Abstract
Operational efficiency is one of the key performance indicators of a port’s service level. In the process of making scheduling plans for container terminals, different types of equipment are usually scheduled separately. The interaction between quay cranes (QCs) and automated guided vehicles (AGVs) is neglected, which results in low operational efficiency. This research explores the integrated scheduling problem of QCs and AGVs. Firstly, a multi-objective mixed integer programming model (MOMIP) is conducted, with the aim of minimizing the makespan of vessels and the unladen time of AGVs. Then, embedded with a new heuristic method, the non-dominated sorting genetic algorithm-II (NSGA-II) is designed for the scheduling problem. The heuristic method includes two parts: a bay-based QC allocation strategy and a container-based QC-AGV scheduling strategy. Finally, in order to test the performance of the proposed algorithm, differently sized benchmark tests are performed, and the results are compared to the multi-objective particle swarm optimization algorithm (MOPSO) and the weighted-sum method. The computational results indicate that the proposed algorithm can effectively solve the multi-objective integrated scheduling problem of QCs and AGVs. For large-scale problems, the NSGA-II algorithm has better performance and more obvious advantages compared to others. The proposed method has the capability of providing a theoretical reference for the QC and AGV scheduling of container terminals.
1. Introduction
1.1. Background and Motivation
Container freight transport has developed rapidly since the 1970s due to the advantages of low cost, high freight quality and volumes. Nowadays, more than 60% of maritime cargo is transported in containers [1]. By 2020, global container throughput reached approximately 800 million TEU, an increase of almost 50% compared to 542 million TEU in 2010. With the development of larger and faster ships, the container throughput is continually increasing, which makes port logistics even more complex [2]. According to UNCTAD [3], the proportion of maritime cargo carried by mega-container ships worldwide has increased from an initial 6% in 2011 to almost 40% in 2021. The rapid development of container freight transportation and the substantial increase in ship carrying capacity have brought great challenges to the operation of the terminal.
However, because of the high price of equipment and the increase in difficulty after adding operating equipment, terminal operators prefer to design a more reasonable scheduling plan to improve service levels.
The equipment in container terminals usually includes three types: the QC, the yard crane (YC) and horizontal transportation equipment (e.g., AGV). Among them, the QC is responsible for unloading (loading) containers from (onto) the ship; the YC is responsible for putting the container from the yard onto the horizontal transportation equipment (unloading from the horizontal transportation equipment to the yard); the horizontal transportation equipment is responsible for transporting the container from the yard to the quay side or from the quay side to the yard side. When evaluating the service level of the container terminal, the makespan of vessels (affected by the operation of the QC, the AGV and the YC) is very important [4]. In the actual operation process, there is usually a situation where the QC and the horizontal transport equipment wait for each other. Taking into account the mutual influence of each type of equipment, the integrated scheduling of multiple types of equipment considers the container terminal as a complete system. Compared to the scheduling of a single type of equipment, integrated scheduling can effectively reduce the waiting time of all kinds of equipment, thereby improving operational efficiency and reducing the turnaround time of vessels.
At present, in the research and real operation of the integrated scheduling of container terminals, a single goal is usually considered, and the main purpose of the scheduling is to minimize the makespan. In order to shorten the makespan, most research will allocate more horizontal transport equipment to ships, resulting in an excess of horizontal transport equipment and a low utilization rate of them. In addition, due to the fact that the cost of ship delays is much higher than the waiting cost of AGVs, the utilization of AGVs will be underestimated if they are all monetized by cost. Therefore, while considering the minimization of makespan, this research takes the unladen time of AGVs (including unladen working time and waiting time) as the second goal.
1.2. Related Work
As the most valuable equipment and the bottleneck in port, QCs has received significant attention from both academics and practitioners. Therefore, this section provides a brief literature review of work on QC scheduling problems (QCSP) and integrated problems that related to QC.
1.2.1. QCSP
QCSP based on complete bays was first studied by Daganzo [5]. He formulated a mixed-integer programming (MIP) model with the assumption that QCs can move freely. Both an exact algorithm and a heuristic algorithm are designed for the problem. Peterkofsky and Daganzo [6] designed a branch-and-bound algorithm for the model developed in Daganzo (1989). Zhu and Lim [7] proved that the QCSP is NP-complete. They designed a branch-and-bound algorithm and simulated an annealing approach for small-scale and large-scale problems, respectively.
Compared with the little research on QCSP with complete bays, most researchers have studied QCSP with container groups. The pioneering work of Kim and Park [8] developed the concept of the container group, and studied the problem with the precedence constraints of containers, safety margins, non-crossing constraints, ready time and other realistic factors. Moccia et al. [9] extended the model proposed by Kim and Park and also developed the branch-and-cut method. The numerical experiments based on the benchmark suite of Kim and Park verified that the computational time was reduced significantly. Sammarra et al. [10] decomposed the QCSP into a routing problem and a scheduling problem. A tabu search algorithm was designed for the routing problem, and the scheduling problem was solved using a local search technique. The algorithm cut down the computational time for the large instances compared to the branch-and-cut algorithm in [9]. The model proposed by Kim and Park has been used as the basis for many subsequent studies of the QCSP. In recent years, more realistic factors are considered in the model, such as vessel stability in [11,12,13,14] and uncertainty in [15,16].
1.2.2. Integrated Scheduling Related to QCs
- (1)
- Integrated scheduling of QCs and horizontal transport equipment
Homayouni et al. [17] studied the integrated scheduling of QCs and AGVs in automated container terminals with a genetic algorithm (GA). However, instead of repairing the chromosomes, they deleted incorrect solutions, which led to an increase in calculation time. Homayouni et al. [18] established a mixed-integer programming (MIP) model and designed a GA for the problem. Cao et al. [19] designed a MIP model for the integrated scheduling of QCs and yard trucks (YTs), with the objective of minimizing the makespan. They developed a GA and a modified Johnson’s rule-based heuristic algorithm for the solution of the problem, but practical factors such as the order of tasks and the interference of QCs were not considered. Tang et al. [20] also studied the joint scheduling problem of QCs and internal trucks (ITs), and extended the problem to bidirectional flow, which means that both inbound and outbound containers were considered. The operation sequence of tasks, the safety distance of QCs, etc., were considered in the model. They used particle swarm optimization (PSO) to solve the problem and improved the speed formula of PSO. Kaveshgar and Huynh [21] extended the research of Tang et al. [20], considering multiple QCs and the blocking factors. Vahdani et al. [22] studied the QC-YT joint scheduling problem in the case of different terminals sharing YTs. They established a multi-objective model with the goal of minimizing operating costs and maximum overflowed workload in the terminals. A modified NSGA-II and a modified multi-objective particle swarm optimization algorithm (MMOPSO) were designed to solve the model. Zhen et al. [23] proved that the integrated problem of QCs and AGVs is strongly NP-hard. They also investigated some properties that could considerably reduce computational complexity. Chen et al. [24] established a joint scheduling model of double-trolley QCs and AGVs, with the aim of minimizing the cost of port operations. A GA embedded with a tabu search algorithm was designed for the problem. CASTILLA-RODRÍGUEZ et al. [25] established an intelligent system which integrated artificial intelligence techniques and simulation tools. They first used an optimization algorithm to obtain a set of high-quality solutions, and then a simulation model was used to simulate each solution to find the optimal solution. On the basis of the literature [20], HOP [26] studied the joint scheduling problem of QCs and YTs considering only unloading operations and improved the model and algorithm in the literature [20]. A brief literature summary for this part is shown in Table 1.

Table 1.
A brief literature summary about QC-YC/AGV integrated scheduling.
- (2)
- Integrated Scheduling Problem of other types of equipment
Chen et al. [27] extended the field by considering the integrated scheduling of QCs, YTs and YCs. However, they did not consider the non-crossing constraints and safety distances of QCs. Lau [28] constructed a MIP model with the goal of minimizing the delayed operation time of QCs and the moving time of YTs and YCs. They also designed a multi-layer genetic algorithm to solve the problem. Chen et al. [29] studied the interaction of crane handling and truck transportation, constructed the joint scheduling problem as a CP model, and designed a three-stage heuristic algorithm to solve it. He et al. [30] took energy consumption into consideration. They proposed an integrated optimization method based on simulation and combined a GA (for global search) and a particle swarm optimization (PSO) algorithm (for local search) in the optimization algorithm. Jonker et al. [31] studied the impact of the single and twin-lift handling of QCs. They constructed a mathematical model in the form of hybrid flow shop with bidirectional flow and job pairing. They designed a simulated annealing algorithm to solve the joint scheduling model. Luo and Wu [32] only considered unloading operations when studying the joint scheduling problem. A MIP model with the goal of minimizing operation time was constructed, and an adaptive GA was designed. Qin et al. [33] used a MIP model and CP techniques to solve the integrated scheduling problem. They first used the MIP solver to solve the MIP model that only considers QC scheduling and obtained a shore crane allocation plan. Then, the QC allocation plan was inputted into the CP model to find the optimal solution. Li et al. [1] considered the constraint of the limited number of devices in the joint scheduling problem and used a GA to solve it. Niu et al. [34] proposed a multi-objective joint scheduling problem with the aim of shortening the makespan and reducing the operating cost. Ahmed [2] studied the joint scheduling problem of container terminals under the double-loop strategy. They also considered the uncertainty of the working time of tasks in the simulation model.
Karam et al. [35] used a functional integration method (according to the hierarchical relationship of the sub-problems to establish an integration mechanism between two levels) to study the joint scheduling problem of berth allocation, QC allocation and specific QC scheduling. Iris et al. [36] studied integrated management, only considering loading operations. They formulated a mathematical model and some enhancements to improve the model. Naeem et al. [37] studied the joint scheduling problem of YCs and AGVs considering the limited buffer capacity of the dual-trolley QCs. A MIP model was established, and a heuristic algorithm was designed to solve the model.
More research on the integrated scheduling of container terminals can be found in the literature [38].
In summary, when it comes to solution methods, due to the complexity of integrated scheduling, most research uses heuristic algorithms for integrated problems to obtain a feasible solution in a reasonable time, and GA is one of the most popular algorithms. In terms of mathematical models, most researchers develop single-objective models, and mostly consider the minimization of the turnaround time of vessels and operating costs. However, in practical operations, multiple objectives are usually considered at the same time, such as efficiency and cost. Only considering a single goal cannot meet the needs of practical port operations. When considering multiple objectives, scholars usually use weight functions to convert them into single-objective models and use single-objective optimization algorithms to solve them.
1.3. Contributions and Structure
Given the above research background and existing challenges, a MOMIP model and NSGA-II algorithm are proposed. The contributions of this research mainly lie in the following aspects:
- (1)
- The majority of the existing literature on integrated scheduling focuses on optimizing a single objective, with less consideration of the efficiency of AGVs. Considering the pooling strategy of AGVs, this research constructs a MOMIP model with the objectives of minimizing vessels’ makespan and AGVs’ unladen time.
- (2)
- An NSGA-II algorithm embedded with a heuristic method is designed to solve the proposed mathematical model, in which the heuristic method consists of two steps: a QC allocation strategy based on bays and a QC-AGV scheduling strategy based on containers. The heuristic method can quickly complete the allocation and scheduling of the QCs and AGVs.
- (3)
- The effectiveness of the proposed model and the NSGA-II algorithm are tested based on differently sized computational experiments, and the results of the sensitivity analysis in this research can provide some references for terminal operators.
The remainder of the paper is organized as follows: Section 2 describes the problem in detail and presents the MOMIP. Section 3 is devoted to the proposed algorithm. Section 4 presents the computational study and the analysis of the results. Finally, Section 5 concludes the work in this research and indicates some research perspectives.
2. Problem Description and Formulation
In this section, we first describe the main components of the problem, followed by a mathematical model with multiple objectives.
2.1. Problem Description
Figure 1 shows the typical layout of the automated container terminal. It also compares two operational strategies for AGVs, namely the single-cycle operational strategy and the pooling strategy. The red arrow represents the process of the single-cycle operation, where the AGV loads the container at the quay side, delivers it to the yard side and then returns empty and waits for another task (take the discharge process as an example). However, with the pooling strategy, the laden AGVs will go to export areas to load an outbound container and deliver it to the quayside. The comparison shows that the empty rate of the AGV with the single-cycle strategy is lower than that with the pooling strategy. As a result, this research explores the integrated problem with the pooling strategy.
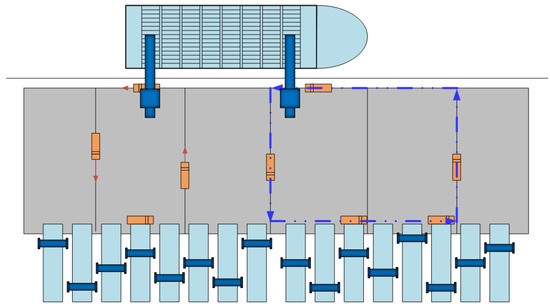
Figure 1.
Layout of an automated container terminal.
The following assumptions are made throughout this research:
- Import containers and export containers are stored in different blocks.
- The stowage plan is already provided. In practice, the stowage plan is usually drawn up by liner companies, and terminals will draw up a handling plan based on it. Thus, this assumption is in line with the real situation.
- There are precedence relationships between containers. For example, the discharging containers are required to be handled before the loading ones when they are both in the same bay. Moreover, tasks on the deck must be performed before those in the hold.
- QCs are not allowed to cross each other. This is because QCs move on the same track while working.
- Two adjacent QCs must be at least one bay apart to perform their tasks without interference.
- Preemption on a task is not allowed, which means that a QC will not stop its operation on a task until it completes it.
- There is enough space to stack containers in the yard, and the AGVs will not wait for the operation of YCs.

Table 2.
Notations used in the scheduling formulation.

Table 3.
Decision variables.
2.2. Mathematical Model
Based on those assumptions and notations, we formulate the problem as the following model.
Objectives:
Equation (1) aims to minimize the makespan. Another object of this paper is to assign and schedule AGVs. In this case, the pooling strategy is adopted to improve the utilization rate of YTs. A proxy of this is the minimization of the unladen time of all containers. In this research, we define the unladen time of AGVs as set-up time. Equation (2) represents the minimization of the total set-up time.
Subject to:
Equations (3)–(10) are QC-related constraints. Equation (3) ensures that each container must be handled once, and only once by a QC. Equation (4) is a flow balance constraint, which ensures that containers are operated one by one. Equations (5) and (6) determine the first task and the last task of every QC, respectively. Equation (7) ensures that the QCs cannot cross each other. Equation (8) denotes that task should be completed before task j. Equation (9) indicates the relationship between variable and . Equation (10) indicates the time window for each container. Equation (11) states that each bay is allocated to one and only one QC. Equation (12) claims the start working time of each bay. Equation (13) indicates that the QC can only proceed to the next bay after processing all containers at the current bay. Equation (14) defines the binary variable .
Equations (15)–(20) are AGV-related constraints. Each container is allocated to one and only one AGV in Equation (15). Equation (16) ensures the flow balance of each AGV. Equations (17) and (18) have the same functions for AGVs as Equations (5) and (6) have for QCs. Similar to Equation (10), Equation (19) complies with the order of handling the containers assigned to each AGV.
The integrated scheduling problem of QCs and AGVs is a strong NP-hard problem [23], so it is difficult to obtain the best solution to the problem with hundreds of containers within a reasonable time. Thus, we propose a NSGA-II embedded with a heuristic method to solve the problem.
3. Solution Development
NSGA-II is one of the most popular multi-objective optimization algorithms [39]. Although there are many other techniques available, NSGA-II is the most suitable method for this research. Firstly, the NSGA-II algorithm can easily realize the encoding of the decision variables used in this paper; secondly, the computational time of the NSGA-II algorithm is relatively short. Therefore, we design an NSGA-II algorithm to solve the problem. The flowchart of NSGA-II is shown in Figure 2.

Figure 2.
Flowchart of NSGA-II.
3.1. Chromosome Encoding
The problem solves three main sub-problems: task sequence decision, QC plan and AGV plan. For our problem, each chromosome consists of three parts. The first part indicates the number of containers, sorting by the operation order of each QC. The second part represents the assigned QCs, and the third corresponds to the number of AGVs allocated to the container at the corresponding location. Figure 3 shows an example with , and , and it can be explained as follows:

Figure 3.
Chromosome illustration.
- (1)
- Take QC 1 as an example; it will serve container 1 first, and then sequentially serve containers 4, 6, 2, 5 and 3.
- (2)
- Now look at AGV 2. It will deliver container 1 first and then deliver containers 5, 8 and finally 10.
- (3)
- Explanations for other QCs and AGVs follow the above steps.
3.2. Population Initialization
We design a new heuristic to generate the initial population. The new heuristics consist of three phases.
- QCs are assigned to bays based on the position and available time, and the process of this part is shown in Figure 4. The strategy specifically includes the following steps: (1) initialize the position and available time of all QCs. (2) Allocate QCs to each bay according to the position and available time. There are mainly two situations while allocating QCs. The first is that only one side of the current bay has QCs. Then, the nearest QC on this side is assigned to the bay. The second is that there are QCs on both sides of the current bay. In this case, the one with the earlier available time among the two QCs closest to the current bay will be assigned. (3) Update the information of the QC and allocate the quay crane for the next bay until all bays are allocated.
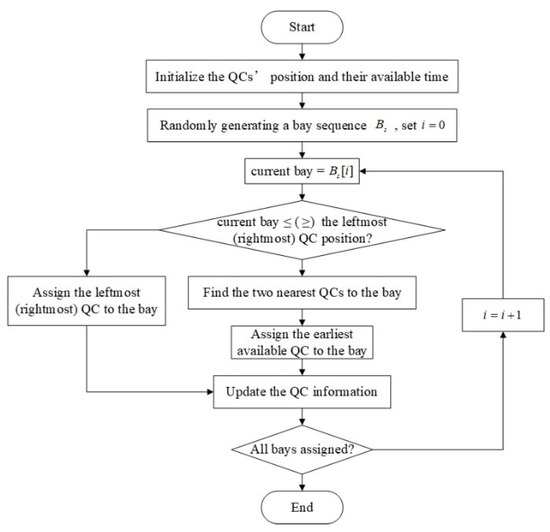 Figure 4. Flowchart of QC assigning.
Figure 4. Flowchart of QC assigning.
- 2.
- The sequence of operations for all tasks in each berth is randomly generated and corrected based on the precedence relationships.
- 3.
- Allocate the AGVs to containers in terms of the quay crane scheduling sequence. Algorithm 1 indicates the strategy for AGV allocation. The specific process is as follows: (1) firstly, calculate the QC operation time of each container according to the QC allocation results. (2) Secondly, assign the AGV with the earliest available time to the current task. (3) Since the allocation of AGVs may require the corresponding QC to wait or wait for QC operations, it is necessary to update the scheduling information of the task according to the type of task (import/export container), available AGV time and the original planned QC operation time. (4) Finally, update the information of AGVs. Do step 2 to 4 until all tasks are scheduled and completed.
| Algorithm 1 AGV Assignment |
| 1: Arrange all tasks in ascending order according to the completion time of QCs’ operations |
| 2: Set , |
| 3. while , do: |
| 4. Assign task i to AGV k with the earliest available time |
| 5. Add the AGV k to |
| 6. Update the information of AGV k, set |
| 7. end while |
| 8. return |
3.3. Genetic Operators Design
We use two techniques for crossover: single-point crossover and uniform order-based crossover. Uniform order-based crossover is an extended version of classical uniform crossover in which, after recombination, conflict genes are deleted, and missing genes are replaced to prevent generating infeasible solutions [40]. Figure 5 is an illustration of the crossover process. Figure 5a,b shows the selected chromosome 1 and 2. The intersection point is generated randomly, as shown by the arrow in Figure 5a. The parts with container numbers 1, 4, 6 and 2 of chromosome 2 are deleted (the red font in Figure 5b), and the child retains the part in front of the intersection in chromosome 1 and the remaining part of chromosome 2, as shown in Figure 5c.
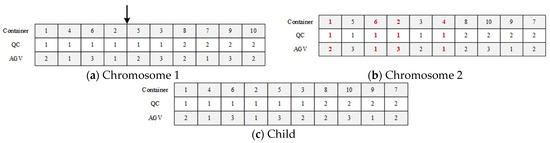
Figure 5.
An illustration of crossover for an example of 10 tasks.
The mutation operation is completed by randomly selecting a location and changing the assigned QC and AGV. The specific operation process is show in Figure 6. The selected task is container 8 (the arrow in Figure 6a), which is in the same bay as container 7. As a result, the child after mutation is shown in Figure 6b.

Figure 6.
An illustration of mutation for an example of 10 tasks.
After the genetic operation, the child chromosome needs to be repaired and the plans need to be updated.
3.4. Stop Criterion
When the maximum number of iterations is reached, stop the iteration and output the non-dominated solution and its corresponding scheduling plan.
4. Experimental Results
To evaluate the proposed algorithm, three performance indicators are introduced firstly, followed by the generation method of the computational experiments. Then, the following sets of experiments are carried out: (1) cases with a small number of containers; (2) cases with a large number of containers. The results are also compared to the weighted-sum method and MOPSO. Finally, a sensitivity analysis is carried out. All the experiments are performed on a computer with Intel Core i7-6700 CPU @3.40 GHz and 8 GB RAM, and the algorithm is coded in Python.
4.1. Performance Indicators
We introduce several indicators to evaluate the performance of the three methods. PF is the reference Pareto solution set, and it can be obtained using multiple calculations. Three performance metrics are introduced, and the specific definitions of the indicators are as follows:
- (1)
- Inverted generational distance (IGD): this metric was developed by Czyzzak et al. [41] and was used to represent the average distance from PF to the non-dominated solution set obtained by the algorithm. So, the smaller the IGD, the better the performance of the algorithm. The specific calculation process is as follows:
- (2)
- Hypervolume (HV) ratio: Zitzler et al. [42] proposed HV to evaluate the performance of a multi-objective evolutionary algorithm. It has excellent theoretical support and is widely used. The calculation formula is
Let be the HV of the optimal solution set, then the HV ratio of the calculated non-dominated solution set can be calculated using the following equation:
A higher HV ratio indicates the solution set has better coverage, and thus the corresponding algorithm is better [43].
- (3)
- Number of Pareto solutions (NOP): NOP indicates the number of solutions in PF, and a larger NOP implies that the algorithm is better.
4.2. Problem Generation
We test the algorithm on 2 types of randomly generated problems—16 small-scale problems (5 to 50 containers) and 25 large-scale problems (70 to 200 containers). The data in the experiments are generated as follows:
- (1)
- The time of unloading or loading a container for a QC is generated following the Gaussian distribution, i.e., .
- (2)
- The speed of the AGV is 210 m/min when loaded and 350 m/min while empty.
- (3)
- The layout of the container terminal is shown in Figure 1, where the length of the quay shoreline is 900 m and the horizontal distance from the quay front to the junction of the yard is 200 m. Let the point (0,0) be the intersection point between the left edge of the shoreline and the yard. So, the y coordinates of all the yards are 0, and the x coordinates of each yard area are shown in Table 4.
 Table 4. Coordinates of yards.
Table 4. Coordinates of yards. - (4)
- The position of import and export containers and their precedence relationship in the experiments are randomly generated according to the layout of the container terminal.
4.3. Experimental Results and Analysis
4.3.1. Parameter Setting
Based on the analysis of calculation results with different crossover probabilities and mutation probabilities, the crossover probability is set to 0.8, and the mutation probability is set to 0.02. Figure 7 shows the influence of changing and on the calculation results when .
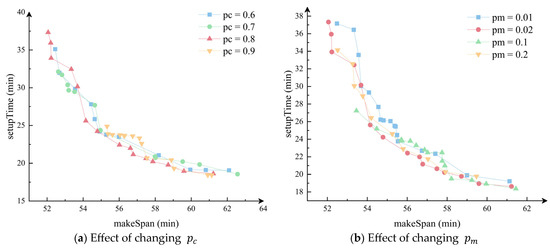
Figure 7.
The effect of changing and in instance 22.
The remaining control parameters were set through empirical tests. We tested the effect of population size and number of iterations on large-scale problems, where the population size was set to and iteration was set to . From the experiments conducted, we were able to observe and conclude that an increase in the does not have a significant effect on the optimization of the objective, while the increase in iterations improves the performance metrics.
As an example, Figure 8 shows the influence of iteration and population size on the solving effect when . The Pareto front was obtained by NSGA-II algorithm with and . As shown in Figure 8, the NSGA-II algorithm is capable of obtaining a uniform and widely spread PF with varied and . However, Figure 8 indicates that the difference between the obtained non-dominated solution sets and the Pareto front gradually decreases as the iteration increases. When , the solution set obtained and NOP are very similar to the Pareto front. Figure 8b shows the effect of on the obtained non-dominated set. It illustrates that gets better solution sets, though the number of non-dominated solutions will be lower. Hence, we decided to set: , and .
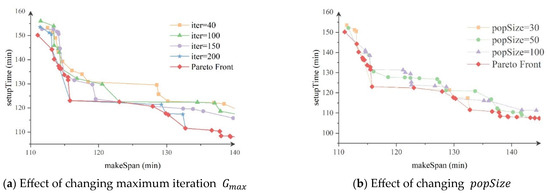
Figure 8.
Effect of changing parameters of NSGA-II algorithm.
4.3.2. Experimental Results
Table 5 compares the results of the weighted-sum method, MOPSO and NSGA-II in small-scale cases. Table 6, Table 7 and Table 8 are the statistical results of each performance indicator with small-scale problems. As can be seen from Table 5, the NSGA-II has the largest average NOP of 6.5, while the average NOPs of MOPSO and weighted-sum are 5.69 and 6.5, respectively. The data in Table 6 also show that among the 16 small-scale experiments, the NSGA-II algorithm can obtain the most NOPs in 13 experiments, which indicates that in the small-scale calculation examples, the NSGA-II algorithm can obtain more Pareto solutions. For the IGD and HV ratio obtained by all the small-scale problems, the NSGA-II algorithm is the best (0.554 for IGD and 0.934 for HV ratio), followed by the MOPSO and the weighted-sum method. The data in Table 7 and Table 8 also show that the NSGA-II algorithm is the easiest for obtaining a better Pareto solution, followed by MOPSO. The solution obtained by the weighted-sum method is the worst. All these show that the NSGA-II algorithm has the best overall performance in small-scale calculation examples among the three methods.

Table 5.
Results of small-scale problems.

Table 6.
Statistical data of NOP in small-scale cases.

Table 7.
Statistical data of IGD in small-scale cases.

Table 8.
Statistical data of HV ratio in small-scale cases.
Table 9 shows the results of the three methods in large-scale cases. Table 10, Table 11 and Table 12 are the statistical data of performance indicators for large-scale experiments. As can be seen from Table 10, the NSGA-II algorithm is able to obtain the most Pareto solutions although its standard deviation is the largest. The NSGA-II also has the best IGD average value of 1.326, while the MOPSO and weighted-sum methods are 10.570 and 10.956, respectively. However, from the statistical data in Table 11, we can conclude that the MOPSO algorithm has a much better performance than the weighted-sum method. The HV ratio value obtained by the NSGA-II algorithm is also optimal (0.955), and the standard deviation is the smallest, followed by MOPSO (0.890). Table 12 also supports this conclusion.

Table 9.
Results of large scale problems.

Table 10.
Statistical data of NOP in large-scale cases.

Table 11.
Statistical data of IGD in large-scale cases.

Table 12.
Statistical data of HV ratio in large-scale cases.
The above comparisons demonstrate that the NSGA-II algorithm has a better performance in terms of the three quality indicators. It can effectively solve the integrated scheduling problem of QC and AGV with multiple objectives.
4.3.3. Sensitivity Analysis
This section first analyzes the effect of the QC configuration on the Pareto solution set for a large-scale scenario with a 1:3 ratio of QC to AGV. Taking instance 32 as an example (as shown in Figure 9), the makespan of vessels significantly decreases when the served QCs changes from two to three. However, the saved time of makespan is much less when the QCs increase from three to four. The analysis shows that in large-scale cases, the makespan and the efficiency of AGVs are optimized with the increase in QCs, but conversely, the marginal benefit will decrease.
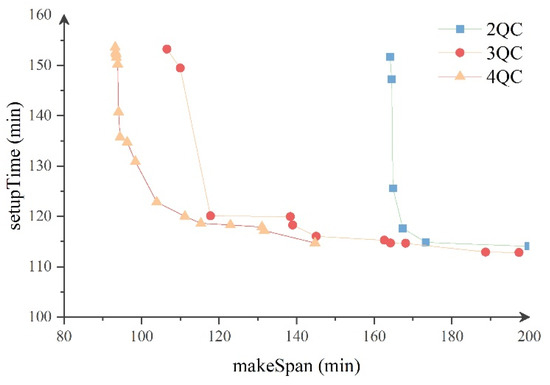
Figure 9.
Effect of changing QC when .
The ratio of the QC and AGV numbers also has a significant impact on the efficiency of the terminal. A reasonable ratio can improve the operational efficiency of each type of equipment in the terminal, so this research analyzes the impact of the ratio on the two target values. Figure 10 shows the Pareto fronts with the ratio of 1:2, 1:3 and 1:4 for 50 and 150 containers, respectively. From Figure 10, we can see that when the ratio of the QCs and AGVs changes from 1:2 to 1:3, the makespan of vessels and the unladen operation time of AGVs are optimized to a certain extent. This is because when the ratio is 1:2, the number of AGVs is not sufficient, and QCs will wait for AGVs during the operation process, which leads to a decrease in the operational efficiency of the bridge and an increase in the makespan of the vessels; in addition, during the scheduling process of the AGVs, in order to reduce the waiting time of the QCs, the pairing of import containers and export containers will be reduced, resulting in a reduction in the number of double-cycle operations of the AGVs and an increase in the unladen traveling time. However, when the ratio is changed from 1:3 to 1:4, the unladen traveling time of the AGV increases when the vessel does not need to operate urgently, although it is possible for the vessel to complete the loading and unloading operation in a shorter time. This is because when the ratio is 1:4, there are relatively more AGVs, and AGVs will be more often found waiting for QCs’ operations, resulting in an increase in their unloaded time. Comparing Figure 10a,b, it can be observed that the strategy with a ratio of 1:4 is not significantly optimized compared to the 1:3 minimum vessel completion time when there are fewer containers in operation, but it results in a significant increase in AGV unladen working time.
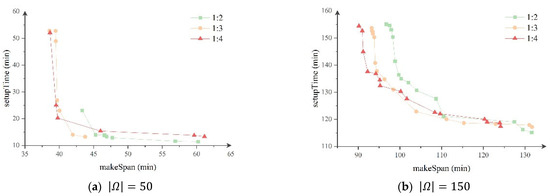
Figure 10.
Effect of changing the ratio of QCs and AGVs.
The analysis shows that If the vessel has a large volume of containers and needs to leave the port quickly, it is possible to assign an average of four AGVs to each served QC; otherwise, given the efficiency of the AGVs, an average of three AGVs should be assigned to each QC.
5. Conclusions
The service level of container terminals is related to the berthing time of vessels and the operational efficiency of the equipment. However, most research studies only take makespan as their goal, neglecting the efficiency of AGVs. This research proposes a multi-objective optimization model with the goals of minimizing the makespan and the duration of no-load AGV operations. We also design an NSGA-II algorithm embedded with a heuristic method for the problem.
We compare the NSGA-II algorithm with the commonly used weighted-sum method and MOPSO algorithm through multiple sets of experiments. The comparison results show that the results obtained by the NSGA-II algorithm are superior to the other two methods, while the MOPSO algorithm is better than the weighted-sum method.
In addition, this research investigates the impact of QC configuration and the operational ratio of QC and AGV on the operational efficiency of the terminal. The results indicate the following:
- The number of QCs has a high influence on the efficiency of terminal operations. The makespan of vessels and the efficiency of AGVs are optimized with the increase in the QCs, but in contrast, the marginal benefit decreases as the number of QCs increases.
- The ratio of QCs and AGVs also affects the efficiency of the terminal. If the vessel has a high volume of containers and needs to leave the port quickly, an average of four AGVs can be assigned to each QC. Otherwise, given the efficiency of the AGVs, an average of three AGVs per bridge should be used.
The research in this paper is in line with the actual loading and unloading processes of the container terminal, but there are still some limitations, such as when considering the operational efficiency of AGVs, only the unloaded traveling time of AGVs is considered, without considering energy consumption or operational costs; uncertainties such as path conflict and path congestion of AGVs and failures of the QC and AGVs are not taken into account. Future research can study the integrated scheduling of QCs and AGVs relative to uncertainties and explore issues such as energy consumption and minimization of operating costs for AGVs or internal trucks.
Author Contributions
Conceptualization, Y.D.; funding acquisition, H.R. and X.Y.; methodology, Y.D., H.R., F.X. and X.Y.; software, Y.D.; supervision, H.R.; validation, Y.D., F.X., X.Y. and Y.M.; writing—original draft, Y.D. and F.X.; writing—review and editing, H.R., X.Y. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (Grant No. 52071312), Key Science and Technology Projects in Transportation Industry (Grant No. 2022-ZD3-035), Applied Basic Research Program Project of Liaoning Province (Grant NO. 2023010126-JH2/1013), Dalian Science and Technology Innovation Fund Project (No. 2022JJ12GX035), the Natural Science Foundation of Liaoning Province of China (Grand No. 2022-BS-099) and the Scientific Research Foundation of the Higher Education Institutions of Liaoning Province of China (Grand No. LJKMZ20220375).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Peng, J.; Wang, X.; Wan, J. Integrated Resource Assignment and Scheduling Optimization with Limited Critical Equipment Constraints at an Automated Container Terminal. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7607–7618. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Abbasy, M.S.; Zayed, T.; Alfalah, G.; Alkass, S. Synchronized scheduling model for container terminals using simulated double-cycling strategy. Comput. Ind. Eng. 2021, 154, 107118. [Google Scholar] [CrossRef]
- UNCTAD. Review of Maritime Transport; United Nations: San Francisco, CA, USA, 2021. [CrossRef]
- He, J.; Zhang, W.; Huang, Y.; Yan, W. A simulation optimization method for internal trucks sharing assignment among multiple container terminals. Adv. Eng. Inform. 2013, 27, 598–614. [Google Scholar] [CrossRef]
- Daganzo, C.F. The crane scheduling problem. Transp. Res. Part B Methodol. 1989, 238, 159–175. [Google Scholar] [CrossRef]
- Peterkofsky, R.I.; Daganzo, C.F. A branch and bound solution method for the crane scheduling problem. Transp. Res. Part B Methodol. 1990, 24, 159–172. [Google Scholar] [CrossRef]
- Zhu, Y.; Lim, A. Crane scheduling with non-crossing constraint. J. Oper. Res. Soc. 2006, 57, 1464–1471. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, Y.-M. A crane scheduling method for port container terminals. Eur. J. Oper. Res. 2004, 156, 752–768. [Google Scholar] [CrossRef]
- Moccia, L.; Cordeau, J.-F.; Gaudioso, M.; Laporte, G. A branch-and-cut algorithm for the quay crane scheduling problem in a container terminal. Nav. Res. Logist. (NRL) 2005, 53, 45–59. [Google Scholar] [CrossRef]
- Sammarra, M.; Cordeau, J.-F.; Laporte, G.; Monaco, M.F. A tabu search heuristic for the quay crane scheduling problem. J. Sched. 2007, 10, 327–336. [Google Scholar] [CrossRef]
- Al-Dhaheri, N.; Jebali, A.; Diabat, A. The quay crane scheduling problem with nonzero crane repositioning time and vessel stability constraints. Comput. Ind. Eng. 2016, 94, 230–244. [Google Scholar] [CrossRef]
- Al-Dhaheri, N.; Diabat, A. The Quay Crane Scheduling Problem. J. Manuf. Syst. 2015, 36, 87–94. [Google Scholar] [CrossRef]
- Chen, J.H.; Bierlaire, M. The study of the unidirectional quay crane scheduling problem: Complexity and risk-aversion. Eur. J. Oper. Res. 2017, 260, 613–624. [Google Scholar] [CrossRef]
- Msakni, M.K.; Diabat, A.; Rabadi, G.; Al-Salem, M.; Kotachi, M. Exact methods for the quay crane scheduling problem when tasks are modeled at the single container level. Comput. Oper. Res. 2018, 99, 218–233. [Google Scholar] [CrossRef]
- Rouky, N.; Abourraja, M.N.; Boukachour, J.; Boudebous, D.; Alaoui, A.E.H.; El Khoukhi, F. Simulation optimization based ant colony algorithm for the uncertain quay crane scheduling problem. Int. J. Ind. Eng. Comput. 2019, 10, 111–132. [Google Scholar] [CrossRef]
- Kizilay, D.; Van Hentenryck, P.; Eliiyi, D.T. Constraint programming models for integrated container terminal operations. Eur. J. Oper. Res. 2020, 286, 945–962. [Google Scholar] [CrossRef]
- Homayouni, S.; Tang, S.; Ismail, N.; Ariffin, M.; Samin, R. A hybrid genetic-heuristic algorithm for scheduling of automated guided vehicles and quay cranes in automated container terminals. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; pp. 96–101. [Google Scholar] [CrossRef]
- Homayouni, M.; Hong, T.S.; Ismail, N.; Khairol, M. A Genetic Algorithm for Optimization of Simultaneous Scheduling of AGVs and QCs in Container Terminals. In Proceedings of the 11th Asia Pacific Industrial Engineering and Management Systems Conference, Melaka, Malaysia, 7–10 December 2010. [Google Scholar]
- Cao, J.; Shi, Q.; Lee, D.-H. Integrated quay crane and yard truck schedule problem in container terminals. Tsinghua Sci. Technol. 2010, 15, 467–474. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, J.; Liu, J. Modeling and solution of the joint quay crane and truck scheduling problem. Eur. J. Oper. Res. 2014, 236, 978–990. [Google Scholar] [CrossRef]
- Kaveshgar, N.; Huynh, N. Integrated quay crane and yard truck scheduling for unloading inbound containers. Int. J. Prod. Econ. 2015, 159, 168–177. [Google Scholar] [CrossRef]
- Vahdani, B.; Mansour, F.; Soltani, M.; Veysmoradi, D. Bi-objective optimization for integrating quay crane and internal truck assignment with challenges of trucks sharing. Knowl.-Based Syst. 2018, 163, 675–692. [Google Scholar] [CrossRef]
- Zhen, L.; Yu, S.; Wang, S.; Sun, Z. Scheduling quay cranes and yard trucks for unloading operations in container ports. Ann. Oper. Res. 2016, 273, 455–478. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Wang, H.; Guo, D. Research on Integrated Scheduling Optimization of Double-trolley Quay Crane and AGV in Automated Terminal. IOP Conf. Ser. Mater. Sci. Eng. 2020, 790, 012071. [Google Scholar] [CrossRef]
- Castilla-Rodríguez, I.; Expósito-Izquierdo, C.; Melián-Batista, B.; Aguilar, R.M.; Moreno-Vega, J.M. Simulation-optimization for the management of the transshipment operations at maritime container terminals. Expert Syst. Appl. 2019, 139, 112852. [Google Scholar] [CrossRef]
- Hop, D.C.; Van Hop, N.; Anh, T.T.M. Adaptive particle swarm optimization for integrated quay crane and yard truck scheduling problem. Comput. Ind. Eng. 2020, 153, 107075. [Google Scholar] [CrossRef]
- Chen, L.; Bostel, N.; Dejax, P.; Cai, J.; Xi, L. A tabu search algorithm for the integrated scheduling problem of container handling systems in a maritime terminal. Eur. J. Oper. Res. 2007, 181, 40–58. [Google Scholar] [CrossRef]
- Lau, H.Y.K.; Zhao, Y. Integrated scheduling of handling equipment at automated container terminals. Ann. Oper. Res. 2007, 159, 373–394. [Google Scholar] [CrossRef]
- Chen, L.; Langevin, A.; Lu, Z. Integrated scheduling of crane handling and truck transportation in a maritime container terminal. Eur. J. Oper. Res. 2013, 225, 142–152. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W.; Wang, S. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption. Expert Syst. Appl. 2015, 42, 2464–2487. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, N.; de Waal, A.; Negenborn, R.R. Coordinated optimization of equipment operations in a container terminal. Flex. Serv. Manuf. J. 2019, 33, 281–311. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Scheduling of container-handling equipment during the loading process at an automated container terminal. Comput. Ind. Eng. 2020, 149, 106848. [Google Scholar] [CrossRef]
- Qin, T.; Du, Y.; Chen, J.H.; Sha, M. Combining mixed integer programming and constraint programming to solve the integrated scheduling problem of container handling operations of a single vessel. Eur. J. Oper. Res. 2020, 285, 884–901. [Google Scholar] [CrossRef]
- Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2020, 20, 89–104. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A. Functional integration approach for the berth allocation, quay crane assignment and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Iris, C.; Christensen, J.; Pacino, D.; Ropke, S. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part B Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Naeem, D.; Eltawil, A.; Iijima, J.; Gheith, M. Integrated Scheduling of Automated Yard Cranes and Automated Guided Vehicles with Limited Buffer Capacity of Dual-Trolley Quay Cranes in Automated Container Terminals. Logistics 2022, 6, 82. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T. A comprehensive review of quay crane scheduling, yard operations and integrations thereof in container terminals. Flex. Serv. Manuf. J. 2020, 33, 1–42. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 49–64. [Google Scholar] [CrossRef]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—A metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Tang, L.; Li, Y.; Bai, D.; Liu, T.; Coelho, L.C. Bi-objective optimization for a multi-period COVID-19 vaccination planning problem. Omega 2022, 110, 102617. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).