Flexible Riser Tensile Armor Modelling Method and Application to Fatigue Analysis

Abstract

In this paper, we present a new stress calculation method for flexible structures, particularly, tensile armors, and apply it to flexible riser fatigue analysis. The method is based on a 3-dimensional curved bar theory. First, the tensile armor center line was described as a cylindrical helix curve; its bent curve length and bending migration length were derived and studied under different friction scenarios. Second, the tensile and bending stiffness was derived with consideration of more accurate shape parameters and the frictional hysteretic effect, and verified through FEA analysis results. Third, we presented the stress calculation formula for tensile armor under tension and bending load. All stress components were considered, including tensile, bending and shear stresses. Fourth, the method was benchmarked with published experimental results on a flexible prototype tension and bending tests, and comparisons showed general agreements. Fifth, the method was applied to an in-service 8″ flexible riser for fatigue assessment and lifetime extension evaluation, and showed the flexible riser has sufficient remaining fatigue life, and is suitable to continue its service under the current operating conditions. Last, conclusions were drawn. We concluded that the presented tensile armor stress calculation method and modelling techniques are valid for flexible riser fatigue analysis. This method is time efficient, and can be implemented into other multi-scale models for riser dynamic analysis. It is also applicable to other similar helix structure stress analysis, such as wire ropes, submarine hoses, and subsea umbilicals.

1. Introduction

Flexible risers are commonly used in offshore oil and gas industry to connect the subsea wells and surface platforms. It has the advantages ofbeing flexible, or being able to bend over a small radius, and can accommodate relative movements between surface platforms and subsea facilities. However, flexible risers also have complex structural component layers, and the friction between layers are highly uncertain, imposing technical challenges to predict the actual structural behaviors, including the stress calculation for fatigue assessment. Therefore, flexible-riser stress calculation is still an area of exploration attracting many researchers. A number of researchers are focused on practical application techniques, including analysis method and techniques for riser lifetime extension, as presented by Elosta [1]. Adokiye [2] also presented a practical dynamic analysis method for shallow-water flexible risers for an FPSO, and applied it to riser system configuration optimization. Smith [3] summarized some of the techniques for flexible riser fatigue analysis, particularly the hysteresis damping effect, which is of great importance to fatigue stress prediction. A flexible riser can also be modeled numerically using an FEA analysis software, such as ANSYS and ABAQUS. The modeling of flexible riser structures requires high skills in software usage and a good knowledge of flexible structure behavior. One of the FEA analysis methods for using ABAQUS was presented in the study of Li [4]. In order to include the nonlinear effect of the flexible riser properties in global analysis, researchers also turned to multi-scale techniques. Alfano [5] proposed a constitutive model of flexible risers, and a multi-scale analysis technique, by embedding the constitutive model into the Euler–Bernoulli beam model for flexible-riser stress analysis. Chi [6] also presented a method to couple global analysis and local FEA analysis using user-defined element subroutine techniques in ABAQUS, and Python scripts for multiscale scheme linking.

In this paper, we presented a new stress analysis model for flexible structures, particularly tensile armors, and applied it to flexible riser fatigue analysis. Being the most fatigue-load-bearing and hence, the most critical component in the flexible riser structural layers, tensile armors are usually helically wounded in multiple layers, with high pitch angles and rectangular cross section. In the present method, we mathematically described the armor wire center line as a 3D space curve, or a cylindrical helix, then applied the curved bar theory to derive the stiffness and stress formula, with empirical coefficients expressed in terms of the armor wire cross section aspect ratio. Comparisons to ANSYS FEA analysis results confirmed our formulae are more accurate than the conventional curved bar formula. Further comparisons to published experimental data showed good agreement, and validated the suitability of this method in flexible armor wire stress analysis. Then, it was applied to an in-service 8” flexible riser fatigue analysis, achieved reasonable results, and showed its validity for industrial applications.

2. Curved Bar Model

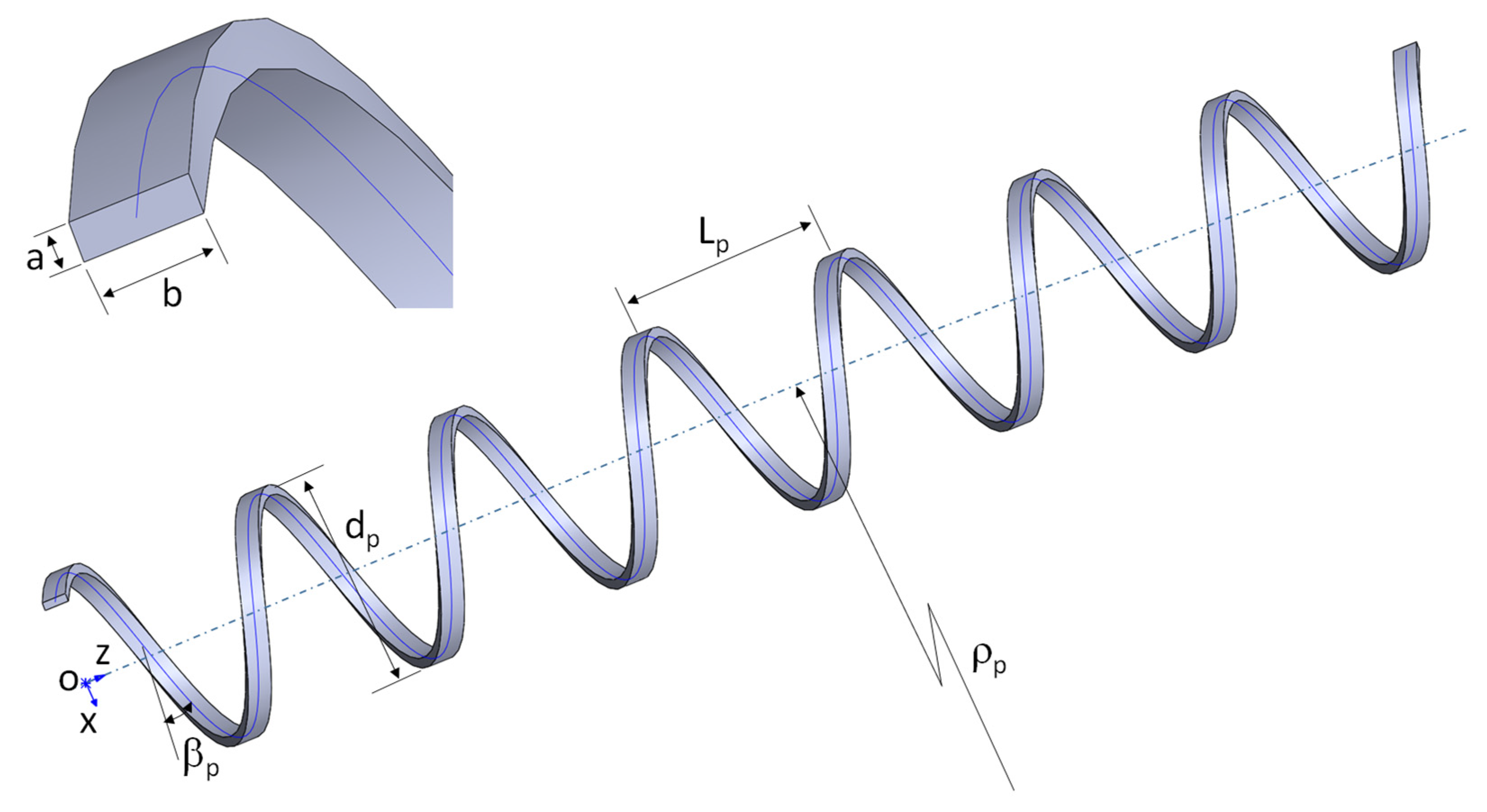
Tensile armors are the major load-bearing components in flexible riser. Physically it is in helix shape, and spirally wounded layer by layer during flexible riser manufacturing. Tensile armors usually have a cross section of a rectangular shape, and a constant pitch angle at each layer. Pitch angles are selected based on the design tensile load and balance of the tension-induced twisting. An illustration of a tensile armor is shown in Figure 1.

As illustrated in Figure 1, the cross section of the rectangular bar had a width of b, and thickness of a (in this paper the aspect ratio was defined as b/a). When a helix is straight in Z direction, or has no bending deformation, the mathematical representation of its center line is given in Equation (1), where $d_p$ is the pitch diameter, $L_p$ is the pitch length, and pitch angle ${\beta }_p=atan\frac{L_p}{\pi d_p}$. A helix can be right-handed or left-handed; within studied scope of this paper, they are the same, and Equation (1) is a right-handed helix. Note that in this paper, we intended to minimize the quantity of new variables in our formulae; as such, the initially selected variables were carried throughout our theoretical derivations.

$$\left\{\begin{array}{c}x=\frac{d_p}{2}cos\theta \\ y=\frac{d_p}{2}sin\theta \\ z=\frac{L_p}{2\pi }\theta \end{array}\right.$$

(1)

For a tensile armor with span length L (or length of the helix center line), the helix angle $\theta =\frac{2\pi L}{L_p}$, and the wire length $s_0\left(\theta \right)=\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}\theta$. When the tensile armor helix bends in x-z plane, with radius of ${\rho }_p$, then the curve follows Equation (2).

$$\left\{\begin{array}{c}x=\left({\rho }_p+\frac{d_p}{2}\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)cos\frac{L_p\theta }{2\pi {\rho }_p}-{\rho }_p\\ y=\frac{d_p}{2}sin\theta \\ z=\left({\rho }_p+\frac{d_p}{2}cos\theta \right)sin\frac{L_p\theta }{2\pi {\rho }_p}\end{array}\right.$$

(2)

For any span length $L=\frac{L_p\theta }{2\pi }$, the bending angle can be calculated as $\varnothing =\frac{L_p\theta }{2\pi {\rho }_p}$ . The helix length $s\left(\theta \right)$ is the curve integration from the coordinate origin, and can be expressed as Equation (3). Compared to a straight helix length $s_0\left(\theta \right)$, it has an additional term that varies with helix angle $\theta$, and was defined as the migration length term in the study of Luo [7]. The physical meaning of this term is that when a helix bends, it requires extra length on the outer side to make the bend curve; at the same time, the inner side has an excessive length for the bend curve; what happens is that the excessive length on the inner side of the bend will shift to the outer side of the bend, causing an axial movement along the tensile armor. When the bending radius is large, the migration length is minor, and can be resisted by frictions between the tensile armor and its adjacent layers, and the tensile armor would be stretched or shortened slightly to accommodate the migration-length requirement. When the bending radius decreases, the friction reaches the upper threshold limit, and cannot stop the tensile armor from moving anymore, and the tensile armor starts to slide axially until the migration-length requirement is satisfied.

$$s\left(\theta \right)=\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}\theta +\frac{d_p^2{L}_p^2}{4{\pi }^2{\rho }_p\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}sin\theta$$

(3)

Depending on the frictions between the armor layer and its neighboring layers, there are three possible scenarios:

• Scenario 1: The friction is high, and tensile armor is fully constrained with no sliding. In this case, the tensile armor has to stretch or shorten itself to accommodate the bending. From Equation (3), the axial strain of the tensile armor is calculated as $\epsilon \left(\theta \right)=\frac{\frac{d(s\left(\theta \right)-s_0\left(\theta \right))}{d\theta }}{\frac{d{s}_0\left(\theta \right)}{d\theta }}$, or $\frac{d_p^2{L}_p^2}{2{\pi }^2{\rho }_p\left(d_p^2+\frac{L_p^2}{{\pi }^2}\right)}\mathrm{c}\mathrm{o}\mathrm{s}\theta$, where $s_0\left(\theta \right)=\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}\theta$, and is the curve length before bending. The axial stress distribution in the tensile armor is $\sigma \left(\theta \right)=E\epsilon \left(\theta \right)$, or $\sigma \left(\theta \right)=\frac{E{d}_p^2{L}_p^2}{2{\pi }^2{\rho }_p\left(d_p^2+\frac{L_p^2}{{\pi }^2}\right)}cos\theta$, where E is the Young’s modulus. And the friction distribution would be $F_{\mu }\left(\theta \right)=ab\frac{d\sigma \left(\theta \right)}{d\theta }/\frac{d{s}_0\left(\theta \right)}{d\theta }=\frac{abE{d}_p^2{L}_p^2}{{\pi }^2{\rho }_p{\left(d_p^2+\frac{L_p^2}{{\pi }^2}\right)}^{3/2}}sin\theta$.
• Scenario 2, the friction is negligible, and the tensile armor is free to slide. In this case, we assume the innermost and outermost points do not change position during bending, i.e., remain as innermost and outermost points after bending; then, the shifting distance at each point in between the inner most point ($\theta$ = 0) and outer most point ($\theta$ = $\pi$) is $∆s\left(\theta \right)=\left[s\left(\theta \right)-s\left(0\right)\right]-\left[s_0\left(\theta \right)-s_0\left(0\right)\right]=\frac{d_p^2{L}_p^2}{4{\pi }^2{\rho }_p\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}sin\theta$. The axial strain and stress are zero since tensile armor will not experience any axial stretching or shortening.
• Scenario 3, the friction is not negligible, but not high enough to restrict the tensile armor from sliding. In this case, only part of the tensile armor will slide, while the remaining part will not. Assuming the static friction is $F_{{\mu }_0}$, from scenario (1), we can calculate the friction–internal stress balance point as $F_{\mu }\left(\theta \right)=\frac{abE{d}_p^2{L}_p^2}{{\pi }^2{\rho }_p{\left(d_p^2+\frac{L_p^2}{{\pi }^2}\right)}^{3/2}}sin\theta =F_{{\mu }_0}$, or ${\theta }_{\mathrm{1,2}}=asin\left(\frac{{\pi }^2{\rho }_p{\left(d_p^2+\frac{L_p^2}{{\pi }^2}\right)}^{3/2}}{abE{d}_p^2{L}_p^2}{F}_{{\mu }_0}\right)$, where ${\theta }_1$ and ${\theta }_2$ are the two roots, and satisfy 0 < ${\theta }_1$ < ${\theta }_2$ < $\pi$. The tensile armor section between ${\theta }_1$ and ${\theta }_2$ will slide, and the sliding distance is now $∆s^{\text{'}}\left(\theta \right)=\frac{d_p^2{L}_p^2}{4{\pi }^2{\rho }_p\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}sin\theta -\frac{F_{{\mu }_0}}{2abE}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}\theta$, where ${\theta }_1\le \theta \le {\theta }_2$.

After we had the above bended tensile armor wire equations, we continued to investigate the stiffness and stresses in following sections.

3. Axial and Bending Stiffness

Tensile armor axial stiffness can also be derived using the bended helix curve equations. For a free tensile armor helix with a rectangular cross section, if the tensile armor wire length elongation is negligible compared to the coil elongation, then only the coil elongation needs to be considered. We developed an axial stiffness formula that is more accurate than Wahl (1944) for a rectangular helix, by introducing a pitch angle correction factor, as in Equation (4):

$$k_0=\frac{4{\xi }_0{a}^{3}b{L}_{p}G}{\pi L{d}_p^3}\left(\frac{\pi d_p}{\sqrt{{\pi }^2{d}_p^2+L_p^2}}+\frac{L_p^2}{(1+\nu )\pi d_p\sqrt{{\pi }^2{d}_p^2+L_p^2}}\right)$$

(4)

where ${\xi }_0=\frac{1}{10}+\frac{1}{9}ln\frac{b}{a}$ is a factor related to the aspect ratio b/a, and as listed in

Table 1. Factor of ${\xi }_0$ .

b/a	1	1.2	1.5	2	2.5	3	4	5	10
${\xi }_0$ (Eq)	0.100	0.120	0.145	0.177	0.202	0.222	0.254	0.279	0.356
${\xi }_0$ (FEA)	0.109	0.122	0.141	0.171	0.201	0.225	0.242	0.256	0.386
Diff %	−8.8%	−1.1%	2.9%	3.5%	0.5%	−1.2%	4.6%	8.3%	−8.5%

for different aspect ratios, G is the shear modulus of the tensile armor, and L is the span length of the tensile armor in tensile armor axial direction. The term in the bracket is the pitch angle correction factor. An FEA model was generated in ANSYS with the following parameters: a = 4 mm, b/a = 1~10, $d_p$ = 250 mm, tensile armor pitch angle 55°, and $L_p$ = 1121.7 mm, L = $L_p$, as shown in Figure 2. And the results are compared to expression ${\xi }_0=\frac{1}{10}+\frac{1}{9}ln\frac{b}{a}$ in Table 1 and Figure 3, the difference is within 10%, which indicates Equation (4) is a good representative of the tensile armor axial stiffness calculation.

The bending stiffness (flexural rigidity) was derived as in Equation (5), which is also more accurate than the round bar helix formula presented by Wahl [8], by introducing an empirical shape correction factor ${\xi }_b$.

$$k_{\theta }=\frac{2{\xi }_b(1+\nu )a^{3}b{L}_{p}G}{3\pi (3+2\nu )d_p^{}}$$

(5)

where ${\xi }_b$ is the rectangular shape bending correction factor, and selected as ${\xi }_b=2+\frac{2}{3}ln\frac{b}{a}$. An FEA model was generated in ANSYS with the following parameters: a = 4 mm, b/a = 1~10, $d_p$ = 250 mm, tensile armor pitch angle 55°, $L_p$ = 1121.7 mm, and L = $L_p$, as shown in Figure 4. The results are compared to expression ${\xi }_b=2+\frac{2}{3}ln\frac{b}{a}$ in Figure 5; the difference is within±10%, which indicates Equation (5) is a good representative of the tensile armor bending stiffness calculation.

For a constrained tensile armor helix, the axial stiffness is more complicated, and all variables, including pitch length, helix diameter, helix angle, and wire elongation, need to be considered. By taking the differentiation of the curve length $s$, we have $∆s=\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}∆\theta +\frac{d_p}{2\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}∆d_p+\frac{L_p}{2{\pi }^2\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}∆L_p$. It clearly shows the relationship between the curve length and the changes in the helix angle, pitch diameter, and pitch length. On the other hand, the tensile armor wire elongation can be calculated through the external force Fz as $∆s=\frac{F_{z}L}{Eab}sin{\beta }_p$. With consideration to these two length variation expressions, we have $\frac{F_{z}L}{Eab}sin{\beta }_p=\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}∆\theta +\frac{d_p}{2\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}∆d_p+\frac{L_p}{2{\pi }^2\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}∆L_p$. By substituting in $\theta =\frac{2\pi L}{L_p}$, $L=\frac{\theta L_p}{2\pi }$, and $∆L=\frac{\theta ∆L_p}{2\pi }$ , Equation (6) is derived.

$$\frac{F_z}{∆L}=\frac{2{\pi }^{2}Eabsin{\beta }_p}{{\theta }^2{L}_p}\left[\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}\frac{∆\theta }{∆L_p}+\frac{d_p}{\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}\frac{∆d_p}{∆L_p}+\frac{L_p}{{\pi }^2\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}}\right]$$

(6)

The left hand side of Equation (6) is the definition of tensile armor axial stiffness $k_z=\frac{F_z}{∆L}$. To the authors’ knowledge, this paper is the first to derive Equation (6) and apply it to study the relationship between helix angle variation, coil diameter variation, and axial stiffness.

If we assume $∆\theta$ and $∆d_p$ are negligible, and compare Equation (6) to Equation (4), we have $\frac{k_z}{k_0}~{\left(\frac{d_p}{a}\right)}^2$. Since $d_p\gg a$, it shows that $k_z\gg k_0$. In other words, when a tensile armor is tightly constrained in the helix angle and helix diameter, i.e., the helix angle and helix diameter cannot be changed, then the tensile armor will have much higher axial stiffness than the free helix condition.

When the friction is considered, the friction force can be calculated using the contact pressure and friction coefficient as $F_{\mu }=\mu \left(P_o+P_i\right)b∆s$, where $\mu$ is the friction coefficient, $P_o$ is the external contact pressure, $P_i$ is the internal contact pressure, and $∆s$ is the tensile armor wire length in the concerned range. The friction-induced hysteretic effect on the tension–displacement curve can then be generated, as shown in Figure 6.

The bending stiffness for constrained tensile armor is the same as Equation (5) for the frictionless condition, since in this case, tensile armor is free to slide to achieve the length of migration during bending. When friction is not negligible, the friction-induced bending moment is $M_{\mu }=\frac{b}{\pi d_{p}sin{\beta }_p}{\int }_0^{2\pi }{\frac{d_p}{2}F}_{\mu }\frac{1}{2}\sqrt{d_p^2+\frac{L_p^2}{{\pi }^2}}sin{\beta }_{p}sin\theta d\theta$, or given in Equation (7):

$$M_{\mu }=\frac{b}{{\pi }^2}{F}_{\mu }\sqrt{{\pi }^2{d}_p^2+L_p^2}$$

(7)

Equation (7) shows the bending moment is equal to the friction force acting at a distance of $d_{\mu }$ from the center line, where $d_{\mu }=\frac{b}{{\pi }^2}\sqrt{{\pi }^2{d}_p^2+L_p^2}$. The friction-induced hysteretic effect on the bending moment–curvature curve can be generated as shown in Figure 7.

4. Tensile Armor Stresses

For a free tensile armor, when it is under tension T, the tension will generate all three stress components: tensile stress, bending stress, and shear stress. Its tensile stress is ${\sigma }_t=\frac{Tsin{\beta }_p}{ab}$, bending stress is ${\sigma }_b=\frac{3T{d}_{p}sin{\beta }_p}{a^{2}b}$, and torsion-induced shear stress is ${\tau }_t=\frac{T{d}_{p}cos{\beta }_p}{2{\xi }_{\sigma }{a}^{2}b}$, where ${\xi }_{\sigma }$ is the stress shape factor. The recommended values were given by Wahl [8], as listed in

Table 2. Factor of ${\xi }_{\sigma }$ .

b/a	1	1.2	1.5	2	2.5	3	4	5	10
${\xi }_{\sigma }$ (Wahl)	0.208	0.219	0.231	0.246	0.258	0.267	0.282	0.291	0.312
${\xi }_{\sigma }$ (FEA)	0.205	0.220	0.231	0.245	0.258	0.267	0.282	0.292	0.312
Diff %	−1.6%	0.6%	−0.1%	−0.2%	−0.2%	0.1%	−0.1%	0.2%	0.1%

. Table 2 also listed the FEA results to compare ${\xi }_{\sigma }$ under different aspect (b/a) ratios with a = 4 mm, and comparisons showed an almost-exact match.

The combined principal stresses are calculated as ${\sigma }_{\mathrm{1,2}}=\frac{{\sigma }_t+{\sigma }_b}{2}\pm \sqrt{\frac{{({\sigma }_t+{\sigma }_b)}^2}{4}+{{\tau }_t}^2}$.

When a tensile armor is under a bending moment, and bent with a curve radius of ${\rho }_p$, then its equivalent bending moment is $M_{\rho }=\frac{k_{\theta }}{{\rho }_p}$, the bending stress is ${\sigma }_b=\frac{6M_{p}sin{\beta }_p}{a^{2}b}$, and the shear stress is ${\tau }_t=\frac{M_{p}cos{\beta }_p}{{\xi }_{\sigma }{a}^{2}b}$. Furthermore, when the tensile armor is under both tension and bending, then the bending and stresses could be superimposed as ${\sigma }_b=\frac{sin{\beta }_p}{a^{2}b}\left(3T{d}_p+\frac{6k_{\theta }}{{\rho }_p}\right)$, and ${\tau }_t=\frac{cos{\beta }_p}{{\xi }_{\sigma }{a}^{2}b}\left(\frac{T{d}_p}{2}+\frac{k_{\theta }}{{\rho }_p}\right)$.

For a constrained tensile armor, the tensile stress calculation remains ${\sigma }_t=\frac{Tsin{\beta }_p}{ab}$; however, for bending and shear stresses, the bending moment and torsion will be partially resisted by the contact force $F_c$, which depends on the contact stiffness and contact deformation distance. Contact force generates a counteracting moment $F_{c}b$, which is subtracted from the external bending moment during bending and shear stress calculation. In summary, the stress calculations are given in Equation (8):

$${\sigma }_t=\frac{Tsin{\beta }_p}{ab}, {\sigma }_b=\frac{sin{\beta }_p}{a^{2}b}\left(3(T{d}_p-2F_{c}b)+\frac{6k_{\theta }}{{\rho }_p}\right), {\tau }_t=\frac{cos{\beta }_p}{{\xi }_{\sigma }{a}^{2}b}\left(\frac{T{d}_p}{2}-F_{c}b+\frac{k_{\theta }}{{\rho }_p}\right)$$

(8)

If contact stiffness is rigid, $T{d}_p-2F_{c}b\approx 0$, and Equation (8) can be reduced to a simpler form.

5. Benchmark Case of Tensile Armor under Tension and Bending

Full-scale flexible structure experiments are usually done in fabrication factories, and testing results are confidential and not available to the public. Some researchers have done experiments on prototype samples, and provided valuable test results, such as Norouzi [9]. In this section, we compared the calculation results between our method and experimental data published by Norouzi [9]. The experimental sample is a simplified flexible riser with four layers: the carcass layer, inner tube, tensile armor layer, and outer tube. The properties are as follows:

• Carcass, ANSI 10180 material, outer diameter 94 mm, cross section 3 mm × 12 mm, pitch length 43.4 mm, overall length 651 mm.
• Inner tube, polycarbonate, outer diameter 100 mm, thickness 3 mm, overall length 668 mm.
• Tensile armor, ANSI 10180 material, outer diameter 106 mm, cross section 3 mm × 12 mm, pitch length 108.5 mm, overall length 651 mm.
• Outer tube, polycarbonate, outer diameter 120 mm, thickness 5 mm, overall length 681 mm.

Tensile loading experiments were done only on the tensile armor, with two end fittings, as shown in Figure 8. The end of the tensile armor was rigidly connected to the end fitting through welding, and the middle section was free. Before the displacement was measured, there was a dead weight of 1.75 kg hanging below the tensile armor, which was included in the measured tension. As such, the tension-displacement curve started at (0, 17) instead of (0, 0). Tension-displacement curves were also calculated using Equation (4) for the free section and Equation (6) for the restrained section, and the combined results were compared to the experimental results in Figure 9. The comparison shows that the calculated stiffness curve has similar hysteretic behavior as the experimental data, and there is slight difference at the high-displacement region.

Bending experiments were performed on the flexible prototype assembly, with both ends fixed, and a vertical load was applied to the center of the assembly. Figure 10 shows the testing assembly. The bending moment and curvature were reported at the center of the assembly. Equation (5) was used to calculate the bending moment–curvature relationship, with friction included as Equation (7), and the results are compared to the experimental data in Figure 11. In general they show good agreement, especially in the low curvature range of 0~0.02 1/m. When curvature exceeds 0.02 1/m, the experimental data showed a higher hysteretic effect, which could be linked to the tension change in the testing assembly. When the testing assembly has high deflections, it will also be stretched in the axial direction due to the fixed boundary conditions at both ends. An increasing tension in the testing assembly would enhance the hysteretic effect.

6. Flexible Riser Fatigue Analysis

In this section, we applied the presented method to an in-service flexible riser fatigue analysis. The studied flexible riser is in Lufeng oil field in the South China Sea, with water depth ranges from 130–146 m. The field consists of a jacket type-LF13-2 production platform, a single-point mooring system and a 121,000 ton floating storage and offloading unit (FSOU), and a 8” flexible riser with a length of 1.8 km to connect the jacket to the FSOU, as shown in Figure 12. The flexible riser has been in service since 2012, and its fatigue damage needs to be assessed for life-extension assessment purposes. The general arrangement of the flexible riser is shown in Figure 13. The upper end of the flexible riser is connected to a disconnectable turret, which can be disconnected from the FSOU and lowered into the water column during a typhoon or planned maintenance periods. A middle water arch structure is used to suspend the flexible riser in water, and provides flexibility to the riser system to accommodate the FSOU motions. The flexible riser system operational records showed that:

• The turret has been disconnected a total of 43 times, of which 30 times were due to typhoon evacuation, and 13 times were due to maintenance and repairs. The total duration of the flexible riser being in a disconnected condition was 237 days.
• From 2012 to 2022, Nanhaishengkai FSOU was used for crude-oil storage and offloading, with a total in-place service duration of 2782 days.
• From 2020 to present, HYSY121 FSOU (a replacement of Nanhaishengkai FSOU) was used for crude-oil storage and offloading, with a total in-place service duration of 469 days.

The operational records also showed that the flexible riser internal pressure varied from 0 to 0.9 MPa; most of the time the internal pressure was below 0.1 MPa, and there were 21 days (less than 1% of the service time) in which the internal pressure had been higher than 0.1 MPa. Internal fluid temperatures varied from 50 to 80 deg C, except during shutdown period, where the fluid temperature reduced to ambient temperature.

The flexible riser structural layers are illustrated in Figure 14, and with properties listed in

Table 3. Flexible riser layer properties.

Layer No	Layer Name	ID	Thickness	Mass	Tensile Strength
		mm	mm	kg/m	MPa
1	Interlocked Carcass	203.2	6	19.11	600
2	Pressure Sheath Crossflex	215.2	6	4.29	-
3	Zeta Wire	227.2	6.2	30.54	1000
4	Anti-wear Tape	239.6	1.5	1.08	-
5	First Armor Layer	242.6	4	21.7	1400
6	Anti-wear Tape	250.6	1.5	1.13	-
7	Second Armor Layer	253.6	4	22.66	1400
8	High Strength Tape	261.6	3.05	1.53	-
9	Inner Sheath	267.7	6.8	5.55	-
10	Insulation Layer 1	281.3	11	5.15	-
11	Insulation Layer 2	303.3	11	5.53	-
12	Fabric Tape	325.3	1.4	0.86	-
13	External Sheath	328.1	9.1	9.13	-
14	Protective Sheath	346.3	9.1	9.62	-

. It has 14 layers, including 2 tensile armor layers. The tensile armor wire has a thickness of 4 mm, a width of 12 mm, and a helix angle of 55°. Refer to API 17B [10] for more details on the flexible riser’s structural definitions and functionalities.

The fatigue analysis was performed using the following procedures:

• Perform global dynamic analysis on the flexible riser systems in Orcaflex, with hysteretic tension and bending stiffness calculated from Equations (6) and (7). The dynamic analysis was performed on each of the fatigue sea states, in combination with different host vessels, i.e., Nanhaishengkai FSOU, HYSY121 FSOU, and the disconnected turret, and two internal pressure levels: 0.1 MPa and 1.0 MPa. The global model is shown in Figure 15, with the flexible riser dynamic envelope under sea state Hs = 3 m, Tp = 8 s. Refer to API RP 2RD [11] for more details about riser dynamic modelling and analysis.
• Retrieve the tension and curvature time histories at the critical locations along the flexible riser, including the hang-off section, sag bend section, hog bend section, and touchdown section. The flexible riser tension and bending curvature range distributions along the riser are shown in Figure 16 and Figure 17, respectively.
• Build the flexible structure model in the FEA analysis software (ANSYS), verify the maximum stresses in the outer-layer tensile armor, and compare it with the predicted stresses using Equation (8) under a selected loading case, as shown in Figure 18. Comparison results of the flexible riser hang-off region, with a tension of 5 Te and a curvature of 0.1 1/m, are presented in

  Table 4. Tensile armor maximum stress comparisons.

  Case	Equation (8)	FEA Model	Difference %
  Tension = 5 Te Curvature = 0	8.2 MPa	7.8 MPa	3.8%
  Tension = 0 Curvature = 0.05 1/m	81.1 MPa	83.5 MPa	−2.9%
  Tension = 5 Te Curvature = 0.05 1/m	88.3 MPa	90.8 MPa	−2.8%

  .
• Calculate the stress time histories for each fatigue bin and critical location using Equation (8), and process the stress ranges through the rain-flow counting technique.
• Calculate the fatigue damages using selected S-N fatigue curves and the Miner–Palmgren rule. The fatigue analysis results are presented in

  Table 5. Summary of tensile armor fatigue-damage results.

  Item	Unit	Hang Off Section	Sag Bend Section	Hog Bend Section	Touchdown Section
  Nanhaishengkai FSOU (2782 days)	1/yr	2.78 × 10−4	9.25 × 10−9	1.43 × 10−6	2.84 × 10−8
  HYSY121 FSOU (469 days)	1/yr	5.97 × 10−5	1.43 × 10−9	1.65 × 10−7	4.60 × 10−9
  Turret Disconnected (237 days)	1/yr	2.21 × 10−7	7.59 × 10−11	8.88 × 10−9	4.18 × 10−9
  Total Fatigue Damage	1/yr	3.38 × 10−4	1.08 × 10−8	1.61 × 10−6	3.72 × 10−8
  Safety Factor		10	10	10	10
  Remaining Fatigue Life	yr	2.14 × 103	9.01 × 107	7.79 × 105	1.55 × 107

  . Refer to DNV RP C203 [12] for more details on fatigue damage calculations.

Figure 15 shows the flexible riser movement range during a typical sea state. The middle water arch provided flexibility to accommodate the FSOU offsets and motions, and limited the flexible riser dynamic motions to a few meters in range.

Flexible riser tension and curvature are readily available after global analysis. Figure 16 shows a typical tension range distribution along the flexible riser. An arc length of zero refers to the to hang-off point, and the middle water arch is located at arc length 180 m; the touchdown point is located at arc length 280 m. The highest tension occurs at the top hang-off area, which ranges from 4 Te to 7 Te. The tension reduction at the middle water arch area is due to the clamps on the middle water arch.

Figure 17 shows a typical dynamic curvature distribution along the flexible riser. The flexible riser is supported on the middle water arch, with a radius of 3.8 m. For other areas, the bending radius is higher than 20 m.

Figure 18 shows the flexible riser ANSYS FEA model for stress check. The FEA model included all structural layers (except the anti-wear tape layers) for one full pitch length, and meshed with more than 10 million elements. ANSYS Solid185 elements were used for all structural layers, and target170/contact175 elements were used at the contact surface. The inner armor wire layer has 50 armor wires in a clockwise spiral; the outer armor wire layer has 52 armor wires in an anti-clockwise spiral. Contact surfaces were defined between adjacent layers, with an internal friction coefficient of 0.1. An external tension of 5 Te and a bending curvature of 0.1 1/m were applied to the model, and the maximum principal stresses on the tensile armors were listed and compared with Equation (8) in Table 4. It showed a difference of less than 5%, which is considered satisfactory. Note that FEA stresses are averaged stresses across the tensile armor thickness, and exclude the localized hot spots at the contact points.

Flexible-structure FEA analysis also identified that the outer tensile armor layer is the fatigue-governing component, and its fatigue damage results are summarized in Table 5. Overall, the fatigue damages are mild; the highest fatigue damage occurs at the top hang-off region, with the expected remaining fatigue life being more than 2000 years. In order to cover the statistical nature of the fatigue phenomenon, a safety factor of 10 was applied. The analysis results supported the lifetime extension of the flexible riser.

7. Conclusions

This paper presented an analytical modelling method of the flexible riser tensile armors. The method was derived using the curved bar theory, and included tensile, shear and bending stress, and tensile and bending stiffnesses. For tensile armor with various aspect ratios, empirical shape coefficients were considered in the stiffness formula, and validated through FEA analysis. Tension and bending hysteretic models were also derived and compared to published experimental data, and comparisons showed good agreements. Tensile and bending stresses were calculated using the rigid beam model, while torsion-induced shear stress was calculated using the Wahl formula, and verified through the FEA results for typical aspect ratios (i.e., b/a ranges from 1 to 10). Finally, the method was applied to an 8″ flexible riser fatigue analysis, which predicted a fatigue life of more than 2000 years, thus being favorable to the decision to extend the service period of this flexible riser.

The highlights of the main findings are as follows:

• Equations (4) and (5) provide improved accuracy for the calculation of rectangular-shape armor-wire tensile and bending stiffnesses, and Equation (6) provides valuable insights into the relationship between the axial stiffness of an armor wire, and the helix angle change and coil diameter change.
• Tensile and bending stiffness could be derived from a curved beam model. Tensile-armor tensile stiffness depends on the pitch length change (axial slippage) and helix diameter change (fabrication gap between layers). Bending stiffness is small if the tensile armor is allowed to slide freely in the axial direction.
• Friction between tensile armor layers generates a hysteretic effect on both the tension and bending stiffness. The tension hysteretic curve can be defined by a vertex with non-dimensional coordinates (0.5, 1); the bending hysteretic curve can be defined by a vertex with non-dimensional coordinates (0, 1).
• The outer tensile armor layer is the most fatigue-onerous component in the flexible riser. For the middle water arch arrangement, the top hang-off section has the highest fatigue damage, mainly due to FSOU dynamic motions. The hog-bend section may also have considerable fatigue damage on its bending chute. In general, the mid water arch arrangement accommodates the FSOU motion very well, and the flexible riser fatigue damage is well below the allowables.

In summary, the presented method for flexible-riser tensile-armor modelling is efficient and effective; hence, it is suitable for flexible-riser fatigue analysis. Future work may include friction models between flexible layers, and stress models for all the layers in the flexible pipe.