Bearing Characteristics of Tripod Bucket Foundation under Horizontal and Moment Load in Sand
Abstract
:1. Introduction
2. Materials and Methods
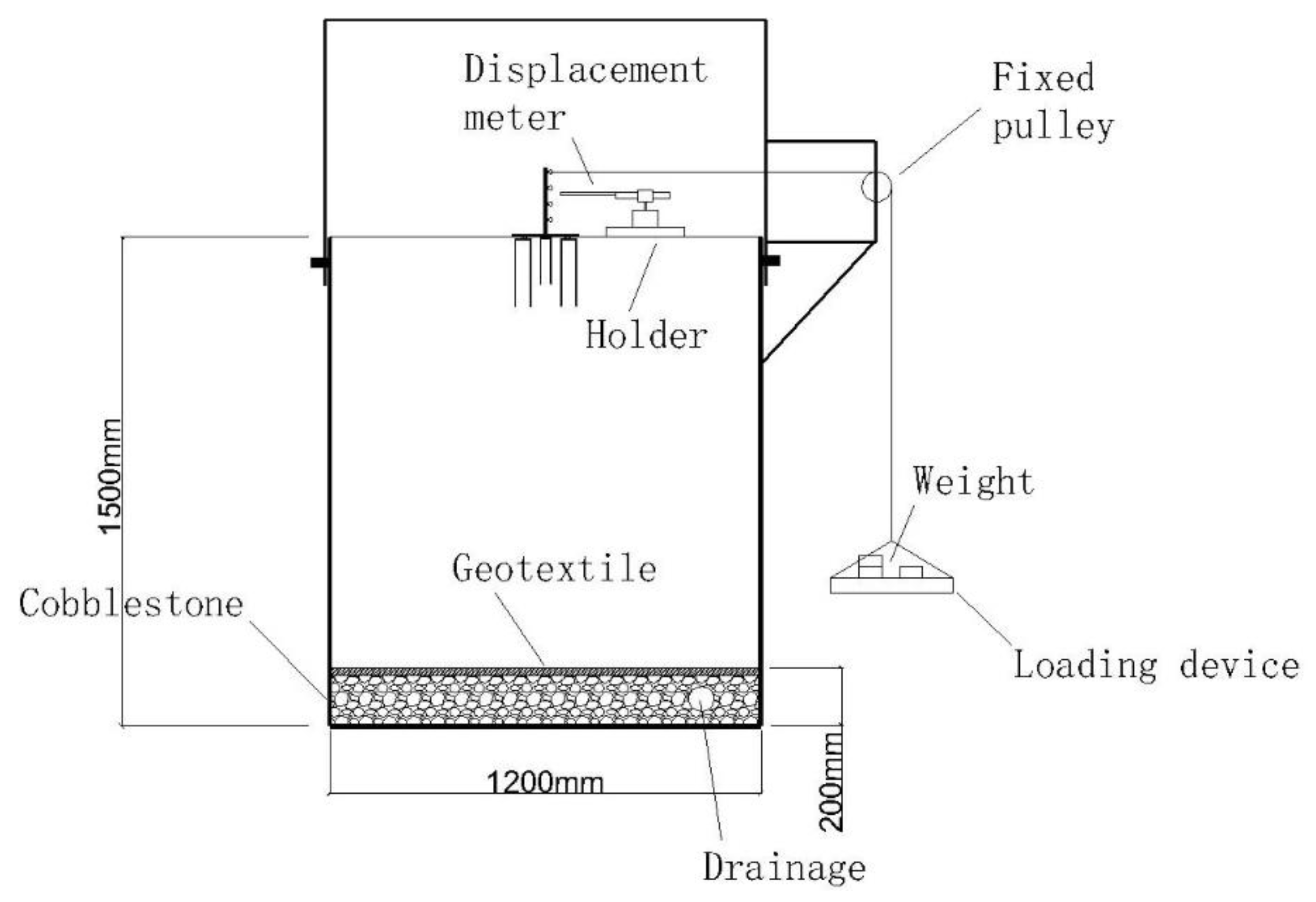
2.1. Physical Model Test
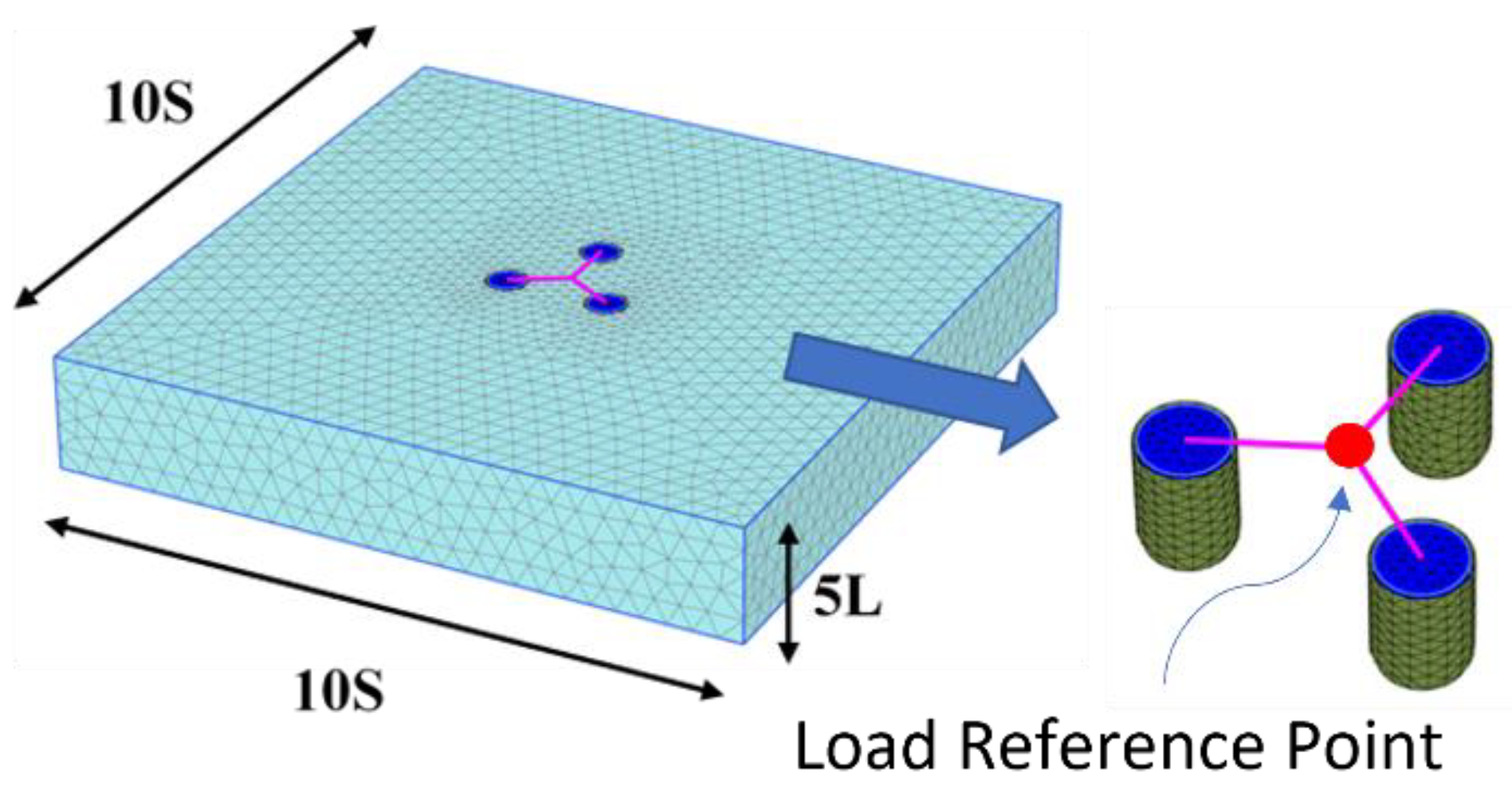
2.2. Numerical Simulation
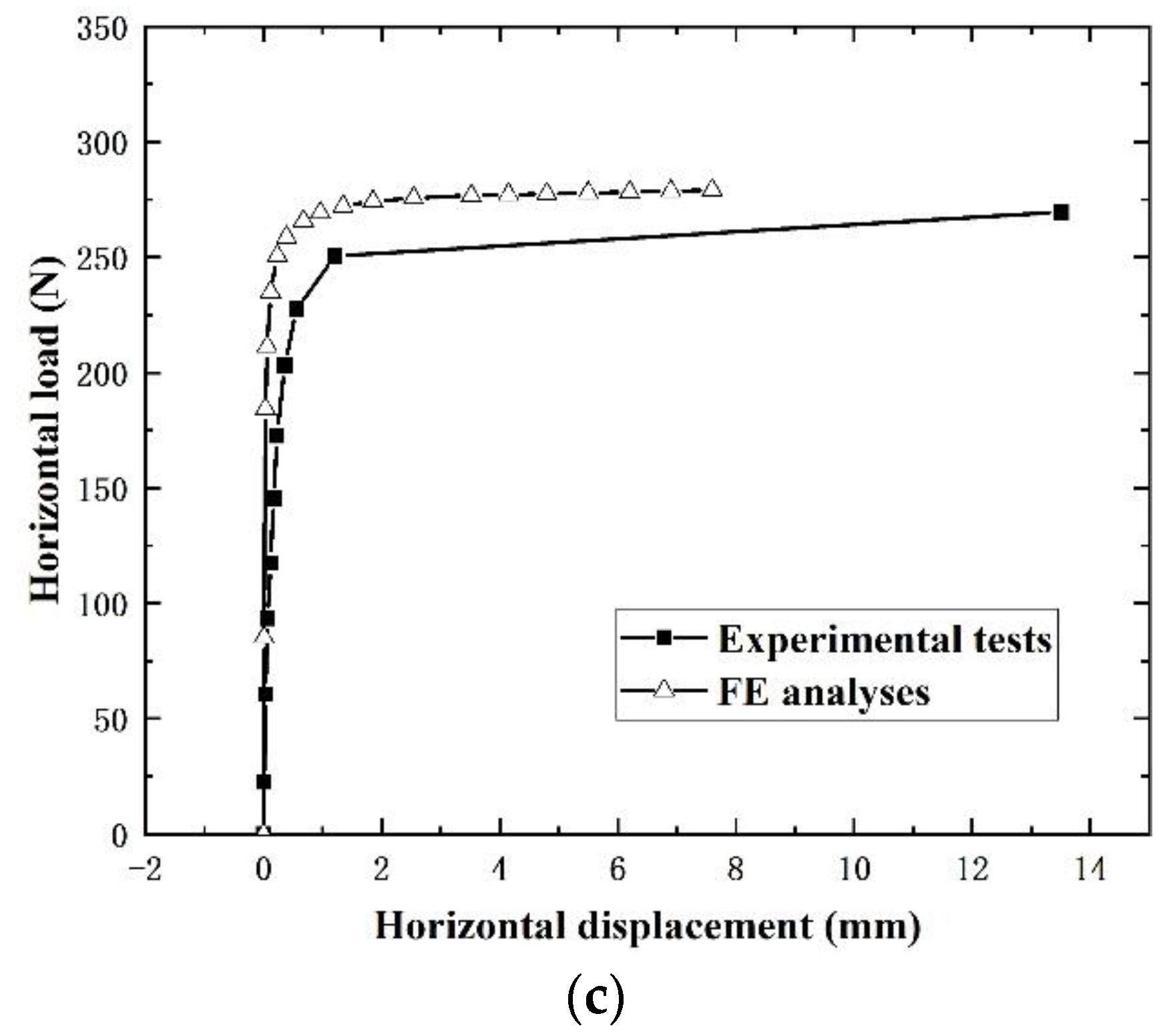
2.3. Validation of Numerical Modeling
3. Results
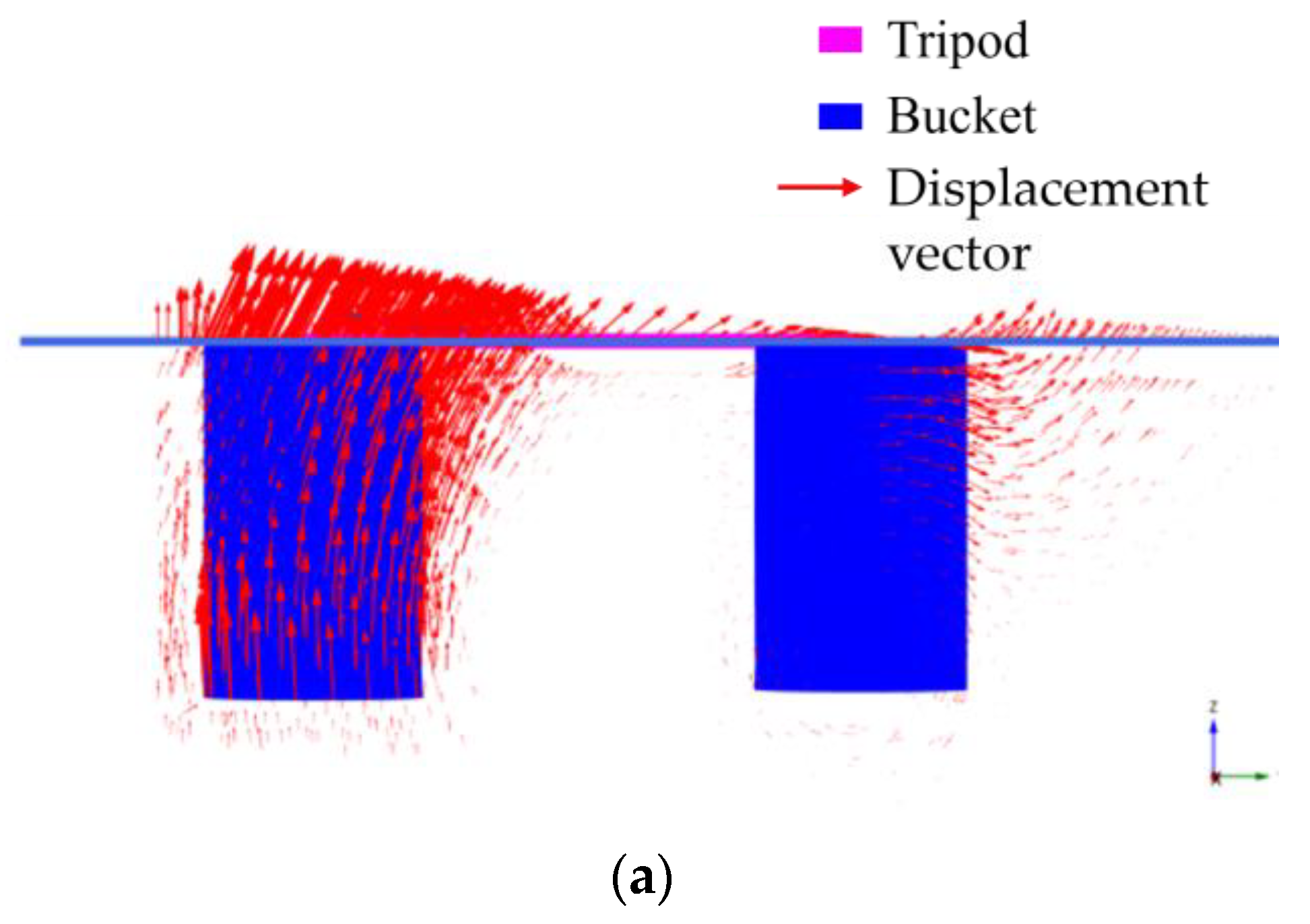
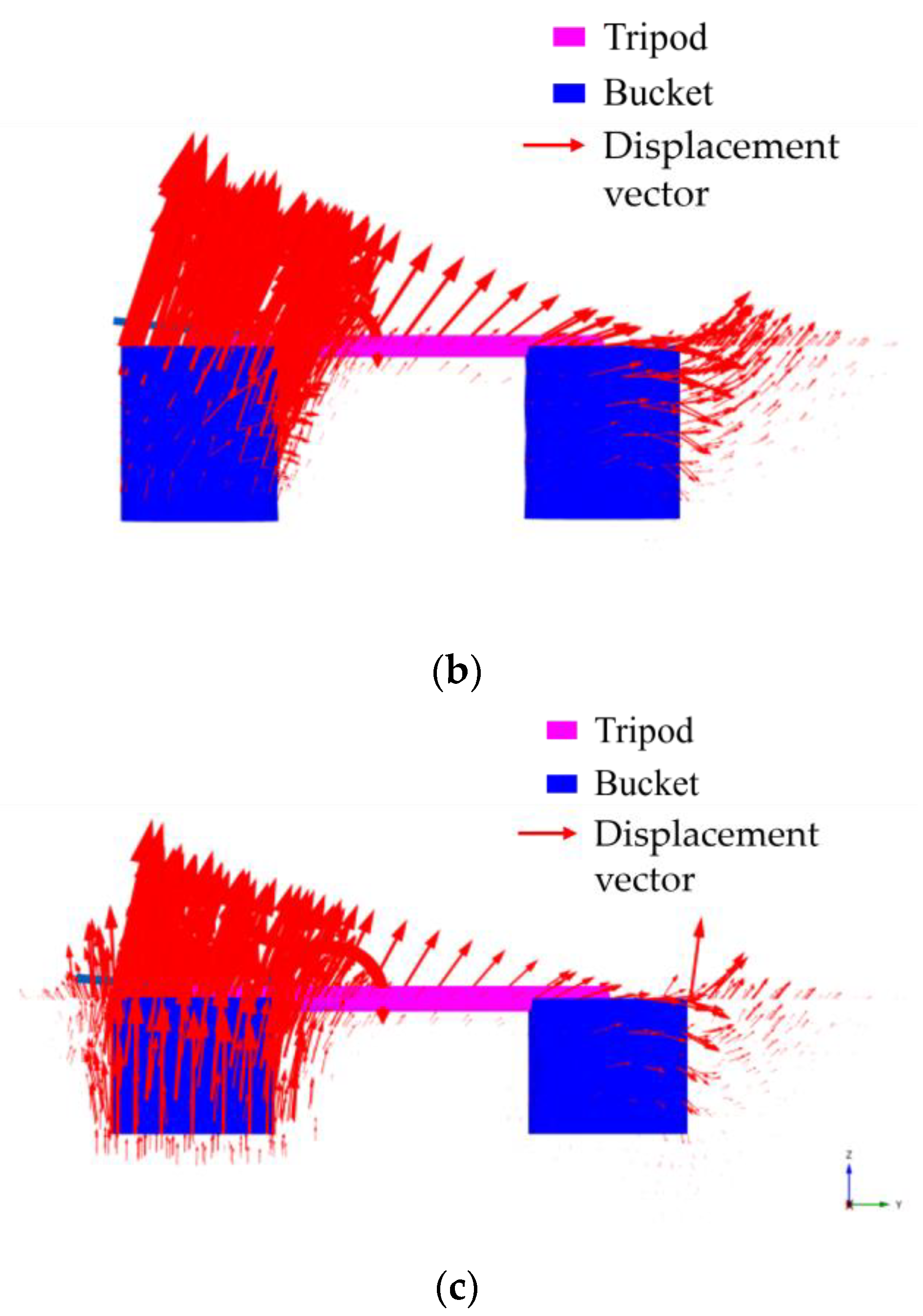
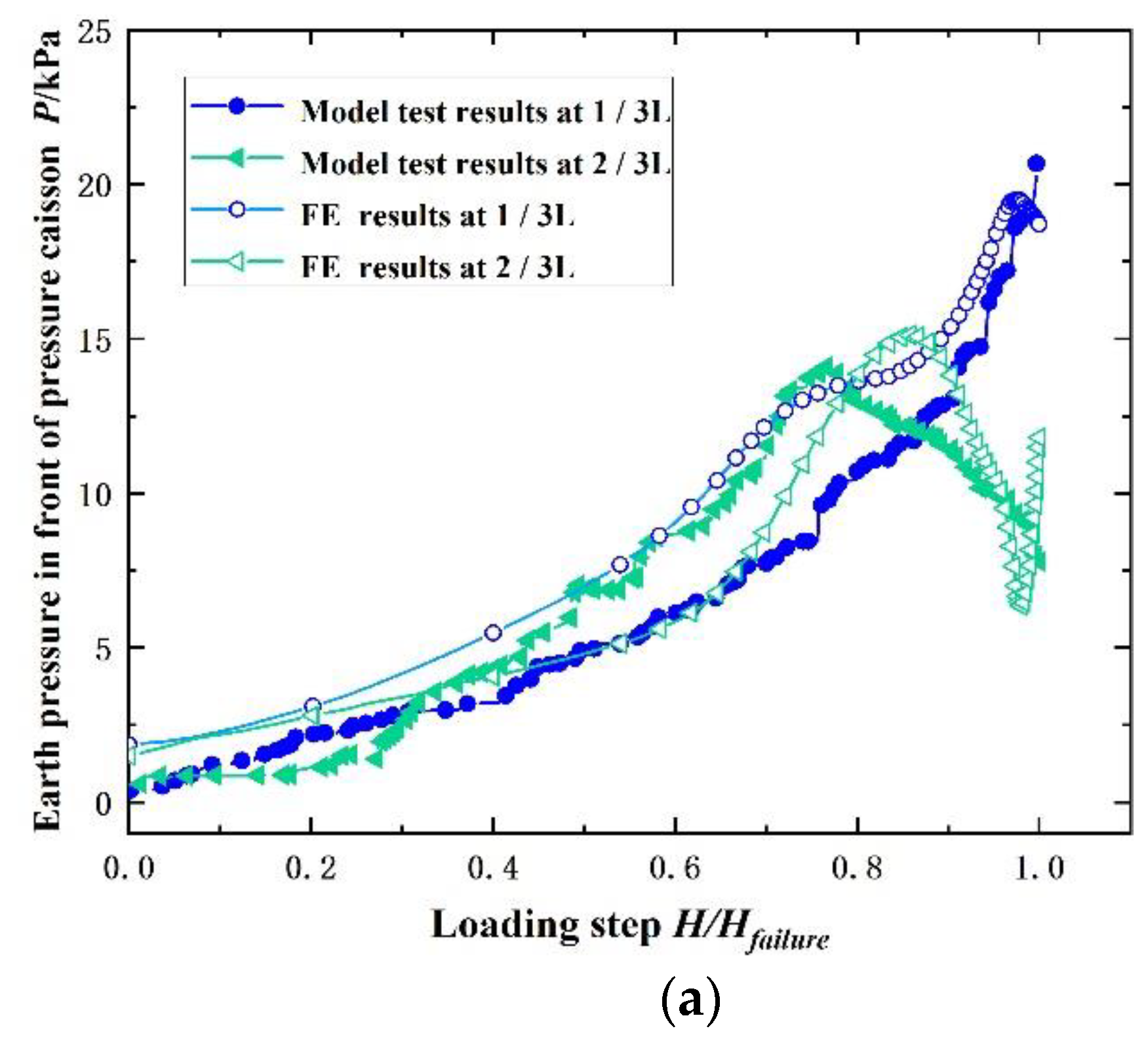
3.1. Failure Mechanism under H–M Loadings
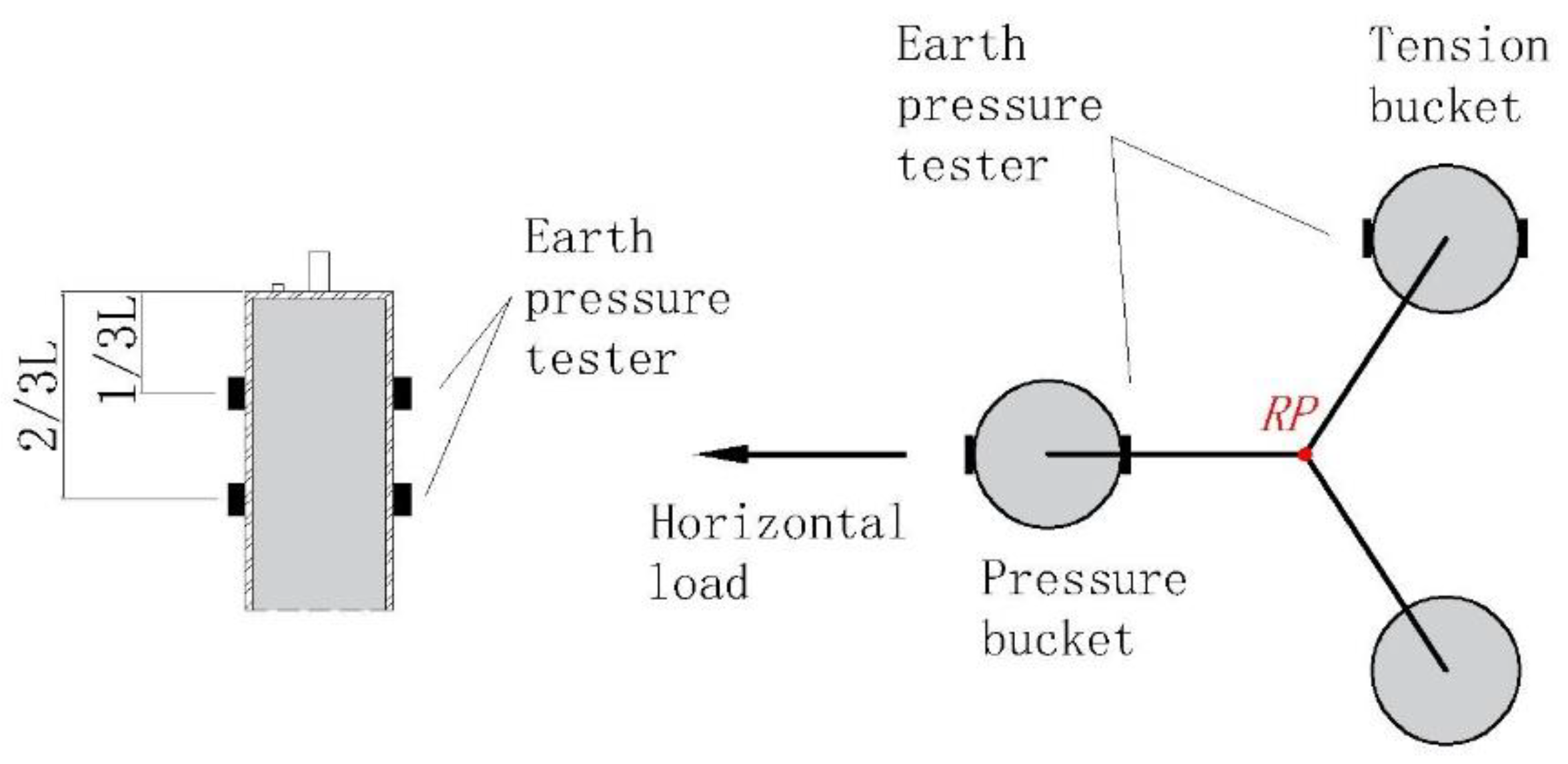
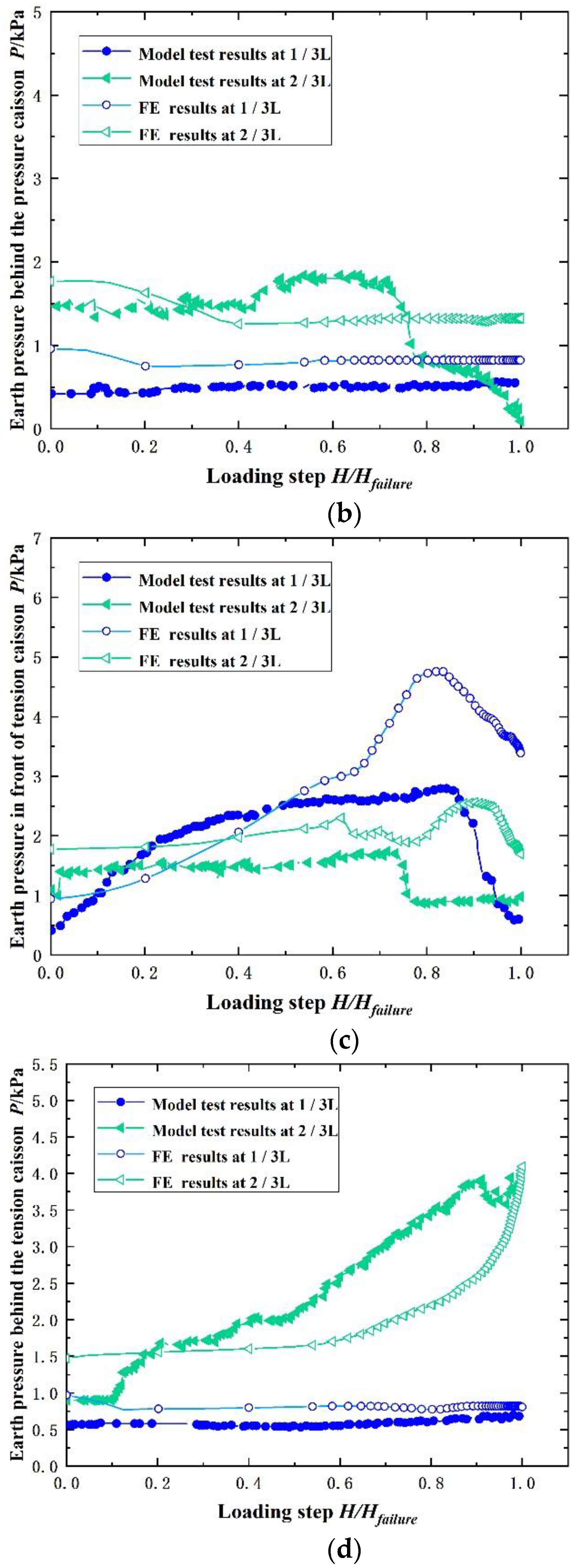
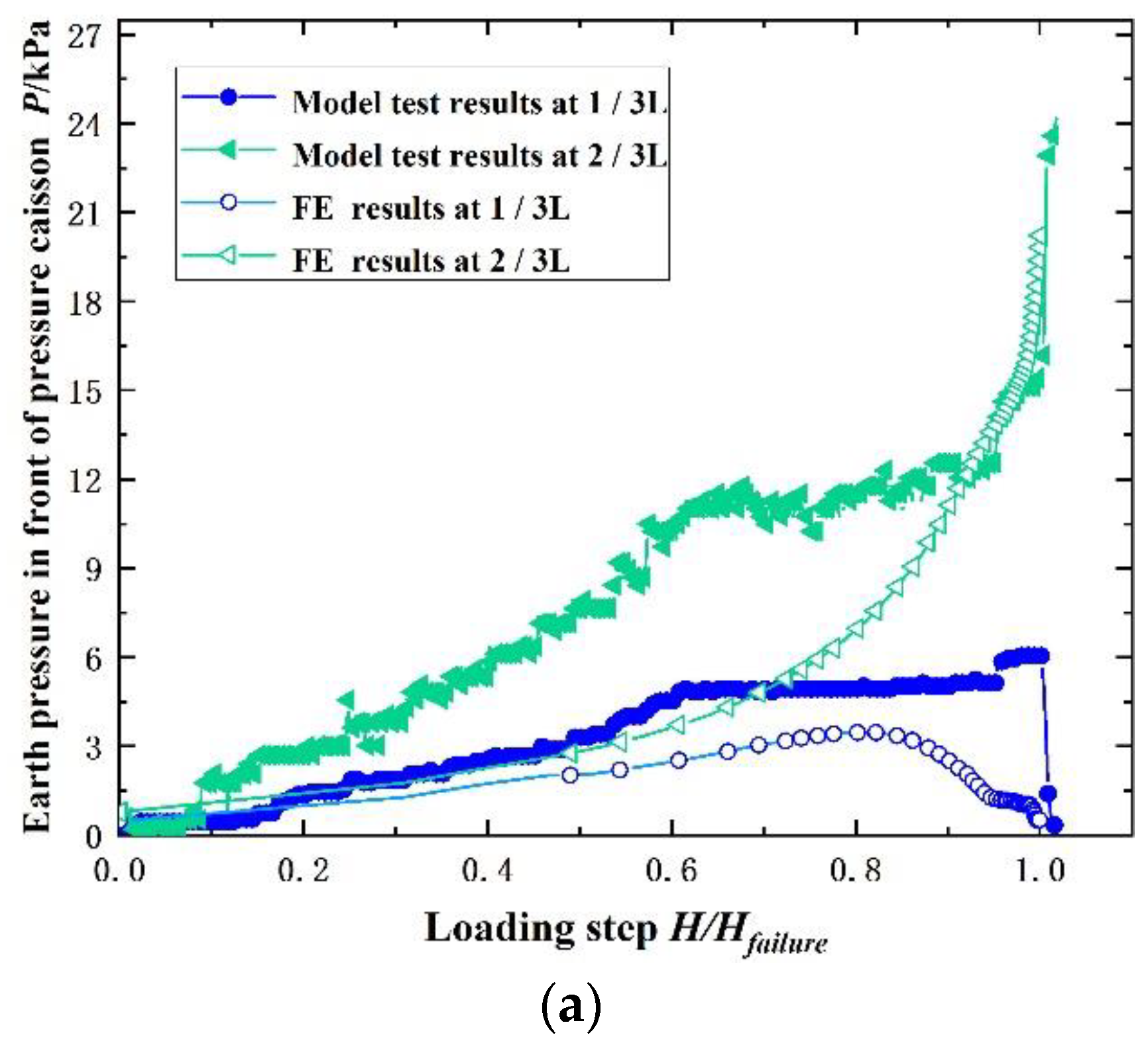
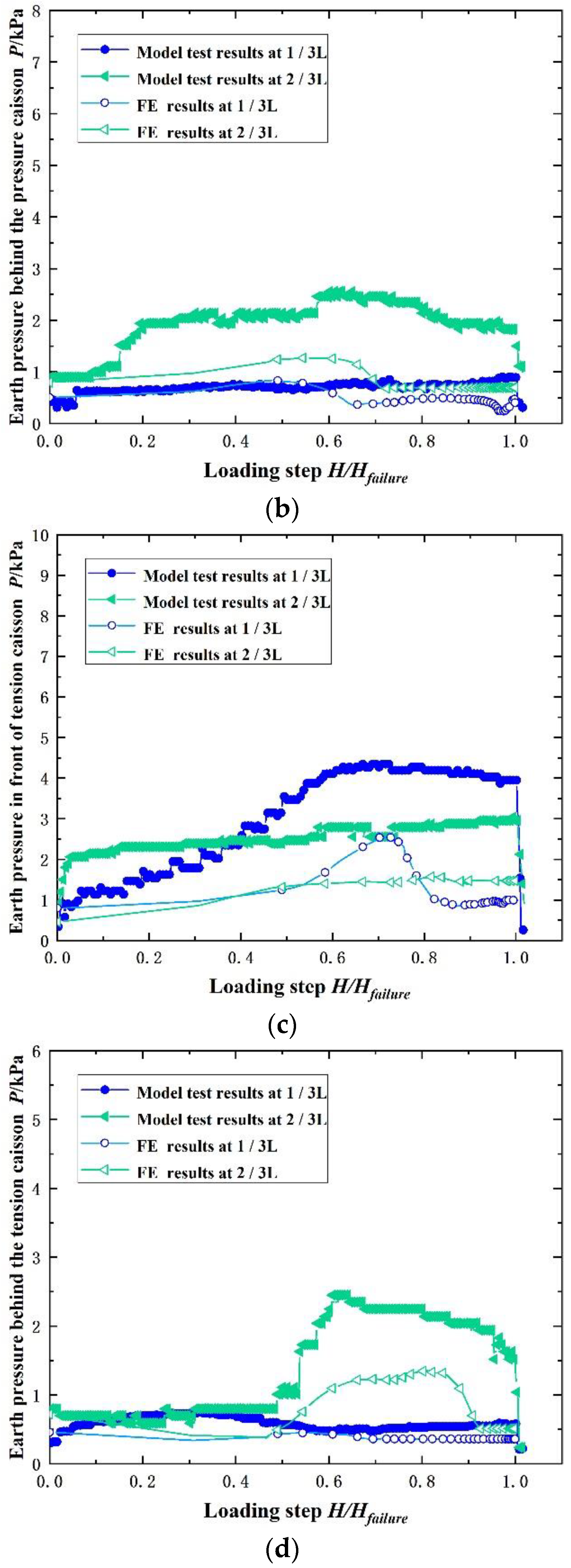
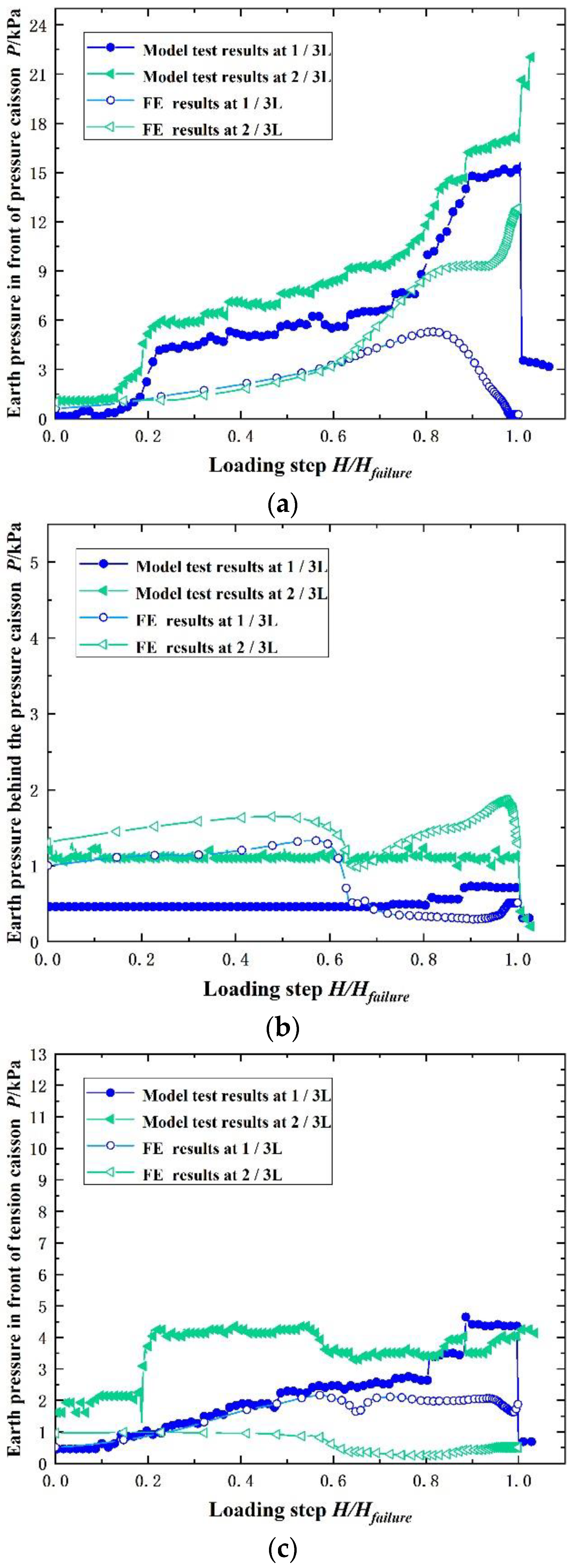
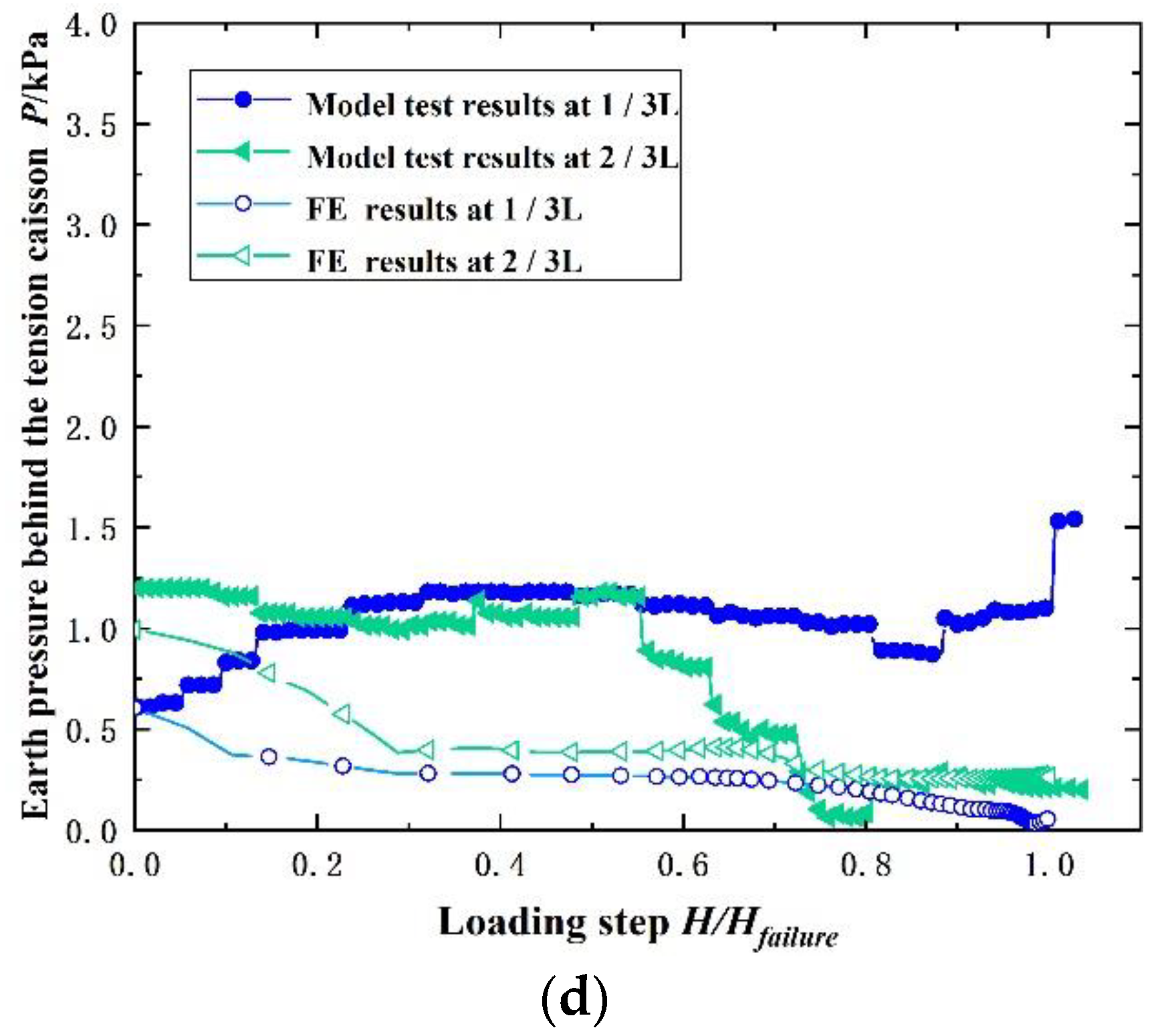
3.2. Earth Pressure Analysis
3.3. Moment Bearing Capacity of Tripod Bucket Foundation under M-H
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.-H.; Jeong, Y.-H.; Ha, J.-G.; Park, H.-J. Evaluation of Soil–Foundation–Structure Interaction for Large Diameter Monopile Foundation Focusing on Lateral Cyclic Loading. J. Mar. Sci. Eng. 2023, 11, 1303. [Google Scholar] [CrossRef]
- Shi, Y.; Yao, W.; Yu, G. Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load. J. Mar. Sci. Eng. 2022, 10, 1024. [Google Scholar] [CrossRef]
- Luke, A.M.; Rauch, A.F.; Olson, R.E.; Mecham, E.C. Components of suction caisson capacity measured in axial pullout tests. Ocean Eng. 2005, 32, 878–891. [Google Scholar] [CrossRef]
- Standard, O. Design of offshore wind turbine structures. Det Nor Ske Veritas 2007, 567–581, 567–581. [Google Scholar]
- Achmus, M.; Kuo, Y.-S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Al-Ramthan, A.Q.O.; Aubeny, C.P. Numerical investigation of the performance of caissons in cohesive soils under cyclic loading. Int. J. Geomech. 2020, 20, 04020042. [Google Scholar] [CrossRef]
- Ghorai, B.; Chatterjee, S. Estimation of installation resistance and subsequent short-term capacities of offshore skirted foundations in clay. Int. J. Geomech. 2020, 20, 04020133. [Google Scholar] [CrossRef]
- Zhang, Y.; Bienen, B.; Cassidy, M.J.; Gourvenec, S. The undrained bearing capacity of a spudcan foundation under combined loading in soft clay. Mar. Struct. 2011, 24, 459–477. [Google Scholar] [CrossRef]
- Kuo, Y.-S.; Achmus, M.; Abdel-Rahman, K. Minimum embedded length of cyclic horizontally loaded monopiles. J. Geotech. Geoenviron. Eng. 2012, 138, 357–363. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Ibsen, L.B.; Byrne, B.W. Suction caissons for wind turbines. In Frontiers in Offshore Geotechnics, Proceedings of the ISFOG, Perth, WA, Australia, 19–21 September 2005; CRC Press: Boca Raton, FL, USA, 2005; pp. 75–93. [Google Scholar]
- Yun, G.; Bransby, M.F. The horizontal-moment capacity of embedded foundations in undrained soil. Can. Geotech. J. 2007, 44, 409–424. [Google Scholar] [CrossRef]
- Achmus, M.; Akdag, C.; Thieken, K. Load-bearing behavior of suction bucket foundations in sand. Appl. Ocean Res. 2013, 43, 157–165. [Google Scholar] [CrossRef]
- Bransby, F.; Randloph, M. The effect of embedment depth on the undrained response of skirted foundations to combined loading. Soils Found. 1999, 39, 19–33. [Google Scholar] [CrossRef]
- Bransby, M.; Yun, G.-J. The undrained capacity of skirted strip foundations under combined loading. Géotechnique 2009, 59, 115–125. [Google Scholar] [CrossRef]
- Gourvenec, S. Effect of embedment on the undrained capacity of shallow foundations under general loading. Géotechnique 2008, 58, 177–185. [Google Scholar] [CrossRef]
- Ni, D.; Lu, M. Review on Bearing Capacity of Offshore Wind Turbine Single Pile and New Pile-barrel Combination Foundation. Int. Core J. Eng. 2022, 8, 433–442. [Google Scholar]
- Sørensen, E.S.; Clausen, J.; Damkilde, L. Comparison of numerical formulations for the modeling of tensile loaded suction buckets. Comput. Geotech. 2017, 83, 198–208. [Google Scholar] [CrossRef]
- Zhao, X.-L.; Wang, X.; Ding, P.-C.; Sui, S.-H.; Deng, W.-N. Development and Influence of Pore Pressure around a Bucket Foundation in Silty Soil. J. Mar. Sci. Eng. 2022, 10, 2020. [Google Scholar] [CrossRef]
- Martin, C.; Hazell, E. Bearing capacity of parallel strip footings on non-homogeneous clay. In Proceedings of the International Symposium on Frontiers in Offshore Geotechnics, Perth, WA, Australia, 19–21 September 2005; pp. 427–433. [Google Scholar]
- Gourvenec, S.; Jensen, K. Effect of embedment and spacing of cojoined skirted foundation systems on undrained limit states under general loading. Int. J. Geomech. 2009, 9, 267–279. [Google Scholar] [CrossRef]
- Bang, S.; Leahy, J.C.; Cho, Y.; Kwon, O. Horizontal bearing capacity of suction piles in sand. Transp. Res. Rec. 2006, 1975, 21–27. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, D.; Zhang, F.; Qiu, Y. Ultimate lateral bearing capacity of tetrapod jacket foundation in clay. Comput. Geotech. 2017, 84, 164–173. [Google Scholar] [CrossRef]
- Kim, S.-R.; Oh, M. Group effect on bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 79, 1–9. [Google Scholar] [CrossRef]
- Hung, L.C.; Kim, S.-R. Evaluation of undrained bearing capacities of bucket foundations under combined loads. Mar. Georesour. Geotechnol. 2014, 32, 76–92. [Google Scholar] [CrossRef]
- He, B.; Jiang, J.; Cheng, J.; Zheng, J.; Wang, D. The capacities of tripod bucket foundation under uniaxial and combined loading. Ocean Eng. 2021, 220, 108400. [Google Scholar] [CrossRef]
- Tran, N.X.; Kim, S.-R. Evaluation of horizontal and moment bearing capacities of tripod bucket foundations in sand. Ocean Eng. 2017, 140, 209–221. [Google Scholar] [CrossRef]
- Brinkgreve, R.; Kumarswamy, S.; Swolfs, W.; Waterman, D.; Chesaru, A.; Bonnier, P. PLAXIS 2016; PLAXIS BV: Delft, The Netherlands, 2016. [Google Scholar]
- Gourvenec, S.; Steinepreis, M. Undrained limit states of shallow foundations acting in consort. Int. J. Geomech. 2007, 7, 194–205. [Google Scholar] [CrossRef]
- Kim, S.R. Evaluation of vertical and horizontal bearing capacities of bucket foundations in clay. Ocean Eng. 2012, 52, 75–82. [Google Scholar]
- Palix, E.; Willems, T.; Kay, S. Caisson capacity in clay: VHM resistance envelope—Part 1: 3D FEM numerical study. Frontiers in Offshore Geotechnics II; CRC Press: Boca Raton, FL, USA, 2010; pp. 771–776. [Google Scholar]


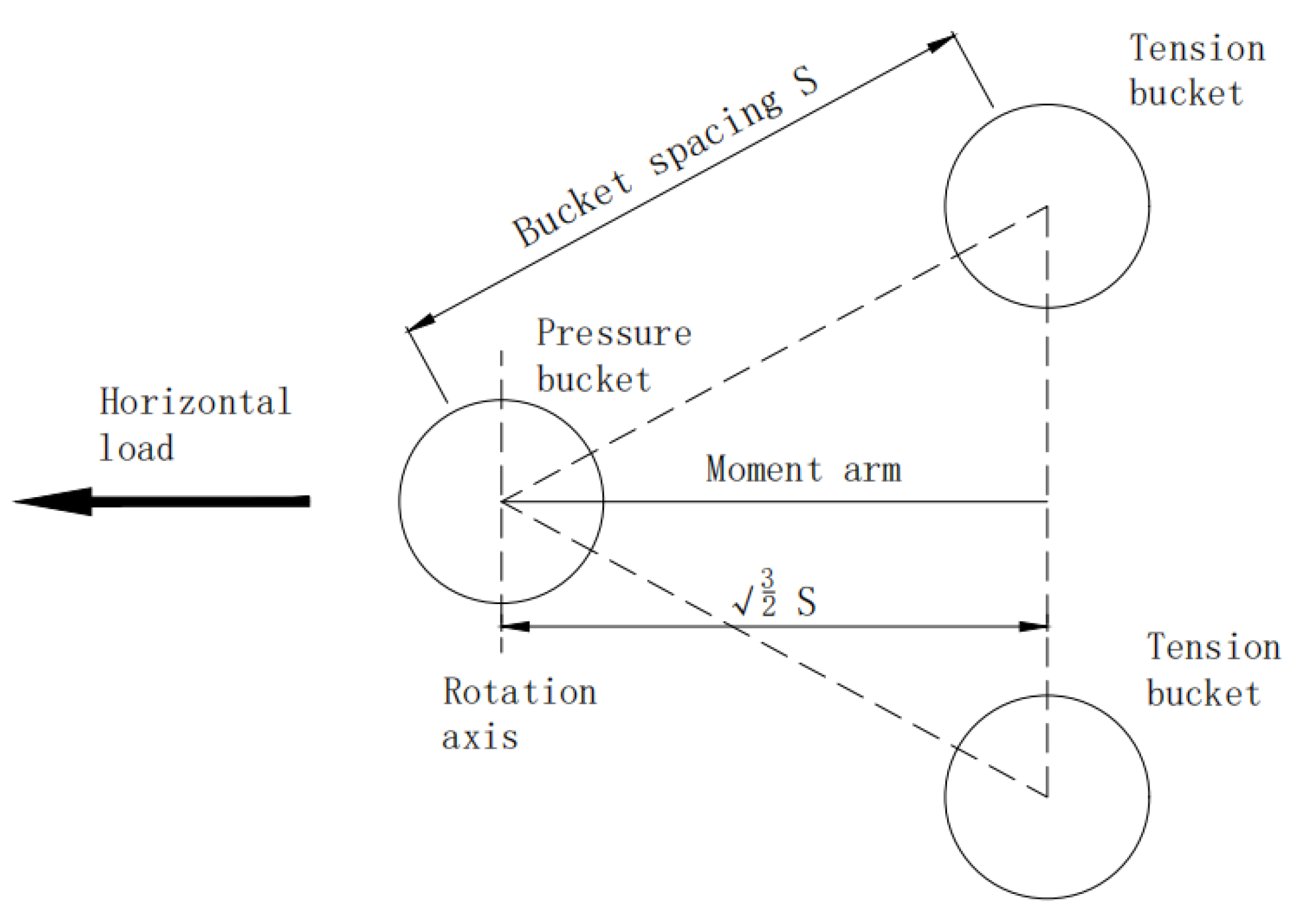
| Sand | Saturated Density γsat (kN/m3) | Natural Density γnat (kN/m3) | Friction Angel φ (°) | Poisson’s Ratio v |
| 19.6 | 15.9 | 35 | 0.26 | |
| Steel pipe | Modulus of elasticity Es (Mpa) | Unit weight γsteel (kN/m3) | Poisson’s Ratio v | |
| 2.06 × 105 | 78.5 | 0.31 | ||
| Model | Diameter (mm) | Length (mm) | Aspect Ratio L/D | Wall Thickness (mm) |
|---|---|---|---|---|
| 1 | 102 | 164.7 | 1.61 | 3 |
| 2 | 120 | 134 | 1.12 | 3 |
| 3 | 133 | 112.6 | 0.85 | 3 |
| L/D | Diameter (mm) | Deviation from the Axis (mm) | Ratio of Deviation Distance to Bucket Diameter (%) | Depth of the Rotation Center |
|---|---|---|---|---|
| 1.61 | 102 | 14.4 | 14.1 | 0.86 L |
| 1.12 | 120 | 16 | 13.3 | 0.97 L |
| 0.85 | 133 | 14 | 10.5 | >1 L |
| Test | D (mm) | V0(S) (N) | fM | M0_FE (N·cm) | M0_cal (N·cm) | Error (%) |
|---|---|---|---|---|---|---|
| 1 | 102 | 235.8 | 1.63 | 19,960 | 20,371 | 2.06 |
| 2 | 120 | 182.7 | 1.45 | 17,570 | 16,518 | 6.37 |
| 3 | 133 | 144 | 1.33 | 12,810 | 13,235 | 3.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, X.-L.; Sui, S.-H.; Hu, Z.-B.; Deng, W.-N.; Song, Q.-M. Bearing Characteristics of Tripod Bucket Foundation under Horizontal and Moment Load in Sand. J. Mar. Sci. Eng. 2023, 11, 1631. https://doi.org/10.3390/jmse11081631
Wang X, Zhao X-L, Sui S-H, Hu Z-B, Deng W-N, Song Q-M. Bearing Characteristics of Tripod Bucket Foundation under Horizontal and Moment Load in Sand. Journal of Marine Science and Engineering. 2023; 11(8):1631. https://doi.org/10.3390/jmse11081631
Chicago/Turabian StyleWang, Xin, Xue-Liang Zhao, Shu-Huan Sui, Zi-Bei Hu, Wen-Ni Deng, and Qi-Ming Song. 2023. "Bearing Characteristics of Tripod Bucket Foundation under Horizontal and Moment Load in Sand" Journal of Marine Science and Engineering 11, no. 8: 1631. https://doi.org/10.3390/jmse11081631
APA StyleWang, X., Zhao, X.-L., Sui, S.-H., Hu, Z.-B., Deng, W.-N., & Song, Q.-M. (2023). Bearing Characteristics of Tripod Bucket Foundation under Horizontal and Moment Load in Sand. Journal of Marine Science and Engineering, 11(8), 1631. https://doi.org/10.3390/jmse11081631






