A Hybrid Probabilistic Risk Analytical Approach to Ship Pilotage Risk Resonance with FRAM
Abstract
:1. Introduction
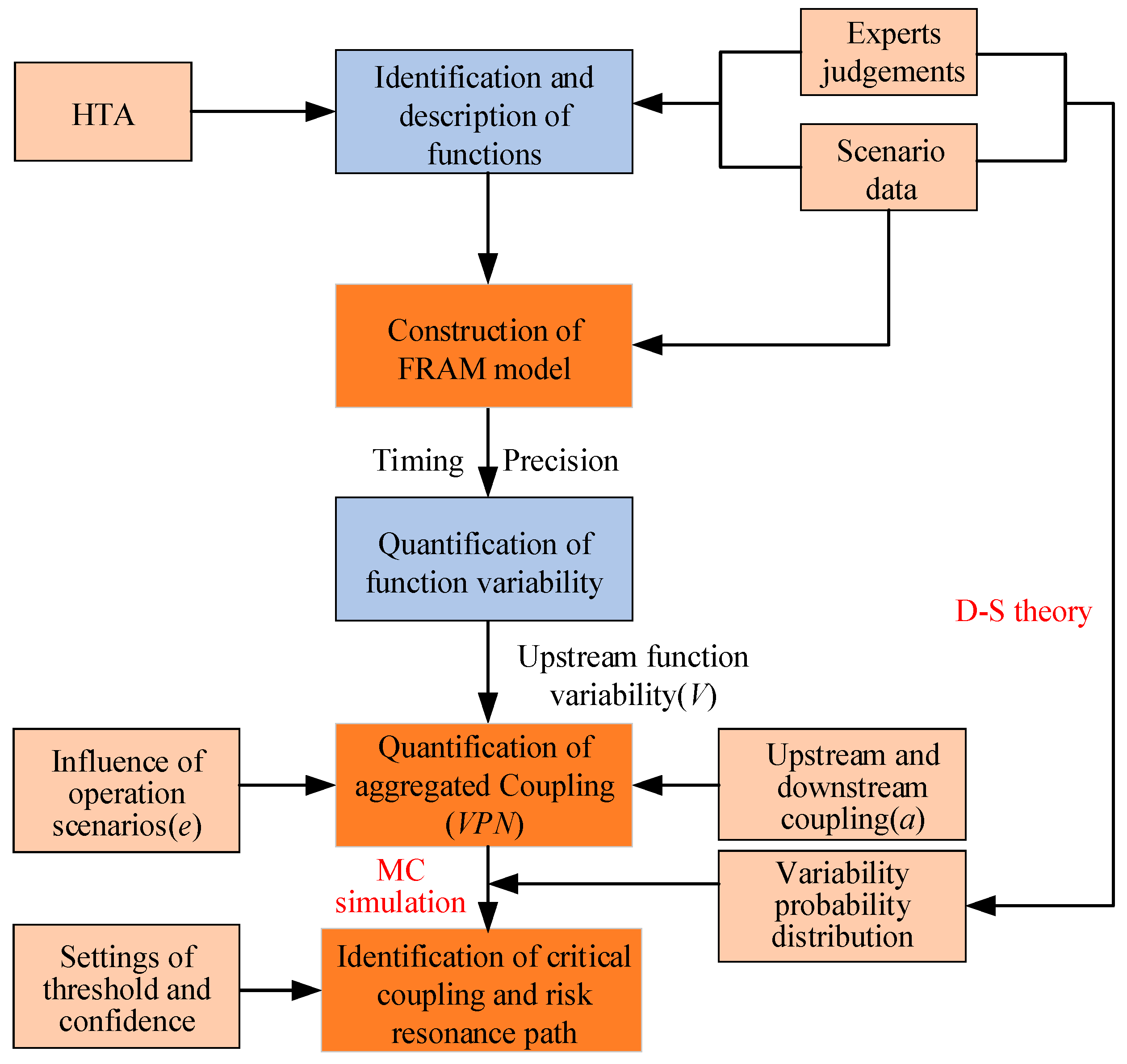
2. Methodology
2.1. Problem Description and Framework
2.1.1. Problem Description of Ship Pilotage Risk Resonance
2.1.2. A Hybrid Probabilistic Risk Analytical Approach
2.2. Modelling
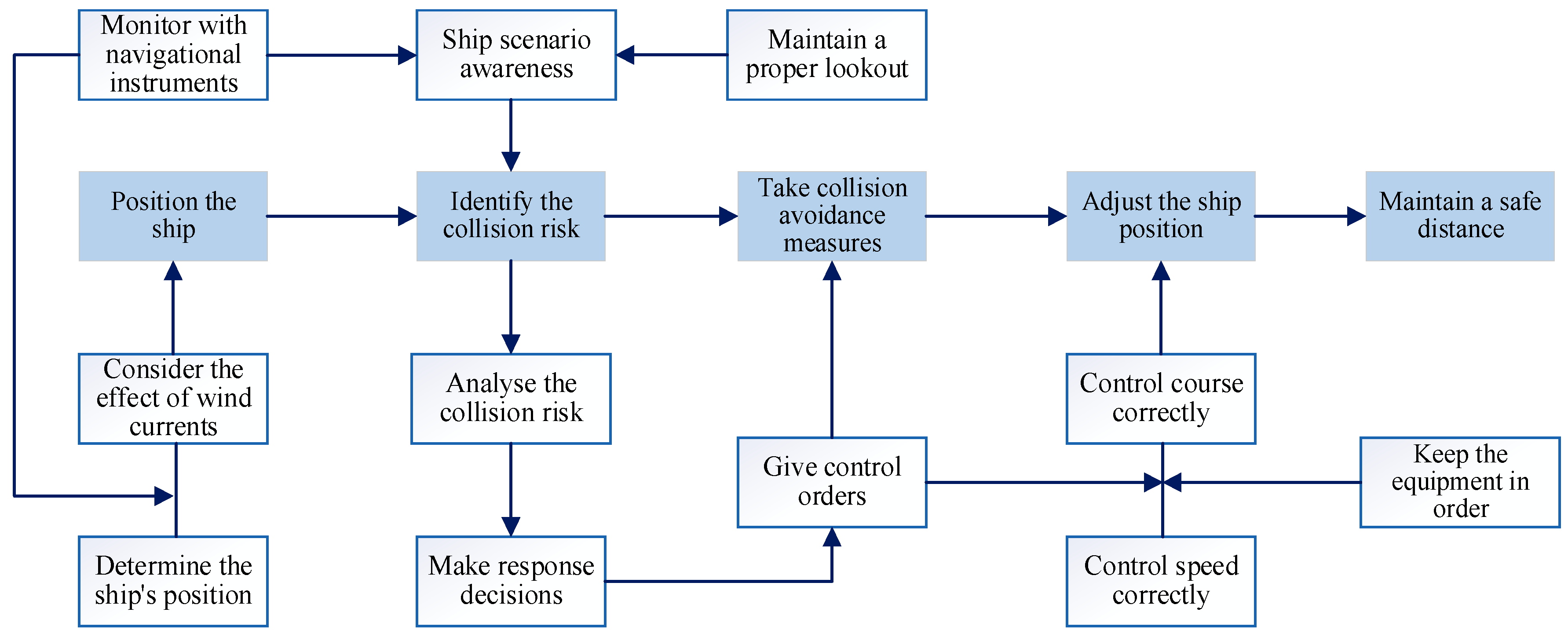
2.2.1. FRAM in Ship Pilotage Risk Resonance
2.2.2. Quantitative Analysis Method of Aggregated Coupling
Quantification of Function Output Variability
Quantification of Coupling Effects between Functions
Quantification the Influence of Operation Scenario
2.2.3. Monte Carlo Simulation
2.2.4. D–S Evidence Theory
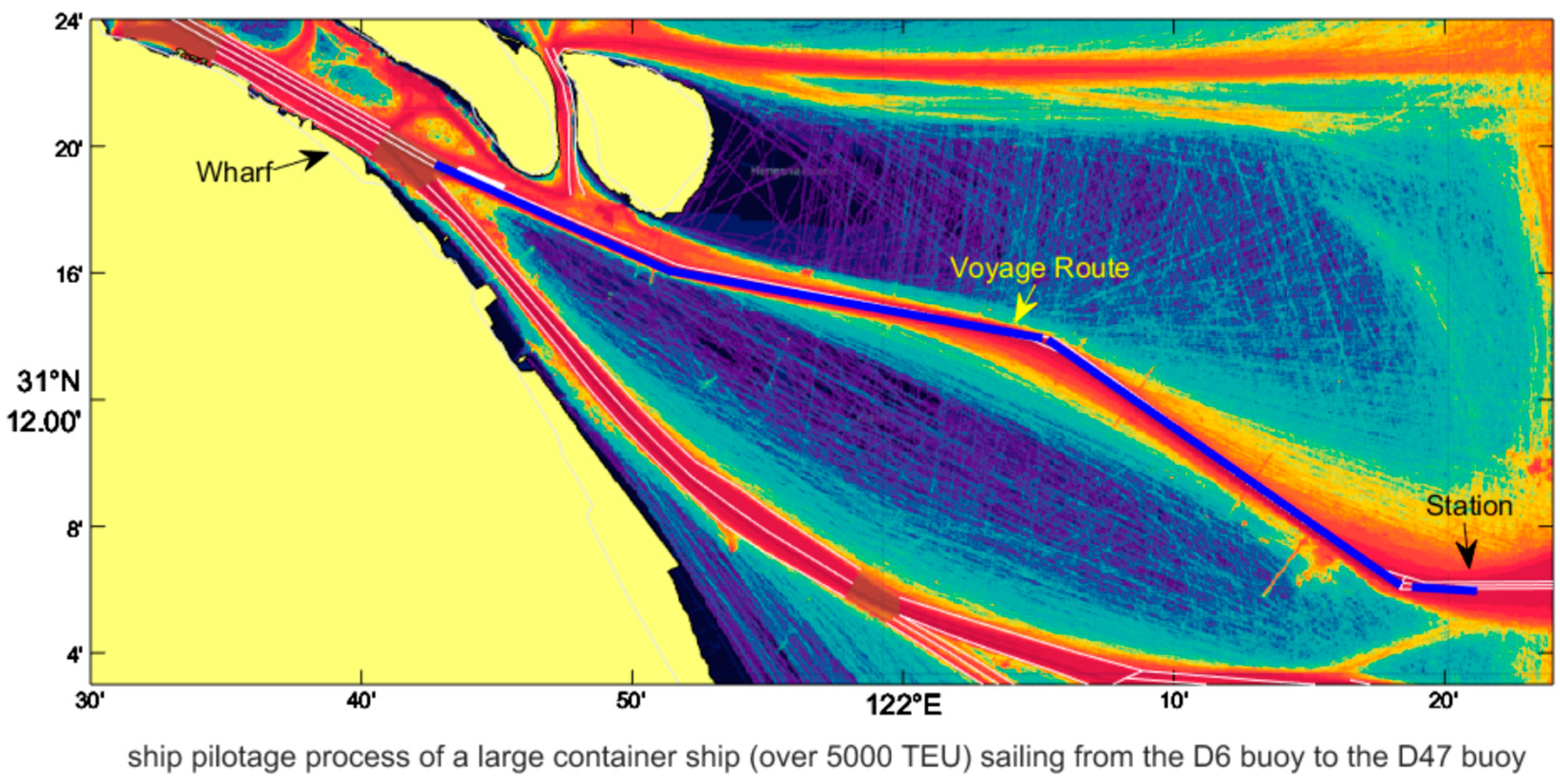
2.3. Scenario and Data
2.3.1. Scenario
2.3.2. Data
Quantification of Variability in Function Output
Quantification of Aggregated Coupling
3. Results
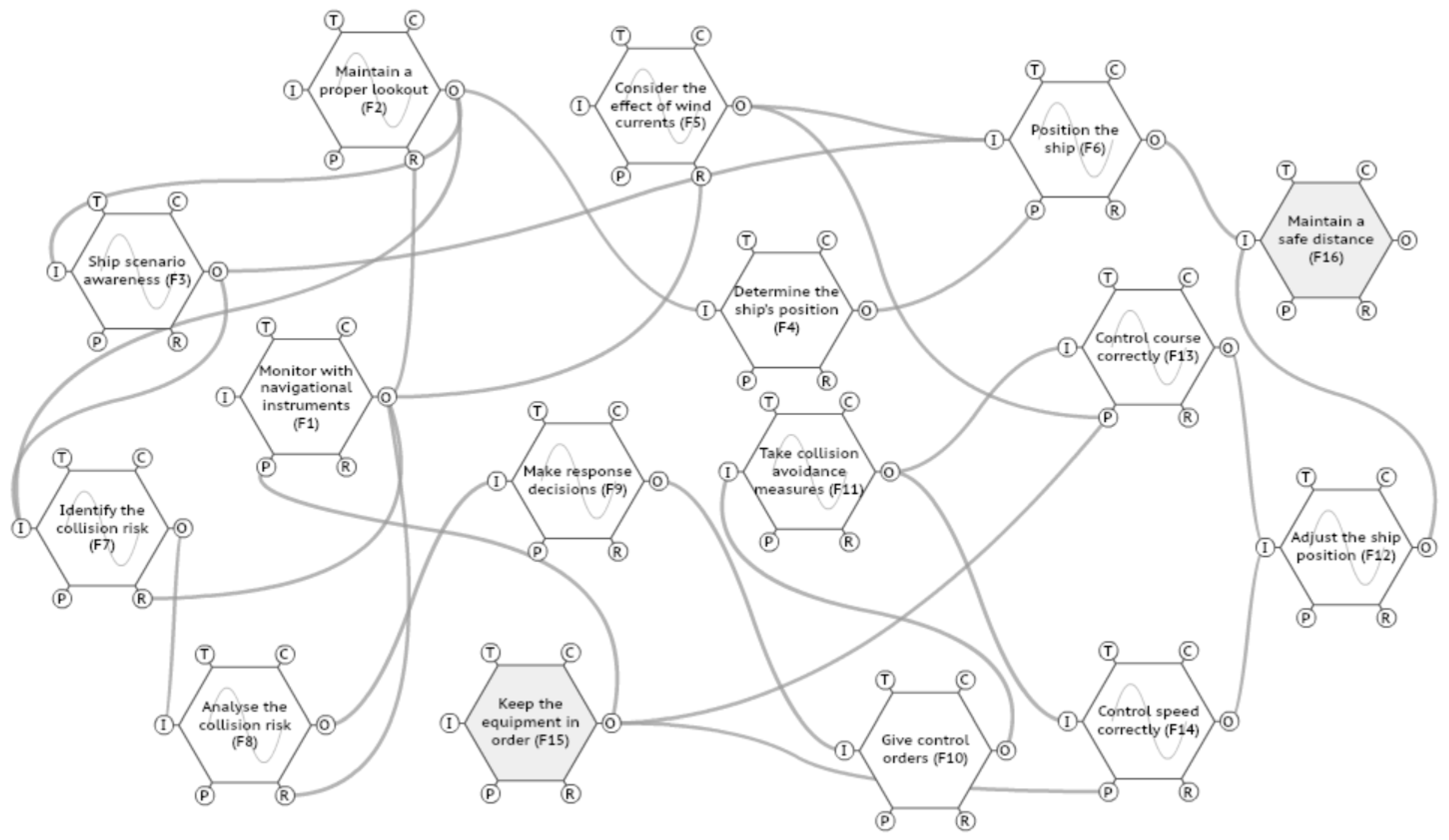
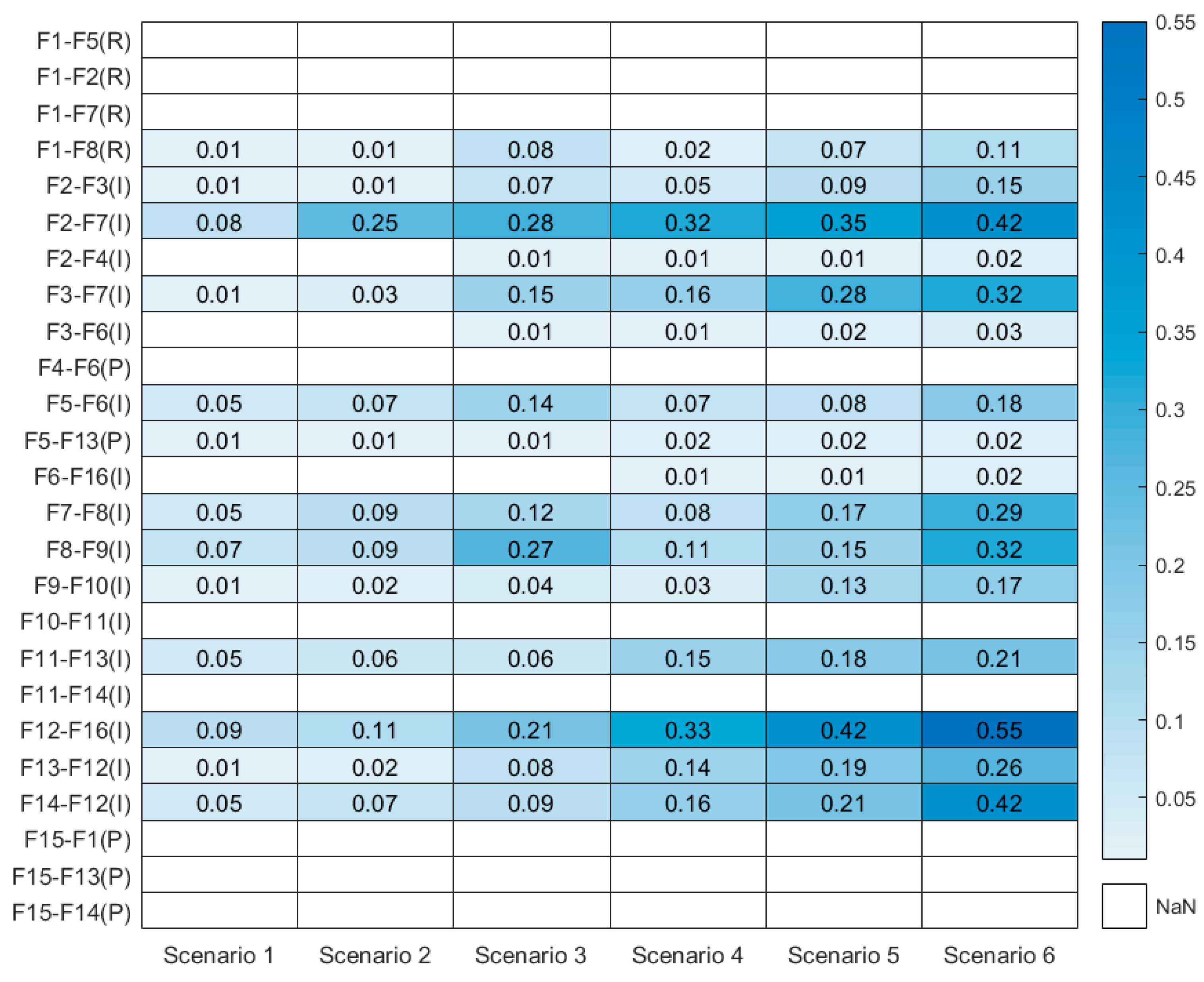
3.1. Quantification of Function Coupling of Ship Pilotage System
3.2. Risk Resonance Analysis in Ship Pilotage Process
3.2.1. Determination of Threshold and Identification of Critical Coupling
3.2.2. Analysis of Collision Risk Resonance during Ship Pilotage Process
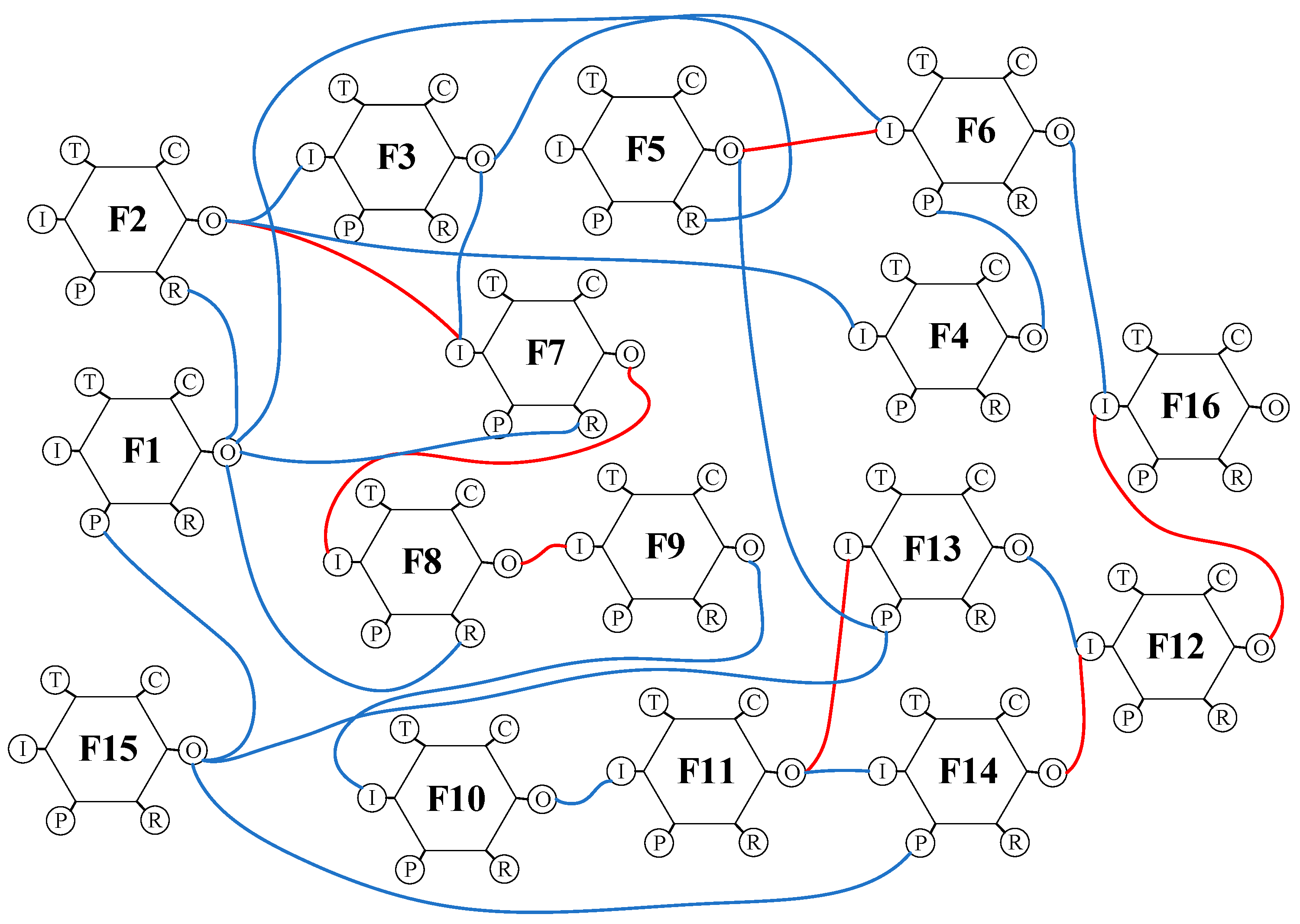
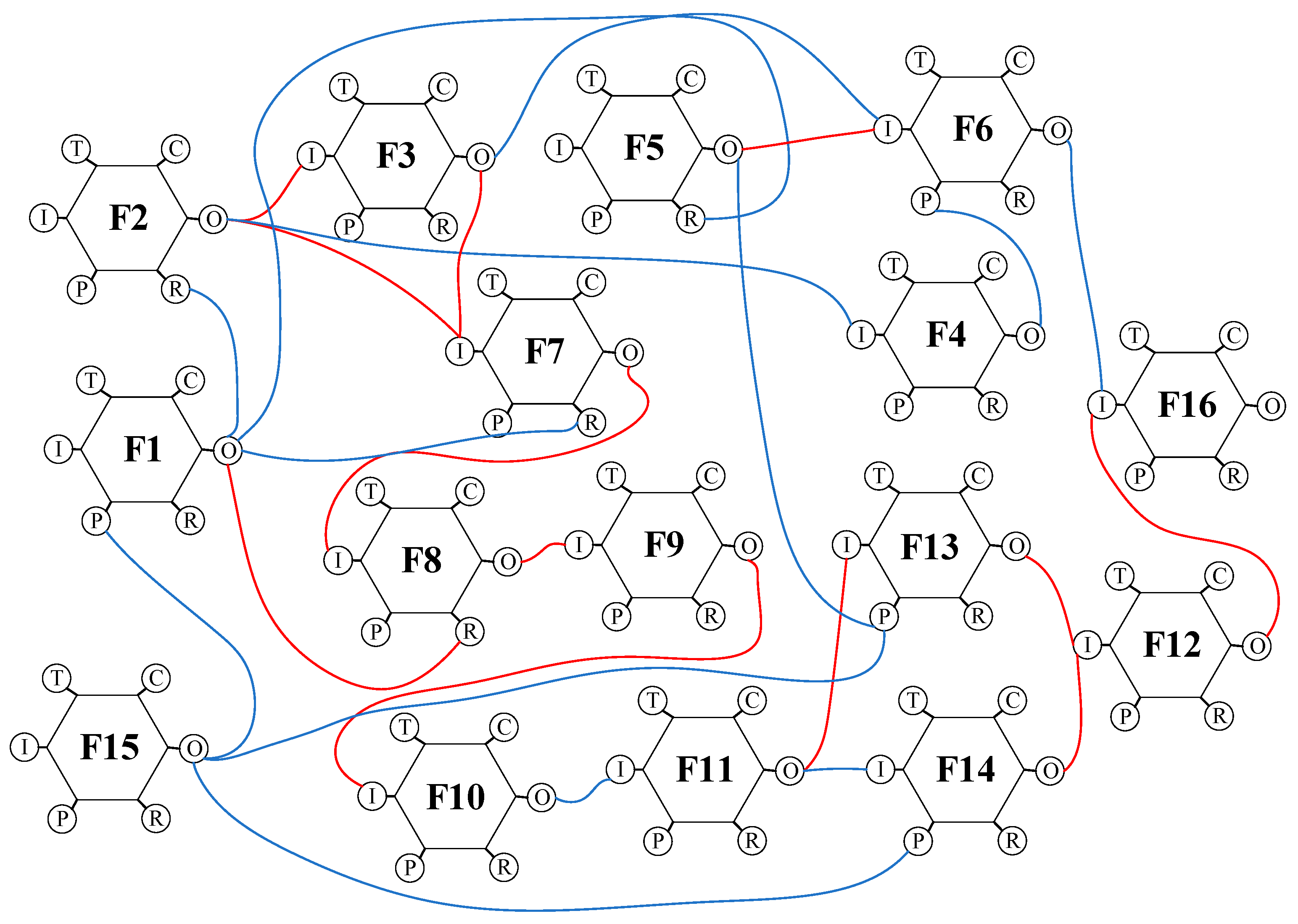
- There are seven critical couplings of the pilotage operation system in scenario 1 (Figure 7) that are relatively dispersed, indicating that the adverse output of some functions may be damped and weakened in the downstream functions. The probability of a collision accident risk arising from the system function resonance was low. In operation scenario 6, new critical couplings emerged in the pilotage system as the variability of traffic conditions, and pilot status increased. Hence, the number of critical couplings increased to twelve in Figure 8, and a relatively continuous function resonance path appeared, such as ‘F2-F7(I)-F8(I)-F9(I)-F10(I)’. In the pilotage operation scenario 6, the adverse output of the system functions was more likely to be transmitted through the function resonance path, causing system function resonance effects and increasing the risk of accidents.
- The comparative assessment between scenarios 1 and 6 further demonstrated the role of operation conditions in shaping system risks. The critical coupling ‘F2-F7(I)’ emerged as a consistent factor in both scenarios, emphasizing the significance of maintaining a proper lookout. In scenario 6, where complexities in traffic conditions prevailed, lookout negligence (‘F2-F3(I)’) became a critical coupling, showcasing the direct impact of operational challenges on risk factors. Moreover, the deterioration of the pilot status further reduced the ability to identify collision risk. Therefore, pilot and crews needed to strengthen their cooperation, fair usage of navigational instruments, and maintain a proper lookout during the entire pilotage process to identify collision risks in time [38].
- Furthermore, the study identified the necessity of combining ‘changing speed’ and ‘changing course’ methods during ship pilotage in narrow waters, as evidenced by the emergence of a new critical coupling (‘F13-F12(I)’) in scenario 6. This result underscored the alignment between MC simulation outcomes and real-world operational conditions, bolstering the method’s effectiveness. In conclusion, the study’s comparative analysis of different scenarios showcased the interplay between operational conditions and system risks, affirming the efficacy of the proposed quantitative FRAM approach. The findings provided valuable insights into collision risk management during ship pilotage operations and laid the groundwork for future studies focused on addressing real-world complexities and temporal risk evaluation.
- Critical coupling and function resonance paths were identified through a quantitative analysis of the coupling effects for different functions under different operation scenarios to analyse the transmission mechanism of system risks. This method indicated the causative mechanism of system risk from the perspective of the system operation mechanism, emphasising that strong coupling between system functions was the main reason for risk transmission and accidents. The coupling between system functions indicated the amplifying effect of risk transmission and the damping effect. Therefore, the focus of risk management differed from the previous concern about failure factors. However, this was to select appropriate monitoring indicators for the critical coupling and functions of the system, restrain the adverse output of the functions, and improve the ability of functions to address variability. Alternatively, introducing new system functions to manage critical functions could block a function’s resonance path.
- The operation conditions of a real ship pilotage process changed constantly as the ship moved. The ship pilotage system could be represented as a state vector that changed with time, and the state space of the system was determined by the function output and the coupling effect of the functions. Thus, the variability of the function output and the system risk in the ship pilotage process represented a temporal state transition.
4. Discussion
4.1. Analysis of Risk Resonance in Ship Pilotage Process
4.2. Analysis of FRAM Quantisation
4.3. Human Factors in Ship Collision Risk
4.4. The Uncertainty and Limitation Analysis of This Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.; Wang, H. Exploring the failure mechanism of container port logistics system based on multi-factor coupling. J. Mar. Sci. Eng. 2023, 11, 1067. [Google Scholar] [CrossRef]
- Wu, L.; Jia, S.; Wang, S. Pilotage planning in seaports. Eur. J. Oper. Res. 2020, 287, 90–105. [Google Scholar] [CrossRef]
- Basnet, S.; Bahootoroody, A.; Chaal, M.; Valdez Banda, O.A.; Lahtinen, J. A decisionmaking framework for selecting an MBSE language—A case study to ship pilotage. Exp. Syst. Appl. 2022, 193, 116451. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Xi, Y.; Hu, S.; Tang, L. Dynamics simulation of the risk coupling effect between maritime pilotage human factors under the HFACS framework. J. Mar. Sci. Eng. 2020, 8, 144. [Google Scholar] [CrossRef]
- Zhang, D.; Yan, X.; Yang, Z.; Wall, A.; Wang, J. Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze river. Reliab. Eng. Syst. Saf. 2013, 118, 93–105. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.; Mou, J.; Gelder, P. Probabilistic risk analysis for ship-ship collision: State-of-the-art. Saf. Sci. 2019, 117, 108–122. [Google Scholar] [CrossRef]
- Kujala, P.; Hanninen, M.; Arola, T.; Ylitalo, J. Analysis of the marine traffic safety in the Gulf of Finland. Reliab. Eng. Syst. Saf. 2009, 8, 1349–1357. [Google Scholar] [CrossRef]
- Fan, C.; Wróbel, K.; Montewka, J.; Gil, M.; Wan, C.; Zhang, D. A framework to identify factors influencing navigational risk for maritime autonomous surface ships. Ocean Eng. 2020, 202, 107188. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Goerlandt, F.; Yan, X.; Kujala, P. Use of HFACS and fault tree model for collision risk factors analysis of icebreaker assistance in ice-covered waters. Saf. Sci. 2019, 111, 128–143. [Google Scholar] [CrossRef]
- Yang, Z.; Abujaafar, K.M.; Qu, Z.; Wang, J.; Nazir, S.; Wan, C. Use of evidential reasoning for eliciting Bayesian subjective probabilities in human reliability analysis: A maritime case. Ocean Eng. 2019, 186, 106095. [Google Scholar] [CrossRef]
- Wu, B.; Yip, T.L.; Yan, X.; Soares, C.G. Review of techniques and challenges of human and organizational factors analysis in maritime transportation. Reliab. Eng. Syst. Saf. 2022, 219, 108249. [Google Scholar] [CrossRef]
- Chang, C.H.; Kontovas, C.; Yu, Q.; Yang, Z. Risk assessment of the operations of maritime autonomous surface ships. Reliab. Eng. Syst. Saf. 2021, 207, 107324. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, P.; Wu, B.; Wan, C.; Yang, Z. A trustable architecture over blockchain to facilitate maritime administration for MASS systems. Reliab. Eng. Syst. Saf. 2022, 219, 108246. [Google Scholar] [CrossRef]
- Yu, Q.; Teixeira, Â.P.; Liu, K.; Rong, H.; Soares, C.G. An integrated dynamic ship risk model based on Bayesian networks and evidential reasoning. Reliab. Eng. Syst. Saf. 2021, 216, 107993. [Google Scholar] [CrossRef]
- Gil, M.; Kozioł, P.; Wróbel, K.; Montewka, J. Know your safety indicator–A determination of merchant vessels bow crossing range based on big data analytics. Reliab. Eng. Syst. Saf. 2022, 220, 108311. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, D.; Montewka, J.; Yan, X.; Zio, E. Towards a probabilistic model for predicting ship besetting in ice in Arctic waters. Reliab. Eng. Syst. Saf. 2016, 155, 124–136. [Google Scholar] [CrossRef]
- Khan, B.; Khan, F.; Veitch, B. A dynamic Bayesian network model for ship-ice collision risk in the Arctic waters. Saf. Sci. 2020, 130, 104858. [Google Scholar] [CrossRef]
- Baksh, A.; Abbassi, R.; Garaniya, V.; Khan, F. Marine transportation risk assessment using Bayesian network: Application to Arctic waters. Ocean. Eng. 2018, 159, 422–436. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, K.; Yang, Z.; Wang, H.; Yang, Z. Geometrical risk evaluation of the collisions between ships and offshore installations using rule-based Bayesian reasoning. Reliab. Eng. Syst. Saf. 2021, 210, 107474. [Google Scholar] [CrossRef]
- Xi, Y.; Yang, Z.; Fang, Q.; Chen, W.; Wang, J. A new hybrid approach to human error probability quantification–applications in maritime operations. Ocean Eng. 2017, 138, 45–54. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, C.; Guo, W.; Dai, J.; Zhao, Z. Systems theoretic accident model and process (STAMP): A literature review. Saf. Sci. 2022, 152, 105596. [Google Scholar] [CrossRef]
- Salihoglu, E.; Beşikçi, E. The use of Functional Resonance Analysis Method (FRAM) in a maritime accident: A case study of Prestige. Ocean Eng. 2021, 219, 108223. [Google Scholar] [CrossRef]
- Hollnagel, E. Barriers and Accident Prevention; Ashgate Publishing: Aldershot, UK, 2004. [Google Scholar]
- De Carvalho, P.V.R. The use of Functional Resonance Analysis Method (FRAM) in a mid-air collision to understand some characteristics of the air traffic management system resilience. Reliab. Eng. Syst. Saf. 2011, 96, 1482–1498. [Google Scholar] [CrossRef]
- Patriarca, R.; Di Gravio, G.; Woltjer, R.; Costantino, F.; Praetorius, G.; Ferreira, P.; Hollnagel, E. Framing the FRAM: A literature review on the functional resonance analysis method. Saf. Sci. 2020, 129, 104827. [Google Scholar] [CrossRef]
- Saldanha, M.C.W.; Carvalho, R.J.M.; Arcuri, R.; Amorim, A.G.; Vidal, M.C.R.; Carvalho, P.V.R. Understanding and improving safety in artisanal fishing: A safety-II approach in raft fishing. Saf. Sci. 2020, 122, 104522. [Google Scholar] [CrossRef]
- Patriarca, R.; Gravio, G.D.; Costantino, F. A Monte Carlo evolution of the Functional Resonance Analysis Method (FRAM) to assess performance variability in complex systems. Saf. Sci. 2017, 91, 49–60. [Google Scholar] [CrossRef]
- Kaya, G.K.; Ozturk, F.; Sariguzel, E.E. System-based risk analysis in a tram operating system: Integrating Monte Carlo simulation with the functional resonance analysis method. Reliab. Eng. Syst. Saf. 2021, 215, 107835. [Google Scholar] [CrossRef]
- Yu, M.; Erraguntla, M.; Quddus, N.; Kravaris, C. A data-driven approach of quantifying function couplings and identifying paths towards emerging hazards in complex systems. Process Saf. Environ. Prot. 2021, 150, 464–477. [Google Scholar] [CrossRef]
- Zinetullina, A.; Yang, M.; Khakzad, N.; Golman, B.; Li, X. Quantitative resilience assessment of chemical process systems using functional resonance analysis method and dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2021, 205, 107232. [Google Scholar] [CrossRef]
- Shepherd, A. Hierarchial Task Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hollnagel, E. FRAM: The Functional Resonance Analysis Method Modelling Complex Socio-Technical Systems; Ashgate: Surrey, UK, 2012. [Google Scholar]
- Kaya, G.K.; Ovali, H.F.; Ozturk, F. Using the functional resonance analysis method on the drug administration process to assess performance variability. Saf. Sci. 2019, 118, 835–840. [Google Scholar] [CrossRef]
- Palluotto, L.; Dumont, N.; Rodrigues, P.; Gicquel, O.; Vicquelin, R. Assessment of randomized Quasi-Monte Carlo method efficiency in radiative heat transfer simulations. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106570. [Google Scholar] [CrossRef]
- Gong, Y.; Su, X.; Qian, H.; Yang, N. Research on fault diagnosis methods for the reactor coolant system of nuclear power plant based on D-S evidence theory. Ann. Nucl. Energy. 2018, 112, 395–399. [Google Scholar] [CrossRef]
- Li, B.; Pang, F.W. An approach of vessel collision risk assessment based on the D-S evidence theory. Ocean Eng. 2013, 74, 16–21. [Google Scholar] [CrossRef]
- Fu, S.; Yu, Y.; Chen, J.; Han, B.; Wu, Z. Towards a probabilistic approach for risk analysis of nuclear-powered icebreakers using FMEA and FRAM. Ocean Eng. 2022, 260, 112041. [Google Scholar] [CrossRef]
- Guo, Y.; Jin, Y.; Hu, S.; Yang, Z.; Xi, Y.; Han, B. Risk evolution analysis of ship pilotage operation by an integrated model of FRAM and DBN. Reliab. Eng. Syst. Saf. 2023, 229, 108850. [Google Scholar] [CrossRef]
- Huang, W.; Yin, D.; Xu, Y.; Zhang, R.; Xu, M. Using N-K Model to quantitatively calculate the variability in Functional Resonance Analysis Method. Reliab. Eng. Syst. Saf. 2022, 217, 108058. [Google Scholar] [CrossRef]
- Hirose, T.; Sawaragi, T. Extended FRAM model based on cellular automaton to clarify complexity of socio-technical systems and improve their safety. Saf. Sci. 2020, 123, 104556. [Google Scholar] [CrossRef]
- Uddin, M.I.; Awal, Z.I. Systems-theoretic approach to safety of inland passenger ship operation in Bangladesh. Saf. Sci. 2020, 126, 104629. [Google Scholar] [CrossRef]
- Guo, X.; Ji, J.; Khan, F.; Ding, L.; Tong, Q. A novel fuzzy dynamic Bayesian network for dynamic risk assessment and uncertainty propagation quantification in uncertainty environment. Saf. Sci. 2021, 141, 105285. [Google Scholar] [CrossRef]

| Pilotage Scenarios | SPC1 | SPC2 | SPC3 | SPC4 |
|---|---|---|---|---|
| Scenario 1 | 1 | 2 | 1 | 1 |
| Scenario 2 | 1 | 2 | 2 | 1 |
| Scenario 3 | 1 | 2 | 4 | 1 |
| Scenario 4 | 4 | 2 | 1 | 1 |
| Scenario 5 | 4 | 2 | 2 | 1 |
| Scenario 6 | 4 | 2 | 4 | 1 |
| Aspects | Variability | Value | Aspects | Variability | Value |
|---|---|---|---|---|---|
| Timing | On time | 1 | Precision | Precise | 1 |
| Too early | 2 | Acceptable | 2 | ||
| Too late | 3 | Imprecise | 3 | ||
| Not at all | 4 | Wrong | 4 |
| Variability | Technical | Human | Organisational |
|---|---|---|---|
| On time | 0.8 | 0.6 | 0.7 |
| Too early | 0.05 | 0.15 | 0.1 |
| Too late | 0.1 | 0.2 | 0.1 |
| Not at all | 0.05 | 0.05 | 0.1 |
| Precise | 0.85 | 0.2 | 0.25 |
| Acceptable | 0.1 | 0.5 | 0.45 |
| Imprecise | 0.04 | 0.2 | 0.25 |
| Wrong | 0.01 | 0.1 | 0.05 |
| Functions | SPC1 | SPC2 | SPC3 | SPC4 |
|---|---|---|---|---|
| Monitor with navigational instruments (F1) | 0 | 0 | 0.5 | 1 |
| Maintain a proper lookout (F2) | 1 | 0.5 | 1 | 0 |
| Ship scenario awareness (F3) | 1 | 0.5 | 1 | 0.5 |
| Determine the ship’s position (F4) | 0 | 1 | 0.5 | 0 |
| Consider the effect of wind currents (F5) | 0 | 1 | 0.5 | 0.5 |
| Position the ship (F6) | 0.5 | 1 | 1 | 0.5 |
| Identify the collision risk (F7) | 1 | 0.5 | 1 | 0 |
| Analyse the collision risk (F8) | 0.5 | 0 | 1 | 0 |
| Make response decisions (F9) | 0.5 | 0.5 | 1 | 0 |
| Give control orders (F10) | 1 | 0.5 | 0.5 | 0 |
| Take collision avoidance measures (F11) | 0 | 1 | 0.5 | 1 |
| Adjust the ship position (F12) | 0 | 0.5 | 0 | 1 |
| Control course correctly (F13) | 0 | 0.5 | 0.5 | 1 |
| Control speed correctly (F14) | 0 | 0.5 | 0.5 | 1 |
| Keep the equipment in order (F15) | 0 | 0 | 0.5 | 1 |
| Maintain a safe distance (F16) | 0.5 | 0.5 | 1 | 0.5 |
| NO | Institutions | Education | Age | Experience | Gender |
|---|---|---|---|---|---|
| 1 | Maritime Safety Administration | Master degree | 35 | As a Wusong VTS officer of Shanghai MSA, he has 8 years of experience in ship safety supervision in the studied waters. | Male |
| 2 | Pilot station | Bachelor degree | 48 | As a senior pilot at Shanghai pilot station, he has extensive experience piloting large container ships in the studied waters. | Male |
| 3 | Shipping company | Bachelor degree | 52 | As a captain of a large container ship, he steered the ship through the studied waters at least 10 times. | Male |
| 4 | Pilot station | Bachelor degree | 46 | As an officer of Shanghai Pilot Station, he has rich pilotage experience and participated in formulating pilotage operation plans. | Male |
| 5 | Maritime University | Doctoral degree | 49 | As a professor at Maritime University, he has more than 10 years of research experience in ship pilotage safety. | Male |
| Variability | Benchmark | SME 1 | SME 2 | SME 3 | SME 4 | SME 5 | Fused Probability |
|---|---|---|---|---|---|---|---|
| On time | 0.60 | 0.50 | 0.30 | 0.65 | 0.25 | 0.10 | 0.63 |
| Too early | 0.15 | 0.05 | 0.25 | 0.15 | 0.35 | 0.55 | 0.09 |
| Too late | 0.20 | 0.30 | 0.35 | 0.15 | 0.25 | 0.20 | 0.27 |
| Not at all | 0.05 | 0.15 | 0.10 | 0.05 | 0.15 | 0.15 | 0.01 |
| Upstream Functions | Downstream Functions | Probability Distribution of Upstream Function Output | Amplifying Factors | ||||
|---|---|---|---|---|---|---|---|
| Symbol | Output | Symbol | Aspect | ||||
| F2 | Encounter situation | F3 | Input | 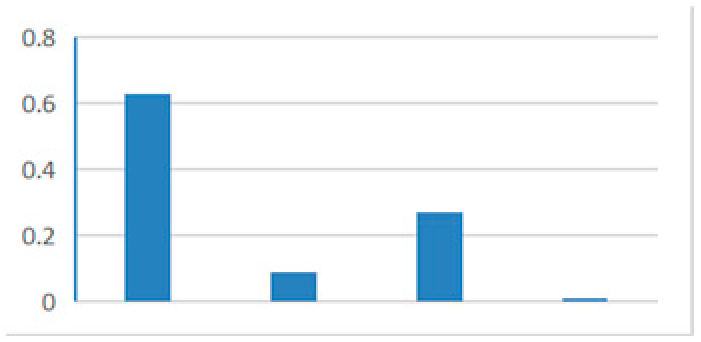 | 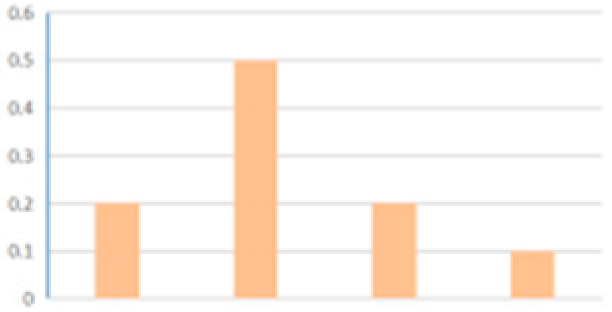 | 1 | 0.5 |
| F1 | Ship’s movement | F7 | Resource | 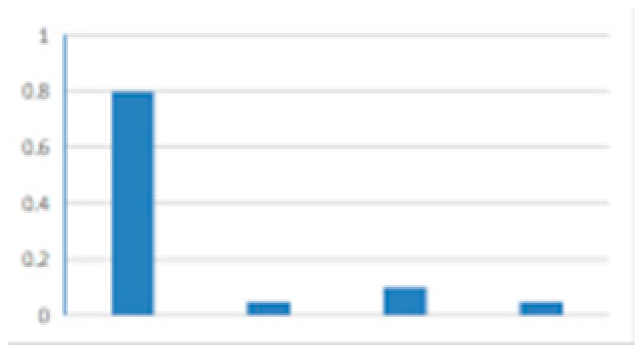 | 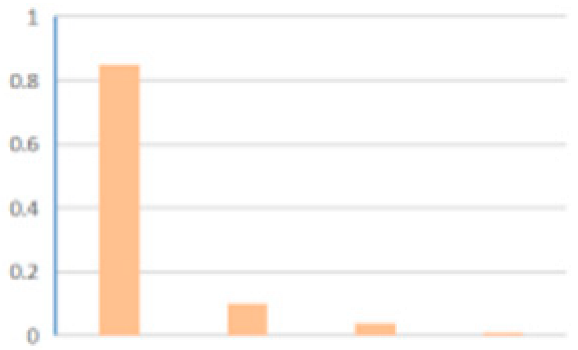 | 0.5 | 0.5 |
| F11 | Steer by order | F13 | Input | 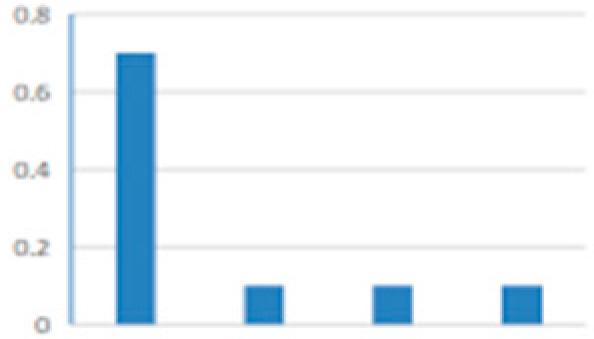 |  | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Hu, S.; Jin, Y.; Xi, Y.; Li, W. A Hybrid Probabilistic Risk Analytical Approach to Ship Pilotage Risk Resonance with FRAM. J. Mar. Sci. Eng. 2023, 11, 1705. https://doi.org/10.3390/jmse11091705
Guo Y, Hu S, Jin Y, Xi Y, Li W. A Hybrid Probabilistic Risk Analytical Approach to Ship Pilotage Risk Resonance with FRAM. Journal of Marine Science and Engineering. 2023; 11(9):1705. https://doi.org/10.3390/jmse11091705
Chicago/Turabian StyleGuo, Yunlong, Shenping Hu, Yongxing Jin, Yongtao Xi, and Wei Li. 2023. "A Hybrid Probabilistic Risk Analytical Approach to Ship Pilotage Risk Resonance with FRAM" Journal of Marine Science and Engineering 11, no. 9: 1705. https://doi.org/10.3390/jmse11091705
APA StyleGuo, Y., Hu, S., Jin, Y., Xi, Y., & Li, W. (2023). A Hybrid Probabilistic Risk Analytical Approach to Ship Pilotage Risk Resonance with FRAM. Journal of Marine Science and Engineering, 11(9), 1705. https://doi.org/10.3390/jmse11091705









