Numerical Investigation of Global Ice Loads of Maneuvering Captive Motion in Ice Floe Fields
Abstract
:1. Introduction
2. Numerical Model of Ship Motion in Ice Floe Field
2.1. The Governing Equation of DEM
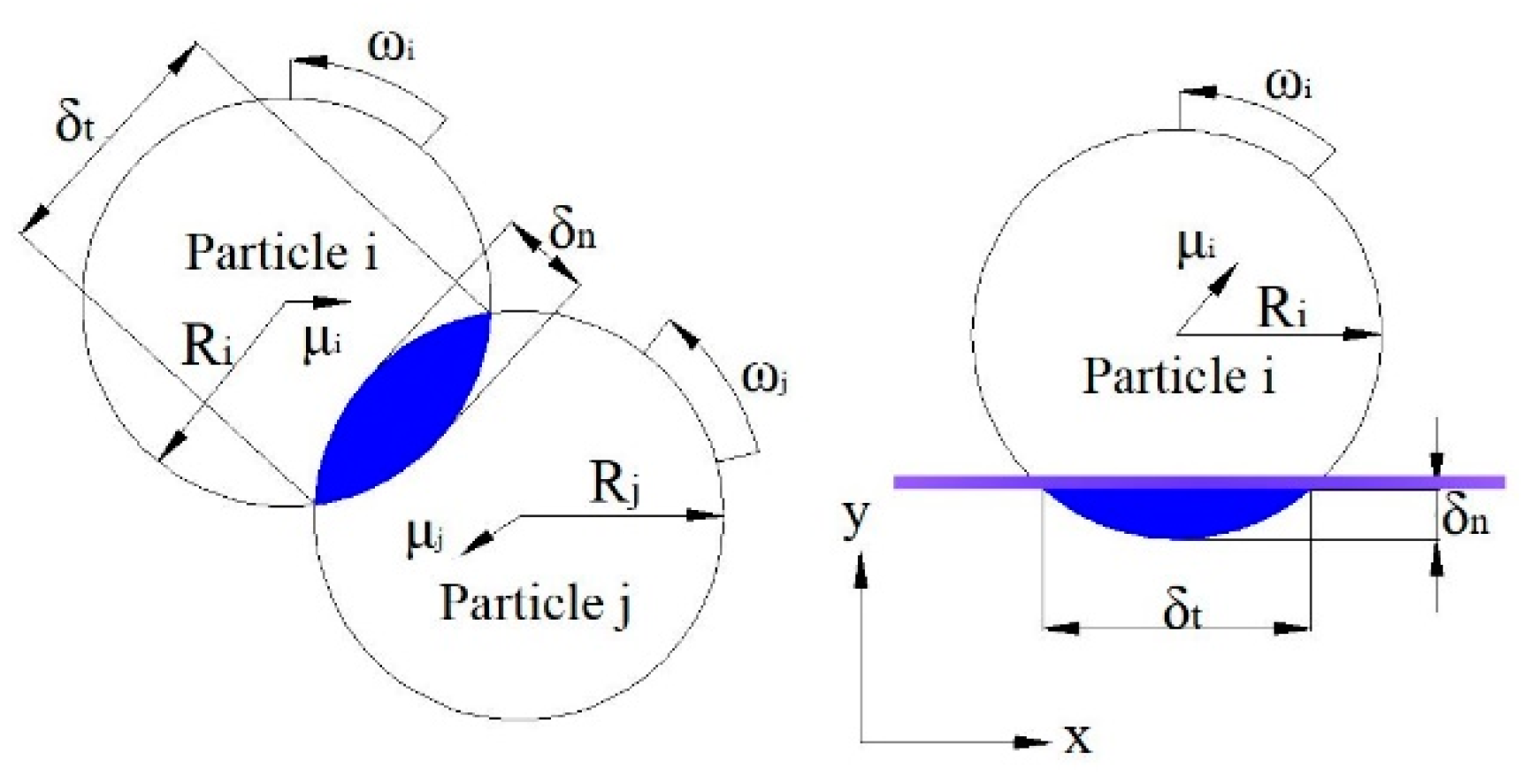
2.2. Interactions of Floe–Floe and Hull–Floe
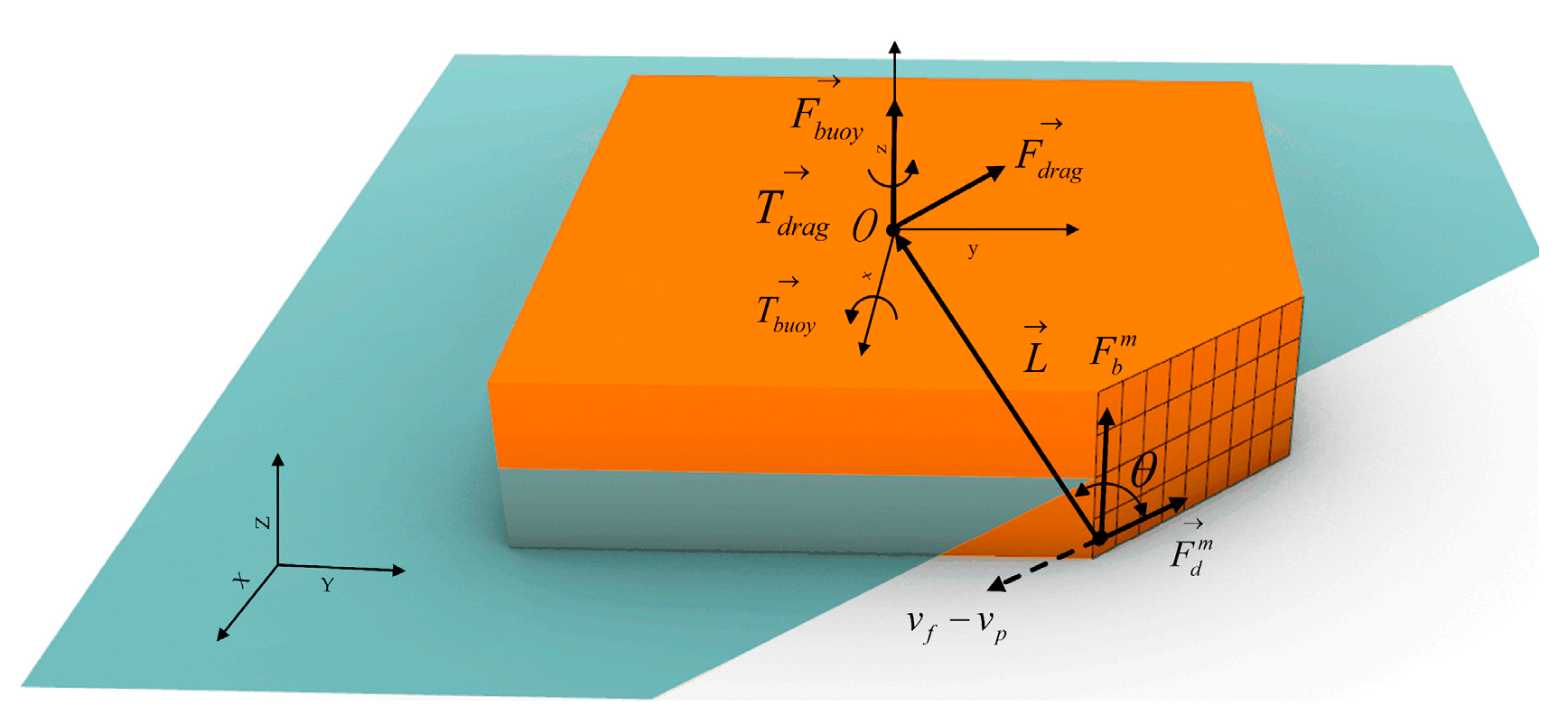
2.3. Interaction of Water–Ice Floe
2.4. DEM Ice Floe Fields
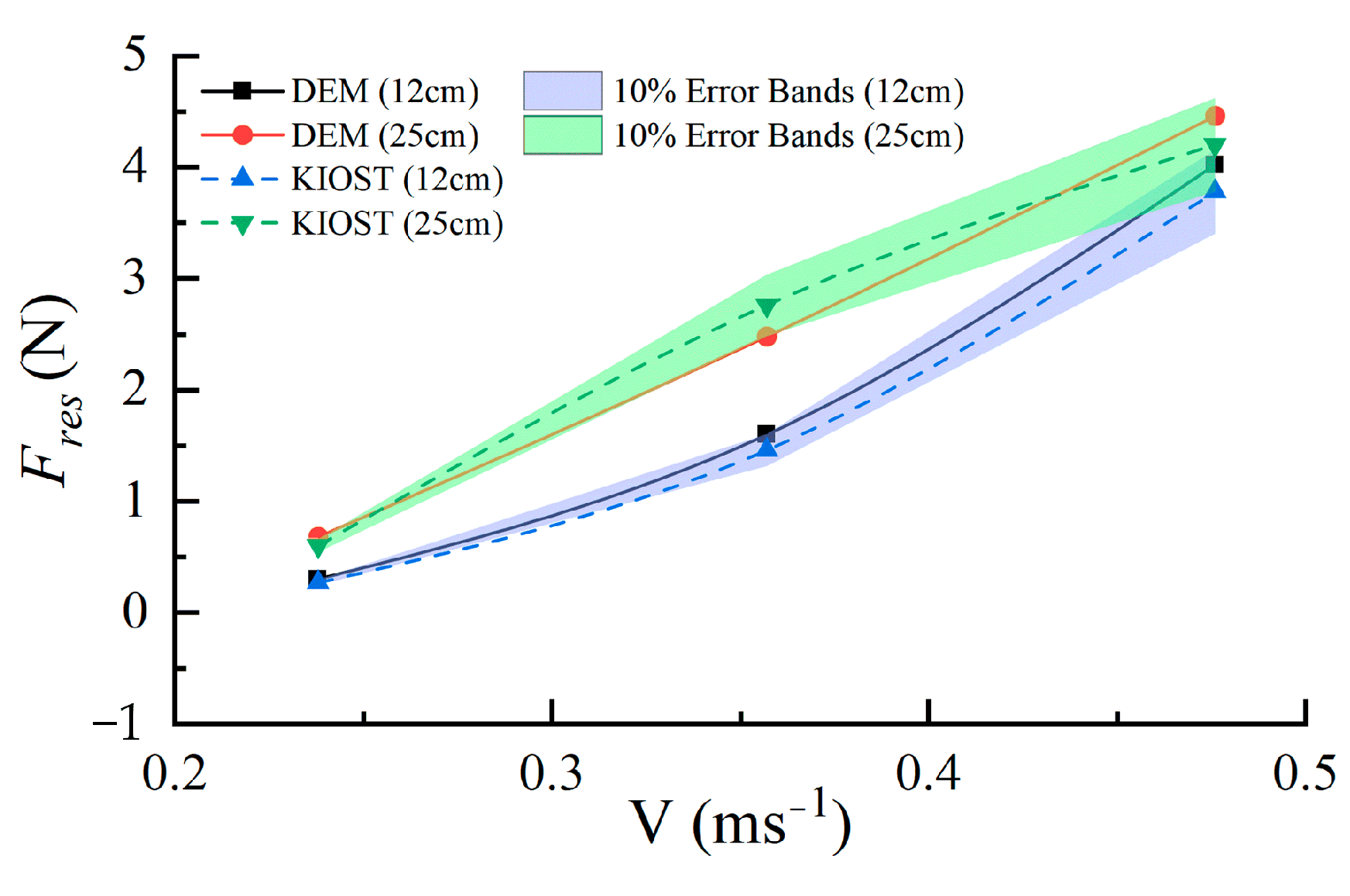
2.5. Validation
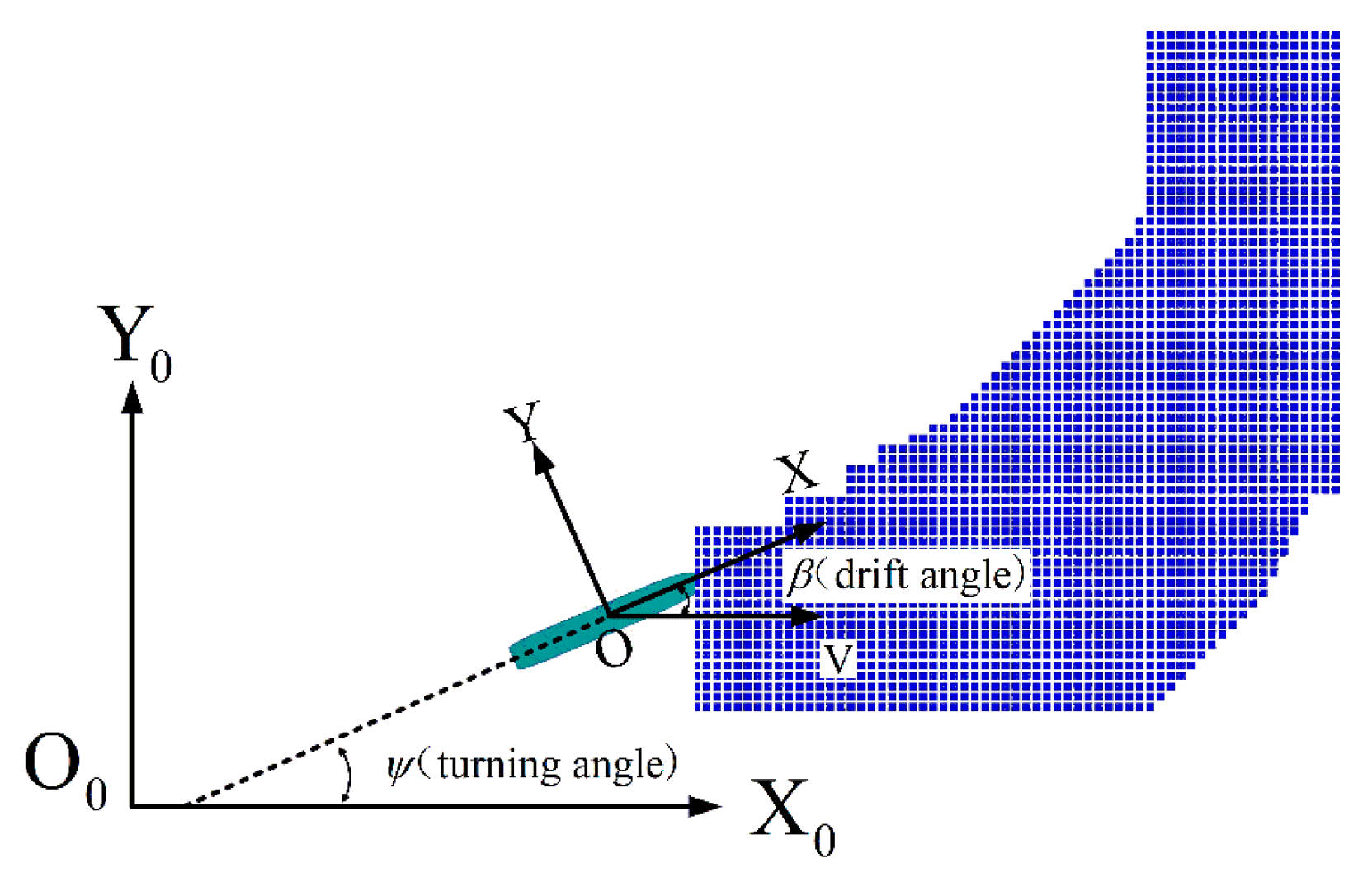
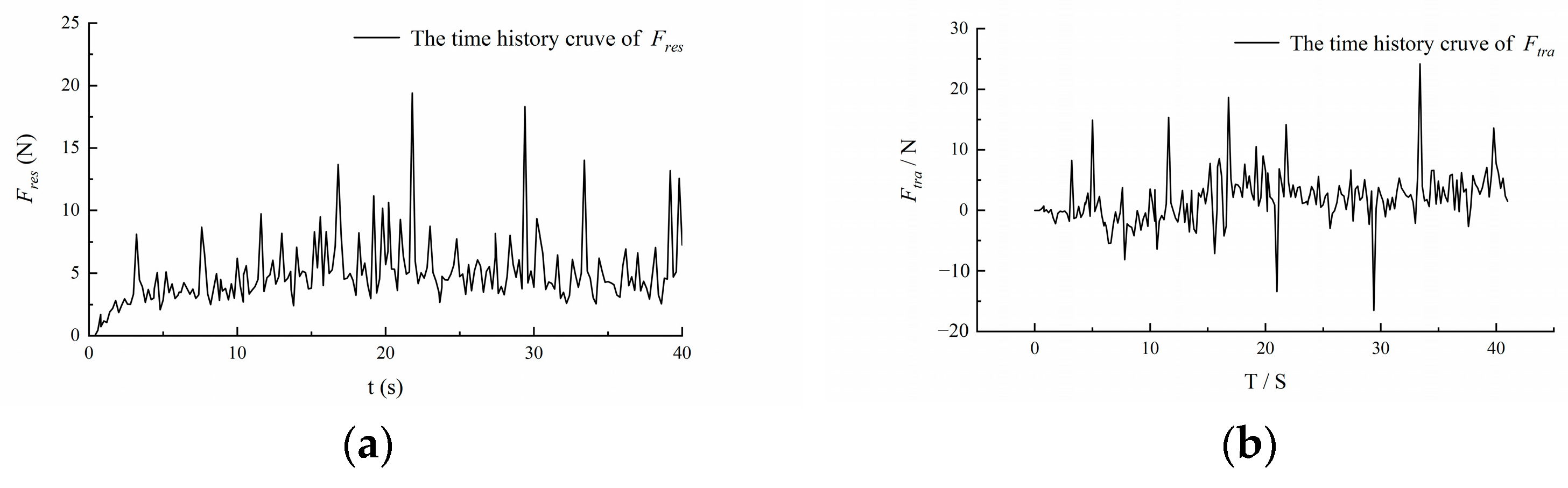
3. Numerical Simulation of Constant Turning Motions: Turning Radius and Drift Angle
3.1. Analysis of the Steady Turning Motion
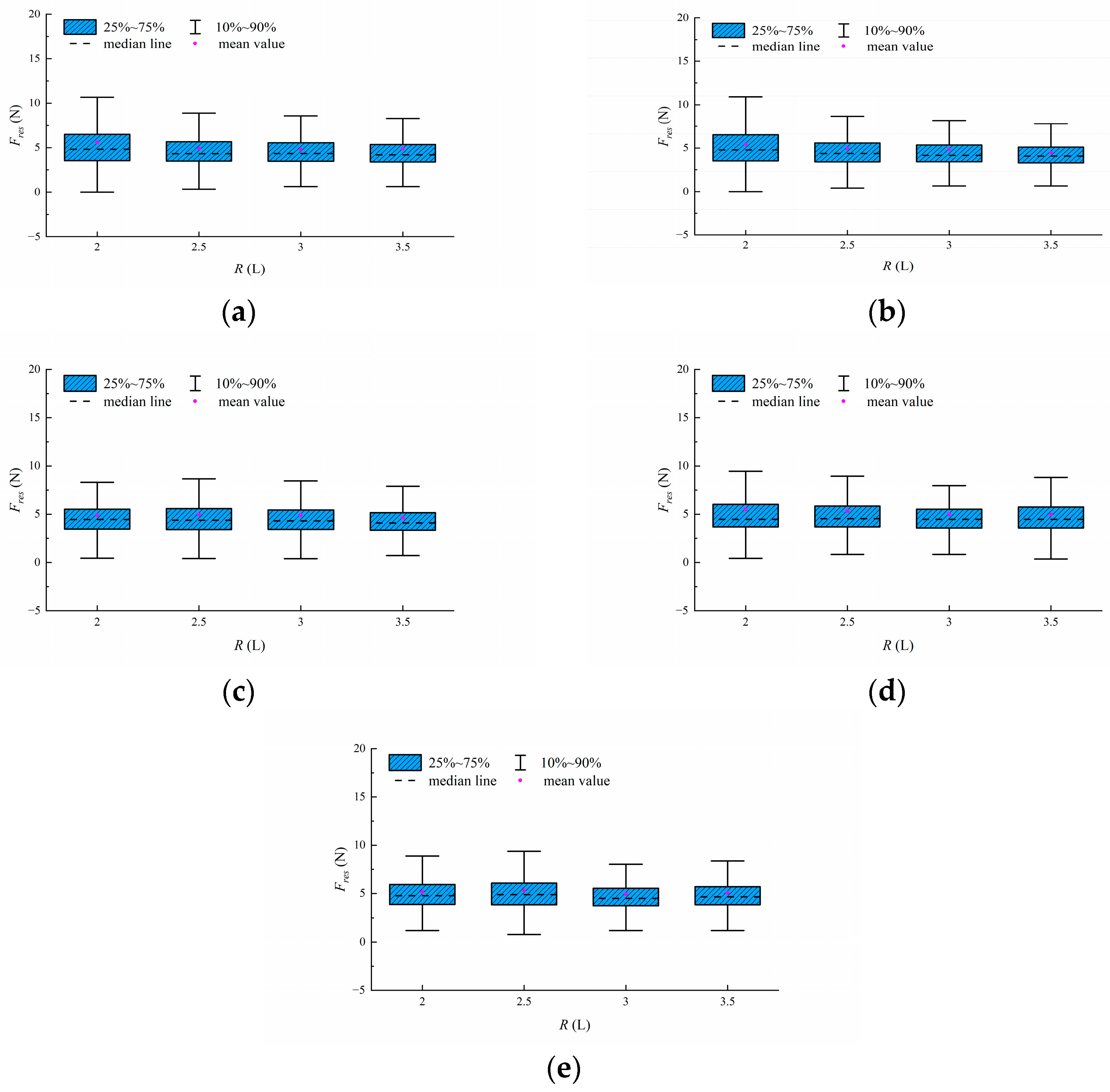
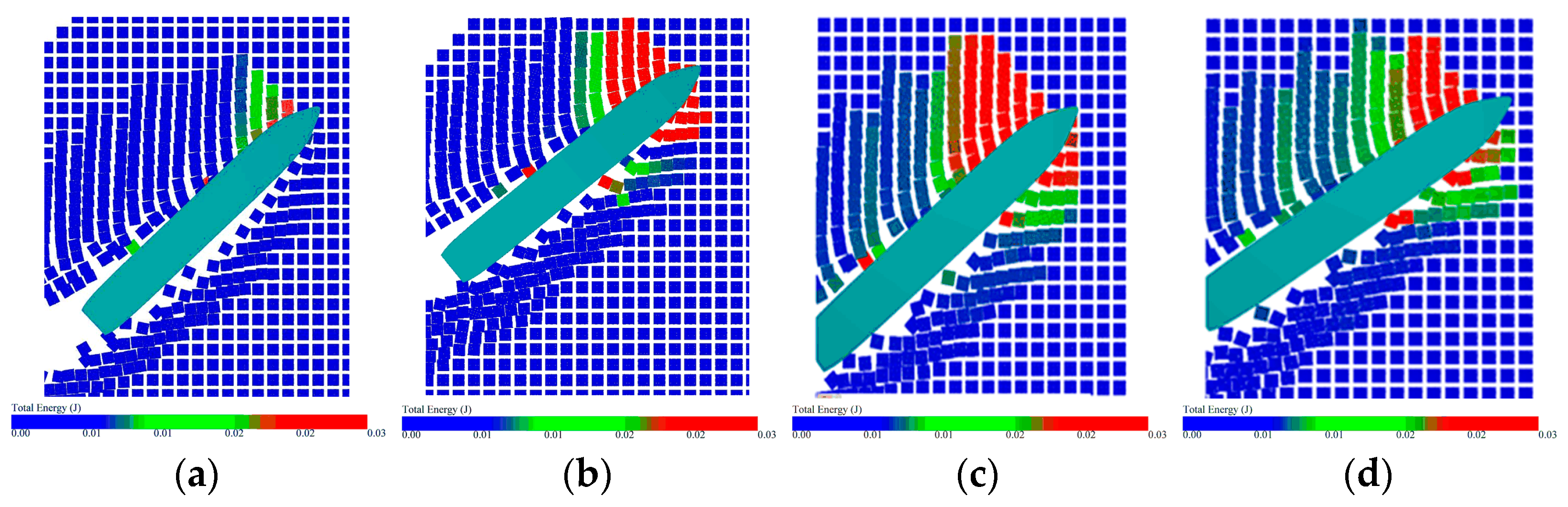
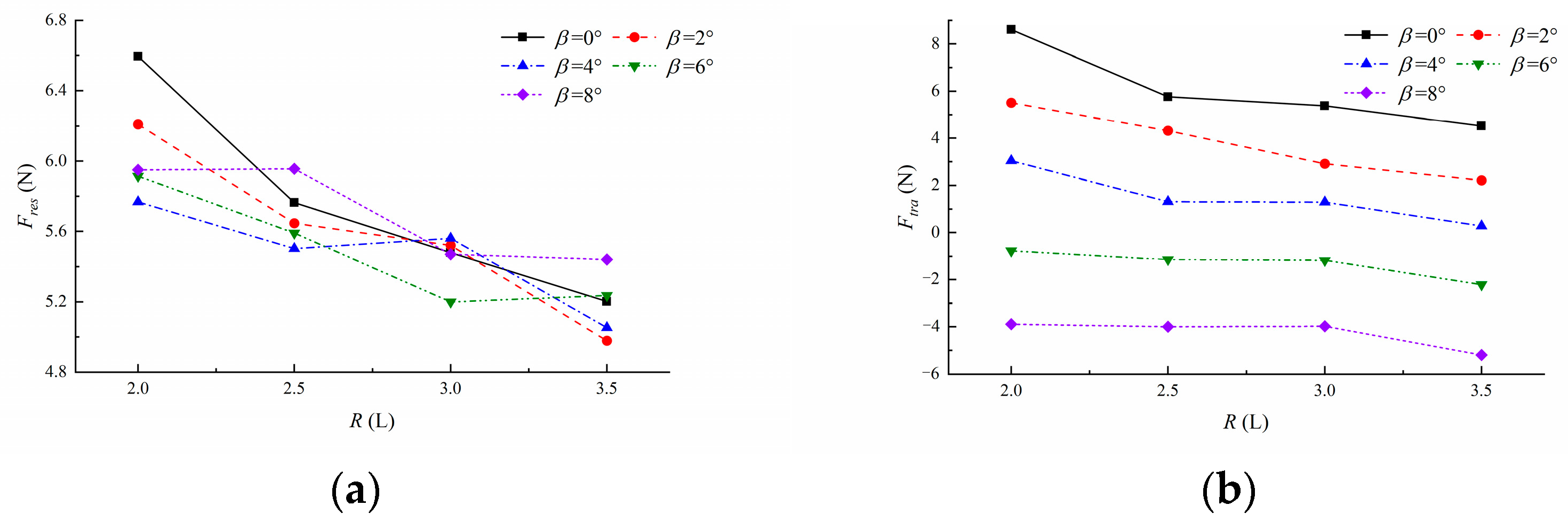
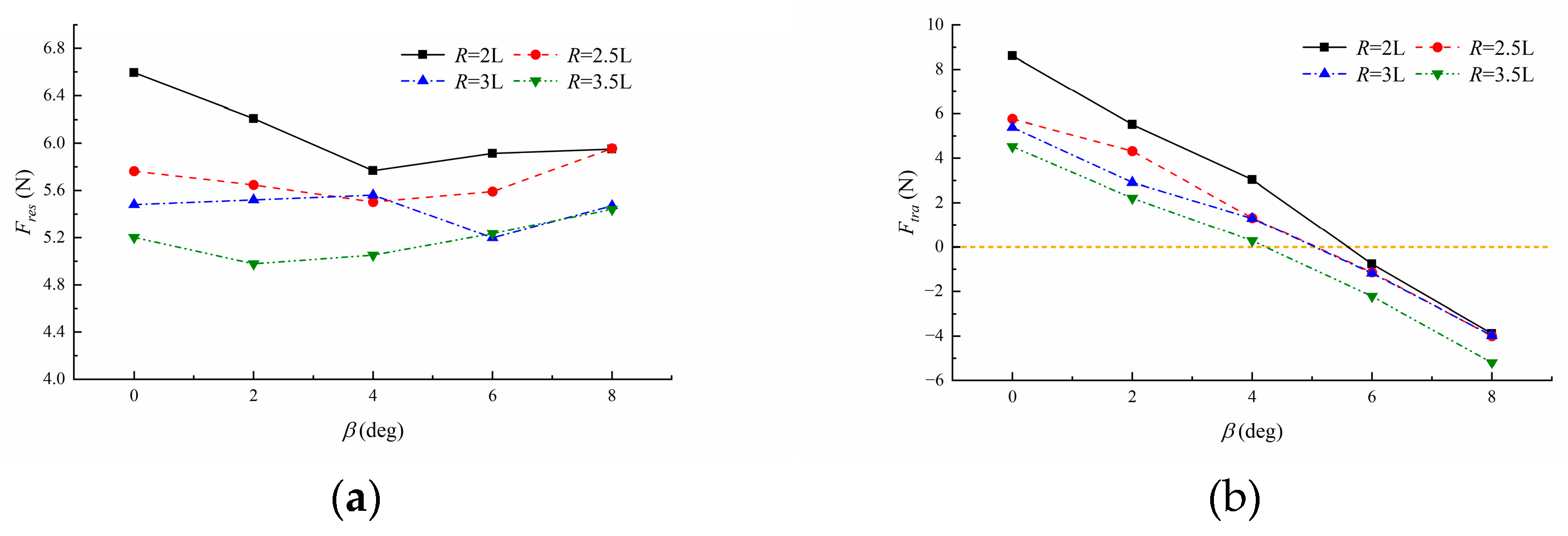
3.2. Analysis Influence of Varying Turning Radius
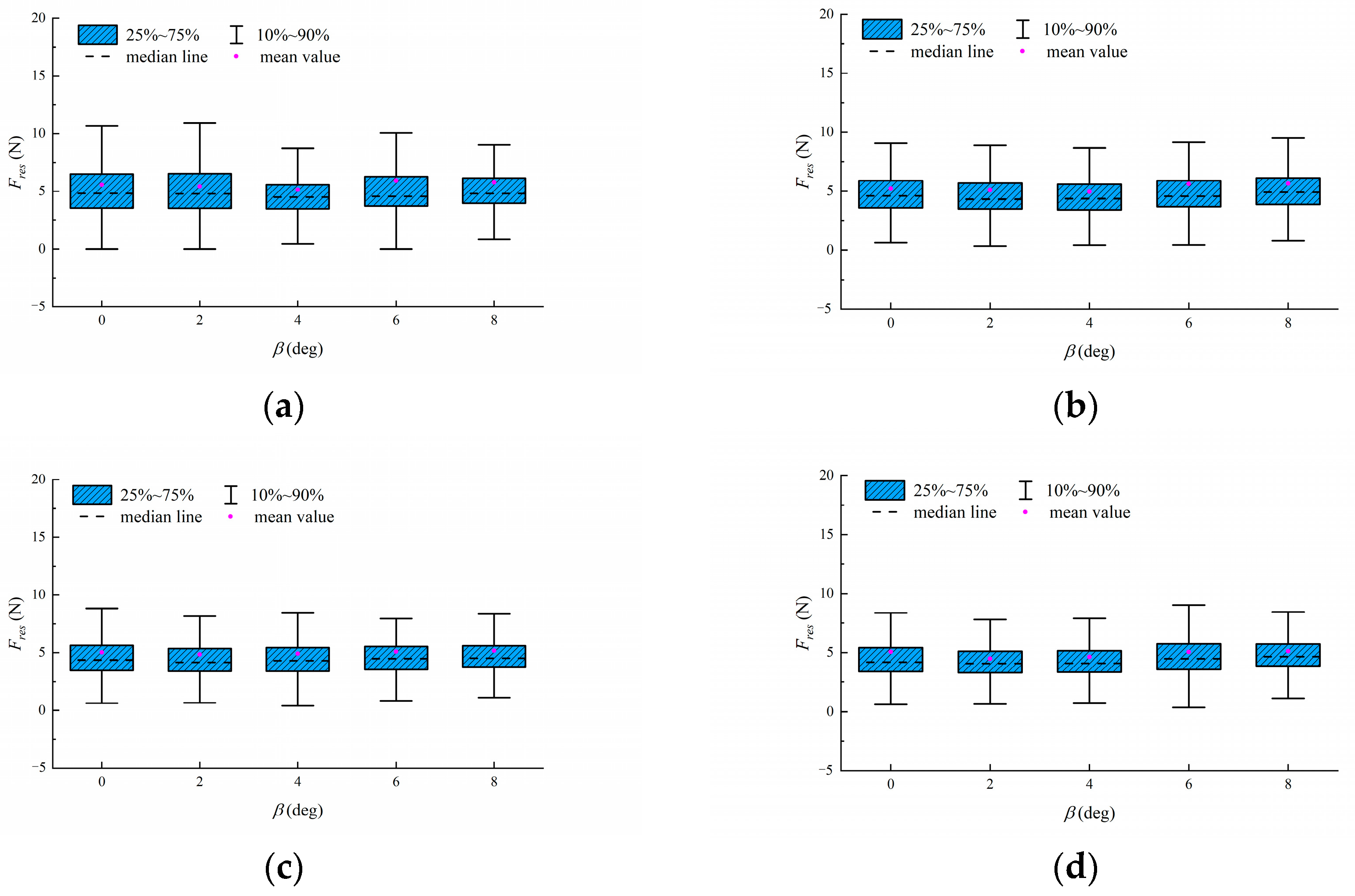
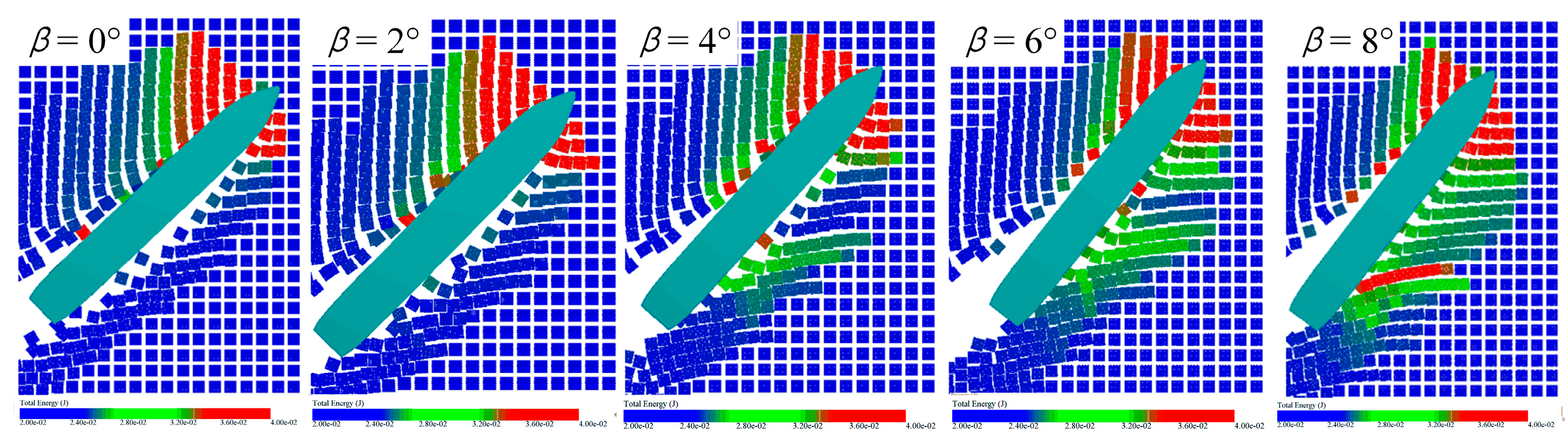
3.3. Analysis of the Influence of Drift Angle
4. Numerical Simulations of Planar Motion Mechanism: Pure Yaw Motion and Pure Sway Motion
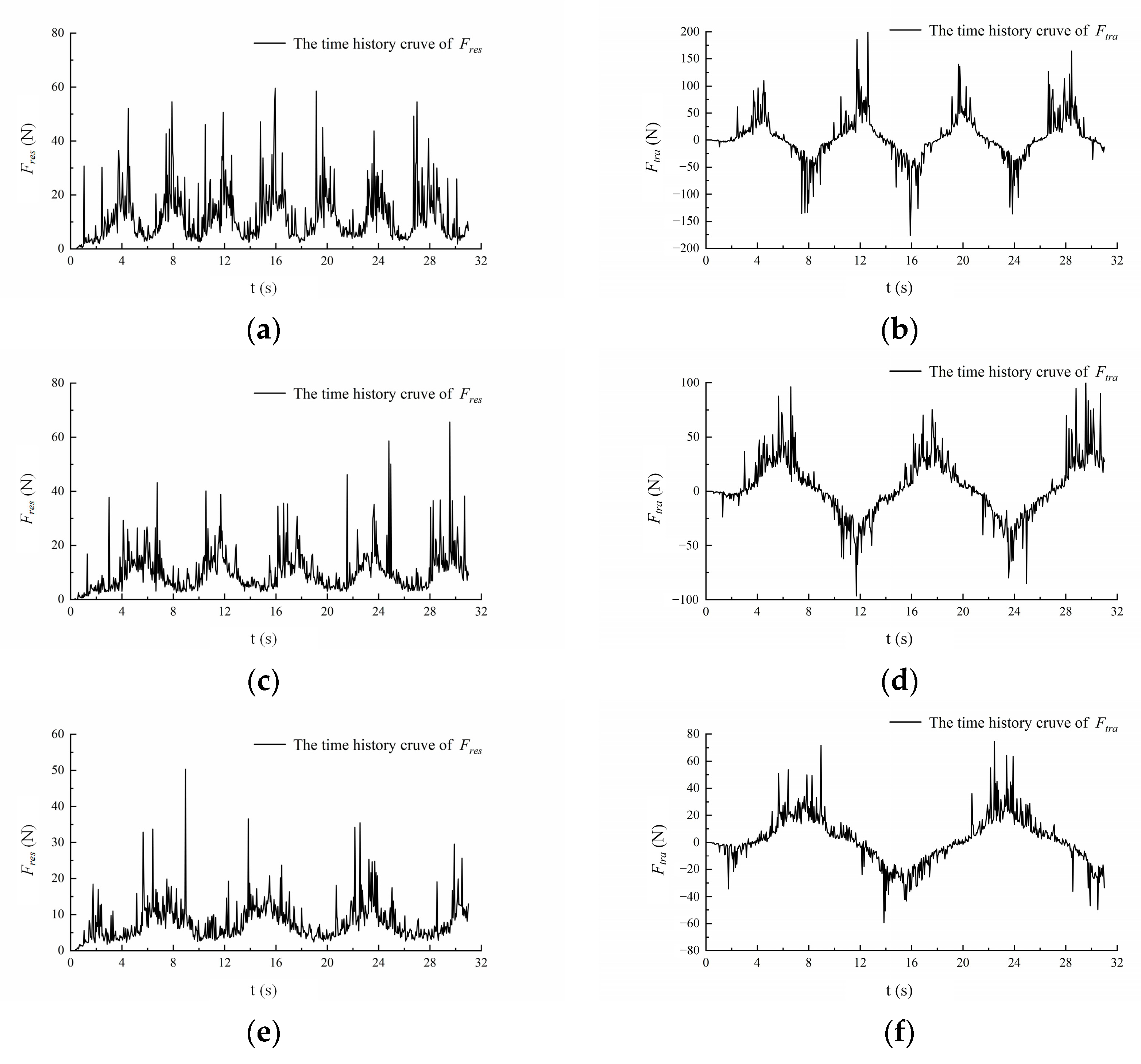
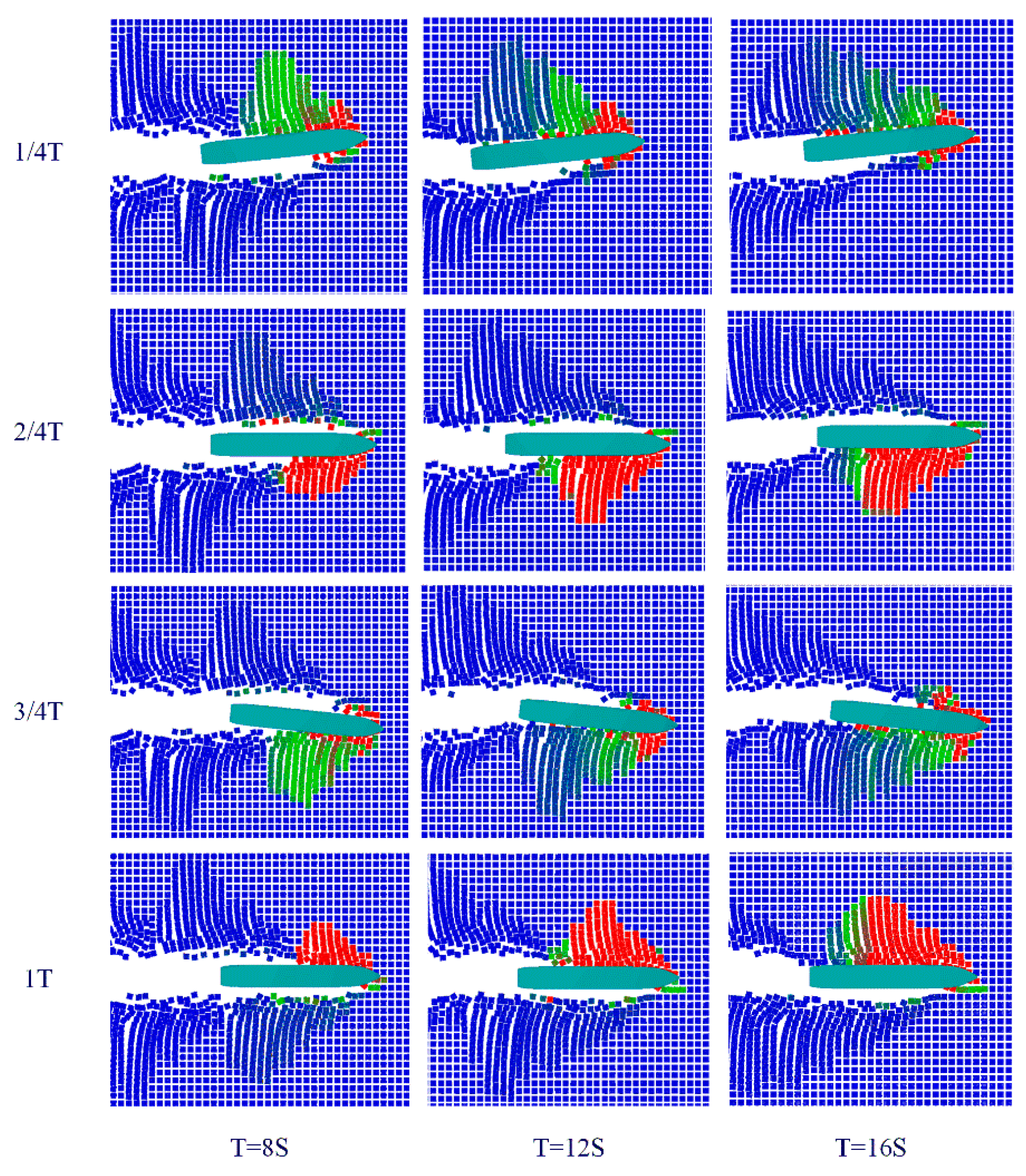
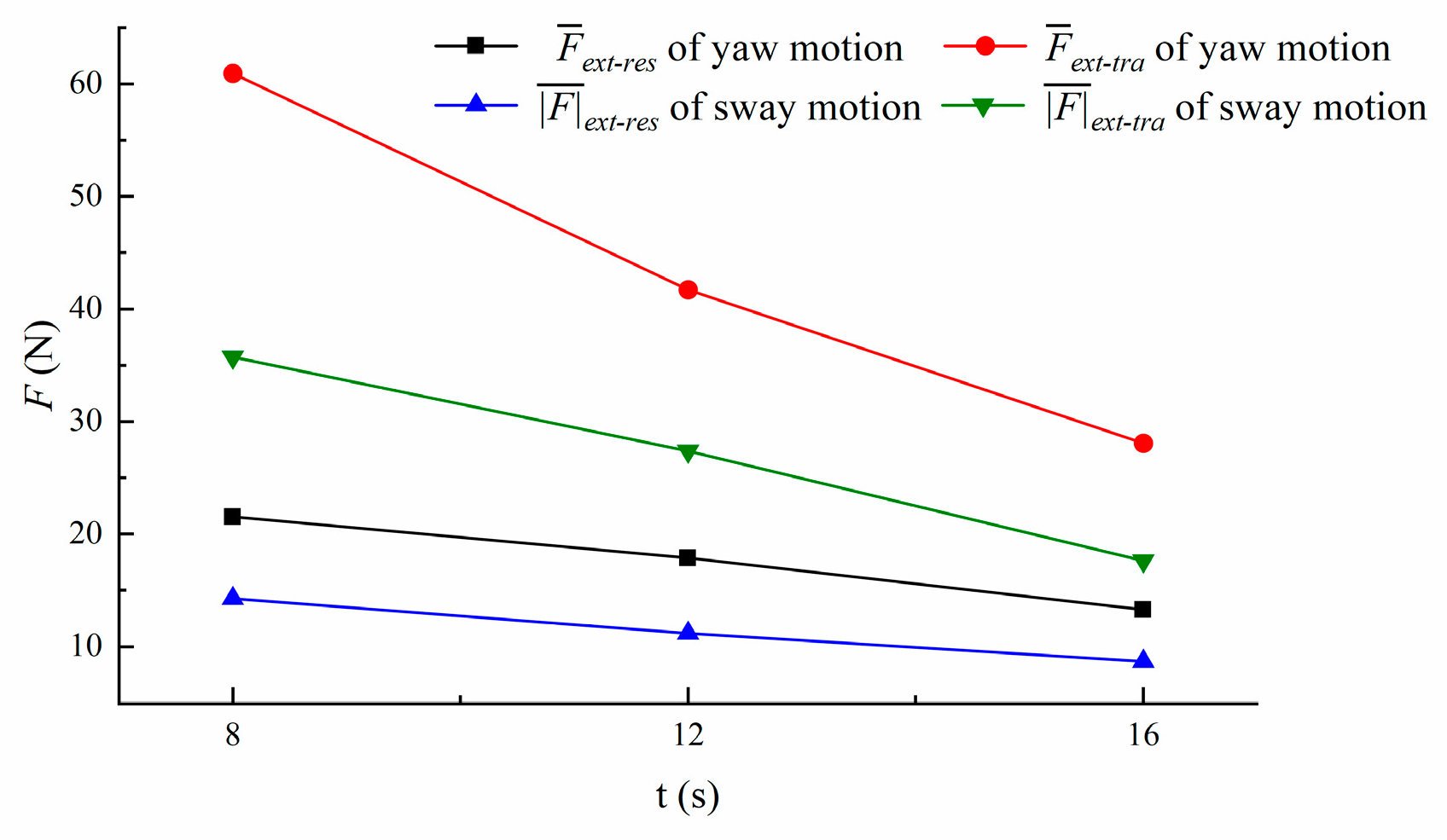
4.1. Pure Yaw Motion under Varying Yaw Periods
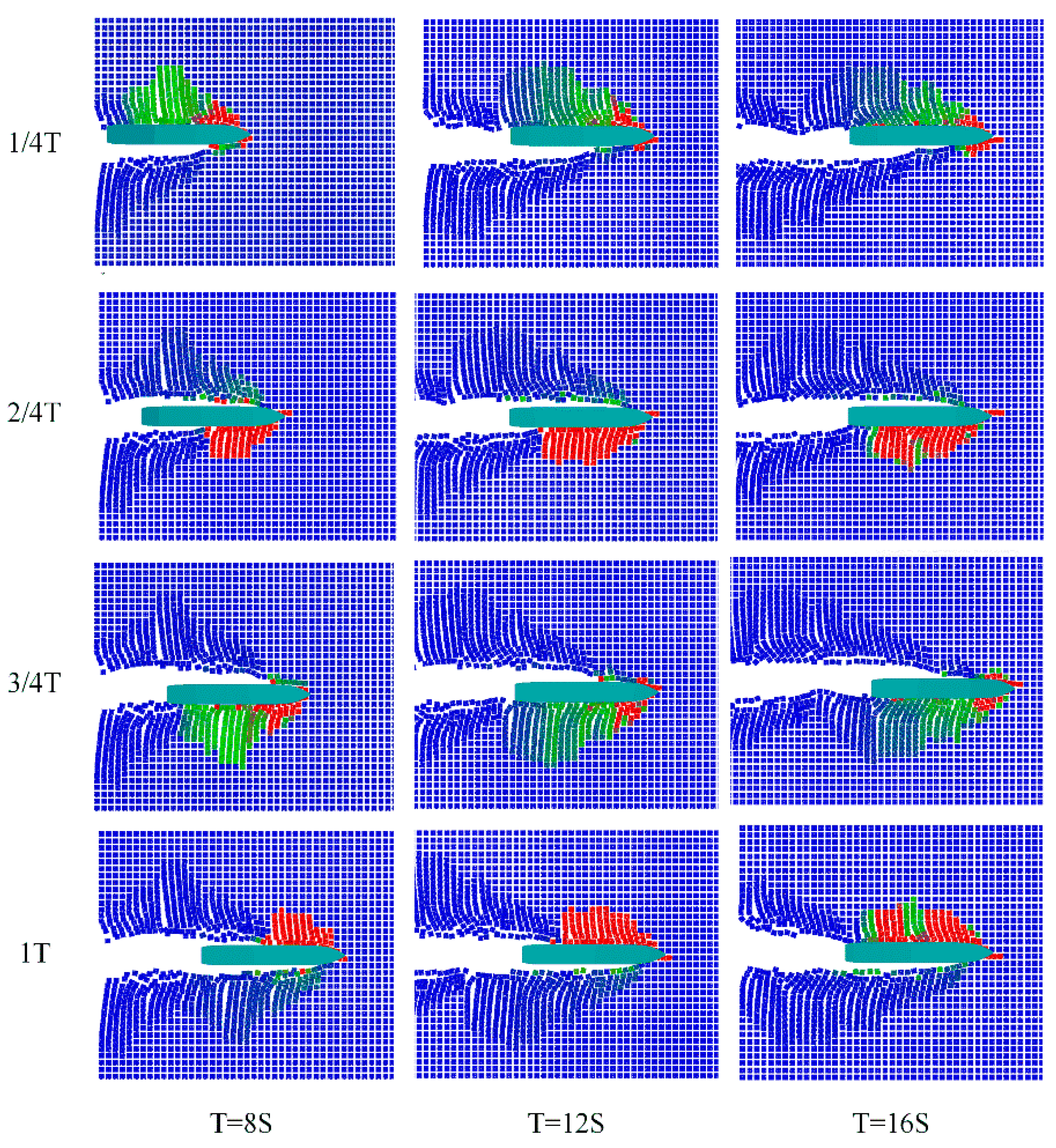
4.2. Pure sway Motion under Varying Sway Periods


5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koçak, S.T.; Yercan, F. Comparative Cost-Effectiveness Analysis of Arctic and International Shipping Routes: A Fuzzy Analytic Hierarchy Process. Transp. Policy 2021, 114, 147–164. [Google Scholar] [CrossRef]
- Melia, N.; Haines, K.; Hawkins, E. Sea Ice Decline and 21st Century Trans-Arctic Shipping Routes: Trans-Arctic Shipping in the 21st Century. Geophys. Res. Lett. 2016, 43, 9720–9728. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Liu, Z.Y.; Xie, D.; Li, W.H. Advancements of the core fundamental technologies and strategies of China regarding the research and development on polar ships. Bull. Natl. Nat. Sci. Found. China 2015, 3, 178–186. [Google Scholar] [CrossRef]
- Cho, S.R.; Jeong, S.Y.; Lee, S. Development of Effective Model Test in Pack Ice Conditions of Square-Type Ice Model Basin. Ocean Eng. 2013, 67, 35–44. [Google Scholar] [CrossRef]
- Hibler, W.D.; Bryan, K. A Diagnostic Ice–Ocean Model. J. Phys. Oceanogr. 1987, 17, 987–1015. [Google Scholar] [CrossRef]
- Bronnikov, A.V. Analysis of resistance of cargo ships going through pack ice. Trans. Leningrad Shipbuild. Inst. 1959, 27, 13. [Google Scholar]
- Buzuev, A.; Ryvlin, A. Calculation of the resistance encountered by an icebreaker moving through ice cakes and brash. Morskoi Flot 1961, 8, 136–138. [Google Scholar]
- Kashteljan, V.I.; Poznyak, I.I.; Ryvlin, A.Y. Ice Resistance to Motion of a Ship; Sudostroyeniye: Leningrad, Russia, 1968. [Google Scholar]
- Nozawa, K. A consideration on ship performance in broken ice sea. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]
- Vance, G.P. Analysis of the Performance of a 140-ft Great Lakes Icebreaker: USCGC Katmai Bay; Report No.80–8; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1980. [Google Scholar]
- Keinonen, A.J.; Browne, R.P.; Revill, C.R.; Reynolds, A. Ice Breaker Characteristics Synthesis; Report for Transportation Development Centre, Transport Canada, TP 12812E; AKAC Inc.: Victoria, BC, Canada, 1996. [Google Scholar]
- Keinonen, A.; Robbins, I. Icebreaker Performance Models, Seakeeping, Icebreaker Escort, Vol. 3—Icebreaker Escort Model User’s Guide; Transport Canada: Calgary, AB, Canada, 1998. [Google Scholar]
- Aboulazm, A.F.; Muggeridge, D. Analytical Investigation of Ship Resistance in Broken or Pack Ice. In Proceedings of the Eighth International Conference on Offshore Mechanics and Arctic Engineering, Hague, The Netherlands, 19–23 March 1989; Volume 4. [Google Scholar]
- Spencer, D.; Molyneux, D. Predicting Pack Ice Loads on Moored Vessels. In Proceedings of the International Conference of Ship and Offshore Technology, Busan, Republic of Korea, 28–29 September 2009. [Google Scholar]
- Hopkins, M.A. Numerical Simulation of Systems of Multitudinous Polygonal Blocks; U.S. Army CRREL: Hanover, NH, USA, 1992. [Google Scholar]
- Løset, S. Discrete Element Modelling of a Broken Ice Field—Part I: Model Development. Cold Reg. Sci. Technol. 1994, 22, 339–347. [Google Scholar] [CrossRef]
- Løset, S. Discrete Element Modelling of a Broken Ice Field—Part II: Simulation of Ice Loads on a Boom. Cold Reg. Sci. Technol. 1994, 22, 349–360. [Google Scholar] [CrossRef]
- Hansen, E.H.; Løset, S. Modelling Floating Offshore Units Moored in Broken Ice: Model Description. Cold Reg. Sci. Technol. 1999, 29, 97–106. [Google Scholar] [CrossRef]
- Konno, A.; Mizuki, T. On the Numerical Analysis of Flow around Ice Piece Moving near Icebreaker Hull (Second report: Application of Physically-Based Modeling to simulation of ice movement). In Proceedings of the 21st International Symposium on Okhotsk Sea & Sea Ice, Mombetsu, Japan, 19–24 February 2006. [Google Scholar]
- Konno, A.; Nakane, A.; Kanamori, S. Validation of Numerical Estimation of Brash Ice Channel Resistance with Model Test. In Proceedings of the 22nd International Conference on Port and Ocean Engineering under Arctic Conditions (POAC’13), Espoo, Finland, 9–13 June 2013. [Google Scholar]
- Alawneh, S.; Dragt, R.; Peters, D.; Daley, C.; Bruneau, S. Hyper-Real-Time Ice Simulation and Modeling Using GPGPU. IEEE Trans. Comput. 2015, 64, 3475–3487. [Google Scholar] [CrossRef]
- Amdahl, T.H.; Bjørnsen, B.; Hagen, O.J.; Søberg, S.R. Numerical Simulations of Ice Loads on an Arctic Floater in Managed Ice. In Proceedings of the OTC Arctic Technology Conference 2014, Houston, TX, USA, 10–12 February 2014. [Google Scholar]
- Metrikin, I.A.; Teigen, S.H.; Gürtner, A.; Uthaug, E.S.; Sapelnikov, D.; Ervik, Å.; Fredriksen, A.; Lundamo, T.; Bonnemaire, B. Experimental and Numerical Investigations of a Ship-Shaped, Turret-Moored Floating Structure in Intact and Managed Sea Ice Conditions. In Proceedings of the OTC Arctic Technology Conference, Copenhagen, Denmark, 23–25 March 2015. [Google Scholar]
- Metrikin, I.; Gürtner, A.; Bonnemaire, B.; Xiang, T.; Arnt, F.; Dmitry, S. SIBIS: A Numerical Environment for Simulating Offshore Operations in Discontinuous Ice. In Proceedings of the 23th International Conference on Port and Ocean Engineering under Arctic Conditions, Trondheim, Norway, 14–18 June 2015. [Google Scholar]
- Lau, M. Ship Manoeuvring-in-Ice Modeling Software OSIS-IHI. In Proceedings of the International Conference on Port and Ocean Engineering Under Arctic Conditions, Montreal, QC, Canada, 10–14 July 2011. [Google Scholar]
- Lau, M.; Lawrence, K.P.; Rothenburg, L. Discrete Element Analysis of Ice Loads on Ships and Structures. Ships Offshore Struct. 2011, 6, 211–221. [Google Scholar] [CrossRef]
- Liu, J.; Lau, M.; Williams, F.M. Numerical Implementation and Benchmark of Ice-Hull Interaction Model for Ship Manoeuvring Simulations. In Proceedings of the 19th IAHR International Symposium on Ice, Vancouver, BC, Canada, 6-11 July 2008; pp. 215–226. [Google Scholar]
- Liu, J.C. Mathematical Modeling Ice-Hull Interaction for Real Time Simulations of Ship Manoeuvring in Level Ice; Memorial University of Newfoundland: St. John’s, NL, Canada, 2009. [Google Scholar]
- Lau, M. Discrete Element Modeling of Ship Manoeuvring in Ice. In Proceedings of the 18th IAHR International Symposium on Ice, Sapporo, Japan, 28 August–1 September 2006. [Google Scholar]
- Lau, M.; Ré, A.S. Performance of Survival Craft in Ice Environments. In Proceedings of the 7th International Conference and Exhibition on Performance of Ships and Structures in Ice, Banff, AB, Canada, 16–19 July 2006; pp. 51–58. [Google Scholar]
- Zhan, D.X.; Agar, D.; He, M.; Spencer, D.; Molyneux, D. Numerical Simulation of Ship Maneuvering in Pack Ice. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering: Volume 4, Shanghai, China, 1 January 2010; ASME: New York, NY, USA, 2010; pp. 855–862. [Google Scholar]
- Zhan, D.X.; Molyneux, D. 3-Dimensional Numerical Simulation of Ship Motion in Pack Ice. In Proceedings of the Volume 6: Materials Technology, Polar and Arctic Sciences and Technology, Petroleum Technology Symposium, American Society of Mechanical Engineers, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 407–414. [Google Scholar]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG Standard Method for Ship Maneuvering Predictions. J. Mar. Sci. Technol. 2015, 20, 37–52. [Google Scholar] [CrossRef]
- Daley, C.; Alawneh, S.; Peters, D.; Colbourne, B. GPU-Event-Mechanics Evaluation of Ice Impact Load Statistics. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 10–12 February 2014. [Google Scholar]
- Daley, C.; Alawneh, S.; Peters, D.; Quinton, B.; Colbourne, B. GPU Modeling of Ship Operations in Pack Ice. In Proceedings of the10th International Conference and Exhibition on Performance of Ships and Structures in Ice, Banff, Alberta, Canada, 17–20 September 2012. [Google Scholar]
- Su, B.; Riska, K.; Moan, T. Numerical Simulation of Ship Turning in Level Ice. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering: Volume 4, Shanghai, China, 1 January 2010; ASME: New York, NY, USA, 2010; pp. 751–758. [Google Scholar]
- Su, B.; Riska, K.; Moan, T. A Numerical Method for the Prediction of Ship Performance in Level Ice. Cold Reg. Sci. Technol. 2010, 60, 177–188. [Google Scholar] [CrossRef]
- Tan, X.; Su, B.; Riska, K.; Moan, T. A Six-Degrees-of-Freedom Numerical Model for Level Ice–Ship Interaction. Cold Reg. Sci. Technol. 2013, 92, 1–16. [Google Scholar] [CrossRef]
- Tan, X. Numerical Investigation of Ship’s Continuous-Mode Icebreaking in Level Ice; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Li, F.; Huang, L. A Review of Computational Simulation Methods for a Ship Advancing in Broken Ice. JMSE 2022, 10, 165. [Google Scholar] [CrossRef]
- Altair Engineering, Inc. Altair EDEM 2022.2 User Guide. Available online: https://2022.help.altair.com/2022/EDEM (accessed on 18 August 2023).
- Government of Canada. Ice Glossary. Environment and Climate Change Canada (ECCC). Available online: https://www.canada.ca/en/environment-climate-change/services/ice-forecasts-observations/latest-conditions/glossary.html (accessed on 18 August 2023).
- Lee, J.M.; Lee, C.J.; Kim, Y.-S.; Choi, G.-G.; Lew, J.-M. Determination of Global Ice Loads on the Ship Using the Measured Full-Scale Motion Data. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 301–311. [Google Scholar] [CrossRef]
- Berman, H.B. Data Patterns in Statistics. Available online: https://stattrek.com/statistics/charts/data-patterns (accessed on 18 August 2023).
- Lau, M. Effects of Hull Geometry and Tightness of Turns on Ship Maneuverability: An OSIS-IHI Simulation. In Proceedings of the Volume 7: Polar and Arctic Sciences and Technology, Online, 21 June 2021; ASME: New York, NY, USA, 2021; p. V007T07A020. [Google Scholar]
- Shi, Y. Model Test Data Analysis of Ship Maneuverability in Ice; Memorial University of Newfoundland: St. John’s, NL, Canada, 2002. [Google Scholar]










| Parameters | Model Scale | Full Scale |
|---|---|---|
| Lpp/m | 5.1 | 95.2 |
| B/m | 1.02 | 19.0 |
| D/m | 0.36 | 6.8 |
| Stem angle/deg | 30 | 30 |
| Parameters | Symbol | Value |
|---|---|---|
| Water density | ρw | 1020 kgm−3 |
| Ice density | ρice | 920 kgm−3 |
| Ice elasticity modulus | E | 0.8 GPa |
| Restitution coefficient of ice–ice | ei | 0.4 |
| Restitution coefficient of ice–ship | es | 0.3 |
| Friction of ice–ice | μi | 0.2 |
| Friction of ice–ship | μs | 0.02/0.22 |
| Parameters | Model Scale | Full Scale |
|---|---|---|
| Lpp/m | 4.91 | 147.0 |
| B/m | 0.75 | 22.6 |
| D/m | 0.45 | 13.5 |
| T/m | 0.27 | 8.0 |
| Item | R = 2 L | R = 2.5 L | R = 3 L | R = 3.5 L | ||||
|---|---|---|---|---|---|---|---|---|
| 0 deg | 6.59 | 8.61 | 5.76 | 5.76 | 5.48 | 5.38 | 5.20 | 4.52 |
| 2 deg | 6.21 | 5.51 | 5.65 | 4.32 | 5.52 | 2.91 | 4.98 | 2.21 |
| 4 deg | 5.77 | 3.04 | 5.50 | 1.32 | 5.56 | 1.29 | 5.05 | 0.276 |
| 6 deg | 5.91 | −0.764 | 5.59 | −1.14 | 5.20 | −1.18 | 5.24 | −2.22 |
| 8 deg | 5.95 | −3.89 | 5.96 | −4.00 | 5.47 | −3.98 | 5.44 | −5.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xuan, S.; Zhan, C.; Liu, Z.; Feng, B.; Chang, H.; Wei, X. Numerical Investigation of Global Ice Loads of Maneuvering Captive Motion in Ice Floe Fields. J. Mar. Sci. Eng. 2023, 11, 1778. https://doi.org/10.3390/jmse11091778
Xuan S, Zhan C, Liu Z, Feng B, Chang H, Wei X. Numerical Investigation of Global Ice Loads of Maneuvering Captive Motion in Ice Floe Fields. Journal of Marine Science and Engineering. 2023; 11(9):1778. https://doi.org/10.3390/jmse11091778
Chicago/Turabian StyleXuan, Shenyu, Chengsheng Zhan, Zuyuan Liu, Baiwei Feng, Haichao Chang, and Xiao Wei. 2023. "Numerical Investigation of Global Ice Loads of Maneuvering Captive Motion in Ice Floe Fields" Journal of Marine Science and Engineering 11, no. 9: 1778. https://doi.org/10.3390/jmse11091778
APA StyleXuan, S., Zhan, C., Liu, Z., Feng, B., Chang, H., & Wei, X. (2023). Numerical Investigation of Global Ice Loads of Maneuvering Captive Motion in Ice Floe Fields. Journal of Marine Science and Engineering, 11(9), 1778. https://doi.org/10.3390/jmse11091778







