Optimization of Ship’s Navigational Parameters to Improve the Stowage and Securing Criteria of Non-Standardized Cargo in Ships
Abstract
:1. Introduction
2. Materials and Methods
2.1. IMO Regulations
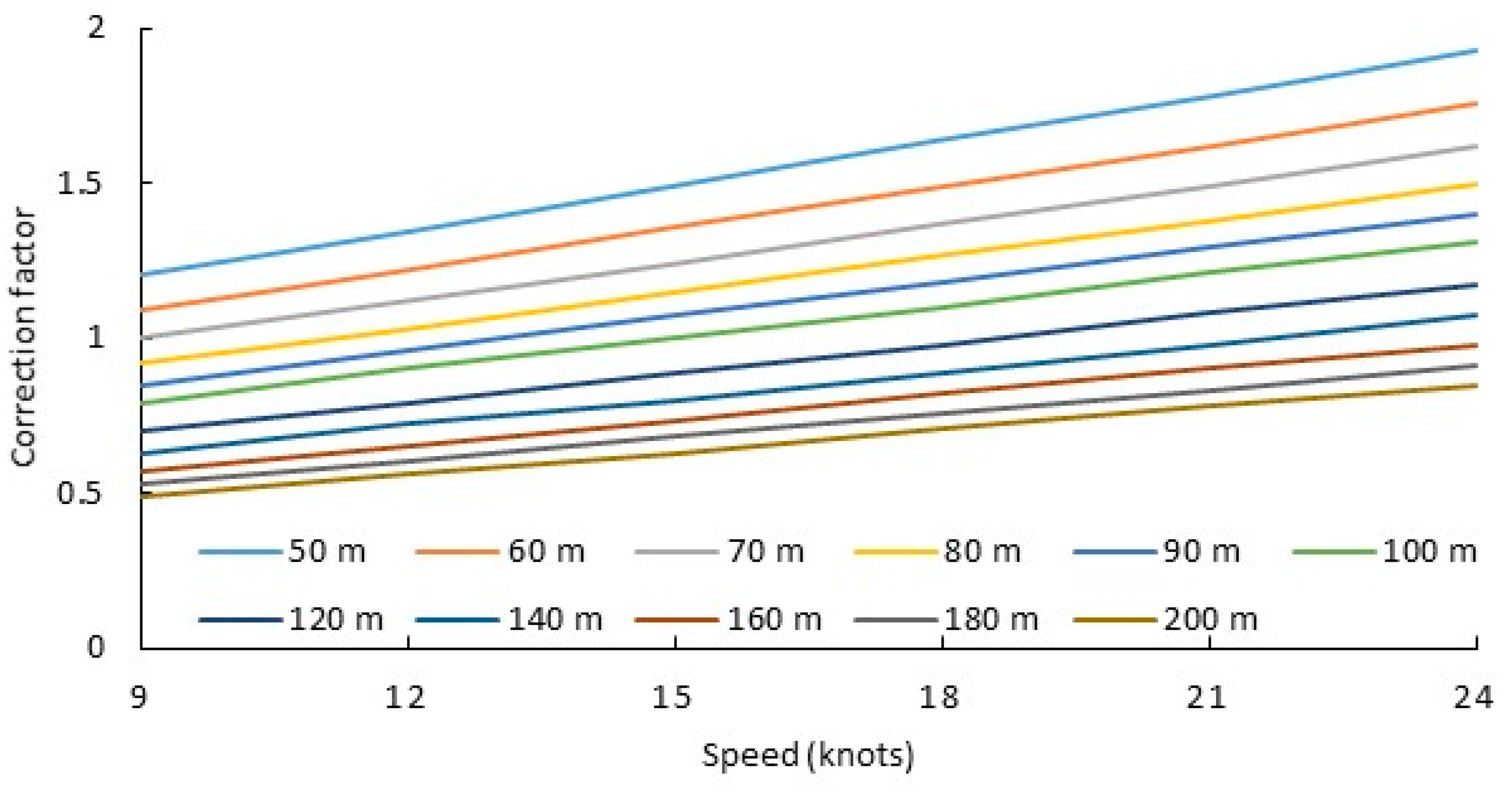
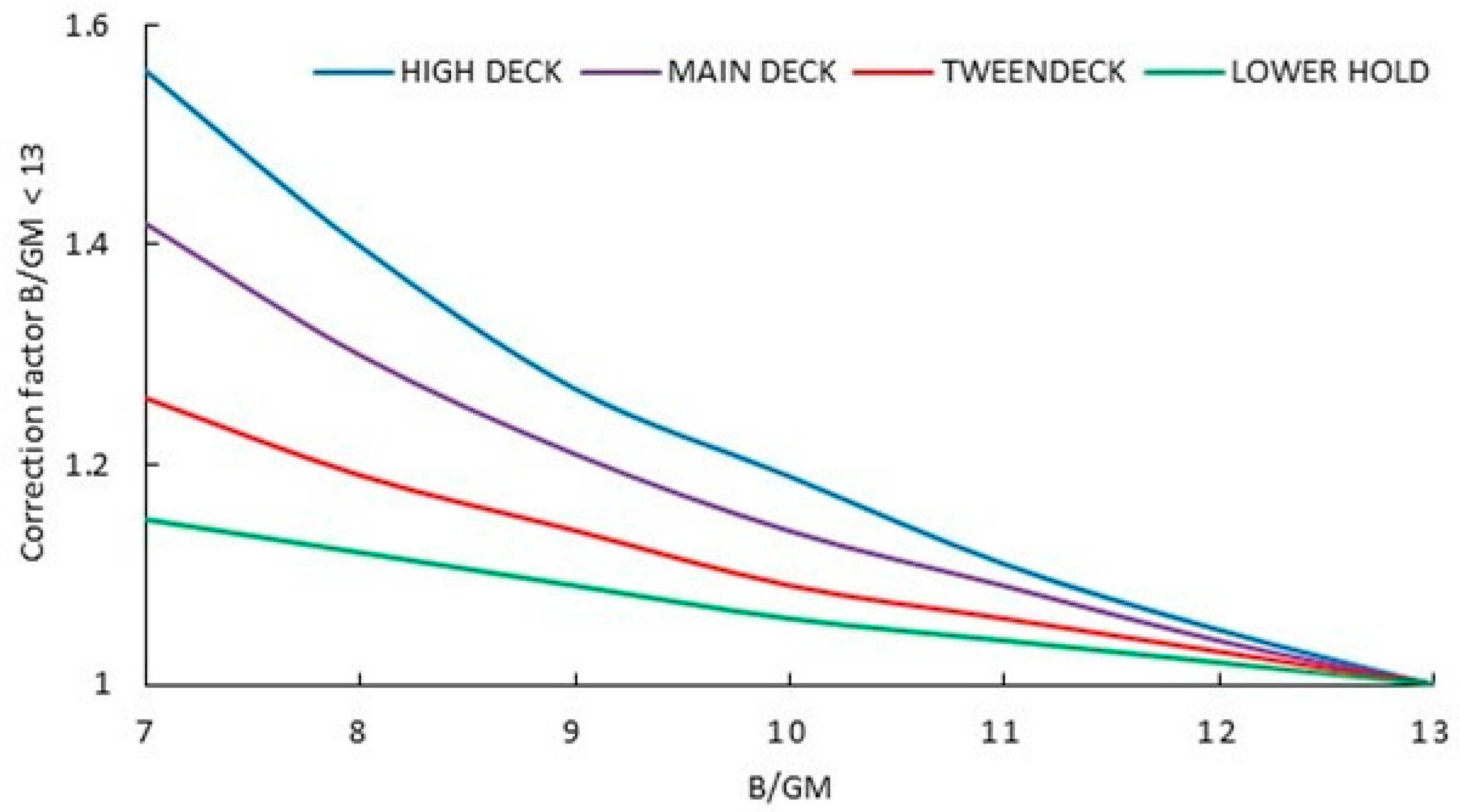
2.2. Classification Society Guidelines
2.3. Ship’s Rolling Motion Influenced by Constant Trochoidal Waves
2.4. Waves’ Study
3. Results
3.1. Case Study
- Ship in upright position;
- 12° as average initial angle of rolling.
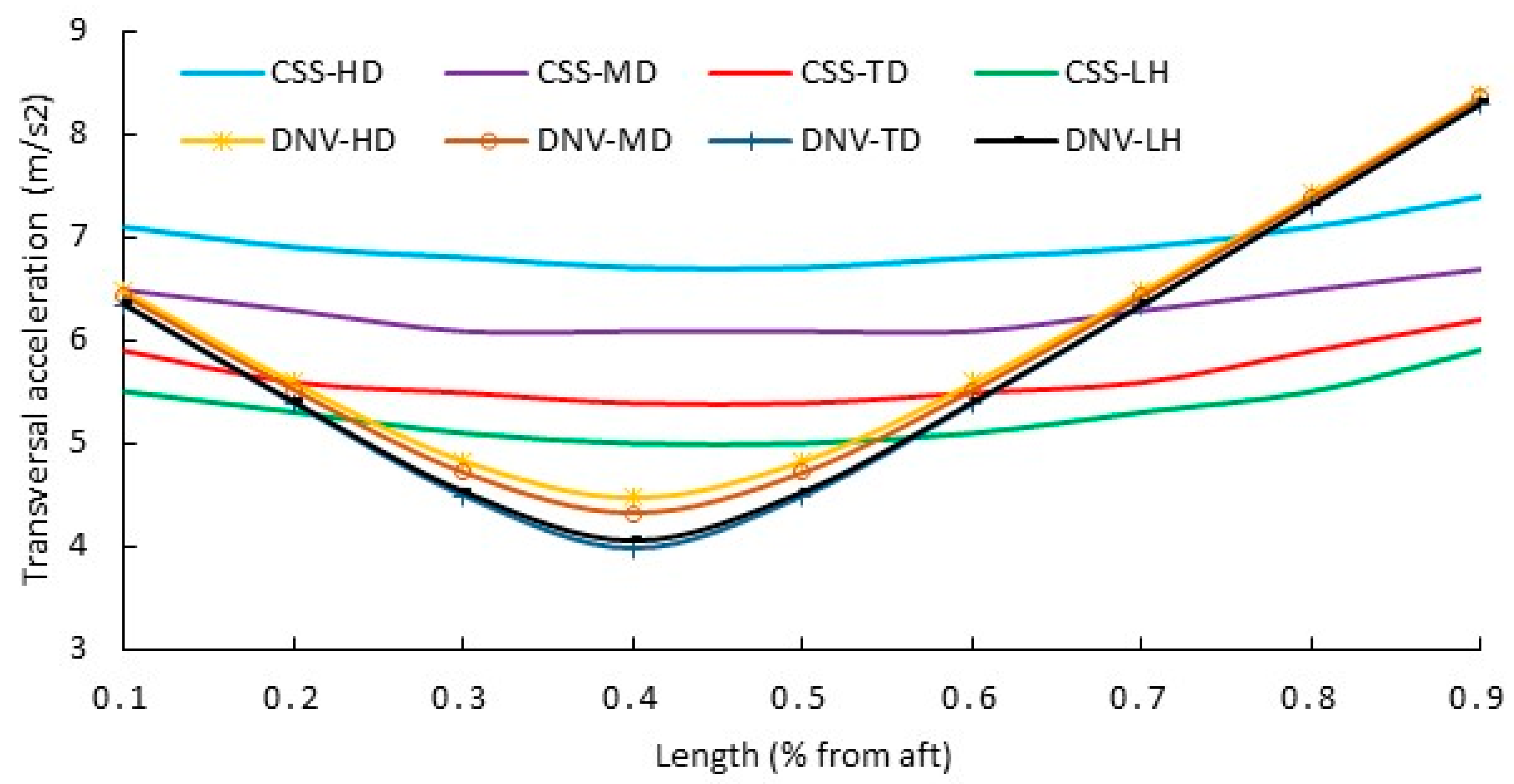
3.2. Comparative Results Analysis between the IMO and the Classification Societies Methods
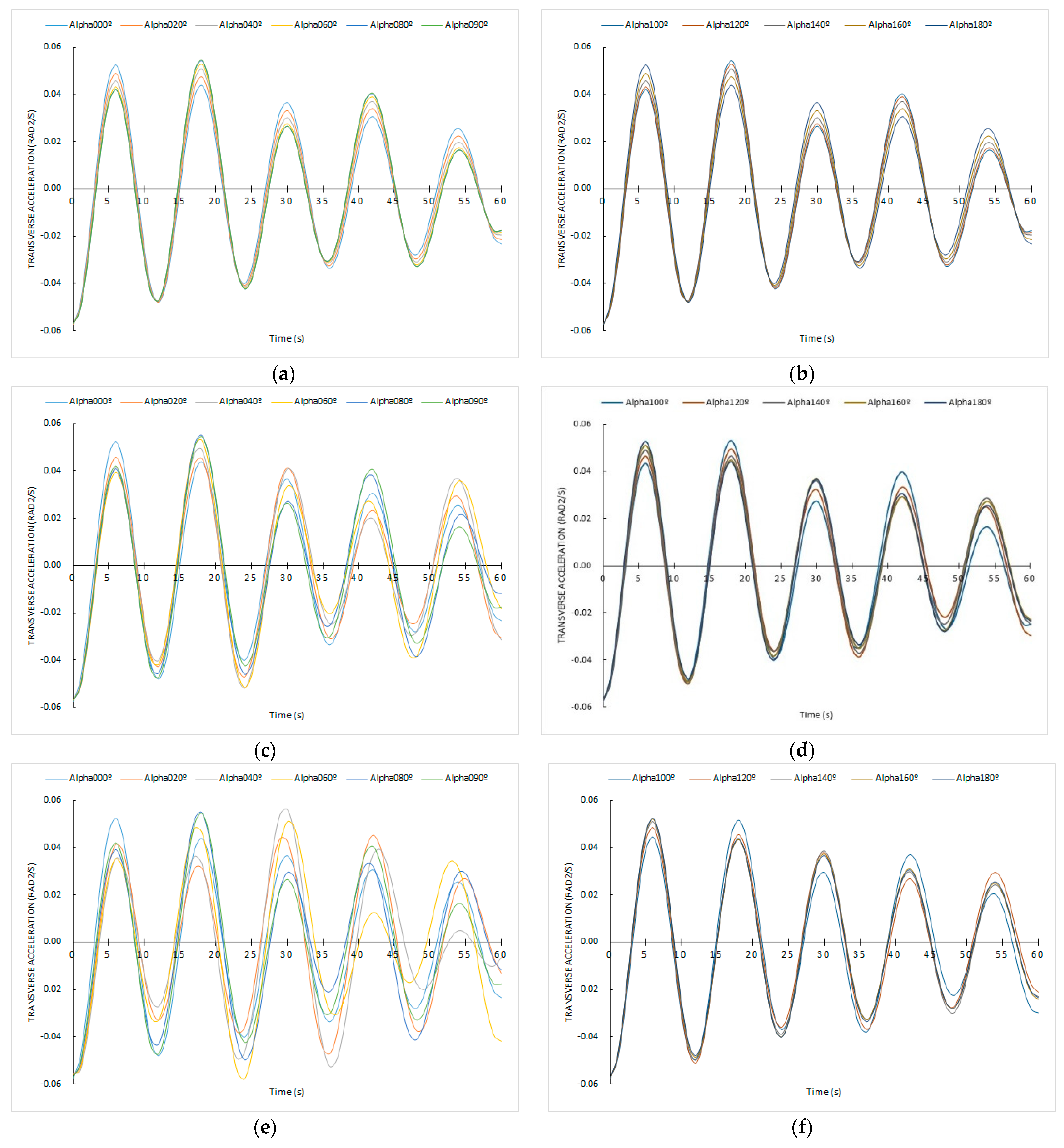
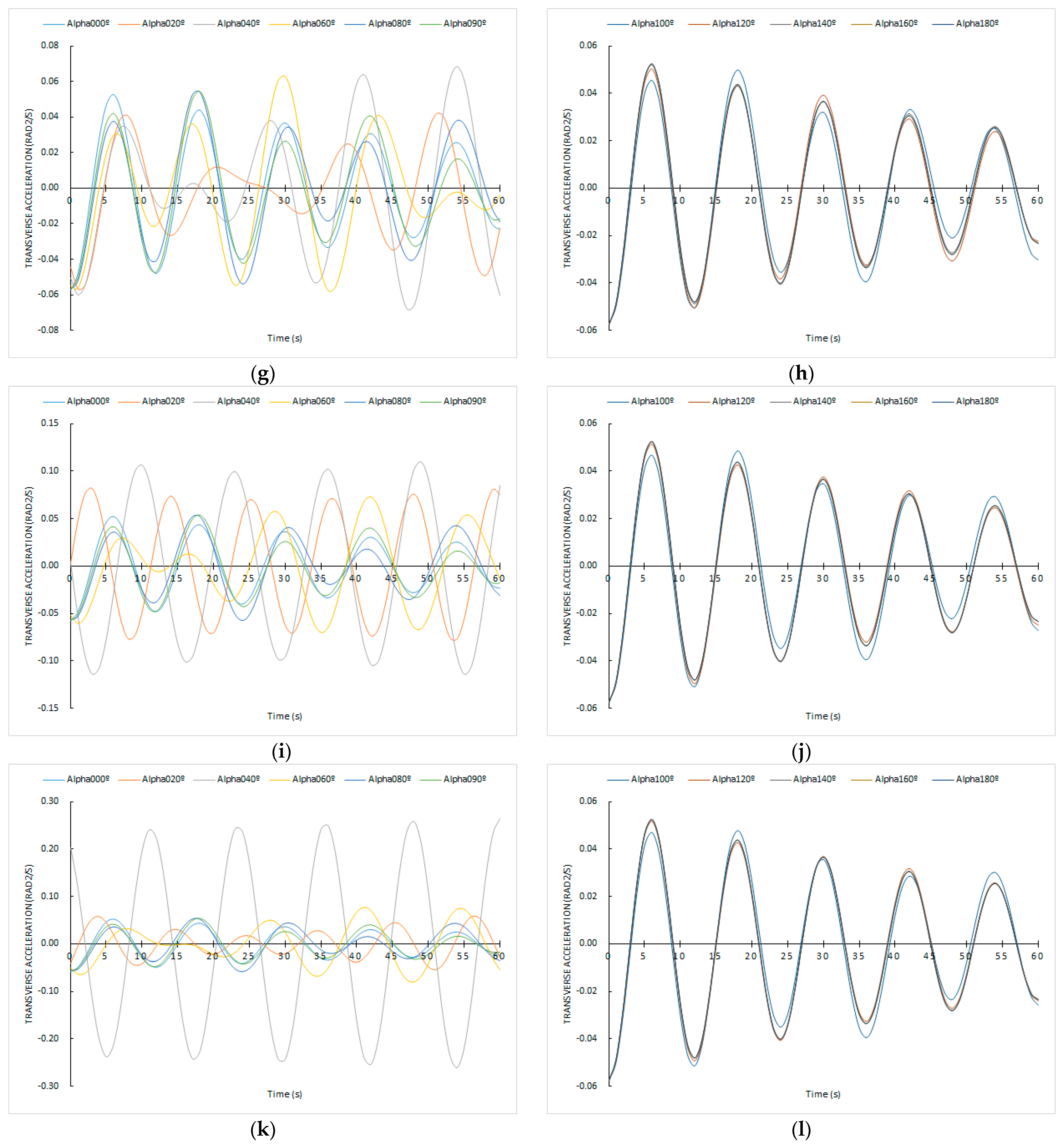
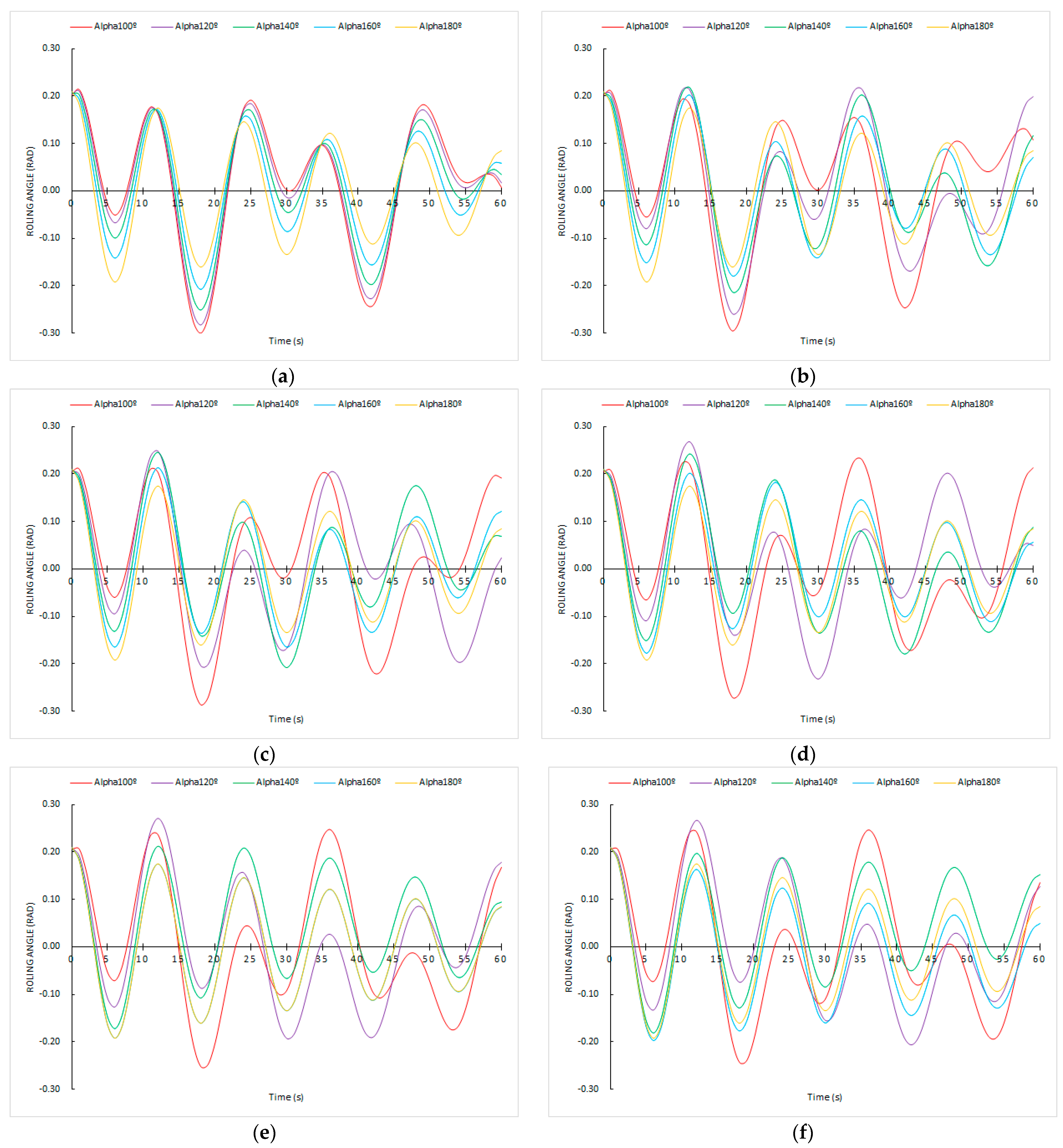
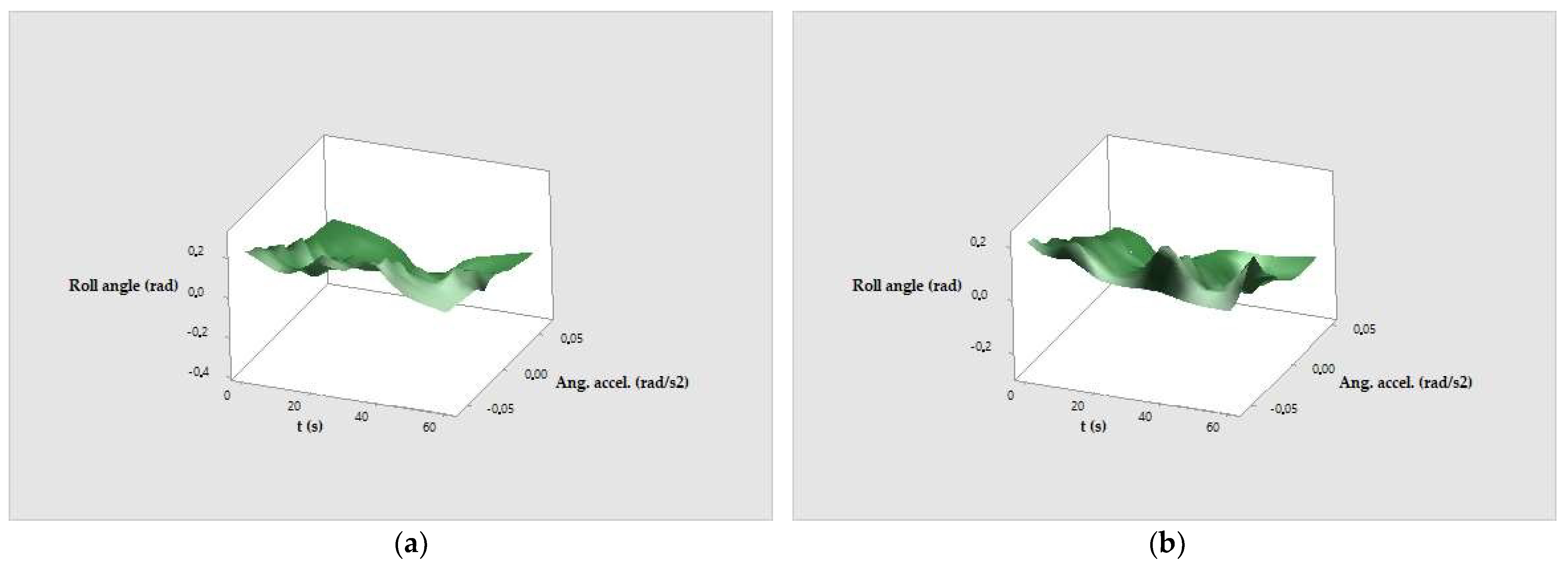
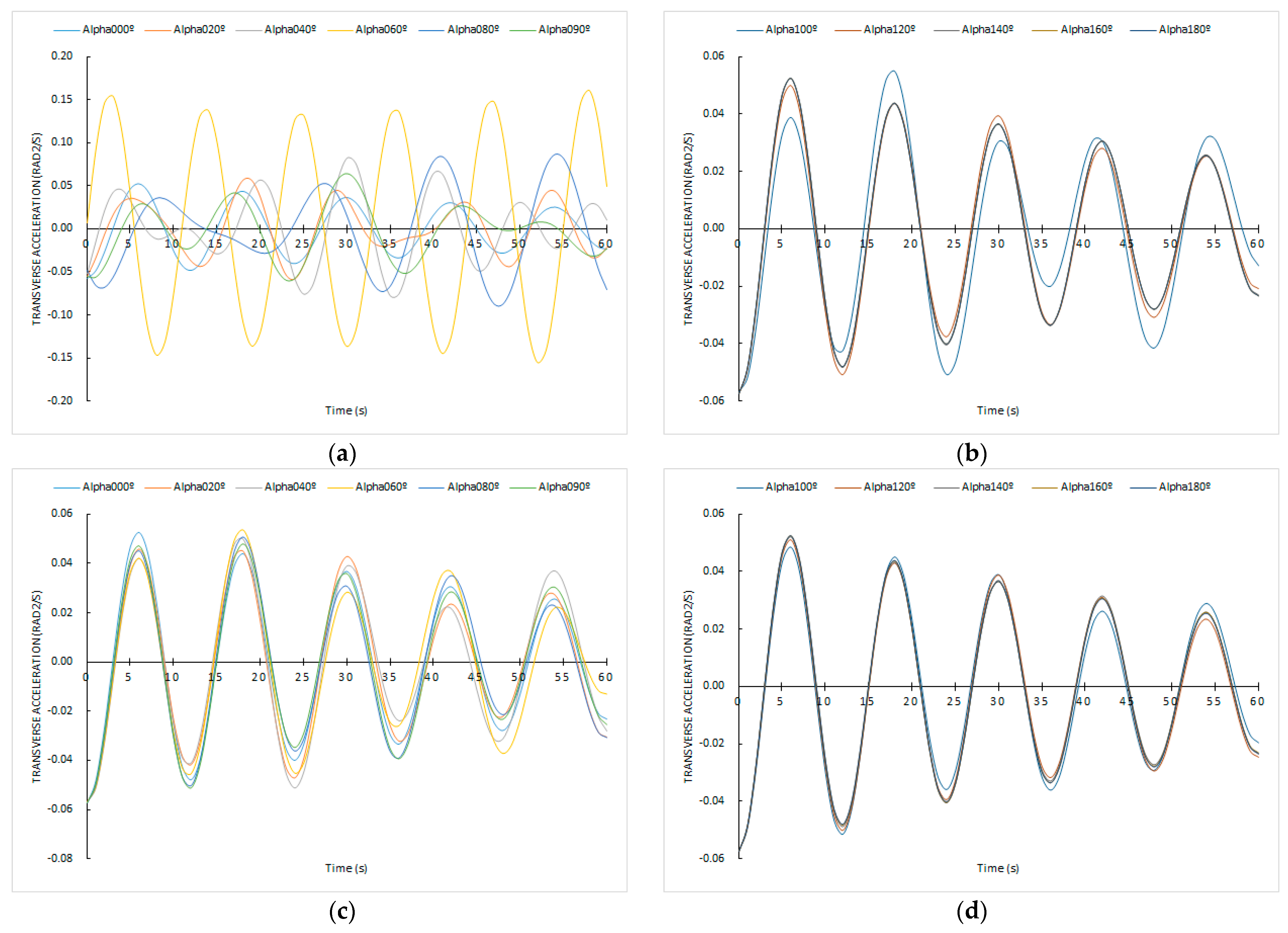
3.3. Ship’s Rolling Motion Sailing in a Resistant Environment and Receiving Successive Trochoidal Waves from Any Constant Direction
4. Discussion
4.1. IMO vs. DNV Criteria
4.2. About the Novel Mathematical Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| α | Angle formed between the ship’s center line (heading) and the waves direction |
| θ | Rolling angle |
| θMW | Maximum wave slope |
| θM | Maximum initial rolling angle |
| at | Tangential acceleration during rolling motion |
| aw | Angular acceleration during rolling motion |
| B | Ship’s beam |
| Cb | Ship’s block coefficient |
| CSS | Code of safe practice for cargo stowage and securing |
| d | Ship’s draught |
| DNV | Classification Society Det Norske Veritas—Germanischer Lloyd |
| g | Gravity acceleration |
| gx | Gravity acceleration parallel to deck |
| GM | Transverse metacentric height |
| HD | High deck |
| Hw | Wave height |
| k1 | Radius of rotation of the ship’s displacement with respect to the longitudinal axis passing through the center of gravity |
| KG | Height of ship’s center of gravity from the keel |
| k | Factor which depends of presence and shape of bilge keels |
| L | Ship’s length |
| LH | Lower hold |
| Lw | Wavelength |
| MD | Main deck |
| RR | Distance from ship’s center of gravity to center of mass of cargo |
| Td | Ship’s natural rolling period |
| TD | Tween deck |
| Tw | Wave period |
| Vw | Wave translation velocity |
| X1 | Factor dependent of relationship B/d |
| X2 | Factor dependent of block coefficient |
References
- EQUASIS. The 2021 World Fleet Report. Statistics from Equasis. The World Merchant Fleet in 2021. Available online: http://www.equasis.org/EquasisWeb/public/HomePage (accessed on 4 August 2023).
- UNCTAD. Handbook of Statistics 2022. Maritime Transport. Merchant Fleet by Flag of Registration and by Type of Ship, Annual. Available online: https://unctad.org/ (accessed on 4 August 2023).
- Jiang, S.; Wang, Y. A Study on Securing Non-standardized Cargo. In Software Engineering and Knowledge Engineering: Theory and Practice; Zhang, W., Ed.; Advances in Intelligent and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2012; Volume 162, pp. 293–301. [Google Scholar] [CrossRef]
- UK P&I Club. Lashing and Securing Deck Cargoes. In Carefully to Carry, 2nd ed.; Witherby Publishing Group. Ltd.: Scotland, UK, 2023; pp. 543–569. [Google Scholar]
- The London P&I Club; TMC Marine; Bureau Veritas. Reducing the Risk of Damage to or Loss of non-Standardized Cargo; Operational Guidance for Securing during Transportation. Available online: www.londonpandi.com/knowledge/publications/reducing-the-risk-of-damage-to-or-loss-of-non-standardized-cargo-operational-guidance-for-securing-during-transportation/ (accessed on 3 August 2023).
- Li, C.; Zhang, W.; Zhou, T.; Ma, S.; Wang, C. Prediction of ship rolling motion based on NARX neural network. In Proceedings of the 33rd Chinese Control and Decision Conference, Kunming, China, 22–24 May 2021. [Google Scholar] [CrossRef]
- Bliault, C.; North of England P&I Association. Cargo Stowage and Securing: A Guide to Good Practice, 2nd ed.; North of England P&I Association Limited: Newcastle upon Tyne, UK, 2007. [Google Scholar]
- International Maritime Organization (IMO). Code of Safe Practice for Cargo Stowage and Securing, 2021 ed.; Witherbys: Scotland, UK, 2021. [Google Scholar]
- 0030/ND Rev. 6.1. 28 June 2016; Technical Standards Committee Guidelines for Marine Transportations. GL Noble Denton: Loughborough, UK, 2016.
- Söding, H.; Shigunov, V.; Zorn, T.; Soukup, P. Method rolls for simulating roll motions of ships. Ship Technol. Res. 2013, 60, 70–84. [Google Scholar] [CrossRef]
- Umadevi, R.; Venugopal, K.; Jeyabarathi, P.; Rajendran, L.; Abukhaled, M. Analytical study of nonlinear roll motion of ships: A homotopy perturbation approach. Palest. J. Math. 2022, 11, 316–325. [Google Scholar]
- Gowthaman, D.; Balagnesan, P.; Rajendra, L. Mathematical modeling of roll motion of ships: New approach of homotopy perturbation method. Int. J. Sci. Technol. Res. 2019, 8, 2539–2545. [Google Scholar]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Laouini, G.; Alshammari, F.S. Study of Rolling Motion of Ships in Random Beam Seas with Nonlinear Restoring Moment and Damping Effects Using Neuroevolutionary Technique. Materials 2022, 15, 674. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.Y. Nonlinear rolling motion of ship in random beam seas. J. Mar. Sci. Technol. 2004, 12, 273–279. [Google Scholar] [CrossRef]
- Son, K.-S.; Kim, S.-M.; Kwak, M.K.; Zhu, W. Development of a control algorithm for active control of rolling motion of a ship using a gyrostabilizer. Ocean Eng. 2023, 280, 114669. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, X.; Wang, Z.-H.; Peng, Y.; Xie, S.-R. A data driven method for multi-step prediction of ship roll motion in high sea states. Ocean Eng. 2023, 276, 114230. [Google Scholar] [CrossRef]
- Begovic, E.; Boccadamo, G.; Rinauro, B.; Rosano, G. Excessive acceleration simplified Operational Guidance. Ocean Eng. 2022, 14, 100473. [Google Scholar] [CrossRef]
- Ma, S.; Ge, W.-P.; Ertekin, R.C.; He, Q.; Duan, W.-Y. Experimental and numerical investigations of ship parametric rolling in regular head waves. China Ocean Eng. 2018, 32, 431–442. [Google Scholar] [CrossRef]
- Deleanu, D.; Dumitrache, C.L. Controlling the parametric roll of a container ship model by changing the forward velocity. IOP Conf. Ser. Mater. Eng. 2020, 916, 012024. [Google Scholar] [CrossRef]
- Shin, D.; Sung, Y.; Jeong, H.; Kim, D.; Moon, B. Evaluation of Parametric Roll Mode Applying the IMO Second Generation Intact Stability Criteria for 13K Chemical Tanker. J. Mar. Sci. Eng. 2023, 11, 1462. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). International Code on Intact Stability, 2008; IMO: London, UK, 2020. [Google Scholar]
- Petacco, N.; Gualeni, P. IMO second generation intact stability criteria: General overview and focus on operational measures. J. Mar. Sci. Eng. 2020, 8, 494. [Google Scholar] [CrossRef]
- Pérez-Canosa, J.M.; Iglesias-Baniela, S.; Salgado Don, A. The Limitations on the Use of the IMO CSS Code in Project Cargo—Case Study: Grillage Design for the Sea Transport of Gas Slug Catchers. App. Mech. 2020, 1, 123–141. [Google Scholar] [CrossRef]
- DNV. Rules for Classification of Ships. Part 3. Chapter 1. Hull Structural Design—Ships with Length 100 Metres and Above. 2016. Available online: https://civamblog.files.wordpress.com/2016/11/ts301.pdf (accessed on 9 September 2023).
- Pérez-Canosa, J.M.; Orosa, J.A.; Galdo, M.I.L.; Barros, J.J.C. A New Theoretical Dynamic Analysis of Ship Rolling Motion Considering Navigational Parameters, Loading Conditions and Sea State Conditions. J. Mar. Sci. Eng. 2022, 10, 1646. [Google Scholar] [CrossRef]
- Orosa, J.A.; Pérez-Canosa, J.M.; Pérez-Castelo, F.J.; Durán-Grados, V. Research on the Improvement of Safety Navigation Based on the Shipmaster’s Control of Ship Navigational Parameters When Sailing in Different Sea State Conditions. Appl. Sci. 2023, 13, 4486. [Google Scholar] [CrossRef]
- Medina, M. The Sea and the Weather. Nautical Meteorology, 3rd ed.; Juventud: Barcelona, Spain, 2007. [Google Scholar]
- Pérez-Canosa, J.M.; Orosa, J.A.; Fraguela, F.; López-Varela, P. Proposal of Optimal Operation in Ship Rolling Motion Considering Sea State Conditions. J. Mar. Sci. Eng. 2022, 10, 669. [Google Scholar] [CrossRef]
- Olivella-Puig, J. Ship’s Theory: Trochoidal Wave, Movements and Forces, 2nd ed.; Universitat Politécnica de Catalunya: Barcelona, Spain, 2011. [Google Scholar]
- Bonilla de la Corte, A. Ship’s Theory, 4th ed.; Librería San José: Vigo, Spain, 1994. [Google Scholar]
- International Maritime Organization (IMO). International Convention on Load Lines, 1966, 2021 ed.; International Maritime Organization: London, UK, 2021. [Google Scholar]



| Variable | Value |
|---|---|
| Length (L) | 100 m |
| Beam (B) | 15.6 m |
| Depth cargo hold (Dep) | 9.0 m |
| Draught (d) | 6.0 m |
| Displacement (D) | 5500 Tm |
| KG | 4.0 m |
| GM | 1.1 m |
| Hatch cover coaming height | 2.0 m |
| Roll natural period (Td) | 12 s |
| Block coefficient (Cb) | 0.812 |
| Bilge keels | Nil |
| θ mean (initial) | 12° |
| Wave and Ship Parameters | New Model | CSS | DNV | ||
|---|---|---|---|---|---|
| Tw (average) | 12 s | 0.058 | 12 s | 0.061 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (low) | 6 s | 0.071 | 6 s | 0.068 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (high) | 20 s | 0.057 | 20 s | 0.068 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (average) | 12 s | 0.057 | 12 s | 0.061 | 0.099 |
| α angle (high) | 080° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (average) | 12 s | 0.056 | 12 s | 0.061 | 0.099 |
| α angle (low) | 010° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (average) | 12 s | 0.094 | 12 s | 0.084 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (high) | 20 kt | 20 kt | |||
| Tw (average) | 12 s | 0.057 | 12 s | 0.047 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (low) | 5 kt | 5 kt | |||
| Tw (high) | 20 s | 0.057 | 20 s | 0.068 | 0.099 |
| α angle (low) | 010° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (high) | 20 s | 0.057 | 20 s | 0.052 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (low) | 5 kt | 5 kt | |||
| Tw (low) | 6 s | 0.107 | 6 s | 0.068 | 0.099 |
| α angle (high) | 080° | - | |||
| Vship (average) | 10 kt | 10 kt | |||
| Tw (low) | 6 s | 0.073 | 6 s | 0.083 | 0.099 |
| α angle (average) | 045° | - | |||
| Vship (high) | 20 kt | 20 kt |
| Tw (s) | Lw (m) | Hw (m) |
|---|---|---|
| 9 | 124.76 | 4.15 |
| 15 | 349.50 | 11.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Canosa, J.M.; Orosa, J.A.; de Osés, F.X.M.; Lama-Carballo, F.J. Optimization of Ship’s Navigational Parameters to Improve the Stowage and Securing Criteria of Non-Standardized Cargo in Ships. J. Mar. Sci. Eng. 2023, 11, 1782. https://doi.org/10.3390/jmse11091782
Pérez-Canosa JM, Orosa JA, de Osés FXM, Lama-Carballo FJ. Optimization of Ship’s Navigational Parameters to Improve the Stowage and Securing Criteria of Non-Standardized Cargo in Ships. Journal of Marine Science and Engineering. 2023; 11(9):1782. https://doi.org/10.3390/jmse11091782
Chicago/Turabian StylePérez-Canosa, José M., José A. Orosa, Francesc Xavier Martínez de Osés, and Fco. Javier Lama-Carballo. 2023. "Optimization of Ship’s Navigational Parameters to Improve the Stowage and Securing Criteria of Non-Standardized Cargo in Ships" Journal of Marine Science and Engineering 11, no. 9: 1782. https://doi.org/10.3390/jmse11091782
APA StylePérez-Canosa, J. M., Orosa, J. A., de Osés, F. X. M., & Lama-Carballo, F. J. (2023). Optimization of Ship’s Navigational Parameters to Improve the Stowage and Securing Criteria of Non-Standardized Cargo in Ships. Journal of Marine Science and Engineering, 11(9), 1782. https://doi.org/10.3390/jmse11091782








