A Machine-Learning Approach Based on Attention Mechanism for Significant Wave Height Forecasting
Abstract
:1. Introduction
2. Materials
2.1. Experimental Data
2.2. Feature Selection
2.3. Data Preprocessing
2.4. Wave Scale Classification Criteria
3. Methodology
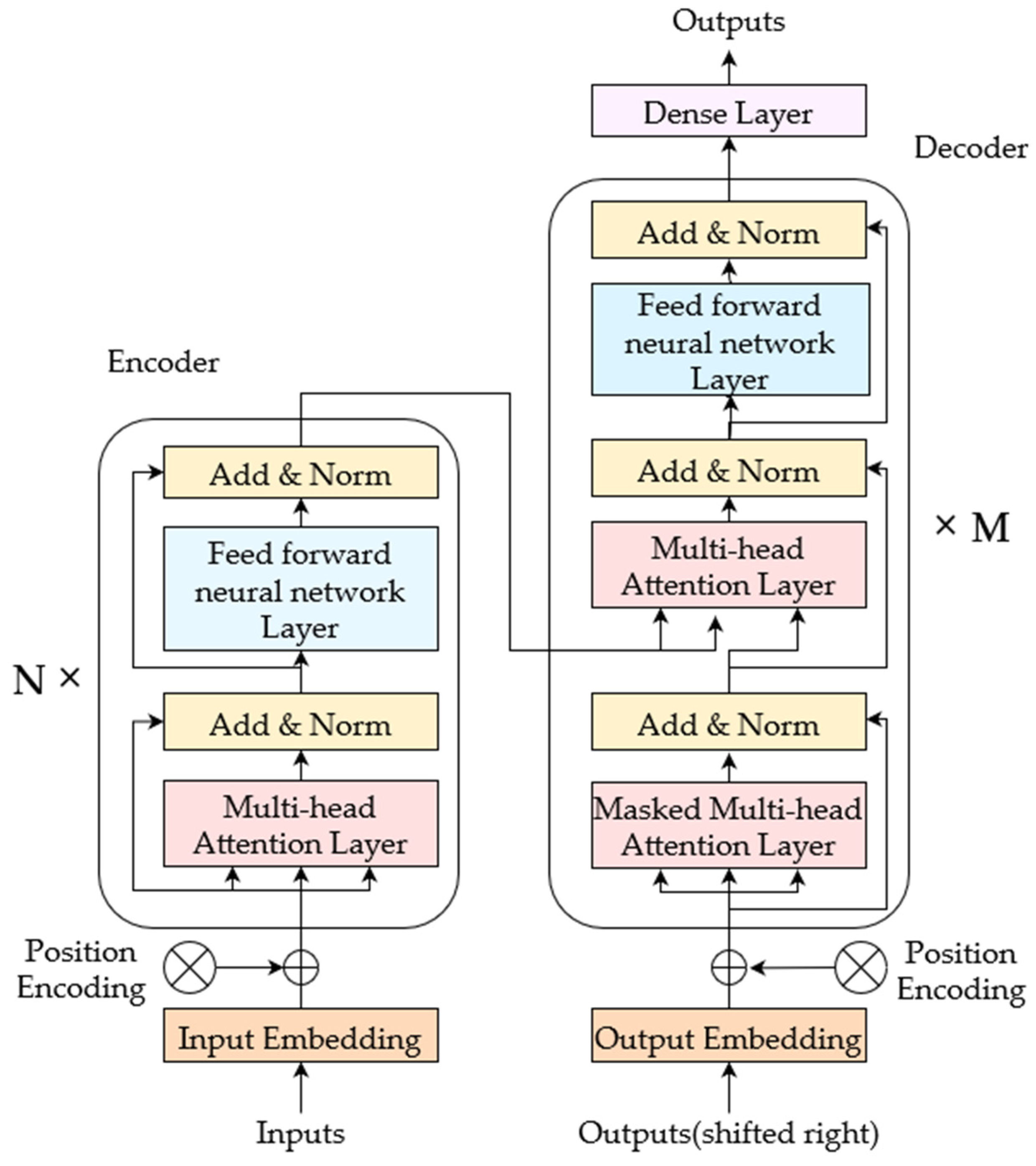
3.1. Model Structure
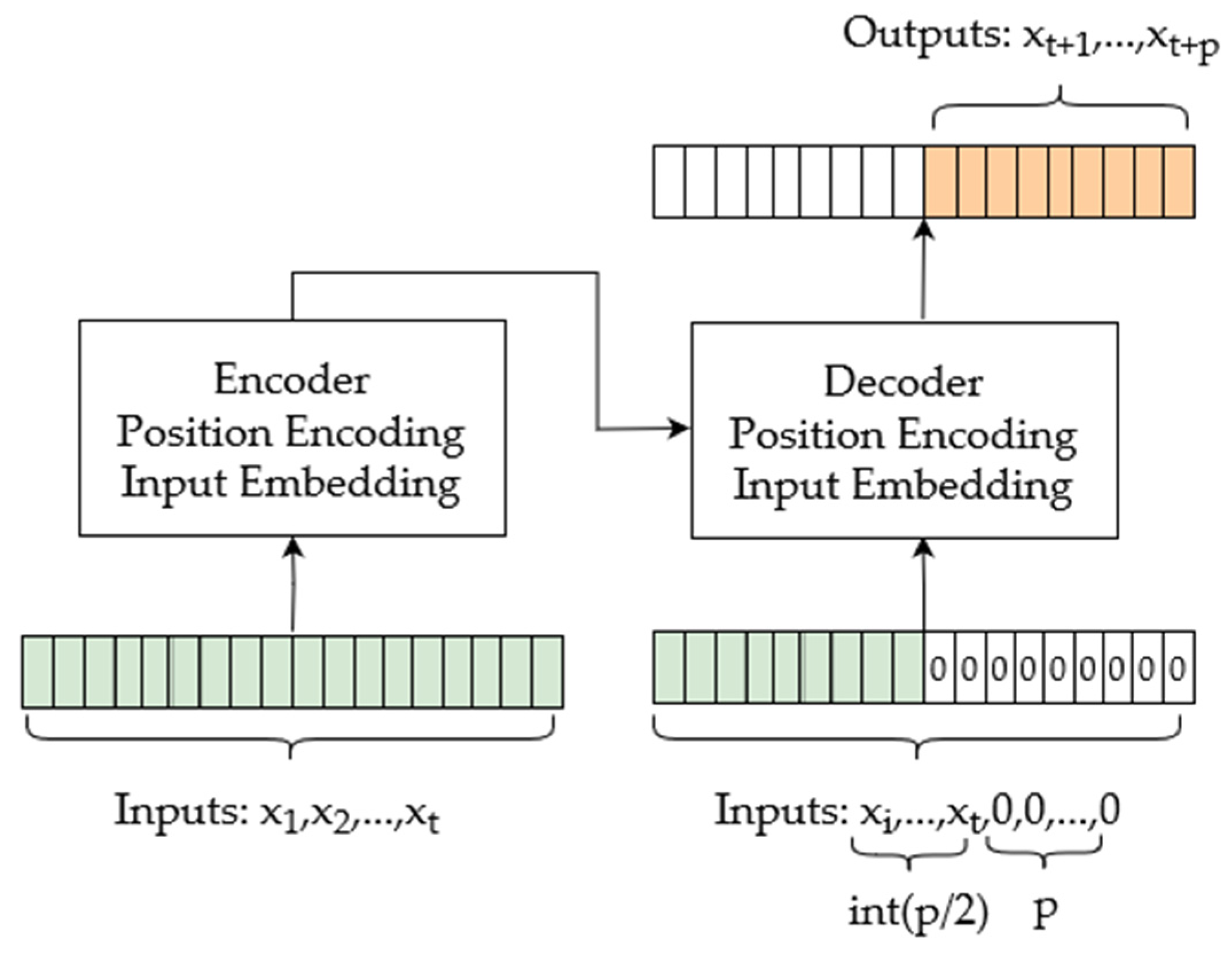
3.2. Introduction of the Output Method
3.3. Parameter Settings
3.4. MASNUM Ocean Wave Numerical Model
3.5. Evaluation Metrics
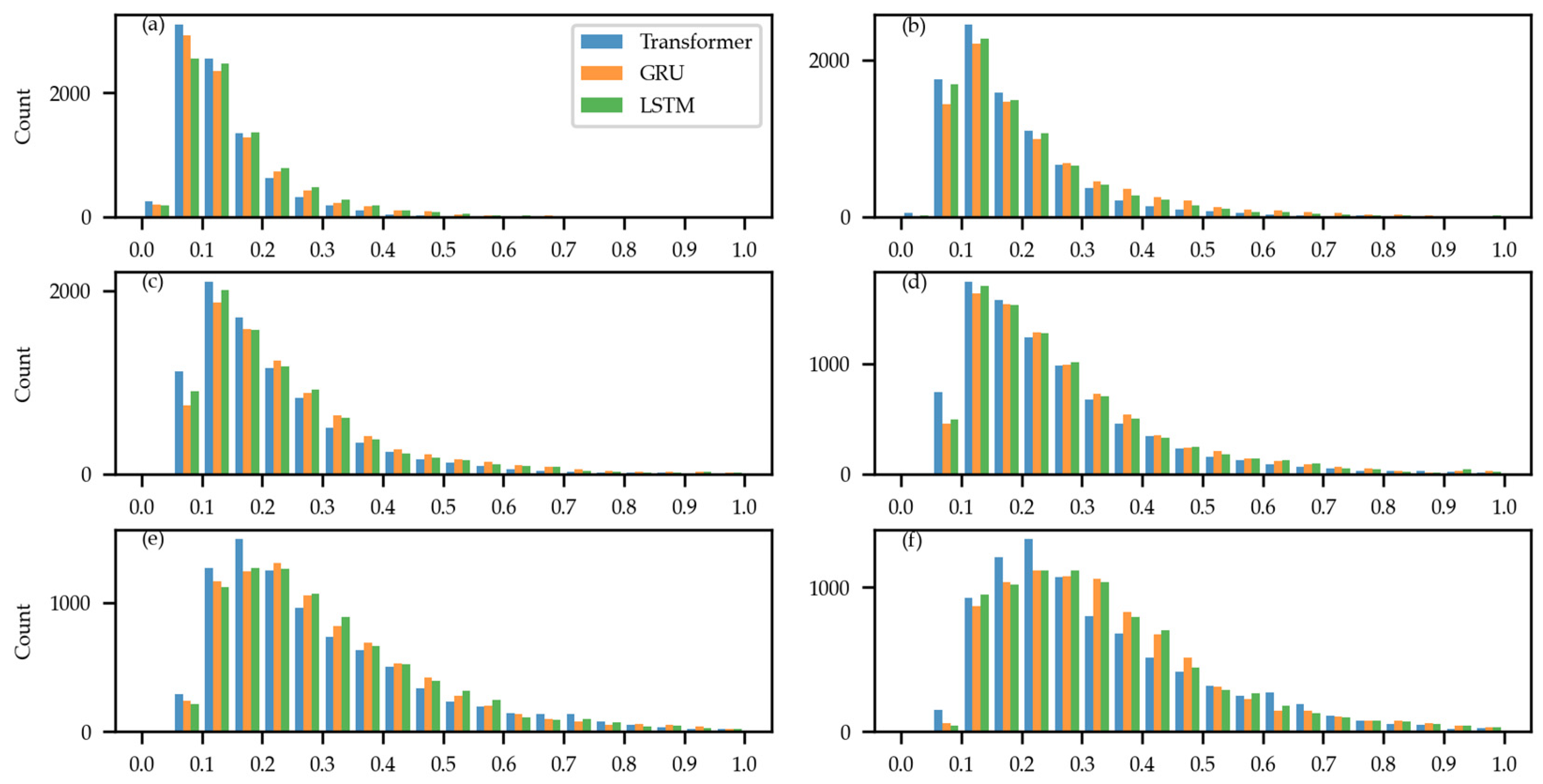
4. Results and Discussion
5. Conclusions
- The transformer model extracted key information from wave data, realizing the continuous forecasting of waves and early warning of wave scale levels, with higher forecasting accuracies than those of the MASNUM numerical model and GRU and LSTM.
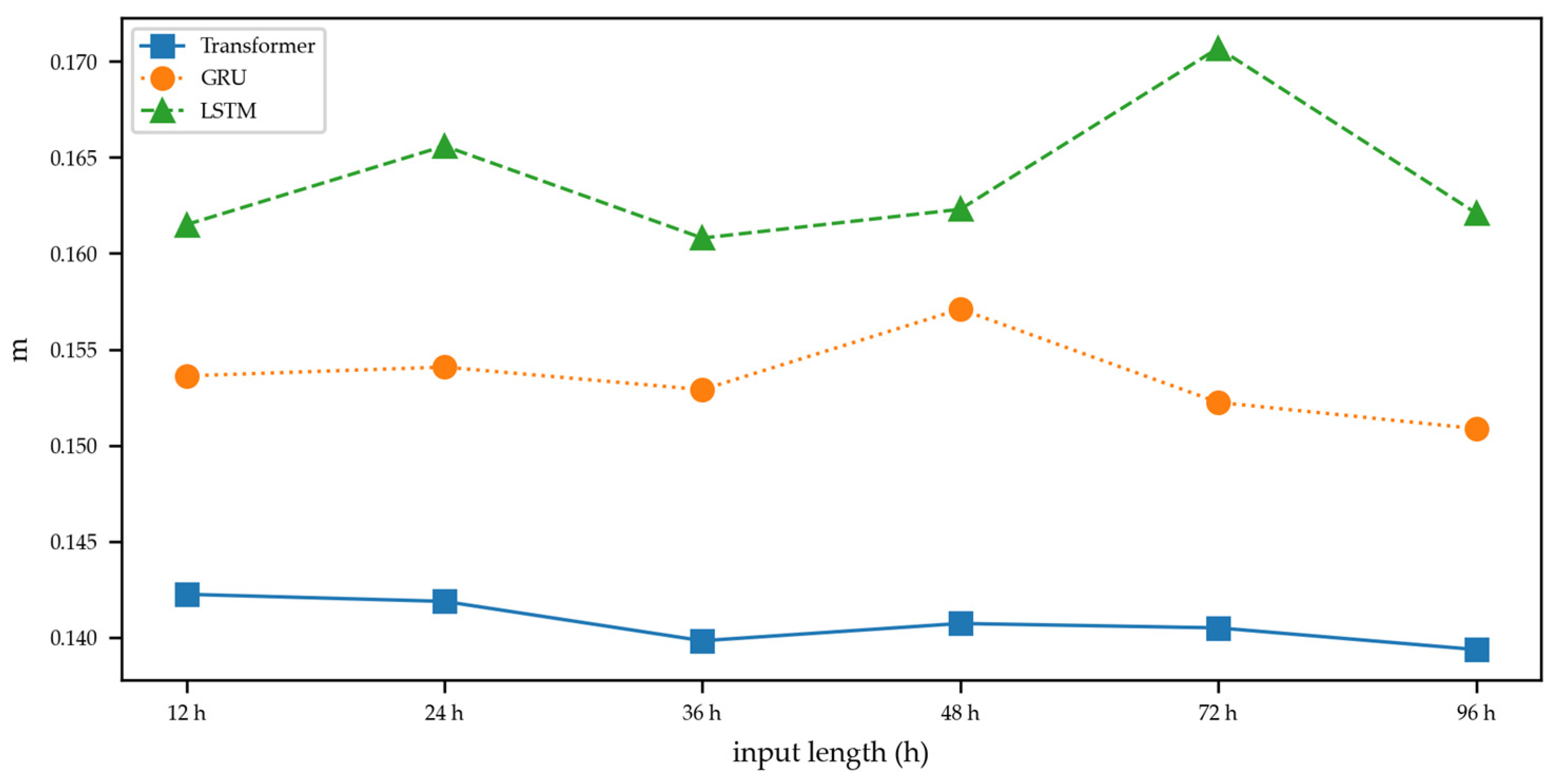
- Unlike the GRU and LSTM models, our transformer method was less affected by the time length of the input sequence.
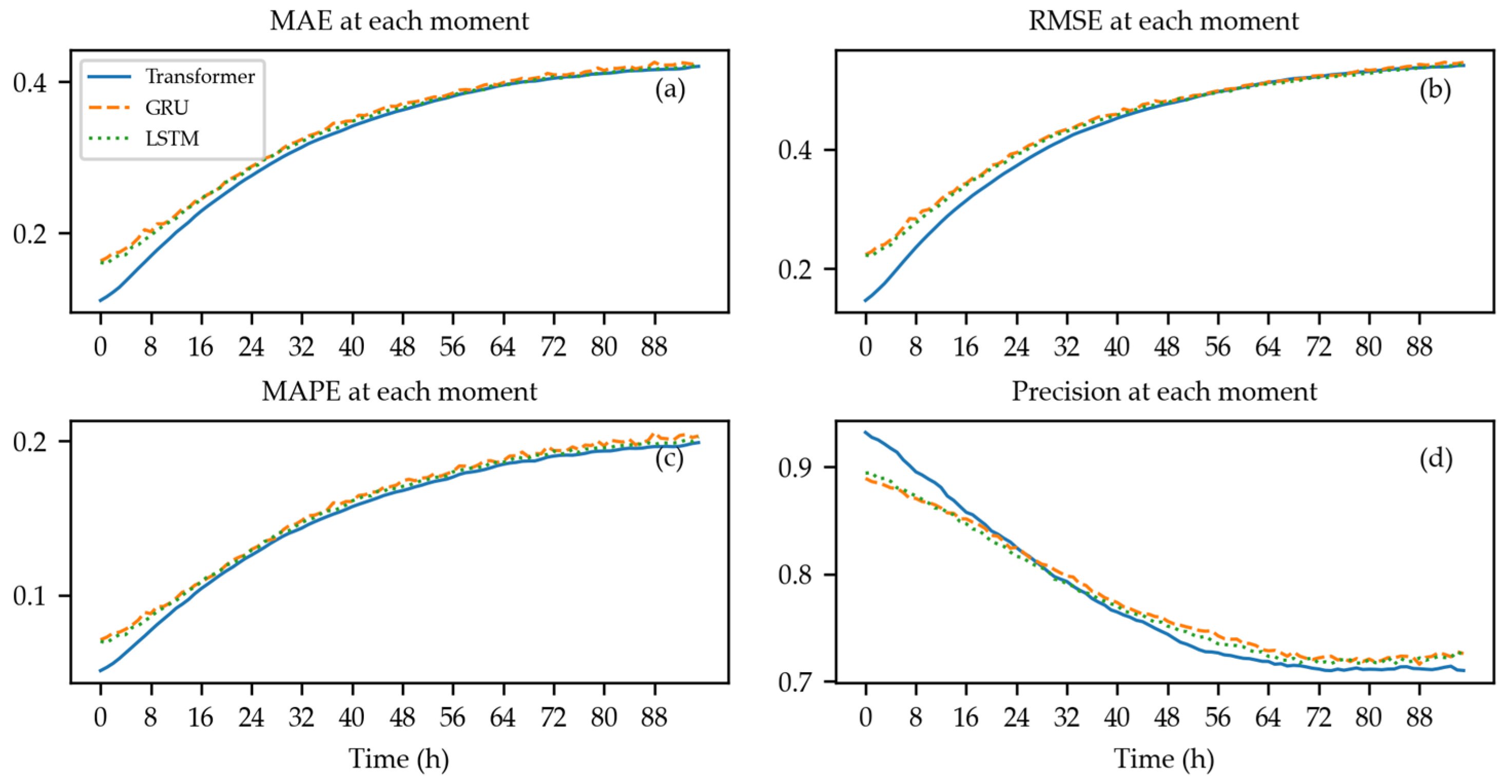
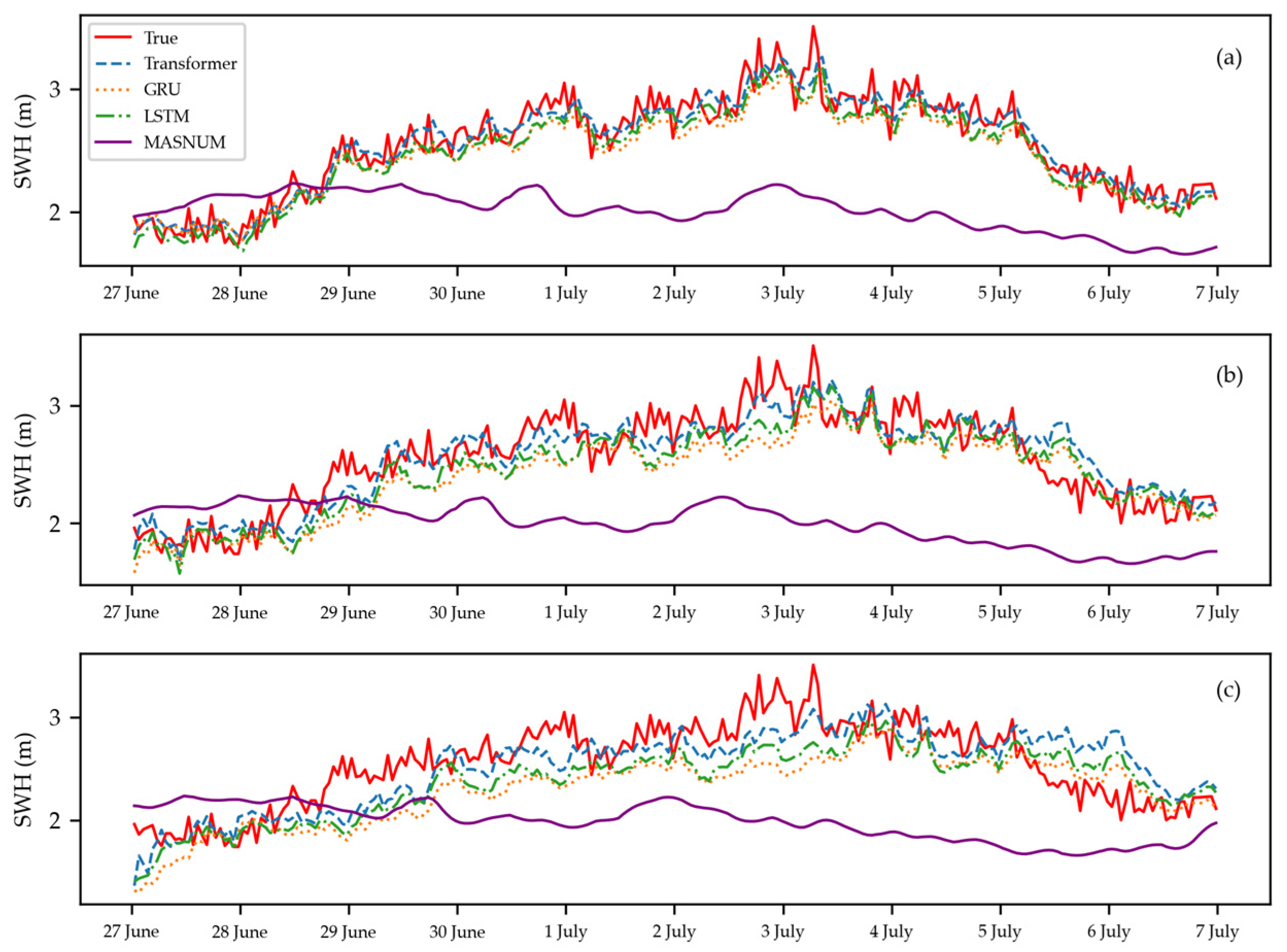
- In the long-sequence forecasting process, the transformer model significantly outperformed the GRU and LSTM models in accurately forecasting future short-term wave height.
- The wave scale levels in the sea area where the buoy was located were mainly moderate sea and rough sea, and the transformer model performed better in SWH forecasting and scale classification for these.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, C.; Xu, G.; Han, G.; Bethel, B.J.; Xie, W.; Zhou, S. Recent Developments in Artificial Intelligence in Oceanography. Ocean. Land Atmos. Res. 2022, 2022, 9870950. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Z.; Guo, X. Research progress in the application of deep learning to ocean information detection: Status and prospect. Mar. Sci. 2022, 46, 145–155. [Google Scholar]
- Prahlada, R.; Deka, P.C. Forecasting of Time Series Significant Wave Height Using Wavelet Decomposed Neural Network. In Proceedings of the International Conference on Water Resources, Coastal and Ocean Engineering (ICWRCOE), Mangaluru, India, 11–14 March 2015; pp. 540–547. [Google Scholar]
- Xia, T.; Li, X.; Yang, S. Prediction of wave height based on BAS-BP model in the northern part of the South China Sea. Trans. Oceanol. Limnol. 2021, 9–16. [Google Scholar]
- Jin, Q.; Hua, F.; Yang, Y. Prediction of the Significant Wave Height Based on the Support Vector Machine. Adv. Mar. Sci. 2019, 37, 199–209. [Google Scholar]
- Wang, Y.; Zhong, J.; Zhang, Z. Application of support vector regression in significant wave height forecasting. Mar. Forecast 2020, 37, 29–34. [Google Scholar]
- Berbic, J.; Ocvirk, E.; Carevic, D.; Loncar, G. Application of neural networks and support vector machine for significant wave height prediction. Oceanologia 2017, 59, 331–349. [Google Scholar] [CrossRef]
- Zhou, S.; Bethel, B.J.; Sun, W.; Zhao, Y.; Xie, W.; Dong, C. Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition-Long Short-Term Memory Network. J. Mar. Sci. Eng. 2021, 9, 744. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, W.; Lu, Y.; Wang, Y.; Zhou, Y.; Hui, N.; Dong, C. ConvLSTM-Based Wave Forecasts in the South and East China Seas. Front. Mar. Sci. 2021, 8, 680079. [Google Scholar] [CrossRef]
- Fan, S.; Xiao, N.; Dong, S. A novel model to predict significant wave height based on long short-term memory network. Ocean Eng. 2020, 205, 107298. [Google Scholar] [CrossRef]
- Jörges, C.; Berkenbrink, C.; Stumpe, B. Prediction and reconstruction of ocean wave heights based on bathymetric data using LSTM neural networks. Ocean Eng. 2021, 232, 109046. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Gao, S.; Ren, P. Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. J. Mar. Sci. Eng. 2021, 9, 514. [Google Scholar] [CrossRef]
- Ma, J.; Xue, H.; Zeng, Y.; Zhang, Z.; Wang, Q. Significant wave height forecasting using WRF-CLSF model in Taiwan strait. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1400–1419. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, P.; Li, S.; Mo, D. Prediction of Significant Wave Height in Offshore China Based on the Machine Learning Method. J. Mar. Sci. Eng. 2022, 10, 836. [Google Scholar] [CrossRef]
- Xie, C.; Liu, X.; Man, T.; Xie, T.; Dong, J.; Ma, X.; Zhao, Y.; Dong, G. PWPNet: A Deep Learning Framework for Real-Time Prediction of Significant Wave Height Distribution in a Port. J. Mar. Sci. Eng. 2022, 10, 1375. [Google Scholar] [CrossRef]
- Meng, F.; Xu, D.; Song, T. ATDNNS: An adaptive time–frequency decomposition neural network-based system for tropical cyclone wave height real-time forecasting. Future Gener. Comput. Syst. 2022, 133, 297–306. [Google Scholar] [CrossRef]
- Alqushaibi, A.; Abdulkadir, S.J.; Rais, H.M.; Al-Tashi, Q.; Ragab, M.G.; Alhussian, H. Enhanced Weight-Optimized Recurrent Neural Networks Based on Sine Cosine Algorithm for Wave Height Prediction. J. Mar. Sci. Eng. 2021, 9, 524. [Google Scholar] [CrossRef]
- Hao, P.; Li, S.; Yu, C.; Wu, G. A Prediction Model of Significant Wave Height in the South China Sea Based on Attention Mechanism. Front. Mar. Sci. 2022, 9, 895212. [Google Scholar] [CrossRef]
- Wang, L.; Deng, X.; Ge, P.; Dong, C.; Bethel, B.J.; Yang, L.; Xia, J. CNN-BiLSTM-Attention Model in Forecasting Wave Height over South-East China Seas. Comput. Mater. Contin. 2022, 73, 2151–2168. [Google Scholar] [CrossRef]
- Luo, Q.; Xu, H.; Bai, L. Prediction of significant wave height in hurricane area of the Atlantic Ocean using the Bi-LSTM with attention model. Ocean Eng. 2022, 266, 112747. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Guo, J.; Liu, C.; Wang, W.; Jia, Z.; Su, T. Multi-step forecasting of ocean wave height using gate recurrent unit networks with multivariate time series. Ocean Eng. 2022, 248, 110689. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yang, J. Forecasting of Significant Wave Height Based on Gated Recurrent Unit Network in the Taiwan Strait and Its Adjacent Waters. Water 2021, 13, 86. [Google Scholar] [CrossRef]
- Yevnin, Y.; Chorev, S.; Dukan, I.; Toledo, Y. Short-term wave forecasts using gated recurrent unit model. Ocean Eng. 2022, 268, 113389. [Google Scholar] [CrossRef]
- Meng, F.; Song, T.; Xu, D.; Xie, P.; Li, Y. Forecasting tropical cyclones wave height using bidirectional gated recurrent unit. Ocean Eng. 2021, 234, 108795. [Google Scholar] [CrossRef]
- Sukanda, A.J.T.; Adytia, D. Wave Forecast using Bidirectional GRU and GRU Method Case Study in Pangandaran, Indonesia. In Proceedings of the 2022 International Conference on Data Science and Its Applications (ICODSA), Bandung, Indonesia, 6–7 July 2022; pp. 278–282. [Google Scholar]
- Celik, A. Improving prediction performance of significant wave height via hybrid SVD-Fuzzy model. Ocean Eng. 2022, 266, 113173. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems, Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Dong, L.; Xu, S.; Xu, B. Speech-Transformer: A No-Recurrence Sequence-to-Sequence Model for Speech Recognition. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5884–5888. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2021, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In AAAI Conference on Artificial Intelligence, Proceedings of the 35th AAAI Conference on Artificial Intelligence 33rd Conference on Innovative Applications of Artificial Intelligence 11th Symposium on Educational Advances in Artificial Intelligence, Washington, DC, USA, 2–9 February 2021; AAAI Press: Washington, DC, USA, 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Advances in Neural Information Processing Systems, Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Electr Network, 6–14 December 2021; NeurIPS Proceedings: San Diego, CA, USA, 2021; Volume 34. [Google Scholar]
- Tuli, S.; Casale, G.; Jennings, N.R. TranAD: Deep Transformer Networks for Anomaly Detection in Multivariate Time Series Data. Proc. Vldb. Endow. 2022, 15, 1201–1214. [Google Scholar] [CrossRef]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Electr Network, 14–18 August 2021; AAAI Press: Washington, DC, USA, 2021; pp. 2114–2124. [Google Scholar]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Immas, A.; Do, N.; Alam, M.R. Real-time in situ prediction of ocean currents. Ocean Eng. 2021, 228, 108922. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, R. A self-attention-based neural network for three-dimensional multivariate modeling and its skillful ENSO predictions. Sci. Adv. 2023, 9, eadf2827. [Google Scholar] [CrossRef]
- Ye, F.; Hu, J.; Huang, T.; You, L.; Weng, B.; Gao, J. Transformer for EI Niño-Southern Oscillation Prediction. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1003305. [Google Scholar] [CrossRef]
- Pokhrel, P.; Ioup, E.; Simeonov, J.; Hoque, M.T.; Abdelguerfi, M. A Transformer-Based Regression Scheme for Forecasting Significant Wave Heights in Oceans. IEEE J. Ocean Eng. 2022, 47, 1010–1023. [Google Scholar] [CrossRef]
- Chang, W.; Li, X.; Dong, H.; Wang, C.; Zhao, Z.; Wang, Y. Real-Time Prediction of Ocean Observation Data Based on Transformer Model. In Proceedings of the 2021 ACM International Conference on Intelligent Computing and its Emerging Applications, Jinan, China, 28–29 December 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 83–88. [Google Scholar]
- Ham, Y.G.; Kim, J.H.; Luo, J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Putri, D.A.; Adytia, D. Time Series Wave Forecasting with Transformer Model, Case Study in Pelabuhan Ratu, Indonesia. In Proceedings of the 2022 10th International Conference on Information and Communication Technology (ICoICT), Bandung, Indonesia, 2–3 August 2022; pp. 430–434. [Google Scholar]
- Li, J.; Zhou, L.; Zheng, C.; Han, X.; Chen, X. Spatial-temporal variation analysis of sea wave field in the Pacific Ocean. Mar. Sci. 2012, 36, 94–100. [Google Scholar]
- Liu, J.; Jiang, W.; Yu, M.; Ni, J.; Liang, G. An analysis on annual variation of monthly mean sea wave fields in north Pacific Ocean. J. Trop. Oceanogr. 2002, 21, 64–69. [Google Scholar]
- Allahdadi, M.N.; Ruoying, H.R.; Neary, V.S. Predicting ocean waves along the US east coast during energetic winter storms: Sensitivity to whitecapping parameterizations. Ocean Sci. 2019, 15, 691–715. [Google Scholar] [CrossRef]
- GB/T 12763.2-2007; Specifications for Oceanographic Survey—Part 2: Marine Hydrographic Observation. Inspection and Quarantine of the People’s Republic of China and Standardization Administration of China: Qingdao, China, 2007.
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yang, Y.; Qiao, F.; Zhao, W.; Teng, Y.; Yuan, L. MASNUM ocean wave numerical model in spherical coordinates and its application. Acta Oceanol. Sin. 2005, 27, 1–2. [Google Scholar]

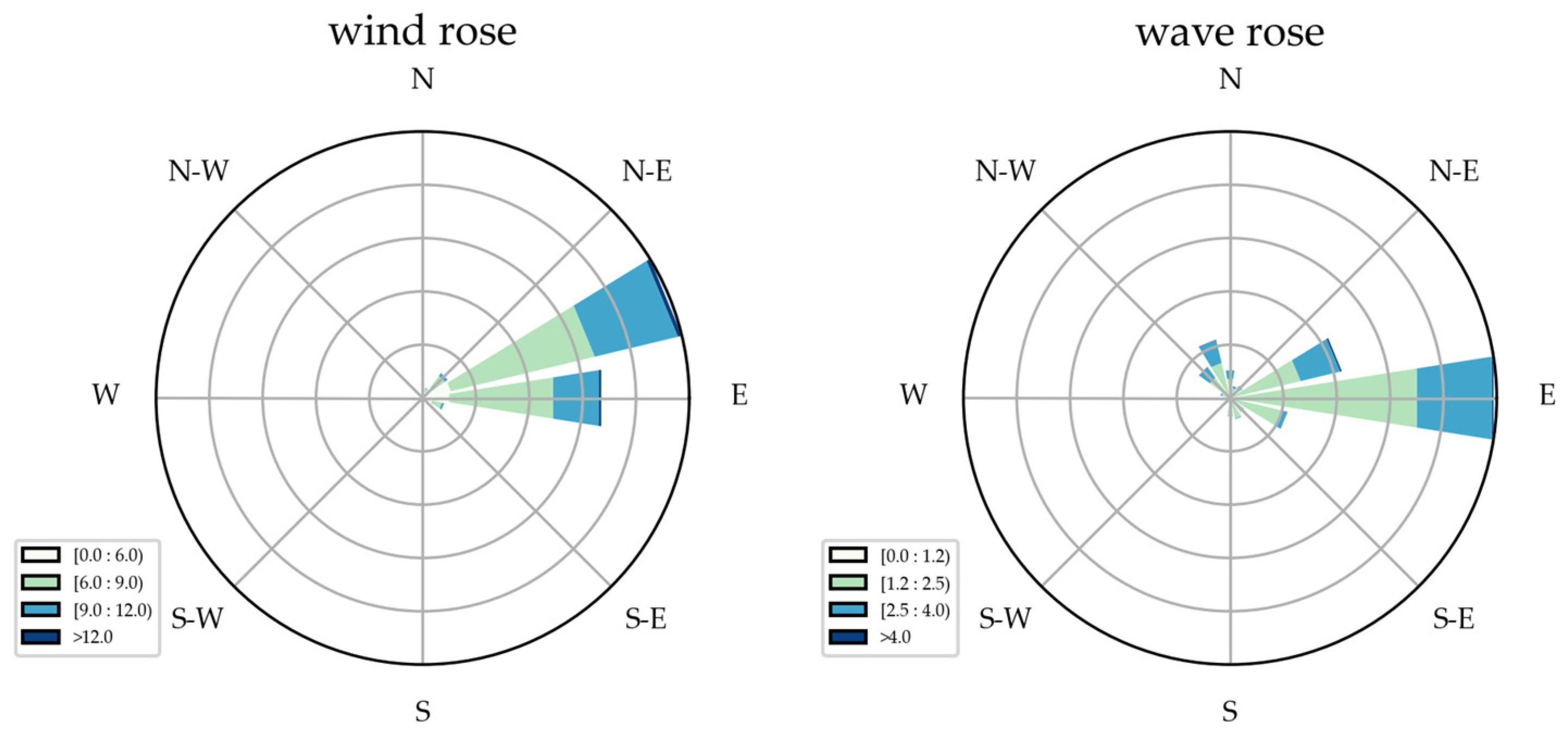
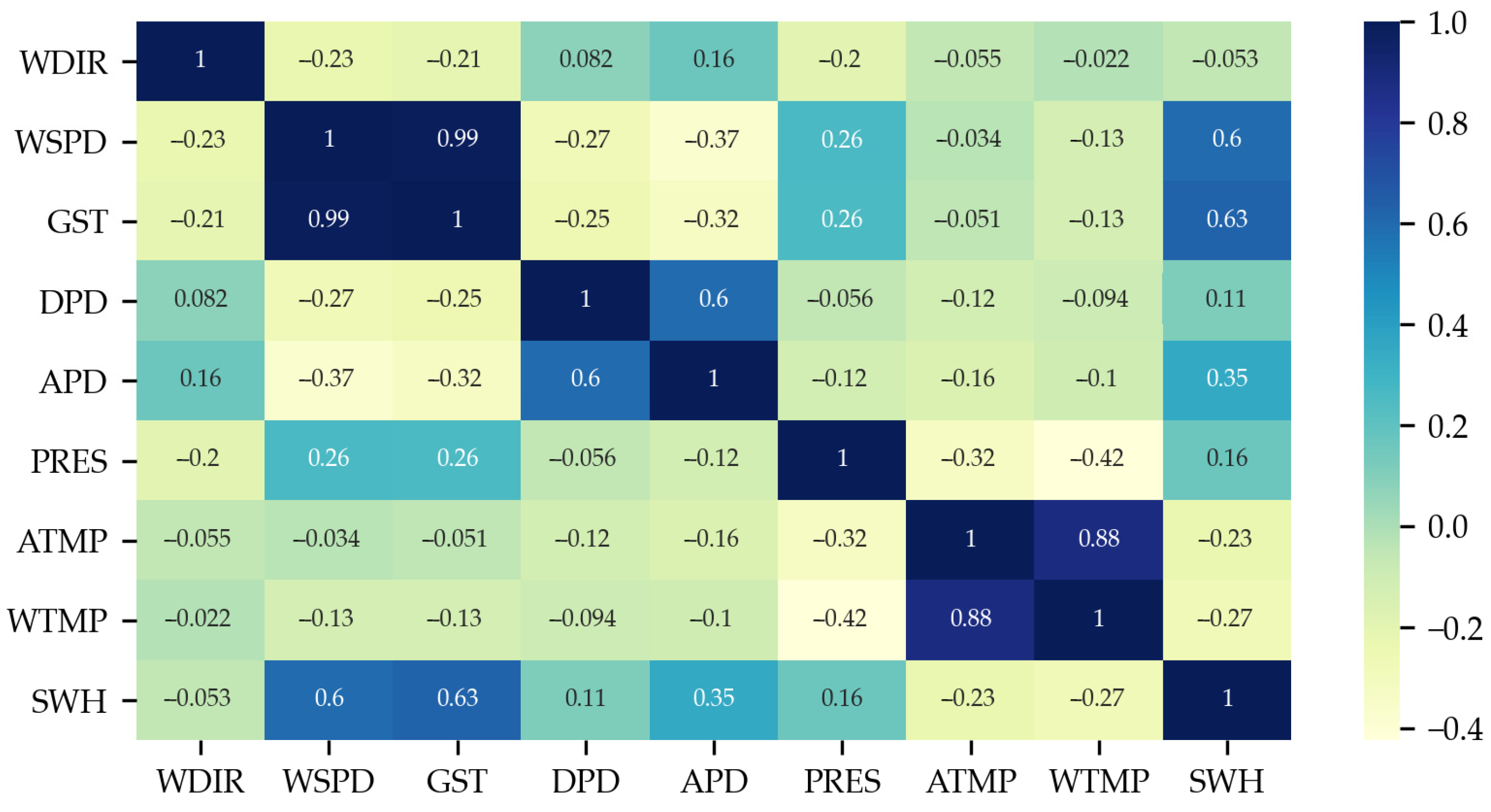

| Location | 17°2′32″ N, 157°44′47″ W |
|---|---|
| Site elevation | sea level |
| Air temp height | 3.7 m above site elevation |
| Anemometer height | 4.1 m above site elevation |
| Barometer elevation | 2.7 m above mean sea level |
| Sea temp depth | 1.5 m below water line |
| Water depth | 4997 m |
| Watch circle radius | 4691.7864 m |
| Station Id | Max_SWH | Min_SWH | Mean_SWH | Variance_SWH |
|---|---|---|---|---|
| 51002 | 5.92 m | 0.49 m | 2.33 m | 0.36 |
| Dataset | Time_Range | Valid Sample Numbers |
|---|---|---|
| Training set | 1 January 2000–31 December 2018 | 117,706 |
| Validation set | 1 October 2019–31 December 2021 | 18,716 |
| Test set | 1 January 2022–31 December 2022 | 8760 |
| Forecast Hours | Encoder Stacks (N) | Decoder Stacks (M) |
|---|---|---|
| 12 | 1 | 1 |
| 24 | 1 | 1 |
| 36 | 2 | 1 |
| 48 | 6 | 1 |
| 72 | 2 | 2 |
| 96 | 4 | 2 |
| Forecast Hours | Model | Bias | MAE | RMSE | MAPE | Precision |
|---|---|---|---|---|---|---|
| 12 h | Transformer | −0.0035 | 0.1394 | 0.1939 | 6.36% | 91.09% |
| GRU | 0.0656 | 0.1522 | 0.2192 | 6.72% | 90.31% | |
| LSTM | 0.0713 | 0.1621 | 0.2265 | 7.18% | 89.58% | |
| MASNUM | 0.0148 | 0.3239 | 0.4077 | 15.12% | 81.16% | |
| 24 h | Transformer | −0.0146 | 0.1864 | 0.2613 | 8.57% | 88.38% |
| GRU | 0.1141 | 0.2256 | 0.3203 | 9.82% | 85.53% | |
| LSTM | 0.0830 | 0.2054 | 0.2910 | 9.05% | 86.76% | |
| MASNUM | 0.0153 | 0.3242 | 0.4121 | 15.16% | 81% | |
| 36 h | Transformer | 0.0261 | 0.2230 | 0.3146 | 10.17% | 85.97% |
| GRU | 0.1100 | 0.2567 | 0.3580 | 11.32% | 83.51% | |
| LSTM | 0.0859 | 0.2423 | 0.3407 | 10.75% | 84.26% | |
| MASNUM | 0.0151 | 0.3242 | 0.4234 | 15.16% | 80.67% | |
| 48 h | Transformer | 0.0236 | 0.2542 | 0.3547 | 11.67% | 83.3% |
| GRU | 0.0683 | 0.2776 | 0.3845 | 12.53% | 82.35% | |
| LSTM | 0.0787 | 0.2708 | 0.3761 | 12.14% | 82.15% | |
| MASNUM | 0.0163 | 0.3243 | 0.4351 | 15.2% | 80.5% | |
| 72 h | Transformer | 0.0186 | 0.3020 | 0.4145 | 13.93% | 78.9% |
| GRU | 0.041 | 0.3110 | 0.4236 | 14.285 | 79.62% | |
| LSTM | 0.0578 | 0.3133 | 0.4256 | 14.29% | 78.79% | |
| MASNUM | 0.0168 | 0.3275 | 0.4556 | 15.31% | 80.01% | |
| 96 h | Transformer | 0.0004 | 0.3290 | 0.4465 | 15.29% | 77.47% |
| GRU | 0.0247 | 0.3398 | 0.4558 | 15.79% | 77.73% | |
| LSTM | 0.0258 | 0.3362 | 0.4521 | 15.62% | 77.42% | |
| MASNUM | 0.0172 | 0.3363 | 0.4783 | 15.45% | 79.75% |
| Classification | 12 h_Mean | 24 h_Mean | 36 h_Mean | 48 h_Mean | 72 h_Mean | 96 h_Mean |
|---|---|---|---|---|---|---|
| Slight sea | 40% | 33% | 24% | 18% | 17% | 37% |
| Moderate sea | 94% | 92% | 89% | 88% | 84% | 82% |
| Rough sea | 83% | 77% | 76% | 69% | 61% | 57% |
| Very rough sea | 39% | 36% | 40% | 41% | 41% | 24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Su, T.; Li, X.; Wang, F.; Cui, J.; Liu, Z.; Wang, J. A Machine-Learning Approach Based on Attention Mechanism for Significant Wave Height Forecasting. J. Mar. Sci. Eng. 2023, 11, 1821. https://doi.org/10.3390/jmse11091821
Shi J, Su T, Li X, Wang F, Cui J, Liu Z, Wang J. A Machine-Learning Approach Based on Attention Mechanism for Significant Wave Height Forecasting. Journal of Marine Science and Engineering. 2023; 11(9):1821. https://doi.org/10.3390/jmse11091821
Chicago/Turabian StyleShi, Jiao, Tianyun Su, Xinfang Li, Fuwei Wang, Jingjing Cui, Zhendong Liu, and Jie Wang. 2023. "A Machine-Learning Approach Based on Attention Mechanism for Significant Wave Height Forecasting" Journal of Marine Science and Engineering 11, no. 9: 1821. https://doi.org/10.3390/jmse11091821
APA StyleShi, J., Su, T., Li, X., Wang, F., Cui, J., Liu, Z., & Wang, J. (2023). A Machine-Learning Approach Based on Attention Mechanism for Significant Wave Height Forecasting. Journal of Marine Science and Engineering, 11(9), 1821. https://doi.org/10.3390/jmse11091821






