Kelp Aquaculture as a Nature-Based Solution for Coastal Protection: Wave Attenuation by Suspended Canopies
Abstract
:1. Introduction
2. Materials and Methods
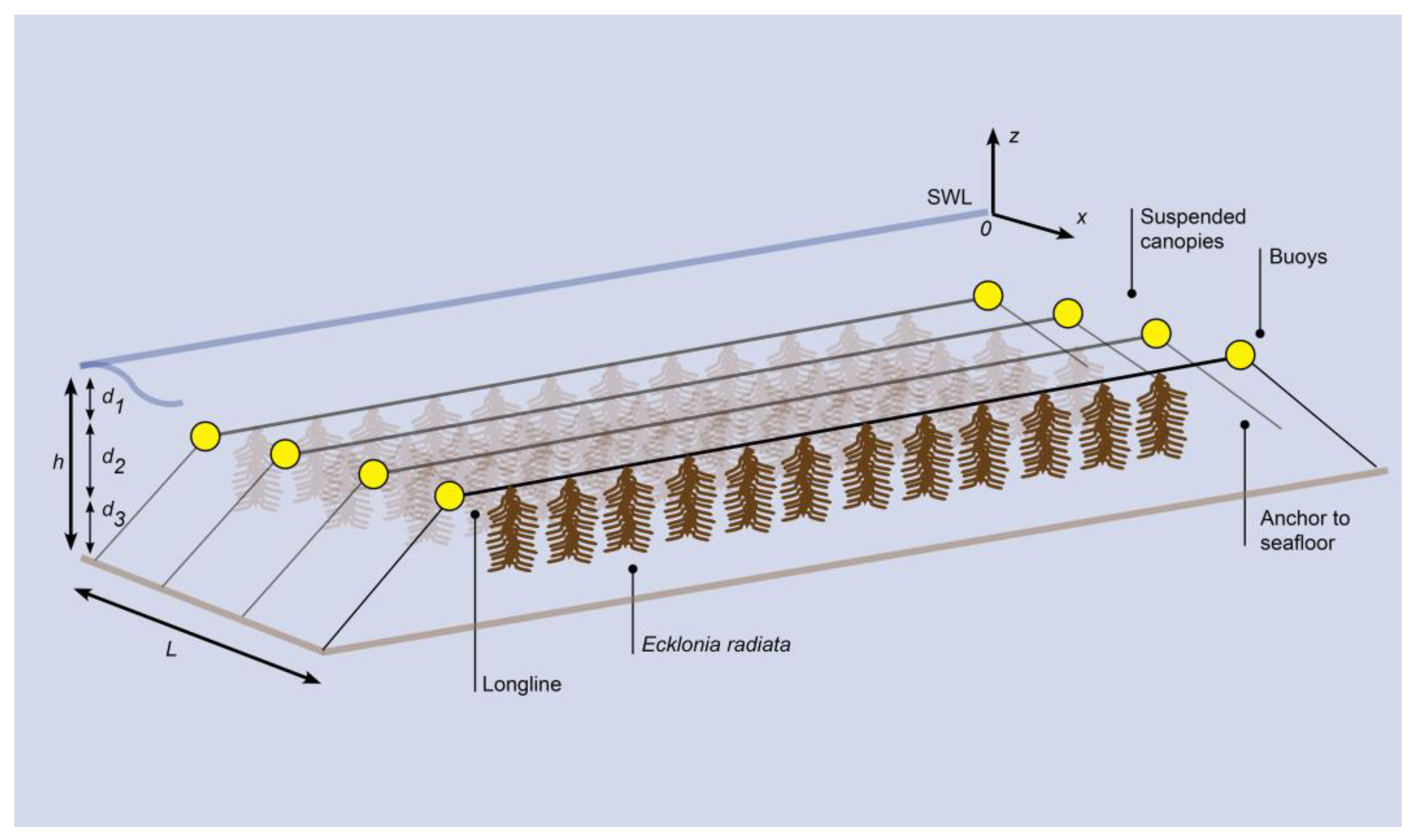
2.1. Model Overview
2.2. Model Adjustments
2.3. Modelled Scenarios (Parameters)
3. Results
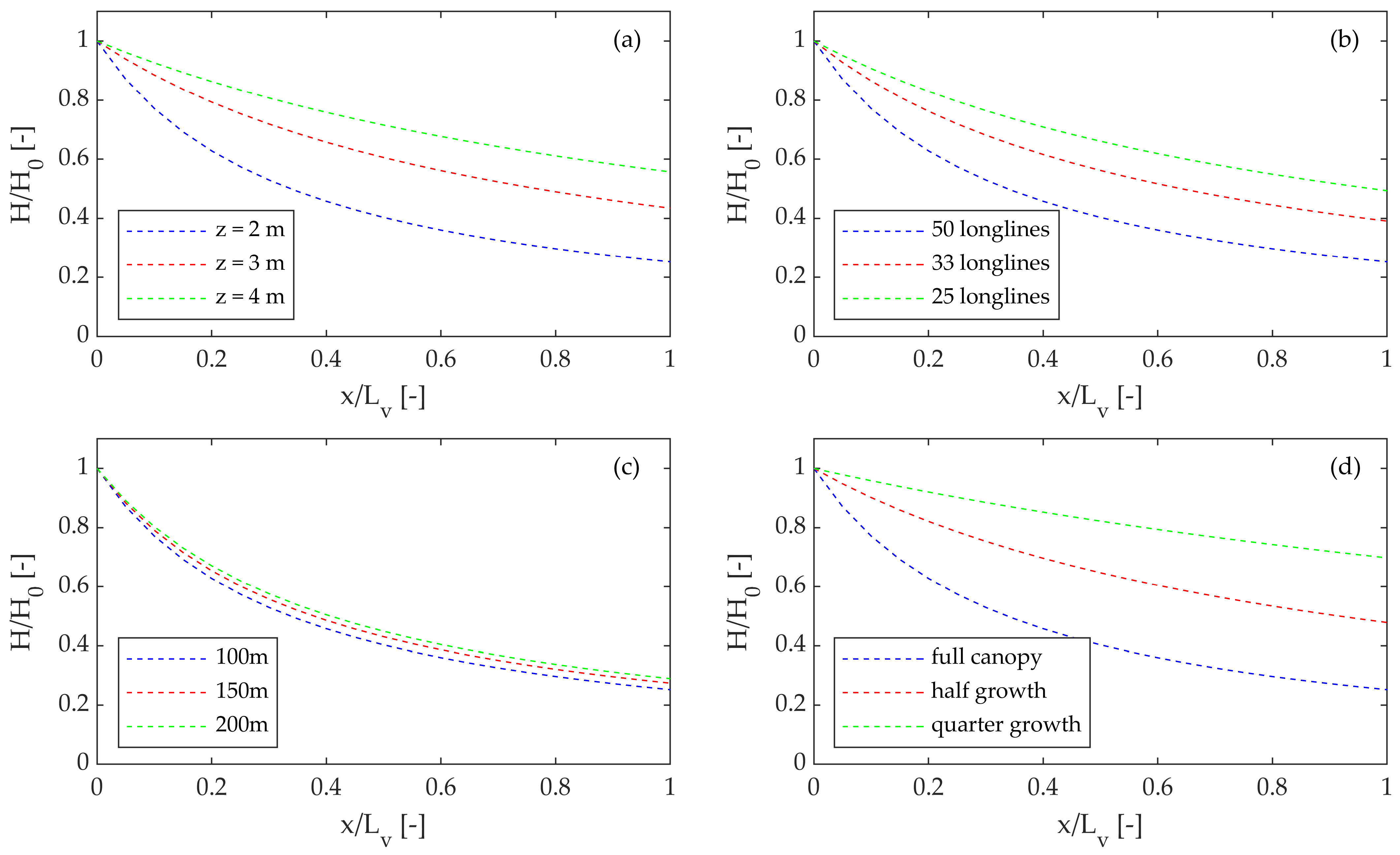
3.1. Water Depth
3.2. Vegetation Density
3.3. Area of Vegetation (Number of Longlines)
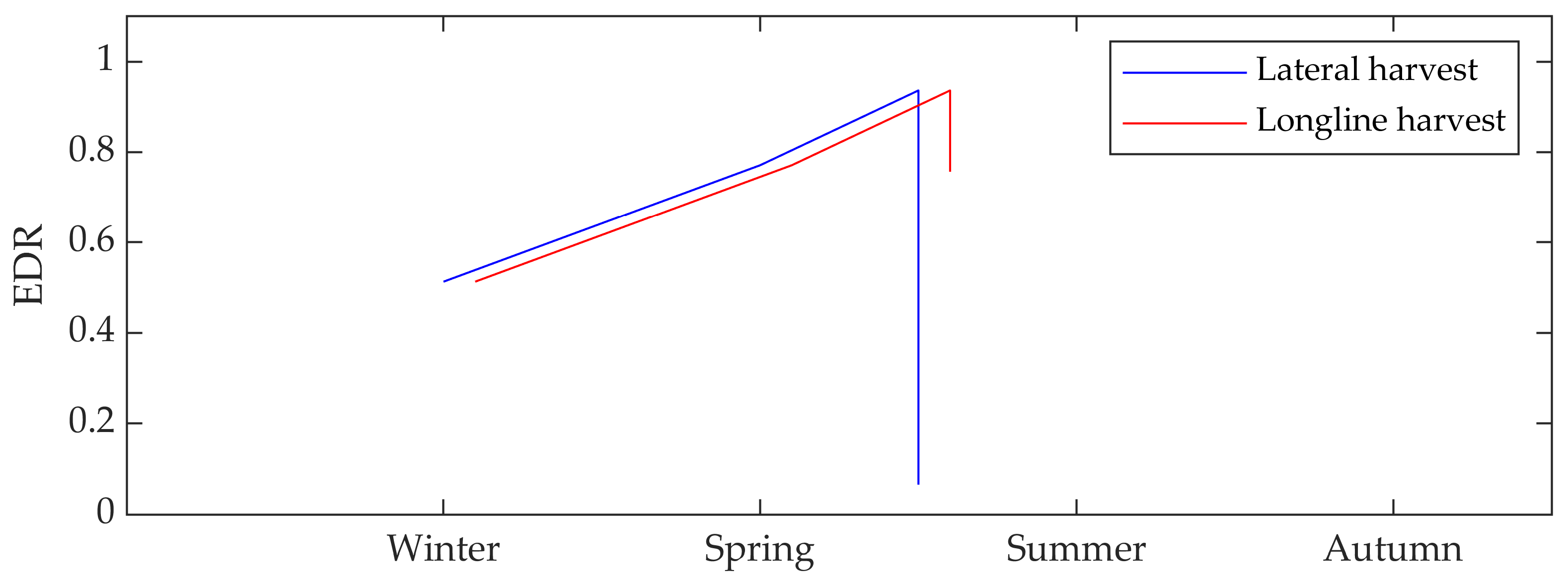
3.4. Seasonal Patterns
3.5. Harvesting Periods
4. Discussion
4.1. Water Depth
4.2. Vegetation Density
4.3. Vegetation Morphology
4.4. The Impact of Seasonality
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cohen-Shacham, E.; Walters, G.; Janzen, C.; Maginnis, S. Nature-based solutions to address global societal challenges. IUCN Gland Switz. 2016, 97, 2016–2036. [Google Scholar]
- Kirezci, E.; Young, I.R.; Ranasinghe, R.; Muis, S.; Nicholls, R.J.; Lincke, D.; Hinkel, J. Projections of global-scale extreme sea levels and resulting episodic coastal flooding over the 21st Century. Sci. Rep. 2020, 10, 11629. [Google Scholar] [CrossRef] [PubMed]
- Narayan, S.; Beck, M.W.; Reguero, B.G.; Losada, I.J.; van Wesenbeeck, B.; Pontee, N.; Burks-Copes, K.A. The Effectiveness, Costs and Coastal Protection Benefits of Natural and Nature-Based Defences. PLoS ONE 2016, 11, e0154735. [Google Scholar] [CrossRef]
- Chowdhury, M.S.N.; La Peyre, M.; Coen, L.D.; Morris, R.L.; Luckenbach, M.W.; Ysebaert, T.; Smaal, A.C. Ecological engineering with oysters enhances coastal resilience efforts. Ecol. Eng. 2021, 169, 106320. [Google Scholar] [CrossRef]
- Bilkovic, D.M.; Mitchell, M.M.; La Peyre, M.K.; Toft, J.D. (Eds.) Living Shorelines: The Science and Management of Nature-Based Coastal Protection; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Morris, R.L.; Konlechner, T.M.; Ghisalberti, M.; Swearer, S.E. From grey to green: Efficacy of eco-engineering solutions for nature-based coastal defence. Glob. Change Biol. 2018, 24, 1827–1842. [Google Scholar] [CrossRef] [PubMed]
- Möller, I. Applying Uncertain Science to Nature-Based Coastal Protection: Lessons from Shallow Wetland-Dominated Shores. Front. Environ. Sci. 2019, 7, 49. [Google Scholar] [CrossRef]
- Smith, C.S.; Rudd, M.E.; Gittman, R.K.; Melvin, E.C.; Patterson, V.S.; Renzi, J.J.; Silliman, B.R. Coming to Terms with Living Shorelines: A Scoping Review of Novel Restoration Strategies for Shoreline Protection. Front. Mar. Sci. 2020, 7, 434. [Google Scholar] [CrossRef]
- Duarte, C.M.; Bruhn, A.; Krause-Jensen, D. A seaweed aquaculture imperative to meet global sustainability targets. Nat. Sustain. 2022, 5, 185–193. [Google Scholar] [CrossRef]
- Möller, I. Quantifying saltmarsh vegetation and its effect on wave height dissipation: Results from a UK East coast saltmarsh. Estuar. Coast. Shelf Sci. 2006, 69, 337–351. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Morris, R.L.; Bilkovic, D.M.; Walles, B.; Strain, E. Nature-based coastal defence: Developing the knowledge needed for wider implementation of living shorelines. Ecol. Eng. 2022, 185, 106798. [Google Scholar] [CrossRef]
- Ferrario, F.; Beck, M.W.; Storlazzi, C.D.; Micheli, F.; Shepard, C.C.; Airoldi, L. The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat. Commun. 2014, 5, 3794. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Thomas, E.L. Influence of the Seagrass, Zostera marina, on Wave Attenuation and Bed Shear Stress Within a Shallow Coastal Bay. Front. Mar. Sci. 2018, 5, 397. [Google Scholar] [CrossRef]
- Morris, R.L.; Graham, T.D.J.; Kelvin, J.; Ghisalberti, M.; Swearer, S.E. Kelp beds as coastal protection: Wave attenuation of Ecklonia radiata in a shallow coastal bay. Ann. Bot. 2019, 125, 235–246. [Google Scholar] [CrossRef] [PubMed]
- FAO. The State of World Fisheries and Aquaculture 2020. In Sustainability in Action; FAO: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Cai, J.; Lovatelli, A.; Garrido Gamarro, E.; Geehan, J.; Lucente, D.; Mair, G.; Roubach, R. Seaweeds and Microalgae: An Overview for Unlocking Their Potential in Global Aquaculture Development; FAO: Rome, Italy, 2021. [Google Scholar]
- Spillias, S.; Valin, H.; Batka, M.; Sperling, F.; Havlík, P.; Leclère, D.; McDonald-Madden, E. Reducing global land-use pressures with seaweed farming. Nat. Sustain. 2023, 6, 380–390. [Google Scholar] [CrossRef]
- Overton, K.; Dempster, T.; Swearer, S.E.; Morris, R.L.; Barrett, L.T. Achieving conservation and restoration outcomes through ecologically beneficial aquaculture. Conserv. Biol. 2023, 2023, e14065. [Google Scholar] [CrossRef] [PubMed]
- Carballeira Braña, C.B.; Cerbule, K.; Senff, P.; Stolz, I.K. Towards environmental sustainability in marine finfish aquaculture. Front. Mar. Sci. 2021, 8, 343. [Google Scholar] [CrossRef]
- Stevens, C.; Plew, D.; Hartstein, N.; Fredriksson, D. The physics of open-water shellfish aquaculture. Aquac. Eng. 2008, 38, 145–160. [Google Scholar] [CrossRef]
- Stevens, C.; Plew, D. Bridging the Separation Between Studies of the Biophysics of Natural and Built Marine Canopies. Front. Mar. Sci. 2019, 6, 217. [Google Scholar] [CrossRef]
- Zhu, L.; Huguenard, K.; Zou, Q.-P.; Fredriksson, D.W.; Xie, D. Aquaculture farms as nature-based coastal protection: Random wave attenuation by suspended and submerged canopies. Coast. Eng. 2020, 160, 103737. [Google Scholar] [CrossRef]
- Zhu, L.; Lei, J.; Huguenard, K.; Fredriksson, D.W. Wave attenuation by suspended canopies with cultivated kelp (Saccharina latissima). Coast. Eng. 2021, 168, 103947. [Google Scholar] [CrossRef]
- Zhu, L.; Huguenard, K.; Fredriksson, D.W.; Lei, J. Wave attenuation by flexible vegetation (and suspended kelp) with blade motion: Analytical solutions. Adv. Water Resour. 2022, 162, 104148. [Google Scholar] [CrossRef]
- Bennett, S.; Wernberg, T.; Connell, S.D.; Hobday, A.J.; Johnson, C.R.; Poloczanska, E.S. The ‘Great Southern Reef’: Social, ecological and economic value of Australia’s neglected kelp forests. Mar. Freshw. Res. 2015, 67, 47–56. [Google Scholar] [CrossRef]
- Carnell, P.E.; Keough, M.J. Reconstructing Historical Marine Populations Reveals Major Decline of a Kelp Forest Ecosystem in Australia. Estuaries Coasts 2019, 42, 765–778. [Google Scholar] [CrossRef]
- Australian Seaweed Industry. Australian Seaweed Industry Blueprint—A Blueprint for Growth (Publication No. 20-072). AgriFutures Australia. 2020. Available online: https://www.australianseaweedinstitute.com.au/australian-national-seaweed-industry-blueprint-report-agrifutures (accessed on 10 May 2022).
- Wiltshire, K.H. Application of Seaweeds to Integrated Multi-Trophic Aquaculture in Southern Australia: Identifying and Investigating Suitable Native Species. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2020. [Google Scholar]
- Dalrymple, R.A.; Kirby, J.T.; Hwang, P.A. Wave Diffraction Due to Areas of Energy Dissipation. J. Waterw. Port Coast. Ocean. Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave Attenuation by Vegetation. J. Waterw. Port Coast. Ocean. Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Luhar, M.; Infantes, E.; Nepf, H. Seagrass blade motion under waves and its impact on wave decay. J. Geophys. Res. Ocean. 2017, 122, 3736–3752. [Google Scholar] [CrossRef]
- Lei, J.; Nepf, H. Wave damping by flexible vegetation: Connecting individual blade dynamics to the meadow scale. Coast. Eng. 2019, 147, 138–148. [Google Scholar] [CrossRef]
- Wernberg, T.; Coleman, M.; Fairhead, A.; Miller, S.; Thomsen, M. Morphology of Ecklonia radiata (Phaophyta: Laminarales) along its geographic distribution in south-western Australia and Australasia. Mar. Biol. 2003, 143, 47–55. [Google Scholar] [CrossRef]
- Fowler-Walker, M.J.; Wernberg, T.; Connell, S.D. Differences in kelp morphology between wave sheltered and exposed localities: Morphologically plastic or fixed traits? Mar. Biol. 2006, 148, 755–767. [Google Scholar] [CrossRef]
- Australian Seaweed Industry. Marine Seaweed Aquaculture Risk Assessment (Publication No. 23-024). AgriFutures Australia. 2023. Available online: https://agrifutures.com.au/wp-content/uploads/2023/02/23-024.pdf (accessed on 30 March 2023).
- Wilding, C.; Tillin, H.M.; Corrigan, S.E.; Stuart, E.; Ashton, I.A.; Felstead, P.; Smale, D.A. Seaweed Aquaculture and Mechanical Harvesting: An Evidence Review to Support Sustainable Management; Natural England: Bristol, UK, 2021.
- Flavin, K.; Flavin, N.; Flahive, B. Kelp Farming Manual. 2013. Available online: https://algaefoundationatec.org/aces/library/Kelp%20Farming%20Manual.pdf (accessed on 10 April 2023).
- Juanich, G. Manual of running water fish culture 1 Eucheuma spp. In Projected Reports Cebu, Philippines, FAO; Marine Agronomy Group: Hilo, HI, USA, 1988. [Google Scholar]
- Hansen, J.C.R.; Reidenbach, M.A. Wave and tidally driven flows in eelgrass beds and their effect on sediment suspension. Mar. Ecol. Prog. Ser. 2012, 448, 271–287. [Google Scholar] [CrossRef]
- Geldard, J.; Lowe, R.; Draper, S.; Ellwood, G.; Wood, A.; Roe, T.; Allen, M. Performance of engineered wave attenuating structures. In Proceedings of the Australasian Coast and Ports 2021 Conference, Christchurch, New Zealand, 30 November–3 December 2021. [Google Scholar]
- Bearham, D.; Vanderklift, M.A.; Gunson, J.R. Temperature and light explain spatial variation in growth and productivity of the kelp Ecklonia radiata. Mar. Ecol. Prog. Ser. 2013, 476, 59–70. [Google Scholar] [CrossRef]
- Thurstan, R.; Brittain, Z.; Jones, D.; Cameron, E.; Dearnaley, J.; Bellgrove, A. Aboriginal uses of seaweeds in temperate Australia: An archival assessment. J. Appl. Phycol. 2018, 30, 1821–1832. [Google Scholar] [CrossRef]
- Christie, E.; Möller, I.; Spencer, T.; Yates, M. Modelling wave attenuation due to saltmarsh vegetation using a modified SWAN model. Coast. Eng. Proc. 2018, 1, 73. [Google Scholar] [CrossRef]
| Variables | Unit | Base Case | Geometric Configuration | Seasonal Variability | Harvesting Strategies | ||
|---|---|---|---|---|---|---|---|
| Lateral | Longline | ||||||
| Wave height | m | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| Wave period | s | 6 | 6 | 6 | 6 | 6 | |
| Water mass density | kg/m3 | 1000 | 1000 | 1000 | 1000 | 1000 | |
| Water depth | m | 2 | 2–4 | 2 | 2 | 2 | |
| Stipe length | m | 0.053 | 0.053 | 0.013–0.053 | 0.053 | 0.053 | |
| Stipe diameter | m | 0.0093 | 0.0093 | 0.0023–0.0093 | 0.0093 | 0.0093 | |
| Lamina length | m | 0.24 | 0.24 | 0.061–0.24 | 0.24 | 0.24 | |
| Lamina width | m | 0.054 | 0.054 | 0.013–0.054 | 0.054 | 0.054 | |
| Lamina thickness | m | 0.0020 | 0.0020 | 0.00051–0.00020 | 0.0020 | 0.0020 | |
| Lateral length | m | 0.22 | 0.22 | 0.056–0.22 | - | 0.22 | |
| Lateral width | m | 0.046 | 0.046 | 0.011–0.046 | - | 0.046 | |
| Lateral thickness | m | 0.00076 | 0.00076 | 0.00019–0.00076 | - | 0.00076 | |
| Average no. of laterals | - | 47.63 | 47.63 | 11.91–47.63 | - | 47.63 | |
| Lamina flexural rigidity | Nm2 | 3.49 (10−5) | 3.49 (10−5) | 3.49 (10−5) | 3.49 (10−5) | 3.49 (10−5)2 | |
| Lateral flexural rigidity | Nm2 | 2.25 (10−6) | 2.25 (10−6) | 2.25 (10−6) | 2.25 (10−6) | 2.25 (10−6) | |
| Canopy length | m | 100 | 100–200 | 100 | 100 | 100 | |
| No. of longlines | - | 50 | 25–50 | 50 | 50 | 50 | |
| Canopy density (number per unit horizontal area) | |||||||
| stipe | - | 5 | 2.5–5 | 5 | 5 | 2.5 | |
| lamina | - | 5 | 2.5–5 | 5 | 5 | 2.5 | |
| laterals | - | 238.15 | 119.08–238.15 | 59.54–238.15 | - | 119.08 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodycomb, R.; Pomeroy, A.W.M.; Morris, R.L. Kelp Aquaculture as a Nature-Based Solution for Coastal Protection: Wave Attenuation by Suspended Canopies. J. Mar. Sci. Eng. 2023, 11, 1822. https://doi.org/10.3390/jmse11091822
Bodycomb R, Pomeroy AWM, Morris RL. Kelp Aquaculture as a Nature-Based Solution for Coastal Protection: Wave Attenuation by Suspended Canopies. Journal of Marine Science and Engineering. 2023; 11(9):1822. https://doi.org/10.3390/jmse11091822
Chicago/Turabian StyleBodycomb, Roma, Andrew W. M. Pomeroy, and Rebecca L. Morris. 2023. "Kelp Aquaculture as a Nature-Based Solution for Coastal Protection: Wave Attenuation by Suspended Canopies" Journal of Marine Science and Engineering 11, no. 9: 1822. https://doi.org/10.3390/jmse11091822
APA StyleBodycomb, R., Pomeroy, A. W. M., & Morris, R. L. (2023). Kelp Aquaculture as a Nature-Based Solution for Coastal Protection: Wave Attenuation by Suspended Canopies. Journal of Marine Science and Engineering, 11(9), 1822. https://doi.org/10.3390/jmse11091822






