Influence of Natural Gas Hydrate Distribution Patterns on the Macroscale–Mesoscale Mechanical Properties of Hydrate-Bearing Sediments
Abstract
:1. Introduction
2. Discrete Element Method for PFC
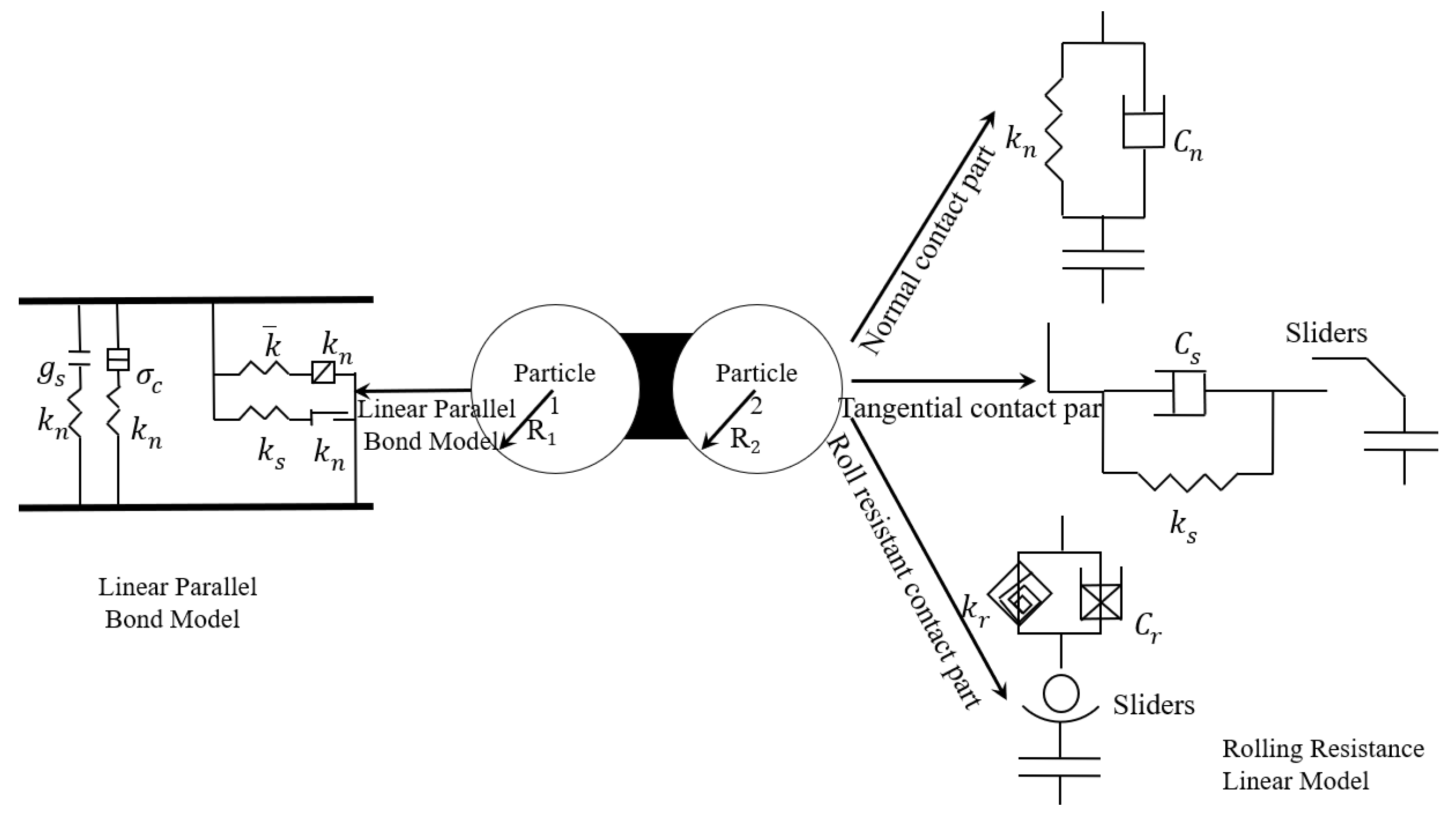
2.1. Particle Contact Model
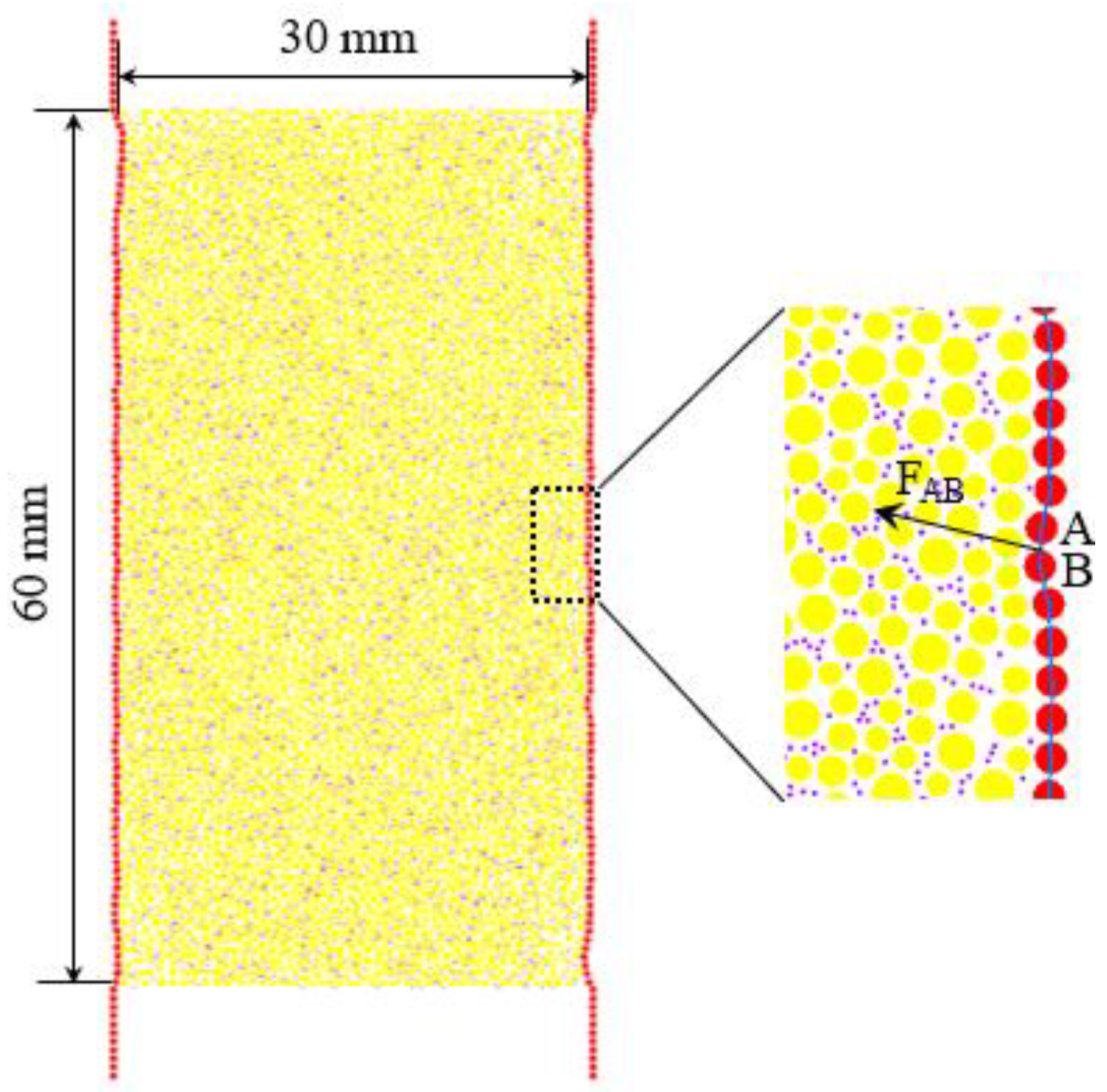
2.2. Model Construction
2.3. Flexible Boundary
2.4. Mesoscale Parameters
2.4.1. Materials and Methods
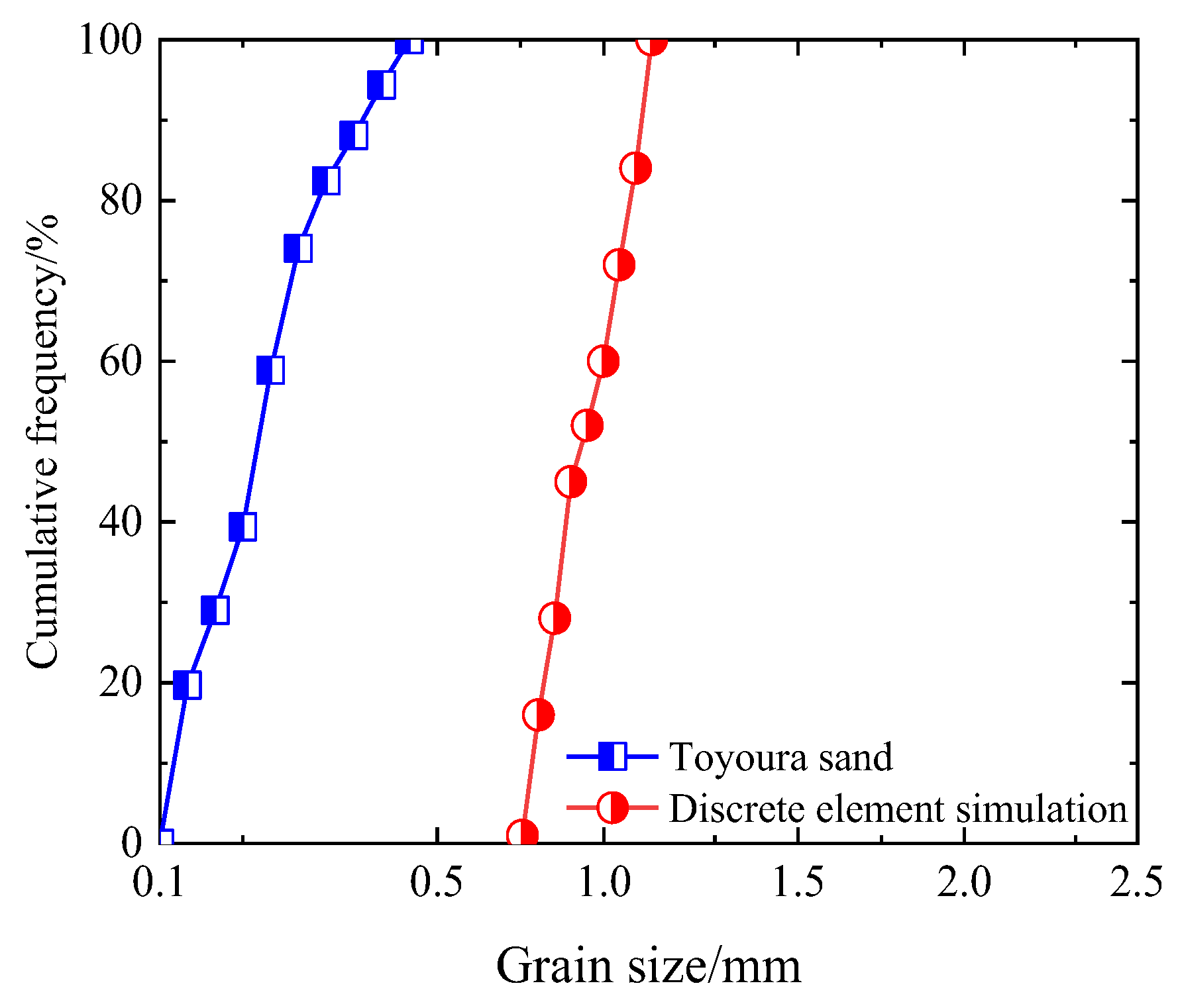
2.4.2. Mesoscopic Parameter Determination
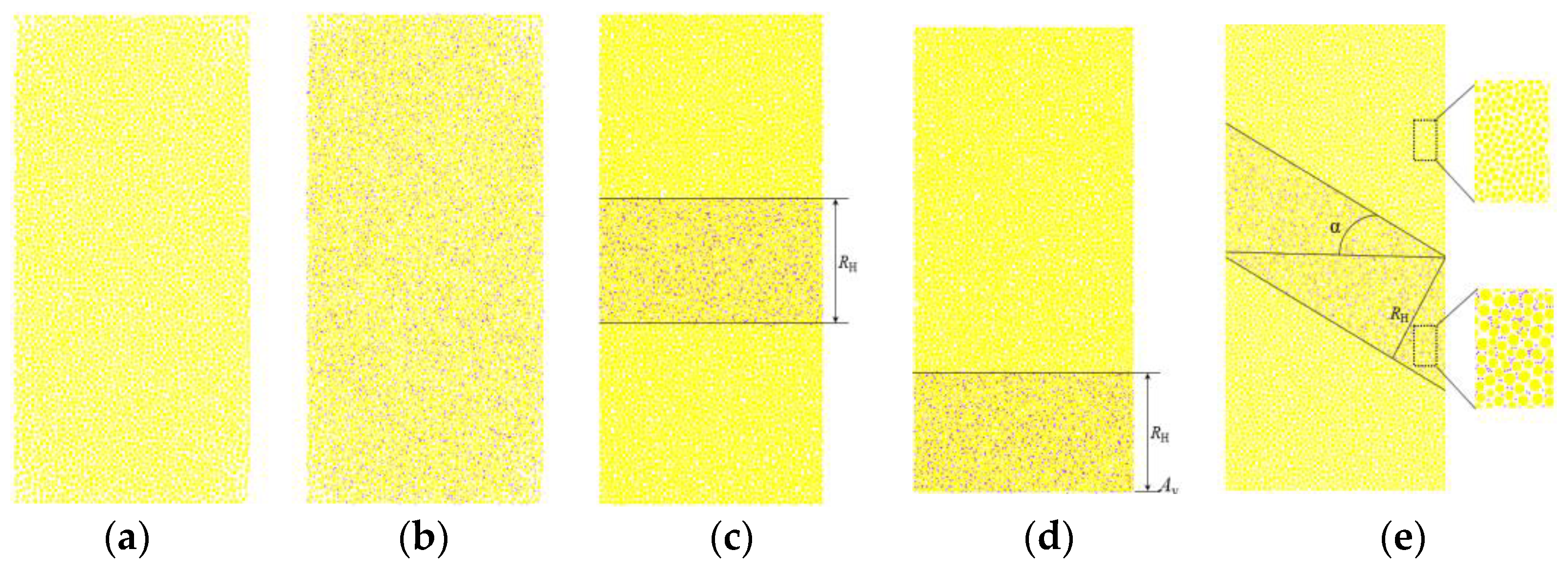
2.5. Test Scheme
3. Macroscale–Mesoscale Shear Mechanical Properties
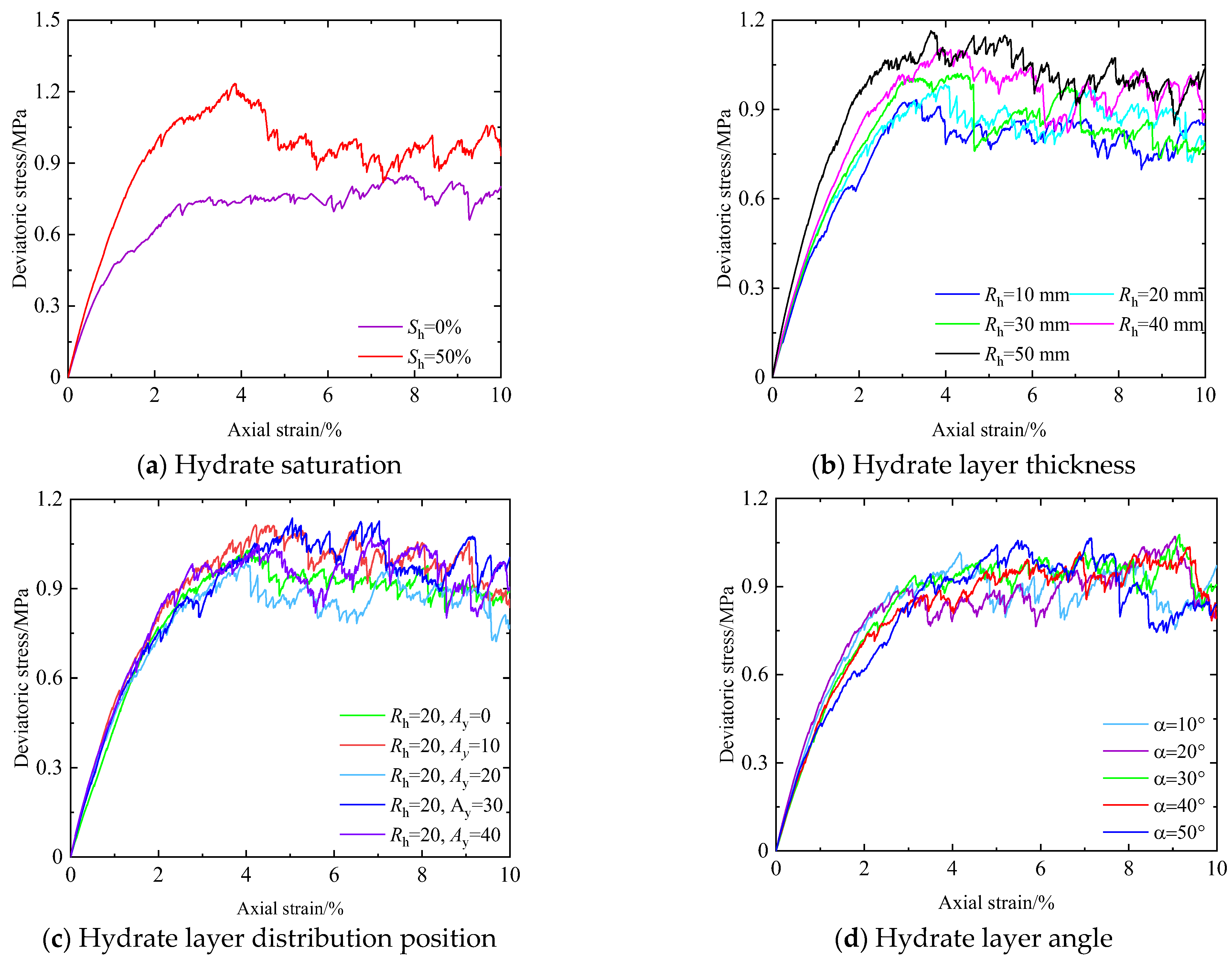
3.1. Stress and Deformation Characteristics
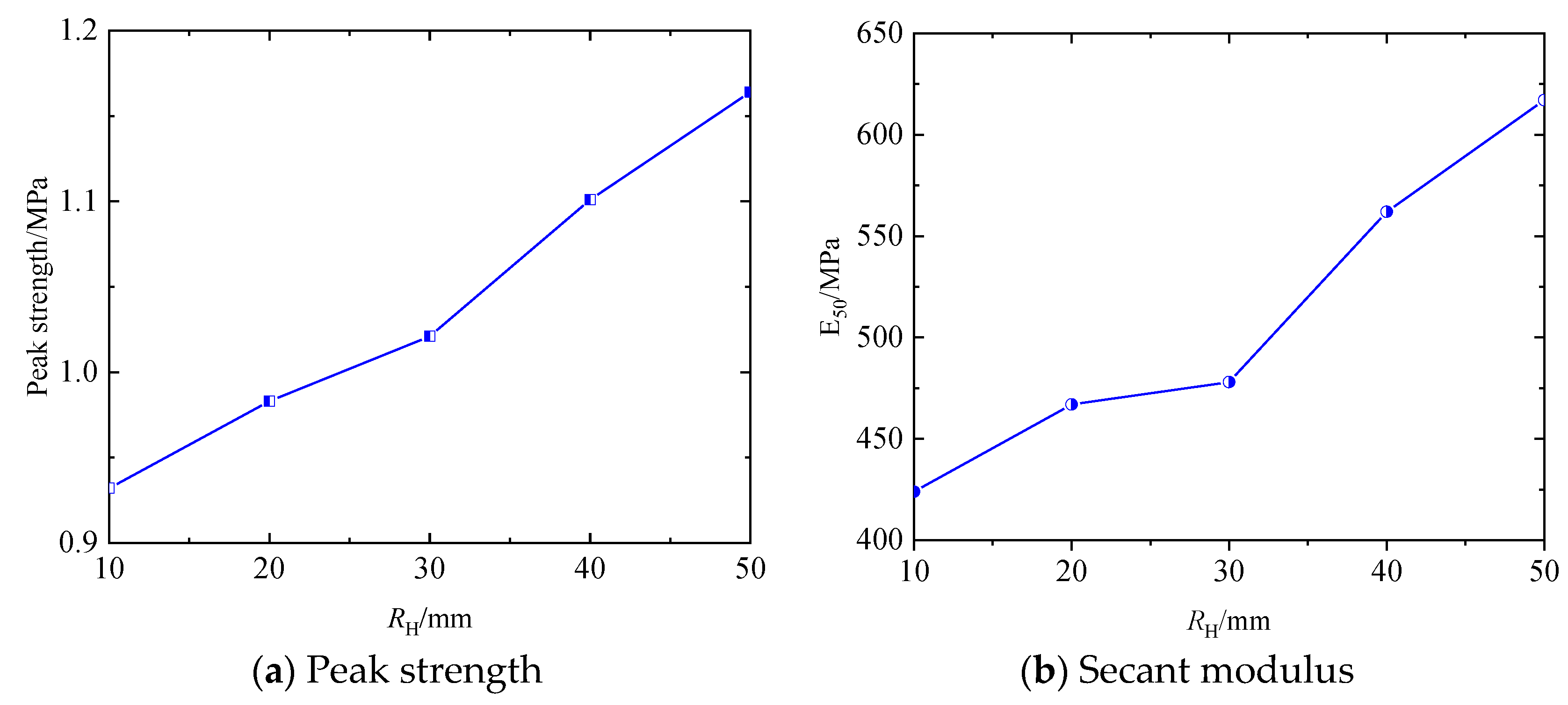
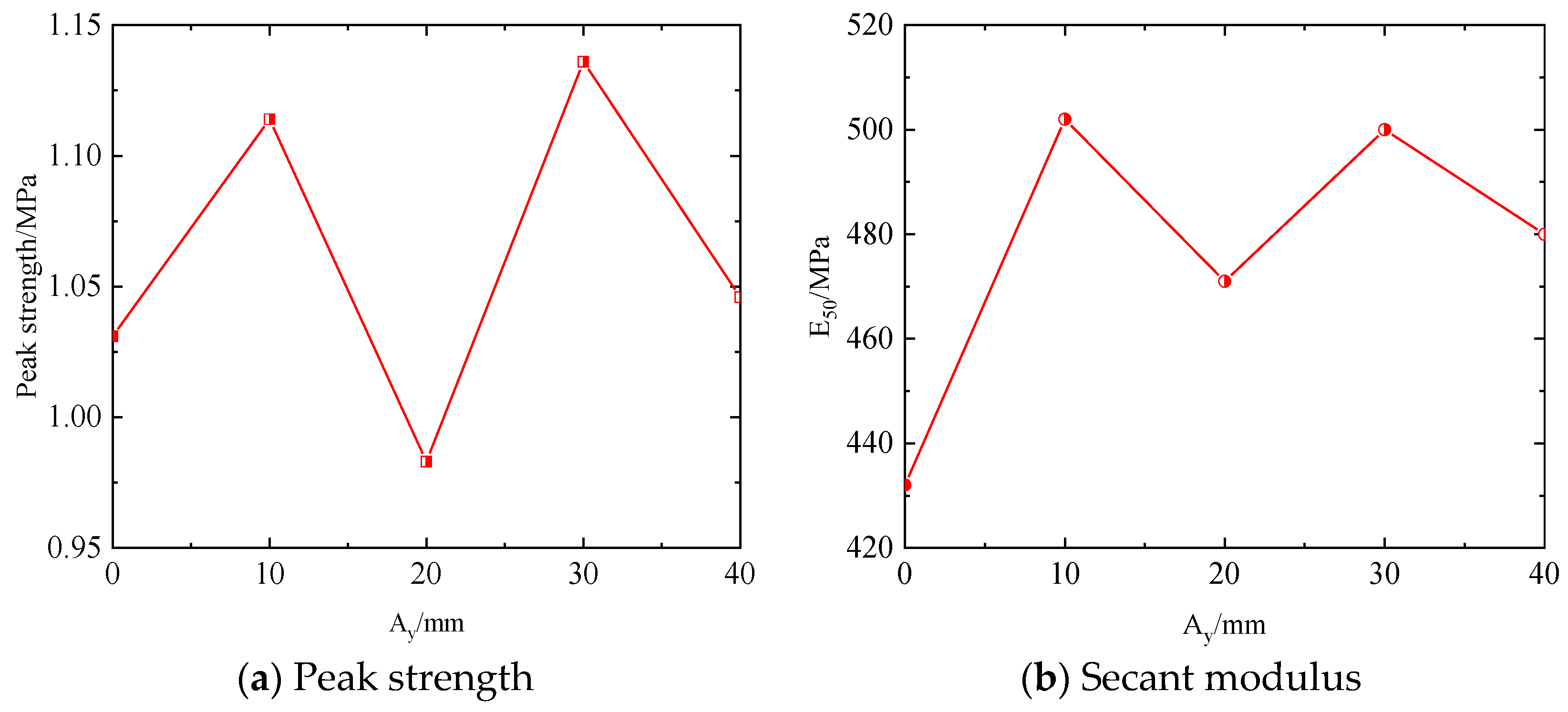
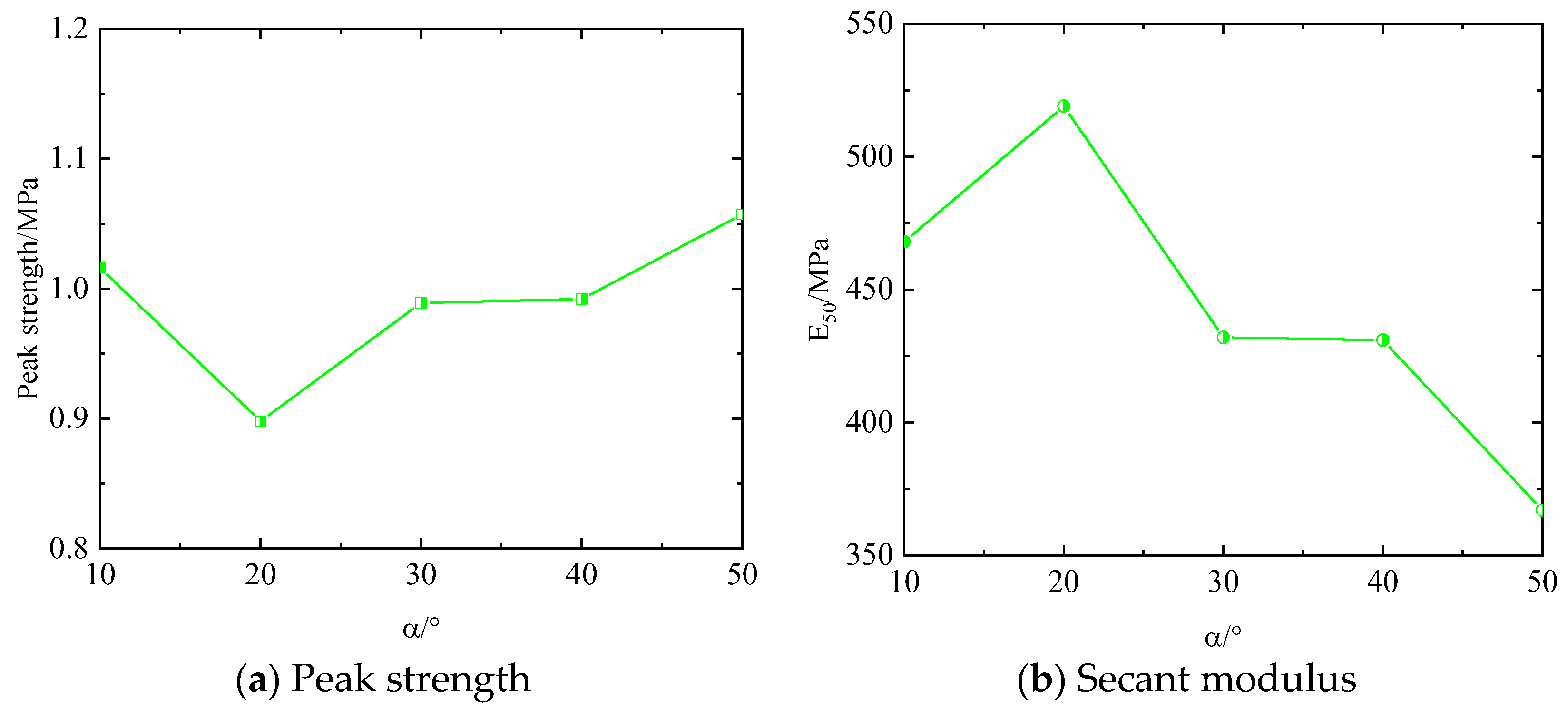
3.2. Strength Characteristics
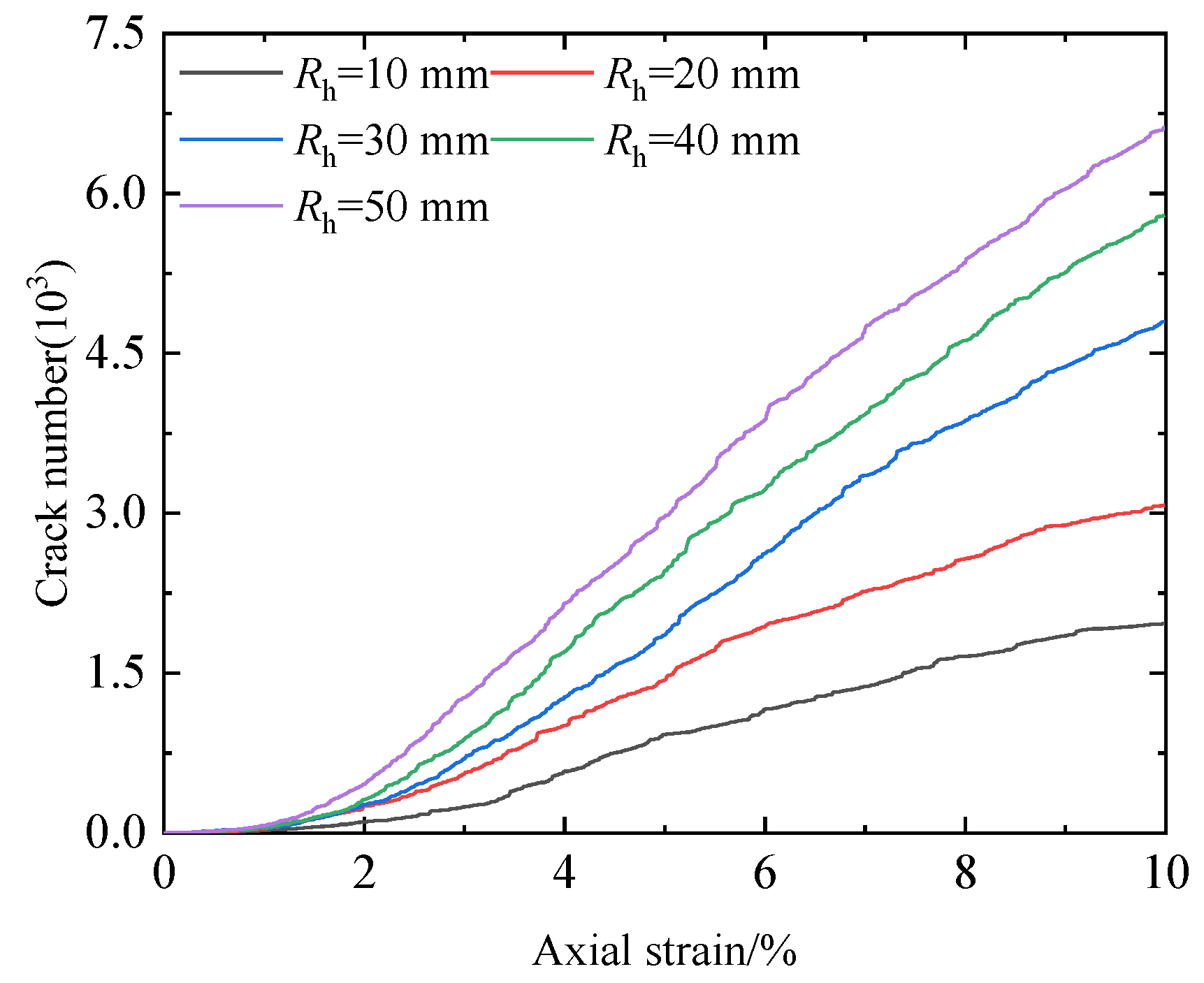
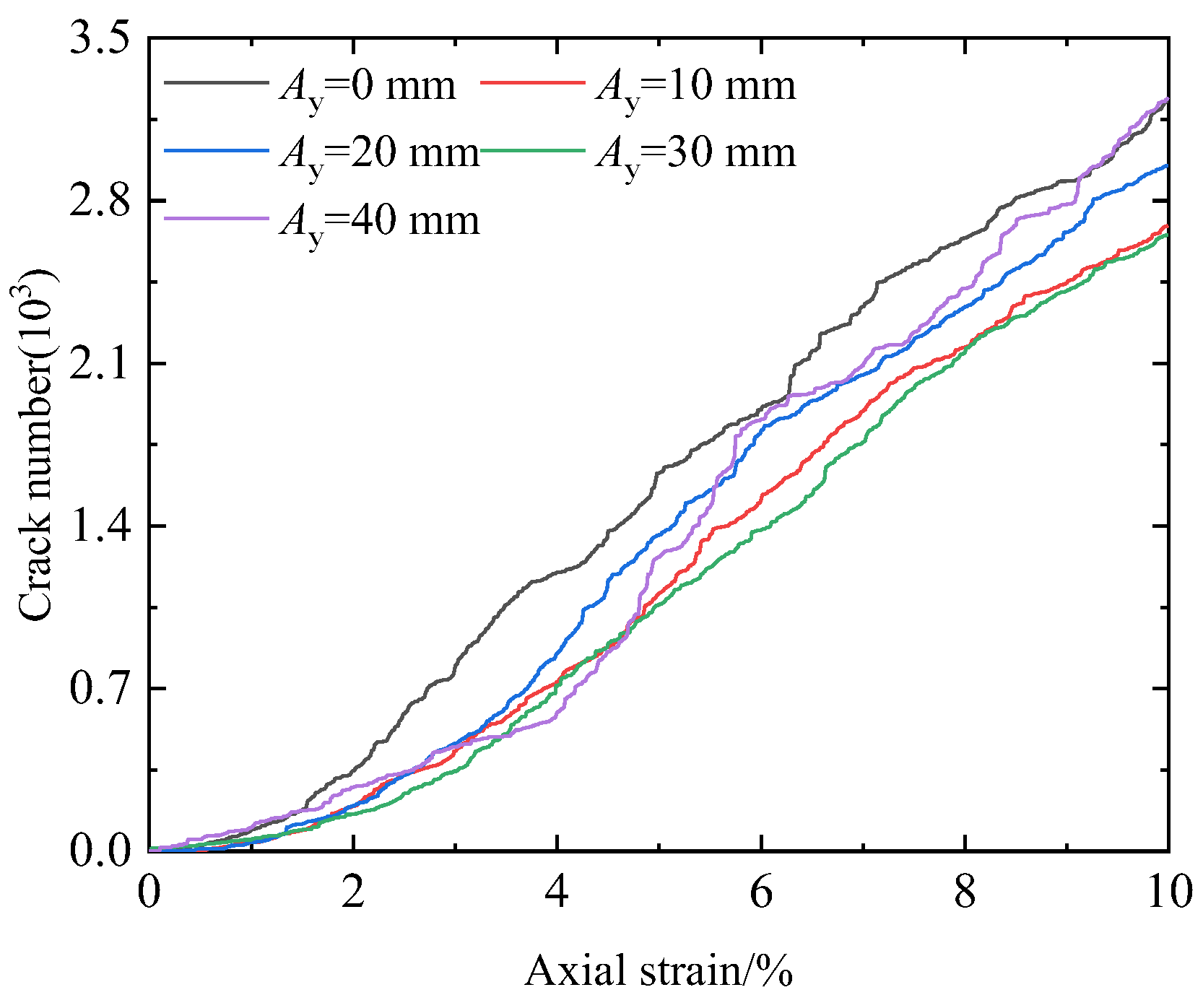
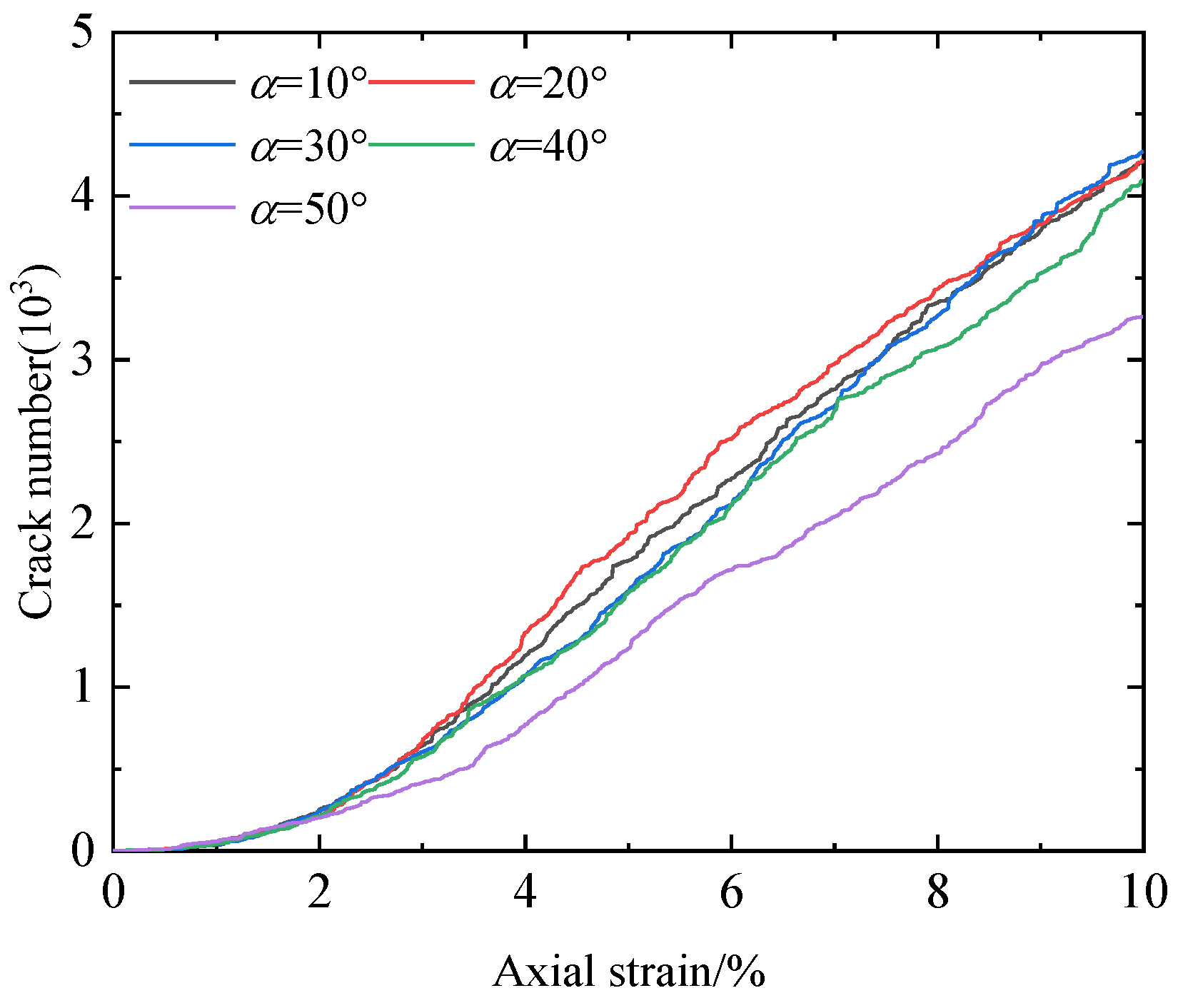
3.3. Typical Damage Law of HBS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kvenvolden, K.A. Methane hydrate-A major reservoir of carbon in the shallow geosphere. Chem. Geol. 1988, 71, 41–51. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47, 465–484. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.-S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energ. 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Li, Y.; Wu, N.; Ning, F.; Gao, D.; Hao, X.; Chen, Q.; Liu, C.; Sun, J. Hydrate-induced clogging of sand-control screen and its implication on hydrate production operation. Energy 2020, 206, 118030. [Google Scholar] [CrossRef]
- Vedachalam, N.; Ramesh, S.; Jyothi, V.; Prasad, N.T.; Ramesh, R.; Sathianarayanan, D.; Ramadass, G.; Atmanand, M. Evaluation of the depressurization based technique for methane hydrates reservoir dissociation in a marine setting, in the Krishna Godavari Basin, east coast of India. J. Nat. Gas Sci. Eng. 2015, 25, 226–235. [Google Scholar] [CrossRef]
- Jin, G.; Xu, T.; Xin, X.; Wei, M.; Liu, C. Numerical evaluation of the methane production from unconfined gas hydrate-bearing sediment by thermal stimulation and depressurization in Shenhu area, South China Sea. J. Nat. Gas Sci. Eng. 2016, 33, 497–508. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Liao, H.; Dong, L.; Bu, Q.; Liu, Z. Mechanical properties of the mixed system of clayey-silt sediments and natural gas hydrates. Nat. Gas Ind. 2020, 40, 10. [Google Scholar] [CrossRef]
- Yan, P.; Luan, H.; Jiang, Y.; Yu, H.; Liang, W.; Cheng, X.; Liu, M.; Chen, H. Experimental Investigation Into Effects of Thermodynamic Hydrate Inhibitors on Natural Gas Hydrate Synthesis in 1D Reactor. Energy Technol. 2023, 11, 2300262. [Google Scholar] [CrossRef]
- Li, Y.; Wu, N.; Gao, D.; Chen, Q.; Liu, C.; Yang, D.; Jin, Y.; Ning, F.; Tan, M.; Hu, G. Optimization and analysis of gravel packing parameters in horizontal wells for natural gas hydrate production. Energy 2021, 219, 119585. [Google Scholar] [CrossRef]
- Li, Y.; Hu, G.; Wu, N.; Liu, C.; Chen, Q.; Li, C. Undrained shear strength evaluation for hydrate-bearing sediment overlying strata in the Shenhu area, northern South China Sea. Acta Oceanol. Sin. 2019, 38, 114–123. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, J.S.; Li, D.L.; Liang, D.Q. Experimental study of mechanical properties of hydrate-bearing sediments during depressurization mining. Rock Soil Mech. 2018, 39, 4508–4516. [Google Scholar] [CrossRef]
- Hyodo, M.; Yoneda, J.; Yoshimoto, N.; Nakata, Y. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed. Soils Found 2013, 53, 299–314. [Google Scholar] [CrossRef]
- Li, Y.; Dong, L.; Wu, N.; Nouri, A.; Liao, H.; Chen, Q.; Sun, J.; Liu, C. Influences of hydrate layered distribution patterns on triaxial shearing characteristics of hydrate-bearing sediments. Eng. Geol. 2021, 294, 106375. [Google Scholar] [CrossRef]
- Winters, W.; Waite, W.; Mason, D.; Gilbert, L.; Pecher, I. Methane gas hydrate effect on sediment acoustic and strength properties. J. Petrol. Sci. Eng. 2007, 56, 127–135. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Egawa, K.; Kida, M.; Ito, T.; Nagao, J.; Tenma, N. Mechanical behavior of hydrate-bearing pressure-core sediments visualized under triaxial compression. Mar. Petrol. Geol. 2015, 66, 451–459. [Google Scholar] [CrossRef]
- Luo, T.; Song, Y.; Zhu, Y.; Liu, W.; Liu, Y.; Li, Y.; Wu, Z. Triaxial experiments on the mechanical properties of hydrate-bearing marine sediments of South China Sea. Mar. Petrol. Geol. 2016, 77, 507–514. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Xin, X.; Yuan, Y.; Jiang, Z. Numerical investigation of natural gas hydrate production performance via a more realistic three-dimensional model. J. Nat. Gas Sci. Eng. 2022, 107, 104793. [Google Scholar] [CrossRef]
- Bosikov, I.I.; Klyuev, R.V.; Silaev, I.V.; Pilieva, D.E. Estimation of multistage hydraulic fracturing parameters using 4D simulation. Gorn. Nauk. I Tekhnologii=Min. Sci. Technol. 2023, 8, 141–149. [Google Scholar] [CrossRef]
- Jiang, M.J.; Sun, Y.G.; Yang, Q.J. A simple distinct element modeling of the mechanical behavior of methane hydrate-bearing sediments in deep seabed. Granul. Matter. 2013, 15, 209–220. [Google Scholar] [CrossRef]
- Jiang, M.J.; Yu, H.S.; Harris, D. Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses. Int. J. Numer. Anal. Meth. Geomech. 2006, 30, 723–761. [Google Scholar] [CrossRef]
- Jiang, M.; Peng, D.; Ooi, J.Y. DEM investigation of mechanical behavior and strain localization of methane hydrate bearing sediments with different temperatures and water pressures. Eng. Geol. 2017, 223, 92–109. [Google Scholar] [CrossRef]
- Jiang, M.; Liu, J.; Kwok, C.Y.; Shen, Z. Exploring the undrained cyclic behavior of methane-hydrate-bearing sediments using CFD–DEM. Comptes Rendus Mécanique 2018, 346, 815–832. [Google Scholar] [CrossRef]
- Wang, H. Discrete Element Simulation Analysis of Mechanical Behavior of the Gas Hydrate-Bearing Sediments. Ijm 2018, 7, 85–94. [Google Scholar] [CrossRef]
- Yu, Y.; Cheng, Y.P.; Xu, X.; Soga, K. Discrete element modelling of methane hydrate soil sediments using elongated soil particles. Comput. Geotech. 2016, 80, 397–409. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, H.; Ma, Q.; Xia, Q.; Yang, X.; Li, F.; Li, X.; Xing, L. Discrete element simulation analysis of damage and failure of hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2022, 102, 104557. [Google Scholar] [CrossRef]
- Jiang, Y.; Gong, B. Discrete-element numerical modelling method for studying mechanical response of methane-hydrate-bearing specimens. Mar. Georesour. Geotec. 2020, 38, 1082–1096. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, M.; Luan, H.; Shi, Y.; Zhang, S.; Yan, P.; Li, B. Discrete Element Simulation of the Macro-Meso Mechanical Behaviors of Gas-Hydrate-Bearing Sediments under Dynamic Loading. Jmse 2022, 10, 1042. [Google Scholar] [CrossRef]
- Gong, B.; Jiang, Y.; Yan, P.; Zhang, S. Discrete element numerical simulation of mechanical properties of methane hydrate-bearing specimen considering deposit angles. J. Nat. Gas Sci. Eng. 2020, 76, 103182. [Google Scholar] [CrossRef]
- Dong, L.; Li, Y.; Liu, C.; Liao, H.; Chen, G.; Chen, Q.; Liu, L.; Hu, G. Mechanical Properties of Methane Hydrate-Bearing Interlayered Sediments. J. Ocean Univ. China 2019, 18, 1344–1350. [Google Scholar] [CrossRef]
- Zhou, M.; Soga, K.; Yamamoto, K. Upscaled Anisotropic Methane Hydrate Critical State Model for Turbidite Hydrate-Bearing Sediments at East Nankai Trough. J. Geophys. Res. Solid Earth 2018, 123, 6277–6298. [Google Scholar] [CrossRef]
- Brugada, J.; Cheng, Y.P.; Soga, K.; Santamarina, J.C. Discrete element modelling of geomechanical behaviour of methane hydrate soils with pore-filling hydrate distribution. Granul. Matter. 2010, 12, 517–525. [Google Scholar] [CrossRef]
- Kumar Saw, V.; Udayabhanu, G.N.; Mandal, A.; Laik, S. Methane Hydrate Formation and Dissociation in the presence of Bentonite Clay Suspension. Chem. Eng. Technol. 2013, 36, 810–818. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, C.F.; Zhou, J.Z.; Chen, P.; Wei, H.Z. Development and application of gas hydrate injection synthesis and direct shear test system. Rock Soil Mech. 2021, 42, 2311–2320. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Q.; Wang, S. Numerical Simulation Technology and Application with Particle Flow Code (PFC5.0); China Architecture & Building Press: Beijing, China, 2018; p. 1. [Google Scholar]
- Belheine, N.; Plassiard, J.P.; Donzé, F.V.; Darve, F.; Seridi, A. Numerical simulation of drained triaxial test using 3D discrete element modeling. Comput. Geotech. 2009, 36, 320–331. [Google Scholar] [CrossRef]
- Evans, T.M.; Valdes, J.R. The microstructure of particulate mixtures in one-dimensional compression: Numerical studies. Granul. Matter. 2011, 13, 657–669. [Google Scholar] [CrossRef]
- Ding, Y.; Qian, A.; Lu, H.; Li, Y.; Zhang, Y. DEM investigation of the effect of hydrate morphology on the mechanical properties of hydrate-bearing sands. Comput. Geotech. 2022, 143, 104603. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.Y.; Zhou, B.; Xue, S.F.; Lin, Y.S. Impact of rolling resistance effect of particles on macro/micro mechanical properties of hydrate-bearing sediments. Acta Pet. Sin. 2020, 41, 885–894. [Google Scholar] [CrossRef]
- Kajiyama, S.; Wu, Y.; Hyodo, M.; Nakata, Y.; Nakashima, K.; Yoshimoto, N. Experimental investigation on the mechanical properties of methane hydrate-bearing sand formed with rounded particles. J. Nat. Gas Sci. Eng. 2017, 45, 96–107. [Google Scholar] [CrossRef]
- Ding, Y.; Qian, A.; Lu, H. Three-dimensional discrete element modeling of the shear behavior of cemented hydrate-bearing sands. J. Nat. Gas Sci. Eng. 2022, 101, 104526. [Google Scholar] [CrossRef]
- Colwell, F.; Matsumoto, R.; Reed, D. A review of the gas hydrates, geology, and biology of the Nankai Trough. Chem. Geol. 2004, 205, 391–404. [Google Scholar] [CrossRef]




| Round Particles | Sediment Particles | NGH Particles |
|---|---|---|
| Density/g·cm−3 | 2.65 | 0.9 |
| Normal stiffness/N·m−1 | 4 × 109 | 4 × 108 |
| Normal tangential stiffness ratio | 4/3 | 4/3 |
| Particle size/mm | 0.727~1.136 | 0.10 |
| Friction coefficient | 0.5 | 0.2 |
| Contact Model | Between Sediment Particles | Between NGH and Sediment Particles | Between NGH Particles |
|---|---|---|---|
| Normal stiffness/N·m−1 | - | 16 × 109 | 16 × 109 |
| Normal tangential stiffness ratio | - | 4/3 | 4/3 |
| Tensile strength/MPa | - | 2 × 106 | 2 × 106 |
| Bond strength/MPa | - | 2 × 106 | 2 × 106 |
| Friction angle/° | - | 38 | 38 |
| Rolling friction coefficient | 0.5 | - | - |
| Groups | Confining Pressure /MPa | Saturation/% | RH 1/mm | Ay 2/mm | α 3/° |
|---|---|---|---|---|---|
| a | 6 | 50 | 0 | 0 | 0 |
| b | 6 | 50 | 60 | 0 | 0 |
| c | 6 | 50 | 10/20/30/40/50 | 0 | 0 |
| d | 6 | 50 | 20 | 0/10/20/30/40 | 0 |
| e | 6 | 50 | 20 | - | 10/20/30/40/50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Du, X.; Yan, P.; Li, M.; Luan, H.; Ma, X.; Shi, Y. Influence of Natural Gas Hydrate Distribution Patterns on the Macroscale–Mesoscale Mechanical Properties of Hydrate-Bearing Sediments. J. Mar. Sci. Eng. 2024, 12, 20. https://doi.org/10.3390/jmse12010020
Jiang Y, Du X, Yan P, Li M, Luan H, Ma X, Shi Y. Influence of Natural Gas Hydrate Distribution Patterns on the Macroscale–Mesoscale Mechanical Properties of Hydrate-Bearing Sediments. Journal of Marine Science and Engineering. 2024; 12(1):20. https://doi.org/10.3390/jmse12010020
Chicago/Turabian StyleJiang, Yujing, Xiaoyu Du, Peng Yan, Meng Li, Hengjie Luan, Xianzhuang Ma, and Yichen Shi. 2024. "Influence of Natural Gas Hydrate Distribution Patterns on the Macroscale–Mesoscale Mechanical Properties of Hydrate-Bearing Sediments" Journal of Marine Science and Engineering 12, no. 1: 20. https://doi.org/10.3390/jmse12010020
APA StyleJiang, Y., Du, X., Yan, P., Li, M., Luan, H., Ma, X., & Shi, Y. (2024). Influence of Natural Gas Hydrate Distribution Patterns on the Macroscale–Mesoscale Mechanical Properties of Hydrate-Bearing Sediments. Journal of Marine Science and Engineering, 12(1), 20. https://doi.org/10.3390/jmse12010020








