Prediction-Based Submarine Cable-Tracking Strategy for Autonomous Underwater Vehicles with Side-Scan Sonar
Abstract
1. Introduction
2. Related Work
- (1)
- Applying the non-myopic method to the submarine cable tracking task, we optimize the AUV’s heading by combining the characteristics of SSS measurements. This ensures high-quality imaging of the side-scan sonar while achieving stable tracking of the cable.
- (2)
- The measured sequence of cable states is viewed as a set of time series arranged at equal time intervals, utilizing LSTM networks to predict future cable trends, thereby mitigating the negative impact of the myopia of onboard sensors.
3. Preliminaries
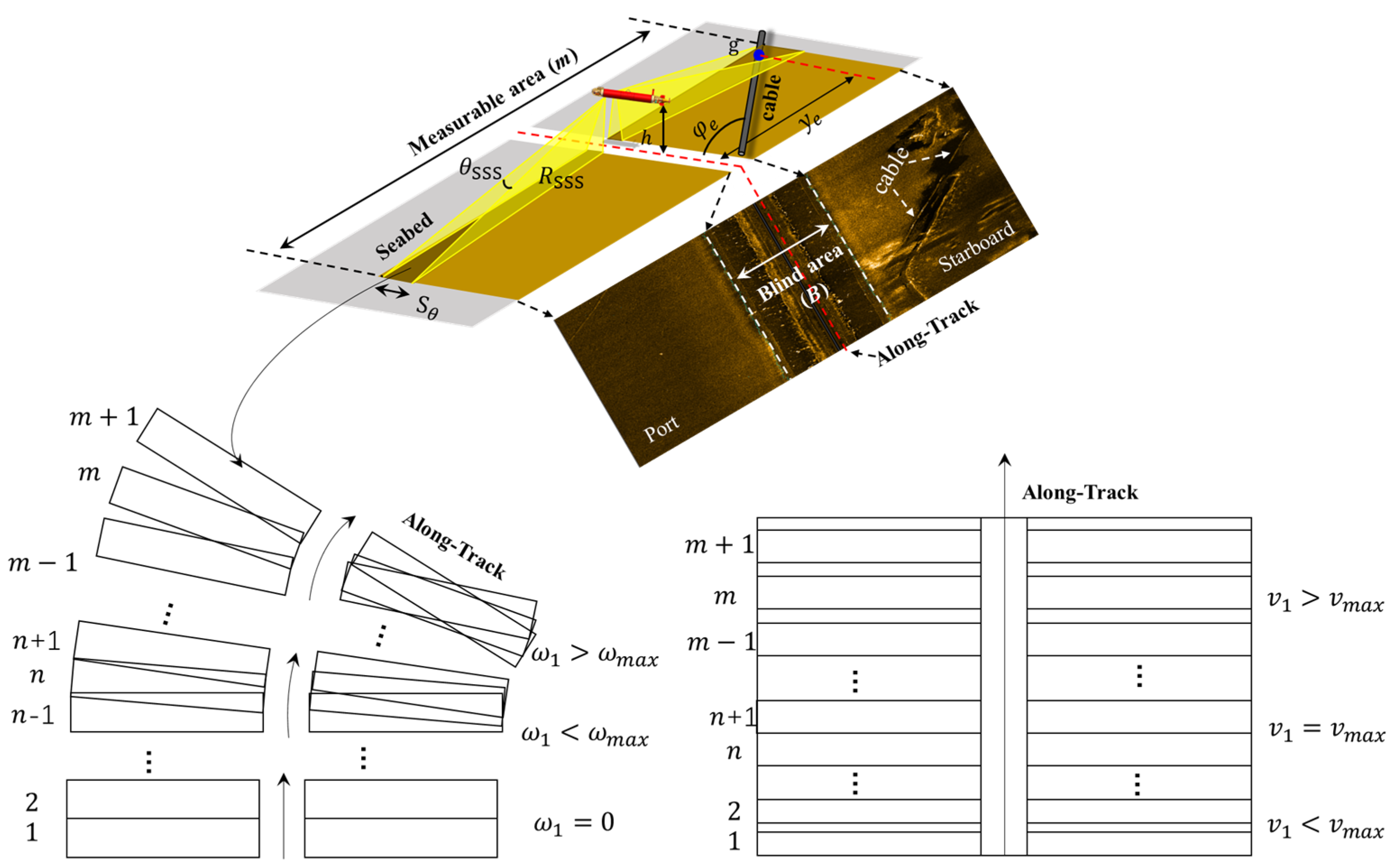
3.1. Introduction to Side-Scan Sonar Imaging
- (1)
- During any sharp turns of the sonar device, any areas outside the turn were completely missed owing to the finite ping rate of the SSS, while areas within the turn could be heavily distorted. In both cases, identifying targets in the images could be challenging [28];
- (2)
- The relative angle between the sonar beam and the underwater cable was a crucial factor influencing target imaging. When the SSS moved parallel to the cable, the strongest acoustic echoes could be obtained because of specular reflection [29];
- (3)
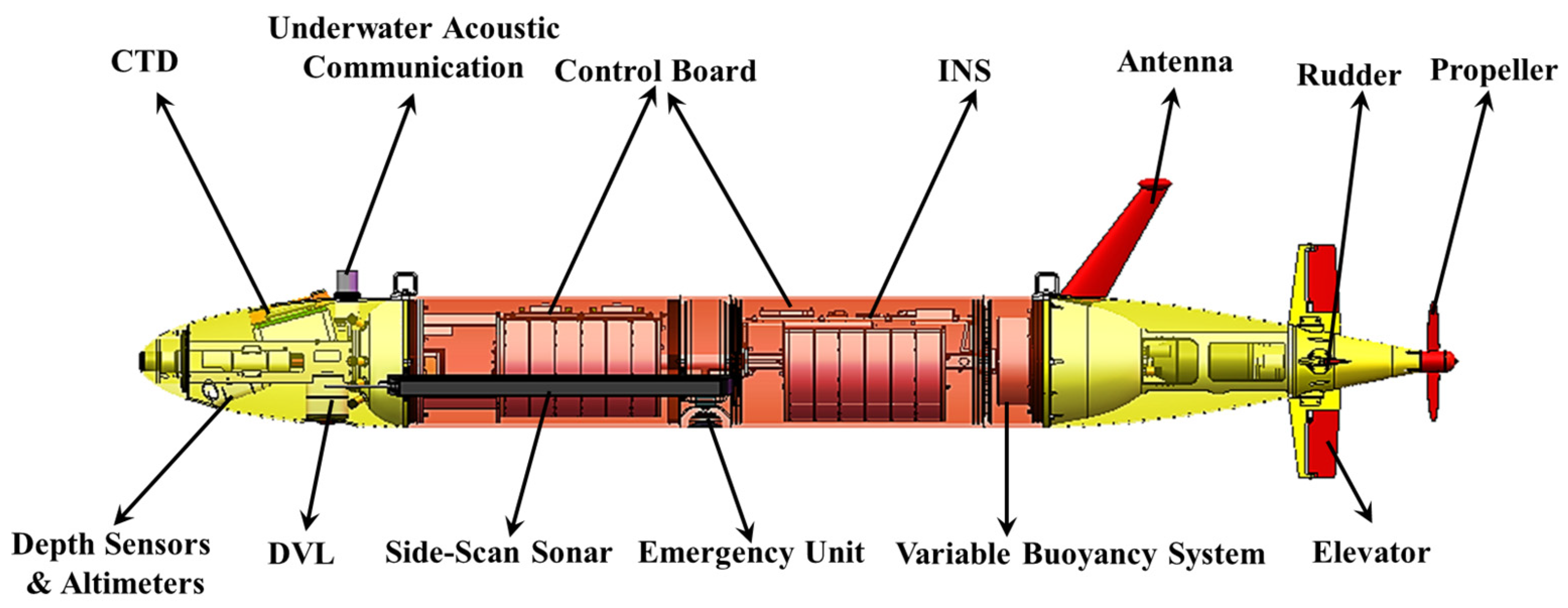
3.2. “Sea Whale” AUV
3.3. Problem Statement
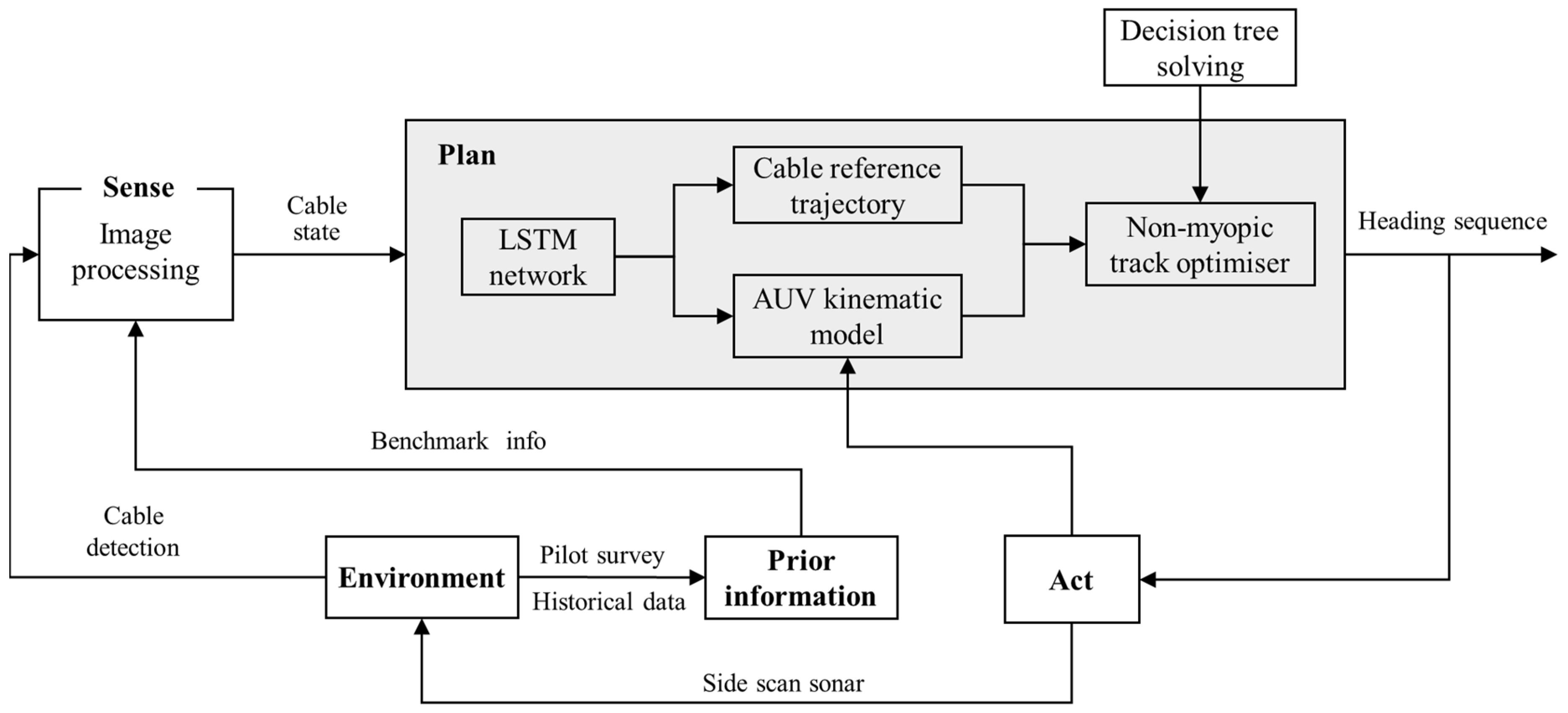
4. Methodology
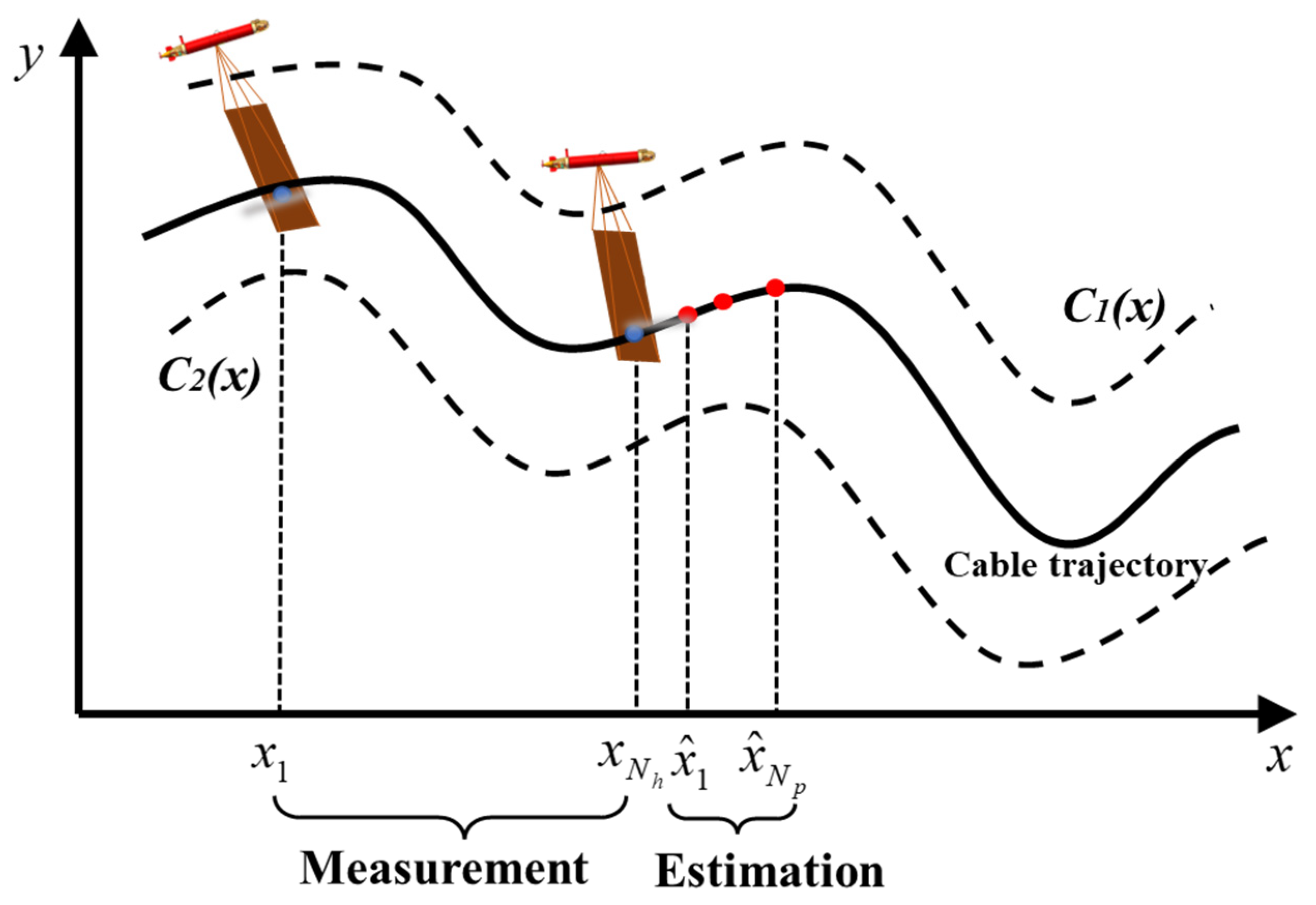
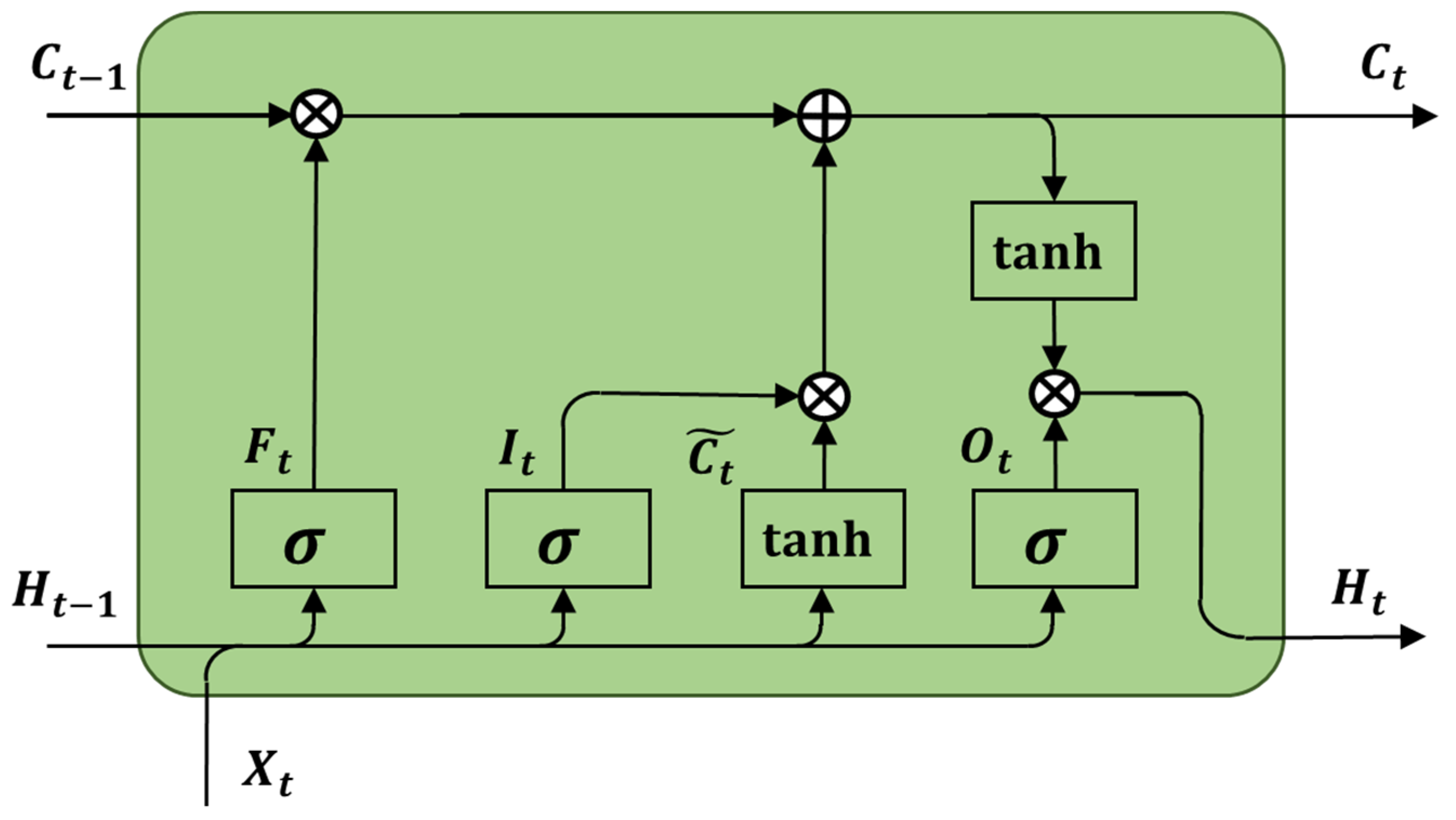
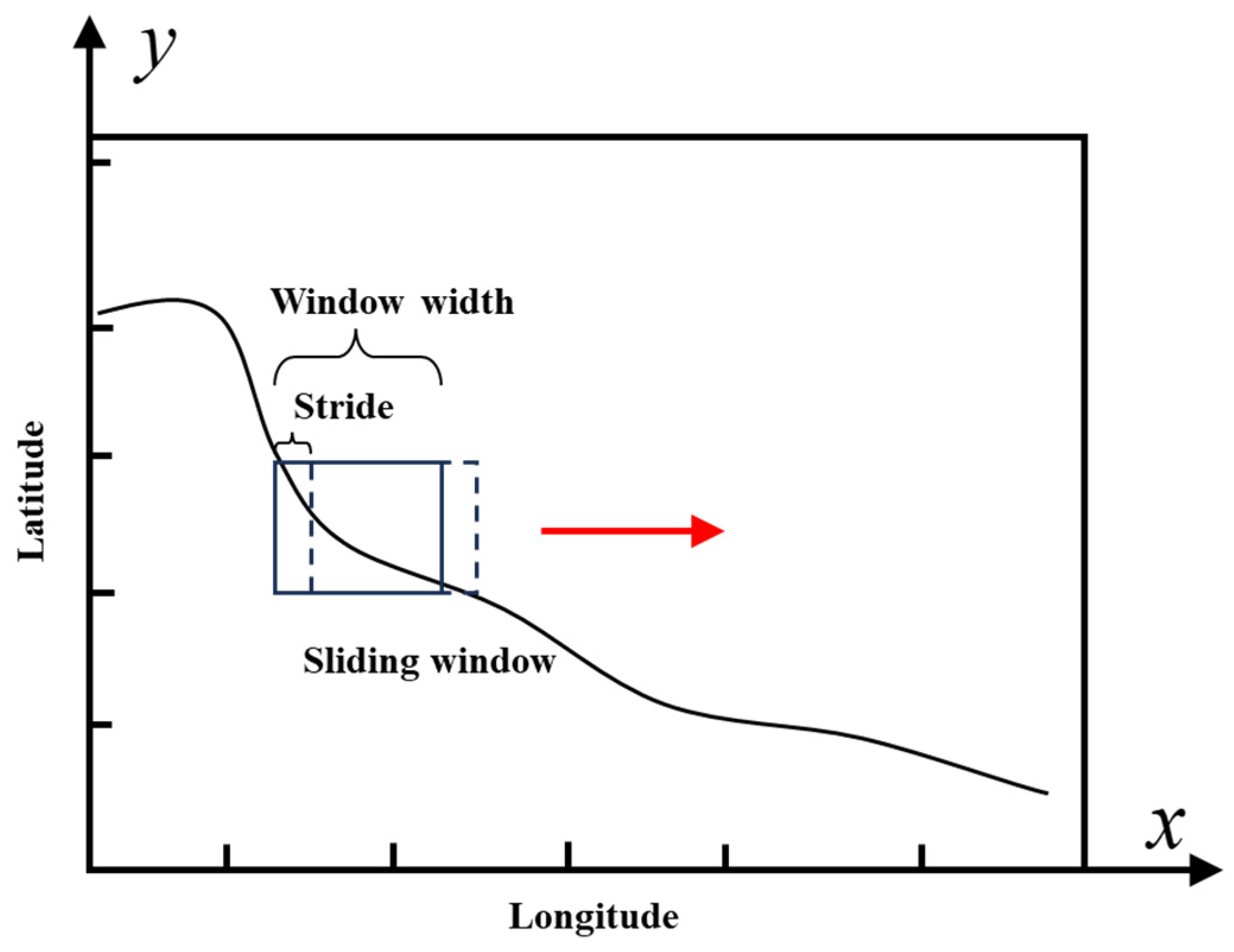
4.1. Cable State Prediction
4.2. Cable-Tracking Method Based on Receding-Horizon Strategy
4.2.1. Construct Cost Function Based on SSS Characteristics
- (1)
- A smaller turning angle avoids distortion of the sonar image;
- (2)
- Imaging is best when the cable and AUV are parallel; and
- (3)
- The cable is kept at a certain distance from the AUV, to locate it in the middle of the sonar image.
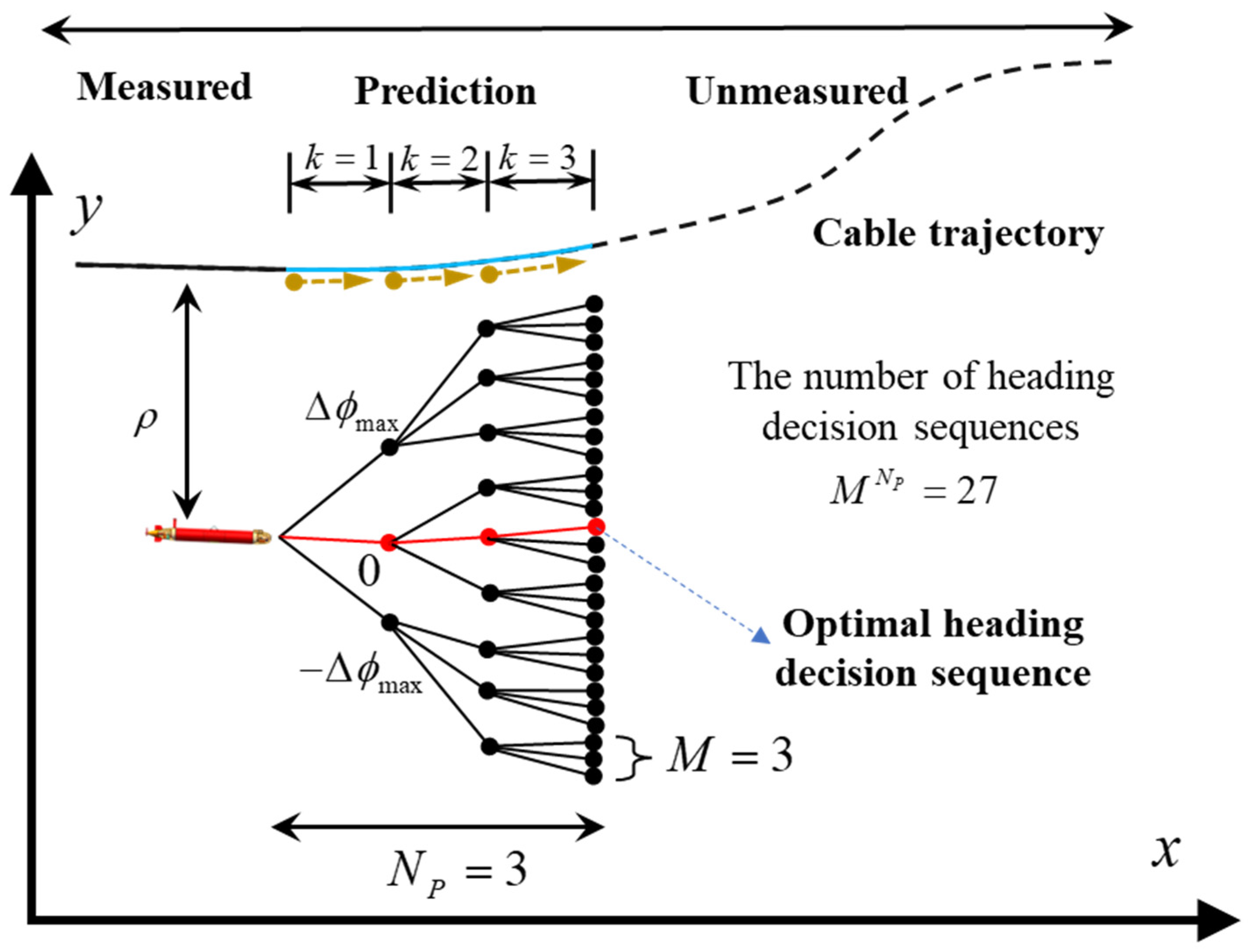
4.2.2. Non-Myopic Optimization Algorithm
| Algorithm 1: Non-myopic cable-tracking algorithm |
| Input: (1) ; (2) steps based on the given sequence of heading decisions: (1) , ; (2) Predict the AUV position by combining the kinematic model (Equation (1)): , where u denotes the axial velocity of the AUV; (3) ; (4) |
4.3. Strategies for Solving Non-Myopic Optimization Problems
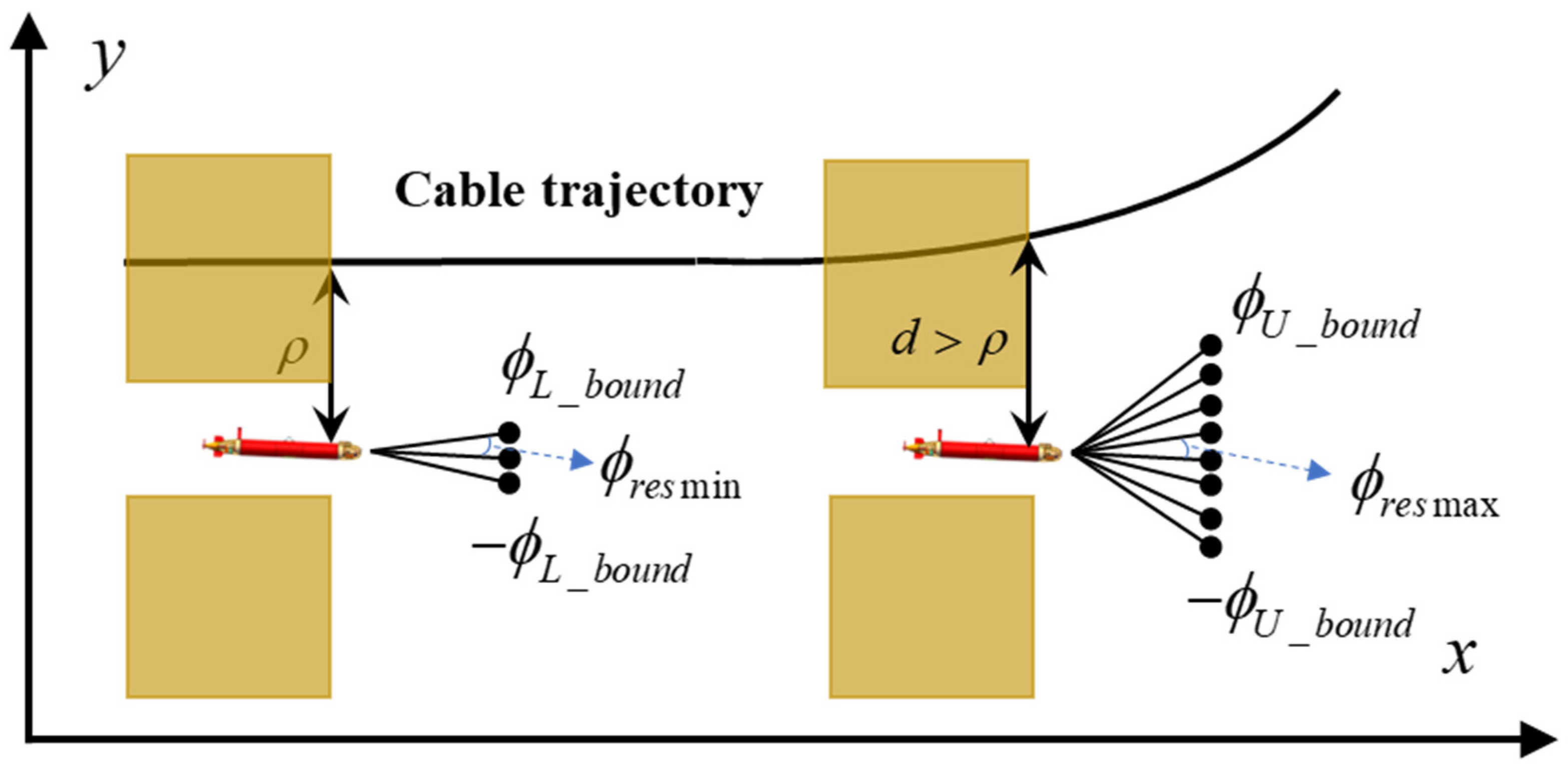
4.3.1. Adaptive Heading-Search Space Method
4.3.2. Tree Search and Pruning Algorithms
- (1)
- Initialize the minimum cost , perform a uniform cost search (UCS), and expand the nodes until reaching the end node of the tree (at a depth of ). Set the decision sequence with the lowest cost as the initial optimal solution and set to the cost of that decision sequence. Repeat until all nodes in the tree are opened.
- (2)
- During node expansion, the lower bound is compared with , and nodes with lower bounds greater than or equal to are pruned. If the search for nodes is completed (end nodes are opened) and the corresponding decision sequence cost is lower than , the decision sequence is considered the new best-decision sequence and is set as the cost of the sequence.
Algorithm 2: Branch-and-bound algorithm (1) ;
(2) ;
(3) to ;
(4) in ascending order of cost;
(5) While there is a node in the list Do
Expands the first node in the list R;
If the sequence corresponding to a node has a cost >Jmin
Stop the expansion of the node;
Remove it from R;
End
If the depth of the children of this node == NP
If decision sequence costs with minimum costs
5. Simulation and Discussion
5.1. Simulation Setup and Environment
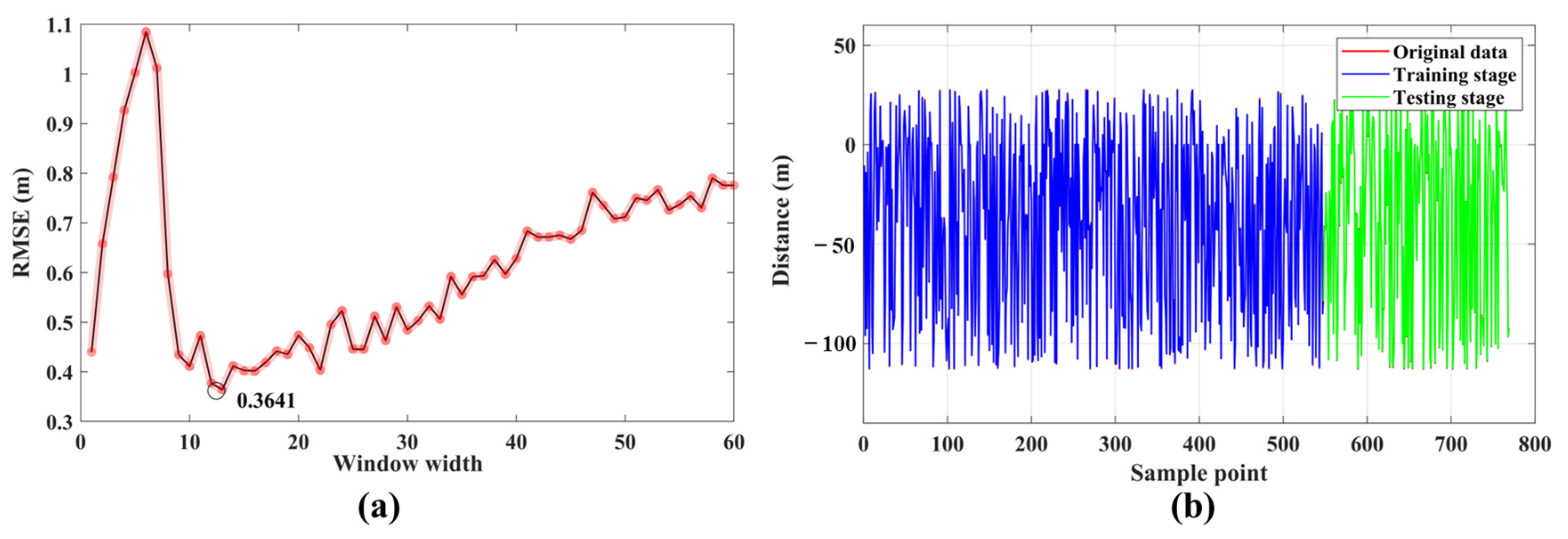
5.2. The Results of Cable State Prediction
5.3. Tracking Performance and Method Comparison
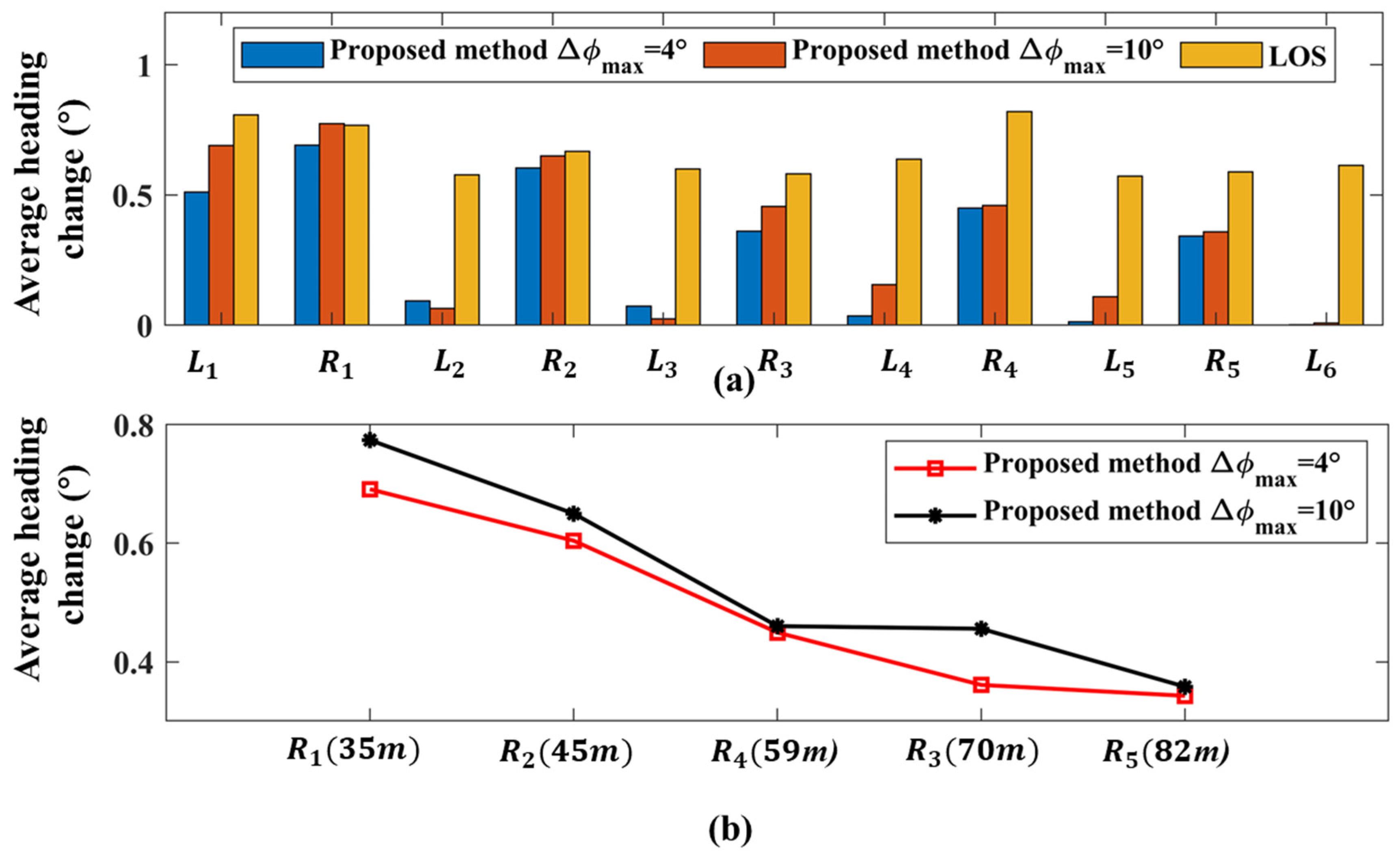
5.3.1. Tracking Performance Analysis
5.3.2. Impact of Cable Curvature on AUV Stability
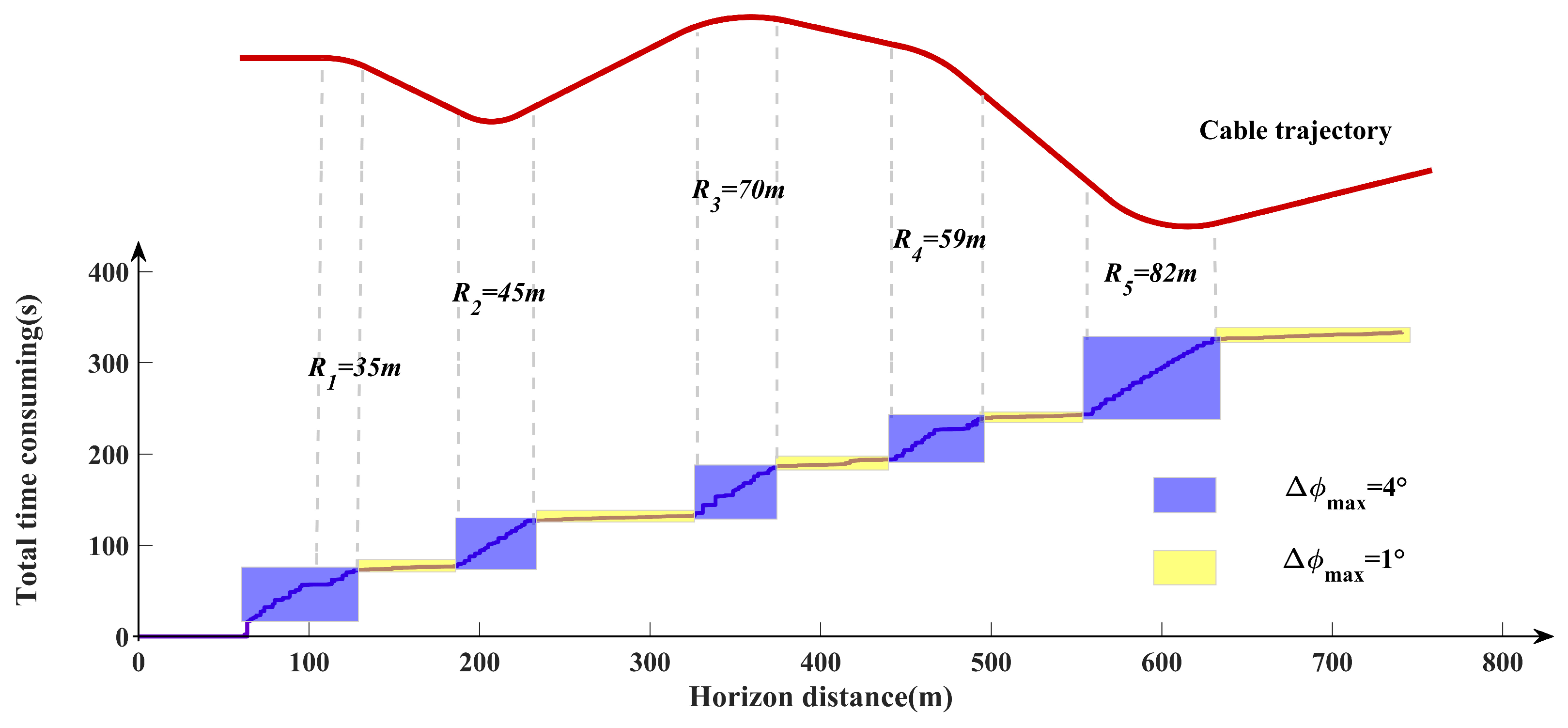
5.3.3. Time-Consumption Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bueger, C.; Liebetrau, T.; Franken, J. In-Depth Analysis Requested by the SEDE Sub-Committee Security Threats to Undersea Communications Cables and Infrastructure—Consequences for the EU; European Parliament: Strasbourg, France, 2022. [Google Scholar] [CrossRef]
- Gheorghe, A.V.; Vamanu, D.V.; Katina, P.F. Critical Infrastructures, Key Resources, Key Assets; Springer: Cham, Switzerland, 2018; ISBN 9783319692234. [Google Scholar]
- Adegboye, M.A.; Fung, W.; Karnik, A. Recent Advances in Pipeline Monitoring and Oil Leakage Detection Technologies: Principles and Approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef] [PubMed]
- Gritzalis, D.A. Cyber-Attacks on the Oil & Gas Sector: A Survey on Incident Assessment and Attack Patterns. IEEE Access 2020, 8, 1–37. [Google Scholar] [CrossRef]
- Shama, A.M.; El-Rashid, A.; El-Shaib, M.; Kotb, D.M. Review of Leakage Detection Methods for Subsea Pipeline. Marit. Transp. Harvest. Sea Resour. 2018, 2, 1141–1149. [Google Scholar]
- Jacobi, M.; Karimanzira, D. Multi Sensor Underwater Pipeline Tracking with AUVs. In Proceedings of the Oceans 2014 MTS/IEEE, St. John’s, NL, Canada, 14–19 September 2014; pp. 2–7. [Google Scholar] [CrossRef]
- Littlefield, R.H.; Soenen, K.; Packard, G.; Kaeli, J. Seafloor Cable Based Navigation and Monitoring with Autonomous Underwater Vehicles. In Proceedings of the Oceans 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019. [Google Scholar] [CrossRef]
- Bobkov, V.; Shupikova, A.; Inzartsev, A. Recognition and Tracking of an Underwater Pipeline from Stereo Images during AUV-Based Inspection. J. Mar. Sci. Eng. 2023, 11, 2002. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Li, W. Adaptive Neural Control of Flight-Style AUV for Subsea Cable Tracking Under Electromagnetic Localization Guidance. IEEE/ASME Trans. Mechatron. 2023, 28, 2976–2987. [Google Scholar] [CrossRef]
- Szyrowski, T.; Sharma, S.K.; Sutton, R.; Kennedy, G.A. Developments in Subsea Power and Telecommunication Cables Detection: Part 1–Visual and Hydroacoustic Tracking. Underw. Technol. 2013, 31, 123–132. [Google Scholar] [CrossRef]
- Evans, J.; Patron, P.; Privat, B.; Johnson, N.; Capus, C. AUTOTRACKER: Autonomous Inspection–Capabilities and Lessons Learned in Offshore Operations. In Proceedings of the Oceans ’09 MTS/IEEE Biloxi–Marine Technology for Our Future: Global and Local Challenges, Biloxi, MI, USA, 26–29 October 2009. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Niu, Z.; Zhang, Q. Subsea Cable Tracking by Autonomous Underwater Vehicle with Magnetic Sensing Guidance. Sensors 2016, 16, 1335. [Google Scholar] [CrossRef]
- Feng, H.; Yu, J.; Huang, Y.; Cui, J.; Qiao, J. Automatic Tracking Method for Submarine Cables and Pipelines of AUV Based on Side Scan Sonar. Ocean Eng. 2023, 280, 114689. [Google Scholar] [CrossRef]
- El-Fakdi, A.; Carreras, M. Policy Gradient Based Reinforcement Learning for Real Autonomous Underwater Cable Tracking. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems IROS, Nice, France, 22–26 September 2008; pp. 3635–3640. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Liu, J.; Zhang, S.; Liu, Z.; Lyu, E.; Chen, W. Submarine Pipeline Tracking Technology Based on AUVs with Forward Looking Sonar. Appl. Ocean Res. 2022, 122, 103128. [Google Scholar] [CrossRef]
- Bagnitsky, A.; Inzartsev, A.; Pavin, A.; Melman, S.; Morozov, M. Side Scan Sonar Using for Underwater Cables & Pipelines Tracking by Means of AUV. In Proceedings of the 2011 IEEE Symposium on Underwater Technology, UT’11 and Workshop on Scientific Use of Submarine Cables and Related Technologies, SSC’11, Tokyo, Japan, 5–8 April 2011. [Google Scholar] [CrossRef]
- Antich, J.; Ortiz, A. Development of the Control Architecture of an Underwater Cable Tracker. Int. J. Intell. Syst. 2005, 20, 477–498. [Google Scholar] [CrossRef]
- Naeem, W.; And, R.S.; Ahmad, S.M. Pure Pursuit Guidance and Model Predictive Control of an Autonomous Underwater Vehicle for Cable/Pipeline Tracking. Proc. Inst. Mar. Eng. Sci. Technol. Part C J. Mar. Sci. Environ. 2004, 279–283. [Google Scholar]
- Cai, M.; Member, S.; Wang, Y.; Wang, S.; Wang, R.; Cheng, L.; Member, S.; Tan, M. Prediction-Based Seabed Terrain Following Control for an Underwater Vehicle-Manipulator System. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 4751–4760. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Integrated Path Planning and Tracking Control of an AUV: A Unified Receding Horizon Optimization Approach. IEEE/ASME Trans. Mechatron. 2017, 22, 1163–1173. [Google Scholar] [CrossRef]
- Cao, X.; Ren, L.; Sun, C. Dynamic Target Tracking Control of Autonomous Underwater Vehicle Based on Trajectory Prediction. IEEE Trans. Cybern. 2023, 53, 1968–1981. [Google Scholar] [CrossRef]
- Ferri, G.; Munafo, A.; Lepage, K.D. An Autonomous Underwater Vehicle Data-Driven Control Strategy for Target Tracking. IEEE J. Ocean. Eng. 2018, 43, 323–343. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. Sensor-Driven Online Coverage Planning for Autonomous Underwater Vehicles. IEEE/ASME Trans. Mechatron. 2013, 18, 1827–1838. [Google Scholar] [CrossRef]
- Williams, D.P. AUV-Enabled Adaptive Underwater Surveying for Optimal Data Collection. Intell. Serv. Robot. 2012, 5, 33–54. [Google Scholar] [CrossRef]
- Cai, C.; Chen, J.; Yan, Q.; Liu, F.; Zhou, R. A Prior Information-based Coverage Path Planner for Underwater Search and Rescue Using Autonomous Underwater Vehicle (AUV) with Side-scan Sonar. IET Radar Sonar Navig. 2022, 16, 1225–1239. [Google Scholar] [CrossRef]
- Lee, E.M. Geomorphological Mapping. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 2001, 18, 53–56. [Google Scholar] [CrossRef]
- Dondurur, D. Acquisition and Processing of Marine Seismic Data; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 0128114916. [Google Scholar]
- Paull, L.; Saeedi, S.; Li, H.; Myers, V. An Information Gain Based Adaptive Path Planning Method for an Autonomous Underwater Vehicle Using Sidescan Sonar. In Proceedings of the 2010 IEEE International Conference on Automation Science and Engineering, Toronto, ON, USA, 21–24 August 2010; pp. 835–840. [Google Scholar] [CrossRef]
- Midtgaard, Ø.; Krogstad, T.R.; Hagen, P.E. Sonar Detection and Tracking of Seafloor Pipelines. In Proceedings of the UAM Conference, Kos, Greece, 20–24 June 2011. [Google Scholar]
- Yordanova, V.; Gips, B. Coverage Path Planning with Track Spacing Adaptation for Autonomous Underwater Vehicles. IEEE Robot. Autom. Lett. 2020, 5, 4774–4780. [Google Scholar] [CrossRef]
- Williams, D.P. On Optimal AUV Track-Spacing for Underwater Mine Detection. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 4755–4762. [Google Scholar]
- Feng, H.; Yu, J.; Huang, Y.; Qiao, J.; Wang, Z.; Xie, Z.; Liu, K. Adaptive Coverage Sampling of Thermocline with an Autonomous Underwater Vehicle. Ocean Eng. 2021, 233, 109151. [Google Scholar] [CrossRef]
- Nie, Y.; Yang, H.; Song, D.; Huang, Y.; Liu, X.; Hui, X. A New Cross-Platform Instrument for Microstructure Turbulence Measurements. J. Mar. Sci. Eng. 2021, 9, 1051. [Google Scholar] [CrossRef]
- Qiu, C.; Liang, H.; Huang, Y.; Mao, H.; Yu, J.; Wang, D.; Su, D. Development of Double Cyclonic Mesoscale Eddies at around Xisha Islands Observed by a ‘Sea-Whale 2000’ Autonomous Underwater Vehicle. Appl. Ocean Res. 2020, 101, 102270. [Google Scholar] [CrossRef]
- Hu, F.; Huang, Y.; Xie, Z.; Yu, J.; Wang, Z.; Qiao, J. Conceptual Design of a Long-Range Autonomous Underwater Vehicle Based on Multidisciplinary Optimization Framework. Ocean Eng. 2022, 248, 110684. [Google Scholar] [CrossRef]
- Qiao, J.; Yu, J.; Huang, Y.; Cui, J.; Wang, B.; Wang, Z. Sea-Whale Series AUV-Extending the Range to 4000 Kilometers. In Proceedings of the OCEANS 2022 Hampton Roads, Virtual, 17–20 October 2022. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lei, L.; Tang, T.; Gang, Y.; Jing, G. Hierarchical Neural Network-Based Hydrological Perception Model for Underwater Glider. Ocean Eng. 2022, 260, 112101. [Google Scholar] [CrossRef]
- Clausen, J. Branch and Bound Algorithms—Principles and Examples; University of Copenhagen: København, Demark, 1999; pp. 1–30. [Google Scholar]
- Chhetri, A.S.; Morrell, D.; Papandreou-Suppappola, A. Nonmyopic Sensor Scheduling and Its Efficient Implementation for Target Tracking Applications. EURASIP J. Adv. Signal Process. 2006, 2006, 031520. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F.; Jiang, J.; Liu, P.; Cui, Z. Continuous Arc-Shaped Laying Technique for Large Diameter Flexible Pipeline in Complicated Sea Conditions. Pet. Eng. Constr. 2018, 44, 36–40. [Google Scholar] [CrossRef]
- Guowei, C.; Chen, B.M.; Lee, T.H. Unmanned Rotorcraft Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; ISBN 1852338288. [Google Scholar]
- Huang, Y. Research on Key Technologies and Control Problems of Lightweight Long-Range AUV; University of Chinese Academy of Sciences: Beijing, China, 2020. [Google Scholar]





| Samples | Depth | Longitude | Latitude | Angle |
|---|---|---|---|---|
| 7820 | 20 m | 123.65821E | 41.93709N | 74° |
| Label | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Radius of curvature/Length (m) | 50 | 35 | 75 | 45 | 125 | 70 | 71 | 59 | 166 | 82 | 135 |
| Hyperparameters | Description | Value |
|---|---|---|
| numHiddenUnits | Number of hidden units | 40 |
| MaxEpochs | Number of training rounds | 400 |
| MiniBatchsize | Minimum batch number of samples | 26 |
| InitialLearnRate | Initial learning rate | 0.005 |
| LearnRateDropPeriod | Learn rate drop period | 200 |
| LearnRateDropFactor | Learn rate drop factor | 0.1 |
| Method | MD (m) | SD (m) | MA (°) | SA (°) | SH (°) |
|---|---|---|---|---|---|
| 1.5 | 1.07 | 1.37 | 1.81 | 0.17 | |
| 0.69 | 0.34 | 1.22 | 1.72 | 0.22 | |
| LOS-based method | 0.89 | 0.65 | 6.93 | 3.92 | 0.62 |
| Number | Parameters | Value | Number | Parameters | Value |
|---|---|---|---|---|---|
| 1 | 4 m | 5 | 0.5° | ||
| 2 | 4° | 6 | 1° | ||
| 3 | 1° | 7 | 0.5*Δφmax | ||
| 4 | 4° | 8 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, H.; Huang, Y.; Qiao, J.; Wang, Z.; Hu, F.; Yu, J. Prediction-Based Submarine Cable-Tracking Strategy for Autonomous Underwater Vehicles with Side-Scan Sonar. J. Mar. Sci. Eng. 2024, 12, 1725. https://doi.org/10.3390/jmse12101725
Feng H, Huang Y, Qiao J, Wang Z, Hu F, Yu J. Prediction-Based Submarine Cable-Tracking Strategy for Autonomous Underwater Vehicles with Side-Scan Sonar. Journal of Marine Science and Engineering. 2024; 12(10):1725. https://doi.org/10.3390/jmse12101725
Chicago/Turabian StyleFeng, Hao, Yan Huang, Jianan Qiao, Zhenyu Wang, Feng Hu, and Jiancheng Yu. 2024. "Prediction-Based Submarine Cable-Tracking Strategy for Autonomous Underwater Vehicles with Side-Scan Sonar" Journal of Marine Science and Engineering 12, no. 10: 1725. https://doi.org/10.3390/jmse12101725
APA StyleFeng, H., Huang, Y., Qiao, J., Wang, Z., Hu, F., & Yu, J. (2024). Prediction-Based Submarine Cable-Tracking Strategy for Autonomous Underwater Vehicles with Side-Scan Sonar. Journal of Marine Science and Engineering, 12(10), 1725. https://doi.org/10.3390/jmse12101725






