Corrected Method for Scaling the Structural Response Subjected to Blast Load
Abstract
:1. Introduction
2. Similarity Law and Correction for Blast Response
2.1. Similarity Law of Blast Response
2.2. Similarity Distortion and Correction
3. Simulation Verification for Correction Method
3.1. Ideal Elastic–Plastic Model
3.1.1. Setting of Simulations and Conditions
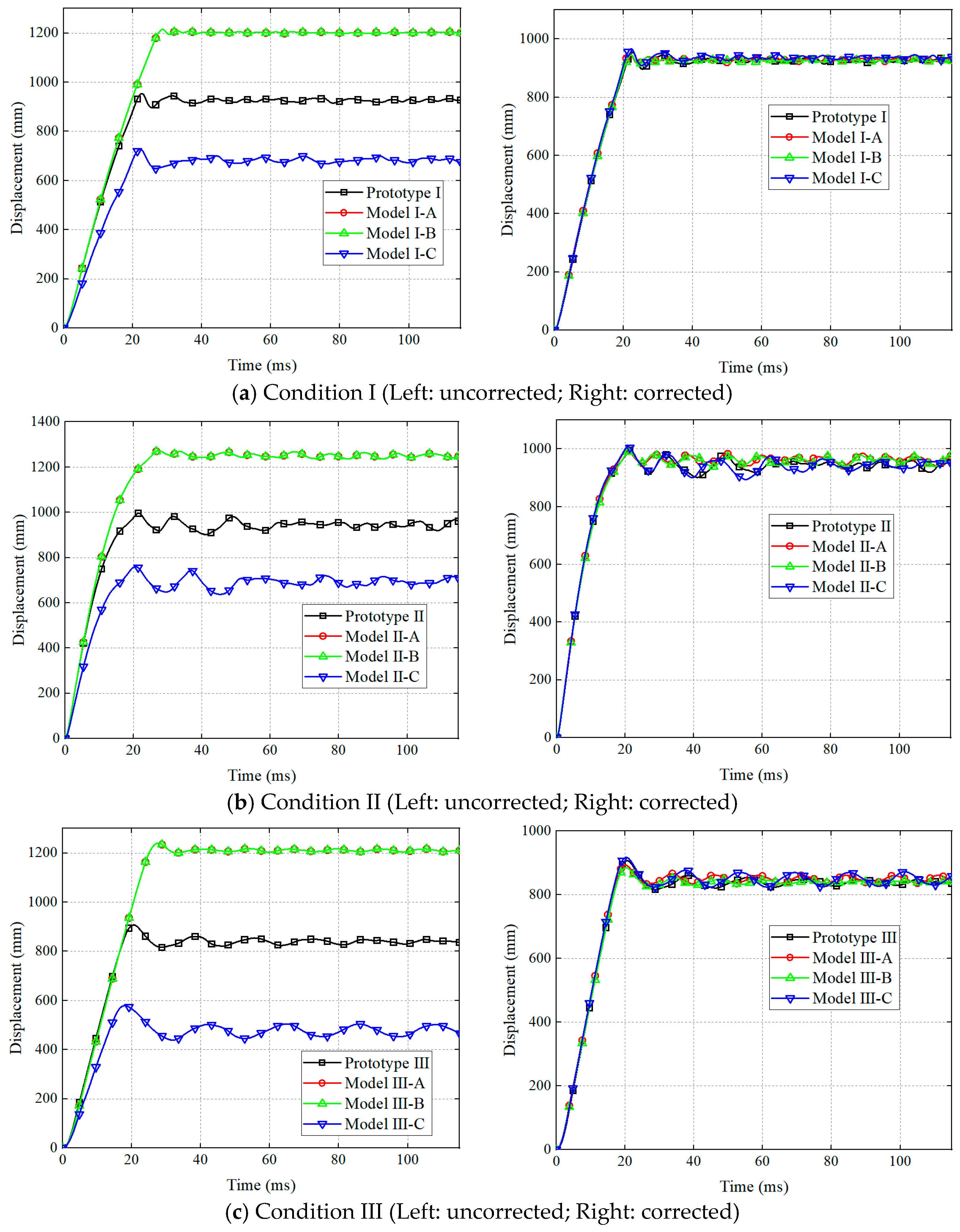
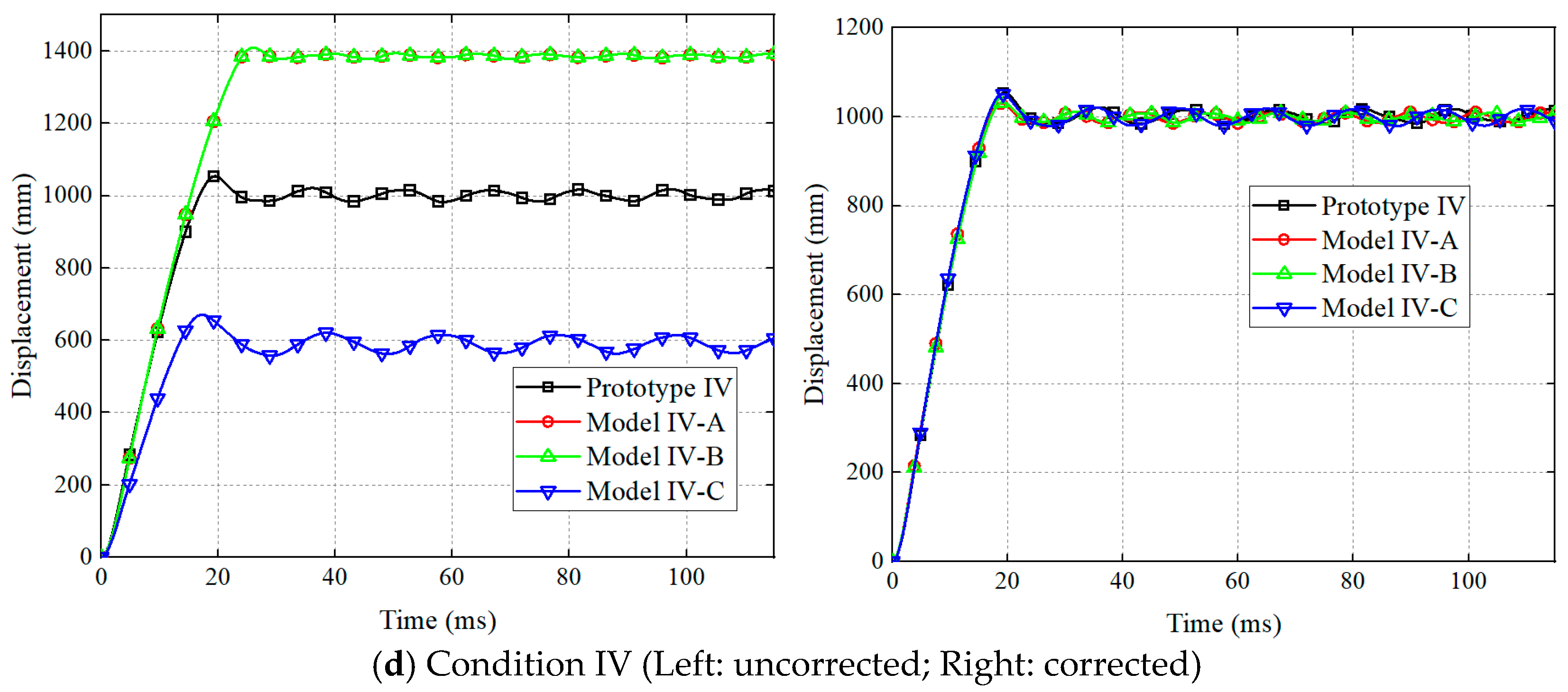
3.1.2. Comparison of Structural Response
3.1.3. Validation of Scaling Factor for Work Done by Explosive Load
3.2. Johnson–Cook Constitutive Model
3.2.1. Setting of Prototype Conditions
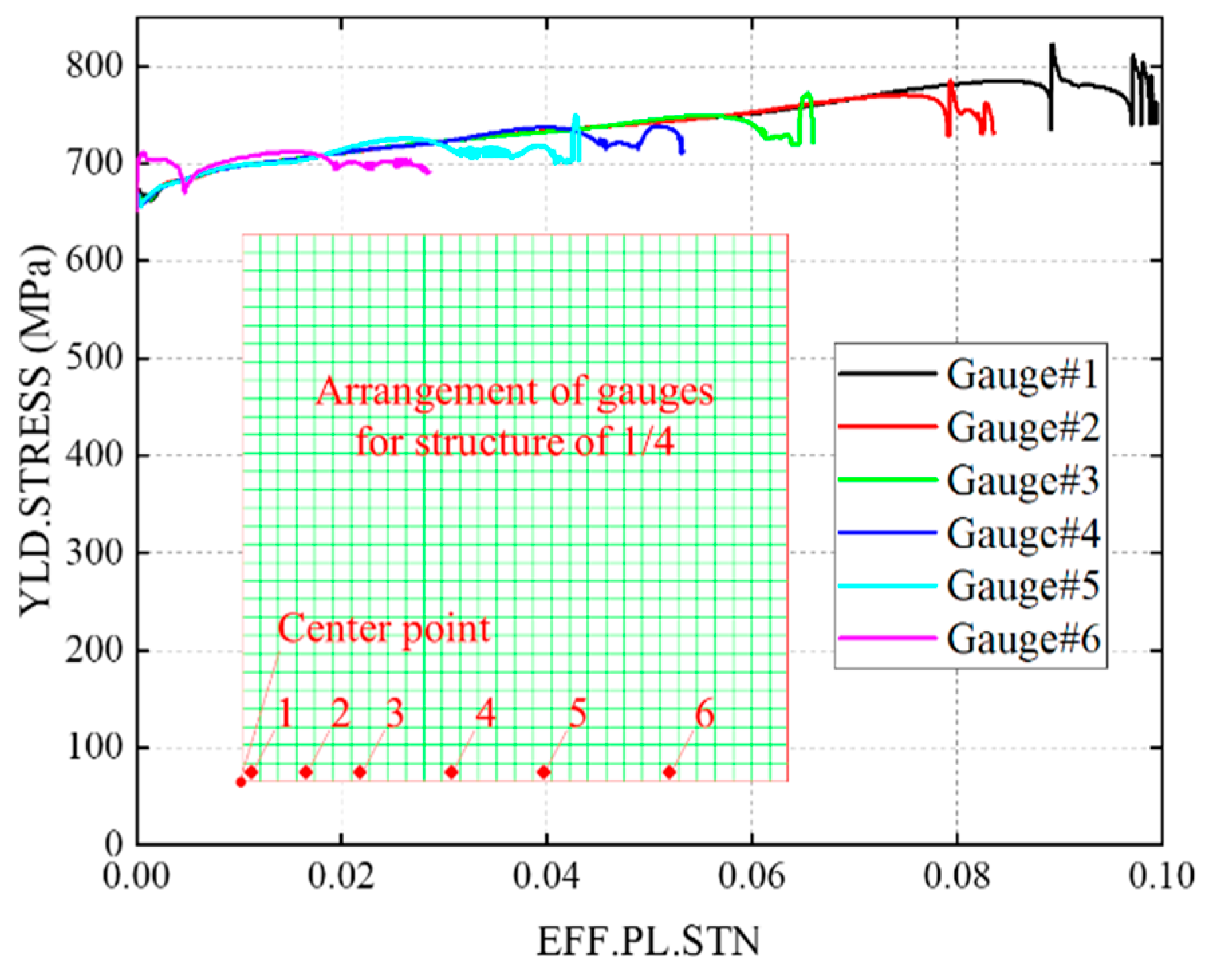
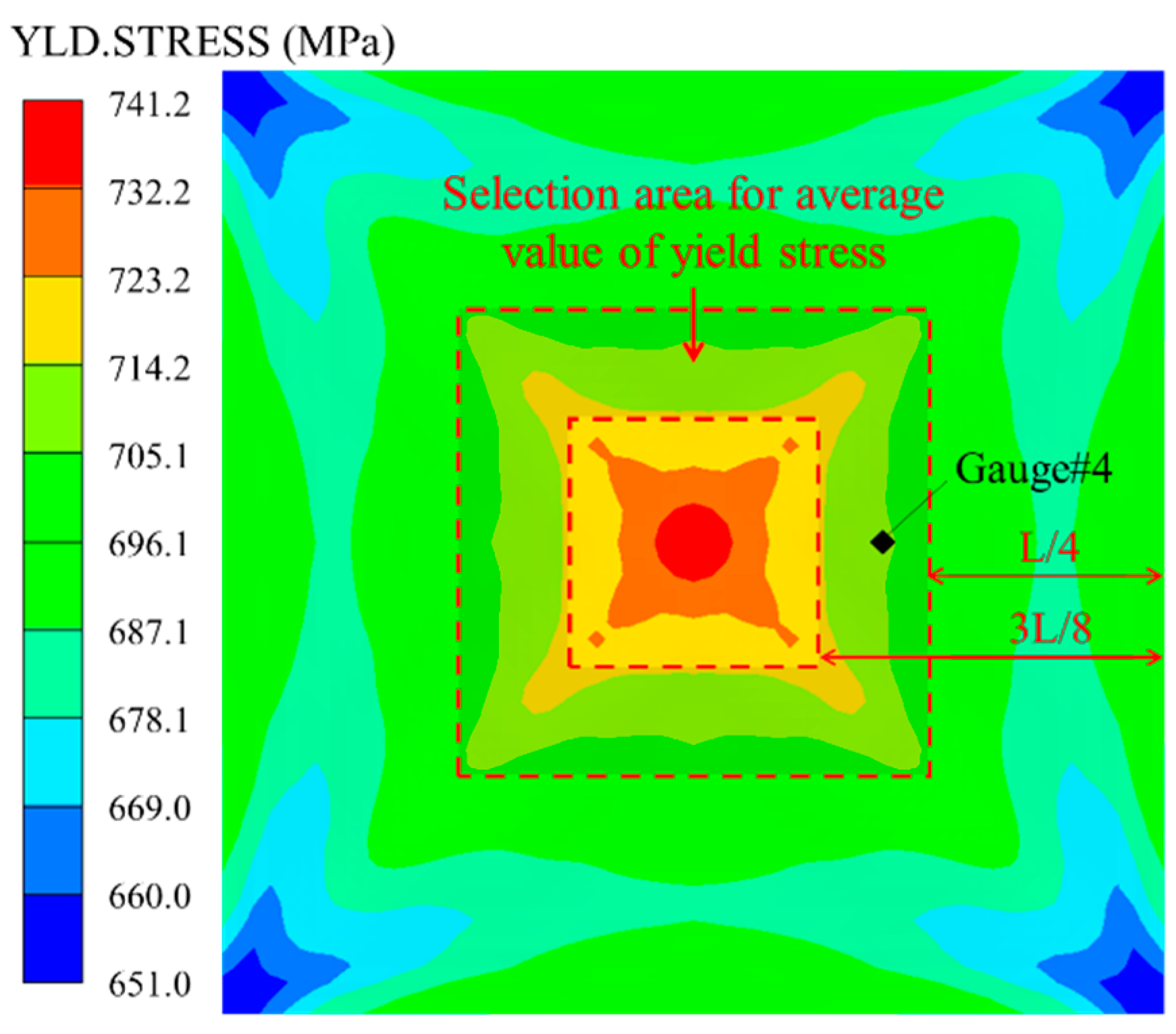
3.2.2. Analysis of Dynamic Yield Stress and Setting of Scaling Condition
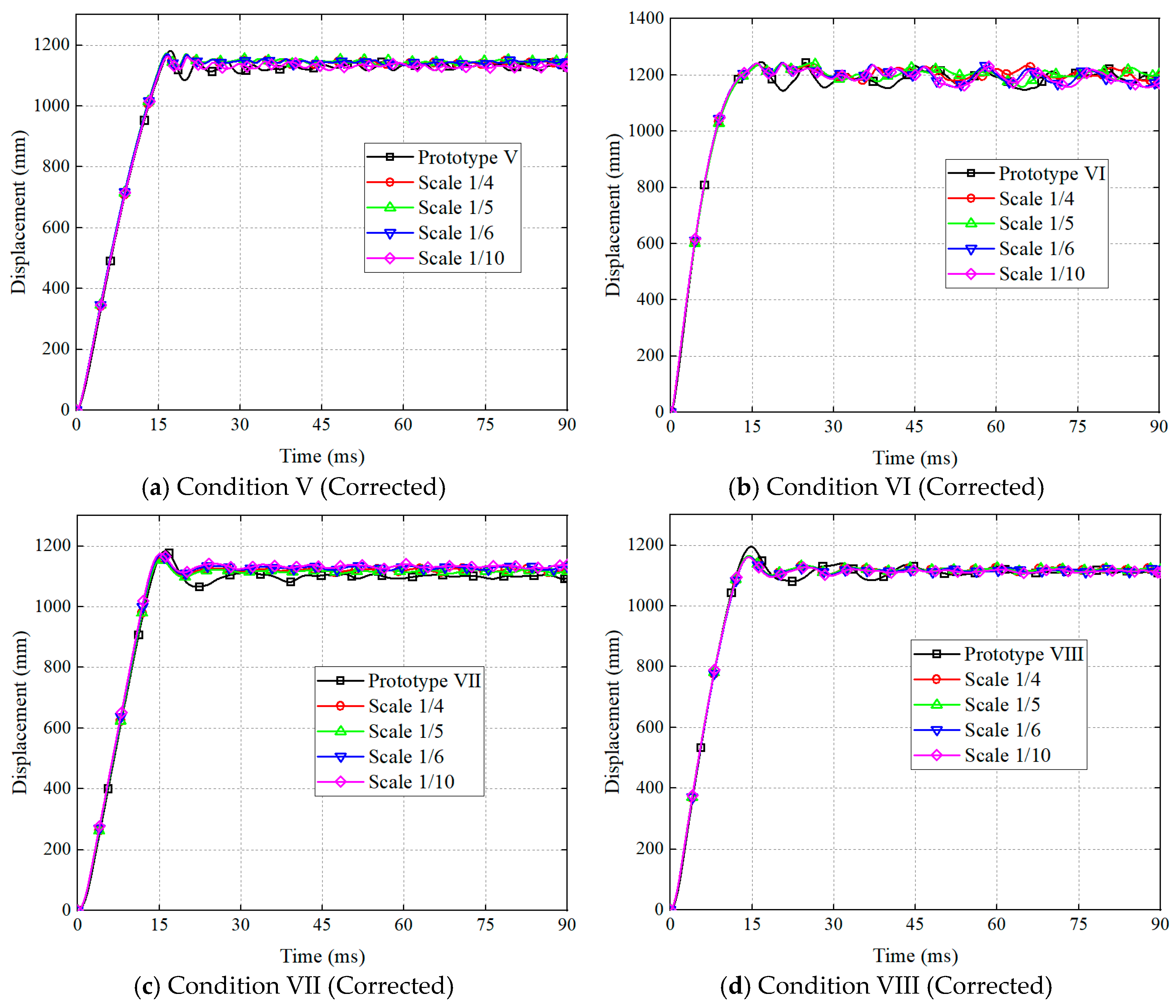
3.2.3. Comparison of Structural Response
4. Similar Distortion Prediction of Blast Response
4.1. Similar Prediction Method
4.1.1. Scaling Factor for Effective Plastic Strain
4.1.2. Establishment of Prediction Method
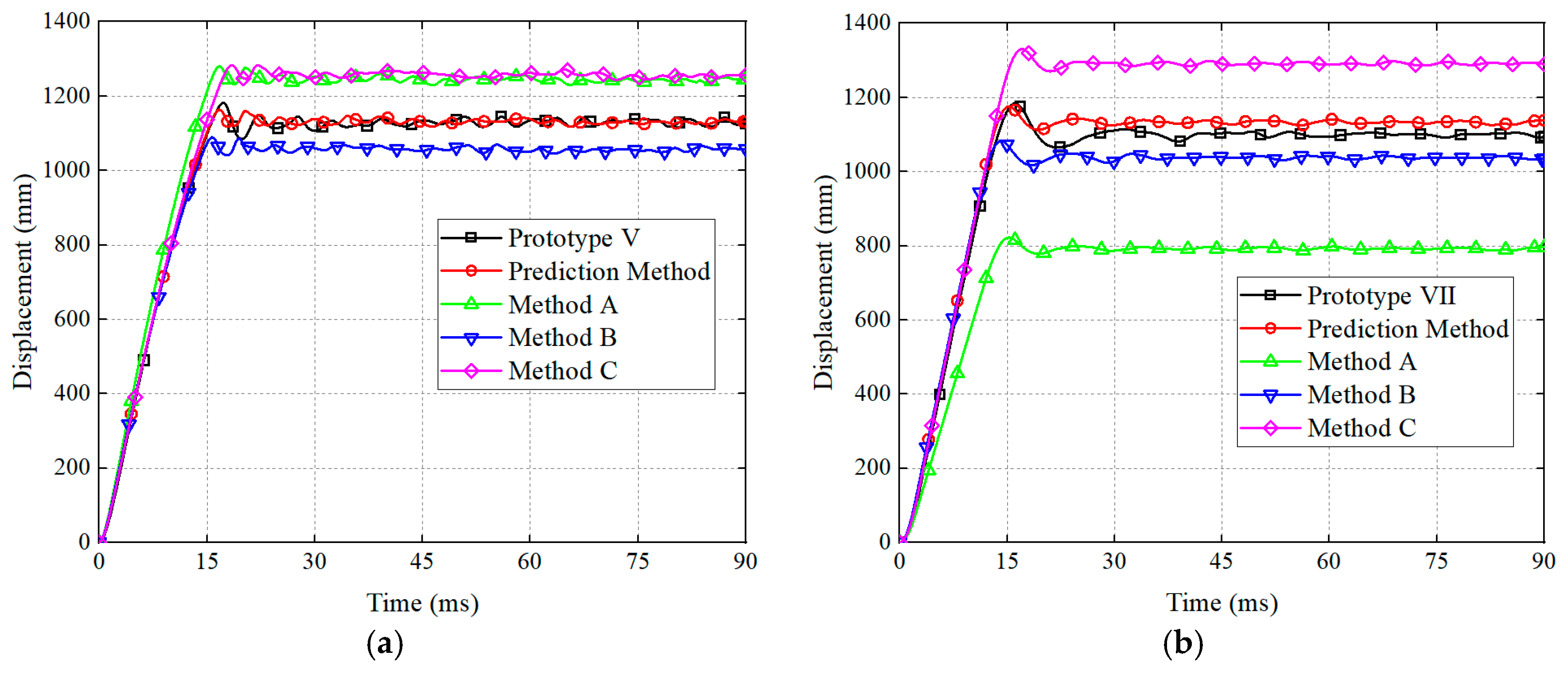
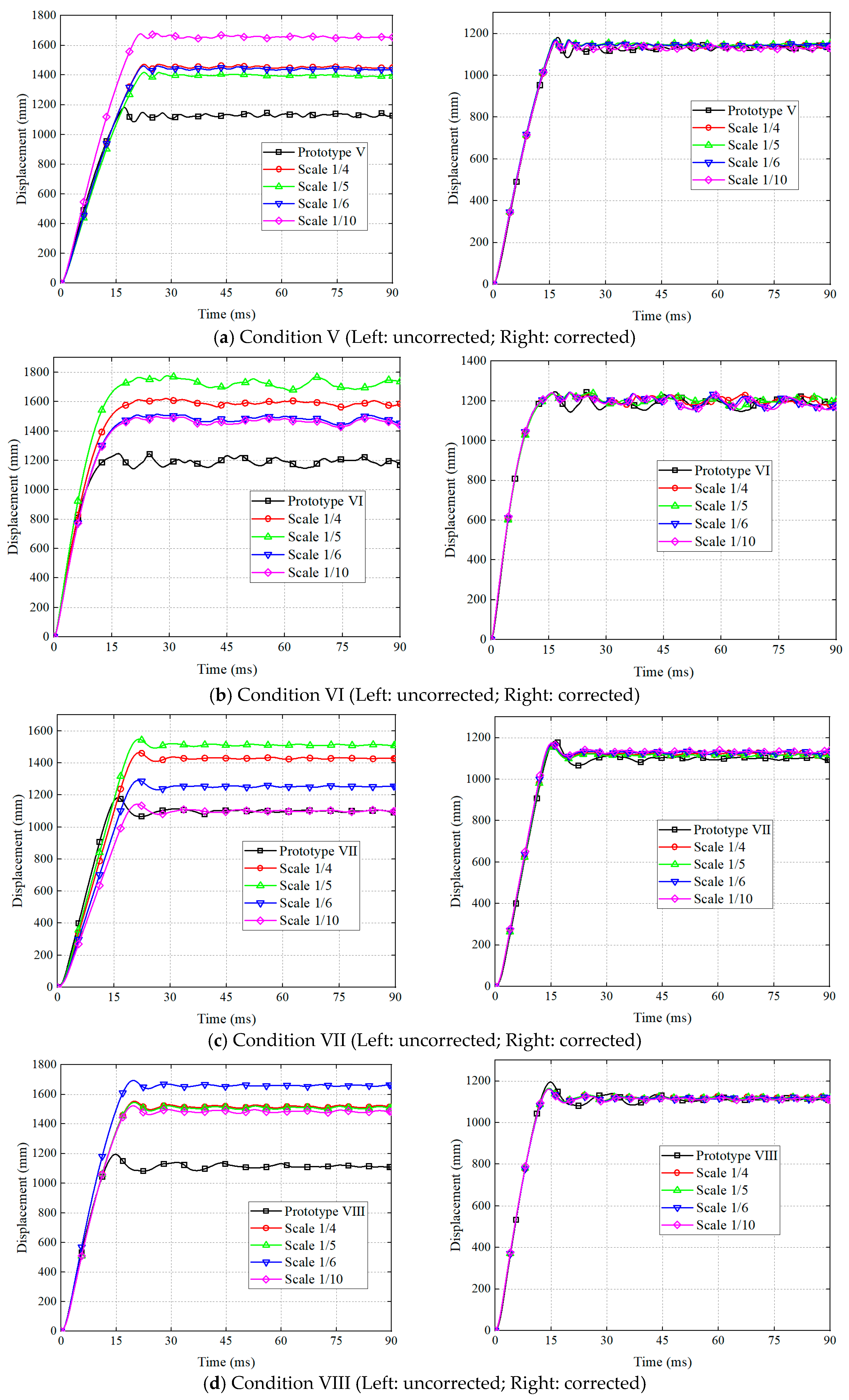
4.2. Simulation Verification for Prediction Method
5. Discussion and Conclusions
- (1)
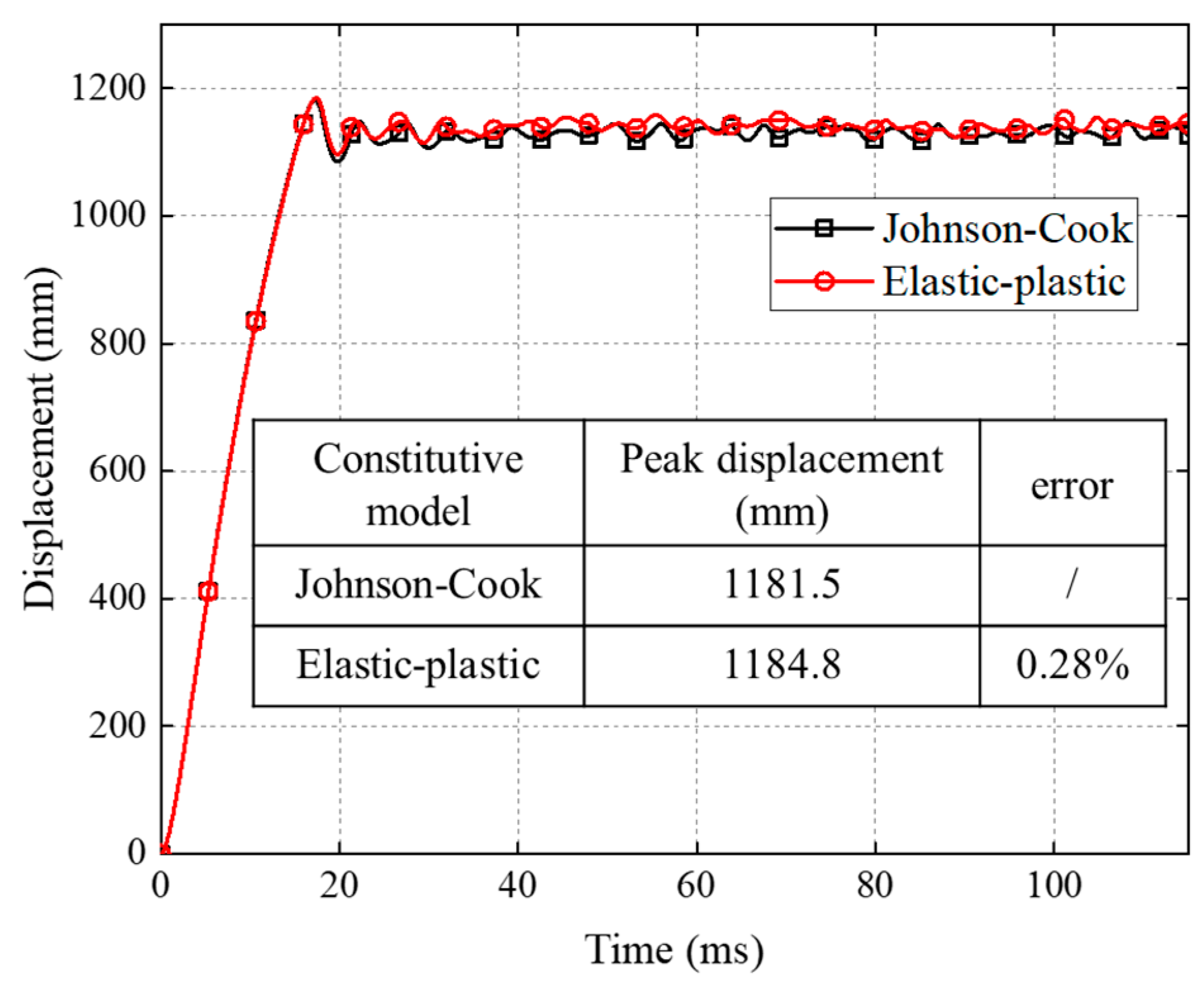
- The structural dynamic response difference between the model and the prototype under explosive loading due to the distortion of yield stress and thickness can be effectively compensated by using the combined corrected equation of impulse, yield stress and thickness. Numerical simulations of the explosion response for thin plates and stiffened plates with an ideal elastic–plastic model were carried out. The results showed that the maximum error in the peak displacement of the corrected models does not exceed 3%, demonstrating the accuracy and applicability of the correction method. Additionally, the predicted work input of the explosive load by was consistent with the prototype, with a maximum error within 2%.
- (2)
- The analysis of the response characteristics of dynamic yield stress with Johnson–Cook constitutive model was carried out, and the average yield stress based on equal plastic strain energy was proposed. A consistent structural response can be obtained by applying the average yield stress to the ideal elastic–plastic model. An accurate prediction can be obtained by correcting the distortion factor based on the average yield stress.
- (3)
- The distortion of the effective plastic strain was analyzed, and the average effective plastic strain between the corrected model and the prototype was equal. Based on the distortion conversion relationship of effective plastic strain and strain rate, a prediction method based on the model structural response parameter is established. Simulation results indicate that the maximum error in the peak displacement of the corrected model is within 3%, demonstrating that the prediction accuracy can be effectively improved by using this method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| W | Mass of the explosive | t | Time |
| R | Stand-off distance | ε | Strain |
| Peak overpressure of the shockwave | Strain rate | ||
| I | impulse | Ei | Work done by impulse load |
| L | Length of the plate | Em | Maximum deformation energy |
| B | Width of the plate | S′ | Structural planar area |
| h | Thickness of the plate | εep | Effective plastic strain |
| n0 | Number of stiffeners | A | Static yield stress |
| ρ | Material density | B | Strain hardening constant |
| σd | Dynamic yield stress | n | Strain hardening index |
| M0 | Plastic limit bending moment | C | Strain rate factor |
| N0 | Plastic limit neutral plane force | m | Thermal softening index |
| δ | Midpoint deflection | Average yield stress | |
| v | Velocity | Average effective plastic strain |
Appendix A
References
- Zheng, C.; Kong, X.-S.; Wu, W.-G.; Liu, F. The elastic-plastic dynamic response of stiffened plates under confined blast load. Int. J. Impact Eng. 2016, 95, 141–153. [Google Scholar] [CrossRef]
- Zheng, C.; Kong, X.-S.; Wu, W.-G.; Xu, S.-X.; Guan, Z.-W. Experimental and numerical studies on the dynamic response of steel plates subjected to confined blast loading. Int. J. Impact Eng. 2018, 113, 144–160. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, P.; Hu, K. Nonlinear dynamic response of blast-loaded stiffened plates considering the strain rate sensitivity. Mar. Struct. 2020, 70, 102699. [Google Scholar] [CrossRef]
- Suresh, C.; Ramajeyathilagam, K. Large deformation behaviour of thin mild steel rectangular plates subjected to underwater explosion loading under air and water backed conditions. Appl. Ocean. Res. 2021, 114, 102780. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Chen, P.Y.; Qi, W. Scaling law of dynamic response of stiffened plates for a ship subjected to under water shock. J. Vi Bration Shock. 2008, 27, 81–86. [Google Scholar]
- Li, H.T.; Zhu, X.; Zhang, Z.H. Similarity law for dynamic response of hull girder subjected to underwater explosion in near field. J. Vib. Shock. 2010, 29, 28–32. [Google Scholar]
- Qin, Y.; Yao, X.; Wang, Z.; Wang, Y. Experimental investigation on damage features of stiffened cabin structures subjected to internal blast loading. Ocean Eng. 2022, 265, 112639. [Google Scholar] [CrossRef]
- Kong, X.; Zhou, H.; Xu, J.; Zheng, C.; Lu, A.; Wu, W. Scaling of confined explosion and structural response. Thin Walled Struct. 2023, 186, 110656. [Google Scholar] [CrossRef]
- Fu, S.; Gao, X.; Chen, X. The similarity law and its verification of cylindrical lattice shell model under internal explosion. Int. J. Impact Eng. 2018, 122, 38–49. [Google Scholar] [CrossRef]
- Oshiro, R.E.; Alves, M. Scaling impacted structures. Arch. Appl. Mech. 2004, 74, 130–145. [Google Scholar] [CrossRef]
- Alves, M.; Oshiro, R.E. Scaling the impact of a mass on a structure. Int. J. Impact Eng. 2006, 32, 1158–1173. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, D.; Lu, F.; Chen, X.; Zhao, P. A combined experimental and numerical investigation on the scaling laws for steel box structures subjected to internal blast loading. Int. J. Impact Eng. 2017, 102, 36–46. [Google Scholar] [CrossRef]
- Ren, X.B.; Huang, Z.X.; Jiang, Y.B.; Chen, Z.H.; Cao, X.F.; Zhao, T.; Li, Y. The scaling laws of cabin structures subjected to internal blast loading: Experimental and numerical studies. Def. Technol. 2022, 18, 811–822. [Google Scholar] [CrossRef]
- Alves, M.; Oshiro, R.E. Scaling impacted structures when the prototype and the model are made of different materials. Int. J. Solids Struct. 2006, 43, 2744–2760. [Google Scholar] [CrossRef]
- Mazzariol, L.M.; Alves, M. Experimental study on scaling of circular tubes subjected to dynamic axial crushing using models of different materials. In Proceedings of the 22nd International Congress of Mechanical Engineering, Ribeirão Preto, Brazil, 3–7 November 2013. [Google Scholar]
- Mazzariol, L.M.; Oshiro, R.E.; Alves, M. A method to represent impacted structures using scaled models made of different materials. Int. J. Impact Eng. 2016, 90, 81–94. [Google Scholar] [CrossRef]
- Wang, S.; Xu, F.; Dai, Z.; Liu, X.; Li, X.; Yang, L.; Xi, X. A direct scaling method for the distortion problems of structural impact. Chin. J. Theor. Appl. Mech. 2020, 52, 774–786. [Google Scholar]
- Wang, S.; Xu, F.; Zhang, X.; Yang, L.; Liu, X. Material similarity of scaled models. Int. J. Impact Eng. 2021, 156, 103951. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Ya, L.; Wa, S.; Li, X.; Xi, X.; Li, J. Study on the similarity of elasticity and ideal plasticity response of thin plate under impact loading. Explos. Shock. 2021, 41, 113103. [Google Scholar]
- Wang, Y.; Liang, D.; Xi, X.; Wang, J.; Liu, X.; He, H. Prediction techniques for the scaled models made of different materials under impact loading. Int. J. Impact Eng. 2023, 179, 104642. [Google Scholar] [CrossRef]
- Wang, S.; Chang, X.; Xu, F.; Li, J.; Wang, J. Similarity laws of geometric and material distortion for anisotropic elastic plate subjected to impact loads. Int. J. Impact Eng. 2023, 180, 104683. [Google Scholar] [CrossRef]
- Wang, T.; Ni, L.; Wu, T.; Wang, Y.; Xi, X.; He, H. Dynamic similitude technique for predicting the behaviour of structures subjected to impact loads. Int. J. Impact Eng. 2022, 163, 104160. [Google Scholar] [CrossRef]
- Oshiro, R.E.; Alves, M. Predicting the behaviour of structures under impact loads using geometrically distorted scaled models. J. Mech. Phys. Solids 2012, 60, 1330–1349. [Google Scholar] [CrossRef]
- Mazzariol, L.M.; Alves, M. Similarity laws of structures under impact load: Geometric and material distortion. Int. J. Mech. Sci. 2019, 157, 633–647. [Google Scholar] [CrossRef]
- Mazzariol, L.M.; Alves, M. Experimental verification of similarity laws for impacted structures made of different materials. Int. J. Impact Eng. 2019, 133, 103364. [Google Scholar] [CrossRef]
- Wang, S.; Xu, F.; Zhang, X.; Dai, Z.; Liu, X.; Bai, C. A directional framework of similarity laws for geometrically distorted structures subjected to impact loads. Int. J. Impact Eng. 2022, 161, 104092. [Google Scholar] [CrossRef]
- Ya, L.; Ch, X.; Xu, F.; Wa, S.; Li, X.; Xi, X.; Li, X. Study on the scaling law of geometrically-distorted thin-walled cylindrical shells subjected to axial impact. Explos. Shock. 2022, 42, 150–161. [Google Scholar]
- Chang, X.; Xu, F.; Yang, L.; Wang, S.; Li, X.; Hui, X.; Wang, J. Study on the similarity of axial crushing of thin-walled square tubes. J. Vib. Shock. 2023, 42, 284–294. [Google Scholar]
- Chang, X.; Xu, F.; Feng, W.; Li, X.; Liu, X. Similarity laws of geometric distortion for stiffened plate under low velocity impact loads. Thin Walled Struct. 2024, 199, 111830. [Google Scholar] [CrossRef]
- Kong, X.; Li, X.; Zheng, C.; Liu, F.; Wu, W.-G. Similarity considerations for scale-down model versus prototype on impact response of plates under blast loads. Int. J. Impact Eng. 2017, 101, 32–41. [Google Scholar] [CrossRef]
- Gao, X.; Fu, S.; Liu, Q.; Chen, D.; Zheng, Q.; Chen, X.; Wang, W. Dynamic scaling laws of spatial grid structures under inner explosion considering material and geometric distortions. Mech. Adv. Mater. Struct. 2022, 29, 5163–5176. [Google Scholar]
- Fu, T.; Zhang, M.; Zheng, Q.; Zhou, D.; Sun, X.; Wang, X. Scaling the response of armor steel subjected to blast loading. Int. J. Impact Eng. 2021, 153, 103863. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Y.; Wang, Z.; Yao, X. Investigation on similarity laws of cabin structure under internal blast loading. Ocean Eng. 2022, 260, 111998. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, Z.H. A scaling method for predicting dynamic responses of stiffened plates made of materials different from experimental models. Explos. Shock. Waves 2010, 30, 511–516. [Google Scholar]
- Zhou, H.; Wang, D. Corrected similarity laws of stiffened panels considering geometric distortion under low speed impact load. Ocean Eng. 2021, 240, 109937. [Google Scholar] [CrossRef]
- Zhou, H.; Okada, T.; Kawamura, Y.; Wang, D.; Hayakawa, G. Improved Similarity Law for Scaling Dynamic Responses of Stiffened Plates with Distorted Stiffener Configurations. Appl. Sci. 2024, 14, 6265. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Y.; Wang, Z.; Yao, X. Investigation on similarity laws of cabin structure for the material distortion correction under internal blast loading. Thin Walled Struct. 2022, 177, 109371. [Google Scholar] [CrossRef]
- Kang, H.; Guo, X.; Zhang, Q.; Cui, H.; Wang, S.; Yan, W. Predicting the behavior of armored plates under shallow-buried landmine explosion using incomplete scaling models. Int. J. Impact Eng. 2021, 156, 103970. [Google Scholar] [CrossRef]
- Kong, X.; Zhou, H.; Kuang, Z.; Zheng, C.; Li, X.; Wu, W.; Guan, Z. Corrected method for scaling the dynamic response of stiffened plate subjected to blast load. Thin Walled Struct. 2021, 159, 107214. [Google Scholar] [CrossRef]
- Chen, C.; Liu, R.; Han, Z.; Cheng, Y. Dynamic response prediction of prototype from scale-down model for I-core sandwich panels subjected to internal explosion. Int. J. Impact Eng. 2023, 174, 104496. [Google Scholar] [CrossRef]
- Nurick, G.N.; Martin, J.B. Deformation of thin plates subjected to impulsive loading—A review: Part i: Theoretical considerations. Int. J. Impact Eng. 1989, 8, 159–170. [Google Scholar] [CrossRef]
- Zhao, Y.P. Suggestion of a new dimensionless number for dynamic plastic response of beams and plates. Arch. Appl. Mech. 1998, 68, 524–538. [Google Scholar] [CrossRef]
- AUTODYN Theory Manual. USA: Century Dynamics Incorporated. Available online: https://www.researchgate.net/profile/Alireza_Rashiddel/post/Is_there_a_way_to_implement_a_large_strain_viscoelastic_material_model_in_AUTODYN/attachment/5f85890de66b860001a8503c/AS%3A946132159045637%401602586893515/download/0-theory_manual_AUTODYN.pdf (accessed on 29 September 2024).
- Lei, X.; Lu, Y. Mechanical properties and constitutive relation of steel 921A under effects of fire and explosion. Ship Eng. 2019, 1, 69–73. [Google Scholar]
- Kong, X.-S.; Wu, W.-G.; Li, J.; Chen, P.; Liu, F. Experimental and numerical investigation on a multi-layer protective structure under the synergistic effect of blast and fragment loadings. Int. J. Impact Eng. 2014, 65, 146–162. [Google Scholar] [CrossRef]

| Variable | Scale Factors | Variable | Scale Factors |
|---|---|---|---|
| Length, L | Plastic limit bending moment, M0 | ||
| Density, ρ | Plastic limit neutral plane force, N0 | ||
| Yield stress, σd | Displacement, δ | ||
| Specific impulse, I | Velocity, v | ||
| Width, B | Time, t | ||
| Thickness, h | Strain, ε | ||
| Number of stiffeners, n0 | Strain rate, |
| Prototype | Length (m) | Thickness (mm) | Stiffener (mm) | TNT Mass (kg) | Stand-Off (m) | Yield Stress (MPa) |
|---|---|---|---|---|---|---|
| I | 10 | 30 | / | 3000 | 10 | 385 |
| II | 36 | / | 2000 | 5 | ||
| III | 20 | 4000 | 10 | |||
| IV | 24 | 2400 | 5 |
| Distortion Model | βI | βh | βσd | βt |
|---|---|---|---|---|
| I-A | 0.0500 | 0.0640 | 0.61 | 0.0640 |
| I-B | 0.0391 | 0.0500 | 0.61 | 0.0639 |
| I-C | 0.0667 | 0.0667 | 1.00 | 0.0500 |
| II-A | 0.0500 | 0.0640 | 0.61 | 0.0640 |
| II-B | 0.0391 | 0.0500 | 0.61 | 0.0639 |
| II-C | 0.0667 | 0.0667 | 1.00 | 0.0500 |
| III-A | 0.0500 | 0.0640 | 0.61 | 0.0640 |
| III-B | 0.0391 | 0.0500 | 0.61 | 0.0639 |
| III-C | 0.0700 | 0.0700 | 1.00 | 0.0500 |
| IV-A | 0.0500 | 0.0640 | 0.61 | 0.0640 |
| IV-B | 0.0391 | 0.0500 | 0.61 | 0.0639 |
| IV-C | 0.0708 | 0.0708 | 1.00 | 0.0500 |
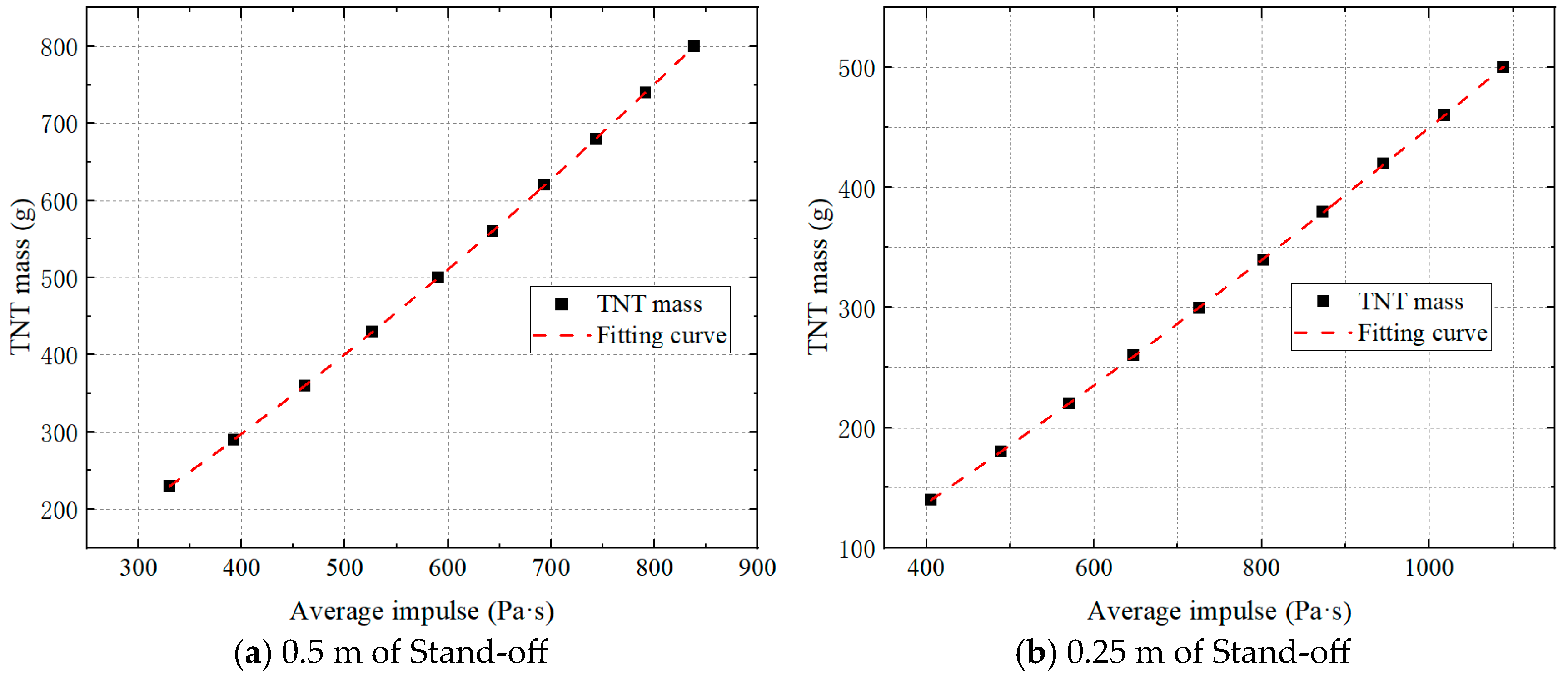
| TNT Mass (g) | 230 | 290 | 360 | 430 | 500 | 560 | 620 | 680 | 740 | 800 |
|---|---|---|---|---|---|---|---|---|---|---|
| Average impulse (Pa·s) | 330.3 | 392.7 | 460.9 | 526.8 | 590.4 | 643.1 | 693.2 | 743.5 | 791.2 | 838.4 |
| TNT Mass (g) | 140 | 180 | 220 | 260 | 300 | 340 | 380 | 420 | 460 | 500 |
|---|---|---|---|---|---|---|---|---|---|---|
| Average impulse (Pa·s) | 405.2 | 489.2 | 570.4 | 646.8 | 725.6 | 802.4 | 872.8 | 945.2 | 1017.6 | 1088.0 |
| Distortion Model | TNT Mass (g) | Distortion Model | TNT Mass (g) |
|---|---|---|---|
| I-A | 375.0 | III-A | 500.0 |
| I-B | 269.7 | III-B | 359.0 |
| I-C | 294.3 | III-C | 370.5 |
| II-A | 250.0 | IV-A | 300.0 |
| II-B | 181.7 | IV-B | 218.8 |
| II-C | 197.9 | IV-C | 222.6 |
| Uncorrected | Corrected | |||
|---|---|---|---|---|
| Condition | Peak Displacement (mm) | Error (%) | Peak Displacement (mm) | Error (%) |
| Prototype I | 953.8 | |||
| Model I-A | 1215.0 | 27.39 | 948.9 | −0.51 |
| Model I-B | 1215.0 | 27.39 | 945.0 | −0.92 |
| Model I-C | 727.1 | −23.77 | 966.4 | 1.32 |
| Prototype II | 996.6 | |||
| Model II-A | 1272.9 | 27.72 | 996.5 | −0.01 |
| Model II-B | 1272.9 | 27.72 | 990.7 | −0.59 |
| Model II-C | 759.8 | −23.76 | 1007.5 | 1.09 |
| Prototype III | 907.3 | |||
| Model III-A | 1240.3 | 36.70 | 893.6 | −1.51 |
| Model III-B | 1240.3 | 36.70 | 885.5 | −2.40 |
| Model III-C | 578.7 | −36.22 | 917.5 | 1.12 |
| Prototype IV | 1054.2 | |||
| Model IV-A | 1409.4 | 33.69 | 1030.6 | −2.24 |
| Model IV-B | 1409.4 | 33.69 | 1032.4 | −2.07 |
| Model IV-C | 670.8 | −36.37 | 1051.2 | −0.28 |
| Condition | Work Done (MJ) | Error (%) | Condition | Work Done (MJ) | Error (%) |
|---|---|---|---|---|---|
| Prototype I | 23.320 | / | Prototype III | 37.296 | / |
| Model I-A | 23.36 | 0.16 | Model III-A | 38.16 | 2.33 |
| Model I-B | 23.25 | 0.30 | Model III-B | 38.02 | 1.95 |
| Model I-C | 23.62 | 1.27 | Model III-C | 37.58 | 0.77 |
| Prototype II | 34.528 | / | Prototype IV | 51.024 | / |
| Model II-A | 34.50 | 0.09 | Model IV-A | 51.24 | 0.42 |
| Model II-B | 34.27 | 0.74 | Model IV-B | 51.67 | 1.26 |
| Model II-C | 35.10 | 1.66 | Model IV-C | 50.58 | 0.88 |
| Prototype | Length (m) | Thickness (mm) | Stiffener (mm) | TNT Mass (kg) | Average (Pa·s) | Stand-Off (m) | Material |
|---|---|---|---|---|---|---|---|
| Ⅴ | 10 | 22 | / | 4000 | 11,792 | 10 | 921A |
| Ⅵ | 27 | / | 2800 | 16,368 | 5 | ||
| Ⅶ | 14 | 5000 | 13,936 | 10 | |||
| Ⅷ | 19 | 3000 | 17,264 | 5 |
| Material | A/MPa | B/MPa | n | C | m |
|---|---|---|---|---|---|
| 921A | 651 | 395 | 0.64 | 0.024 | 1.03 |
| Q235 | 249.2 | 889 | 0.746 | 0.058 | 0.94 |
| Model | βL | βh | First Correction | Second Correction | |||
|---|---|---|---|---|---|---|---|
| βI | W (kg) | βσd | βI | W (kg) | |||
| V | 1/4 | 0.273 | 0.201 | 46.50 | 0.494 | 0.192 | 43.76 |
| 1/5 | 0.227 | 0.167 | 25.14 | 0.501 | 0.161 | 23.88 | |
| 1/6 | 0.182 | 0.134 | 13.78 | 0.505 | 0.129 | 13.16 | |
| 1/10 | 0.0909 | 0.0669 | 2.330 | 0.516 | 0.0653 | 2.256 | |
| VI | 1/4 | 0.259 | 0.191 | 30.98 | 0.505 | 0.184 | 29.62 |
| 1/5 | 0.185 | 0.136 | 13.70 | 0.509 | 0.132 | 13.16 | |
| 1/6 | 0.185 | 0.136 | 10.03 | 0.514 | 0.133 | 9.701 | |
| 1/10 | 0.111 | 0.0817 | 2.166 | 0.526 | 0.0806 | 2.126 | |
| VII | 1/4 | 0.286 | 0.210 | 61.82 | 0.494 | 0.201 | 58.16 |
| 1/5 | 0.214 | 0.158 | 29.04 | 0.498 | 0.151 | 27.48 | |
| 1/6 | 0.214 | 0.158 | 21.44 | 0.504 | 0.152 | 20.45 | |
| 1/10 | 0.143 | 0.105 | 5.333 | 0.517 | 0.103 | 5.171 | |
| VIII | 1/4 | 0.263 | 0.194 | 33.80 | 0.507 | 0.187 | 32.44 |
| 1/5 | 0.211 | 0.155 | 17.31 | 0.512 | 0.151 | 16.71 | |
| 1/6 | 0.158 | 0.116 | 8.749 | 0.515 | 0.113 | 8.476 | |
| 1/10 | 0.105 | 0.0774 | 2.163 | 0.527 | 0.0764 | 2.126 | |
| Model | βL | /s−1 | W (kg) | ||
|---|---|---|---|---|---|
| V | 1/4 | 0.02358 | 15.26 | 0.1911 | 43.58 |
| 1/5 | 0.02408 | 19.54 | 0.1604 | 23.79 | |
| 1/6 | 0.02397 | 23.57 | 0.1289 | 13.12 | |
| 1/10 | 0.02340 | 38.69 | 0.06518 | 2.251 | |
| VI | 1/4 | 0.02822 | 20.64 | 0.1842 | 29.62 |
| 1/5 | 0.02803 | 25.31 | 0.1322 | 13.17 | |
| 1/6 | 0.02765 | 31.38 | 0.1328 | 9.706 | |
| 1/10 | 0.02743 | 51.83 | 0.08064 | 2.129 | |
| VII | 1/4 | 0.02361 | 17.72 | 0.2006 | 58.10 |
| 1/5 | 0.02351 | 21.13 | 0.1512 | 27.48 | |
| 1/6 | 0.02356 | 27.38 | 0.1521 | 20.44 | |
| 1/10 | 0.02365 | 45.68 | 0.1027 | 5.171 | |
| VIII | 1/4 | 0.02740 | 22.93 | 0.1869 | 32.32 |
| 1/5 | 0.02715 | 27.64 | 0.1502 | 16.65 | |
| 1/6 | 0.02747 | 30.05 | 0.1131 | 8.455 | |
| 1/10 | 0.02634 | 54.17 | 0.07626 | 2.122 |
| βL | Peak Displacement (mm) | Error (%) | βL | Peak Displacement (mm) | Error (%) | ||
|---|---|---|---|---|---|---|---|
| V | 1 | 1181.5 | / | VII | 1 | 1183.6 | / |
| 1/4 | 1170.5 | −0.93 | 1/4 | 1162.0 | −1.82 | ||
| 1/5 | 1173.6 | −0.66 | 1/5 | 1157.1 | −2.23 | ||
| 1/6 | 1171.2 | −0.87 | 1/6 | 1169.0 | −1.23 | ||
| 1/10 | 1163.4 | −1.53 | 1/10 | 1175.4 | −0.69 | ||
| VI | 1 | 1246.2 | / | VIII | 1 | 1195.1 | / |
| 1/4 | 1243.3 | −0.23 | 1/4 | 1164.8 | −2.53 | ||
| 1/5 | 1242.2 | −0.32 | 1/5 | 1164.7 | −2.54 | ||
| 1/6 | 1243.2 | −0.23 | 1/6 | 1161.4 | −2.82 | ||
| 1/10 | 1241.5 | −0.38 | 1/10 | 1160.2 | −2.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Kong, X.; Zhou, H.; Zheng, C.; Wu, W. Corrected Method for Scaling the Structural Response Subjected to Blast Load. J. Mar. Sci. Eng. 2024, 12, 1767. https://doi.org/10.3390/jmse12101767
Liu Y, Kong X, Zhou H, Zheng C, Wu W. Corrected Method for Scaling the Structural Response Subjected to Blast Load. Journal of Marine Science and Engineering. 2024; 12(10):1767. https://doi.org/10.3390/jmse12101767
Chicago/Turabian StyleLiu, Yihao, Xiangshao Kong, Hu Zhou, Cheng Zheng, and Weiguo Wu. 2024. "Corrected Method for Scaling the Structural Response Subjected to Blast Load" Journal of Marine Science and Engineering 12, no. 10: 1767. https://doi.org/10.3390/jmse12101767






