Development of a Hierarchical Clustering Method for Anomaly Identification and Labelling of Marine Machinery Data
Abstract
1. Introduction
2. Literature Review
- The introduction of histogram similarity for evaluating differences between distinct faults.
- The combination of histogram similarity with hierarchical clustering for effective fault labelling, while facilitating model’s explainability.
- The consideration of the silhouette coefficient for the selection of parameters.
- The application of the above fault labelling framework to the case of a main engine of a tanker vessel to assess the effectiveness of the proposed methodology.
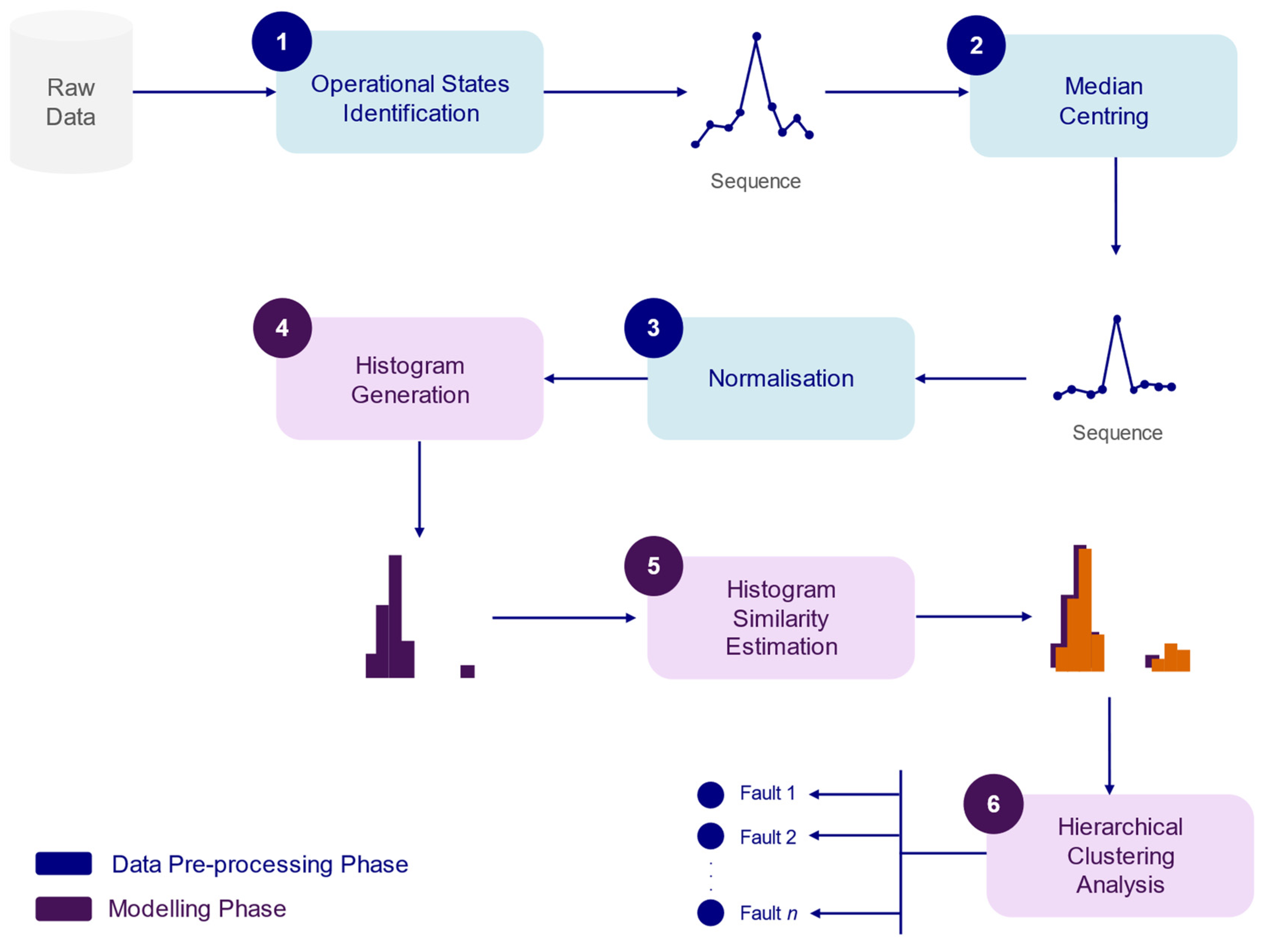
3. Methodology
3.1. Operational States Identification
3.2. Median Centring
3.3. Normalisation
3.4. Histogram Generation
3.5. Histogram Similarity Estimation
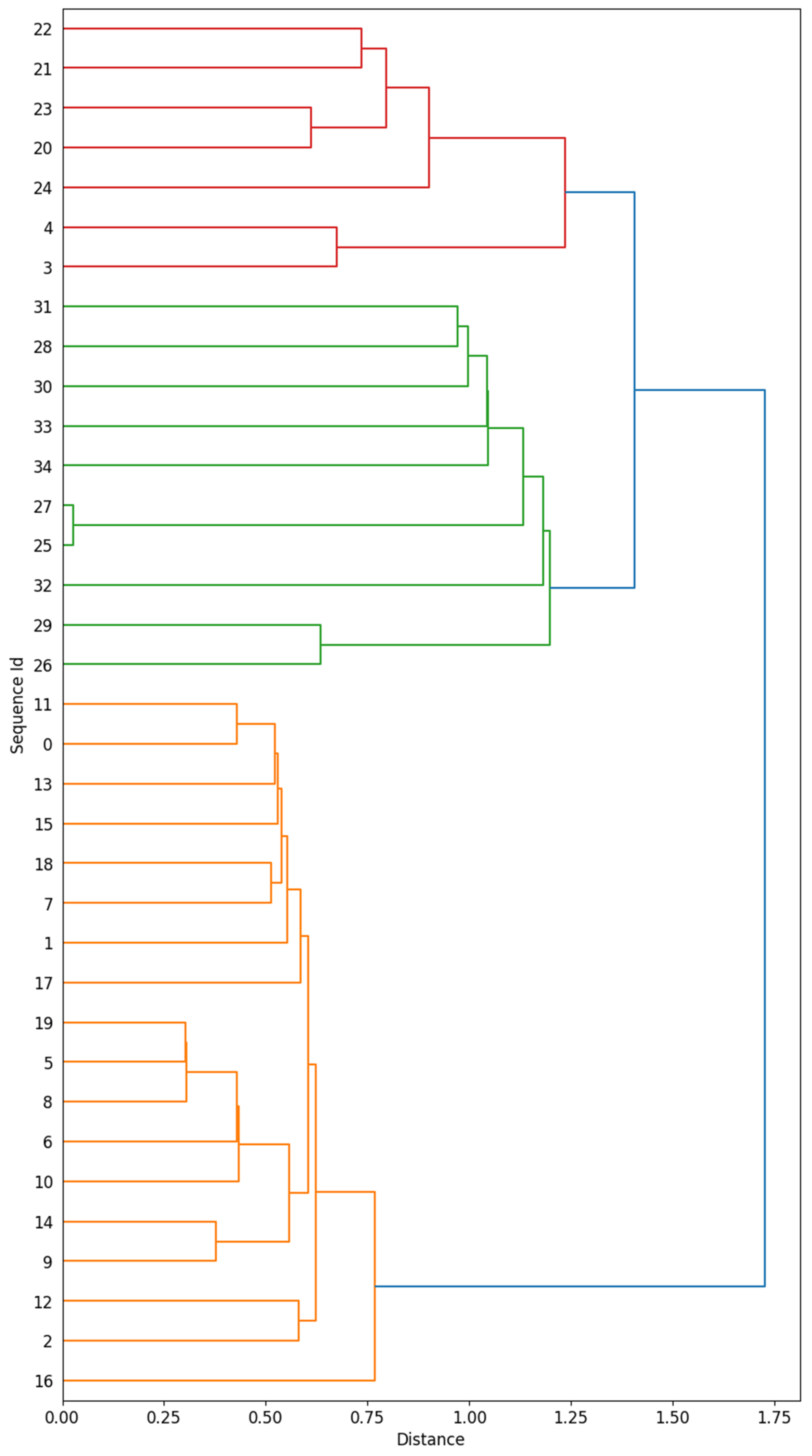
3.6. Hierarchical Clustering Analysis
- (1)
- There is no need to define the number of clusters before implementing the model.
- (2)
- It does not focus on the distribution of the data, so this model can be implemented for different distribution types.
- (3)
- It enhances the interpretability by enabling the visualisation of results through dendrograms.
- (4)
- Nested structures in the data can be revealed, which commonly occurs when dealing with distinct faults in marine machinery.
| Algorithm 1. Hierarchical clustering model |
| Input: similarity matrix, similarity_matrix. distance search space, distances_search. Output: resulting clusters, c. 1. Initialisation. The model considers as many clusters as sequences being analysed. 2. The similarity_matrix of dimensions n × n, where n is the number of sequences being analysed, is set as the distance matrix that is considered during the clustering process. 3. Set the number of clusters, n_clusters, to n. 4. while n_clusters > 1 do 5. Apply centroid linkage as follows: 6. Group the two most similar clusters/instances according to the results of the centroid linkage. 7. Update the similarity matrix. 8. Set n_clusters to n_clusters—1. 9. end while 10. The silhouette array is initialised as an empty matrix. 11. for each distance in distances_search do 12. The distance is set as the cut-off distance to determine the distinct clusters. 13. Each instance is associated with its respective label based on the configuration of clusters. 14. The silhouette index is estimated and stored in silhouette. 15. end for 16. The maximum value in silhouette array is detected, which relates to the best results obtained. 17. The distance associated to the best silhouette value is obtained, best_distance. 18. The final clusters are obtained by considering the best_dinstance, and the resulting labels are returned. |
| Algorithm 2. Proposed methodology |
| Input: Sequences to be analysed, sequences. Number of bins to be considered for histogram generation, n_bins. Definition of the distance search space, distances_search. Output: resulting clusters, c. 1. Median centring is applied individually in each of the sequences. 2. Normalisation is applied individually in each of the sequences. 3. for each b in n_bins do 4. Generate the histogram for each sequence and store it in histograms. 5. Obtain the similarity matrix following the process in Section 3.5. 6. Apply Algorithm 1 to obtain the resulting clusters in this iteration. 7. Store the clustering results. 8. end for 9. Obtain the configuration that leads to the maximum silhouette score. 10. Return the clusters that relates to the best configuration obtained. |
4. Case Study and Results
- The limited number of faults. Faults can be considered rare events if compared to normal operations, as a fault during operational conditions may lead to an inadequate functioning of marine machinery. Thus, preventive actions are usually performed in advance to avert any fault that can jeopardise the operations of the systems. This results in a lack of fault data, which can limit most of the studies that utilise deep learning approaches, as they require significant amounts of data for training. For this reason, recent studies focus on data augmentation techniques. Nevertheless, this study aims to provide an alternative for the labelling of fault data based on histogram similarity and hierarchical clustering. While the first case study contained a significant amount of fault sequences (2420 sequences), the third case study considers a total of 35 anomaly sequences to analyse whether the proposed model is effective with a limited amount of fault data.
- Fault imbalance. It is not uncommon when dealing with this type of case study that the different fault types exhibit varying frequencies. This is because certain fault types may occur more frequently than others, which can be rare. To validate whether the proposed model can handle fault imbalance, the model is tested using three types of anomaly sequences. The distribution of the anomaly sequences is as follows: 20 out of 35 anomaly sequences relate to point anomalies, 5 out of 35 relate to change point anomalies, and 10 out of 35 relate to contextual anomalies (please see Table 3 for further details).
- Explainability. The proposed model considers hierarchical clustering to understand the classifications provided through the model based on the histogram similarity.
- Anomalies needed to be injected to validate the proposed methodology due to the lack of fault data. An implementation of a real-world case study is expected once fault data is available to the authors.
- Additional key ship machinery parameters such as auxiliary engine cylinder pressure and temperature can be explored and trialled further.
- Analogously, due to the lack of fault data, univariate analysis was performed. However, a multivariate analysis could also be performed, while then adapting the proposed methodology accordingly.
- Utilise other histogram similarity methods to generate a more robust similarity matrix.
- Develop an ensemble model that can be adapted to the dimensions and characteristics of the data.
- The silhouette coefficient is suggested as a metric for identifying the optimal parameters. However, other coefficients need to be evaluated to create a more robust model.
- Create a holistic framework where the proposed methodology is incorporated as a preceding step of a fault diagnosis tool.
- Develop a more efficient method to reduce the computational cost, as the introduced agglomerative clustering approach has a complexity of O(n3), resulting in an average execution time of 35.59 s for the first case study.
- Even though the model showed good performance when the data was imbalanced, this performance is reduced when the dataset is severely imbalanced. Therefore, further work needs to be conducted to ensure that the methodology can handle highly imbalanced datasets.
- Develop a framework that integrates the developed methodology with a fault diagnosis model so that a fault diagnosis model can be trained and deployed when fault label data are missing in real industrial applications.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Jiang, X.; Ke, W.; Zhu, Q.; He, Y.; Zhang, Y.; Wang, Z. A novel pattern classification integrated GLPP with improved AROMF for fault diagnosis. Process Saf. Environ. Prot. 2023, 171, 299–311. [Google Scholar] [CrossRef]
- Mou, M.; Zhao, X.; Liu, K.; Hui, Y. Variational autoencoder based on distributional semantic embedding and cross-modal reconstruction for generalized zero-shot fault diagnosis of industrial processes. Process Saf. Environ. Prot. 2023, 177, 1154–1167. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Feng, Z.; Ruifang, L.V.; Lu, C.; Dai, Y.; Dong, L. Gated recurrent unit-enhanced deep convolutional neural network for real-time industrial process fault diagnosis. Process Saf. Environ. Prot. 2023, 175, 129–149. [Google Scholar] [CrossRef]
- Liu, J.; Hou, L.; He, S.; Zhang, X.; Yu, Q.; Yang, K.; Li, Y. Two-dimensional explainability method for fault diagnosis of fluid machine. Process Saf. Environ. Prot. 2023, 178, 1148–1160. [Google Scholar] [CrossRef]
- Galar, D.; Kumar, U. Diagnosis. In eMaintenance; Elsevier: Amsterdam, The Netherlands, 2017; pp. 235–310. [Google Scholar] [CrossRef]
- Dai, Y.; Qiu, Y.; Feng, Z. Research on faulty antibody library of dynamic artificial immune system for fault diagnosis of chemical process. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2018; pp. 493–498. [Google Scholar] [CrossRef]
- Xia, J.; Huang, R.; Chen, Z.; He, G.; Li, W. A novel digital twin-driven approach based on physical-virtual data fusion for gearbox fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 240, 109542. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, M.; Xu, H.; Wang, C.; Yang, W. A cross-domain intelligent fault diagnosis method based on deep subdomain adaptation for few-shot fault diagnosis. Appl. Intell. 2023, 53, 24474–24491. [Google Scholar] [CrossRef]
- Yin, M.; Li, J.; Li, H. A CNN approach based on correlation metrics to chemical process fault classifications with limited labelled data. Can. J. Chem. Eng. 2023, 101, 3982–3997. [Google Scholar] [CrossRef]
- Huang, H.; Wang, R.; Zhou, K.; Ning, L.; Song, K. CausalViT: Domain generalization for chemical engineering process fault detection and diagnosis. Process Saf. Environ. Prot. 2023, 176, 155–165. [Google Scholar] [CrossRef]
- Safaei, M.; Soleymani, S.A.; Safaei, M.; Chizari, H.; Nilashi, M. Deep learning algorithm for supervision process in production using acoustic signal. Appl. Soft Comput. 2023, 146, 110682. [Google Scholar] [CrossRef]
- Liu, H. Application of industrial Internet of things technology in fault diagnosis of food machinery equipment based on neural network. Soft Comput. 2023, 27, 9001–9018. [Google Scholar] [CrossRef]
- Yang, C.; Ma, S.; Han, Q. Robust discriminant latent variable manifold learning for rotating machinery fault diagnosis. Eng. Appl. Artif. Intell. 2023, 126, 106996. [Google Scholar] [CrossRef]
- Wang, R.; Huang, W.; Lu, Y.; Zhang, X.; Wang, J.; Ding, C.; Shen, C. A novel domain generalization network with multidomain specific auxiliary classifiers for machinery fault diagnosis under unseen working conditions. Reliab. Eng. Syst. Saf. 2023, 238, 109463. [Google Scholar] [CrossRef]
- Yang, C.; Ma, S.; Han, Q. Unified discriminant manifold learning for rotating machinery fault diagnosis. J. Intell. Manuf. 2023, 34, 3483–3494. [Google Scholar] [CrossRef]
- Jieyang, P.; Kimmig, A.; Dongkun, W.; Niu, Z.; Zhi, F.; Jiahai, W.; Liu, X.; Ovtcharova, J. A systematic review of data-driven approaches to fault diagnosis and early warning. J. Intell. Manuf. 2023, 34, 3277–3304. [Google Scholar] [CrossRef]
- Balaji, P.A.; Sugumaran, V. Comparative study of machine learning and deep learning techniques for fault diagnosis in suspension system. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 215. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Arslanoğlu, Y. Development of condition-based maintenance strategy for fault diagnosis for ship engine systems. Ocean Eng. 2022, 256, 111515. [Google Scholar] [CrossRef]
- Wang, R.; Chen, H.; Guan, C.; Gong, W.; Zhang, Z. Research on the fault monitoring method of marine diesel engines based on the manifold learning and isolation forest. Appl. Ocean Res. 2021, 112, 102681. [Google Scholar] [CrossRef]
- Ellefsen, A.L.; Han, P.; Cheng, X.; Holmeset, F.T.; Aesoy, V.; Zhang, H. Online Fault Detection in Autonomous Ferries: Using Fault-type Independent Spectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2020, 69, 8216–8225. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, J.; Tian, H.; Jiang, D.; Guo, L.; Wang, G.; Lin, Y. Multi-label classification for simultaneous fault diagnosis of marine machinery: A comparative study. Ocean Eng. 2021, 239, 109723. [Google Scholar] [CrossRef]
- Lei, Y. Individual intelligent method-based fault diagnosis. In Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Elsevier: Amsterdam, The Netherlands, 2017; pp. 67–174. [Google Scholar] [CrossRef]
- Zhong, B.; Zhao, M.; Wang, L.; Fu, S.; Zhong, S. DCSN: Focusing on hard samples mining in small-sample fault diagnosis of marine engine. Measurement 2024, 235, 114929. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J.; Sun, B.; Wang, Y. A universal fault diagnosis framework for marine machinery based on domain adaptation. Ocean Eng. 2024, 302, 117729. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, Y.; Wu, R.; Li, J.; Cai, Z. Sustainable Maritime Transport: A Review of Intelligent Shipping Technology and Green Port Construction Applications. J. Mar. Sci. Eng. 2024, 12, 1728. [Google Scholar] [CrossRef]
- Chen, X.; Ma, D.; Liu, R.W. Application of Artificial Intelligence in Maritime Transportation. J. Mar. Sci. Eng. 2024, 12, 439. [Google Scholar] [CrossRef]
- Ren, X.; Guo, Y.; Gong, Y. Fault diagnosis study of ship solar photovoltaic power generation system. J. Phys. Conf. Ser. 2024, 2771, 012024. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Xie, Y.; Wu, M.; Li, Z.; Mu, W.; Liu, G. Multi-sensor cross-domain fault diagnosis method for leakage of ship pipeline valves. Ocean Eng. 2024, 299, 117211. [Google Scholar] [CrossRef]
- Lu, B.; Dibaj, A.; Gao, Z.; Nejad, A.R.; Zhang, Y. A class-imbalance-aware domain adaptation framework for fault diagnosis of wind turbine drivetrains under different environmental conditions. Ocean Eng. 2024, 296, 116902. [Google Scholar] [CrossRef]
- Velasco-Gallego, C.; De Maya, B.N.; Molina, C.M.; Lazakis, I.; Mateo, N.C. Recent advancements in data-driven methodologies for the fault diagnosis and prognosis of marine systems: A systematic review. Ocean Eng. 2023, 284, 115277. [Google Scholar] [CrossRef]
- Wang, R.; Chen, H.; Guan, C. DPGCN Model: A Novel Fault Diagnosis Method for Marine Diesel Engines Based on Imbalanced Datasets. IEEE Trans. Instrum. Meas. 2023, 72, 3504011. [Google Scholar] [CrossRef]
- Zhong, K.; Li, J.; Wang, J.; Han, M. Fault Detection for Marine Diesel Engine Using Semi-supervised Principal Component Analysis. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST), Hulunbuir, China, 2–5 August 2019; pp. 146–151. [Google Scholar] [CrossRef]
- Su, Y.; Gan, H.; Ji, Z. Research on Multi-Parameter Fault Early Warning for Marine Diesel Engine Based on PCA-CNN-BiLSTM. J. Mar. Sci. Eng. 2024, 12, 965. [Google Scholar] [CrossRef]
- Cheliotis, M.; Lazakis, I.; Theotokatos, G. Machine learning and data-driven fault detection for ship systems operations. Ocean Eng. 2020, 216, 107968. [Google Scholar] [CrossRef]
- Xu, F.; Jia, S.; Qu, C.; Chen, D.; Ma, L. Diesel Engine Fault Diagnosis Based on Convolutional Autoencoder Using Vibration Signals. Autom. Control. Comput. Sci. 2024, 58, 185–194. [Google Scholar] [CrossRef]
- Wu, H.; Jiang, R.; Wu, X.; Chen, X.; Liu, T. Marine Diesel Engine Fault Detection Based on Xilinx ZYNQ SoC. Appl. Sci. 2024, 14, 5152. [Google Scholar] [CrossRef]
- Wang, J.; Cao, H.; Cui, Z.; Ai, Z.; Jiang, K. Intelligent Fault Diagnosis of Marine Diesel Engines Based on Efficient Channel Attention-Improved Convolutional Neural Networks. Processes 2023, 11, 3360. [Google Scholar] [CrossRef]
- Zhu, G.; Huang, L.; Yin, J.; Gai, W.; Wei, L. Multiple faults diagnosis for ocean-going marine diesel engines based on different neural network algorithms. Sci. Prog. 2023, 106, 00368504231212765. [Google Scholar] [CrossRef] [PubMed]
- Pająk, M.; Kluczyk, M.; Muślewski, Ł.; Lisjak, D.; Kolar, D. Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning. Electronics 2023, 12, 3860. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J. Fault Diagnosis of Marine Diesel Engines under Partial Set and Cross Working Conditions Based on Transfer Learning. J. Mar. Sci. Eng. 2023, 11, 1527. [Google Scholar] [CrossRef]
- Shi, Q.; Hu, Y.; Yan, G. Hierarchical Multiscale Fluctuation Dispersion Entropy for Fuel Injection System Fault Diagnosis. Pol. Marit. Res. 2023, 30, 98–111. [Google Scholar] [CrossRef]
- Gokcek, V.; Genc, Y.; Kocak, G. Condition Monitoring and Fault Diagnosis of a Marine Diesel Engine with Machine Learning Techniques. Pomorstvo 2023, 37, 32–46. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Chen, N. Thermal fault diagnosis of marine diesel engine based on LSTM neural network algorithm. Vibroengineering Procedia 2022, 41, 198–203. [Google Scholar] [CrossRef]
- Yang, M.; Chen, H.; Guan, C. Research on diesel engine fault diagnosis method based on machine learning. In Proceedings of the 2022 4th International Conference on Frontiers Technology of Information and Computer (ICFTIC), Qingdao, China, 2–4 December 2022; pp. 1078–1082. [Google Scholar] [CrossRef]
- Chu, Z.; Gu, Z.; Chen, Y.; Zhu, D.; Tang, J. A Fault Diagnostic Approach for Underwater Thrusters Based on Generative Adversarial Network. IEEE Trans. Instrum. Meas. 2024, 73, 3524614. [Google Scholar] [CrossRef]
- Ai, Z.; Cao, H.; Wang, M.; Yang, K. Ship Ballast Water System Fault Diagnosis Method Based on Multi-Feature Fusion Graph Convolution. J. Phys. Conf. Ser. 2024, 2755, 012028. [Google Scholar] [CrossRef]
- Xu, X.; Lin, Y.; Ye, C. Fault diagnosis of marine machinery via an intelligent data-driven framework. Ocean Eng. 2023, 289, 116302. [Google Scholar] [CrossRef]
- Ai, Z.; Cao, H.; Wang, J.; Cui, Z.; Wang, L.; Jiang, K. Research Method for Ship Engine Fault Diagnosis Based on Multi-Head Graph Attention Feature Fusion. Appl. Sci. 2023, 13, 12421. [Google Scholar] [CrossRef]
- Zhengjie, L.; Xiaohui, Y.; Mengmeng, W.; Weilei, M.; Guijie, L. Leveraging deep learning techniques for ship pipeline valve leak monitoring. Ocean Eng. 2023, 288, 116167. [Google Scholar] [CrossRef]
- Wang, L.; Cao, H.; Cui, Z.; Ai, Z. A Fault Diagnosis Method for Marine Engine Cross Working Conditions Based on Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 270. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, D.; Shi, P. Semi-supervised prototype network based on compact-uniform-sparse representation for rotating machinery few-shot class incremental fault diagnosis. Expert Syst. Appl. 2024, 255, 124660. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, R.; Luo, Y.; Shao, H. A holistic semi-supervised method for imbalanced fault diagnosis of rotational machinery with out-of-distribution samples. Reliab. Eng. Syst. Saf. 2024, 250, 110297. [Google Scholar] [CrossRef]
- Velasco-Gallego, C.; Lazakis, I. A real-time data-driven framework for the identification of steady states of marine machinery. Appl. Ocean Res. 2022, 121, 103052. [Google Scholar] [CrossRef]
- Dalheim, Ø.Ø.; Steen, S. Preparation of in-service measurement data for ship operation and performance analysis. Ocean Eng. 2020, 212, 107730. [Google Scholar] [CrossRef]
- Dalheim, Ø.Ø.; Steen, S. A computationally efficient method for identification of steady state in time series data from ship monitoring. J. Ocean Eng. Sci. 2020, 5, 333–345. [Google Scholar] [CrossRef]
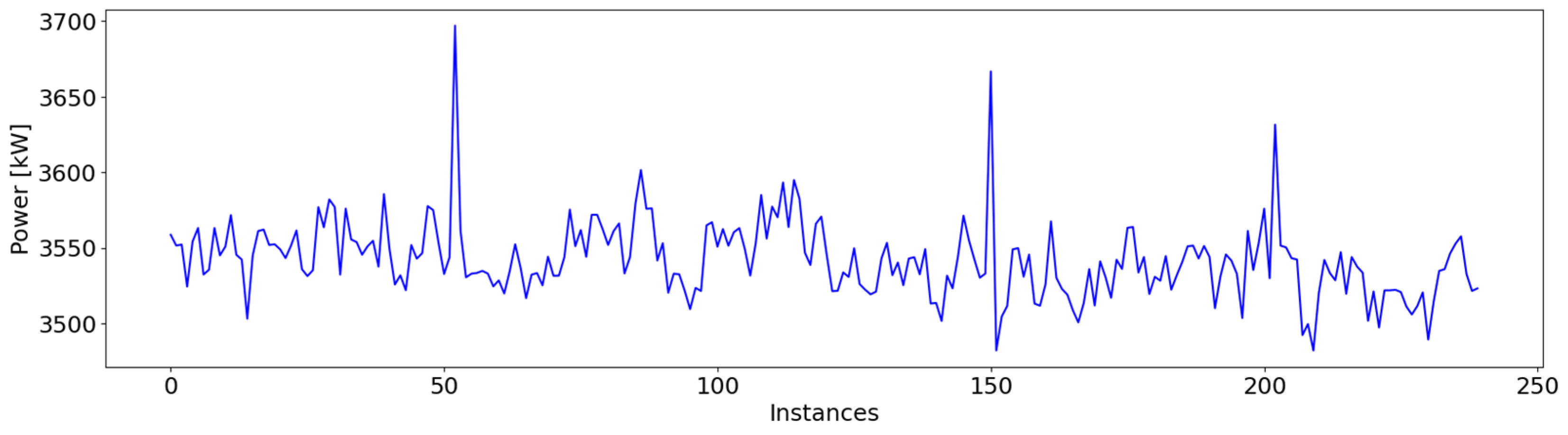
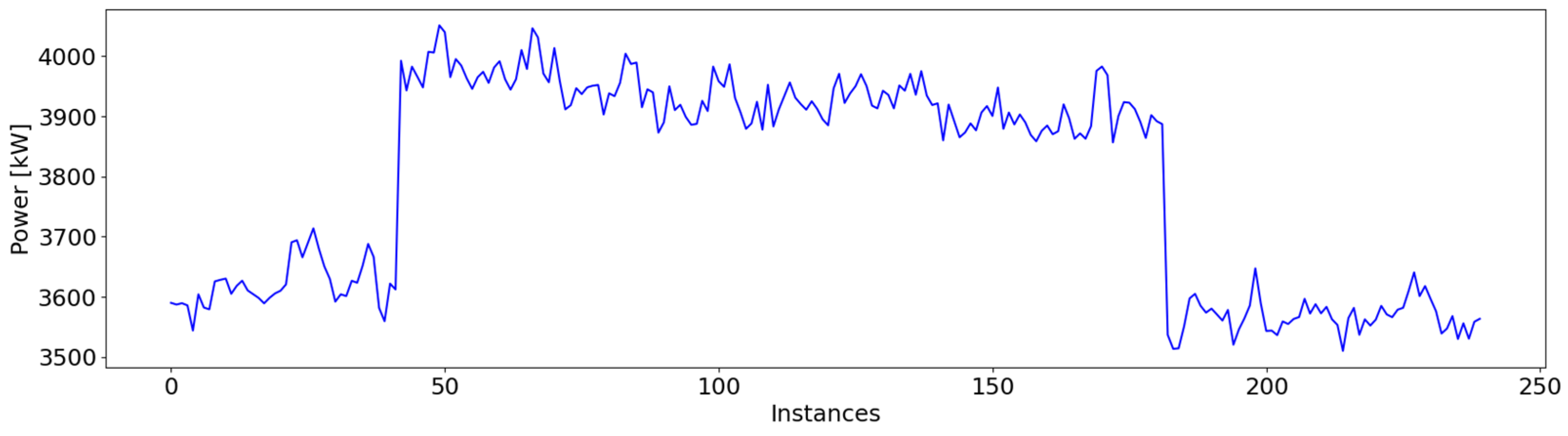
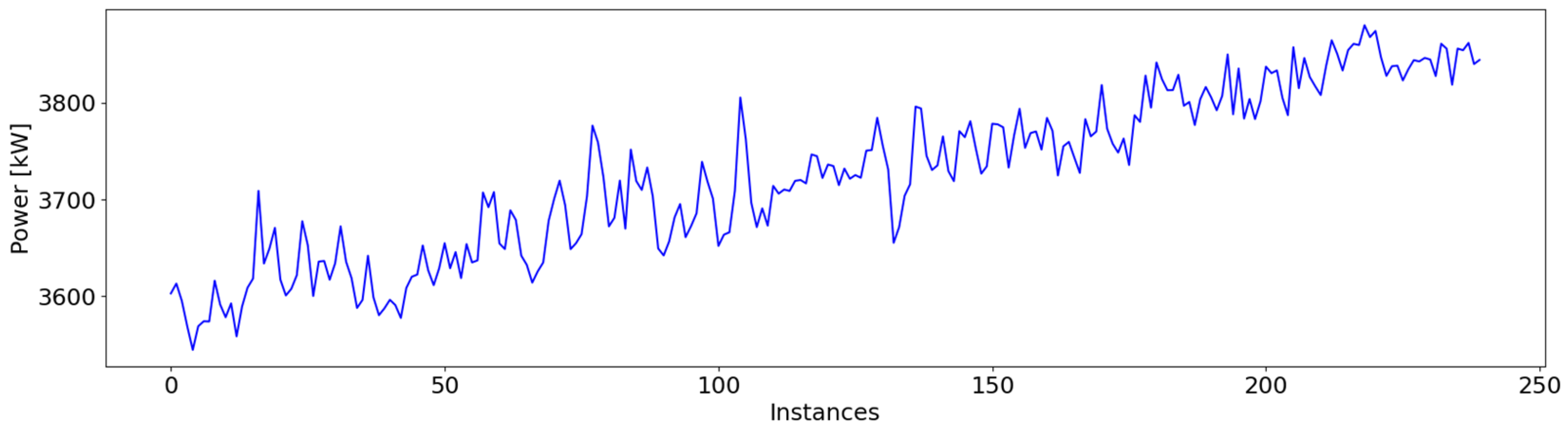
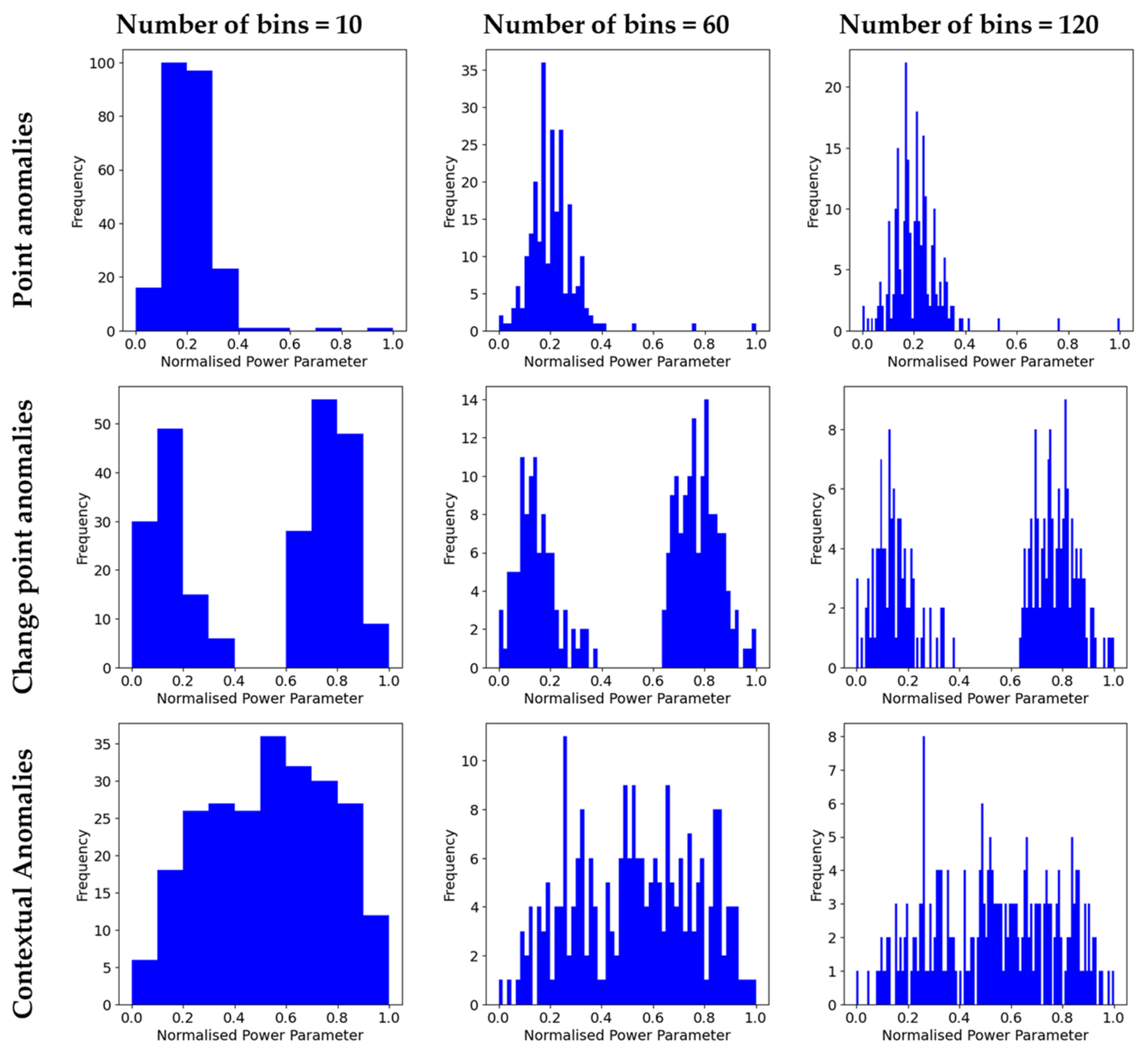


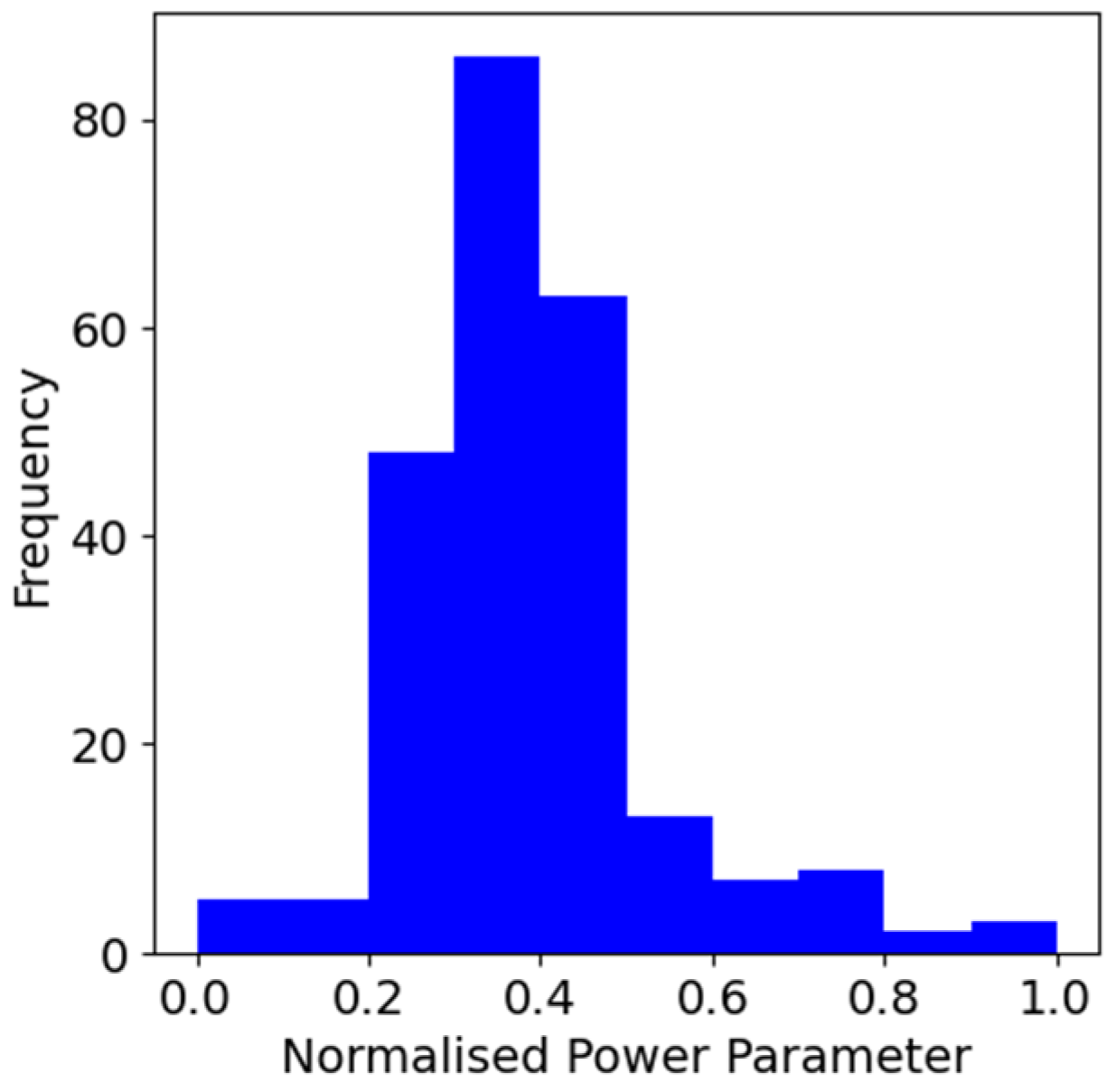
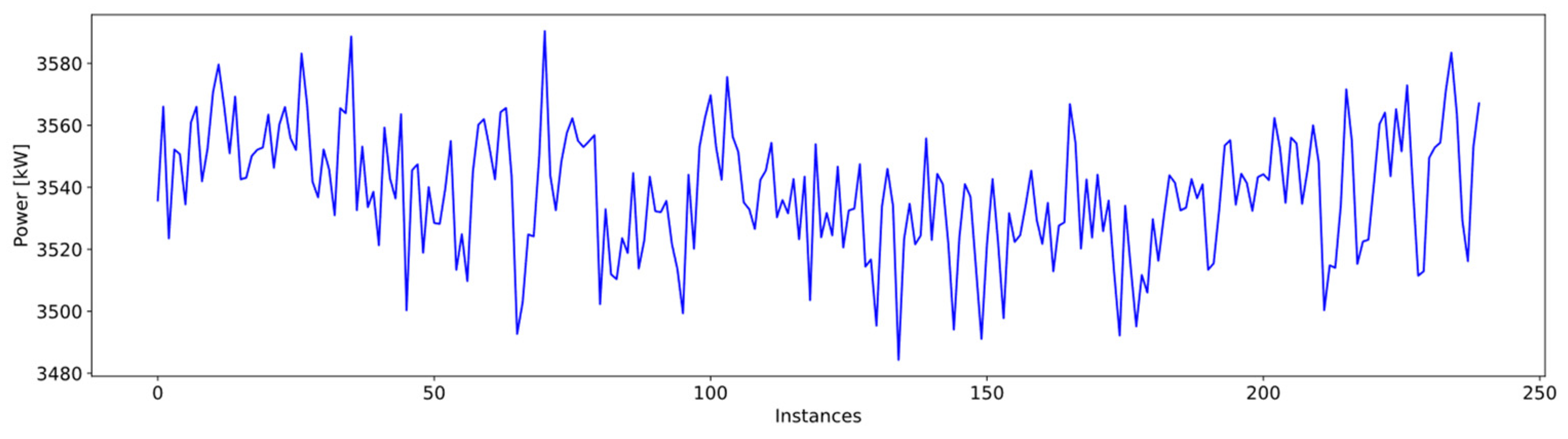

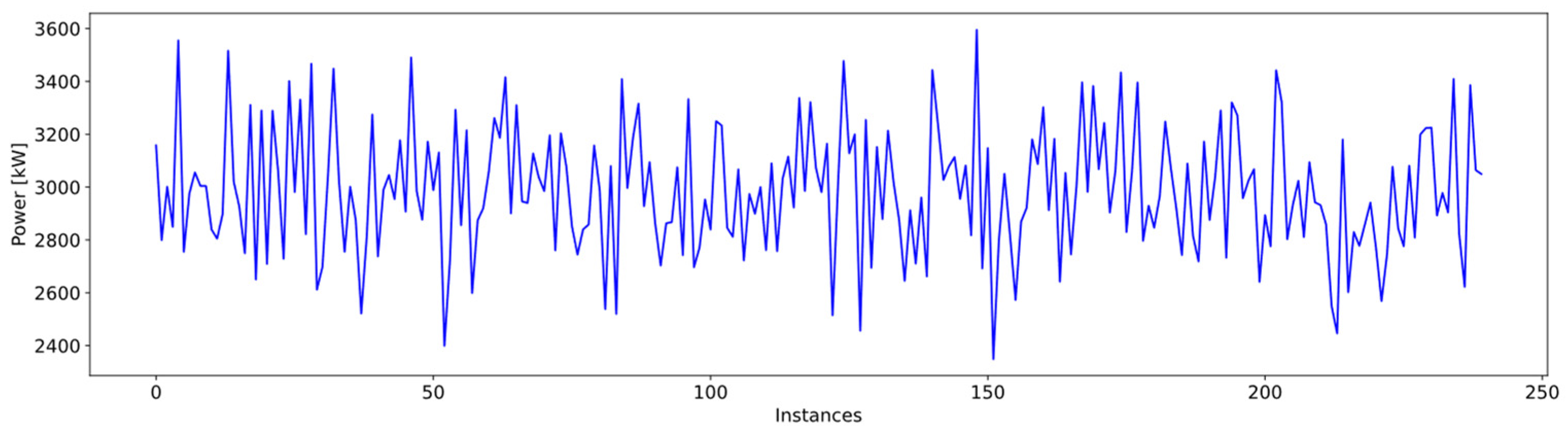
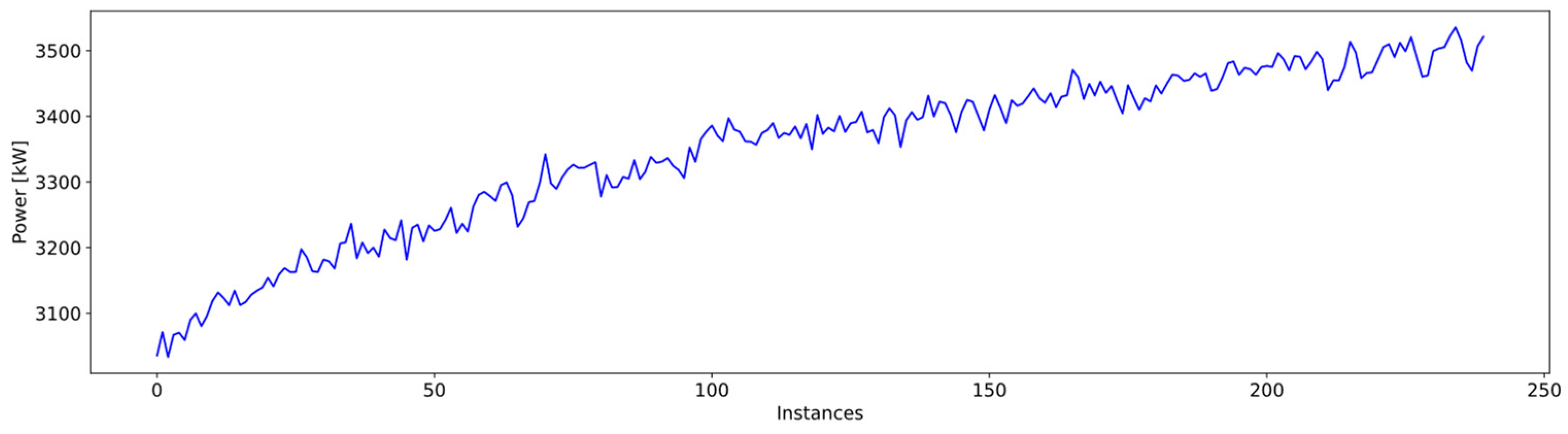
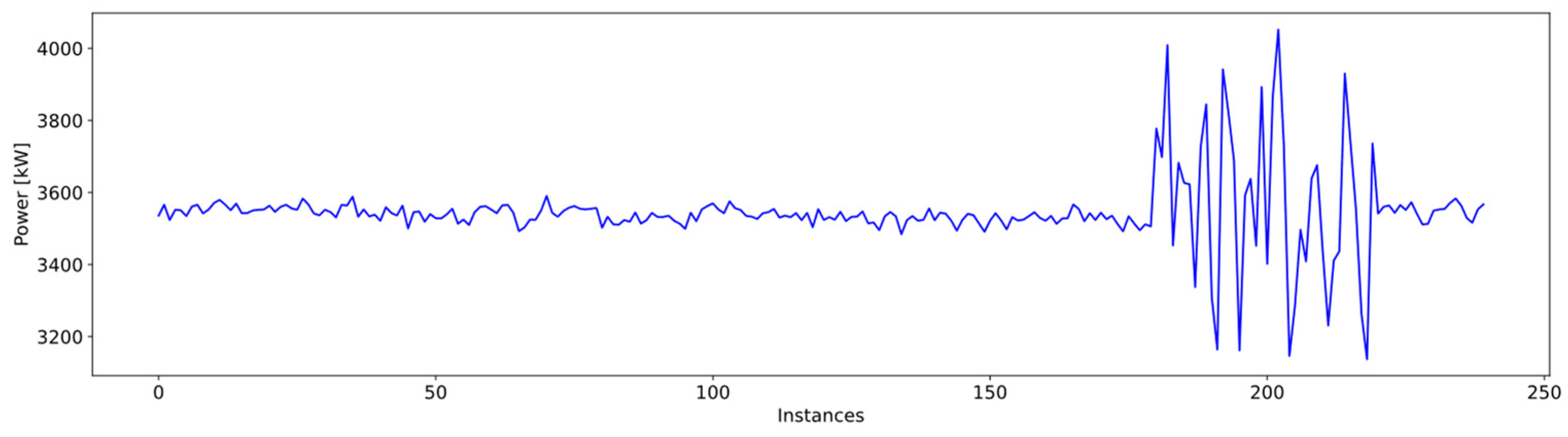
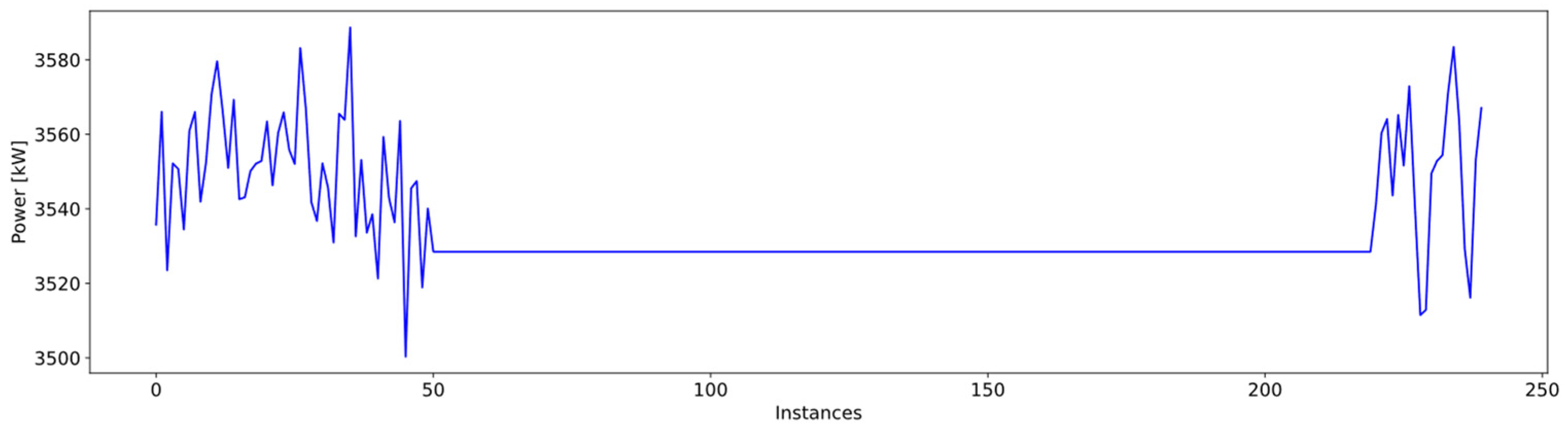

| Type of Anomaly | Number of Instances | % of Total |
|---|---|---|
| Point | 799 | 33.0% |
| Change Point | 811 | 33.5% |
| Contextual | 810 | 33.5% |
| 2420 | 100.0% |
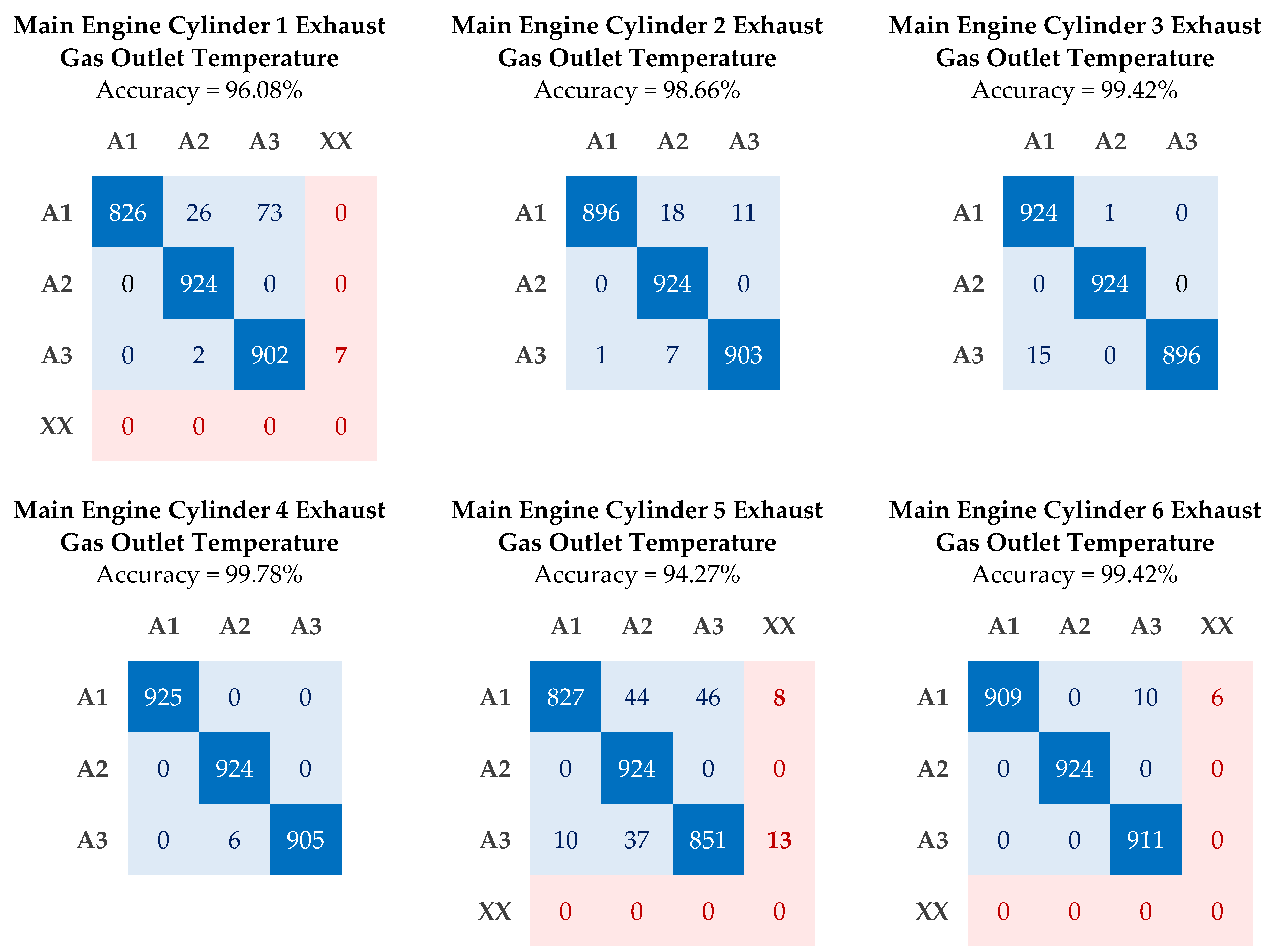
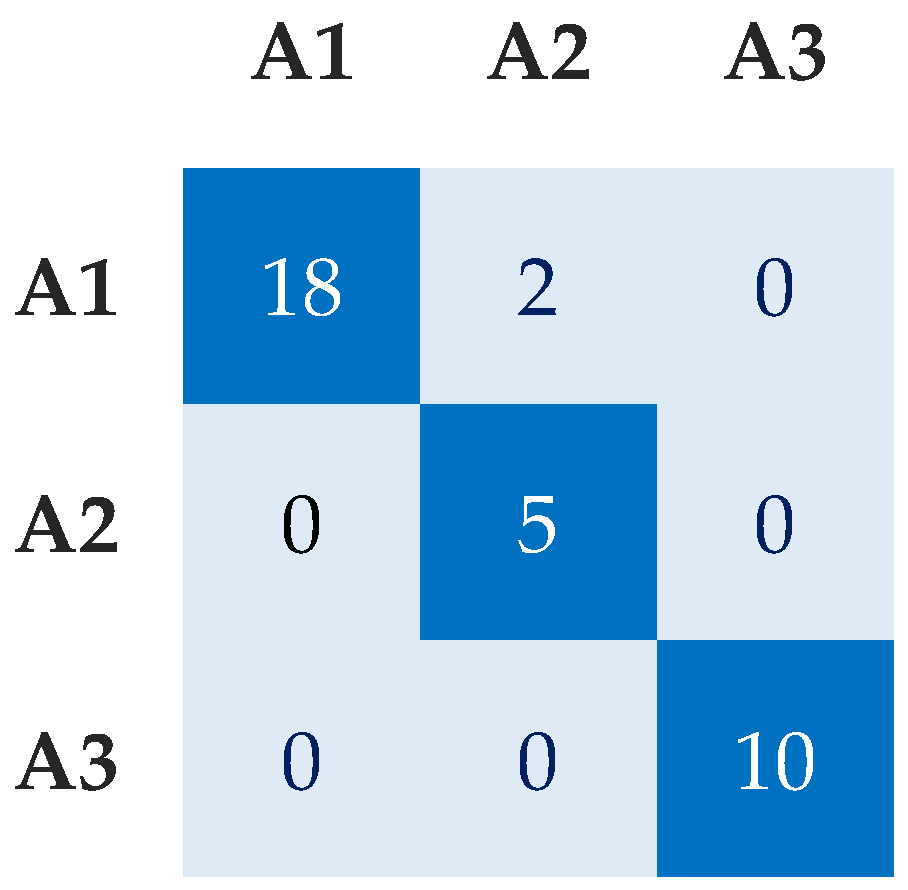
| Parameter | Accuracy | Micro Precision | Micro Recall | Micro F1 | MCC | K | Average Execution Time (s) |
|---|---|---|---|---|---|---|---|
| Power | 0.952 | 0.952 | 0.952 | 0.952 | 0.930 | 0.928 | 32.77 |
| Cylinder 1 Exh. Gas Out. Temp. | 0.960 | 0.960 | 0.960 | 0.960 | 0.940 | 0.940 | 46.50 |
| Cylinder 2 Exh. Gas Out. Temp. | 0.986 | 0.986 | 0.986 | 0.986 | 0.980 | 0.979 | 46.15 |
| Cylinder 3 Exh. Gas Out. Temp. | 0.994 | 0.994 | 0.994 | 0.994 | 0.991 | 0.991 | 46.06 |
| Cylinder 4 Exh. Gas Out. Temp. | 0.997 | 0.997 | 0.997 | 0.997 | 0.996 | 0.996 | 47.50 |
| Cylinder 5 Exh. Gas Out. Temp. | 0.942 | 0.942 | 0.942 | 0.942 | 0.910 | 0.910 | 45.70 |
| Cylinder 6 Exh. Gas Out. Temp. | 0.994 | 0.994 | 0.994 | 0.994 | 0.996 | 0.996 | 46.67 |
| Type of Anomaly | Number of Instances | % of Total |
|---|---|---|
| Point | 20 | 57% |
| Change point | 5 | 14% |
| Contextual | 10 | 29% |
| 35 | 100.0% |
| Percentage of One Fault Type Data Compared to the Total Number of Normal Instances | Balanced Accuracy |
|---|---|
| 10% | 0.82 |
| 20% | 0.85 |
| 30% | 0.92 |
| 40% | 0.93 |
| 50% | 0.93 |
| 60% | 0.94 |
| 70% | 0.94 |
| 80% | 0.95 |
| 90% | 0.95 |
| 100% | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velasco-Gallego, C.; Lazakis, I.; Cubo-Mateo, N. Development of a Hierarchical Clustering Method for Anomaly Identification and Labelling of Marine Machinery Data. J. Mar. Sci. Eng. 2024, 12, 1792. https://doi.org/10.3390/jmse12101792
Velasco-Gallego C, Lazakis I, Cubo-Mateo N. Development of a Hierarchical Clustering Method for Anomaly Identification and Labelling of Marine Machinery Data. Journal of Marine Science and Engineering. 2024; 12(10):1792. https://doi.org/10.3390/jmse12101792
Chicago/Turabian StyleVelasco-Gallego, Christian, Iraklis Lazakis, and Nieves Cubo-Mateo. 2024. "Development of a Hierarchical Clustering Method for Anomaly Identification and Labelling of Marine Machinery Data" Journal of Marine Science and Engineering 12, no. 10: 1792. https://doi.org/10.3390/jmse12101792
APA StyleVelasco-Gallego, C., Lazakis, I., & Cubo-Mateo, N. (2024). Development of a Hierarchical Clustering Method for Anomaly Identification and Labelling of Marine Machinery Data. Journal of Marine Science and Engineering, 12(10), 1792. https://doi.org/10.3390/jmse12101792








