A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels
Abstract
:1. Introduction
2. Preliminaries
2.1. Mathematical Model of Ship Maneuvering Motion
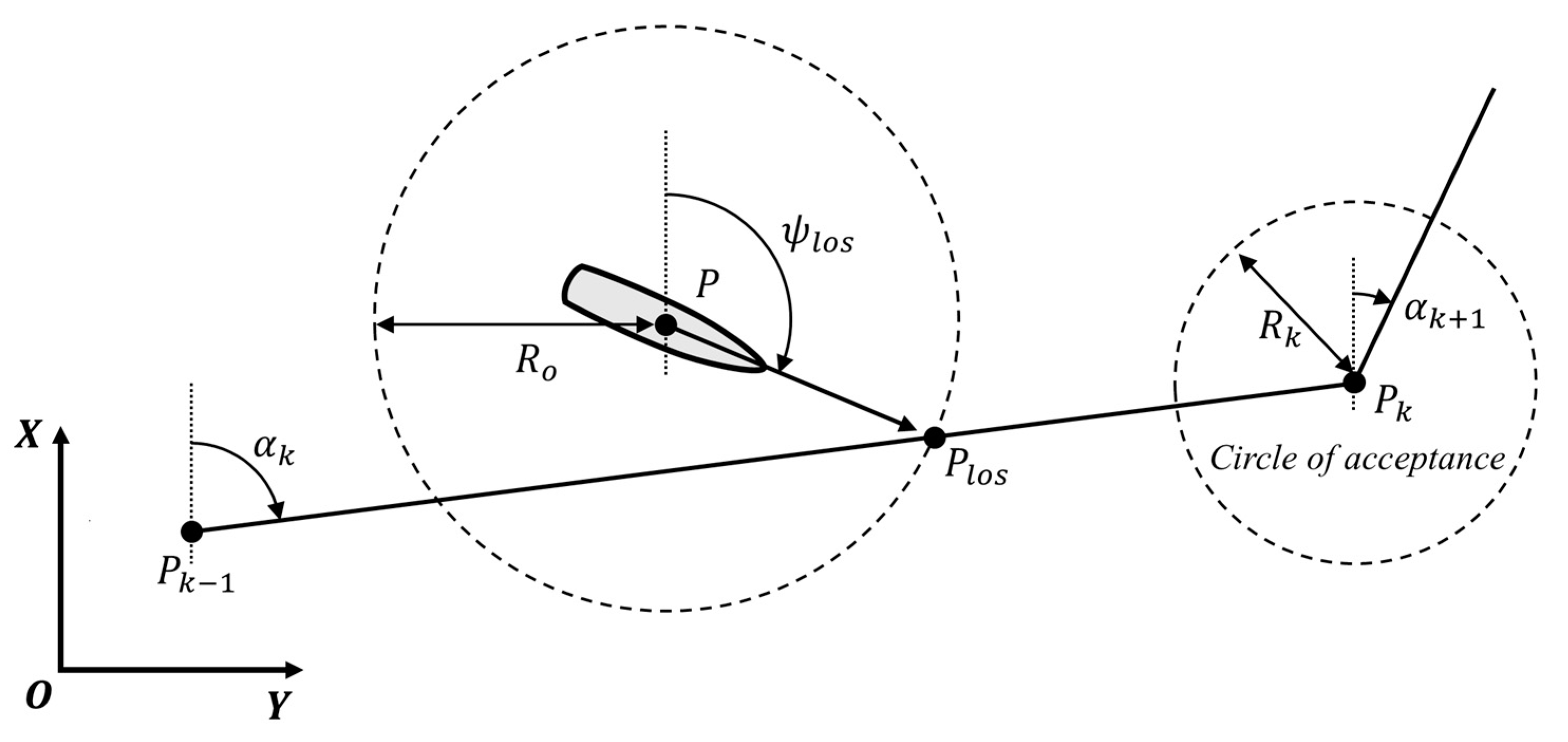
2.2. LOS Guidance Law
2.2.1. Traditional LOS Guidance Law
2.2.2. LOS Guidance Using Minimum Dynamic Circle
2.2.3. Time-Varying Lookahead Distance Guidance Law
2.3. Distance of New Course Mathematical Model
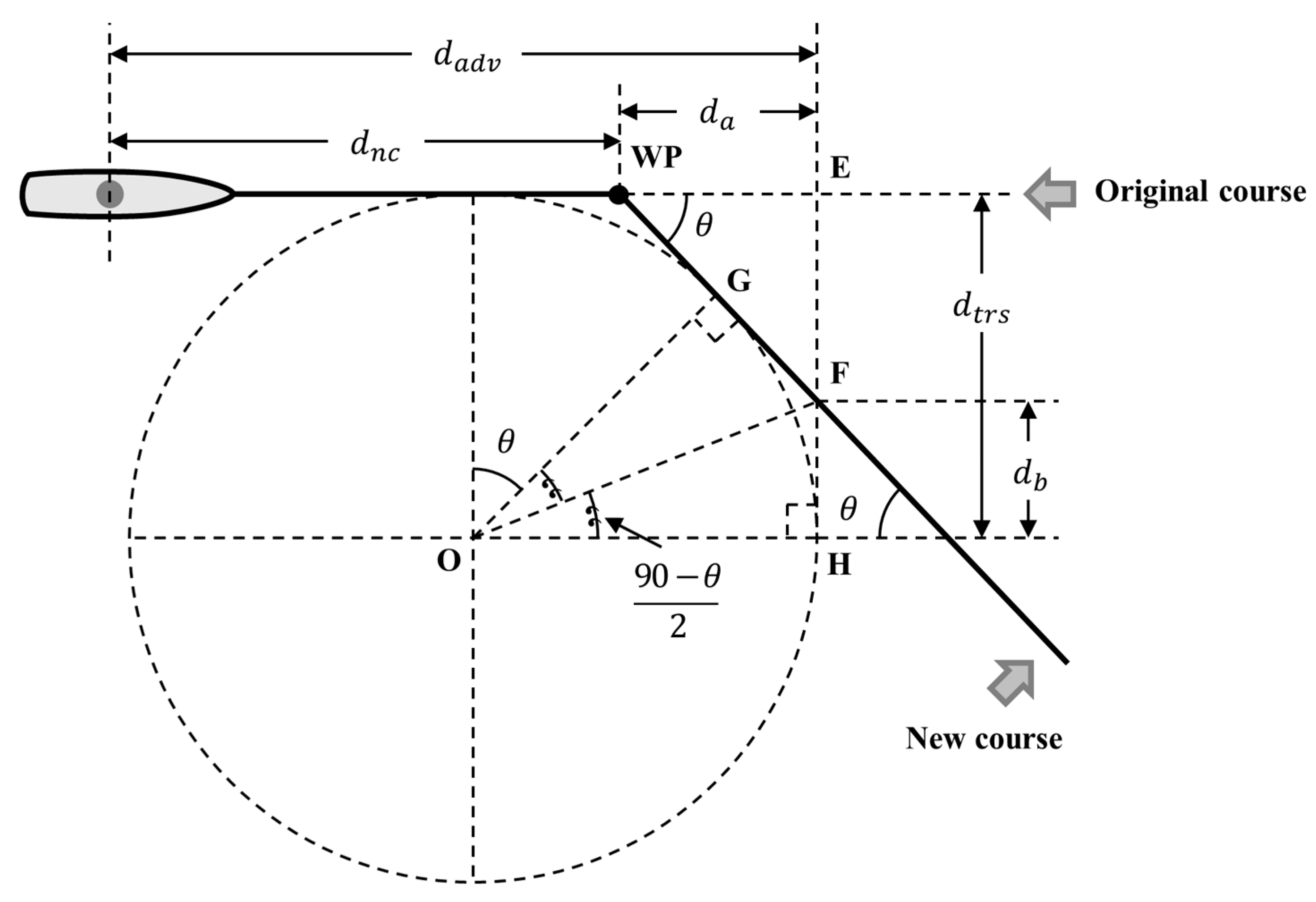
3. Balanced Path-Following Approach
3.1. Waypoint Switching Point
3.2. Balanced LOS Guidance
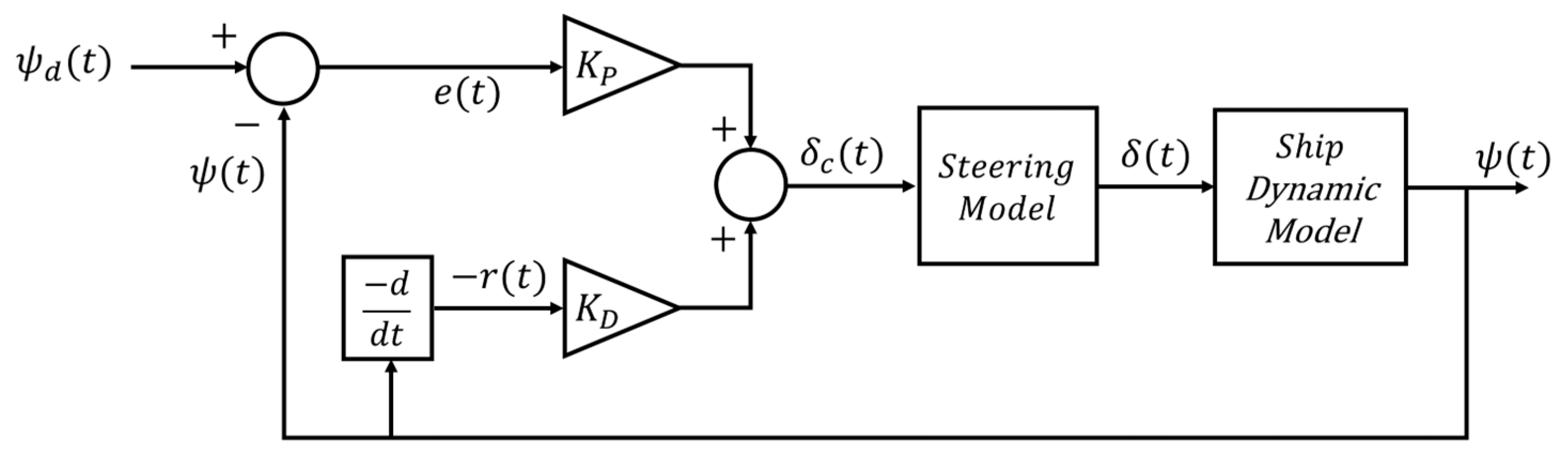
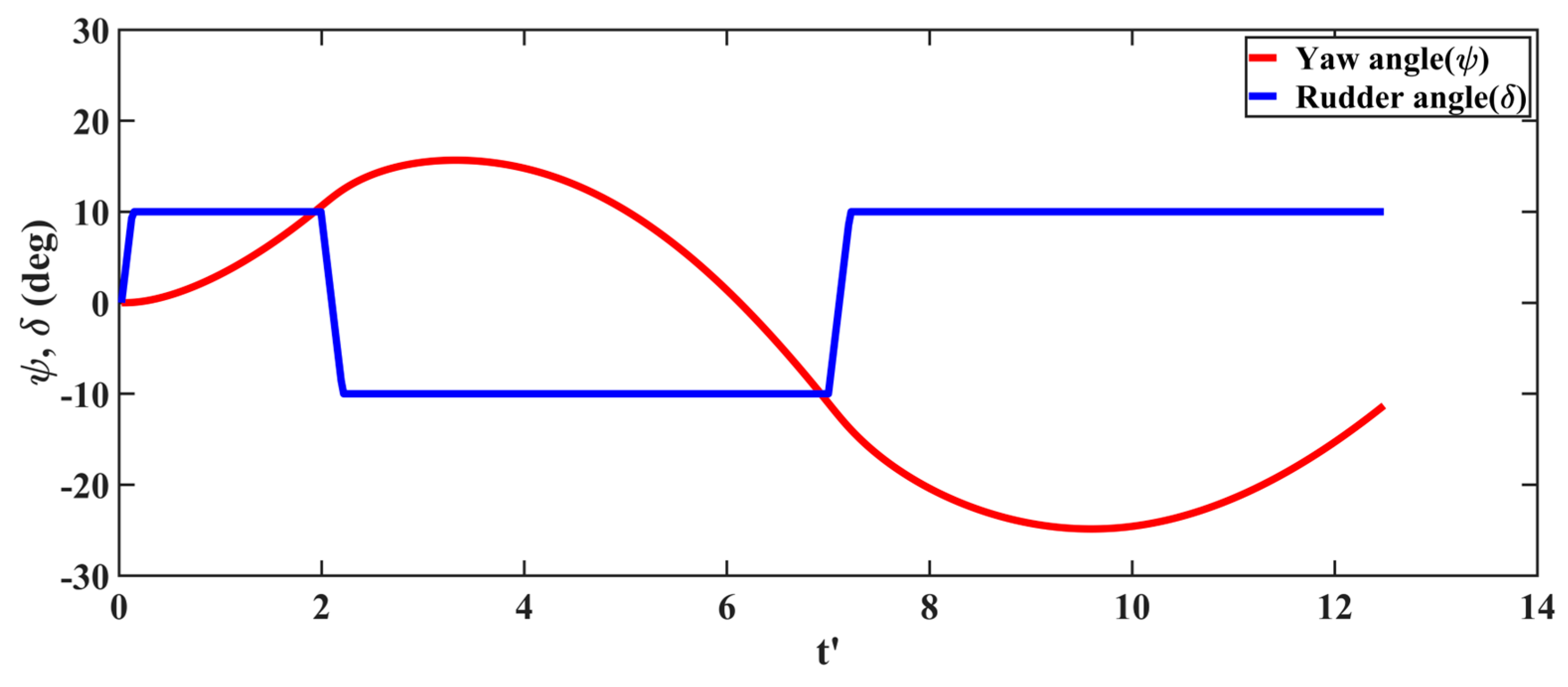
3.3. Heading Controller Design
4. Model Validation and Simulation Results
4.1. Validation of KVLCC2 Maneuvering Model
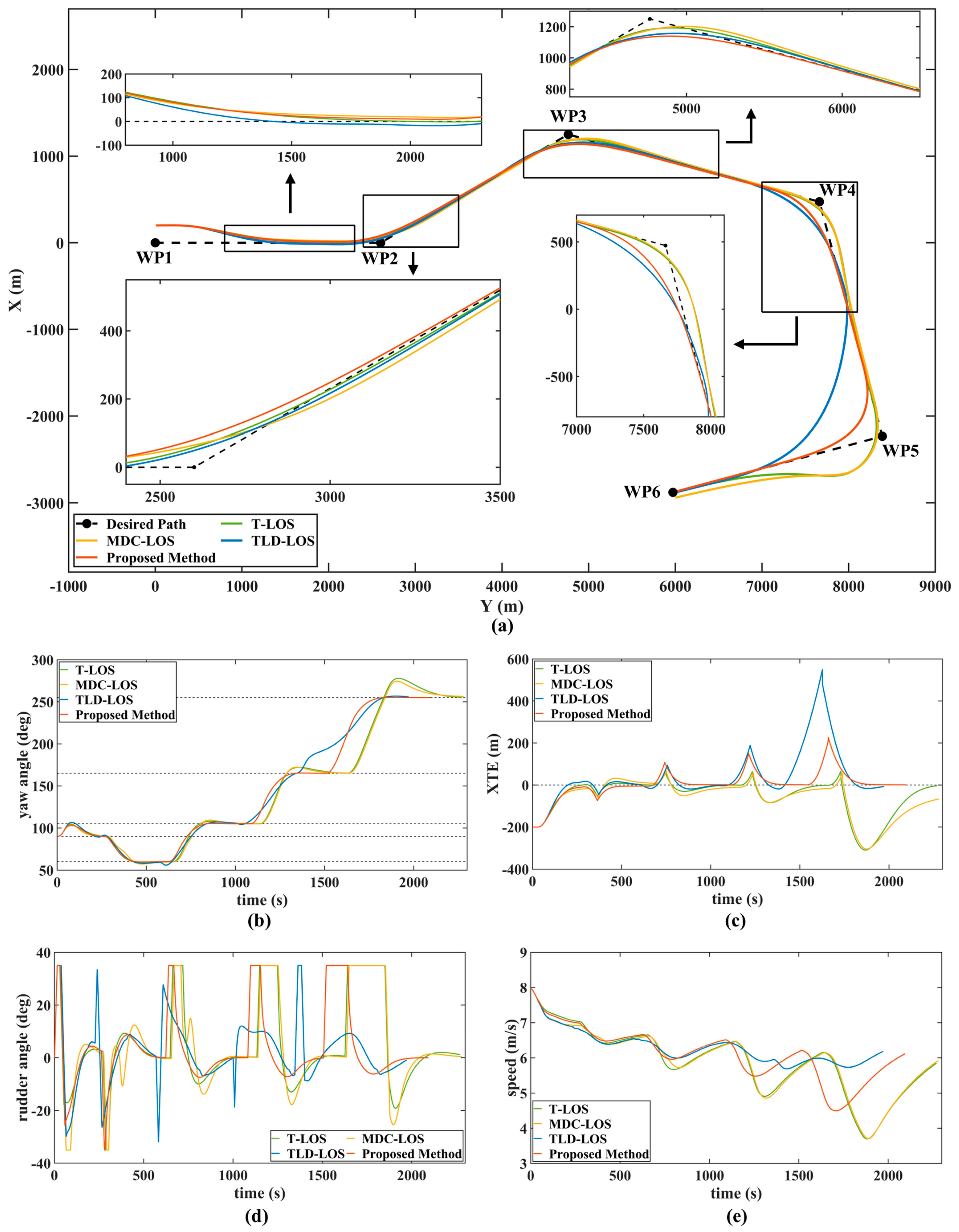
4.2. Path Following Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barrera, C.; Padron, I.; Luis, F.S.; Llinas, O.; Marichal, G.N. Trends and Challenges in Unmanned Surface Vehicles (USV): From Survey to Shipping. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2021, 15, 135–142. [Google Scholar] [CrossRef]
- Munim, Z.H.; Haralambides, H. Advances in maritime autonomous surface ships (MASS) in merchant shipping. Marit. Econ. Logist. 2022, 24, 181–188. [Google Scholar] [CrossRef]
- Lynch, K.M.; Banks, V.A.; Roberts, A.P.; Radcliffe, S.; Plant, K.L. What factors may influence decision-making in the operation of Maritime autonomous surface ships? A systematic review. Theor. Issues Ergon. Sci. 2024, 25, 98–142. [Google Scholar] [CrossRef]
- Qiao, Y.; Yin, J.; Wang, W.; Duarte, F.; Yang, J.; Ratti, C. Survey of Deep Learning for Autonomous Surface Vehicles in Marine Environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3678–3701. [Google Scholar] [CrossRef]
- Statheros, T.; Howells, G.; Maier, K.M. Autonomous ship collision avoidance navigation concepts, technologies and techniques. J. Navig. 2008, 61, 129–142. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, Y.; Li, T.; Chen, C.L.P. A Survey of Technologies for Unmanned Merchant Ships. IEEE Access 2020, 8, 224461. [Google Scholar] [CrossRef]
- Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A review of path planning algorithms in maritime autonomous surface ships: Navigation safety perspective. Ocean Eng. 2022, 251, 111010. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Jiang, L.; An, L.; Yang, R. Collision-avoidance navigation systems for Maritime Autonomous Surface Ships: A state of the art survey. Ocean Eng. 2021, 235, 109380. [Google Scholar] [CrossRef]
- Akdağ, M.; Solnør, P.; Johansen, T.A. Collaborative collision avoidance for maritime autonomous surface ships: A review. Ocean Eng. 2022, 250, 110920. [Google Scholar] [CrossRef]
- Issa, M.; Llinca, A.; Ibrahim, H.; Rizk, P. Maritime autonomous surface ships: Problems and challenges facing the regulatory process. Sustainability 2022, 14, 15630. [Google Scholar] [CrossRef]
- Liu, C.; Chu, X.; Wu, W.; Li, S.; He, Z.; Zheng, M.; Zhou, H.; Li, Z. Human–machine cooperation research for navigation of maritime autonomous surface ships: A review and consideration. Ocean Eng. 2022, 246, 110555. [Google Scholar] [CrossRef]
- Budak, G.; Beji, S. Controlled course-keeping simulations of a ship under external disturbances. Ocean Eng. 2020, 218, 108126. [Google Scholar] [CrossRef]
- Healey, A.J.; Lienard, D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles. IEEE J. Ocean. Eng. 1993, 18, 327–339. [Google Scholar] [CrossRef]
- Breivik, M. Nonlinear Maneuvering Control of Underactuated Ships. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2003. [Google Scholar]
- Lekkas, A.M.; Fossen, T.I. Line-of-sight guidance for path following of marine vehicles. In Advanced in Marine Robotics; Gal, O., Ed.; Academic: San Francisco, CA, USA, 2013; pp. 63–92. [Google Scholar]
- Gu, N.; Wang, D.; Peng, Z.; Wang, J.; Han, Q. Advances in Line-of-Sight Guidance for Path Following of Autonomous Marine Vehicles: An Overview. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 12–28. [Google Scholar] [CrossRef]
- Børhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS Path Following for Curved Paths Based on a Monotone Cubic Hermite Spline Parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Wan, L.; Su, Y.; Zhang, H.; Shi, B.; Abouomar, M.S. An improved integral light-of-sight guidance law for path following of unmanned surface vehicles. Ocean Eng. 2020, 205, 107302. [Google Scholar] [CrossRef]
- Han, B.; Duan, Z.; Peng, Z.; Chen, Y. A Ship Path Tracking Control Method Using a Fuzzy Control Integrated Line-of-Sight Guidance Law. J. Mar. Sci. Eng. 2024, 12, 586. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-Sight Path Following for Dubins Paths With Adaptive Sideslip Compensation of Drift Forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.; Wang, H. Predictor-based LOS guidance law for path following of underactuated marine surface vehicles with sideslip compensation. Ocean Eng. 2016, 124, 340–348. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles With Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Nie, J.; Lin, X. FAILOS guidance law based adaptive fuzzy finite-time path following control for underactuated MSV. Ocean Eng. 2020, 195, 106726. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws. Automatica 2014, 50, 2912–2917. [Google Scholar] [CrossRef]
- Rout, R.; Cui, R.; Han, Z. Modified line-of-sight guidance law with adaptive neural network control of underactuated marine vehicles with state and input constraints. IEEE Trans. Control Syst. Technol. 2020, 28, 1902–1914. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y. Predictor LOS-based trajectory linearization control for path following of underactuated unmanned surface vehicle with input saturation. Ocean Eng. 2020, 214, 107874. [Google Scholar] [CrossRef]
- Fossen, T.I. Line-of-sight path-following control utilizing an extended Kalman filter for estimation of speed and course over ground from GNSS positions. J. Mar. Sci. Eng. 2022, 27, 806–813. [Google Scholar] [CrossRef]
- Lv, C.; Liu, L.; Wang, D.; Peng, Z.; Li, Y.; Li, T. Human-machine Shared Line-of-Sight Path Following Control of Intelligent Surface Vehicles. IEEE Trans. Veh. Technol, 2024; early access. [Google Scholar] [CrossRef]
- Fossen, T.I.; Breivik, M.; Skjetne, R. Line-of-sight path following of underactuated marine craft. In Proceedings of the 2003 6th IFAC Conference on Manoeuvring and Control of Marine Craft, Girona, Spain, 17–19 September 2003; Volume 36, pp. 211–216. [Google Scholar] [CrossRef]
- Moreira, L.; Fossen, T.I.; Guedes Soares, C. Path following control system for a tanker ship model. Ocean Eng. 2007, 34, 2074–2085. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. A time-varying lookahead distance guidance law for path following. In Proceedings of the 2012 9th IFAC Conference on Manoeuvring and Control of Marine Craft, Arenzano, Italy, 19–21 September 2012; Volume 45, pp. 398–403. [Google Scholar] [CrossRef]
- Su, Z.; Zhang, X. Nonlinear Feedback-Based Path Following Control for Underactuated Ships via an Improved Compound Line-of-Sight Guidance. IEEE Access 2021, 9, 81535–81545. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicle; John Wiley & Sons Ltd.: Chichester, UK, 1994. [Google Scholar]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG standard method for ship maneuvering predictions. J. Mar. Sci. Technol. 2014, 20, 37–52. [Google Scholar] [CrossRef]
- SIMMAN. Part C: Captive and free model test data. In Proceedings of the Workshop on Verification and Validation of Ship Manoeuvring Simulation Methods (SIMMAN), Copenhagen, Denmark, 14–16 April 2008; SIMMAN: Copenhagen, Denmark, 2008.
- Sukas, O.F.; Kinaci, O.K.; Bal, S. Theoretical background and application of MANSIM for ship maneuvering simulations. Ocean Eng. 2019, 192, 106239. [Google Scholar] [CrossRef]
- Paramesh, S.; Rajendran, S. A unified seakeeping and manoeuvring model with a PID controller for path following of a KVLCC2 tanker in regular waves. Appl. Ocean Res. 2021, 116, 102860. [Google Scholar] [CrossRef]
- Adams, J.; Dubey, A.C.; Rajendran, S. A Model Predictive based Controller (MPC) for the Path Following of a KVLCC2 Tanker in waves. In Proceedings of the IEEE OCEANS Conferences 2022, Chennai, India, 21–24 February 2022. [Google Scholar] [CrossRef]
- Kim, D.J.; Choi, H.; Yun, K.; Yeo, D.J.; Kim, Y.G. Experimental study on turning characteristics of KVLCC2 tanker in long-crested irregular waves. Ocean Eng. 2022, 244, 110362. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems C Guidance. Navigation, and Control of Ships, Rigs and Underwater Vehicles; Marine Cybern.: Trondheim, Norway, 2002. [Google Scholar]
- Papoulias, F.A. Bifurcation analysis of line of sight vehicle guidance using sliding modes. Int. J. Bifurc. Chaos 1991, 1, 849–865. [Google Scholar] [CrossRef]
- Kamis, A.S.; Ahmad Fuad, A.F.; Ashaari, A.; Mohd Noor, C.W. Development of WOP mathematical model for efficient course alteration: LNG tanker manoeuvring analysis and Mann-Whitney U test. Ocean Eng. 2021, 239, 109768. [Google Scholar] [CrossRef]
- Fossen, T.I. Recent Developments in Ship Control Systems Design. World Superyacht Review; Sterling Publication Limited: London, UK, 1999. [Google Scholar]
- Zhang, R.; Chen, Y.; Sun, Z.; Sun, F.; Xu, H. Path control of a surface ship in restricted waters using sliding mode. IEEE Trans. Control Syst. Technol. 2000, 8, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Perera, L.P.; Soares, C.G. Pre-filtered sliding mode control for nonlinear ship steering associated with disturbances. Ocean Eng. 2012, 51, 49–62. [Google Scholar] [CrossRef]
- Layne, J.R.; Passino, K.M. Fuzzy model reference learning control for cargo ship steering. IEEE Control Syst. 1993, 13, 23–34. [Google Scholar] [CrossRef]
- Velagic, J.; Vukic, Z.; Omerdic, E. Adaptive fuzzy ship autopilot for track-keeping. Control Eng. Pract. 2003, 11, 433–443. [Google Scholar] [CrossRef]
- Zhang, Y.; Hearn, G.E.; Sen, P. A neural network approach to ship track-keeping control. IEEE J. Ocean. Eng. 1996, 21, 513–527. [Google Scholar] [CrossRef]
- Dai, S.L.; Wang, C.; Luo, F. Identification and learning control of ocean surface ship using neural networks. IEEE Trans. Ind. Inform. 2012, 8, 801–810. [Google Scholar] [CrossRef]
- Dubey, A.C.; Gajapathy, R.; Rajendran, S. An experimental and numerical investigation on the autopilot design of a KVLCC2 tanker. In Proceedings of the IEEE OCEANS Conferences, San Diego, CA, USA, 20–23 September 2021. [Google Scholar] [CrossRef]
- Sandeepkumar, R.; Rajendran, S.; Mohan, R.; Pascoal, A. A unified ship manoeuvring model with a nonlinear model predictive controller for path following in regular waves. Ocean Eng. 2022, 243, 110165. [Google Scholar] [CrossRef]
- Paramesh, S.; Rajendran, S. Numerical investigation of the manoeuvring motions and trajectory tracking of a kvlcc2 tanker using PID controller in regular waves. In Proceedings of the Global Oceans 2020, Biloxi, MS, USA, 5–30 October 2020. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–765. [Google Scholar] [CrossRef]
- McCormack, A.S.; Godfrey, K.R. Rule-based autotuning based on frequency domain identification. IEEE Trans. Control Syst. Technol. 1998, 6, 43–61. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). Standards for Ship Manoeuvrability (IMO Resolution MSC.137(76)); IMO: London, UK, 2002. [Google Scholar]




| Parameters | Values |
|---|---|
| ) | 320.0 m |
| 58.0 m | |
| 20.8 m | |
| 312,600 m3 | |
| ) | 11.2 m |
| ) | 0.810 |
| ) | 9.86 m |
| ) | 15.80 m |
| ) | 112.5 m2 |
| −0.040 | −0.391 | 0.022 | 1.6 | ||||
| 0.002 | 0.008 | 0.223 | 1.1 | ||||
| 0.011 | −0.137 | 0.011 | 0.640 | ||||
| 0.771 | −0.049 | 0.220 | 0.395 | ||||
| −0.315 | −0.030 | 0.387 | −0.710 | ||||
| 0.083 | −0.294 | 0.312 | 1.09 | ||||
| −1.607 | 0.055 | −0.464 | 0.50 | ||||
| 0.379 | −0.013 | 2.0 | 2.747 |
| MARIN FR | MANSIM | Yasukawa & Yoshimura | Present Code | ||
|---|---|---|---|---|---|
| +35° | 3.25 | 3.10 | 3.62 | 3.24 | |
| 1.36 | 1.35 | 1.58 | 1.37 | ||
| 3.34 | 3.16 | 3.71 | 3.18 | ||
| −35° | 3.11 | 3.10 | 3.56 | 3.09 | |
| −1.22 | −1.23 | −1.51 | −1.24 | ||
| −3.08 | −2.90 | −3.59 | −2.89 |
| MARIN FR | MANSIM | Yasukawa & Yoshimura | Present Code | ||
|---|---|---|---|---|---|
| +10° | 1st OA | 8.2 | 5.3 | 5.8 | 5.7 |
| 2nd OA | 21.9 | 14.1 | 20.5 | 14.9 | |
| −10° | 1st OA | 9.5 | 7.5 | 8.8 | 8.2 |
| 2nd OA | 15 | 9.4 | 12.6 | 9.6 | |
| +20° | 1st OA | 13.7 | 11.1 | 11.8 | 11.7 |
| 2nd OA | 14.9 | 15.5 | 19.7 | 15.6 | |
| −20° | 1st OA | 15.1 | 14.2 | 16.1 | 14.7 |
| 2nd OA | 13.3 | 11.8 | 14.6 | 11.9 |
| X (m) | Y (m) | Course (°) | Distance (m) | Course Change Angle (°) | (m) | |
|---|---|---|---|---|---|---|
| Waypoint 1 | 0 | 0 | ||||
| 090 | 2600 | |||||
| Waypoint 2 | 0 | 2600 | −30 | 669 | ||
| 060 | 2500 | |||||
| Waypoint 3 | 1250 | 4765 | 45 | 781 | ||
| 105 | 3000 | |||||
| Waypoint 4 | 473 | 7663 | 60 | 853 | ||
| 165 | 2800 | |||||
| Waypoint 5 | −2232 | 8388 | 90 | 1038 | ||
| 255 | 2500 | |||||
| Waypoint 6 | −2879 | 5973 | ||||
| Max. XTE (m) | Max. Overshoot (m) | Time (s) | MAE (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 30° | 45° | 60° | 90° | 30° | 45° | 60° | 90° | |||
| T-LOS | 54.2 | 61.3 | 84.6 | 309.6 | 8.4 | 30.4 | 84.6 | 309.6 | 2270 | 58.33 |
| MDC-LOS | 61.6 | 67.0 | 83.1 | 305.0 | 32.0 | 50.6 | 83.1 | 305.0 | 2281 | 70.79 |
| TLD-LOS | 46.0 | 94.4 | 188.5 | 548.8 | 15.8 | 19.0 | 18.9 | 16.4 | 1972 | 69.31 |
| Proposed method | 72.9 | 103.2 | 146.0 | 221.4 | - | 0.2 | 0.5 | - | 2098 | 34.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, W.-J.; Lee, J.-S. A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels. J. Mar. Sci. Eng. 2024, 12, 1831. https://doi.org/10.3390/jmse12101831
Choi W-J, Lee J-S. A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels. Journal of Marine Science and Engineering. 2024; 12(10):1831. https://doi.org/10.3390/jmse12101831
Chicago/Turabian StyleChoi, Won-Jin, and Jeong-Seok Lee. 2024. "A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels" Journal of Marine Science and Engineering 12, no. 10: 1831. https://doi.org/10.3390/jmse12101831
APA StyleChoi, W.-J., & Lee, J.-S. (2024). A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels. Journal of Marine Science and Engineering, 12(10), 1831. https://doi.org/10.3390/jmse12101831






