Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Required During Ship Mooring Operations
Abstract
:1. Introduction
2. Ship Mooring Operations with Tug Assistance in Ports and Literature Analysis
3. Theoretical Basis for Tug Bollard Pull Evaluation During Ship Mooring Operations in Ports
3.1. Research Methodology: Basic Ideas
- -
- Collection and analysis of the aforementioned primary data;
- -
- Assessment of the manoeuvrability of the ship and the tugboats in the port area during various operations;
- -
- Optimum selection of the number of tugboats and the required pulling power (bollard pull) of the tugboats;
- -
- Planning the timing of towing operations and possible costs;
- -
- Drawing conclusions and recommendations for specific conditions.
3.2. Mathematical Model

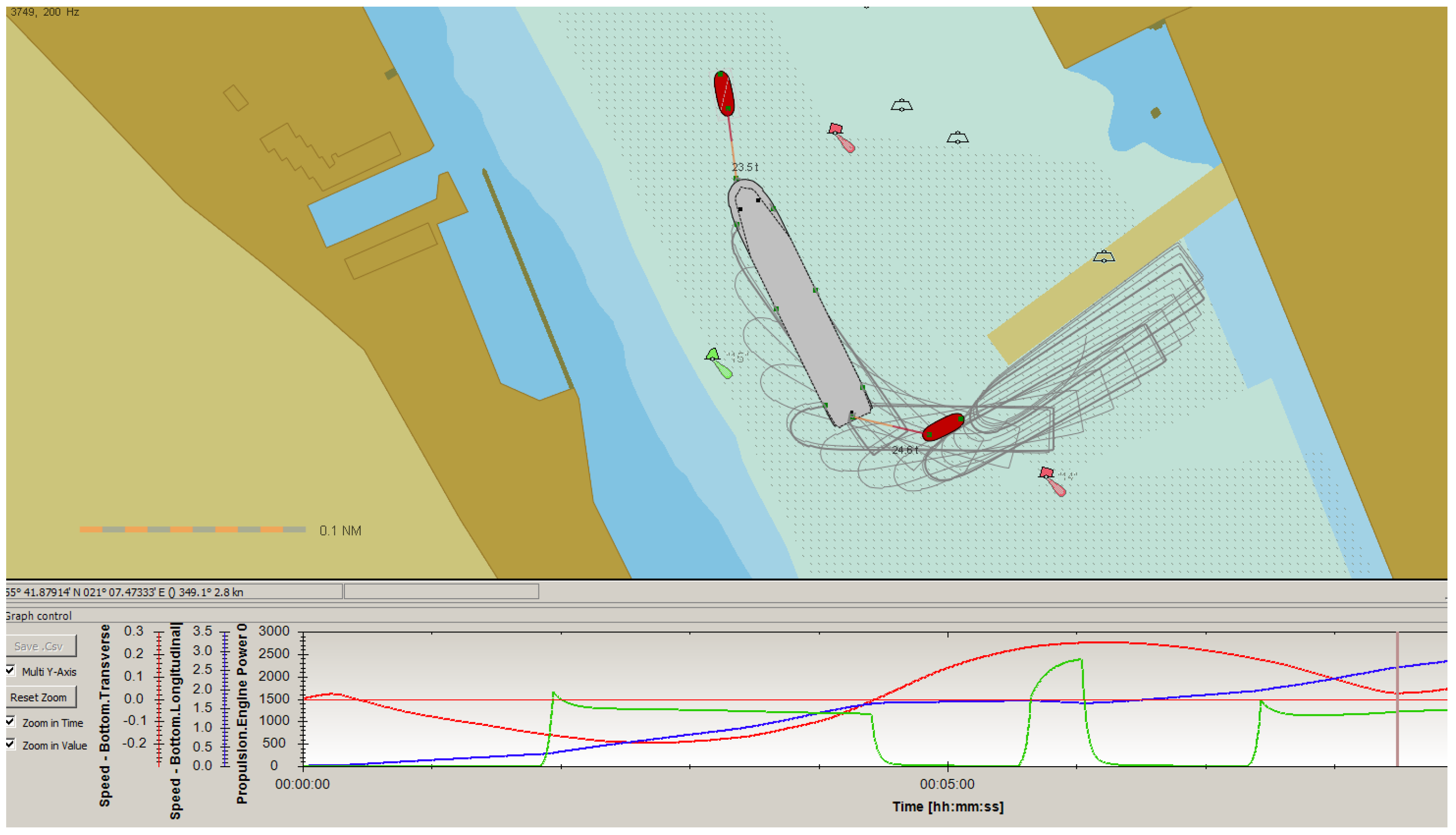
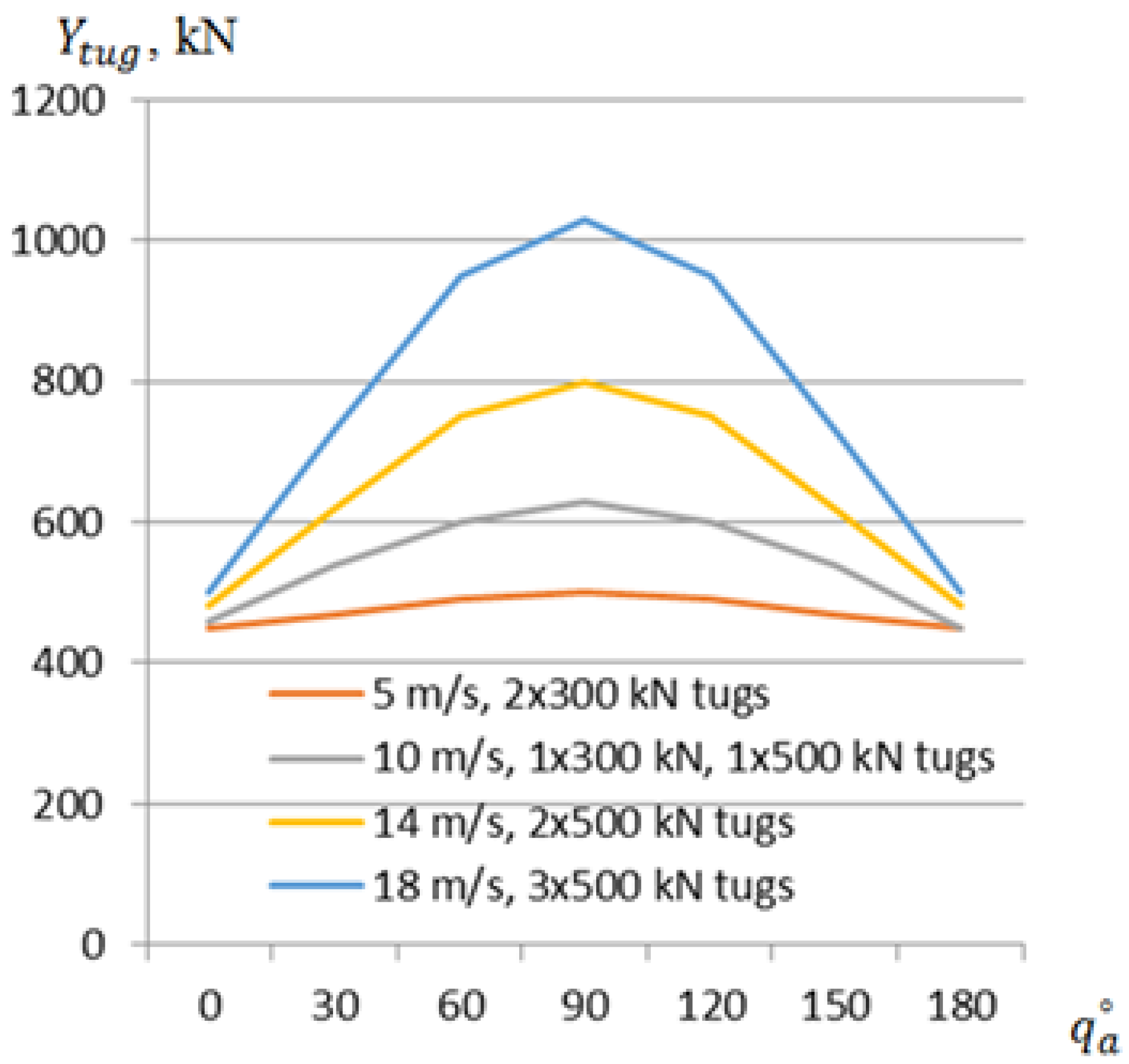
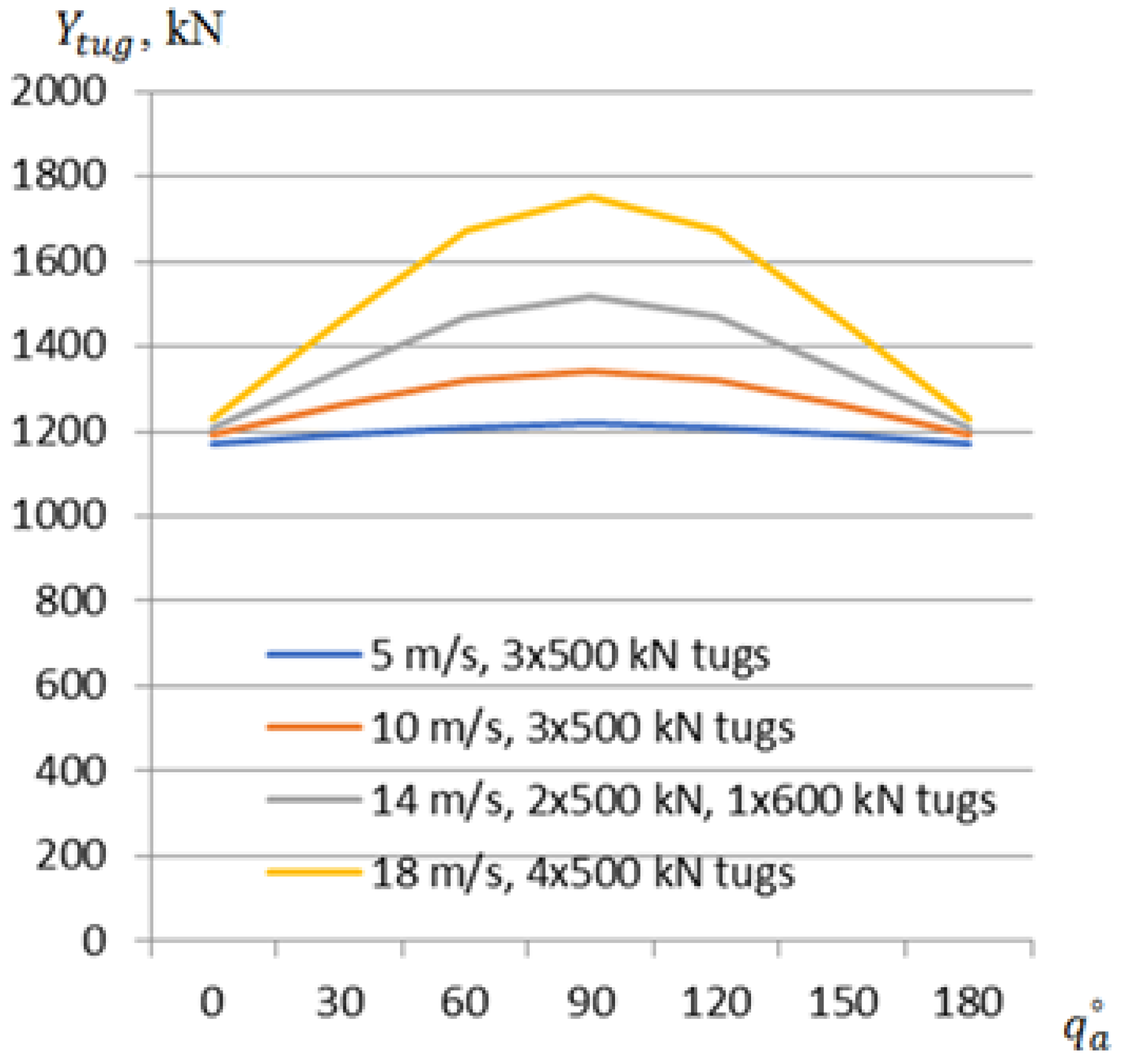
4. Case Study of Tug Bollard Pull Evaluation During Ship Mooring Operations
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toma, A.; Oncica, V.; Atodiresei, D. The study of ships behavior during port maneuvering with tugs. Mircea Cel Batran Nav. Acad. Sci. Bull. 2016, 19, 109–115. [Google Scholar] [CrossRef]
- Piaggio, B.; Viviani, M.; Martelli, M.; Figari, M. Z-Drive Escort Tug manoeuvrability model and simulation. Ocean. Eng. 2019, 191, 106461. [Google Scholar] [CrossRef]
- Paulauskas, V.; Simutis, M.; Placiene, B.; Barzdžiukas, R.; Jonkus, M.; Paulauskas, D. The Influence of Port Tugs on Improving the Navigational Safety of the Port. J. Mar. Sci. Eng. 2021, 9, 342. [Google Scholar] [CrossRef]
- Artyszuk, J. Types and Power of Harbour Tugs—the Latest Trends. Pr. Nauk. Politech. Warsz. 2013, 98, 12. [Google Scholar]
- Aydın, Ç.; Ünal, U.O.; Karabulut, U.C.; Sarıöz, K. Practical Computational Procedures for Predicting Steering and Braking Forces of Escort Tugs. Ocean. Eng. 2018, 166, 159–171. [Google Scholar] [CrossRef]
- Paulauskas, V.; Paulauskas, D. Research on work methods for tugs in ports//Transport/Vilniaus Gedimino Technikos Universitetas. Vilnius Tech. 2011, 26, 310–314. [Google Scholar] [CrossRef]
- Kornacki, J.; Galor, W. Analysis of Ships Turn Manoeuvres in Port Water Area. Int. J. Mar. Navi-Gation Saf. Sea Transp. 2007, 1, 95–100. [Google Scholar]
- Chou, C.C.; Wen, C.C.; Huang, Y.J. Analysis of Tugboat Operation and Towage Fees in a Taiwanese Port and Alternatives for Improving Tugboat Operation by the Delphi Method. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 235, 176–187. [Google Scholar] [CrossRef]
- Abhijit, S. Hazards Identification and Safety Management Practices for Major Hazards in Routine Ship Towage Operation in Indian Coastal Waters; University of Petroleum and Energy Studies (UPES): Dehradun, India, 2016. [Google Scholar]
- Nowy, A.; Gucma, L.; Perkovič, M. Advances in the Collision and Grounding of Ships and Offshore Structures: Proceedings of the 9th International Conference on Collision and Grounding of Ships and Offshore Structures (ICCGS 2023), Nantes, France, 11–13 September 2023; International Conference on Collision and Grounding of Ships and Offshore Structures; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- European Maritime Safety Agency. Annual Overview of Marine Casualties and Incidents 2023 European Maritime Safety Agency; European Maritime Safety Agency: Lisbon, Portugal, 2023; pp. 1–66. Available online: https://emsa.europa.eu/publications/item/5052-annual-overview-of-marine-casualties-and-incidents.html (accessed on 15 October 2024).
- Bondarenko, O.V.; Nekrasov, V.O.; Yastreba, O.P. Effectiveness Harbour Tug Fleet: Problem Formulation and Methodology of Its Solution. Brodogradnja 2016, 67, 33–46. [Google Scholar] [CrossRef]
- Kang, L.; Gao, S.; Meng, Q. Capacity Analysis of Ship-Tugging Operations in a Large Container Port. Asian Transp. Stud. 2020, 6, 100011. [Google Scholar] [CrossRef]
- Aro, E.; Rytter, N.G.M.; Itälinna, T. Maritime Industry Processes in the Baltic Sea Region. 2020. Available online: https://www.utupub.fi/bitstream/handle/10024/156199/ECOPRODIGI%20Research%20Report%201%202020%20final.pdf?sequence=1 (accessed on 15 October 2024).
- Paulauskas, V. Ships Entering the Ports; N.I.M.S Publish House: Riga, Latvia, 2013; 240p, ISBN 9984-679-71-3. [Google Scholar]
- Sun, C.; Li, M.; Chen, L.; Chen, P. Dynamic Tugboat Scheduling for Large Seaports with Multiple Terminals. J. Mar. Sci. Eng. 2024, 12, 170. [Google Scholar] [CrossRef]
- Havsmiljöinstitutet. Mapping Shipping Intensity and Routes in the Baltic Sea. 2014, 1, 6. Available online: http://havsmiljoinstitutet.se/digitalAssets/1506/1506887_sime_ais_report_2014_5.pdf (accessed on 15 August 2024).
- BPO. The Baltic Sea as a Model Region for Green Ports and Maritime Transport; BPO: Navi Mumbai, India, 2016. Available online: http://www.bpoports.com/BPC/Helsinki/BPO_report_internet-final.pdf (accessed on 15 October 2024).
- BSMIR Project Team, Finnish Border Guard Headquarters. Baltic Sea Maritime Incident Response Survey. 2014. Available online: https://cbss.org/wp-content/uploads/2020/04/CBSS_AnnualReport_2013-14.pdf (accessed on 15 October 2024).
- Mazaheri, A.; Montewka, J.; Kotilainen, P.; Sormunen, O.V.E.; Kujala, P. Assessing Grounding Frequency Using Ship Traffic and Waterway Complexity. J. Navig. 2015, 68, 89–106. [Google Scholar] [CrossRef]
- Kang, L.; Meng, Q.; ChoonTan, K. Tugboat Scheduling under Ship Arrival and Tugging Process Time Uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2020, 144, 102125. [Google Scholar] [CrossRef]
- Wei, X.; Jia, S.; Meng, Q.; Tan, K.C. Tugboat Scheduling for Container Ports. Transp. Research. Logist. Transp. Rev. 2020, 142, 102125. [Google Scholar] [CrossRef]
- Paulauskas, V.; Paulauskas, D.; Wijffels, J. Ship Safety in Open Ports. Transport 2009, 24, 113–120. [Google Scholar] [CrossRef]
- Nitonye, S.; Adumene, S.; Howells, U.U. Numerical Design and Performance Analysis of a Tug Boat Propulsion System. J. Power Energy Eng. 2017, 5, 80–98. [Google Scholar] [CrossRef]
- Karaçay, Ö.E.; Özsoysal, O.A. Techno-Economic Investigation of Alternative Propulsion Systems for Tugboats. Energy Convers. Manag. 2021, 10, 12. [Google Scholar] [CrossRef]
- Gucma, L. The Risk Assessment of Ships Maneuvering on the Waterways Based on Generalized Simulation Data Safety and Security Engineering II. WIT Transactions on the Built Environment. 2007. Available online: https://www.witpress.com/Secure/elibrary/papers/SAFE07/SAFE07041FU1.pdf (accessed on 15 October 2024).
- SimFlex Navigator Simulator. Force Technology; SimFlex: Copenhage, Denmark, 2014. Available online: https://forcetechnology.com/en/services/simulations-and-cfd/cloud-based-maritime-simulator?gad_source=1&gclid=Cj0KCQjw4Oe4BhCcARIsADQ0csn5m_Yw9VTmQyUy8_JJFs1UmfHcOU7zsFIXm4k7IooxG9LAM5WjECsaAiqmEALw_wcB (accessed on 15 October 2024).
- Wu, G.; Zhao, X.; Sun, Y.; Wang, L. Cooperative Maneuvering Mathematical Modeling for Multi-Tugs Towing a Ship in the Port Environment. J. Mar. Sci. Eng. 2021, 9, 384. [Google Scholar] [CrossRef]
- HTG. Recommendations of the Committee for Waterfront Structures—Harbours and Waterways: EAU 2012, 9th ed.; Ernst & Sohn: Hoboken, NJ, USA, 2012; Available online: https://www.wiley.com/en-ae/Recommendations+of+the+Committee+for+Waterfront+Structures+Harbours+and+Waterways%3A+EAU+2012%2C+9th+Edition-p-9783433605202 (accessed on 15 October 2024).
- McBride, M.W.; Smallman, J.V.; Huntington, S.W. Guidelines for Design of Approach Channels. In Proceedings PORTS ’98; ASCE: Long Beach, CA, USA, 1998; pp. 1315–1324. [Google Scholar]
- Recommendations for the Design of the Maritime Configuration of Ports, Approach Channels and Harbour Basins; ROM 3.1-99; Puertos del Estado: Madrid, Spain, 1999; 350p.
- Feeny, B.F. D’Alembert’s Principle and the Equations of Motion for Nonholonomic Systems. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Seattle, WA, USA, 11–15 November 2007; IMECE2006-14533. pp. 561–570. [Google Scholar] [CrossRef]
- Rawson, K.J.; Tupper, E.C. Basic Ship Theory, 5th ed.; Elsever: Amsterdam, The Netherlands, 2001; 727p. [Google Scholar]
- Paulauskas, V.; Paulauskas, D. Ship’s Steering in Port Areas; Klaipeda University Publish House: Klaipeda, Lithuania, 2009; 256p. [Google Scholar]
- IALA Recommendation V-128 on Operational and Technical Performance of VTS Systems Edition 4. Saint-Germain France. 2015. Available online: https://www.iala-aism.org/content/uploads/2016/09/V-128-Ed.-4-Operational-and-Technical-Performance-Requirements-for-VTS-Equipment.pdf (accessed on 15 October 2024).
- Chauhan, S.; Patil, C.; Sinha, M.; Halder, A. Fuzzy state noise-driven Kalman filter for sensor fusion. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 1091–1097. [Google Scholar] [CrossRef]
- Hanqing, J.; Shige, P. Optimal unbiased estimation for maximal distribution. Am. Inst. Math. Sci. 2021, 6, 189–198. [Google Scholar] [CrossRef]
- PIANC Fender Guidelines. Guidelines for the Design, Manufacturing and Testing of Fender Systems; 2024; 274p, ISBN 978-2-87223-036-5. [Google Scholar]
- Klaipeda Seaport Manual, Maps and Charts. 2024. Available online: www.portofklaipeda.lt (accessed on 25 August 2024).
- Openseamap. Available online: https://map.openseamap.org/ (accessed on 25 August 2024).
 ) and the help of calibrated simulator (red line).
) and the help of calibrated simulator (red line).
 ) and the help of calibrated simulator (red line).
) and the help of calibrated simulator (red line).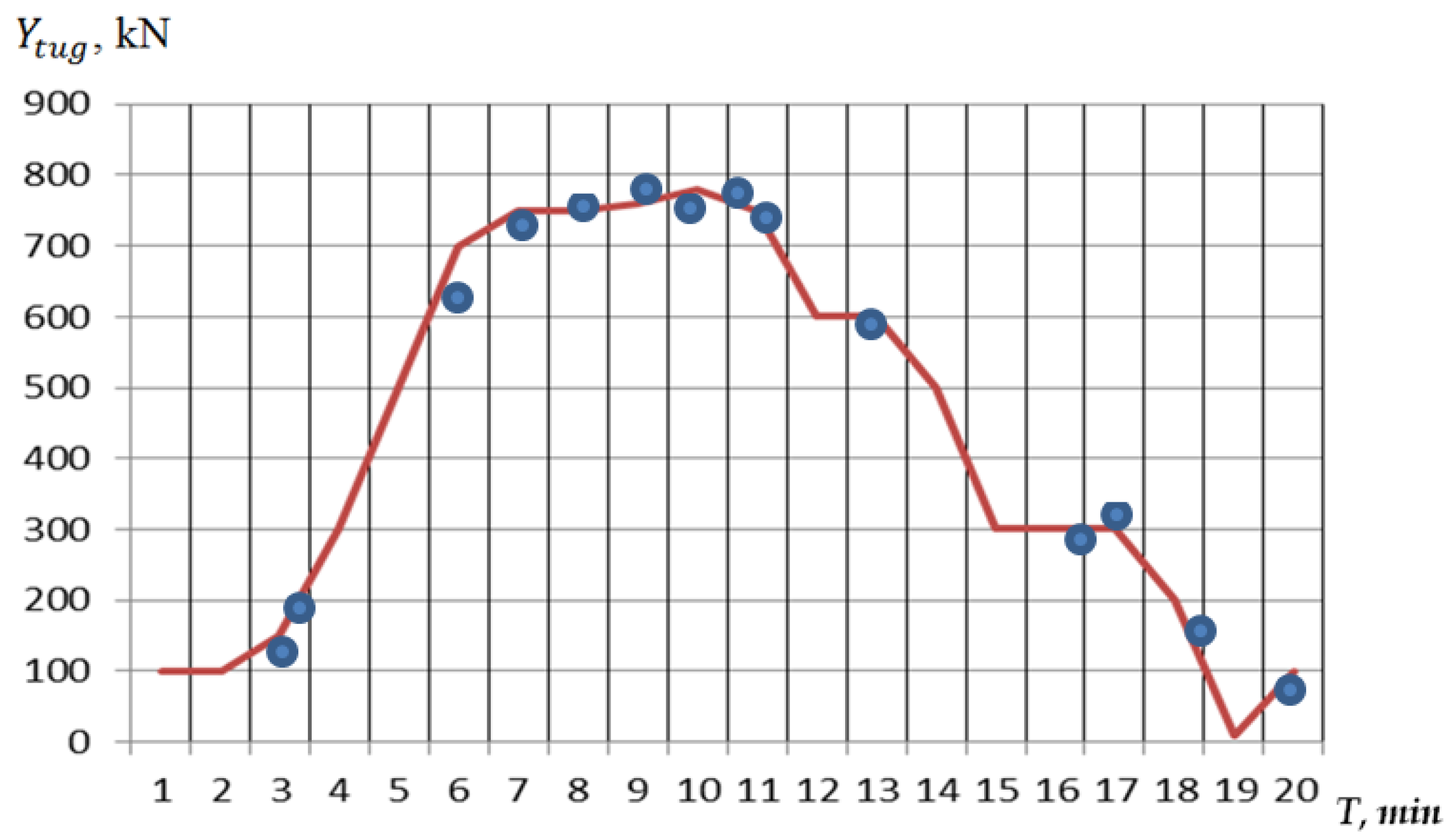
 ) and the help of calibrated simulator (green line).
) and the help of calibrated simulator (green line).
 ) and the help of calibrated simulator (green line).
) and the help of calibrated simulator (green line).
 ) and the help of calibrated simulator (purple line).
) and the help of calibrated simulator (purple line).
 ) and the help of calibrated simulator (purple line).
) and the help of calibrated simulator (purple line).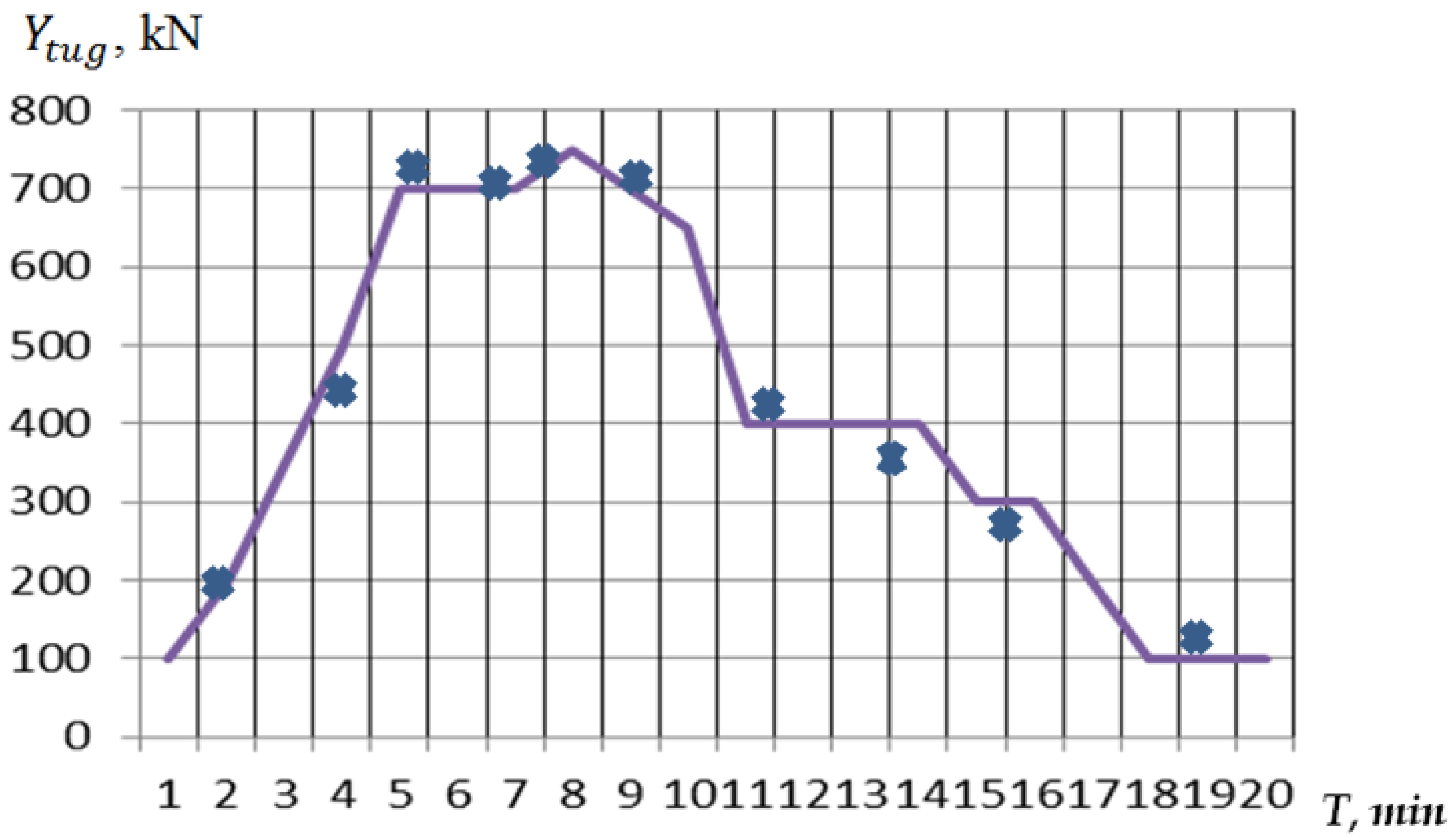

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulauskas, V.; Paulauskas, D.; Simutis, M. Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Required During Ship Mooring Operations. J. Mar. Sci. Eng. 2024, 12, 1959. https://doi.org/10.3390/jmse12111959
Paulauskas V, Paulauskas D, Simutis M. Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Required During Ship Mooring Operations. Journal of Marine Science and Engineering. 2024; 12(11):1959. https://doi.org/10.3390/jmse12111959
Chicago/Turabian StylePaulauskas, Vytautas, Donatas Paulauskas, and Martynas Simutis. 2024. "Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Required During Ship Mooring Operations" Journal of Marine Science and Engineering 12, no. 11: 1959. https://doi.org/10.3390/jmse12111959
APA StylePaulauskas, V., Paulauskas, D., & Simutis, M. (2024). Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Required During Ship Mooring Operations. Journal of Marine Science and Engineering, 12(11), 1959. https://doi.org/10.3390/jmse12111959








