Shore-Side Downfall Pressures Due to Waves Impacting a Vertical Seawall: An Experimental Study
Abstract
:1. Introduction
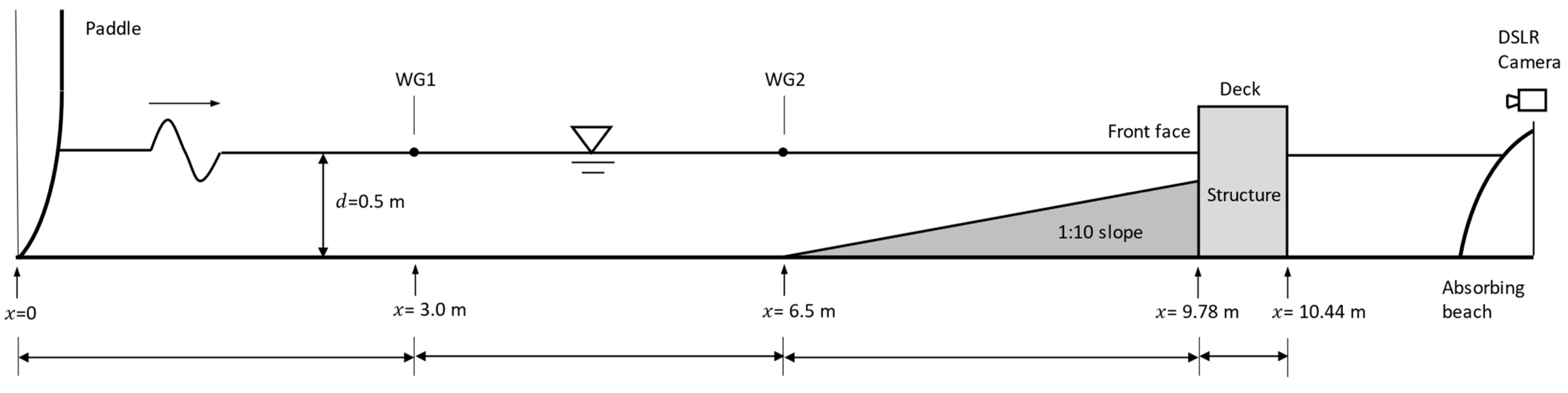
2. Experimental Arrangements
2.1. The Physical Model
2.2. Experimental Instrumentation
2.3. Wave Conditions
2.3.1. Regular Wave Properties
2.3.2. Focused Wave Properties
2.4. Scale Considerations
2.5. Data Processing
2.6. Wave Generation
2.6.1. Accuracy and Reflection Analysis
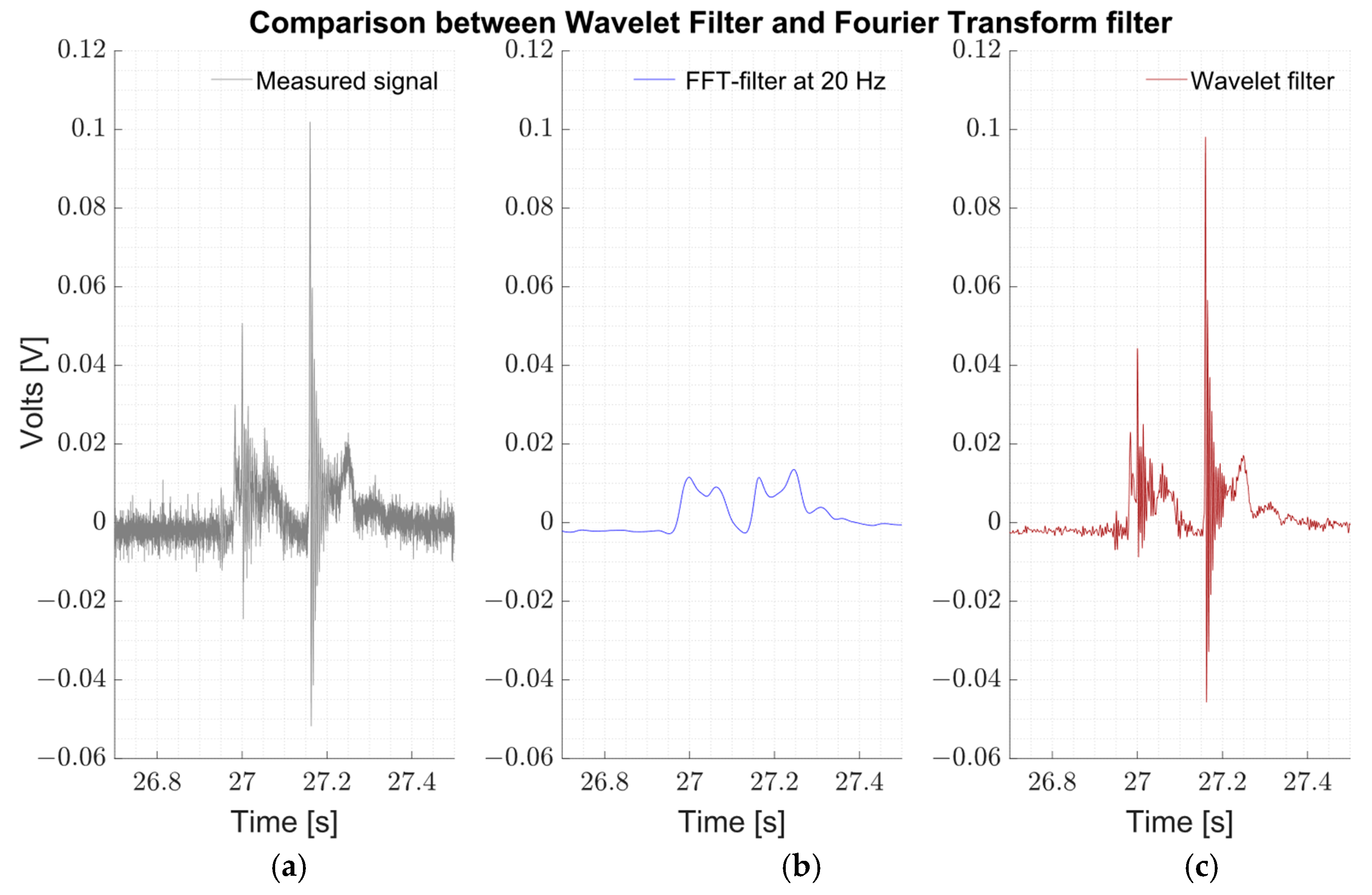
2.7. Signal Filtering
Wavelet Filtering
3. Results and Discussion
3.1. Regular Waves
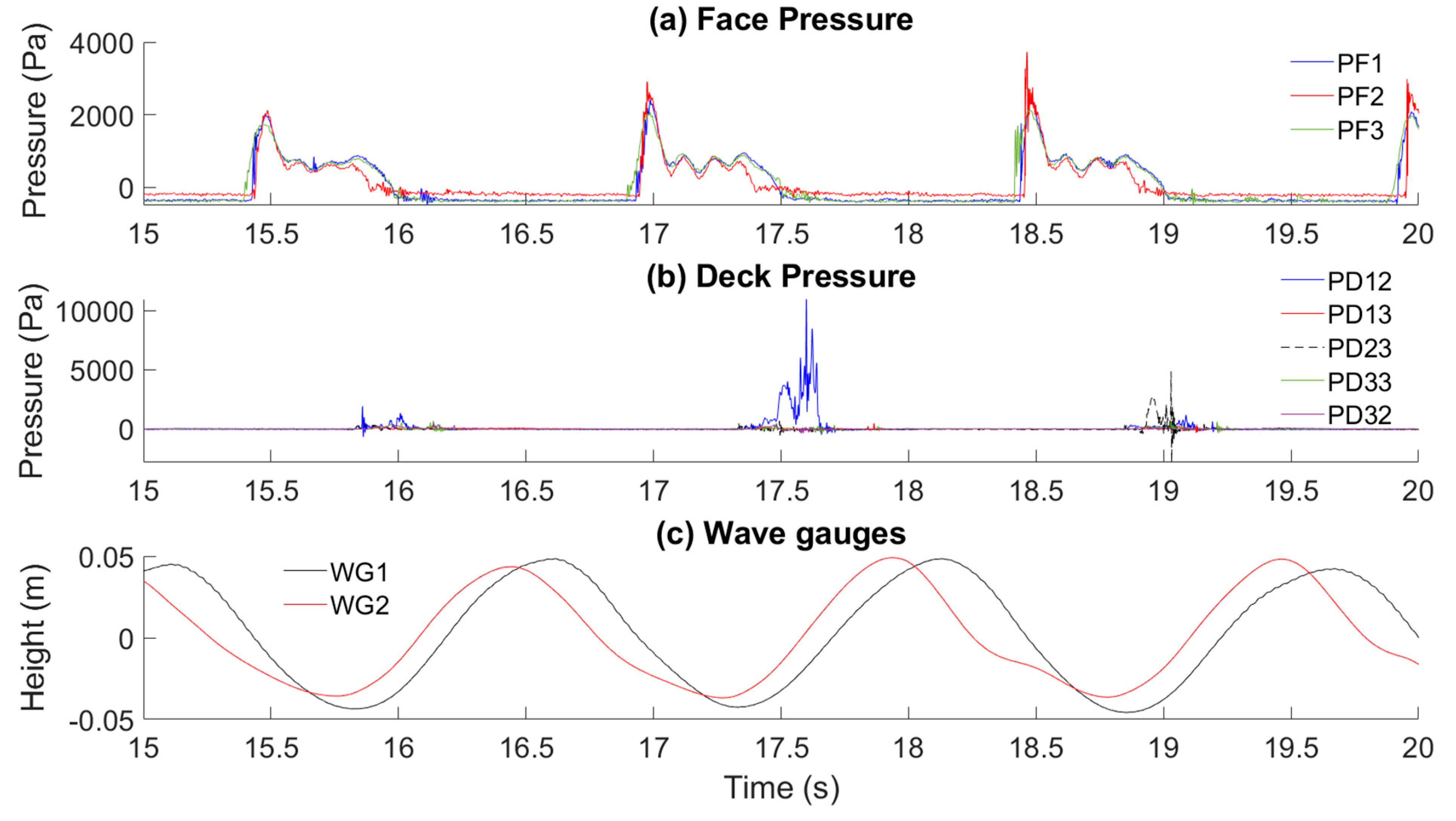
3.1.1. Wave-by-Wave Analysis
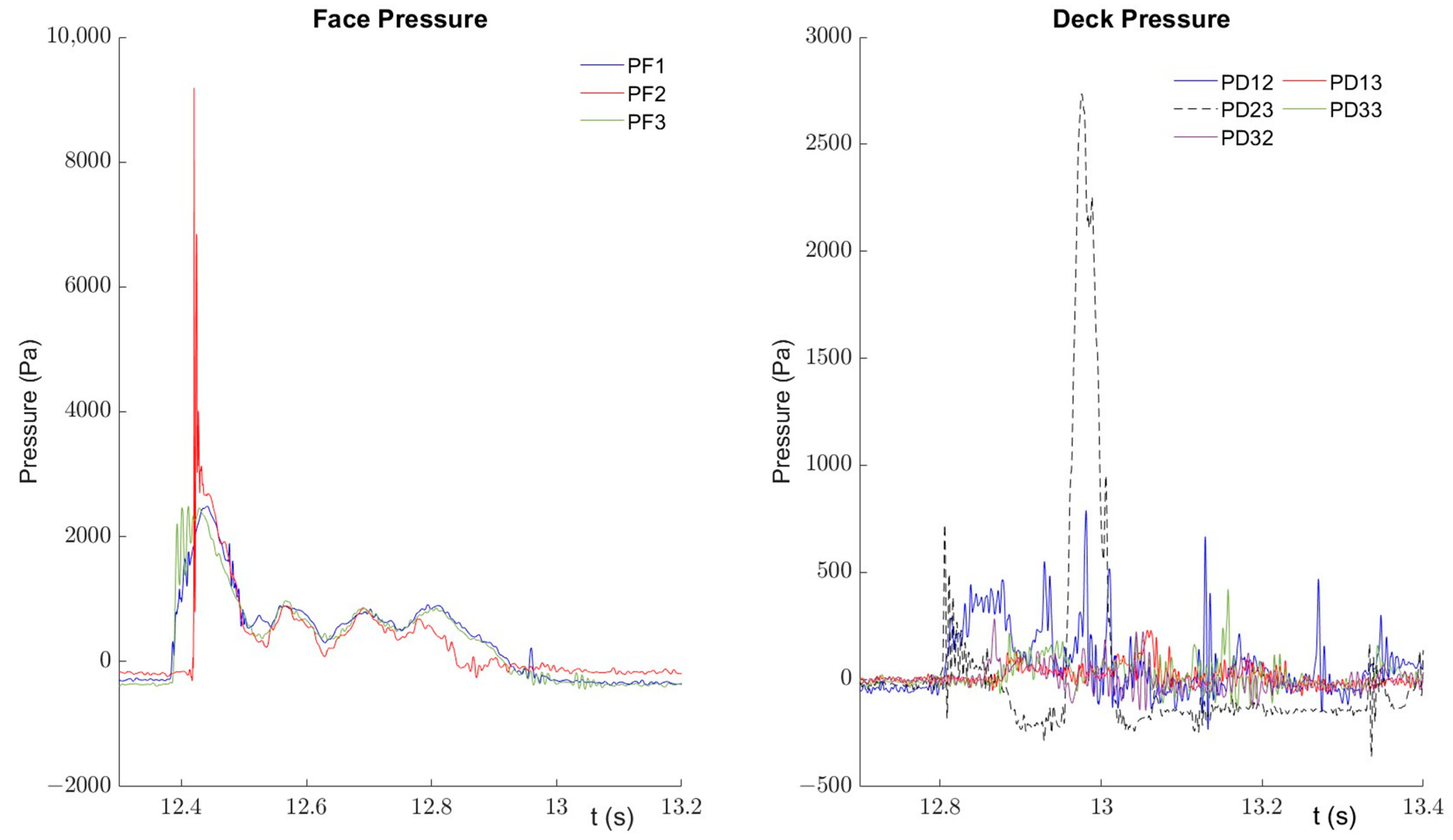
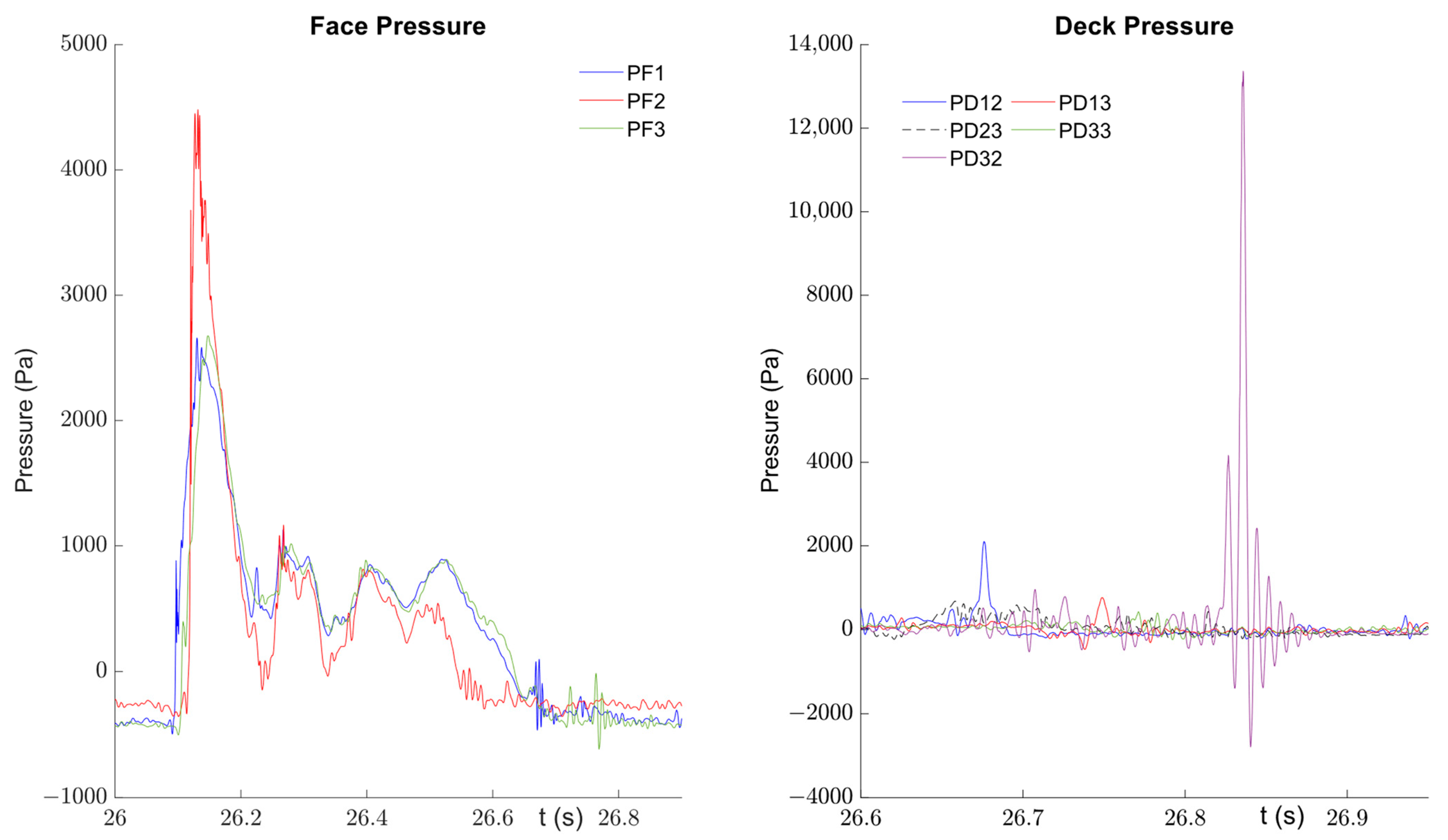
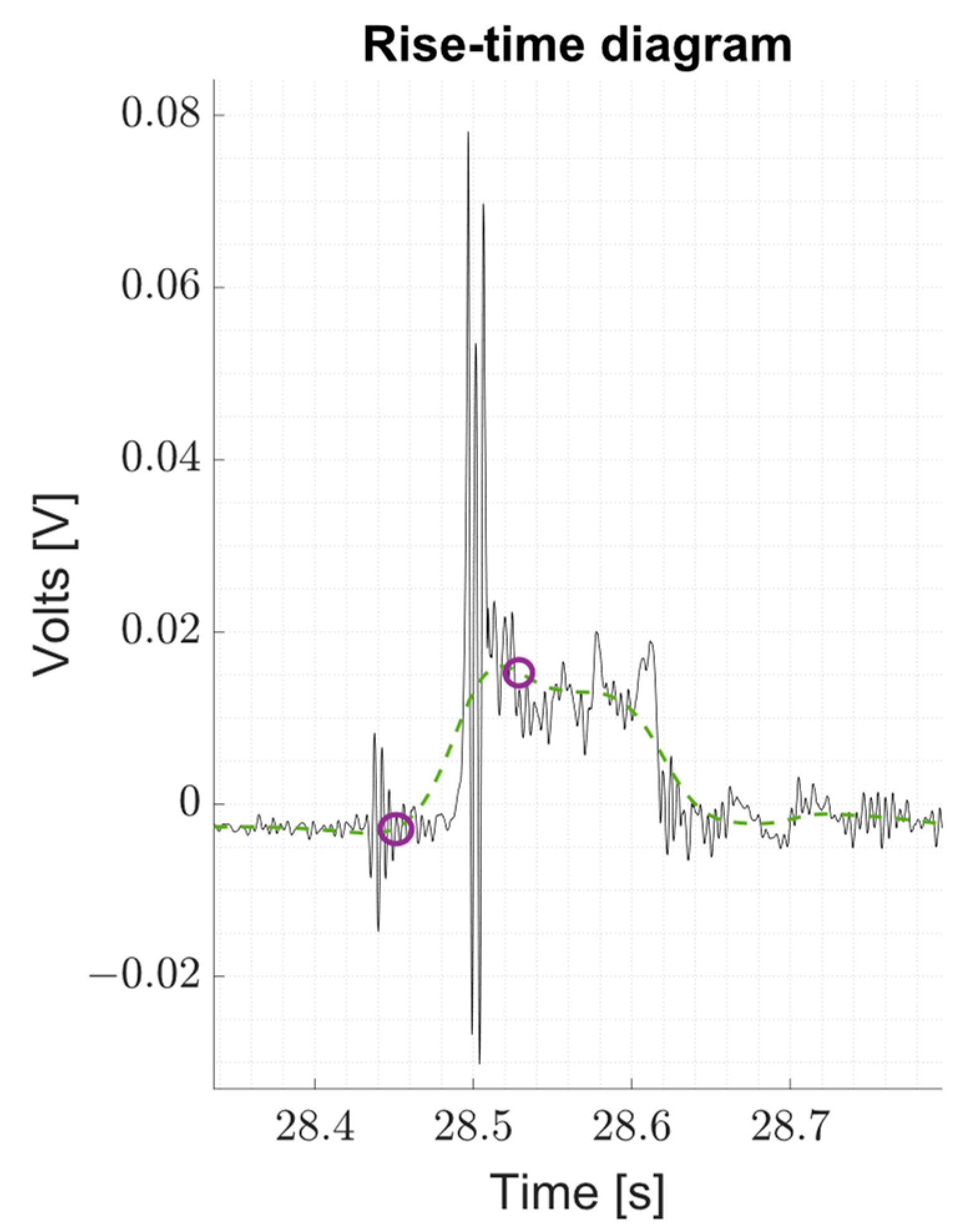
3.1.2. Characterisation of Individual Impact Events
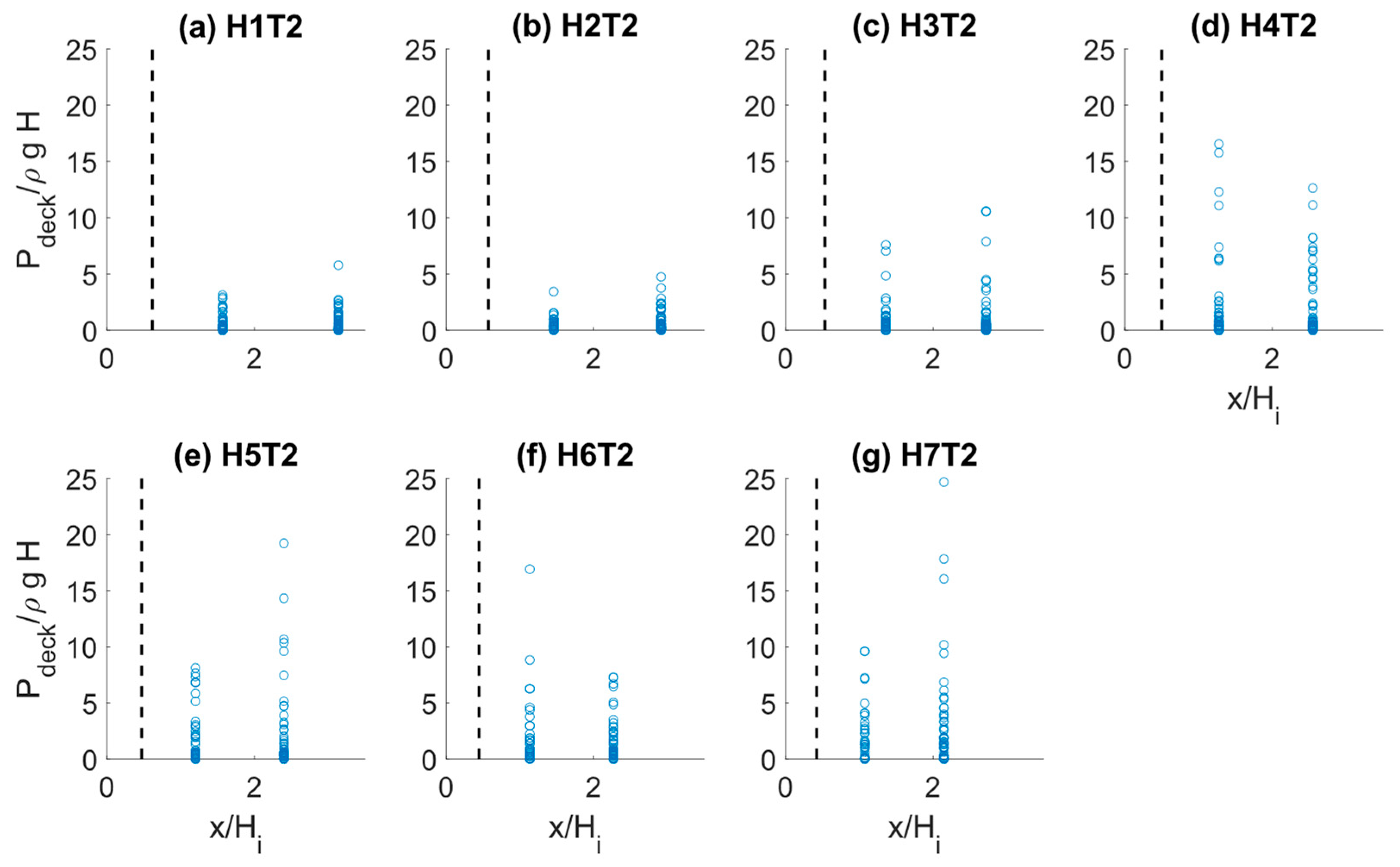
3.1.3. Deck Impact Pressure and Incident Wave Conditions
3.1.4. Further Characterisation of the Impacts
Relationship of Impact Times and Peak Pressures
Spatial Distribution of Pressure on the Deck
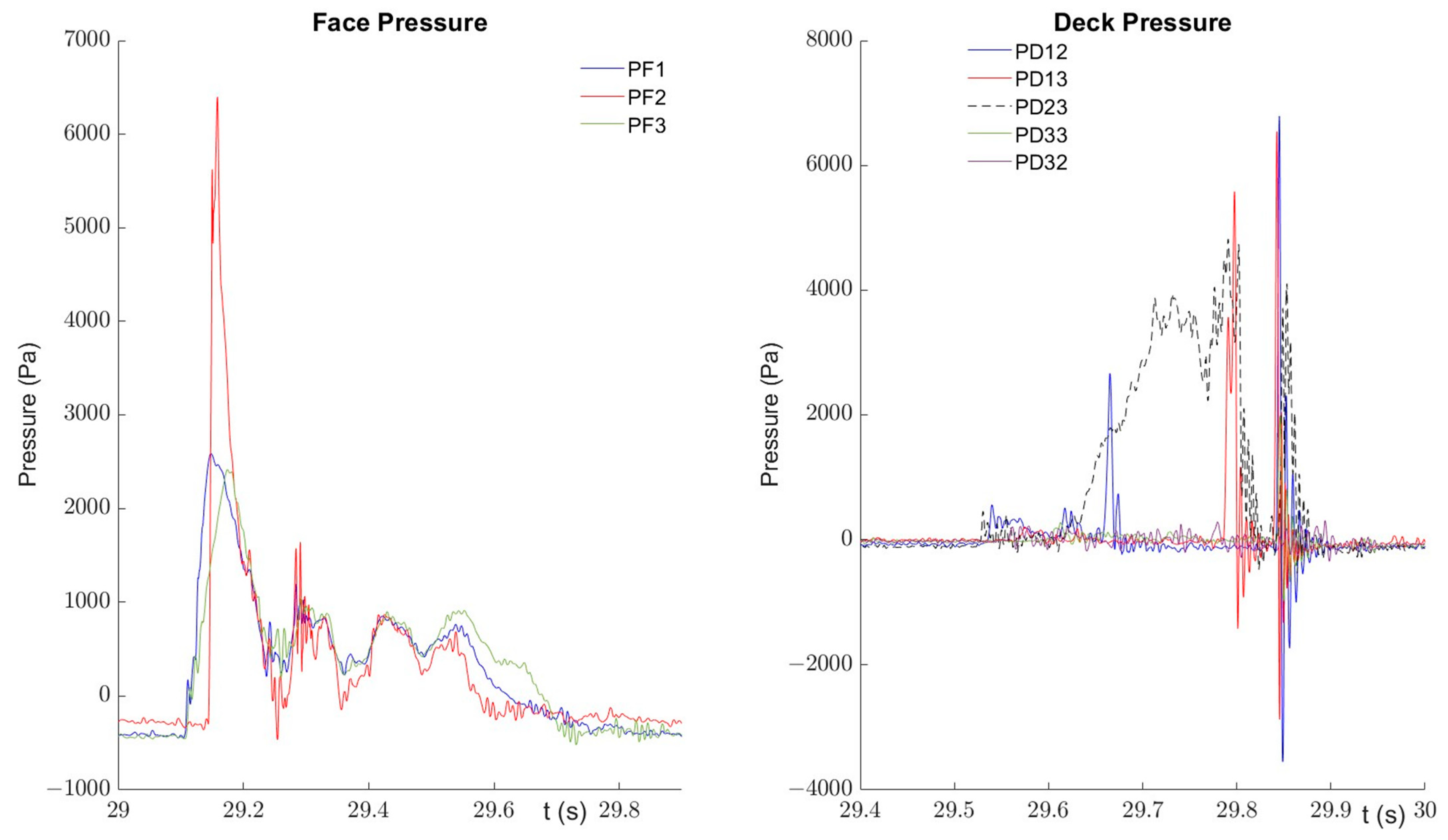
3.2. Focused Waves
4. Discussion and Limitations
4.1. Limitations
4.1.1. Implications of Scale Effects on the Reported Deck Pressures
4.1.2. Implications of Improper Weber Scaling
4.2. Design Implications and Recommendations for Further Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bullock, G.N.; Obhrai, C.; Peregrine, D.H.; Bredmose, H. Violent Breaking Wave Impacts. Part 1: Results from Large-Scale Regular Wave Tests on Vertical and Sloping Walls. Coast. Eng. 2007, 54, 602–617. [Google Scholar] [CrossRef]
- Ravindar, R.; Sriram, V. Impact Pressure and Forces on a Vertical Wall with Different Types of Parapet. J. Waterw. Port Coast. Ocean. Eng. 2021, 147, 04021007. [Google Scholar] [CrossRef]
- van der Meer, J.W.; Allsop, W.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Zanuttigh, B.; Schuttrumpf, H.; Troch, P. EurOtop-Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application. 2018. Available online: https://www.overtopping-manual.com/assets/downloads/EurOtop_II_2018_Final_version.pdf (accessed on 18 November 2024).
- BBC Dawlish’s Storm-Damaged Railway Line Reopens. Available online: https://www.bbc.co.uk/news/uk-england-devon-26874503 (accessed on 22 June 2021).
- The British Standards Institution. BS 6349-1-2:2016+A1:2017: Maritime Works; British Standards Institute: London, UK, 2017; ISBN 9780580988318. [Google Scholar]
- U.S. Army Corps of Engineers. Coastal Engineering Manual Part VI, 1st ed.; U.S. Army Corps of Engineers: Los Angeles, CA, USA, 2012; ISBN 1782661980. [Google Scholar]
- FEMA. FEMA-55: Coastal Construction Manual-Principles and Practices of Planning, Siting, Designing, Constructing, and Maintaining Residential Buildings in Coastal Areas, 4th ed.; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 2005; Volume I, ISBN 1482079291. [Google Scholar]
- Allsop, W.; Franco, L.; Bellotti, G.; Bruce, T.; Geeraerts, J. Hazards to People and Property from Wave Overtopping at Coastal Structures. In Proceedings of the Coastlines, Structures and Breakwaters 2005, London, UK, 20–22 April 2005; pp. 153–165. [Google Scholar]
- Bodaghkhani, A.; Dehghani, S.R.; Muzychka, Y.S.; Colbourne, B. Understanding Spray Cloud Formation by Wave Impact on Marine Objects. Cold Reg. Sci. Technol. 2016, 129, 114–136. [Google Scholar] [CrossRef]
- Bodaghkhani, A.; Muzychka, Y.S.; Colbourne, B. An Analytical Model of Final Average Droplet Size Prediction of Wave Spray Cloud. Int. J. Heat Fluid Flow 2018, 74, 110–117. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.R.; Muzychka, Y.S.; Naterer, G.F. Droplet Trajectory and Thermal Analysis of Impinging Saline Spray Flow on Marine Platforms in Cold Seas and Ocean Regions. Ocean. Eng. 2018, 148, 538–547. [Google Scholar] [CrossRef]
- Watanabe, Y.; Ingram, D.M. Size Distributions of Sprays Produced by Violent Wave Impacts on Vertical Sea Walls. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160423. [Google Scholar] [CrossRef]
- BBC Blackpool North Pier to Reopen after £1m Storm Damage Repairs. Available online: https://www.bbc.co.uk/news/uk-england-lancashire-26704975 (accessed on 22 June 2021).
- BBC Aberystwyth Seafront Storm Damage Clean-Up Attracts 200. Available online: https://www.bbc.co.uk/news/uk-wales-mid-wales-25682802 (accessed on 18 June 2021).
- Wolters, G.; Müller, G.; Bruce, T.; Obhrai, C. Large-Scale Experiments on Wave Downfall Pressures. Marit. Eng. 2005, 158, 137–145. [Google Scholar] [CrossRef]
- Bruce, T.; Pearson, J.; Allsop, W. Violent Overtopping of Seawalls-Extended Prediction Methods. In Proceedings of the Breakwaters, Coastal Structures and Coastlines; Allsop, W.H., Ed.; Institute of Civil Engineers: London, UK, 2002; pp. 245–255. [Google Scholar]
- Bruce, T.; Franco, L.; Alberti, P.; Pearson, J.; Allsop, W. Violent Wave Overtopping: Discharge Throw Velocities, Trajectories and Resulting Crown Deck Loading. In Ocean Wave Measurement and Analysis (2001); American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 1783–1796. ISBN 9780784406045. [Google Scholar]
- Watson, P.J.; Nuyts, S.; Murphy, J.; Lizondo, S.; Avgeris, I. Wave Overtopping Pressures and Spatial Distribution behind Rubble Mound Breakwaters. In Proceedings of the 3rd International Conference on Protection against Overtopping, Grange-over-Sands, UK, 6–8 June 2018; HR Wallingford: Grange-over-Sands, UK, 2018. [Google Scholar]
- Baines, A.; Watson, P.; Cunningham, L.S.; Rogers, B.D.; Murphy, J.; Lizondo, S. Modelling Shore-Side Pressure Distributions from Violent Wave Breaking at a Seawall. Proc. Inst. Civ. Eng.-Eng. Comput. Mech. 2019, 172, 118–123. [Google Scholar] [CrossRef]
- Cuomo, G.; Tirindelli, M.; Allsop, W. Wave-in-Deck Loads on Exposed Jetties. Coast. Eng. 2007, 54, 657–679. [Google Scholar] [CrossRef]
- de Almeida, E.; Hofland, B. Validation of Pressure-Impulse Theory for Standing Wave Impact Loading on Vertical Hydraulic Structures with Short Overhangs. Coast. Eng. 2020, 159, 103702. [Google Scholar] [CrossRef]
- Bredmose, H.; Peregrine, D.H.; Bullock, G.N. Violent Breaking Wave Impacts. Part 2: Modelling the Effect of Air. J. Fluid Mech. 2009, 641, 389–430. [Google Scholar] [CrossRef]
- Bredmose, H.; Bullock, G.N.; Hogg, A.J. Violent Breaking Wave Impacts. Part 3. Effects of Scale and Aeration. J. Fluid Mech. 2015, 765, 82–113. [Google Scholar] [CrossRef]
- Bagnold, R.A. Interim Report on Wave-Pressure Research; Institute of Civil Engineers: London, UK, 1939. [Google Scholar]
- Cuomo, G.; Allsop, W.; Takahashi, S. Scaling Wave Impact Pressures on Vertical Walls. Coast. Eng. 2010, 57, 604–609. [Google Scholar] [CrossRef]
- Bullock, G.N.; Crawford, A.R.; Hewson, P.J.; Walkden, M.J.A.; Bird, P.A.D. The Influence of Air and Scale on Wave Impact Pressures. Coast. Eng. 2001, 42, 291–312. [Google Scholar] [CrossRef]
- Bullock, G.N.; Bredmose, H. Violent Breaking-Wave Impacts. Part 4: A Detailed Analysis and Comparison of Field and 1:4 Scale Measurements on Sloping and Vertical Walls Including the Influence of Air and Scale Effects. Coast. Eng. 2024, 191, 104520. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Chen, J.; Zhai, G. Multiscale Air Entrainment in Wave-in-Deck Loads. Coast. Eng. 2024, 188, 104431. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Zhai, G.; Chen, J. Wave-in-Deck Loads Induced by Regular Wave Impact: The Role of Compressible Air Entrainment. J. Fluids Struct. 2023, 122, 103974. [Google Scholar] [CrossRef]
- Edinburgh Designs Piston Coastal Wave Generators. Available online: http://www4.edesign.co.uk/product/piston-wave-generators/ (accessed on 10 July 2021).
- Pepi, Y.; Streicher, M.; Ricci, C.; Franco, L.; Bellotti, G.; Hughes, S.; Troch, P. The Effect of Variations in Water Level on Wave Overtopping Discharge over a Dike: An Experimental Model Study. Coast. Eng. 2022, 178, 104199. [Google Scholar] [CrossRef]
- Altomare, C.; Gironella, X. Characterization of Overtopping Volumes from Focused Wave Groups over Smooth Dikes with an Emerged Toe: Insights from Physical Model Tests. J. Mar. Sci. Eng. 2024, 12, 1143. [Google Scholar] [CrossRef]
- Kerpen, N.B.; Daemrich, K.F.; Lojek, O.; Schlurmann, T. Effect of Variations Inwater Level and Wave Steepness on the Robustness Ofwave Overtopping Estimation. J. Mar. Sci. Eng. 2020, 8, 63. [Google Scholar] [CrossRef]
- Van Gent, M.R.A.; Zwanenburg, S.A.A.; Kramer, J. Effects of Water Level Variations on the Stability of Rock Armoured Slopes. Coast. Eng. Proc. 2018, 1, 44. [Google Scholar] [CrossRef]
- Baines, A.; Cunningham, L.S.; Rogers, B.D. Numerical Modelling of Wave Downfall Pressures on the Deck Landward of a Vertical Breakwater. In Proceedings of the Coasts, Marine Structures and Breakwaters 2017; ICE Publishing: Manchester, England, 2018; pp. 1051–1061. [Google Scholar]
- Hunt-Raby, A.C.; Borthwick, A.G.L.; Stansby, P.K.; Taylor, P.H. Experimental Measurement of Focused Wave Group and Solitary Wave Overtopping. J. Hydraul. Res. 2011, 49, 450–464. [Google Scholar] [CrossRef]
- Whittaker, C.N.; Fitzgerald, C.J.; Raby, A.C.; Taylor, P.H.; Borthwick, A.G.L. Extreme Coastal Responses Using Focused Wave Groups: Overtopping and Horizontal Forces Exerted on an Inclined Seawall. Coast. Eng. 2018, 140, 292–305. [Google Scholar] [CrossRef]
- Schäffer, H.A. Accurate Determination of Internal Kinematics from Numerical Wave Model Results. Coast. Eng. 2004, 50, 199–211. [Google Scholar] [CrossRef]
- Raby, A.; Jayaratne, R.; Bredmose, H.; Bullock, G. Individual Violent Wave-Overtopping Events: Behaviour and Estimation. J. Hydraul. Res. 2019, 58, 34–46. [Google Scholar] [CrossRef]
- Katsardi, V.; Swan, C. The Evolution of Large Non-Breaking Waves in Intermediate and Shallow Water. I. Numerical Calculations of Uni-Directional Seas. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2011, 467, 778–805. [Google Scholar] [CrossRef]
- Schaffer, H.A. Second-order wavemaker theory for irregular waves. Ocean. Eng. 1995, 23, 47–88. [Google Scholar] [CrossRef]
- McCormick, M.E. Ocean Engineering Mechanics: With Applications; Cambridge University Press: Cambridge, UK, 2009; ISBN 0521859522. [Google Scholar]
- Oshana, R. Overview of Digital Signal Processing Algorithms. In DSP Software Development Techniques for Embedded and Real-Time Systems; Elsevier: Oxford, UK, 2006; pp. 59–121. [Google Scholar] [CrossRef]
- McCabe, M.V.; Stansby, P.K.; Apsley, D.D. Random Wave Runup and Overtopping a Steep Sea Wall: Shallow-Water and Boussinesq Modelling with Generalised Breaking and Wall Impact Algorithms Validated against Laboratory and Field Measurements. Coast. Eng. 2013, 74, 33–49. [Google Scholar] [CrossRef]
- Whittaker, C.N.; Fitzgerald, C.J.; Raby, A.C.; Taylor, P.H.; Orszaghova, J.; Borthwick, A.G.L. Optimisation of Focused Wave Group Runup on a Plane Beach. Coast. Eng. 2017, 121, 44–55. [Google Scholar] [CrossRef]
- Weller, S. Wave Energy Extraction from Device Arrays Experimental Investigation in a Large Wave Facility. Ph.D Thesis, University of Manchester, Manchester, UK, 2010. [Google Scholar]
- Baines, A.S. Resilience of Coastal Structures to Spray Dominated Wave Impacts: An Experimental and Numerical Investigation. Ph.D. Thesis, University of Manchester, Manchester, UK, 2020. [Google Scholar]
- Orszaghova, J.; Taylor, P.H.; Borthwick, A.G.L.; Raby, A.C. Importance of Second-Order Wave Generation for Focused Wave Group Run-up and Overtopping. Coast. Eng. 2014, 94, 63–79. [Google Scholar] [CrossRef]
- Dassanayake, D.T.; Raby, A.; Antonini, A. Efficacy of Analysis Techniques in Assessing Broken Wave Loading on a Cylinder upon a Shoal. Proc. Int. Conf. Offshore Mech. Arct. Eng.-OMAE 2019, 7A-2019, 1–10. [Google Scholar] [CrossRef]
- Massel, S.R. Wavelet Analysis for Processing of Ocean Surface Wave Records. Ocean Eng. 2001, 28, 957–987. [Google Scholar] [CrossRef]
- Baines, A.; Cunningham, L.S.; Rogers, B.D. Simulation of Wave Downfall Pressures on Coastal Protection Structures: Energy Considerations. In Proceedings of the 2017 MACE PGR Conference, Manchester, UK, 6 September 2017; pp. 26–28. [Google Scholar]
- Hattori, M.; Arami, A.; Yui, T. Wave Impact Pressure on Vertical Walls under Breaking Waves of Various Types. Coast. Eng. 1994, 22, 79–114. [Google Scholar] [CrossRef]
- Yan, B.; Luo, M.; Bai, W. An Experimental and Numerical Study of Plunging Wave Impact on a Box-Shape Structure. Mar. Struct. 2019, 66, 272–287. [Google Scholar] [CrossRef]
- De Finis, S.; Lugni, C.; Bellotti, G.; Brocchini, M. Filling Flows by Wave Impacts on Walls: Laboratory and Numerical Experiments. Phys. Fluids 2022, 34. [Google Scholar] [CrossRef]
- Wolters, G.; Müller, G. The Propagation of Wave Impact Induced Pressures into Cracks and Fissures. Eng. Geol. Spec. Publ. 2007, 20, 121–130. [Google Scholar] [CrossRef]
- Horriche, Z.; Etienne, S.; Béguin, C.; Brosset, L. Numerical Study of the Influence of Weber and Reynolds Numbers on Global Wave Shapes before Impact. In Proceedings of the 33rd International Ocean and Polar Engineering Conference, Ottawa, ON, Canada, 18–23 June 2023; pp. 2542–2551. [Google Scholar]
- Bodaghkhani, A.; Colbourne, B.; Muzychka, Y.S. Prediction of Droplet Size and Velocity Distribution for Spray Formation Due to Wave-Body Interactions. Ocean Eng. 2018, 155, 106–114. [Google Scholar] [CrossRef]










| Parameter | Wolters et al. [15] | Bruce et al. [16] | Watson et al. [18] |
|---|---|---|---|
| Scale | 1:4 | 1:100 | 1:25 |
| m | |||
| s | s | s | |
| Toe depth (d) | m | (toe of rubble mound) | |
| Spectrum type | Joint North Sea Wave Project (JONSWAP) | JONSWAP | JONSWAP |
| Model Seawall type | Vertical | Vertical | Rubble mound with crown |
| Probe positions | Face and deck | Face and deck | Face and 4 elevations above deck |
| Peak Downfall Pressures | |||
| Rise time of impact | N/A |
| Make | Model | Type | Range | Output | Accuracy | |
|---|---|---|---|---|---|---|
| Face | GE UNIK 5000 | PMP5074-TBA1-CAH1PA | Relative | Industrial | ||
| Deck | PMP5074-TBA1-CAH1PA | Premium |
| Test Name | T (s) | H (m) | Wave Length (m) | Iribarren Number | Test Name | T (s) | H (m) | Wave Length (m) | Iribarren Number | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | H1 | 1.33 | 0.065 | 2.399 | 0.65 | T4 | H1 | 2.22 | 0.065 | 4.586 | 1.09 |
| H2 | 0.07 | 0.63 | H2 | 0.07 | 1.05 | ||||||
| H3 | 0.075 | 0.61 | H3 | 0.075 | 1.02 | ||||||
| H4 | 0.08 | 0.59 | H4 | 0.08 | 1.02 | ||||||
| H5 | 0.085 | 0.57 | H5 | 0.085 | 0.98 | ||||||
| H6 | 0.09 | 0.56 | H6 | 0.09 | 0.95 | ||||||
| H7 | 0.095 | 0.54 | H7 | 0.095 | 0.93 | ||||||
| T2 | H1 | 1.54 | 0.065 | 2.924 | 0.75 | T5 | H1 | 2.86 | 0.065 | 6.067 | 1.41 |
| H2 | 0.07 | 0.73 | H2 | 0.07 | 1.36 | ||||||
| H3 | 0.075 | 0.70 | H3 | 0.075 | 1.31 | ||||||
| H4 | 0.08 | 0.68 | H4 | 0.08 | 1.27 | ||||||
| H5 | 0.085 | 0.66 | H5 | 0.085 | 1.23 | ||||||
| H6 | 0.09 | 0.64 | H6 | 0.09 | 1.20 | ||||||
| H7 | 0.095 | 0.63 | H7 | 0.095 | 1.16 | ||||||
| T3 | H1 | 1.82 | 0.065 | 3.616 | 0.75 | New wave focused wave groups | |||||
| H2 | 0.07 | 0.72 | FG1 | 1.82 | 0.065 | 3.616 | 0.75 | ||||
| H3 | 0.075 | 0.69 | FG2 | 1.54 | 0.07 | 2.924 | 0.65 | ||||
| H4 | 0.08 | 0.67 | FG3 | 2.86 | 0.075 | 6.067 | 0.90 | ||||
| H5 | 0.085 | 0.65 | |||||||||
| H6 | 0.09 | 0.63 | |||||||||
| H7 | 0.095 | 0.62 | |||||||||
| Test Name | |||
|---|---|---|---|
| H1T2 | 0.065 | 1.5–2.0 | 1.0–3.0 |
| H2T2 | 0.07 | 1.5–4.0 | 1.0–3.5 |
| H3T2 | 0.075 | 2.5–6.0 | 4.0–8.0 |
| H4T2 | 0.08 | 5.0–12.0 | 6.0–14.0 |
| H5T2 | 0.085 | 7.5–20.0 | 5.0–11.0 |
| H6T2 | 0.09 | 10.0–20.0 | 5.0–7.0 |
| H7T2 | 0.095 | 10.0–22.0 | 8.0–18.0 |
| Test | ||||||
|---|---|---|---|---|---|---|
| PF1 | PD12 | PD13 | PD23 | PD32 | PD33 | |
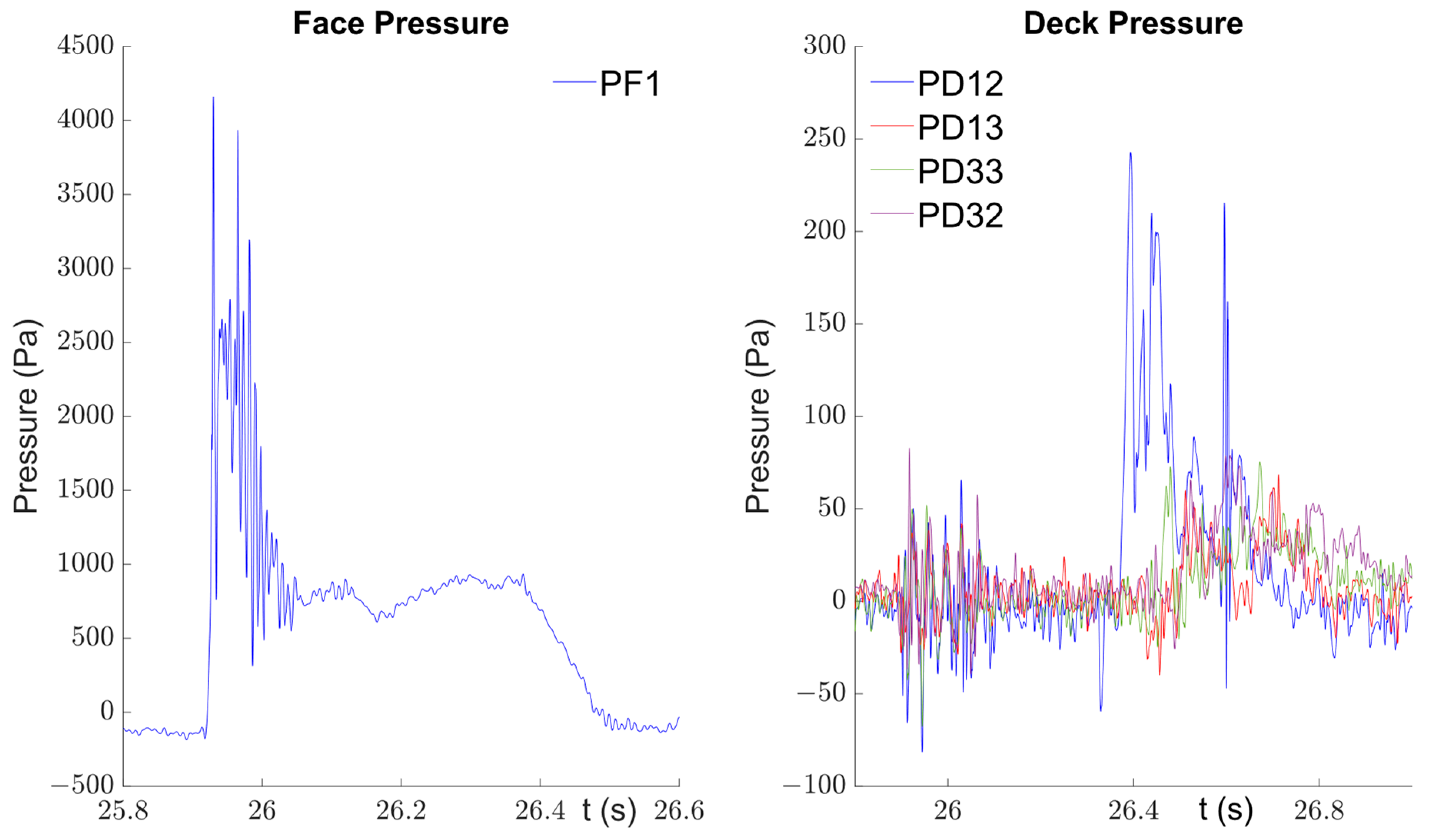
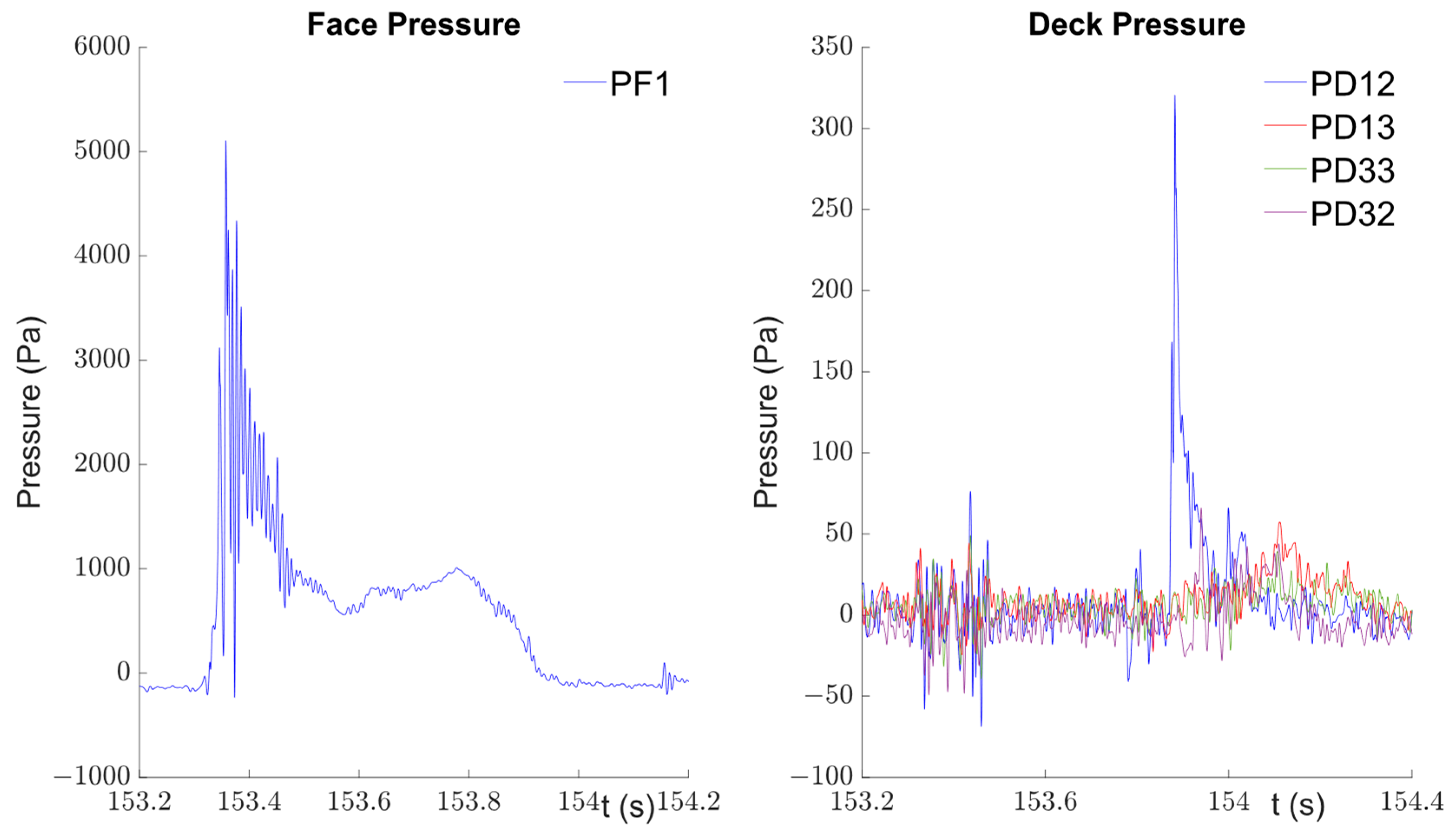
| R1 | 6379.37 | 292.46 | 174.23 | 177.55 | 181.52 | 111.04 |
| R2 | 4915.41 | 232.33 | 66.06 | 60.05 | 399.75 | 55.71 |
| R3 | 7839.17 | 96.92 | 98.04 | 199.50 | 53.99 | 23.11 |
| R4 | 4849.62 | 269.68 | 87.36 | 87.53 | 106.05 | 89.94 |
| R5 | 4070.35 | 408.99 | 131.05 | 176.25 | 99.44 | 57.06 |
| 5610.78 | 260.08 | 111.35 | 140.18 | 168.15 | 67.37 | |
| 1341.07 | 100.71 | 37.81 | 55.51 | 122.82 | 30.39 | |
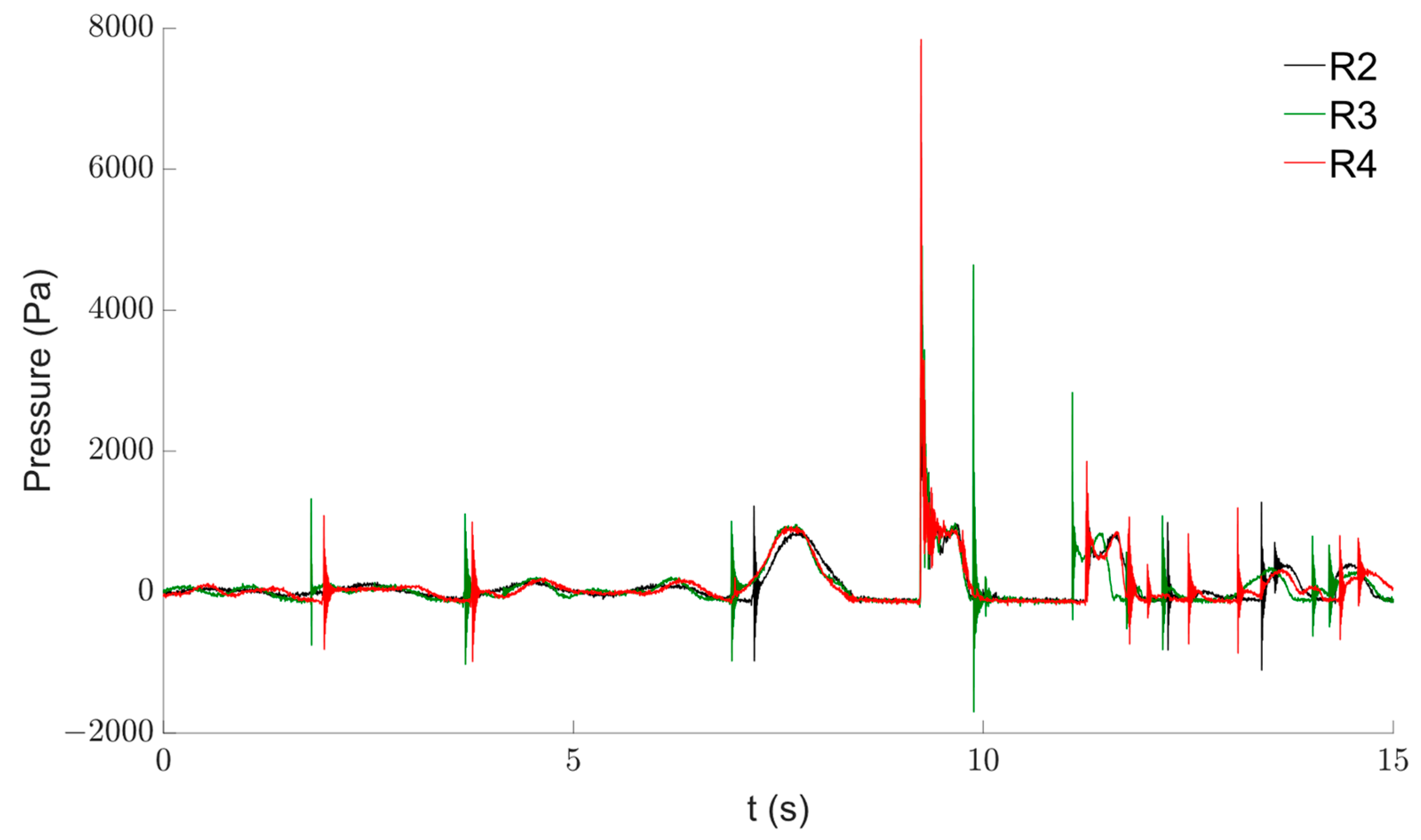
| Test | R2 | R3 | R4 |
|---|---|---|---|
| Dynamic impulse time (ms) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baines, A.; Cunningham, L.S.; Rogers, B.D. Shore-Side Downfall Pressures Due to Waves Impacting a Vertical Seawall: An Experimental Study. J. Mar. Sci. Eng. 2024, 12, 2149. https://doi.org/10.3390/jmse12122149
Baines A, Cunningham LS, Rogers BD. Shore-Side Downfall Pressures Due to Waves Impacting a Vertical Seawall: An Experimental Study. Journal of Marine Science and Engineering. 2024; 12(12):2149. https://doi.org/10.3390/jmse12122149
Chicago/Turabian StyleBaines, Annelie, Lee S. Cunningham, and Benedict D. Rogers. 2024. "Shore-Side Downfall Pressures Due to Waves Impacting a Vertical Seawall: An Experimental Study" Journal of Marine Science and Engineering 12, no. 12: 2149. https://doi.org/10.3390/jmse12122149
APA StyleBaines, A., Cunningham, L. S., & Rogers, B. D. (2024). Shore-Side Downfall Pressures Due to Waves Impacting a Vertical Seawall: An Experimental Study. Journal of Marine Science and Engineering, 12(12), 2149. https://doi.org/10.3390/jmse12122149





