Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode
Abstract
1. Introduction
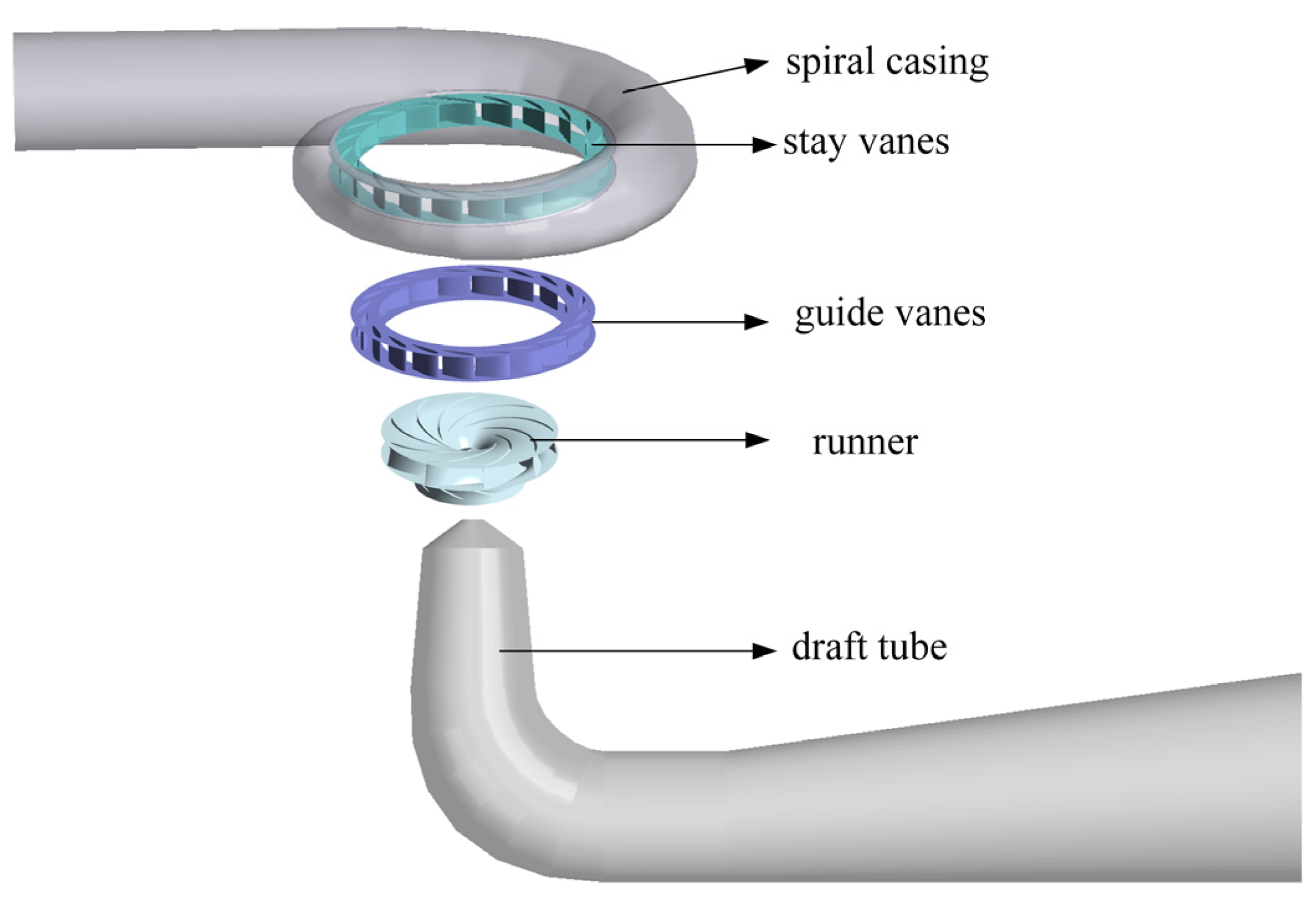
2. Specifications of the Pump Turbine
3. Numerical Simulation
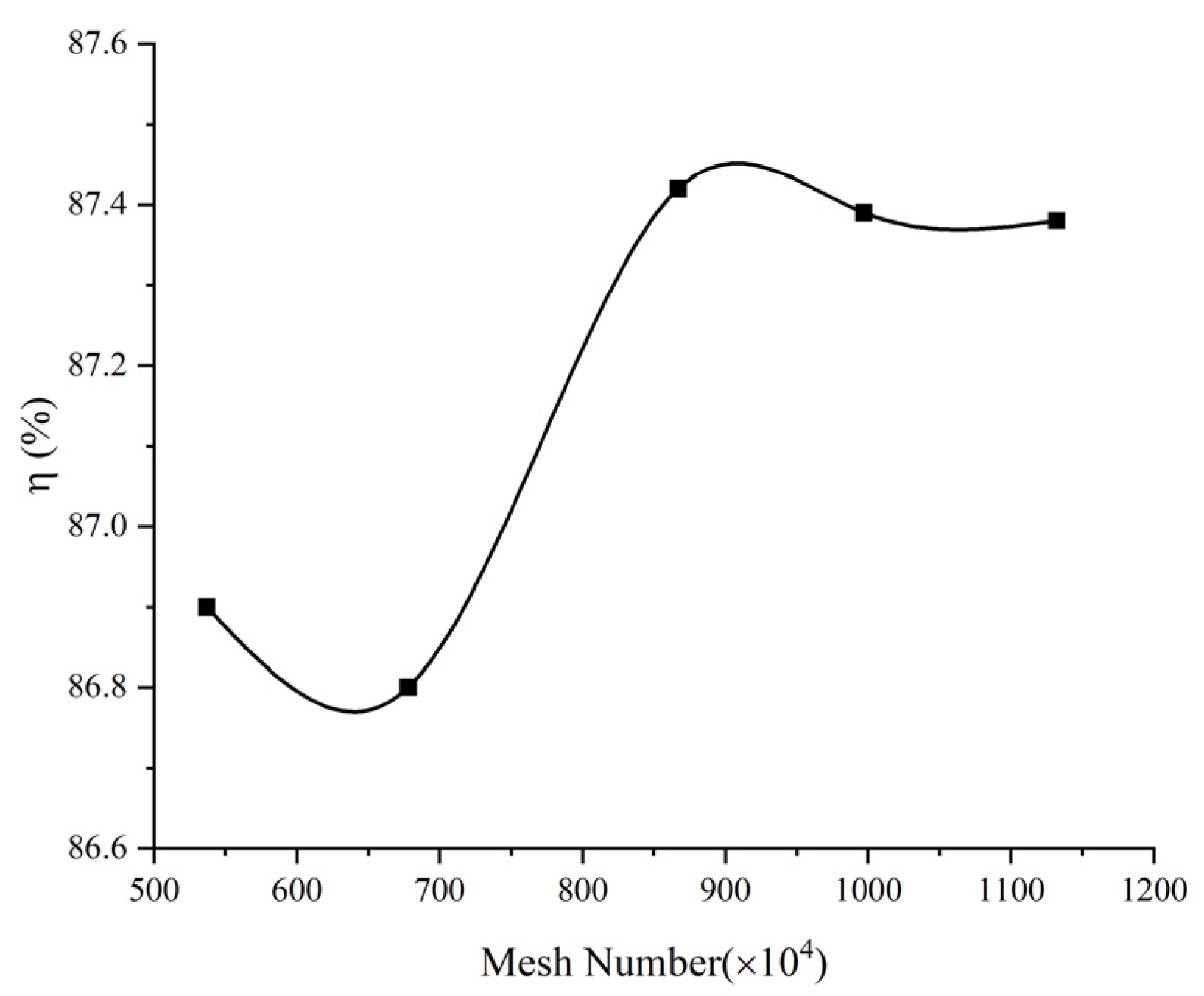
3.1. Mesh Generation and Irrelevance Verification
3.2. Turbulence Model Selection and Boundary Condition Setting
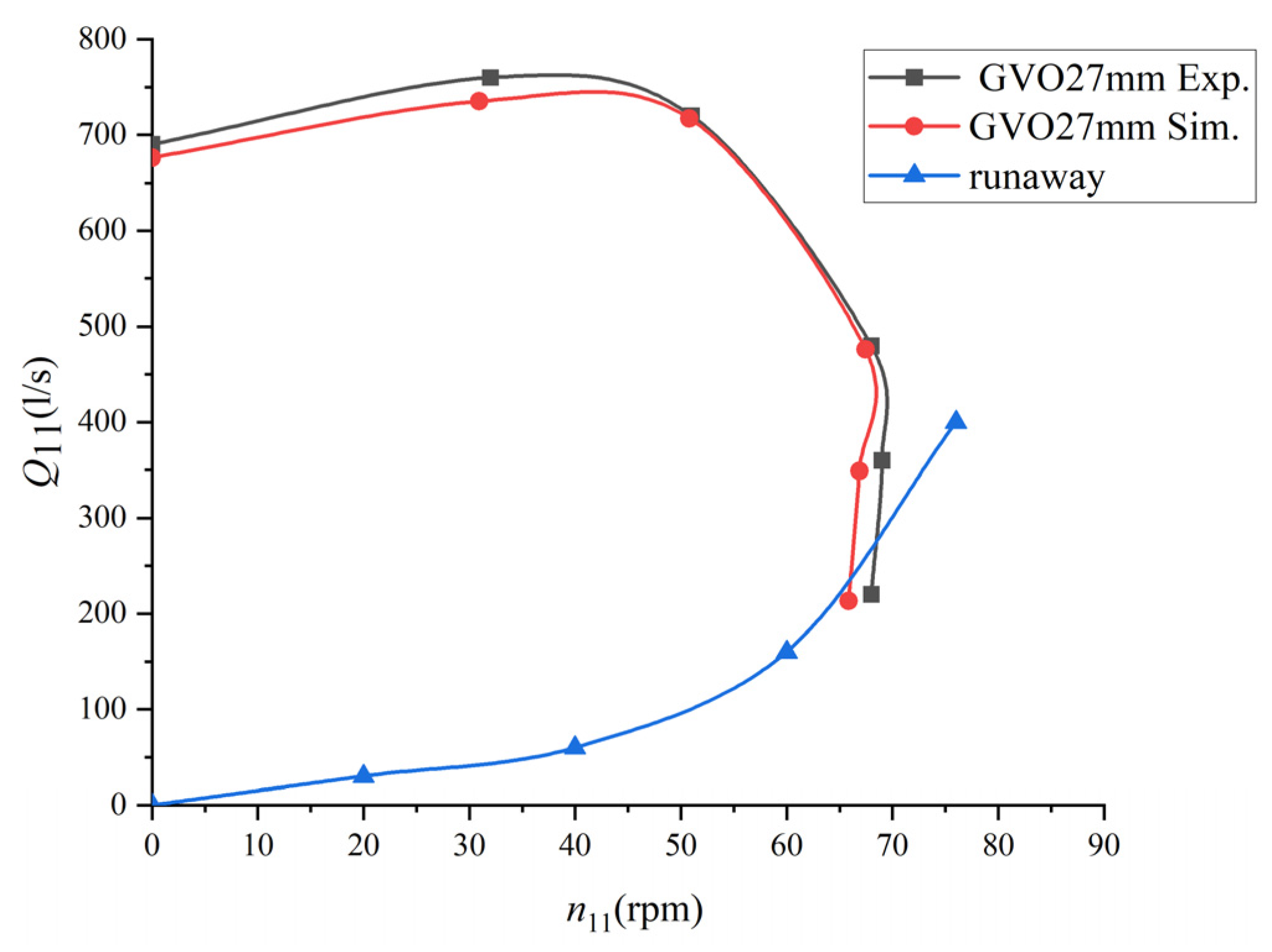
4. Numerical Simulations and Validation
5. Results and Discussion
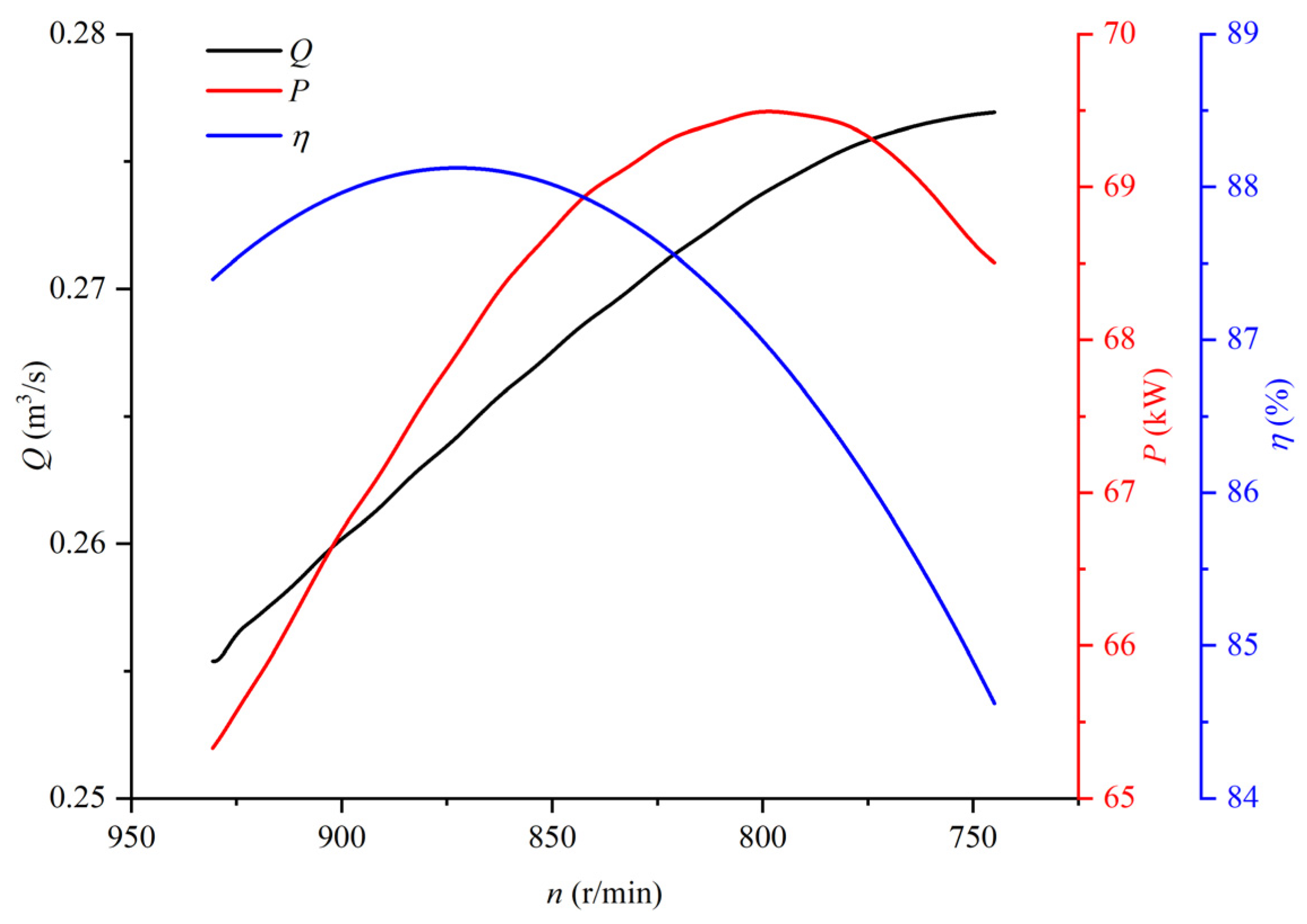
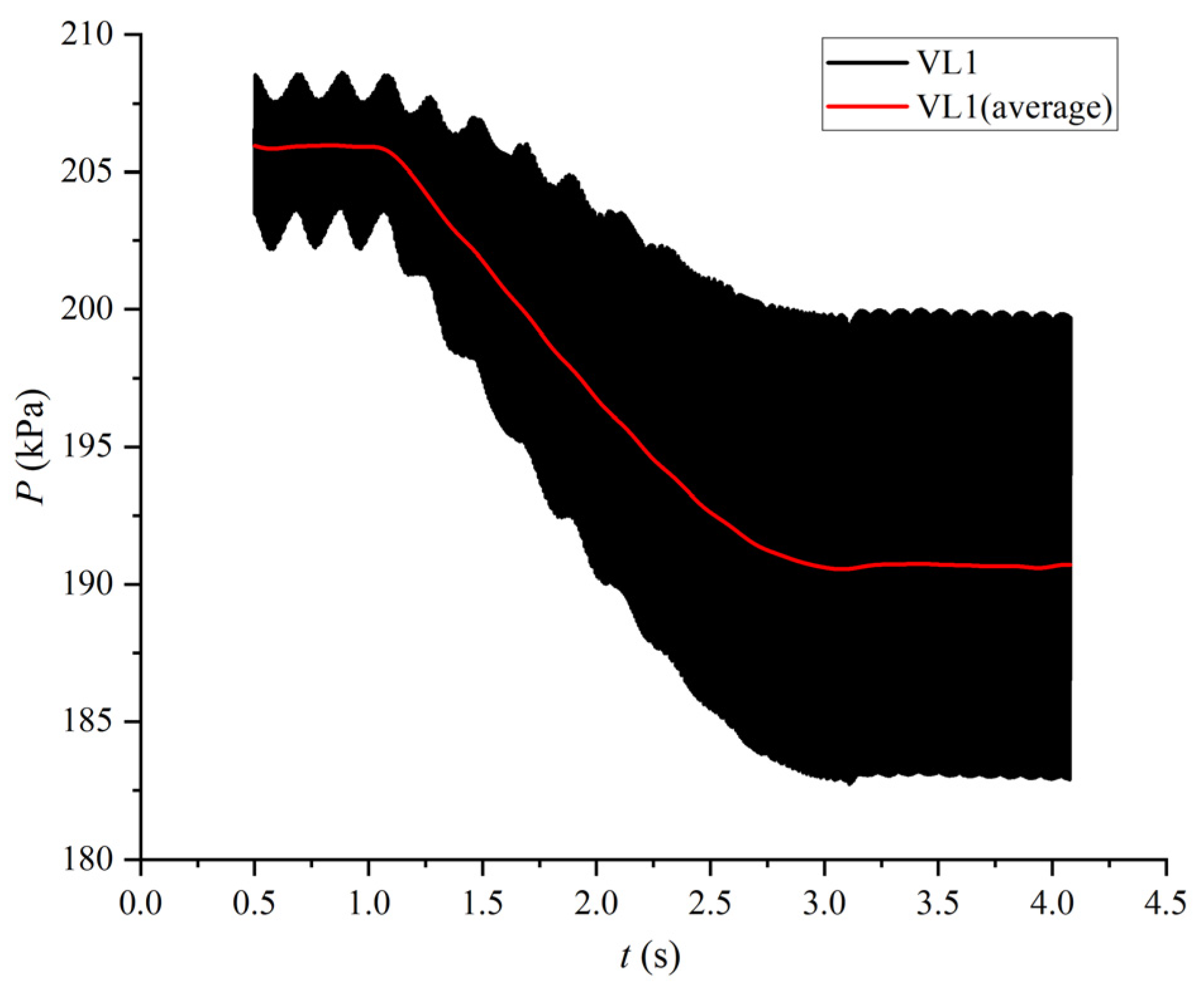
5.1. External Characteristics
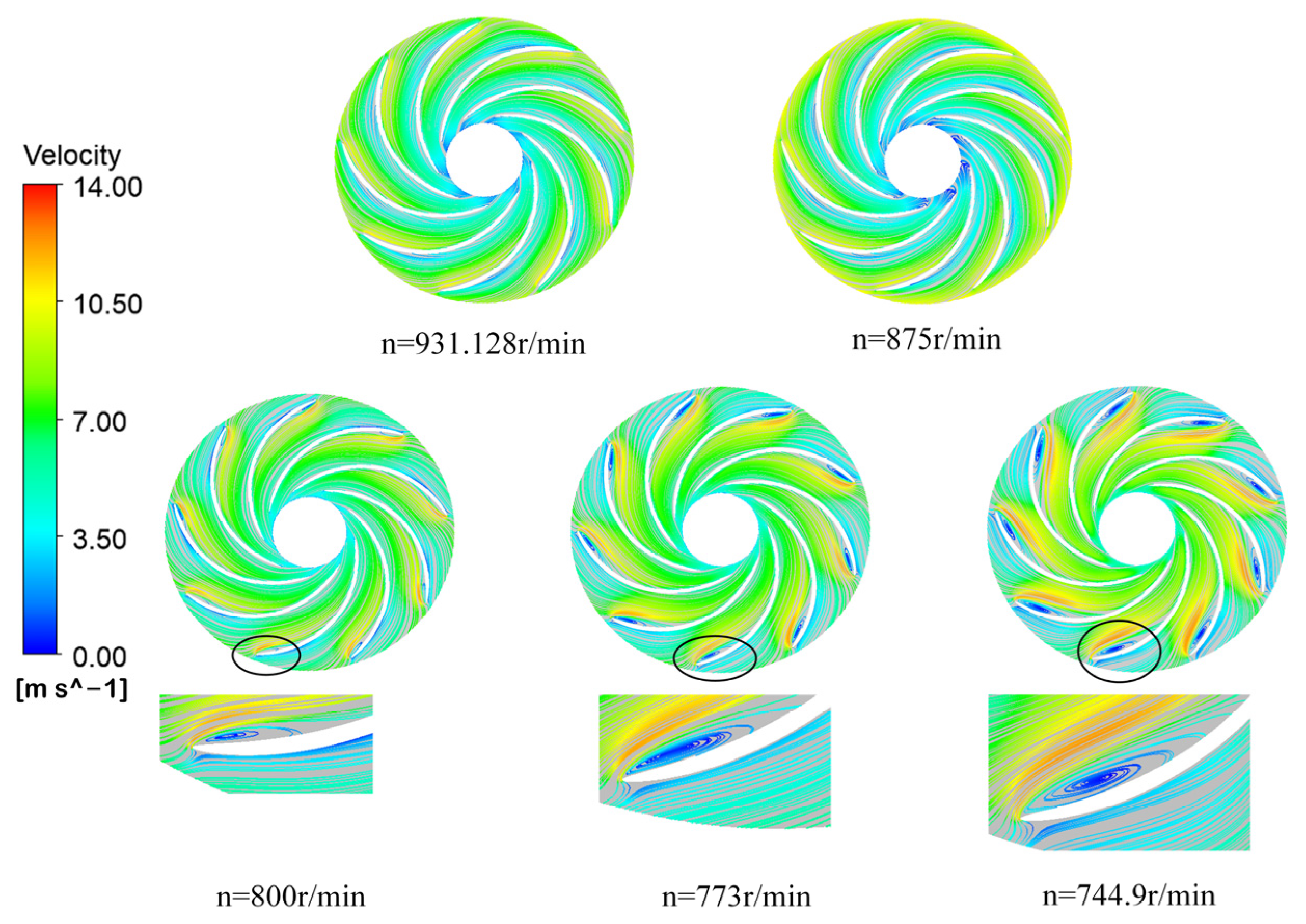
5.2. Internal Flow Characteristics in the Runner
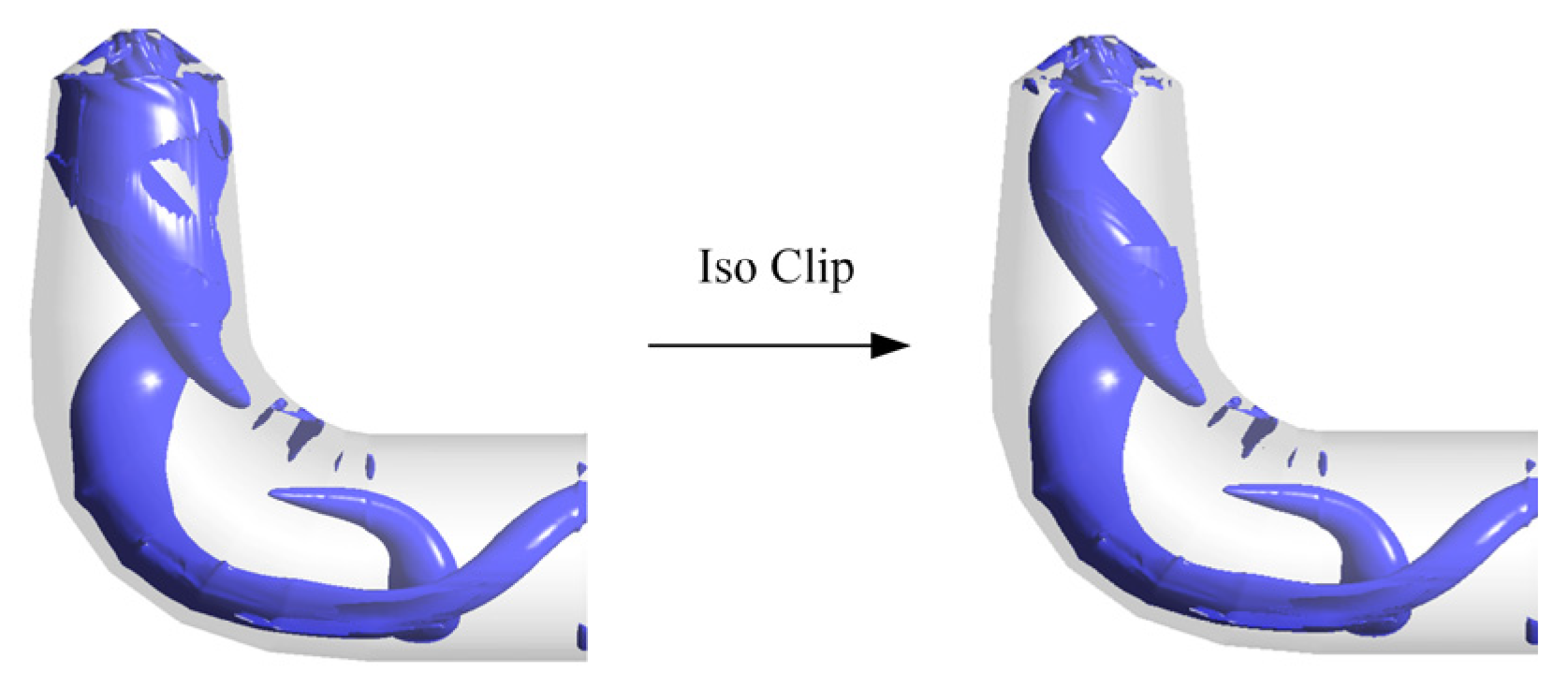
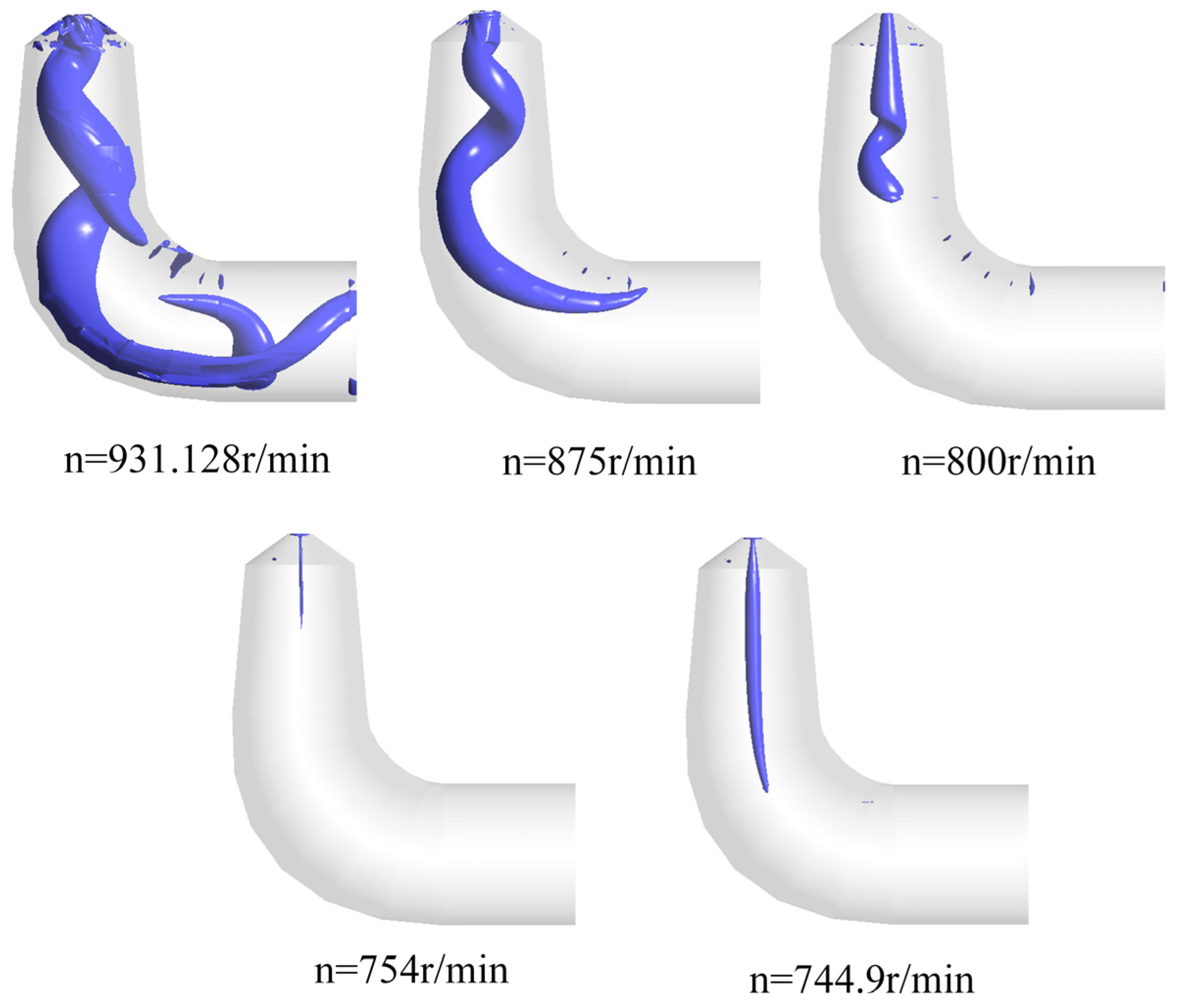
5.3. Evolution of Vortex Structure in the Draft Tube
5.4. Change of Axial Velocity of Draft Tube
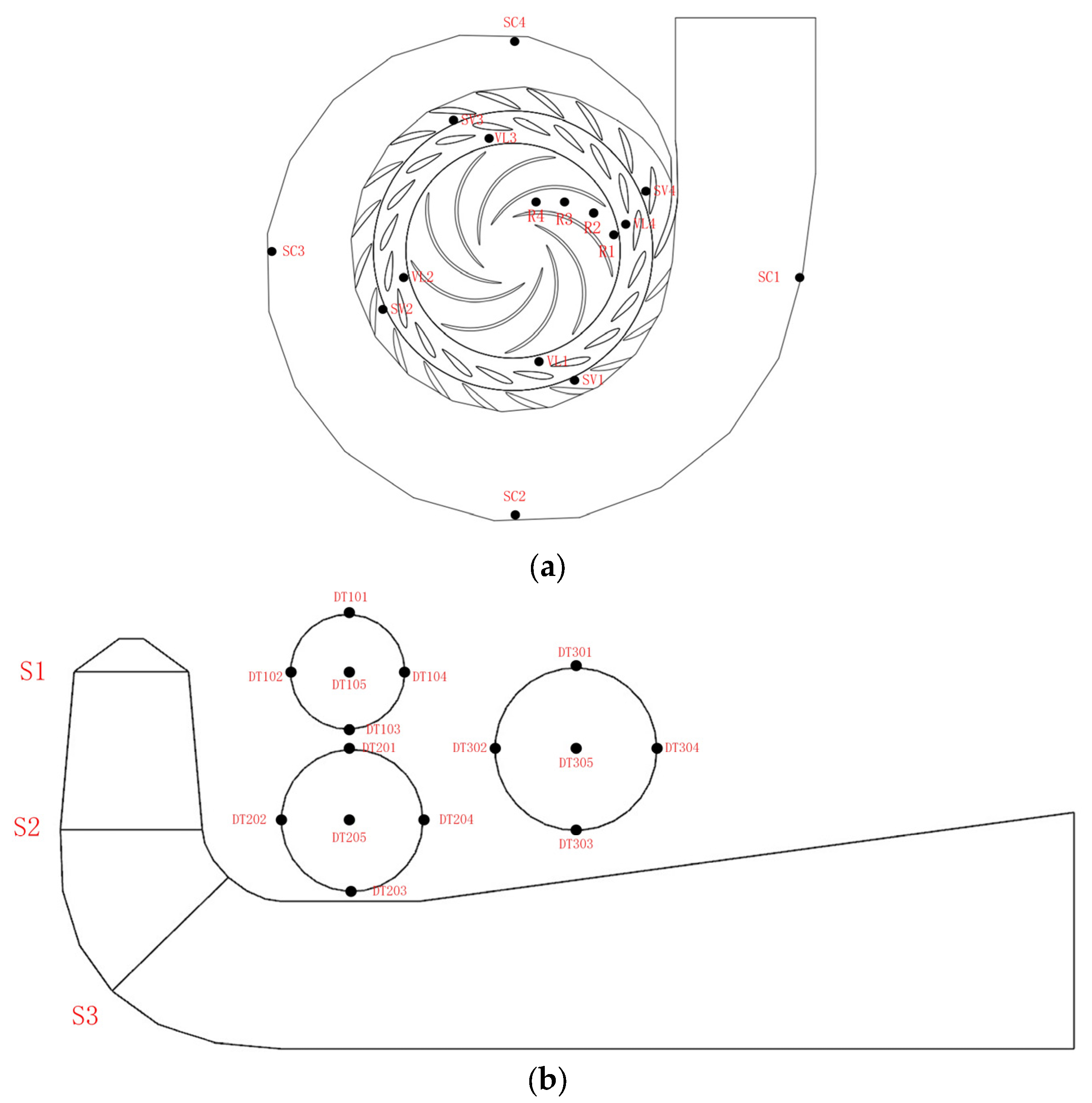
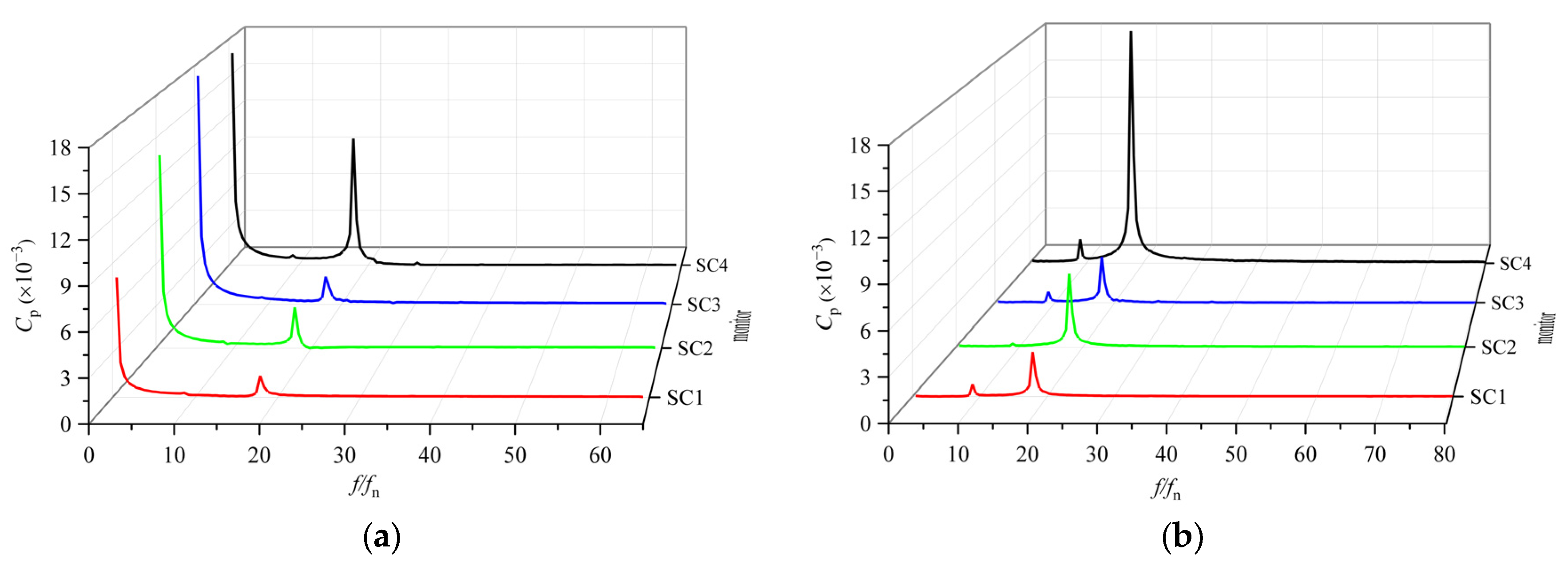
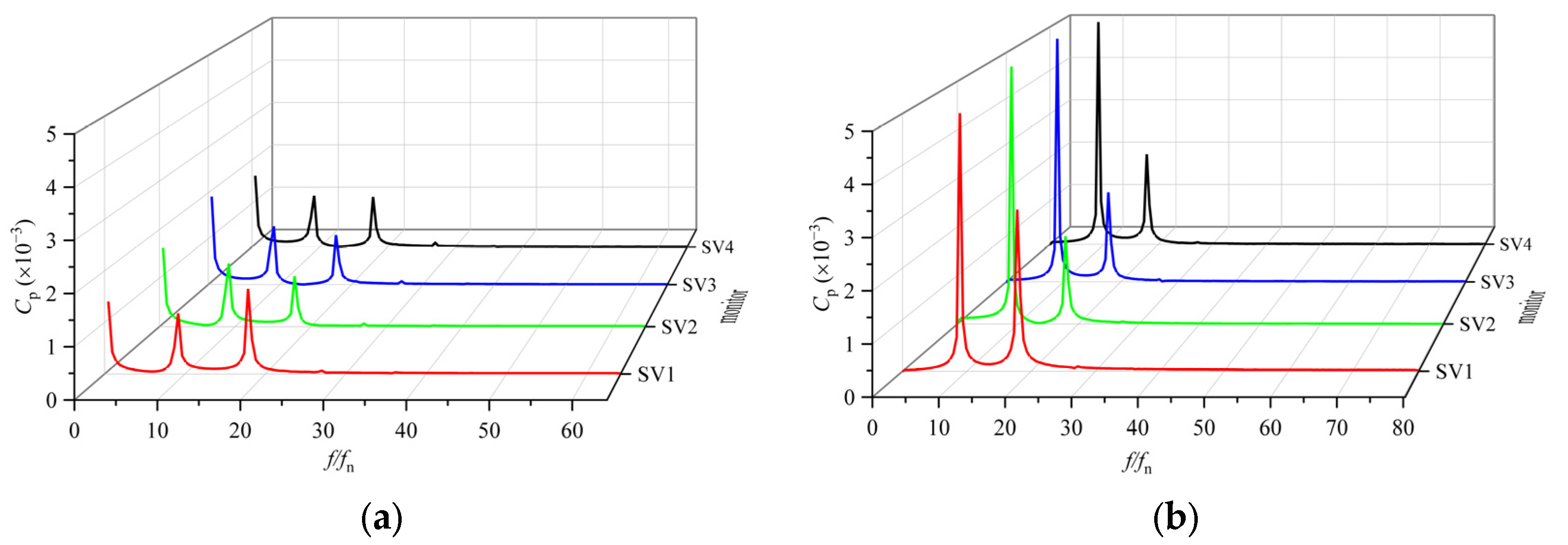
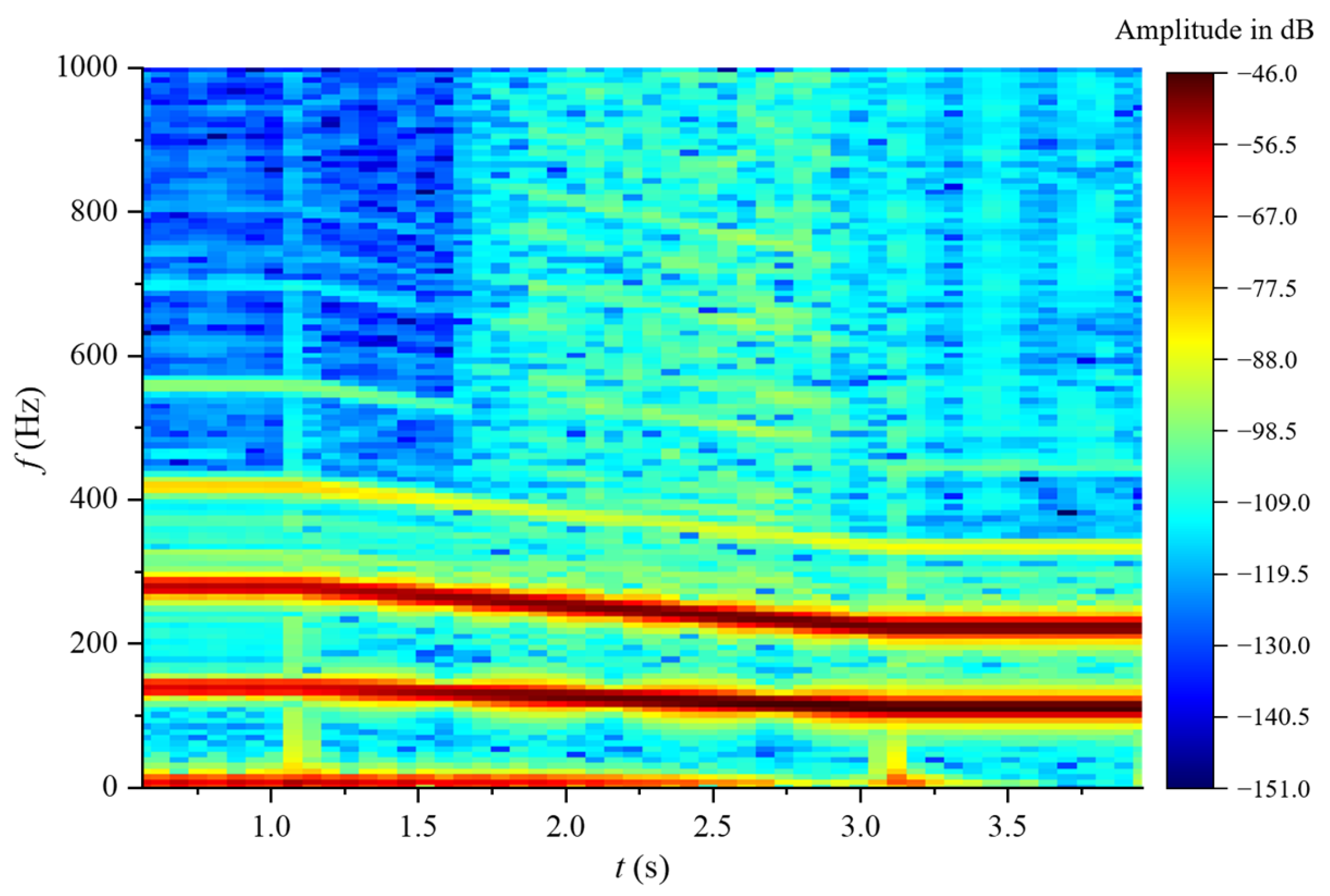
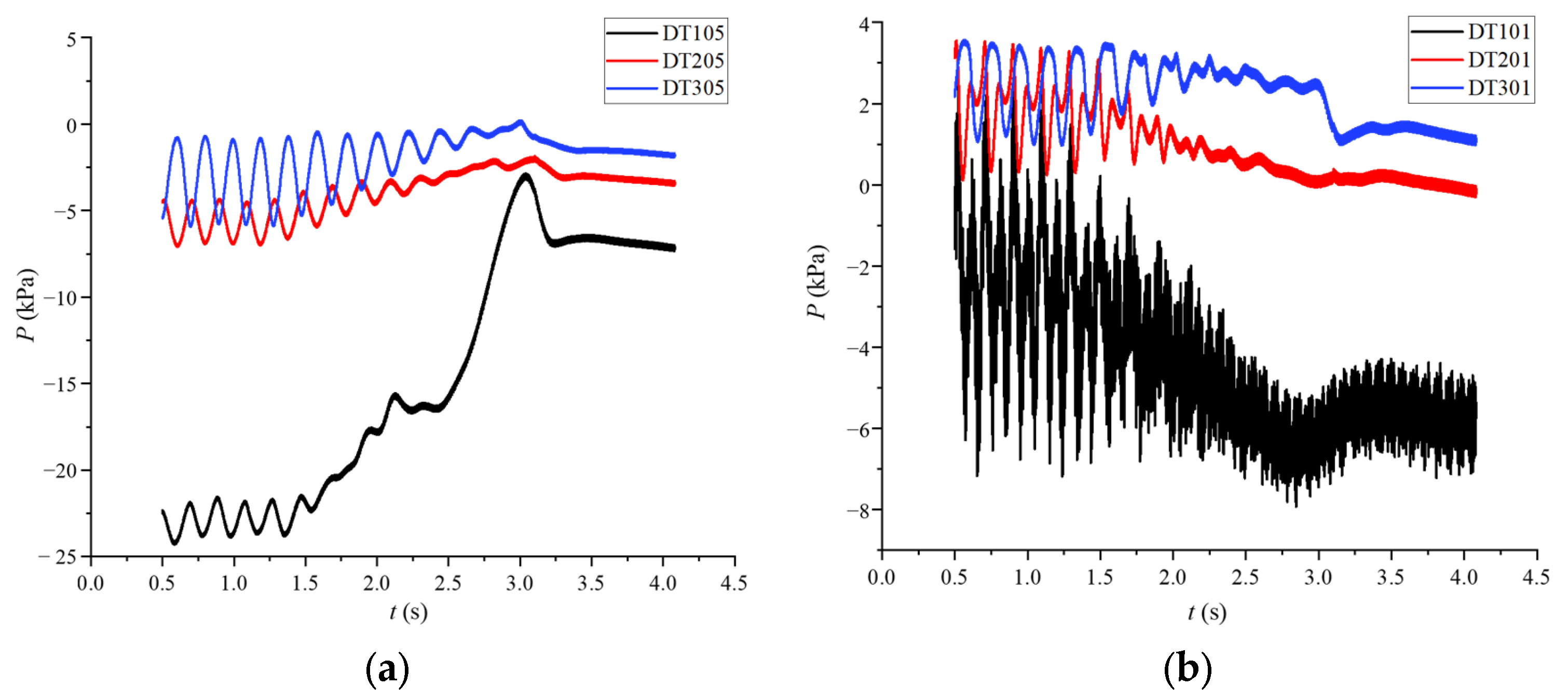
5.5. Pressure Pulsation
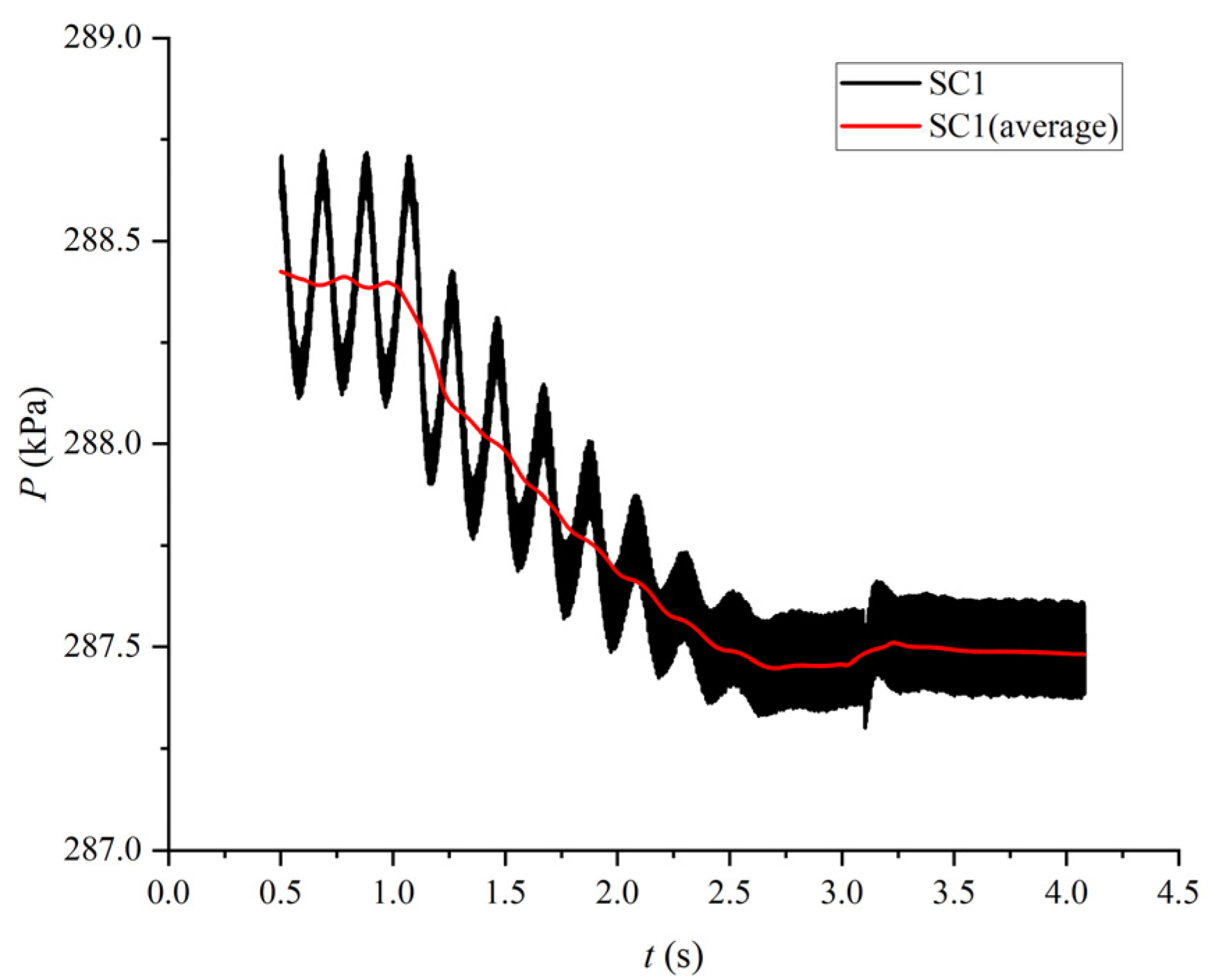
5.5.1. Spiral Casing
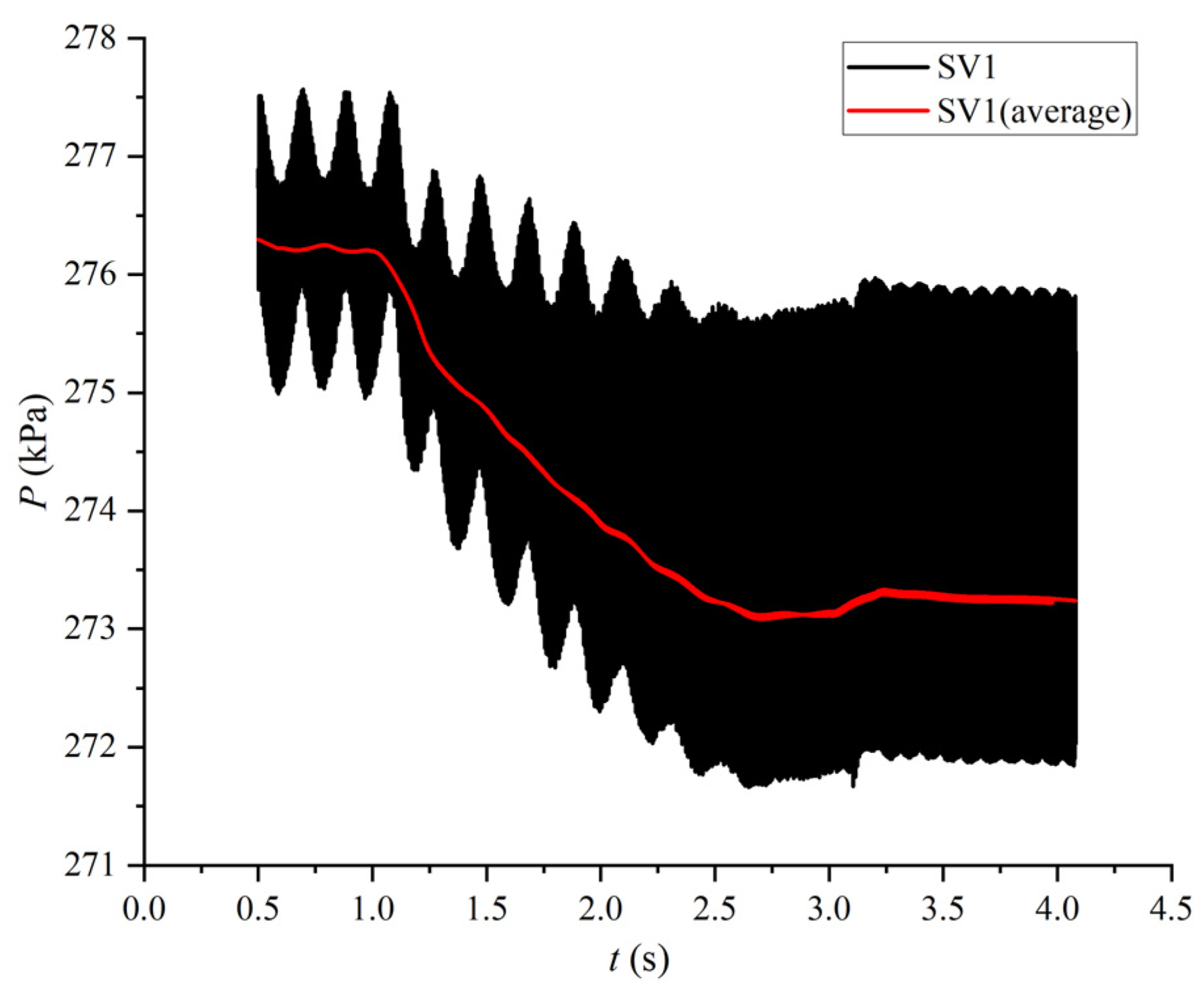
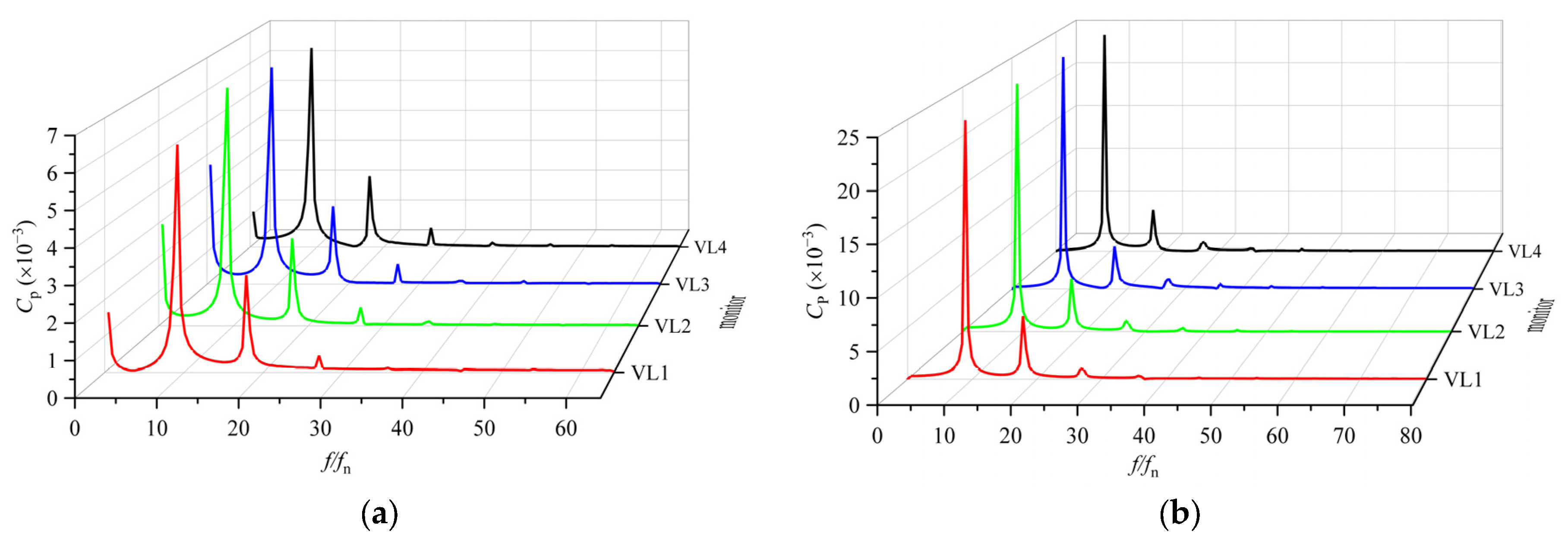
5.5.2. Stay Vanes
5.5.3. Vaneless Region
5.5.4. Runner
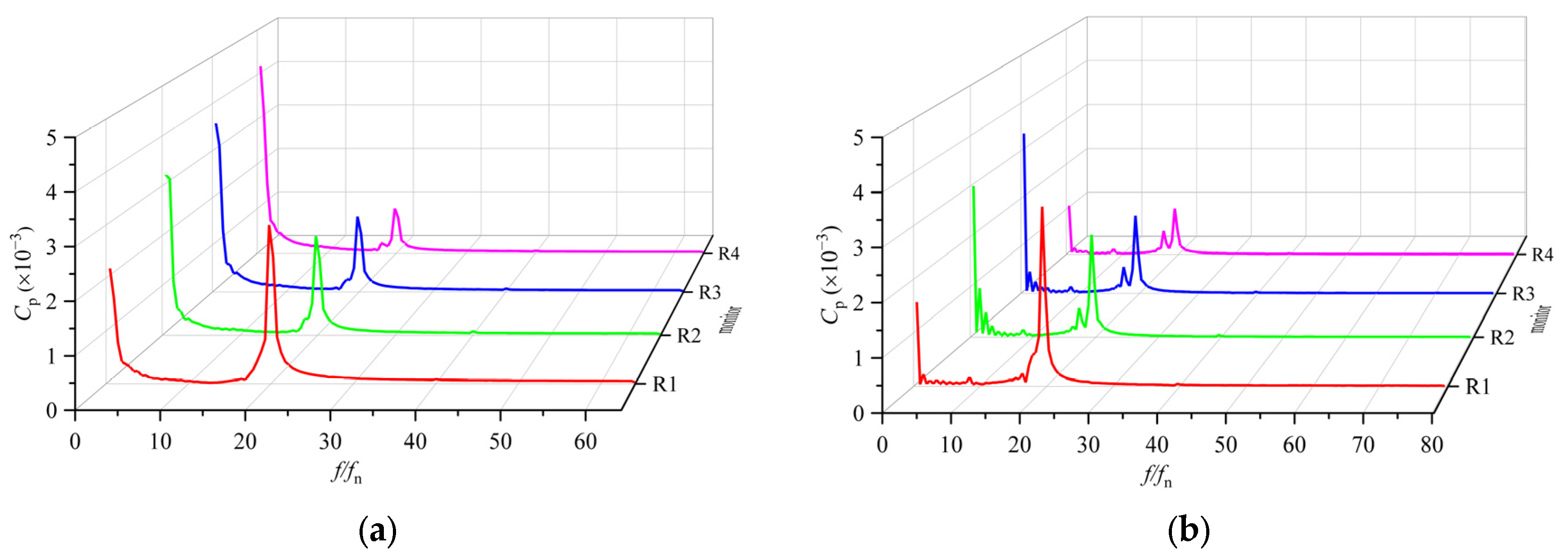
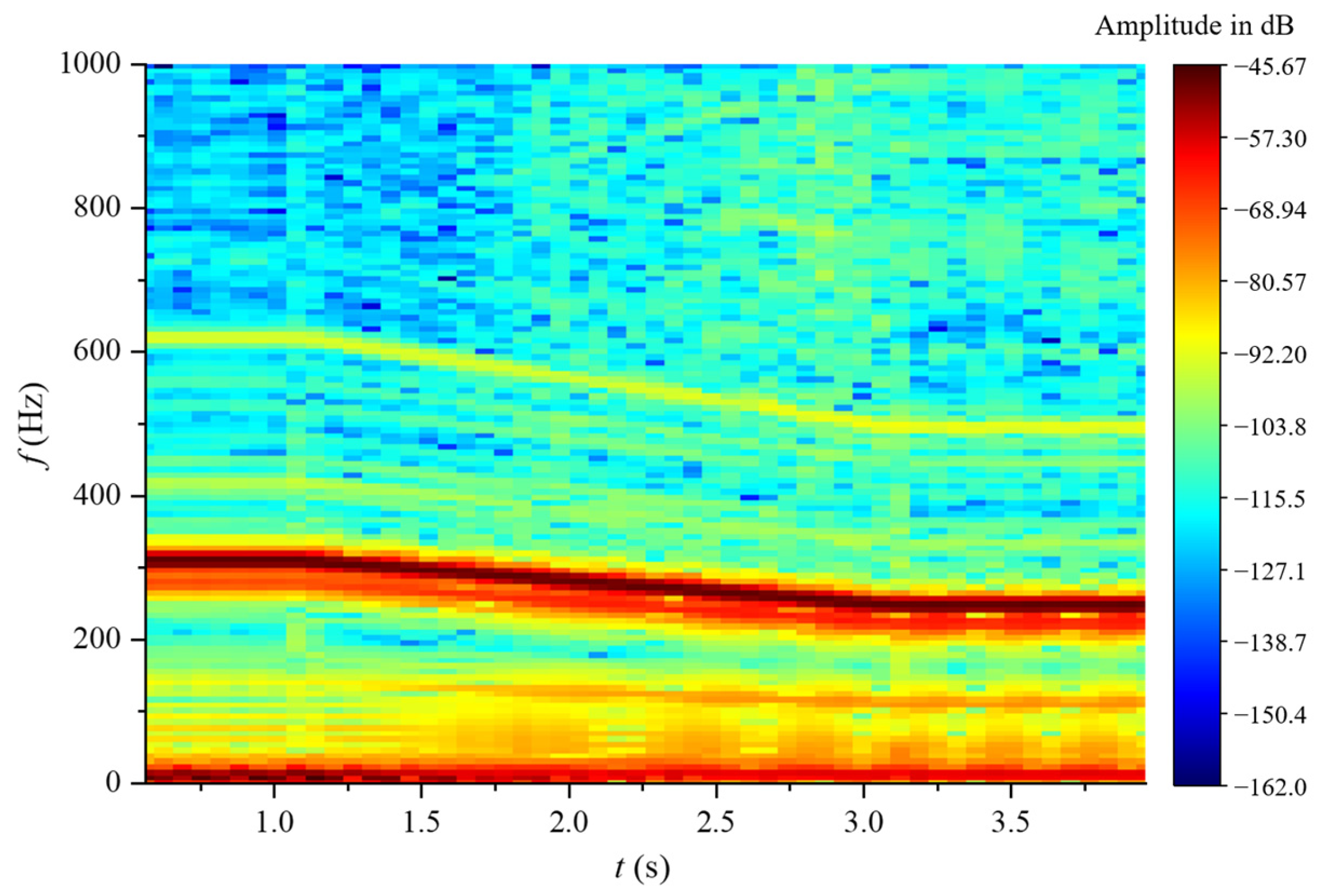
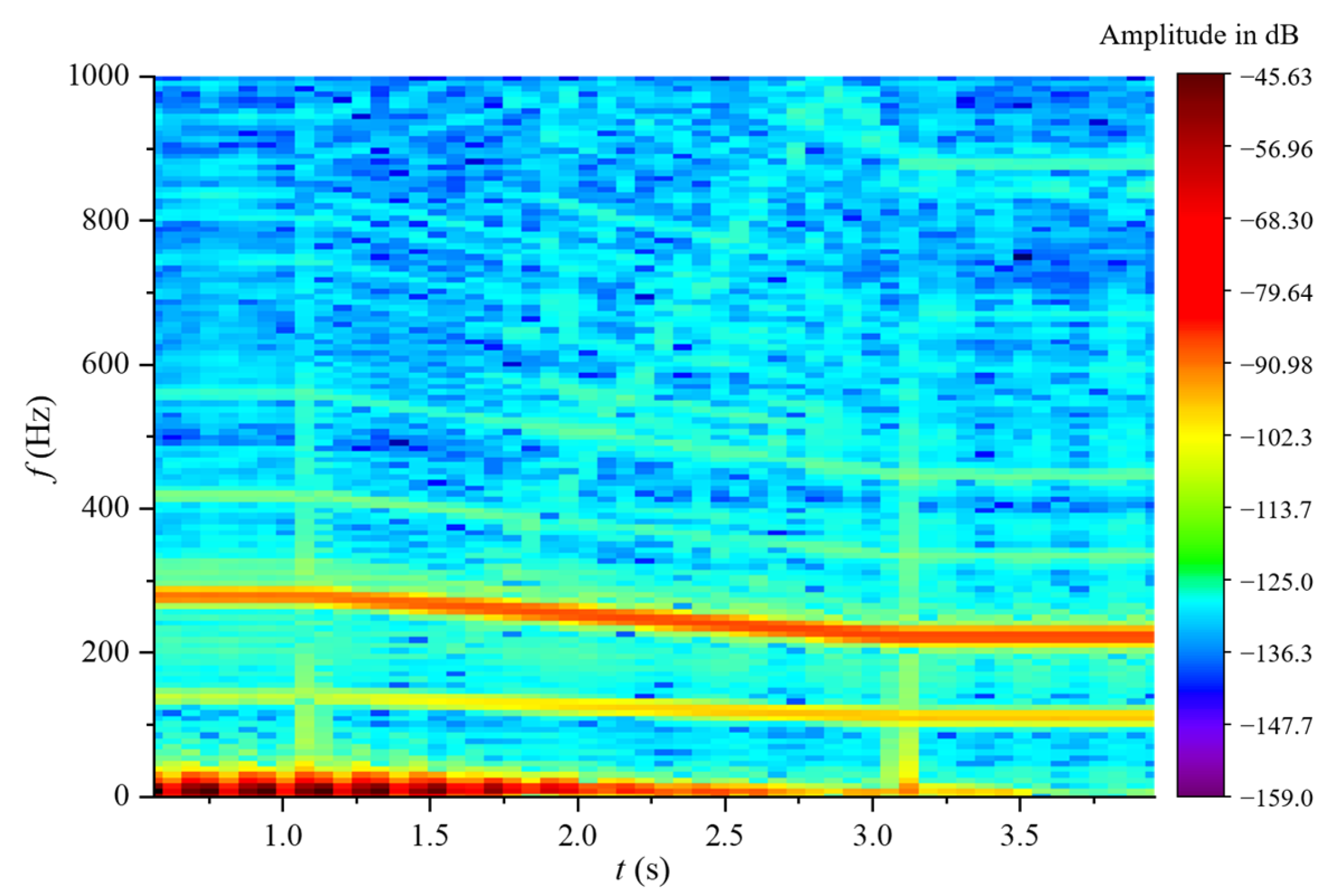
5.5.5. Draft Tubes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Chen, S.; Wu, Y.; Wang, Q.; Liu, X.; Qi, L.; Lu, X.; Gao, L. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Lopes, R.; Barbosa, P.S.F.; Nascimento, A.; de Castro, N.J.; Brandão, R.; Schneider, P.S.; Wada, Y. Existing and new arrangements of pumped-hydro storage plants. Renew. Sustain. Energy Rev. 2020, 129, 109914. [Google Scholar] [CrossRef]
- Javed, S.M.; Ma, T.; Jurasz, J.; Armin, M.Y. Solar and wind power generation systems with pumped hydro storage: Review and future perspectives. Renew. Energy 2020, 148, 176–192. [Google Scholar] [CrossRef]
- Sun, K.; Li, K.-J.; Pan, J.; Liu, Y.; Liu, Y. An optimal combined operation scheme for pumped storage and hybrid wind-photovoltaic complementary power generation system. Appl. Energy 2019, 242, 1155–1163. [Google Scholar] [CrossRef]
- Abdelfattah, A.I.; Shaaban, M.F.; Osman, A.H.; Ali, A. Optimal Management of Seasonal Pumped Hydro Storage System for Peak Shaving. Sustainability 2023, 15, 11973. [Google Scholar] [CrossRef]
- Suh, J.-W.; Kim, S.-J.; Kim, J.-H.; Joo, W.-G.; Park, J.; Choi, Y.-S. Effect of interface condition on the hydraulic characteristics of a pump-turbine at various guide vane opening conditions in pump mode. Renew. Energy 2020, 154, 986–1004. [Google Scholar] [CrossRef]
- Yu, A.; Wang, Y.; Tang, Q.; Lv, R.; Yang, Z. Investigation of the vortex evolution and hydraulic excitation in a pump-turbine operating at different conditions. Renew. Energy 2021, 171, 462–478. [Google Scholar] [CrossRef]
- Shi, G.; Hao, Z.; Peng, X.; Wen, H.; Lv, W.; Fu, J. Analysis of vortex characteristics in the S-shaped region of a reversible Pump-Turbine with different guide vane openings based on Omega vortex identification method. J. Energy Storage 2024, 84, 110921. [Google Scholar] [CrossRef]
- Yao, W.; Deng, C.; Li, D.; Chen, M.; Peng, P.; Zhang, H.; Yao, W.; Deng, C.; Li, D.; Chen, M.; et al. Optimal Sizing of Seawater Pumped Storage Plant with Variable-Speed Units Considering Offshore Wind Power Accommodation. Sustainability 2019, 11, 1939. [Google Scholar] [CrossRef]
- Iliev, I.; Trivedi, C.; Dahlhaug, O.G. Variable-speed operation of Francis turbines: A review of the perspectives and challenges. Renew. Sustain. Energy Rev. 2019, 103, 109–121. [Google Scholar] [CrossRef]
- Bidgoli, M.A.; Yang, W.J.; Ahmadian, A. DFIM versus synchronous machine for variable speed pumped storage hydropower plants: A comparative evaluation of technical performance. Renew. Energy 2020, 159, 72–86. [Google Scholar] [CrossRef]
- Gao, C.; Yu, X.; Nan, H.; Men, C.; Fu, J. A Fast High-Precision Model of the Doubly-Fed Pumped Storage Unit. J. Electr. Eng. Technol. 2021, 16, 797–808. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Venugopal, G.; Ekanayake, J.B.; Tiong, S.K. Variable speed pumped hydro storage: A review of converters, controls and energy management strategies. Renew. Sustain. Energy Rev. 2021, 135, 11156. [Google Scholar] [CrossRef]
- Zhu, K.K.; Ruan, L. Self-starting control strategy of variable speed pumped storage unit based on adaptive full order state observer. Meas. Control 2023, 56, 630–637. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, P.; Morabito, A.; Feng, W.; Mahmud, A.; Chen, D.; Hendrick, P. Dynamic analysis of variable-speed pumped storage plants for mitigating effects of excess wind power generation. Int. J. Electr. Power Energy Syst. 2022, 135, 107453. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, W.; Zhao, Z.; Han, W.; Li, Y.; Yang, J. Dynamic modeling and favorable speed command of variable-speed pumped-storage unit during power regulation. Renew. Energy 2023, 206, 769–783. [Google Scholar] [CrossRef]
- Heckelsmueller, G.P. Application of variable speed operation on Francis turbines. Ing. Investig. 2015, 35, 12–16. [Google Scholar] [CrossRef]
- Bortoni, E.; Souza, Z.d.; Viana, A.; Villa-Nova, H.; Rezek, Â.; Pinto, L.; Siniscalchi, R.; Bragança, R.; Bernardes, J., Jr. The Benefits of Variable Speed Operation in Hydropower Plants Driven by Francis Turbines. Energies 2019, 12, 3719. [Google Scholar] [CrossRef]
- Yu, Z.-F.; Wang, W.-Q.; Yan, Y.; Wang, H.-Y.; Wu, W.-L. Evaluating energy-efficiency improvement of variable-speed operation with the help of entropy: A case study of low-head Francis turbine. Sustain. Energy Technol. Assess. 2022, 53, 102468. [Google Scholar] [CrossRef]
- Feng, C.; Li, C.; Chang, L.; Ding, T.; Mai, Z. Advantage analysis of variable-speed pumped storage units in renewable energy power grid: Mechanism of avoiding S-shaped region. Int. J. Electr. Power Energy Syst. 2020, 120, 105976. [Google Scholar] [CrossRef]
- Deng, W.; Xu, L.; Li, Z.; Tang, W.; Wang, X.; Shang, L.; Liu, D.; Liu, X. Stability Analysis of Vaneless Space in High-Head Pump-Turbine under Turbine Mode: Computational Fluid Dynamics Simulation and Particle Imaging Velocimetry Measurement. Machines 2022, 10, 143. [Google Scholar] [CrossRef]
- Lai, X.; Chen, X.; Liang, Q.; Ye, D.; Gou, Q.; Wang, R.; Yan, Y. Experimental and numerical investigation of vortex flows and pressure fluctuations in a high-head pump-turbine. Renew. Energy 2023, 211, 236–247. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, L.; Liang, Q.; Guan, Z.; Liu, D.; Wang, Z.; Kang, W. A method of evaluating the vortex rope strength in draft tube of Francis turbine. Renew. Energy 2020, 152, 770–780. [Google Scholar] [CrossRef]
- Zhu, D.; Yan, W.; Guang, W.; Wang, Z.; Tao, R. Influence of Guide Vane Opening on the Runaway Stability of a Pump-Turbine Used for Hydropower and Ocean Power. J. Mar. Sci. Eng. 2023, 11, 1218. [Google Scholar] [CrossRef]
- Trivedi, C.; Agnalt, E.; Dahlhaug, O.G. Experimental study of a Francis turbine under variable-speed and discharge conditions. Renew. Energy 2018, 119, 447–458. [Google Scholar] [CrossRef]
- Trivedi, C.; Agnalt, E.; Dahlhaug, O.G. Investigations of unsteady pressure loading in a Francis turbine during variable-speed operation. Renew. Energy 2017, 113, 397–410. [Google Scholar] [CrossRef]
- Rode, B.R.; Kumar, A. Rotor-stator interaction investigations in variable speed reversible pump-turbine at higher head. Phys. Fluids 2024, 36, 035122. [Google Scholar] [CrossRef]
- Shang, L.; Cao, J.; Wang, L.; Yu, S.; Ding, S.; Wei, Z.; Wang, Z.; Liu, X. Analysis of Flow and Runner Dynamic Response Characteristics under Pump Conditions of Variable-Speed Pump Turbine. J. Mar. Sci. Eng. 2023, 11, 1493. [Google Scholar] [CrossRef]
- Li, Y.; Yang, W.; Huang, Y.; Ma, W.; Zhao, Z.; Yang, J.; Cheng, Y.; Qian, Z.; Yang, J. Reduction of Pressure Pulsation for Pump-Turbine by Variable Speed Operation. J. Energy Resour. Technol.-Trans. ASME 2023, 145, 081301. [Google Scholar] [CrossRef]
- Trivedi, C.; Iliev, I.; Dahlhaug, O.G.; Markov, Z.; Engstrom, F.; Lysaker, H. Investigation of a Francis turbine during speed variation: Inception of cavitation. Renew. Energy 2020, 166, 147–162. [Google Scholar] [CrossRef]
- Lv, Y.; Li, S.G.; Wang, Z.W.; Zhou, L.J. Study on pump mode cavitation characteristic of variable speed pump turbine. Phys. Fluids 2023, 35, 065111. [Google Scholar]









| Parameters | Symbols | Values |
|---|---|---|
| Diameter of impeller inlet | D1 | 470 mm |
| Diameter of impeller outlet | D2 | 300 mm |
| Number of stay vanes | ZS | 20 |
| Number of guide vanes | Zg | 20 |
| Number of impeller blades | Zr | 9 |
| Guide vane opening | a | 19 mm |
| Head | H | 30 m |
| Rated speed | n1 | 931.128 r/min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Li, B.; Xiao, Y.; Tang, M.; Yang, X. Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode. J. Mar. Sci. Eng. 2024, 12, 2243. https://doi.org/10.3390/jmse12122243
Shi G, Li B, Xiao Y, Tang M, Yang X. Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode. Journal of Marine Science and Engineering. 2024; 12(12):2243. https://doi.org/10.3390/jmse12122243
Chicago/Turabian StyleShi, Guangtai, Binyan Li, Yexiang Xiao, Manqi Tang, and Xi Yang. 2024. "Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode" Journal of Marine Science and Engineering 12, no. 12: 2243. https://doi.org/10.3390/jmse12122243
APA StyleShi, G., Li, B., Xiao, Y., Tang, M., & Yang, X. (2024). Effect of Speed Linear Decrease on Internal Flow Characteristics and Pressure Pulsations of Variable-Speed Pump Turbine in Turbine Mode. Journal of Marine Science and Engineering, 12(12), 2243. https://doi.org/10.3390/jmse12122243







