Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage
Abstract
:1. Introduction
2. Numerical Method
- The test environment and experimental setup are close to the real working environment of a gravity cage under uniform flow.
- The cage used in the test is full-scale for offshore aquaculture.
- The authors provided enough information to build an approximate numerical model. The numerical model and the physical model are shown in Figure 1.
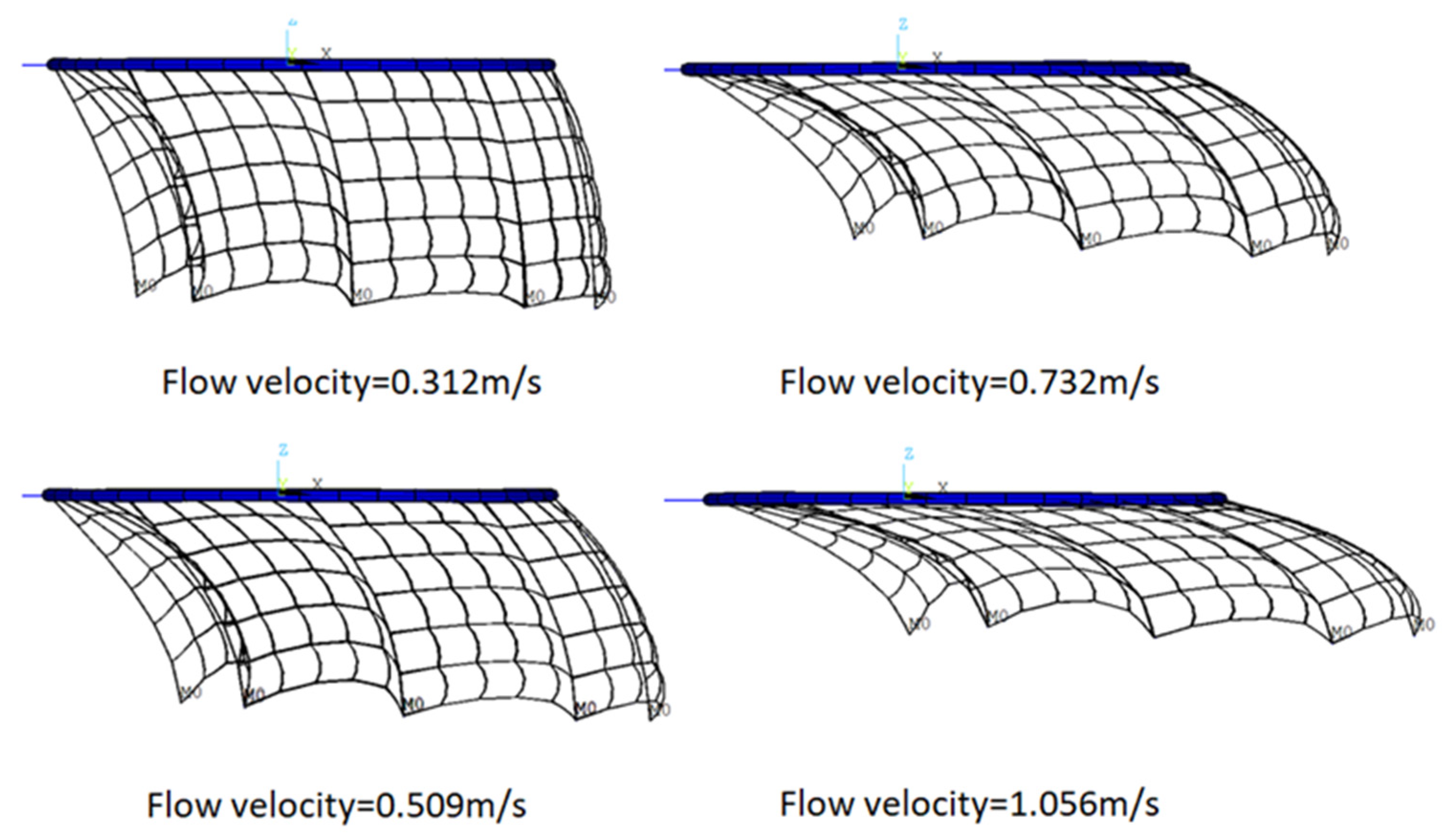
3. Numerical Results and Comparison with Test Results
3.1. Numerical Model without Considering Flow Velocity Reduction
3.2. Numerical Model Subjected to Waves of Different Heights
4. Assessment of Model Uncertainty
4.1. Velocity-Independent Model Error
4.2. Velocity-Dependent Model Error
4.3. Results
5. Discussion
5.1. Comparison between the Results in This Work and Published Results
5.2. Increasing the Quantity of Experiment and Field Test Results
5.3. Improvement of the Experimental Technology
5.4. Improvement of the Numerical Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FAO. The State of World Fisheries and Aquaculture 2020; Fisheries and Aquaculture Department, Food and Agriculture Organization of the United Nations: Rome, Italy; Publishing Policy and Support Branch, Office of Knowledge Exchange, Research and Extension: Rome, Italy, 2020. [Google Scholar]
- Holmer, M. Environmental issues of fish farming in offshore waters: Perspectives, concerns and research needs. Aquac. Environ. Interact. 2010, 1, 57–70. [Google Scholar] [CrossRef]
- Lader, P.; Dempster, T.; Fredheim, A.; Jensen, F. Current induced net deformations in full-scale cages for Atlantic salmon (Salmo salar). Aquac. Eng. 2008, 38, 52–65. [Google Scholar] [CrossRef]
- Fu, S.; Xu, Y.; Hu, K.; Zhang, Y. Experimental investigation on hydrodynamics of floating cylinder in oscillatory and steady flows by forced oscillation test. Mar. Struct. 2013, 34, 41–55. [Google Scholar] [CrossRef]
- Moe-Føre, H.; Lader, P.; Lien, E.; Hopperstad, O. Structural response of high solidity net cage models in uniform flow. J. Fluids Struct. 2016, 65, 180–195. [Google Scholar] [CrossRef]
- Gansel, L.; Oppedal, F.; Birkevold, J.; Tuene, S. Drag forces and deformation of aquaculture cages-Full-scale towing tests in the field. Aquac. Eng. 2018, 81, 46–56. [Google Scholar] [CrossRef]
- Hou, H.; Dong, G.; Xu, T. Assessment of fatigue damage of mooring line for fish cage under wave groups. Ocean. Eng. 2020, 210, 107568. [Google Scholar] [CrossRef]
- Liu, Z.; Mohapatra, S.; Guedes Soares, C. Finite Element Analysis of the Effect of Currents on the Dynamics of a Moored Flexible Cylindrical Net Cage. J. Mar. Sci. Eng. 2021, 9, 159. [Google Scholar] [CrossRef]
- Liu, Z.; Guedes Soares, C. Experimental Study of the Behaviour of a Circular Gravity Cage in Linear Waves. Aquac. Eng. 2022, 99, 102291. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H.; Guedes Soares, C. Experimental study on the mooring forces and motions of a fish cage under regular waves. Ocean Eng. 2023, 280, 114612. [Google Scholar] [CrossRef]
- Cheng, H.; Li, L.; Ong, M. Comparative study of five commonly used gravity type fish cages under pure current conditions. Ocean Eng. 2022, 250, 110977. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, S.; Xu, Y.; Li, S.; Moan, T. Loads on a vessel-shaped fish cage steel structures, nets and connectors considering the effects of diffraction and radiation waves. Mar. Struct. 2022, 86, 103301. [Google Scholar] [CrossRef]
- Ye, H.; Li, W.; Lin, S.; Ge, Y.; Lv, Q. A framework for fault detection method selection of oceanographic multi-layer winch fibre rope arrangement. Measurement 2024, 2024, 114168. [Google Scholar] [CrossRef]
- Park, S.; Zhou, J.; Dong, S.; Li, Q.; Yoshida, T.; Kitazawa, D. Characteristics of the flow field inside and around a square fish cage considering the circular swimming pattern of a farmed fish school: Laboratory experiments and field observations. Ocean Eng. 2022, 261, 112097. [Google Scholar] [CrossRef]
- Wang, G.; Martin, T.; Huang, L.; Bihs, H. Numerical investigation of the hydrodynamics of a submersible steel-frame offshore fish farm in regular waves using CFD. Ocean Eng. 2022, 256, 111528. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, H.; Bai, X.; Hao, Z.; Sun, Y.; Wu, D.; Johanning, L. Numerical investigations on fluid characteristics around the bottom-fixed aquacultural farm. Ocean Eng. 2022, 266, 112689. [Google Scholar] [CrossRef]
- Zeng, X.; Gualtieri, C.; Cuthbertson, A.; Shao, D. Experimental study of flow and mass transport in the near-wake region of a rigid planar metal net panel. Aquac. Eng. 2022, 98, 102267. [Google Scholar] [CrossRef]
- Shao, D.; Huang, L.; Wang, R.-Q.; Gualtieri, C.; Cuthbertson, A. Flow turbulence characteristics and mass transport in the near-wake region of an aquaculture cage net panel. Water 2021, 13, 294. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, X.; Gualtieri, C.; Cuthbertson, A.; Wang, R.-Q.; Shao, D. Numerical Simulation of Scalar Mixing and Transport through a Fishing Net Panel. J. Mar. Sci. Eng. 2022, 10, 1511. [Google Scholar] [CrossRef]
- Liu, Z.; Guedes Soares, C. Sensitivity analysis of a numerical model of the dynamics of gravity cages subjected to current and waves. Ocean Eng. 2023, 287, 115715. [Google Scholar] [CrossRef]
- Fredheim, A. Current Forces on Net Structures. Ph.D. Thesis, NTNU Trondheim, Trondheim, Norway, 2005. [Google Scholar]
- Friedman, Z.; Kosmatka, J. An improved two-node Timoshenko beam finite element. Comput. Struct. 1993, 47, 473–481. [Google Scholar] [CrossRef]
- Kosmatka, J. An improved two-node finite element for stability and natural frequencies of axial-loaded Timoshenko beams. Comput. Struct. 1995, 57, 141–149. [Google Scholar] [CrossRef]
- Gansel, L.C.; McClimans, T.A.; Myrhaug, D. Average flow inside and around fish cages with and without fouling in a uniform flow. J. Offshore Mech. Arct. Eng. Trans. ASME 2012, 134, 041201. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Bi, C.-W.; Chen, C.-P.; Li, Y.-C.; Dong, G.-H. Experimental study on flow velocity and mooring loads for multiple net cages in steady current. Aquac. Eng. 2015, 67, 24–31. [Google Scholar] [CrossRef]
- DeCew, J.; Fredriksson, D.W.; Lader, P.F.; Chambers, M.; Howell, W.H.; Osienki, M.; Celikkol, B.; Frank, K.; Høy, E. Field measurements of cage deformation using acoustic sensors. Aquac. Eng. 2013, 57, 114–125. [Google Scholar] [CrossRef]
- Klebert, P.; Patursson, Ø.; Endresen, P.; Rundtop, P.; Birkevold, J.; Rasmussen, H. Three-dimensional deformation of a large circular flexible sea cage in high currents: Field experiment and modeling. Ocean Eng. 2015, 104, 511–520. [Google Scholar] [CrossRef]
- Dong, G.; Hou, H.; Xu, T. Model uncertainty in hydrodynamic characteristics by numerical models for aquaculture plant and mooring system. Ocean Eng. 2021, 219, 108383. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Li, Y.C.; Dong, G.H.; Gui, F.K.; Teng, B. Numerical simulation of the effects of structure size ratio and mesh type on three-dimensional deformation of the fishing-net gravity cage in current. Aquac. Eng. 2007, 36, 285–301. [Google Scholar] [CrossRef]
- Lader, P.F.; Enerhaug, B. Experimental investigation of forces and geometry of a net cage in uniform flow. IEEE J. Ocean. Eng. 2005, 30, 79–84. [Google Scholar] [CrossRef]
- Lee, C.W.; Kim, Y.B.; Lee, G.H.; Choe, M.Y.; Lee, M.K.; Koo, K.Y. Dynamic simulation of a fish cage system subjected to currents and waves. Ocean Eng. 2008, 35, 1521–1532. [Google Scholar] [CrossRef]




| Properties | Adjusted Net Strucutres |
|---|---|
| Single twine diameter | 2 mm |
| Number of horizontal lines | 6 |
| Number of vertical lines | 40 |
| Diameter of horizontal lines | 17.07 mm |
| Diameter of vertical lines | 16.57 mm |
| Young’s modulus | 3.5 × 106 |
| Density | 1015 kg/m3 |
| Mass of the counterweight | 35 kg |
| Number of the counterweight | 8 |
| Flow Velocity(m/s) | Volume of Physical Model | Volume of Numerical Model with no Flow Reduction | Volume of Numerical Model with Plan I Flow Reduction | Volume of Numerical Model with Plan II Flow Reduction |
|---|---|---|---|---|
| 0.312 | 75% | 79.2% | 76.94% | 77.44% |
| 0.509 | 59% | 70.17% | 72.1% | 68.57% |
| 0.732 | 44% | 59.45% | 59.49% | 55.89% |
| 1.056 | 33% | 45.02% | 47.65% | 47.2% |
| Flow Velocity (m/s) | Plan I | Plan II |
|---|---|---|
| 0.312 | 20% | 50% |
| 0.509 | 20% | 70% |
| 0.732 | 20% | 70% |
| 1.056 | 20% | 70% |
| Velocity-Independent Model | Velocity-Dependent Model | |
|---|---|---|
| a | 0.8592 | 1.0319 |
| b | n/a. | −0.3333 |
| Flow Velocity (m/s) | Velocity-Independent Model | Velocity-Dependent Model |
|---|---|---|
| 0.312 | 0.0792 | 0.0169 |
| 0.509 | −0.0044 | −0.0136 |
| 0.732 | −0.061 | −0.0249 |
| 1.056 | −0.0521 | 0.024 |
| Q | 0.0127 | 0.0017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Guedes Soares, C. Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage. J. Mar. Sci. Eng. 2024, 12, 289. https://doi.org/10.3390/jmse12020289
Liu Z, Guedes Soares C. Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage. Journal of Marine Science and Engineering. 2024; 12(2):289. https://doi.org/10.3390/jmse12020289
Chicago/Turabian StyleLiu, Zhongchi, and C. Guedes Soares. 2024. "Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage" Journal of Marine Science and Engineering 12, no. 2: 289. https://doi.org/10.3390/jmse12020289
APA StyleLiu, Z., & Guedes Soares, C. (2024). Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage. Journal of Marine Science and Engineering, 12(2), 289. https://doi.org/10.3390/jmse12020289







