Wave-Induced Instantaneous Liquefaction of a Non-Cohesive Seabed around Buried Pipelines: A Liquefaction-Associated Non-Darcy Flow Model Approach
Abstract
:1. Introduction
2. The Liquefaction-Associated Non-Darcy Flow Model
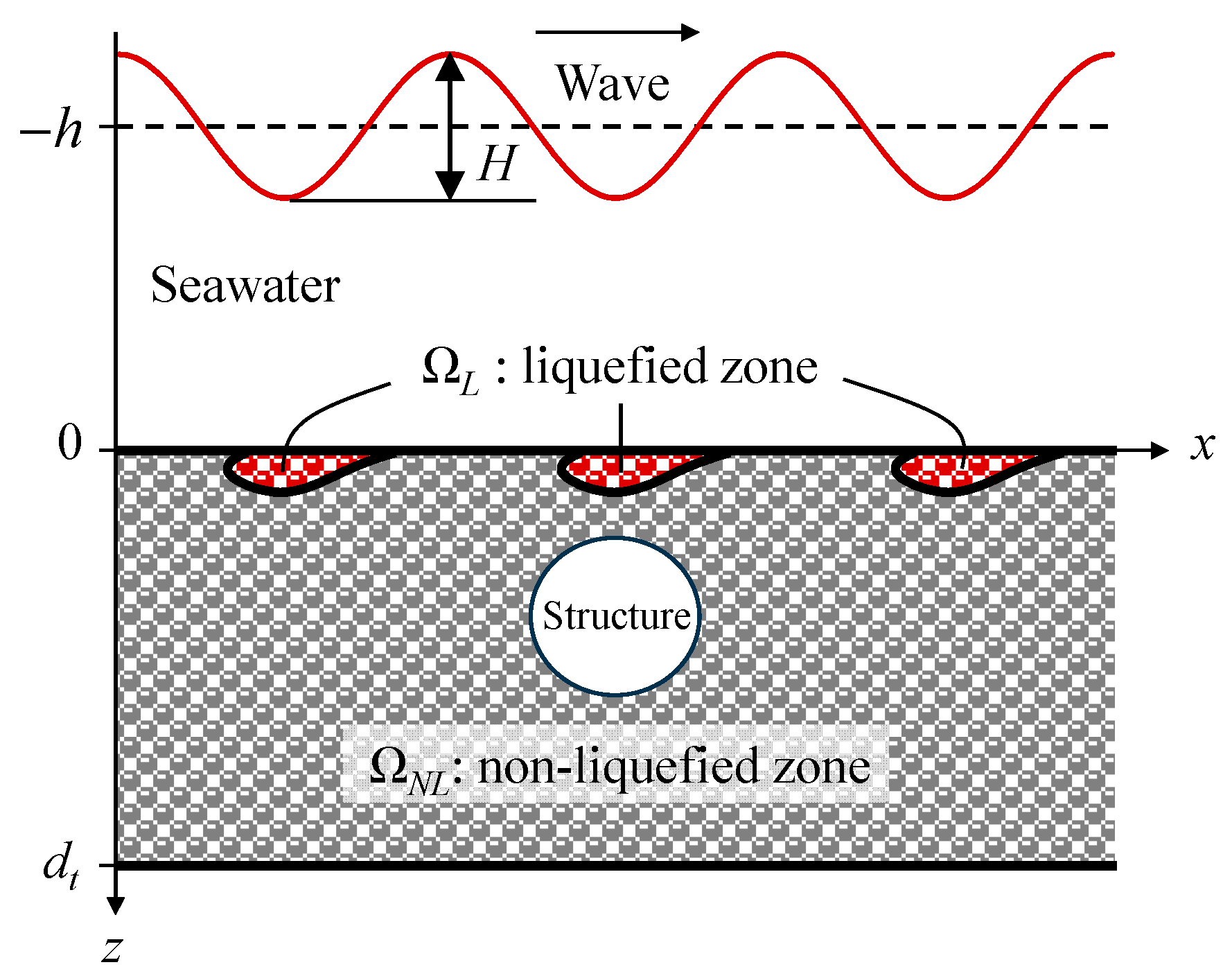
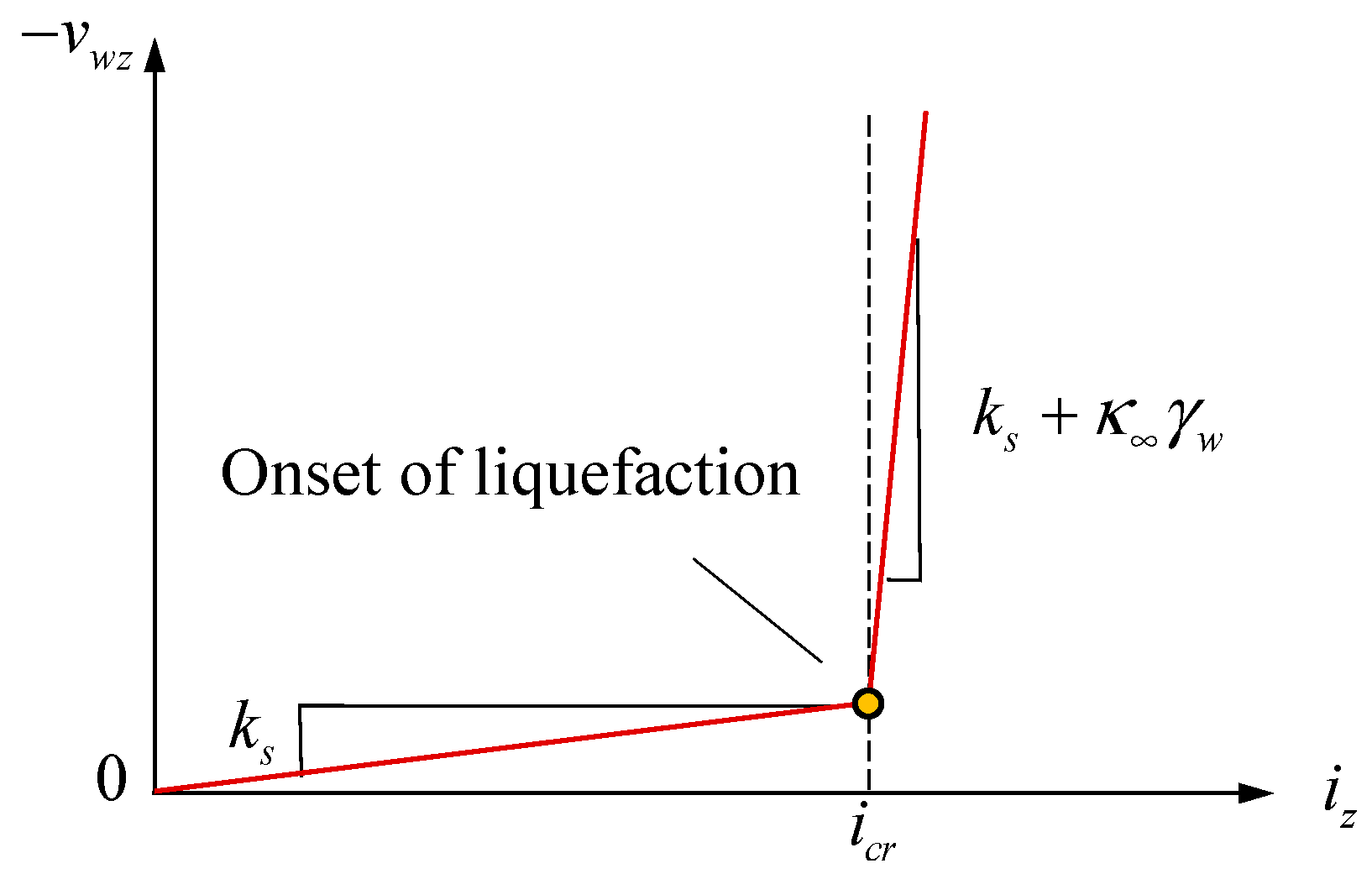
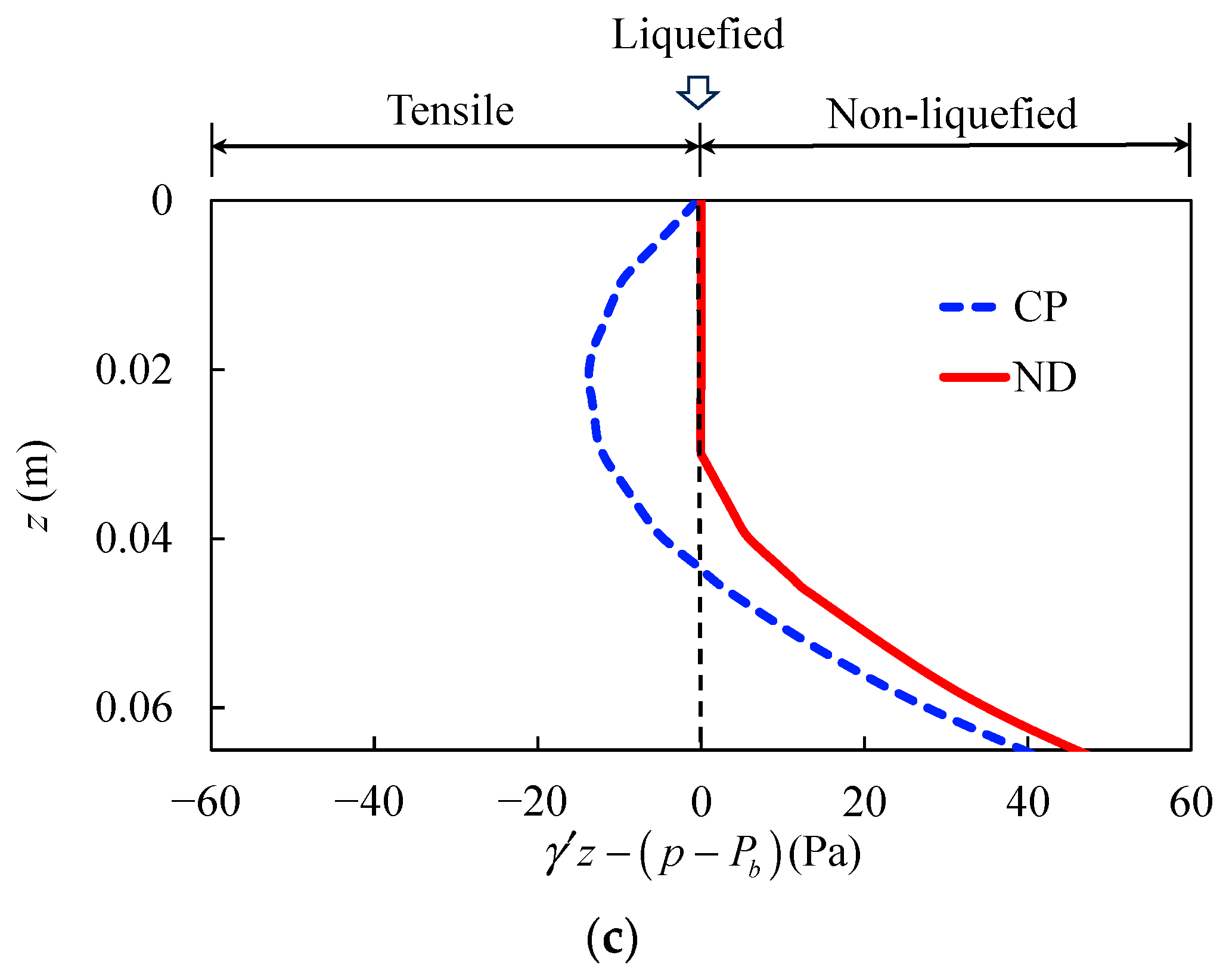
2.1. Wave–Seabed–Structure Model and Liquefaction Criteria
2.2. Numerical Implementation of the Non-Darcy Flow Model
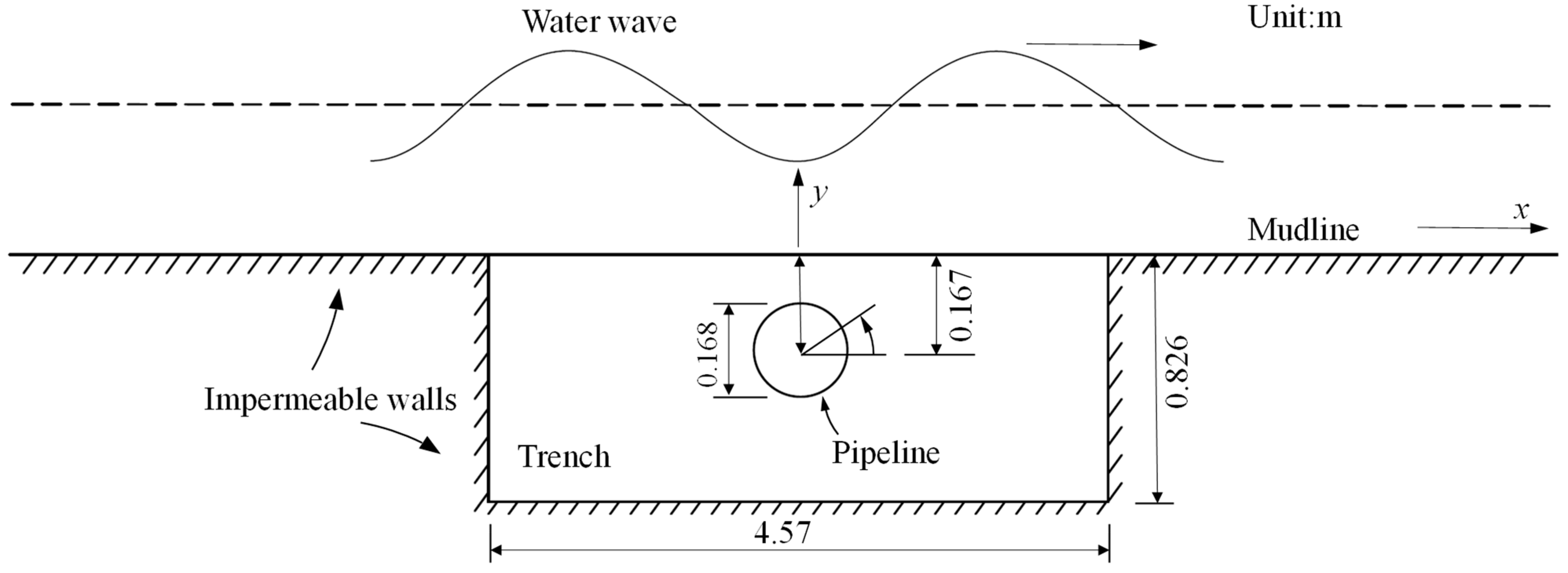
3. Validation of the Wave–Seabed–Structure Model without Seabed Liquefaction
3.1. Computational Model
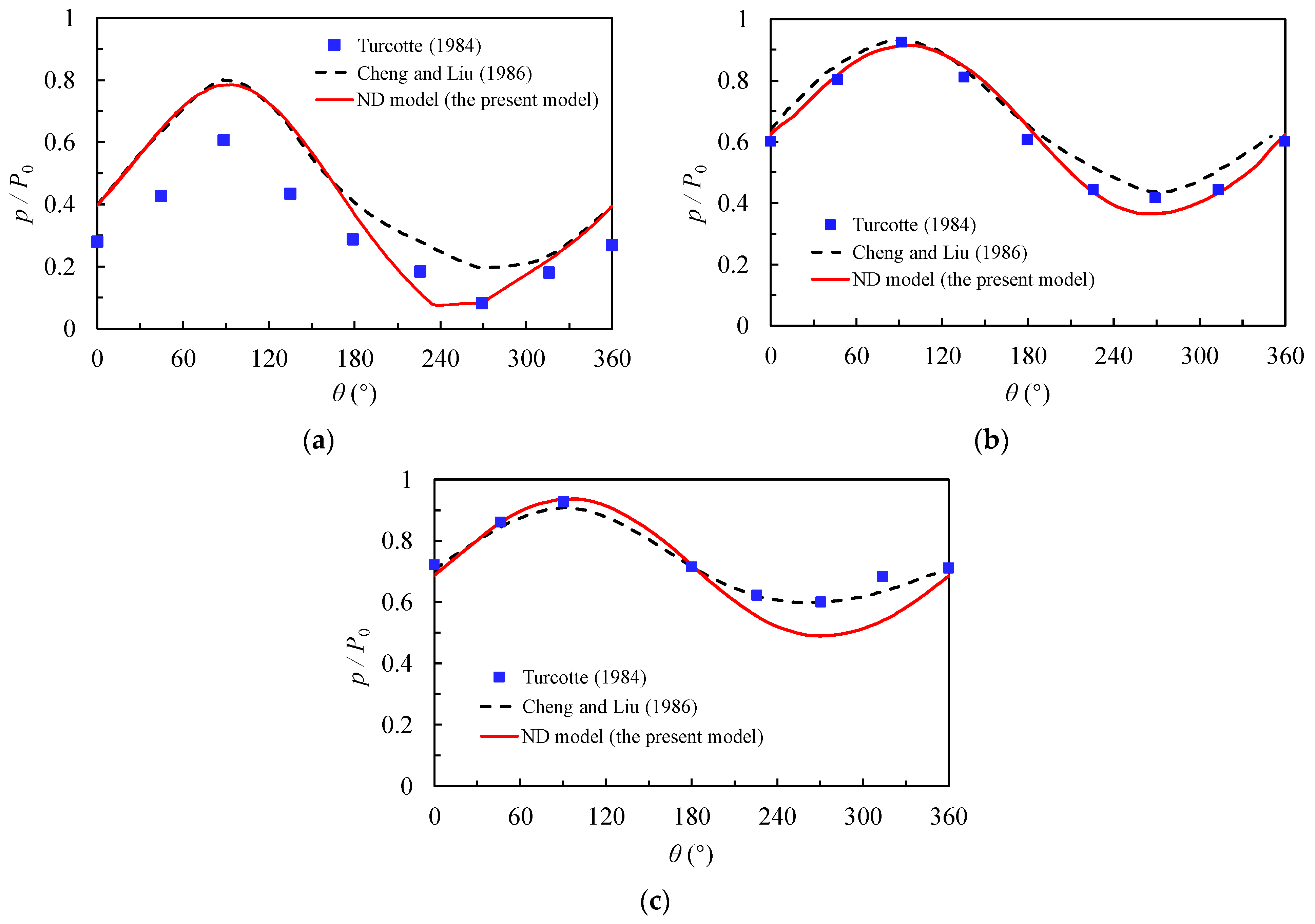
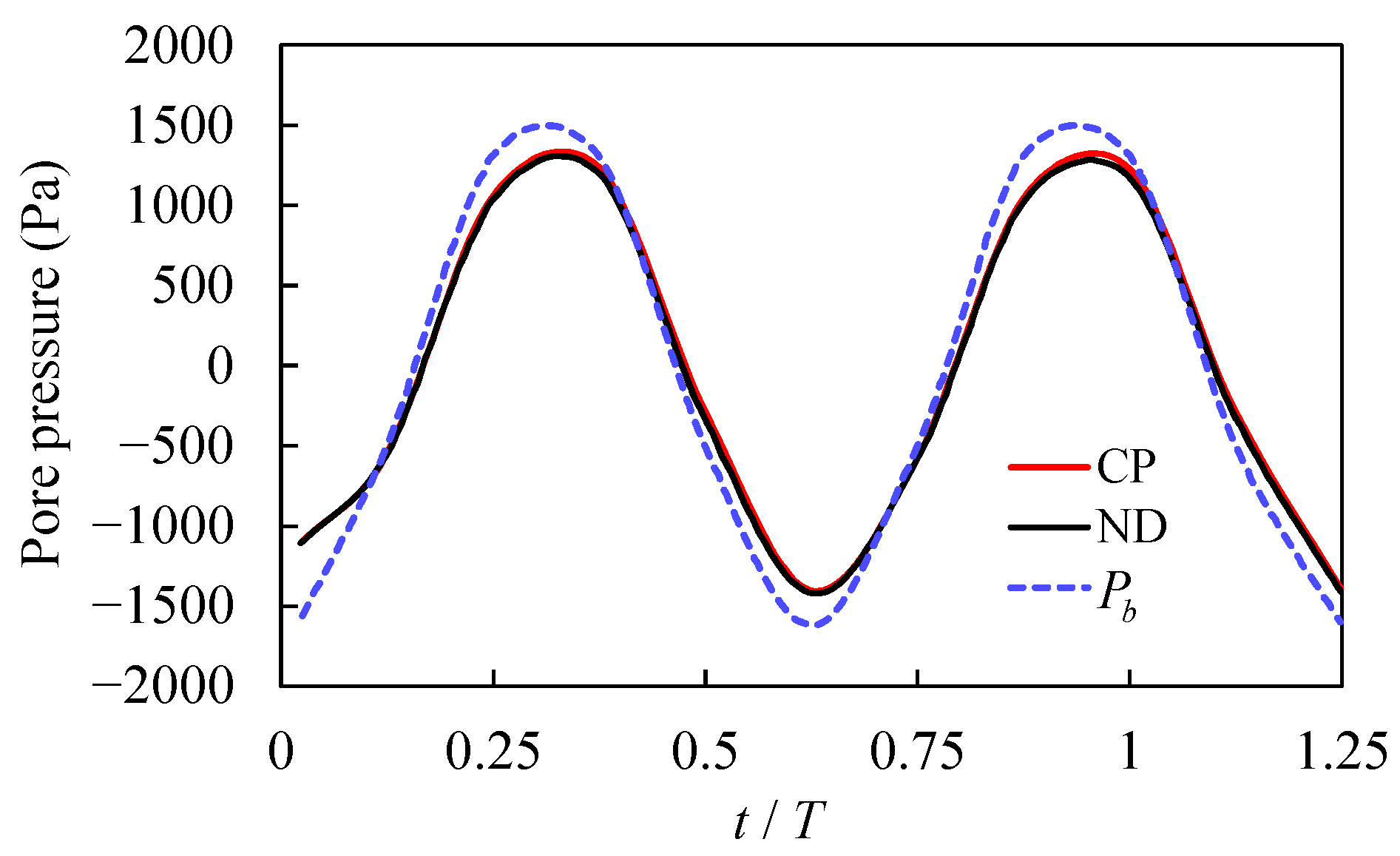
3.2. Pore Pressure Response
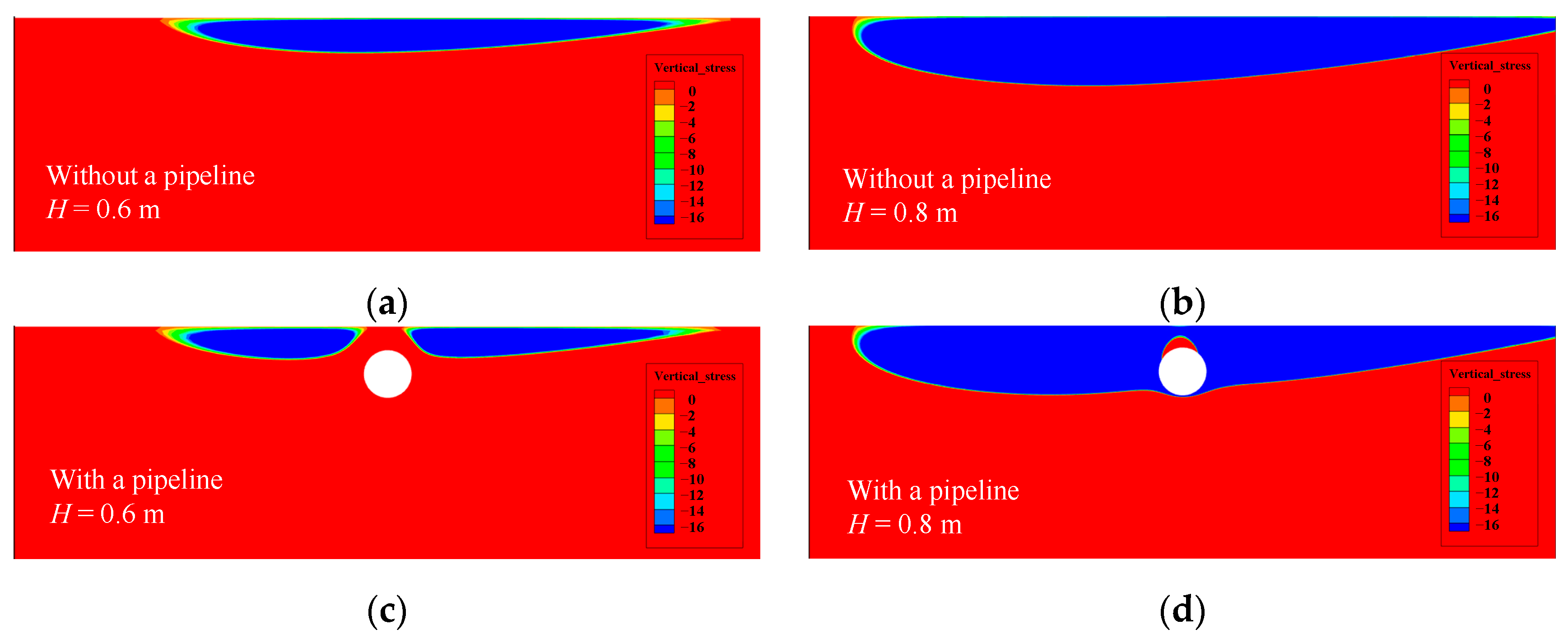
4. Numerical Results of the Wave–Seabed–Structure Model with Seabed Liquefaction
4.1. Computational Model
4.2. Pore Pressure Response
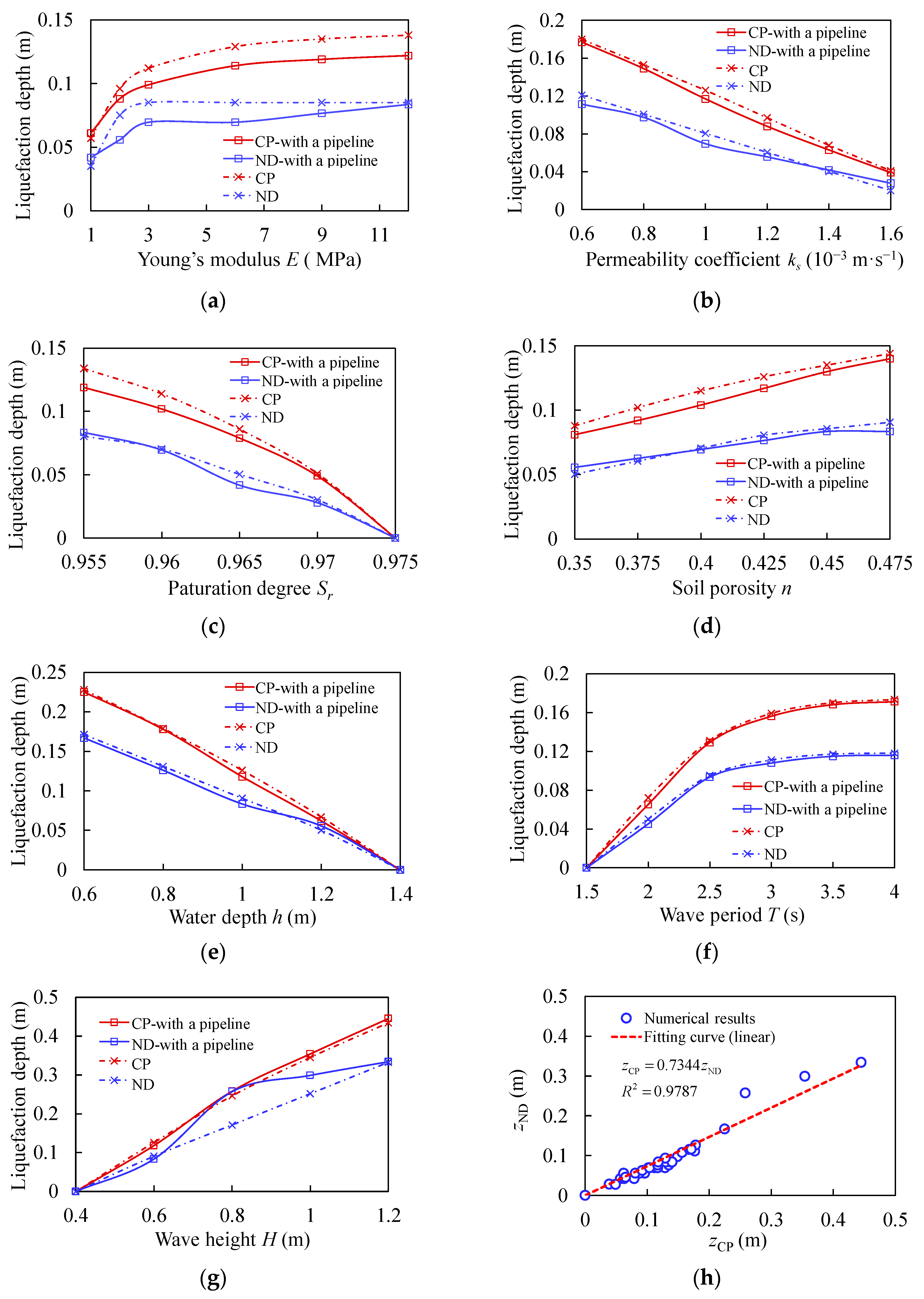
4.3. Parametric Study on the Liquefaction Depth
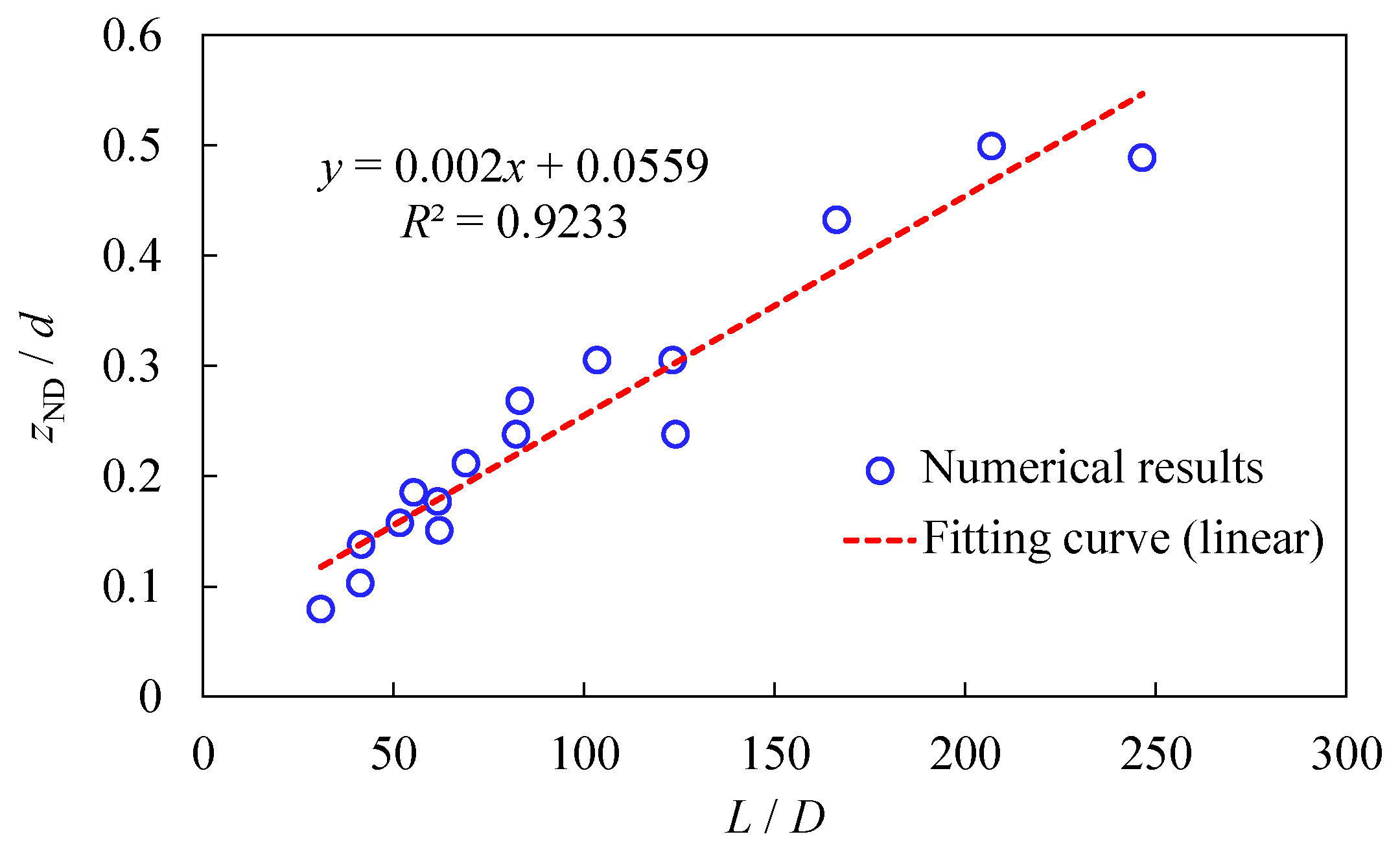
4.4. Study on Non-Dimensional Parameters
5. The Shielding Phenomenon of a Structure in the Seabed under a Liquefaction Condition
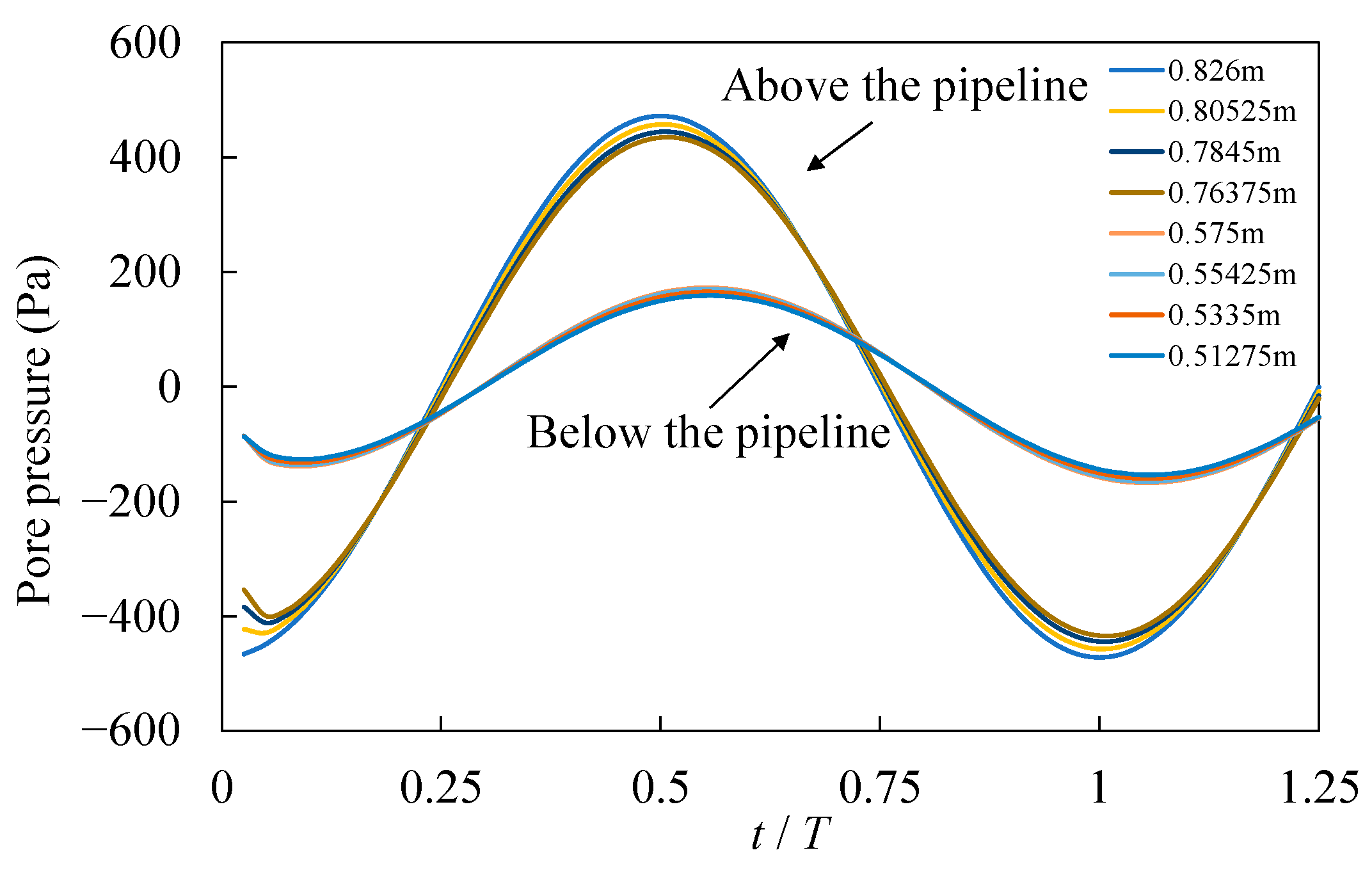
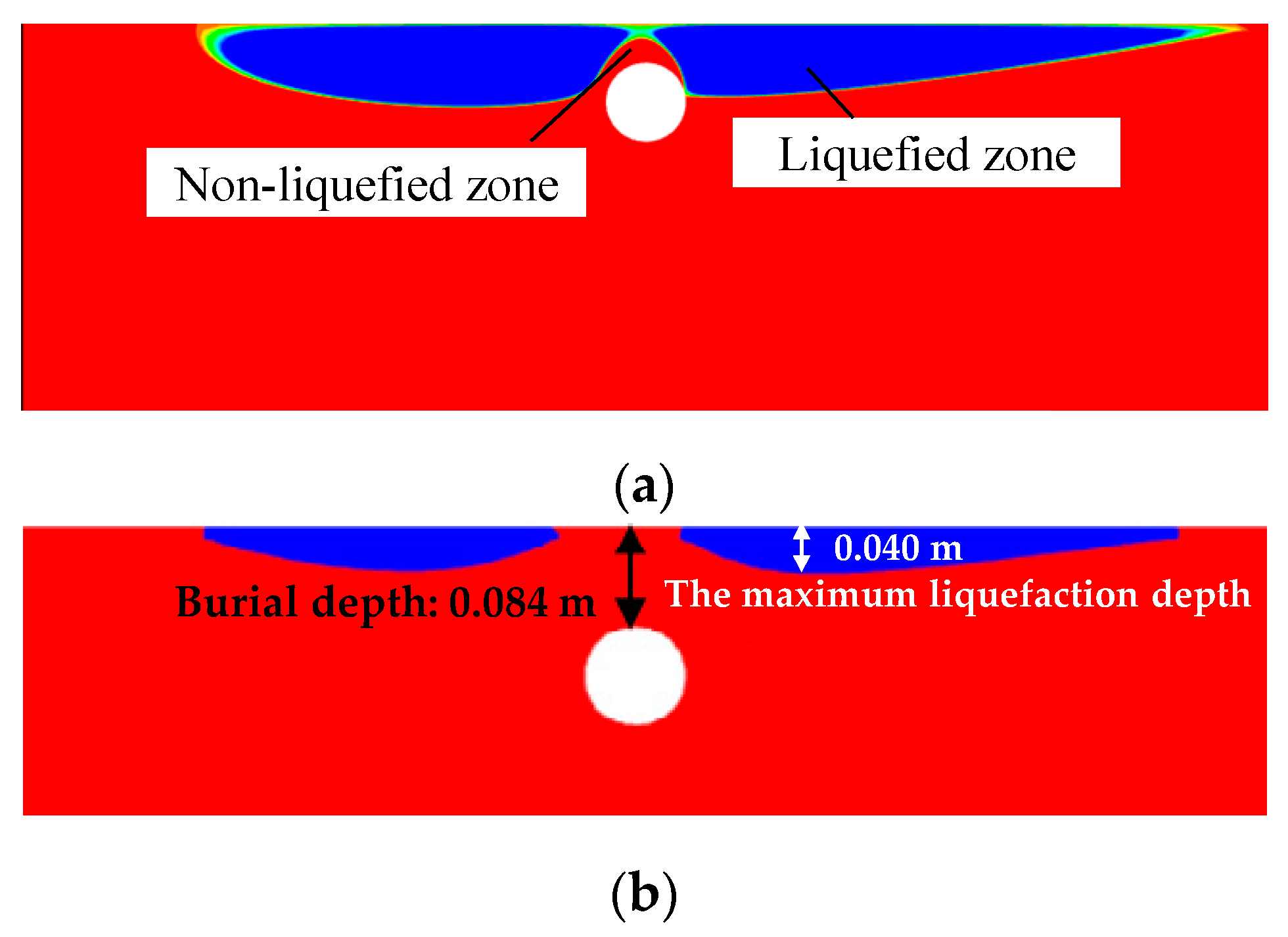
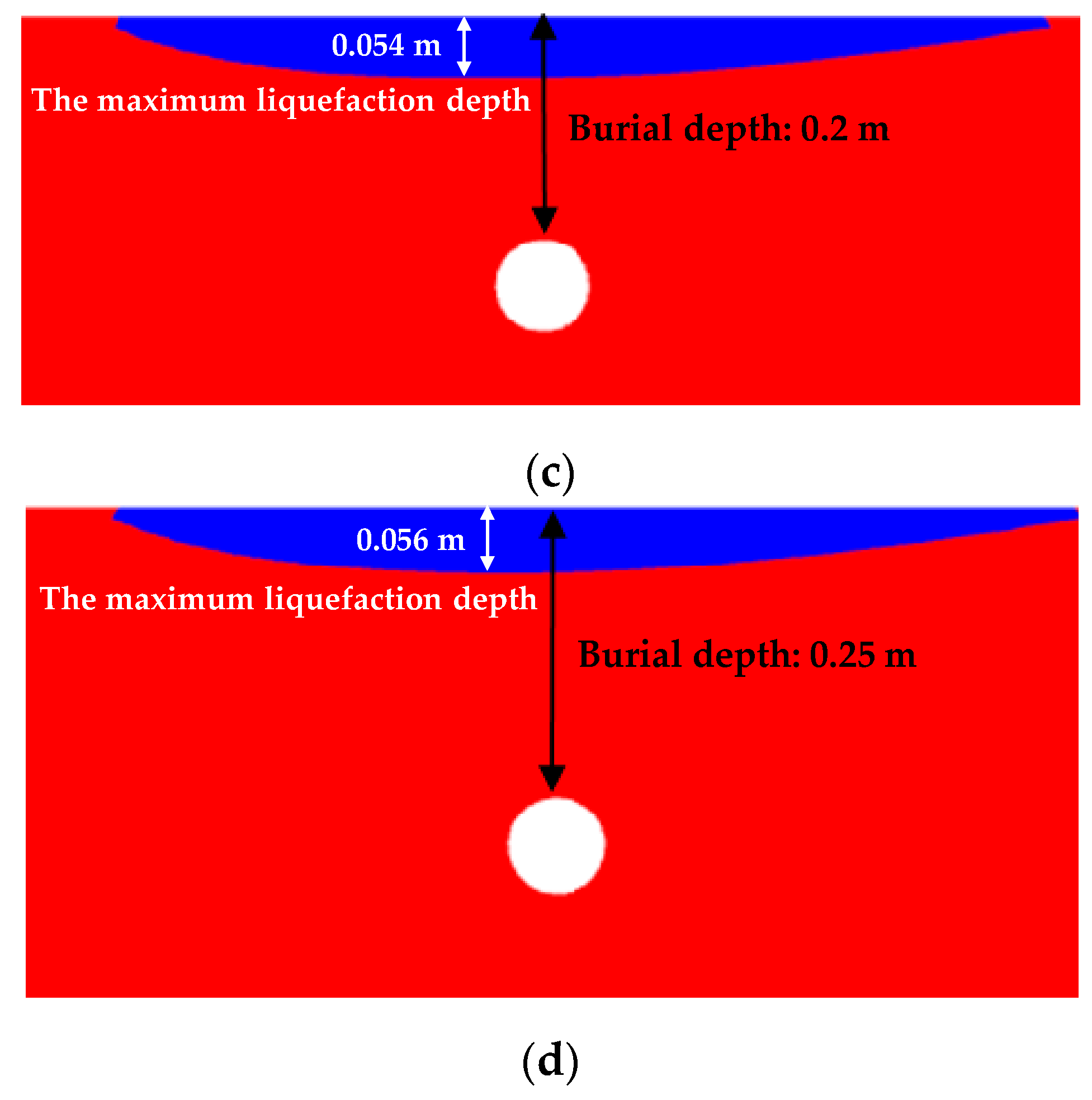
5.1. The Shielding Effect of the Pipeline on the Liquefied Zone
5.2. Onset Conditions for Liquefaction Occurrence above the Pipeline
6. Conclusions
- (1)
- Numerical simulations were conducted based on Turcotte’s flume experiment, validating the reliability of our in-house code in modeling wave–seabed–structure interactions.
- (2)
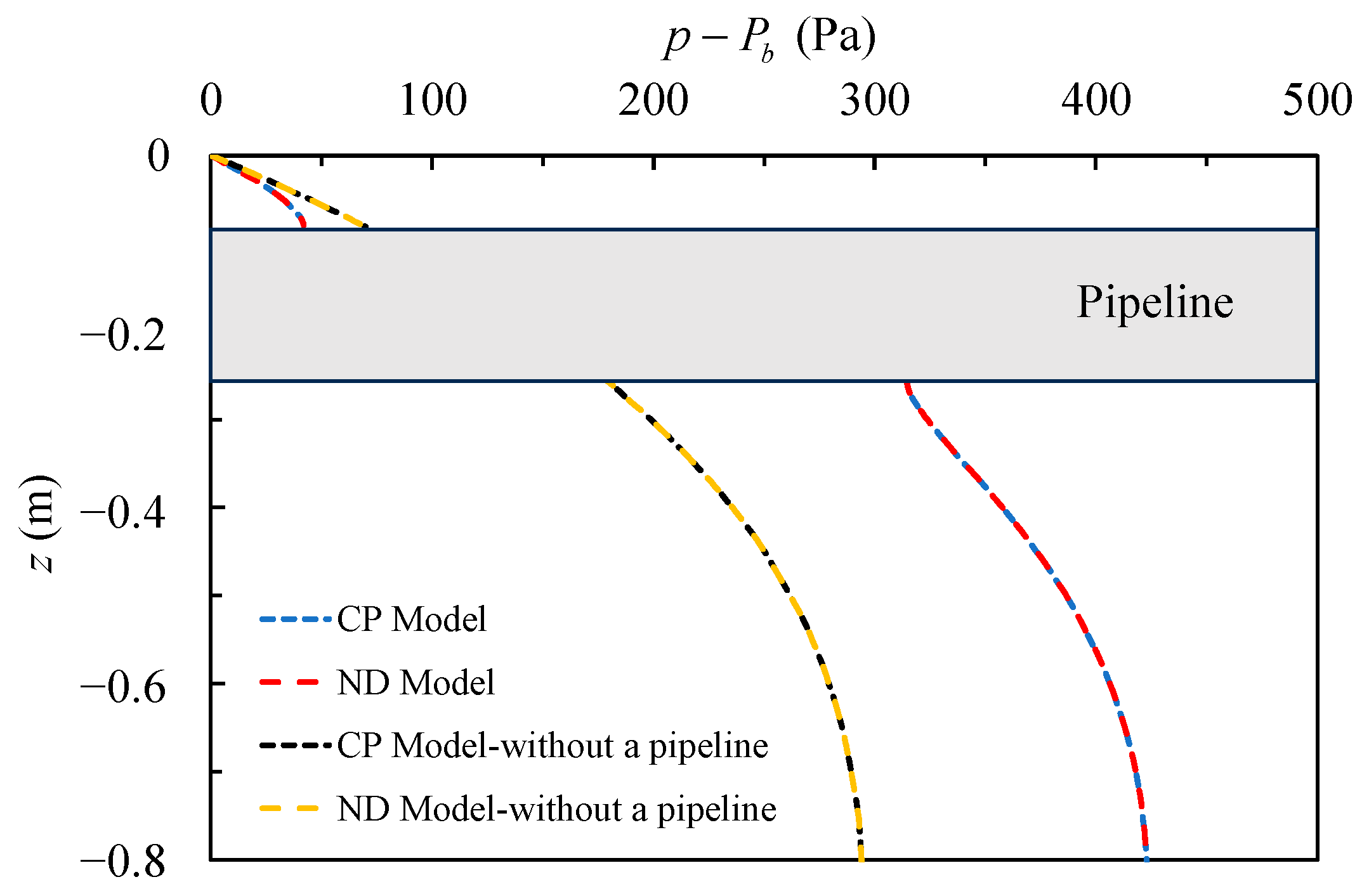
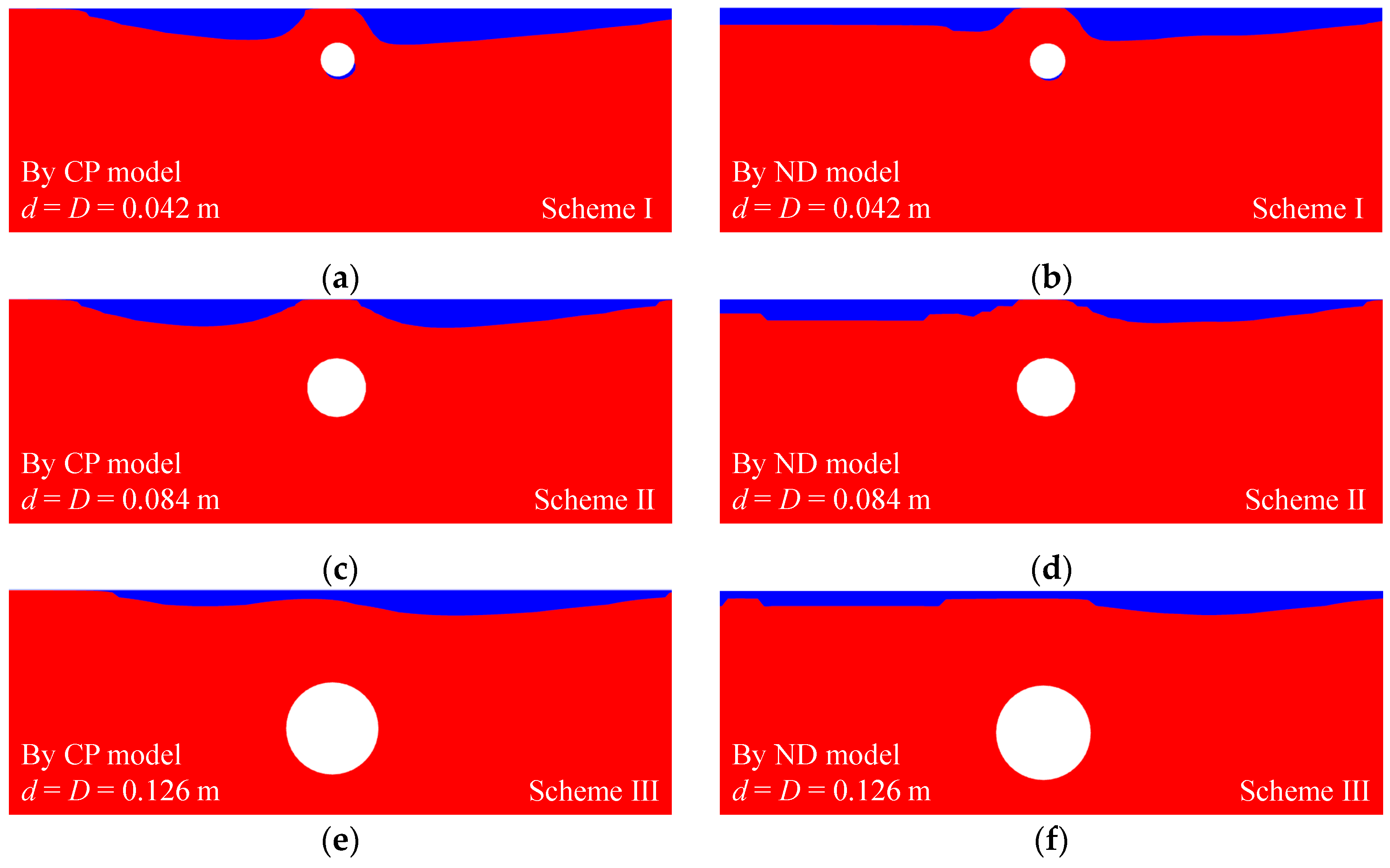
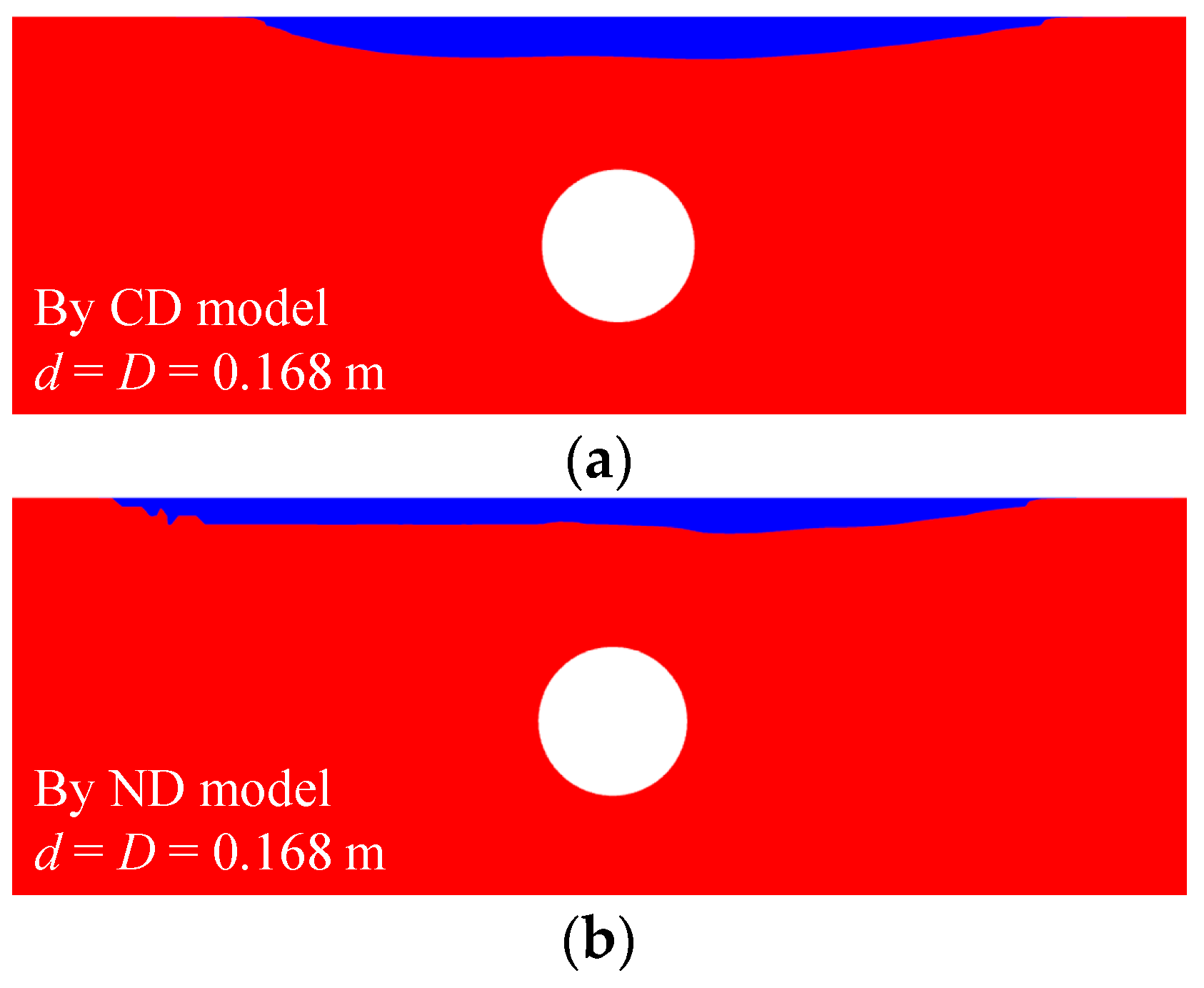
- A numerical study was conducted by varying the burial depth and diameter of the pipeline, revealing that the existence of a pipeline weakens the degree of amplitude attenuation and the phase lag. Therefore, when the pipeline is shallow, the liquefied zone of the seabed with a pipeline is smaller than that in the pure seabed, which is called the “liquefaction shielding effect” in this work.
- (3)
- Under some conditions, liquefaction can even completely disappear above the pipeline, while horizontally distant areas still have liquefied zones. The onset conditions for liquefaction occurrence above the pipeline are then discussed.
- (4)
- As the burial depth of the pipeline increases, the liquefaction shielding effect weakens, resulting in an increase in the liquefaction depth above the pipeline. Once the pipeline is sufficiently far from the seabed surface, it no longer influences the liquefied zone.
- (5)
- Based on the parametric study, it was observed that the liquefaction depth predicted by the non-Darcy model is approximately 0.73 times the value estimated by the conventional Darcy model, regardless of whether or not a pipeline is involved.
- (6)
- The quantitative relationship between wave loadings and structural sizes is studied. A highly linear relationship between two sets of non-dimensional parameters, i.e., “liquefaction depth/burial depth” and “wavelength/diameter”, is discovered.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, X.; Sun, Y.; Song, Y.; Zhu, C. In-Situ Observation of Wave-Induced Pore Water Pressure in Seabed Silt in the Yellow River Estuary of China. J. Mar. Environ. Eng. 2021, 10, 305–317. [Google Scholar]
- Jia, Y.; Zhang, L.; Zheng, J.; Liu, X.; Jeng, D.-S.; Shan, H. Effects of wave-induced seabed liquefaction on sediment re-suspension in the Yellow River Delta. Ocean Eng. 2014, 89, 146–156. [Google Scholar] [CrossRef]
- Mory, M.; Michallet, H.; Bonjean, D.; Piedra-Cueva, I.; Barnoud, J.M.; Foray, P.; Abadie, S.; Breul, P. A Field Study of Momentary Liquefaction Caused by Waves around a Coastal Structure. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 28–38. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, T.; Yu, L.; Guo, X.; Jia, Y. Penetration depth of the dynamic response of seabed induced by internal solitary waves. Appl. Ocean Res. 2019, 90, 101867. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, Y.; Zhang, Y.; Liu, X.; Shan, H. In situ observations of wave pumping of sediments in the Yellow River Delta with a newly developed benthic chamber. Mar. Geophys. Res. 2018, 39, 463–474. [Google Scholar] [CrossRef]
- Jeng, D.-S. Mechanics of Wave-Seabed-Structure Interactions: Modelling, Processes and Applications; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Sumer, T.B.M. Liquefaction around Marine Structures; World Scientific: Singapore, 2014. [Google Scholar]
- Jeng, D.-S. Wave-induced sea floor dynamics. Appl. Mech. Rev. 2003, 56, 407–429. [Google Scholar] [CrossRef]
- Zen, K.; Yamazaki, H. Mechanism of Wave-Induced Liquefaction and Densification in Seabed. Soils Found. 1990, 30, 90–104. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, J.; Sassa, S.; Sekiguchi, H. Progressive solidification of a liquefied sand layer during continued wave loading. Géotechnique 2004, 54, 617–629. [Google Scholar] [CrossRef]
- Mutlu Sumer, B.; Hatipoglu, F.; Fredsøe, J.; Kaan Sumer, S. The sequence of sediment behaviour during wave-induced liquefaction. Sedimentology 2006, 53, 611–629. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Jeng, D.S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Anal. Methods Geomech. 1994, 18, 785–807. [Google Scholar] [CrossRef]
- Madsen, O.S. Wave-Induced Pore Pressures and Effective Stresses in A Porous Bed. Geotechnique 1978, 28, 377–393. [Google Scholar] [CrossRef]
- Yamamoto, T.; Koning, H.L.; Sellmeijer, H.; Vanhijum, E.P. Response of A Poro-Elastic Bed to Water-Waves. J. Fluid Mech. 1978, 87, 193–206. [Google Scholar] [CrossRef]
- Zhang, Y.; Jeng, D.S.; Gao, F.P.; Zhang, J.S. An analytical solution for response of a porous seabed to combined wave and current loading. Ocean Eng. 2013, 57, 240–247. [Google Scholar] [CrossRef]
- Duan, L.; Liao, C.; Jeng, D.; Chen, L. 2D numerical study of wave and current-induced oscillatory non-cohesive soil liquefaction around a partially buried pipeline in a trench. Ocean Eng. 2017, 135, 39–51. [Google Scholar] [CrossRef]
- Gao, F.P.; Jeng, D.S.; Sekiguchi, H. Numerical study on the interaction between non-linear wave, buried pipeline and non-homogenous porous seabed. Comput. Geotech. 2003, 30, 535–547. [Google Scholar] [CrossRef]
- Jeng, D.S.; Lin, Y.S. Wave–induced pore pressure around a buried pipeline in Gibson soil: Finite element analysis. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 1559–1578. [Google Scholar] [CrossRef]
- Li, K.; Guo, Z.; Wang, L.; Jiang, H. Effect of seepage flow on shields number around a fixed and sagging pipeline. Ocean Eng. 2019, 172, 487–500. [Google Scholar] [CrossRef]
- Liang, Z.; Jeng, D.-S. PORO-FSSI-FOAM model for seafloor liquefaction around a pipeline under combined random wave and current loading. Appl. Ocean Res. 2021, 107, 102497. [Google Scholar] [CrossRef]
- Liang, Z.; Jeng, D.-S.; Liu, J. Combined wave–current induced seabed liquefaction around buried pipelines: Design of a trench layer. Ocean Eng. 2020, 212, 107764. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, Y.; Jeng, D.S.; Liao, C.; Rey, N. An integrated numerical model for wave–soil–pipeline interactions. Coast. Eng. 2016, 108, 25–35. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Jeng, D.-S. Accumulated Pore Pressures around Submarine Pipeline Buried in Trench Layer with Partial Backfills. J. Eng. Mech. 2016, 142, 04016042. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Jeng, D.S.; Guo, Z.; Zhang, J.S. Two-Dimensional Model for Pore Pressure Accumulations in the Vicinity of a Buried Pipeline. J. Offshore Mech. Arct. Eng. 2014, 136, 042001. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Tong, L.; Sun, K.; Guo, Y.; Wei, C. Experimental study of soil responses around a pipeline in a sandy seabed under wave-current load. Appl. Ocean Res. 2023, 130, 103409. [Google Scholar] [CrossRef]
- Duan, L.; Zhan, B.; Shen, L.; Fan, M.; Wang, D. Nonlinear Wave-Induced Uplift Force onto Pipelines Buried in Sloping Seabeds. Appl. Sci. 2023, 13, 7519. [Google Scholar] [CrossRef]
- Celli, D.; Li, Y.; Ong, M.C.; Di Risio, M. The role of submerged berms on the momentary liquefaction around conventional rubble mound breakwaters. Appl. Ocean Res. 2019, 85, 1–11. [Google Scholar] [CrossRef]
- Jeng, D.S.; Ye, J.H.; Zhang, J.S.; Liu, L.F. An integrated model for the wave-induced seabed response around marine structures: Model verifications and applications. Coast. Eng. 2013, 72, 1–19. [Google Scholar] [CrossRef]
- Jisheng, Z.; Linlong, T.; Jinhai, Z.; Rui, H.; Yakun, G. Effects of Soil-Resistance Damping on Wave-Induced Pore Pressure Accumulation around a Composite Breakwater. J. Coast. Res. 2018, 34, 573–585. [Google Scholar] [CrossRef]
- Young, Y.L.; White, J.A.; Xiao, H.; Borja, R.I. Liquefaction potential of coastal slopes induced by solitary waves. Acta Geotech. 2009, 4, 17–34. [Google Scholar] [CrossRef]
- Chang, K.-T.; Jeng, D.-S. Numerical study for wave-induced seabed response around offshore wind turbine foundation in Donghai offshore wind farm, Shanghai, China. Ocean Eng. 2014, 85, 32–43. [Google Scholar] [CrossRef]
- Li, Y.; Ong, M.C.; Tang, T. Numerical analysis of wave-induced poro-elastic seabed response around a hexagonal gravity-based offshore foundation. Coast. Eng. 2018, 136, 81–95. [Google Scholar] [CrossRef]
- Lin, Z.; Pokrajac, D.; Guo, Y.; Jeng, D.-S.; Tang, T.; Rey, N.; Zheng, J.; Zhang, J. Investigation of nonlinear wave-induced seabed response around mono-pile foundation. Coast. Eng. 2017, 121, 197–211. [Google Scholar] [CrossRef]
- Qi, W.-G.; Gao, F.-P. Physical modeling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef]
- Sui, T.; Zhang, C.; Guo, Y.; Zheng, J.; Jeng, D.; Zhang, J.; Zhang, W. Three-dimensional numerical model for wave-induced seabed response around mono-pile. Ships Offshore Struct. 2016, 11, 667–678. [Google Scholar] [CrossRef]
- Zhao, H.; Alam, A.; San, C.-Y.; Eguchi, S.; Chen, Q.; Lian, Q.; Ma, D. Molecular mechanisms of brain-derived neurotrophic factor in neuro-protection: Recent developments. Brain Res. 2017, 1665, 1–21. [Google Scholar] [CrossRef]
- Sui, T.; Zheng, J.; Zhang, C.; Jeng, D.-S.; Zhang, J.; Guo, Y.; He, R. Consolidation of unsaturated seabed around an inserted pile foundation and its effects on the wave-induced momentary liquefaction. Ocean Eng. 2017, 131, 308–321. [Google Scholar] [CrossRef]
- Cui, L.; Jeng, D.-S.; Liu, J. Numerical analysis of the seabed liquefaction around a fixed gravity-based structure (GBS) of an offshore platform and protection. Ocean Eng. 2022, 249, 110844. [Google Scholar] [CrossRef]
- Qin, C.; Duan, L.; Wang, D.; Duan, B.; Fan, M.; Wang, H. Three-dimensional numerical simulation of wave-induced seabed response around a dumbbell-shaped cofferdam. Appl. Ocean Res. 2023, 134, 103501. [Google Scholar] [CrossRef]
- Chen, W.; Liu, C.; He, R.; Chen, G.; Jeng, D.; Duan, L. Stability of the foundation trench of the immersed tunnel subjected to combined wave and current loading. Appl. Ocean Res. 2021, 110, 102627. [Google Scholar] [CrossRef]
- Han, S.; Jeng, D.-S.; Tsai, C.-C. Response of a Porous Seabed around an Immersed Tunnel under Wave Loading: Meshfree Model. J. Mar. Sci. Eng. 2019, 7, 369. [Google Scholar] [CrossRef]
- Li, Y.; Ong, M.C.; Tang, T. A numerical toolbox for wave-induced seabed response analysis around marine structures in the OpenFOAM® framework. Ocean Eng. 2020, 195, 106678. [Google Scholar] [CrossRef]
- Cuéllar, P.; Mira, P.; Pastor, M.; Fernández Merodo, J.A.; Baeßler, M.; Rücker, W. A numerical model for the transient analysis of offshore foundations under cyclic loading. Comput. Geotech. 2014, 59, 75–86. [Google Scholar] [CrossRef]
- Kudella, M.; Oumeraci, H.; de Groot, M.B.; Meijers, P. Large-Scale Experiments on Pore Pressure Generation underneath a Caisson Breakwater. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 310–324. [Google Scholar] [CrossRef]
- Liao, C.; Chen, J.; Zhang, Y. Accumulation of pore water pressure in a homogeneous sandy seabed around a rocking mono-pile subjected to wave loads. Ocean Eng. 2019, 173, 810–822. [Google Scholar] [CrossRef]
- Sumer, S.K.; Sumer, B.M.; Dixen, F.H.; Fredsøe, J. Pore pressure buildup in the subsoil under a caisson breakwater. In Proceedings of the Eighteenth International Offshore and Polar Engineering Conference, Ottawa, ON, Canada, 6–11 July 2008; pp. 664–671. [Google Scholar]
- Wang, Z.; Yang, Y.; Yu, H.-S. Effects of principal stress rotation on the wave–seabed interactions. Acta Geotech. 2017, 12, 97–106. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.S. Effects of principal stress rotation on wave-induced soil response in a poro-elastoplastic sandy seabed. Acta Geotech. 2019, 14, 1717–1739. [Google Scholar] [CrossRef]
- Qi, W.-G.; Shi, Y.-M.; Gao, F.-P. Uplift soil resistance to a shallowly-buried pipeline in the sandy seabed under waves: Poro-elastoplastic modeling. Appl. Ocean Res. 2020, 95, 102024. [Google Scholar] [CrossRef]
- Qi, W.-G.; Gao, F.-P. A modified criterion for wave-induced momentary liquefaction of sandy seabed. Theor. Appl. Mech. Lett. 2015, 5, 20–23. [Google Scholar] [CrossRef]
- Qi, W.-G.; Gao, F.-P. Wave induced instantaneously-liquefied soil depth in a non-cohesive seabed. Ocean Eng. 2018, 153, 412–423. [Google Scholar] [CrossRef]
- Zhou, M.-Z.; Jeng, D.-S.; Qi, W.-G. A new model for wave-induced instantaneous liquefaction in a non-cohesive seabed with dynamic permeability. Ocean Eng. 2020, 213, 107597. [Google Scholar] [CrossRef]
- Wu, S.; Jeng, D.S. Effects of dynamic soil permeability on the wave-induced seabed response around a buried pipeline. Ocean Eng. 2019, 186, 106132. [Google Scholar] [CrossRef]
- Wu, S.; Jeng, D.S.; Seymour, B.R. Numerical Modelling of consolidation-induced solute transport in unsaturated soil with dynamic hydraulic conductivity and degree of saturation. Adv. Water Resour. 2020, 135, 103466. [Google Scholar] [CrossRef]
- Arulandan, K.; Sybico, J.; Houlsby, G.T.; Schofield, A.N. Post-liquefaction settlement of sands. Géotechnique 2009, 59, 739–749. [Google Scholar]
- Ha, I.S.; Park, Y.H.; Kim, M.M. Dissipation Pattern of Excess Pore Pressure After Liquefaction in Saturated Sand Deposits. Transp. Res. Rec. 2003, 1821, 59–67. [Google Scholar] [CrossRef]
- Haigh, S.K.; Eadington, J.; Madabhushi, S.P.G. Permeability and stiffness of sands at very low effective stresses. Géotechnique 2012, 62, 69–75. [Google Scholar] [CrossRef]
- Shahir, H.; Mohammadi-Haji, B.; Ghassemi, A. Employing a variable permeability model in numerical simulation of saturated sand behavior under earthquake loading. Comput. Geotech. 2014, 55, 211–223. [Google Scholar] [CrossRef]
- Ueng, T.-S.; Wang, Z.-F.; Chu, M.-C.; Ge, L. Laboratory tests for permeability of sand during liquefaction. Soil Dyn. Earthq. Eng. 2017, 100, 249–256. [Google Scholar] [CrossRef]
- Wang, B.; Zen, K.; Chen, G.Q.; Zhang, Y.B.; Kasama, K. Excess pore pressure dissipation and solidification after liquefaction of saturated sand deposits. Soil Dyn. Earthq. Eng. 2013, 49, 157–164. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, H.; Jeng, D.-S.; Qi, W.; Fang, Q. Modelling the wave-induced instantaneous liquefaction in a non-cohesive seabed as a nonlinear complementarity problem. Comput. Geotech. 2021, 137, 104275. [Google Scholar] [CrossRef]
- Kunisch, K.; Rösch, A. Primal-Dual Active Set Strategy for a General Class of Constrained Optimal Control Problems. SIAM J. Optim. 2002, 13, 321–334. [Google Scholar] [CrossRef]
- Zhou, M.-Z.; Qi, W.-G.; Jeng, D.-S.; Gao, F.-P. A non-Darcy flow model for a non-cohesive seabed involving wave-induced instantaneous liquefaction. Ocean Eng. 2021, 239, 109807. [Google Scholar] [CrossRef]
- Fukumoto, Y.; Ohtsuka, S. 3-D direct numerical model for failure of non-cohesive granular soils with upward seepage flow. Comput. Part. Mech. 2018, 5, 443–454. [Google Scholar] [CrossRef]
- Skempton, A.W.; Brogan, J.M. Experiments on piping in sandy gravels. Géotechnique 1994, 44, 449–460. [Google Scholar] [CrossRef]
- Scholtès, L.; Chareyre, B.; Michallet, H.; Catalano, E.; Marzougui, D. Modeling wave-induced pore pressure and effective stress in a granular seabed. Contin. Mech. Thermodyn. 2015, 27, 305–323. [Google Scholar] [CrossRef]
- Turcotte, B.R. Laboratory Evaluation of Wave Tank Parameters for Wave-Sediment Interaction; Cornell University: Ithaca, NY, USA, 1984. [Google Scholar]
- Zhou, X.-L.; Zhang, J.; Wang, J.-H.; Xu, Y.-F.; Jeng, D.-S. Stability and liquefaction analysis of porous seabed subjected to cnoidal wave. Appl. Ocean Res. 2014, 48, 250–265. [Google Scholar] [CrossRef]
- Dean, R.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1984. [Google Scholar]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Verruijt, A. Elastic storage of aquifers. In Flow Through Porous Media; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Cheng, A.H.D.; Liu, P.L.F. Seepage Force on a Pipeline Buried in a Poroelastic Seabed under Wave Loadings. Appl. Ocean Res. 1986, 8, 22–32. [Google Scholar] [CrossRef]
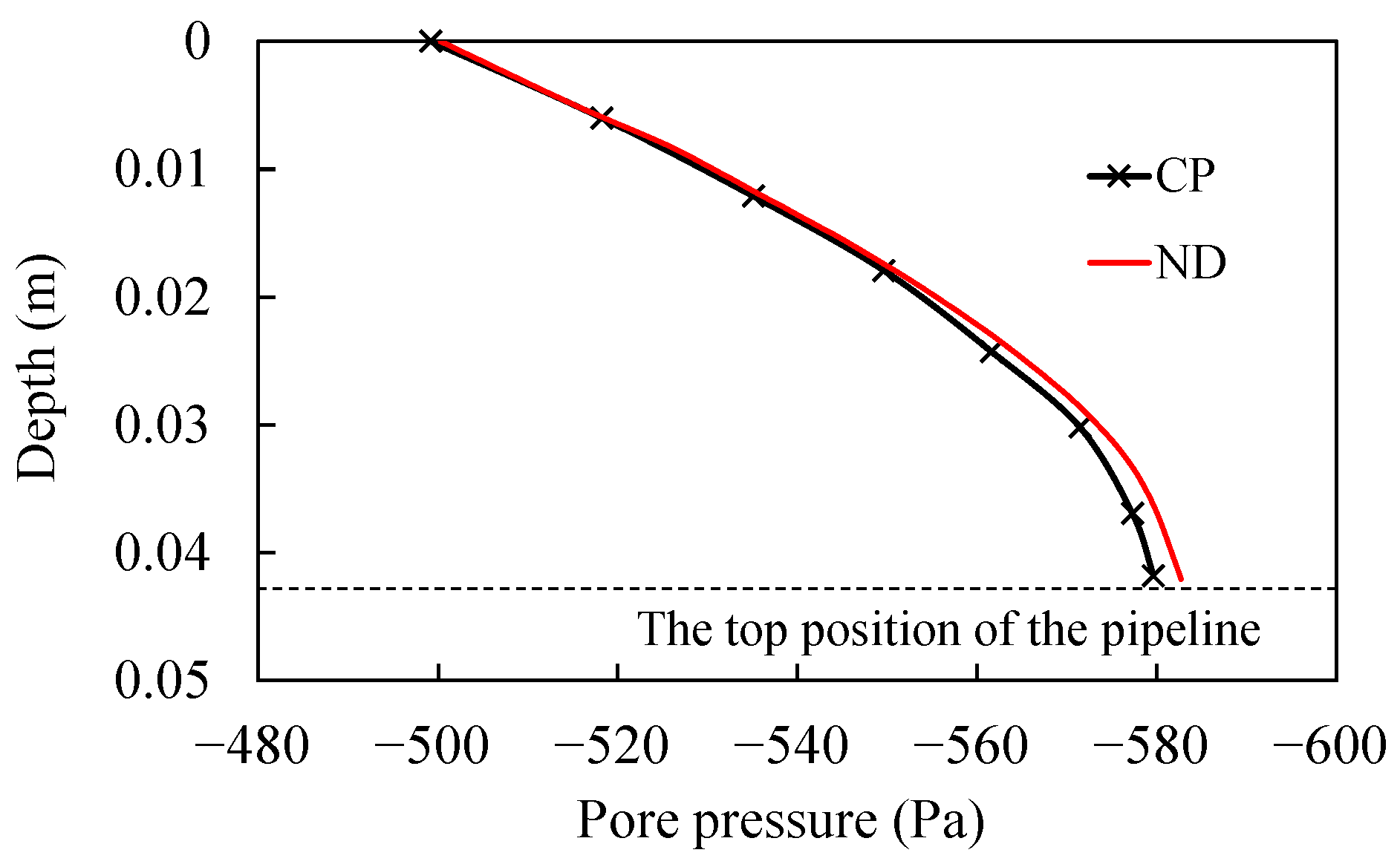
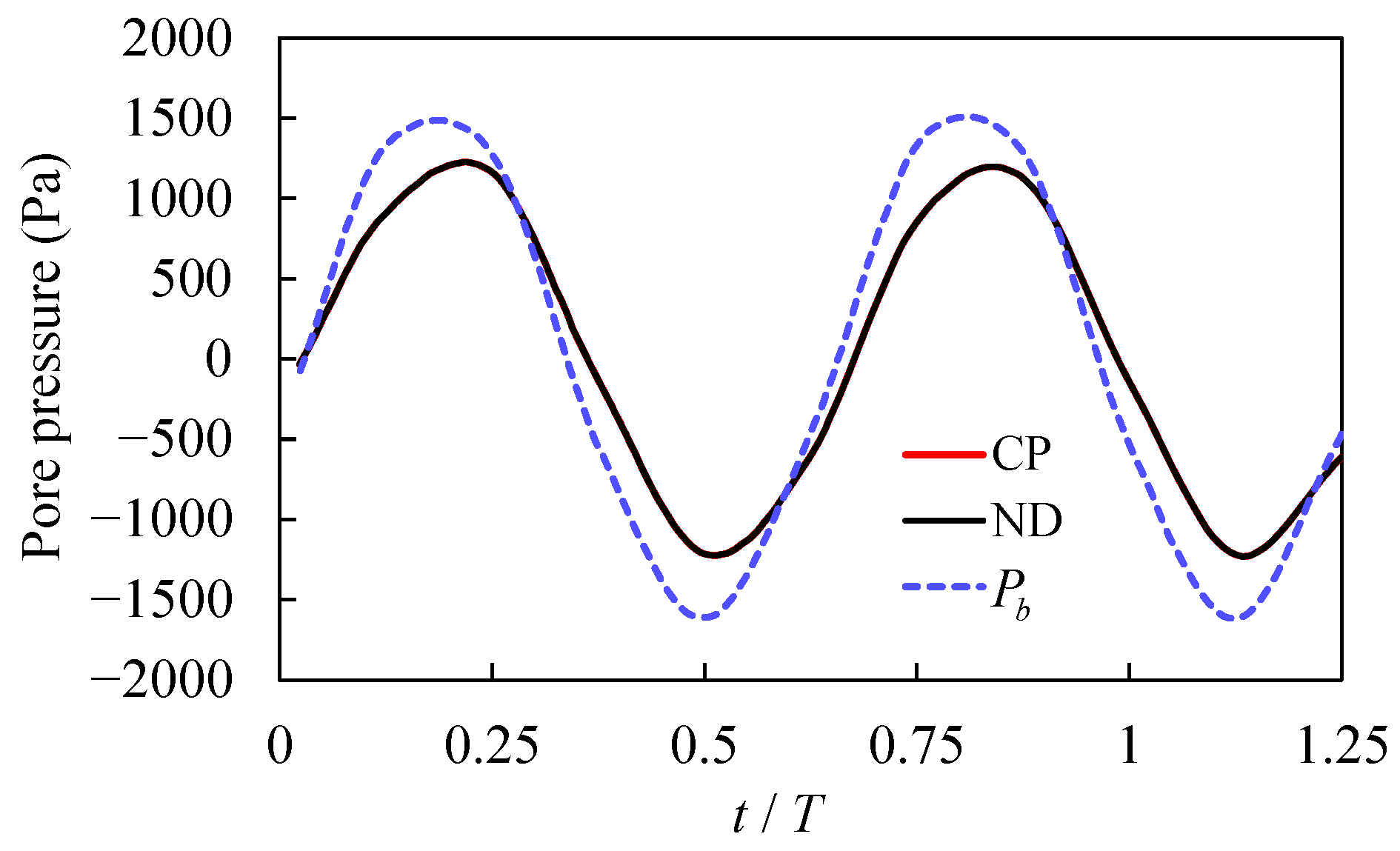
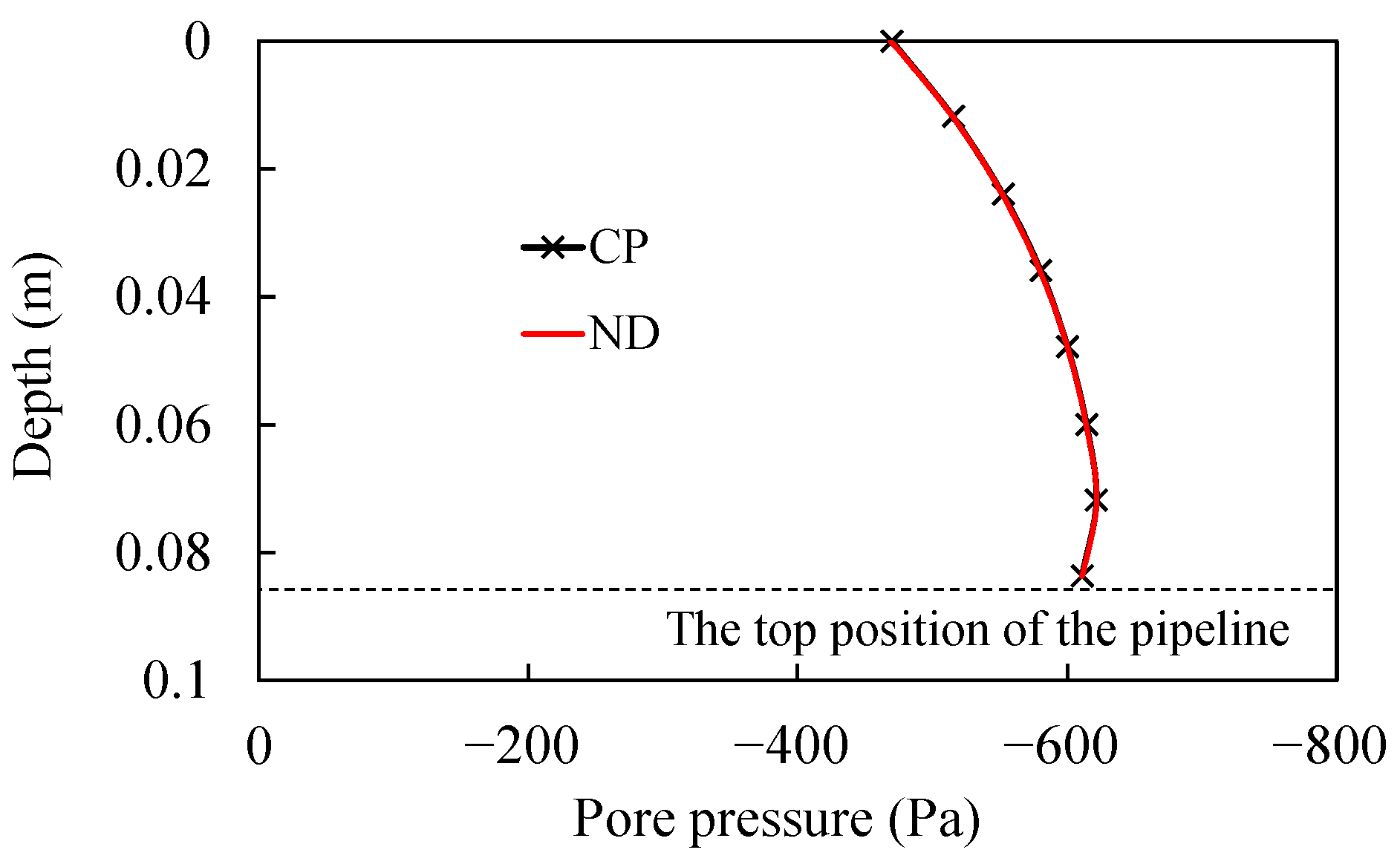
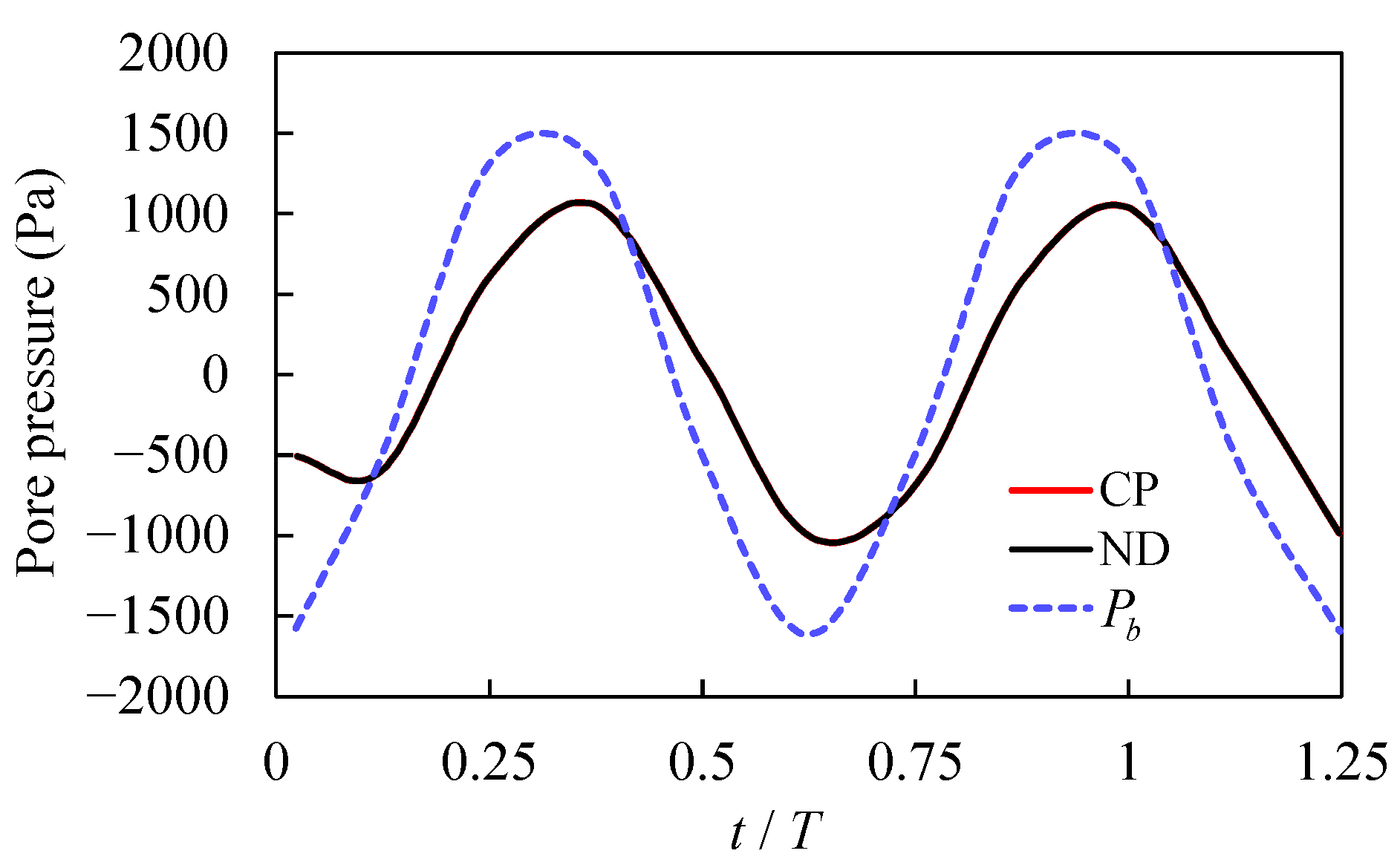


| Parameter | T (s) | L (m) | H (m) | h (m) | (-) | n (-) | γ′ (kN/m3) | (m·s−1) | E (MPa) | (-) |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 2 | 5.21 | 0.6 | 1 | 0.95 | 0.425 | 5.3 | 0.001 | 3 | 0.33 |
| Scheme No. | Burial Depth d (m) | Diameter D (m) |
|---|---|---|
| I | 0.042 | 0.042 |
| II | 0.084 | 0.084 |
| III | 0.126 | 0.126 |
| D (m) | d = D (m) | d = 2D (m) | d = 3D (m) | d = 4D (m) | d = 5D (m) |
|---|---|---|---|---|---|
| 0.042 | 0.042 | 0.084 | 0.126 | 0.168 | 0.21 |
| 0.084 | 0.084 | 0.168 | 0.252 | 0.336 | 0.42 |
| 0.126 | 0.126 | 0.252 | 0.378 | 0.504 | 0.63 |
| 0.168 | 0.168 | 0.336 | 0.504 | 0.672 | 0.84 |
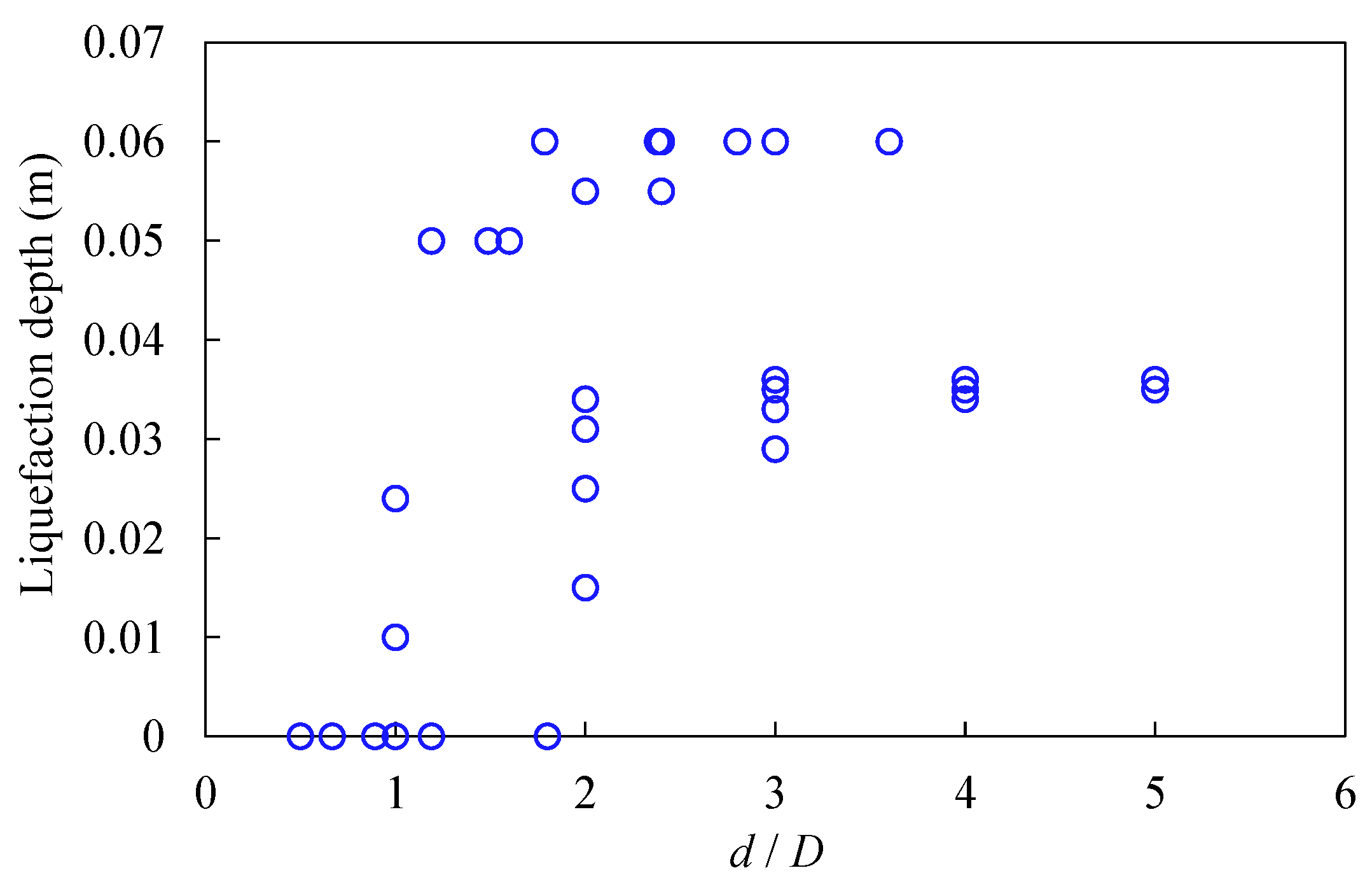
| D (m) | d (m) | d/D | Liquefaction Depths (m) |
|---|---|---|---|
| 0.084 | 0.3 | 3.6 | 0.06 |
| 0.25 | 3 | 0.06 | |
| 0.2 | 2.4 | 0.055 | |
| 0.15 | 1.8 | 0 | |
| 0.084 | 1 | 0 | |
| 0.126 | 0.35 | 2.8 | 0.06 |
| 0.3 | 2.4 | 0.06 | |
| 0.25 | 2 | 0.055 | |
| 0.2 | 1.6 | 0.05 | |
| 0.15 | 1.190476 | 0 | |
| 0.084 | 0.666667 | 0 | |
| 0.168 | 0.4 | 2.380952 | 0.06 |
| 0.3 | 1.785714 | 0.06 | |
| 0.25 | 1.488095 | 0.05 | |
| 0.2 | 1.190476 | 0.05 | |
| 0.15 | 0.892857 | 0 | |
| 0.084 | 0.5 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Zhou, M.; Zhang, D.; Qi, W.; Xue, C.; Fang, Q. Wave-Induced Instantaneous Liquefaction of a Non-Cohesive Seabed around Buried Pipelines: A Liquefaction-Associated Non-Darcy Flow Model Approach. J. Mar. Sci. Eng. 2024, 12, 373. https://doi.org/10.3390/jmse12030373
Han S, Zhou M, Zhang D, Qi W, Xue C, Fang Q. Wave-Induced Instantaneous Liquefaction of a Non-Cohesive Seabed around Buried Pipelines: A Liquefaction-Associated Non-Darcy Flow Model Approach. Journal of Marine Science and Engineering. 2024; 12(3):373. https://doi.org/10.3390/jmse12030373
Chicago/Turabian StyleHan, Shichong, Mozhen Zhou, Dingli Zhang, Wengang Qi, Chaodong Xue, and Qian Fang. 2024. "Wave-Induced Instantaneous Liquefaction of a Non-Cohesive Seabed around Buried Pipelines: A Liquefaction-Associated Non-Darcy Flow Model Approach" Journal of Marine Science and Engineering 12, no. 3: 373. https://doi.org/10.3390/jmse12030373
APA StyleHan, S., Zhou, M., Zhang, D., Qi, W., Xue, C., & Fang, Q. (2024). Wave-Induced Instantaneous Liquefaction of a Non-Cohesive Seabed around Buried Pipelines: A Liquefaction-Associated Non-Darcy Flow Model Approach. Journal of Marine Science and Engineering, 12(3), 373. https://doi.org/10.3390/jmse12030373








