Next Article in Journal
Impact of Operational Configuration Onboard a Drillship on Main Generator Engine Subcomponents Interval and Maintenance Strategies
Previous Article in Journal
Coastal Management: A Review of Key Elements for Vulnerability Assessment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 12
Issue 3
10.3390/jmse12030385
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

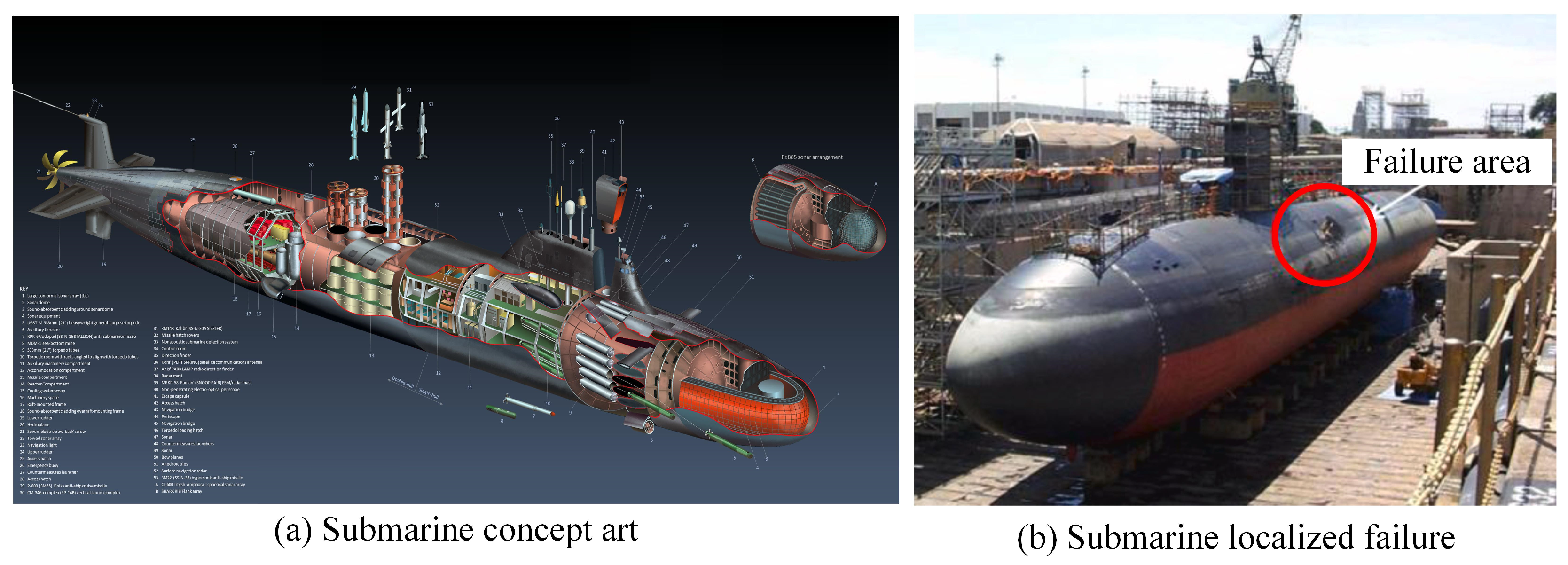
Failure Behavior of Corrugated Pressure Cylindrical Shells with Variable Wall Thickness under Uniform External Pressure

by
Jianliang Sun
1,*,
Xu Zhang
1,
Yuanhe Zhang
1,
Xianghui Lu
2 and
Yan Peng
1
1
National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China
2
Department of Electromechanics, Hebei Vocational and Technical College of Building Materials, Qinhuangdao 066004, China
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2024, 12(3), 385; https://doi.org/10.3390/jmse12030385
Submission received: 17 January 2024 / Revised: 14 February 2024 / Accepted: 17 February 2024 / Published: 23 February 2024
(This article belongs to the Section Ocean Engineering)
Browse Figures
Versions Notes

Abstract

:
The main load-bearing structure of submarines is the pressure shell. Shell failures are usually caused by high hydrostatic pressure and its own potential geometric imperfections. This paper proposes a cylindrical shell with a strong corrugated stiffening structure. Two theoretically geometrically identical shells are fabricated using CNC machining to ensure the reproducibility and reasonableness of the results. Firstly, the point cloud data of all the geometric parameters of the corrugated pressure cylindrical shells were obtained using a 3D scanner. Geomagic Control X 3D inspection software was used to determine the geometric deviations of the shells. Geometric reconstruction was performed using Geomagic Design X reverse modeling software to capture potential imperfections of the shells. The aluminum shells were then welded and placed in the pressure chamber. Failure loads were obtained for all shells by constant water injection and pressurization. Considering the confined nature of the pressure chamber, a nonlinear finite element analysis of the corrugated pressure cylindrical shell was carried out using Abaqus/Riks, taking into account actual fabrication imperfections. Finally, the failure behavior of the shells under uniform external pressure was determined. The results show that both corrugated pressure cylindrical shells have high machining accuracy. The numerical simulation results of the critical buckling load of the corrugated pressure cylindrical shells were in good agreement with the test results. The corrugated structure has additional advantages in retarding the generation and expansion of shell surface defects. The equilibrium path of the corrugated pressure cylindrical shell can be maintained in a smooth and continuous state, showing stable buckling behavior. This study will provide new inspiration for the structural design and failure prediction of the submarine pressure shell.

1. Introduction

The submarine is a naval vessel with the ability to operate underwater and complete various specialized missions, such as covert attacks against the enemy [1,2], intelligence gathering [3], surveillance, and special deployments [4,5,6]. Under combat conditions, it can dive to reasonable depths for underwater operations [7]. The most important load-bearing structure of a submarine is the pressure shell. Pressure shell dimensions and compressive properties largely determine its maximum operating depth [8,9,10,11].
Many researchers are pursuing pressure structures that combine greater diving depths, higher pressure resistance, and better safety features. This is due to the presence of a leaping layer at depths of 300–350 m, i.e., the salinity, water temperature, and density of the ocean water have a significant leap. As a result, most sonar signals are unable to detect objects below this layer, which increases the concealment of submarines [3,12]. Secondly, the substantial rise in seawater pressure below 300 m diminishes the air bubble effect created by the submarine propeller operating at high speed. Additionally, all kinds of turbulence generated by the submarine in high-speed motion are easily compressed and diluted by the water pressure [13,14,15,16]. Thirdly, once the submarine submerges to a depth of 400–500 m, most of the anti-submarine means in the world today would have difficulty attacking it effectively [7].
Based on hydrodynamics, the teardrop or nearly cylindrical pressure shells made up of a series of cylindrical shells and end spherical conical shells remain the most effective design for modern submarines [17,18,19,20,21]. This design can significantly reduce seawater resistance at high speeds [22], increase sailing speeds [23], and lower energy consumption [24,25].
Based on structural mechanics, cylindrical pressure shells are widely used due to the convenience of processing and fabricating, high utilization rate of inside space, and the ability to be combined with hemispherical, ellipsoidal, and conical heads [26,27,28,29]. Nevertheless, cylindrical pressure shells have limited compressive strength. Structural buckling failure frequently takes place before the shell material yields, which severely limits their application in offshore engineering [30,31]. Welding ring reinforcing ribs on the shell surface can significantly increase its buckling resistance, fully utilizing the advantages of material strength [32,33,34,35]. Due to the giant size of the submarine pressure shell, local buckling failure can easily occur under external hydrostatic pressure. Therefore, based on welded stiffening ribs, a few strong stiffening ribs (king stiffening ribs) are usually welded to delay the occurrence of local buckling failure [36,37]. The welding process induces varied mechanical properties in different regions of the pressure shell. Such differences are likely to result in early failure of the submarine in the vicinity of the welded areas during service. Employing CNC machining to fabricate the stiffening shell can reduce the number of weld seams to a certain extent and ensure the overall machining accuracy of the shell [38]. However, this approach would unavoidably result in material waste.
Compared to the ideal pressure shell shape, the geometry of the actual fabricated pressure shell will deviate somewhat. Sometimes this deviation is defined as geometric imperfections. Geometric imperfections are one of the most important factors affecting the failure behavior of pressure shells [39,40]. These imperfections typically arise during the machining, assembly, transportation, and operating processes of pressure shells and are virtually impossible to avoid completely. The initial geometric imperfections result in a lower failure load of the pressure shell than the theoretically calculated value and are distributed in a discrete manner. They also lead to the shell exhibiting instability and dynamic failure characteristics after reaching the failure load, which, in some cases, may lead to catastrophic results. During submarine service, various types of loads such as explosions, wave impacts, shock loads, hydrodynamic pressure, hydrostatic pressure, and gravity are often applied to the pressure shell, and the most important load is the hydrostatic pressure [41]. In addition, these loads will inevitably lead to a certain impact on the structural integrity of the pressure-resistant shells [42,43]. As the submarine dives deeper, the external seawater pressure will continue to increase. Under a high hydrostatic pressure environment and its own potential imperfections, the submarine is likely to undergo unstable local buckling and sudden collapse in a short period of time [44].
The rapid advancement of computers has led to the development and improvement of industrial software. By integrating nonlinear finite element analysis into the structural design of pressure shells, pressure-resistant structures can now be more accurately evaluated for integrity and failure behavior. Due to the limitations of the current pressure shell fabrication process, little attention has been paid to the influence of the true geometry of pressure shells, including deterministic imperfections derived from more accurate measurements, on their ultimate failure behavior [45,46]. For a conventional cylindrical pressure shell of equal wall thickness, the global thickness variation is usually ignored. The shell is simply defined as an equal wall thickness cylindrical pressure shell. However, for the variable wall thickness corrugated pressure shell investigated in this study, the wall thickness variation cannot be ignored.
The overall structure of the submarine is shown in Figure 1 [47,48]. In this work, two corrugated pressure cylindrical shells with high machining accuracy were fabricated by CNC machining. Hydrostatic pressure tests were performed on the sealed aluminum shells to determine their failure loads. In addition, a nonlinear finite element analysis using Abaqus/Riks was performed on the corrugated pressure cylindrical shells, taking into account actual fabrication imperfections, to investigate the safety and robustness of the shells under uniform external pressure.

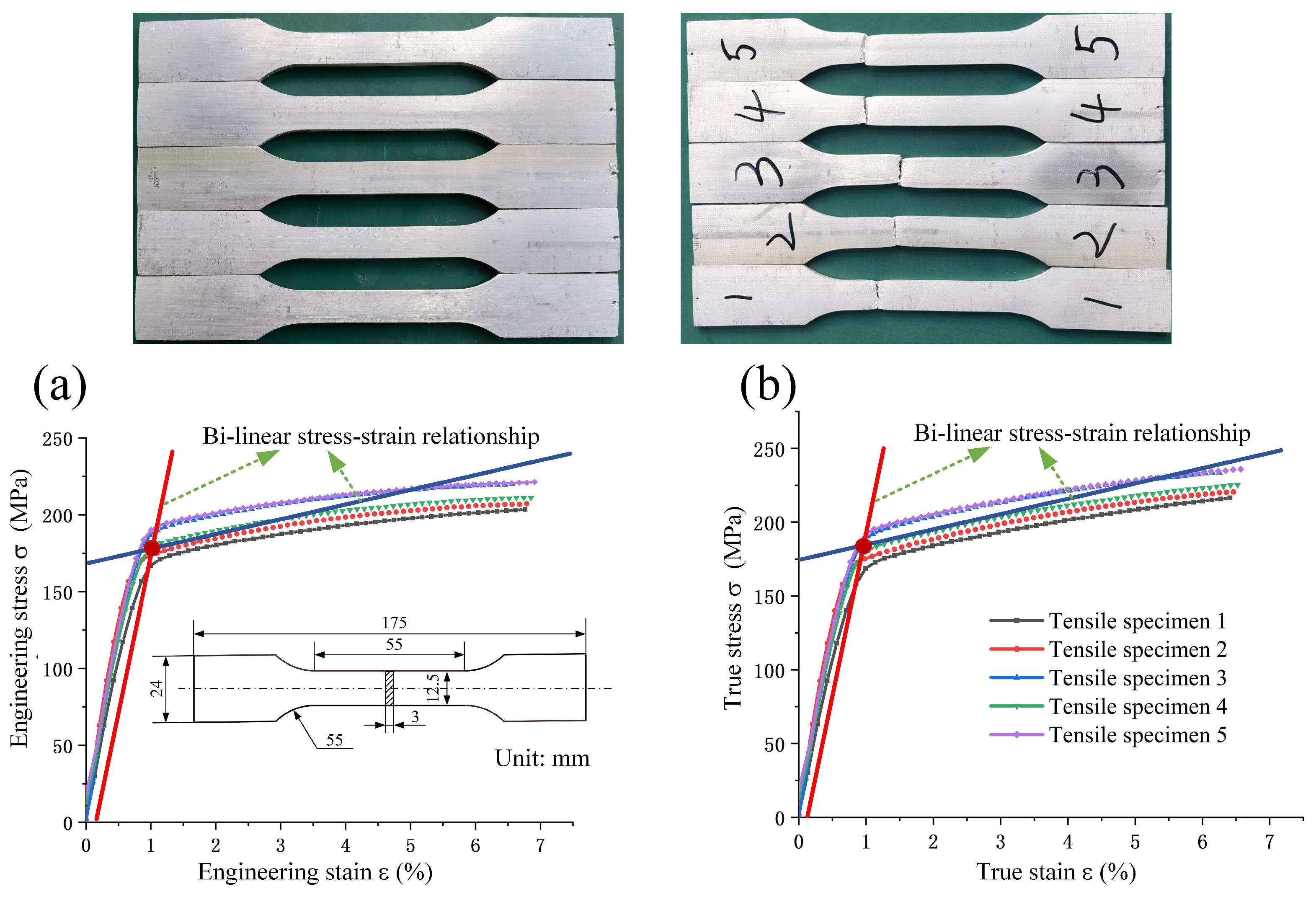
2. Specimen Design and Measurement Methods

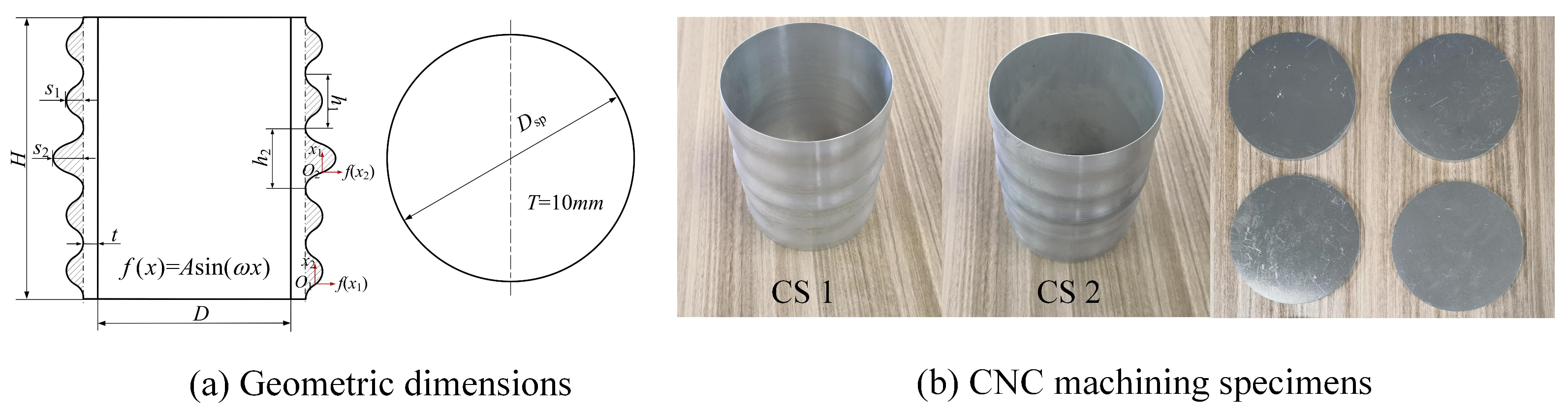
2.1. Specimen Design

Corrugated sheets and bellows construction can provide excellent compressive performance [49,50]. The utilization of variable thickness plates can considerably minimize the product weight without reducing the component service performance [51]. Therefore, this study aims to explore the impact of potential imperfections of the corrugated pressure cylindrical shell on the final failure behavior.
In practical engineering applications, the stiffening structure can be placed either inside or outside the pressure shell. The inner stiffening structure has a wider range of application scenarios, while the outer stiffening structure has the advantage of easy processing. Essentially, the corrugated structure is a form of stiffening structure with a smoother axial cross-section. In the American Bureau of Shipping (ABS) [52] and China Classification Society (CCS) [53], the compressive performance of pressure shells is stipulated primarily, with no specific requirement on stiffening location. To more accurately evaluate the failure behavior of the pressure shell, in this study, the outer corrugated pressure cylindrical shell was selected as the object to ensure the machining accuracy of the corrugated structure. In addition, we designed a strong corrugated stiffening structure in the middle region of the shell to make the corrugated structure more consistent with practical engineering applications. For ease of description, the remainder of the paper uses corrugated shells instead of pressure shells with strong corrugated stiffening structures.
The dimensions and actual specimens of the corrugated shell are displayed in Figure 2. The ideal corrugated shell has an inner diameter of D = 150 mm and a height of H = 200 mm. Two types of uniformly distributed sinusoidal corrugations can be found on the shell’s outer surface. The main parameters of the first sinusoidal corrugation are as follows: number of corrugations n1 = 4, corrugation amplitude A1 = 1 mm, corrugation span h1 = 2π/ω = 40 mm, where ω represents the frequency 0.05π. The main parameters of the second sinusoidal corrugation are as follows: number of corrugations n2 = 1, corrugation amplitude A2 = 2 mm, corrugation span h2 = 2π/ω = 40 mm. The two sinusoidal corrugations have the same corrugation span and frequency, and the main difference lies in the number of corrugations and corrugation amplitude. The distribution locations of the two sinusoidal corrugations are shown in Figure 2a.
For corrugated shells, the shell wall thickness varies periodically along the axial direction. In this study, wall thickness t is defined as the shortest horizontal distance, i.e., the theoretical thinnest wall thickness t = 1.0 mm. The corrugation height s is defined as the maximum horizontal distance. Under ideal conditions, the corrugation height s1 = 2A1 = 2.0 mm and the strong corrugation height s2 = 2A2 = 4.0 mm. However, the results are slightly different when actual fabrication errors are considered. In order to ensure that the sealing circular plates can effectively seal all ends of the corrugated shells in the subsequent welding and minimize their impact on the failure behavior, define Dsp = 154 mm and T = 10 mm, where Dsp and T are the sealing circular plate diameter and thickness, respectively.
Extruded Al6061-T6 aluminum alloy seamless cylindrical preforms were used as the raw material for the experiment. To guarantee the reproducibility and reasonableness of the test outcomes, two theoretically identical corrugated shells were acquired through CNC machining. The machining results are shown in Figure 2b, where the two corrugated shells are defined as CS1 and CS2, respectively. The sealing circular plate was cut from a 10 mm thick square plate, as shown in Figure 2b.

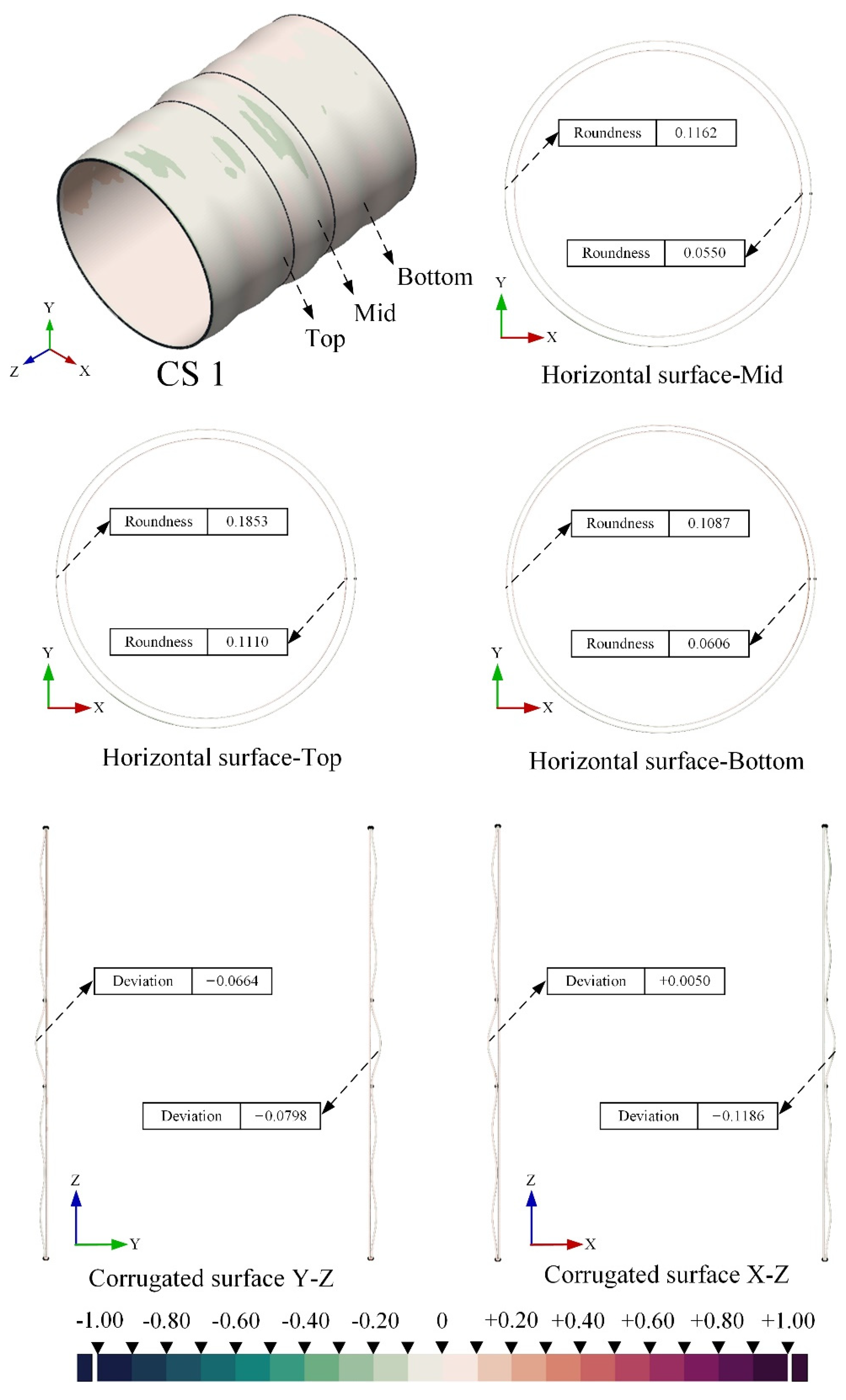
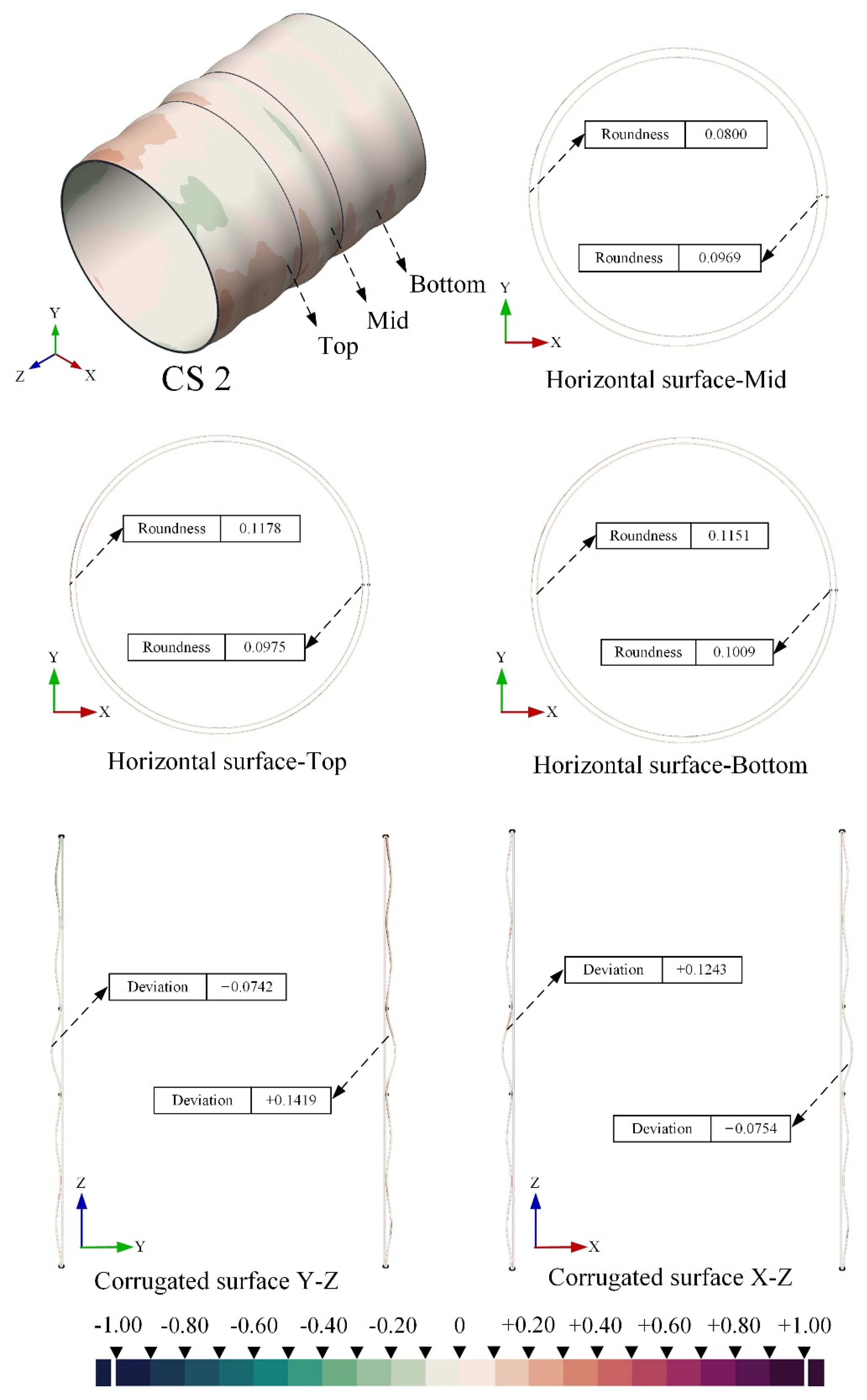
2.2. Geometric Parameter Measurements

Submarine pressure shell failures typically result from high external hydrostatic pressures and their own potential imperfections. The potential imperfections can be divided into two main types: geometric imperfections and material imperfections. The former mainly includes out-of-roundness [54] and thickness deviation [55], while the latter mainly includes material anisotropy [56] and residual stress [57,58]. These two sets of factors interact with each other. Material anisotropy and residual stresses can be eliminated by proper heat treatment [59,60]. The underlying geometric imperfections of the pressure shell are the key factors influencing the failure behavior of the pressure shell.
For conventional cylindrical pressure shells with equal wall thickness, out-of-roundness is one of the main factors influencing their failure behavior [54]. Therefore, it is possible to ignore their global thickness variation without affecting the accuracy of the final calculation. However, for pressure shells with variable thickness, it is essential to consider their thickness variations. Ultrasonic gauges can be utilized to precisely measure the thickness variation of each section of the pressure shell [61]. For corrugated shells, the wall thickness varies periodically along the axial direction. Obtaining complete information on wall thickness variation through an ultrasonic measuring instrument for the shell would be a huge amount of work. Therefore, it is necessary to propose a new method to obtain the potential imperfections of corrugated shells.
We chose the DUUMM V900 handheld 3D laser scanner to measure the geometric point cloud data of the corrugated shell, as shown in Figure 3. On the surface of the shell, approximately 100 marking points were randomly taped at approximately 2–3 cm intervals. Taking into account the presence of corrugated morphology on the outer surface of the shell, we employed a higher number of marking points on this surface. Subsequently, the shell surface was scanned smoothly along axial and circumferential directions using a 3D laser scanner to capture the full information of the corrugated morphology. The scanner has an accuracy of 0.025 mm. The final output of the point cloud data is approximately 2,120,000 laser points. In this study, the wall thickness of the ideal corrugated shell is 1 mm, and measurement error is 2.5%, which is within the acceptable range.

2.3. Reverse Modeling and Geometric Imperfections Characterization

After obtaining the point cloud data of corrugated morphology information, it is necessary to perform reverse modeling processing and geometric imperfections characterization. The basic process is shown in Figure 4. In addition, this study neglected the impact of welding residual stresses on the corrugated shells.
The point cloud data obtained from 3D laser scanning tend to have local scanning blind spots and noise, which cannot fully meet the requirements of realism and real time of the digital model. The corrugated shell point cloud data were preprocessed using Geomagic Design X 2020 software, followed by reverse modeling, and the results are shown in Figure 5. The initial geometric imperfections clouds of the corrugated shell are all on the same scale (−1 mm~1 mm). It can be observed that the reverse modeling results have high accuracy (±0.1 mm, green area). Therefore, the authors concluded that the reverse modeling results of the corrugated shell CS1 and CS2 are good.
Geomagic Control X was utilized to identify geometric deviations in the actual fabricated corrugated shells. Considering that the geometric deviation of different planes of corrugated shells all have some differences, three X-Y horizontal planes, top, middle, and bottom, are selected to observe the roundness variation and thickness deviation. In addition, the X-Z and Y-Z vertical planes are taken as an example to analyze the local thickness deviation variation of corrugated shells, as shown in Figure 6. The initial geometric imperfections clouds of the corrugated shells are all on the same scale (−1 mm to 1 mm). Positive values represent large thicknesses and negative values represent small thicknesses. Compared to the ideal model, the actual fabrication errors of the corrugated shells are relatively small, and the overall corrugated morphology is good. The only slight difference in the local region is in CS 1 and CS 2, which is due to the randomness of the fabrication errors caused by the CNC machining. Nevertheless, the overall fabrication error is largely within ±0.20 mm, demonstrating the high machining accuracy of the corrugated shell.

3. Hydrostatic Uniform External Pressure Test

The corrugated shell underwent hydrostatic pressure testing by using a deep-sea pressure simulation chamber to simulate an underwater high-pressure environment, as shown in Figure 7. As the corrugated shell does not contain a power unit, it may float on the water surface during the test due to its lower gravity compared to the buoyancy force. This may result in non-uniform distribution of external water pressure on the corrugated shell. The test results will be significantly affected by this [62]. The decision was made to secure the shell in the water using a rope. In this study, the pressure loading history of the corrugated shell is divided into three stages, as shown in Figure 8, following the pressurization curve of a spherical shell under hydrostatic pressure proposed by Pan et al. [63].
The pressure chamber was first filled with water and then pressurized to test that the equipment is working properly. Afterwards, the shell was placed into the pressure chamber and the chamber was filled with water to exhaust the air. The chamber was slowly pressurized with water to about 0.2 MPa by manually adjusting the pressure pump. The pressure was then removed to minimize residual stresses in the welded areas of the shell. Finally, manually adjust the pressure pump again to slowly pressurize the chamber with water, and when the bursting sound is heard from the destruction of the shell, the pressurization is stopped and the test data are recorded. After the chamber is depressurized, open the chamber cover and remove the model. Record the experimental data and observe the failure of the corrugated shell morphology. The test results are shown in Table 1. The critical buckling loads of the corrugated shells CS1 and CS2 were 3.2 MPa and 3.4 MPa, respectively. The difference on the critical buckling load between the two shells is only 0.2 MPa. It proves the reproducibility and reasonableness of the test results. The failures all occurred close to the thin-walled area of the corrugated shell, and the sealing plates at both ends were essentially undeformed. Both have very similar failure loads and failure modes.

4. Nonlinear Buckling Failure Analysis

To ensure the safety and robustness of the corrugated shell under external hydrostatic pressure, it is necessary to understand the collapse behavior accompanied by buckling and to estimate the failure behavior as well as the defect generation on the corrugated shell surface with high accuracy. It is unrealistic to try to fully obtain the buckling behavior and failure mechanism of the corrugated shell at different stages purely through tests, and a nonlinear analysis of the geometric model for reverse modeling of the corrugated shell was performed using Abaqus with reference to ABS [52] and CCS [53].

4.1. Solver Selection

In general, the theoretical buckling strength of the pressure shell can be determined by solving the characteristic equations. Solving the eigenvalues and corresponding eigenmodes of the pressure shell under uniform external pressure is called “eigenvalue buckling analysis”. However, in practical engineering applications, due to the limitations of the fabrication process, there is inevitably a certain error between the actual fabricated pressure shell and the theoretical model. Therefore, only calculating the eigenvalue buckling does not represent the actual buckling strength of the structure. The Arc Length Method (Riks) proves to be particularly advantageous in solving the nonlinear buckling strength of the pressure shell under uniform external pressure. Abaqus/Riks was finally chosen for nonlinear analysis of the corrugated shell reverse modeling model.
A 10 mm thick sealing circular plate is selected to minimize the effect of plate thickness on the failure behavior of the corrugated shell. In the finite element simulation, a “Tie” connection is defined for the connection area between the upper and lower ends of the corrugated shell and the end circular plates. It is assumed that no welding failure would occur in the corrugated shell under hydrostatic pressure. The uniform pressure acting on the outer surface of the sealed corrugated shell is defined as 1 MPa, resulting in a final load scaling factor that was numerically equal to the critical buckling load of the corrugated shell. The effects of geometric nonlinearity and material nonlinearity are considered in the Riks, and the solving parameters are tabulated in Table 2. The mechanical property parameters of 6061-T6 are shown in Figure 9 and Table 3. Repeated tensile tests were carried out on five identical specimens, taking into account the various errors that may exist during the experiment. More detailed measurements of aluminum alloy material parameters can be found in the literature [55].

4.2. Mesh Selection

Considering that the wall thickness of the corrugated shell varies periodically along the axial direction, the thickness variation cannot be ignored. Consequently, the corrugated shell, considering actual geometric imperfections, is defined as a three-dimensional solid unit with mesh type C3D8R. The sealing circular plate is defined as a shell unit with mesh type S4R. We found that when the mesh number of the corrugated shell is 47,800 (there is a slight difference in the mesh number between corrugated shells CS1 and CS2 due to the different actual fabrication imperfections) and the mesh number of the sealing circular plate is 5760, the increase in the mesh number thereafter has less effect on the failure loads of the corrugated shells. The boundary conditions for the sealed corrugated shell are shown in Figure 10. In order to show the boundary conditions more clearly, only half of the model is shown. With reference to CCS [53], a symmetric setting of the three-point support boundary condition is chosen, which eliminates the rigid displacement of the entire sealing pressure shell and has no effect on the shell deformation.

4.3. Results Analysis and Discussion

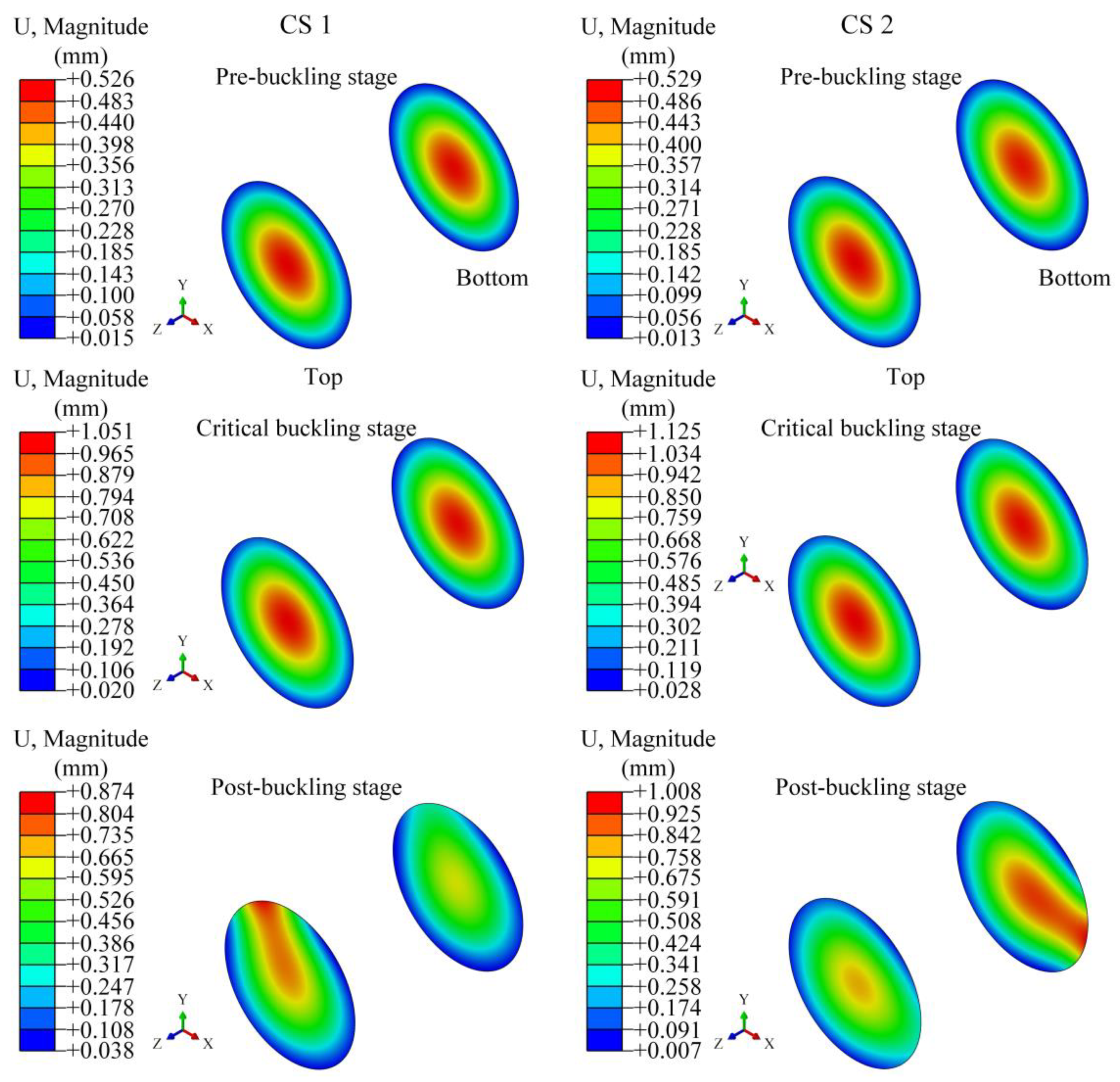
4.3.1. Sealing Circular Plates Variations

The displacement variations of the sealing circular plates in different buckling states are shown in Figure 11. The sealing circular plates of CS1 and CS2 are highly similar in different buckling states. In the pre-buckling and critical buckling stages, the ends of the sealing plates basically do not change, and the displacement in the center is relatively large, with the overall tendency of inward concavity. The sealing circular plates exhibit regular changes. In the post-buckling stage, the displacement changes of the sealing circular plates of the corrugated shells CS1 and CS2 can also be considered to be very similar, and only the nominal coordinates have some differences. This is due to the potential imperfections of the corrugated shells considered in the finite element simulation process. For CS1, the shell near the positive direction of the z-axis has a larger localized error, resulting in a larger displacement variation of the sealing circular plate top. For CS2, the shell near the negative direction of the z-axis has a larger local error, resulting in a larger displacement variation of the sealing plate bottom.
For the sealing circular plates, the maximum displacement occurs in the critical buckling stage. This is due to the fact that at this time, the corrugated shell is subjected to the largest external pressure, and the pressure acting on the outer surface of the sealing circular plates is also the largest. As a result, the displacement of the sealing circular plates in this state changes significantly. The displacement magnitude of the sealing circular plates in the whole buckling process is relative. Through observation, it can be found that due to the fact that the sealing circular plates are thicker, the maximum displacement in the whole buckling process is only about 1 mm. It can be considered that the sealing circular plates have sufficient stiffness.

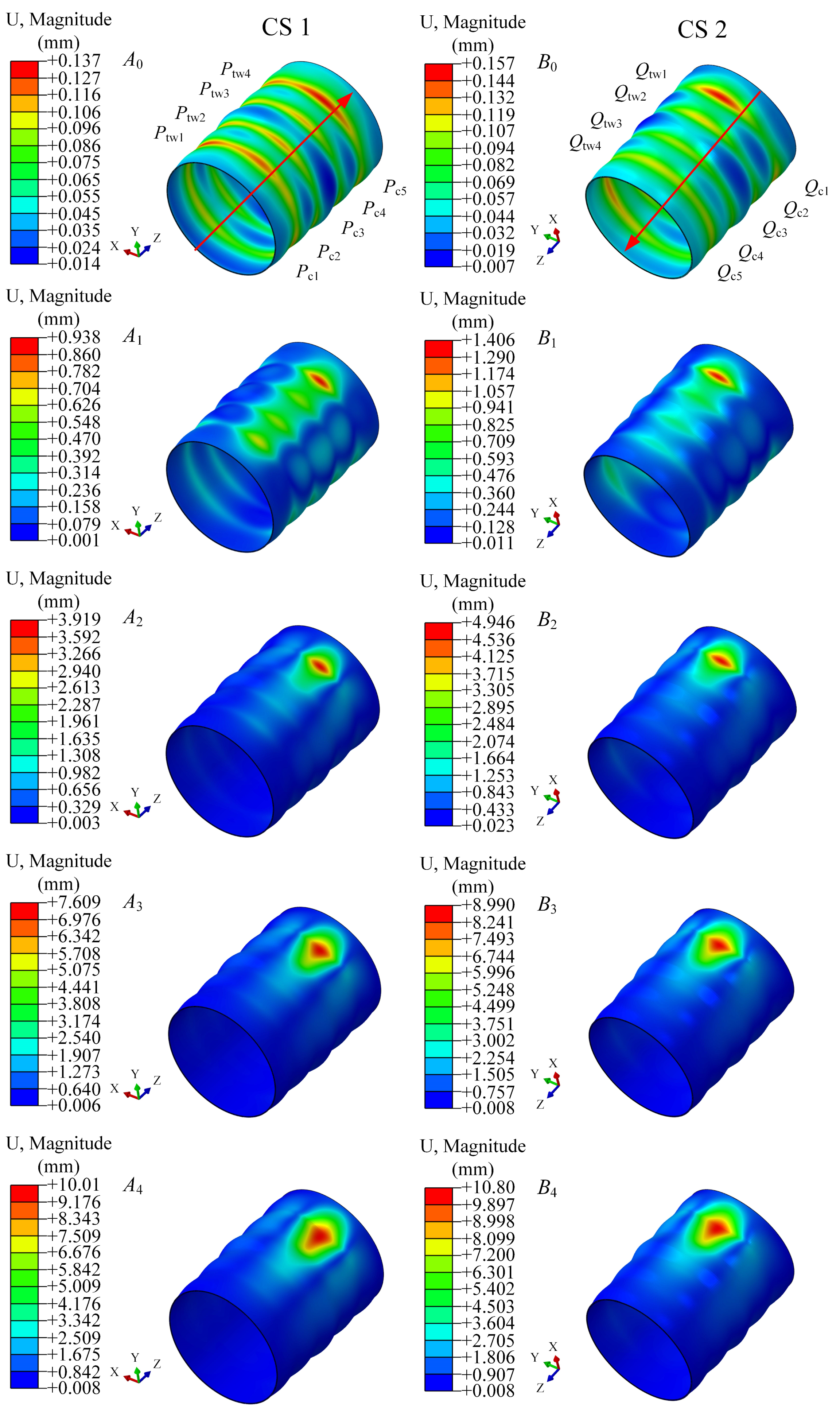
4.3.2. Corrugated Shell Variations

In solving the equilibrium path of the sealed corrugated shell model, the displacement changes at different nodes of the model are different. The node at which the maximum displacement occurs on the corrugated shell is selected as the object of study, and the equilibrium path is shown in Figure 12. Where A0 represents the pre-buckling state, A1 represents the critical buckling state, and A2–A5 represent the post-buckling state. We can find that the critical buckling loads for the corrugated shells CS1 and CS2 are 3.063 and 3.188 MPa, respectively. In addition, the corrugated shell equilibrium paths show a regular variation, which is a typical steady-state buckling.
For corrugated shell CS1, we divide the outer surface along the z-axis positive direction into thin-walled region Ptwi (i = 1–4) and corrugated region Pcj (j = 1–5). For corrugated shell CS2, we also divide the outer surface along the z-axis positive direction into thin-walled region Qtwi (i = 1–4) and corrugated region Qcj (j = 1–5). Figure 13 shows the displacement variation of the corrugated shell in different buckling states. Theoretically, the maximum displacement of the corrugated shell should appear near the middle region of the corrugated shell under the symmetric boundary condition. However, the simulation results show that the maximum displacement of the corrugated shell CS1 occurs in the thin-walled region Ptw4, and the maximum displacement of the corrugated shell CS2 occurs in the thin-walled region Qtw1. The failures of the two corrugated shells in different buckling states are very similar, and only the nominal coordinates have some differences. This shows that even if the CNC machining of the corrugated shells has reasonable machining accuracy, local geometric imperfections are still unavoidable.
Pre-buckling stage: For the corrugated shell CS1, the displacement changes in the thin-walled regions Ptw1 and Ptw4 are more obvious and coordinated. The displacement changes in the corrugated region are relatively small. For corrugated shell CS2, the displacement change in the thin-walled region Qtw1 is more obvious. The displacement changes in the corrugated region are relatively small. The regions where the maximum displacements occur are similar for CS1 and CS2, but the overall displacement changes for CS1 are somewhat more symmetrical.
Critical buckling stage: For corrugated shell CS1, the displacement change in the thin-walled region Ptw4 is more pronounced. The displacement changes in other thin-walled and corrugated regions are more coordinated. For corrugated shell CS2, the displacement change in the thin-walled region Qtw1 is more obvious. The overall displacement changes in CS1 and CS2 are very similar, except that CS2 has a larger maximum displacement in the critical buckling state. This also explains why the critical buckling load is higher for CS2.
Post-buckling stage: There are three periods with different pressure decrease rates. As the displacement of the corrugated shell increases, the pressure decrease rate gradually slows down and finally stabilizes. For the corrugated shell CS1, the maximum displacement occurs near the thin-walled region Ptw4, and there is a tendency to expand in the negative direction of the z-axis. For the corrugated shell CS2, the maximum displacement occurs near the thin-walled region Qtw1, and there is a tendency to expand to the positive direction of the z-axis. The corrugated structure can suppress the expansion to some extent and slow down the rate of pressure drop. The presence of a strong corrugated structure can enhance this suppression effect to some extent.

4.3.3. Surface Defect Generation

Figure 14 shows the stress variation of the corrugated shells in different buckling states. In the pre-buckling state, the overall stress variations of CS1 and CS2 are very similar. The maximum Mises stresses mainly appear at the end of the corrugated shell. The overall stress variation in the thin-walled region is lower than that in the corrugated region, which is due to the larger thickness of the corrugated region. In the critical buckling state, the overall stress variation of CS1 is more symmetrical, and the maximum stress region mainly occurs in the thin-wall region Ptw1, Ptw4 and the end, while the maximum stress region of CS2 mainly occurs in the thin-wall region Qtw1 and the end. At this time, some scattered ring defects (Ptw2, Ptw3 and Qtw2, Qtw3, Qtw4) appear in the thin-walled regions of corrugated shells CS1 and CS2, thereafter entering the post-buckling state. The stress variations of CS1 and CS2 in the post-buckling stage are very similar. For the corrugated shell CS1: at the moment A2, the maximum Mises stress occurs mainly in the thin-walled region Ptw4, and there is a tendency for small defects near Ptw4 to be connected. At the moment A3, the corrugated shell as a whole is subjected to a larger Mises stress, and the small defect near Ptw4 starts to expand into an approximate small diamond-shaped defect. At the moment of A4, the small diamond-shaped defect expands along the negative direction of the z-axis and gradually forms a large diamond-shaped defect.
In general, with the increase in external pressure, the corrugated shell surface will produce some sporadic ring defects. They gradually deepen and expand and eventually form a large diamond-shaped defect. The existence of a corrugated structure can inhibit the generation of scattered ring-shaped defects to a certain extent. When the small diamond-shaped defect starts to expand, the corrugated structure can also delay the transformation of the small diamond-shaped defect to the large diamond-shaped defect to a certain extent. We observe the defect expansion path of the corrugated shell and find that the defect expansion rate is not uniform. This is because the initial geometric imperfections of the corrugated shell are considered in the nonlinear analysis, and the distribution of the geometric imperfections has a certain randomness. In addition, in the nonlinear analysis of the corrugated shell model, the thickness distribution at the corrugated shell end is not uniform, which is the main reason for the end stress concentration phenomenon in the early stage. In this study, the main failure regions of the corrugated shell are near the thin-walled region of the corrugated shell, which also indicates that it is reasonable to ignore the effect of weld strength when analyzing the shell failure.

5. Discussion

During submarine service, various types of loads such as explosions, wave impacts, shock loads, hydrodynamic pressure, hydrostatic pressure, and gravity are often applied to the pressure shell, and the most important load is the hydrostatic pressure applied to the shell’s outer surface. Submarine failure is often the result of multiple loads acting together. This study focuses on hydrostatic pressure and uses a combination of numerical simulations and experiments to investigate the influence of the potential imperfections of the corrugated shell itself on its failure behavior. To ensure the accuracy and repeatability of the test results, two theoretically identical corrugated shells are fabricated by CNC machining, taking the external corrugated structure as an example.
In terms of fluid mechanics, the inner corrugated structure has better practical engineering application scenarios. However, when the authors attempted to fabricate the inner corrugated structure, the overall fabrication accuracy was found to be low. This phenomenon becomes more pronounced when strong corrugated structures are considered. Therefore, the subsequent research work can put more energy into the inner corrugated structure under the premise of ensuring the machining accuracy. Furthermore, due to the military and classified nature of submarines, many relevant test data have not been disclosed. This results in fewer relevant reference materials. Considering the cost of specimen machining and the actual test conditions, only laboratory-level hydrostatic pressure tests were conducted in this study for aluminum corrugated shells. How to apply the existing small-scale results with high fidelity to actual submarine pressure shell structures will be the focus of future work.
In addition, the fabrication process for ring- and T-shaped stiffening pressure shells, which are in very mature operation at this stage, can be divided into two main steps. The first step is the large plate rolling machine, which is subsequently longitudinally welded into a cylindrical part. The second step is to weld circumferential stiffening ribs inside it. The presence of welded areas (axial welds of the cylinder and circumferential welds of the stiffening ribs) will inevitably degrade the overall mechanical properties of the pressure shell. For the corrugated shell proposed in this study, its structure is characterized by the continuous smooth variation of the corrugated stiffening part. This characteristic contributes to the innovation of the fabrication process of the corrugated stiffening shell.
In this study, numerical simulations and test validation were conducted only for aluminum corrugated shells. Considering that, the failure behavior of different pressure shell materials under uniform external pressure will be different. How the existing research on corrugated structures can be applied to other commonly used pressure shell materials such as high-strength steel or composite materials will help to further promote the use of corrugated structures in the marine field.
It is a long process from the proposal of a pressure shell structure to its practical application. In this study, we choose the von Mises criterion for a simple analysis of the corrugated cylindrical shell stress case. However, when applying the corrugated structure to the submarine pressure shell, we also need to pay more attention to the stress concentration situation near the shell load transfer nodes and opening regions. Moreover, for a 3-axis stress state, one of which has a negative value, the intensity criterion more accurately captures the maximum shear stresses that threaten the integrity of the shell. We also need to increase the stress calculations by 2–5% to eliminate the effects of numerical errors and other factors.
Compared with the traditional finite element, this study used a 3D scanner to obtain the potential imperfections information of the corrugated shell itself and performed the inverse modeling process. It makes the finite element simulation results have better agreement with the test results. However, the cumbersome process of reverse modeling is a major constraint to its wide-scale application.
Boundary conditions have a strong influence on the failure behavior of pressure shells. Submarines achieve submergence in the ocean mainly through internal power units. Considering the cost of the experiment, the size of the pressure shell and the limitation of the test conditions, the pressure shell in this paper does not have any internal power unit. In order to avoid the influence of buoyancy on the failure behavior of the pressure shell, it is chosen to tie a rope on the outer surface of the shell to realize the fixation of the pressure shell in the water. This will inevitably have some influence on the boundary conditions. The best way to fully determine whether the immobilization of the pressure shell by the rope will have a significant effect on its buckling critical load and failure behavior is still to improve the existing hydrostatic pressure device. Installing a high-speed camera in the pressure chamber is a good option.

6. Conclusions

(1)
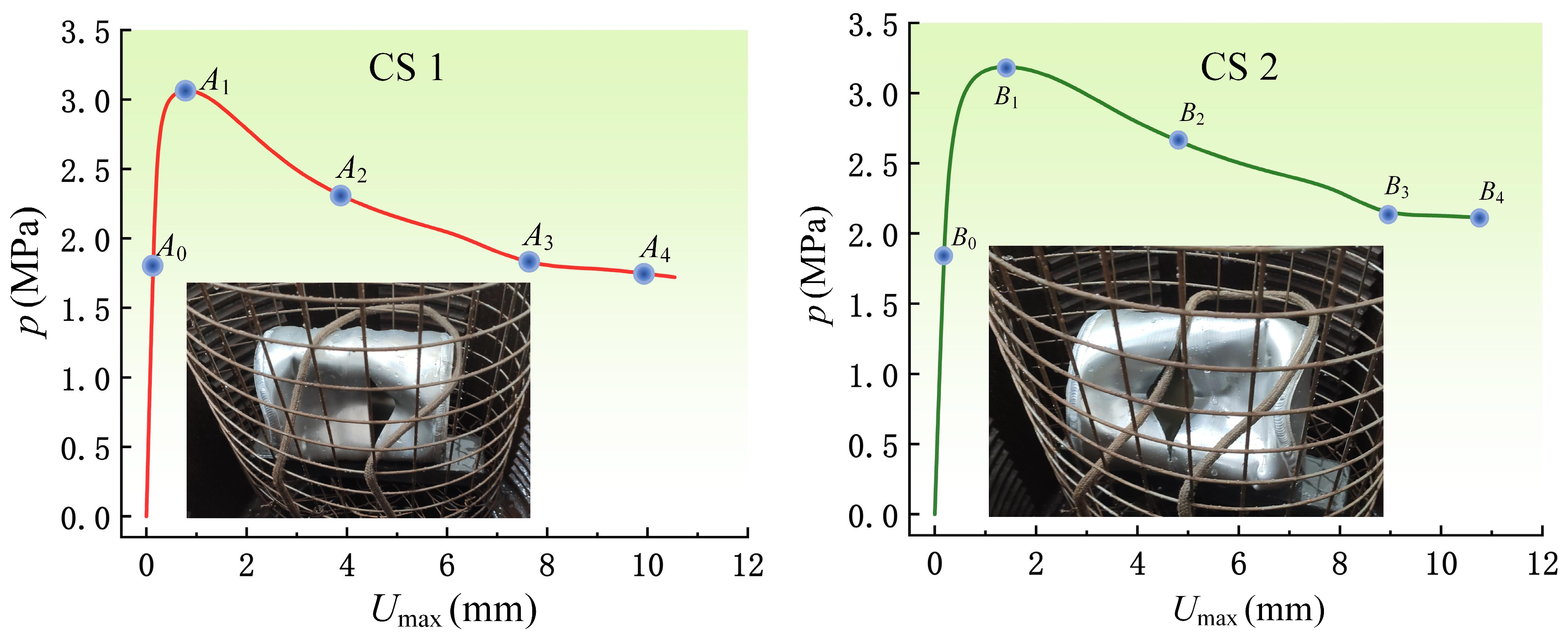
The hydrostatic pressure test results show that the critical buckling load of the two corrugated pressure cylindrical shells differed by only 0.2 MPa. The reproducibility and reasonableness of the test results are proved.
(2)
The numerical simulation results for the critical buckling load of the corrugated pressure cylindrical shell considering fabrication imperfections were in good agreement with the test results. It is demonstrated that the reverse modeling technique has great potential in reproducing the shell failure behavior.
(3)
The corrugated shell equilibrium path exhibits a regular variation that is a typical steady-state buckling. The corrugated structure provides an additional advantage in retarding the generation and expansion of defects on the shell surface.

Author Contributions

J.S. Conceptualization, Funding acquisition, Supervision, Project administration, Resources, Writing—Review & Editing. X.Z. Formal analysis, Methodology, Software, Validation, Visualization, Writing—Original Draft. Y.Z. Methodology, Validation, Visualization. X.L. Methodology, Software. Y.P. Project administration, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 52075473), the Natural Science Foundation of Hebei Province (No. E2021203190), the Central Government Guides Local Science and Technology Development Fund Projects (No. 216Z1602G and No. 206Z1601G), and the Qinhuangdao Science and Technology Research and Development Program Projects (No. 202301A007). And the authors would like to express their gratitude to the Institute of Underwater Engineering, Shanghai Jiao Tong University, for their support in hydrostatic pressure testing.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from Jianliang Sun ([email protected]).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Stefan, S.; Baljit, S.; John, W. Submarine Hull Impacts: Validation of Finite Element Models from Submarine Impact Trials; Rolls-Royce and the UK MoD: London, UK, 2009. [Google Scholar]
  2. Donner, R.; Besnier, F.; Le, S.H. Numerical simulation of ship-submarine collisons. In Proceedings of the Practical Design of Ships and Other Floating Structure Conference, PRADS, Shanghai, China, 16–21 September 2001. [Google Scholar]
  3. Wikipedia. ARA San Juan (S-42), the Free Encyclopedia. 2019. Available online: https://en.wikipedia.org/wiki/ARASanJuan(S-42) (accessed on 2 August 2019).
  4. Geoffrey, P.C. The Design of an Intelligent Decision Support Tool for Submarine Commanders. Master’s Thesis, Engineering Systems at the Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
  5. Burcher, R.; Rydill, L. Concepts in Submarine Design, 1st ed.; Cambridge University Press: Cambridge, MA, USA, 1995. [Google Scholar]
  6. DPA. SSP 74 Design of Submarine Structures; Defence Procurement Agency, Sea Technology Group: London, UK, 2001. [Google Scholar]
  7. Wikipedia. The Manhattan Project, the Free Encyclopedia. 2019. Available online: https://en.wikipedia.org/wiki/Manhattan_Project (accessed on 1 August 2019).
  8. MacKay, J.R.; Smith, M.J.; Keulen, F.V.; Bosman, T.N.; Pegg, N.G. Experimental investigation of the strength and stability of submarine pressure hulls with and without artificial corrosion damage. Mar. Struct. 2010, 23, 339–359. [Google Scholar] [CrossRef]
  9. MacKay, J.R.; Keulen, F.V. Partial safety factor approach to the design of submarine pressure hulls using nonlinear finite element analysis. Finite Elem. Anal. Des. 2013, 65, 1–16. [Google Scholar] [CrossRef]
  10. Smith, M.J.; Macadam, T.; MacKay, J.R. Integrated modelling, design and analysis of submarine structures. Ships Offshore Struct. 2015, 10, 349–366. [Google Scholar] [CrossRef]
  11. Yu, C.L.; Guo, Q.B.; Gong, X.B.; Yang, Y.F.; Zhang, J. Fatigue life assessment of pressure hull of deep-sea submergence vehicle. Ocean Eng. 2022, 245, 110528. [Google Scholar] [CrossRef]
  12. Wen, G.L.; Lu, Y.Z.; Zhang, Z.Y.; Ma, C.S.; Yin, H.F.; Cui, Z. Line spectra reduction and vibration isolation via modified projective synchronization for acoustic stealth of submarines. J. Sound Vib. 2009, 324, 954–961. [Google Scholar] [CrossRef]
  13. Jeong, S.J.; Hong, S.Y.; Song, J.H.; Kwon, H.W.; Seol, H.S. Numerical method to determine the cavitation inception speed of a submarine propeller based on the noise obtained from bubble dynamics. Ocean Eng. 2022, 245, 110464. [Google Scholar] [CrossRef]
  14. Chen, F.; Chen, Y.; Hua, H.X. Vibration analysis of a submarine elastic propeller-shaft-hull system using FRF-based substructuring method. J. Sound Vib. 2019, 443, 460–482. [Google Scholar] [CrossRef]
  15. Han, H.; Jeon, S.; Kim, Y.; Lee, C.; Lee, D.; Lee, G.; Lee, S. Monitoring of the cavitation inception speed and sound pressure level of the model propeller using accelerometer attached to the model ship in the cavitation tunnel. Ocean Eng. 2022, 266, 112906. [Google Scholar] [CrossRef]
  16. Yu, K.; Park, D.; Choi, J.; Seol, H.; Park, I.; Lee, S.G. Effect of skew on the tonal noise characteristics of a full-scale submarine propeller. Ocean Eng. 2023, 276, 114218. [Google Scholar] [CrossRef]
  17. Sarigiguzel, F.; Kilavuz, A.; Ozgoren, M.; Durhasan, T.; Sahin, B.; Kavurmacioglu, L.A.; Akilli, H.; Sekeroglu, E.; Yaniktepe, B. Experimental investigation of free-surface effects on flow characteristics of a torpedo-like geometry having a cambered nose. Ocean Eng. 2022, 253, 111174. [Google Scholar] [CrossRef]
  18. Bridges, D.H.; Blanton, J.N.; Brewer, W.H.; Park, J.T. Experimental investigation of the flow past a submarine at angle of drift. AIAA J. 2003, 41, 71–81. [Google Scholar] [CrossRef]
  19. Palomba, G.; Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E. Static and Fatigue Full-Scale Tests on a Lightweight Ship Balcony Overhang with Al/Fe Structural Transition Joints. J. Mar. Sci. Eng. 2022, 10, 1382. [Google Scholar] [CrossRef]
  20. Ekmekci, A.; Rockwell, D. Effects of a geometrical surface disturbance on flow past a circular cylinder: A large-scale spanwise wire. J. Fluid Mech. 2010, 665, 120–157. [Google Scholar] [CrossRef]
  21. Gao, T.; Wang, Y.; Pang, Y.; Cao, J. Hull shape optimization for autonomous underwater vehicles using CFD. Eng. Appl. Comput. Fluid Mech. 2016, 10, 599–607. [Google Scholar] [CrossRef]
  22. Myring, D.F. A theoretical study of body drag in subcritical axisymmetric flow. Aeronaut. Q. 1976, 27, 186–194. [Google Scholar] [CrossRef]
  23. Tian, W.L.; Song, B.W.; Ding, H. Numerical research on the influence of surface waves on the hydrodynamic performance of an AUV. Ocean Eng. 2019, 183, 40–56. [Google Scholar] [CrossRef]
  24. Wu, H.Y.; Niu, W.D.; Wang, S.X.; Yan, S.Z. A feedback control strategy for improving the motion accuracy of underwater gliders in currents: Performance analysis and parameter optimization. Ocean Eng. 2022, 252, 111250. [Google Scholar] [CrossRef]
  25. Wang, G.H.; Yang, Y.A.; Wang, S.X. Ocean thermal energy application technologies for unmanned underwater vehicles: A comprehensive review. Appl. Energy 2020, 278, 115752. [Google Scholar] [CrossRef]
  26. Moustabchir, H.; Azari, Z.; Hariri, S.; Dmytrakh, I. Experimental and numerical study of stress–strain state of pressurised cylindrical shells with external defects. Eng. Fail. Anal. 2010, 17, 506–514. [Google Scholar] [CrossRef]
  27. Ismail, M.S.; Purbolaksono, J.; Andriyana, A.; Tan, C.J.; Muhammad, N.; Liew, H.L. The use of initial imperfection approach in design process and buckling failure evaluation of axially compressed composite cylindrical shells. Eng. Fail. Anal. 2015, 51, 20–28. [Google Scholar] [CrossRef]
  28. Mehretehran, A.M.; Maleki, S. Axial buckling of imperfect cylindrical steel silos with isotropic walls under stored solids loads: FE analyses versus Eurocode provisions. Eng. Fail. Anal. 2022, 137, 106282. [Google Scholar] [CrossRef]
  29. Jo, B.; Kasahara, N.; Okamoto, K. Buckling of cylindrical stainless-steel tubes subjected to external pressure at extremely high temperatures. Eng. Fail. Anal. 2018, 92, 61–70. [Google Scholar] [CrossRef]
  30. Christensen, C.F.; Wang, F.W.; Sigmund, O. Topology optimization of multiscale structures considering local and global buckling response. Comput. Methods Appl. Mech. Eng. 2023, 408, 115969. [Google Scholar] [CrossRef]
  31. Viswanath, A.; Khalil, M.; Maskari, F.A.; Cantwell, W.J.; Khan, K.A. Harnessing buckling response to design lattice structures with improved buckling strength. Mater. Des. 2023, 232, 112113. [Google Scholar] [CrossRef]
  32. Gannon, L. Submerged aluminum cylinder response to close-proximity underwater explosions—A comparison of experiment and simulation. Int. J. Impact Eng. 2019, 133, 103339. [Google Scholar] [CrossRef]
  33. Cho, S.R.; Muttaqie, T.; Do, Q.T.; So, H.Y.; Sohn, J.M. Ultimate strength formulation considering failure mode interactions of ring-stiffened cylinders subjected to hydrostatic pressure. Ocean Eng. 2018, 161, 242–256. [Google Scholar] [CrossRef]
  34. Barlag, S.; Rothert, H. An idealization concept for the stability analysis of ring reinforced cylindrical shells under external pressure. Int. J. Non-Linear Mech. 2002, 37, 745–756. [Google Scholar] [CrossRef]
  35. Tian, K.; Wang, B.; Hao, P.; Waas, A.M. A high-fidelity approximate model for determining lower-bound buckling loads for stiffened shells. Int. J. Solids Struct. 2018, 148–149, 14–23. [Google Scholar] [CrossRef]
  36. Do, Q.T.; Muttaqie, T.; Nhut, P.T.; Vu, M.T.; Khoa, N.D.; Prabowo, A.R. Residual ultimate strength assessment of submarine pressure hull under dynamic ship collision. Ocean Eng. 2022, 266, 112951. [Google Scholar] [CrossRef]
  37. Viljoen, H.C.; Mahomed, N.; Cupido, L.H.; Mitchell, G.P. Effect of corrosion thinning on depth of operation: Case study of an HY-80 steel submarine pressure hull. Mar. Struct. 2022, 81, 103103. [Google Scholar] [CrossRef]
  38. Ma, X.T.; Hao, P.; Wu, H.; Wang, B.; Bi, X.J.; Du, K.F.; Ke, X.G. High-fidelity numerical simulation and experimental validation of a 1600-mm-diameter axial loaded grid stiffened cylindrical shell. Int. J. Solids Struct. 2023, 273, 112262. [Google Scholar] [CrossRef]
  39. Shen, K.C.; Yang, Z.Q.; Jiang, L.L.; Pan, G. Buckling and post-buckling behavior of perfect/perforated composite cylindrical shells under hydrostatic pressure. J. Mar. Sci. Eng. 2022, 10, 278. [Google Scholar] [CrossRef]
  40. Li, Z.; Pasternak, H.; Andreas, J. A Buckling of ring-stiffened cylindrical shell under axial compression: Experiment and numerical simulation. Thin-Walled Struct. 2021, 164, 107888. [Google Scholar] [CrossRef]
  41. Lee, S.K.; Jones, M.B.; Quick, H. Loads and hull-pressure measurements on a generic submarine in different stages of model build-up. Ocean Eng. 2023, 271, 113677. [Google Scholar] [CrossRef]
  42. Chmelko, V.; Biro, D. Safety of pressure pipe operation with corrosive defect. Procedia Struct. Integr. 2019, 17, 520–525. [Google Scholar] [CrossRef]
  43. Chmelko, V.; Šulko, M.; Garan, M.; Zvirko, O. Influence of additional factors on the integrity of pipelines with small corrosion defects. Procedia Struct. Integr. 2022, 42, 315–320. [Google Scholar] [CrossRef]
  44. Wei, C.Q.; Chen, G.; Sergeev, A.; Yeh, J.; Chen, J.H.; Wang, J.M.; Ji, S.C.; Wang, J.; Yang, D.H.; Xiang, S.H.; et al. Implosion of the argentinian submarine ARA san Juan S-42 undersea: Modeling and simulation. Commun. Nonlinear Sci. Numer. Simulat. 2020, 91, 105397. [Google Scholar] [CrossRef]
  45. Cho, S.R.; Muttaqie, T.; Do, Q.T.; Kim, S.; Kim, S.M.; Han, D.H. Experimental investigations on the failure modes of ring-stiffened cylinders under external hydrostatic pressure. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 711–729. [Google Scholar] [CrossRef]
  46. Wang, H.K.; Yu, Y.; Yu, J.X.; Duan, J.H.; Zhang, Y.; Li, Z.M.; Wang, C.M. Effect of 3D random pitting defects on the collapse pressure of pipe—Part I: Experiment. Thin-Walled Struct. 2018, 129, 512–526. [Google Scholar] [CrossRef]
  47. Covert, S. Yasen-M Cruise Missile Submarine. Available online: http://www.hisutton.com (accessed on 4 August 2021).
  48. Kristina, D.; William, L.B. USS Greenville collides with Japan’s Ehime Maru: Cultural issues in image repair discourse. Publ. Relat. Rev. 2004, 30, 177–185. [Google Scholar] [CrossRef]
  49. Li, W.X.; Sun, F.F.; Wei, W.Y.; Liu, D.B.; Zhang, X.; Li, M.; Fan, H.L. Fabrication and testing of composite corrugated-core sandwich cylinder. Compos. Sci. Technol. 2018, 156, 127–135. [Google Scholar] [CrossRef]
  50. Wang, Q.S.; Li, Z.; Qin, B.; Zhong, R.; Zhai, Z.Y. Vibration characteristics of functionally graded corrugated plates by using differential quadrature finite element method. Compos Struct. 2021, 274, 114344. [Google Scholar] [CrossRef]
  51. Wang, S.; Wang, X.G.; Liu, X.H.; Li, C.S. Experiment and simulation of variable thickness rolling for 3D-profiled blank. J. Mater. Process. Technol. 2021, 290, 116971. [Google Scholar] [CrossRef]
  52. American Bureau of Shipping (ABS). Rules for Building and Classing Underwater Vehicles; System and Hyperbaric Facilities: Houston, TX, USA, 2012. [Google Scholar]
  53. China Classification Society (CCS). Submersible Systems and Submersible Classification Specification; China Classification Society: Beijing, China, 2018. [Google Scholar]
  54. Luo, G.M.; Hsu, Y.C. Nonlinear buckling strength of out-of-roundness pressure hull. Thin-Walled Struct. 2018, 130, 424–434. [Google Scholar] [CrossRef]
  55. Zhang, X.; Sun, J.L.; Wu, R.Z.; Peng, Y. Buckling performance of inner corrugated pressure shells under external hydrostatic pressure. Ocean Eng. 2023, 288, 115963. [Google Scholar] [CrossRef]
  56. Schmidová, E.; Klejch, F.; Sunilkumar, M.R. Development of anisotropy and strain hardening in damaged stamped parts made of IF steel. Eng. Fail. Anal. 2023, 145, 107015. [Google Scholar] [CrossRef]
  57. Ribeiro, V.; Correia, J.; Mourão, A.; Lesiuk, G.; Gonçalves, A.; De, J.A.; Berto, F. Fatigue crack growth modelling by means of the strain energy density-based Huffman model considering the residual stress effect. Eng. Fail. Anal. 2022, 140, 106543. [Google Scholar] [CrossRef]
  58. Samadi, F.; Mourya, J.; Wheatley, G.; Khan, M.N.; Nejad, R.M.; Branco, R.; Macek, W. An investigation on residual stress and fatigue life assessment of T-shape welded joints. Eng. Fail. Anal. 2022, 141, 106685. [Google Scholar] [CrossRef]
  59. Zhang, K.; Dai, S.H.; Jiang, B.Y.; Wang, D.H.; Han, C.; Liu, Q.Y. Simulation optimization and experimental research on heat-treatment process for ring remanufacturing of TBM disc cutters. Surf. Coat. Technol. 2023, 475, 130133. [Google Scholar] [CrossRef]
  60. Alizadeh, M.; Vahdatinejad, F.; Pashangeh, S. Feasibility study of producing Al–5Zn–1 Mg alloy by accumulative roll bonding process and subsequent heat treatment. Eng. Fail. Anal. 2023, 143, 106927. [Google Scholar] [CrossRef]
  61. Zhang, J.; Wang, M.L.; Wang, W.B.; Tang, W.X.; Zhu, Y.M. Investigation on egg-shaped pressure hulls. Mar. Struct. 2017, 52, 50–66. [Google Scholar] [CrossRef]
  62. Yang, M.; Yang, S.H.; Wang, Y.H.; Liang, Y.; Wang, S.X.; Zhang, L.H. Optimization design of neutrally buoyant hull for underwater gliders. Ocean Eng. 2020, 209, 107512. [Google Scholar] [CrossRef]
  63. Pan, B.B.; Cui, W.C.; Shen, Y.S. Experimental verification of the new ultimate strength equation of spherical pressure hulls. Mar. Struct. 2012, 29, 169–176. [Google Scholar] [CrossRef]
Jmse 12 00385 g001
Figure 1. Schematic diagram of submarine structure [47,48].
Figure 1. Schematic diagram of submarine structure [47,48].
Jmse 12 00385 g001
Jmse 12 00385 g002
Figure 2. Corrugated shell geometrical dimensions and machining results.
Figure 2. Corrugated shell geometrical dimensions and machining results.
Jmse 12 00385 g002
Jmse 12 00385 g003
Figure 3. Measurement of corrugated shell parameters.
Figure 3. Measurement of corrugated shell parameters.
Jmse 12 00385 g003
Jmse 12 00385 g004
Figure 4. Reverse modeling processing and geometric imperfections characterization of corrugated shell point cloud data.
Figure 4. Reverse modeling processing and geometric imperfections characterization of corrugated shell point cloud data.
Jmse 12 00385 g004
Jmse 12 00385 g005
Figure 5. Reverse modeling results for two corrugated shells.
Figure 5. Reverse modeling results for two corrugated shells.
Jmse 12 00385 g005
Jmse 12 00385 g006aJmse 12 00385 g006b
Figure 6. Global and local deviation of corrugated shells.
Figure 6. Global and local deviation of corrugated shells.
Jmse 12 00385 g006aJmse 12 00385 g006b
Jmse 12 00385 g007
Figure 7. Hydrostatic pressure test device.
Figure 7. Hydrostatic pressure test device.
Jmse 12 00385 g007
Jmse 12 00385 g008
Figure 8. Pressure–time curve.
Figure 8. Pressure–time curve.
Jmse 12 00385 g008
Jmse 12 00385 g009
Figure 9. Bi-linear stress–strain curves of 6061 aluminum alloy under tensile condition: (a) engineering stress–strain curve, (b) true stress–strain curve [55].
Figure 9. Bi-linear stress–strain curves of 6061 aluminum alloy under tensile condition: (a) engineering stress–strain curve, (b) true stress–strain curve [55].
Jmse 12 00385 g009
Jmse 12 00385 g010
Figure 10. Mesh division and boundary conditions in finite element simulation.
Figure 10. Mesh division and boundary conditions in finite element simulation.
Jmse 12 00385 g010
Jmse 12 00385 g011
Figure 11. Displacement variation of sealing circular plates in different buckling states.
Figure 11. Displacement variation of sealing circular plates in different buckling states.
Jmse 12 00385 g011
Jmse 12 00385 g012
Figure 12. Equilibrium path variation of corrugated shells.
Figure 12. Equilibrium path variation of corrugated shells.
Jmse 12 00385 g012
Jmse 12 00385 g013
Figure 13. Displacement variation of corrugated shells in different buckling states.
Figure 13. Displacement variation of corrugated shells in different buckling states.
Jmse 12 00385 g013
Jmse 12 00385 g014
Figure 14. Stress variation of corrugated shells in different buckling states.
Figure 14. Stress variation of corrugated shells in different buckling states.
Jmse 12 00385 g014
Table 1. Comparing experimental and numerical results of critical buckling loads for different corrugated shells.
Table 1. Comparing experimental and numerical results of critical buckling loads for different corrugated shells.
Corrugated Shells CS1CS2
Ptest/MPa3.23.4
Pnum/MPa3.0633.188
(Ptest − Pnum)/Ptest4.28%6.24%
Ptest: test critical buckling load. Pnum: scanning model critical buckling load.
Table 2. Solution parameters for numerical analysis of hydrostatic buckling.
Table 2. Solution parameters for numerical analysis of hydrostatic buckling.
NmaxΔlinΔlminΔlmax
5000.0051e−150.05
Nmax = maximum number; Δlin = initial increment in arc length along the static equilibrium path in scaled load–displacement space; Δlmin = minimum arc length increment; Δlmax = maximum arc length increment.
Table 3. Material properties of Al6061-T6 [55].
Table 3. Material properties of Al6061-T6 [55].
PropertiesE (MPa)μσ0 (MPa)Ks (MPa)
Values69,9000.33185940,000
E: Young’s modulus; μ: Poisson’s ratio; σ0: yield stress; Ks: strain hardening factor.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sun, J.; Zhang, X.; Zhang, Y.; Lu, X.; Peng, Y. Failure Behavior of Corrugated Pressure Cylindrical Shells with Variable Wall Thickness under Uniform External Pressure. J. Mar. Sci. Eng. 2024, 12, 385. https://doi.org/10.3390/jmse12030385

AMA Style

Sun J, Zhang X, Zhang Y, Lu X, Peng Y. Failure Behavior of Corrugated Pressure Cylindrical Shells with Variable Wall Thickness under Uniform External Pressure. Journal of Marine Science and Engineering. 2024; 12(3):385. https://doi.org/10.3390/jmse12030385

Chicago/Turabian Style

Sun, Jianliang, Xu Zhang, Yuanhe Zhang, Xianghui Lu, and Yan Peng. 2024. "Failure Behavior of Corrugated Pressure Cylindrical Shells with Variable Wall Thickness under Uniform External Pressure" Journal of Marine Science and Engineering 12, no. 3: 385. https://doi.org/10.3390/jmse12030385

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop