Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure
Abstract
1. Introduction
2. Finite Element Modeling
2.1. Establishment of FE Model
2.2. Validation of FE Model
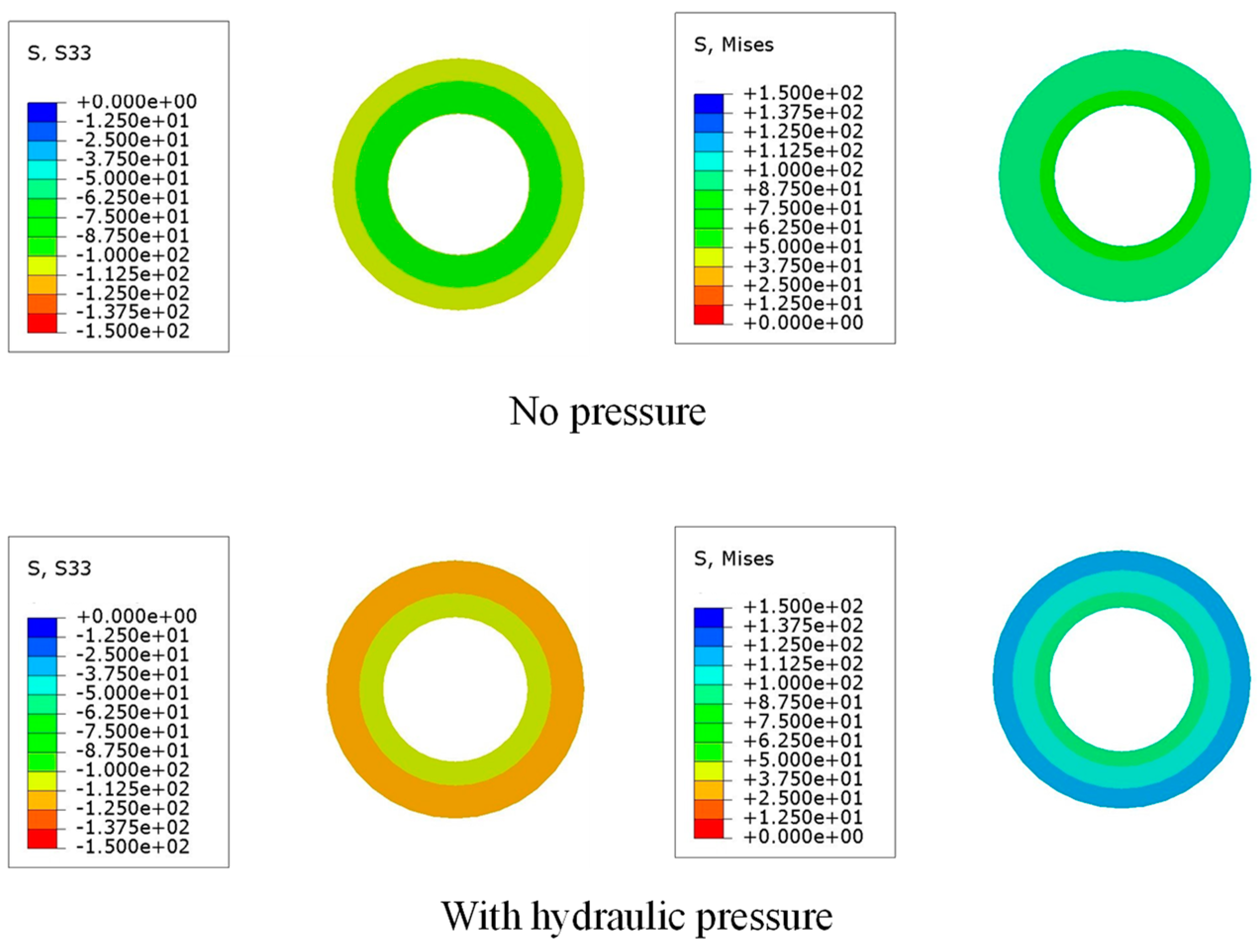
2.3. Analysis on Full-Range Performance with Hydraulic Pressure
3. Parametric Study
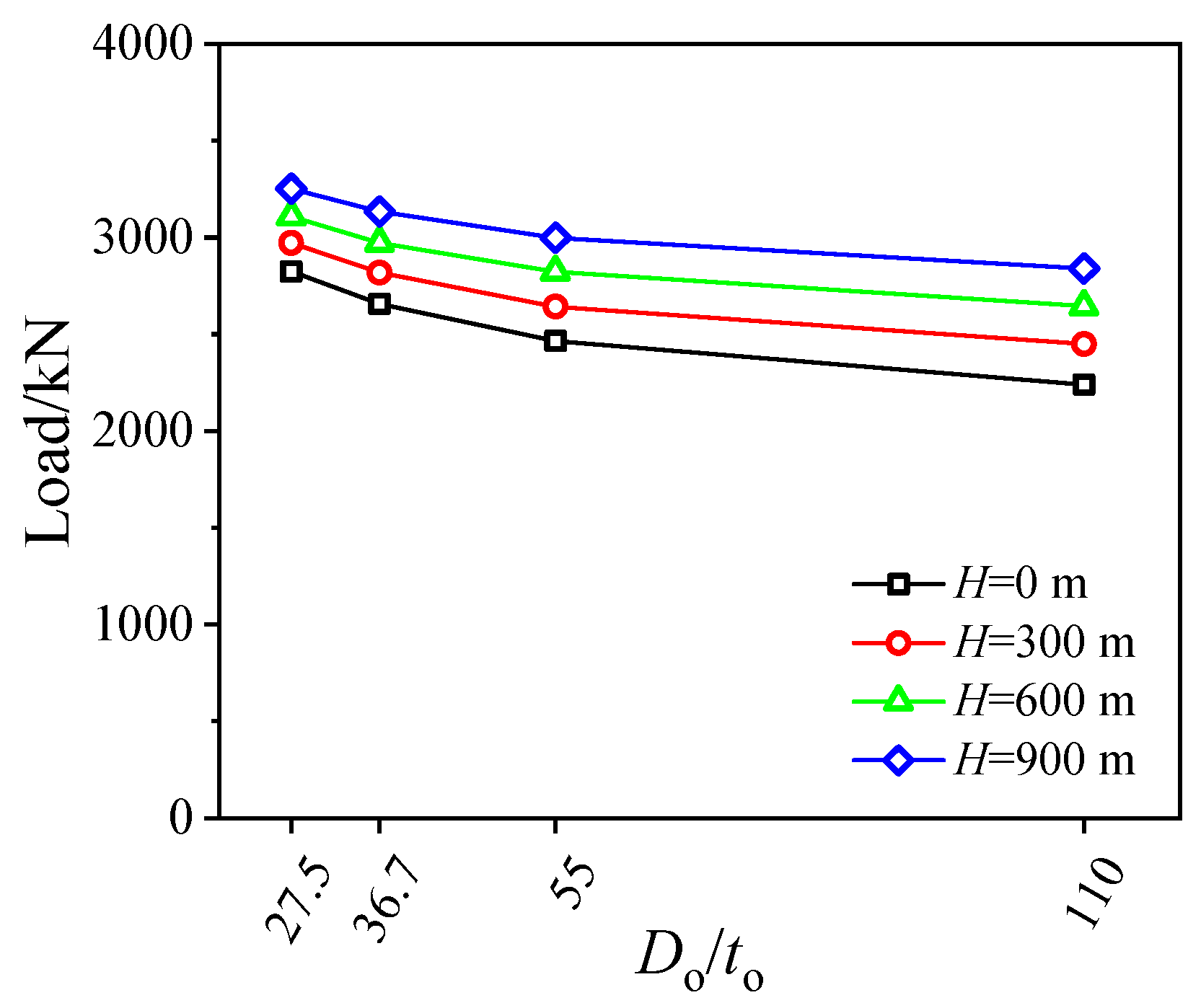
3.1. Influence of Do/to Ratio
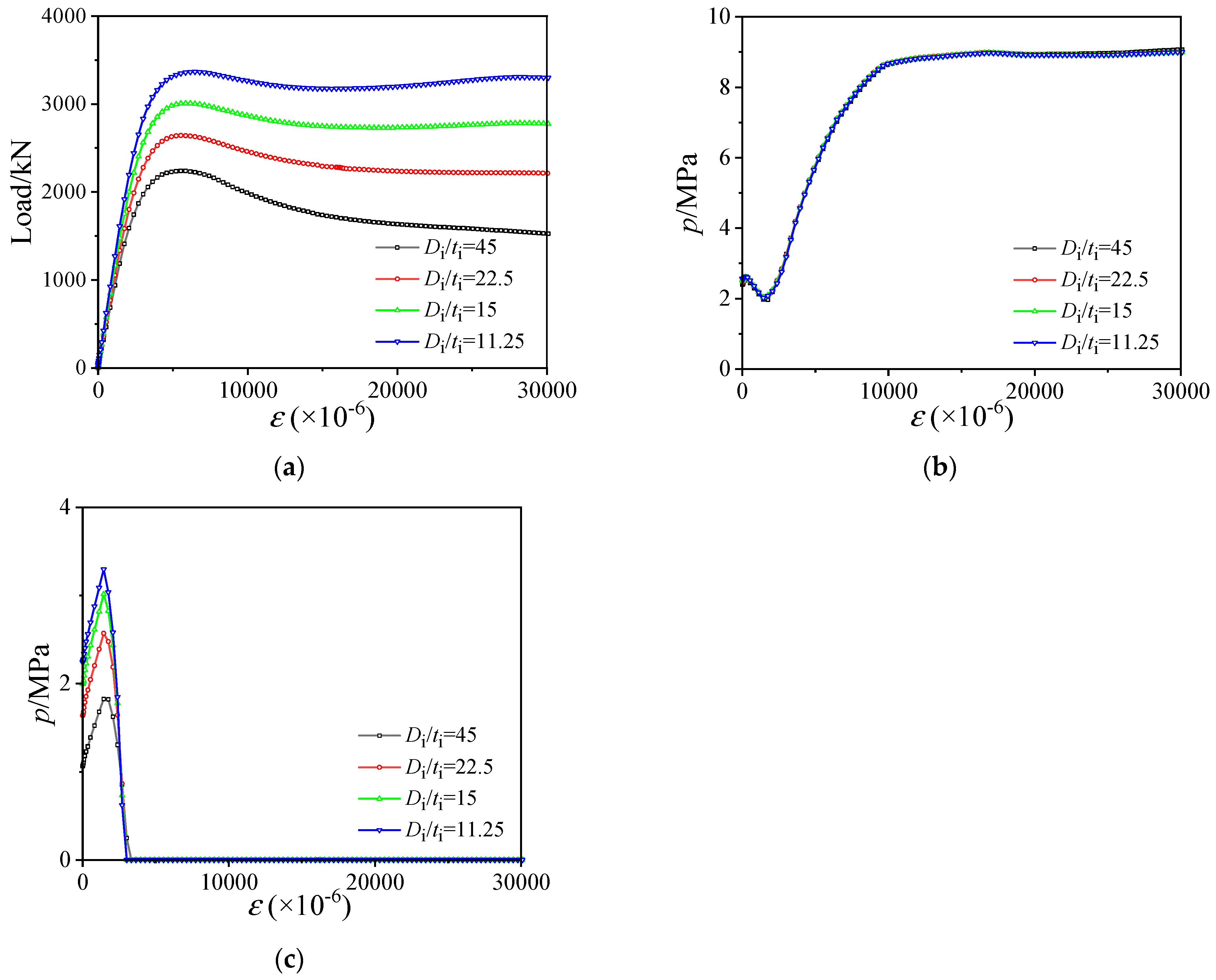
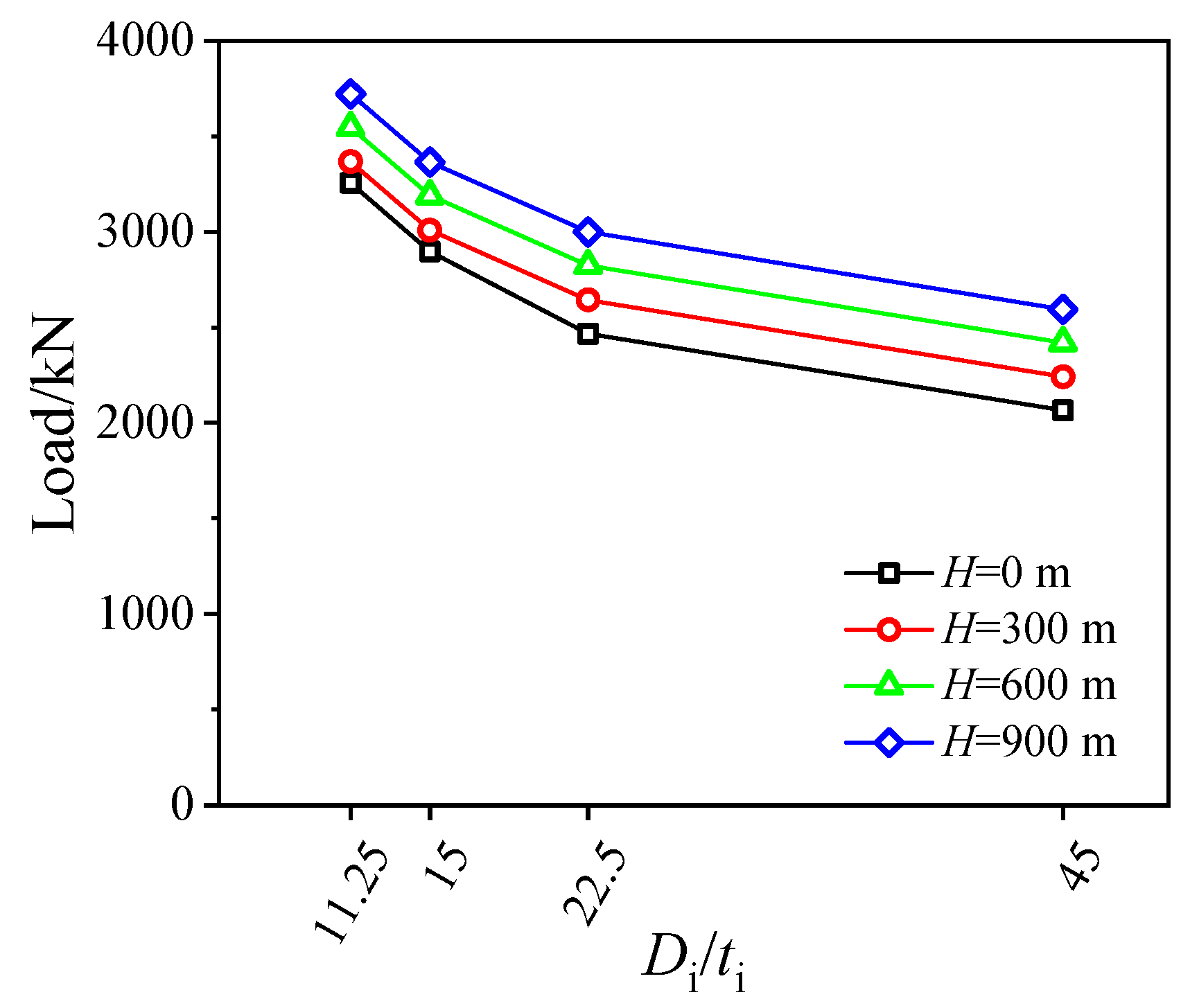
3.2. Influence of Di/ti Ratio
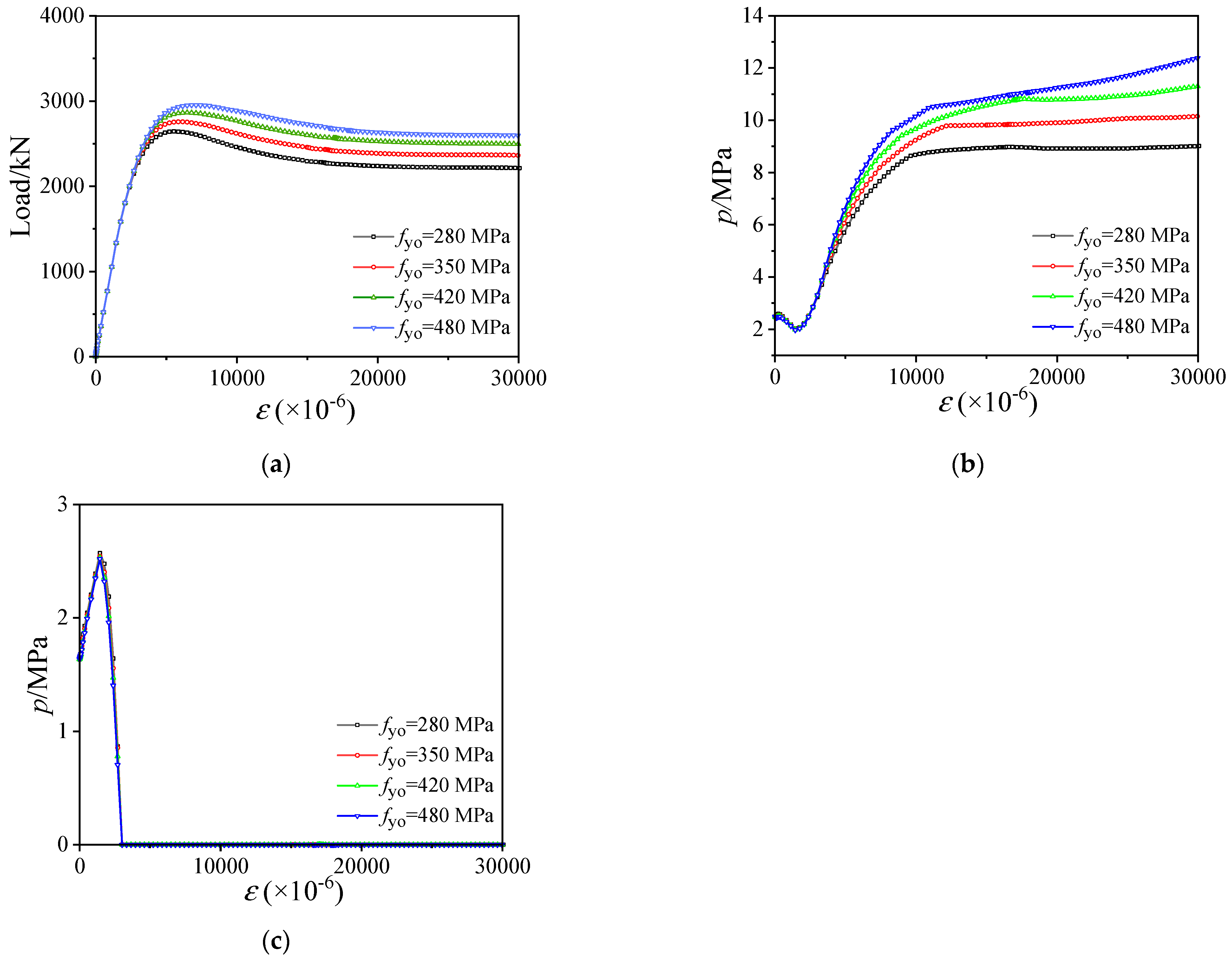
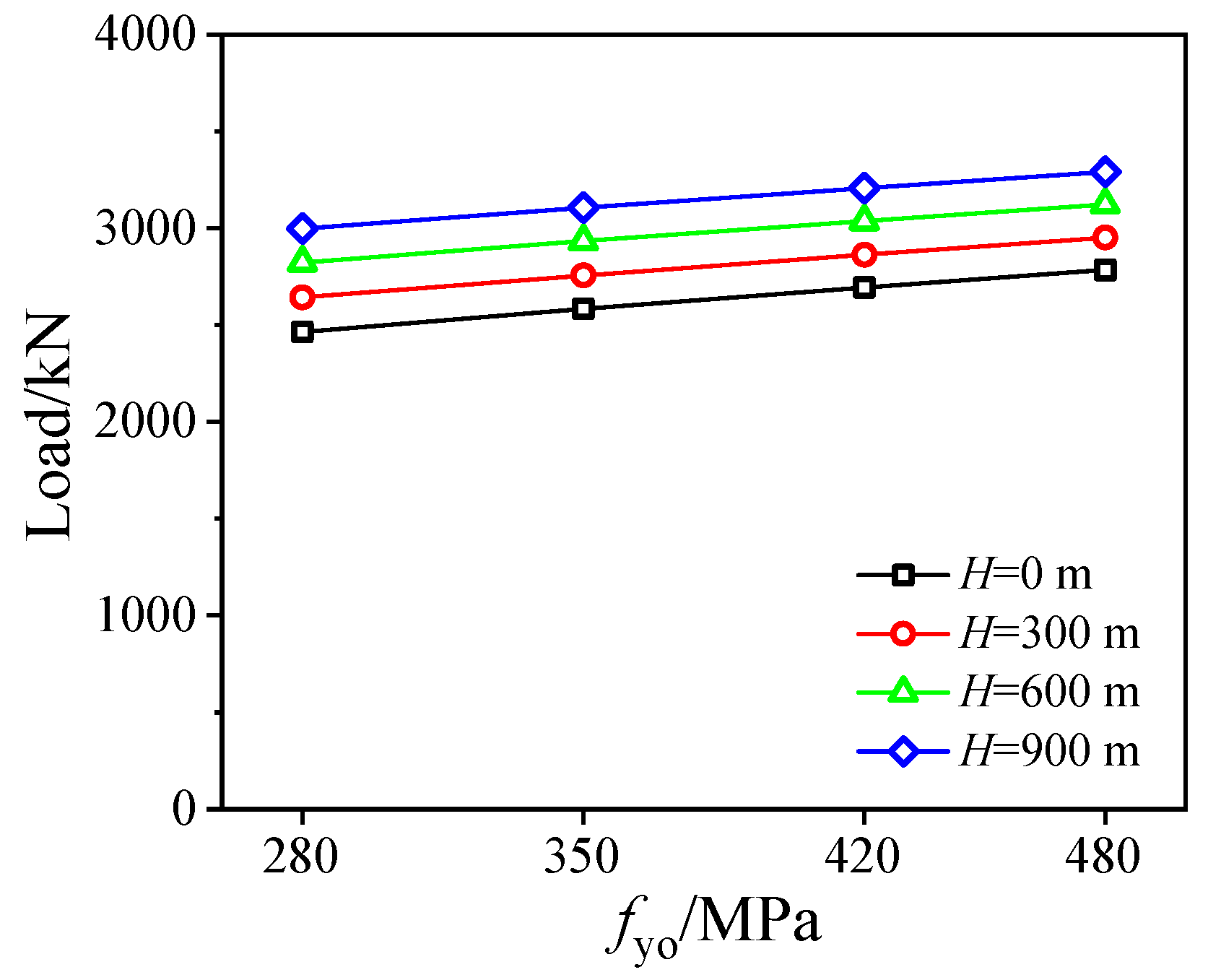
3.3. Influence of fyo
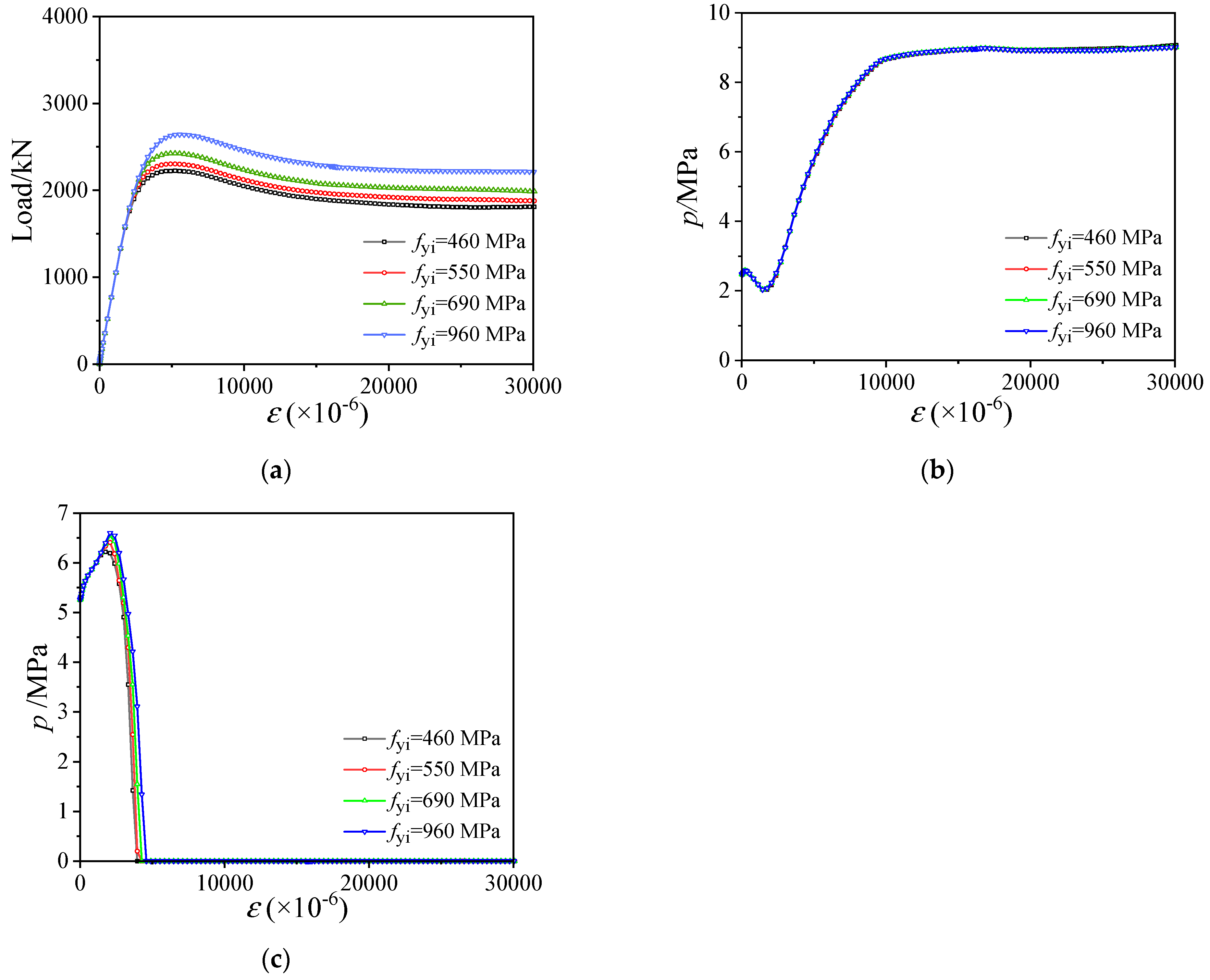
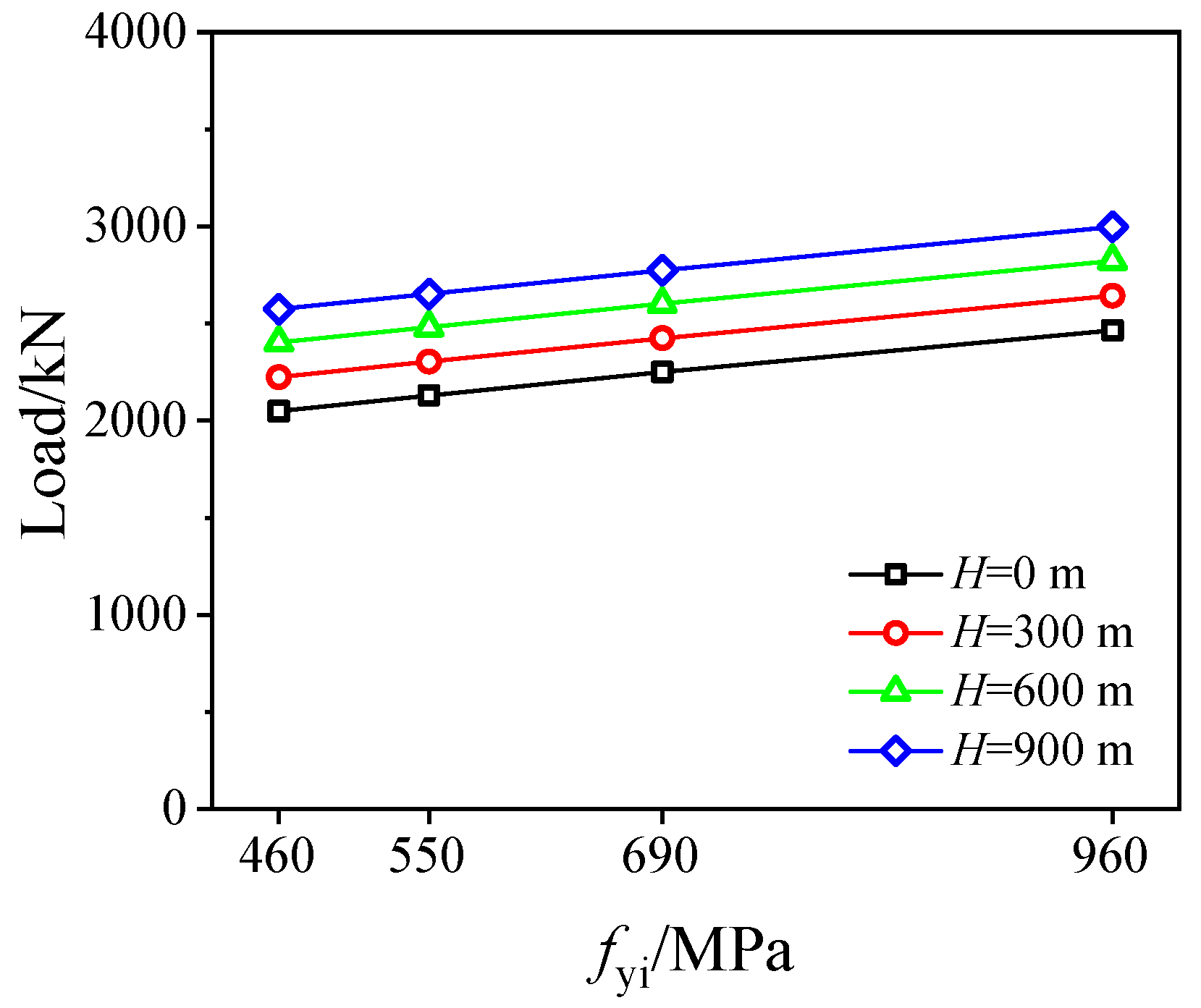
3.4. Influence of fyi
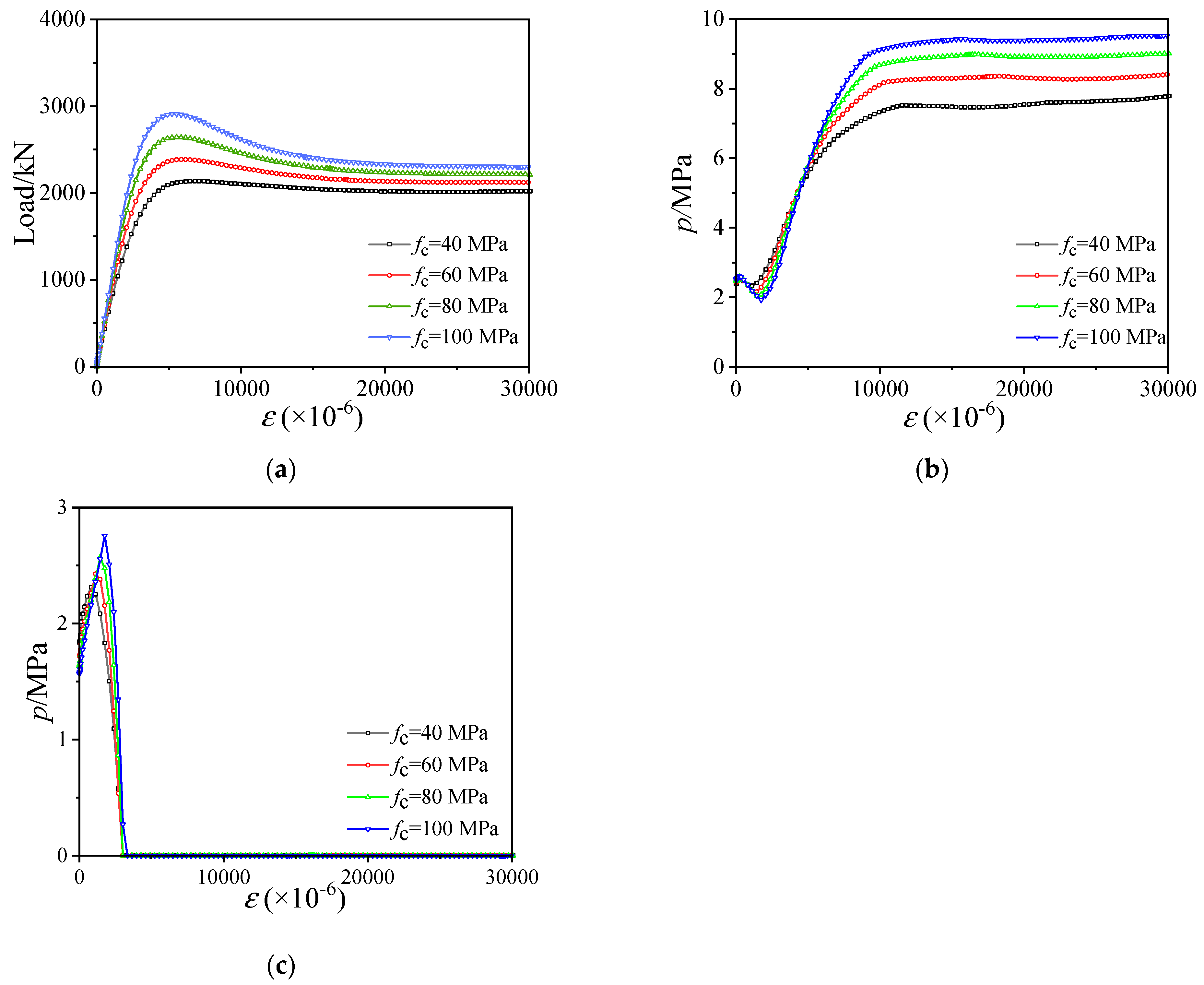
3.5. Influence of fc
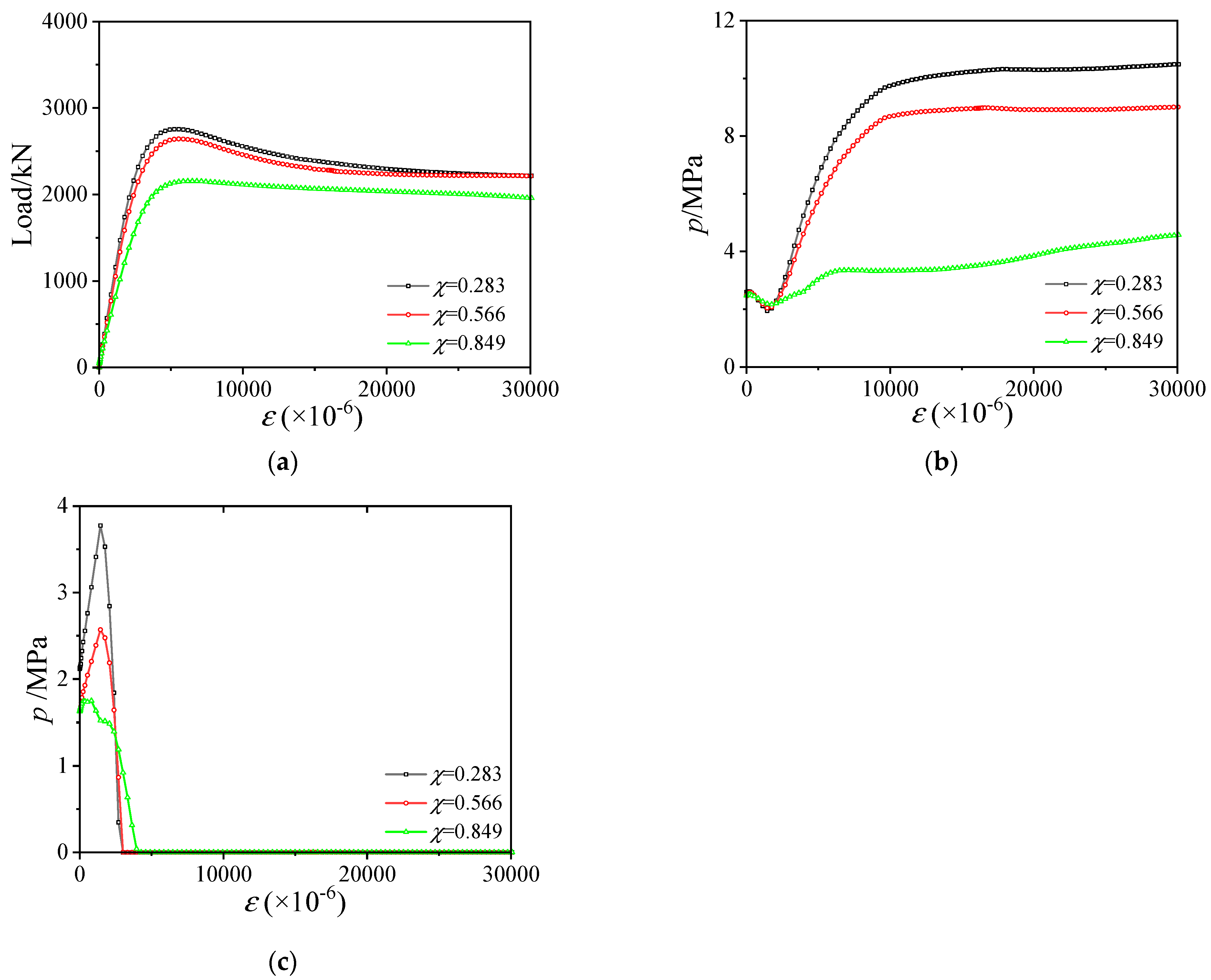
3.6. Influence of χ
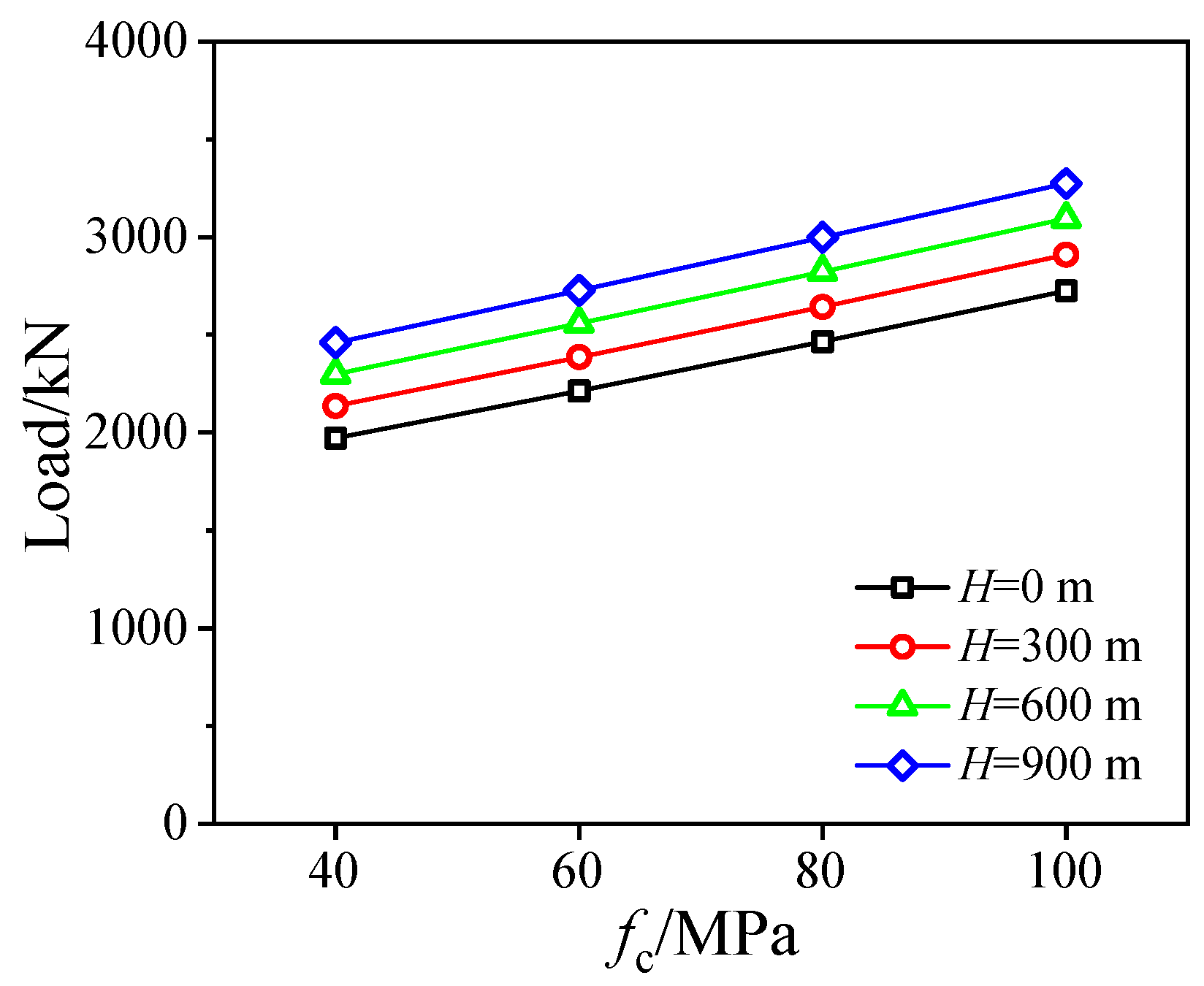
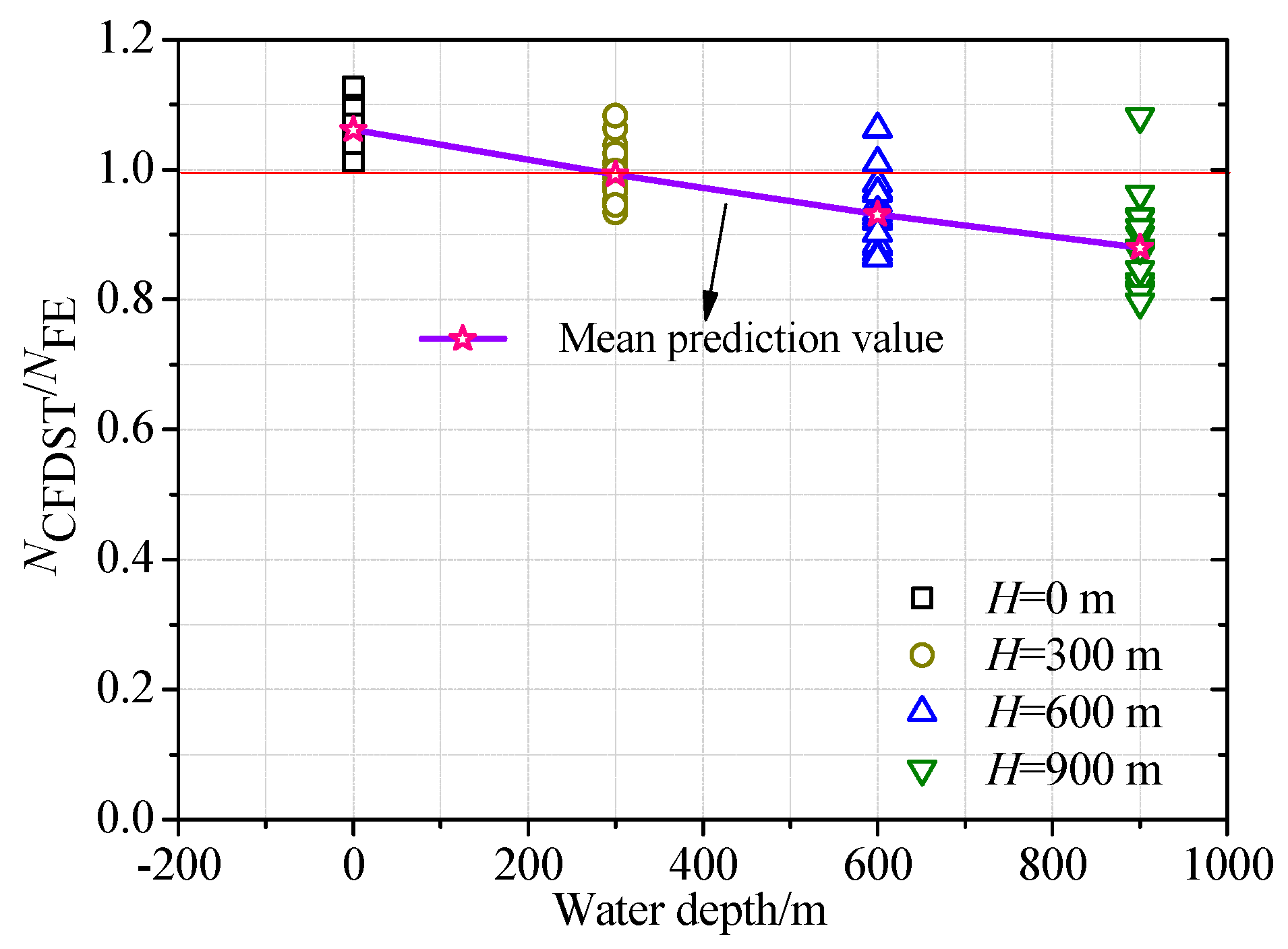
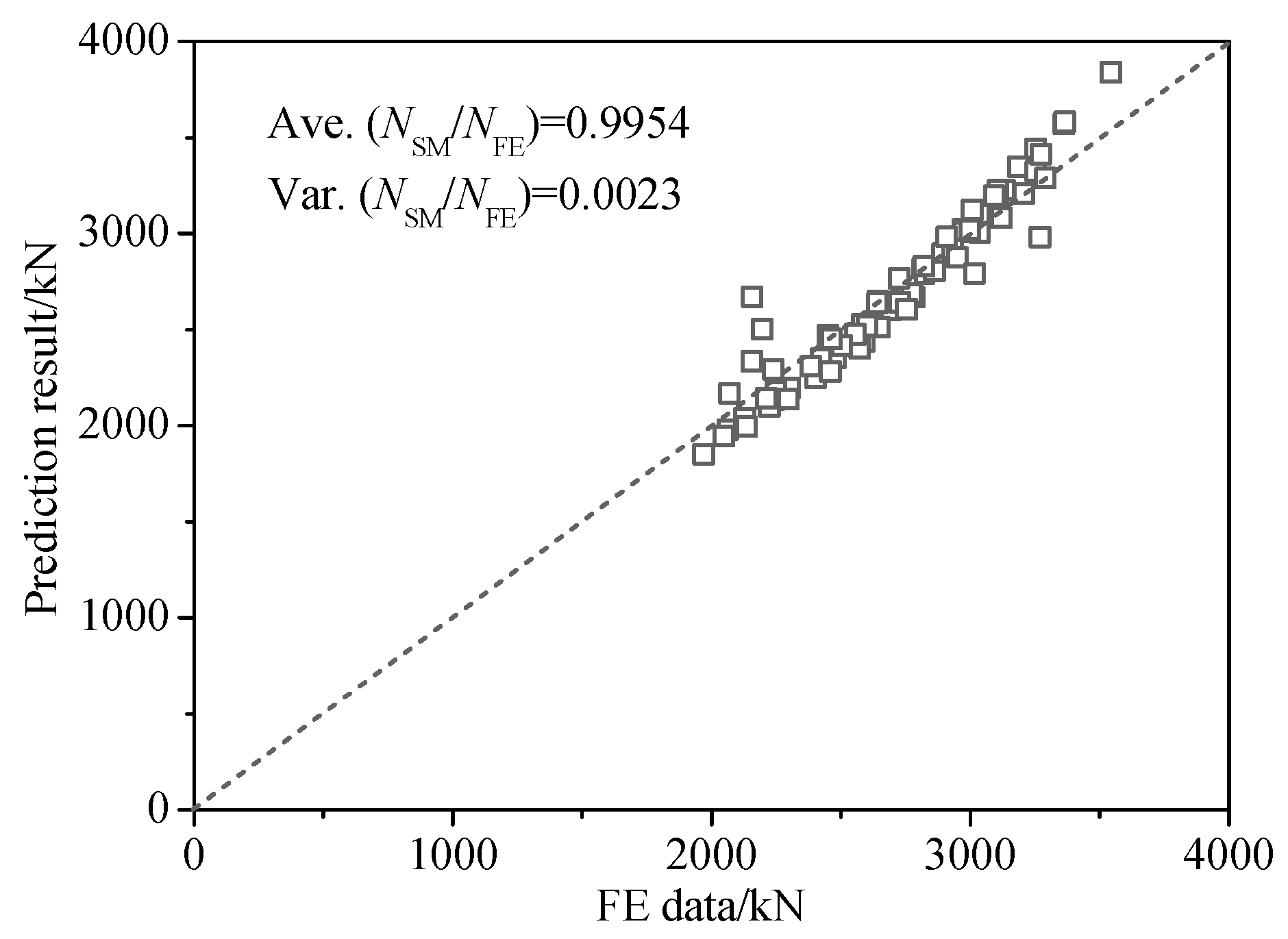
4. Design Method on Bearing Capacity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| fc | compression strength of concrete cylinder |
| fck | prismatic compressive strength of concrete |
| ft0 | tensile strength of concrete |
| fyo | yielding strength of outer steel tube |
| fyi | yielding strength of inner steel tube |
| ti or to | inner/outer tube’s thickness |
| fosc | composite strength of stainless steel tube–sandwich concrete composite part under the double-skin hollow section |
| fsc | composite strength of outer tube and core concrete under solid section |
| fcu | cubic concrete strength under compression |
| Ac | cross-sectional area of sandwich concrete |
| Asi | cross-sectional area of inner steel tube |
| Aso | cross-sectional area of outer steel tube |
| Acc | area of core concrete in solid section |
| Do | diameter of outer steel tube |
| Di | diameter of inner steel tube |
| E0 | elasticity modulus |
| GF | fracture energy |
| H | water depth |
| NCFDST | axial compression capacity for whole traditional CFDST members |
| Nosc | axial strength contribution of outer tube and sandwich concrete |
| Ni | axial strength contribution of inner tube |
| NSM | the modified load-carrying capacity for SCCDST members with hydraulic pressures |
| ξ | confinement coefficient |
| ε0 | peak strain |
| β0 | computing coefficient |
| εs | strain of stainless steel |
| σs | corresponding stress at strain εs |
| σ0.2 | 0.2% proof stress for stainless steel |
| ε0.2 | strain at σ0.2 for stainless steel |
| εssu | ultimate strain for stainless steel |
| σssu | tensile strength for stainless steel |
| n and m | calculation factors |
| σ0.01 | 0.01% proof stress for stainless steel |
| χ | hollow ratio |
References
- Qian, R.; Li, Q.; Fu, C.; Zhang, Y.; Wang, Y.; Jin, X. Atmospheric chloride-induced corrosion of steel-reinforced concrete beam exposed to real marine-environment for 7 years. Ocean Eng. 2023, 286, 115675. [Google Scholar] [CrossRef]
- Xiao, L.; Peng, J.; Cai, C.S.; Chen, H. Experimental and numerical investigations on the mechanical behavior of coastal high performance steel beams with local corrosion within the shear-span. Appl. Ocean Res. 2023, 136, 103581. [Google Scholar] [CrossRef]
- Peng, W.; Duan, T.; Hou, J.; Guo, W.; Ding, K.; Cheng, W.; Xu, L. Long-term corrosion behaviour of 1060 aluminium in deep-sea environment of South China Sea. Corros. Eng. Sci. Technol. 2021, 56, 327–340. [Google Scholar] [CrossRef]
- Katsoudas, A.S.; Silionis, N.E.; Anyfantis, K.N. Structural health monitoring for corrosion induced thickness loss in marine plates subjected to random loads. Ocean Eng. 2023, 273, 114037. [Google Scholar] [CrossRef]
- Li, G.; Hou, C.; Shen, L. Combined compression-bending performance and design of CFST with localised pitting corrosion. J. Constr. Steel Res. 2022, 192, 107247. [Google Scholar] [CrossRef]
- Li, W.; Han, L.H.; Zhao, X.L. Behavior of CFDST stub columns under preload, sustained load and chloride corrosion. J. Constr. Steel Res. 2015, 107, 12–23. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, Y.; Hou, C.; Lu, B. CFDST stub columns with galvanized corrugated steel tubes: Concept and axial behaviour. Thin-Walled Struct. 2020, 157, 107116. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Lam, D.; Hou, C.C.; Zhang, R. Behaviours of circular CFDST with stainless steel external tube: Slender columns and beams. Thin-Walled Struct. 2021, 158, 107172. [Google Scholar] [CrossRef]
- Han, L.H.; Ren, Q.X.; Li, W. Tests on stub stainless steel–concrete–carbon steel double-skin tubular (DST) columns. J. Constr. Steel Res. 2011, 67, 437–452. [Google Scholar] [CrossRef]
- Li, W.; Han, L.H.; Zhao, X.L. Axial strength of concrete-filled double skin steel tubular (CFDST) columns with preload on steel tubes. Thin-Walled Struct. 2012, 56, 9–20. [Google Scholar] [CrossRef]
- Vernardos, S.; Gantes, C. Experimental behavior of concrete-filled double-skin steel tubular (CFDST) stub members under axial compression: A comparative review. Structures 2019, 22, 383–404. [Google Scholar] [CrossRef]
- Wang, F.; Young, B.; Gardner, L. CFDST sections with square stainless steel outer tubes under axial compression: Experimental investigation, numerical modelling and design. Eng. Struct. 2020, 207, 110189. [Google Scholar] [CrossRef]
- Aghamaleki, S.T.N.; Naghipour, M.; Amiri, J.V.; Nematzadeh, M. Compression behavior of the concrete-filled double skin steel tube columns under hydrostatic pressure: Experimental and modeling study. Structures 2023, 58, 105505. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Zhang, D. Analytical model for axially compressed circular concrete-filled double skin steel tubes (CFDSTs): Insights from concrete non-uniformly confined states. Thin-Walled Struct. 2023, 192, 111106. [Google Scholar] [CrossRef]
- Wang, F.C.; Han, L.H. Analytical behavior of carbon steel-concrete-stainless steel double-skin tube (DST) used in submarine pipeline structure. Mar. Struct. 2019, 63, 99–116. [Google Scholar] [CrossRef]
- Zhao, X.L.; Tong, L.W.; Wang, X.Y. CFDST stub columns subjected to large deformation axial loading. Eng. Struct. 2010, 32, 692–703. [Google Scholar] [CrossRef]
- Pagoulatou, M.; Sheehan, T.; Dai, X.H.; Lam, D. Finite element analysis on the capacity of circular concrete-filled double-skin steel tubular (CFDST) stub columns. Eng. Struct. 2014, 72, 102–112. [Google Scholar] [CrossRef]
- Ekmekyapar, T.; Hasan, H.G. The influence of the inner steel tube on the compression behaviour of the concrete filled double skin steel tube (CFDST) columns. Mar. Struct. 2019, 66, 197–212. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, R.; Ning, F.; Liang, Y. Compression behaviour and bearing capacity calculation of concrete filled double skin square steel columns. J. Build. Eng. 2021, 42, 103022. [Google Scholar] [CrossRef]
- Ci, J.; Ahmed, M.; Tran, V.L.; Jia, H.; Chen, S. Axial compressive behavior of circular concrete-filled double steel tubular short columns. Adv. Struct. Eng. 2022, 25, 259–276. [Google Scholar] [CrossRef]
- Abadel, A.A.; Khan, M.I.; Masmoudi, R. Experimental and numerical study of compressive behavior of axially loaded circular ultra-high-performance concrete-filled tube columns. Case Stud. Constr. Mater. 2022, 17, e01376. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z. Axial compressive behavior of ultra-high performance concrete-filled double skin high-strength steel tubular short columns. Struct. Concr. 2023, 24, 3857–3876. [Google Scholar] [CrossRef]
- Yilmaz, B.C.C.; Binbir, E.; Guzelbulut, C.; Yildirim, H.; Celik, O.C. Circular concrete-filled double skin steel tubes under concentric compression: Tests and FEA parametric study. Compos. Struct. 2023, 309, 116765. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F.; Liang, Q.Q. Circular concrete-filled double skin tubular short columns with external stainless steel tubes under axial compression. Thin-Walled Struct. 2013, 73, 252–263. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhao, X.L.; Raman, R.S.; Yu, X. Axial compression tests on seawater and sea sand concrete-filled double-skin stainless steel circular tubes. Eng. Struct. 2018, 176, 426–438. [Google Scholar] [CrossRef]
- Wang, F.; Young, B.; Gardner, L. Compressive testing and numerical modelling of concrete-filled double skin CHS with austenitic stainless steel outer tubes. Thin-Walled Struct. 2019, 141, 345–359. [Google Scholar] [CrossRef]
- Le, T.T.; Patel, V.I.; Liang, Q.Q.; Huynh, P. Numerical modeling of rectangular concrete-filled double-skin steel tubular columns with outer stainless-steel skin. J. Constr. Steel Res. 2021, 179, 106504. [Google Scholar] [CrossRef]
- Le, T.T.; Patel, V.I.; Liang, Q.Q.; Huynh, P. Axisymmetric simulation of circular concrete-filled double-skin steel tubular short columns incorporating outer stainless-steel tube. Eng. Struct. 2021, 227, 111416. [Google Scholar] [CrossRef]
- Castanheira, D.S.; De Lima, L.R.O.; Vellasco, P.D.S.; Cashell, K.A.; Gardner, L. Compressive behaviour of double skin sections with stainless steel outer tubes and recycled aggregate concrete. Structures 2022, 41, 750–763. [Google Scholar] [CrossRef]
- Le, T.T.; Patel, V.I.; Liang, Q.Q.; Huynh, P. Simulation modeling and design of circular concrete-filled double-skin tubular slender beam-columns with outer stainless-steel tube. Eng. Struct. 2023, 285, 116014. [Google Scholar] [CrossRef]
- Zhou, F.; Lama, L.; Zhao, K. Design of stainless steel CHS-concrete infill-carbon steel CHS double-skin stub columns. Eng. Struct. 2023, 278, 115479. [Google Scholar] [CrossRef]
- EN 1994-1-1; Eurcode 4, Design of Composite Steel and Concrete Structures, Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- AS 5100.6-2004; Bridge Design Part 6: Steel and Composite Construction. Standards Australia: Sydney, Australia, 2004.
- ANSI/AISC 360-16; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2016.
- ACI 318-14; Building Code Requirements for Structural Concrete and Commentary. ACI: Farmington Hills, MI, USA, 2014.
- T/CCES 7-2020; Technical Specification for Concrete-Filled Double Skin Steel Tubular Structures. China Architecture & Building Press: Beijing, China, 2020. (In Chinese)
- T/CECS 952-2021; China Association for Engineering Construction Standardization. Technical Specification for Concrete-Filled Stainless Steel Tubular Structures. China Architecture & Building Press: Beijing, China, 2022. (In Chinese)
- Wang, J.T.; Liu, X.H.; Sun, Q.; Li, Y.W. Compressive–flexural failure mechanism and bearing capacity calculation of over-ranging tapered CFDST members for support structures of offshore wind turbines. J. Mar. Sci. Eng. 2023, 11, 1621. [Google Scholar] [CrossRef]
- Wang, J.T.; Liu, X.H.; Sun, Q.; Li, Y.W. Analytical behavior and bearing capacity research on out-of-code tapered CFDST members under pure torsion and compression-torsion combination. Ocean Eng. 2023, 284, 115324. [Google Scholar] [CrossRef]
- Han, L.H. Concrete Filled Steel Tubular Structures—Theory and Practice; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Patel, V.I.; Hassanein, M.F.; Thai, H.T.; Al Abadi, H.; Paton-Cole, V. Behaviour of axially loaded circular concrete-filled bimetallic stainless-carbon steel tubular short columns. Eng. Struct. 2017, 147, 583–597. [Google Scholar] [CrossRef]
- Tang, G.Q.; Xiao, Y.; Zhang, Y.T. Study of bearing capacity and complete stress-strain curves for concrete filled square steel tube columns. Eng. Mech. 2015, 32, 103–111. (In Chinese) [Google Scholar]

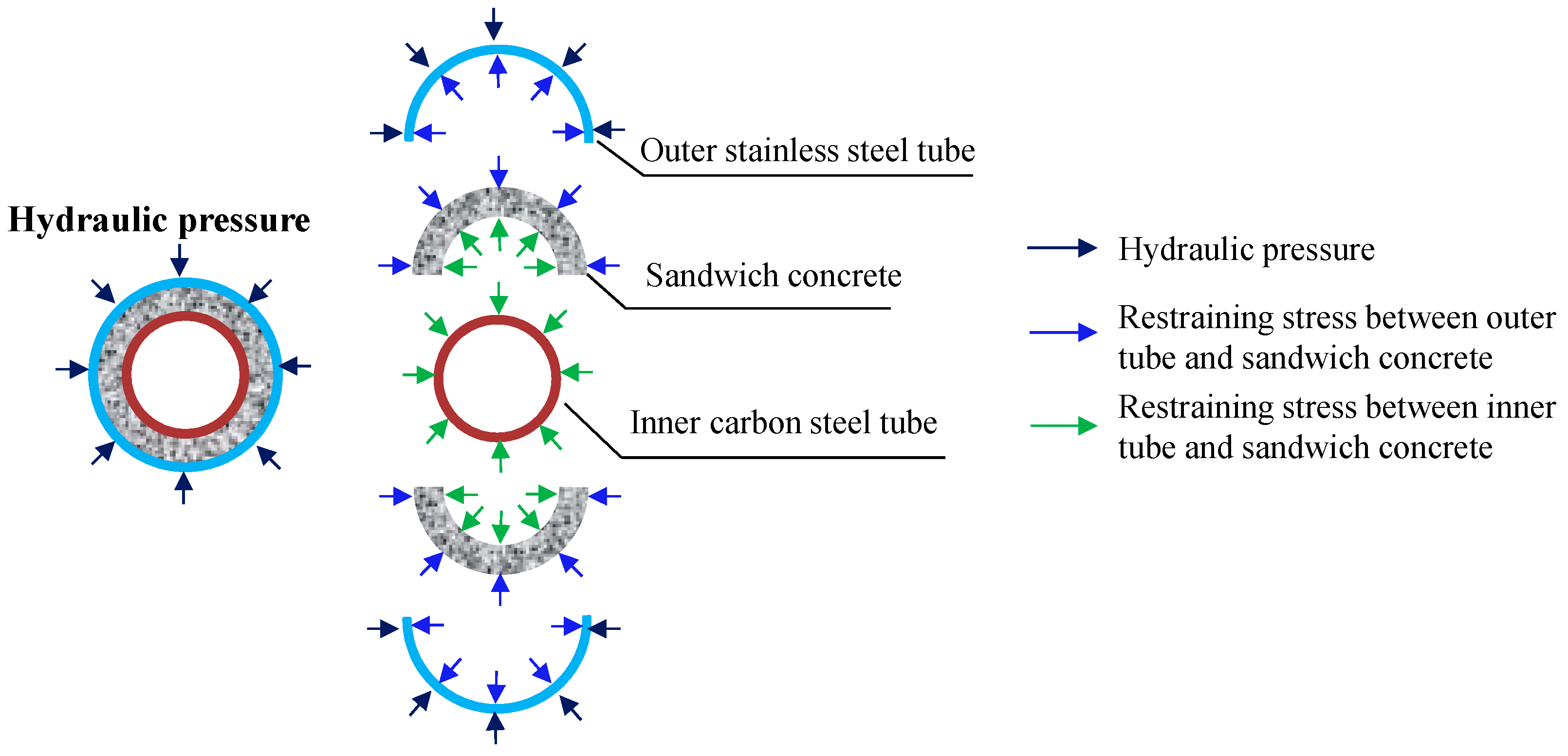


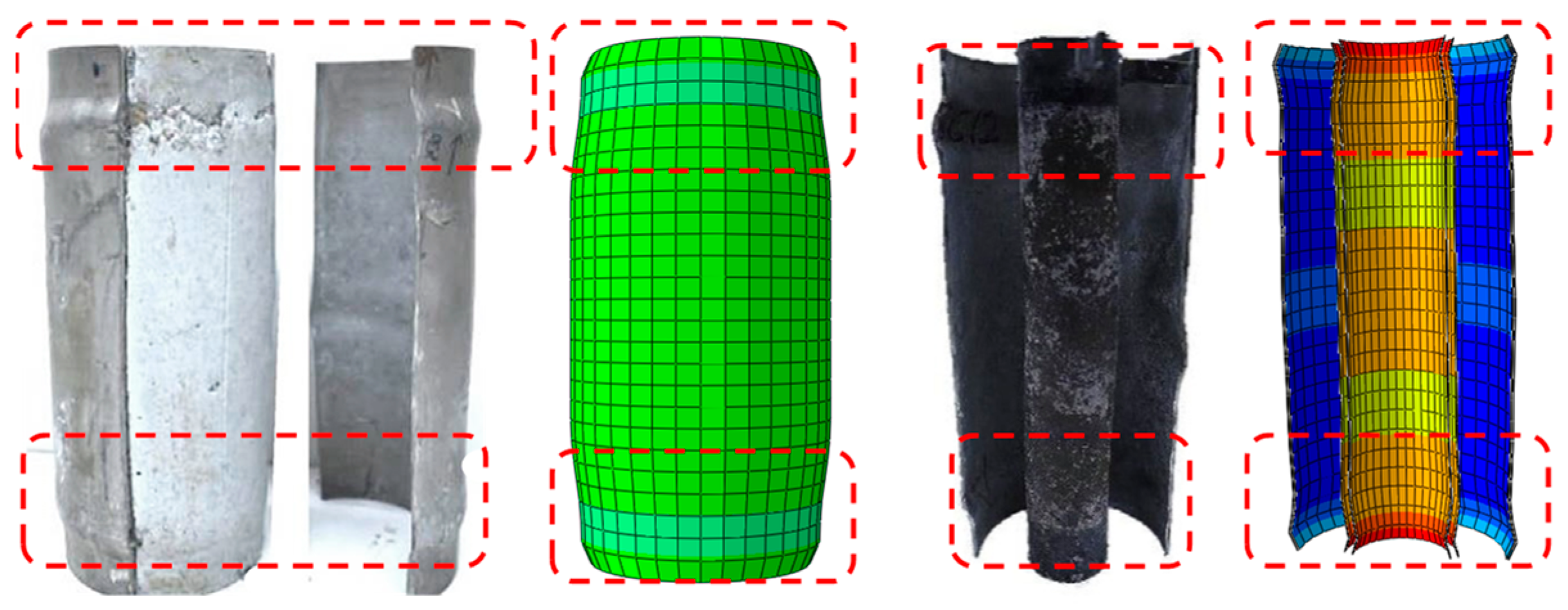

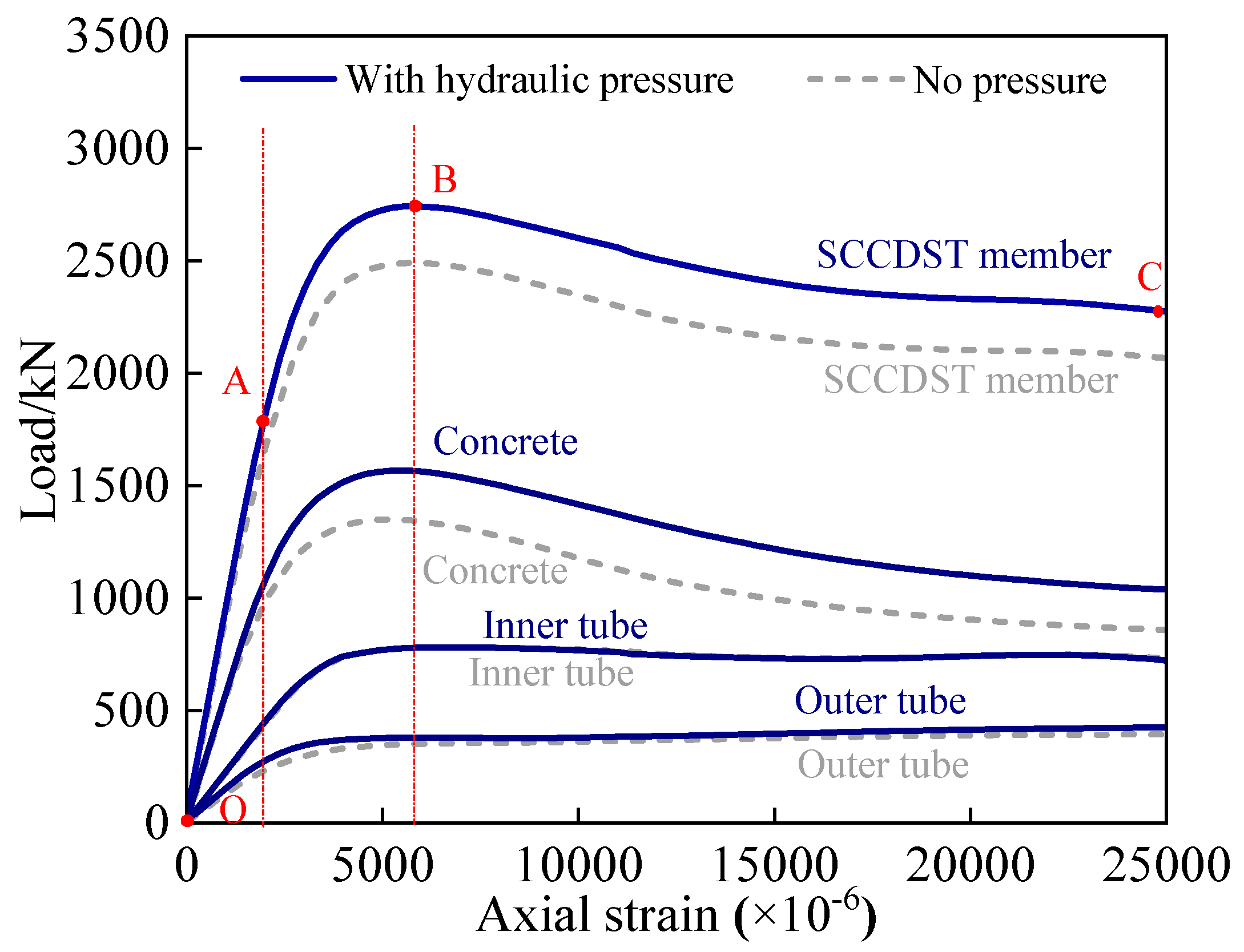
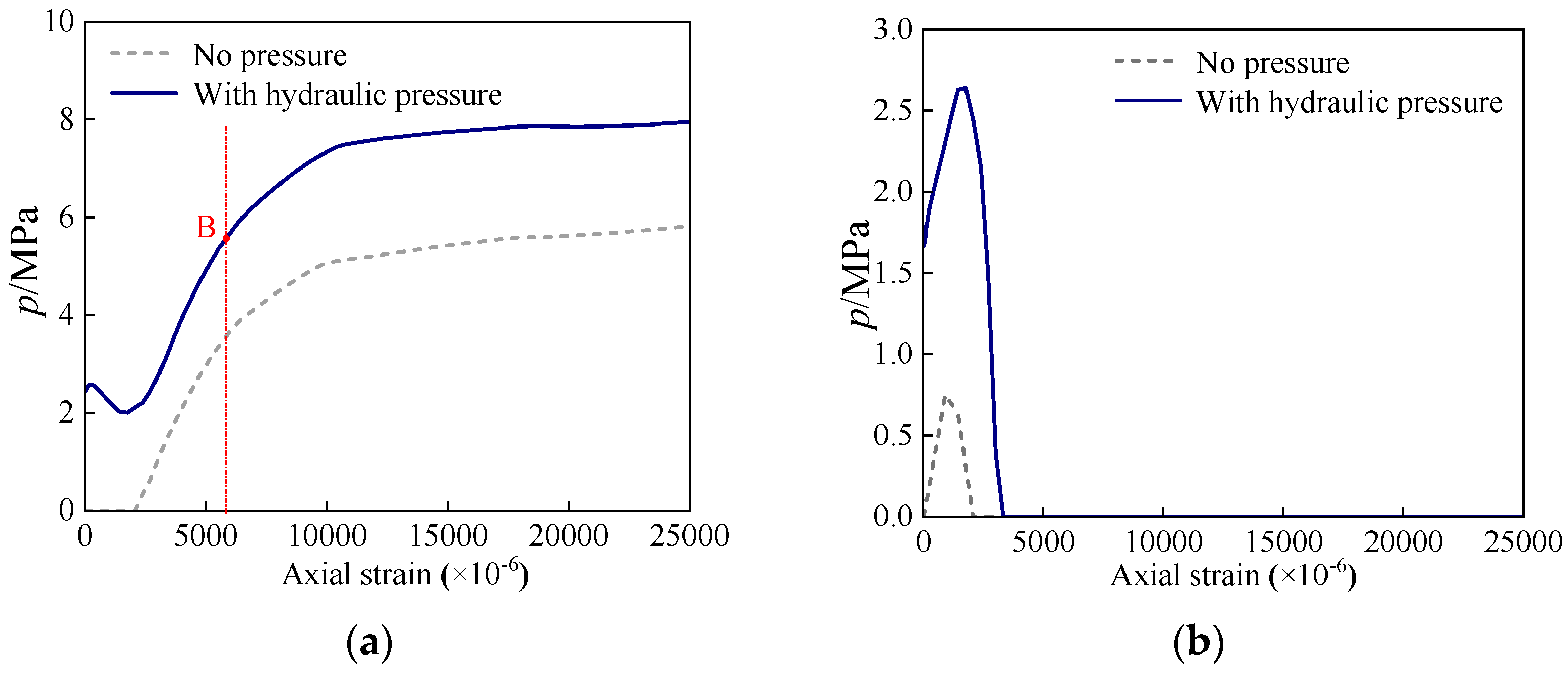


| Specimen [26] | Length/mm | Outer Tube/mm | Inner Tube/mm | Material Strength/MPa | Test Capacity NT/kN | Numerical Capacity NFE/kN | NFE/NT | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Do | to | Di | ti | fyo | fyi | fc | |||||
| AC140×3-HC22×4-C40 | 350 | 140.2 | 2.92 | 22.1 | 4.09 | 300 | 794 | 40.5 | 1410 | 1392 | 0.9872 |
| AC140×3-HC22×4-C80 | 350 | 140.2 | 2.91 | 22.1 | 4.10 | 300 | 794 | 79.9 | 1845 | 1846 | 1.0005 |
| AC140×3-HC22×4-C120 | 350 | 140.2 | 2.89 | 22.1 | 4.08 | 300 | 794 | 115.6 | 2321 | 2316 | 0.9978 |
| AC140×3-HC32×6-C40 | 350 | 140.3 | 2.89 | 32.0 | 5.48 | 300 | 619 | 40.5 | 1423 | 1476 | 1.0372 |
| AC140×3-HC32×6-C80 | 350 | 140.2 | 2.92 | 31.9 | 5.27 | 300 | 619 | 79.9 | 2012 | 2020 | 1.0040 |
| AC140×3-HC32×6-C120 | 350 | 140.1 | 2.91 | 31.9 | 5.36 | 300 | 619 | 115.6 | 2537 | 2566 | 1.0114 |
| AC140×3-HC38×8-C40 | 350 | 140.1 | 2.91 | 38.1 | 7.63 | 300 | 433 | 40.5 | 1626 | 1633 | 1.0043 |
| AC140×3-HC38×8-C80 | 350 | 140.1 | 2.90 | 38.0 | 7.51 | 300 | 433 | 79.9 | 2083 | 2072 | 0.9947 |
| AC140×3-HC38×8-C120 | 350 | 140.2 | 2.90 | 37.9 | 7.39 | 300 | 433 | 115.6 | 2500 | 2483 | 0.9932 |
| AC140×3-HC55×11-C40 | 350 | 140.2 | 2.90 | 55.1 | 10.62 | 300 | 739 | 40.5 | 2543 | 2539 | 0.9984 |
| AC140×3-HC55×11-C80 | 350 | 140.1 | 2.90 | 55.2 | 10.76 | 300 | 739 | 79.9 | 2775 | 2877 | 1.0368 |
| AC140×3-HC89×4-C40 | 350 | 140.1 | 2.87 | 89.0 | 3.89 | 300 | 1029 | 40.5 | 2025 | 2026 | 1.0005 |
| AC140×3-HC89×4-C80 | 350 | 140.1 | 2.86 | 89.1 | 3.91 | 300 | 1029 | 79.9 | 2107 | 2119 | 1.0057 |
| AC140×3-HC89×4-C120 | 350 | 140.2 | 2.88 | 89.1 | 3.91 | 300 | 1029 | 115.6 | 2195 | 2176 | 0.9913 |
| AC165×3-HC22×4-C40 | 413 | 165.3 | 2.94 | 22.0 | 4.14 | 276 | 794 | 40.5 | 1750 | 1598 | 0.9131 |
| AC165×3-HC22×4-C80 | 413 | 165.2 | 2.94 | 22.1 | 4.09 | 276 | 794 | 79.9 | 2413 | 2389 | 0.9901 |
| AC165×3-HC22×4-C120 | 413 | 165.3 | 2.94 | 22.1 | 4.04 | 276 | 794 | 115.6 | 2911 | 2995 | 1.0289 |
| AC165×3-HC32×6-C40 | 413 | 165.3 | 2.93 | 31.9 | 5.35 | 276 | 619 | 40.5 | 1943 | 1980 | 1.0190 |
| AC165×3-HC32×6-C40R | 413 | 165.3 | 2.94 | 31.9 | 5.39 | 276 | 619 | 40.5 | 1891 | 1825 | 0.9651 |
| AC165×3-HC32×6-C80 | 413 | 165.3 | 2.94 | 31.8 | 5.25 | 276 | 619 | 79.9 | 2550 | 2540 | 0.9961 |
| AC165×3-HC89×4-C40 | 413 | 165.5 | 2.92 | 89.0 | 3.92 | 276 | 1029 | 40.5 | 2375 | 2353 | 0.9907 |
| AC165×3-HC89×4-C80 | 413 | 165.4 | 2.91 | 89.1 | 3.91 | 276 | 1029 | 79.9 | 2580 | 2566 | 0.9946 |
| AC165×3-HC89×4-C120 | 413 | 165.2 | 2.92 | 88.9 | 3.88 | 276 | 1029 | 115.6 | 2671 | 2681 | 1.0037 |
| Mean | 0.9985 | ||||||||||
| Variance | 0.0006 | ||||||||||
| Water Depths (H)/m | Do/to | Di/ti | fyo/MPa | fyi/Mpa | fc/Mpa | χ |
|---|---|---|---|---|---|---|
| 0; 300; 600; 900 | 110; 55; 36.7; 27.5 | 45; 22.5; 15; 11.25 | 280; 350; 420; 480 | 460; 550; 690; 960 | 40; 60; 80; 100 | 0.283; 0.566; 0.849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-T.; Yang, K.-L.; Sun, J.-Y. Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure. J. Mar. Sci. Eng. 2024, 12, 406. https://doi.org/10.3390/jmse12030406
Wang J-T, Yang K-L, Sun J-Y. Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure. Journal of Marine Science and Engineering. 2024; 12(3):406. https://doi.org/10.3390/jmse12030406
Chicago/Turabian StyleWang, Jian-Tao, Kai-Lin Yang, and Jia-Yao Sun. 2024. "Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure" Journal of Marine Science and Engineering 12, no. 3: 406. https://doi.org/10.3390/jmse12030406
APA StyleWang, J.-T., Yang, K.-L., & Sun, J.-Y. (2024). Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure. Journal of Marine Science and Engineering, 12(3), 406. https://doi.org/10.3390/jmse12030406






