Experimental Study on the Effect of Wind on Armor Stone Stability
Abstract
:1. Introduction
2. Experiment
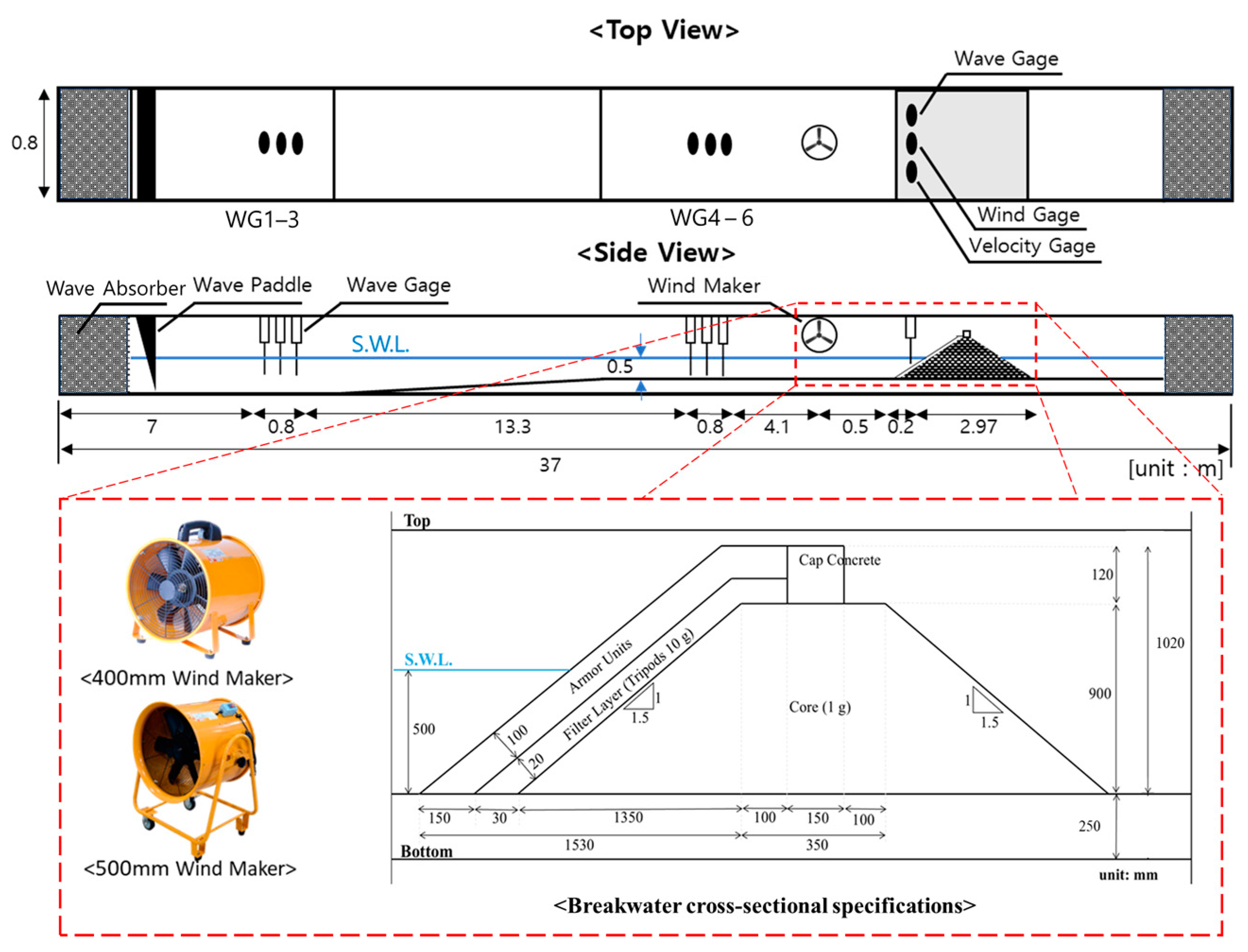
2.1. Laboratory Experiment Setup
2.2. Wave and Wind Conditions
2.3. Breakwater Armor Stone Damage
2.4. Wind Velocity Field
3. Results and Discussion
3.1. Hudson Stability Factor ()
3.2. Hydrodynamics
3.2.1. Wave Spectrum
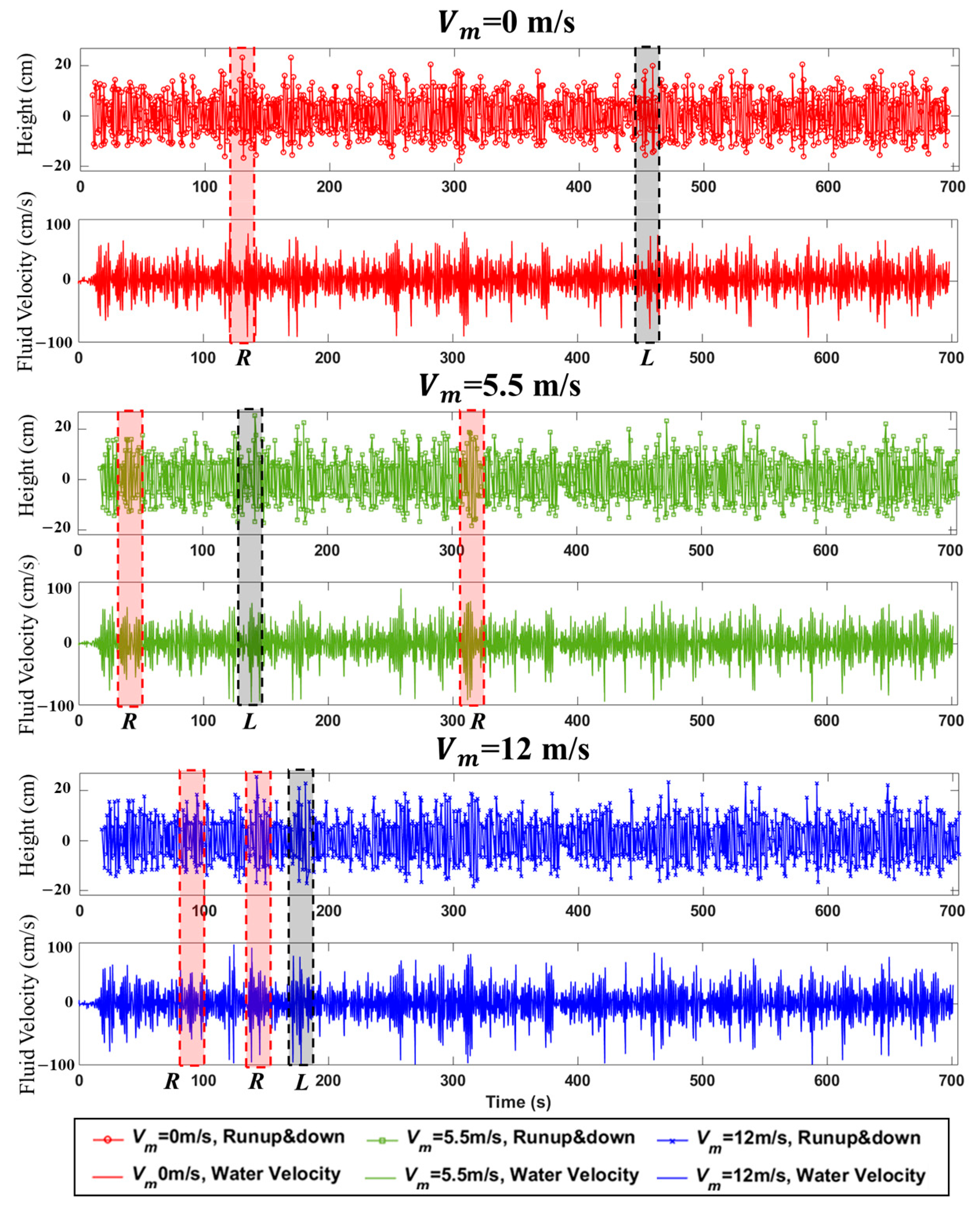
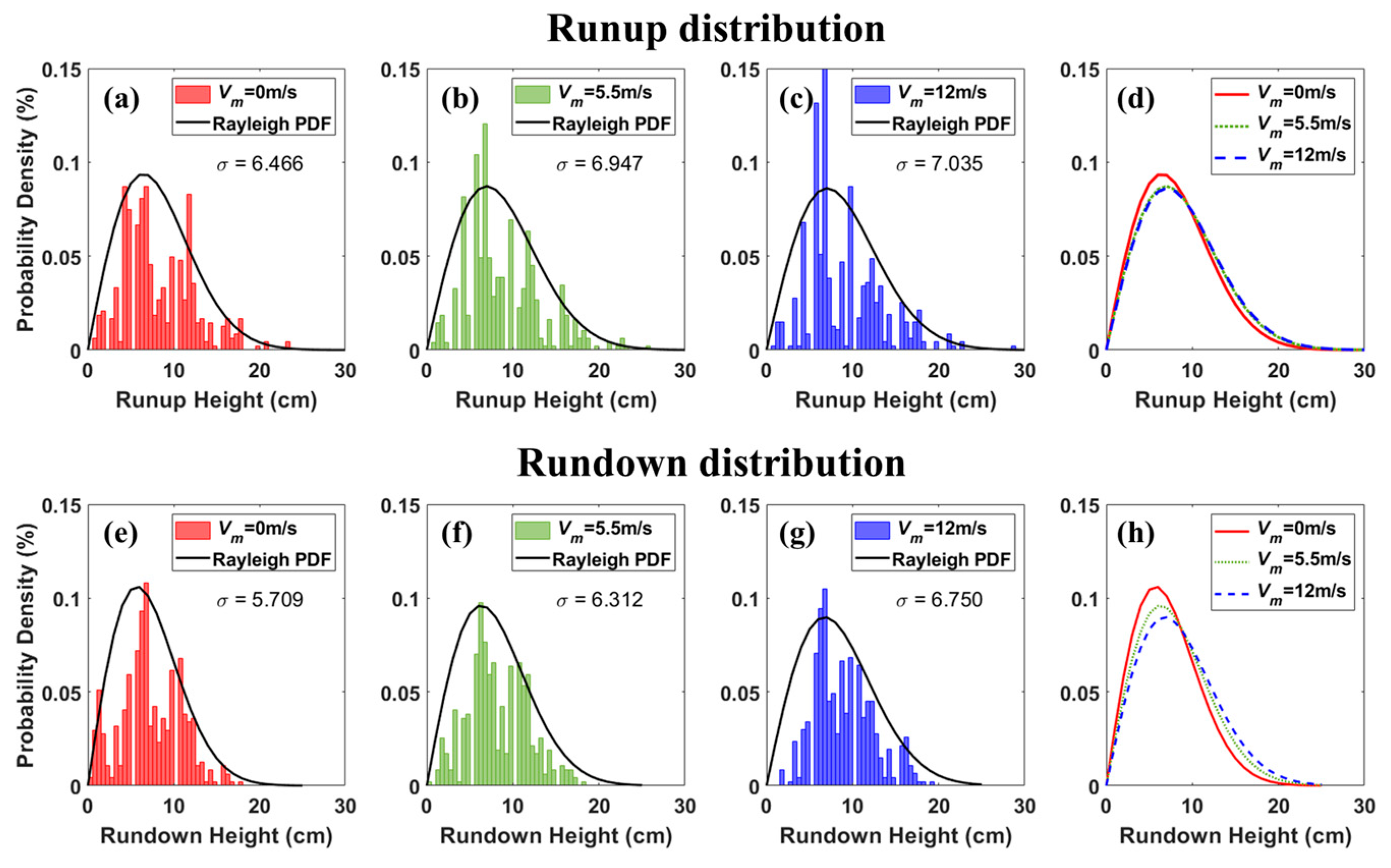
3.2.2. Wave Runup and Rundown
3.2.3. Fluid Velocity
3.2.4. Effect of Wave Period on TTP Damage
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patterson, J.; Ford, G. The damaging impacts of hurricanes upon coastal structures. In Proceedings of the ASEE Southeast Section Conference, Marietta, GA, USA, 5–7 April 2009. [Google Scholar]
- Fukuda, N.; Uno, T.; Irie, I. Field observations of wave overtopping of wave absorbing revetment. Coast. Eng. Jpn. 1974, 17, 117–128. [Google Scholar] [CrossRef]
- Medina, J.R. Wind effects on runup and breakwater crest design. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; pp. 1068–1081. [Google Scholar] [CrossRef]
- Hudson, R.Y. Laboratory investigation of rubble-mound breakwaters. J. Waterw. Harb. Div. 1959, 85, 93–121. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Stability of breakwater armour layers—Design formulae. J. Coast. Eng. 1987, 11, 219–239. [Google Scholar] [CrossRef]
- Hashida, M.; Matsunaga, N.; Irie, I. Landward transport of spray generated from a wave absorbing sea wall. In Proceedings of the International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; pp. 1022–1033. [Google Scholar] [CrossRef]
- Carrasco, A.R.; Reis, M.T.; Neves, M.G.; Ferreira, O.; Matias, A.; Almeida, S. Overtopping hazard on a rubble mound breakwater. J. Coast. Res. 2014, 70, 247–252. [Google Scholar] [CrossRef]
- Diwedar, A.I. Investigating the effect of wave parameters on wave runup. Alex. Eng. J. 2016, 55, 627–633. [Google Scholar] [CrossRef]
- Hughes, S.A. Estimation of wave run-up on smooth, impermeable slopes using the wave momentum flux parameter. J. Coast. Eng. 2004, 51, 1085–1104. [Google Scholar] [CrossRef]
- Yamashiro, M.; Yoshida, A.; Hashimoto, H.; Kurushima, N.; Irie, I. Conversion of the wind velocity in wave-overtopping experiment into the wind velocity of the real coast. Proc. Civ. Eng. Ocean 2004, 20, 653–658. [Google Scholar] [CrossRef]
- Yamashiro, M.; Yoshida, A.; Yoshioka, T.; Hashimoto, H.; Moriya, Y. Effect of wind to wave-overtopping and water spray on non wave-overtopping type seawall in deepwater. Proc. Civ. Eng. Ocean 2005, 21, 611–616. [Google Scholar] [CrossRef]
- Shim, G.-T.; Kim, G.-H. Review of hydraulic characteristics of the entire revetment in a coexistence of waves and wind. J. Korean Soc. Coast. Ocean Eng. 2020, 32, 575–586. [Google Scholar] [CrossRef]
- Sous, D.; Forsberg, P.L.; Touboul, J.; Nogueira, G.G. Laboratory experiments of surf zone dynamics under on- and offshore wind conditions. Coast. Eng. 2021, 163, 103797. [Google Scholar] [CrossRef]
- de Waal, J.P.; Tönjes, P.; van der Meer, J.W. Wave overtopping of vertical structures including wind effect. In Proceedings of the 25th International Conference on Coastal Engineering, ASCE, Orlando, FL, USA, 2–6 September 1996. [Google Scholar] [CrossRef]
- Ward, D.L.; Wibner, C.G.; Zhang, J. Runup on coastal revetments under the influence of onshore wind. J. Coast. Res. 1998, 14, 1325–1333. [Google Scholar]
- Mares-Nasarre, P.; Molines, J.; Gómez-Martín, M.E.; Medina, J.R. Hydraulic stability of cube-armored mound breakwaters in depth-limited breaking wave conditions. Ocean Eng. 2022, 259, 111845. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Rock Slopes and Gravel Beaches under Wave Attack. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 2020. [Google Scholar]
- Kobune, K.; Sasaki, H.; Hashimoto, N. Characteristics of ocean waves off cape Nojima in the North Western Pacific, measured with a discus buoy. Coastal Eng. Jpn. 1988, 30, 45–62. [Google Scholar] [CrossRef]
- Bretschneider, C. Significant waves and wave spectrum. In Ocean Ocean Industry; Gulf Publishing Company: Houston, TX, USA, 1968; pp. 40–46. Available online: https://cir.nii.ac.jp/crid/1574231875266506752 (accessed on 15 March 2024).
- Mitsuyasu, H. On the growth of wind-generated waves (2)—Spectral shape of wind waves at finite fetch. In Proceedings of the 17th Japanese Conference on Coastal Engineering, Kyoto, Japan, 16–21 October 1970; pp. 1–7. Available online: https://cir.nii.ac.jp/crid/1573105975214720000 (accessed on 15 March 2024).
- Korea Meteorological Administration (KMA). Korean Peninsula TYPHOON analysis Report 2020. National Typhoon Center Technical Note, Daejeon–si, Republic of Korea, 11-1360000-001533-10. Available online: https://www.kma.go.kr/download_01/typhoon/typeffect_2020.pdf (accessed on 15 March 2024).
- Inagaki, N.; Shibayama, T.; Nakamura, R.; Ishibashi, K.; Esteban, M. Experimental investigation into the effects of strong winds on the transport of overtopping water mass over a vertical seawall. Coast. Eng. J. 2023, 1–15. [Google Scholar] [CrossRef]
- Lee, J.S.; Suh, K.-D. Development of stability formulas for rock armor and tetrapod using multigene genetic programming. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019027. [Google Scholar] [CrossRef]
- Lee, D.-S.; Oh, S.-H.; Cho, B.-S. Experimental investigation on the change in tetrapod stability coefficient according to the difference in specific gravity. J. Korean Soc. Coast. Ocean Eng. 2016, 28, 124–131. [Google Scholar] [CrossRef]
- Suh, K.-D.; Kim, M.; Kim, S.-W. Comparison of calculation methods of cumulative damage to breakwater armor layer. J. Waterw. Port Coast. Ocean Eng. 2012, 139, 277–285. [Google Scholar] [CrossRef]
- Kim, Y.-T.; Lee, J.-I. Hydraulic experiment on the stable weight and coverage of Tetrapods mounted on the head of an inclined breakwater: Non-crushing wave conditions. J. Korean Soc. Coast. Ocean Eng. 2017, 29, 389–398. [Google Scholar] [CrossRef]
- Ministry of Oceans and Fisheries (MOF). Design Standards for Harbor and Fishery Port 2017, Sejong–si, Republic of Korea, 11-1192000-000184-14 (KDS 64 00 00). Available online: https://www.mof.go.kr/search/selectTotalList.do?menuSeq=955 (accessed on 15 March 2024).
- USACE. Coastal Engineering Manual; U.S. Army Coastal Engineering Research Center, U.S. Army Engineer Waterways Experiment Station: Vicksburg, MI, USA, 2005. [Google Scholar]
- González-Escrivá, J.A. The role of wind in wave runup and overtopping of coastal structures. Coast. Eng. 2006, 5, 4766–4778. [Google Scholar] [CrossRef]
- Suh, K.D.; Park, W.S. Wave reflection from perforated-wall caisson breakwaters. Coast. Eng. 1995, 26, 177–193. [Google Scholar] [CrossRef]
- Pedersen, J. Wave Forces and Overtopping on Crown Walls of Rubble Mound Breakwaters: An Experimental Study. Ph.D. Thesis, Hydraulic & Coastal Engineering Lab, Dept. of Civil Engineering, University of Aalborg, Aalborg, Denmark, 1996. [Google Scholar]
- Shankar, N.J.; Jayaratne, M.P.R. Wave run-up and overtopping on smooth and rough slopes of coastal structures. Ocean Eng. 2003, 30, 221–238. [Google Scholar] [CrossRef]
- Sakakiyama, T.; Liu, P.L.-F. Laboratory experiments for wave motions and turbulence flow in front of a breakwater. Coast. Eng. 2001, 44, 117–139. [Google Scholar] [CrossRef]
- Sundar, V.; Ragu, V. Dynamic pressures and run-up on semicircular breakwaters due to random waves. Ocean Eng. 1998, 25, 221–241. [Google Scholar] [CrossRef]
- Oh, S.-H.; Kwon, O.-S. Comparison of Wave Runup Formula Used in Domestic and Foreign Countries; Korean Society of Coastal and Ocean Engineers: Seoul, Republic of Korea, 2009; Volume 18, pp. 176–179. [Google Scholar]
- Di Leo, A.; Dentale, F.; Buccino, M.; Tuozzo, S.; Carratelli, E.P. Numerical analysis of wind effect on wave overtopping on a vertical seawall. Water 2022, 14, 3891. [Google Scholar] [CrossRef]
- Denissenko, P.; Didenkulova, I.; Rodin, A.; Listak, M.; Pelinovsky, E. Experimental statistics of long wave runup on a plane beach. J. Coast. Res. 2013, 65, 195–200. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave runup distributions on natural beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Ward, D.L.; Wibner, C.G.; Zhang, J.; Edge, B. Wind effects on runup and overtopping. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 1687–1699. [Google Scholar] [CrossRef]
- Aniel-Quiroga, I.; Vidal, C.; Lara, J.L.; González, M.; Sainz, A. Stability of rubble-mound breakwaters under tsunami first impact and overflow based on laboratory experiments. Coast. Eng. 2018, 135, 39–54. [Google Scholar] [CrossRef]
- Latham, J.P. Degradation model for rock armour in coastal engineering. Q. J. Eng. Geol. Hydrogeol. 1991, 24, 101–188. [Google Scholar] [CrossRef]
- Ehsani, M.; Moghim, M.N.; Shafieefar, M. An experimental study on the hydraulic stability of Icelandic-Type berm breakwaters. Coast. Eng. 2020, 156, 103599. [Google Scholar] [CrossRef]
- Hajivalie, F.; Yeganeh-Bakhtiary, A. Numerical study of breakwater steepness effect on the hydrodynamics of standing waves and steady streaming. J. Coast. Res. 2009, 56, 514–518. [Google Scholar]
- Sumer, B.M.; Fredsøe, J. Experimental study of 2D scour and its production at a rubble-mound breakwater. Coast. Eng. 2000, 40, 59–87. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, J.H.; Ma, H.S. Applicability evaluation of tetrapod debris barrier—A case of Honggyeri area in Sanchung county. J. Korean Soc. Environ. Restor. Technol. 2012, 15, 119–132. [Google Scholar] [CrossRef]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Petrol. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Cho, Y.J. Numerical analysis of the beach stabilization effect of an asymmetric ripple mat. J. Korean Soc. Coast. Ocean Eng. 2019, 31, 209–220. [Google Scholar] [CrossRef]
- Goda, Y.; Kishira, Y.; Kamiyama, Y. Laboratory investigation on the overtopping rate of seawalls by irregular waves. Port Harb. Res. Inst. 1975, 14, 4. [Google Scholar]
- USACE. Shore Protection Manual; U.S. Army Coastal Engineering Research Center, U.S. Army Engineer Waterways Experiment Station: Vicksburg, MI, USA, 1984. [Google Scholar]
- Douglass, S.L. Influence of wind on breaking waves. J. Waterw. Port Coast. Ocean Eng. 1990, 116, 651–663. [Google Scholar] [CrossRef]





| Target | Measured Data | |||
|---|---|---|---|---|
| (s) | (s) | (cm) | (cm) | (s) |
| 1.41 | 1.45 | 7 | 7.3 | 1.52 |
| 8 | 8.2 | 1.52 | ||
| 9 | 9.1 | 1.57 | ||
| 10 | 10.3 | 1.54 | ||
| 11 | 11.4 | 1.63 | ||
| 12 | 12.1 | 1.41 | ||
| 13 | 13.0 | 1.41 | ||
| 14 | 14.2 | 1.55 | ||
| 15 | 15.3 | 1.55 | ||
| (m/s) | (m/s) [Froude Scale] | (m/s) [10] |
|---|---|---|
| 0 | 0 | 0 |
| 5.5 | 38.9 | 16.5 |
| 12 | 84.8 | 36 |
| (cm) | Wind Velocity (m/s) | |||
|---|---|---|---|---|
| 0 | 5.5 | 12 | ||
| 7.3 | - | - | - | 1.68 |
| 8.2 | 2.37 | |||
| 9.1 | : 1, : 0 | 3.25 | ||
| 10.3 | : 4, : 0 | : 4, : 0 | 4.86 | |
| 11.4 | : 5, : 0 | : 5, : 1 | 6.50 | |
| 12.1 | : 1, : 0 | : 6, : 1 | : 7, : 1 | 7.79 |
| 13.0 | : 1, : 1 | : 8, : 2 | : 9, : 2 | 9.58 |
| 14.2 | : 2, : 2 | : 8, : 4 | : 9, : 4 | 12.54 |
| 15.3 | : 6, : 3 | 15.59 | ||
| Calculated | 7.79 (-) | 4.86 (−37.61) | 3.25 (−58.28) | |
| (m/s) | (cm) | (cm) | (cm/s) | (cm/s) |
|---|---|---|---|---|
| 0 | 19.97 (-) | 15.53 (-) | 74.85 (-) | 78.21 (-) |
| 5.5 | 25.52 (27.79%) | 17.20 (10.75%) | 68.85 (−8.02%) | 95.50 (22.11) |
| 12 | 23.74 (18.88%) | 17.20 (10.75%) | 78.59 (5.00%) | 98.94 (26.51%) |
| Runup height | (m/s) | Number of runup height data | (cm) | (cm) | (cm) | (cm) | ||||
| ~5 cm | 5~10 cm | 10~15 cm | 15~20 cm | ~20 cm | ||||||
| 0 | 126 [26.1%] | 204 [42.3%] | 118 [24.5%] | 30 [6.2%] | 4 [0.8%] | 23.30 (-) | 19.20 (-) | 13.09 (-) | 8.18 (-) | |
| 5.5 | 85 [17.3%] | 244 [49.8%] | 106 [21.6%] | 47 [9.6%] | 8 [1.6%] | 25.52 (9.5%) | 21.49 (11.9%) | 13.91 (6.3%) | 8.80 (7.6%) | |
| 12 | 66 [14.0%] | 250 [53.1%] | 104 [22.1%] | 43 [9.1%] | 8 [1.7%] | 28.84 (23.8%) | 22.02 (14.7%) | 14.08 (7.6%) | 8.93 (9.2%) | |
| Rundown height | (m/s) | Rundown height data number | (cm) | (cm) | (cm) | (cm) | ||||
| ~5 cm | 5~10 cm | 10~15 cm | 15~20 cm | ~20 cm | ||||||
| 0 | 127 [26.9%] | 235 [49.8%] | 100 [21.2%] | 10 [2.1%] | 0 [0%] | 17.75 (-) | 15.30 (-) | 8.88 (-) | 7.23 (-) | |
| 5.5 | 83 [17.7%] | 241 [51.3%] | 130 [27.7%] | 16 [3.4%] | 0 [0%] | 18.31 (3.2%) | 16.09 (5.2%) | 9.98 (12.4%) | 8.21 (13.6%) | |
| 12 | 48 [10.3%] | 264 [56.5%] | 122 [26.1%] | 33 [7.1%] | 0 [0%] | 19.41 (9.4%) | 16.64 (8.8%) | 10.54 (18.7%) | 8.92 (23.4%) | |
| (m/s) | Fluid Velocity (cm/s) Data Number | Max (cm/s) | Min (cm/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ~−75 | −75~−50 | −50~−25 | −25~0 | 0~25 | 25~50 | 50~75 | ~75 | |||
| 0 | 60 (0.17%) | 554 (1.57%) | 3435 (9.74%) | 12862 (36.49%) | 13518 (38.35%) | 4236 (12.02%) | 570 (1.62%) | 15 (0.04%) | 90.9 | −92.2 |
| 5.5 | 144 (0.41%) | 731 (2.07%) | 4000 (11.35%) | 13384 (37.97%) | 12673 (35.95%) | 3845 (10.91%) | 470 (1.33%) | 3 (0.01%) | 89.3 | −95.5 |
| 12 | 147 (0.42%) | 765 (2.17%) | 3862 (10.96%) | 13343 (37.85%) | 12567 (35.65%) | 3919 (11.12%) | 612 (1.74%) | 35 (0.10%) | 97.0 | −99.2 |
| Target | Measured Data | |||
|---|---|---|---|---|
| (s) | (s) | (cm) | (cm) | (s) |
| 2.26 | 2.33 | 7 | 7.1 | 2.41 |
| 8 | 8.1 | 2.21 | ||
| 9 | 9.1 | 2.64 | ||
| 10 | 10.1 | 2.41 | ||
| 11 | 11.3 | 2.21 | ||
| 12 | 11.9 | 2.64 | ||
| 13 | 13.0 | 2.41 | ||
| 14 | 13.9 | 2.64 | ||
| 15 | 14.9 | 2.48 | ||
| Measured Data | Wind Velocity | ||
|---|---|---|---|
| (cm) | (s) | = 0 m/s | = 5.5 m/s |
| 7.1 | 2.41 | - | - |
| 8.1 | 2.21 | ||
| 9.1 | 2.64 | ||
| 10.1 | 2.41 | ||
| 11.3 | 2.21 | ||
| 11.9 | 2.64 | : 2, : 0 | |
| 13.0 | 2.41 | : 2, : 0 | : 4, : 0 |
| 13.9 | 2.64 | : 4, : 0 | : 7, : 0 |
| 14.9 | 2.48 | : 5, : 1 | : 7, : 1 |
| 9.58 | 7.35 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-M.; Lim, J.-H.; Yoon, H.-D. Experimental Study on the Effect of Wind on Armor Stone Stability. J. Mar. Sci. Eng. 2024, 12, 499. https://doi.org/10.3390/jmse12030499
Kim Y-M, Lim J-H, Yoon H-D. Experimental Study on the Effect of Wind on Armor Stone Stability. Journal of Marine Science and Engineering. 2024; 12(3):499. https://doi.org/10.3390/jmse12030499
Chicago/Turabian StyleKim, Young-Min, Jae-Ho Lim, and Hyun-Doug Yoon. 2024. "Experimental Study on the Effect of Wind on Armor Stone Stability" Journal of Marine Science and Engineering 12, no. 3: 499. https://doi.org/10.3390/jmse12030499
APA StyleKim, Y.-M., Lim, J.-H., & Yoon, H.-D. (2024). Experimental Study on the Effect of Wind on Armor Stone Stability. Journal of Marine Science and Engineering, 12(3), 499. https://doi.org/10.3390/jmse12030499





