Abstract
Incorporating steps into a hull reduces the wetted surface, promoting improved hydrodynamic lift and reduced resistance at high speeds, provided that the step is designed appropriately. Traditional hydrodynamics studies rely on scaled model testing in towing tanks, but numerical tools offer a more efficient alternative. This study focused on investigating the hydrodynamic performance of stepped hulls by modifying the parent hull of the Naples Systematic Series (C1). The Computational Fluid Dynamics (CFD) code SIEMENS PLM STAR CCM+ version 2302 was used for simulations, including four different beam Froude numbers ( = 1.13, 2.22, 2.56, and 2.96) and a total of 15 hull configurations with single and double steps. By employing a three-dimensional computational analysis of multiphase flow using Dynamic Fluid–Body Interaction (DFBI) and overset mesh, various performance parameters such as resistance coefficient, dimensionless wetted surface, sinkage, and dynamic trim were analyzed. The accuracy of the CFD results was confirmed through comparison with experimental data and grid uncertainty assessment. The study demonstrated that placing a single step near the transom decreased trim and increased resistance and wetted surface. Conversely, positioning a step in the forward section reduced the trim angle at lower step heights but increased trim at higher step heights in single-stepped hulls. The application of these findings contributes to the design optimization of stepped hulls for enhanced performance in high-speed maritime applications.
1. Introduction
In recent years, there has been a significant emphasis on designing planing hulls for maximum speed, with researchers and designers adjusting hull geometry to achieve this goal [1]. These modifications include the addition of features like steps [2], tunnels [3], and hydrofoils [4] to enhance planing hull performance. Among these modifications, the addition of steps has gained attention due to its minimal alteration of the hull’s original geometry.
1.1. Comparative Analysis of Single- and Double-Stepped Hull
The stepped hull is renowned for its low hydrodynamic drag-to-lift ratio at high speeds, attributed to a reduction in wetted surface caused by flow separation induced by the step [5]. However, the performance prediction of hulls is influenced by factors such as the position, shape, and height of the step [6]. Consequently, researchers endeavored to investigate the performance prediction and motion in waves of both stepless and stepped hull designs using a combination of towing tank tests, analytical methods, and CFD-based simulations.
Towing tank tests are considered the optimal and most precise method for assessing the performance of planing hulls. This has led to the emergence of various systematic experimental tests documented in the literature. Between 2008 and 2014, Becker et al. [7], Taunton et al. [8], and Lee et al. [9] conducted extensive towing tank tests to evaluate the performance of stepped planing hulls in calm water. These tests focused on the impact of straight steps on planing hulls, revealing that the addition of straight steps can enhance fuel efficiency. In recent years, Vitiello et al. [10] conducted towing tank tests on forward-swept stepped planing hulls with variations in step positions and heights. Their findings indicated that relocating a forward-swept angled step from near the transom to the forward part of the hull (near stagnation lines) reduced the wetted surface but increased spray drag. This spray drag further increased with an increase in step height. However, the parametric study of hulls in a towing tank can sometimes be costly and time-consuming. Consequently, researchers have endeavored to develop alternative methods that offer time and cost savings.
1.2. Numerical Analysis
The evolution of research practices has led to the design of optimized stepless and stepped hulls using analytical/empirical and CFD-based methods. In the realm of empirical methods, Savitsky [11] pioneered a framework for estimating the lift, resistance, and dynamic trim angles of planing hulls in calm water. Utilizing key parameters such as hull dimensions, deadrise angle, longitudinal center of gravity, and forward speed, Savitsky’s method laid the foundation. Subsequent refinements by Savitsky et al. [12] incorporated whisker spray and air resistance to enhance the accuracy of total resistance calculations. This work was further extended by Savitsky and Morabito [13] to investigate the main spray pattern characteristics.
Advancements in applying the Savitsky method to stepped planing hulls ensued, with Savitsky and Morabito [13] conducting experiments to derive mathematical formulations for flow separation from steps. Svahn [14] then leveraged these formulations, extending Savitsky’s [11] method using wake theory for the performance prediction of single-stepped hulls. However, when applied to two-stepped hulls, Danielsson and Stromquist [15] faced challenges due to the limited range of applicability. To overcome this, they introduced an assumption of linear trends for flow separation and reattachment in high-speed scenarios.
Turning to analytical methods, the 2D + t method emerges as a powerful tool for solving fluid field equations around planing hulls. By simplifying the three-dimensional problem into a 2D problem, this method provides insights into the flow field around 2D V-shaped bodies resembling the section of a deep-V boat [16,17]. Despite the advantages of the 2D problem, the 3D problem requires time domain solutions, as seen in water entry problems. The versatility of the 2D + t method extends to various planing vessel designs, encompassing predictions of motions in waves [18], modeling roll motion [19], and maneuvering planing hulls [20,21], even in the early-stage design of stepped planing hulls [6]. While analytical methods prove useful for calculating performance predictions and motion in waves in the early-stage design, CFD simulations offer a higher level of accuracy, making them preferable in the final stages of design where precision is crucial. Numerous researchers have scrutinized the accuracy of CFD in replicating the calm-water behavior of stepped planing hulls, including studies by Brizzolara and Federici [22], De Marco et al. [23], Niazmand Bilandi et al. [24,25], and Park et al. [26]. De Marco et al. [23] and Niazmand Bilandi et al. [24] demonstrated that CFD can reasonably accurately calculate the flow behavior around and beneath swept-stepped hulls. Chooran et al. [27] used ANSYS-FLUENT commercial software to simulate two-phase flow and determine the drag force on a single-stepped planing hull. Their main goal was to investigate the effect of step height on the hull’s performance in terms of drag reduction and stability. They discovered that increasing the step height beyond a certain value led to hydrodynamic issues, resulting in porpoising and hull instability. They observed that up to a step height-to-length ratio of 0.1, drag reduction occurred and the hull remained stable. However, beyond this ratio, such as with step height-to-length ratios of 0.125 and 0.15, ventilation occurred more extensively than the hull length, causing the water to detach from the hull bottom and leading to hull instability. Cucinotta et al. [28] conducted an experimental and numerical campaign on a multi-stepped ACS, varying the velocity and airflow rate under the hull. They demonstrated that CFD simulations could incorporate air injection into the step and simulate the behavior of stepped hulls. Their findings revealed that using CFD enabled the observation of quantities that are challenging to evaluate through traditional experimental tests, such as the frictional component of resistance, airflow path lines, and volume fraction in transversal and longitudinal sections. Zou et al. [29] conducted a combined experimental and numerical study on a double-stepped planing hull, focusing on the hydrodynamic characteristics of the step and stern flap, as well as their coupling effect on the hull body. They determined that increasing the stern flap mounting angle reduced trim and intensified cavity expansion speed, resulting in a reduction in the wetted surface area and friction resistance. This led to slight amplification of total resistance, while also distributing the load more uniformly among the planing surfaces, which helped inhibit porpoising. Yang et al. [30] investigated the use of CFD techniques to study the flow around single-stepped planing hulls. Their numerical results indicated that as the air cavity expanded, it could cover up to 77.8% of the entire wetted surface of the planing hull bottom. Additionally, during the triangle planing stage, there was additional wetting at the aft bilge due to spray from the steps when stagnation lines intersected them, leading to a decrease in the air cavity rate and an increase in the wetted area. In a recent study, Niazmand Bilandi et al. [25] conducted a verification and validation study on CFD simulations of swept-stepped hulls, showcasing how moving mesh techniques and increasing mesh numbers can enhance the flow behavior around and beneath these hulls.
1.3. Objective of Research
This paper builds on previous CFD simulations of stepped planing hulls. It conducts further investigations through additional CFD simulations, exploring how different shapes, heights, and positions of stepped planing hulls influence their performance prediction. The aim is to fill the existing gap in understanding how step shape, height, and position impact the performance prediction of both single and double-stepped planing hulls. The simulation’s outcome demonstrated that placing a single step near the transom decreased trim and increased resistance and wetted surface. Conversely, lower step height and positioning in the forward section reduced the trim angle, subsequently increasing trim at higher step heights in single-stepped hulls. Notably, in this study, the wetted surface is reduced in all step designs except for the “S3-F” model.
1.4. Paper Structure
The rest of the present paper is organized as follows. Section 2 introduces the planing hull and the modified stepped hulls that are studied in the present research, including the dimensional aspect of the steps. Section 3 briefly introduces the fluid assumptions and governing equations and then details the numerical scheme used to replicate the motions of the hulls in a numerical tank, as well as the mesh generation and mesh independence analysis. Section 4 investigates the comparative analysis between CFD data and results obtained from towing tank tests, plotting the results for resistance, wetted surface, sinkage, dynamic trim, pressure distribution, and Volume of Fraction (VOF) contours for CFD. Finally, Section 5 presents the conclusion of this research. Appendix A shows the Y+ contours of all stepped hulls, while Appendix B includes the table of results for all four beam Froude numbers.
2. Hull Models and Methodology
Stepped hulls, a prevalent design feature in boats, have the potential to diminish resistance and wetted surfaces through flow separation at the bottom of the vessel. Nevertheless, the effectiveness of a stepped hull is contingent upon factors like step type, height, and location. This study employs numerical simulations to investigate the influence of steps on the performance of one- and two-stepped planing hulls in calm water, building upon previous research in this domain.
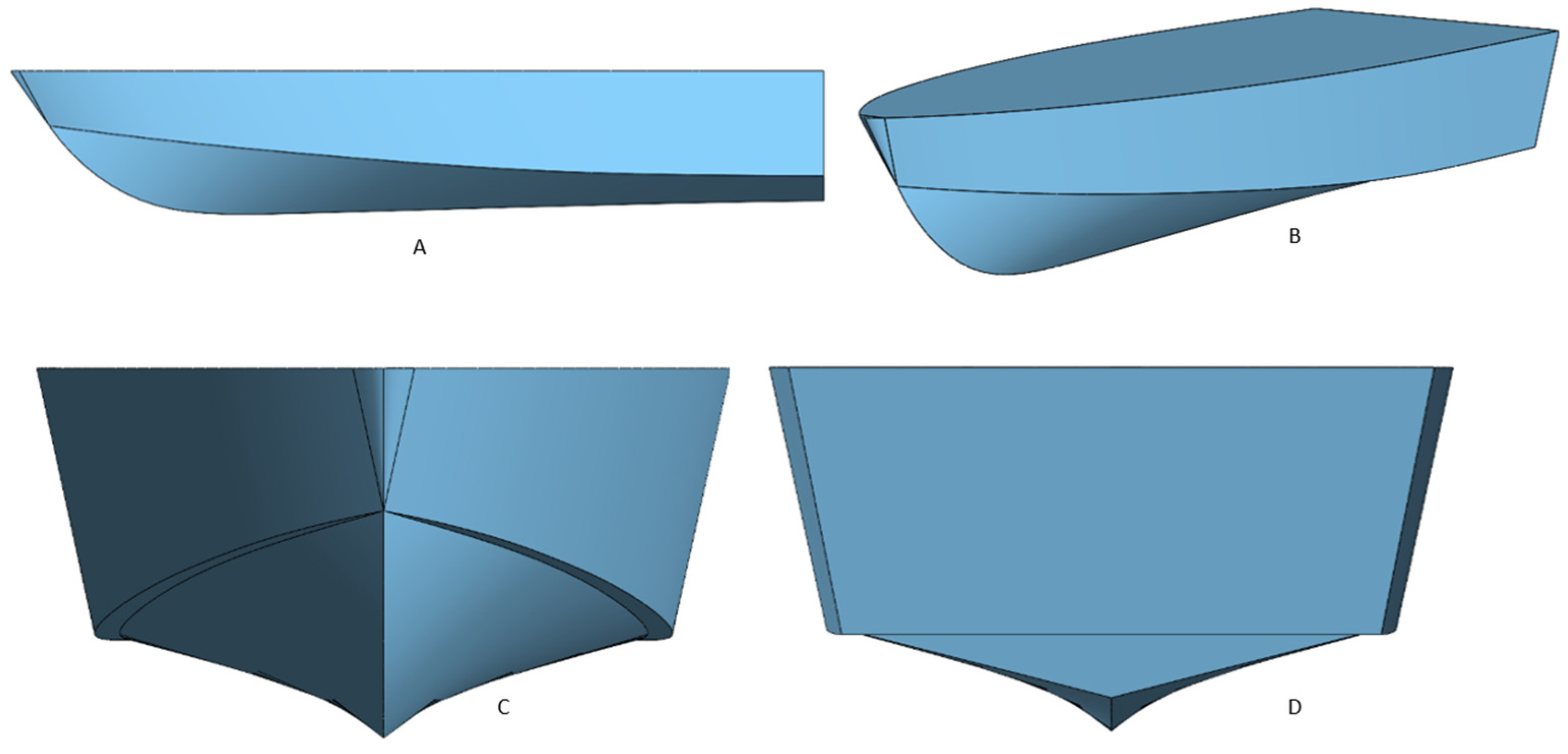
To scrutinize the planing hull’s behavior and the impact of steps, the parent hull (C1) of the Naples Systematic Series (NSS) was chosen as the foundational model. The C1 underwent design and testing at the naval division of the Department of Industrial Engineering of the Università degli Studi di Napoli “Federico II”. Figure 1 illustrates the C1 model, and the key parameters of the hull are presented in Table 1 [31].
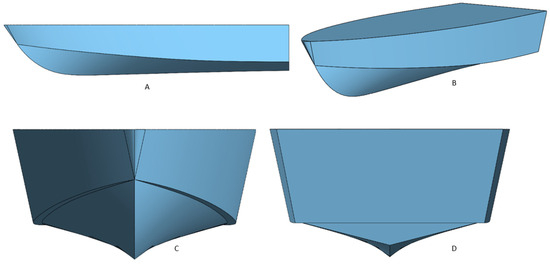
Figure 1.
Different views of C1: (A) longitudinal view (Y-axis), (B) perspective view (3D view), (C) bow view (X-axis), (D) transom view (X-axis from transom).

Table 1.
Principal parameters of C1 [31].
We selected this model for analyzing the effect of step height and position on performance prediction due to the availability of towing tank test results for the non-stepped hull. Additionally, the results of the interceptor’s impact on this hull are accessible, enabling readers to easily compare the results of the interceptor with the added step.
This hull is symmetrical along the Y-axis from the centerline which is why half hull is used to perform CFD simulations to save computational time.
Addition of Steps
The C1 hull served as the base model, and steps were incorporated into the hull. Previous studies indicate that steps can offer an effective solution for controlling the dynamic trim angle, mitigating longitudinal instability phenomena such as the porpoising effect [23].
In this research, single and double steps were introduced by varying their locations, shapes, and sizes. Initially, nine single-stepped hulls were created, each with distinct locations, shapes, and sizes. Subsequently, the second step was added to the hull after fixing the first step, and both steps were adjusted by varying their locations and sizes, resulting in 15 stepped hulls. To facilitate a systematic comparison with the base model, a constant draft was maintained while adjusting hull displacement. This methodological choice aims to isolate the influence of displacement variations on overall performance, with the resistance coefficient employed as a standardized metric for comparative analysis. The resistance coefficient, being a normalized measure, accommodates the diverse hull configurations, ensuring a robust basis for evaluating and comparing the performance of distinct hull designs.
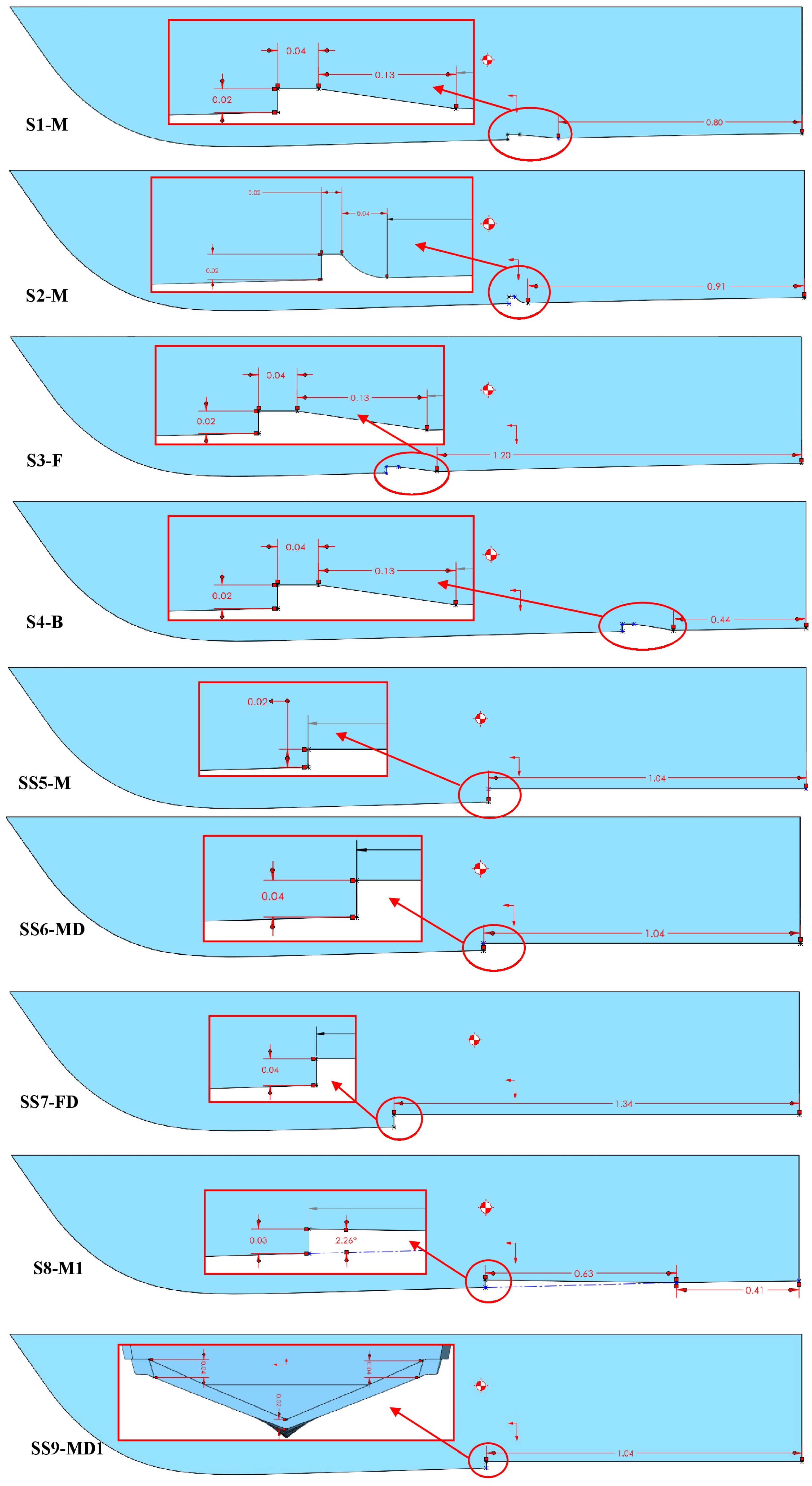
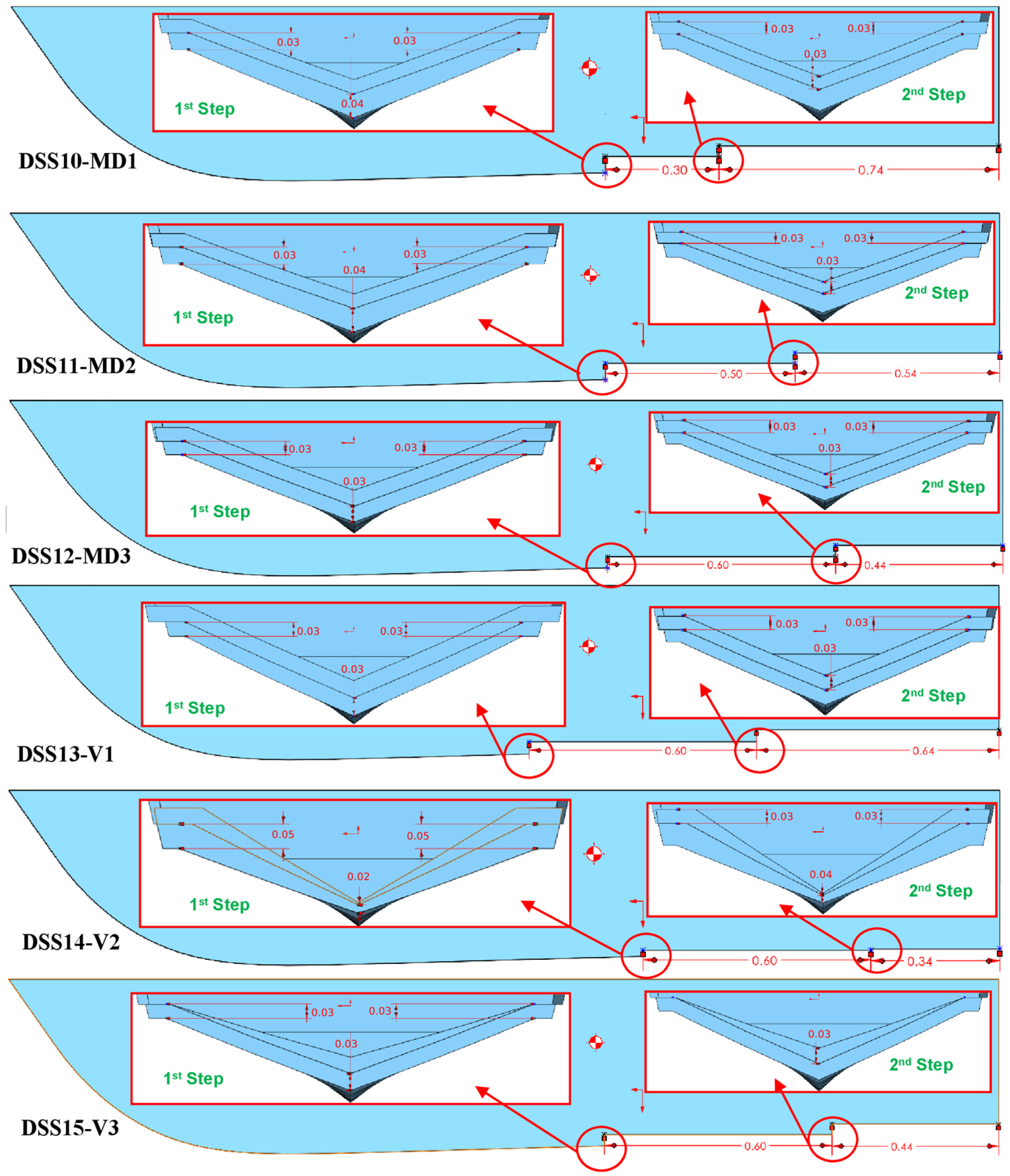
For better comprehension, the longitudinal view of all hulls is presented in Figure 2 and Figure 3. Initially, steps were placed in the center of gravity (COG), and then additional steps were introduced in the forward and aft sections of the hull. The variation in step height was also analyzed.
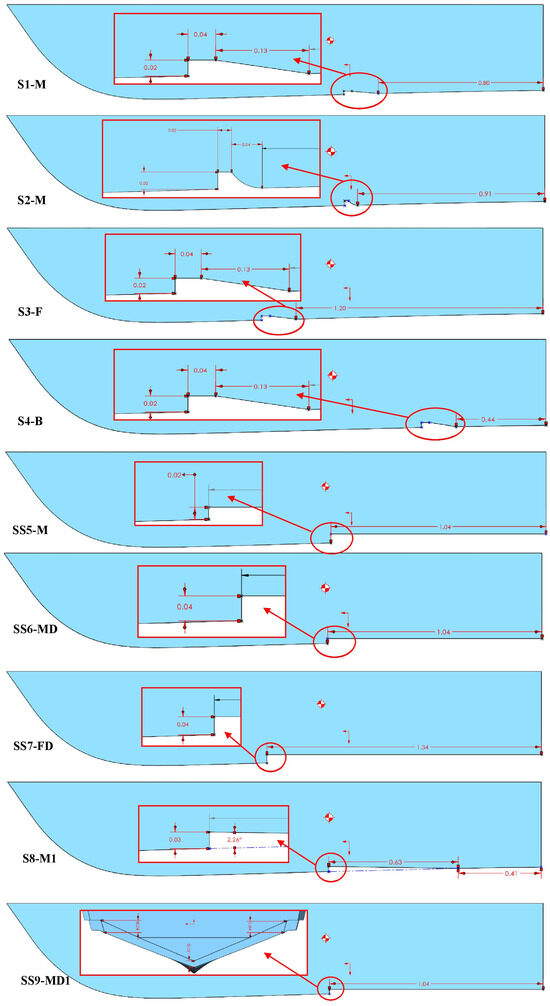
Figure 2.
First nine single-stepped modified hulls (Y-axis view).
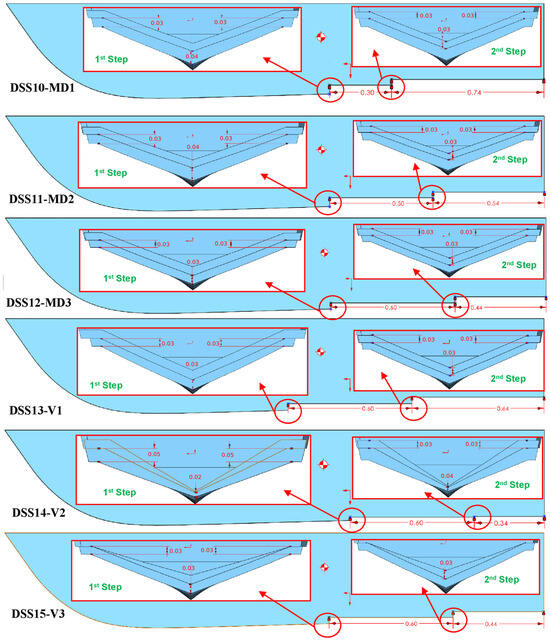
Figure 3.
Six double-stepped modified hulls (Y-axis view).
Table 2 provides the technical specifications of the stepped hull. The “Code” column contains different names for the modified hulls, while subsequent columns detail the hull mass and the location of the COG.

Table 2.
Modified stepped hull details.
In Figure 2, the first nine single-stepped hulls with varying locations, sizes, and shapes are shown. The design SS9-MD1 has different steps, as can be seen in the figure. Notably, its middle step has a slightly lower height than the sides. To facilitate ventilation and airflow from the steps, the edges are curved.
The double-stepped planing hull has a significant advantage in stability and resistance reduction. Therefore, modifications are considered to analyze the behavior of the hull. The hulls from DSS10-MD1 to DSS15-V3 are all double-stepped hulls with different details, which are presented in Figure 3.
The CFD was performed in free motion and using the Dynamic Fluid Body Interaction (DFBI) approach to capture the hull motions. Specifically, two motions were allowed: dynamic trim and heave. Four different speeds are simulated (3.05 m/s, 6.0 m/s, 7.0 m/s, and 8.0 m/s).
3. Numerical Setup
In contrast to the displacement hull, accurate prediction of motion and resistance for planing hulls requires special numerical approaches. For accurate and reliable CFD calculations, it makes use of dynamic, overset grids, and wave damping. These implemented tactics are discussed in the next section, along with how they were applied in the paper.
3.1. Computational Domain Definition
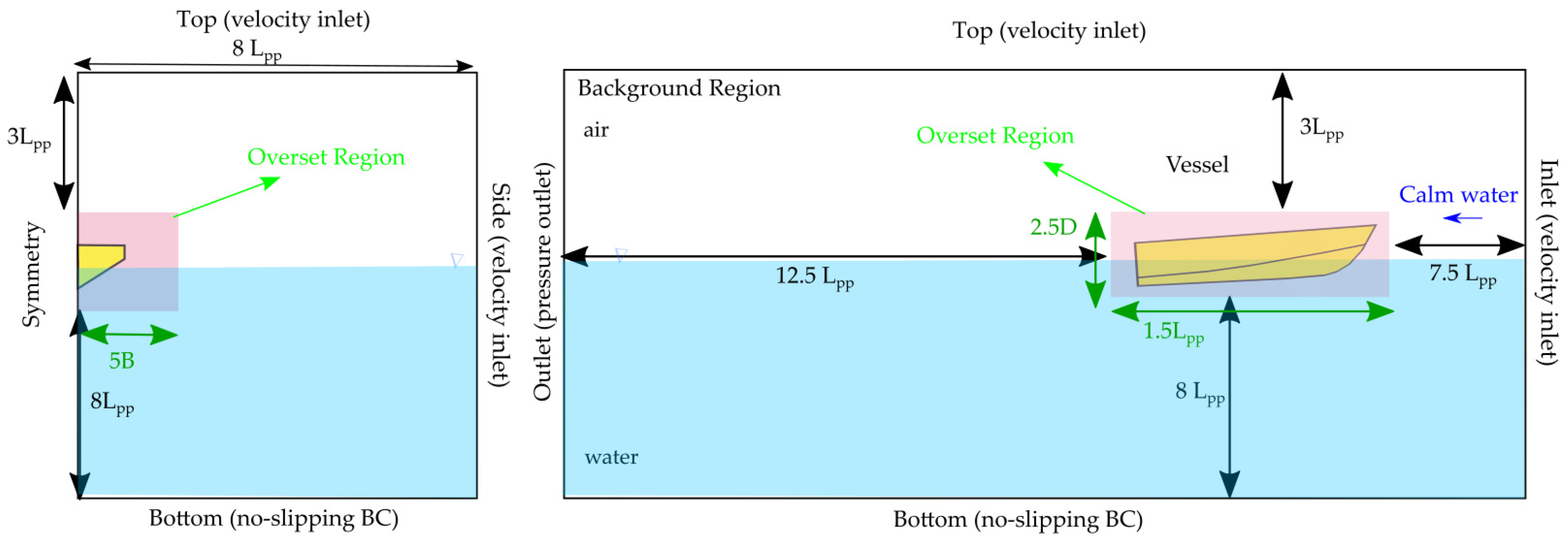
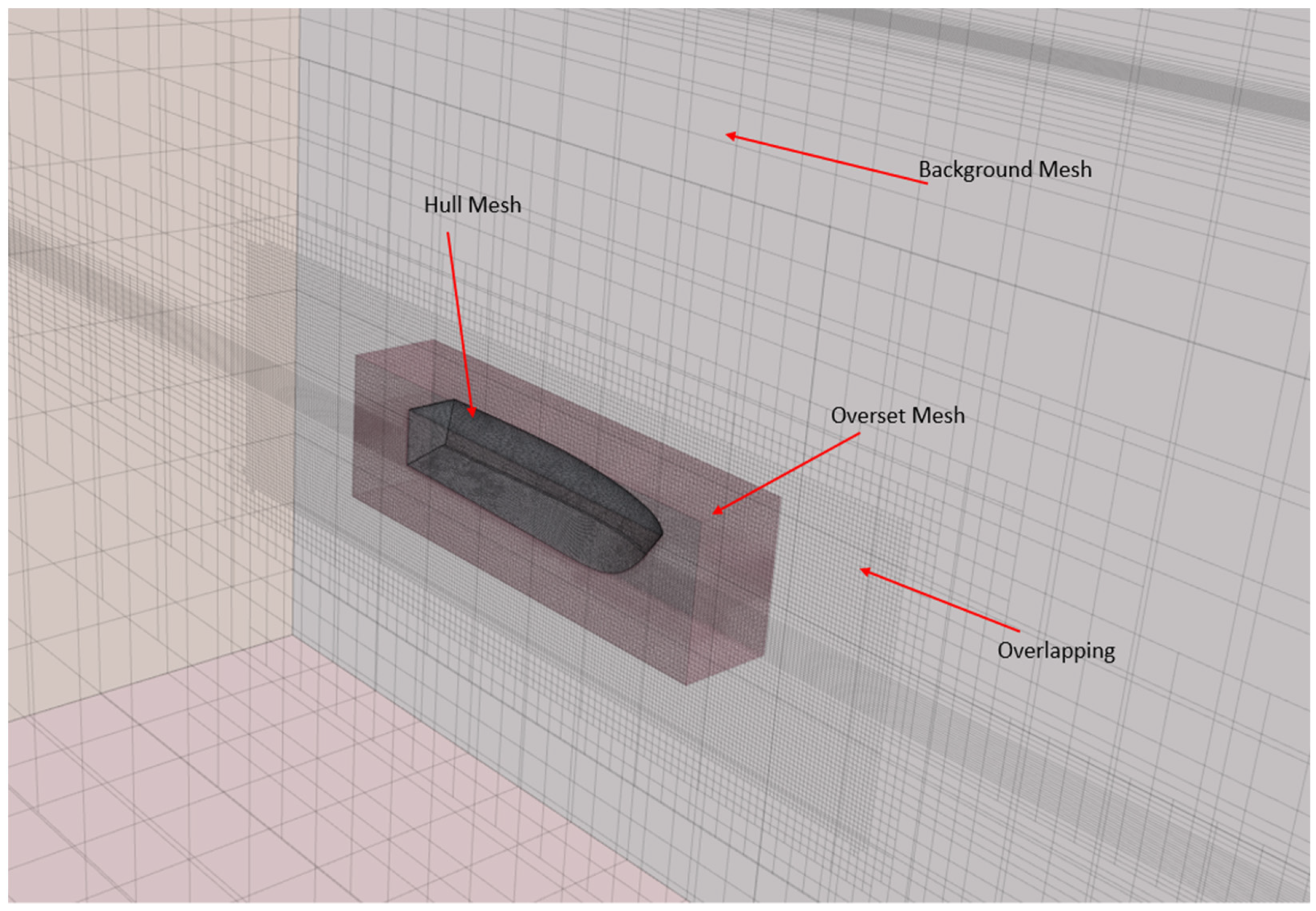
The computational domain serves as the primary representation of the encompassing volume around a subdomain near the hull, where the overset mesh is employed to capture the hydrodynamics of the hull. This approach involves two regions: the overset region, which moves with the hull, and the stationary background. The domain, constructed following the guidelines in [32] and in compliance with ITTC’s CFD recommendations [33], is illustrated in Figure 4. This figure also presents the Overset and Background domains, along with the applied boundary conditions.
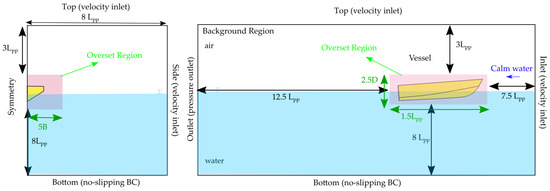
Figure 4.
Dimensions of the computational domain and boundary conditions.
3.2. Physical Models
The physics setup includes an implicit unsteady time domain in which the time step was set to be in the range of the ITTC time-step formula [34]. A segregated flow equation is utilized to solve continuity and momentum equations. A realizable K-Epsilon turbulence model is implemented with a wall function approach turbulence model.
A wall function treatment, specifically the All-wall y+ approach, was used in the simulation to describe the viscous sublayer near the hull’s wall. The y+ parameter utilizes a hybrid approach in the viscous sublayer region to imitate the low-y+ wall (wall y+ < 1) values for fine resolution of the near wall zone and the high-y+ (wall y+ > 30) values for coarse resolution of the near wall zone. This approach provides an effective compromise between the two wall treatment methods. All other main physics setup and solver parameters selected in the simulations are detailed in Table 3.

Table 3.
Selected numerical parameters.
The air and water phases are modeled using the density and viscosity values detailed in Table 4.

Table 4.
Multiphase fluid properties.
3.3. Mesh Generation
The overset mesh approach involves two distinct regions: a static background zone and a moving overset region. This meshing technique is particularly suitable for hulls with significant dynamic trim angles and sinkage, such as planing hulls.
In this study, the meshing process utilized the overset mesh approach ensuring consistency in the cell sizes between the overset and background regions The code SIEMENS PLM STAR-CCM+ was employed for mesh generation in two regions (Figure 5): the first region dealt with the stationary background domain, utilizing a trimmer mesh with hexahedral cells. The second region is the overset region itself and a polyhedral mesh was implemented, similar to the meshing strategy described in De Luca et al. [32].
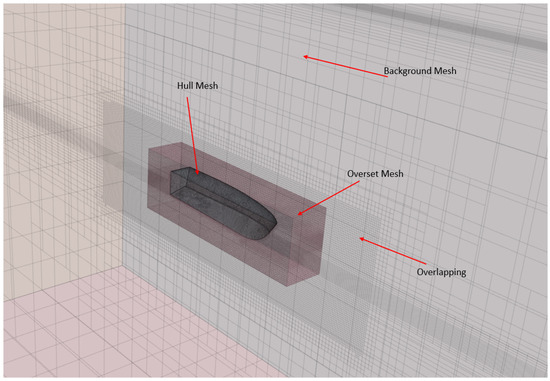
Figure 5.
Mesh configuration on the different mesh regions.
3.4. Mesh Independence and Uncertainty Analysis
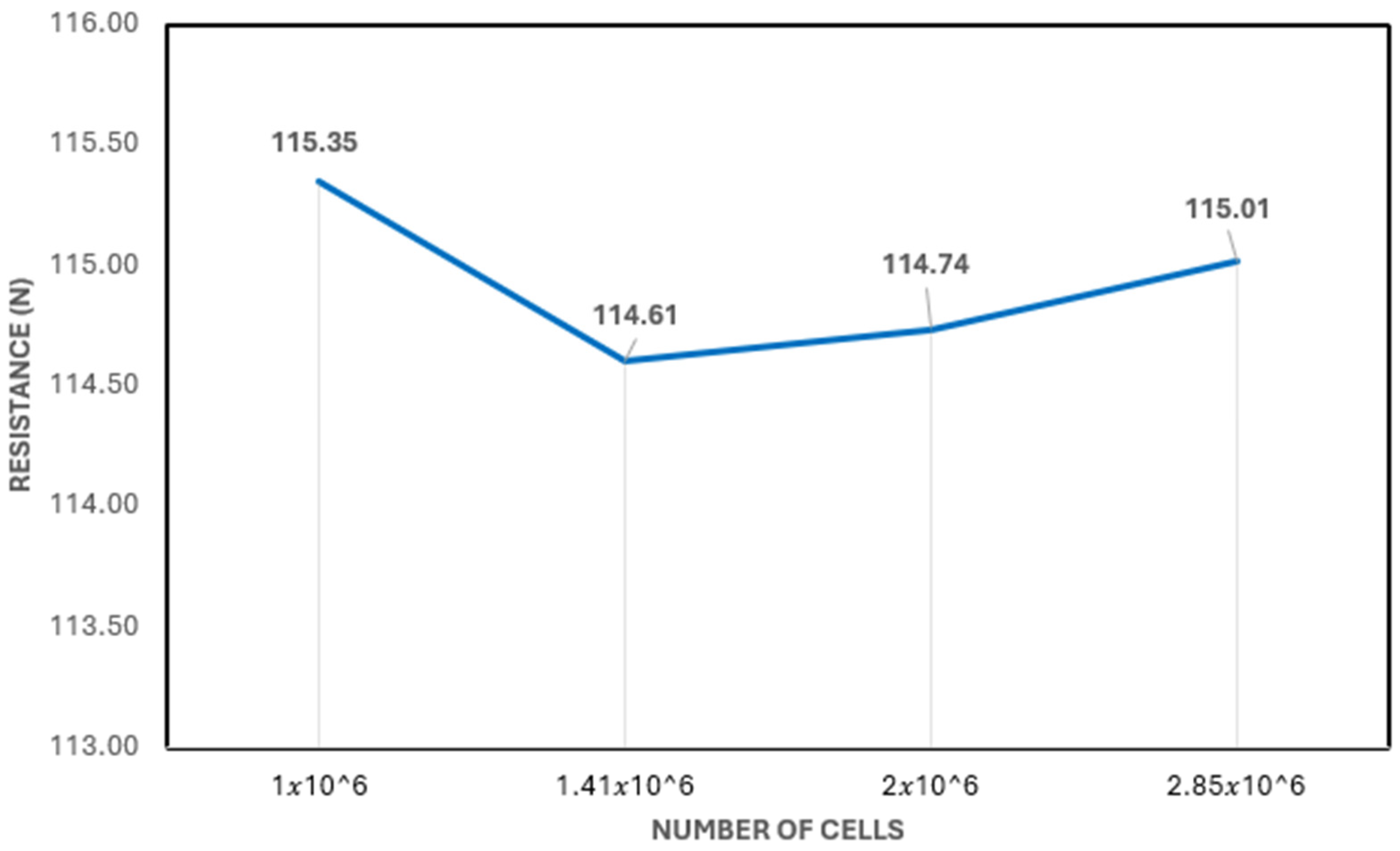
To make the solution independent from the mesh, a mesh independence study was carried out. Four different mesh sizes were used (Table 5). The results noticed from the different grid sizes agreed well with the experimental results. A total of four mesh refinement sizes were used and the resistance percentage error between the EFD and CFD was within the recommended range [34,35] and the asymptotic trend is detected for the latest mesh sizes (M3 and M4), as shown in Figure 6 The ITTC guidelines [33] recommend a uniform refinement ratio in the range of √2 and 2.

Table 5.
Mesh refinement ratio.
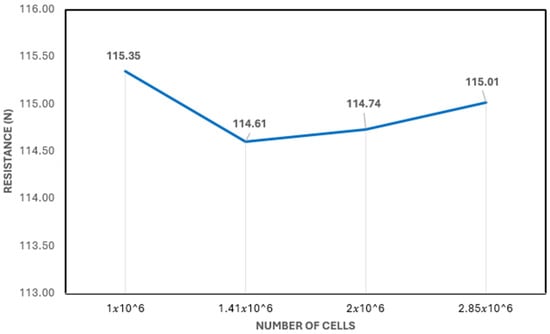
Figure 6.
Mesh convergence study for hull resistance.
In the mesh independence study, four different sizes were used to achieve mesh independence. Different factors were used to maintain the mesh refinement ratio in accordance with ITTC guidelines for overset and background mesh [34]. Table 5 shows that the resistance converged at M3 and M4 mesh sizes. While there was a slight increase in computational time due to a rise in element count, the results did not show a significant difference. Therefore, M1 was chosen to conduct all simulations for both the base hull and the stepped hull. Figure 6 displays the plot of the mesh independence study, which includes the same four mesh sizes. All simulations for mesh independence were conducted at a beam Froude number of 1.13.
With the results of the mesh independence analysis, a grid uncertainty study was performed. The convergence ratio () was defined to provide information about the convergence/divergence of a solution (Equation (1)).
where ε21 and ε32 are the solution changes for the solutions of the cases under analysis. Four different cases of may occur:
- Monotonic convergence: 0 < < 1
- Oscillatory convergence: < 0, || < 1
- Monotonic divergence: > 1
- Oscillatory divergence: < 0, || > 1
In case 1, the generalized Richardson extrapolation is used to assess the uncertainty , as in the ITTC guidelines [33]. For oscillatory convergence (case 2), is estimated by determining the error between the minimum and maximum values of the oscillation (valid only in the asymptotic regime). When the monotonic convergence is reached, and the observed order of accuracy () can be assessed by different solution verification methods. The general form of the uncertainty evaluation can be written as shown in Equation (2).
where is the parameter refinement ratio, ε is the solution change, is the factor of safety, FS = 1.25 for studies with three or more grid cases and is the order of accuracy [33].
The results of the grid uncertainty study are shown in Table 6. For the first set of three grids (M1–M3), no uncertainty can be estimated because the ratio of convergence is as in case 2 but is far from reaching the asymptotic regime. For the second set of three grids (M2–M4), the grid uncertainty () is 0.56%, calculated based on the Grid Convergence Index (GCI), where is the observed grid order of accuracy and is the grid convergence ratio.

Table 6.
Grid uncertainty results at = 1.13 (UG was expressed as a percentage value of the simulation solution for the finest grid).
3.5. Comparison with Experimental Results
To assess the reliability of the CFD setup adopted, a comparison between the CFD and experimental results on the NSS C1 hull was performed. It should be noted that the towing tank data are available on a wide range of speeds and other varying parameters [31]. However, in this study, the comparison was performed at just three different speeds, 3.05 m/s, 6.0 m/s, and 7.0 m/s, to capture the hump in the resistance curve; 8 m/s is the fourth speed that was used to run the CFD, but the validation was not performed on this speed due to the unavailability of experimental data. The output parameters for the comparison are the resistance, dynamics trim, wetted surface area, and sinkage.
Table 7 shows the percentage comparison errors between the experimental and numerical results for the main parameters under analysis. Usually, an error under 5% for resistance and 10–15% for dynamic trim might be considered in the acceptable range for high-speed crafts, as indicated in the ITTC 2014 report of the Specialist Committee on CFD marine hydrodynamics [36].

Table 7.
Comparison errors at three different beam Froude numbers.
From Table 7, it can be observed that the Dynamic Wetted Surface (SWD) estimation has high comparison errors. However, the experimental approach to estimating the wetted surface can partially explain the discrepancies between the experimental wetted surface values and the numerical values. Indeed, as stated in De Luca and Pensa [31], the wetted surface on the C1 hull was calculated with a computerized analysis of camera output and by post-processing it in 3D CAD software, not including the whisker spray area. The dynamic sinkage error is particularly prominent in the pre-planing regime. Notably, the high percentage error for dynamic sinkage is closely associated with the relatively small values of this parameter. In the pre-planing region, where the speed is insufficient for planing, this results in an increased sinkage value vertically downward (negatively).
4. Results and Discussions
The CFD analysis was performed on the single and double-stepped hull and the results were compared with the experimental results. Dimensionless parameters were considered for the analysis such as resistance, wetted surface, sinkage, and dynamic trim. A total of 15 stepped hulls were created from the parent hull of NSS and simulations were performed at four different speeds, 3.05 m/s, 6.0 m/s, 7.0 m/s, and 8.0 m/s, correspondent to = 1.13, 2.22, 2.59, and 2.96, respectively.
In the code column, the last letter of the code such as M, F, B, etc. shows the location and depth of the steps.
- The “M” represents that step is placed in the mid of the hull.
- The “F” represents that the step is placed in the forward region of the hull.
- The “B” represents that the step is placed in the backward region of the hull.
- The “D” represents that the step has more depth, and the location is shown by the attached letter “FD” which means the step is in the forward section but has more depth than the previous step in the forward part of the hull.
- “BH” is for the base hull.
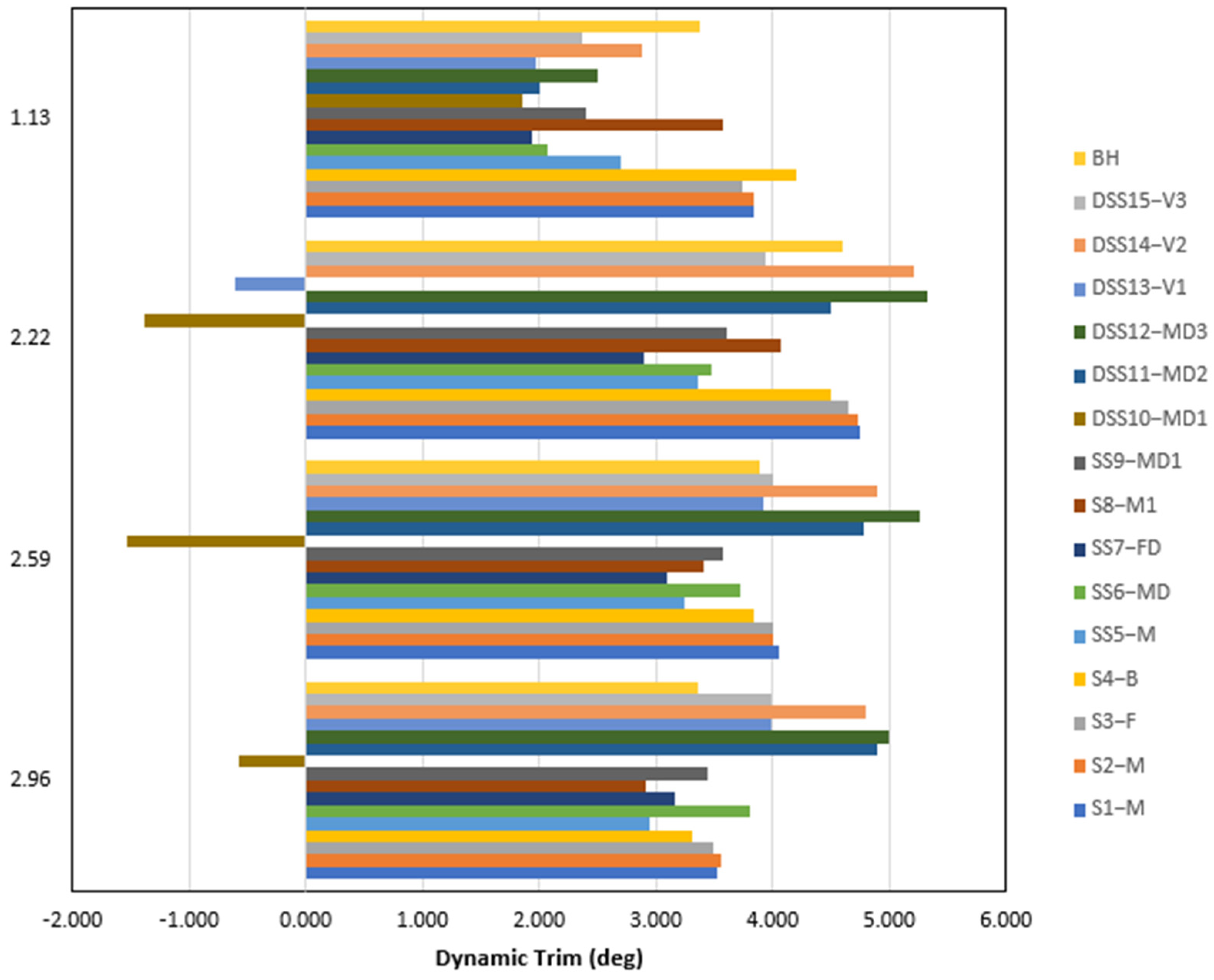
The results of the dynamic trim are plotted in Figure 7. In STAR CCM+, the dynamic trim angle is determined using Dynamic Fluid Body Interaction (DFBI). This involves simulating how the hull interacts with fluid flow, allowing rotation about the y-axis to calculate the trim angle accurately. It can be observed that as the speed increased, the dynamic trim also increased in the semi-planing region and reached its maximum at < 2.22, except for “DSS10-MD1” and “DSS13-V1”, which both show a different trend. As the beam Froude number increased, the planing region was reached, and dynamic trim decreased for all the stepped hulls. The depth and location of the steps play very important roles in step design. Some steps do not have a perfect placement, which raises the dynamic trim as compared to the base hull. Most designs reduce dynamic trim at low speeds except “S8-M1”, “S3-F”, “S2-M”, “S4-B”, and “S1-M” and rose in the semi-planing region which was further reduced as the Froude number increased. “SS5-M”, “SS7-FD”, and “S8-M1” performed well in dynamics trim reduction.
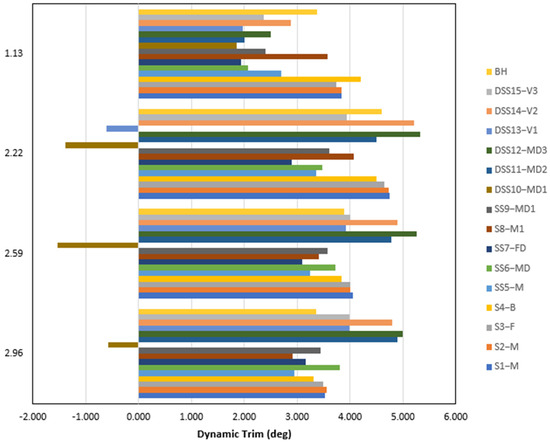
Figure 7.
Comparison of CFD results for dynamic trim among all stepped hulls with the bare hull.
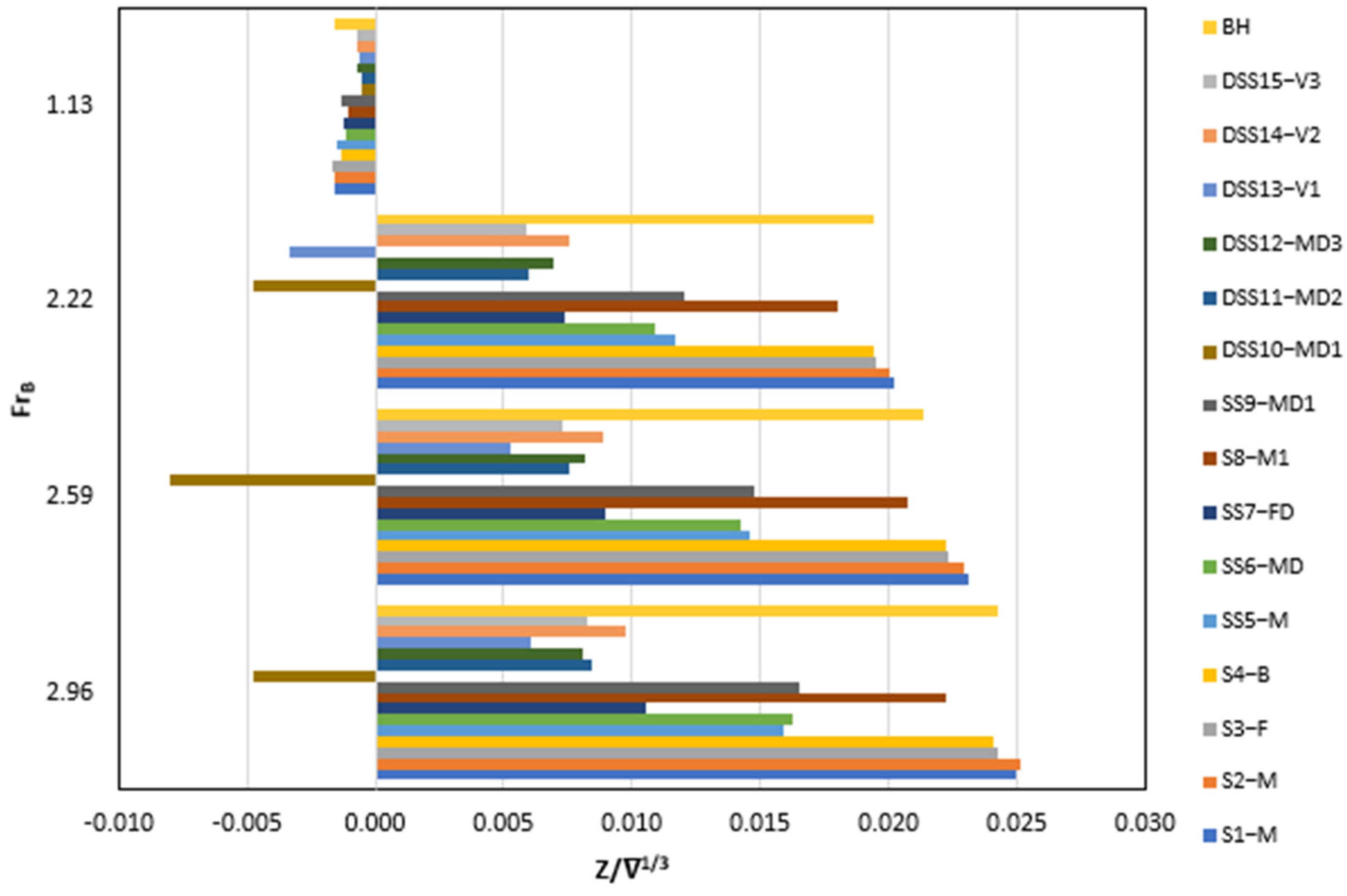
The hull is considered in the planing region when sinkage values increase from negative to positive. When the hull moves out of the water vertically (upward direction on the z-axis), it is considered positive, and vice versa. At a low , the sinkage is almost the same for all the stepped hulls but as the speed increases, the sinkage value starts rising positively upward in the z-axis as shown in Figure 8 for higher speeds as well. This shows the relation of interaction between water and hull, as greater upward motion means less resistance.
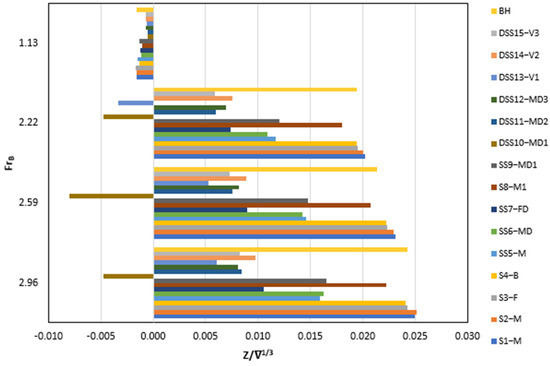
Figure 8.
Comparison of CFD results for sinkage among all stepped hulls with the bare hull.
The “S1-M”, “S2-M”, “S3-F”, and “S4-B” are the step designs that have a greater positive value of sinkage as compared to the base hull. The other designs reduce the sinkage value, as shown in Figure 8. The “DSS10-MD1” and “DSS13-V1” have irregular behavior because the depth of the step is increased in these designs, which moves the center of pressure in the forward section.
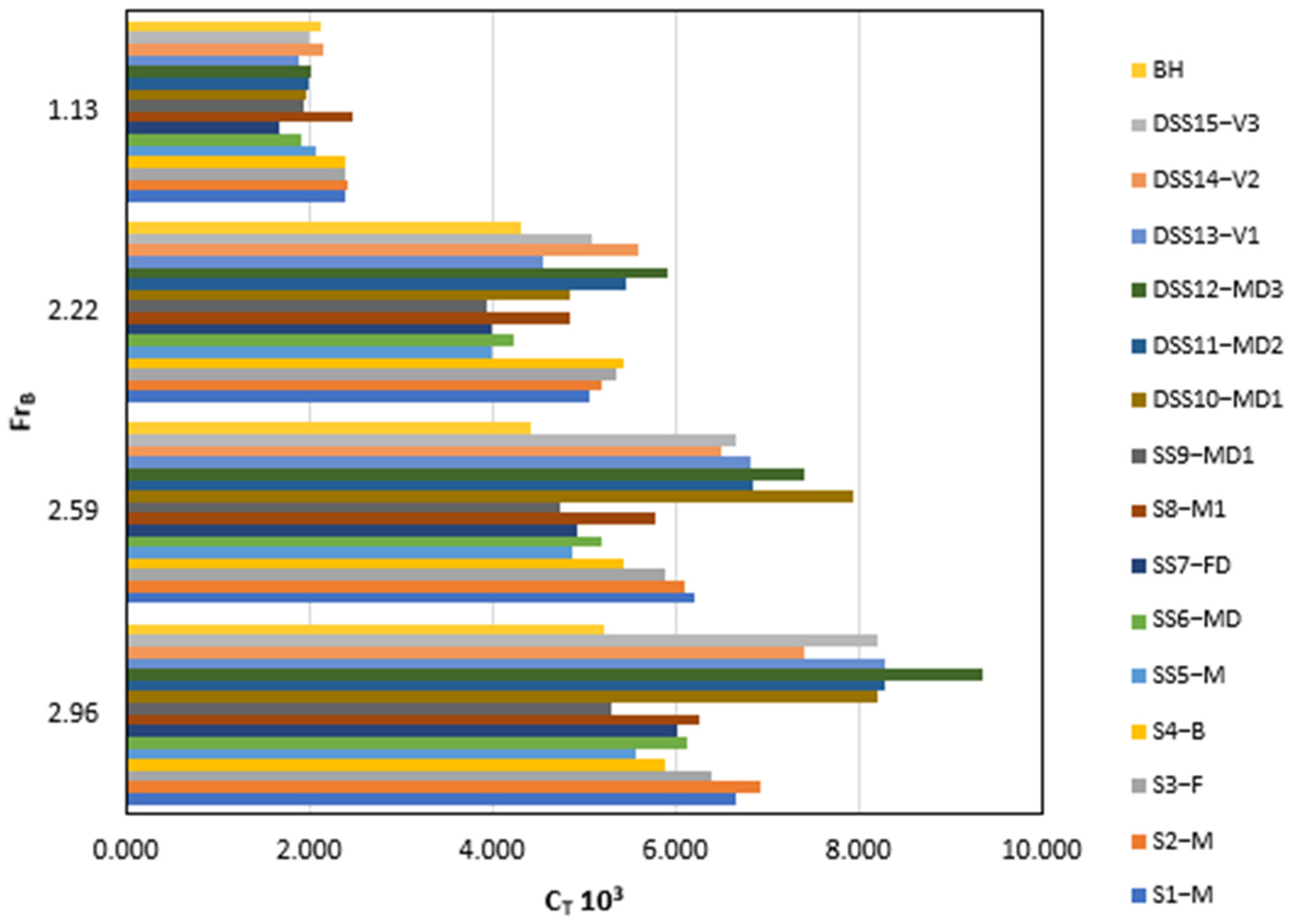
The resistance of the planing hull is a crucial factor for the performance of the planing hull, especially for the stepped hull. The resistance of all stepped hulls and base hulls is plotted in Figure 9. Total resistance depends on the wetted surface area and the shape of the hull, and water spray also plays its role. Figure 9 shows the resistance coefficient (Equation (3)) of the stepped hull as compared with the base hull.
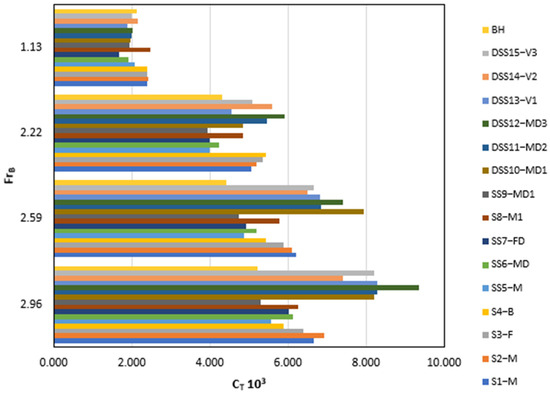
Figure 9.
Comparison of CFD results for the resistance coefficient among all stepped hulls with the bare hull.
At lower beam Froude numbers, all stepped hulls show a lower resistance coefficient compared to the base hull, except for “S1-M”, “S2-M”, “S3-F”, “S4-B”, and “S8-M1”‘ which display higher values at lower Froude numbers. As the speed increases, “SS5-M”, “SS6-MD”, “SS7-FD”, and “SS9-MD1” initially experience a decrease in resistance, but a further speed increment leads to a rise in the resistance coefficient. Notably, “SS9-MD1” demonstrates low resistance compared to the base hull at = 1.13 and 2.22, followed by an increase at = 2.59, maintaining nearly constant values at = 2.96. With its streamlined design, this hull exhibits impressive resistance performance.
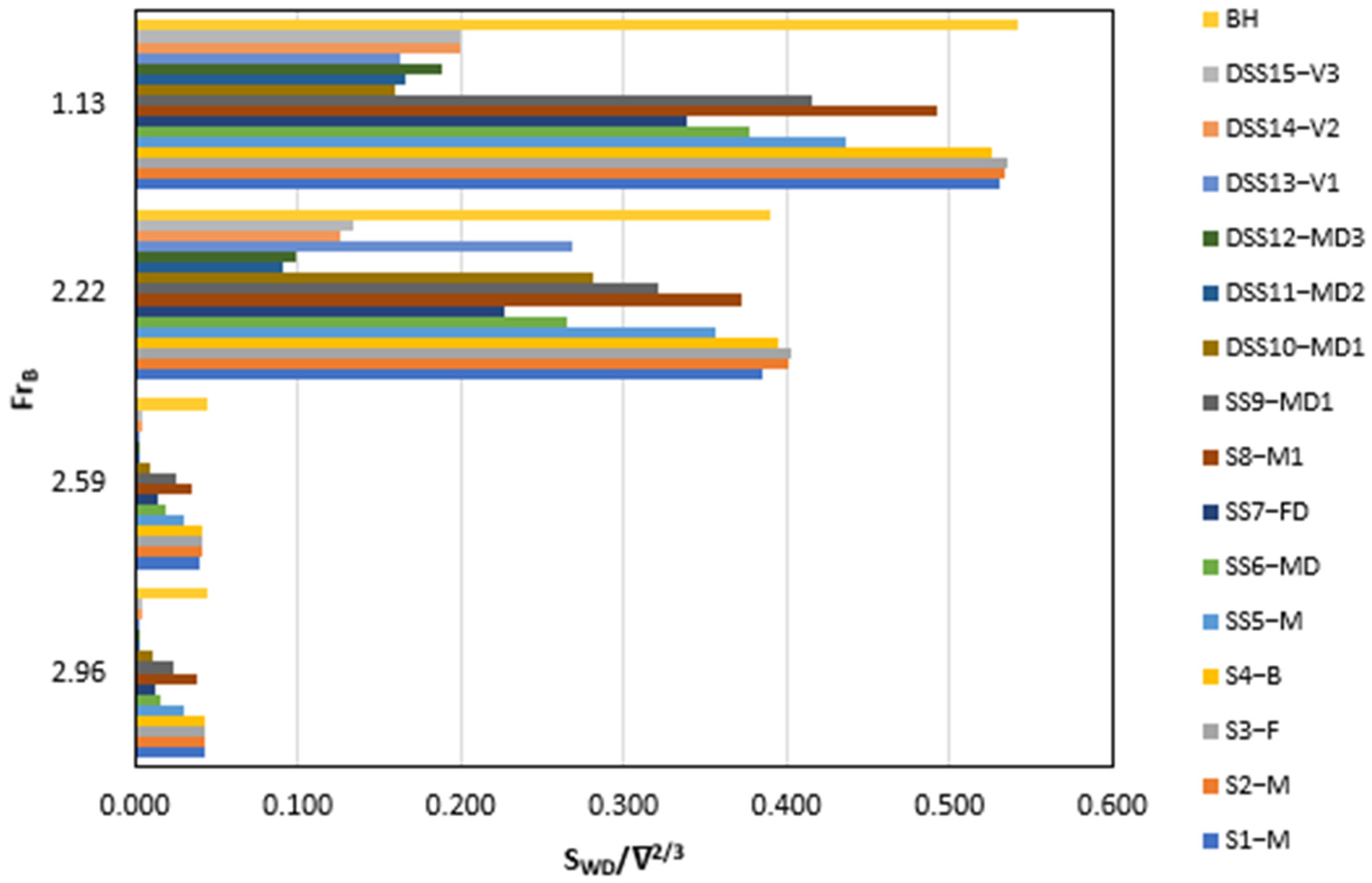
The wetted surface of the stepped hull at the four-beam Froude numbers was investigated. Typically, planing hulls move at high speeds and, due to the generation of hydrodynamic lift, the hull comes out of the water, reducing the wetted surface.
The plot for the wetted surface is in Figure 10. Most stepped hulls reduce wetted surfaces, except for “S1-M”, “S2-M”, “S3-F”, and “SS5-M”. These four designs have slightly higher values or coincide with the base hull at all Froude numbers. The models “DSS10-MD1” and “DSS13-V1” have the lowest wetted surface at = 1.13 and rise as the Froude number increases to = 2.22, further increasing in speed = 2.96 and reducing the values to 2nd or 3rd lowest. The inclusion of steps at significant positions and appropriate step heights will reduce the wetted surface. The augmented spray drag may offset the overall reduction, resulting in an increase in total resistance. In some scenarios, however, the placement and height of the step can lead to an overall increase in resistance.
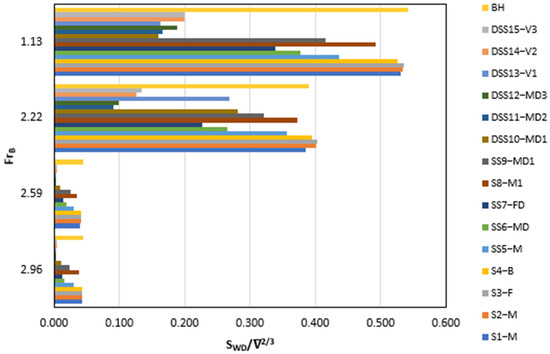
Figure 10.
Comparison of CFD results for wetted surface among all stepped hulls with the bare hull.
4.1. Pressure Distribution Contours
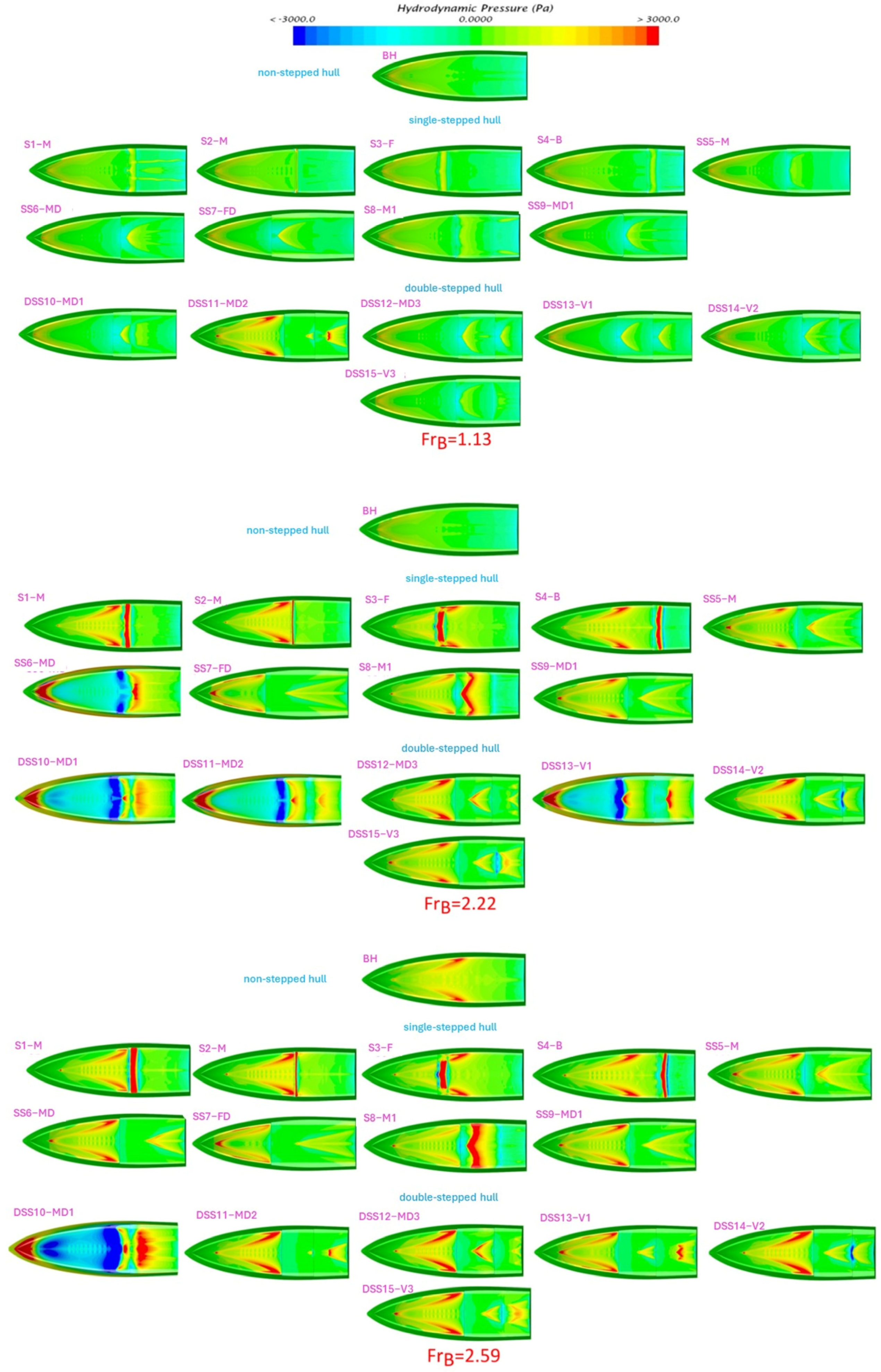
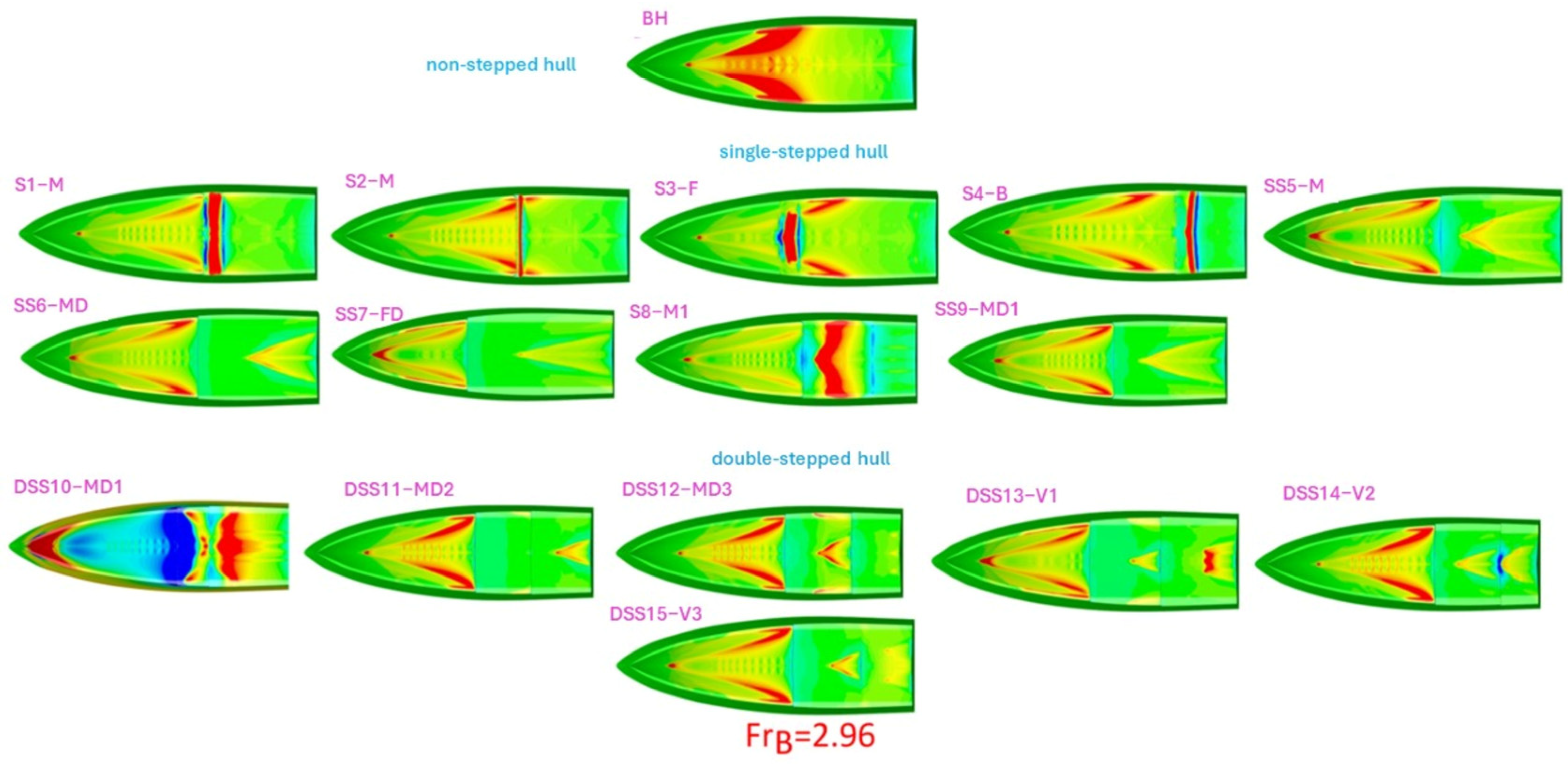
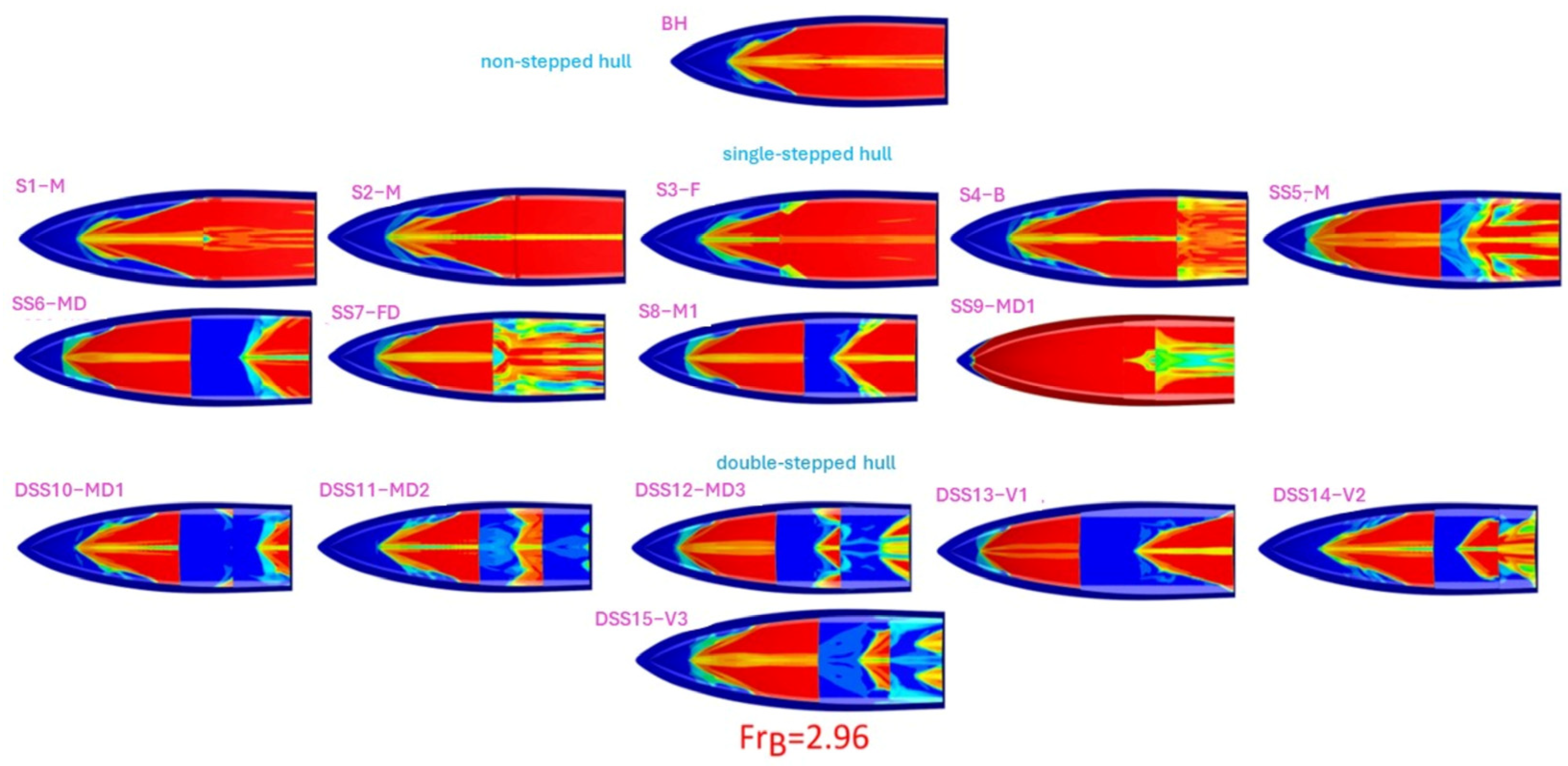
The pressure distribution on the bottom surface of the hull plays a crucial role in hydrodynamic studies. The pressure of steps in the hull creates flow separation, which impacts the pressure distribution and results in a low-pressure region at the location of the step and the high-pressure region aft of the step. The pressure difference generates lift, reducing dynamic trim and sinkage while enhancing hull performance. The pressure distribution in Figure 11 reveals that single-stepped hulls exhibit two pressure regions, while double-stepped hulls have three.
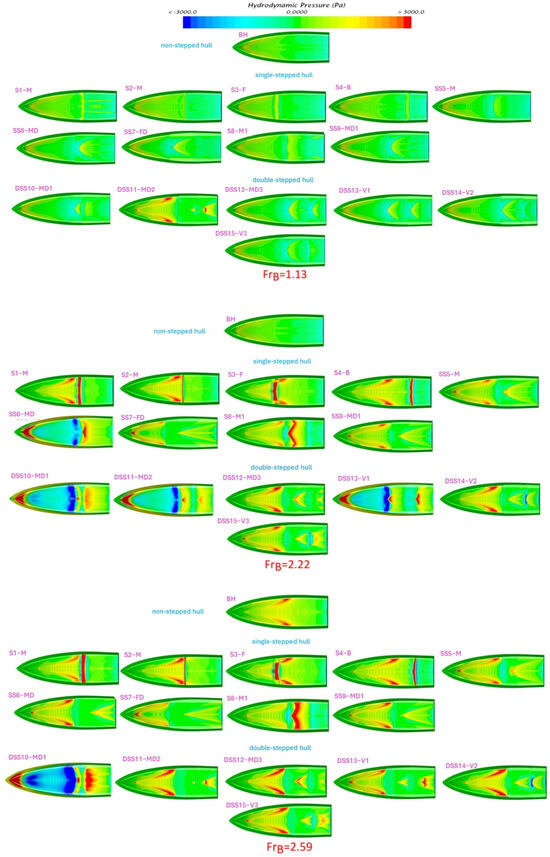
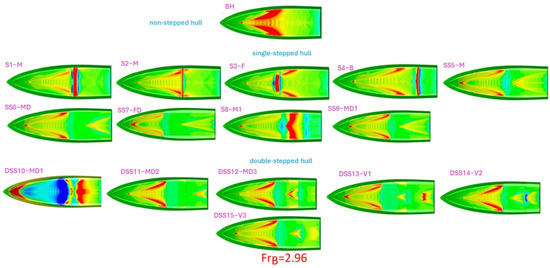
Figure 11.
Pressure distribution for single and double-stepped hulls, as well as the bare hulls at various beam Froud numbers.
In this scientific context, hydrodynamic pressures are chosen as representative values. Figure 11 shows the pressure distribution for all stepped hulls and the bare hull. These pressures can have both negative and positive values and are constrained within the range of −3000 to +3000 Pascal. By limiting the pressure range, a more accurate and comprehensive analysis of pressure variations across the entire hull can be conducted, leading to a better understanding of its hydrodynamic behavior. The same pressure restrictions are also applied to the bare hull for comparison and analysis. The steps influence the pressure distribution across the hull’s bottom. It is observed that regions before and after the step have higher pressure and the step itself experiences lower pressure due to the additional lift generated compared to the base hull. Some designs like “DSS10-MD2” at = 1.13, “DSS10-MD1”, “DSS11-MD2”, “DSS13-V1”, and “SS6-MD” at = 2.22, “DSS10-MD1” at = 2.59 and = 2.96 have more critical pressure distribution as compared to the base hull. The critical pressure distribution refers to a distribution of high or low pressure along the hull’s bottom, where the flow behavior undergoes significant changes and inappropriate pressure can lead to structural damage. Higher or lower pressure on the hull directly affects its structural integrity, potentially leading to stress concentration and deformation. Examining these pressure variations provides valuable insights into how bottom pressure affects structural integrity. Variations in bottom pressure can concentrate localized stresses, which may lead to fatigue, deformation, or even structural collapse over time. Low-pressure areas can cause buckling or collapse, while high-pressure areas can lead to bending of the hull material. Stepped hulls with less depth steps, as seen in the “S3-F” model at all speeds, may not effectively distribute pressure. Conversely, non-stepped hulls at = 2.96 exhibit higher pressure, but with stepped hulls, the pressure distribution is more uniform and reduced.
4.2. Volume of Fraction Contours
The figure depicts the volume fraction of water for various stepped hulls. The value “1” corresponds to water, while “0” represents air. Values between “1” and “0” indicate an air–water mixture. The red portion represents water, the blue portion represents air, and the green portion is the air–water mixture. Potential overestimations of the ventilated part related to numerical ventilation issues are contained using the artificial VOF suppression scheme detailed in De Luca et al. [32] and Mancini et al. [37].
Under low speeds, there is minimal change in the water’s surface. However, as the speed increases, the wake becomes more distinct. Steps play a crucial role in reducing the wetted surface area. Compared to the bare hull, the addition of steps noticeably reduces the wetted surface area at all speeds.
Figure 12 presents the distribution of volume fraction along the bottom of the hulls, considering both stepped configurations and the bare hull, across a range of beam Froude numbers. At = 2.96, the wetted surface of hulls “DSS11-MD2” and “DSS12-MD3” appears “W”-shaped. This shape is characterized by three triangles, with one in the middle and two on the port and starboard sides. The middle triangle represents the wetted surface caused by the solid wake from the forebody, while the other two triangles result from the spray, which increases hydrodynamic resistance, as noted by Savitsky and Morabito [13]. Hence, optimal step design involves positioning it strategically to minimize the impact of the spray area, ensuring that the stagnation line avoids intersecting the steps, particularly in the forward planing surface.
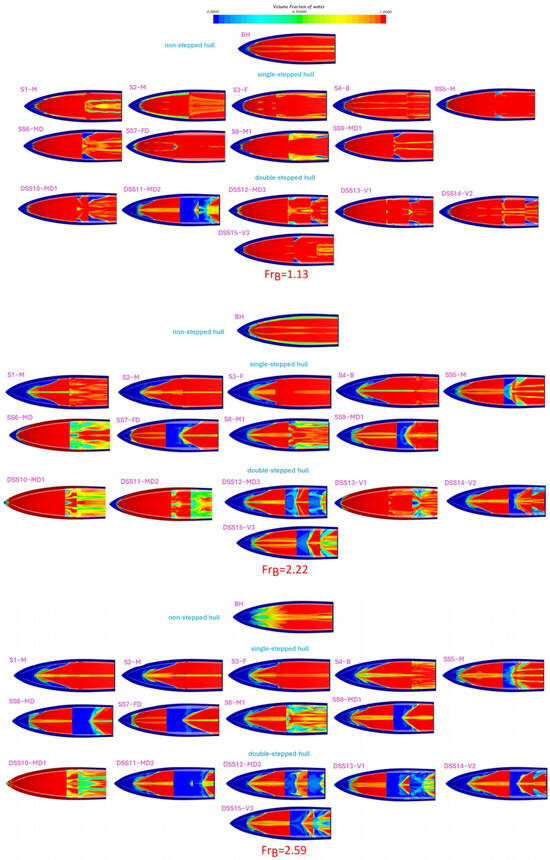
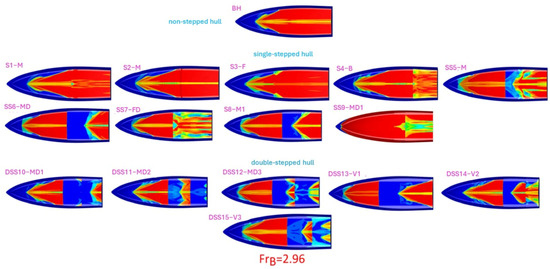
Figure 12.
Volume fraction distribution on the bottom of the hulls for single- and double-stepped hulls, as well as the bare hull at various beam Froud numbers.
5. Conclusions
The aim of the present study is to investigate the behavior of stepped hull shapes, height, and position by modifying the base hull of the NSS (C1 hull). For this purpose, the CFD code SIEMENS PLM STAR CCM+ was utilized, and its accuracy was confirmed against experimental data. Simulations were conducted using different beam Froude numbers, including = 1.13, 2.22, 2.56, and 2.96. A total of 15 stepped hull designs were developed, consisting of 9 single-step hulls and 6 double-step hulls, to explore the effects of step addition, step height, and step position. Control outputs such as resistance coefficient, wetted surface, sinkage, and dynamic trim were considered to evaluate the impact of the proposed modifications. To account for the hull motions (heave and pitch), Dynamic Fluid Body Interaction (DFBI) was employed in conjunction with the overset mesh approach. The main outcomes of the present study can be summarized as follows.
- It was observed from the simulations that the single-stepped hulls “SS5-M”, “SS6-MD”, “SS7-FD”, and “SS9-MD1” had the lowest resistance coefficients at low Froude numbers compared to the base hull.
- The single-stepped hull “SS9-MD1” showed a reduction in resistance at = 1.13 and = 2.22 and had nearly the same value at = 2.96.
- The primary goal of using steps in the hull is to attain high speed by minimizing resistance and controlling trim. The design of these steps requires careful consideration to meet this objective. Notably, the double-stepped hulls “DSS10-MD1” and “DSS12-MD3” exhibited the highest resistance values and started trimming by the bow due to the shift of the center of gravity in the forward section, and these types of designs are advisable to be avoided. Dynamic trim is an important factor for planing hulls at high speeds. The rise in trim and slamming can affect the structure and comfort of the vessel. The single-stepped hulls “SS5-M”, “SS7-FD”, and “S8-M1” were able to control the dynamic trim angle at all Froude numbers.
- Most double-stepped hulls have greater dynamic trim angles at high speed due to the placement of the second step near the transom. At low speeds, the double-step designs have lower trim angles as compared to the base hull. A positive value for sinkage means the hull is coming out of the water, which directly reduces the wetted surface and resistance. The single-stepped hulls “S1-M”, “S2-M”, “S3-F”, and “S4-B” had larger (positive) values of sinkage compared to the base hull.
- When planing a hull, as speed increases, the wetted surface usually decreases due to the generation of hydrodynamic lift, which pushes the hull out of the water. Adding steps also reduces the wetted surface and changes the pressure distribution on the bottom of the hull. In this study, all added steps reduced the wetted surface area except for the “S3-F” model. The placement of the steps close to the transom reduces trim at high speeds but also increases the resistance and wetted surface of the single-step hull. On the contrary, for a single-stepped hull, having a step at the front will reduce the trim angle at low step heights but increase the trim angle at high step heights. Regarding sinkage, hull configurations with a single step exhibit a similar or slightly higher positive sinkage compared to the base hull, unlike what occurs with hulls featuring double-step configurations.
Author Contributions
Conceptualization, M.S.; methodology, M.S.; software, M.S. and S.M.; validation, M.S. and S.M.; formal analysis, M.S. and S.M.; investigation, M.S. and S.M.; data curation, S.M. and M.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S., S.M. and R.N.B.; visualization, M.S., S.M. and R.N.B.; supervision, S.M. and R.N.B.; project administration, M.S. and S.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data might be available per a reasonable request.
Acknowledgments
The authors are thankful for the technical support for the access to the High-Performance Computer Lab (HPC) at the National University of Science and Technology, Pakistan Navy Engineering College (NUST-PNEC). Specifically, thanks to Zeeshan Riaz and Junaid Ahmad Khan for supervision and support throughout the research.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| B | Breath (m) |
| Beam Froude Number | |
| BWL | Breadth Waterline (m) |
| D | Draught (m) |
| LWL | Waterline Length (m) |
| SWS | Static Wetted Surface (m2) |
| SWD | Dynamic Wetted Surface (m2) |
| V | Hull Speed (m/s) |
| ▽ | Displacement Volume (m3) |
| Volumetric Froude Number | |
| L/B | Length-to-Beam Ratio |
| CT | Resistance Coefficient |
| CFD | Computational Fluid Dynamics |
| DFBI | Dynamic Fluid Body Interaction |
| DOF | Degree of Freedom |
| EFD | Experimental Fluid Dynamics |
| GCI | Grid Convergence Index |
| ITTC | International Towing Tank Conference |
| HRIC | High-Resolution Interface Capturing Scheme |
| LCB | Longitudinal Center of Buoyancy |
| LCG | Longitudinal Center of Gravity |
| NSS | Naples Systematic Series |
| RANS | Reynolds Averaged Navier-Stokes |
| SIMPLE | Semi-Implicit Method Pressure-Linked Equations |
| VOF | Volume of Fluid |
Appendix A. Wall Y+
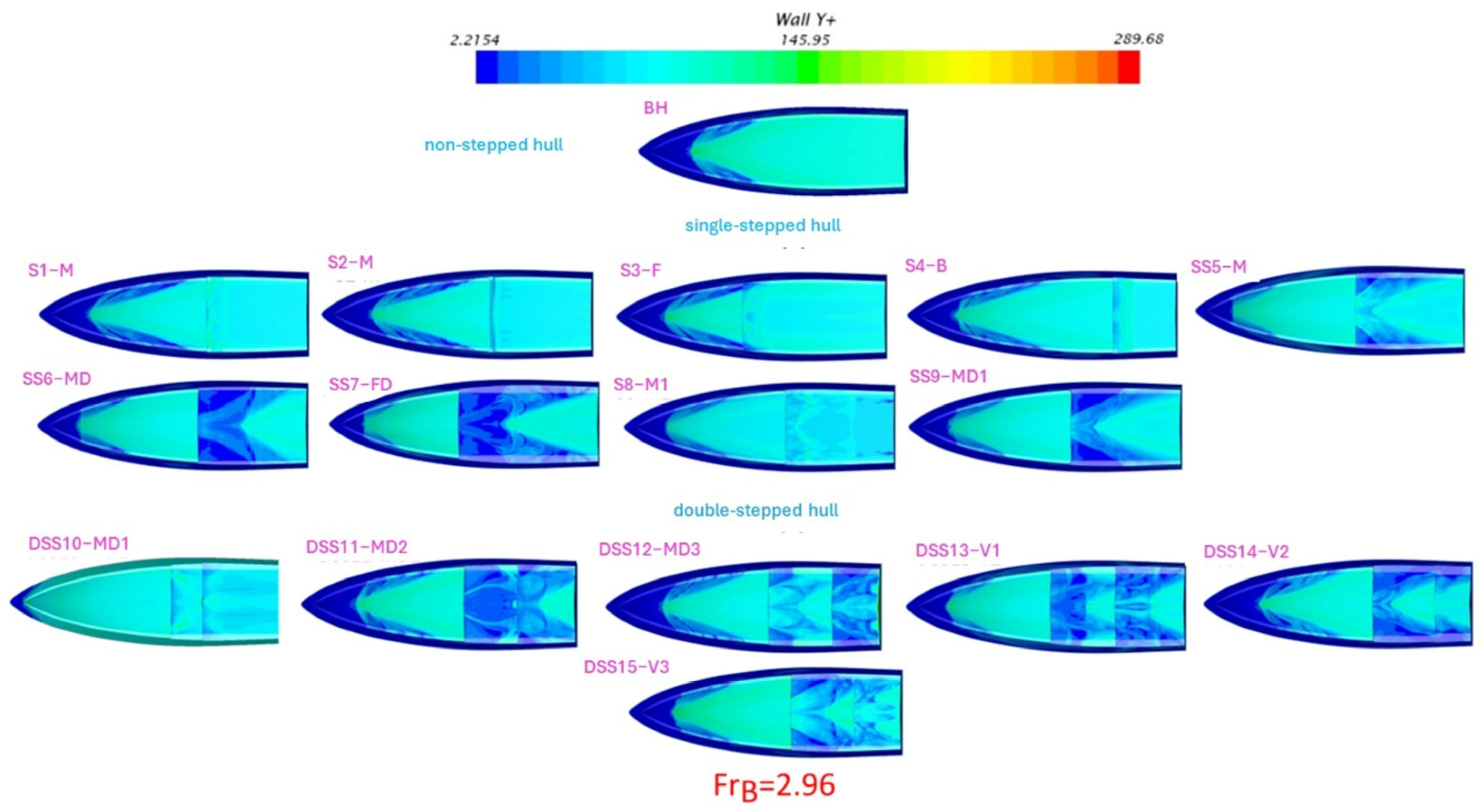
The wall y+ is a dimensionless factor that indicates the accuracy of the results captured by the numerical model. For fine and coarse mesh treatments, a prism layer is used to mention the required y+ value to be < 300. Wall y+ is a crucial factor in hydrodynamic analyses in current simulations. In Figure A1, wall y+ values are displayed for all stepped hulls at the highest simulated speed ( = 2.96). It is considered that if the y+ value for all hulls falls within the appropriate range at high speeds, then the results are accurate at low speeds.
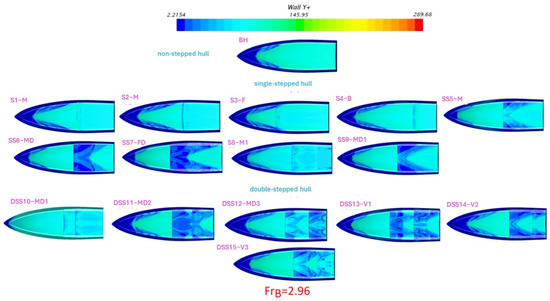
Figure A1.
Wall Y+ contours for non-stepped and stepped hulls at maximum speed.
Figure A1.
Wall Y+ contours for non-stepped and stepped hulls at maximum speed.
Appendix B. Results

Table A1.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.96.
Table A1.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.96.
| Code | Dynamic Trim Angle | CT × 1000 | Sinkage Dimensionless (Z/∇1/3) | Wetted Surface Aera Dimensionless (SWD/∇2/3) | |
|---|---|---|---|---|---|
| [deg] | [-] | [-] | [-] | ||
| S1-M | 2.96 | 3.52 | 6.659 | 0.025 | 0.042 |
| S2-M | 2.96 | 3.55 | 6.916 | 0.025 | 0.042 |
| S3-F | 2.96 | 3.49 | 6.399 | 0.024 | 0.042 |
| S4-B | 2.96 | 3.31 | 5.885 | 0.024 | 0.043 |
| SS5-M | 2.96 | 2.95 | 5.561 | 0.016 | 0.029 |
| SS6-MD | 2.96 | 3.81 | 6.137 | 0.016 | 0.016 |
| SS7-FD | 2.96 | 3.16 | 6.014 | 0.011 | 0.012 |
| S8-M1 | 2.96 | 2.91 | 6.266 | 0.022 | 0.037 |
| SS9-MD1 | 2.96 | 3.44 | 5.302 | 0.017 | 0.024 |
| DSS10-MD1 | 2.96 | -0.57 | 8.2 | −0.005 | 0.010 |
| DSS11-MD2 | 2.96 | 4.89 | 8.284 | 0.008 | 0.002 |
| DSS12-MD3 | 2.96 | 5.00 | 9.342 | 0.008 | 0.003 |
| DSS13-V1 | 2.96 | 3.98 | 8.296 | 0.006 | 0.002 |
| DSS14-V2 | 2.96 | -4.79 | 7.413 | 0.010 | 0.004 |
| DSS15-V3 | 2.96 | 3.99 | 8.195 | 0.008 | 0.004 |
| BH | 2.96 | 3.35 | 5.223 | 0.024 | 0.044 |

Table A2.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.59.
Table A2.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.59.
| Code | Dynamic Trim Angle | CT × 1000 | Sinkage Dimensionless (Z/∇1/3) | Wetted Surface Area Dimensionless (SWD/∇2/3) | |
|---|---|---|---|---|---|
| [deg] | [-] | [-] | [-] | ||
| S1-M | 2.59 | 4.050 | 6.208 | 0.023 | 0.040 |
| S2-M | 2.59 | 4.000 | 6.091 | 0.023 | 0.042 |
| S3-F | 2.59 | 4.010 | 5.894 | 0.022 | 0.042 |
| S4-B | 2.59 | 3.830 | 5.438 | 0.022 | 0.042 |
| SS5-M | 2.59 | 3.240 | 4.869 | 0.015 | 0.030 |
| SS6-MD | 2.59 | 3.720 | 5.196 | 0.014 | 0.018 |
| SS7-FD | 2.59 | 3.100 | 4.935 | 0.009 | 0.013 |
| S8-M1 | 2.59 | 3.410 | 5.774 | 0.021 | 0.035 |
| SS9-MD1 | 2.59 | 3.570 | 4.737 | 0.015 | 0.024 |
| DSS10-MD1 | 2.59 | −1.530 | 7.927 | −0.008 | 0.009 |
| DSS11-MD2 | 2.59 | 4.780 | 6.844 | 0.008 | 0.003 |
| DSS12-MD3 | 2.59 | 5.260 | 7.404 | 0.008 | 0.003 |
| DSS13-V1 | 2.59 | 3.920 | 6.831 | 0.005 | 0.003 |
| DSS14-V2 | 2.59 | 4.900 | 6.488 | 0.009 | 0.005 |
| DSS15-V3 | 2.59 | 4.000 | 6.671 | 0.007 | 0.004 |
| BH | 2.59 | 3.890 | 4.412 | 0.021 | 0.044 |

Table A3.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.22.
Table A3.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 2.22.
| Code | Dynamic Trim Angle | CT × 1000 | Sinkage Dimensionless (Z/∇1/3) | Wetted Surface Area Dimensionless (SWD/∇2/3) | |
|---|---|---|---|---|---|
| [deg] | [-] | [-] | [-] | ||
| S1-M | 2.22 | 4.750 | 5.047 | 0.020 | 0.386 |
| S2-M | 2.22 | 4.730 | 5.186 | 0.020 | 0.401 |
| S3-F | 2.22 | 4.640 | 5.343 | 0.020 | 0.403 |
| S4-B | 2.22 | 4.490 | 5.436 | 0.019 | 0.394 |
| SS5-M | 2.22 | 3.350 | 3.999 | 0.012 | 0.356 |
| SS6-MD | 2.22 | 3.470 | 4.222 | 0.011 | 0.265 |
| SS7-FD | 2.22 | 2.900 | 3.99 | 0.007 | 0.226 |
| S8-M1 | 2.22 | 4.060 | 4.848 | 0.018 | 0.372 |
| SS9-MD1 | 2.22 | 3.600 | 3.943 | 0.012 | 0.321 |
| DSS10-MD1 | 2.22 | −1.390 | 4.854 | −0.005 | 0.281 |
| DSS11-MD2 | 2.22 | 4.490 | 5.465 | 0.006 | 0.090 |
| DSS12-MD3 | 2.22 | 5.320 | 5.923 | 0.007 | 0.099 |
| DSS13-V1 | 2.22 | −0.600 | 4.554 | −0.003 | 0.269 |
| DSS14-V2 | 2.22 | 5.200 | 5.598 | 0.008 | 0.127 |
| DSS15-V3 | 2.22 | 3.930 | 5.073 | 0.006 | 0.134 |
| BH | 2.22 | 4.590 | 4.304 | 0.019 | 0.389 |

Table A4.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 1.13.
Table A4.
Simulation results (total resistance coefficient, dynamic trim angle, non-dimensional sinkage, and wetted surface) at = 1.13.
| Code | Dynamic Trim Angle | CT × 1000 | Sinkage Dimensionless (Z/∇1/3) | Wetted Surface Area Dimensionless (SWD/∇2/3) | |
|---|---|---|---|---|---|
| [deg] | [-] | [-] | [-] | ||
| S1-M | 1.13 | 3.840 | 2.386 | −0.002 | 0.531 |
| S2-M | 1.13 | 3.840 | 2.418 | −0.002 | 0.534 |
| S3-F | 1.13 | 3.730 | 2.386 | −0.002 | 0.535 |
| S4-B | 1.13 | 4.200 | 2.404 | −0.001 | 0.526 |
| SS5-M | 1.13 | 2.690 | 2.075 | −0.002 | 0.436 |
| SS6-MD | 1.13 | 2.070 | 1.901 | −0.001 | 0.377 |
| SS7-FD | 1.13 | 1.940 | 1.683 | −0.001 | 0.339 |
| S8-M1 | 1.13 | 3.580 | 2.462 | −0.001 | 0.493 |
| SS9-MD1 | 1.13 | 2.400 | 1.941 | −0.001 | 0.416 |
| DSS10-MD1 | 1.13 | 1.850 | 1.957 | −0.001 | 0.160 |
| DSS11-MD2 | 1.13 | 2.000 | 1.99 | −0.001 | 0.166 |
| DSS12-MD3 | 1.13 | 2.500 | 2.008 | −0.001 | 0.189 |
| DSS13-V1 | 1.13 | 1.970 | 1.896 | −0.001 | 0.162 |
| DSS14-V2 | 1.13 | 2.880 | 2.152 | −0.001 | 0.200 |
| DSS15-V3 | 1.13 | 2.370 | 1.993 | −0.001 | 0.199 |
| BH | 1.13 | 3.380 | 2.128 | −0.002 | 0.542 |
References
- Yousefi, R.; Shafaghat, R.; Shakeri, M. Hydrodynamic analysis techniques for high-speed planing hulls. Appl. Ocean Res. 2013, 42, 105–113. [Google Scholar] [CrossRef]
- Lee, E.J. Advancements of Stepped Planing Hulls. Doctoral Dissertation, Virginia Tech, Blacksburg, VA, USA, 2014. Available online: https://vtechworks.lib.vt.edu/handle/10919/51123 (accessed on 5 June 2023).
- Yousefi, R.; Shafaghat, R.; Shakeri, M. High-speed planing hull drag reduction using tunnels. Ocean Eng. 2014, 84, 54–60. [Google Scholar] [CrossRef]
- Shen, H.; Xiao, Q.; Zhou, J.; Su, Y.; Bi, X. Design of hydrofoil for the resistance improvement of planing boat based on CFD technology. Ocean Eng. 2022, 255, 111413. [Google Scholar] [CrossRef]
- Garland, W.R. Stepped planing hull investigation. Soc. Naval Archit. Mar. Eng. (SNAME) Trans. 2011, 119, 448–458. [Google Scholar]
- Bilandi, R.N.; Dashtimanesh, A.; Tavakoli, S. Stepped Hulls Early Stage Design by Implementing 2D+ T Method. In Proceedings of the HSMV 2023, Naples, Italy, 23–25 October 2023; IOS Press: Amsterdam, The Netherlands, 2023; pp. 23–32. [Google Scholar] [CrossRef]
- Becker, C.; Loreto, A.; Shell, J. A Systematic Study of Stepped Planing Hulls; Webb Institute: Glen Cove, NY, USA, 2008. [Google Scholar]
- Taunton, D.J.; Hudson, D.A.; Shenoi, R.A. Characteristics of a series of high speed hard chine planing hulls-part 1: Performance in calm water. Int. J. Small Craft Technol. 2010, 152, 55–75. [Google Scholar] [CrossRef]
- Lee, E.; Pavkov, M.; McCue-Weil, L. The Systematic Variation of Step Configuration and Displacement for a Double-step Planing Craft. J. Ship Prod. Des. 2014, 30, 89–97. [Google Scholar] [CrossRef]
- Vitiello, L.; Mancini, S.; Bilandi, R.N.; Dashtimanesh, A.; De Luca, F.; Nappo, V. A comprehensive stepped planing hull systematic series: Part 1—Resistance test. Ocean Eng. 2022, 266, 112242. [Google Scholar] [CrossRef]
- Savitsky, D. Hydrodynamic Design of Planing Hulls. Mar. Technol. SNAME News 1964, 1, 71–95. [Google Scholar] [CrossRef]
- Savitsky, D.; DeLorme, M.F.; Datla, R. Inclusion of Whisker Spray Drag in Performance Prediction Method for High-Speed Planing Hulls. Mar. Technol. SNAME News 2007, 44, 35–56. [Google Scholar] [CrossRef]
- Savistky, D.; Morabito, M. Surface Wave Contours Associated with the Forebody Wake of Stepped Planing Hulls. Mar. Technol. SNAME News 2010, 47, 1–16. [Google Scholar] [CrossRef]
- Svahn, D. Performance Prediction of Hulls with Transverse Steps. Master’s Thesis, The Royal Institute of Technology, KTH, Centre for Naval Architecture, Stockholm, Sweden, 2009. [Google Scholar]
- Jonas, D.; Strømquist, J. Conceptual Design of a High-Speed Superyacht Tender: Hull Form Analysis and Structural Optimization. Master’s Thesis, Marina System Centre for Naval Architecture, Stockholm, Sweden, 2012. [Google Scholar]
- Akers, R.H. Dynamic Analysis of Planing Hulls in the Vertical Plane. Proc. Soc. Nav. Archit. Mar. Eng. N. Engl. Sect. 1999. Available online: https://www.academia.edu/4972207/Dynamic_Analysis_of_Planing_Hulls_in_the_Vertical_Plane (accessed on 29 March 2024).
- Martin, M. Theoretical Prediction of Motions of High-Speed Planing Boats in Waves. J. Ship Res. 1978, 22, 140–169. [Google Scholar] [CrossRef]
- Zarnick, E. A Nonlinear Mathematical Model of Motions of a Planing Boat in Regular Waves; Technical Report DTNSRDC-78/032. David Taylor Naval Ship Research and Development Center, 1978. Available online: https://archive.org/details/nonlinearmathema00zarn (accessed on 15 September 2023).
- Tavakoli, S.; Ghadimi, P.; Dashtimanesh, A.; Sahoo, P.K. Determination of Hydrodynamic Coefficients in Roll Motion of High-Speed Planing Hulls. In Proceedings of the SNAME 13th International Conference on Fast Sea Transportation, Providence, RI, USA, 26–27 October 2021. [Google Scholar]
- Tavakoli, S.; Dashtimanesh, A. A six-DOF theoretical model for steady turning maneuver of a planing hull. Ocean Eng. 2019, 189, 106328. [Google Scholar] [CrossRef]
- Algarín, R.; Bula, A. A numeric study of the maneuverability of planing hulls with six degrees of freedom. Ocean Eng. 2021, 221, 108514. [Google Scholar] [CrossRef]
- Brizzolara, S.; Federici, A. Designing of planing hulls with longitudinal steps: CFD in support of traditional semi-empirical methods. In Proceedings of the Design and Construction of Super and Mega Yachts, Genoa, Italy, 13–14 May 2015. [Google Scholar]
- De Marco, A.; Mancini, S.; Miranda, S.; Scognamiglio, R.; Vitiello, L. Experimental and numerical hydrodynamic analysis of a stepped planing hull. Appl. Ocean Res. 2017, 64, 135–154. [Google Scholar] [CrossRef]
- Bilandi, R.N.; Dashtimanesh, A.; Mancini, S.; Vitiello, L. Comparative study of experimental and CFD results for stepped planing hulls. Ocean Eng. 2023, 280, 114887. [Google Scholar] [CrossRef]
- Bilandi, R.N.; Mancini, S.; Dashtimanesh, A.; Tavakoli, S. A revisited verification and validation analysis for URANS simulation of planing hulls in calm water. Ocean Eng. 2024, 293, 116589. [Google Scholar] [CrossRef]
- Park, S.; Wang, Z.; Stern, F.; Husser, N.; Brizzolara, S.; Morabito, M.; Lee, E. Single- and two-phase CFD V&V for high-speed stepped planing hulls. Ocean Eng. 2022, 261, 112047. [Google Scholar] [CrossRef]
- Tork Chooran, R.; Shafaghat, R.; Yoosefi, R. Numerical Investigation of Step Depth Effects on Hydrodynamic Performance of Planing Hull Using Dynamic Mesh and Two Degree of Freedom Model. AUT J. Mech. Eng. 2019, 3, 139–148. [Google Scholar]
- Cucinotta, F.; Guglielmino, E.; Sfravara, F. A critical CAE analysis of the bottom shape of a multi stepped air cavity planing hull. Appl. Ocean Res. 2019, 82, 130–142. [Google Scholar] [CrossRef]
- Zou, J.; Lu, S.; Jiang, Y.; Sun, H.; Li, Z. Experimental and Numerical Research on the Influence of Stern Flap Mounting Angle on Double-Stepped Planing Hull Hydrodynamic Performance. J. Mar. Sci. Eng. 2019, 7, 346. [Google Scholar] [CrossRef]
- Yang, D.; Sun, Z.; Jiang, Y.; Gao, Z. A Study on the Air Cavity under a Stepped Planing Hull. J. Mar. Sci. Eng. 2019, 7, 468. [Google Scholar] [CrossRef]
- De Luca, F.; Pensa, C. The Naples warped hard chine hulls systematic series. Ocean Eng. 2017, 139, 205–236. [Google Scholar] [CrossRef]
- De Luca, F.; Mancini, S.; Miranda, S.; Pensa, C. An Extended Verification and Validation Study of CFD Simulations for Planing Hulls. J. Ship Res. 2016, 60, 101–118. [Google Scholar] [CrossRef]
- ITTC 7.5-03-01-01 Rev 04, “Uncertainty Analysis in CFD Verification and Validation, Methodology and Procedures”. 2021. Available online: https://ittc.info/media/4184/75-03-01-01.pdf (accessed on 29 March 2024).
- ITTC 7.5-03-02-03 Rev 01, “Recommended Procedures and Guidelines: Practical Guidelines for Ship CFD”. 2014. Available online: https://ittc.info/media/4196/75-03-02-03.pdf (accessed on 29 March 2024).
- Pacuraru, F.; Mandru, A.; Bekhit, A. CFD Study on Hydrodynamic Performances of a Planing Hull. J. Mar. Sci. Eng. 2022, 10, 1523. [Google Scholar] [CrossRef]
- Hino, T. Final report and Recommendations of the Specialist Committee on CFD in Marine Hydrodynamics. In Proceedings of the 27th International Towing Tank Conference (ITTC), Copenhagen, Denmark, 31 August–5 September 2014; pp. 522–567. [Google Scholar]
- Mancini, S.; De Luca, F.; Ramolini, A. Towards CFD Guidelines for Planing Hull Simulations Based on the Naples Systematic Series. In Presented at the MARINE VII: Proceedings of the VII International Conference on Computational Methods in Marine Engineering, Nantes, France, 15–17 May 2017; pp. 1071–1085. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).