Numerical Simulation on the Two-Degree-of-Freedom Flow-Induced Vibration of a Submerged Floating Tunnel under Current

Abstract

The submerged floating tunnel (SFT) is a novel form of transportation infrastructure for crossing deeper and wider seas. One of the primary challenges in designing SFTs is understanding their hydrodynamic response to complex environmental loads. In order to investigate the two-degree-of-freedom (2-DOF) flow-induced vibration (FIV) response of SFTs under current, a two-dimensional (2D) numerical model was developed using the Reynolds-averaged Navier–Stokes (RANS) method combined with the fourth-order Runge–Kutta method. The numerical results were validated by comparing them with the existing literature. The study then addressed the effects of coupled vibration and structural parameters, i.e., the mass ratio and natural frequency ratio, on the response and wake pattern of SFTs, numerically. The results indicated that coupled vibration had a significant impact on the SFT response at reduced velocities of Ur_wx ≥ 4.4. A decrease in mass ratio (m* < 1) notably amplified the 2-DOF vibration amplitudes of SFTs at Ur_wx ≥ 4.4, particularly for in-line vibration. Similarly, a decrease in natural frequency ratio (R_f < 1) significantly suppressed the in-line vibration of SFTs at Ur_wx ≥ 2.5. Therefore, for the design of SFTs, careful consideration should be given to the effect of mass ratio and natural frequency ratio on in-line vibration.

1. Introduction

The submerged floating tunnel (SFT) is considered to be the most effective method for crossing deeper and wider seas. An anchored SFT typically consists of a tube, end constraints, and the on-way support system. It suspends at a specific water depth through buoyancy force to balance the weight of the tunnel, with a mass ratio m* < 1 and natural frequency ratio R_f < 1 [1,2,3,4]. Compared to traditional water crossing structures, anchored SFTs offer several advantages, including flexible on-way configurations and sections, minimal impact on navigation and the ecological environment, better adaptability to water depth and topography, improved spanning capacity, and lower construction costs. As a result, SFTs have garnered extensive attention from both academic and engineering communities.

When exposed to the ocean environment, the flow-induced vibration (FIV) of SFTs is generated by the alternating vortex shedding in wake flow under current. When the response frequency and vortex shedding frequency closely match the natural frequency of the SFT under critical flow velocity, the responses of the SFT can be significantly amplified. This phenomenon is commonly known as lock-in [5,6,7,8]. Frequency lock-in occurs within a certain reduced velocity range. Large-amplitude vibration in this lock-in regime can lead to fatigue damage and significantly affect the safety, operation, and remaining fatigue life of the SFT. Hence, this issue should be given careful attention.

Directive experiments on SFTs are lacking due to the high expenses. However, bluff bodies, which are similar to the tubes in SFTs, have been studied experimentally for a long time. Numerous experiments [9,10,11,12] have demonstrated that the FIV response of a bluff body is influenced by both model parameters, such as mass ratio m*, damping ratio ξ, and natural frequency ratio R_f, etc., as well as flow parameters, including the Reynolds number Re, reduced velocity Ur_w, etc. The non-dimensional vibration amplitude and frequency of a bluff body can be expressed as a function of a series of normalized factors.

Early experiments were conducted on a single elastically mounted rigid cylinder, focusing mainly on large-amplitude vibration only in the cross-flow direction (one-degree-of-freedom, 1-DOF) for a high mass ratio m* = O(100) [13]. These experiments indicated that only two branches (the initial excitation branch and the lower branch) for cross-flow vibration amplitude existed under various reduced velocities, as shown in Figure 1a. The jump from the initial branch to the lower branch corresponded to a wake mode change from 2S (two single vortices shedding per vibration cycle) to 2P (two pairs of vortices shedding per vibration cycle) [14]. The vibration frequency was close to the natural frequency in the lock-in regime and followed the Strouhal relationship outside, as shown in Figure 1b.

A decrease in the mass ratio (m* = O(10)) can significantly enhance the fluid–cylinder interaction and expand the cross-flow lock-in regime. This leads to the generation of a new large-amplitude branch, known as the upper branch. The vortex shedding mode is 2P, with different vortex intensities for each pair of vortices [15,18]. During lock-in, the vibration frequency is larger than the natural frequency (f* ≈ 1.4), a phenomenon known as soft lock-in [16].

When the mass ratio decreases to a critical value (i.e., m_crit* = 0.54 ± 0.02 for a low mass-damping cylinder), the lower branch in the cross-flow direction disappears. This means that the vibration of the cylinder will have a large amplitude and be continuous with the increase in reduced velocity. Additionally, the vibration frequency may approach or even exceed the vortex shedding frequency [16,19].

By confining the vibration of the cylinder only in the cross-flow direction, the true dynamic response and wake pattern may be altered. There, further experiments investigated the in-line vibration of an elastically mounted cylinder and its effect on the cross-flow vibration and wake pattern. These experiments revealed that in-line vibration for a low-mass-ratio cylinder (m* < 4) occurred more easily at low reduced velocities and significantly enhanced the cross-flow vibration with the increase in reduced velocity. A new large-amplitude branch was generated, known as the super-upper branch (m* = 2.6). The wake mode observed was 2T, with two sets of triple vortices shedding per vibration cycle [17].

It is important to note that for the aforementioned experiments, the masses and natural frequencies of the cylinder in the in-line and cross-flow directions are the same.

With the advancement in computer performance, some researchers have begun using computational fluid dynamics (CFD) methods to numerically simulate the vibration of elastically mounted cylinders and the resulting vortex patterns.

Singh and Mittal [20] conducted simulations of the two-degree-of-freedom vibration of a cylinder with a low mass ratio (m* = 10) and low Reynolds number (Re ≤ 500). The finding indicated that the Reynolds number had a significant impact on the vibration of the cylinder and the mode of vortex shedding. Kang et al. [21] established a two-degree-of-freedom numerical model for a cylinder (m* = 2.6) using the Reynolds-averaged Navier–Stokes (RANS) method with a modified shear stress transport (SST) turbulence model. They simulated and compared three initial conditions, including increasing velocity, decreasing velocity, and constant velocity. Their work revealed that the two-degree-of-freedom vibration response of cylinder and hydrodynamic loads were significantly dependent on the initial conditions, and the super-upper branch of the cross-flow amplitude and 2T vortex shedding mode can be approximately reproduced only under increasing velocity. Zhao et al. [22] conducted simulations and analyzed the impact of the natural frequency ratio (R_f = 1–4) on the two-degree-of-freedom vibration of a cylinder (m* = 2.0) with a low Reynolds number (Re = 200). The findings revealed that the vibration of the cylinder and the resulting hydrodynamic loads were complex at R_f = 2.5 or 3, with two or three wake modes (P+S, 2P, N) present in the lock-in regime. These studies focus on the mass ratios of cylinders that are greater than 1.

Liu et al. [23] simulated the cross-flow vibration of a cylinder with m* = 0.7 and compared the results to those of a cylinder with m* = 2.4. They found that no lower branch of cross-flow vibration amplitude was present for m* = 0.7. Additionally, the vibration frequency remained consistent with the vortex shedding frequency under reduced velocities ranging from 1 to 20. However, it is worth noting that the cylinder is constrained to vibrate only in the cross-flow direction.

Yu et al. [24] conducted a numerical investigation into the two-degree-of-freedom maximum vibration amplitude of a cylinder as a function of the Reynolds number (Re = 75–175) under a limiting condition (m* = 0 and ξ = 0) and compared it to the one- or two-degree-of-freedom vibrations of a cylinder with m* = 1. The results indicated that the maximum cross-flow amplitude increased with the rise in the Reynolds number in the laminar flow regime. Notably, this finding differed from the conclusion proposed by Williamson and Govardhan [25] for one-degree-of-freedom vibration. Additionally, the maximum cross-flow amplitude decreased with an increase in mass ratio, and the maximum amplitude of two-degree-of-freedom vibration decreased at a faster rate than that of one-degree-of-freedom vibration. For one- and two-degree-of-freedom vibrations of the cylinder, the critical mass ratios were 0.117 and 0.106, respectively, signifying that the vibration of the cylinder remained stable below the critical mass ratio at high reduced velocity.

So far, previous studies on the two-dimensional vibration of elastically mounted cylinders and wake patterns have primarily focused on low Reynolds numbers, even within the laminar flow regime, a mass ratio m* > 1, and a natural frequency ratio R_f > 1. Additionally, most experiments and numerical simulations have been conducted under low damping to investigate the large-amplitude vibration in the cross-flow direction [22]. However, the numerical studies on the 2-DOF vibration of the cylinder with mass ratio m* < 1 and natural frequency ratio R_f ≤ 1, i.e., an anchored SFT, are limited and should be addressed.

In this study, a two-dimensional numerical model was established for the two-degree-of-freedom FIV of an anchored SFT, using the Reynolds-averaged Navier–Stokes (RANS) method combined with the fourth-order Runge–Kutta method. The specific parameters for the SFT were m* = 0.84, R_f > 0.54, and ξ = 0.05. This model was subjected to current and was verified using the literature results. Our work addressed the effects of two-degree-of-freedom coupled vibration and structural parameters, such as mass ratio and natural frequency ratio, on SFT response and wake pattern. The numerical investigation covered a wide range of reduced velocities, ranging from 0.6 to 10.

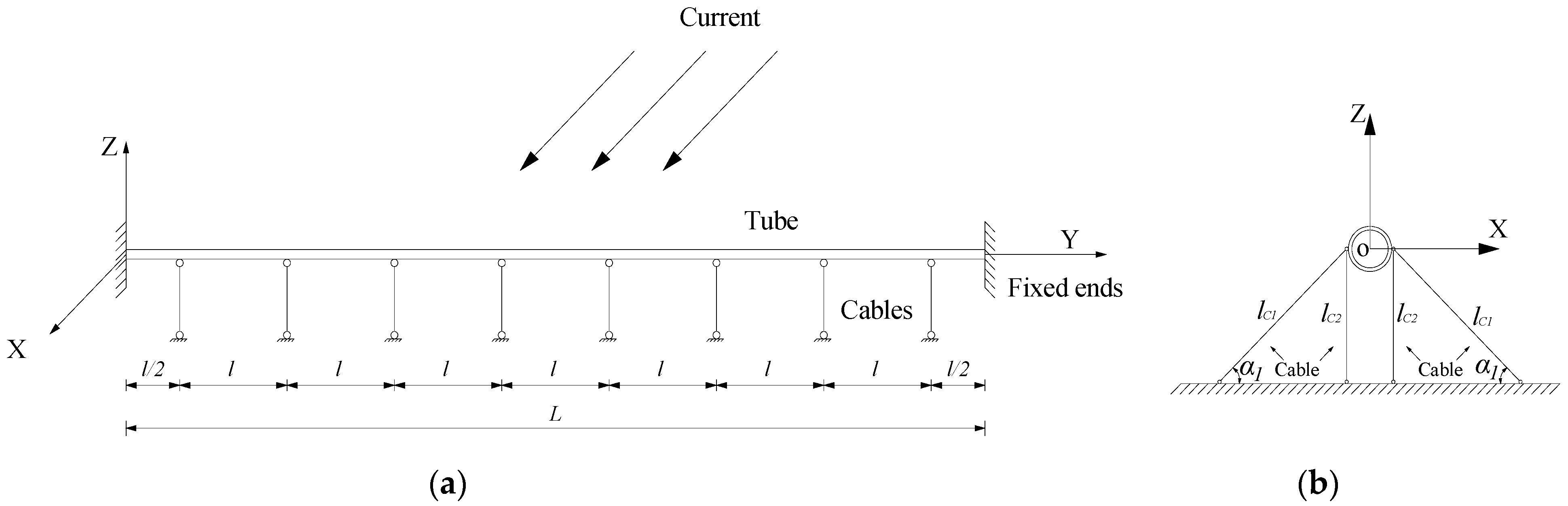
2. Numerical Methods

2.1. Governing Equations

As shown in Figure 2a,b, the left end is defined as the origin, and the axial line of the tube is defined as the Y-axis. The coordinates of an anchored SFT can then be determined by the right-hand rule. Perpendicular to the tube, the direction of incident currents is defined as the X-axis. The vertical up is defined as the Z-axis.

Ignoring the flow–cable interaction, the anchoring cables can be simplified as elastic supports with linear equivalent stiffness in the X- or Z-axis. Thus, the anchored SFT can be considered a mass-spring-damping system, as shown in Figure 2c [26]. Spacing among the on-way anchors is the same, and the material properties of symmetrical anchors are the same. Based on the slicing method, the vibration of an SFT under current can be simplified as two-degree-of-freedom vibration in the plane, and the governing equations [21,22,23] can be expressed in Equation (1):

$$\left\{\begin{array}{l}{m}_0\frac{{\partial }^{2}x}{{\partial }^{2}t}+c_x\frac{\partial x}{\partial t}+k_{x}x=F_x\left(t\right)\\ m_0\frac{{\partial }^{2}z}{{\partial }^{2}t}+c_z\frac{\partial z}{\partial t}+k_{z}z=F_z\left(t\right)\end{array}\right.,$$

(1)

where $x$ and $z$ are the instantaneous displacements of the SFT in the X- and Z-axis, respectively. $c_x=2{\xi }_x\sqrt{k_x{m}_0}$ and $c_z=2{\xi }_z\sqrt{k_z{m}_0}$ are the structural damping coefficients of the SFT in the X- and Z-axis, respectively. $k_x$ and $k_z$ are the equivalent stiffness of elastic supports in the X- and Z-axis, respectively. $F_x\left(t\right)$ and $F_z\left(t\right)$ are the instantaneous hydrodynamic loads acting on the SFT in the X- and Z-axis, respectively. $C_D(t)=\frac{F_x\left(t\right)}{\frac{1}{2}\rho D{U}^2}$ and $C_L(t)=\frac{F_z\left(t\right)}{\frac{1}{2}\rho D{U}^2}$ are the instantaneous drag coefficient and lift coefficient, respectively.

The governing equations in Equation (1) can be solved by the 4th-order Runge–Kutta method, as expressed in Equation (2):

$$\left\{\begin{array}{l}\dot{x}\left(t_{n+1}\right)=\dot{x}\left(t_n\right)+\frac{∆t}{6}\left(k_1+2k_2+{2k}_3+k_4\right)\\ x\left(t_{n+1}\right)=x\left(t_n\right)+\dot{x}\left(t_n\right)∆t+\frac{∆t^2}{6}\left(k_1+k_2+k_3\right)\end{array}\right.,$$

(2)

where k₁, k₂, k₃, and k₄ are the 4th-order Runge–Kutta coefficients, and $∆t$ is the time step.

Based on the Reynolds-averaged Navier–Stokes (RANS) method for incompressible and viscous fluid, the two-dimensional turbulent flow around the SFT is simulated, and the governing equations can be expressed in Equation (3):

$$\left\{\begin{array}{l}\frac{\partial u_i}{\partial x_i}=0\\ \frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left(2\nu S_{ij}-\overline{{u^{\prime }}_i{u^{\prime }}_j}\right)\end{array}\right.,$$

(3)

where $x_i$ = x and $x_j$ = z are the coordinates in the X- and Z-axis, respectively. $u$ and $p$ are the flow velocity and pressure, respectively. $S_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$ is the mean strain rate tensor. $\overline{{u^{\prime }}_i{u^{\prime }}_j}$ is the Reynolds stress tensor. Based on Boussinesq’s hypothesis [27], $\overline{{u^{\prime }}_i{u^{\prime }}_j}=-2{\nu }_t{S}_{ij}+\frac{2}{3}{\delta }_{ij}k$; $u\prime$ is the fluctuating velocity of fluid; ${\delta }_{ij}$ is the Kronecker symbol; ${\nu }_t$ and $k=\frac{1}{2}\overline{{u^{\prime }}_i{u^{\prime }}_i}$ are the turbulent eddy viscosity and kinetic energy both given by the turbulence model, respectively. The shear stress transport (SST) k-ω turbulence model [28] is adopted in this study.

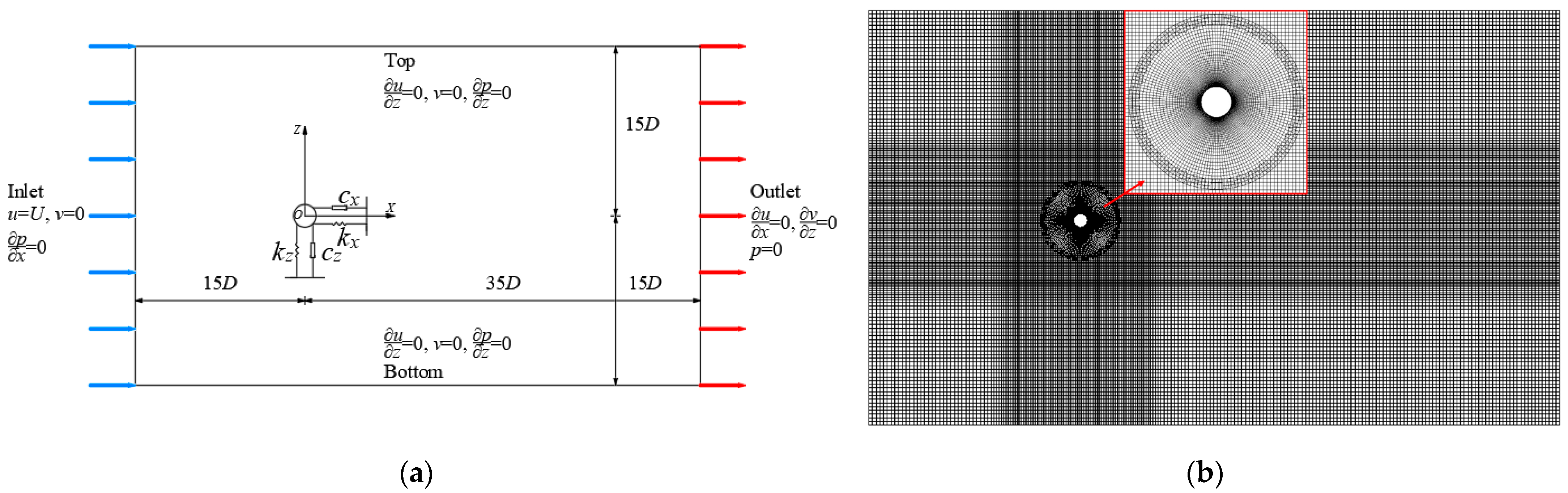
2.2. Computational Domain and Meshes

The commercial software ANSYS v19.0 Fluent with user-defined functions (UDFs) is adopted to solve the two-degree-of-freedom FIV of SFTs under current.

As shown in Figure 3a, the numerical model consists of a 50D × 30D rectangular computational domain and an elastically mounted circular cylinder. For coordinates, the X- and Z-axis are defined as in-line and cross-flow direction, respectively. For the computational domain, the initial condition is that the SFT and fluid are stationary. The inlet boundary is 15D upstream from the center of the cylinder, and the Dirichlet boundary condition is imposed on it. Turbulence is defined by the turbulence intensity ($I=0.16{Re}^{(-1/8)}$) and hydraulic diameter. The outlet boundary is 35D downstream from the center of the cylinder, and the Neumann boundary is set. The top and bottom boundaries are 15D away from the center of the cylinder, and the free-slip boundary is employed. The no-slip boundary is applied on the surface of the cylinder.

The governing Equation (3) can be solved by the finite volume method (FVM). The computational domain is discretized, as shown in Figure 3b. To avoid excessive mesh deformation and ensure mesh quality, the overset mesh method (i.e., background mesh and component mesh) is adopted. To accurately capture the flow characteristics around the cylinder, the O-type component mesh is set (6D in diameter) and moves synchronously with the cylinder. The boundary layer mesh around the cylinder is densified (i.e., thickness of the first layer Δh, node number in radial direction Ns) to ensure the non-dimensional parameter $y^{+}$ <1.0 for the SST k-ω turbulence model. The background mesh is generated to discretize the whole computational domain and is densified (10D in length) around the cylinder. The solver automatically identifies the overset boundary of two meshes and establishes data transmission between them.

The fluid–cylinder interaction is in one-step coupling. And the solution process in numerical simulation is as follows:

(1)

On each time step, Equation (3) is discretely calculated based on the CFD solver first, which provides the pressure and viscous shear force of the fluid acting on the SFT. These forces are then used to integrate F_x(t) and F_z(t) and subsequently determine C_D and C_L for analyzing the interaction of fluid forces and the structure. In CFD calculations, the pressure–velocity coupling is based on the coupled method. The second-order scheme is applied to discretize the pressure term, and the second-order upwind scheme is adopted to discretize the convection term. The time step $∆t$ satisfies the Courant–Friedrichs–Lewy (CFL) condition (the maximum Courant number is less than 1.0 in this study).

(2)

After obtaining F_x(t) and F_z(t), they are input into the UDF code for Equation (1) to calculate the displacement x and z of the SFT. Equation (1) is solved by the 4th-order Runge–Kutta method in Equation (2), and it is commonly utilized in studies related to SFT, as referenced in [21,22,23].

(3)

Once the displacements are calculated, the fluid mesh is updated, and the process continues for the next time step.

In this study, simulations are stopped after at least 30 cycles of stable vibration. The response parameters of the SFT are normalized and summarized in

Table 1. Normalized parameters for SFT vibrating in two-degree of freedom.

Normalized Parameters	Expression
Non-dimensional mean in-line displacement	${\overline{A}}_X=\frac{\overline{x}}{D}$
Non-dimensional amplitude of in-line displacement	$A_X^{\ast }=\frac{\left(x_{max}-x_{min}\right)}{2D}$
Non-dimensional amplitude of cross-flow displacement	$A_Z^{\ast }=\frac{\left(z_{max}-z_{min}\right)}{2D}$
Non-dimensional in-line vibration frequency	$f_X^{\ast }=\frac{f_x}{f_{nwx}}$
Non-dimensional cross-flow vibration frequency	$f_Z^{\ast }=\frac{f_z}{f_{nwz}}$
In-line reduced velocity	${Ur}_{wx}=\frac{U}{f_{nwx}D}$
Cross-flow reduced velocity	${Ur}_{wz}=\frac{U}{f_{nwz}D}$
Root-mean-square value of lift coefficient	$C_{L,rms}=\frac{1}{T}\sqrt{{\int }_0^T{C}_L^2(t)dt}$
Mean drag coefficient	${\overline{C}}_D=\frac{1}{T}{\int }_0^T{C}_D(t)dt$

, where $\overline{x}$, $x_{max}$, and $x_{min}$ are the mean, maximum, and minimum displacements of the SFT in the X-axis, and $z_{max}$ and $z_{min}$ are the maximum and minimum displacements of the SFT in the Z-axis. In addition, $f_x$ and $f_z$ are the vibration frequencies of the SFT in the X- and Z-axis, respectively. $T$ is the vibration period of the SFT.

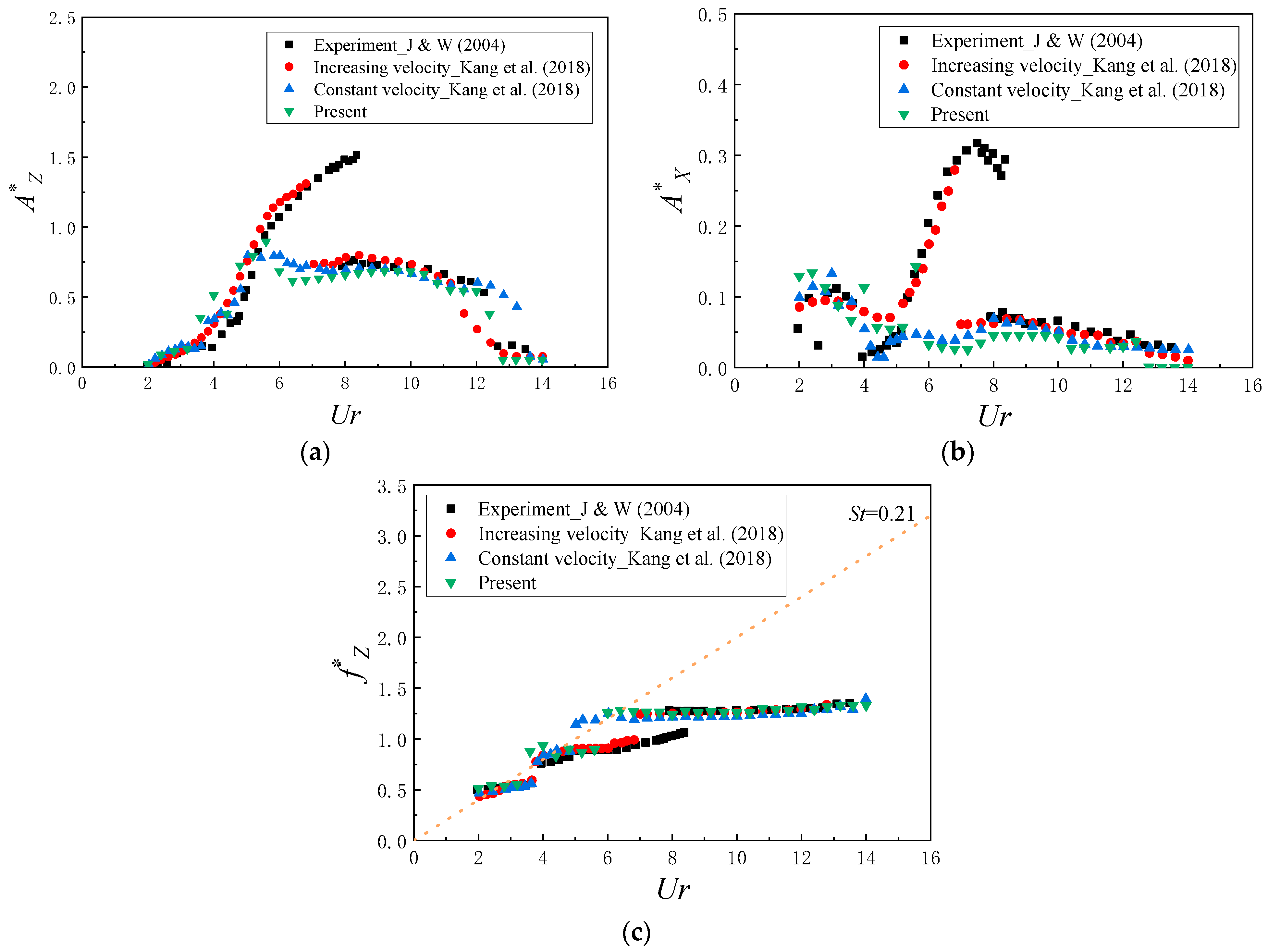
2.3. Model Verification

Comparing the numerical results of two-degree-of-freedom FIV for the SFT and hydrodynamic loads under various mesh densities and time steps, the mesh and time step independence analyses were first validated. The mechanical parameters of the SFT are selected as an outer diameter D = 0.252 m, mass ratio $m^{\ast }$ = 0.84 (BWR = 1.19), structural damping ratio $\xi$ = 0.05, in-line natural frequency in water $f_{nwx}$ = 0.45 Hz, natural frequency ratio $R_f$ = 0.54, reduced velocity ${Ur}_{wx}$ = 3.1, and Reynolds number $Re$ = 8.8 × 104. Note that the parameters of the SFT and reduced velocities in numerical simulations are consistent with the three-dimensional hydro-elastic SFT model test in reference [29].

Comparisons on the non-dimensional two-degree-of-freedom FIV of the SFT and hydrodynamic coefficients under various mesh densities and time steps are summarized in

Table 2. Comparison of the results of mesh and time step independence verification for the two-dimensional computational domain of SFT under current.

Mesh	Ns	Elements	Nodes	$∆\mathit{t}$	${\mathit{A}}_{\mathit{x}}^{\mathbf{\ast }}$	${\mathit{A}}_{\mathit{z}}^{\mathbf{\ast }}$	${\mathit{f}}_{\mathit{x}}^{\mathbf{\ast }}$	${\mathit{f}}_{\mathit{z}}^{\mathbf{\ast }}$	${\overline{\mathit{C}}}_{\mathit{D}}$	${\mathit{C}}_{\mathit{L},\mathit{r}\mathit{m}\mathit{s}}$
Mesh 1	100	20,400	20,726	0.0005	0.0115	0.0416	1.440	0.425	1.04	1.002
Mesh 2	160	58,025	58,588		0.0096	0.0401	1.515	0.410	1.033	0.986
Mesh 3	220	86,400	87,076		0.0097 (1.0%)	0.0398 (−0.7%)	1.516 (0.1%)	0.413 (0.7%)	1.03 (−0.3%)	0.99 (0.4%)
Mesh 2	160	53,025	53,588	0.001	0.0105	0.041	1.529	0.418	1.042	1.005
				0.0001	0.0095 (−1.0%)	0.04 (−0.2%)	1.511 (−0.3%)	0.411 (0.2%)	1.033 (0)	0.985 (−0.1%)

. Comparisons show that, for mesh density, the results simulated with Ns = 160 and Ns = 220 are identical, and the variation is within 1%. For the time step, the variation in the results simulated with $∆t$ = 0.0001 s and $∆t$ = 0.0005 s is within 1%. Hence, Mesh 2 for computational domain discretization and time step $∆t$ = 0.0005 s is applicable for numerical simulation of SFTs under current.

To verify the numerical method, the two-degree-of-freedom FIV of the SFT under current were compared to the literature results (i.e., model test results by Jauvtis and Williamson [17] and numerical results by Kang et al. [21]). The mechanical parameters are selected as diameter D = 0.0381 m, mass ratio $m^{\ast }$ = 2.6, mass-damping parameter $\left(m^{\ast }+C_A\right)\ast \xi$ = 0.013, and natural frequency f_n = 0.4 Hz. Furthermore, the reduced velocity ranged from 2 to 14.

Figure 4a,b show the comparisons of the results of two-degree-of-freedom vibration response versus reduced velocity, respectively. They show that, when the initial condition is constant velocity and the reduced velocity varies from 2 to 14, the two-degree-of-freedom FIV results by the numerical method in this study agree well with those of Kang et al. (2018) [21]. Due to the small amplitude of vibration in the in-line direction, the deviation is larger with an average deviation of 7% and a maximum deviation of 10% (at ${Ur}_{wx}$ = 4). The average deviation of amplitude in the cross-flow direction is 0.5%, and the maximum deviation is 2%.

Figure 4c shows the comparisons of the results of cross-flow vibration frequency versus reduced velocity. It shows that the vibration frequency also agrees well with that of Kang et al. (2018) [21]. The average deviation of vibration frequency in the cross-flow direction is 3%, and the maximum deviation is 9% (at ${Ur}_{wx}$ = 4).

Hence, the present numerical method is applicable for the numerical simulation of the SFT under current. Notably, since the initial condition is constant velocity, it fails to reproduce the super-upper branch in the cross-flow direction observed by Jauvtis and Williamson [17].

It is worth pointing out that, considering the mesh distortion, negative volume of dynamic mesh, and computational cost, this study performed two-dimensional numerical simulations to quickly investigate the dynamic response and vortex pattern of the SFT under the target flow reduced velocities. However, the two-dimensional simulations assumed that the hydrodynamic loads acting on any section of the SFT are the same, and the effects of vortex pattern instability or the non-uniform elastic deformation of the SFT in the spanwise direction for fluid–structure coupling were ignored. In addition, to compare with our SFT physical model test in reference [29] in the next stage, the SFT parameters, Reynolds number, and initial conditions in this study were then consistent with the physical model test.

2.4. Selection of Simulation Parameters

To numerically investigate the two-degree-of-freedom FIV of the SFT and wake pattern in a wide range of reduced velocities, the mechanical parameters of the SFT selected are the same as those in 2.3 for the mesh and time step independence analyses. Three factors were normalized as follows:

(1)

In-line reduced velocity ${Ur}_{wx}=\frac{U}{f_{nwx}D}$ ranged from 0.6 to 10.

(2)

Mass ratio $m^{\ast }=\frac{m_0}{\frac{\pi }{4}{\rho D}^2}$ ranged from 0.5 to 2.0.

(3)

Natural frequency ratio $R_f=\frac{f_{nwx}}{f_{nwz}}$ ranged from 0.54 to 1.85. For $R_f$ = 0.54, the in-line and cross-flow natural frequencies were $f_{nwx}$ = $f_1$ = 0.45 Hz and $f_{nwz}$ = $f_2$ = 0.83 Hz, respectively. For $R_f$ = 1.85, the in-line and cross-flow natural frequencies were $f_{nwx}$ = $f_2$ and $f_{nwz}$ = $f_1$. For $R_f$ = 1.0, two cases were addressed (i.e., $f_{nwx}$ = $f_{nwz}$ = $f_1$, $f_{nwx}$ = $f_{nwz}$ = $f_2$).

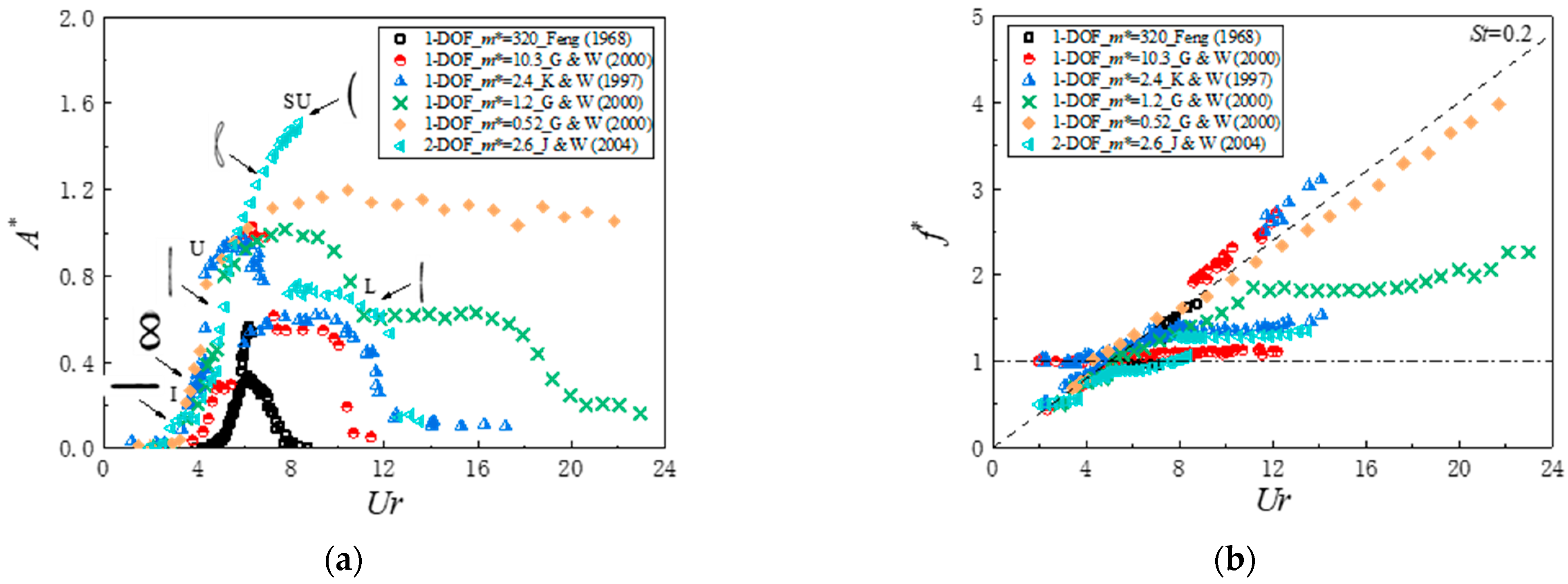
3. Numerical Results

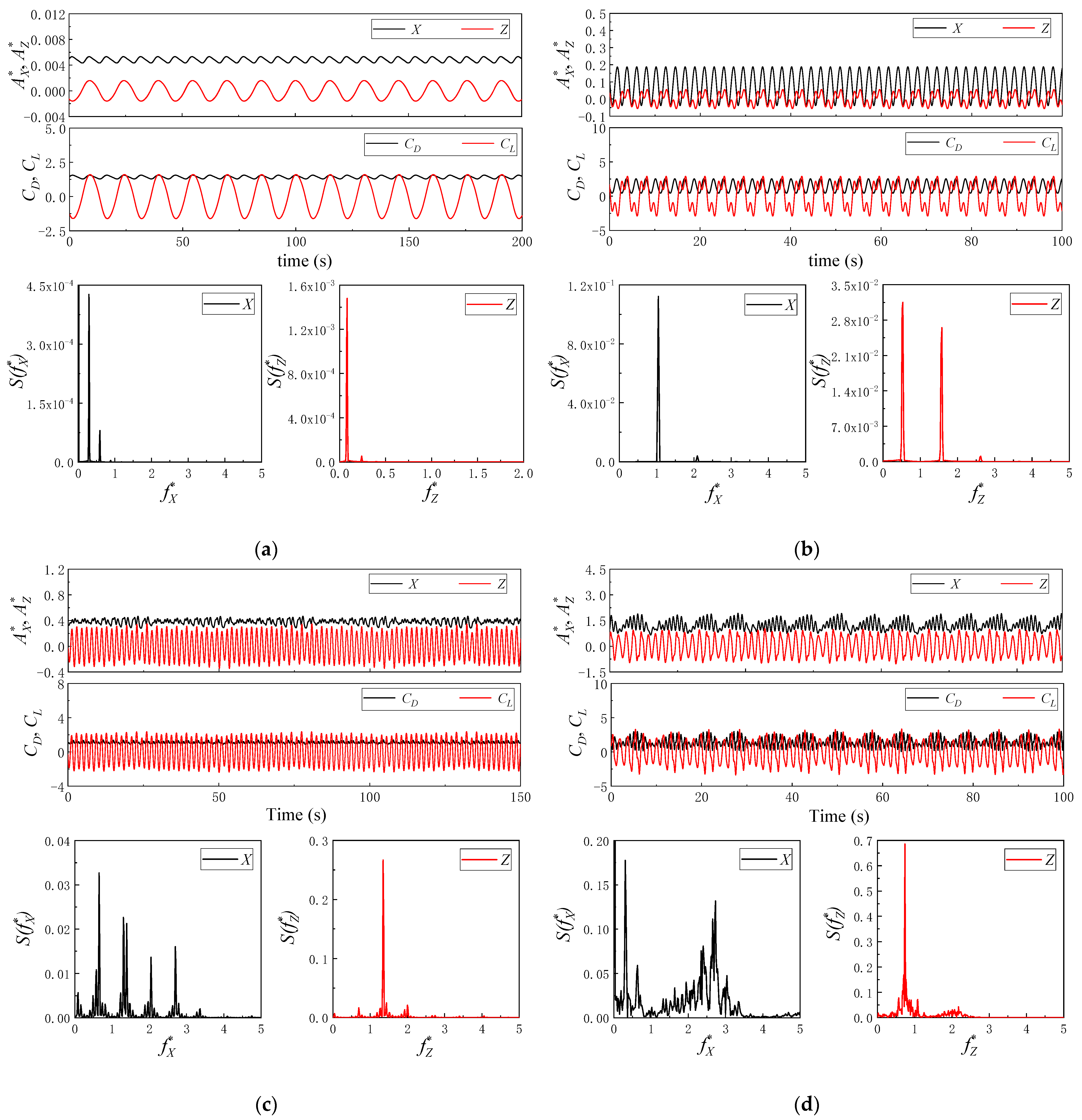
3.1. Two-Degree-of-Freedom FIV

To investigate the effect of coupled vibration for the SFT under current, the two-degree-of-freedom (2-DOF) FIV was simulated numerically in a wide range from 0.6 to 10, and the results were compared to that of one-degree-of-freedom (1-DOF) FIV.

Figure 5 shows the time histories of displacements for the SFT and hydrodynamic coefficients under typical reduced velocities. Note that the spectra of displacements for the SFT are also included. It reveals that, for ${Ur}_{wx}$ = 0.6, the two-degree-of-freedom FIV of the SFT is periodic and dominant at one frequency (narrow peak). The in-line main vibration frequency (i.e., the maximum peak value in the spectrum) is twice that in the cross-flow direction. Phase differences exist between the two-degree-of-freedom vibrations and the hydrodynamic coefficients. For ${Ur}_{wx}$ = 2.5, since the in-line vibration frequency is close to the natural frequency, the amplitude of in-line displacement is larger than that in cross-flow. Cross-flow vibration is irregular and multi-frequency, corresponding to two narrow peaks in the spectrum (i.e., main frequency and its third frequency). For ${Ur}_{wx}$ = 6.3 or 10, the in-line vibration is multi-frequency, corresponding to multiple and wide peaks in the spectrum, and the cross-flow vibration is still in the one-frequency domain.

Figure 6 shows the XZ-trajectories of the SFT versus reduced velocity. It should be noted that the smaller two-degree-of-freedom responses at ${Ur}_{wx}$ ≤ 1.8 are amplified by 10 times synchronously. It reveals that the variation in shape and moving direction for the XZ-trajectory critically affects the vibration of the SFT (i.e., amplitude, frequency, and phase) and wake pattern. Typical “8”-shaped trajectories are present under most reduced velocities corresponding to the 2:1 in-line to cross-flow dominant frequency ratios. For 0.6 ≤ ${Ur}_{wx}$ ≤ 1.8, since the phase difference ${\Psi }_{X-Z}$ between the in-line and cross-flow vibration is close to 270°, the XZ-trajectories bend downstream and appear like a circular arc (“C” shape). The two-degree-of-freedom vibration amplitudes of the SFT are identical. Due to the one-frequency dominant vibration of the SFT, the XZ-trajectories are periodic and regular. For ${Ur}_{wx}$ = 2.5, since the in-line vibration frequency is close to the natural frequency (as shown in Figure 5b), the XZ-trajectory becomes flat. For 3.1 ≤ ${Ur}_{wx}$ ≤ 3.8, the XZ-trajectories bend upstream, and the phase difference ${\Psi }_{X-Z}$ is close to 90°. For ${Ur}_{wx}$ = 4.4, the XZ-trajectory changes to an enclosed loop shape (i.e., the in-line vibration frequency is the same as that in cross-flow). With the further increase in reduced velocity, the cross-flow amplitude of the SFT increases and is larger than the in-line. Due to the in-line multi-frequency vibration, the XZ-trajectories become chaotic and do not repeat the same path from cycle to cycle (even drift from one mode to another). For ${Ur}_{wx}$ = 8.2, the XZ-trajectory restores to the standard “8” shape. For ${Ur}_{wx}$ = 10, the trajectory becomes irregular again since the multi-frequency vibration is in the in-line direction.

Figure 7 shows the non-dimensional responses (i.e., amplitude, frequency, and phase) of the SFT versus reduced velocity. Note that the numerical results of one-degree-of-freedom FIV for the SFT under current are also included for comparison purposes. For the multi-peak spectra, only the maximum peak value is shown in Figure 7.

The comparisons show that the effect of coupled vibration on the SFT is significant.

(1)

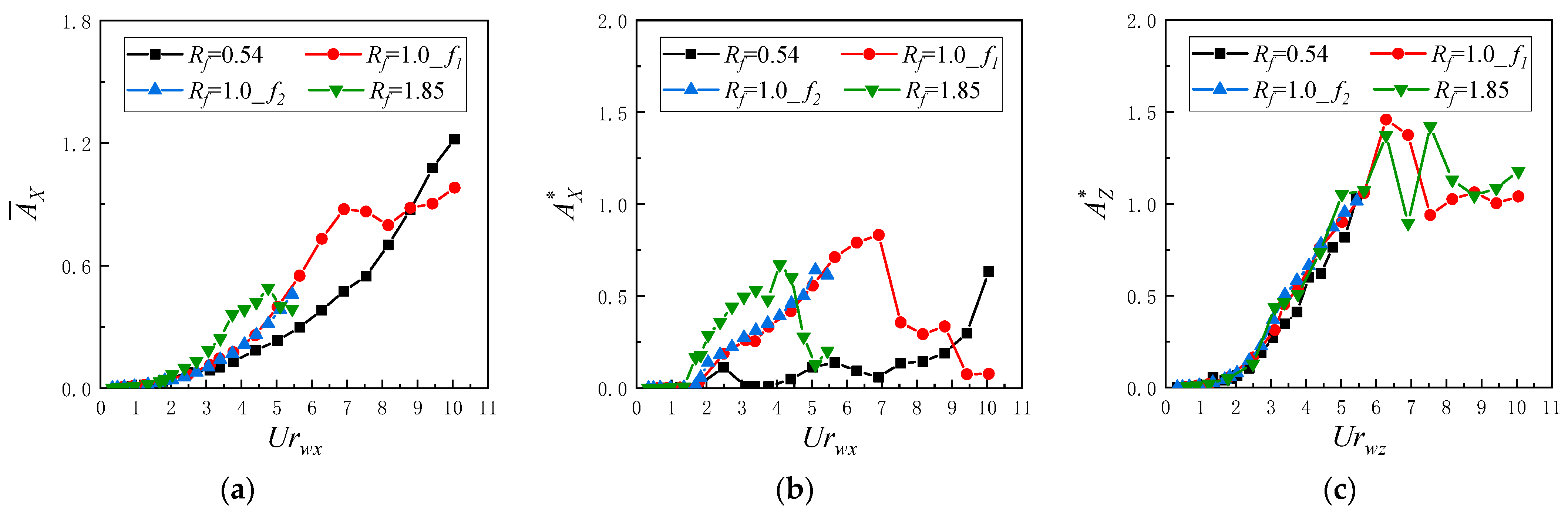
Amplitude

Generally, the 2-DOF vibration amplitudes of the SFT increased with the reduced velocity. For in-line vibration, the maximum vibration amplitude is 0.63D at ${Ur}_{wx}$ = 10. For cross-flow vibration, the initial branch and upper branch are present, and the maximum vibration amplitude is in synchronization with the in-line amplitude (1.03D). In addition, the cross-flow amplitudes are significantly larger than the in-line when ${Ur}_{wx}$ ≥ 3.1.

A comparison with the 1-DOF results reveals that the coupled vibration has a significant impact on the in-line and cross-flow vibration amplitudes of the SFT at ${Ur}_{wx}$ ≥ 4.4 and ${Ur}_{wx}$ ≥ 5.7, respectively.

(2)

Frequency

For ${Ur}_{wx}$ ≤ 3.8, the 2-DOF vibration frequencies follow the Strouhal relationship (i.e., the in-line frequency is twice that in cross-flow). For 4.4 ≤ ${Ur}_{wx}$ ≤ 7.5, the in-line vibrations become multi-frequency and dominated by lower frequency. The in-line main frequencies jump between 0.2$f_{wz}$ and 1.0$f_{wz}$. For 8.2 ≤ ${Ur}_{wx}$ ≤ 9.4, the in-line vibrations recover one frequency, and the non-dimensional vibration frequency (≈2.5$f_{wx}$) is less than 2$f_v^{\ast }$. The in-line vibration becomes multi-frequency again at ${Ur}_{wx}$ = 10, and the non-dimensional vibration frequency (≈0.3$f_{wx}$) is about 0.2$f_Z^{\ast }$. For cross-flow vibration, the frequency locking presents at 5.7 ≤ ${Ur}_{wx}$ ≤ 10 (≈0.7$f_{wz}$).

A comparison with the 1-DOF results reveals that the coupled vibration has a significant impact on the in-line and cross-flow vibration frequencies of the SFT at ${Ur}_{wx}$ ≥ 4.4 and ${Ur}_{wx}$ ≥ 5.7, respectively. Multi-frequency competition and conversion of in-line vibration appear at larger reduced velocities, and the main frequency significantly decreases. 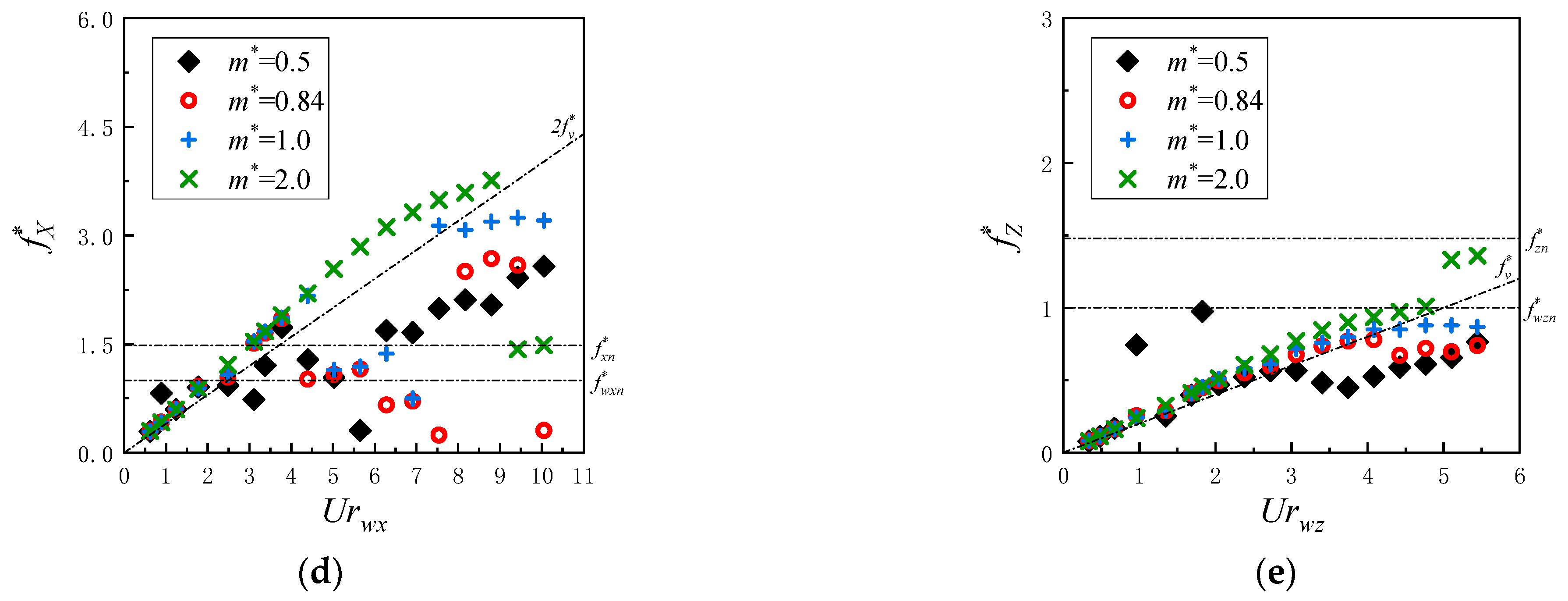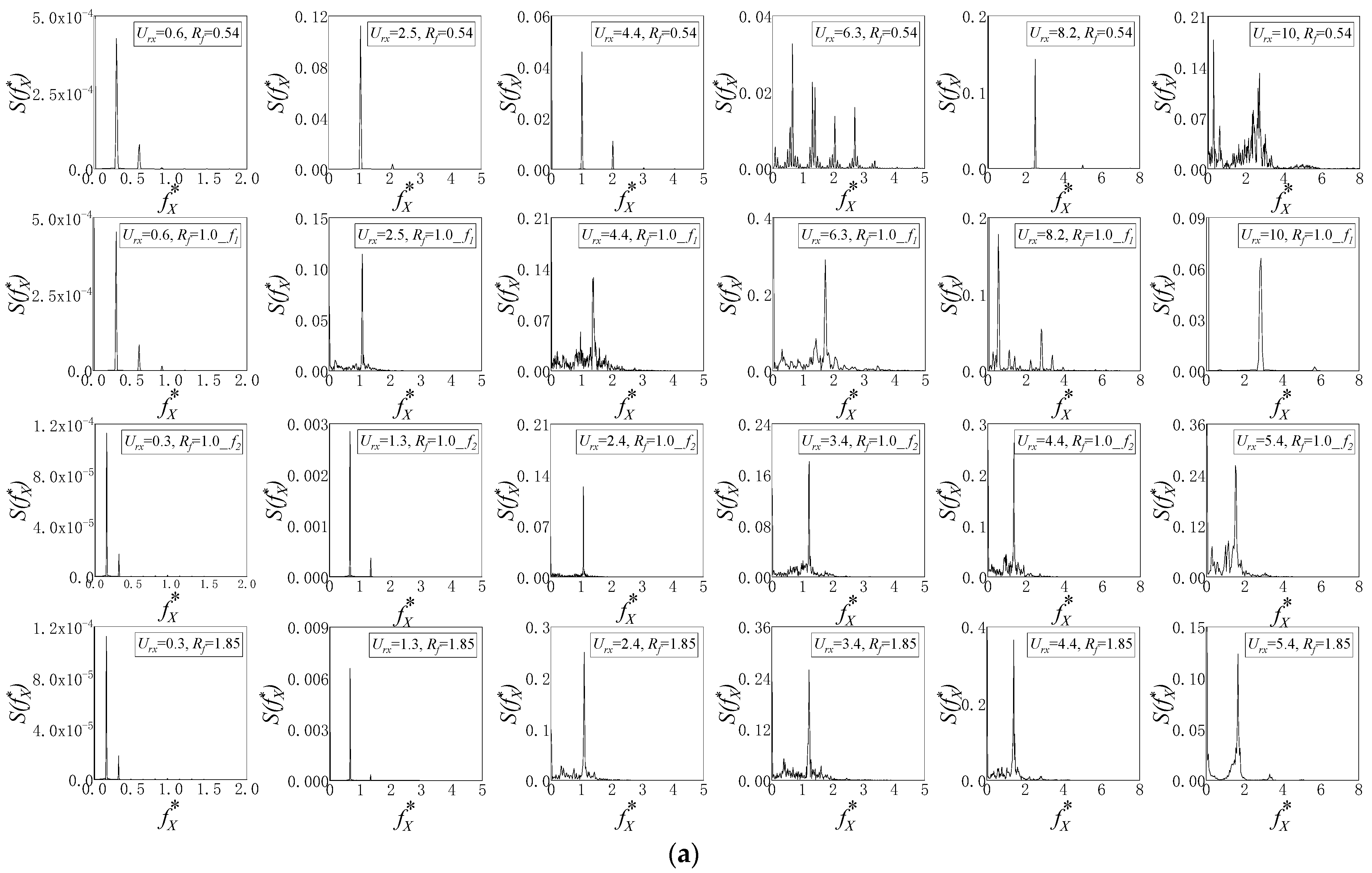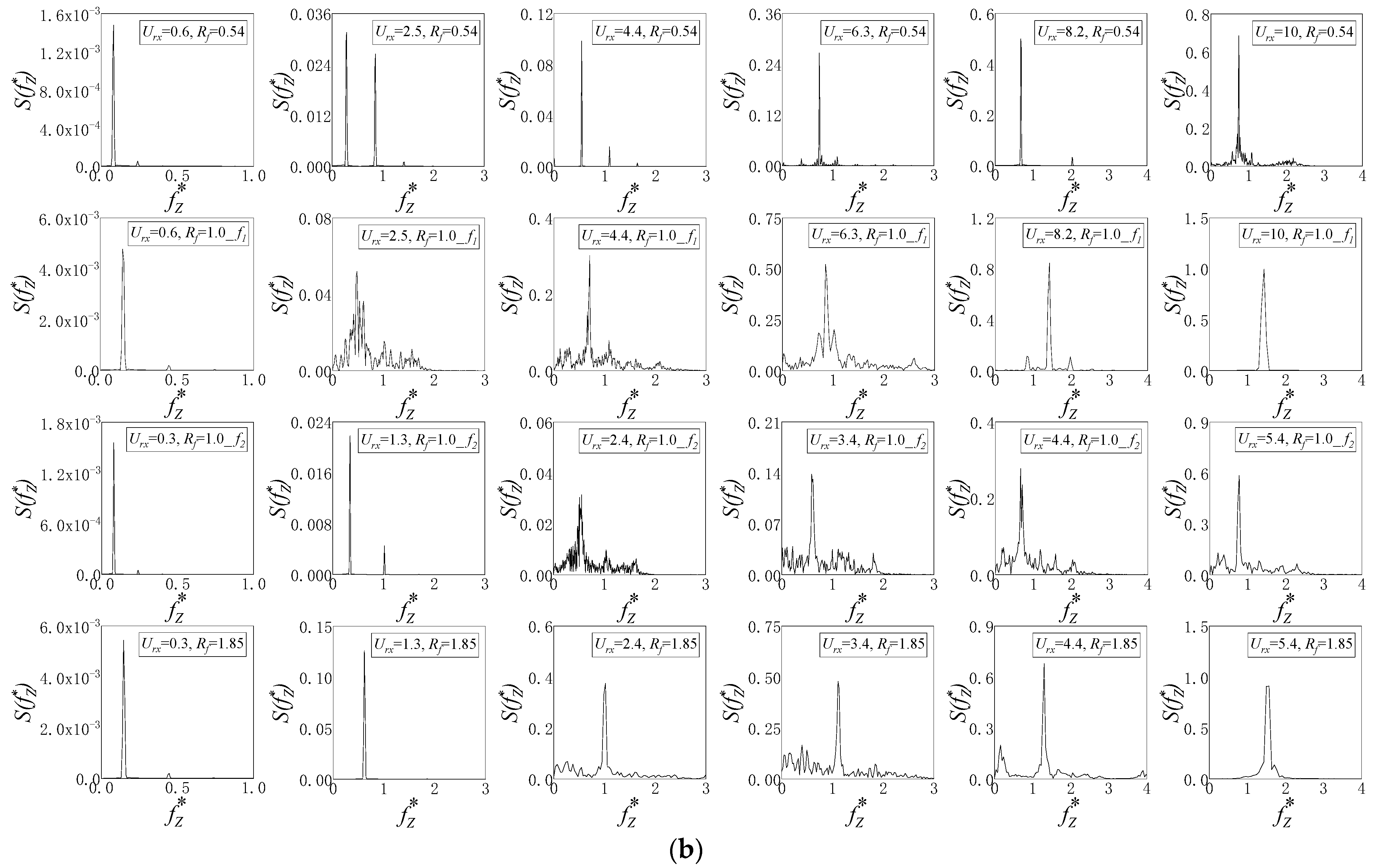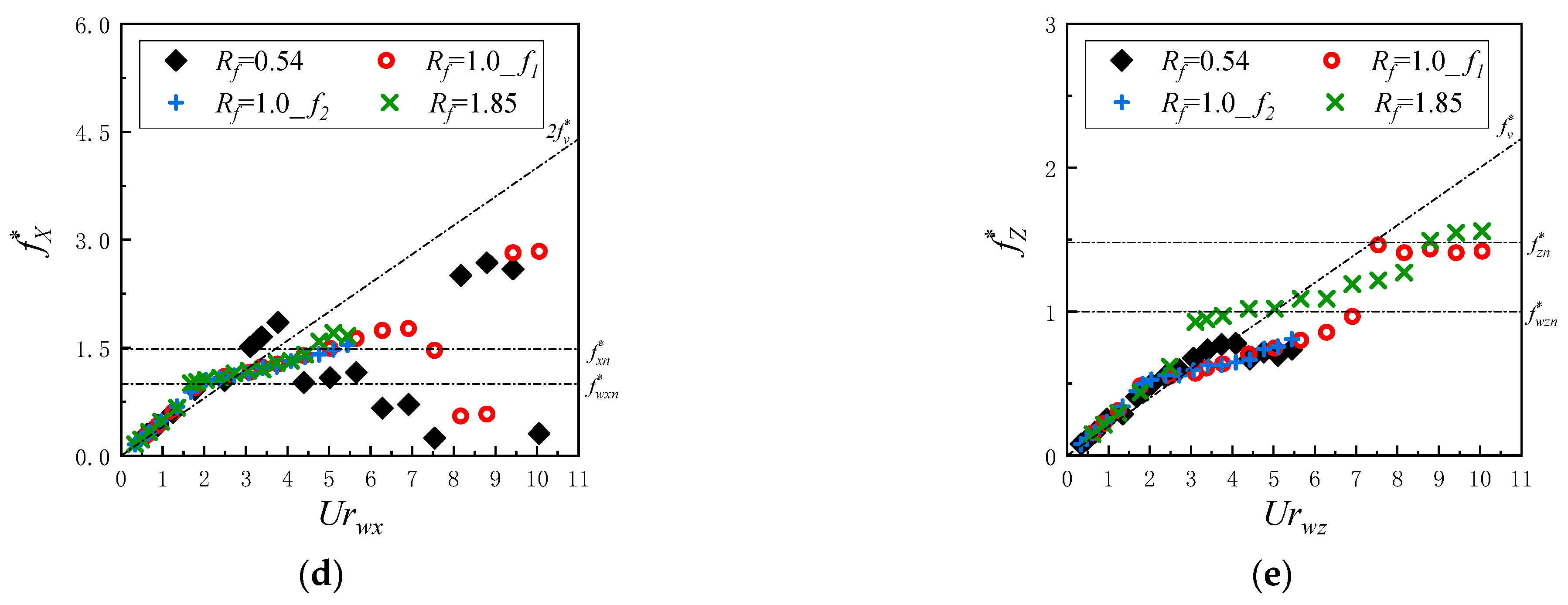The lock-in frequency of cross-flow vibration is less than the natural frequency.

(3)

Phase difference

Variation in phase can affect the vortex pattern. For 0.6 ≤ ${Ur}_{wx}$ ≤ 1.8, the phase difference ${\Psi }_{X-Z}$ is nearly 270°, and the hydrodynamic load is in phase with the vibration of the SFT in the same direction. For 2.5 ≤ ${Ur}_{wx}$ ≤ 5.7, the phase difference ${\Psi }_{X-Z}$ jumps to 90° and then varies irregularly due to the in-line multi-frequency vibration. For 10 > ${Ur}_{wx}$ ≥ 8.2, the phase difference ${\Psi }_{X-Z}$ becomes quasi-steady at 200° and increases again at ${Ur}_{wx}$ = 10.

A comparison with the 1-DOF results reveals that the coupled vibration has a significant impact on the phase difference ${\Psi }_{X-C_D}$ (between the in-line vibration of the SFT and drag force) at ${Ur}_{wx}$ ≥ 4.4) and is limited by the phase difference ${\Psi }_{Z-C_L}$.

Figure 8 shows the transient vorticity magnitude of the SFT at typical reduced velocities. Note that the numerical results of one-degree-of-freedom FIV for the SFT are also included for comparison purposes. It indicates that, for lower reduced velocities, a single vortex sheds from each side of the SFT during one cycle (2S mode). With the increase in reduced velocity, the wake pattern of two-degree-of-freedom FIV for the SFT becomes irregular, and the vortex length becomes larger. The coupled vibration has a significant impact on the wake pattern at ${Ur}_{wx}$ ≥ 4.4.

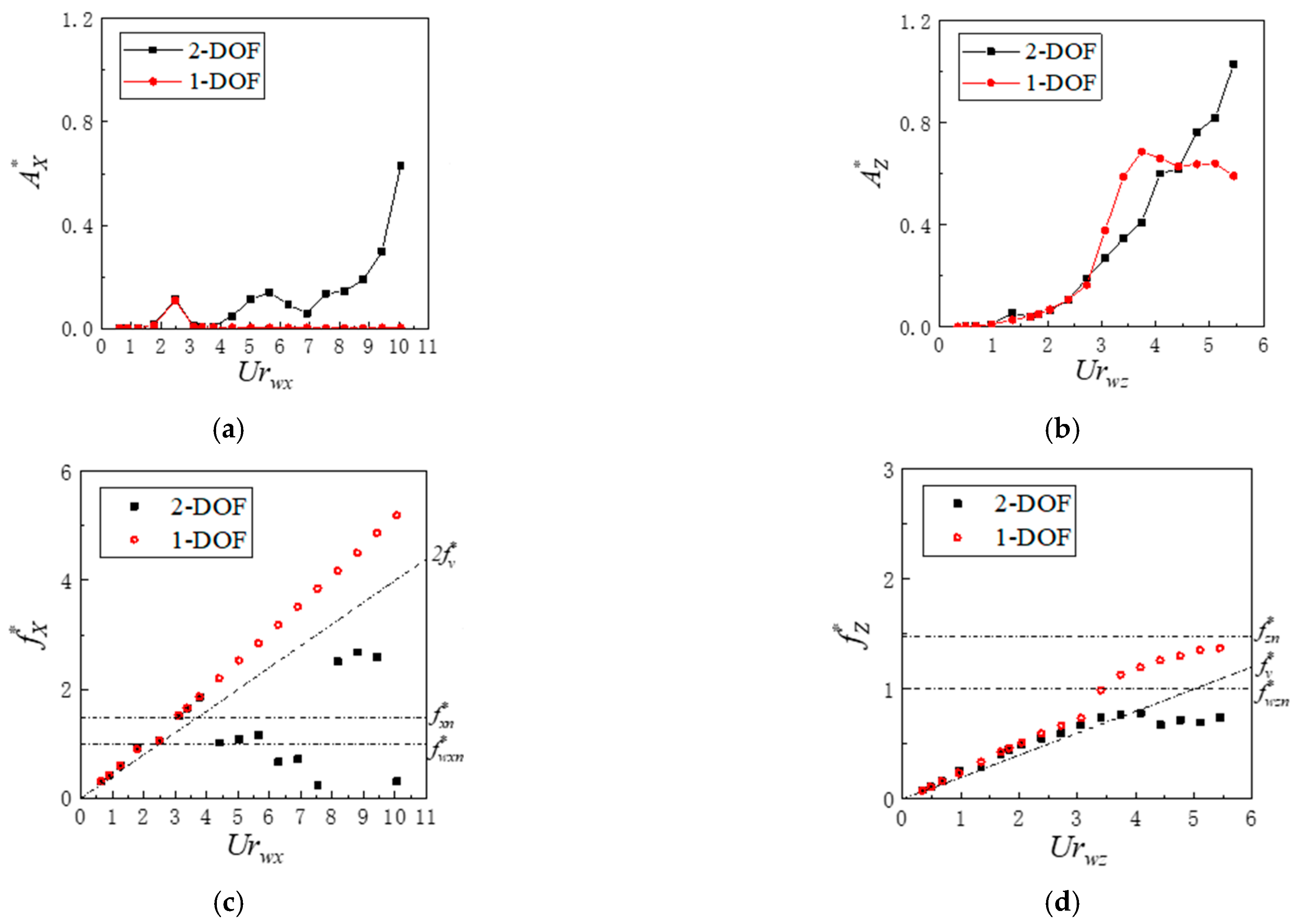
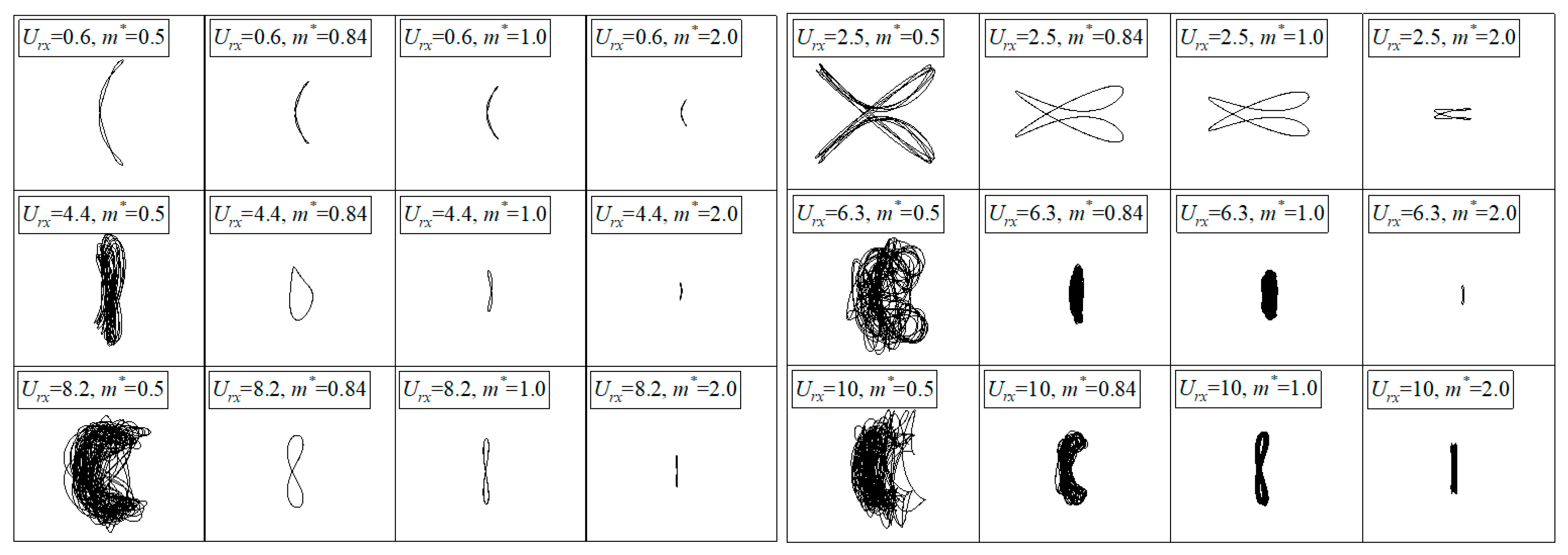
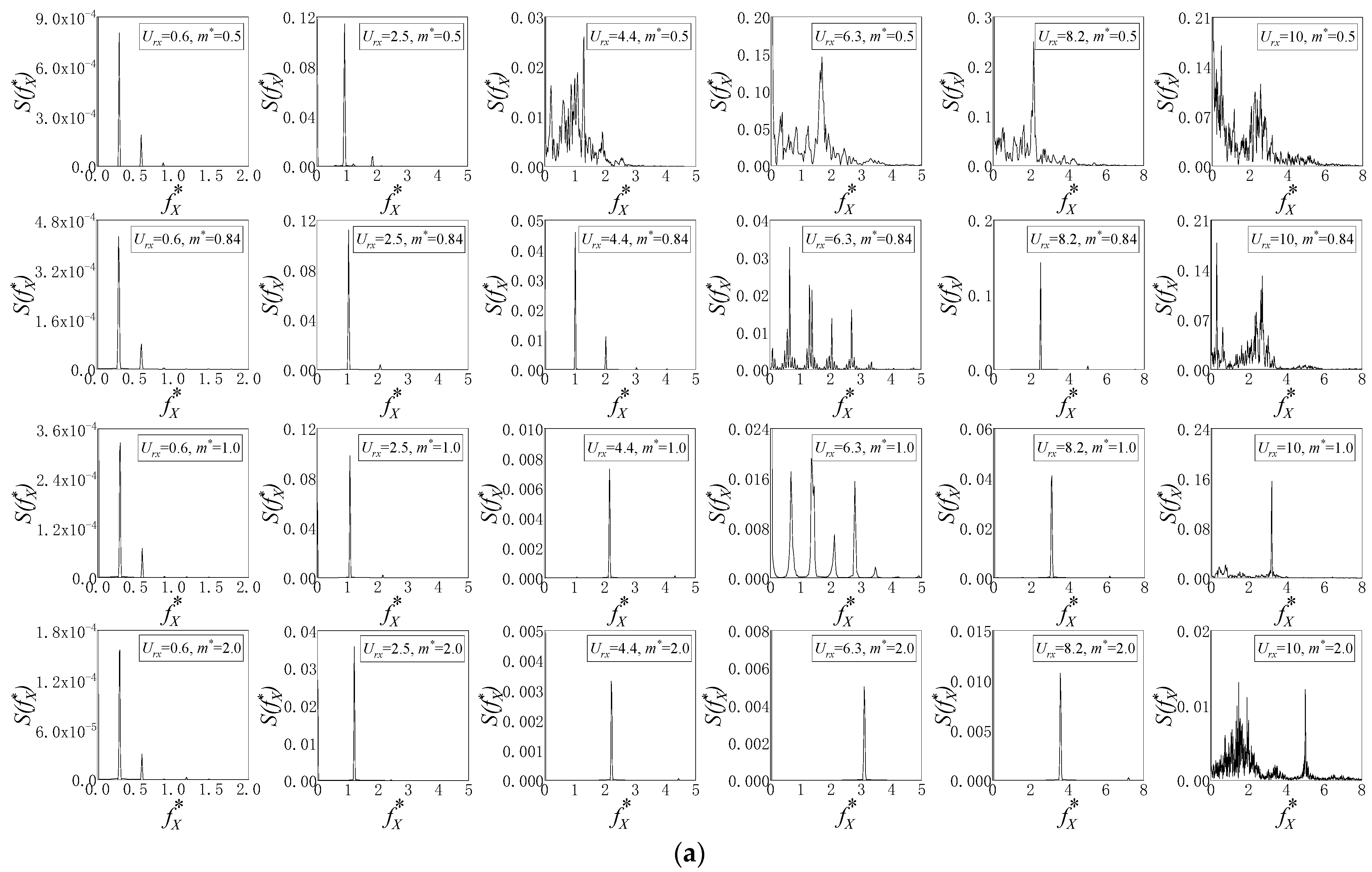
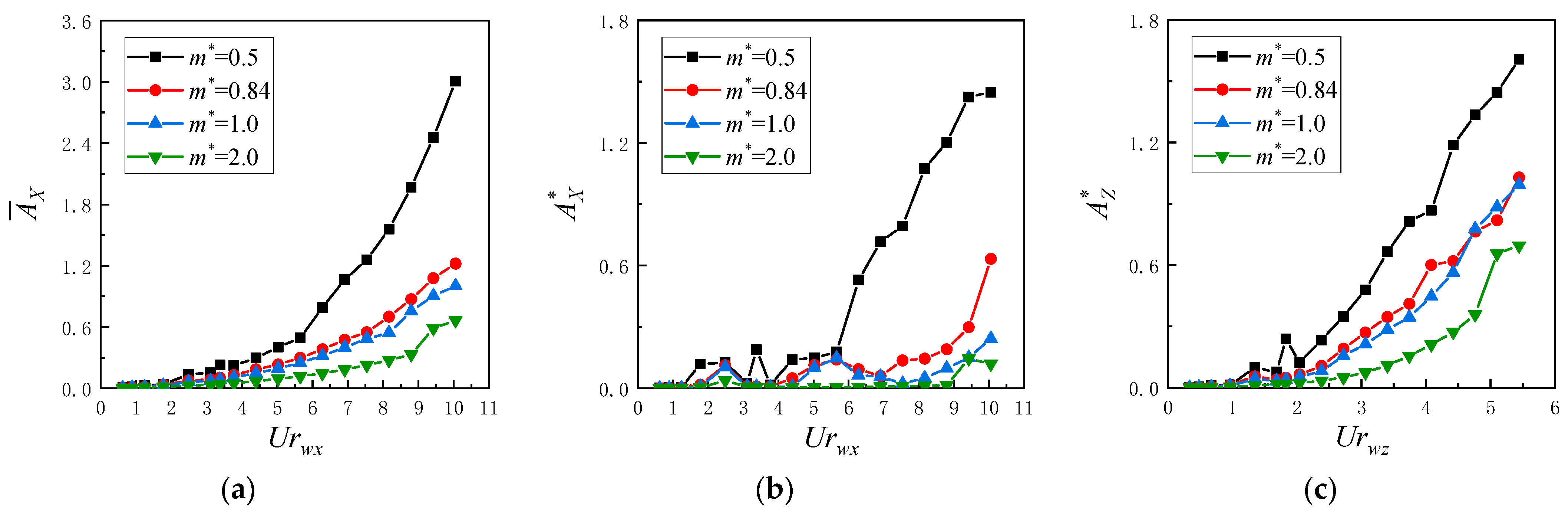
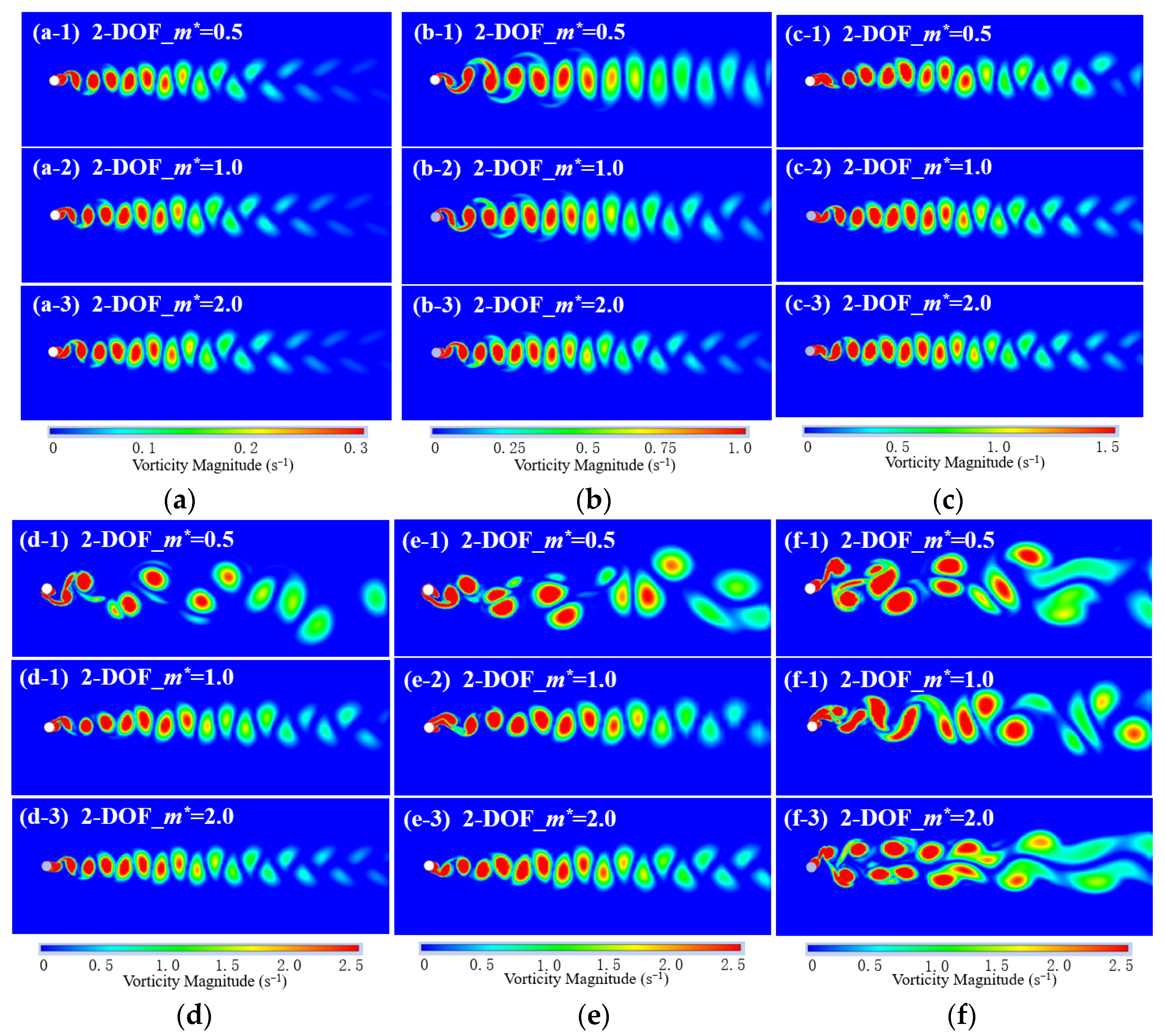
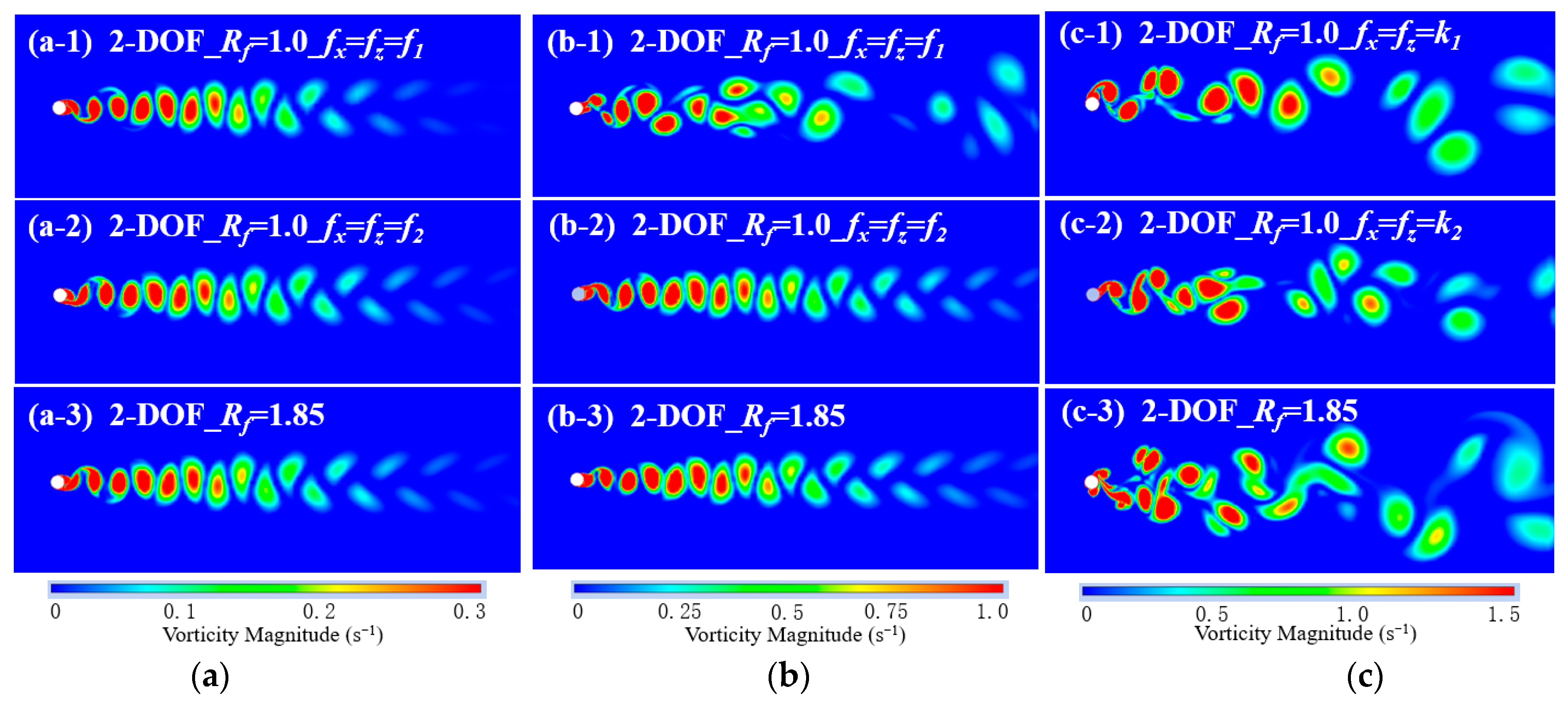
3.2. Effect of Mass Ratio on SFT Vibration

To investigate the effect of mass ratio on the two-degree-of-freedom FIV of the SFT under current, four mass ratios were selected for simulation.

Figure 9 shows the comparison of the XZ-trajectories of SFTs with various mass ratios at typical reduced velocities. Figure 10 shows the spectra of in-line and cross-flow displacements under the same conditions. Comparisons show that the two-degree-of-freedom vibrations of the SFT are significantly suppressed with the increase in mass ratio at ${Ur}_{wx}$ ≥ 4.4, especially for the in-line vibration. Due to the in-line multi-frequency effect at larger velocities, the XZ-trajectories become regular and periodic for the SFT with a larger mass ratio. Furthermore, due to the variations in vibration frequency and phase, the pattern of XZ-trajectories and the width of the spectra also vary with mass ratio.

Figure 11 shows the comparison of the non-dimensional responses (i.e., amplitude, frequency) of the SFT versus reduced velocity under various mass ratios. It shows that the two-degree-of-freedom vibration amplitudes of the SFT increase with the increase in reduced velocity. The increase in mass ratio significantly suppresses SFT vibration due to the multi-frequency vibration and early frequency locking for the SFT with lower mass ratios. For $m^{\ast }$ = 0.5, the in-line and cross-flow amplitudes of the SFT are equal to 1.5D at ${Ur}_{wx}$ = 10. By contrast, they decrease 92% and 57% when $m^{\ast }$ = 2.0, respectively. The in-line and cross-flow vibration frequencies of the SFT when $m^{\ast }$ = 2.0 follow the Strouhal relationship at ${Ur}_{wx}$ ≤ 8.8, and one frequency dominates the vibration with a narrow peak in the spectra.

Figure 12 shows the comparison of the transient vorticity magnitudes of the SFT at typical reduced velocities under various mass ratios. It shows that, for ${Ur}_{wx}$ ≤ 4.4, the effect of mass ratio on vortex pattern and length is limited. With the increase in reduced velocity, the vortex pattern of the SFT with a lower mass ratio becomes unstable, corresponding to the irregular XZ-trajectories. Due to the multi-frequency vibration and early frequency locking, vortex mode switching may occur during the vibration.

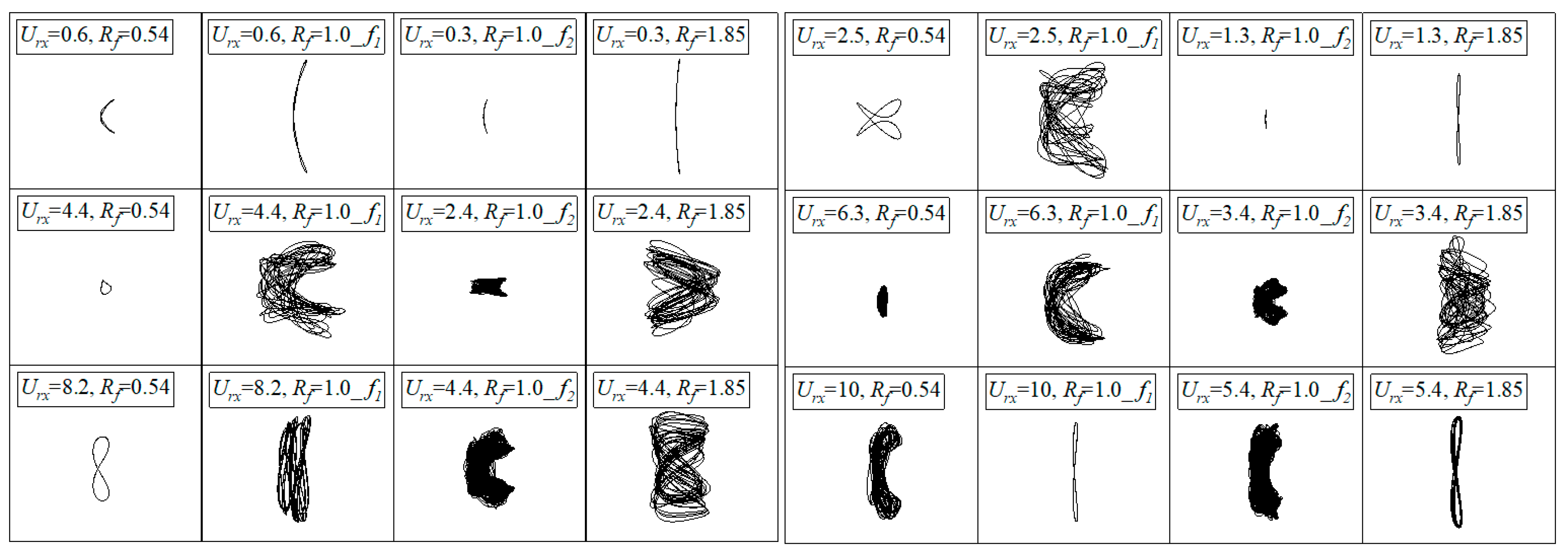
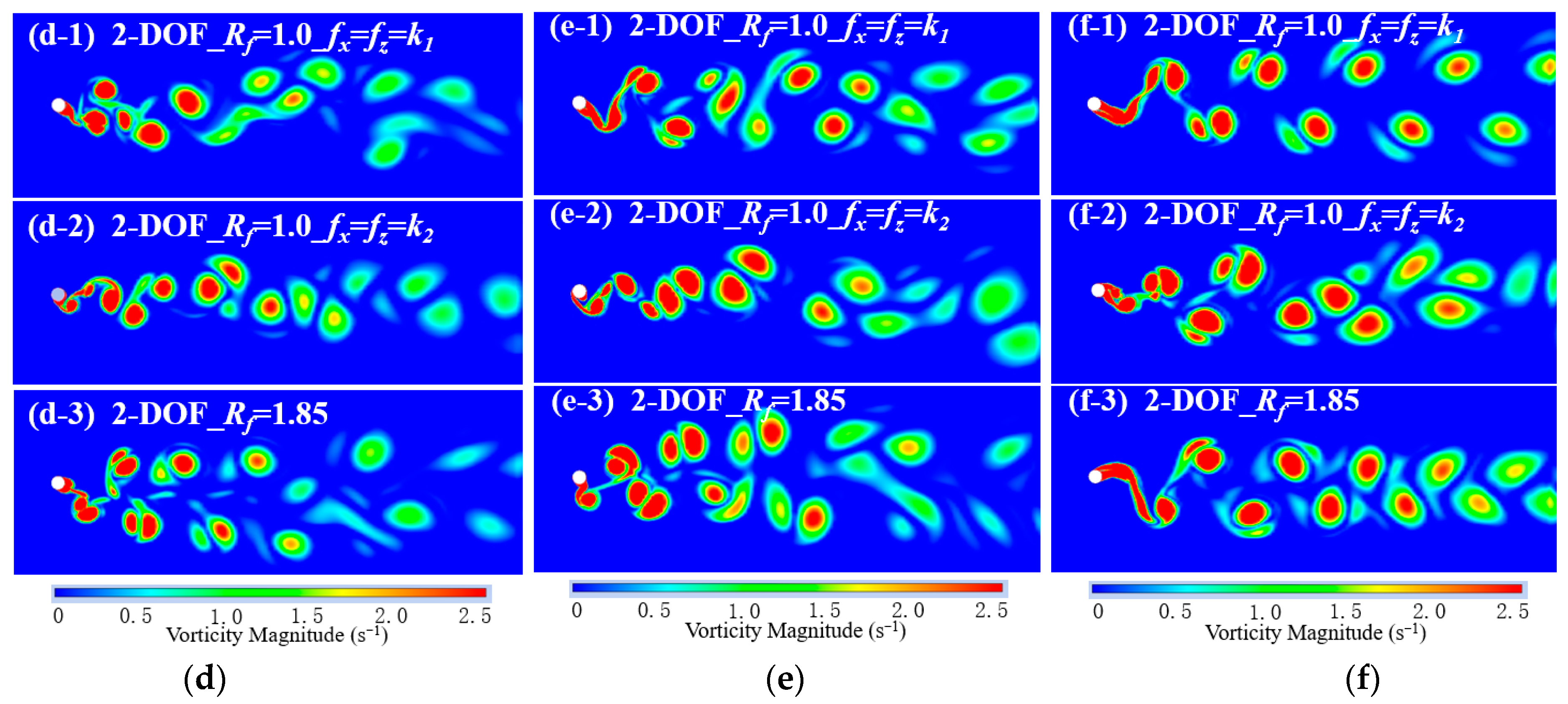
3.3. Effect of Natural Frequency Ratio on SFT Vibration

To investigate the effect of the natural frequency ratio on the two-degree-of-freedom FIV of the SFT under current, three natural frequency ratios were selected for simulation.

Figure 13 shows the comparison of the XZ-trajectories of the SFT under various natural frequency ratios at typical reduced velocities. Figure 14 shows the spectra of in-line and cross-flow displacements under the same conditions. Comparisons show that the two-degree-of-freedom vibration amplitudes of the SFT vary significantly with the increase in natural frequency ratio at ${Ur}_{wx}$ ≥ 2.5. The pattern of XZ-trajectories and the width of spectra also vary with the natural frequency ratio.

Figure 15 shows the non-dimensional response (i.e., amplitude, frequency) of the SFT versus reduced velocity under various natural frequency ratios. It shows that peak points of the two-degree-of-freedom vibration amplitudes exist with the increase in reduced velocity. The increase in the natural frequency ratio significantly affects the peak point and lock-in width of SFT vibration since the frequency-locking relationship varies. For R_f = 1.0 and $f_{nwx}$ = $f_{nwz}$ = $f_1$, the maximum in-line vibration amplitude is 0.8D at ${Ur}_{wx}$ = 6.9, and the maximum cross-flow amplitude is 1.4D. For R_f = 1.85, the maximum in-line vibration amplitude is 0.7D at ${Ur}_{wx}$ = 4.1, and the maximum cross-flow amplitude is 1.4D. In addition, the in-line and cross-flow vibration frequencies of the SFT with various natural frequency ratios follow the Strouhal relationship at ${Ur}_w$ ≤ 3.4.

Figure 16 shows the comparison of the transient vorticity magnitudes of the SFT at typical reduced velocities under natural frequency ratios. It shows that, for ${Ur}_{wx}$ ≥ 2.5, the effect of the natural frequency ratio on vortex pattern and length can be observed. With the increase in reduced velocity, the vortex pattern of the SFT with a larger natural frequency ratio becomes more unstable, corresponding to the irregular XZ-trajectories and various vortex modes.

4. Conclusions

Based on the Reynolds-averaged Navier–Stokes (RANS) method, a two-dimensional numerical model was developed to investigate the two-degree-of-freedom FIV of an anchored SFT under current. The numerical results were verified by the literature results, and the effects of coupled vibration and structural parameters, such as mass ratio and natural frequency ratio, on SFT response and wake pattern were addressed across a wide range of reduced velocities. Based on the numerical results, the following conclusions can be drawn:

(1)

Compared to the 1-DOF numerical results, coupled vibration has a significant impact on SFT response at ${Ur}_{wx}$ ≥ 4.4.

(2)

A decrease in mass ratio (m* < 1) significantly amplified the 2-DOF vibration amplitudes of the SFT at ${Ur}_{wx}$ ≥ 4.4, especially for the in-line vibration. Frequency lock-in was observed in advance for $m^{\ast }$ ≤ 1.0, leading to enhanced in-line multi-frequency vibration, and the vortex pattern became more unstable. For $m^{\ast }$ = 2.0, the cross-flow vibration of the SFT is dominant.

(3)

Decreasing the natural frequency ratio (R_f < 1) significantly suppressed the in-line vibration of the SFT at ${Ur}_{wx}$ ≥ 2.5. The peak points and lock-in width of 2-DOF vibration amplitudes versus reduced velocity showed significant variations. For R_f ≤ 1.0, frequency jumping was observed, leading to smaller in-line vibration amplitude, and the vortex pattern became more steady.

In summary, for SFT design, the effect of mass ratio and natural frequency ratio on the in-line vibration of the SFT should be given more attention.

It should be noted that to quickly investigate the dynamic response of the SFT and to compare it to the physical model test results in the next stage, two-dimensional numerical simulations with the same Reynolds number range as the physical model test [29] were addressed in this study. Additionally, the damping effects, specifically the discussion of hydrodynamic damping, were not covered in this study. We plan to investigate this aspect in more detail in our future work.

For an actual SFT, a higher Reynolds number (i.e., Re = O(10⁷)) is more representative of turbulent flow conditions encountered in practice. The factors, i.e., three-dimensional vortex instability or non-uniform elastic deformation of the SFT in the spanwise direction, can affect the dynamic response of the SFT. The effect will be further investigated based on the three-dimensional fluid–structure coupling simulation, and the difference with the two-dimensional results will be addressed. Furthermore, we will also consider the design of motion response control devices or damping devices, as they have the potential to improve the performance of SFTs under current.