Modes of Weather System-Induced Flows through an Arctic Lagoon

Abstract

With the increasing warming of the Arctic, the summertime ice-free period in the coastal Arctic becomes longer and the water exchange between arctic lagoons and coastal Beaufort Sea becomes more important for land–ocean interaction. This study examined the dynamics of water exchange between the arctic lagoons and the Arctic Ocean under the influence of weather systems (the transient arctic cyclones and hovering Beaufort High pressure system). We implemented rare observations, numerical modeling with the Finite Volume Community Ocean Model (FVCOM), and a forcing-response Empirical Orthogonal Function (fr-EOF) analysis to determine the weather-driven flow patterns and characteristics in the micro-tidal arctic lagoon (Elson Lagoon) with little freshwater discharge. The results were validated for both tidal and subtidal currents with in situ data. The inlets of the lagoon were significantly impacted by wind associated with the weather systems and the flows through the inlets were highly correlated with each other. The fr-EOF analysis for the 1.5-month FVCOM output indicated three significant modes of wind-driven flow. In the deepest (~16 m) northwestern-most inlet, a counter-wind flow occurred more than 96% of the time due to setup and set down of water level inside the lagoon and the vorticity balance related to the wind stress and water depth. For about 60–80% of the time, the exchange flow was out of the lagoon through the northwestern-most and deepest inlet due to the strong easterly winds dictated by the Beaufort High; this dominant flow is mainly caused by the persistent easterly wind as a limb of the Beaufort High pressure system, modified by the transient arctic cyclones with a westerly wind and inward flows at the westernmost inlet of Elson Lagoon. This study shows that the alternating influence from the cyclone-anticyclone weather systems produces a meteorological tide in the subtidal spectrum which dominates the water exchange in the region through the multiple inlets. With the observed increase in cyclone strength and frequency under the warming trend, this may imply a greater contribution from the westerly wind because of the increased cyclonic activities. If this is the case, the inward flow might increase and have an effect on sediment, larval, and nutrient transports through this system.

1. Introduction

1.1. Climate Change and Challenges in Studying Arctic Coastal Water

Global climate change has shown an increasing warming trend in the arctic region [1,2,3]. The warming has lengthened the ice-free period in arctic water corresponding to an increased summertime river runoff along the North American coast bordering the Arctic Ocean [4,5,6]. Recent Arctic Ocean model studies revealed that, in addition to Ekman pumping [7,8,9] and ice melt [10], the change in river runoff along the Alaskan coast plays a major role in freshwater content variability of the Beaufort Gyre [6].

However, to resolve the water exchange between the arctic lagoons/estuaries and the Arctic Ocean, the Arctic Ocean model should include accurate land boundary conditions where complex estuaries and lagoons need to be resolved for reliably simulating the hydrodynamics. The North American arctic coast is characterized by numerous rivers, estuaries, and lagoons for which many of the bathymetry data from these ecosystems remain unavailable or inaccurate, and consequently without which numerical models cannot be validated. Moreover, the frequent severe weather in the region makes in situ field campaigns difficult and also has the potential to modify the physical characteristics of these systems. It is these weather events that play significant roles in driving the variability of exchange flows between the estuaries/lagoons and the Arctic Ocean.

In addition, there is a severe lack of infrastructure and logistic support in the region. As a result, there has been little effort in determining the land–ocean exchange under the changing climate. This coastal system is among the least measured globally.

Since the exchange flows between the estuaries and coastal ocean vary significantly with weather conditions, understanding the complex estuarine–shelf interaction over the Alaskan coast under varying weather systems may provide insight into the interaction between the coastal waters especially between the extensive arctic lagoons/estuaries and the Beaufort Sea and Chukchi Sea.

1.2. Estuarine Gravitational, Tidally Induced and Weather-Induced Circulation

In the estuaries and lagoons, wind-driven currents are not always considered the most important driving factors. For example, in estuaries with large saltmarshes [11] or in an elongated estuary with a single opening to the coastal ocean, the dominant flow is usually due to gravitational circulation and is a result of the momentum balance between the baroclinic pressure gradient and turbulent mixing [12,13], although the wind effect may have a certain spectrum overlapping that of the gravitational circulation.

More recent studies argued that estuarine residual circulation is related to spatiotemporally varying mixing due to tidal mixing and tidal straining or covariance between eddy viscosity and velocity shear [14,15,16,17,18]. In studies on tidally induced residual circulation [19], the wind effect is often excluded, although it was noticed even in the early studies that wind effects can contribute significantly to the dynamics [20]. The wind effect has been discussed in studies with respect to estuarine flushing [21], wind-straining [22,23], stratification [24], and lateral structure [25].

Tidally induced residual flows in estuaries can dominate the circulation under normal weather conditions [26], but they are usually weaker than the wind-driven flows in a multiple-inlet system, particularly when there is a strong weather system such as an atmospheric cold front [27]. The main reason is that tide is oscillatory, and thus the mean is much reduced; while in a multiple-inlet system, the wind-driven flow can produce through-flows so that with a given wind condition some inlets tend to have an inward flow and others an outward flow, especially under severe weather.

1.3. Wind-Driven Circulations in Coastal Embayment

Most surveys in estuaries and lagoons are conducted during fair weather conditions, although there have been theoretical [28,29,30,31] and observational or experimental studies [32,33,34,35,36,37,38] of the wind-driven circulation and storm surge under variable weather conditions. Consequently, results can be biased toward the fair-weather end of the spectrum. The actual circulation within an estuary requires knowledge of the wind effect, which can vary significantly in magnitude as weather changes. These episodic and energetic weather systems cause meteorological tides in sub-inertial or subtidal bands in the spectrum and may have substantial consequences on the distribution and transport of waterborne materials. Understanding the effects of weather systems on the hydrodynamics in coastal embayments including lagoons and estuaries can help better understand the effects of physical forcing on biogeochemical and ecosystem processes.

1.4. This Study

Wind-driven flows can be classified into three different levels under (1) normal weather conditions (i.e., relatively weak wind, e.g., [30,36,38]); (2) severe weather (such as an arctic cyclone, extratropical cyclone, and cold fronts, e.g., [39,40,41]); and (3) extreme weather (such as hurricanes and tornados). Studies for the impact of hurricanes/typhoons are perhaps the most abundant [31,42,43,44], while few efforts are made to examine the impact of arctic cyclones on the arctic estuaries. In [45], a short-term (5-day) study was conducted in Elson Lagoon (Figure 1) and demonstrated that wind and subtidal velocities were highly correlated (R²~0.96) within this system.

The objective of this study is to examine an extended dataset from the summer of 2014 obtained by the authors of this paper, with rare coverage of a severe atmospheric cold front associated with a summertime arctic cyclone passing across the region. We examine the dynamics with a numerical simulation using the Finite Volume Community Ocean Model (FVCOM), and a subsequent forcing-response Empirical Orthogonal Function (fr-EOF) analysis. This study aims to provide a synthesized picture of the weather-driven exchange flows through multiple inlets of a micro-tidal lagoon in the Arctic.

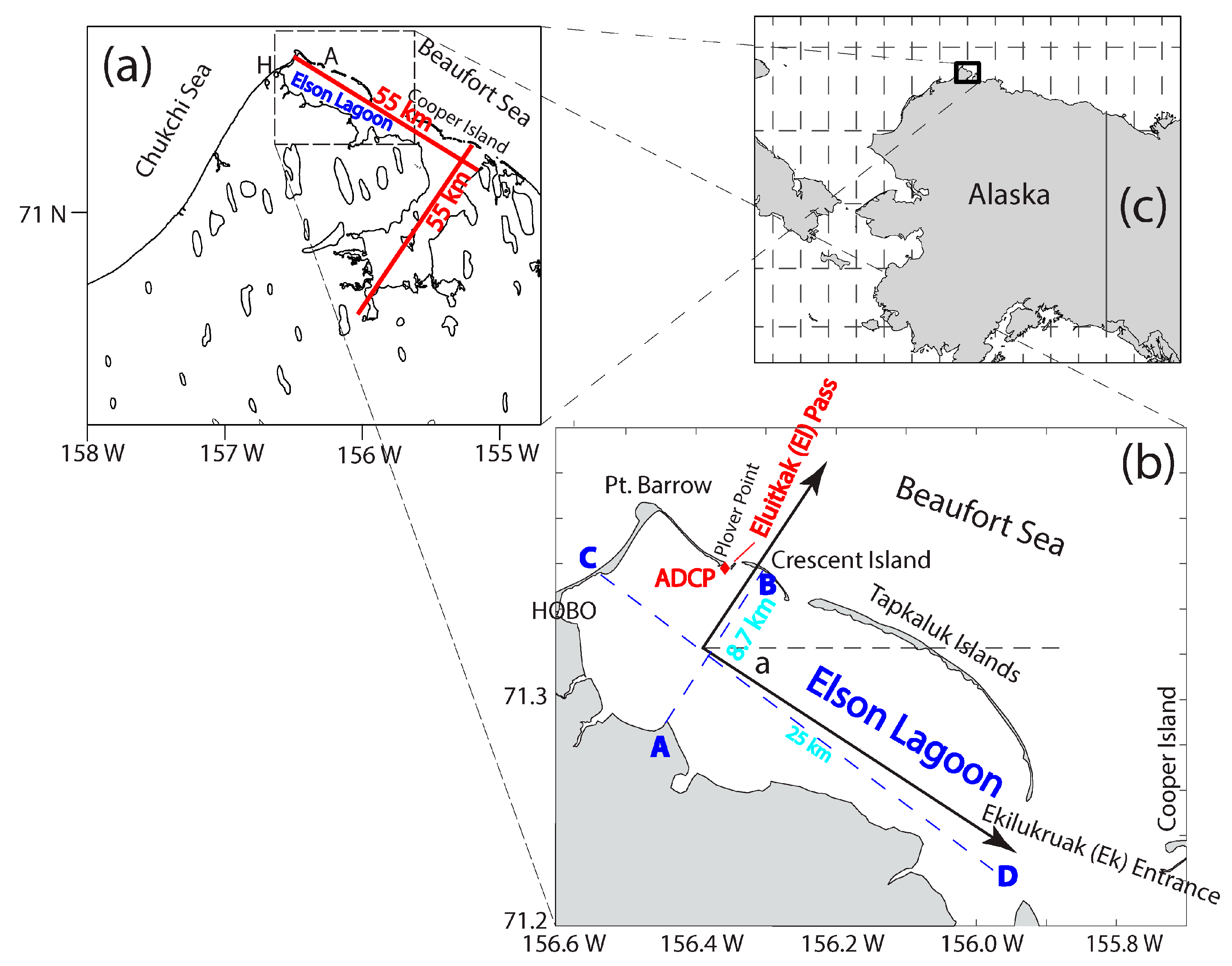
2. Study Site

The study occurred in Elson Lagoon, located on the northernmost coast of the United States (Figure 1). Elson Lagoon is very shallow, with a mean depth of ~2–3 m. It encompasses two connected outer and inner lagoons with the shape of a flipped “L” (Figure 1a), and a length of ~55 km in both directions (Figure 1a). The outer lagoon is approximately rectangular, with a width of ~8.7 km (point A to point B), and a length of ~25 km (point C to point D, Figure 1b). The lagoon is located near the confluence of the Chukchi and Beaufort Seas at the northwestern-most corner of Alaska, roughly bounded within 156°36′ W, 155°54′ W, 71°12′ N, and 71°23′ N. This lagoon is oriented in the northwest-southeast direction, with an axis of ~−30° from the true west-east direction (Figure 1b). All the inlets are on the side of the Beaufort Sea, with the widest width being ~7 km between barrier islands. There is a relatively deep channel at the northwestern corner of the lagoon, Eluitkak Pass, that has a width of ~300 m and a maximum water depth of ~16 m [45]. A chain of islands located east and southeast of Eluitkak Pass acts as the seaward boundary of the lagoon connecting to the coastal ocean. These islands include the Crescent, Tapkaluk, and Cooper Islands. The inlet between Crescent and Tapkaluk Islands is about 700 m wide, while the inlet between Tapkaluk and Cooper Islands (the Ekilukruak Entrance) is 7.1 km wide. Tide in the region is semi-diurnal with very small amplitudes—the tidal range is ~0.2 m.

3. Methods

After initial observations made in 2013 [45], we conducted additional measurements in Elson Lagoon in the summer of 2014, during which an arctic cyclone passed over the region and our data captured the weather-induced flows. In this study, the new data were analyzed and used to validate the FVCOM model to simulate the weather-driven circulation between 15 July and 31 August 2014. Analysis of the FVCOM model results was performed using a force-response Empirical Orthogonal Function (fr-EOF) analysis [37]. The fr-EOF analysis allowed us to examine the wind effects on water transport within this multiple-inlet system. The FVCOM model included the tidal constituents as input at open boundaries and the wind stress from the weather systems. The detailed bathymetry data around the major inlet area and in the lagoon for the FVCOM were obtained by our own observations.

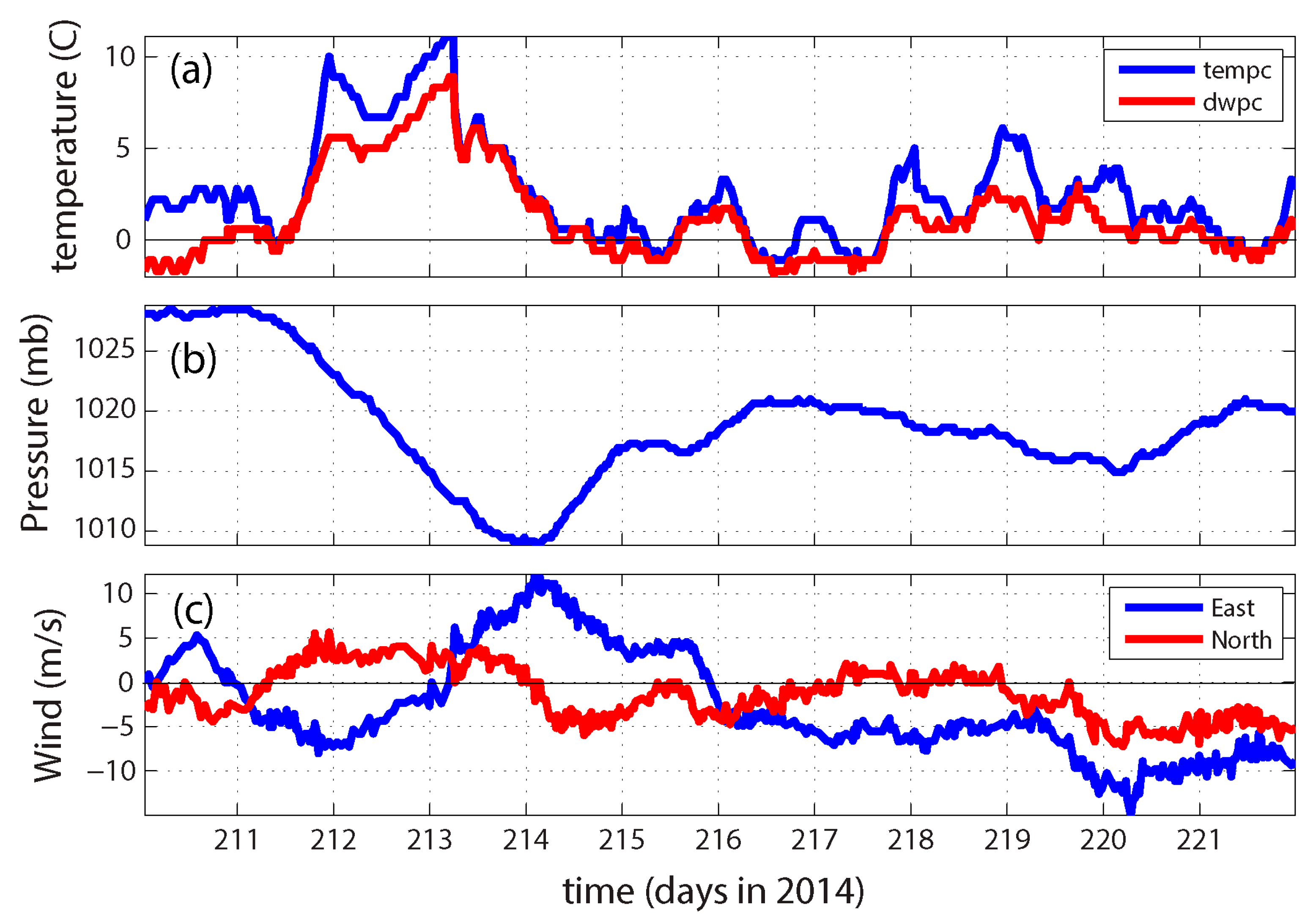
3.1. Observations

The observations were conducted with a bottom-mounted RDI 1200 kHz acoustic Doppler current profiler (ADCP). The ADCP was moored on the bottom with upward-facing transducers in approximately 13 m of water. The total weight of the mooring was about 30 kg. The ADCP was deployed at (~71.3593° N, 156.3561° W) on 29 July 2014 (Figure 1,

Table 1. Information about the ADCP Deployment.

Deploy #	Time Valid Data Starts	Deployed at Longitude Latitude	Time Valid Data Ends	Recovered at Longitude Latitude	Data File Name	Location of Deployment
1	29 July 2014	156.3561° W 71.3593° N	8/3, 01:29	-	Elson2014-1	Eluitkak Pass
2	4 August 2014	156.3561° W 71.3593° N	8/18, 21:01	156.3960° W 71.3749° N	Elson2014-2 Elson2014-3	Eluitkak Pass

), very close to the actual deployment in 2013 [45]. It was retrieved on August 3 and redeployed at a slightly different location (71.3597° N, 156.3538° W) a day later, on 4 August. The second deployment site was a little shallower (~11 m) and located closer to the outside of the inlet. On 19 August, this deployment was recovered at a different location (71.3749° N, 156.3960° W, Table 1), about 2.2 km northwest of the original site outside of the lagoon on the inner shelf where the depth was about 5 m. The area was ice-free until about 13 August, when a storm brought floating ice into the lagoon and then out. As the ice moved out of the lagoon, the instrument was dragged by floating ice for more than 2 km onto the shelf. The first deployment was set up to sample every 80 s, with 45 samples every hour. The data were saved hourly with a vertical bin size of 1.0 m. The first bin with velocity data was 1.53 m above the bottom. During the second deployment, the setup was changed to sample every 6 s. An average was calculated every 50 samples to produce the ensemble data every 5 min. For this study, we excluded the ADCP data after the instrument was moved by sea ice on 9 August. The event was identified by examining significant departures from the relatively consistent pitch and roll sensor data. Thus, the data included two periods from 29 July to 3 August and from 4 August to 9 August. The weather data used in this analysis were recorded at the Wiley Post-Will Rogers Memorial Airport in Utqiaġvik, Alaska at 156.7922° W, 71.2826° N. In the following, for simplicity, we used either the actual date or the consecutive count of days in 2014 (i.e., the short version of Julian date), e.g., 30 July 2014, corresponds to Day 211 of 2014 (the first day being 1 January 2014), and 8 August is Day 220.

3.2. FVCOM Simulation

The unstructured grid FVCOM was used for a numerical simulation of wind-driven flows in Elson Lagoon. FVCOM [46] is suitable for simulating hydrodynamic processes in coastal and estuarine waters [11,26,47,48,49,50] as it has an advantage of satisfying volume conservation and a better resolution of complex coastlines with multiple inlets and variable bathymetry. This model was successfully used to simulate basin–coastal interaction processes in the Arctic Ocean, evident in [51,52,53,54,55]. The governing equations and numerical schemes of the FVCOM model are described in [46]. The bathymetric data used in the model were a combination of the dataset from the National Centers for Environmental Information (formerly National Geophysical Data Center) and our own measurements. The critical water depth data inside the lagoon and in the channel (the Eluitkak Pass) were obtained by the authors. The source of bathymetry data elsewhere in the model (basically the Beaufort Sea and Chukchi Sea) was from the HYbrid Coordinate Ocean Model (HYCOM; hycom.org) and NOAA’s ETOPO1 dataset (https://sos.noaa.gov/catalog/datasets/etopo1-topography-and-bathymetry/, accessed on 1 March 2024), a 1 arc-minute global relief model of Earth’s surface that integrates land topography and ocean bathymetry. The HYCOM datasets with water level and flow were interpolated onto our model grid for the initial condition and boundary condition of the model.

In the model, the vertical eddy viscosity was determined by the level-2.5 (MY-2.5) turbulent closure scheme [56] modified by [57]. The surface and bottom boundary conditions included the wind and bottom stresses, dependent on the quadratic law. The surface drag coefficient $C_{da}$ was calculated based on [58], as shown below:

$$C_{da}=\left\{\begin{array}{c}\left(0.49+0.065\times 11.0\right)\times {10}^{-3}, U_{10}<11.0 \mathrm{m}/\mathrm{s}\\ \left(0.49+0.065\times \left|U_{10}\right|\right)\times {10}^{-3}, 11.0\le U_{10}\le 25.0 \mathrm{m}/\mathrm{s}\\ \left(0.49+0.065\times 25.0\right)\times {10}^{-3}, U_{10}>25.0 \mathrm{m}/\mathrm{s}\end{array}\right.$$

(1)

The bottom drag coefficient $C_d$ was determined by the following equation:

$$C_d=\max (\frac{k^2}{\ln {\left(\frac{z_{ab}}{z_0}\right)}^2},0.0025)$$

(2)

where k is the von Karman constant (0.4), $z_0$ is the bottom roughness, and $z_{ab}$ is the height above the bottom.

The wind velocity time series and atmospheric pressure were specified using the weather data at the airport in Utqiaġvik and assumed spatially uniform in the computational domain.

The simulation period was from 15 July to 31 August 2014, covering the observational period. The mesh had 15,384 nodes and 29,015 cells with the highest resolution of ~20 m in the horizontal and 40-sigma layers in the vertical (Figure 2). The model used a 0.2 s external time step and a 1.0 s internal time step.

3.3. The fr-EOF Analysis

Previous studies have shown that the subtidal through-flows and exchange flows have predictable patterns, given the wind forcing [27,37]. Using the model output, we conducted an fr-EOF analysis similar to that used in [37] in a subtropical system. The fr-EOF analysis includes vectors representing forcing factors in the temporal-spatial data scatter matrix to correlate the characteristics of the data variability with forcings [32,59]. The eigenvectors of the data scatter matrix had information on the variability of forcings by the modes of temporal-spatial data. To resolve the empirical modes, we selected eight transects inside the lagoon or across the inlets (Figure 3). The model-simulated velocity field was integrated across these transects to yield the total volume transport through each transect. These transport time series were then low-pass filtered using the 40-h cut-off and 6th order Butterworth IIR filter. The fr-EOF analysis is similar to the conventional method [59], and the low-pass filtered (subtidal) transport and wind velocity components are grouped to construct the data matrix Z’:

$$Z’=\left(\begin{array}{cc}\begin{array}{c}\begin{array}{ccc}{v}_{tr1}\left(t_1\right)& v_{r2}\left(t_1\right)& \dots \\ v_{r1}\left(t_2\right)& v_{r2}\left(t_2\right)& \dots \\ ⋮& ⋮& ⋮\end{array}\\ \begin{array}{ccc}{v}_{r1}\left(t_n\right)& v_{r2}\left(t_n\right)& \dots \end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}{v}_{r8}\left(t_1\right)& {100\times W}_{E10}\left(t_1\right)& 100\times W_{N10}\left(t_1\right)\\ v_{r8}\left(t_2\right)& {100\times W}_{E10}\left(t_2\right)& {100\times W}_{N10}\left(t_2\right)\\ ⋮& ⋮& ⋮\end{array}\\ \begin{array}{ccc}{v}_{r8}\left(t_n\right)& {100\times W}_{E10}\left(t_n\right)& {100\times W}_{N10}\left(t_n\right)\end{array}\end{array}\end{array}\right)$$

(3)

in which $v_{r1}$, $v_{r2}$, $\dots v_{r8}$ are the low-pass filtered cross transect volume transport for each of the eight transects, respectively; $W_{E10}$ and $W_{N10}$ are the east and north components of the low-pass filtered wind velocity vectors at the 10-m height above the sea level, respectively; $t_1$, $t_2$, …, $t_n$ are times for the first, second, …, and n-th samples, respectively. The wind velocity components were multiplied by 100 because the transport and wind velocity had disparate values. Multiplying by 100 made them more similar in magnitude, so they were “equally considered” in the matrix. It should be noted that the variables in the data matrix do not have to have the same unit. The data matrix was then de-meaned for each column to yield the mean data matrix Z. The data scatter matrix was then constructed by S = Z^TZ. The eigenvalues and associated eigenvectors of S could then be calculated for the EOF modes and the percentage of variability for each mode.

4. Results

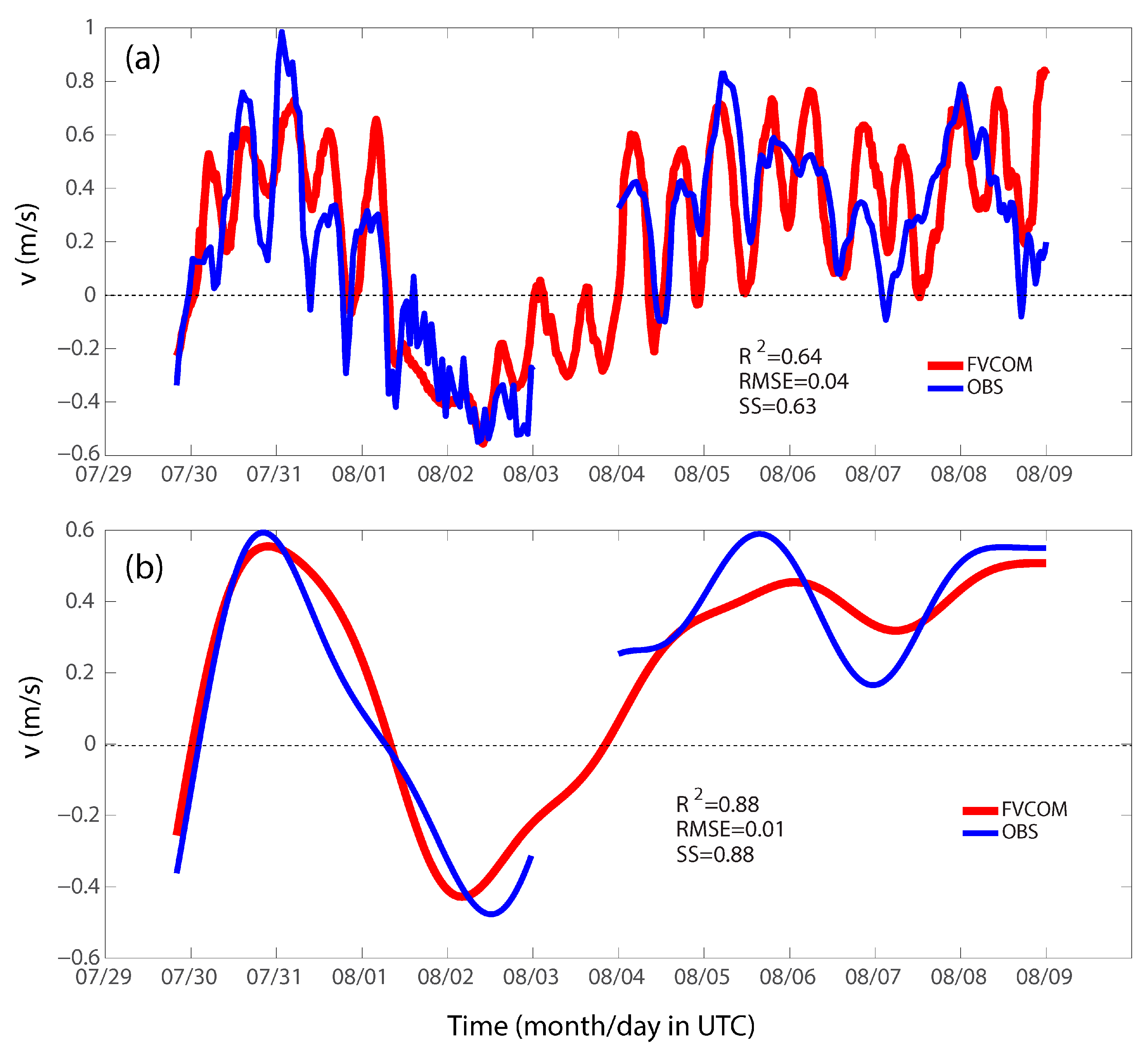
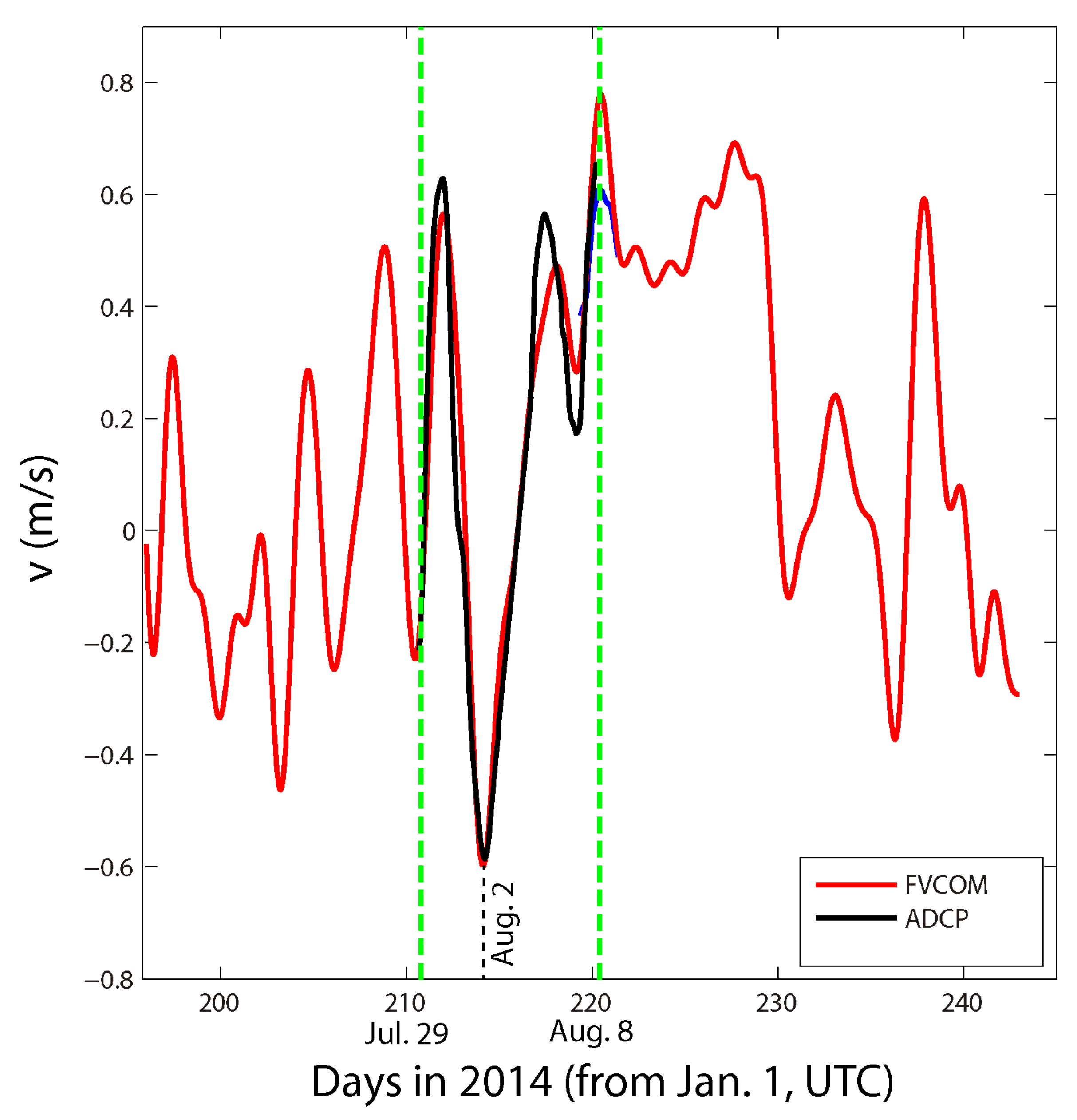
4.1. FVCOM Model-Data Comparison

The FVCOM-simulated velocity was compared with the observed velocity. The simulated velocity was chosen from the model grid point closest to the site of the ADCP deployment. The model reproduced both tidal and subtidal signals. As a general practice, we calculated the model skill score as defined by:

$$SS=1-\frac{\sum _{i=1}^N{\left(v_m-v_o\right)}^2}{\sum _{i=1}^N{\left(v_o-\overline{v_o}\right)}^2}$$

(4)

in which $v_m$, $v_o$, and N are the modeled velocity, observed velocity, and the total number of time series data points, respectively. The overall time series comparison yielded a skill score of 0.63 (Figure 4a). According to the definitions in previous studies [60,61,62], this skill score value corresponds to the “very good” category for the model performance. If only the subtidal signal was examined (i.e., after 40-h low-pass filtering), the skill score would increase to 0.88 (Figure 4b), which is in the “excellent” category. Note that there was a gap in the observations between the first and second deployments in 2014. The calculation of the skill score excluded this data gap.

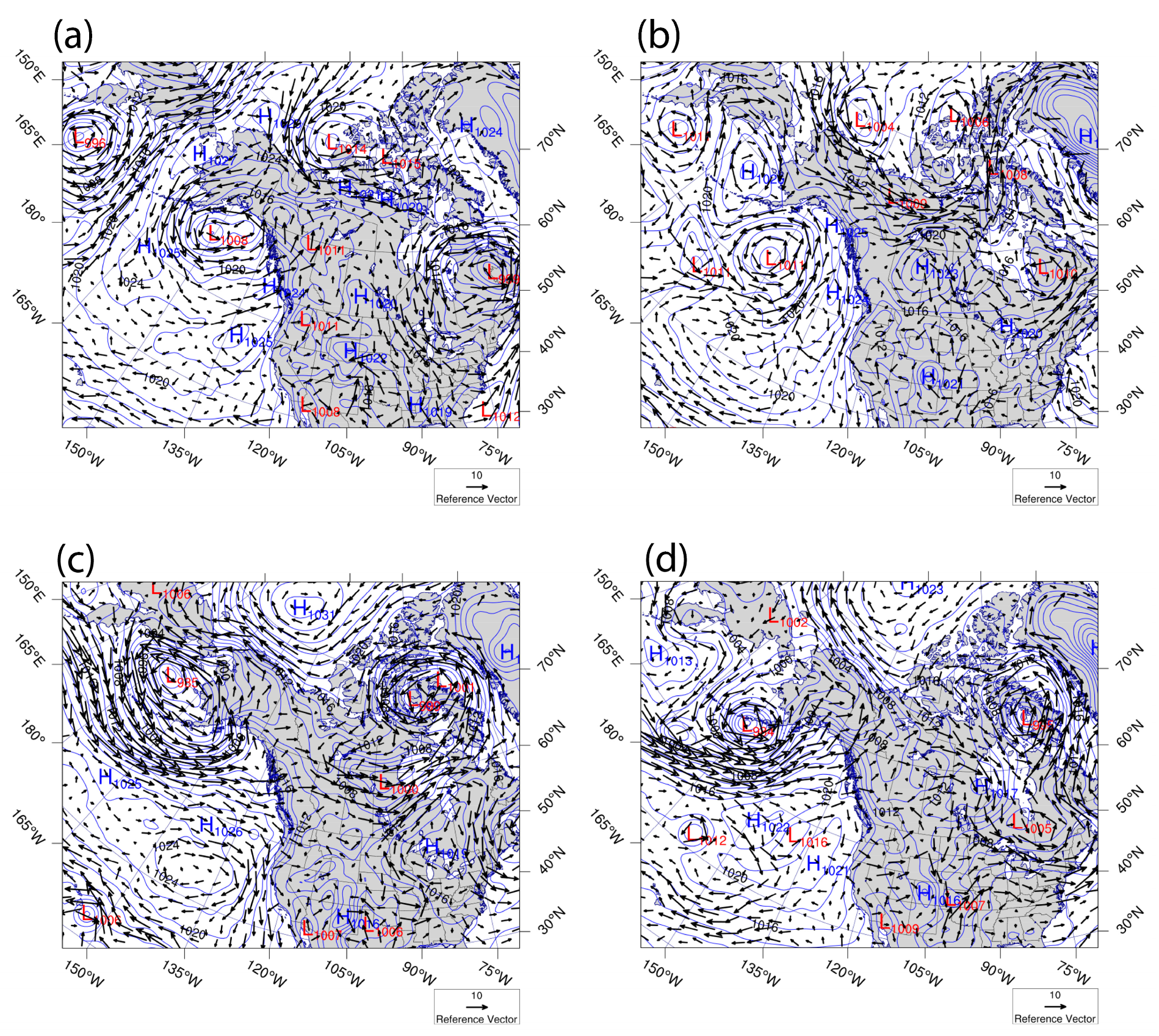
4.2. Weather Conditions and Inlet Flows

It can be seen from Figure 4a,b that most (71%) of the time during the deployment of the ADCP, the flow was from the lagoon to the ocean (positive flows). This finding is consistent with [45] for the observations in 2013 that reported that during 73–80% of the time the net flow was out of the lagoon from the western inlet (the Eluitkak Pass) over about three months. The asymmetric net flow was due to the wind effect associated with the weather systems including the arctic cyclones (low pressure systems) and the Beaufort High pressure system, which produces a persistent easterly wind in the study region. On 30 July (day 211), an arctic cyclone was over the western Canadian Archipelago, northeast of the study region, while a high-pressure system was over the study site (Figure 5a). These two weather systems led to an onshore wind that caused a counter-wind flow at Eluitkak Pass, confirming the findings in [45]. On 31 July or day 212, the high-pressure system was just north of the study site, at which the wind was from the east-southeast. It was a transient period during which the outward flow was diminishing as another low-pressure system moved into the region. The air pressure dropped to a minimum of 1009 mb at the beginning of Day 114 or 2 August (Figure 6b) when the wind became westerly and reached its maximum of ~12 m/s (Figure 6c).

This westerly wind with a maximum speed of ~12 m/s subsequently changed to northwesterly and produced an inward flux through the Eluitkak Pass (Figure 7). This feature of wind variation was also consistent with the 2013 data [45]. Before 8 August (Day 220), i.e., toward the end of the second segment of the data, there had been a strong easterly wind due to the intensive polar high-pressure system located over the Beaufort Sea (the Beaufort High, Figure 5c). This high-pressure system pushed water out of the lagoon through the western inlet, as shown by the velocity data (Figure 7). From August 8 through 18, the high-pressure system located in the Beaufort Sea region was almost stationary (Figure 5d). The persistent easterly and then southeasterly winds contributed to the movement of water in the lagoon from the east or southeast toward the west or northwest, resulting in a water setup against the western end of the lagoon and a continuous (~10 days) outward flow through Eluitkak Pass as verified by the FVCOM model results (Figure 7).

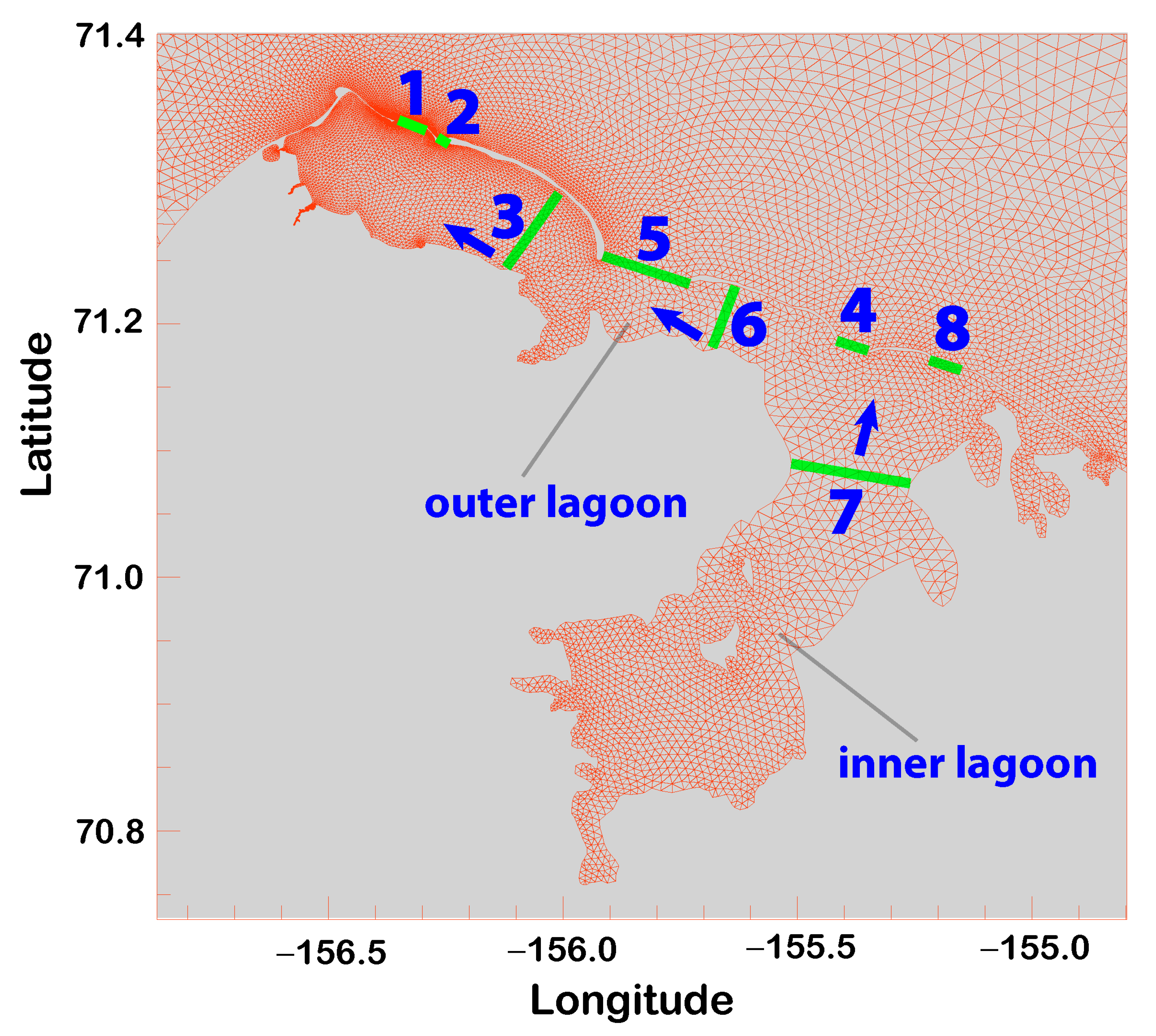
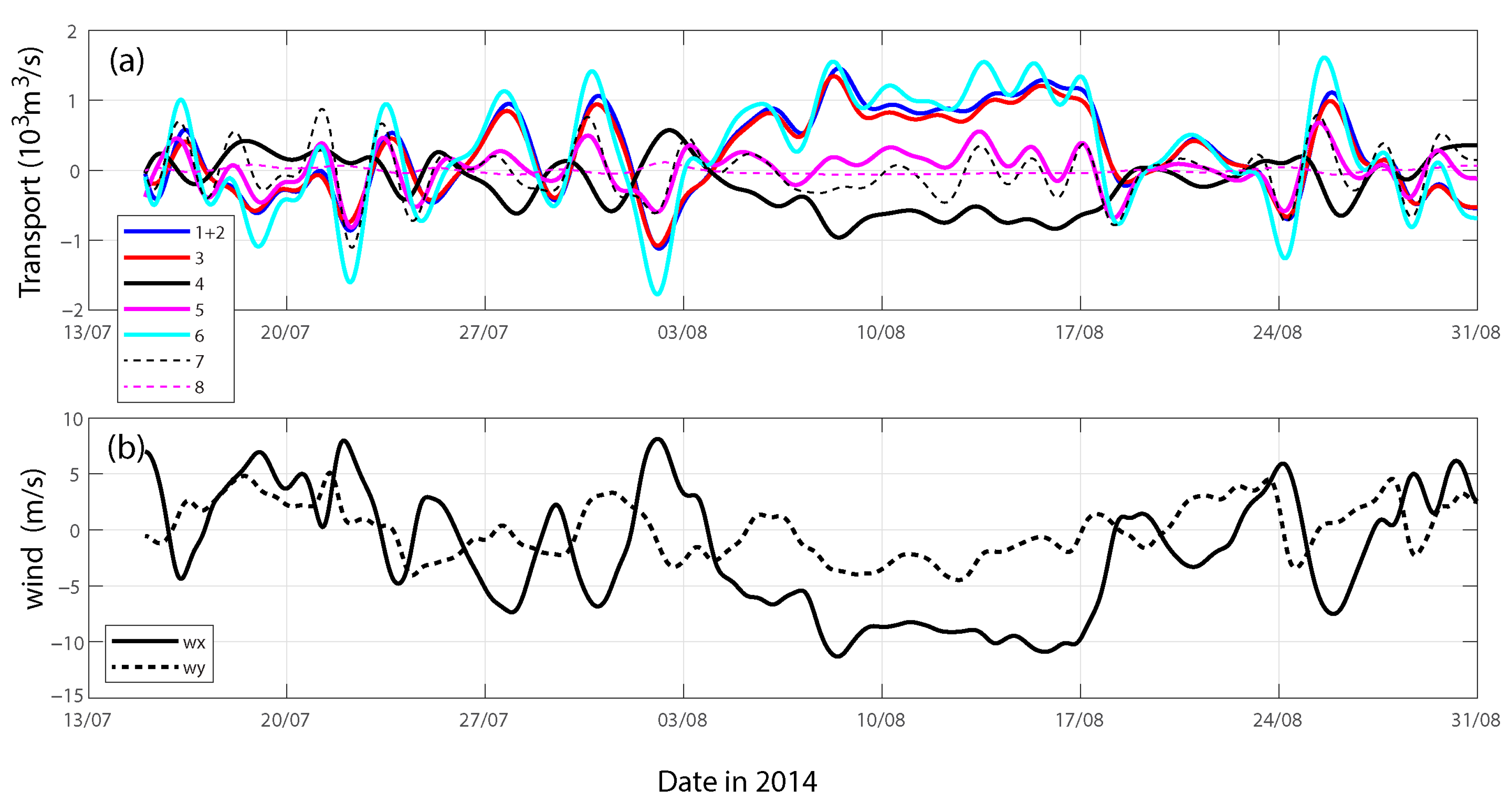
4.3. Transport across Eight Transects

The transport values through the eight selected transects (Figure 3), calculated from the FVCOM results, are shown in Figure 8a with the corresponding east and north wind velocity components for the same period shown in Figure 8b. When water flowed out of the lagoon to the coastal ocean, the sign was positive (for Transects 1, 2, 4, 5, and 8). For Transects 3, 6, and 7 across the channel, the definition of a positive transport direction is shown in Figure 3, i.e., a transport toward the northwest is defined as positive for Transects 3 and 6; in transect 7, a positive transport is defined as northeastward.

Because Transects 1 and 2 are very close together and Transect 2 only has a minimal total transport (only about 4% of that of Transect 1), we summed them together (Figure 8a). The correlation coefficient between the transport estimated through Transect 1 and that through Transect 2 is 0.973 (

Table 2. Correlation coefficients for transports and wind velocity components. T1 through T8 are the transports through Transects 1 through 8, respectively. The wind velocity components in the east and north directions are w_x and w_y, respectively. The last two variables, w_xr and w_yr, are the rotated wind velocity components so that they are the along-channel and cross-channel components, respectively.

Correlation Coefficient	T2	T3	T4	T5	T6	T7	T8	wx	wy	wxr	wyr
T1	0.973	0.996	−0.918	0.592	0.943	0.181	−0.910	−0.974	−0.276	−0.977	−0.792

), indicating that they almost always follow each other. During these 1.5 months of simulation, there was a total of 1.58 × 10⁹ m³ of water flowing from the lagoon to the coastal ocean and 5.56 × 10⁸ m³ of water flowing from the ocean into the lagoon through Transects 1 and 2. During this period, approximately 65% of lagoon water volume transported out to the ocean and 35% was transported into the lagoon. The flow was out of the lagoon from Transect 1 approximately 61% of the time, which was about the same amount of time the flow was through Transect 3 toward the northwest. The transport through Transect 3 was essentially the same as that through Transects 1 and 2 (the red and blue lines in Figure 8a are almost on top of each other). As a result, the correlation coefficient between the transports through Transect 1 and Transect 3 has a high value of 0.996 (Table 2).

The simulated transport through Transect 4 is almost out of phase with that through Transect 1–the correlation coefficient is negative: −0.918. It was similar to the correlation coefficient between the transport through Transect 1 and Transect 8 (correlation coefficient is −0.910, Table 2). This finding confirms the result in [27] that the transport through the two ends of the lagoon is opposite in direction (into or out of, forming a through flow). In [27], an associated result was that the middle inlet had less correspondence or correlation with both inlets at the ends. Indeed, the correlation coefficient between the transports through Transect 1 and Transect 5 is a relatively lower value of 0.592 (Table 2), but it is still a positive correlation. It is particularly striking because Transect 5 is the widest, and yet the transport through it is mostly smaller (Figure 8a) than those through the end inlets (the one in the northwest of Eluitkak Pass and the one in the southeast end—the Transects 4 and 8). This result is consistent with [27] that the middle inlet tends to have a relatively smaller transport. In terms of total transport, Transect 6 has the largest magnitude. This transport through Transect 6 should be consistent with the sum of the transports through Transects 1, 2, and 3 for the most part (when Transect 3 and Transect 1 are in phase). In contrast, Transect 7 has smaller transport values than Transect 1 and is much less correlated with any other transect, and the correlation coefficient between Transect 1 and 7 is a low value of 0.181 (Table 2). Transect 8 is very similar to Transect 4 as they are close together, even though the transport through Transect 8 is minimal due to its very shallow water (less than half a meter). The conclusion is that the constricted inlet (extremely shallow) has much reduced connectivity in the lagoon system.

The correlation between the east wind velocity component and the transport through Transect 1 was −0.974, indicating a strong negative correlation. It means that under easterly wind (negative), the transport at Eluitkak Pass is outward. Under westerly wind, the transport is inward and is consistent with the water level gradient. Under easterly wind, the western lagoon has a higher water level than outside because the coastal ocean is open and unable to pile up as much water mass as inside the lagoon. This wind-induced water setup and water level difference between the inside and outside of the inlet drives water out of the lagoon at the western end.

In contrast, the correlation between the north wind velocity component and transport through Transect 1 was much lower, and negative (−0.276). To examine the effect of the along-channel wind component and the cross-channel wind component on the transport at Eluitkak Pass, we rotated the wind vector by −30 degrees so that w_xr is in the along-channel direction (positive toward the southeast and negative toward the northwest); w_yr is in the cross-channel direction (positive toward the outside of the lagoon, and negative toward the inside). After the rotation, we can see that the transport through Transect 1 has an even more significant negative correlation with the along-channel wind velocity component (−0.977), while the transport has a clear negative correlation with the cross-channel wind velocity component (−0.792). This result is a clear indication of a counter-wind transport at the Eluitkak Pass, further confirming the previous findings based on the 2013 data [45].

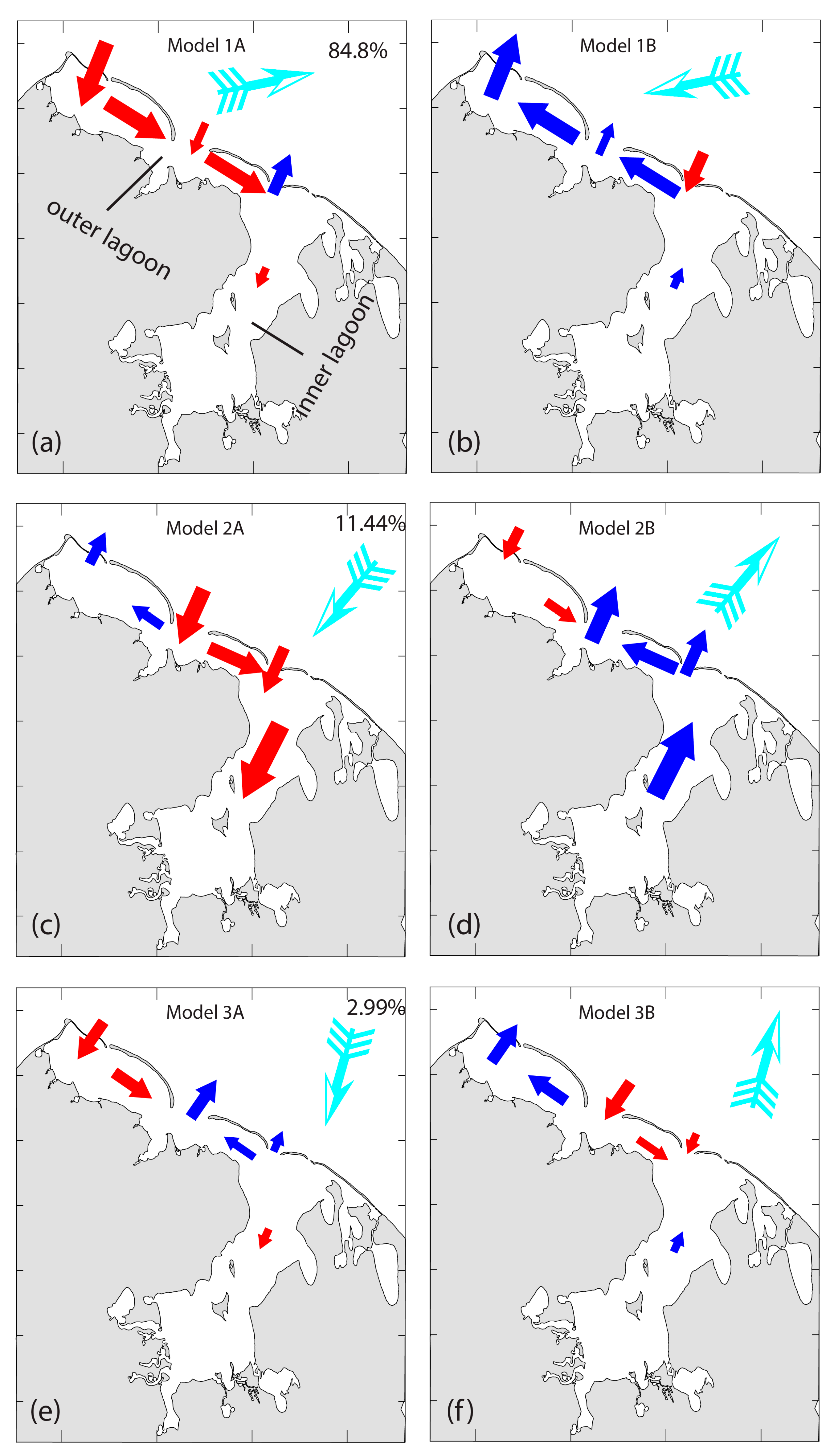
4.4. Modes from fr-EOF Analysis

The EOF analysis yields eight modes with the normalized eigenvalues representing the percentage of variability of 84.8%, 11.4%, 2.99%, 0.38%, 0.19%, 0.14%, 0.04%, 0.016%, 0.009%, 0.00022%, respectively. We will only discuss the first three modes as the other modes are insignificant. The first three eigenvectors are:

$${\mathrm{E}}_1=\left(\begin{array}{c}-0.4507\\ -0.0153\\ \begin{array}{c}-0.4260\\ 0.2524\\ \begin{array}{c}-0.1504\\ -0.5899\\ \begin{array}{c}-0.0755\\ 0.0286\\ \begin{array}{c}0.4131\\ 0.0620\end{array}\end{array}\end{array}\end{array}\end{array}\right), {\mathrm{E}}_2=\left(\begin{array}{c}0.1303\\ 0.0013\\ \begin{array}{c}0.1159\\ -0.3721\\ \begin{array}{c}-0.3935\\ -0.3149\\ \begin{array}{c}-0.7085\\ -0.0252\\ \begin{array}{c}-0.2046\\ -0.1806\end{array}\end{array}\end{array}\end{array}\end{array}\right), {\mathrm{E}}_3=\left(\begin{array}{c}-0.2362\\ -0.0234\\ \begin{array}{c}-0.2006\\ 0.0849\\ \begin{array}{c}0.2675\\ 0.1339\\ \begin{array}{c}-0.0713\\ 0.0060\\ \begin{array}{c}-0.1087\\ -0.8887\end{array}\end{array}\end{array}\end{array}\end{array}\right)$$

(5)

The first eight elements of the above three eigenvectors provide the sign and relative magnitude of the transport through the eight transects. In comparison, the last two elements of each of the above eigenvectors provide the sign and relative magnitude of the wind velocity components in the east and north directions, respectively. The corresponding transport and wind patterns are shown in Figure 9.

First Mode. The first mode accounts for 84.8% of the variability; its positive phase is shown by Figure 9a and the negative phase by Figure 9b. This mode corresponded to a roughly westerly (Figure 9a) or easterly (Figure 9b) wind. When the wind is westerly, the transport at Eluitkak Pass is inward, while the transport at the eastern end (Transects 4 and 8, Figure 3) is outward, and the transport in the outer lagoon is toward the southeast. The transport in the inner lagoon is small. The transport through the middle inlet (Transect 5) is into the lagoon, having the same sign as that through Transect 1, but with a smaller magnitude. When the wind is easterly, the transport at the Eluitkak Pass is outward, and the transport at the eastern end is inward, and as a result, the transport in the outer lagoon is toward the northwest. The transport through Transect 5 is out of the lagoon.

Second Mode. The second mode explained 11.4% of the variability. Its positive phase is shown in Figure 9c and the negative phase in Figure 9d. This mode corresponded to a wind roughly perpendicular to the coastline, i.e., in either the onshore (Figure 9c) or offshore directions (Figure 9d). When the wind is toward the shore, the transport at Eluitkak Pass is against the wind (outward), while the transport at the eastern end (Transects 4 and 8, Figure 3) is in the direction of the wind (inward). In contrast to the first mode, the transport through the middle inlet (Transect 5) is now with the wind as well, or into the lagoon, but with a greater magnitude than the transport through Transect 1. Consequently, transport in the outer lagoon diverges at the position of the middle inlet (Transect 5) so that the upper (northwestern) part has a northwestward transport while the lower (southeastern) part has a southeastward transport. The transport in the inner lagoon is in the direction of the wind and is relatively large, because the wind is in the direction of the major axis of the inner lagoon. For the negative phase of this mode, the wind is toward the offshore direction, and the transport directions are all reversed. This mode corresponds to a counter-wind flow pattern at the deepest inlet (Eluitkak Pass), and the shallower inlets all have transport in the direction of the wind.

Third Mode. The third mode explained only 2.99% of the variability. This mode corresponded to a roughly northerly wind (Figure 9e) for its positive phase and a southerly wind for its negative phase (Figure 9f). For this mode, when the wind is roughly northerly, the transport at Eluitkak Pass is inward, while the transport at the eastern end (Transects 4 and 8, Figure 3) is outward, with a smaller magnitude than that at Eluitkak Pass. The transport at the middle inlet is against the wind. The along-channel transport at the outer lagoon near the central inlet (Transect 5) is convergent. For the negative phase of this mode, the wind is roughly southerly, and the transport directions all reverse.

As in all EOF analysis, the coefficients for these empirical modes are functions of time (Figure 10), with magnitudes representing the importance of each at different times. The actual transport patterns are always a combination of these three modes, and therefore we rarely see the transport patterns described by only a single mode. We do see it, however, when one mode is dominant. For example, we can see episodes when the first mode’s coefficient has a magnitude much greater than those for Modes 2 and 3, during which time we can say that Mode 1 is much more important than the other modes.

4.5. Conceptual Model for Counter-Wind Flows

To further examine the wind-driven flows in a lagoon with more than one inlet, a simplified conceptual model is examined. This model provides a first-order estimate of exchange flows driven by wind based on a general consideration of mass and momentum conservations without resolving the details of the flow field. The model is for a bay with two inlets on the same side of the coastline adjacent to each other (Figure 11). For simplicity, here we only include two inlets that are parallel to each other (denoted as 1 and 2 in the subscripts for the variables). The x-axis is defined to be in the direction of the channel and starts from 0 at the mouth to L at the head (so that the length of the bay is L). In the following the definitions of mathematical symbols are given for convenience.

Definition of Symbols:

$b_{\mathrm{1,2}}$—width of inlets 1 and 2, respectively;

$u_{\mathrm{1,2}}$—depth-averaged velocity in inlets 1 and 2, respectively;

${\overline{u}}_{\mathrm{1,2}}$—cross-inlet averaged and depth-averaged velocity in inlets 1 and 2, respectively;

$u$—depth-averaged velocity in either inlet 1 or 2;

${∆\zeta }_{\mathrm{1,2}}$—water level difference between the end of the bay and the mouth of the bay at inlets 1 and 2, respectively;

$∆\zeta$—water level difference between the end of the bay and the mouth of the bay;

$h_{\mathrm{1,2}}$—depth of inlets 1 and 2, respectively;

$\tau , {\tau }_b$—wind stress (a constant) and bottom stress;

$L$—length of the channel;

$f_p,f_w,f_b$—pressure gradient force, wind-stress, and bottom friction, respectively;

$\rho$—water density;

$C_D, \beta$—bottom drag coefficient and friction coefficient;

At steady state, the velocities are constant and therefore $\frac{\partial }{\partial t}=0$; therefore, the momentum balance would lead to:

$$0=f_p+f_w+f_b$$

(6)

which is applicable to both inlets. This can be more specifically expressed as:

$$0=-g\frac{∆\zeta }{L}+\frac{\tau }{\rho h}-\frac{{\tau }_b}{\rho h}$$

(7)

in which:

$${\tau }_b=\rho C_{D}u\left|u\right|$$

(8)

The quadratic bottom stress can be replaced by a linear friction for the conceptual model:

$$\frac{\tau }{\rho h}=\frac{\beta u}{h}$$

(9)

Applying this to the momentum balance equation for each inlet, we have:

$$0=-g\frac{{∆\zeta }_1}{L}+\frac{\tau }{\rho h_1}-\frac{\beta {\overline{u}}_1}{h_1}, 0=-g\frac{{∆\zeta }_2}{L}+\frac{\tau }{\rho h_2}-\frac{\beta {\overline{u}}_2}{h_2}$$

(10)

By subtraction of the above two equations, we obtain:

$$\frac{{\overline{u}}_2}{h_2}-\frac{{\overline{u}}_1}{h_1}=\frac{\tau }{\rho \beta }\left(\frac{1}{h_1}-\frac{1}{h_2}\right)+\frac{g}{L}\frac{{∆\zeta }_1-{∆\zeta }_2}{\beta }$$

(11)

The volume conservation requires that:

$$h_1{b}_1{\overline{u}}_1+h_2{b}_2{\overline{u}}_2=0$$

(12)

which yields the conceptual model solution for depth and width averaged velocity at the two inlets, respectively,

$${\overline{u}}_1=-\frac{h_2{b}_2}{h_1{b}_1}{\overline{u}}_2$$

(13)

$${\overline{u}}_2=\alpha \left[\frac{\tau }{\rho \beta }\left(1-\frac{h_2}{h_1}\right)+\frac{g{h}_2\left({∆\zeta }_1-{∆\zeta }_2\right)}{L\beta }\right]$$

(14)

in which:

$$\alpha =\frac{1}{1+{\left(\frac{h_2}{h_1}\right)}^2\frac{b_2}{b_1}}$$

(15)

Obviously, the flows in the two inlets under steady state must have opposite signs (as seen from Equation (13)). It should be noted that when the wind stress is parallel to the x-axis, the water level contour lines should be perpendicular to the wind direction, i.e., roughly ${∆\zeta }_1$ and ${∆\zeta }_2$ are the same. Thus, we can take ${∆\zeta }_1~{∆\zeta }_2$. Therefore,

$${\overline{u}}_2~\alpha \frac{\tau }{\rho \beta }\left(1-\frac{h_2}{h_1}\right)$$

(16)

If the depth in the second inlet is deeper than that in the first inlet, i.e.,

$$h_2>h_1,$$

(17)

the flow in the deeper inlet must be opposite of the wind direction. This can also be explained from a vorticity point of view (the wind stress working on the water with different depths results in a vorticity tendency). In our case, the outer lagoon has several inlets, the westernmost inlet (Eluitkak Pass) is the deep inlet (~16 m) and the eastern inlet is much shallower (~1 m). As a result, Eluitkak Pass experiences counter-wind the most; both Mode 1 and Mode 2 show counter-wind at Eluitkak Pass, which accounts for approximately ~96% of the total variability.

5. Discussion

5.1. Significance of Study and Major New Findings

An observational campaign in the arctic lagoons is generally challenging because of the remote location, harsh environmental conditions, frequent severe weather, rough sea state, the lack of infrastructure, and very limited logistic support. Only small boats can be used and these rely on very rudimentary makeshift boat launches, which can be damaged by storms. Our moorings were once lost in a severe storm that almost ruined the entire project. As a result, the data from this arctic lagoon presented here are unique in capturing the impact of arctic weather systems.

Because of the lack of data, there have been very few numerical experimental studies on the hydrodynamics of such a coastal lagoon system—much of the arctic study has been heavily focused on the continental shelf, Bering Strait, and deep ocean basins. Part of the reason is that numerical models cannot be validated unless accurate bathymetry data are available which we were able to provide in Elson Lagoon for the model application.

In terms of the subject, this study deals with a meteorological setup that is different from those in the mid and low latitudes: the region is dominated by the arctic east wind regime as a limb of the Beaufort High pressure system. The competition between the passing arctic cyclones and the hovering Beaufort High pressure system makes the lagoon’s hydrodynamics unique, which has rarely been examined. The alternating high- and low-pressure systems provide a pulsing influence of the atmosphere to the arctic lagoons in the summer ice-free period, which is becoming longer as the arctic warming trend continues, making the impact of this meteorological tide even more important.

To date, there has been no study demonstrating the major modes of exchange flows in this system, or any arctic lagoon system, as presented here. The counter-wind flows through the narrow inlet were verified by observations, numerical modeling, and the conceptual model results, and are explained by the prevailing physical forcing determined in subsequent analysis. The identified modes have significant implications on the routes of exchange flows and subsequent impact on ecological processes and dynamics of the ecosystem.

5.2. Meteorological Tides

Migrating weather systems under the influence of large-scale atmospheric circulations such as the westerly winds, trade winds (in tropical regions), and arctic easterly winds, are often demonstrated by the alternating warm advections and cold advections and change in wind regimes. This in turn provides an alternating forcing to the coastal lagoons and estuaries, resulting in meteorological tides. These meteorological tides are shown as mainly subtidal oscillations of water level and associated exchange flows which are mostly within the spectrum of storm surges. In the present study, the migrating arctic cyclones and anti-cyclone (the high-pressure system over the Beaufort Sea region) produced the asymmetric meteorology-induced exchange flows that are more influenced by the easterly wind from the arctic high-pressure system. Our study is still quite preliminary due to the lack of longer time series of data.

5.3. Limitations and Future Studies

Given the harsh conditions in the Arctic and the lack of infrastructure, the data obtained are still limited in quantity and in covering a more complete spectrum of weather conditions. Secondly, our numerical model is a three-dimensional barotropic model without inclusion of the baroclinic circulation. The lagoon has a very small variability in salinity (1 PSU) during a week-long observational period; we anticipate that the shelf process might exhibit more influence of stratified flows. We expect that this study will prepare and motivate further research as the interest in climate change becomes greater. Future studies may focus on the long-term climate change, continued warming in the Arctic, and the ecological consequence of the increased weather system-related exchange flows through the coastal arctic lagoons.

6. Concluding Remarks

Because of the rapid warming of the Arctic Ocean and the increased length of the ice-free period each summer, it is imperative that we understand the response of the arctic estuaries and lagoons to such dramatic climate changes. An understanding of the hydrodynamics, including the exchange flows, is the first step which provides the basis for further investigation on the ecological impact. The lack of studies in the coastal semi-enclosed water bodies will hinder the attempt to understand better the fast-changing system and its impact on the global climate. This study attempts to illustrate the importance of attention on the exchange flow under the less-known changing arctic weather systems. Understanding the lagoon’s response to weather systems is a better approach compared to simply wind-driven circulations. The method is a combination of met-ocean observations, numerical simulation, fr-EOF analysis to the numerical model results, and a conceptual model. The major conclusions include:

(1)

Studies on the exchange flows at the multiple inlets of arctic lagoons must consider the wind variations as part of the arctic weather systems. Despite the complications of weather systems, the dominant Beaufort High (BH) is more common than the transient arctic cyclones. The BH provides a dominant easterly wind at the study site which pushes water into the lagoon (water setup) causing an outward flow at Eluitkak Pass, producing a counter-wind flow. The migrating arctic cyclone on the other hand, usually brings in a westerly wind over the lagoon and pushes the water out (water set-down) of the lagoon through the eastern inlets. This causes an inward flow at Eluitkak Pass, and also a counter-wind flow;

(2)

Three major exchange flow modes are identified by this study. The first two modes (accounting for a total of ~96% of the variability) are all counter-wind flows, consistent with the weather system-induced wind-driven flows as concluded in (1);

(3)

In addition to the water setup and set down by the direct wind forcing from the weather systems, the wind stress and water depth work together to generate a velocity shear and vorticity tendency. This vorticity effect produces the same type of exchange flow as the water setup and set-down mechanisms in this arctic lagoon. Together they produce an overwhelming counter-wind flow in Eluitkak Pass. In other lagoon systems, however, these two mechanisms may compete with each other, depending on the geometry, such as the orientations of the lagoon and inlets, and the wind directions.