Buckling Behavior of Stainless Wave-Shaped Pressure Hulls
Abstract
:1. Introduction
2. Materials and Methods
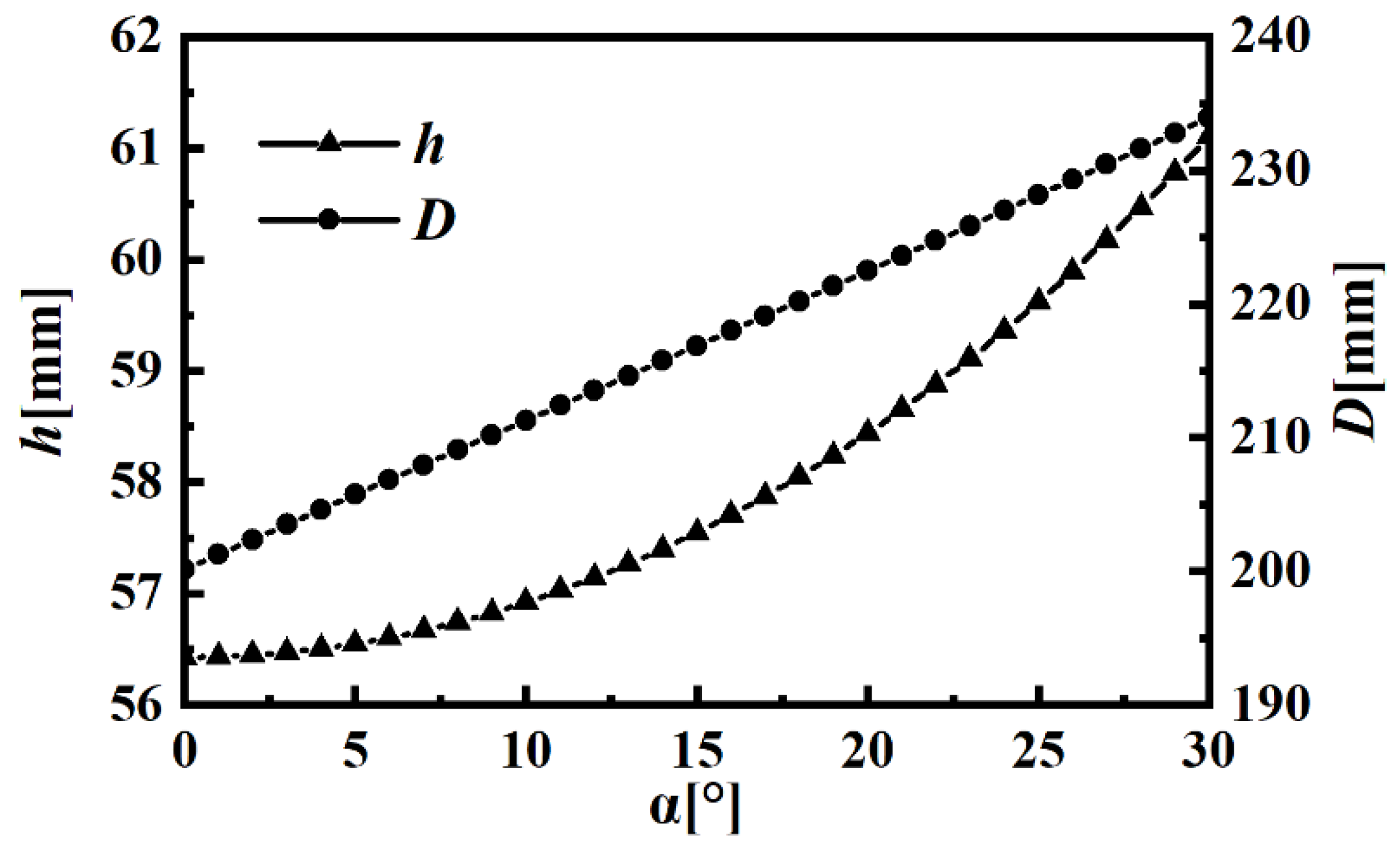
2.1. Problem Identification
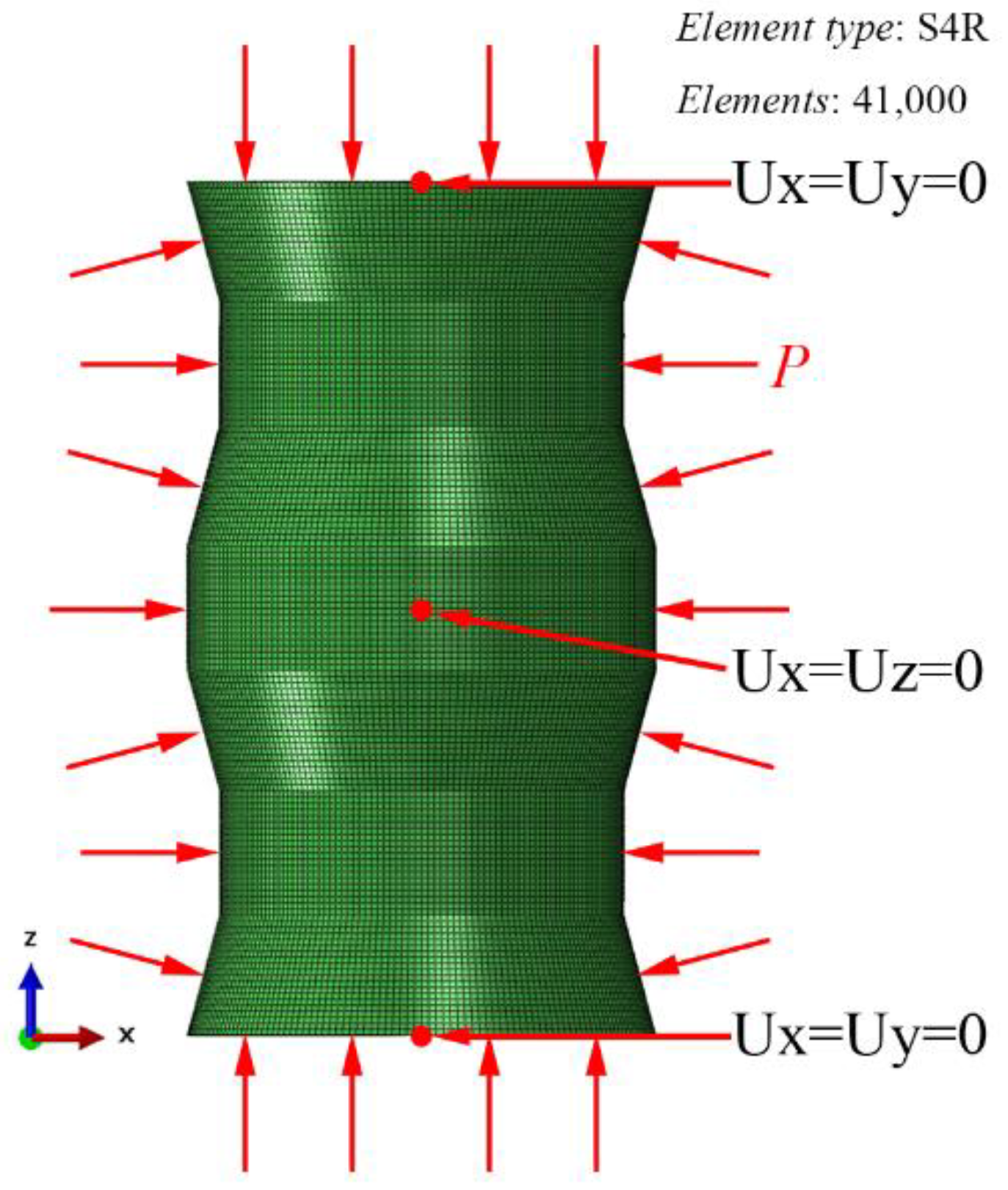
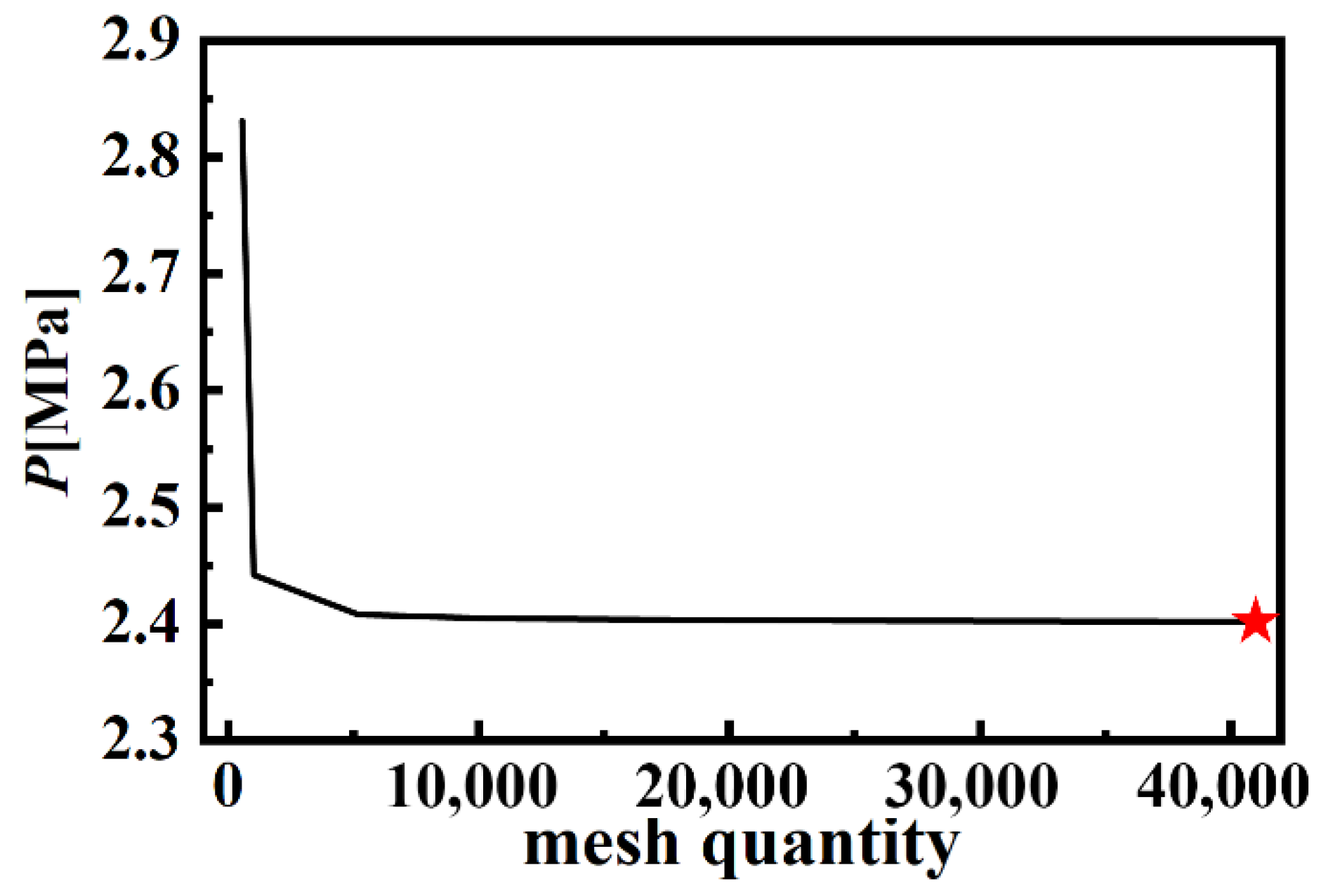
2.2. Numerical Methods
2.3. Experimental Methods
3. Numerical Results
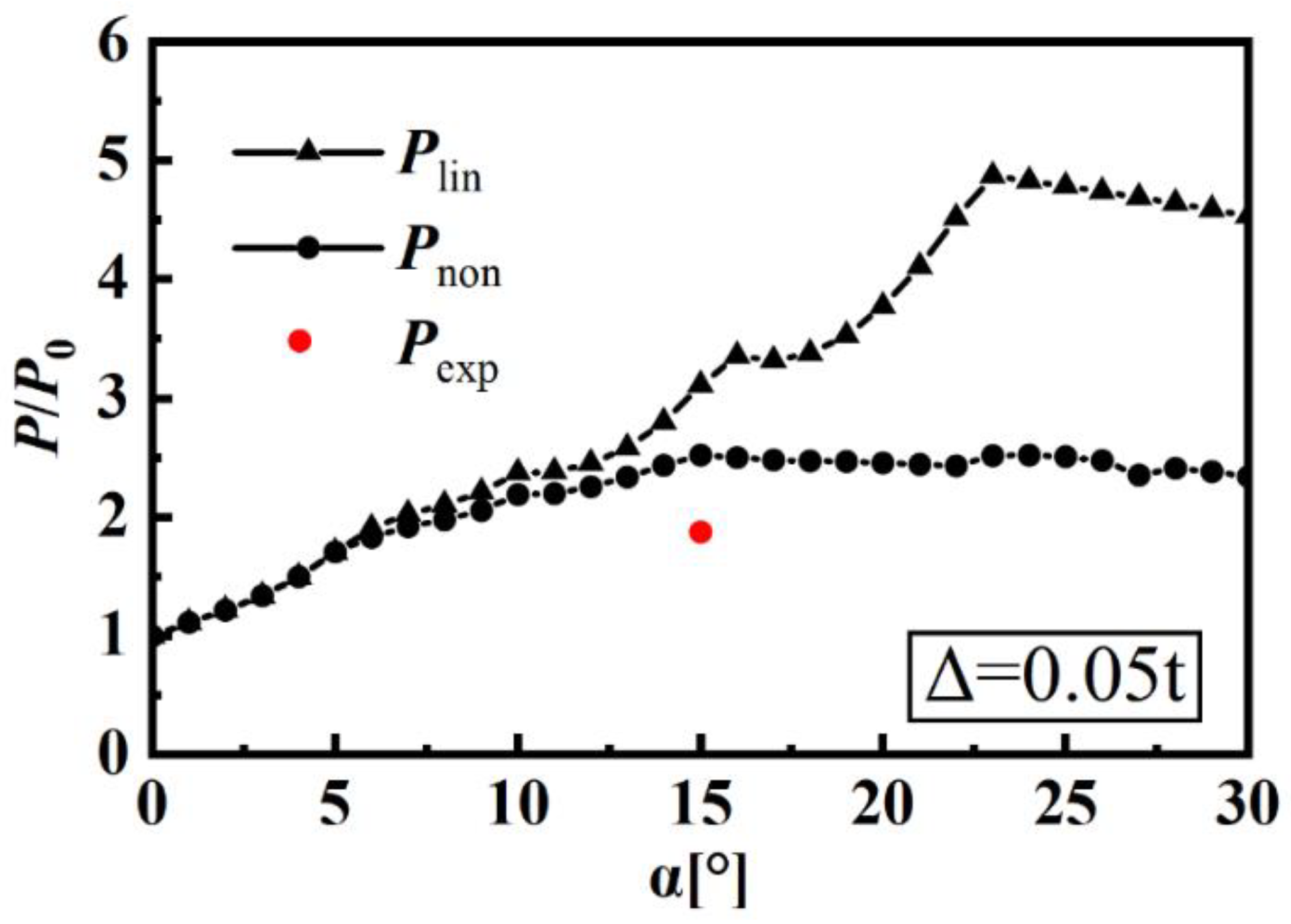
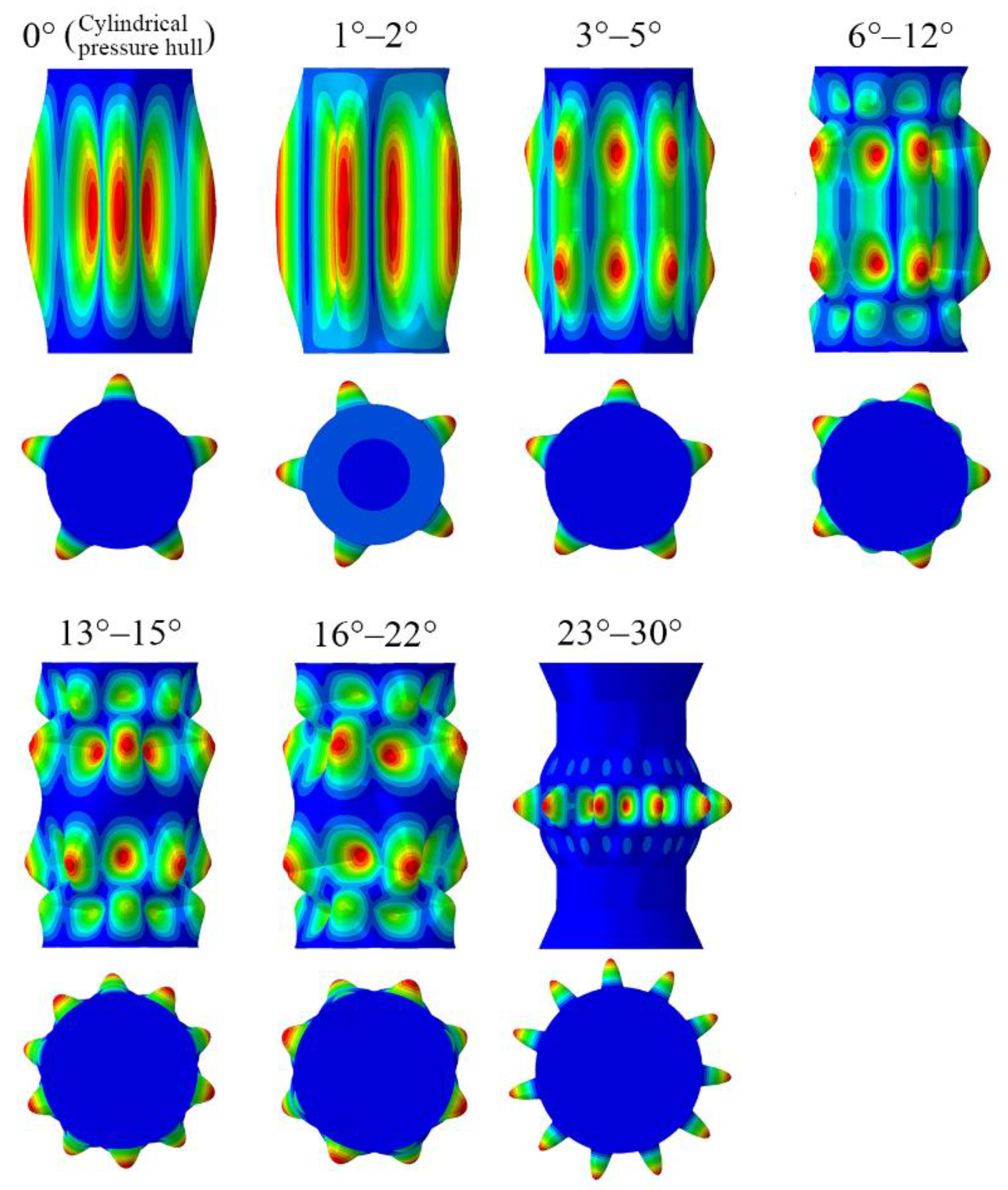
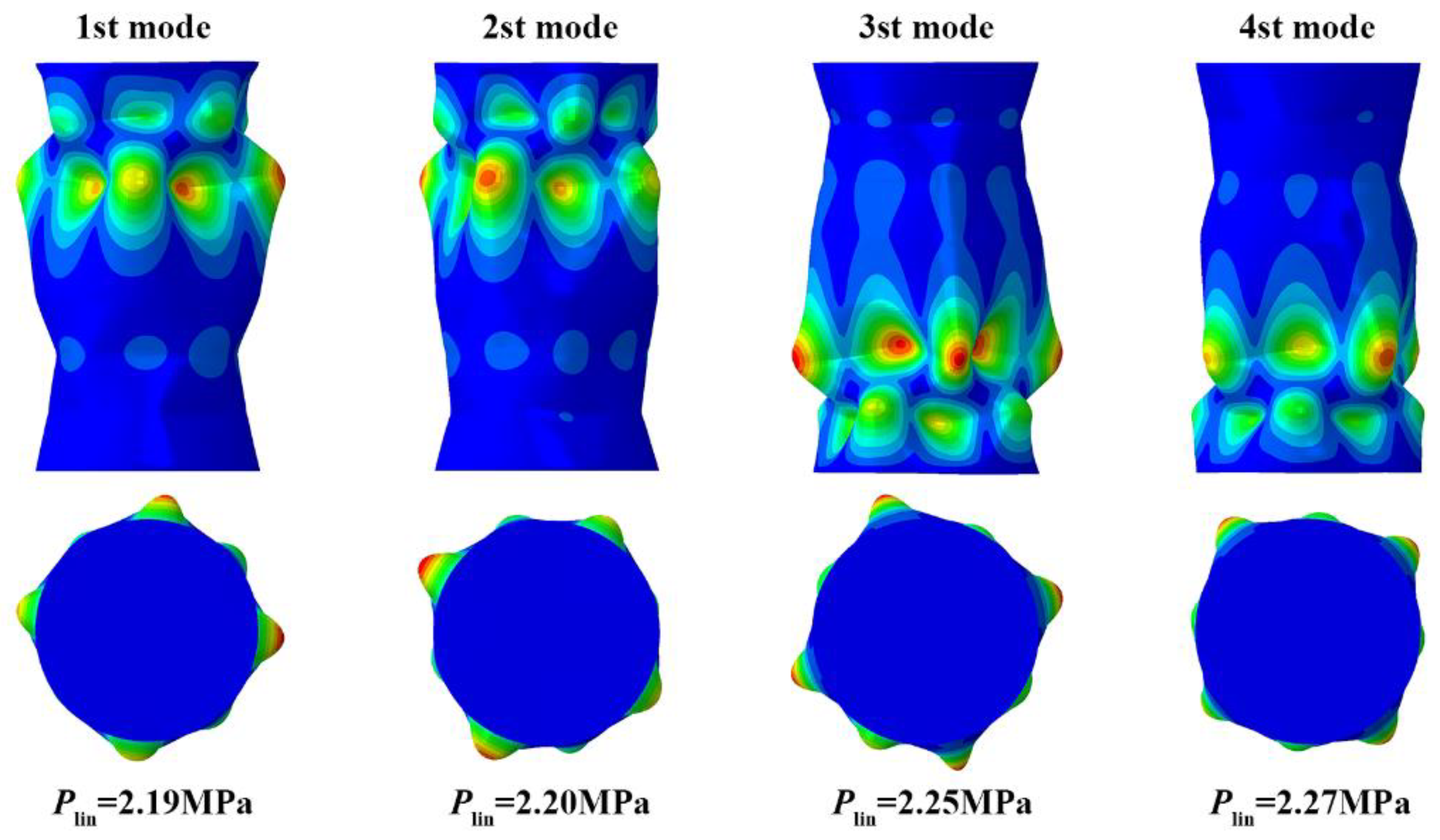
3.1. Linear Buckling Analysis
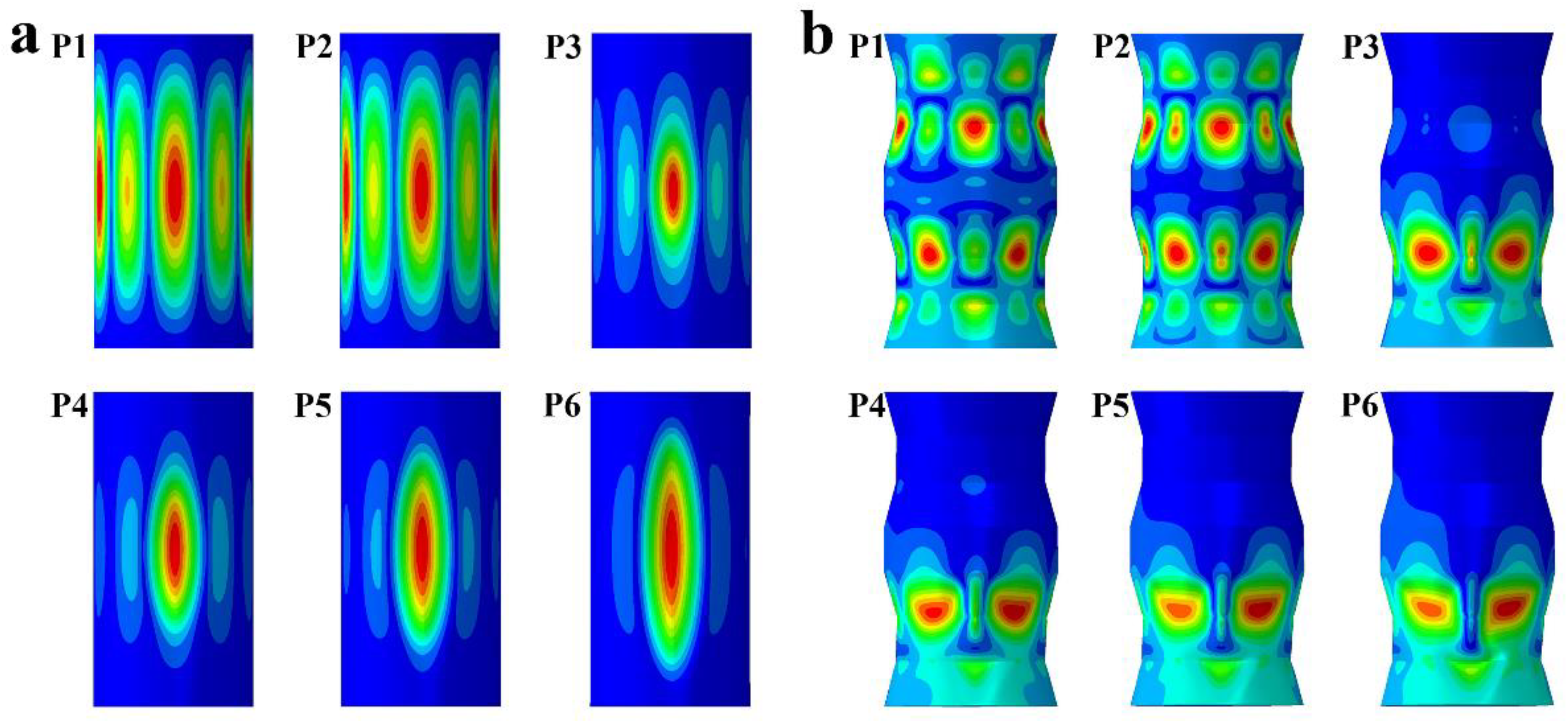
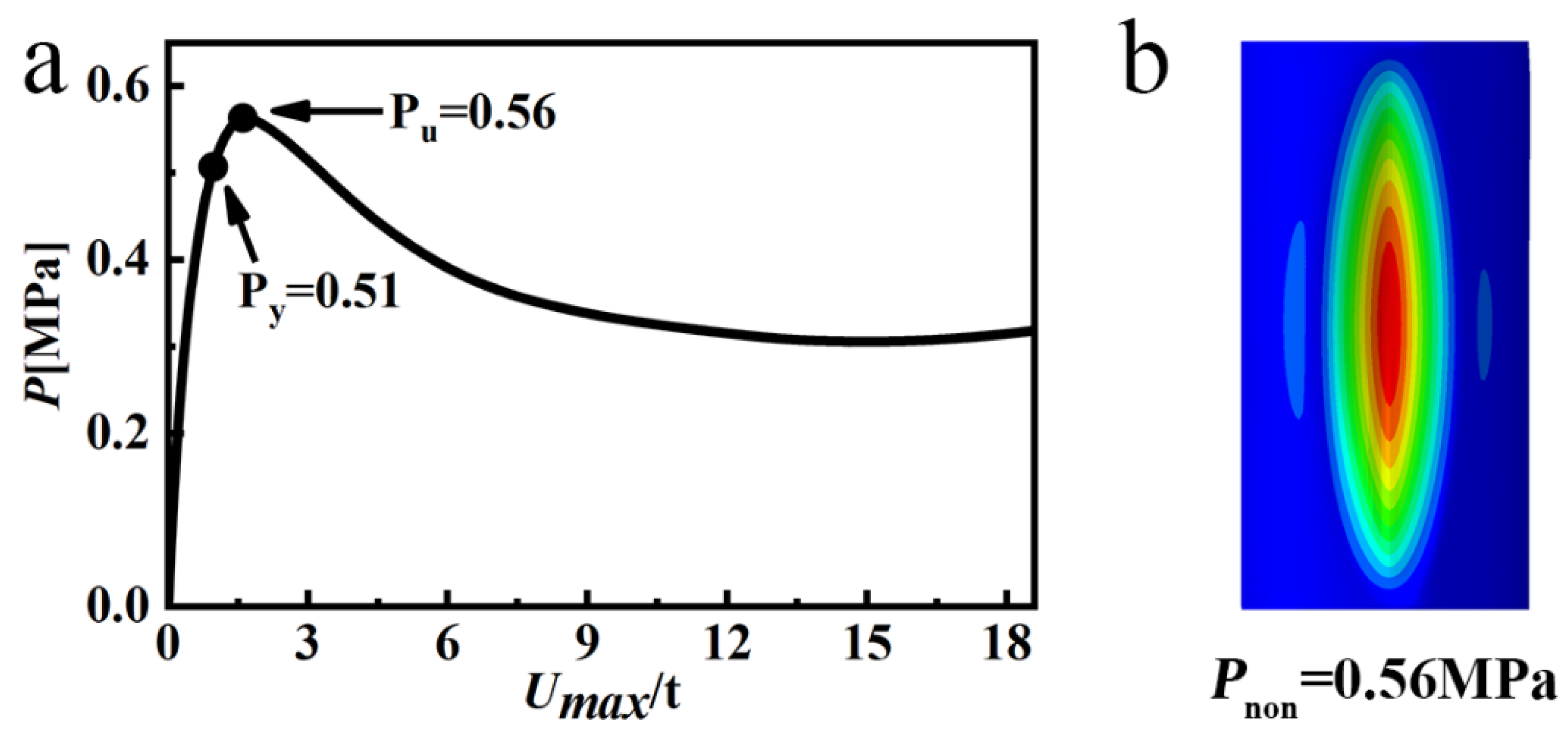
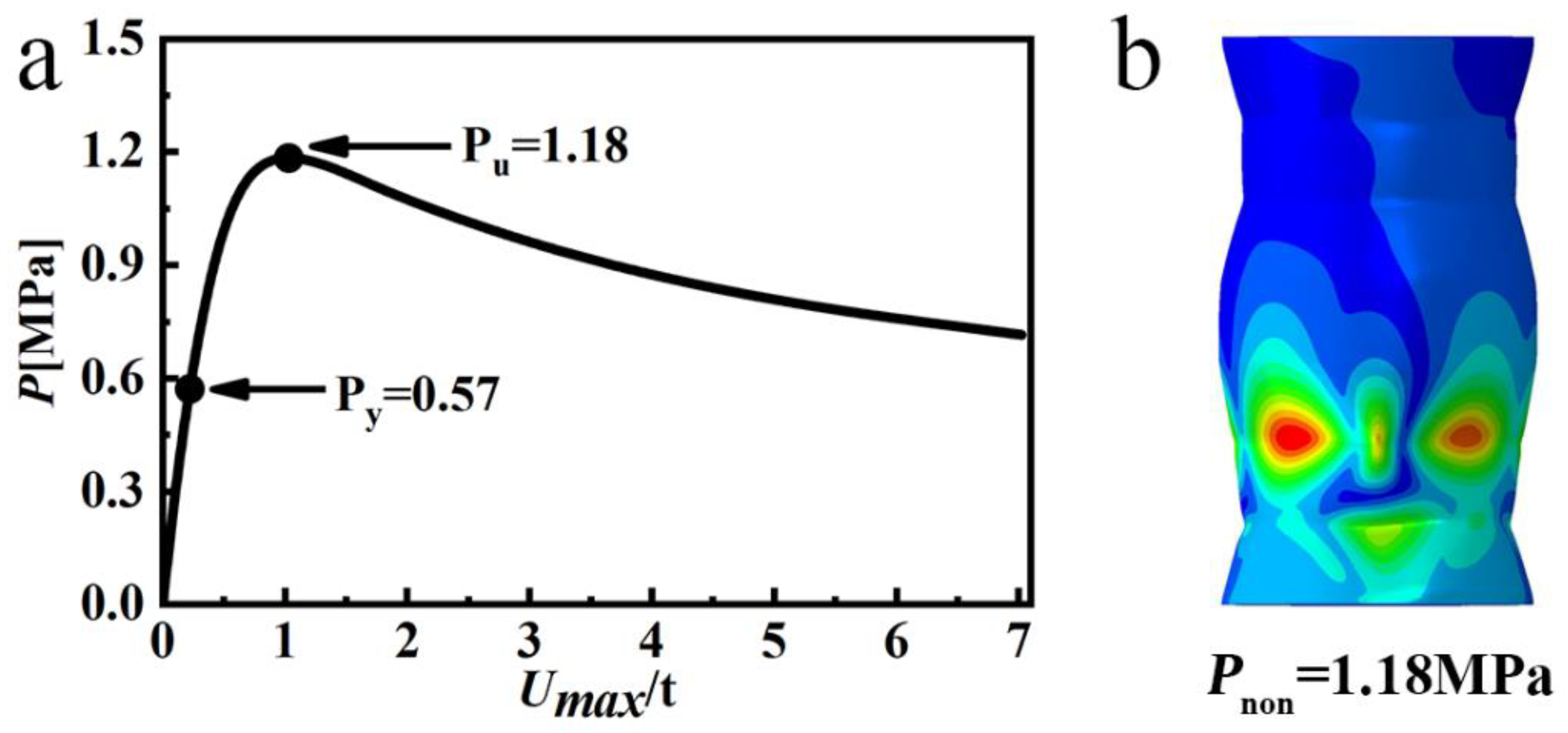
3.2. Nonlinear Buckling Analysis
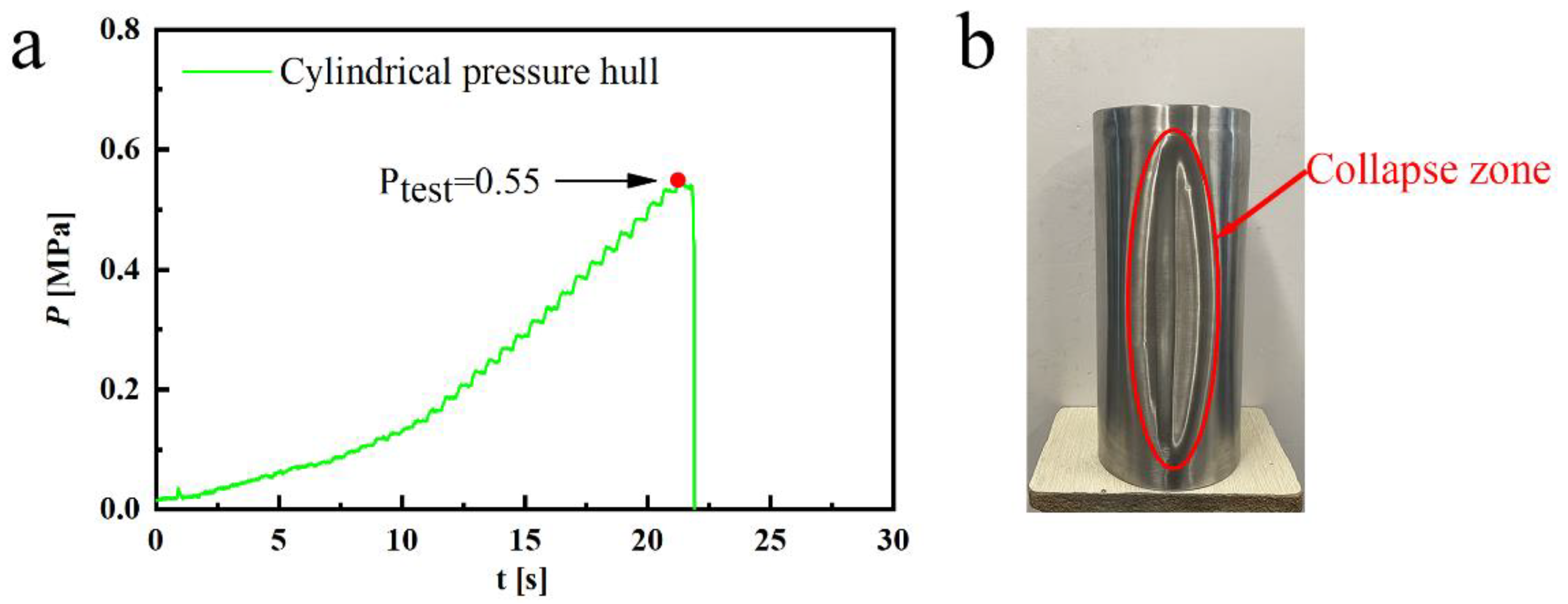
4. Experimental Results
4.1. Analysis of Measurement Results
4.2. Numerical Analysis of Fabricated Pressure Hulls
4.3. Semi-Analytical Evaluation of the Fabricated Wave-Shaped Pressure Hull
5. Conclusions
- (1)
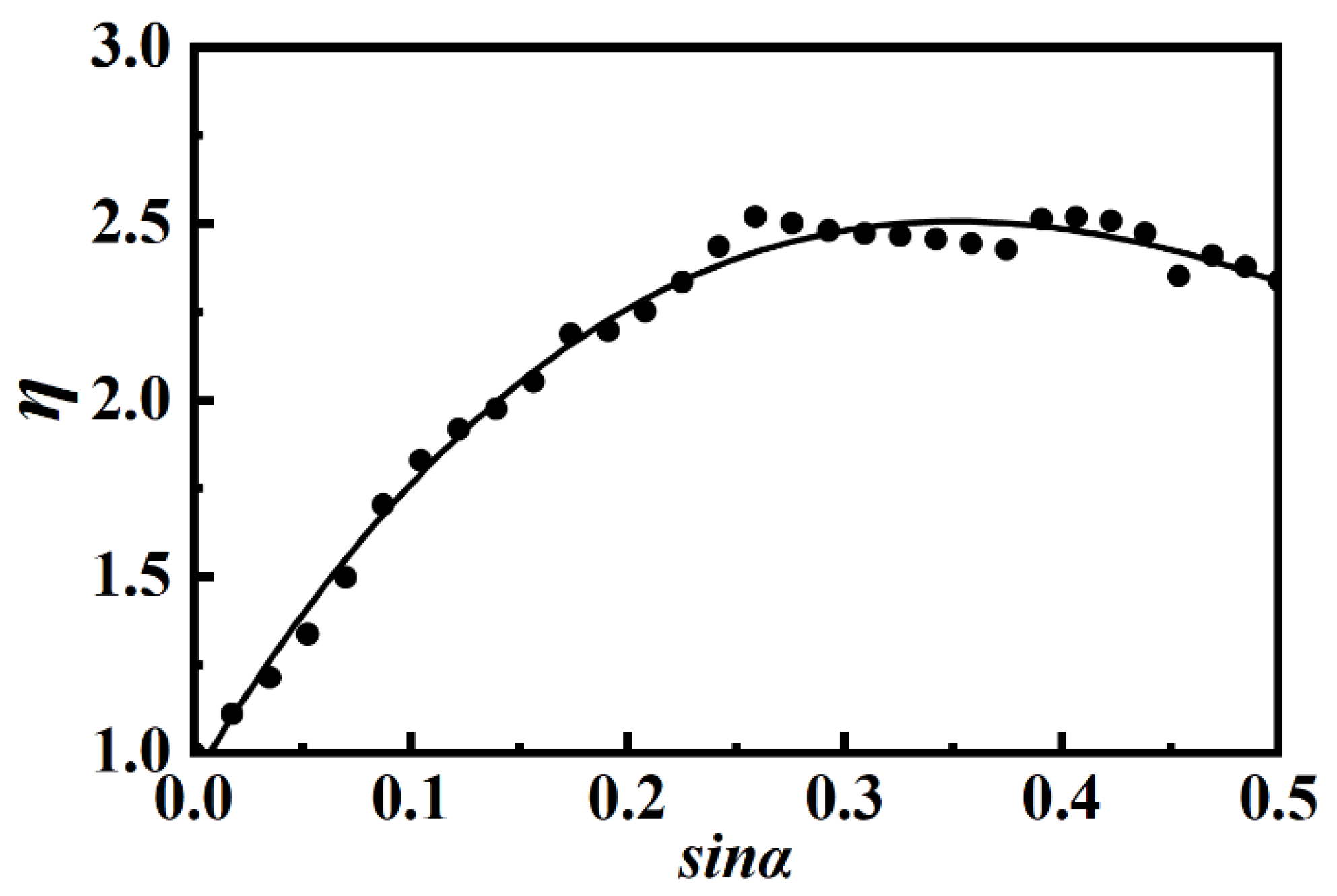
- The slant angle of a wave-shaped pressure hull affected the hull’s linear and nonlinear buckling loads. In terms of load-bearing capacity, the 30 wave-shaped pressure hulls outperformed the equivalent cylindrical pressure hull. Furthermore, the optimal slant angle for wave-shaped pressure hulls was 14°–16°.
- (2)
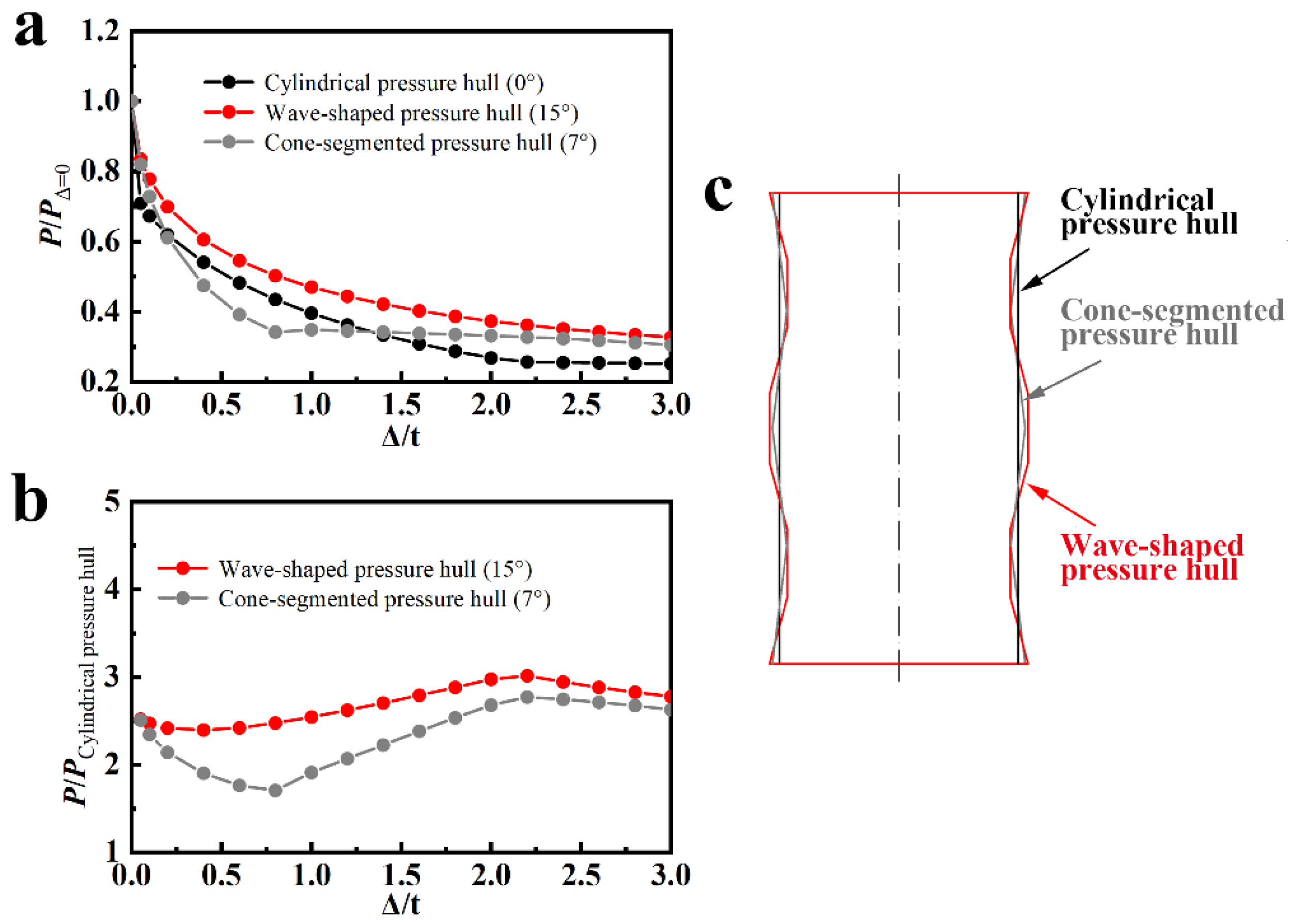
- A wave-shaped pressure hull was less sensitive to imperfections at any amplitude compared with the equivalent cylindrical pressure hull. This finding extends the literature on segmented pressure hulls, which only exhibit lower imperfection sensitivity than equivalent cylindrical pressure hulls when large imperfections are involved.
- (3)
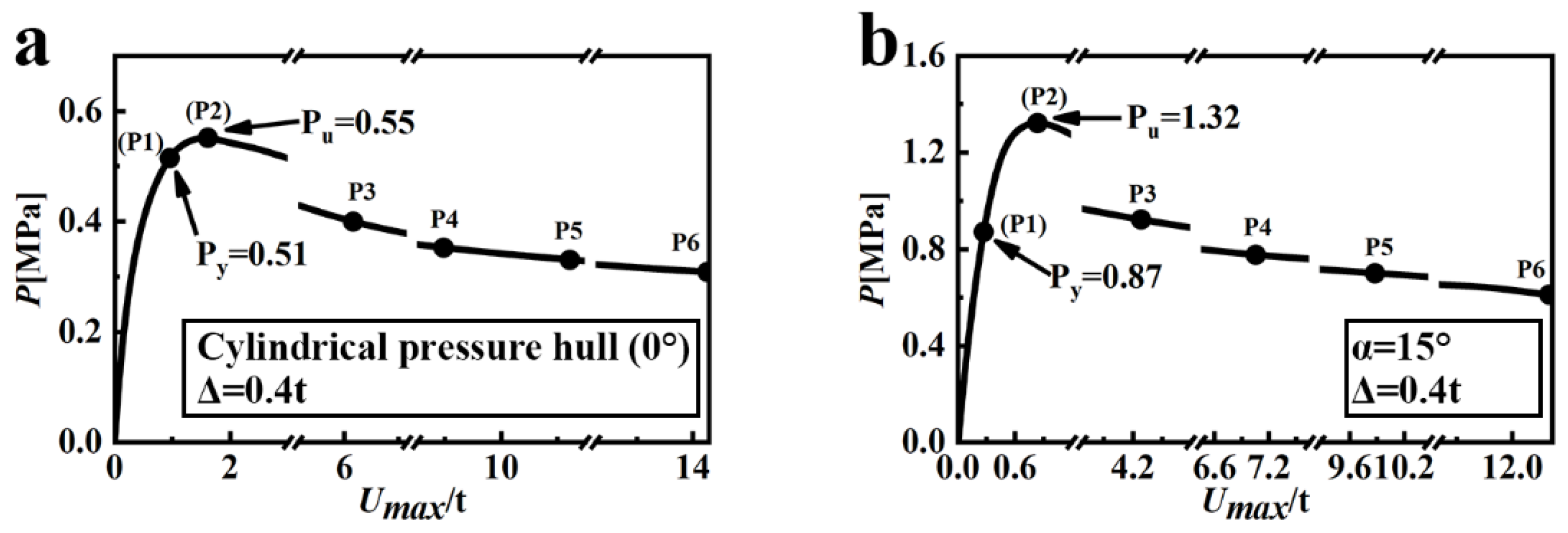
- The experimental and numerical results were consistent. The simulated and experimental buckling loads of the wave-shaped pressure hull were 1.18 and 1.03 MPa, respectively. The simulated load of the cylindrical pressure hull was 0.56 MPa, which was close to its experimental load of 0.55 MPa. The simulated-to-experimental buckling load ratio ranged from 1.018 to 1.146, confirming the accuracy of the FEM.
- (4)
- The experimental buckling load of the equivalent cylindrical pressure hull (0.55 MPa) was considerably lower than that of the wave-shaped pressure hull (1.03 MPa). That is, the buckling load of the wave-shaped pressure hull was approximately 1.87 times that of the equivalent cylindrical pressure hull.
- (5)
- A formula for estimating the load-bearing capacity of a wave-shaped pressure hull was designed in this study. This formula incorporated a correction coefficient and the classical semi-analytical formula for cylindrical pressure hulls. The formula for calculating the correction coefficient was obtained on the basis of numerical evaluation and regression analysis results. The estimated-to-tested buckling load ratios of 0.912, 1.291, and 1.320 were obtained using the Modify-NASA, Modify-Ven, and Modify-Ross equations, respectively. The corresponding findings suggest that the Modify-NASA equation provided an accurate but slightly conservative estimation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ross, C.T.F.; Little, A.P.F. The Buckling of a Corrugated Carbon Fibre Cylinder under External Hydrostatic Pressure. Ocean Eng. 2001, 28, 1247–1264. [Google Scholar] [CrossRef]
- Ross, C.T.F. A Conceptual Design of an Underwater Vehicle. Ocean Eng. 2006, 33, 2087–2104. [Google Scholar] [CrossRef]
- Błachut, J.; Smith, P. Buckling of Multi-Segment Underwater Pressure Hull. Ocean Eng. 2008, 35, 247–260. [Google Scholar] [CrossRef]
- Nho, I.S.; Ryu, J.W.; Lim, S.J.; Cho, S.R.; Cho, Y.S. Buckling Analysis of Circular Cylinders with Initial Imperfection Subjected to Hydrostatic Pressure. J. Soc. Nav. Archit. Korea 2017, 54, 267–273. [Google Scholar] [CrossRef]
- Basaglia, C.; Camotim, D.; Silvestre, N. GBT-Based Buckling Analysis of Steel Cylindrical Shells under Combinations of Compression and External Pressure. Thin-Walled Struct. 2019, 144, 106274. [Google Scholar] [CrossRef]
- Li, Z.; Pasternak, H.; Geißler, K. Experiment-based Statistical Distribution of Buckling Loads of Cylindrical Shells. Ce/Papers 2023, 6, 1816–1820. [Google Scholar] [CrossRef]
- Li, Z.; Pasternak, H.; Geißler, K. Buckling Analysis of Cylindrical Shells Using Stochastic Finite Element Method with Random Geometric Imperfections. Ce/Papers 2022, 5, 653–658. [Google Scholar] [CrossRef]
- Sowiński, K. Experimental and Numerical Verification of Stress Distribution in Additive Manufactured Cylindrical Pressure Vessel—A Continuation of the Dished End Optimization Study. Thin-Walled Struct. 2023, 183, 110336. [Google Scholar] [CrossRef]
- Zingoni, A. Liquid-Containment Shells of Revolution: A Review of Recent Studies on Strength, Stability and Dynamics. Thin-Walled Struct. 2015, 87, 102–114. [Google Scholar] [CrossRef]
- Foryś, P. Optimization of Cylindrical Shells Stiffened by Rings under External Pressure Including Their Post-Buckling Behaviour. Thin-Walled Struct. 2015, 95, 231–243. [Google Scholar] [CrossRef]
- Shiomitsu, D.; Yanagihara, D. Elastic Local Shell and Stiffener-Tripping Buckling Strength of Ring-Stiffened Cylindrical Shells under External Pressure. Thin-Walled Struct. 2020, 148, 106622. [Google Scholar] [CrossRef]
- Ghanbari Ghazijahani, T.; Jiao, H.; Holloway, D. An Experimental Study on Externally Pressurized Stiffened and Thickened Cylindrical Shells. Thin-Walled Struct. 2014, 85, 359–366. [Google Scholar] [CrossRef]
- Do, Q.T.; Muttaqie, T.; Park, S.-H.; Shin, H.K.; Cho, S.-R. Ultimate Strength of Intact and Dented Steel Stringer-Stiffened Cylinders under Hydrostatic Pressure. Thin-Walled Struct. 2018, 132, 442–460. [Google Scholar]
- Ross, C.T.F.; Waterman, G.A. Inelastic Instability of Circular Corrugated Cylinders under External Hydrostatic Pressure. Ocean Eng. 2000, 27, 331–343. [Google Scholar] [CrossRef]
- Ross, C.T.F. Collapse of Corrugated Circular Cylinders under Uniform External Pressure. Int. J. Struct. Stab. Dyn. 2005, 5, 241–257. [Google Scholar] [CrossRef]
- Ross, C.T.F.; Terry, A.; Little, A.P.F. A Design Chart for the Plastic Collapse of Corrugated Cylinders under External Pressure. Ocean Eng. 2001, 28, 263–277. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Cui, W.; Zhao, X.; Tang, W.; Wang, F. Buckling of Circumferentially Corrugated Cylindrical Shells under Uniform External Pressure. Ships Offshore Struct. 2019, 14, 879–889. [Google Scholar] [CrossRef]
- Chrysanidis, T. The Effect of Longitudinal Reinforcement Ratio on the Lateral Buckling Behavior of R/C Walls Modelled Using Prism Elements. J. Build. Eng. 2021, 42, 102456. [Google Scholar] [CrossRef]
- Cho, S.-R.; Muttaqie, T.; Do, Q.T.; Kim, S.; Kim, S.M.; Han, D.-H. Experimental Investigations on the Failure Modes of Ring-Stiffened Cylinders under External Hydrostatic Pressure. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 711–729. [Google Scholar] [CrossRef]
- Cho, S.R.; Muttaqie, T.; Do, Q.T.; Park, S.H.; Kim, S.M.; So, H.Y.; Sohn, J.M. Experimental Study on Ultimate Strength of Steel-Welded Ring-Stiffened Conical Shell under External Hydrostatic Pressure. Mar. Struct. 2019, 67, 102634. [Google Scholar] [CrossRef]
- Ghanbari Ghazijahani, T.; Jiao, H.; Holloway, D. Longitudinally Stiffened Corrugated Cylindrical Shells under Uniform External Pressure. J. Constr. Steel Res. 2015, 110, 191–199. [Google Scholar] [CrossRef]
- Ghanbari Ghazijahani, T.; Sadighi Dizaji, H.; Nozohor, J.; Zirakian, T. Experiments on Corrugated Thin Cylindrical Shells under Uniform External Pressure. Ocean Eng. 2015, 106, 68–76. [Google Scholar] [CrossRef]
- Ross, C.T.F. Pressure Vessels: External Pressure Technology, 2nd ed.; Woodhead Publishing: Sawston, UK, 2011; ISBN 9780857092489. [Google Scholar]
- Zhang, J.; Zheng, L.; Kaewunruen, S.; Zhan, M.; Liu, P. Nonlinear Buckling of Steel Cone-Segmented Cylinders under External Pressure: Numerical and Experimental Evaluations. Ships Offshore Struct. 2024, 1–12. [Google Scholar] [CrossRef]
- Documentation, A. Abaqus Analysis User’s Guide; Simulia: Johnston, RI, USA, 2014. [Google Scholar]
- Ismail, M.S.; Ifayefunmi, O.; Fadzullah, S.H.S.M.; Johar, M. Buckling of Imperfect Cone-Cylinder Transition Subjected to External Pressure. Int. J. Press. Vessel. Pip. 2020, 187, 104173. [Google Scholar] [CrossRef]
- Rules for Classification of Diving Systems and Submersibles; China Classification Society: Beijing, China, 2018.
- Zhang, J.; Tan, J.; Tang, W.; Wang, F.; Zhao, X. International Journal of Pressure Vessels and Piping Collapse Performance of Externally Pressurized Resin Egg-Shaped Shells with Corrosion Thinning. Int. J. Press. Vessel. Pip. 2019, 177, 103993. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, J.; Tang, W.; Zhao, X.; Zhu, Y. Experimental and Numerical Collapse Properties of Externally Pressurized Egg-Shaped Shells under Local Geometrical Imperfections. Int. J. Press. Vessel. Pip. 2019, 175, 103893. [Google Scholar] [CrossRef]
- Zhang, J.; Hua, Z.; Wang, F.; Tang, W. Buckling of an Egg-Shaped Shell with Varying Wall Thickness under Uniform External Pressure. Ships Offshore Struct. 2018, 14, 559–569. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.M.; Cui, W.C.; Tang, W.X.; Wang, F.; Chen, Y. Buckling of Longan-Shaped Shells under External Pressure. Mar. Struct. 2018, 60, 218–225. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, Y.; Liu, J. A Domain-Decomposition Generalized Finite Difference Method for Stress Analysis in Three-Dimensional Composite Materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A Robust Bézier Based Solution for Nonlinear Vibration and Post-Buckling of Random Checkerboard Graphene Nano-Platelets Reinforced Composite Beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential Quadrature: A Powerful New Technique for Analysis of Composite Structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Błachut, J. Buckling of Externally Pressurised Barrelled Shells: A Comparison of Experiment and Theory. Int. J. Press. Vessel. Pip. 2002, 79, 507–517. [Google Scholar] [CrossRef]
- Bałchut, J.; Wang, P. Buckling of Barreled Shells Subjected to External Hydrostatic Pressure. J. Press. Vessel Technol. Trans. ASME 2001, 123, 232–239. [Google Scholar] [CrossRef]
- Błachut, J.; Smith, P. Tabu Search Optimization of Externally Pressurized Barrels and Domes. Eng. Optim. 2007, 39, 899–918. [Google Scholar] [CrossRef]
- Błachut, J. Optimal Barreling of Steel Shells via Simulated Annealing Algorithm. Comput. Struct. 2003, 81, 1941–1956. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Zhang, J.; Tang, W. On the Imperfection Sensitivity and Design of Spherical Domes under External Pressure. Int. J. Press. Vessel. Pip. 2020, 179, 104015. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Niemann, S. Robust Knockdown Factors for the Design of Spherical Shells under External Pressure: Development and Validation. Int. J. Mech. Sci. 2018, 141, 58–77. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). Buckling of Thin-Walled Circular Cylinders; NASA: Washington, DC, USA, 1965.
- Hilburger, M.W. Developing the next Generation Shell Buckling Design Factors and Technologies. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Struct, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; pp. 1–15. [Google Scholar] [CrossRef]
- Hilburger, M.W.; Nemeth, M.P.; Starnes, J.H. Shell Buckling Design Criteria Based on Manufacturing Imperfection Signatures. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Struct, Structural Dynamics and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; Volume 44. [Google Scholar]
- Cartwright, R. Book Reviews: Book Reviews. Perspect. Public Health 2010, 130, 239. [Google Scholar] [CrossRef]
- Ross, C.T.F. A Proposed Design Chart to Predict the Inelastic Buckling Pressures for Conical Shells under Uniform External Pressure. Mar. Technol. SNAME News 2007, 44, 77–81. [Google Scholar] [CrossRef]







| H [mm] | T [mm] | T [mm] | V [mm3] |
|---|---|---|---|
| 395 | 30 | 1.074 | 12,427,945 |
| Sample | Tmin [mm] | Tmax [mm] | Tave [mm] | St.dev. [mm] | S [mm2] | V [mm3] |
|---|---|---|---|---|---|---|
| Cylindrical pressure hull | 1.072 | 1.090 | 1.083 | 0.003 | 349,100(1.000) | 14,438,837(1.009) |
| Wave-shaped pressure hull | 1.008 | 1.098 | 1.075 | 0.016 | 363,845(0.990) | 14,581,047(0.996) |
| Pcr [MPa] | Pexp [MPa] | Pcr/Pexp | |
|---|---|---|---|
| Modify-NASA | 0.94 | 1.03 | 0.912 |
| Modify-Ven | 1.33 | 1.03 | 1.291 |
| Modify-Ross | 1.36 | 1.03 | 1.320 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Hu, Y.; Jiao, H.; Zhang, J. Buckling Behavior of Stainless Wave-Shaped Pressure Hulls. J. Mar. Sci. Eng. 2024, 12, 821. https://doi.org/10.3390/jmse12050821
Zheng L, Hu Y, Jiao H, Zhang J. Buckling Behavior of Stainless Wave-Shaped Pressure Hulls. Journal of Marine Science and Engineering. 2024; 12(5):821. https://doi.org/10.3390/jmse12050821
Chicago/Turabian StyleZheng, Lingtong, Yunsen Hu, Huifeng Jiao, and Jian Zhang. 2024. "Buckling Behavior of Stainless Wave-Shaped Pressure Hulls" Journal of Marine Science and Engineering 12, no. 5: 821. https://doi.org/10.3390/jmse12050821
APA StyleZheng, L., Hu, Y., Jiao, H., & Zhang, J. (2024). Buckling Behavior of Stainless Wave-Shaped Pressure Hulls. Journal of Marine Science and Engineering, 12(5), 821. https://doi.org/10.3390/jmse12050821









