Numerical Simulation of Extreme Ice Loads on Complex Pile Legs of Offshore Substation Structures
Abstract
:1. Introduction
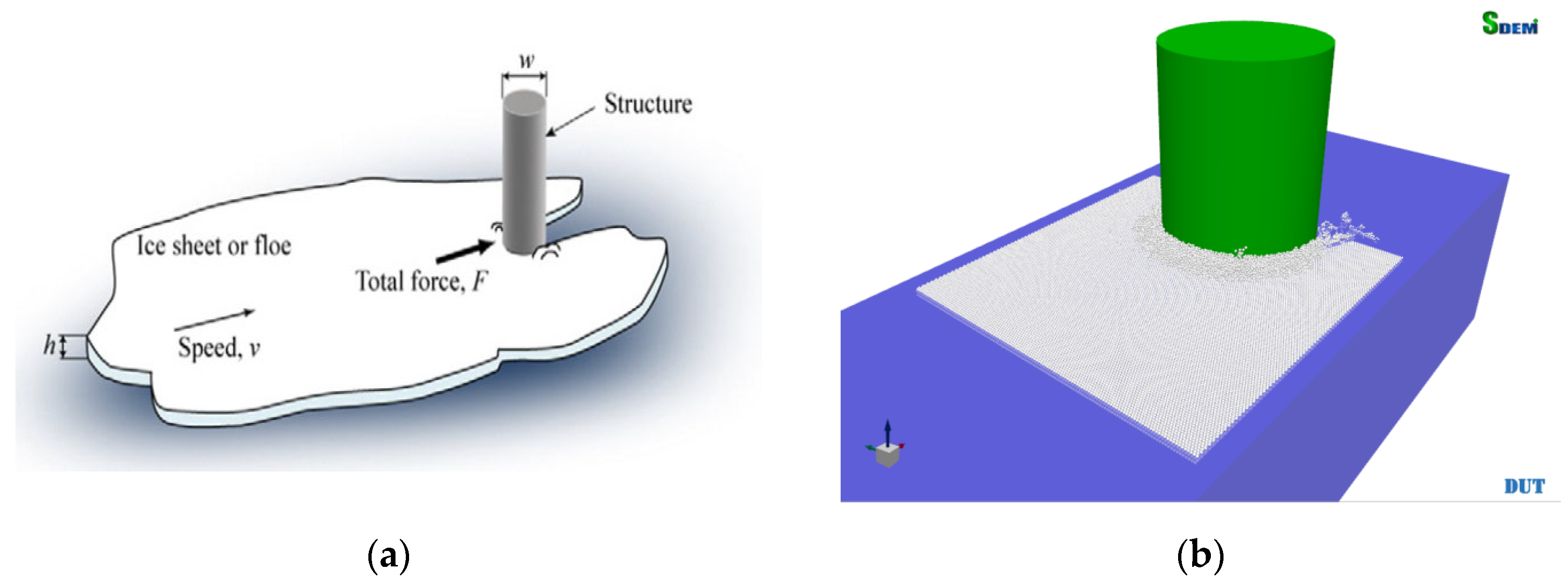
2. Numerical Simulation of Interaction between Sea Ice and Offshore Substation Structures
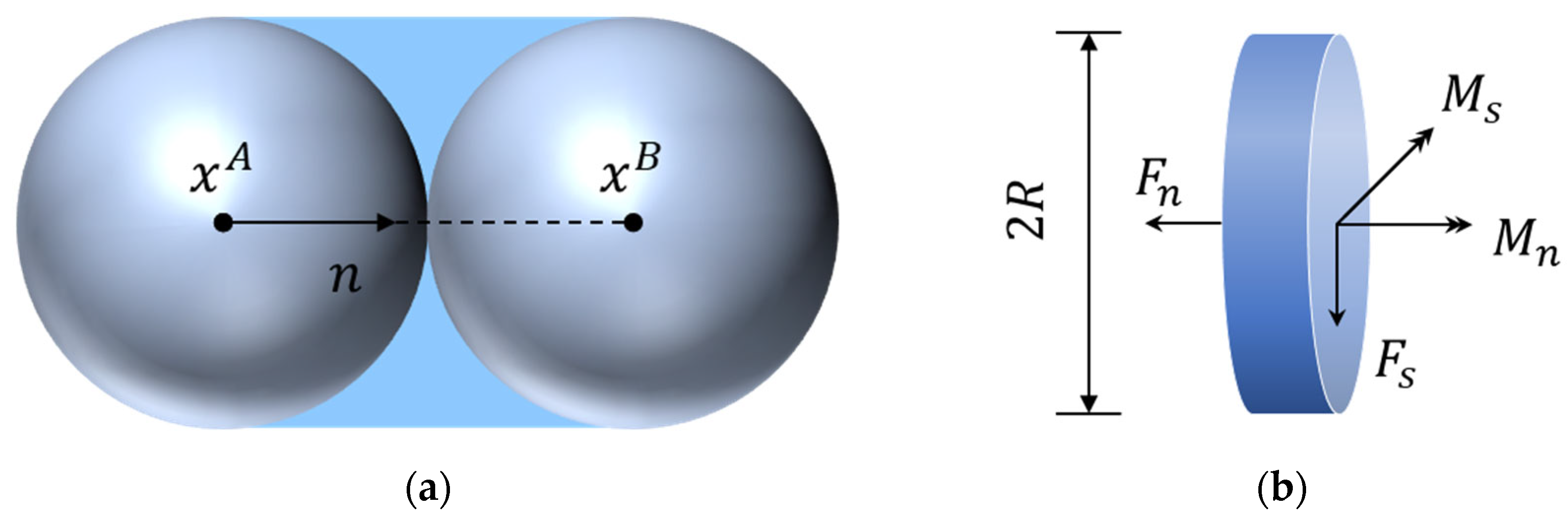
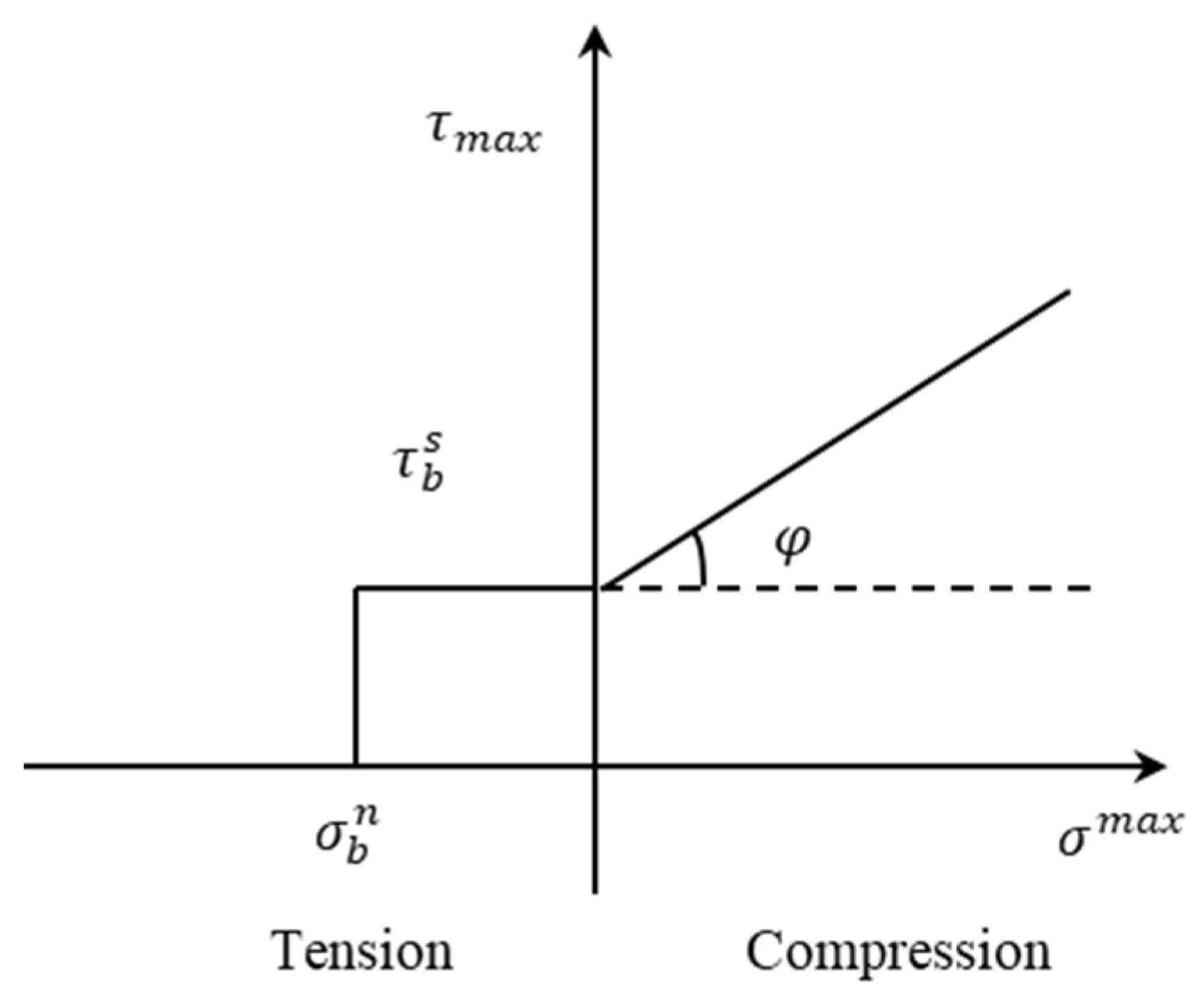
2.1. Numerical Simulation Methods
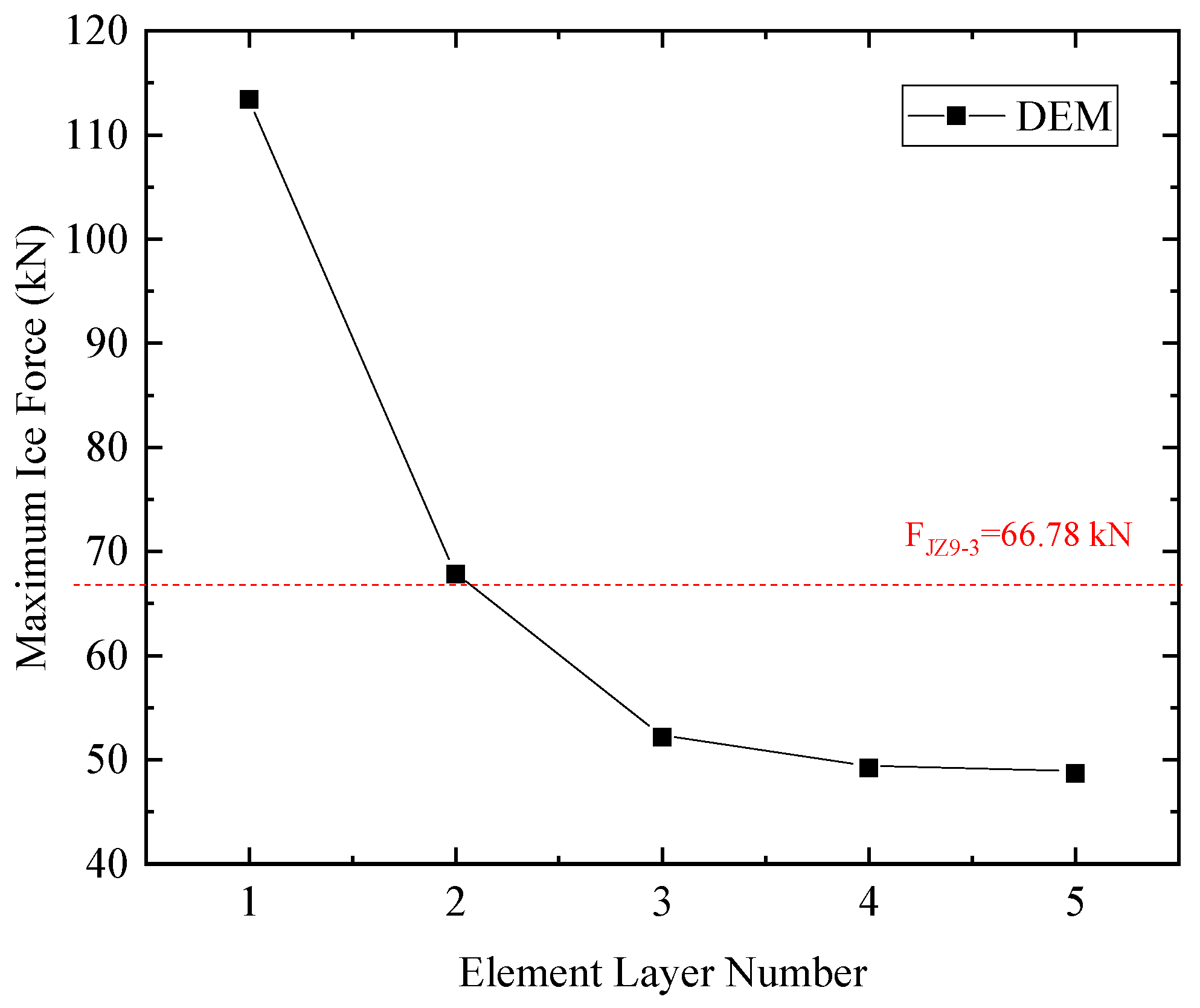
2.2. Numerical Model
3. Results and Discussion
3.1. Sea Ice Failure Mode
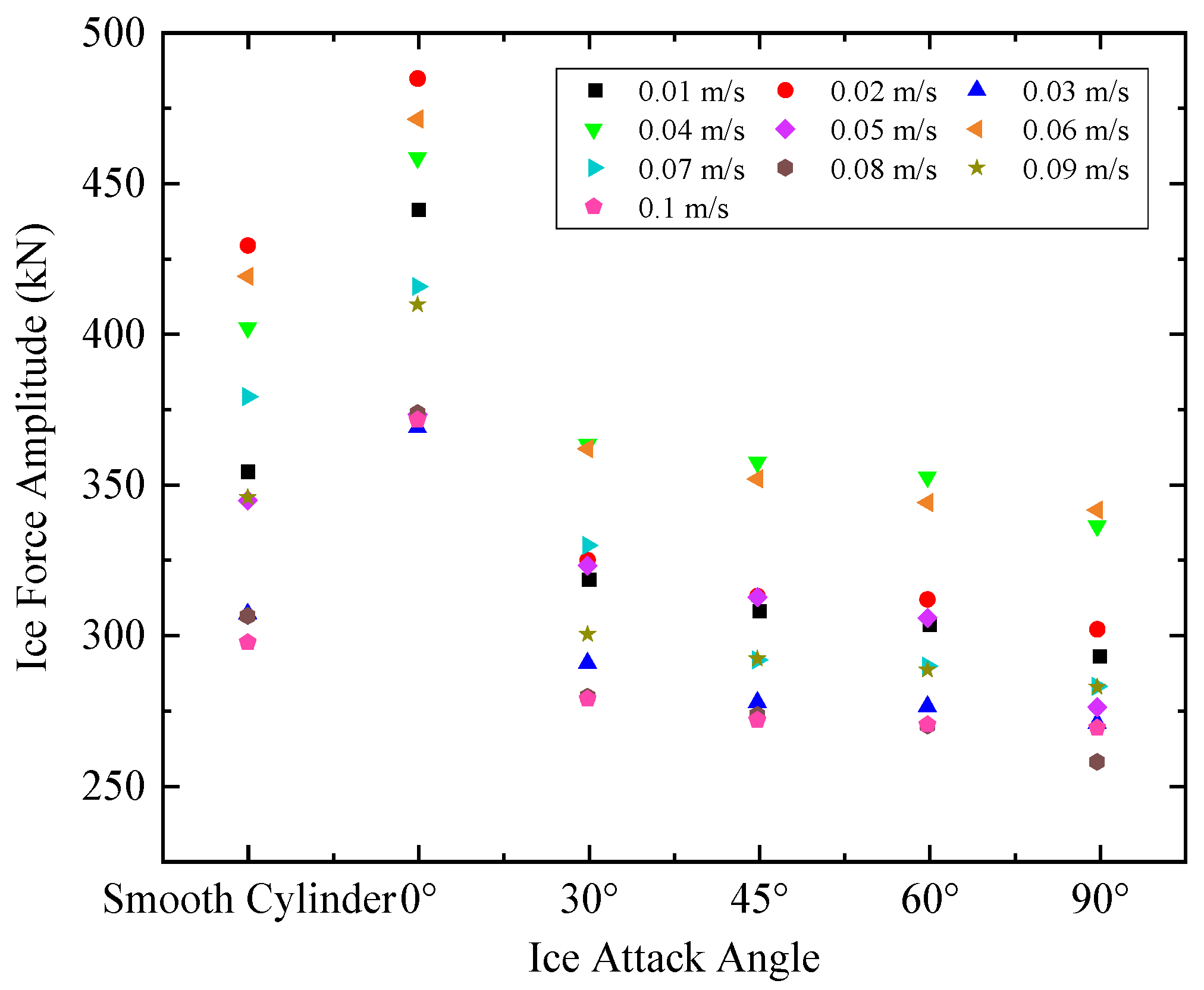
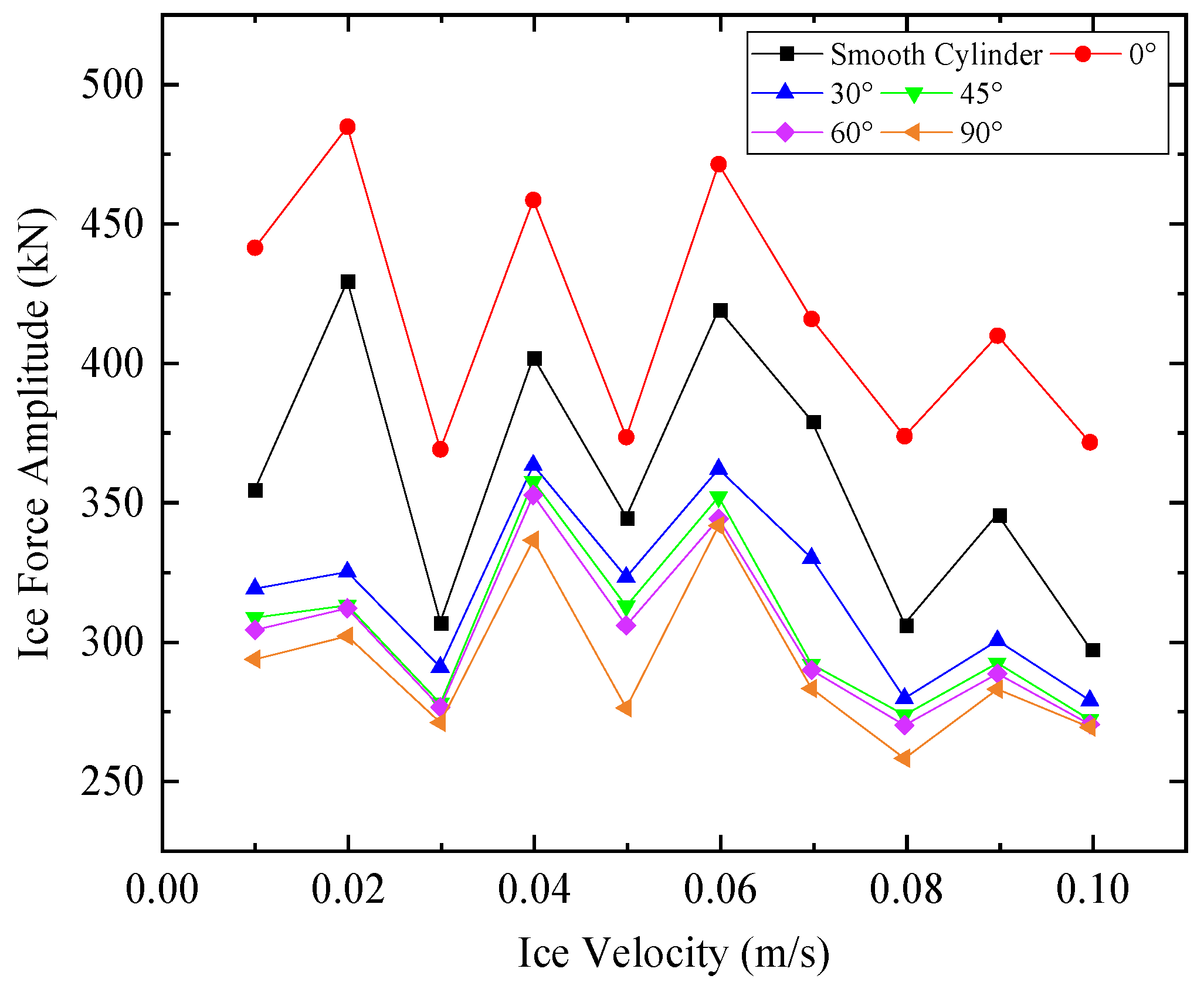
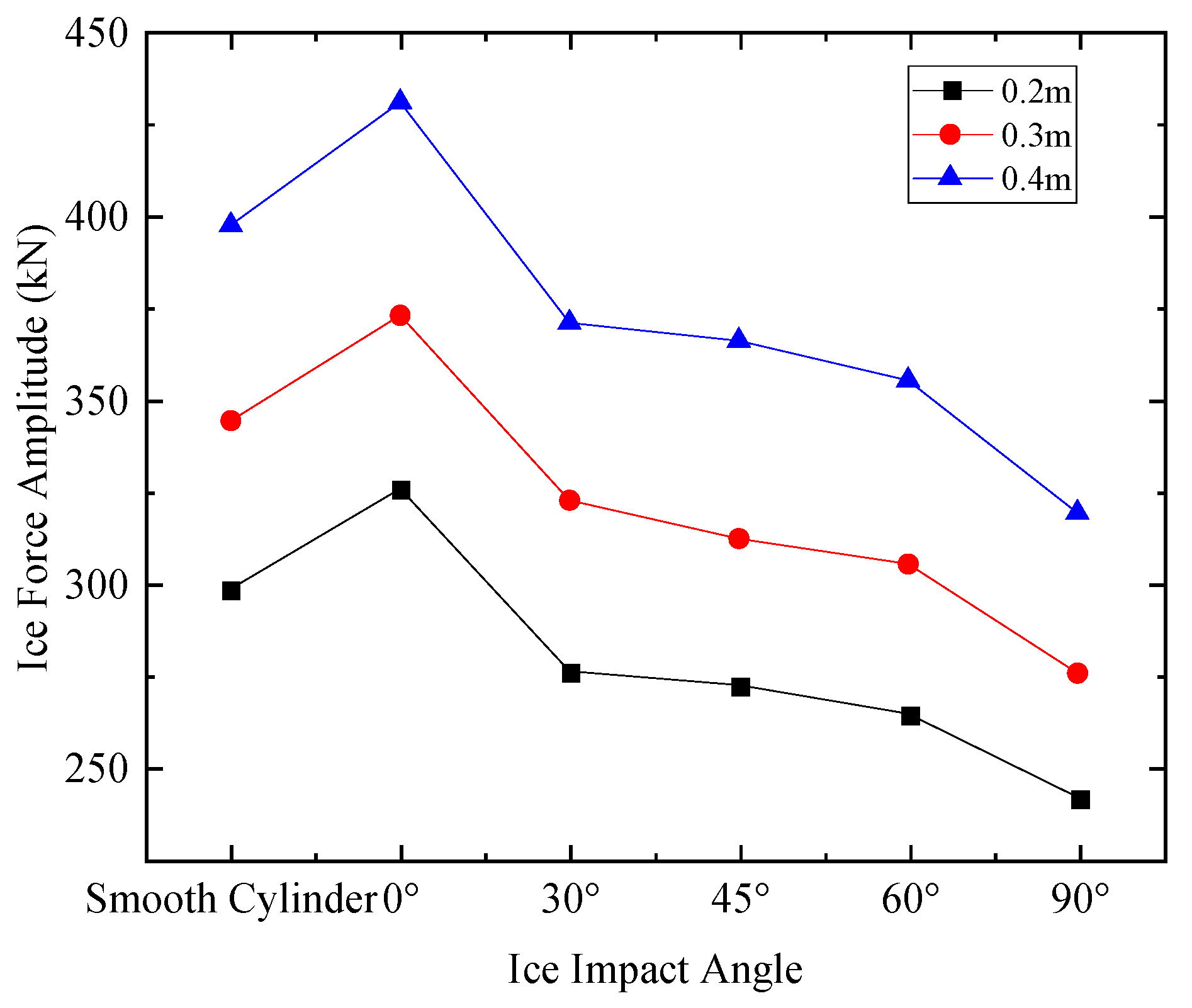
3.2. Ice Force Amplitude
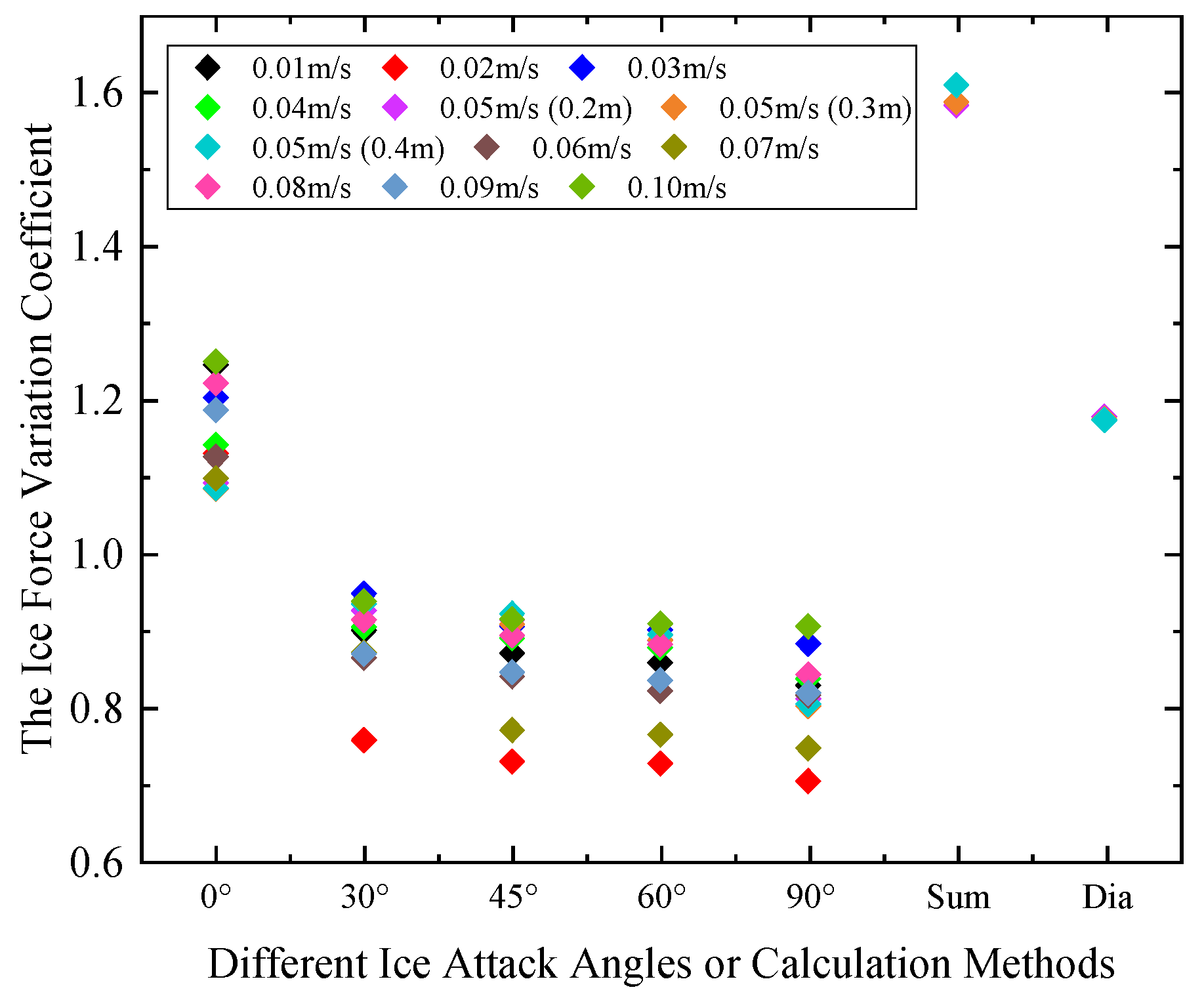
3.3. Ice Force Variation Coefficient
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, A.L.; Tang, M.N.; Zhao, Q.; Liu, Y.; Li, B.H.; Shi, Y.Y.; Sui, J.P. Analysis of sea ice parameters for the design of an offshore wind farm in the Bohai Sea. Ocean Eng. 2021, 239, 109902. [Google Scholar] [CrossRef]
- Haselibozchaloee, D.; Correia, J.; Mendes, P.; Jesus, A.D.; Berto, F. A review of fatigue damage assessment in offshore wind turbine support structure. Int. J. Fatigue 2022, 164, 107145. [Google Scholar] [CrossRef]
- Wang, G.J.; Yue, Q.J.; Zhang, D.Y.; Fu, Y.H.; Peng, X.; Dong, R. Distribution analysis of local ice pressures in the indentation test at various velocities. J. Mar. Sci. Eng. 2022, 10, 433. [Google Scholar] [CrossRef]
- Timco, G.W.; Johnston, M. Ice loads on the caisson structures in the Canadian Beaufort Sea. Cold Reg. Sci. Technol. 2004, 38, 185–209. [Google Scholar] [CrossRef]
- Kärnä, T.; Kamesaki, K.; Tsukuda, H. A numerical model for dynamic ice-structure interaction. Comput. Struct. 1999, 72, 645–658. [Google Scholar] [CrossRef]
- Kärnä, T.; Jochmann, P. Field observations on ice failure modes. In Proceedings of the 17th International Conference on Port and Ocean Engineering under Arctic Conditions, Trondheim, Norway, 16–19 June 2003. [Google Scholar]
- Hendrikse, H.; Metrikine, A. Ice-induced vibrations and ice buckling. Cold Reg. Sci. Technol. 2016, 131, 129–141. [Google Scholar] [CrossRef]
- Yue, Q.J.; Guo, F.W.; Kärnä, T. Dynamic ice forces of slender vertical structures due to ice crushing. Cold Reg. Sci. Technol. 2009, 56, 77–83. [Google Scholar] [CrossRef]
- Sanderson, T. Ice Mechanics and Risks to Offshore Structures; Kluwer Academic Publishers: Norwell, MA, USA, 1988. [Google Scholar]
- Ji, S.Y.; Di, S.C.; Liu, S.W. Analysis of ice load on conical structure with discrete element method. Eng. Comput. 2015, 32, 1121–1134. [Google Scholar] [CrossRef]
- Long, X.; Liu, L.; Ji, S.Y. Discrete element analysis of ice-induced vibrations of offshore wind turbines in level ice. J. Mar. Sci. Eng. 2023, 11, 2153. [Google Scholar] [CrossRef]
- Izumiyama, K.; Kitagawa, H.; Koyama, K.; Uto, S. On the interaction between a conical structure and ice sheet. In Proceedings of the 11th International Conference on Port and Ocean Engineering under Arctic Conditions, St. John’s, NL, Canada, 24–28 September 1991; Volume 1, pp. 155–166. [Google Scholar]
- Li, F.; Yue, Q.J. Failure mode effect on conical structure dynamic ice forces. In Proceedings of the 19th International Conference on Port and Ocean Engineering under Arctic Conditions, Dalian, China, 27–30 June 2007; pp. 113–121. [Google Scholar]
- Paavilainen, J.; Tuhkuri, J. Ice loads on sloping structures: Influence of parameters in virtual experiments. In Proceedings of the 21st IAHR International Symposium on Ice, Dalian, China, 11–15 June 2012; pp. 842–852. [Google Scholar]
- Qu, Y.; Yue, Q.J.; Bi, X.J.; Kärnä, T. A random ice force model for narrow conical structures. Cold Reg. Sci. Technol. 2006, 45, 148–157. [Google Scholar]
- Ranta, J.; Polojarvi, A.; Tuhkuri, J. Limit mechanisms for ice loads on inclined structures: Buckling. Cold Reg. Sci. Technol. 2018, 147, 34–44. [Google Scholar] [CrossRef]
- Ranta, J.; Polojarvi, A.; Tuhkuri, J. Ice loads on inclined marine structures-Virtual experiments on ice failure process evolution. Mar. Struct. 2018, 57, 72–86. [Google Scholar] [CrossRef]
- Ranta, J.; Polojarvi, A.; Tuhkuri, J. The statistical analysis of peak ice loads in a simulated ice-structure interaction process. Cold Reg. Sci. Technol. 2017, 13, 46–55. [Google Scholar] [CrossRef]
- Di, S.C.; Xue, Y.Z.; Wang, Q.; Bai, X.L. Discrete element simulation of ice loads on narrow conical structures. Ocean Eng. 2017, 146, 282–297. [Google Scholar] [CrossRef]
- Jou, O.; Celigueta, M.A.; Latorre, S.; Arrufat, F.; Onate, E. A bonded discrete element method for modeling ship–ice interactions in broken and unbroken sea ice fields. Comput. Part. Mec. 2019, 6, 739–765. [Google Scholar] [CrossRef]
- Chen, Y.H.; Liu, H.Y. Overview of the development of offshore wind power generation in China. Sustain. Energy Technol. Assess. 2022, 53, 102766. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Qu, Y.; Yue, Q.J.; Xu, N. Ice-Resistant performance analysis of jackup structures. J. Cold Reg. Eng. 2018, 32, 04017022. [Google Scholar] [CrossRef]
- Liu, H.J.; Tian, Y.F. Model test of ice load on high pile cap foundation of offshore wind power. China Offshore Platf. 2020, 35, 54–59. [Google Scholar]
- Regulations for Offshore Ice Condition & Application in China Sea: Q/HSn 3000-2002; China National Offshore Oil Corporation: Beijing, China, 2002.
- Chen, Z.A.; Huang, Y.T.; Zhang, D.Y. Machine learning assisted in forecasting the ice-induced vibration for jacket platforms. Appl. Ocean Res. 2023, 141, 103778. [Google Scholar] [CrossRef]
- Shen, H.H.; Ackley, S.F.; Yong, Y. Limiting diameter of pancake ice. J. Geophys. Res.-Oceans 2004, 109, 1–13. [Google Scholar] [CrossRef]
- Dempsey, J.P. Research trends in ice mechanics. Int. J. Solids Struct. 2000, 37, 131–153. [Google Scholar] [CrossRef]
- Hopkins, M.A. Four stages of pressure ridging. J. Geophys. Res-Oceans 1998, 103, 21883–21891. [Google Scholar] [CrossRef]
- Liu, M.H.; Wang, Q.; Lu, W. Peridynamic simulation of brittle-ice crushed by a vertical structure. Int. J. Nav. Arch. Ocean Eng. 2017, 9, 209–218. [Google Scholar] [CrossRef]
- Long, X.; Liu, S.W.; Ji, S.Y. Discrete element modelling of relationship between ice breaking length and ice load on conical structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Ji, S.Y.; Li, Z.L.; Li, C.H.; Shang, J. Discrete element modeling of ice loads on ship hulls in broken ice fields. Acta Oceanol. Sin. 2013, 32, 50–58. [Google Scholar] [CrossRef]
- Ji, S.Y. Discrete Element Modeling of Ice loads on ship and offshore structures. In Proceedings of the 7th International Conference on Discrete Element Methods, Dalian, China, 1–4 August 2016; pp. 45–54. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Wilchinsky, A.V.; Feltham, D.L.; Hopkins, M.A. Modelling the reorientation of sea-ice faults as the wind changes direction. Ann. Glaciol. 2011, 52, 83–90. [Google Scholar] [CrossRef]
- Jang, H.K.; Kim, M. Dynamic ice force estimation on a conical structure by discrete element method. Int. J. Nav. Arch. Ocean Eng. 2021, 13, 136–146. [Google Scholar] [CrossRef]
- Timco, G.W.; Sudom, D. Revisiting the Sanderson pressure–area curve: Defining parameters that influence ice pressure. Cold Reg. Sci. Technol. 2013, 95, 53–66. [Google Scholar] [CrossRef]
- Sodhi, D.S.; Haehnel, R.B. Crushing ice forces on structures. J. Cold Reg. Eng. 2003, 17, 135–184. [Google Scholar] [CrossRef]

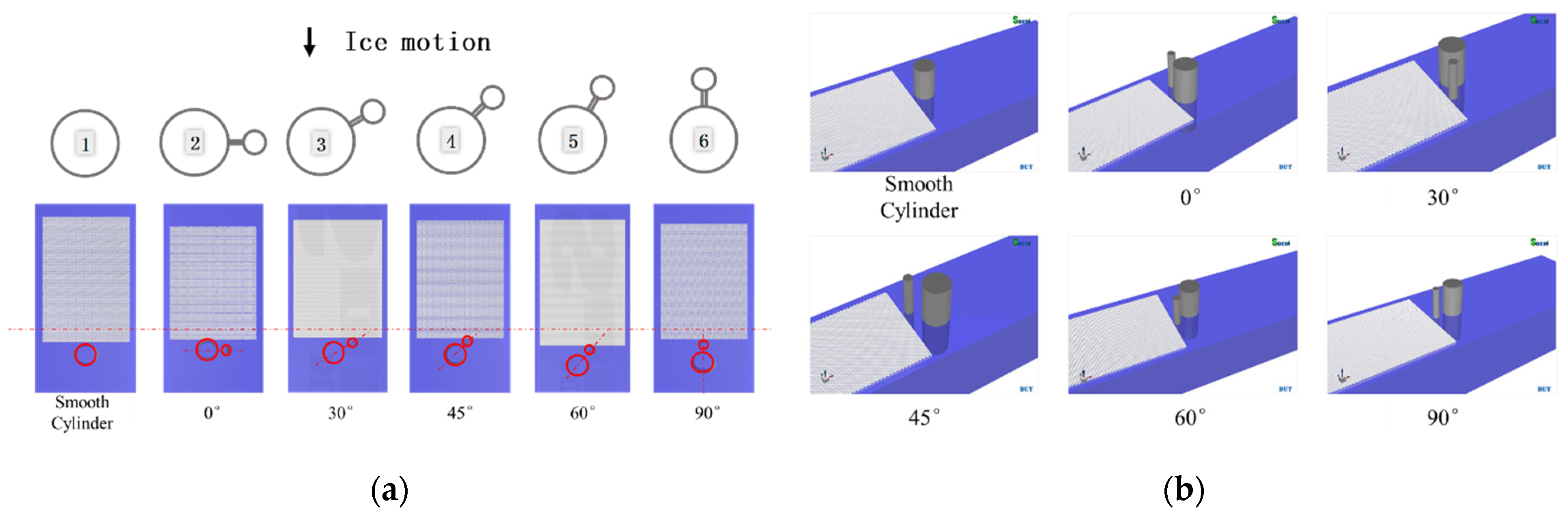
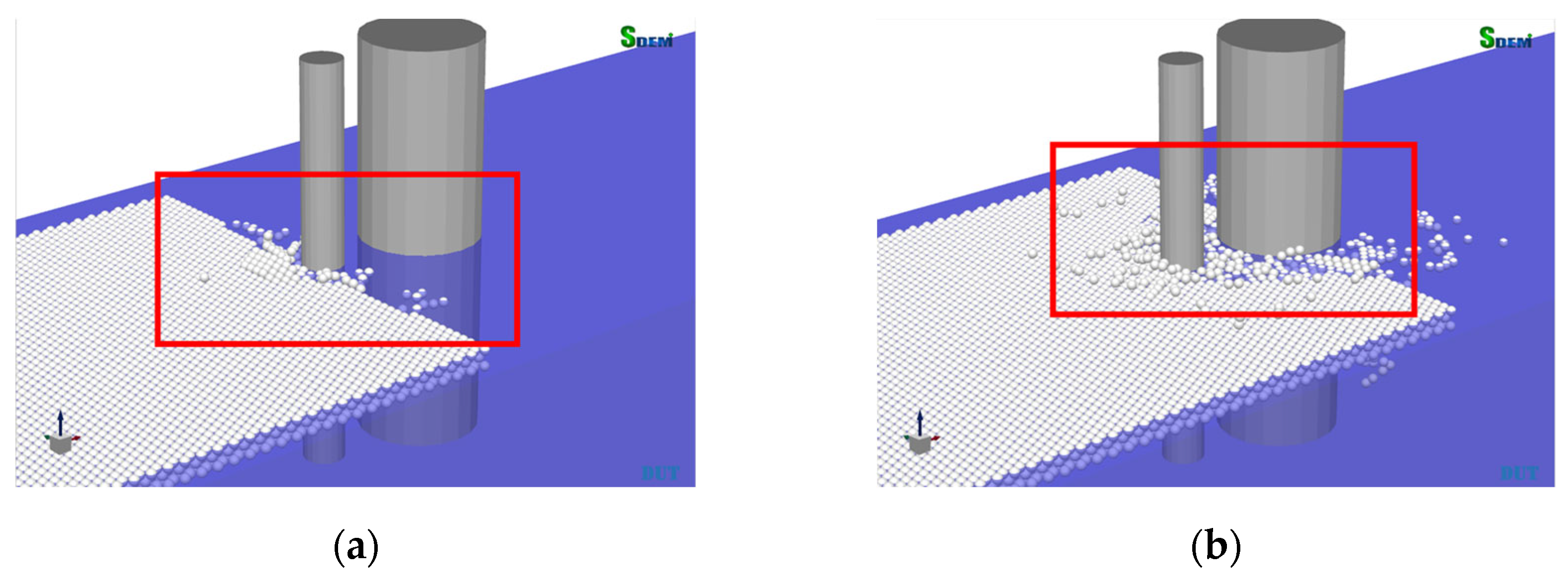

| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Sea Ice Density/(kg/m3) | 920.0 | Element Diameter/m | 0.1 | ||
| Seawater Density/(kg/m3) | 1035.0 | Distance Between Structure Centers/m | 1.5 | ||
| Sea Ice Elastic Modulus/GPa | 1.0 | Pile Leg Diameter/m | 1.5 | ||
| Sea Ice Compressive Strength/MPa | 2.0 | Cable Pipe Diameter/m | 0.508 | ||
| Sea Ice Bending Strength/MPa | 0.7 | Sea Ice Thickness/m | 0.2/0.3/0.4 | ||
| Sea Ice Friction Coefficient | 0.16 | Sea Ice Velocity/(m/s) | 0.01–0.1 | ||
| Element Bonding Strength/MPa | 0.94 | Ice Attack Angle/° | a | 0–90 |
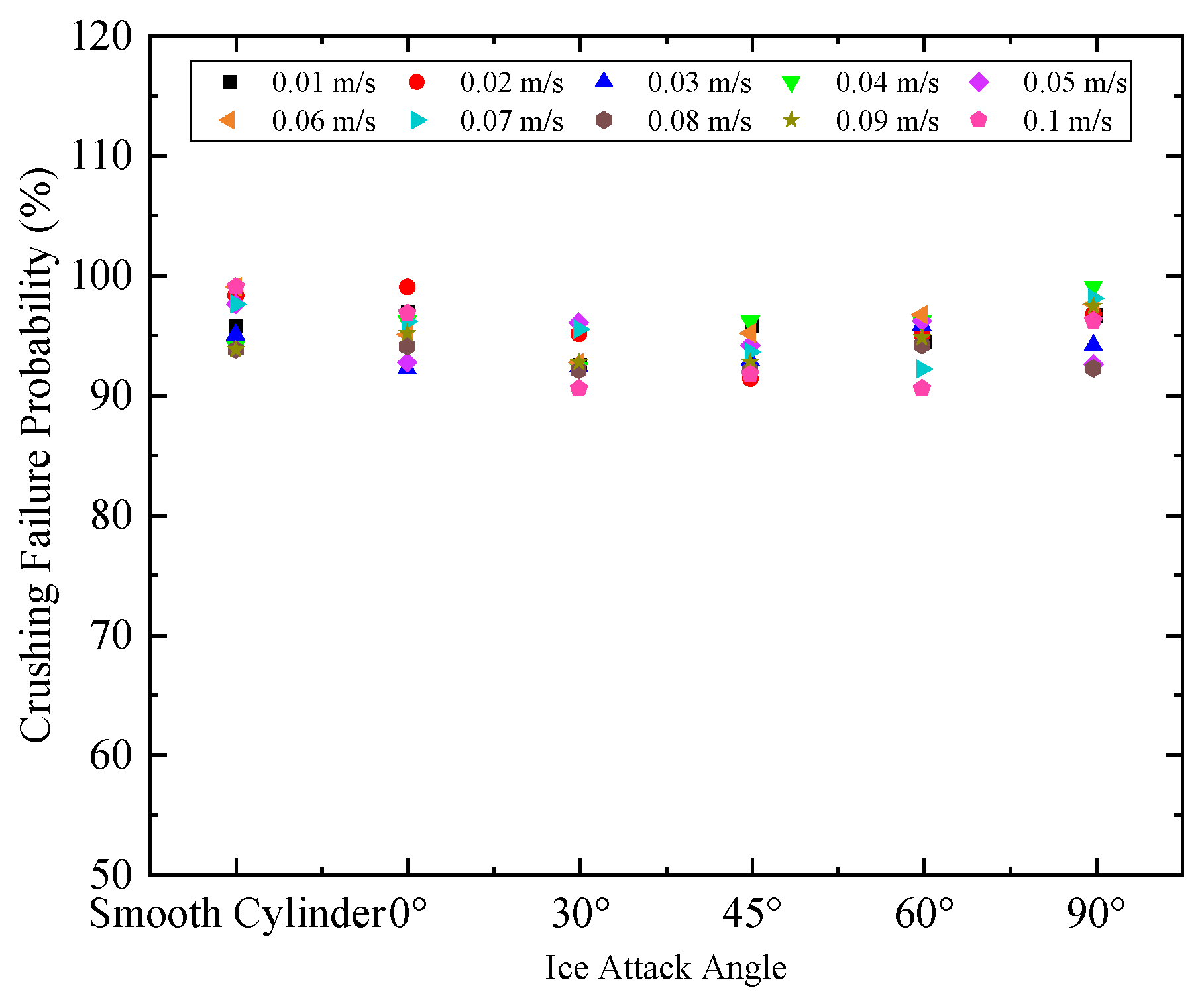
| Crushing Failure Probability/% | ||||||
|---|---|---|---|---|---|---|
| Ice Velocity/m/s | Ice Attack Angle/° | |||||
| Smooth Cylinder | 0 | 30 | 45 | 60 | 90 | |
| 0.01 | 95.76 | 96.88 | 92.50 | 95.76 | 94.44 | 96.67 |
| 0.02 | 98.31 | 100.00 | 95.08 | 91.30 | 95.00 | 96.72 |
| 0.03 | 95.00 | 92.16 | 92.31 | 92.86 | 95.83 | 94.12 |
| 0.04 | 94.00 | 96.08 | 92.16 | 96.08 | 96.08 | 100.00 |
| 0.05 | 97.56 | 92.68 | 96.00 | 94.12 | 96.15 | 92.50 |
| 0.06 | 100.00 | 95.00 | 92.68 | 95.12 | 96.67 | 97.56 |
| 0.07 | 97.56 | 96.08 | 95.45 | 93.55 | 92.11 | 98.04 |
| 0.08 | 93.75 | 94.00 | 92.00 | 92.00 | 94.12 | 92.16 |
| 0.09 | 93.75 | 95.12 | 92.68 | 92.68 | 94.74 | 97.37 |
| 0.1 | 100.00 | 96.77 | 90.48 | 91.67 | 90.48 | 96.15 |
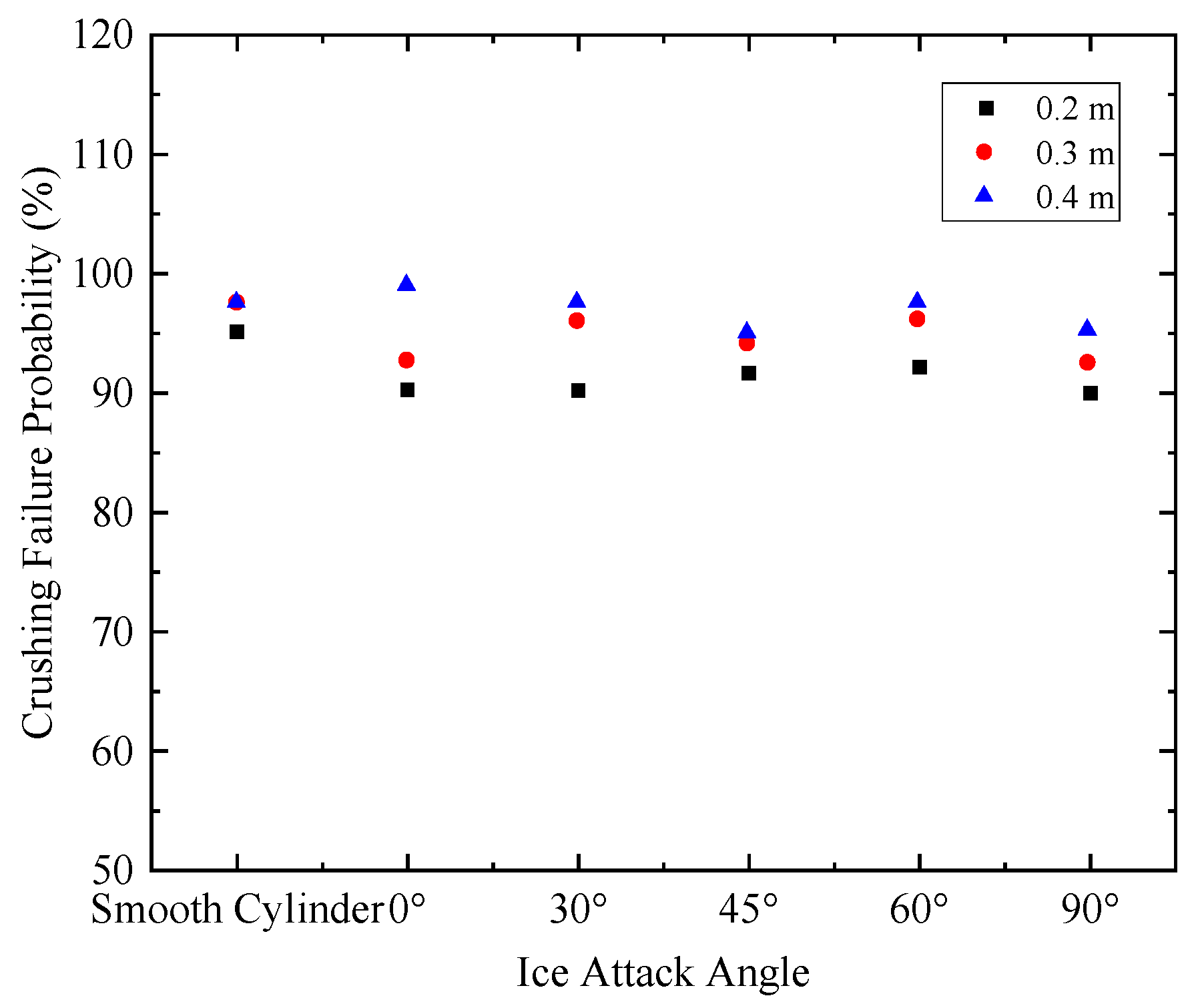
| Crushing Failure Probability/% | ||||||
|---|---|---|---|---|---|---|
| Ice Thickness/m | Ice Attack Angle/° | |||||
| Smooth Cylinder | 0 | 30 | 45 | 60 | 90 | |
| 0.2 | 95.12 | 90.24 | 90.20 | 91.67 | 92.16 | 90.00 |
| 0.3 | 97.56 | 92.68 | 96.00 | 94.12 | 96.15 | 92.50 |
| 0.4 | 97.56 | 100.00 | 97.56 | 95.00 | 97.56 | 95.24 |
| Ice Force Amplitude/kN | ||||||
|---|---|---|---|---|---|---|
| Ice Velocity/m/s | Ice Attack Angle/° | |||||
| Smooth Cylinder | 0 | 30 | 45 | 60 | 90 | |
| 0.01 | 354.36 | 441.23 | 318.47 | 308.03 | 303.62 | 293.12 |
| 0.02 | 429.21 | 484.79 | 324.46 | 312.47 | 311.42 | 301.43 |
| 0.03 | 306.59 | 368.65 | 290.21 | 277.11 | 275.78 | 270.21 |
| 0.04 | 401.86 | 458.38 | 362.95 | 357.11 | 352.20 | 335.86 |
| 0.05 | 344.32 | 373.05 | 322.62 | 312.18 | 305.25 | 275.52 |
| 0.06 | 419.00 | 471.31 | 361.53 | 351.45 | 343.59 | 341.13 |
| 0.07 | 378.87 | 415.55 | 329.42 | 291.20 | 289.14 | 282.46 |
| 0.08 | 305.83 | 373.42 | 278.99 | 272.93 | 269.34 | 257.32 |
| 0.09 | 345.33 | 409.57 | 299.76 | 291.65 | 287.93 | 282.23 |
| 0.1 | 297.07 | 371.16 | 278.20 | 271.25 | 269.64 | 268.58 |
| Ice Force Amplitude/kN | |||
|---|---|---|---|
| Ice Attack Angle/° | Ice Thickness/m | ||
| 0.2 | 0.3 | 0.4 | |
| Smooth Cylinder | 298.46 | 344.32 | 397.61 |
| 0° | 325.70 | 373.05 | 431.12 |
| 30° | 275.99 | 322.62 | 371.01 |
| 45° | 272.25 | 312.18 | 366.11 |
| 60° | 264.41 | 305.25 | 355.23 |
| 90° | 241.68 | 275.52 | 319.17 |
| Dia Method | 472.59 | 546.63 | 640.05 |
| Sum Method | 351.44 | 404.37 | 466.49 |
| Different Ice Attack Angles or Calculation Methods | Different Ice Attack Angles or Calculation Methods | ||
|---|---|---|---|
| 0° | 1.10 | 90° | 0.78 |
| 30° | 0.90 | Sum Method | 1.59 |
| 45° | 0.87 | Dia Method | 1.18 |
| 60° | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Dong, R.; Li, W.; Zhao, Y.; Wang, G.; Zhang, D. Numerical Simulation of Extreme Ice Loads on Complex Pile Legs of Offshore Substation Structures. J. Mar. Sci. Eng. 2024, 12, 838. https://doi.org/10.3390/jmse12050838
Zhang B, Dong R, Li W, Zhao Y, Wang G, Zhang D. Numerical Simulation of Extreme Ice Loads on Complex Pile Legs of Offshore Substation Structures. Journal of Marine Science and Engineering. 2024; 12(5):838. https://doi.org/10.3390/jmse12050838
Chicago/Turabian StyleZhang, Baofeng, Rui Dong, Wei Li, Yue Zhao, Guojun Wang, and Dayong Zhang. 2024. "Numerical Simulation of Extreme Ice Loads on Complex Pile Legs of Offshore Substation Structures" Journal of Marine Science and Engineering 12, no. 5: 838. https://doi.org/10.3390/jmse12050838
APA StyleZhang, B., Dong, R., Li, W., Zhao, Y., Wang, G., & Zhang, D. (2024). Numerical Simulation of Extreme Ice Loads on Complex Pile Legs of Offshore Substation Structures. Journal of Marine Science and Engineering, 12(5), 838. https://doi.org/10.3390/jmse12050838






