The Role of Different Total Water Level Definitions in Coastal Flood Modelling on a Low-Elevation Dune System
Abstract
1. Introduction
2. Study Area
3. Datasets
3.1. Definition of the Total Water Levels
3.2. Inundation Modelling
4. Methodology
4.1. Definitions
- Component: the representative value of one or more components of the total water level. The components can be either static or dynamic according to their nature. They can also be divided into three categories according to the method used to calculate the extreme value;
- Static Component: a component whose variability in time is limited and whose physical behaviour can be represented by a static (fixed) value;
- Dynamic Component: a component whose value cannot be represented correctly by attributing a fixed value. The only component in this category is the dynamic runup.
4.2. Extreme Event Analysis
4.2.1. Extreme Value Analysis
- Number of extreme events per year. Based on the literature and local studies, the area of Emilia-Romagna is affected by 2 to 6 storms per year. If the results of the combinations of variables for the EVA did not fit this range, it was not considered for the final analysis;
- Statistical values of Pearson r PP and QQ. The pyextremes package provided statistical values of extreme events analyses, in which Pearson r PP and QQ are included. If the statistics’ values were considered statistically representative (>0.97), the extreme value was included in the analysis of TWL.
4.2.2. Total Water Level Combinations
4.2.3. Selection of Representative Values
4.3. Flood Model Configuration
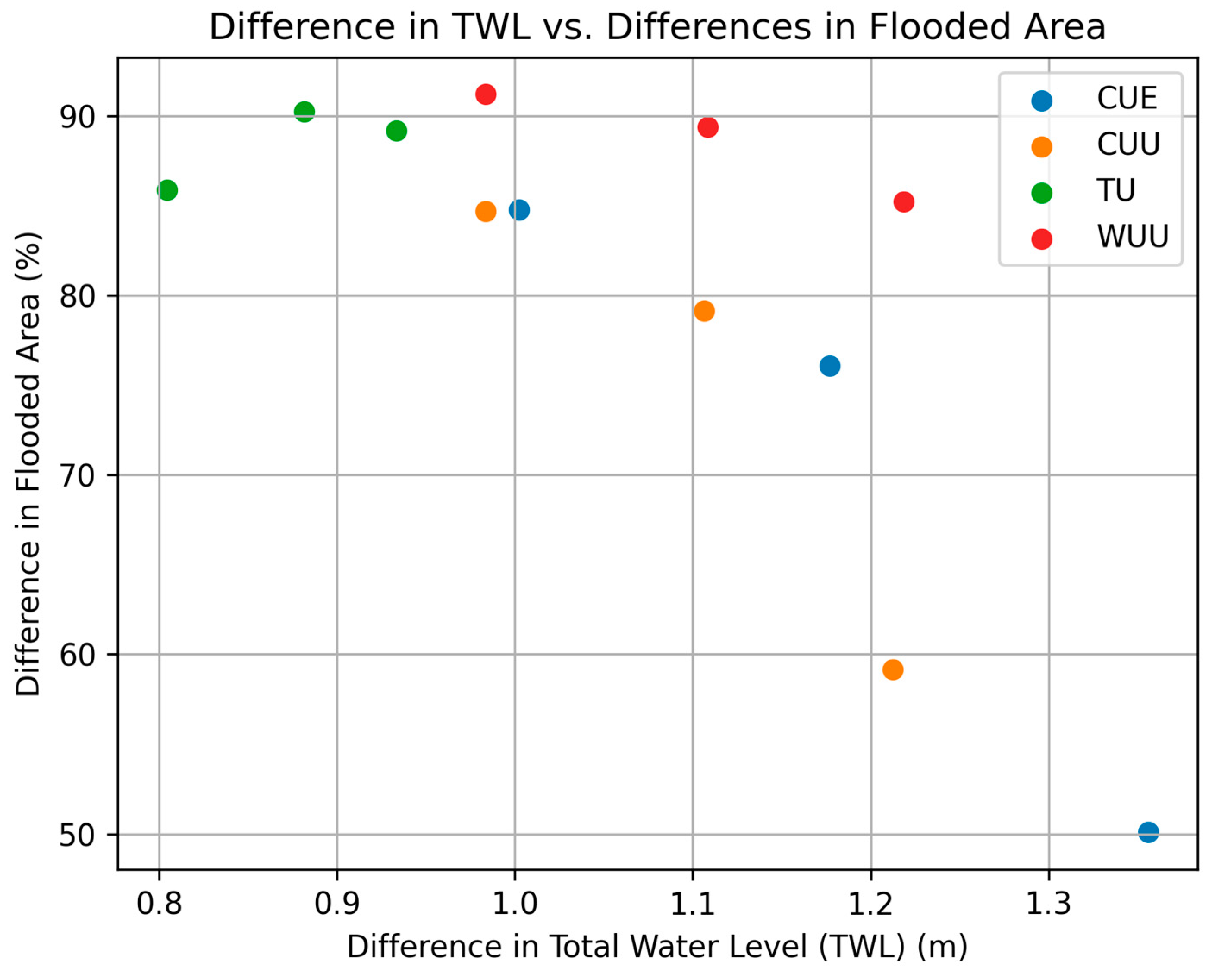
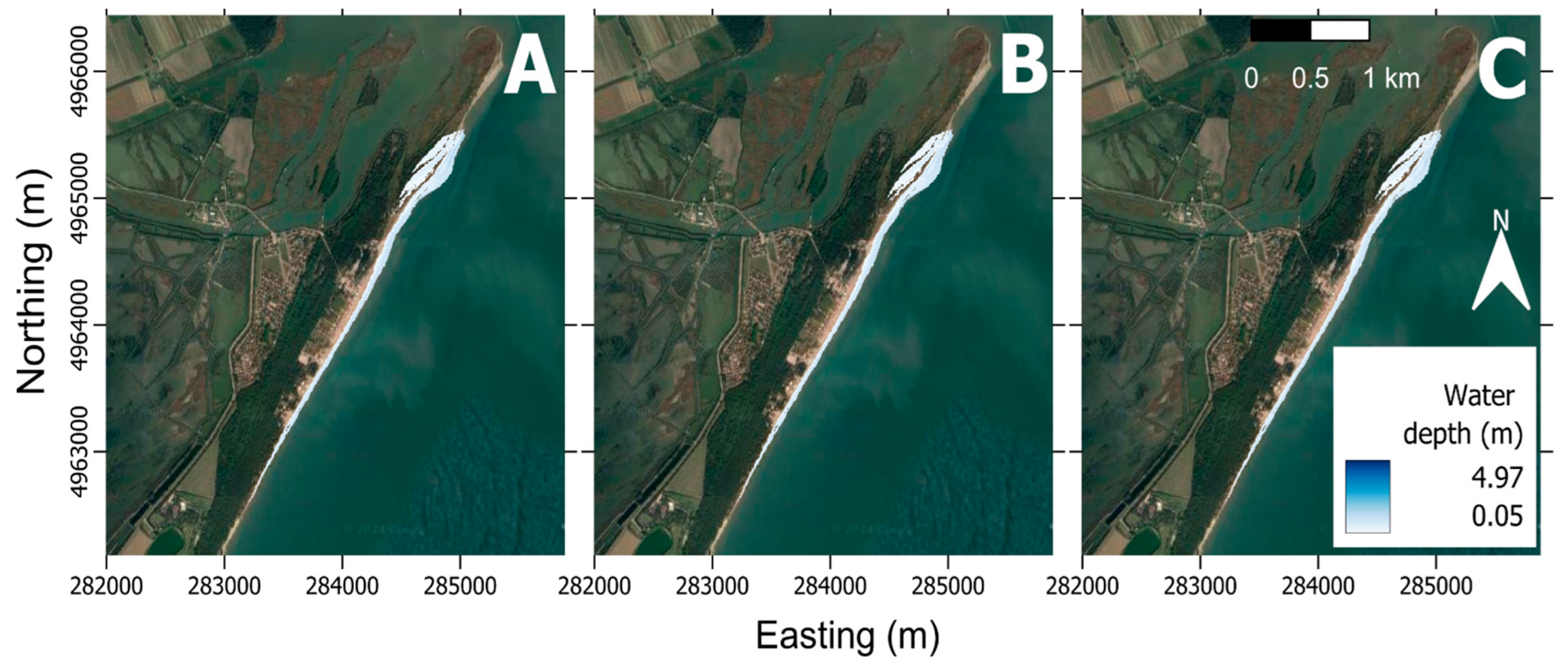
5. Results
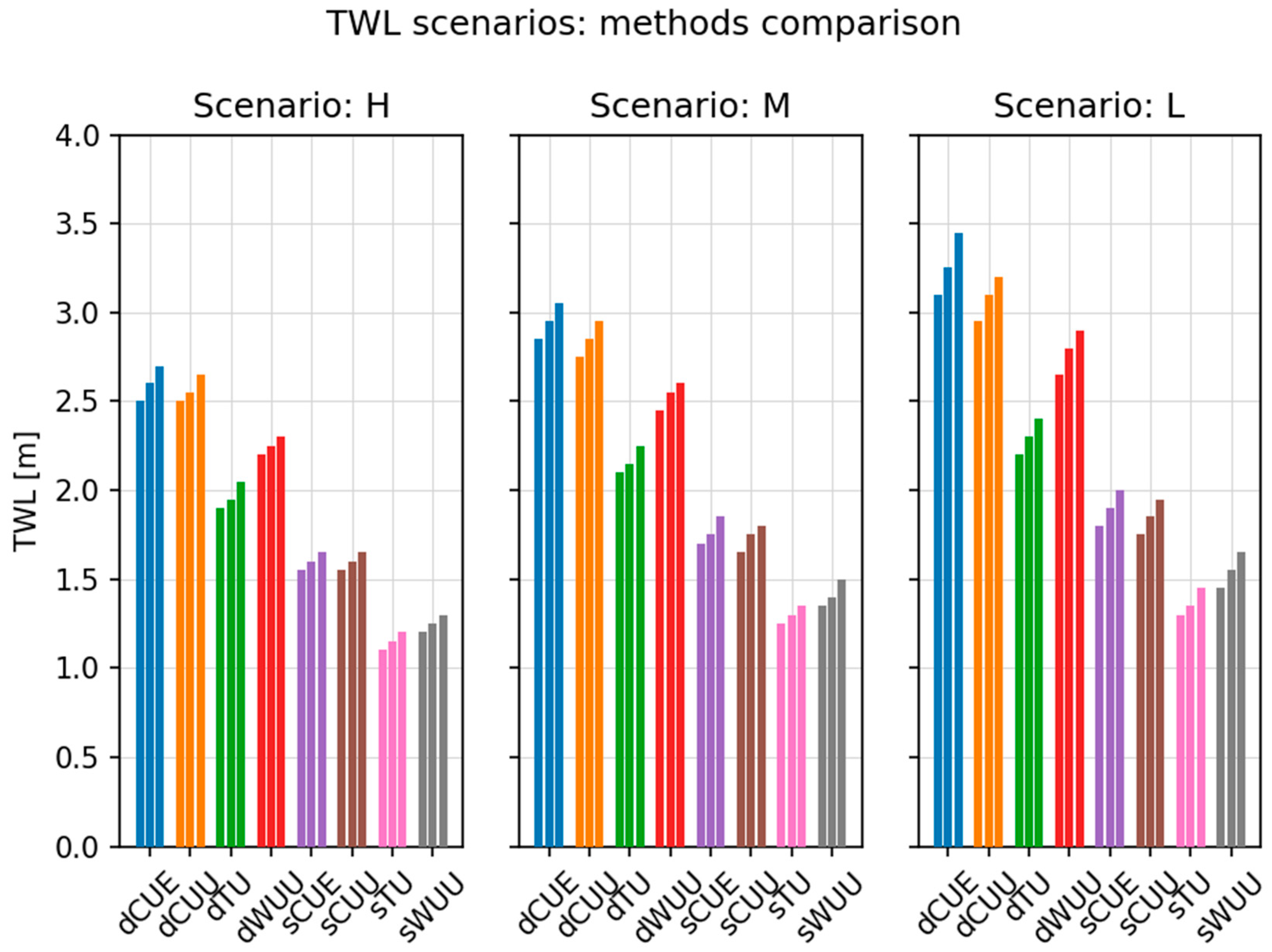
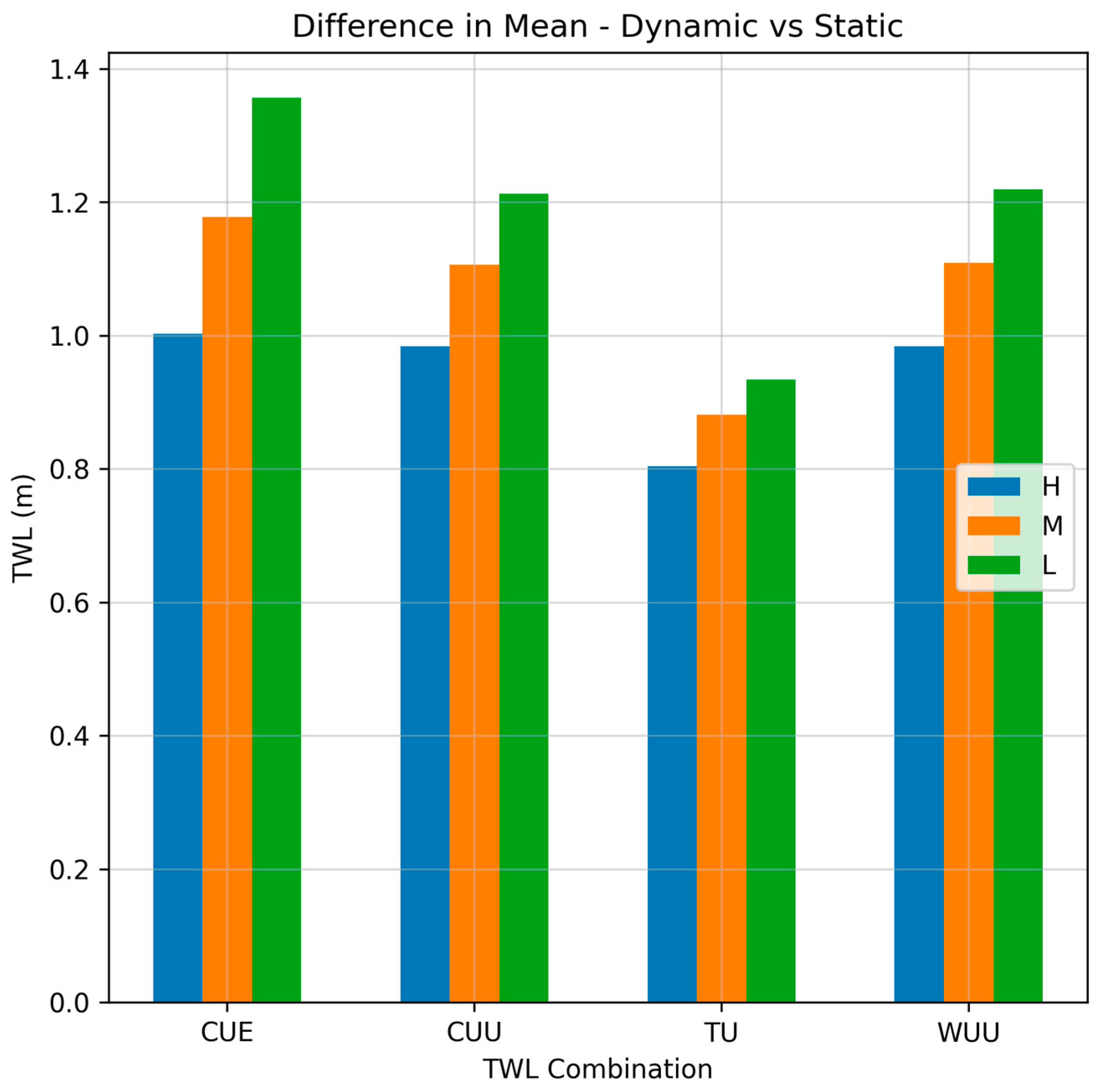
5.1. Nearshore Total Water Levels
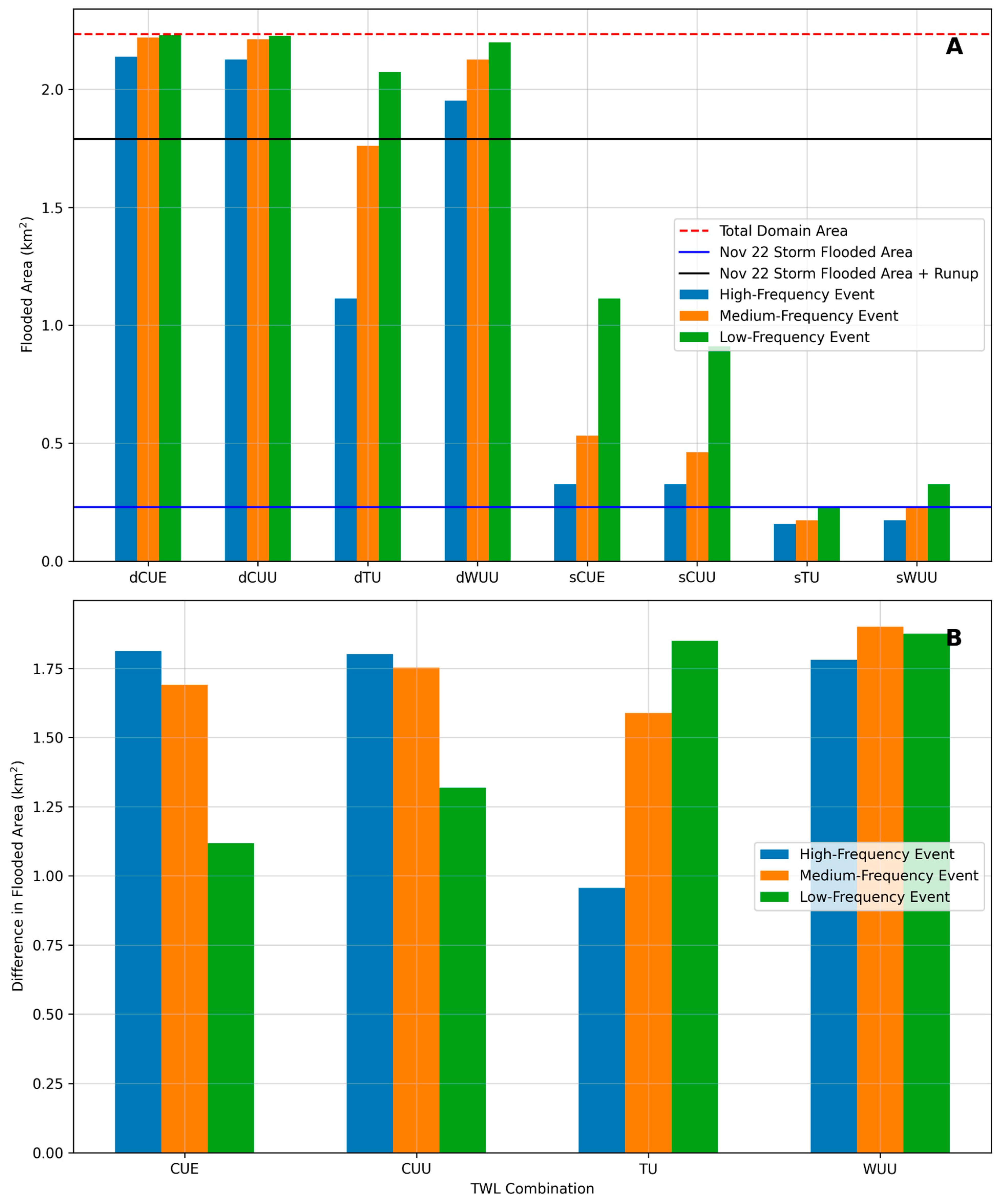
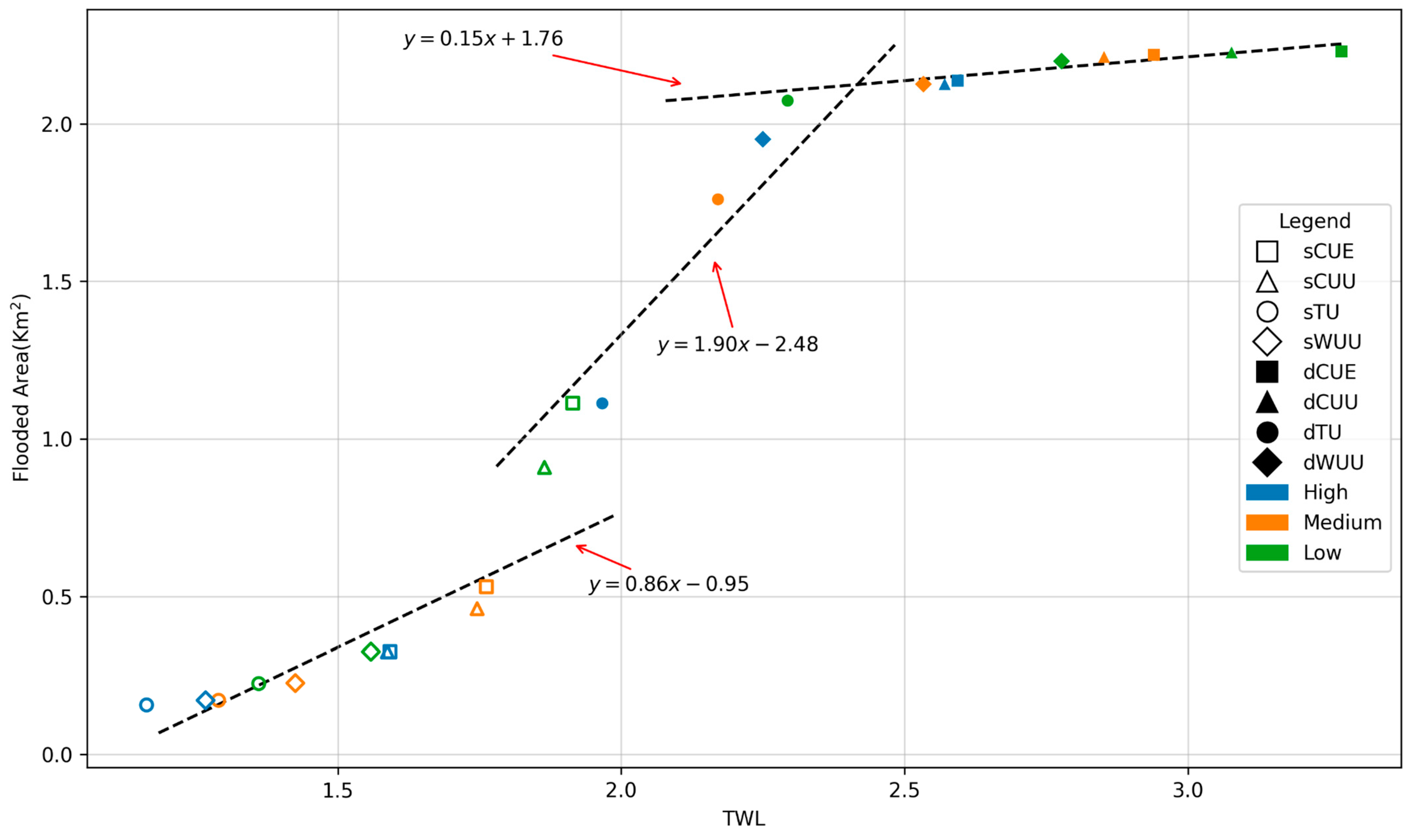
5.2. Flood Extension Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harley, M. Coastal Storm Definition. In Coastal Storms; Coco, G., Ciavola, P., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 1–21. [Google Scholar]
- Reimann, L.; Vafeidis, A.T.; Honsel, L.E. Population Development as a Driver of Coastal Risk: Current Trends and Future Pathways. Camb. Prism. Coast. Futures 2023, 1, e14. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling Storm Impacts on Beaches, Dunes and Barrier Islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Deltares. Delft3D Flexible Mesh Suite 1D/2D/3D Modelling Suite for Integral Water Solutions; Deltares: Delft, The Netherlands, 2023. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-Generation Wave Model for Coastal Regions 1. Model Description and Validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Tolman, H.L.; Balasubramaniyan, B.; Burroughs, L.D.; Chalikov, D.V.; Chao, Y.Y.; Chen, H.S.; Gerald, V.M. Development and Implementation of Wind-Generated Ocean Surface Wave Models at NCEP. Weather. Forecast. 2001, 17, 311–333. [Google Scholar] [CrossRef]
- Kir, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0 Fully Nonlinear Boussinesq Wave Mode. Documentation and User’s Manual. 1998. Available online: https://repository.tudelft.nl/islandora/object/uuid:d79bba08-8d35-47e2-b901-881c86985ce4/datastream/OBJ/download (accessed on 9 June 2024).
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A High-Order Adaptive Time-Stepping TVD Solver for Boussinesq Modeling of Breaking Waves and Coastal Inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Liu, W.; Ning, Y.; Shi, F.; Sun, Z. A 2DH Fully Dispersive and Weakly Nonlinear Boussinesq-Type Model Based on a Finite-Volume and Finite-Difference TVD-Type Scheme. Ocean Model. 2020, 147, 101559. [Google Scholar] [CrossRef]
- Ning, Y.; Liu, W.; Zhao, X.; Zhang, Y.; Sun, Z. Study of Irregular Wave Run-up over Fringing Reefs Based on a Shock-Capturing Boussinesq Model. Appl. Ocean. Res. 2019, 84, 216–224. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A Simple Raster-Based Model for Flood Inundation Simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Bates, P.D.; Dawson, R.J.; Hall, J.W.; Horritt, M.S.; Nicholls, R.J.; Wicks, J.; Ali Mohamed Hassan, M.A. Simplified Two-Dimensional Numerical Modelling of Coastal Flooding and Example Applications. Coast. Eng. 2005, 52, 793–810. [Google Scholar] [CrossRef]
- Sharifian, M.K.; Kesserwani, G.; Chowdhury, A.A.; Neal, J.; Bates, P. LISFLOOD-FP 8.1: New GPU-Accelerated Solvers for Faster Fluvial/Pluvial Flood Simulations. Geosci. Model. Dev. 2023, 16, 2391–2413. [Google Scholar] [CrossRef]
- Warner, J.C.; Defne, Z.; Haas, K.; Arango, H.G. A Wetting and Drying Scheme for ROMS. Comput. Geosci. 2013, 58, 54–61. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless Cross-Scale Modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Galland, J.-C.; Goutal, N.; Hervouet, J.-M. TELEMAC: A New Numerical Model for Solving Shallow Water Equations. Adv. Water Resour. 1991, 14, 138–148. [Google Scholar] [CrossRef]
- DHI MIKE 21 Flow Model & MIKE 21 Flood Screening Tool. Hydrodynamic Module Scientific Documentation; 2022. Available online: https://manuals.mikepoweredbydhi.help/2017/Coast_and_Sea/M21HDFST_Scientific_Doc.pdf (accessed on 13 June 2024).
- Le Gal, M.; Fernández-Montblanc, T.; Duo, E.; Montes Perez, J.; Cabrita, P.; Souto Ceccon, P.; Gastal, V.; Ciavola, P.; Armaroli, C. A New European Coastal Flood Database for Low–Medium Intensity Events. Nat. Hazards Earth Syst. Sci. 2023, 23, 3585–3602. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Mentaschi, L.; Dottori, F.; Giardino, A.; Bouziotas, D.; Bianchi, A.; Salamon, P.; Feyen, L. Developments in Large-Scale Coastal Flood Hazard Mapping. Nat. Hazards Earth Syst. Sci. 2016, 16, 1841–1853. [Google Scholar] [CrossRef]
- Armaroli, C.; Duo, E.; Viavattene, C. From Hazard to Consequences: Evaluation of Direct and Indirect Impacts of Flooding Along the Emilia-Romagna Coastline, Italy. Front. Earth Sci. 2019, 7, 1–20. [Google Scholar] [CrossRef]
- Smith, R.A.E.; Bates, P.D.; Hayes, C. Evaluation of a Coastal Flood Inundation Model Using Hard and Soft Data. Environ. Model. Softw. 2012, 30, 35–46. [Google Scholar] [CrossRef]
- Carneiro-Barros, J.E.; Plomaritis, T.A.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F. Coastal Flood Mapping with Two Approaches Based on Observations at Furadouro, Northern Portugal. Remote Sens. 2023, 15, 5215. [Google Scholar] [CrossRef]
- Purvis, M.J.; Bates, P.D.; Hayes, C.M. A Probabilistic Methodology to Estimate Future Coastal Flood Risk Due to Sea Level Rise. Coast. Eng. 2008, 55, 1062–1073. [Google Scholar] [CrossRef]
- Lyddon, C.E.; Brown, J.M.; Leonardi, N.; Plater, A.J. Sensitivity of Flood Hazard and Damage to Modelling Approaches. J. Mar. Sci. Eng. 2020, 8, 724. [Google Scholar] [CrossRef]
- Paprotny, D.; Morales-Nápoles, O.; Vousdoukas, M.I.; Jonkman, S.N.; Nikulin, G. Accuracy of Pan-European Coastal Flood Mapping. J. Flood Risk Manag. 2019, 12, e12459. [Google Scholar] [CrossRef]
- Plomaritis, T.A.; Costas, S.; Ferreira, Ó. Use of a Bayesian Network for Coastal Hazards, Impact and Disaster Risk Reduction Assessment at a Coastal Barrier (Ria Formosa, Portugal). Coast. Eng. 2018, 134, 134–147. [Google Scholar] [CrossRef]
- Poelhekke, L.; Jäger, W.S.; van Dongeren, A.; Plomaritis, T.A.; McCall, R.; Ferreira, Ó. Predicting Coastal Hazards for Sandy Coasts with a Bayesian Network. Coast. Eng. 2016, 118, 21–34. [Google Scholar] [CrossRef]
- Pugh, D. Tides, Surges, and Mean Sea-Level; J. Wiley and Sons: Hoboken, NJ, USA, 1987; ISBN 047191505X. [Google Scholar]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global Probabilistic Projections of Extreme Sea Levels Show Intensification of Coastal Flood Hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef]
- Jiménez, J.; Ciavola, P.; Balouin, Y.; Armaroli, C.; Bosom, E.; Gervais, M. Geomorphic Coastal Vulnerability to Storms in Microtidal Fetch-Limited Environments: Application to NW Mediterranean & N Adriatic Seas. J. Coast. Res. 2009, 56, 1641–1645. [Google Scholar]
- Del Río, L.; Plomaritis, T.A.; Benavente, J.; Valladares, M.; Ribera, P. Establishing Storm Thresholds for the Spanish Gulf of Cádiz Coast. Geomorphology 2012, 143–144, 13–23. [Google Scholar] [CrossRef]
- Rulent, J.; Calafat, F.M.; Banks, C.J.; Bricheno, L.M.; Gommenginger, C.; Green, J.A.M.; Haigh, I.D.; Lewis, H.; Martin, A.C.H. Comparing Water Level Estimation in Coastal and Shelf Seas From Satellite Altimetry and Numerical Models. Front. Mar. Sci. 2020, 7, 549467. [Google Scholar] [CrossRef]
- Croteau, R.; Pacheco, A.; Ferreira, Ó. Flood Vulnerability under Sea Level Rise for a Coastal Community Located in a Backbarrier Environment, Portugal. J. Coast. Conserv. 2023, 27, 28. [Google Scholar] [CrossRef]
- Caruso, M.F.; Marani, M. Extreme-Coastal-Water-Level Estimation and Projection: A Comparison of Statistical Methods. Nat. Hazards Earth Syst. Sci. 2022, 22, 1109–1128. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A.; Archetti, R. Coastal Flooding: A Copula Based Approach for Estimating the Joint Probability of Water Levels and Waves. Coast. Eng. 2015, 97, 37–52. [Google Scholar] [CrossRef]
- Perini, L.; Calabrese, L.; Lorito, S.; Luciani, P. Costal Flood Risk in Emilia-Romagna (Italy): The Sea Storm of February 2015. In Proceedings of the Coastal and Maritime Mediterranean Conference, Edition 3, Ferrara, Italy, 25–27 November 2015; pp. 225–230. [Google Scholar]
- Perini, L.; Calabrese, L.; Lorito, S.; Luciani, P. Il Rischio Da Mareggiata in Emilia-Romagna: L’evento Del 5–6 Febbraio 2015. Il Geol. Vol. 2015, 53, 8–17. [Google Scholar]
- Harley, M.D.; Valentini, A.; Armaroli, C.; Perini, L.; Calabrese, L.; Ciavola, P. Can an Early-Warning System Help Minimize the Impacts of Coastal Storms? A Case Study of the 2012 Halloween Storm, Northern Italy. Nat. Hazards Earth Syst. Sci. 2016, 16, 209–222. [Google Scholar] [CrossRef]
- Duo, E.; Chris Trembanis, A.; Dohner, S.; Grottoli, E.; Ciavola, P. Local-Scale Post-Event Assessments with GPS and UAV-Based Quick-Response Surveys: A Pilot Case from the Emilia-Romagna (Italy) Coast. Nat. Hazards Earth Syst. Sci. 2018, 18, 2969–2989. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P.; Perini, L.; Calabrese, L.; Lorito, S.; Valentini, A.; Masina, M. Critical Storm Thresholds for Significant Morphological Changes and Damage along the Emilia-Romagna Coastline, Italy. Geomorphology 2012, 143–144, 34–51. [Google Scholar] [CrossRef]
- Perini, L.; Calabrese, L.; Lelli, J.; Fabbri, S.; Ciavola, P. Le Dune Costiere al 2019—Stato e Analisi Evolutive Periodo 2004–2019; Regione Emilia-Romagna: Bologna, Italy, 2023; Available online: https://ambiente.regione.emilia-romagna.it/it/geologia/pubblicazioni/poster/le-dune-costiere-al-2019-stato-e-analisi-evolutive-periodo-2004-2019-2023 (accessed on 13 June 2024).
- Masina, M.; Ciavola, P. Analisi Dei Livelli Marini Estremi e Delle Acque Alte Lungo Il Litorale Ravennate. Studi Costieri 2011, 18, 84–98. [Google Scholar]
- Perini, L.; Calabrese, L.; Deserti, M.; Valentini, A.; Ciavola, P.; Armaroli, C. Le Mareggiate e Gli Impatti Sulla Costa in Emilia-Romagna 1946–2010; Arpa Emilia-Romagna: Bologna, Italy, 2011; ISBN 88-87854-27-5. [Google Scholar]
- Mel, R.A.; Coraci, E.; Morucci, S.; Crosato, F.; Cornello, M.; Casaioli, M.; Mariani, S.; Carniello, L.; Papa, A.; Bonometto, A.; et al. Insights on the Extreme Storm Surge Event of the 22 November 2022 in the Venice Lagoon. J. Mar. Sci. Eng. 2023, 11, 1750. [Google Scholar] [CrossRef]
- Ferrarin, C.; Bajo, M.; Barbariol, F.; Benetazzo, A. Sea Level and Wave Hindcast for the Northern Adriatic Sea, 2024 [Data Set]. Available online: https://doi.org/10.5281/zenodo.10683078 (accessed on 13 June 2024).
- Umgiesser, G.; Canu, D.M.; Cucco, A.; Solidoro, C. A Finite Element Model for the Venice Lagoon. Development, Set up, Calibration and Validation. J. Mar. Syst. 2004, 51, 123–145. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical Parameterization of Setup, Swash, and Runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Innerbichler, F.; Kreisel, A.; Gruber, C. Nomenclature and Mapping Guideline—Coastal Zones Land Cover/Land Use 2012 and 2018 and Land Cover/Land Use Change 2012–2018. 2021. Available online: https://land.copernicus.eu/en/technical-library/coastal-zones-nomenclature-and-mapping-guideline/@@download/file (accessed on 9 June 2024).
- European Environment Agency Coastal Zones Land Cover/Land Use 2018 (Vector), Europe, 6-Yearly, Feb. 2021. 2020. Available online: https://doi.org/10.2909/205e2db2-4e35-4b1b-bf84-271c4a82248c (accessed on 13 June 2024).
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Papaioannou, G.; Efstratiadis, A.; Vasiliades, L.; Loukas, A.; Papalexiou, S.M.; Koukouvinos, A.; Tsoukalas, I.; Kossieris, P. An Operational Method for Flood Directive Implementation in Ungauged Urban Areas. Hydrology 2018, 5, 24. [Google Scholar] [CrossRef]
- Korres, G.; Oikonomou, C.; Denaxa, D.; Sotiropoulou, M. Mediterranean Sea Waves Analysis and Forecast (Copernicus Marine Service MED-Waves, MEDWAΜ4 System) (Version 1), Copernic. Mar. Serv., 2023 [Data Set]. Available online: https://doi.org/10.25423/CMCC/MEDSEA_ANALYSISFORECAST_WAV_006_017_MEDWAM4 (accessed on 13 June 2024).
- Duo, E.; Sanuy, M.; Jiménez, J.A.; Ciavola, P. How Good Are Symmetric Triangular Synthetic Storms to Represent Real Events for Coastal Hazard Modelling. Coast. Eng. 2020, 159, 103728. [Google Scholar] [CrossRef]
- Beniston, M.; Stephenson, D.B. Extreme Climatic Events and Their Evolution under Changing Climatic Conditions. Glob. Planet. Change 2004, 44, 1–9. [Google Scholar] [CrossRef]
- Sanuy, M.; Jiménez, J.A.; Ortego, M.I.; Toimil, A. Differences in Assigning Probabilities to Coastal Inundation Hazard Estimators: Event versus Response Approaches. J. Flood Risk Manag. 2020, 13, e12557. [Google Scholar] [CrossRef]
- Bergeson, C.B.; Martin, K.L.; Doll, B.; Cutts, B.B. Soil Infiltration Rates Are Underestimated by Models in an Urban Watershed in Central North Carolina, USA. J. Environ. Manag. 2022, 313, 115004. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A Simple Inertial Formulation of the Shallow Water Equations for Efficient Two-Dimensional Flood Inundation Modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How Much Physical Complexity Is Needed to Model Flood Inundation? Hydrol. Process. 2012, 26, 2264–2282. [Google Scholar] [CrossRef]
- Shaw, J.; Kesserwani, G.; Neal, J.; Bates, P.; Sharifian, M.K. LISFLOOD-FP 8.0: The New Discontinuous Galerkin Shallow-Water Solver for Multi-Core CPUs and GPUs. Geosci. Model. Dev. 2021, 14, 3577–3602. [Google Scholar] [CrossRef]
- Le Gal, M.; Fernández-Montblanc, T.; Montes Perez, J.; Duo, E.; Souto Ceccon, P.; Ciavola, P.; Armaroli, C. Influence of Model Configuration for Coastal Flooding across Europe. Coast. Eng. 2024, 192, 104541. [Google Scholar] [CrossRef]
- Sanuy, M.; Duo, E.; Jäger, W.S.; Ciavola, P.; Jiménez, J.A. Linking Source with Consequences of Coastal Storm Impacts for Climate Change and Risk Reduction Scenarios for Mediterranean Sandy Beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 1825–1847. [Google Scholar] [CrossRef]
- Sallenger, A.H. Storm Impact Scale for Barrier Islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Stockdon, H.F.; Long, J.W.; Palmsten, M.L.; Van der Westhuysen, A.; Doran, K.S.; Snell, R.J. Operational Forecasts of Wave-Driven Water Levels and Coastal Hazards for US Gulf and Atlantic Coasts. Commun. Earth Environ. 2023, 4, 169. [Google Scholar] [CrossRef]
- Haigh, I.D.; Wijeratne, E.; Macpherson, L.R.; Mason, M.S. Estimating Present Day Extreme Total Water Level Exceedance Probabilities around the Coastline of Australia; Antarctic Climate and Ecosystems Cooperative Research Centre: Hobart, Australia, 2012; ISBN 978-0-9871939-2-6. [Google Scholar]
- Serafin, K.A.; Ruggiero, P. Simulating Extreme Total Water Levels Using a Time-Dependent, Extreme Value Approach. J. Geophys. Res. Ocean. 2014, 119, 6305–6329. [Google Scholar] [CrossRef]
- Duo, E.; Fabbri, S.; Grottoli, E.; Ciavola, P. Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes. Remote Sens. 2021, 13, 1823. [Google Scholar] [CrossRef]
- Serafin, K.A.; Ruggiero, P.; Stockdon, H.F. The Relative Contribution of Waves, Tides, and Nontidal Residuals to Extreme Total Water Levels on U.S. West Coast Sandy Beaches. Geophys. Res. Lett. 2017, 44, 1839–1847. [Google Scholar] [CrossRef]
- van Ormondt, M.; Roelvink, D.; van Dongeren, A. A Model-Derived Empirical Formulation for Wave Run-up on Naturally Sloping Beaches. J. Mar. Sci. Eng. 2021, 9, 1185. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Moradkhani, H.; Pappenberger, F.; Moftakhari, H.; Bates, P.; Abbaszadeh, P.; Marsooli, R.; Ferreira, C.; Cloke, H.L.; Ogden, F.; et al. Recent Advances and New Frontiers in Riverine and Coastal Flood Modeling. Rev. Geophys. 2023, 61, e2022RG000788. [Google Scholar] [CrossRef]
- Cueto, J.E.; Otero Díaz, L.J.; Ospino-Ortiz, S.R.; Torres-Freyermuth, A. The Role of Morphodynamics in Predicting Coastal Flooding from Storms on a Dissipative Beach with Sea Level Rise Conditions. Nat. Hazards Earth Syst. Sci. 2022, 22, 713–728. [Google Scholar] [CrossRef]
- Ferreira, Ó.; Plomaritis, T.A.; Costas, S. Effectiveness Assessment of Risk Reduction Measures at Coastal Areas Using a Decision Support System: Findings from Emma Storm. Sci. Total Environ. 2019, 657, 124–135. [Google Scholar] [CrossRef]
- Zornoza-Aguado, M.; Pérez-Díaz, B.; Cagigal, L.; Castanedo, S.; Méndez, F.J. An Efficient Metamodel to Downscale Total Water Level in Open Beaches. Estuar. Coast. Shelf Sci. 2024, 299, 108705. [Google Scholar] [CrossRef]
- Taramelli, A.; Di Matteo, L.; Ciavola, P.; Guadagnano, F.; Tolomei, C. Temporal Evolution of Patterns and Processes Related to Subsidence of the Coastal Area Surrounding the Bevano River Mouth (Northern Adriatic)—Italy. Ocean Coast. Manag. 2015, 108, 74–88. [Google Scholar] [CrossRef]
- Fernández-Montblanc, T.; Duo, E.; Ciavola, P. Dune Reconstruction and Revegetation as a Potential Measure to Decrease Coastal Erosion and Flooding under Extreme Storm Conditions. Ocean Coast. Manag. 2020, 188, 105075. [Google Scholar] [CrossRef]




| Component | Base | Univariate | Estimated |
|---|---|---|---|
| MSL | Local (0 m) | - | - |
| Tide | MHW: Mean High Water | ||
| MHWS: Mean High Water Springs | - | - | |
| HAT: Maximum Astronomical Tide | |||
| Residual | - | Time series (water level—tide time series) | - |
| Setup | - | Stockdon et al. [47] time series | Stockdon et al. [47] Single value |
| Dynamic Runup | - | Stockdon et al. [47] Runup-Setup, time series | Stockdon et al. [47] Runup-Setup, Single value |
| Water level | - | Time series (Residual + Tide) | - |
| TWL static | - | Time series (water level + setup) | - |
| TWL dynamic | - | Time series (water level + setup + dynamic Runup) | - |
| TWL Acronyms | Used Component |
|---|---|
| dCUE | MSL (base) + Tide (Highs) + Residual + Estimated nearshore components (setup and dynamic runup) |
| dCUU | MSL (base) + Tide (Highs) + Residual + Univariated nearshore components (setup and dynamic runup) |
| dTU | TWL dynamic [MSL (base) + Tide (Highs) + Residual + Univariated nearshore components (setup and dynamic runup)] Based on Sanuy et al. [55] |
| dWUU | Water Level [MSL (base) + Tide (Highs) + Residual] + Univariated nearshore components (setup and dynamic runup) |
| sCUE | MSL (base) + Tide (Highs) + Residual + Estimated Setup |
| sCUU | MSL (base) + Tide (Highs) + Residual + Univariated Setup |
| sTU | TWL static[ MSL (base) + Tide (Highs) + Residual + Univariated setup] Based on Sanuy et al. [55] |
| sWUU | Water Level [ MSL (base) + Tide (Highs) + Residual] + Univariated Setup |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrita, P.; Montes, J.; Duo, E.; Brunetta, R.; Ciavola, P. The Role of Different Total Water Level Definitions in Coastal Flood Modelling on a Low-Elevation Dune System. J. Mar. Sci. Eng. 2024, 12, 1003. https://doi.org/10.3390/jmse12061003
Cabrita P, Montes J, Duo E, Brunetta R, Ciavola P. The Role of Different Total Water Level Definitions in Coastal Flood Modelling on a Low-Elevation Dune System. Journal of Marine Science and Engineering. 2024; 12(6):1003. https://doi.org/10.3390/jmse12061003
Chicago/Turabian StyleCabrita, Paulo, Juan Montes, Enrico Duo, Riccardo Brunetta, and Paolo Ciavola. 2024. "The Role of Different Total Water Level Definitions in Coastal Flood Modelling on a Low-Elevation Dune System" Journal of Marine Science and Engineering 12, no. 6: 1003. https://doi.org/10.3390/jmse12061003
APA StyleCabrita, P., Montes, J., Duo, E., Brunetta, R., & Ciavola, P. (2024). The Role of Different Total Water Level Definitions in Coastal Flood Modelling on a Low-Elevation Dune System. Journal of Marine Science and Engineering, 12(6), 1003. https://doi.org/10.3390/jmse12061003








