Numerical Investigation of Solitary Wave Attenuation by a Vertical Plate-Type Flexible Breakwater Constructed Using Hyperelastic Neo-Hookean Material
Abstract
1. Introduction
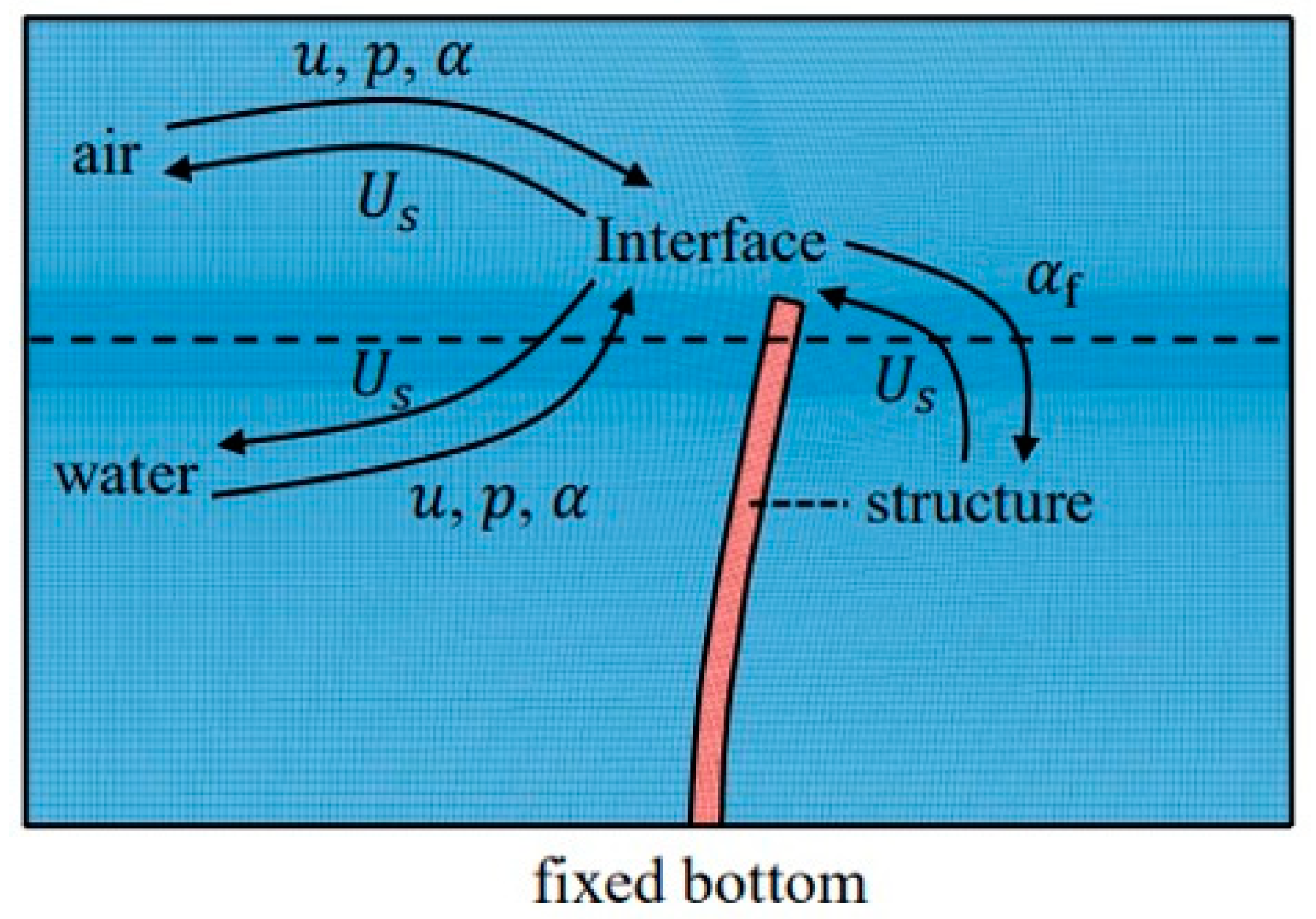
2. Numerical Methods
2.1. Fluid Solver
2.2. Structural Solver
2.3. Coupling Algorithm
3. Results
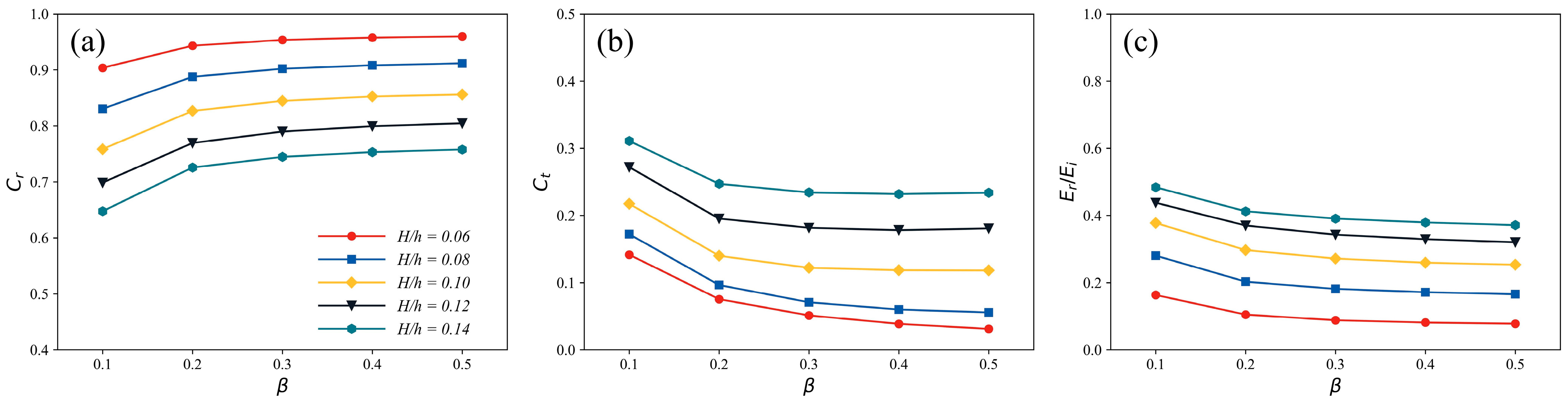
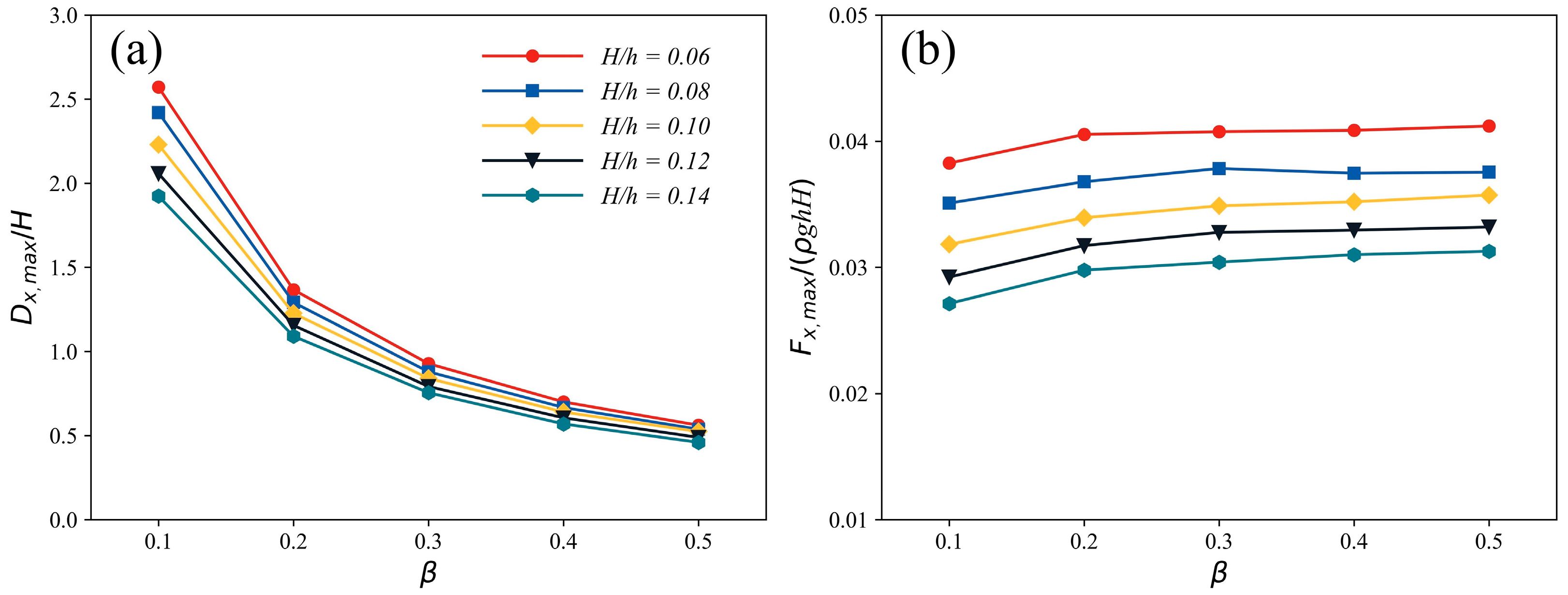
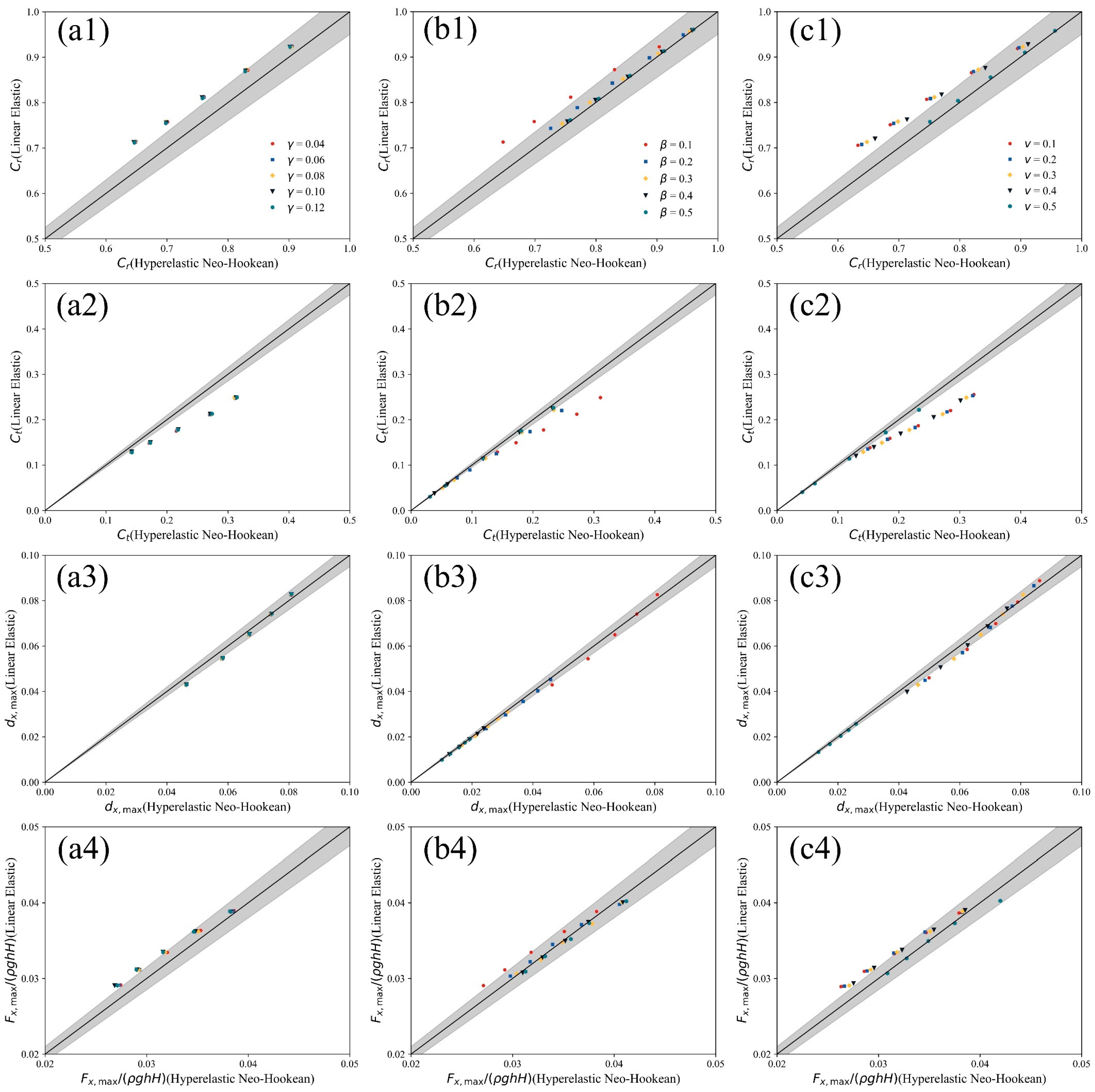
3.1. Effects of Mass Coefficient
3.2. Effects of Stiffness Coefficient
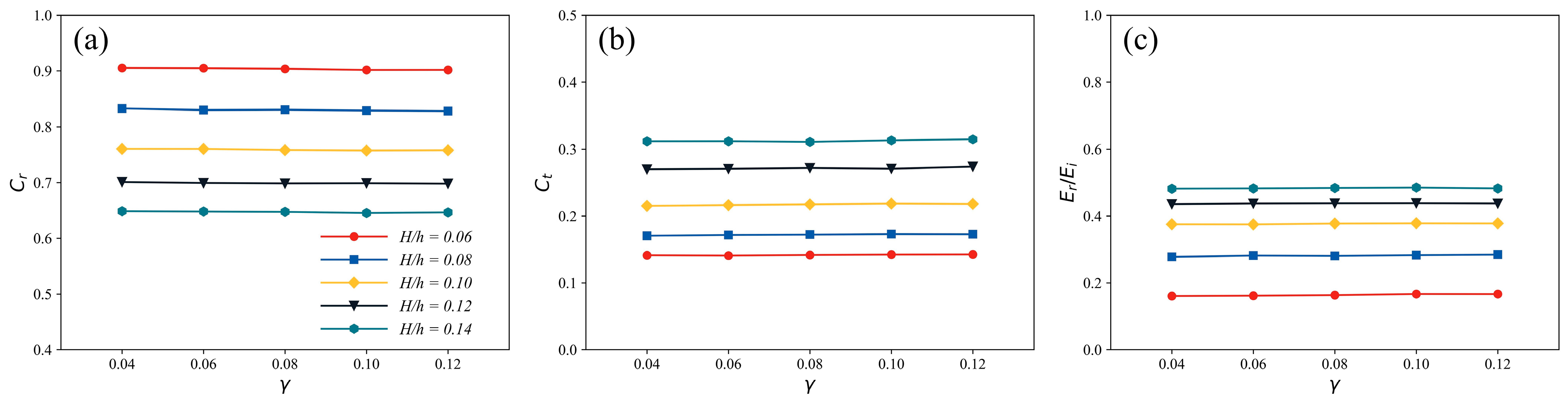
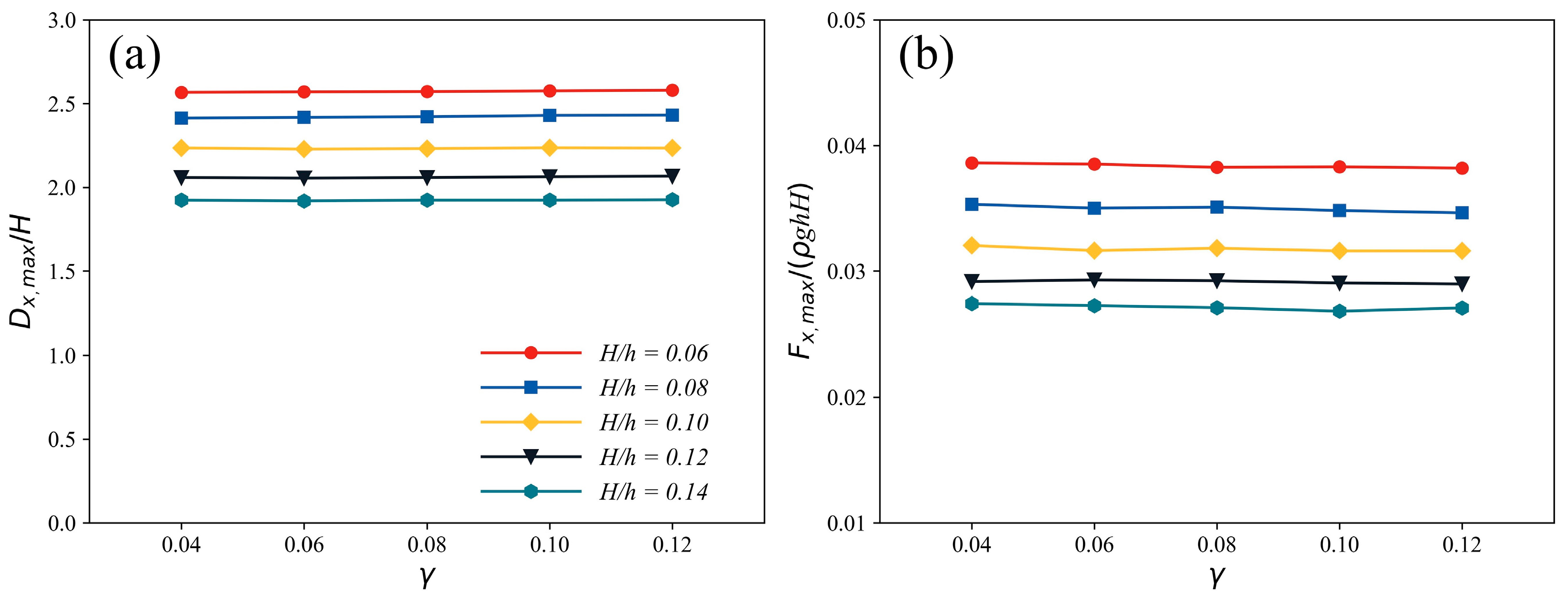
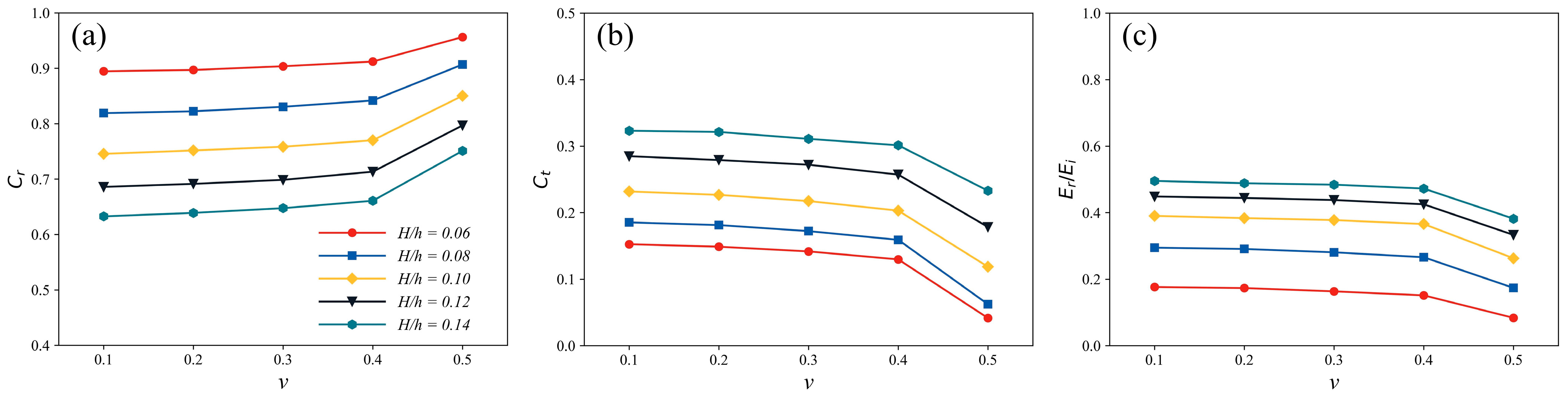
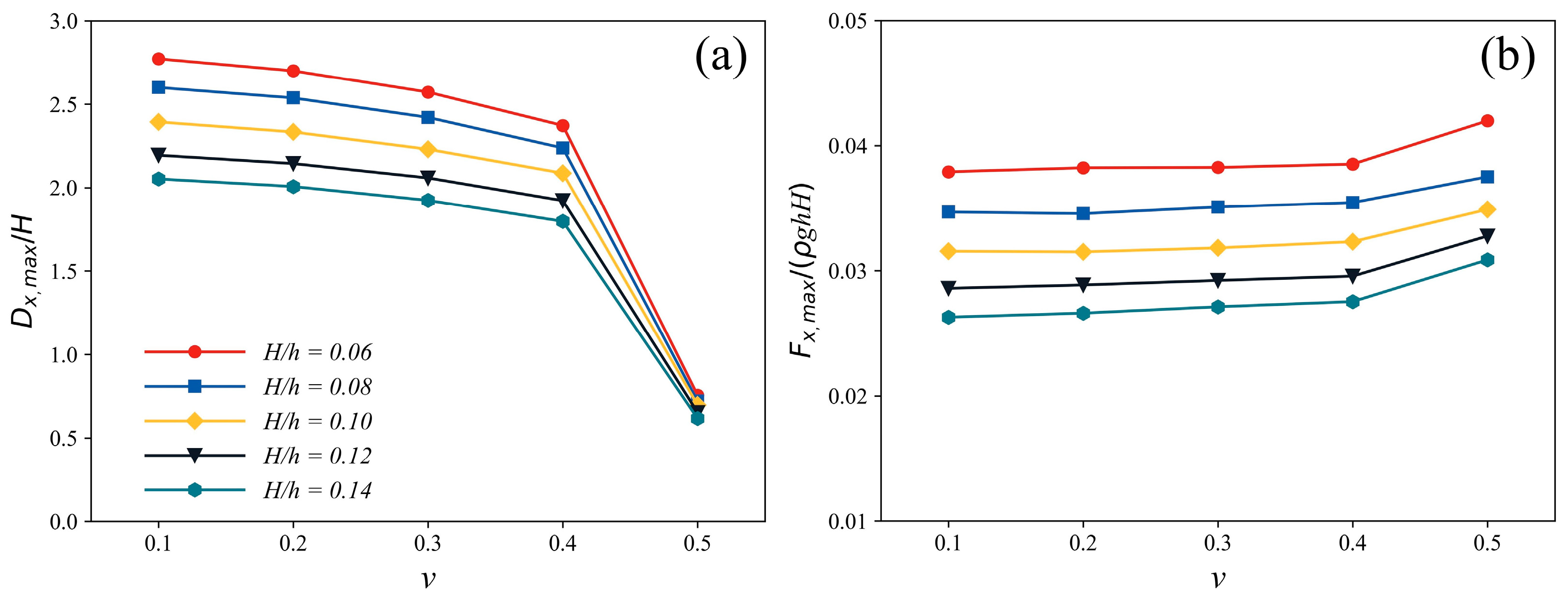
3.3. Effects of Poisson’s Ratio
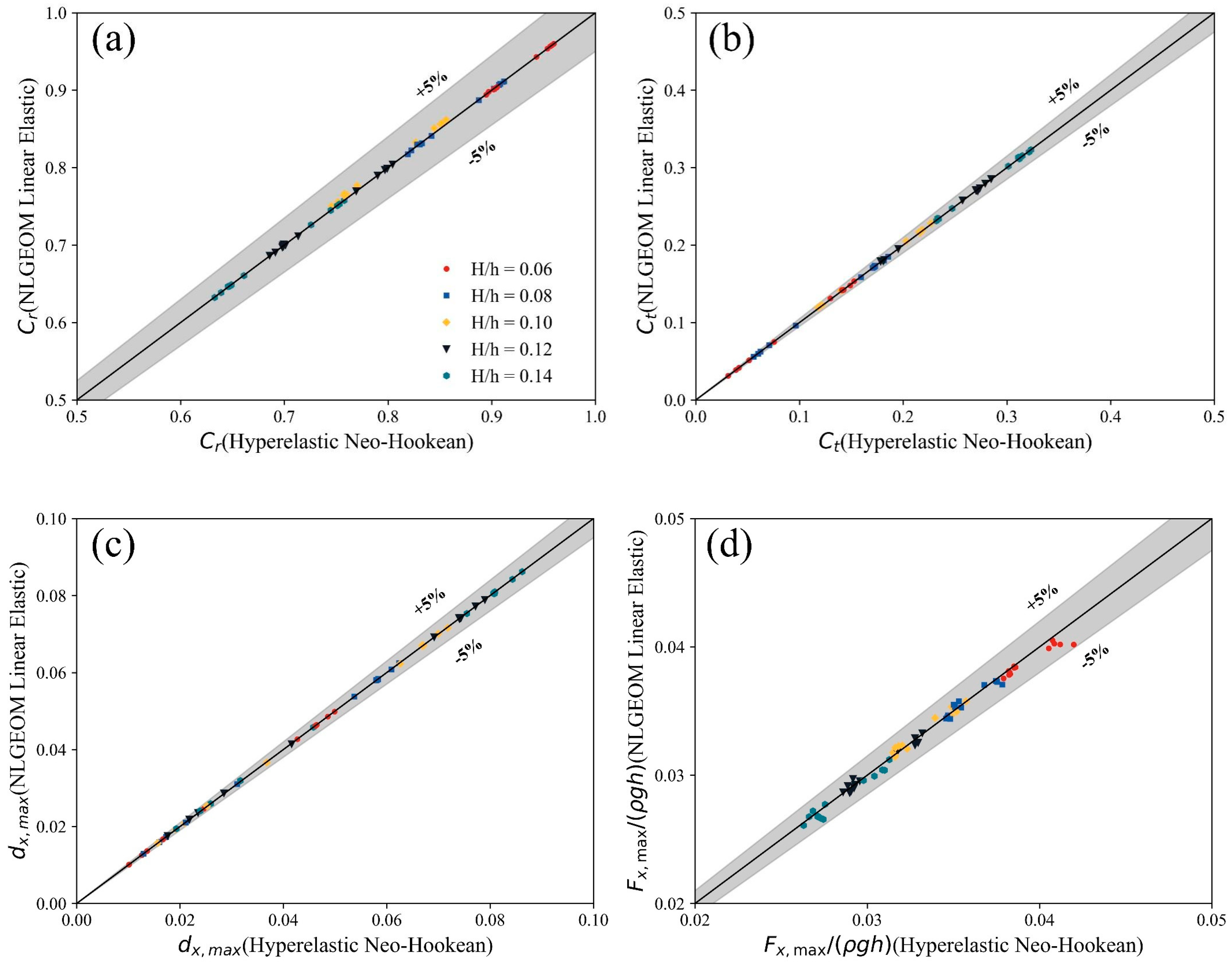
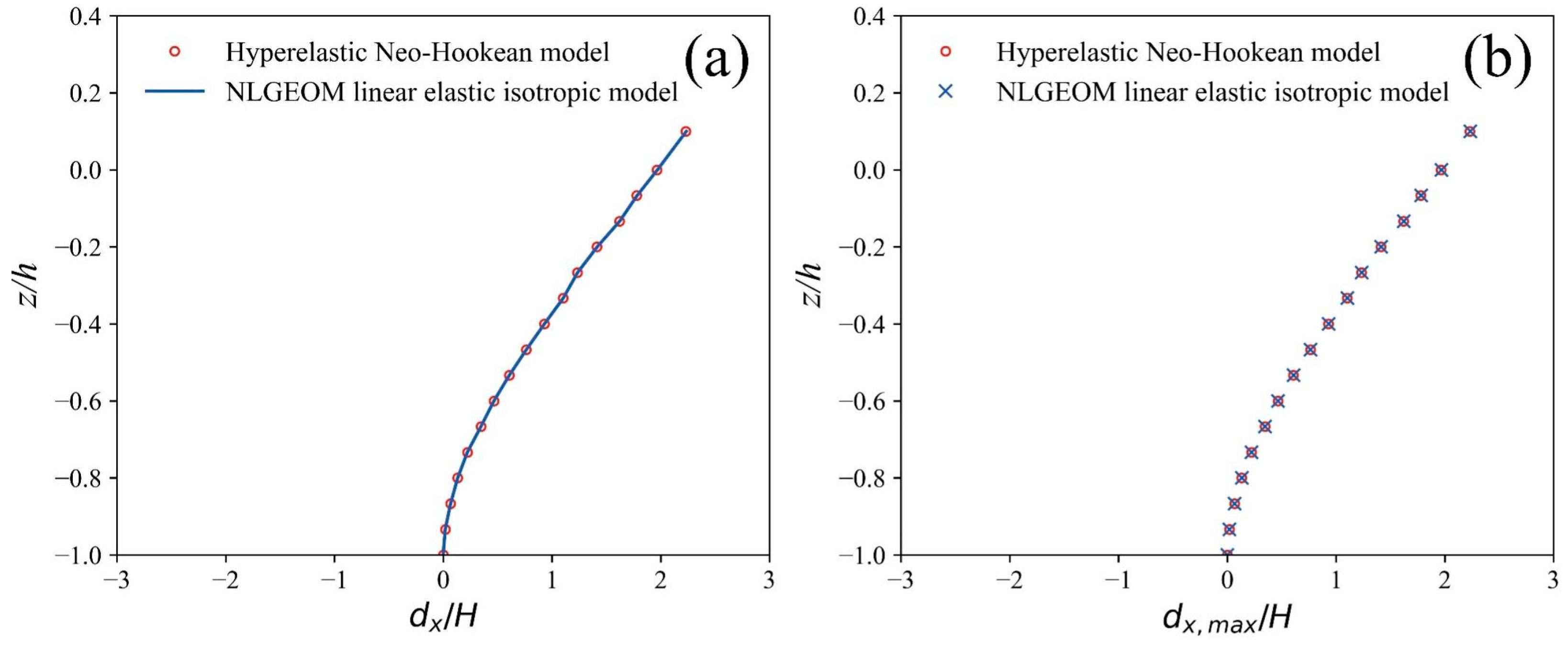
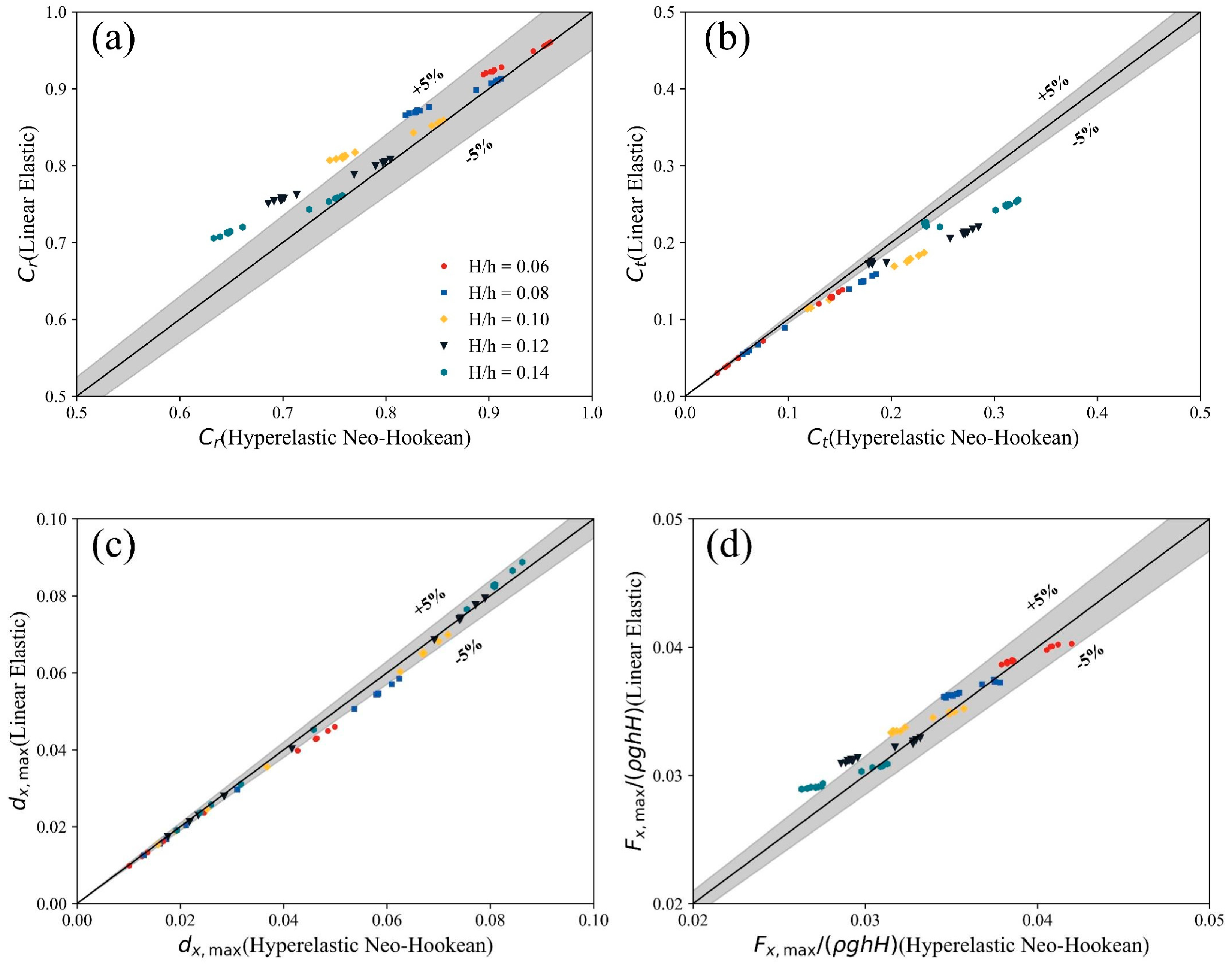
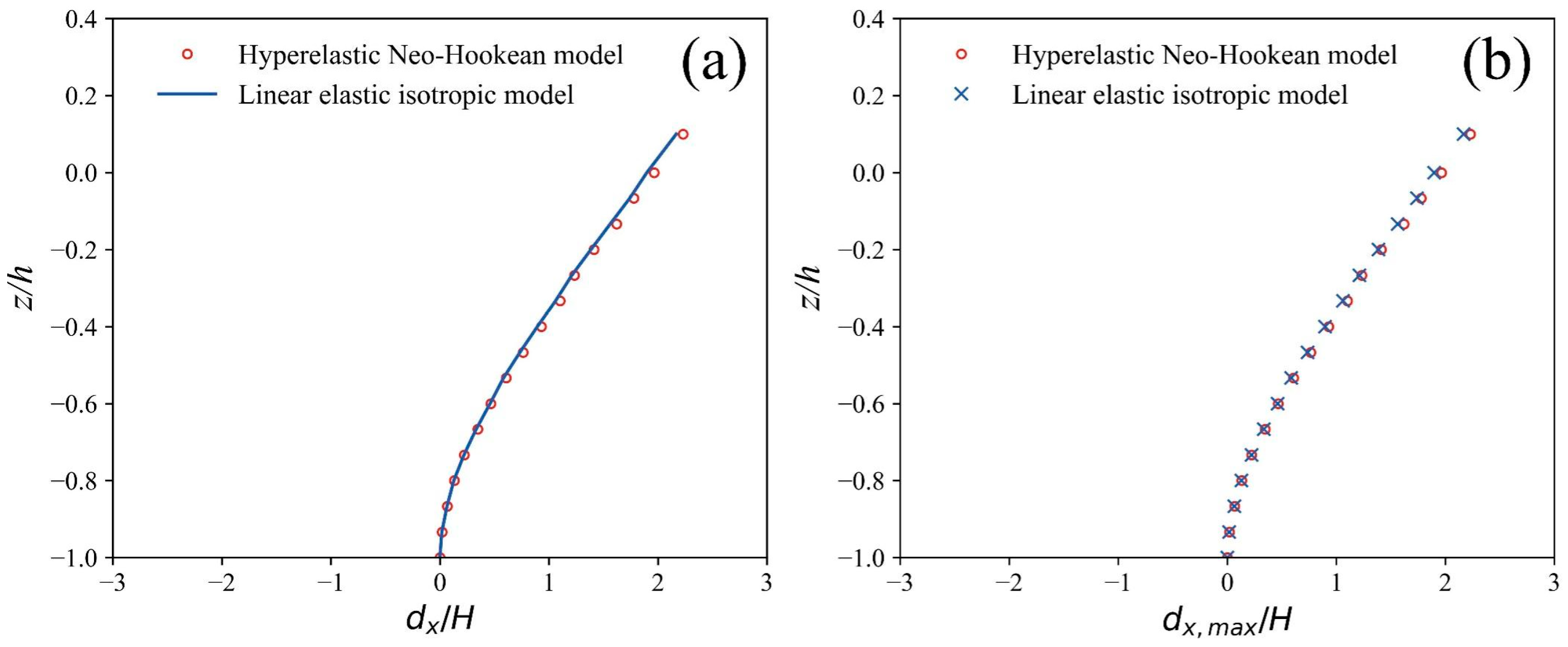
3.4. Comparisons of Three Elastic Material Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanaka, M.; Ohyama, T.; Kiyokawa, T.; Uda, T.; Omata, A. Characteristics of wave dissipation by flexible submerged breakwater and utility of the device. In Coastal Engineering 1992; American Society of Civil Engineers: Reston, VA, USA, 1993; pp. 1613–1624. [Google Scholar]
- Guo, Y.C.; Mohapatra, S.C.; Guedes Soares, C. Experimental study on the performance of an array of vertical flexible porous membrane type breakwater under regular waves. Ocean Eng. 2022, 264, 112328. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Yagci, O.; Kabdasli, M.S. 3D Experimental investigation of the structural response and the effectiveness of a moored floating breakwater with flexibly connected modules. Coast. Eng. 2014, 91, 164–180. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Lentsiou, E.N.; Aksel, M.; Yagci, O. Experimental investigation of the hydroelastic and the structural response of a moored pontoon-type modular floating breakwater with flexible connectors. Coast. Eng. 2017, 121, 240–254. [Google Scholar] [CrossRef]
- Sree, D.K.K.; Mandal, S.; Law, A.W.K. Surface wave interactions with submerged horizontal viscoelastic sheets. Appl. Ocean Res. 2021, 107, 102483. [Google Scholar] [CrossRef]
- Hsiao, Y.; Hsiao, S.C. Experimental study on the interaction of solitary wave with elastic submerged plate. Ocean Eng. 2022, 261, 112106. [Google Scholar] [CrossRef]
- Abul-Azm, A.G. Wave diffraction through submerged flexible breakwaters. Ocean Eng. 1996, 23, 403–422. [Google Scholar] [CrossRef]
- Peter, M.A.; Meylan, M.H. A general spectral approach to the time-domain evolution of linear water waves impacting on a vertical elastic plate. SIAM J. Appl. Math. 2010, 70, 2308–2328. [Google Scholar] [CrossRef]
- Lan, Y.J.; Hsu, T.W.; Lai, J.W.; Chang, C.C.; Ting, C.H. Bragg scattering of waves propagating over a series of poro-elastic submerged breakwaters. Wave Motion 2011, 48, 1–12. [Google Scholar] [CrossRef]
- Li, A.J.; Liu, Y.; Liu, X.; Zhao, Y. Analytical and experimental studies on Bragg scattering of water waves by multiple submerged perforated semi-circular breakwaters. Ocean Eng. 2020, 209, 107419. [Google Scholar] [CrossRef]
- Das, S.; Cheung, K.F. Coupled boundary element and finite element model for fluid-filled membrane in gravity waves. Eng. Anal. Bound. Elem. 2009, 33, 802–814. [Google Scholar] [CrossRef]
- Liao, K.; Hu, C. A coupled FDM–FEM method for free surface flow interaction with thin elastic plate. J. Mar. Sci. Technol. 2013, 18, 1–11. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, Y.; Zong, Y.; Yang, Z.; Luo, M. A CIP-based numerical simulation of wave interaction with a fluid-filled membrane submerged breakwater. Ocean Eng. 2022, 260, 111819. [Google Scholar] [CrossRef]
- Tuković, Ž.; Karač, A.; Cardiff, P.; Jasak, H.; Ivanković, A. OpenFOAM finite volume solver for fluid-solid interaction. Trans. FAMENA 2018, 42, 1–31. [Google Scholar] [CrossRef]
- Cardiff, P.; Karač, A.; De Jaeger, P.; Jasak, H.; Nagy, J.; Ivanković, A.; Tuković, Ž. An open-source finite volume toolbox for solid mechanics and fluid-solid interaction simulations. arXiv 2018, arXiv:1808.10736. [Google Scholar]
- Huang, L.; Ren, K.; Li, M.; Tuković, Ž.; Cardiff, P.; Thomas, G. Fluid-structure interaction of a large ice sheet in waves. Ocean Eng. 2019, 182, 102–111. [Google Scholar] [CrossRef]
- Huang, L.; Li, Y. Design of the submerged horizontal plate breakwater using a fully coupled hydroelastic approach. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 915–932. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, L.; Li, Y. Fully-coupled hydroelastic modeling of a deformable wall in waves. Coast. Eng. 2022, 179, 104245. [Google Scholar] [CrossRef]
- Bungartz, H.J.; Lindner, F.; Gatzhammer, B.; Mehl, M.; Scheufele, K.; Shukaev, A.; Uekermann, B. preCICE—A fully parallel library for multi-physics surface coupling. Comput. Fluids 2016, 141, 250–258. [Google Scholar] [CrossRef]
- Dhondt, G. The Finite Element Method for Three-Dimensional Thermomechanical Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Vilmar, F. Numerische Modellierung von Fluid-Struktur-Wechselwirkungen an Wellenbeaufschlagten Strukturen. Ph.D. Thesis, Universität Kassel, Fachbereich Maschinenbau, Kassel, Germany, 2014. [Google Scholar]
- Sun, W.Y.; Nakamura, T.; Cho, Y.H.; Mizutani, N. Numerical investigation of solitary wave attenuation by a vertical plate-type flexible breakwater using an FVM–FEM coupled model. Part 1: Linear elastic isotropic material. Ocean Eng. 2023, 285, 115368. [Google Scholar] [CrossRef]
- Jacobsen, N.G. Waves2foam Manual; Deltares: Delft, The Netherlands, 2017; p. 570. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Uekermann, B.; Bungartz, H.; Yau, L.C.; Chourdakis, G.; Rusch, A. Official preCICE Adapters for Standard Open-Source Solvers. In Proceedings of the 7th GACM Colloquium on Computational Mechanics for Young Scientists from Academia, Stuttgart, Germany, 11–13 October 2017. [Google Scholar]
- Haelterman, R.; Bogaers, A.E.J.; Scheufele, K.; Uekermann, B.; Mehl, M. Improving the performance of the partitioned QN-ILS procedure for fluid–structure interaction problems: Filtering. Comput. Struct. 2016, 171, 9–17. [Google Scholar] [CrossRef]
- Lindner, F.; Mehl, M.; Uekermann, B. Radial basis function interpolation for black-box multi-physics simulations. In Proceedings of the VII International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED 2017), Rhodes Island, Greece, 12–14 June 2017. [Google Scholar]


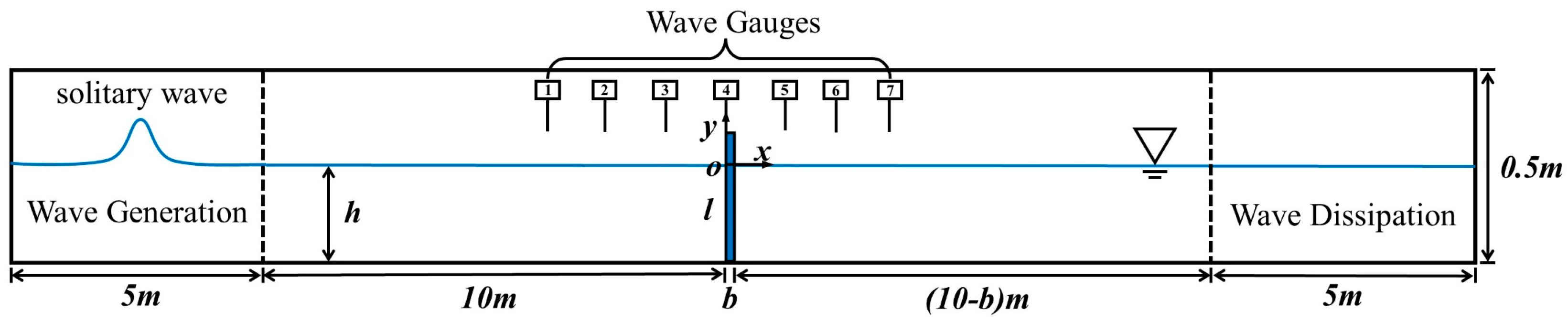
| Case | Structure Properties | Wave Properties | |||||
|---|---|---|---|---|---|---|---|
| 1 | 600 | 0.012 | 0.3 | 0.04 | 0.1 | 0.018 0.024 0.030 0.036 0.042 | 0.3 |
| 2 | 900 | 0.012 | 0.3 | 0.06 | 0.1 | ||
| 3 | 1200 | 0.012 | 0.3 | 0.08 | 0.1 | ||
| 4 | 1500 | 0.012 | 0.3 | 0.10 | 0.1 | ||
| 5 | 1800 | 0.012 | 0.3 | 0.12 | 0.1 | ||
| 6 | 1200 | 0.024 | 0.3 | 0.08 | 0.2 | ||
| 7 | 1200 | 0.036 | 0.3 | 0.08 | 0.3 | ||
| 8 | 1200 | 0.048 | 0.3 | 0.08 | 0.4 | ||
| 9 | 1200 | 0.060 | 0.3 | 0.08 | 0.5 | ||
| 10 | 1200 | 0.012 | 0.1 | 0.08 | 0.1 | ||
| 11 | 1200 | 0.012 | 0.2 | 0.08 | 0.1 | ||
| 12 | 1200 | 0.012 | 0.4 | 0.08 | 0.1 | ||
| 13 | 1200 | 0.012 | 0.5 | 0.08 | 0.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Nakamura, T.; Cho, Y.; Mizutani, N. Numerical Investigation of Solitary Wave Attenuation by a Vertical Plate-Type Flexible Breakwater Constructed Using Hyperelastic Neo-Hookean Material. J. Mar. Sci. Eng. 2024, 12, 1004. https://doi.org/10.3390/jmse12061004
Sun W, Nakamura T, Cho Y, Mizutani N. Numerical Investigation of Solitary Wave Attenuation by a Vertical Plate-Type Flexible Breakwater Constructed Using Hyperelastic Neo-Hookean Material. Journal of Marine Science and Engineering. 2024; 12(6):1004. https://doi.org/10.3390/jmse12061004
Chicago/Turabian StyleSun, Weiyi, Tomoaki Nakamura, Yonghwan Cho, and Norimi Mizutani. 2024. "Numerical Investigation of Solitary Wave Attenuation by a Vertical Plate-Type Flexible Breakwater Constructed Using Hyperelastic Neo-Hookean Material" Journal of Marine Science and Engineering 12, no. 6: 1004. https://doi.org/10.3390/jmse12061004
APA StyleSun, W., Nakamura, T., Cho, Y., & Mizutani, N. (2024). Numerical Investigation of Solitary Wave Attenuation by a Vertical Plate-Type Flexible Breakwater Constructed Using Hyperelastic Neo-Hookean Material. Journal of Marine Science and Engineering, 12(6), 1004. https://doi.org/10.3390/jmse12061004






