Robust Prescribed-Time ESO-Based Practical Predefined-Time SMC for Benthic AUV Trajectory-Tracking Control with Uncertainties and Environment Disturbance
Abstract
:1. Introduction
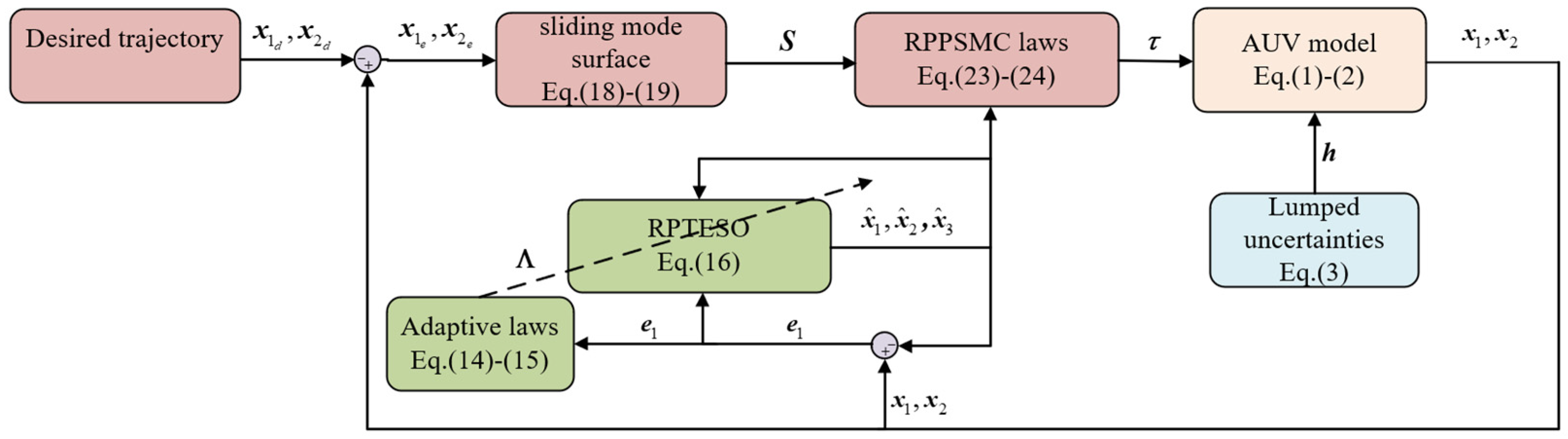
- A new RPTESO was proposed to observe the AUV states and lumped disturbances, and its conservative upper bound of convergence time can be directly designed as only one explicit parameter, regardless of the initial state. An adaptive law was proposed to effectively enhance the robustness of the observer.
- Considering the dynamic and kinematic characteristics of AUV, a new RPPSMC method was proposed. Additionally, it was proven that the sliding mode surface and the RPPSMC is predefined-time stable. A new control scheme with strong robustness was designed in combination with RPTESO.
- Compared with some existing AUV trajectory-tracking control systems such as those that are based on finite-time and fixed-time theories, the proposed control scheme does not require a complicated parameter adjustment process and can flexibly adjust the convergence time of the system according to the actual requirements.
2. Preliminaries and Problem Formulation
2.1. AUV Mathematical Model
2.2. Preliminaries
2.3. Control Objective
3. Main Results
3.1. Design of RPTESO
3.2. Design of a Predefined-Time Sliding Mode Control
4. Stability Analysis
5. Simulation Verification
5.1. Comparative Verification with Fixed-Time ESO
5.2. Comparative Verification with Fixed-Time SMC
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Xu, Y.; Wan, L.; Chen, G.; Cao, Y. Rotation matrix-based finite-time trajectory tracking control of AUV with output constraints and input quantization. Ocean. Eng. 2024, 293, 116570. [Google Scholar] [CrossRef]
- Chen, G.F.; Wan, L.; Jiang, C.M.; Zhang, Y.; Liu, Y.; Zhang, Z.; Xu, Y. Dynamic event-triggered observer-based control for autonomous underwater vehicles in the Trans-Atlantic Geotraverse hydrothermal field using rotation matrices. Ocean. Eng. 2023, 281, 114961. [Google Scholar] [CrossRef]
- Li, J.; Du, J.L.; Sun, Y.Q.; Lewis, F.L. Robust adaptive trajectory tracking control of underactuated autonomous underwater vehicles with prescribed performance. Int. J. Robust Nonlinear Control 2019, 29, 4629–4643. [Google Scholar] [CrossRef]
- Li, D.L.; Du, L. AUV Trajectory Tracking Models and Control Strategies: A Review. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- Yan, Z.P.; Zhang, C.; Tian, W.D.; Cai, S.; Zhao, L. Distributed observer-based formation trajectory tracking method of leader-following multi-AUV system. Ocean. Eng. 2022, 260, 112019. [Google Scholar] [CrossRef]
- Klein, I.; Gutnik, Y.; Lipman, Y. Estimating DVL Velocity in Complete Beam Measurement Outage Scenarios. IEEE Sens. J. 2022, 22, 20730–20737. [Google Scholar] [CrossRef]
- Jia, K.K.; Xu, W.J.; Ma, L. Correction of velocity estimation bias caused by phase-shift beamforming in acoustic Doppler velocity logs. IET Radar Sonar Navig. 2024. [Google Scholar] [CrossRef]
- Hou, C.; Li, X.G.; Wang, H.B.; Zhai, P.; Lu, H. Fuzzy linear extended states observer-based iteration learning fault-tolerant control for autonomous underwater vehicle trajectory-tracking system. IET Control Theory Appl. 2023, 17, 270–283. [Google Scholar] [CrossRef]
- Huang, F.; Xu, J.; Yin, L.A.; Wu, D.; Cui, Y.; Yan, Z.; Chen, T. A general motion control architecture for an autonomous underwater vehicle with actuator faults and unknown disturbances through deep reinforcement learning. Ocean. Eng. 2022, 263, 112424. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, J.; Yue, D.; Xie, X.; Yue, W. Observer-Based Containment Control for a Class of Nonlinear Multiagent Systems with Uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 588–600. [Google Scholar] [CrossRef]
- Liu, P.; Xue, W.; Chen, S.; Huang, Y.; Sun, Z. An integrated solution to ACMM problem of spacecraft with inertia uncertainty. Int. J. Robust Nonlinear Control 2018, 28, 5575–5589. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Wu, W.J.; Ma, J.; Wang, D.; Peng, Z.; Fang, Y. Finite-time ESO-based cascade-free FCS-MPC for NNPC converter. Int. J. Electr. Power Energy Syst. 2023, 148, 108939. [Google Scholar] [CrossRef]
- Gao, C.Y.; Dai, J.; Li, J.; Li, J.X. Finite-Time Convergence ESO-Based Nonsingular Fast Terminal Sliding Mode Control for PMSM with Unknown Parameters and Time-Varying Load. Math. Probl. Eng. 2022, 2022, 9080445. [Google Scholar] [CrossRef]
- Cui, L.; Jin, N.; Chang, S.P.; Zuo, Z.; Zhao, Z. Fixed-time ESO based fixed-time integral terminal sliding mode controller design for a missile. ISA Trans. 2022, 125, 237–251. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.Y.; Li, Z.C.; Yan, H.C.; Zhang, H. Adaptive fixed-time control for nonlinear systems subject to mismatched uncertainties and external disturbance: An ESO-based strategy. Int. J. Robust Nonlinear Control 2024, 34, 3499–3515. [Google Scholar] [CrossRef]
- Yang, X.F.; Zhu, X.N.; Liu, W.; Ye, H.; Xue, W.; Yan, C.; Xu, W. A Hybrid Autonomous Recovery Scheme for AUV Based Dubins Path and Non-Singular Terminal Sliding Mode Control Method. IEEE Access 2022, 10, 61265–61276. [Google Scholar] [CrossRef]
- Zhang, L.L.; Liu, X.L.; Hua, C.C. Prescribed-Time Control for Stochastic High-Order Nonlinear Systems with Parameter Uncertainty. IEEE Trans. Circuits Syst. II-Express Briefs 2023, 70, 4083–4087. [Google Scholar] [CrossRef]
- Ye, H.; Song, Y. Prescribed-time Control for Linear Systems in Canonical Form Via Nonlinear Feedback. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 1126–1135. [Google Scholar] [CrossRef]
- Chang, L.; Han, Q.L.; Ge, X.; Zhang, C.; Zhang, X. On Designing Distributed Prescribed Finite-Time Observers for Strict-Feedback Nonlinear Systems. IEEE Trans. Cybern. 2019, 51, 4695–4706. [Google Scholar] [CrossRef]
- Cui, L.; Jin, N. Prescribed-time ESO-based prescribed-time control and its application to partial IGC design. Nonlinear Dyn. 2021, 106, 491–508. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, C.; Liu, Y. Barrier Lyapunov Function-based adaptive prescribed-time extended state observers design for unmanned surface vehicles subject to unknown disturbances. Ocean. Eng. 2023, 270, 113671–113676. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.H.; Li, Z.X.; Du, X.; Yan, Z. Three-Dimensional Trajectory Tracking of AUV Based on Nonsingular Terminal Sliding Mode and Active Disturbance Rejection Decoupling Control. J. Mar. Sci. Eng. 2023, 11, 959. [Google Scholar] [CrossRef]
- Hu, Y.H.; Song, Z.K.; Zhang, H.C. Adaptive sliding mode control with pre-specified performance settings for AUV’s trajectory tracking. Ocean. Eng. 2023, 287, 115882. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ceglarek, D. Global finite-time cooperative control for multiple manipulators using integral sliding mode control. Asian J. Control 2022, 24, 2862–2876. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Plestan, F. Robust Fixed-Time Stability: Application to Sliding-Mode Control. IEEE Trans. Autom. Control 2022, 67, 1061–1066. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Liu, J.Y.; Jiang, G.P.; Li, C. Consensus of multi-agent systems via prescribed-time sliding mode control method. Trans. Inst. Meas. Control 2022, 44, 2369–2377. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Sanchez, E.N.; Loukianov, A.G. Predefined-time stability of dynamical systems with sliding modes. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Becerra, H.M.; Vazquez, C.R.; Arechavaleta, G.; Delfin, J. Predefined-Time Convergence Control for High-Order Integrator Systems Using Time Base Generators. IEEE Trans. Control Syst. Technol. 2017, 26, 1866–1873. [Google Scholar] [CrossRef]
- Munoz-Vazquez, A.J.; Sanchez Torres, J.D.; Jimenez Rodriguez, E.; Loukianov, A. Predefined-Time Robust Stabilization of Robotic Manipulators. IEEE/ASME Trans. Mechatron. 2019, 24, 1033–1040. [Google Scholar] [CrossRef]
- Dong, F.; You, K.; Xie, L.; Hu, Q. Coordinate-free Circumnavigation of a Moving Target via a Simple PD-like Controller. IEEE Trans. Aerosp. Electron. Syst. 2020, 58, 2012–2025. [Google Scholar] [CrossRef]
- Xu, Y.F.; Wan, L.; Zhang, Z.Y.; Chen, G.F. Robust adaptive path following control of autonomous underwater vehicle with uncertainties and communication bandwidth limitation. Ocean. Eng. 2023, 287, 115895. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q. Adaptive Nonsingular Predefined-Time Control for Attitude Stabilization of Rigid Spacecrafts. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 189–193. [Google Scholar] [CrossRef]
- Wang, W.C.; Hou, M.S.; Feng, D.; Liu, B.J. Predefined-time control for Euler-Lagrange systems with model uncertainties and actuator faults. Asian J. Control 2023, 25, 1591–1605. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A. Levant’s Arbitrary Order Exact Differentiator: A Lyapunov Approach. IEEE Trans. Autom. Control 2018, 64, 3034–3039. [Google Scholar] [CrossRef]
- Polyakov, A.; Fridman, L. Stability notions and Lyapunov functions for sliding mode control systems. J. Frankl. Inst. 2014, 351, 1831–1865. [Google Scholar] [CrossRef]
- Qin, H.; Wu, Z.; Sun, Y.; Sun, Y. Prescribed performance adaptive fault-tolerant trajectory tracking control for an ocean bottom flying node. Int. J. Adv. Robot. Syst. 2019, 16, 172988141984194. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, D.; Sun, Y.; Qin, H.; Cao, Y.; Chen, G. Fast fixed-time vertical plane motion control of autonomous underwater gliders in shallow water. J. Frankl. Inst. 2022, 359, 10483–10509. [Google Scholar] [CrossRef]











| Component | Value |
|---|---|
| RPTSESO | |
| Fixed-time ESO | , , , , , , , , , , , |
| Fixed-time SMC | , , , , , , , , , , , |
| Method | e31 | e32 | e33 | e34 | e35 | |
|---|---|---|---|---|---|---|
| 2.16 | 6.38 | 9.79 | 7.22 | 12.2 | ||
| 11.8 | 20.8 | 34.4 | 24.2 | 46.7 | ||
| Fixed-time ESO | 13.9 | 7.71 | 7.69 | 10.7 | 19 | |
| 2.06 | 2.79 | 3.15 | 2.29 | 2.66 | ||
| 2.6 | 3.6 | 3.32 | 2.98 | 3.8 | ||
| Fixed-time ESO | 14.34 | 13.64 | 15.3 | 14.06 | 14.24 |
| Component | Value |
|---|---|
| RPPSMC-1 | , , , |
| RPPSMC-2 | , , , |
| Method | ||||||
|---|---|---|---|---|---|---|
| RPPSMC-1 | 1.85 | 2.43 | 2.15 | 0.6 | 1.81 | |
| RPPSMC-2 | 2.3 | 3.12 | 2.83 | 0.7 | 2.31 | |
| Fixed-time SMC | 2.53 | 3.89 | 3.44 | 0.71 | 2.66 | |
| RPPSMC-1 | 2.37 | 3.97 | 1.48 | 0.53 | 1.96 | |
| RPPSMC-2 | 6.2 | 8.3 | 8.48 | 0.54 | 3.51 | |
| Fixed-time SMC | 6.31 | 6.41 | 8.16 | 0.50 | 3.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, Z.; Wan, L. Robust Prescribed-Time ESO-Based Practical Predefined-Time SMC for Benthic AUV Trajectory-Tracking Control with Uncertainties and Environment Disturbance. J. Mar. Sci. Eng. 2024, 12, 1014. https://doi.org/10.3390/jmse12061014
Xu Y, Zhang Z, Wan L. Robust Prescribed-Time ESO-Based Practical Predefined-Time SMC for Benthic AUV Trajectory-Tracking Control with Uncertainties and Environment Disturbance. Journal of Marine Science and Engineering. 2024; 12(6):1014. https://doi.org/10.3390/jmse12061014
Chicago/Turabian StyleXu, Yufei, Ziyang Zhang, and Lei Wan. 2024. "Robust Prescribed-Time ESO-Based Practical Predefined-Time SMC for Benthic AUV Trajectory-Tracking Control with Uncertainties and Environment Disturbance" Journal of Marine Science and Engineering 12, no. 6: 1014. https://doi.org/10.3390/jmse12061014






