Numerical Investigation of the Seabed Dynamic Response to a Perforated Semi-Circular Breakwater
Abstract
:1. Introduction
2. Numerical Model
2.1. Flow Model
2.2. Seabed Model
3. Model Validation and Numerical Setup
3.1. Model Validation
3.2. Numerical Setup
4. Results and Discussion
4.1. Impact of the Marine Environment
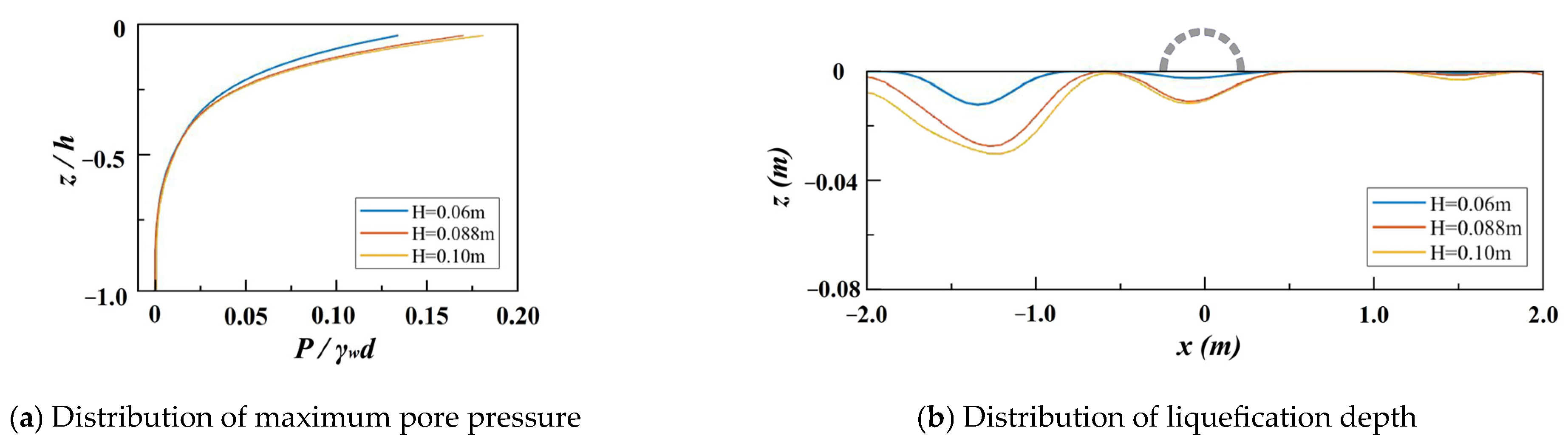
4.1.1. Wave Height
4.1.2. Water Depth
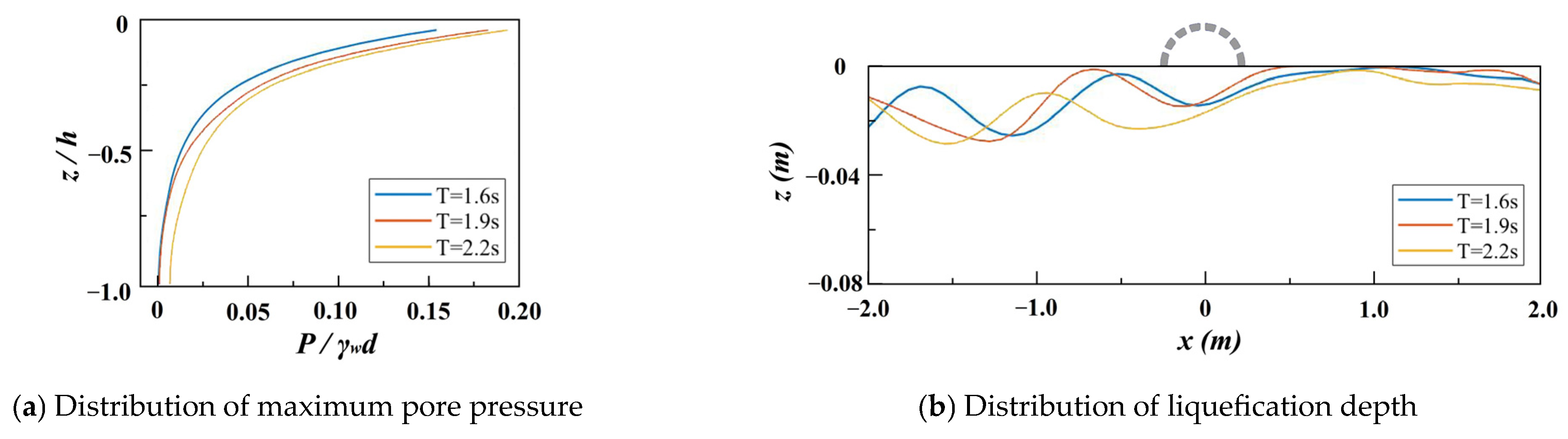
4.1.3. Wave Period
4.2. Impact of Breakwater Structure
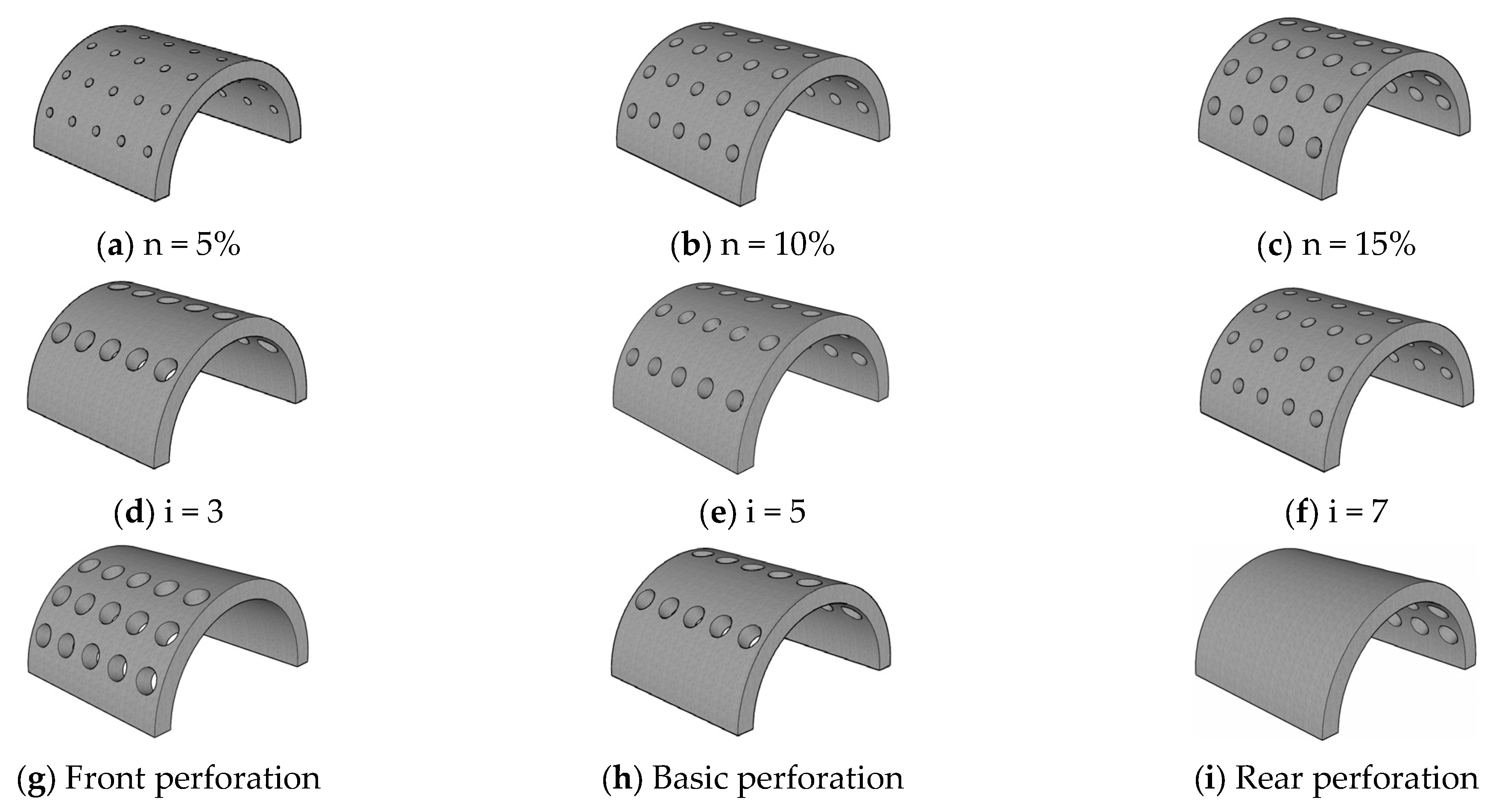
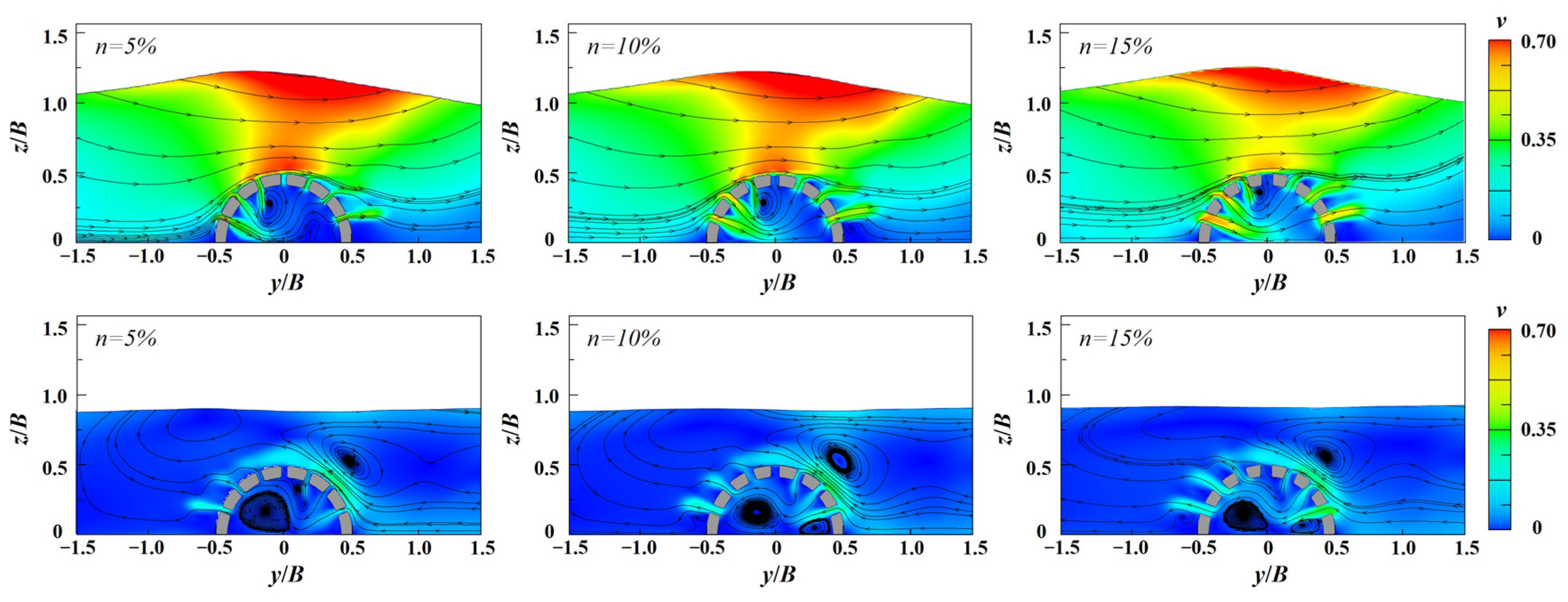
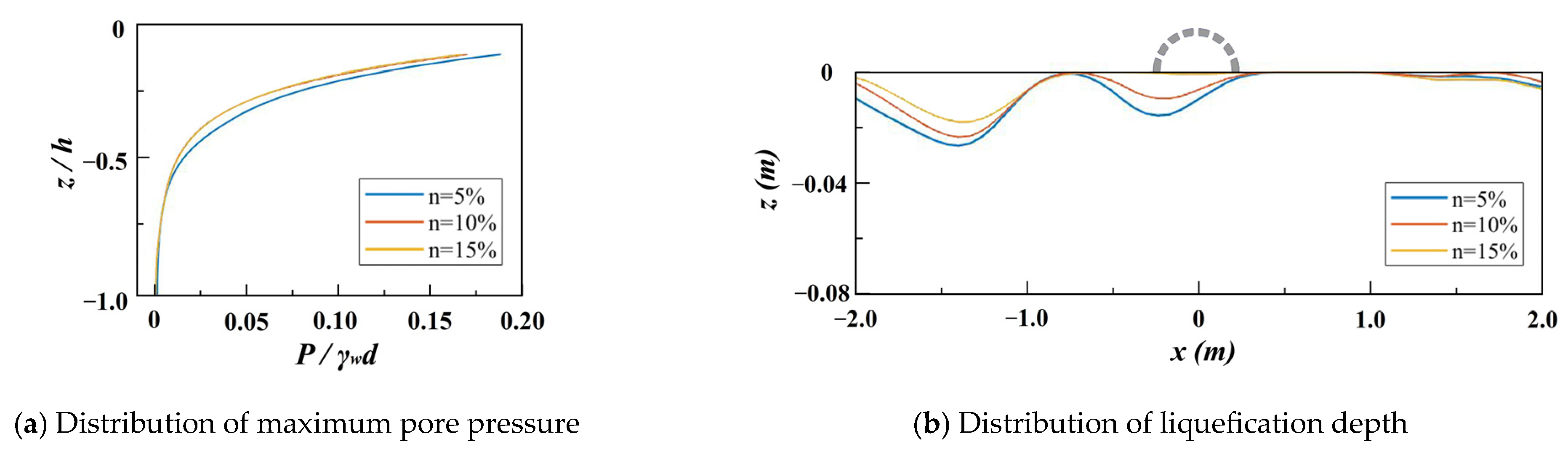
4.2.1. Breakwater Perforation Rate
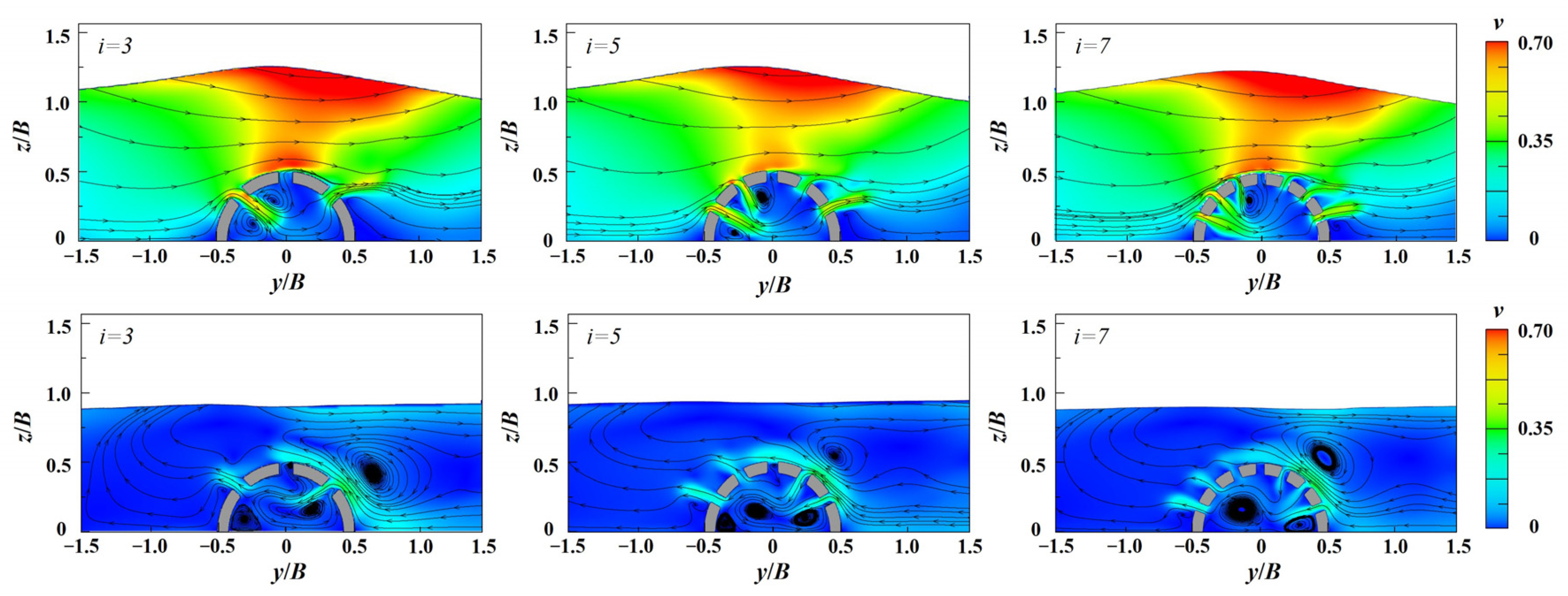
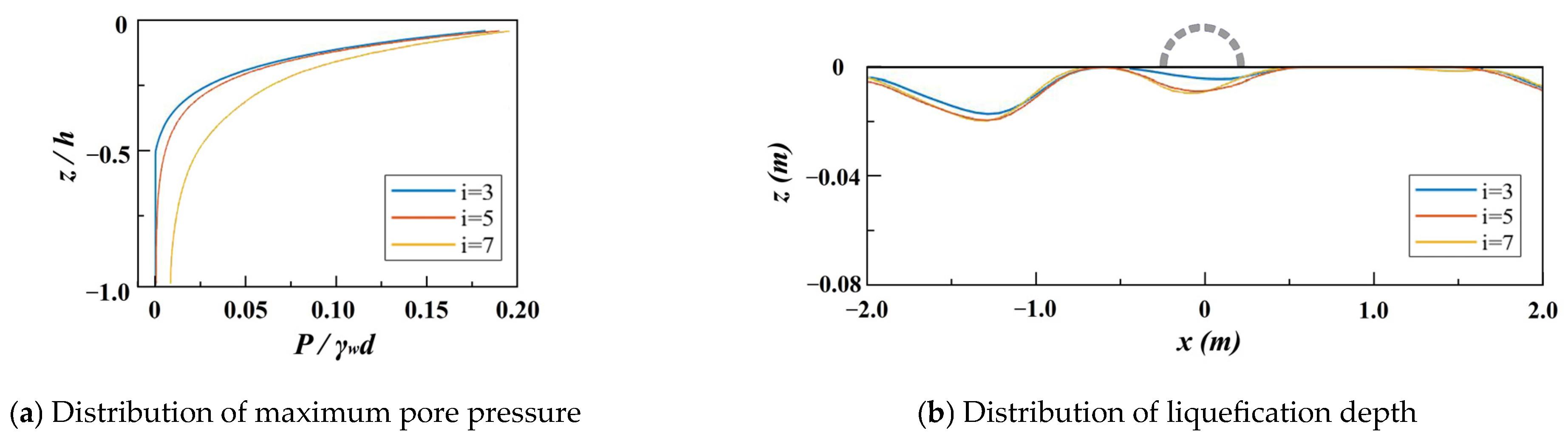
4.2.2. Breakwater Perforation Number
4.2.3. Breakwater Perforation Type
5. Conclusions
- The model developed in this study is well suited for investigating the dynamic response of the seabed. The wave model accurately simulates wave generation, propagation, and reflection processes. Additionally, the seabed model effectively captures liquefaction in the seabed foundation.
- Wave characteristics significantly influence the dynamic response of the seabed. Pore pressure and liquefaction show a positive correlation with wave height and wave period, while exhibiting a negative correlation with water depth.
- The perforation rate of the SBW has a minor effect on pore pressure. Increasing the perforation rate from 5% to 10% leads to a 32% decrease in the average liquefaction depth. The increasing perforation number slightly enhances pore pressure and deepens liquefaction due to complex wave reflection and transmission. Among the three different perforation types, basic perforation exerts the minimum seabed pressure. Front perforation increases liquefaction by 22.9% in the seaside, and rear perforation increases liquefaction by 45.9% in the leeside.
- In the design of SBWs, it is crucial to consider both wave dissipation and the stability of seabed liquefaction comprehensively. Measures such as reducing the permeability of the seabed can be implementing to enhance the stability of the seabed soil.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanimoto, K.; Takahashi, S. Design and construction of caisson breakwaters—The Japanese experience. Coast. Eng. 1994, 22, 57–77. [Google Scholar] [CrossRef]
- Xie, S. Waves forces on submerged semicircular breakwater and similar structures. China Ocean Eng. 1999, 13, 63–72. [Google Scholar]
- Liu, Y.; Li, H.-J. Analysis of wave interaction with submerged perforated semi-circular breakwaters through multipole method. Appl. Ocean Res. 2012, 34, 164–172. [Google Scholar] [CrossRef]
- Dhinakaran, G.; Sundar, V.; Sundaravadivelu, R.; Graw, K. Dynamic pressures and forces exerted on impermeable and seaside perforated semicircular breakwaters due to regular waves. Ocean Eng. 2002, 29, 1981–2004. [Google Scholar] [CrossRef]
- Guo, L.; Cai, Y.; Jardine, R.J.; Yang, Z.; Wang, J. Undrained behaviour of intact soft clay under cyclic paths that match vehicle loading conditions. Can. Geotech. J. 2018, 55, 90–106. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Yan, Z.; Wang, Y.-C. Numerical analyses of caisson breakwaters on soft foundations under wave cyclic loading. China Ocean Eng. 2016, 30, 1–18. [Google Scholar] [CrossRef]
- Hu, C.; Liu, H.; Huang, W. Anisotropic bounding-surface plasticity model for the cyclic shakedown and degradation of saturated clay. Comput. Geotech. 2012, 44, 34–47. [Google Scholar] [CrossRef]
- Mynett, A.E.; Mei, C. Wave-induced stresses in a saturated poro-elastic sea bed beneath a rectangular caisson. Geotechnique 1982, 32, 235–247. [Google Scholar] [CrossRef]
- Tsai, Y.; McDougal, W.; Sollitt, C. Response of finite depth seabed to waves and caisson motion. J. Waterw. Port Coast. Ocean. Eng. 1990, 116, 1–20. [Google Scholar] [CrossRef]
- Mase, H.; Sakai, T.; Sakamoto, M. Wave-induced porewater pressures and effective stresses around breakwater. Ocean Eng. 1994, 21, 361–379. [Google Scholar] [CrossRef]
- Jeng, D.; Cha, D.; Lin, Y.; Hu, P. Analysis on pore pressure in an anisotropic seabed in the vicinity of a caisson. Appl. Ocean Res. 2000, 22, 317–329. [Google Scholar] [CrossRef]
- Jeng, D.; Cha, D.; Lin, Y.; Hu, P. Wave-induced pore pressure around a composite breakwater. Ocean Eng. 2001, 28, 1413–1435. [Google Scholar] [CrossRef]
- Zhang, J.-S.; Jeng, D.-S.; Liu, P.-F. Numerical study for waves propagating over a porous seabed around a submerged permeable breakwater: PORO-WSSI II model. Ocean Eng. 2011, 38, 954–966. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Zhang, H.; Zhao, H.; Jeng, D. Three-dimensional model for wave-induced dynamic soil response around breakwaters. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–23 June 2012; ISOPE: Mountain View, CA, USA, 2012. [Google Scholar]
- Zhao, H.Y.; Jeng, D.S.; Zhang, Y.; Zhang, J.S.; Zhang, H.J.; Zhang, C. 3D numerical model for wave-induced seabed response around breakwater heads. Geomech. Eng. 2013, 5, 595–611. [Google Scholar] [CrossRef]
- Mizutani, N.; McDougal, W.; Mostafa, A. BEM-FEM combined analysis of nonlinear interaction between wave and submerged breakwater. In Coastal Engineering 1996, Proceedings of the Twenty-fifth International Conference, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: Reston, VA, USA, 1997; pp. 2377–2390. [Google Scholar]
- Mostafa, A.M.; Mizutani, N.; Iwata, K. Nonlinear wave, composite breakwater, and seabed dynamic interaction. J. Waterw. Port Coast. Ocean. Eng. 1999, 125, 88–97. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, H.; Sun, X. Tests on wave-induced dynamic response and instability of silty clay seabeds around a semi-circular breakwater. Appl. Ocean Res. 2018, 78, 1–13. [Google Scholar] [CrossRef]
- Vastenholz, H. The Interdependent Effects of Wave Reflection and Seabed Erosion. In Proceedings of the 3rd International Conference on Scour and Erosion (ICSE-3), Amsterdam, The Netherlands, 1–3 November 2006; CURNET: Gouda, The Netherlands, 2006; pp. 669–674. [Google Scholar]
- Xu, W.; Chen, C.; Htet, M.H.; Sarkar, M.S.I.; Tao, A.; Wang, Z.; Fan, J.; Jiang, D. Experimental Investigation on Bragg Resonant Reflection of Waves by Porous Submerged Breakwaters on a Horizontal Seabed. Water 2022, 14, 2682. [Google Scholar] [CrossRef]
- Brunone, B.; Tomasicchio, G.R. Wave kinematics at steep slopes: Second-order model. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 223–232. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, L.M. The renormalization group, the ε-expansion and derivation of turbulence models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Chang, C.; Bettess, P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Geotechnique 1980, 30, 385–395. [Google Scholar] [CrossRef]
- Sui, T.; Zhang, C.; Guo, Y.; Zheng, J.; Jeng, D.; Zhang, J.; Zhang, W. Three-dimensional numerical model for wave-induced seabed response around mono-pile. Ships Offshore Struct. 2016, 11, 667–678. [Google Scholar] [CrossRef]
- Sui, T.; Zheng, J.; Zhang, C.; Jeng, D.S.; Zhang, J.; Guo, Y.; He, R. Consolidation of unsaturated seabed around an inserted pile foundation and its effects on the wave-induced momentary liquefaction. Ocean Eng. 2017, 131, 308–321. [Google Scholar] [CrossRef]
- Mizutani, N.; Mostafa, A.M. Nonlinear wave-induced seabed instability around coastal structures. Coast. Eng. J. 1998, 40, 131–160. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Hsiao, S.-C. Propagation of solitary waves over a submerged permeable breakwater. Coast. Eng. 2013, 81, 1–18. [Google Scholar] [CrossRef]
- Deng, B.; Yin, L.; Huang, J.; Xiong, K.; Jiang, C. Three dimensional numerical simulation of wave interaction with a new type of double row perforated cylinder breakwater. Chin. J. Theor. Appl. Mech. 2023, 55, 845–857. [Google Scholar]
- Zhang, T. Three-Dimensional Numerical Simulation of Waves and Its Application. Master’s Thesis, Tianjin University, Tianjin, China, 2009. [Google Scholar]
- Ye, J. 3D liquefaction criteria for seabed considering the cohesion and friction of soil. Appl. Ocean Res. 2012, 37, 111–119. [Google Scholar] [CrossRef]
- Pan, T.; Feng, X.; Ni, X.; Feng, W.; Ma, G. Study on the response of wave transmission coefficient to various incident wave elements of a permeable sloping breakwater. J. Hohai Univ. (Nat. Sci.) 2022, 50, 45–53. [Google Scholar]
- Teh, H.M. Wave Transmission over a Submerged Porous Breakwater: An Experimental Study. In Proceedings of the 2nd International Conference on Civil, Offshore and Environmental Engineering (ICCOEE), Kuala Lumpur, Malaysia, 3–5 June 2014. [Google Scholar]
- Sasajima, H. Field demonstration test on a semi-circular breakwater. In HYDRO-PORT’94, Proceedings of the International Conference on Hydro-Technical Engineering for Port and Harbor Construction, Yokosuka, Japan, 19–21 October 1994; Coastal Development Institute of Technology: Tokyo, Japan, 1994. [Google Scholar]
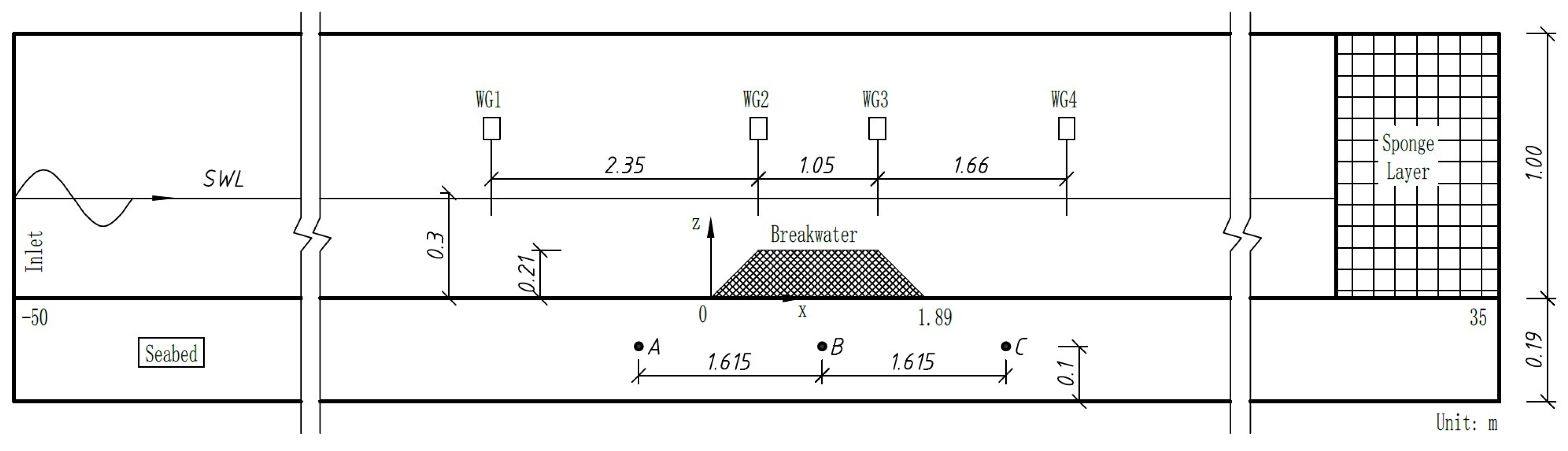
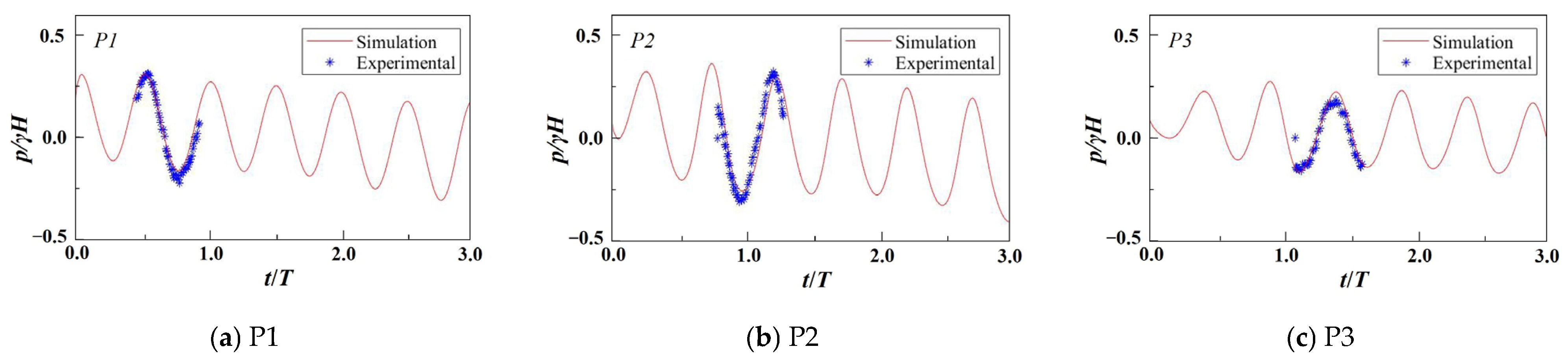
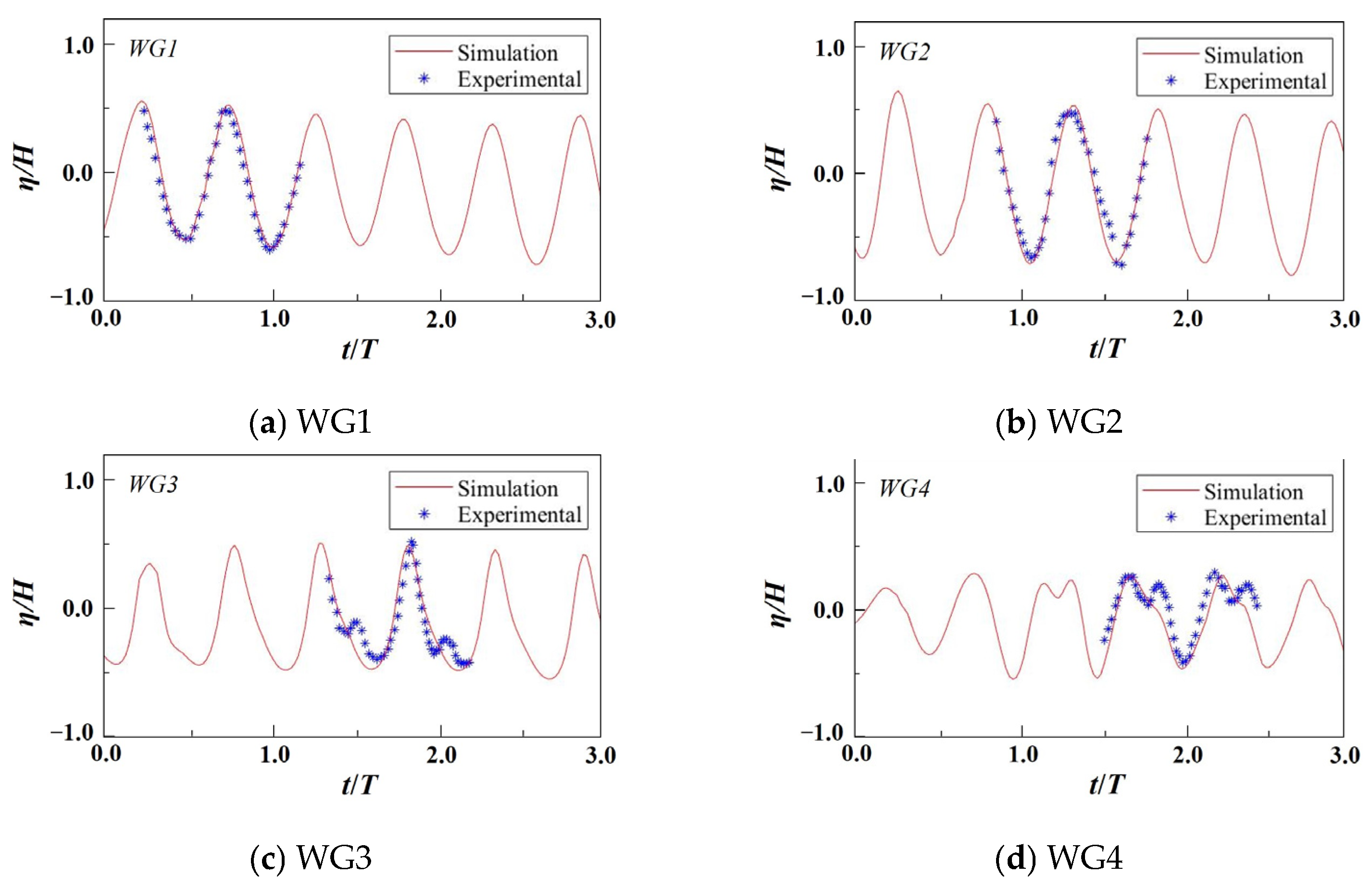

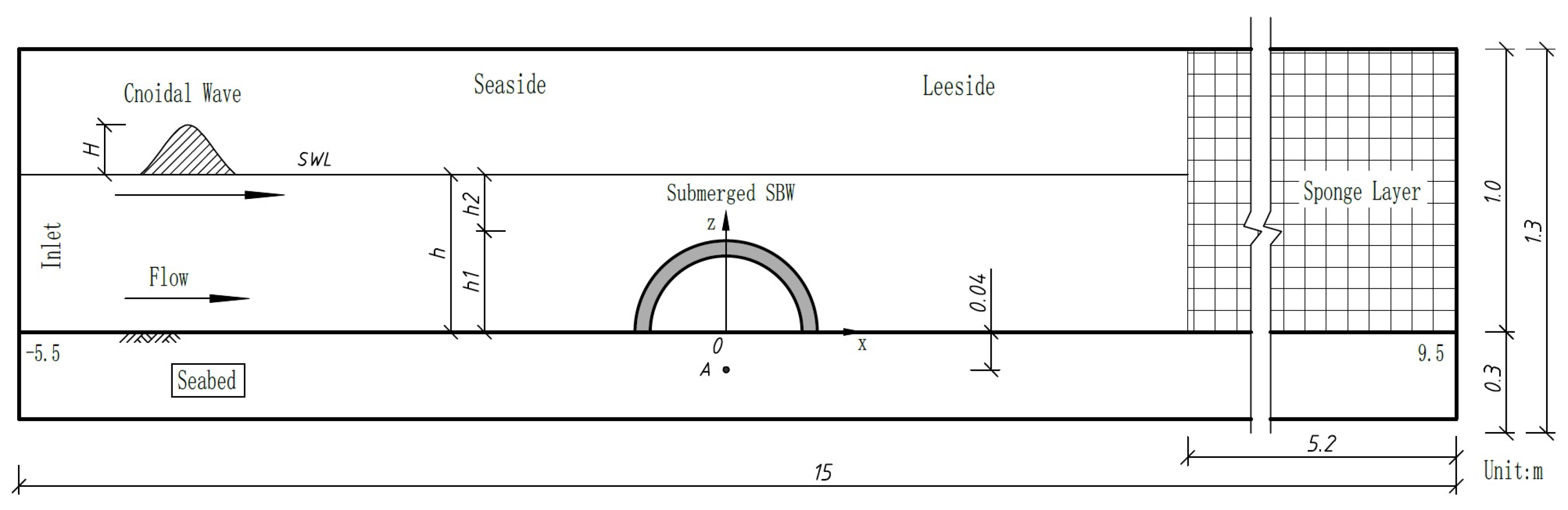




| Wave | Seabed Soil | Breakwater Soil | ||||||
|---|---|---|---|---|---|---|---|---|
| Wave Height (m) | Water Depth (m) | Wave Period (s) | Permeability (m/s) | Porosity | Saturation | Permeability (m/s) | Porosity | Median Diameter (mm) |
| 0.03 | 0.3 | 1.4 | 2.2 × 10−3 | 0.3 | 0.98 | 1.8 × 10−3 | 0.24 | 27 |
| Cases | Flow Velocity (m/s) | Wave Height (m) | Water Depth (m) | Wave Period (s) | Perforation Rate (n) | Perforation Number (i) | Perforation Type |
|---|---|---|---|---|---|---|---|
| 1 | 0.08 | 0.060 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 2 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 3 | 0.08 | 0.100 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 4 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 5 | 0.08 | 0.088 | 0.292 | 1.9 | 10% | 7 | Basic perforation |
| 6 | 0.08 | 0.088 | 0.312 | 1.9 | 10% | 7 | Basic perforation |
| 7 | 0.08 | 0.088 | 0.228 | 1.6 | 10% | 7 | Basic perforation |
| 8 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 9 | 0.08 | 0.088 | 0.228 | 2.2 | 10% | 7 | Basic perforation |
| 10 | 0.08 | 0.088 | 0.228 | 1.9 | 5% | 7 | Basic perforation |
| 11 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 12 | 0.08 | 0.088 | 0.228 | 1.9 | 15% | 7 | Basic perforation |
| 13 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 3 | Basic perforation |
| 14 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 5 | Basic perforation |
| 15 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 16 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 3 | Front perforation |
| 17 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Basic perforation |
| 18 | 0.08 | 0.088 | 0.228 | 1.9 | 10% | 7 | Rear perforation |
| Cases | Flow Velocity (m/s) | Wave Height (m) | Water Depth (m) | Wave Period (s) | Maximum Liquefaction Depth in the Seaside (cm) | Maximum Liquefaction Depth in the Leeside (cm) | Average Liquefaction Depth (cm) |
|---|---|---|---|---|---|---|---|
| 1 | 0.08 | 0.060 | 0.228 | 1.9 | 1.22 | 0.07 | 0.18 |
| 2 | 0.08 | 0.088 | 0.228 | 1.9 | 2.74 | 0.14 | 0.63 |
| 3 | 0.08 | 0.100 | 0.228 | 1.9 | 3.02 | 0.30 | 0.82 |
| 4 | 0.08 | 0.088 | 0.228 | 1.9 | 2.74 | 0.14 | 0.63 |
| 5 | 0.08 | 0.088 | 0.292 | 1.9 | 2.69 | 0.08 | 0.70 |
| 6 | 0.08 | 0.088 | 0.312 | 1.9 | 2.47 | 0.06 | 0.65 |
| 7 | 0.08 | 0.088 | 0.228 | 1.6 | 2.55 | 0.51 | 0.90 |
| 8 | 0.08 | 0.088 | 0.228 | 1.9 | 2.76 | 0.71 | 1.06 |
| 9 | 0.08 | 0.088 | 0.228 | 2.2 | 2.85 | 0.90 | 1.30 |
| Cases | Perforation Rate (n) | Perforation Number (i) | Perforation Type | Maximum Liquefaction Depth in the Seaside (cm) | Maximum Liquefaction Depth in the Leeside (cm) | Average Liquefaction Depth (cm) |
|---|---|---|---|---|---|---|
| 10 | 5% | 7 | Basic perforation | 2.64 | 0.58 | 0.75 |
| 11 | 10% | 7 | Basic perforation | 2.33 | 0.37 | 0.54 |
| 12 | 15% | 7 | Basic perforation | 1.79 | 0.27 | 0.37 |
| 13 | 10% | 3 | Basic perforation | 1.65 | 0.85 | 0.53 |
| 14 | 10% | 5 | Basic perforation | 1.78 | 0.79 | 0.61 |
| 15 | 10% | 7 | Basic perforation | 1.92 | 0.64 | 0.69 |
| 16 | 10% | 3 | Front perforation | 2.49 | 0.46 | 0.90 |
| 17 | 10% | 7 | Basic perforation | 1.92 | 0.64 | 0.69 |
| 18 | 10% | 7 | Rear perforation | 1.90 | 1.11 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Wang, G.; Yu, T.; Yang, Y.; Sui, T.; Liu, J.; Guan, D. Numerical Investigation of the Seabed Dynamic Response to a Perforated Semi-Circular Breakwater. J. Mar. Sci. Eng. 2024, 12, 873. https://doi.org/10.3390/jmse12060873
Gao Y, Wang G, Yu T, Yang Y, Sui T, Liu J, Guan D. Numerical Investigation of the Seabed Dynamic Response to a Perforated Semi-Circular Breakwater. Journal of Marine Science and Engineering. 2024; 12(6):873. https://doi.org/10.3390/jmse12060873
Chicago/Turabian StyleGao, Yikang, Guangsheng Wang, Tong Yu, Yanhao Yang, Titi Sui, Jingang Liu, and Dawei Guan. 2024. "Numerical Investigation of the Seabed Dynamic Response to a Perforated Semi-Circular Breakwater" Journal of Marine Science and Engineering 12, no. 6: 873. https://doi.org/10.3390/jmse12060873





