Numerical Study on the Performance of an OWC under Breaking and Non-Breaking Waves
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrodynamic Model
2.2. Pneumatic Model
3. Results and Discussion
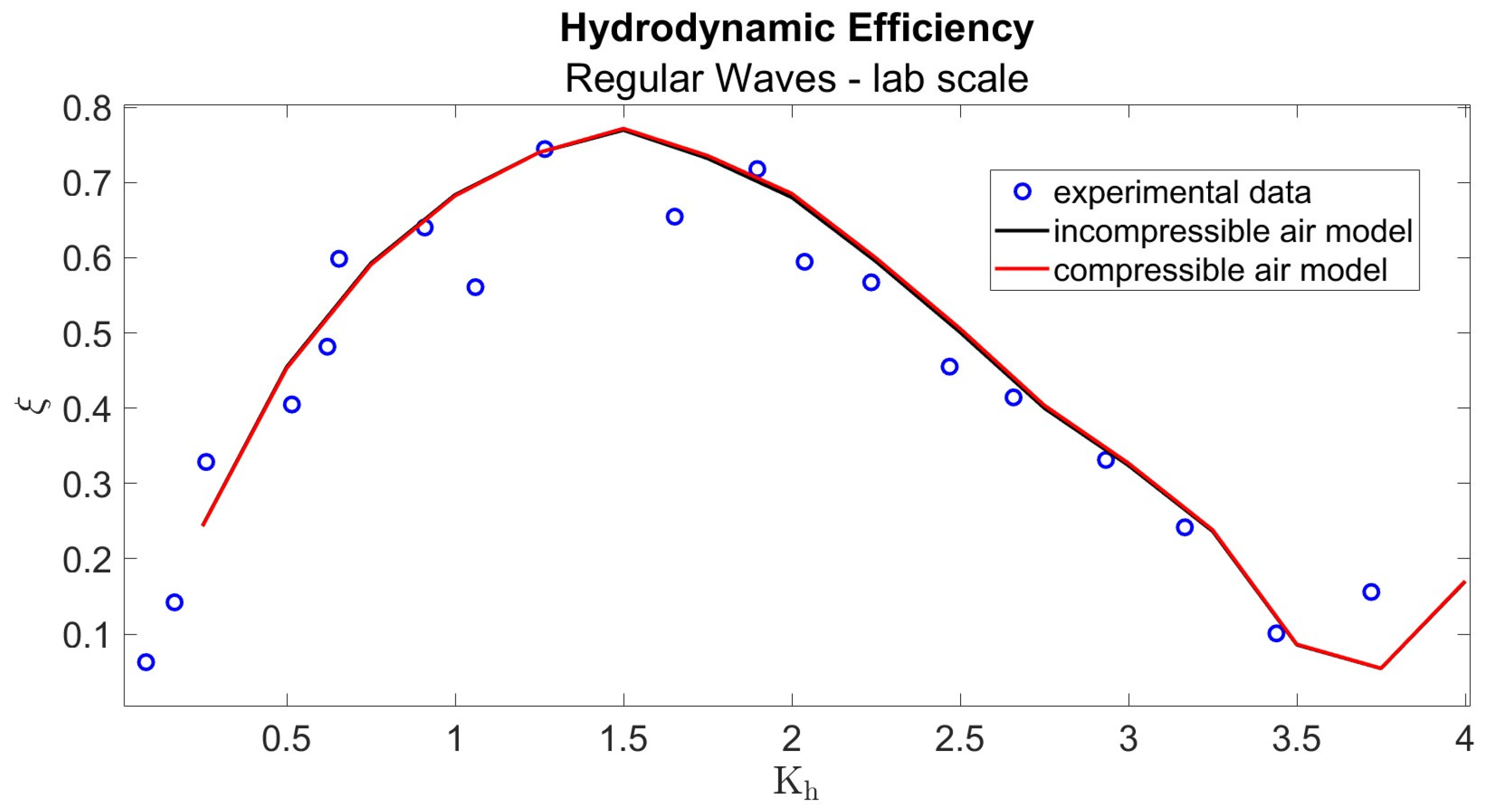
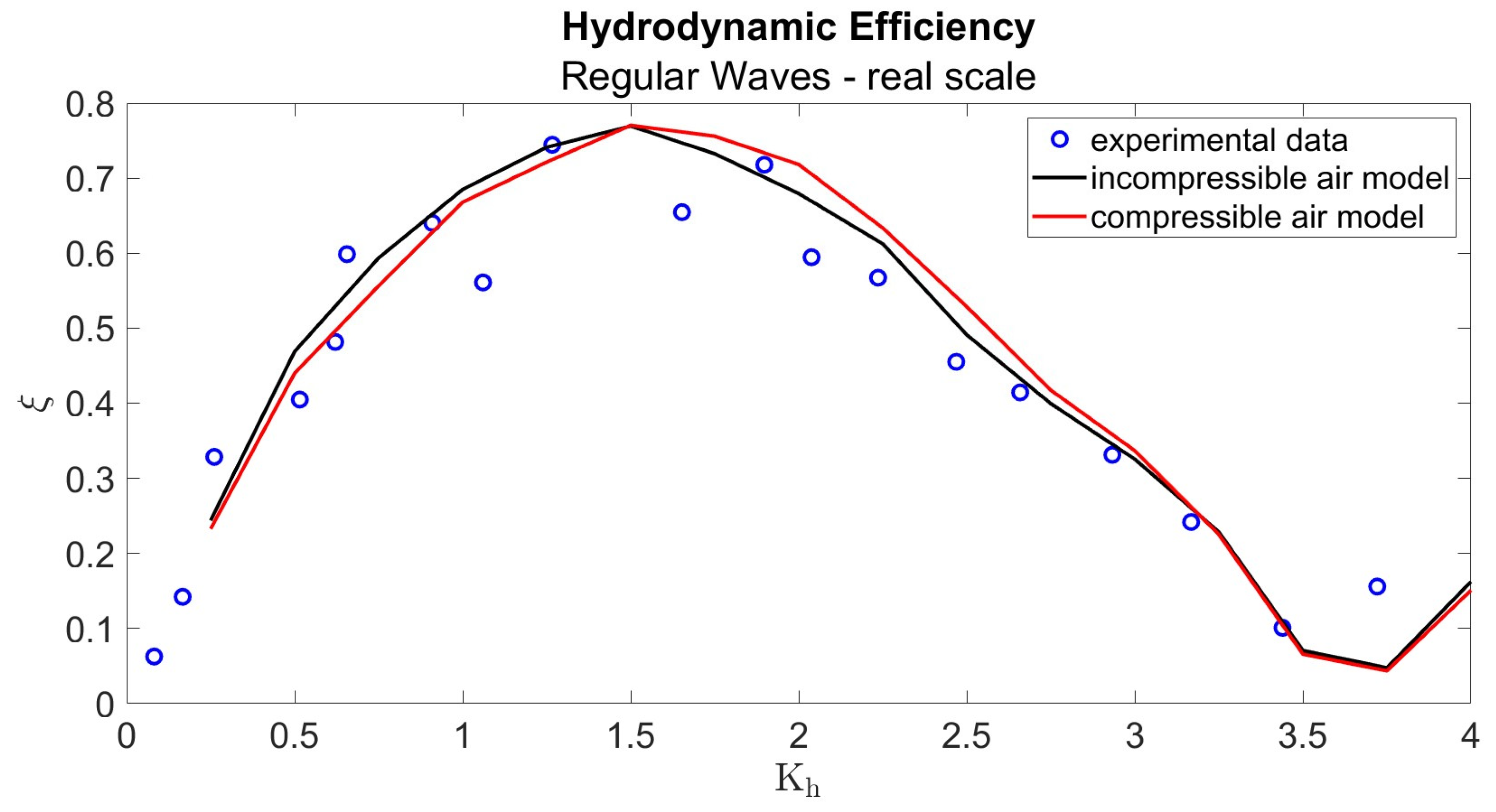
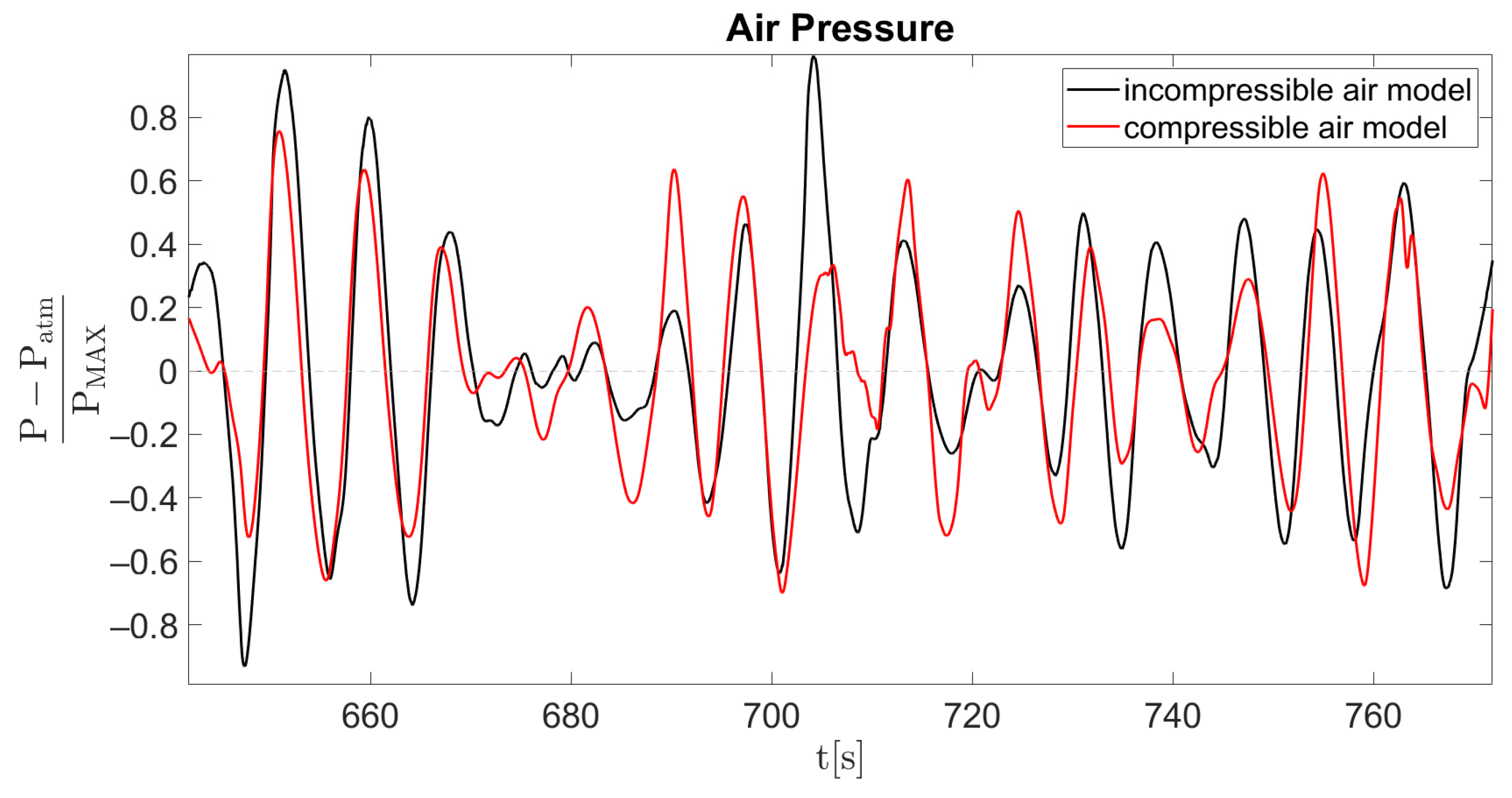
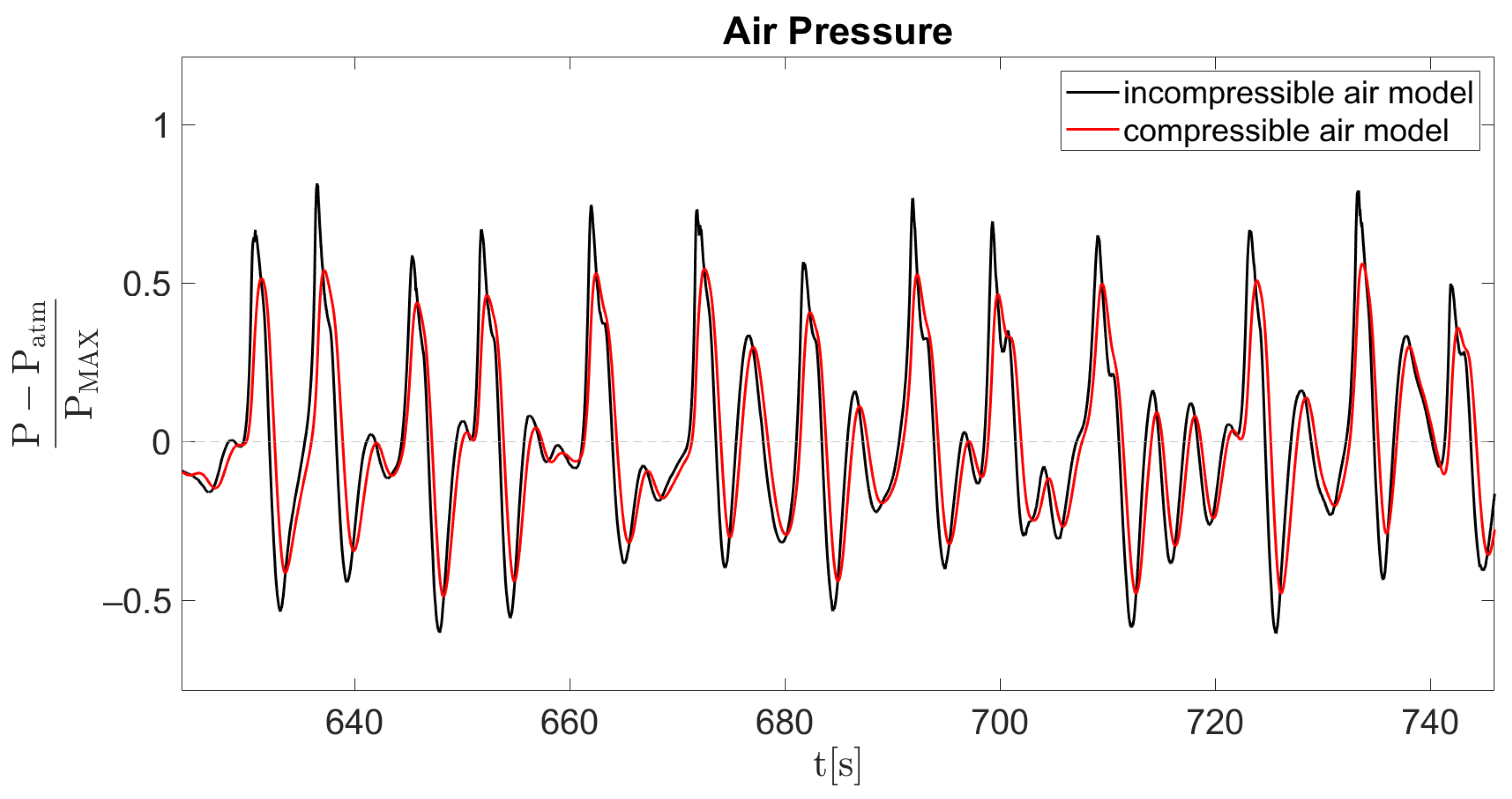
3.1. Validation
3.2. Real Cases Applications
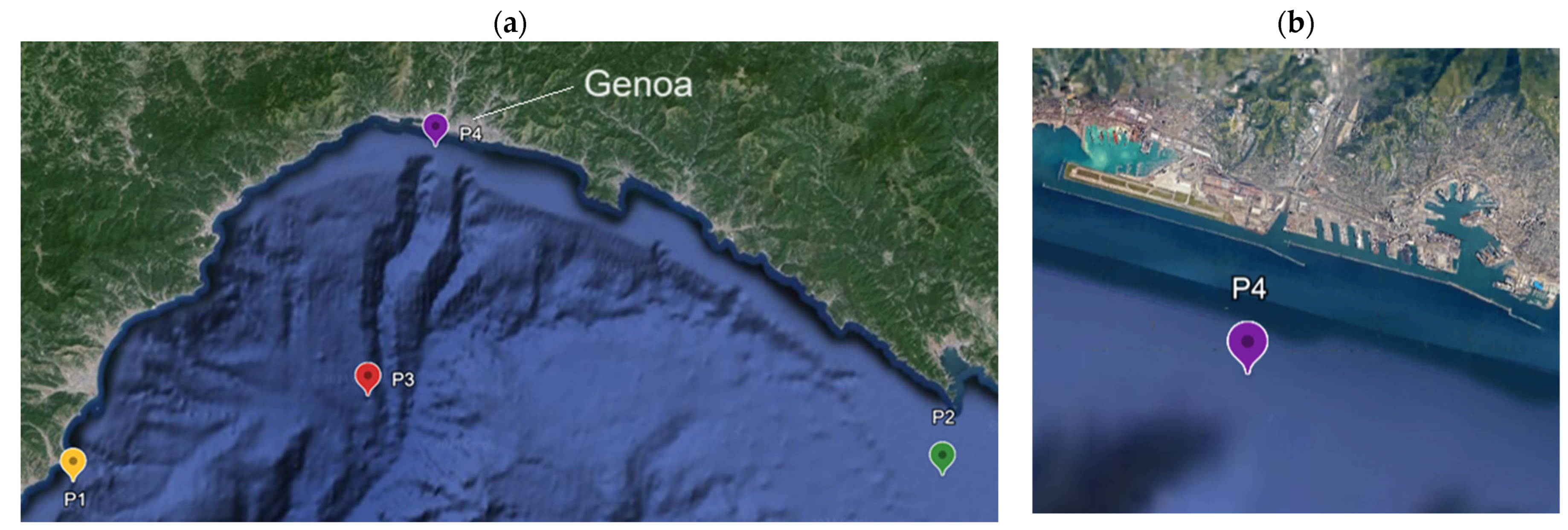
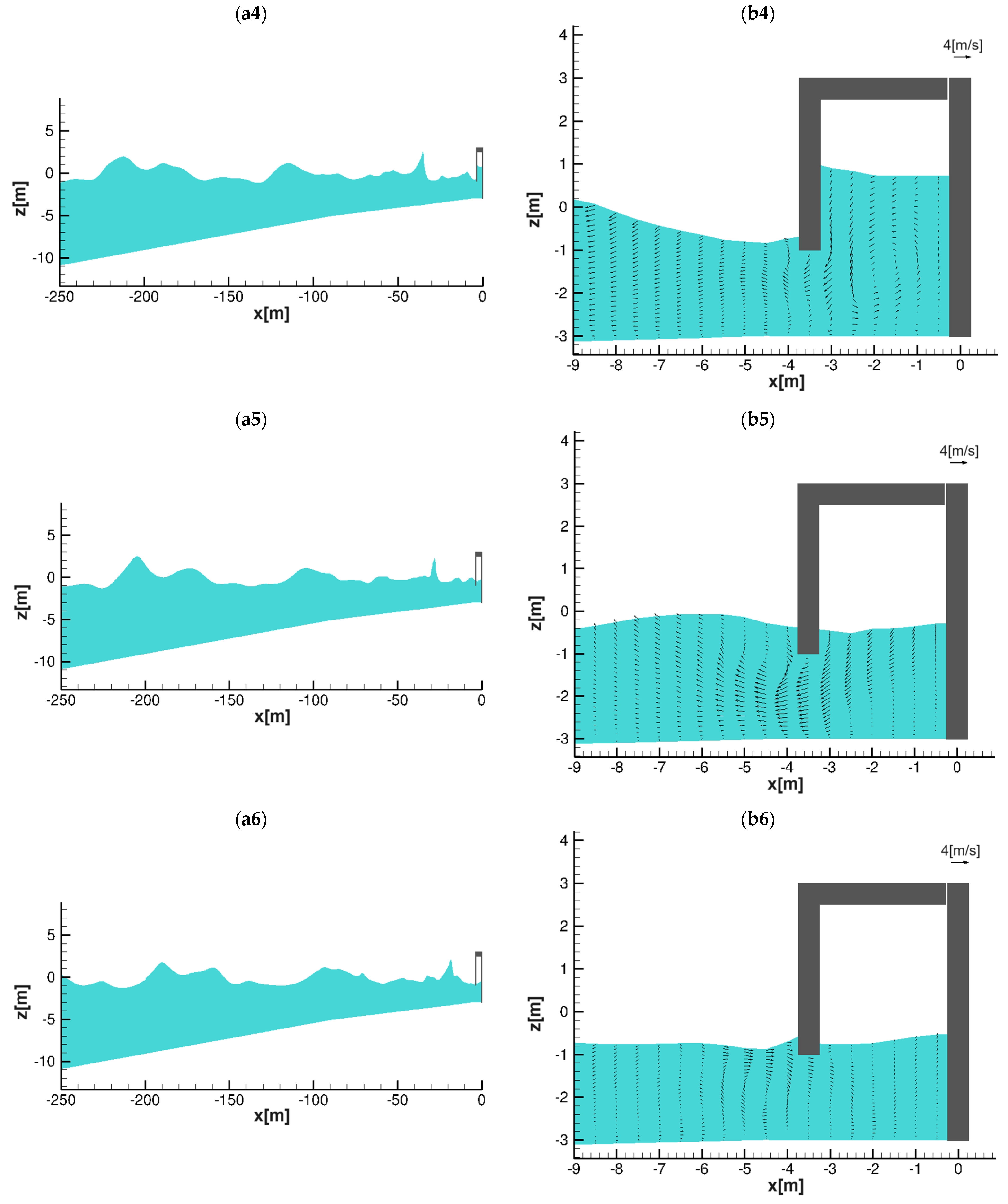
3.2.1. Performance of an OWC Subjected to Non-Breaking Waves (Genoa Port)
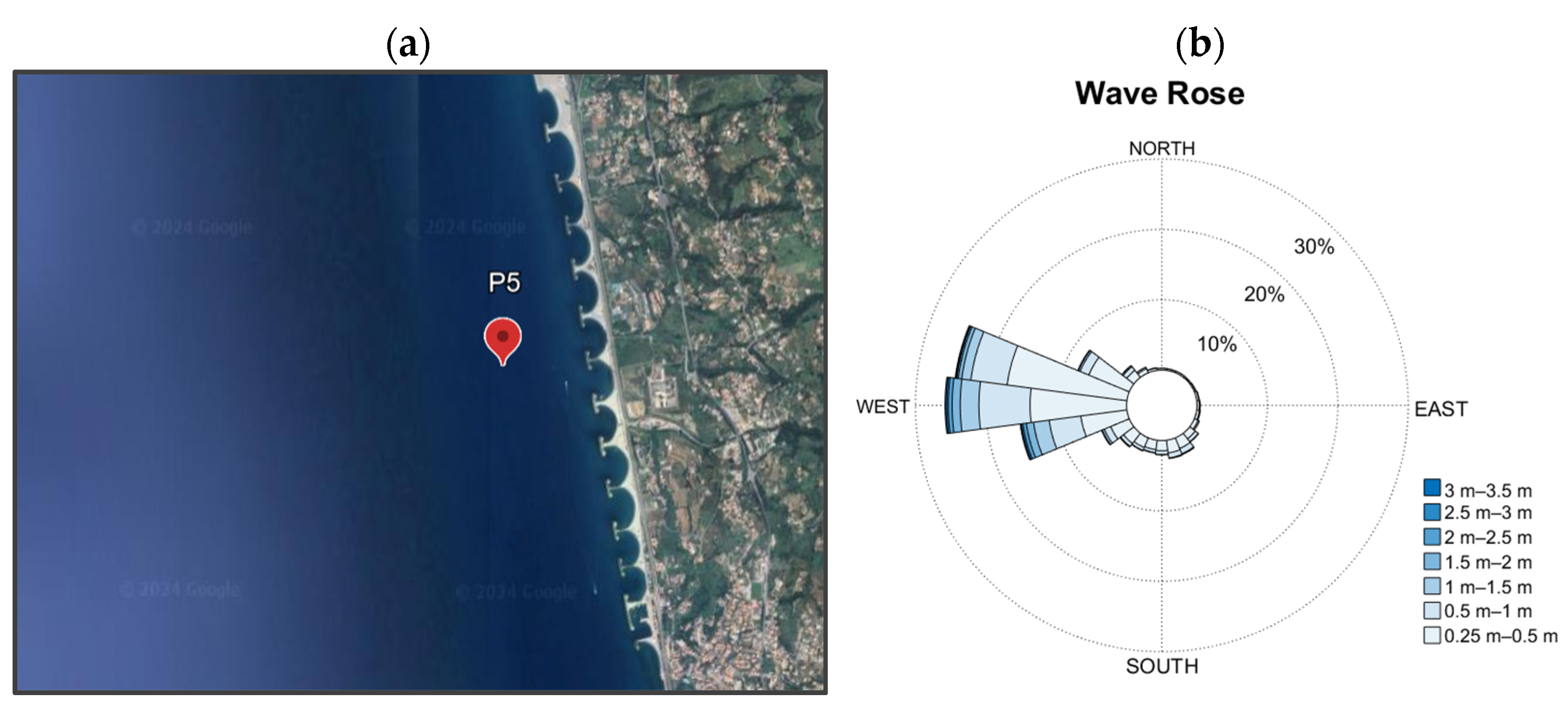
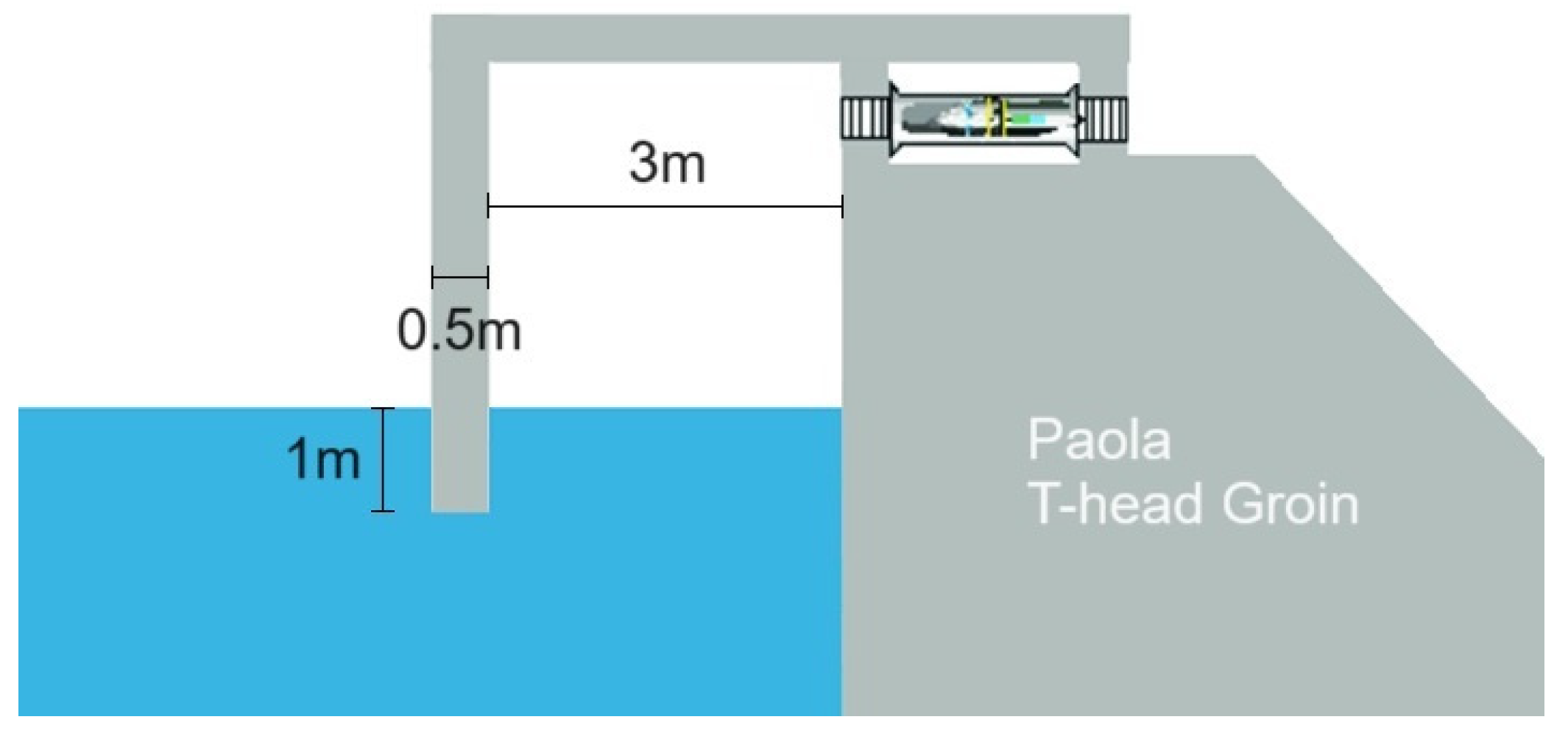
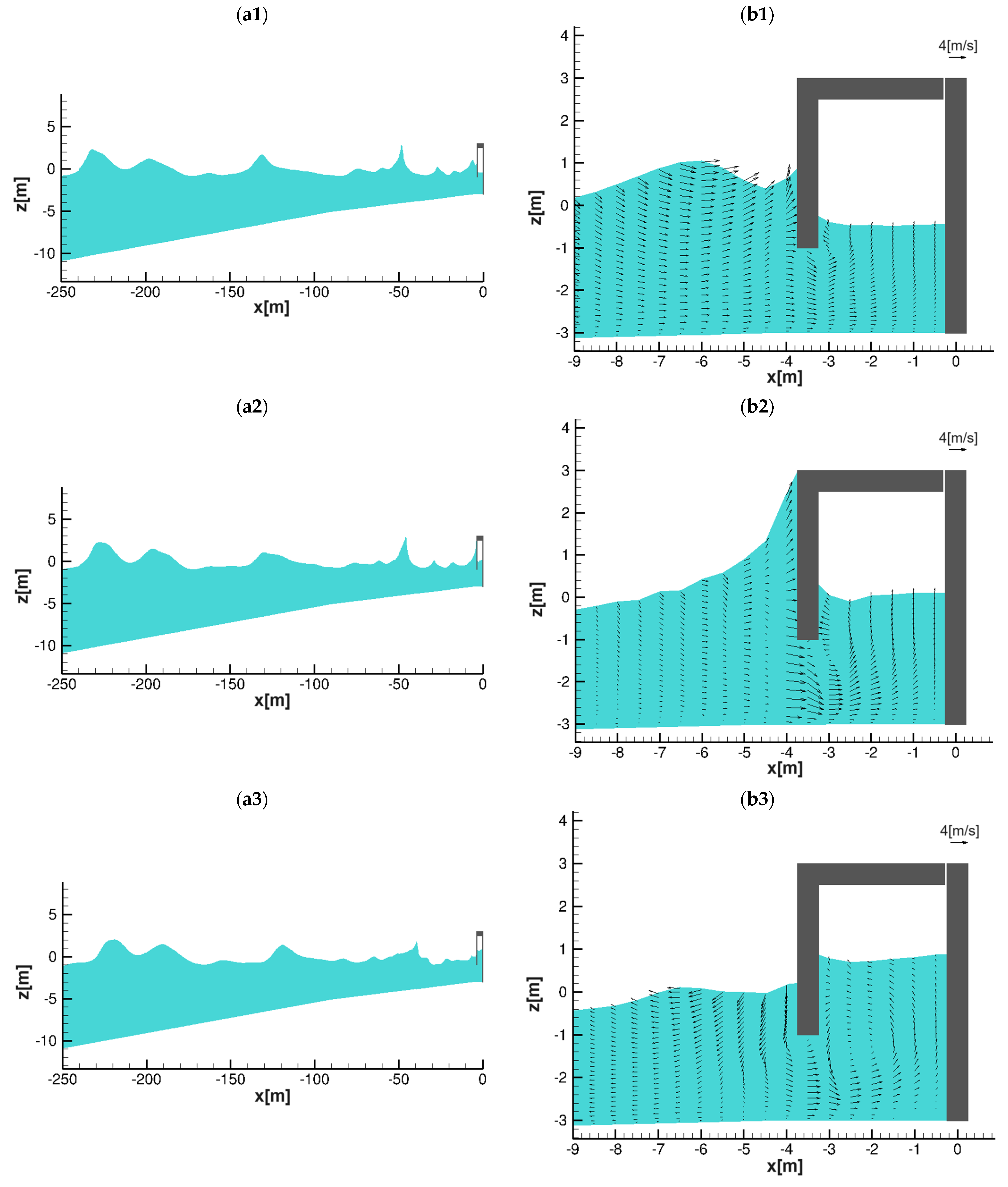
3.2.2. Performance of an OWC Subjected to Breaking Waves (Paola Coast)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Falcão, A.F.O. Overview on Oscillating Water Column Devices. Mater. Res. Proc. 2022, 20, 1–9. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C.; Gato, L.M.C. Self-rectifying air turbines for wave energy conversion: A comparative analysis. Renew. Sustain. Energy Rev. 2018, 91, 1231–1241. [Google Scholar] [CrossRef]
- Morris-Thomas, M.T.; Irvin, R.J.; Thiagarajan, K.P. An investigation into the hydrodynamic efficiency of an oscillating water column. J. Offshore Mech. Arct. Eng. 2007, 129, 273–278. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zou, Q.P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Romolo, A.; Timpano, B.; Laface, V.; Fiamma, V.; Arena, F. Experimental Investigation of Wave Loads on U-OWC Breakwater. J. Mar. Sci. Eng. 2023, 11, 19. [Google Scholar] [CrossRef]
- Ning, D.; Shi, J.; Zou, Q.; Teng, B. Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method). Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- Kim, J.S.; Nam, B.W.; Park, S.; Kim, K.H.; Shin, S.H.; Hong, K. Numerical investigation on hydrodynamic energy conversion performance of breakwater-integrated oscillating water column-wave energy converters. Ocean Eng. 2022, 253, 111287. [Google Scholar] [CrossRef]
- Koo, W.; Kim, M. Nonlinear time-domain simulation of a land-based oscillating water column. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 276–285. [Google Scholar] [CrossRef]
- Wan, C.; Yang, C.; Bai, X.; Bi, C.; Chen, H.; Li, M.; Jin, Y.; Zhao, L. Numerical investigation on the hydrodynamics of a hybrid OWC wave energy converter combining a floating buoy. Ocean Eng. 2023, 281, 114818. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43, 22–35. [Google Scholar] [CrossRef]
- Derakhti, M.; Kirby, J.T.; Shi, F.; Ma, G. Wave breaking in the surf zone and deep-water in a non-hydrostatic RANS model. Part 1: Organized wave motions. Ocean Model. 2016, 107, 125–138. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Gallerano, F. Numerical integration of the contravariant integral form of the Navier-Stokes equations in time-dependent curvilinear coordinate system for three-dimensional free surface flows. Contin. Mech. Thermodyn. 2019, 31, 491–519. [Google Scholar] [CrossRef]
- Cannata, G.; Simone, M.; Gallerano, F. Numerical Investigation into the Performance of an OWC Device under Regular and Irregular Waves. J. Mar. Sci. Eng. 2023, 11, 735. [Google Scholar] [CrossRef]
- Torres, F.R.; Teixeira, P.R.F.; Didier, E. Study of the turbine power output of an oscillating water column device by using a hydrodynamic—Aerodynamic coupled model. Ocean Eng. 2016, 125, 147–154. [Google Scholar] [CrossRef]
- Teixeira, P.R.F.; Davyt, D.P.; Didier, E.; Ramalhais, R. Numerical simulation of an oscillating water column device using a code based on Navier.Stokes equations. Energy 2013, 61, 513–530. [Google Scholar] [CrossRef]
- Josset, C.; Clément, A.H. A time-domain numerical simulator for oscillating water column wave power plants. Renew. Energy 2007, 32, 1379–1402. [Google Scholar] [CrossRef]
- Cannata, G.; Palleschi, F.; Iele, B.; Gallerano, F. A Wave-Targeted Essentially Non-Oscillatory 3D Shock-Capturing Scheme for Breaking Wave Simulation. J. Mar. Sci. Eng. 2022, 10, 810. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 5th ed.; Wiley: Chichester, UK, 2006; pp. 128–131. [Google Scholar]
- Booij, N.; Holthuijsen, L.H.; Ris, R.C. The “SWAN” wave model for shallow water. Coast. Eng. 1996, 25, 668–676. [Google Scholar] [CrossRef]
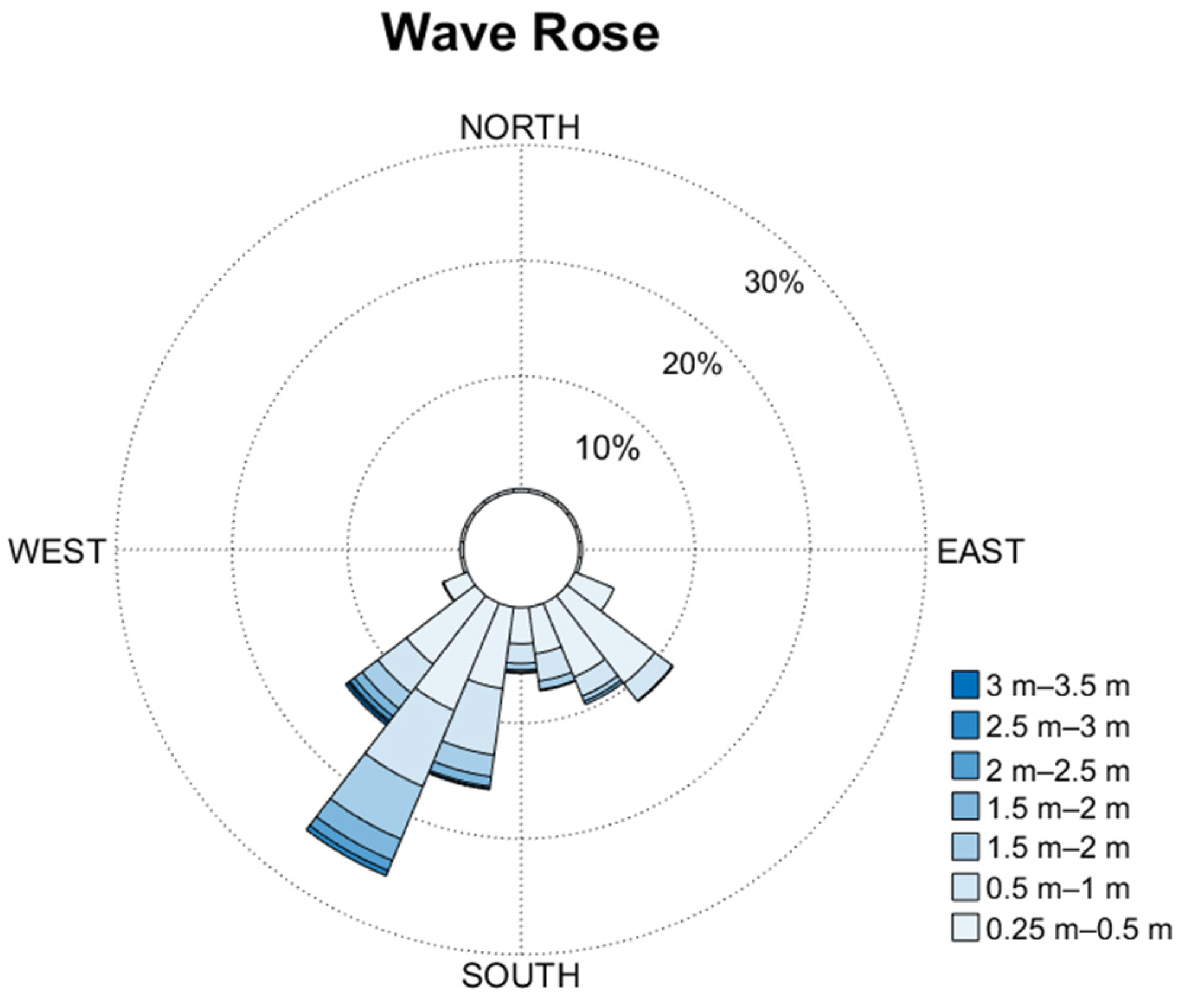

| θ [° North] | Hs [m] |  | ||||||
| 0.25–0.5 | 0.5–1.0 | 1.0–1.5 | 1.5–2.0 | 2.0–2.5 | 2.5–3.0 | 3.0–3.5 | ||
| 165 | 4.6 s | 5.3 s | 6.4 s | 7.2 s | 7.8 s | 8.2 s | 9.1 s | |
| 180 | 4.9 s | 5.6 s | 6.7 s | 7.4 s | 8.1 s | 8.8 s | 9.6 s | |
| 195 | 4.8 s | 5.8 s | 6.9 s | 7.7 s | 8.2 s | 8.8 s | 9.7 s | |
| 210 | 5.5 s | 7.3 s | 8.1 s | 8.4 s | 8.8 s | 9.1 s | 9.7 s | |
| θ [° North] | Hs [m] | 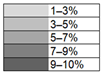 | |||||
| 0.25–0.5 | 0.5–1.0 | 1.0–1.5 | 1.5–2.0 | 2.0 – 2.5 | 2.5–3.0 | ||
| 225 | 6.5 s | 7.2 s | 8.0 s | 8.2 s | 8.8 s | 9.8 s | |
| 240 | 6.3 s | 7.0 s | 8.0 s | 8.4 s | 8.9 s | 9.6 s | |
| 255 | 6.2 s | 7.1 s | 8.0 s | 8.6 s | 9.1 s | 9.6 s | |
| 270 | 5.6 s | 6.9 s | 8.0 s | 8.7 s | 9.3 s | 9.7 s | |
| 285 | 5.2 s | 6.8 s | 8.1 s | 8.8 s | 9.7 s | 10.1 s | |
| 300 | 5.5 s | 6.7 s | 7.8 s | 8.5 s | 9.6 s | 10.0 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cannata, G.; Biondi, F.; Simone, M. Numerical Study on the Performance of an OWC under Breaking and Non-Breaking Waves. J. Mar. Sci. Eng. 2024, 12, 936. https://doi.org/10.3390/jmse12060936
Cannata G, Biondi F, Simone M. Numerical Study on the Performance of an OWC under Breaking and Non-Breaking Waves. Journal of Marine Science and Engineering. 2024; 12(6):936. https://doi.org/10.3390/jmse12060936
Chicago/Turabian StyleCannata, Giovanni, Francesco Biondi, and Marco Simone. 2024. "Numerical Study on the Performance of an OWC under Breaking and Non-Breaking Waves" Journal of Marine Science and Engineering 12, no. 6: 936. https://doi.org/10.3390/jmse12060936
APA StyleCannata, G., Biondi, F., & Simone, M. (2024). Numerical Study on the Performance of an OWC under Breaking and Non-Breaking Waves. Journal of Marine Science and Engineering, 12(6), 936. https://doi.org/10.3390/jmse12060936







