Innovations in Offshore Wind: Reviewing Current Status and Future Prospects with a Parametric Analysis of Helical Pile Performance for Anchoring Mooring Lines
Abstract
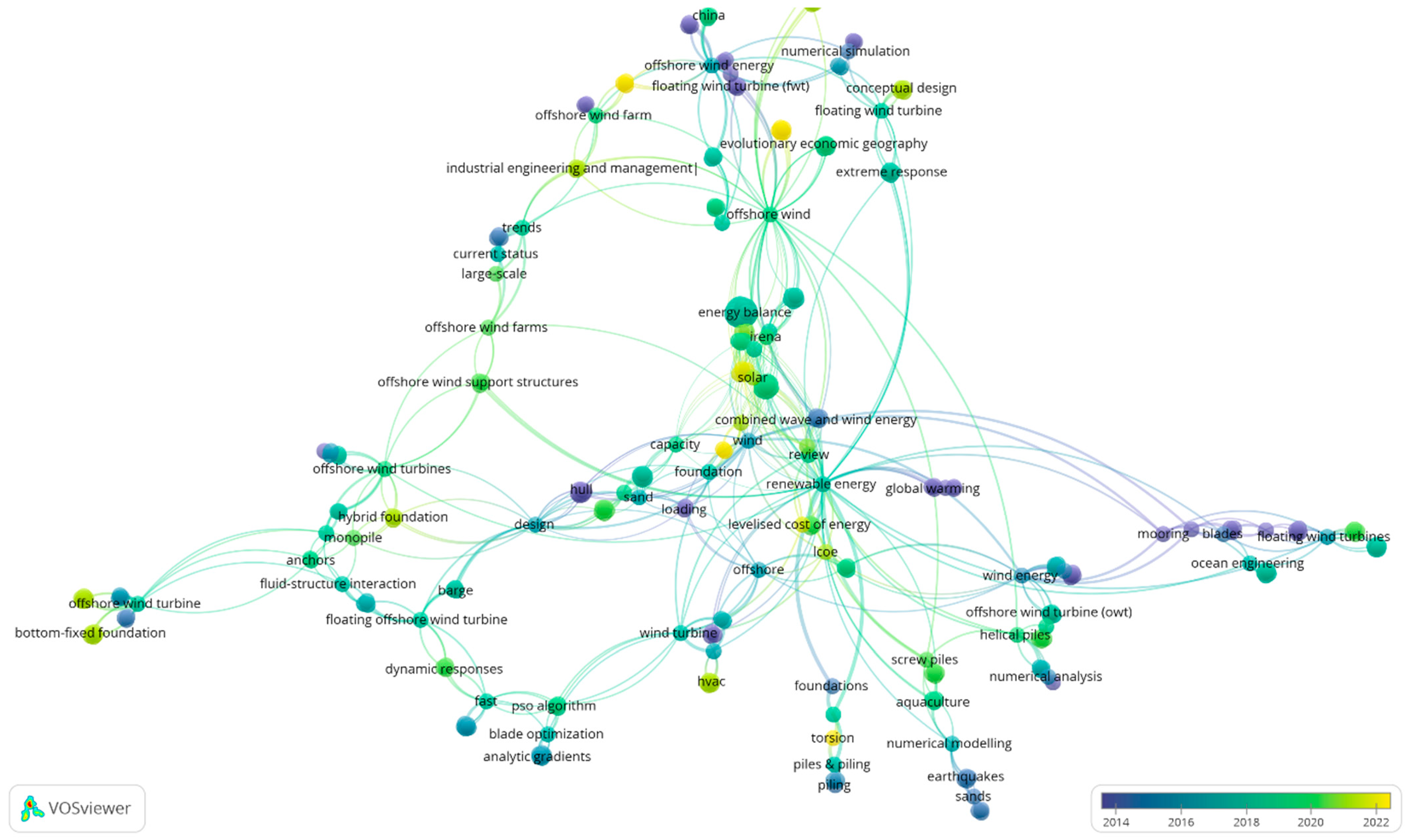
:1. Introduction
- Surveying the database and selecting pertinent keywords to ensure a comprehensive coverage of the relevant literature.
- Assembling and screening research papers to extract valuable insights and identify emerging trends in the offshore wind sector.
- Comparing various offshore wind foundation types to discern their strengths, weaknesses, potential areas for further research and improvement, as well as determining prospects for offshore wind.
- Applying numerical modeling techniques to investigate the efficacy of helical piles with two helices at varied loading inclinations as anchors for resisting loads from floating offshore mooring lines. These piles are installed utilizing machine-mounted hydraulic or electrically powered drilling equipment that screws them directly into the ground, thus allowing for easy installation in marine environments.
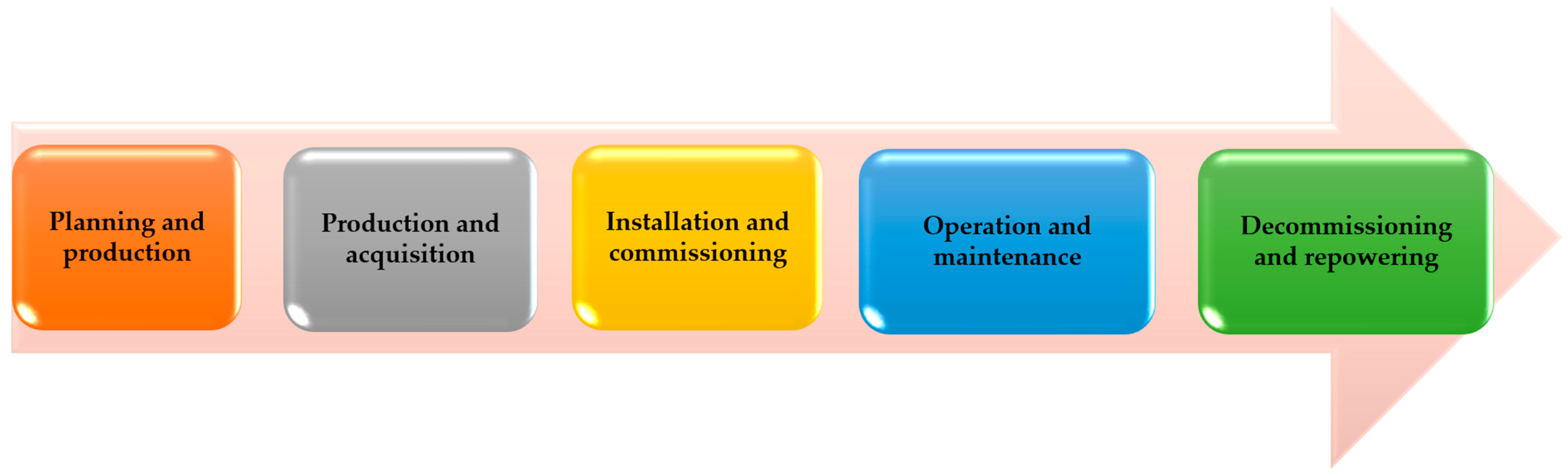
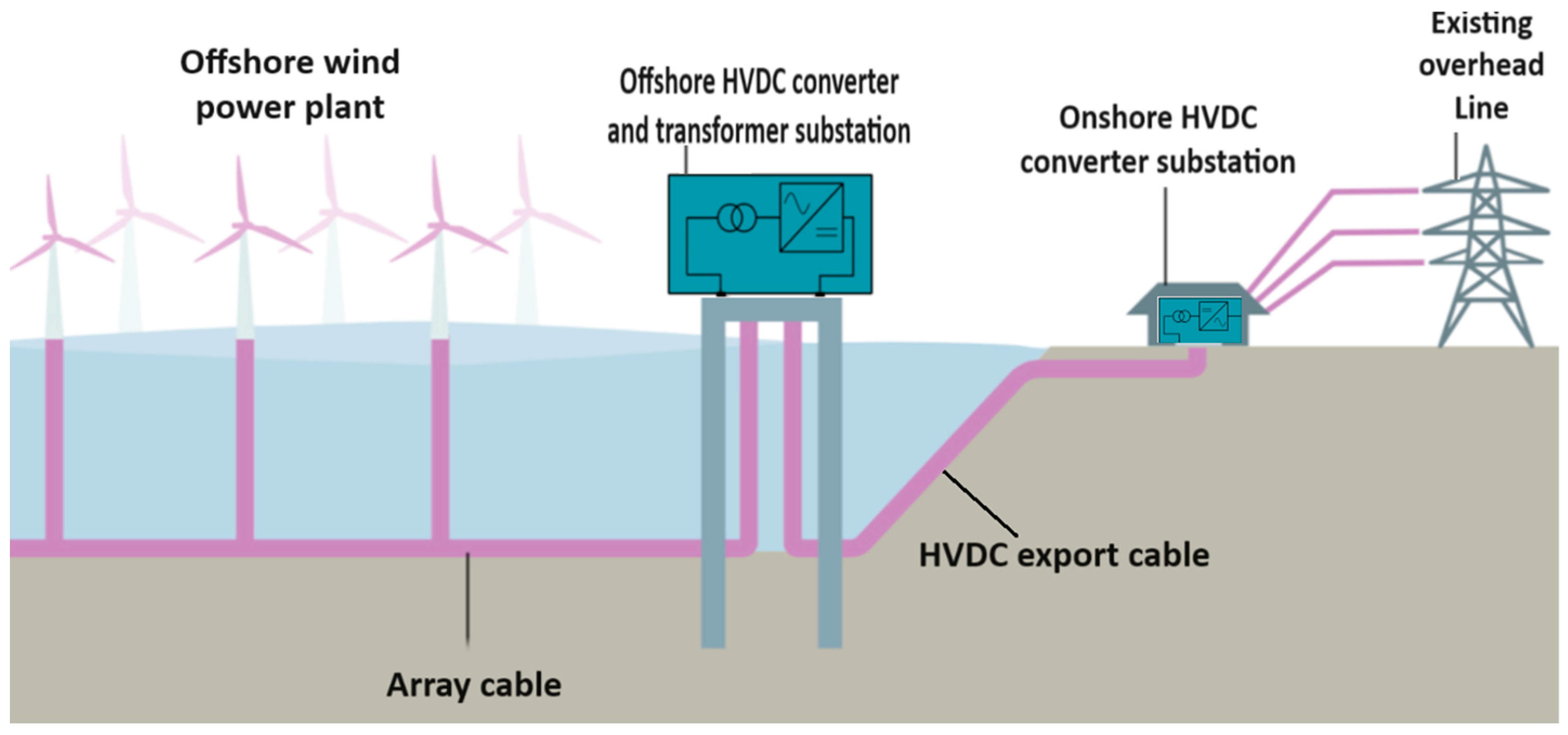
2. Offshore Wind Farms
2.1. Offshore Wind Turbine
2.2. Foundations
2.2.1. Monopile
2.2.2. Gravity Foundations
2.2.3. Jacket
3. Prospects for Offshore Wind
- Semi-Submersible Platform (SSP): This platform floats above the water’s surface while remaining partially submerged. Mooring lines are used by both spar and SSP to keep a loose connection to the seafloor. Suitable for water depths up to 120 m, SSP is a flexible sort of floating foundation [37].
- Tension Leg Platform (TLP): TLPs are well known in the O&G sector, and they are commonly used as FOWT substructures. TLP wind turbines have significantly lower heave, roll, and pitch motions than other floating foundations. It might drastically reduce manufacturing costs in deep oceans compared to stationary platforms. A seafloor-supported underwater platform is supported vertically by tendons. TLP is a lightweight, highly stable construction that can be used in water up to 120 m deep. But, TLP is not employed much because of its complicated and expensive mooring method [37,47].
- Barge: The barge-type FOWT uses wind turbines mounted on a shallow-draft barge frame. The barge type is stable because of its broad waterplane surface. Similar to semisubmersibles, quayside assembly and wet towing are possible. The barge-type foundation has the advantage of being simple to manufacture. Barge-type wind turbines are typically employed in calm seas, such as harbors, due to their sensitivity to wave motions.
4. Utilizing Helical Piles: A Solution for Anchoring Mooring Lines
4.1. Introduction
4.2. Plaxis Validation
4.2.1. The Case Study of Sharkia Governorate, Egypt (According to Salem and Hussein [82])
4.2.2. Centrifuge Test Undertaken at the University of Dundee (According to Davidson et al. [78,83])
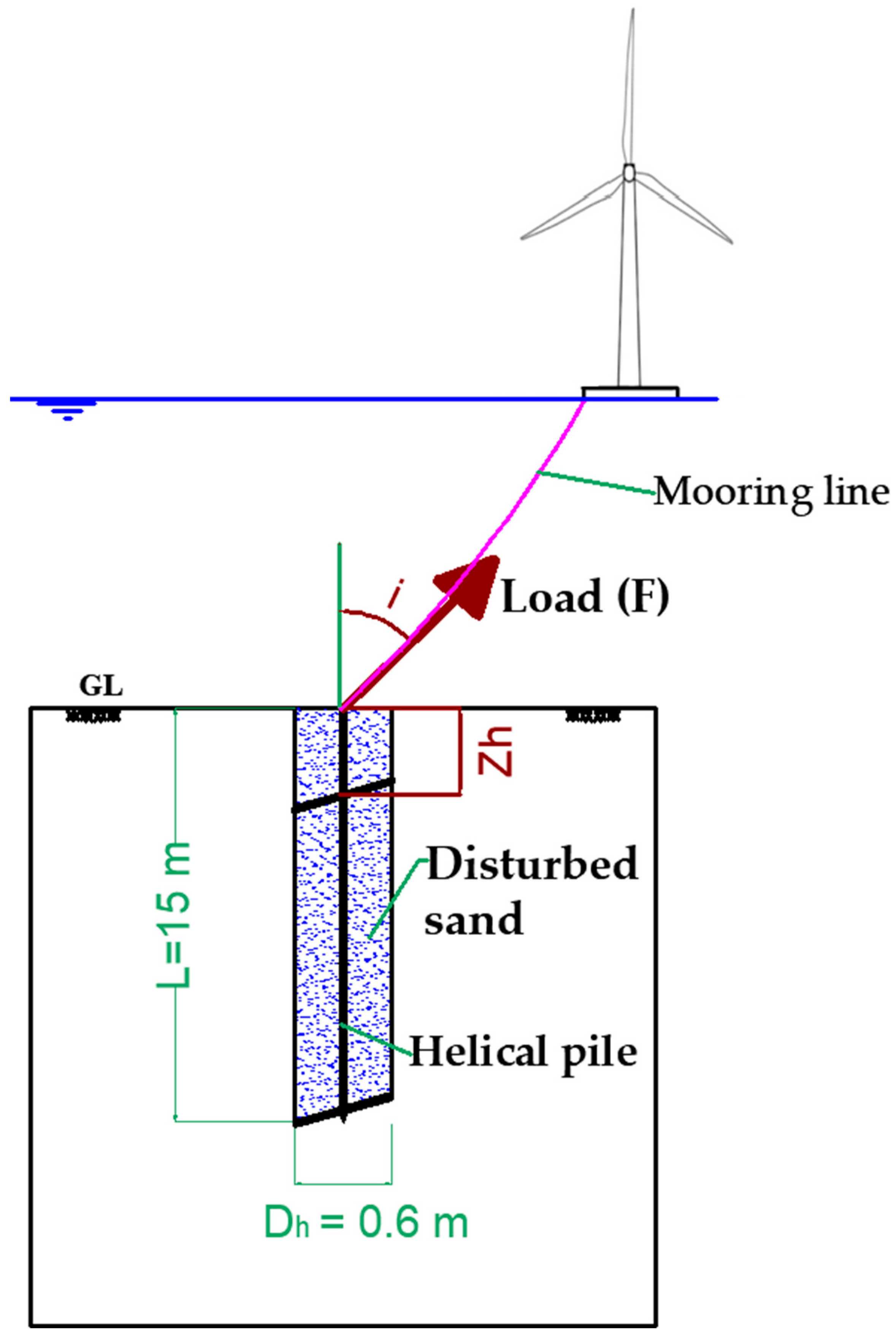
4.3. Problem Description
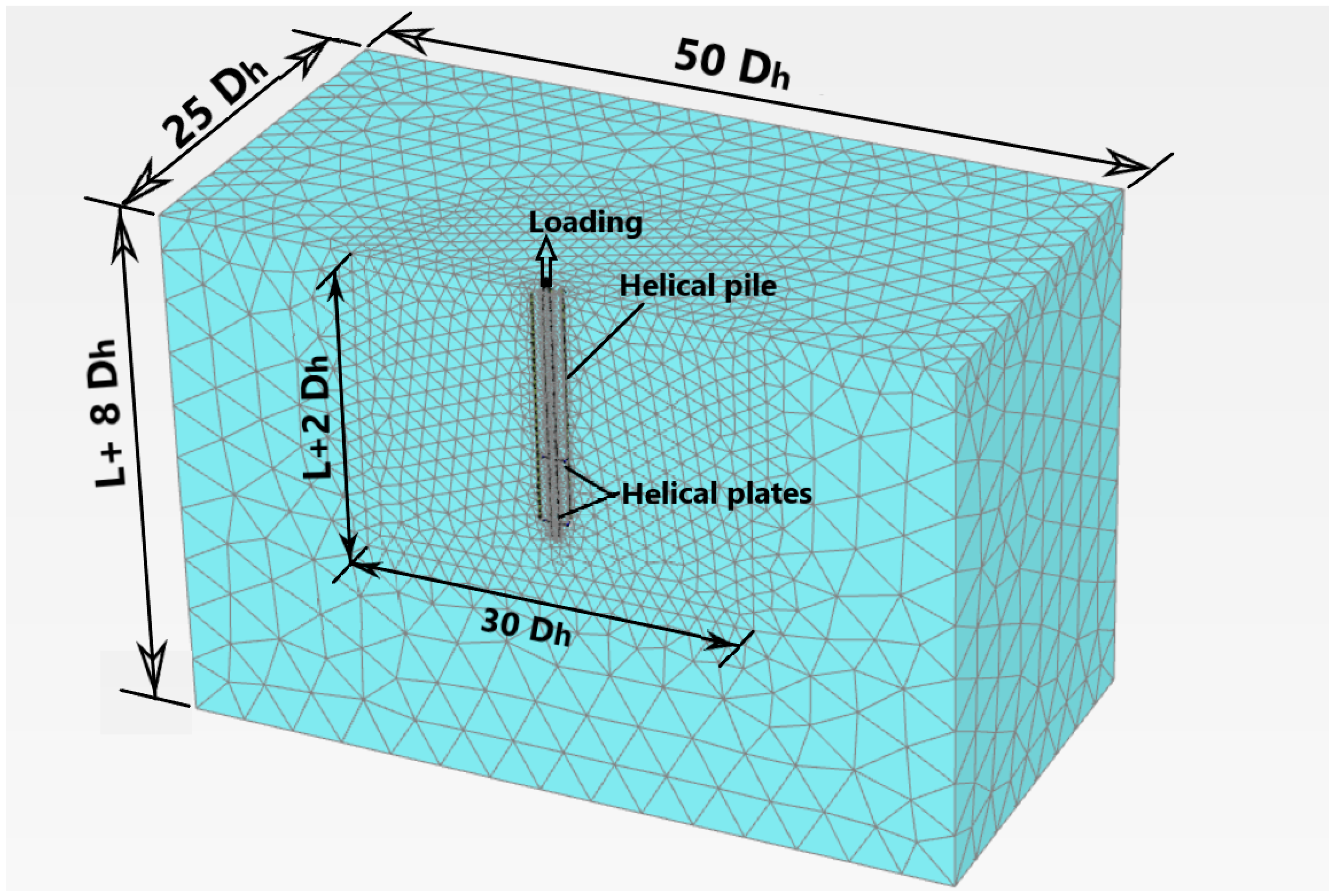
4.4. Methodology
Boundary and Initial Conditions
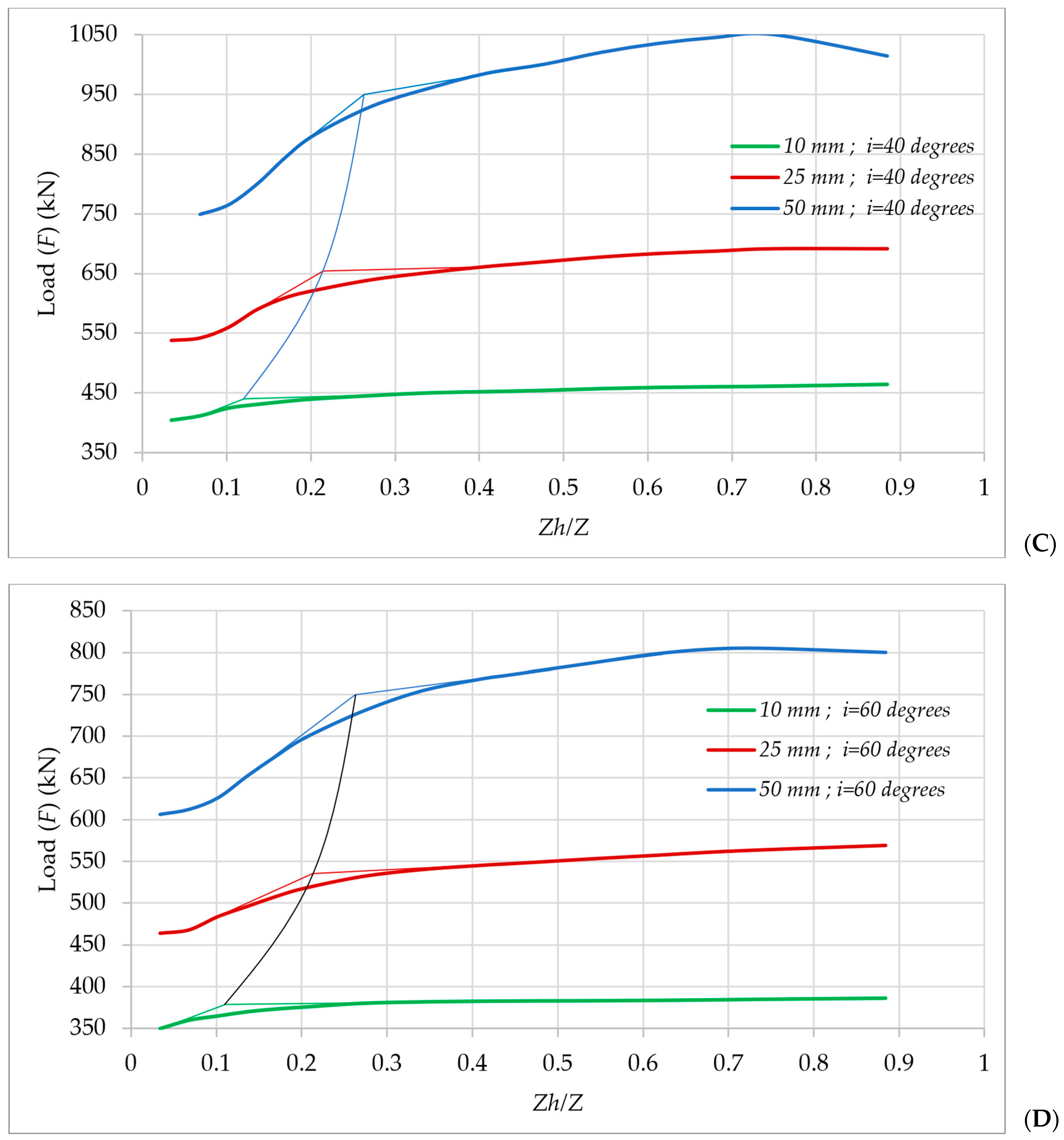
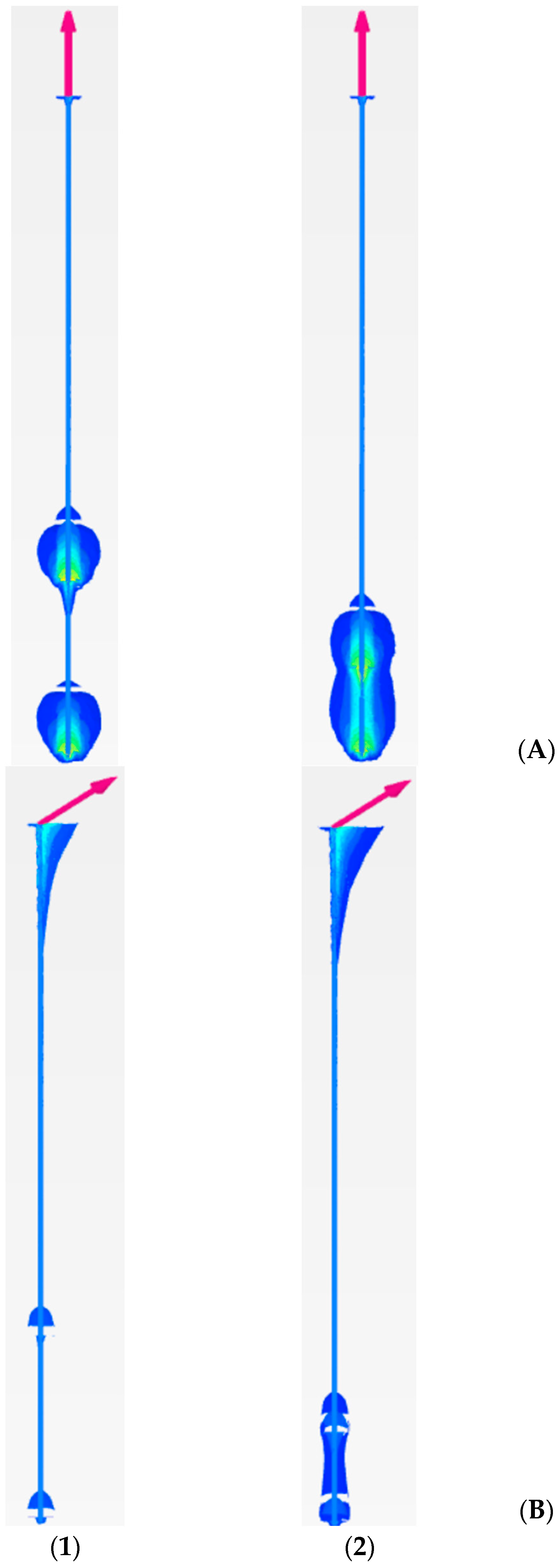
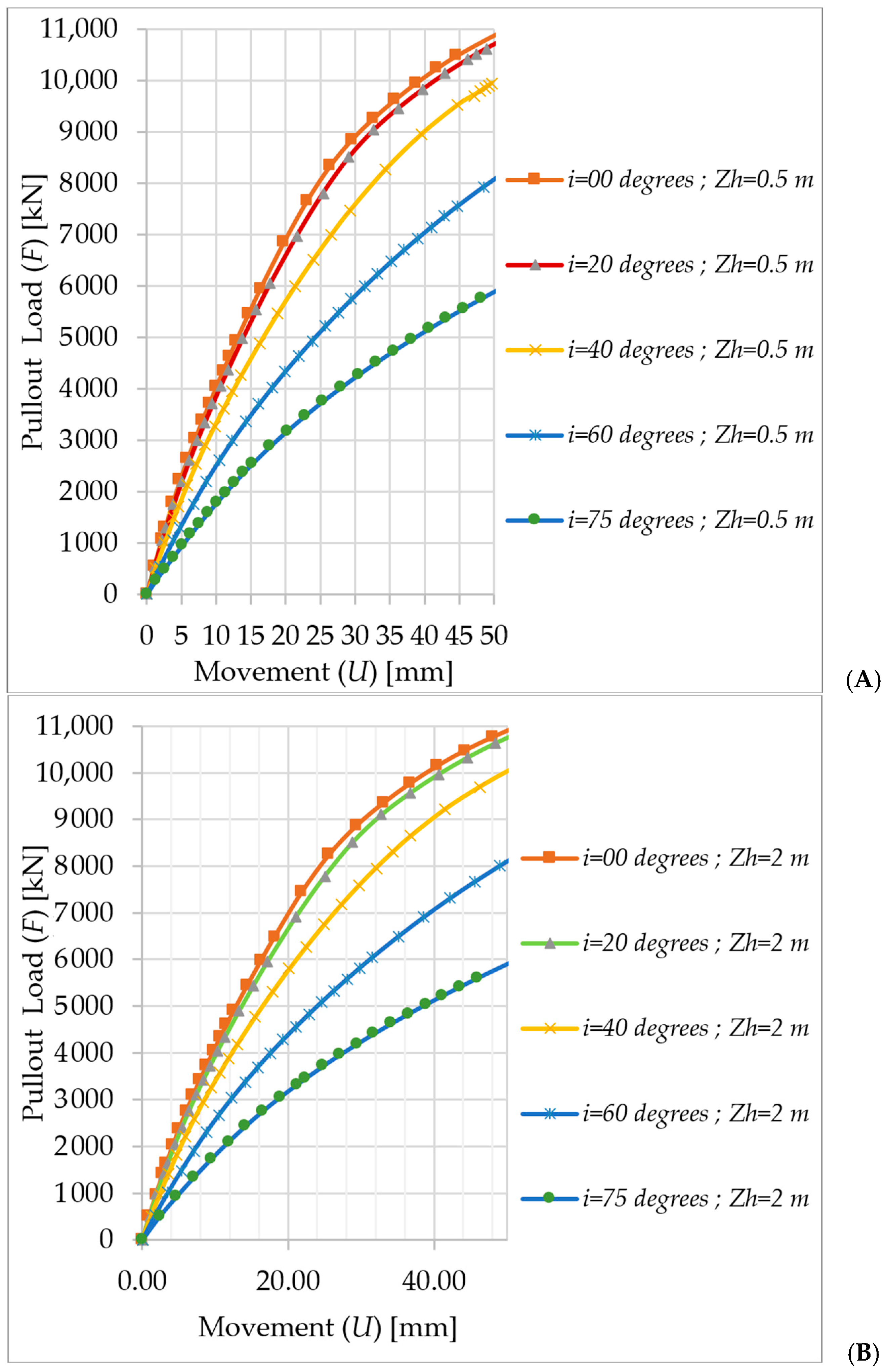
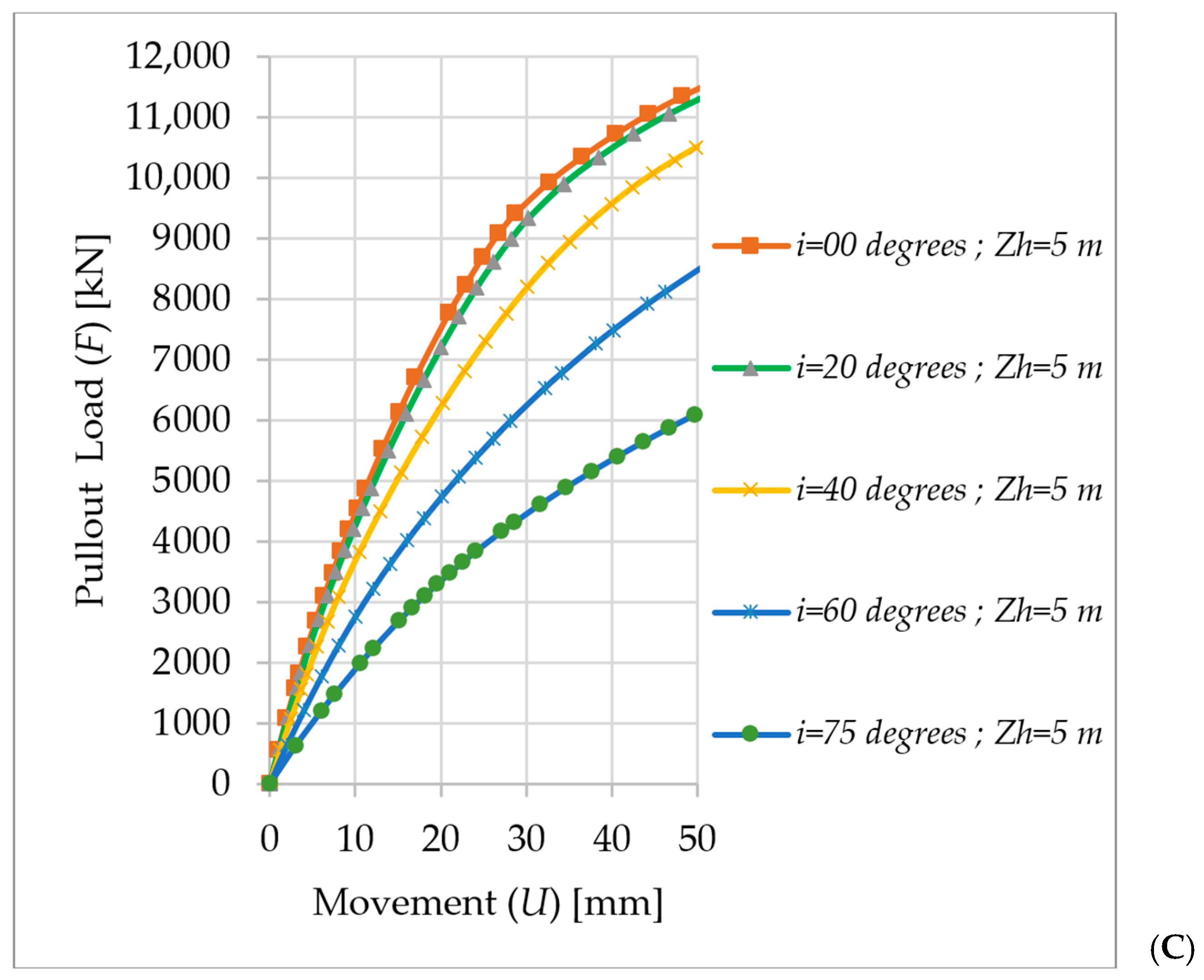
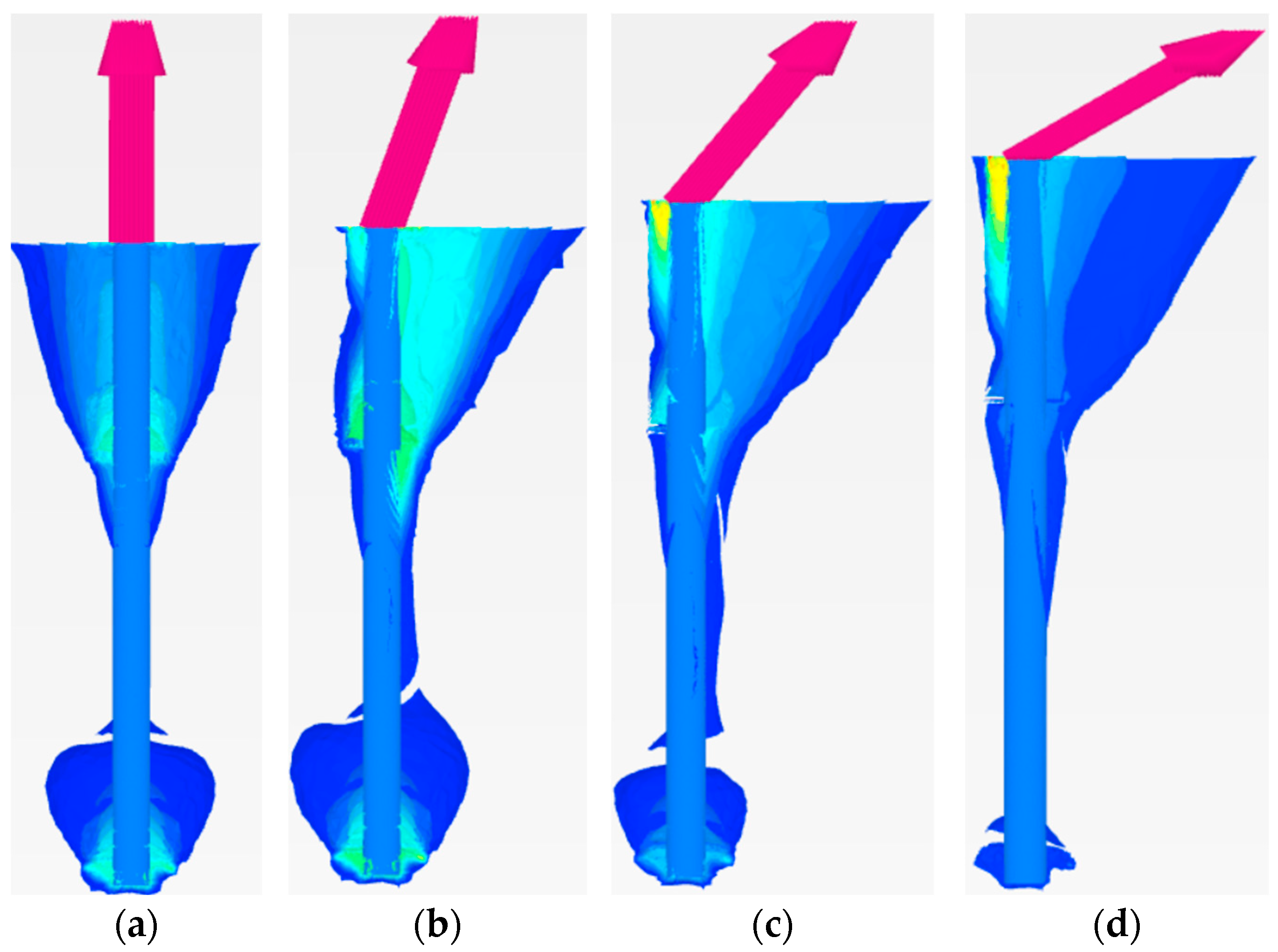
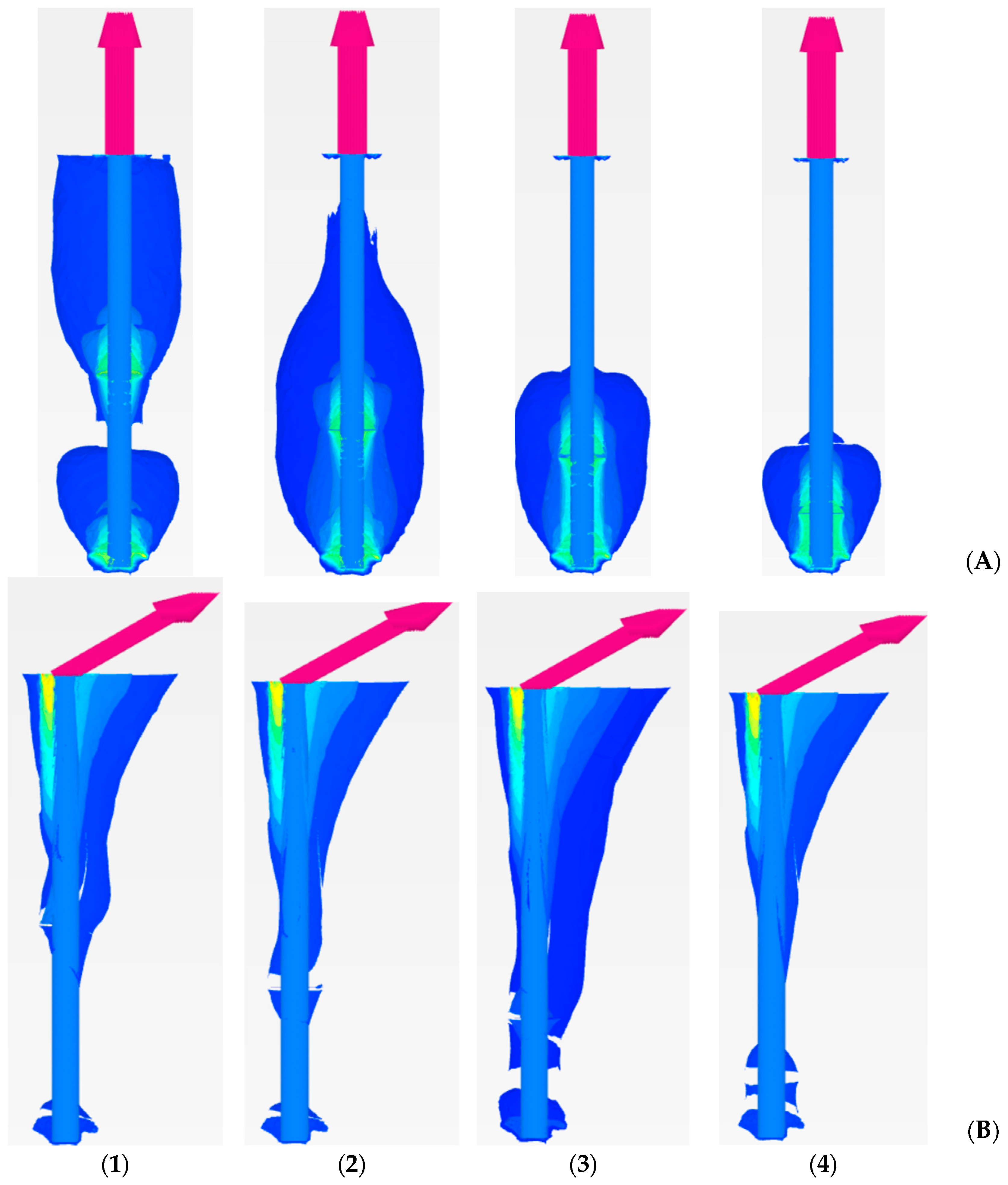
4.5. Results and Discussion
4.5.1. Small-Shaft-Diameter Helical Piles
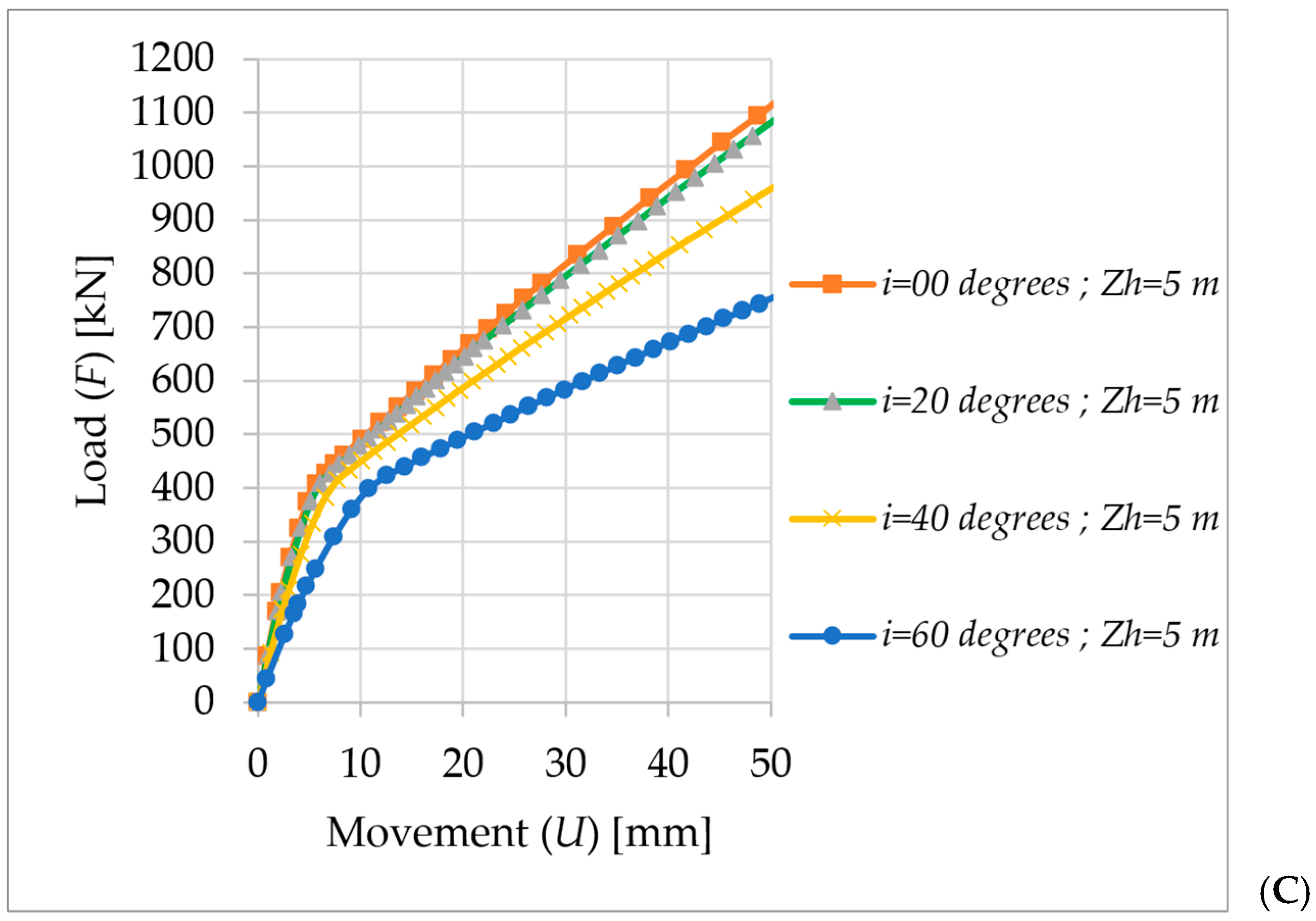
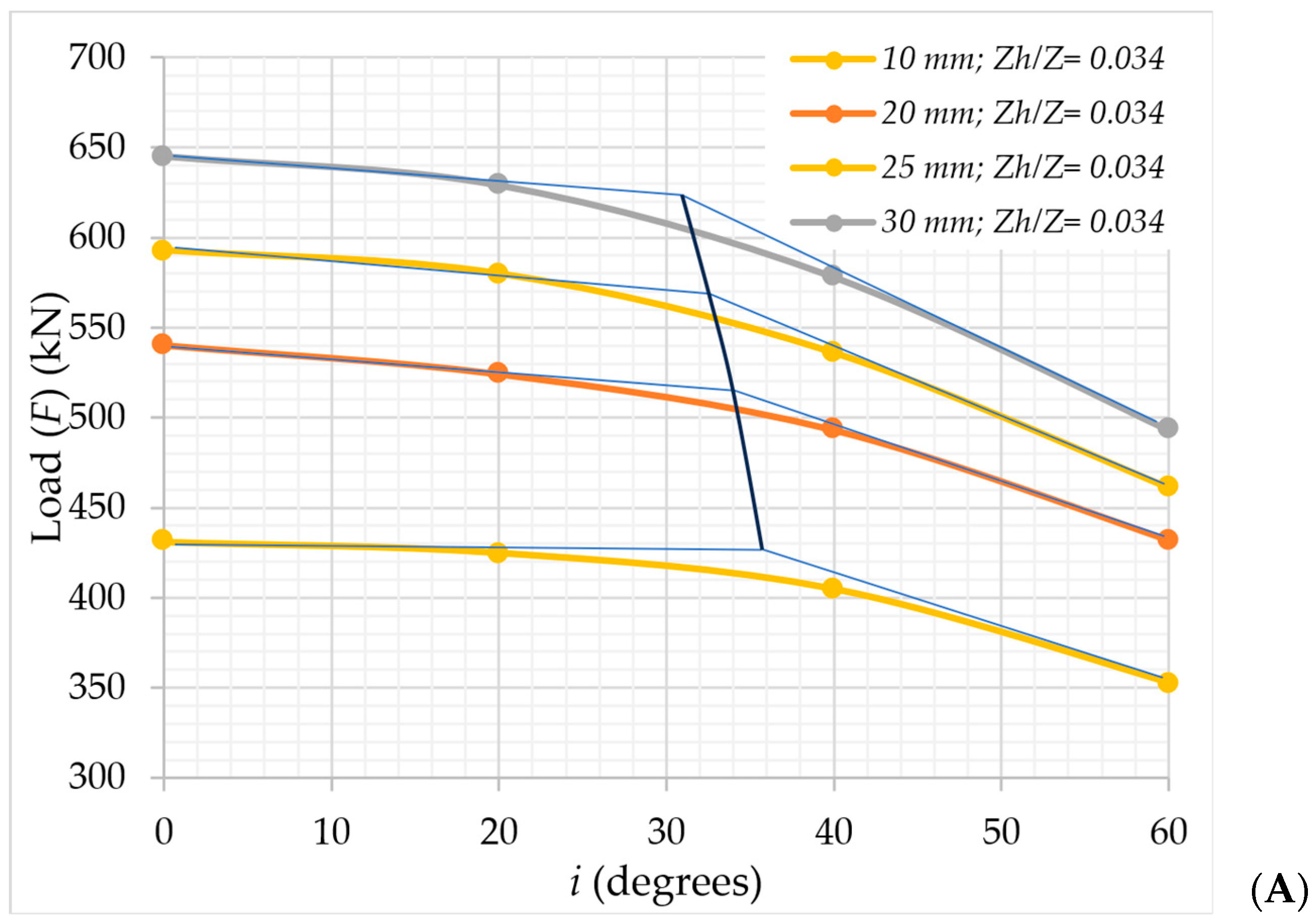
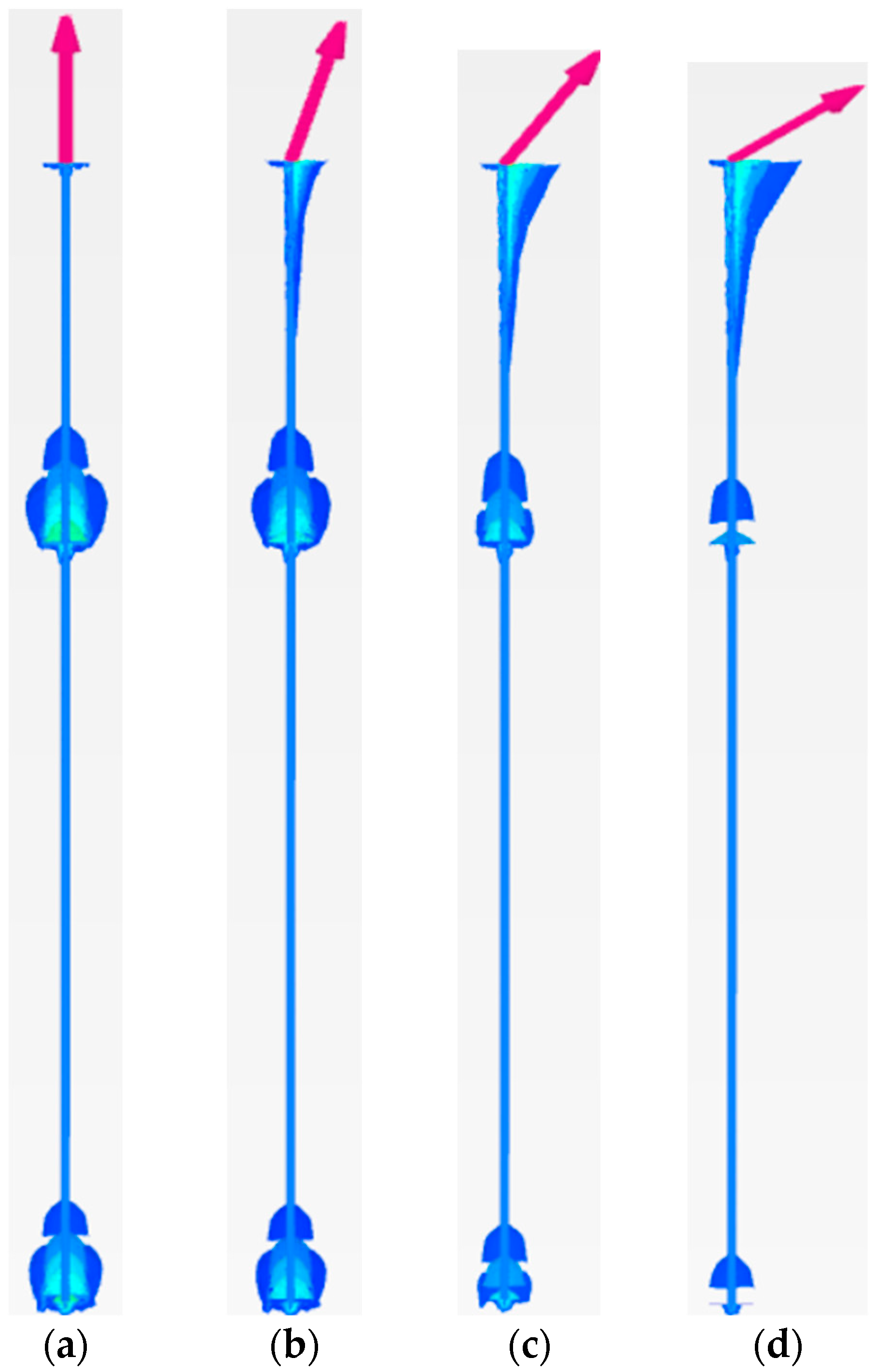
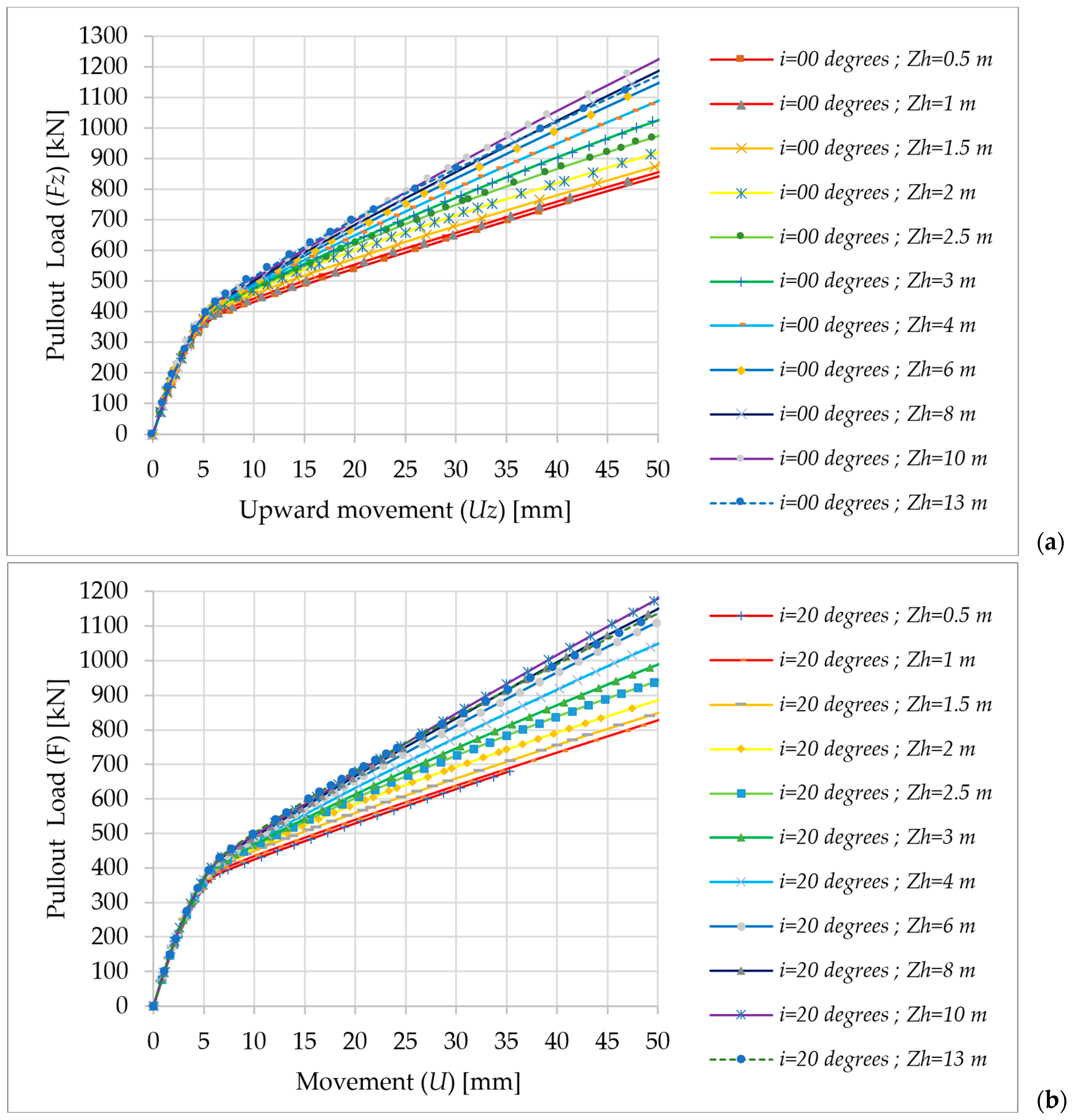
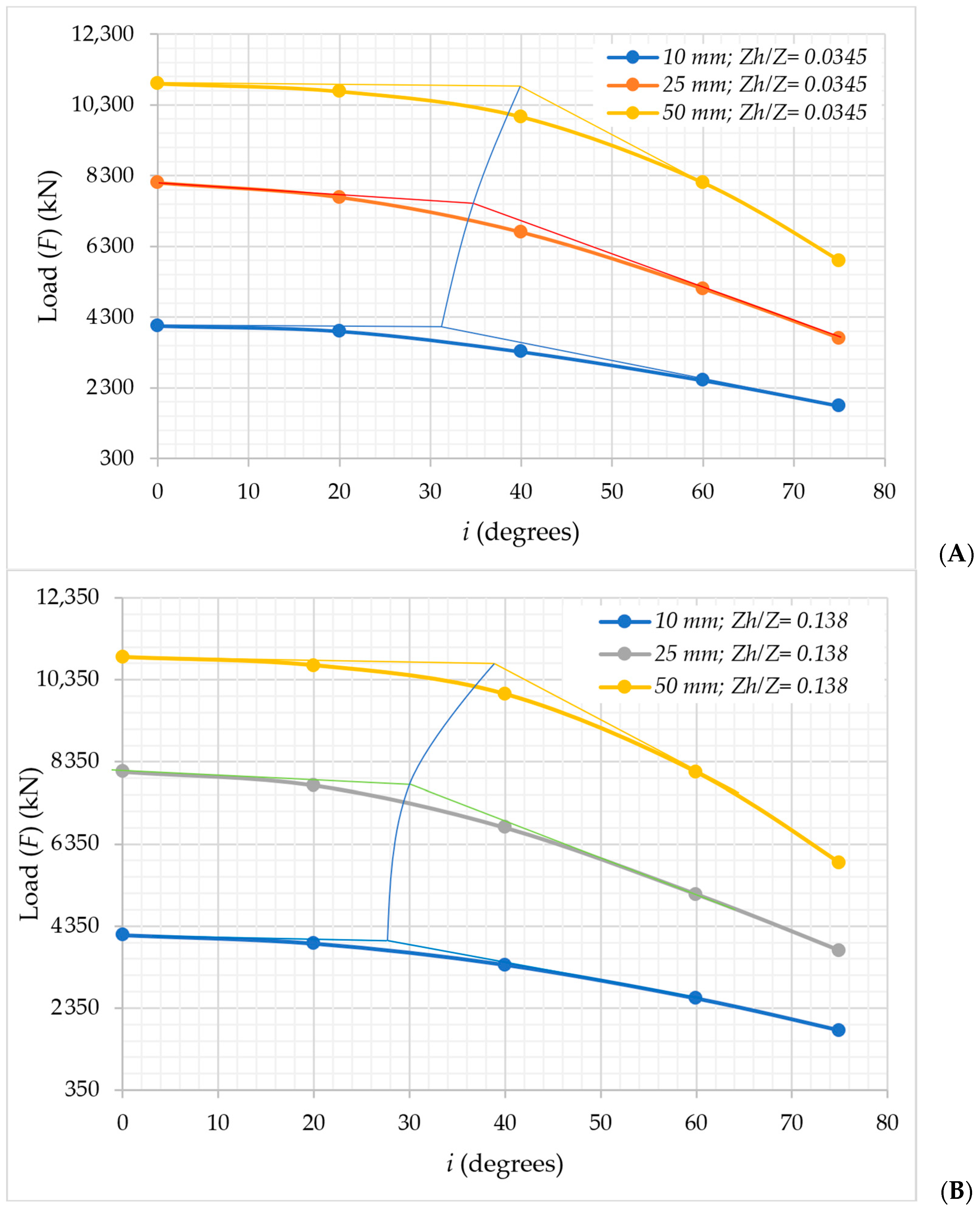
Impact of Load Inclination (i) on Pullout Behavior
Impact of Top Helical Plate Location (Zh) on the Pullout Load (F) Behavior
4.5.2. Large-Shaft-Diameter Helical Piles
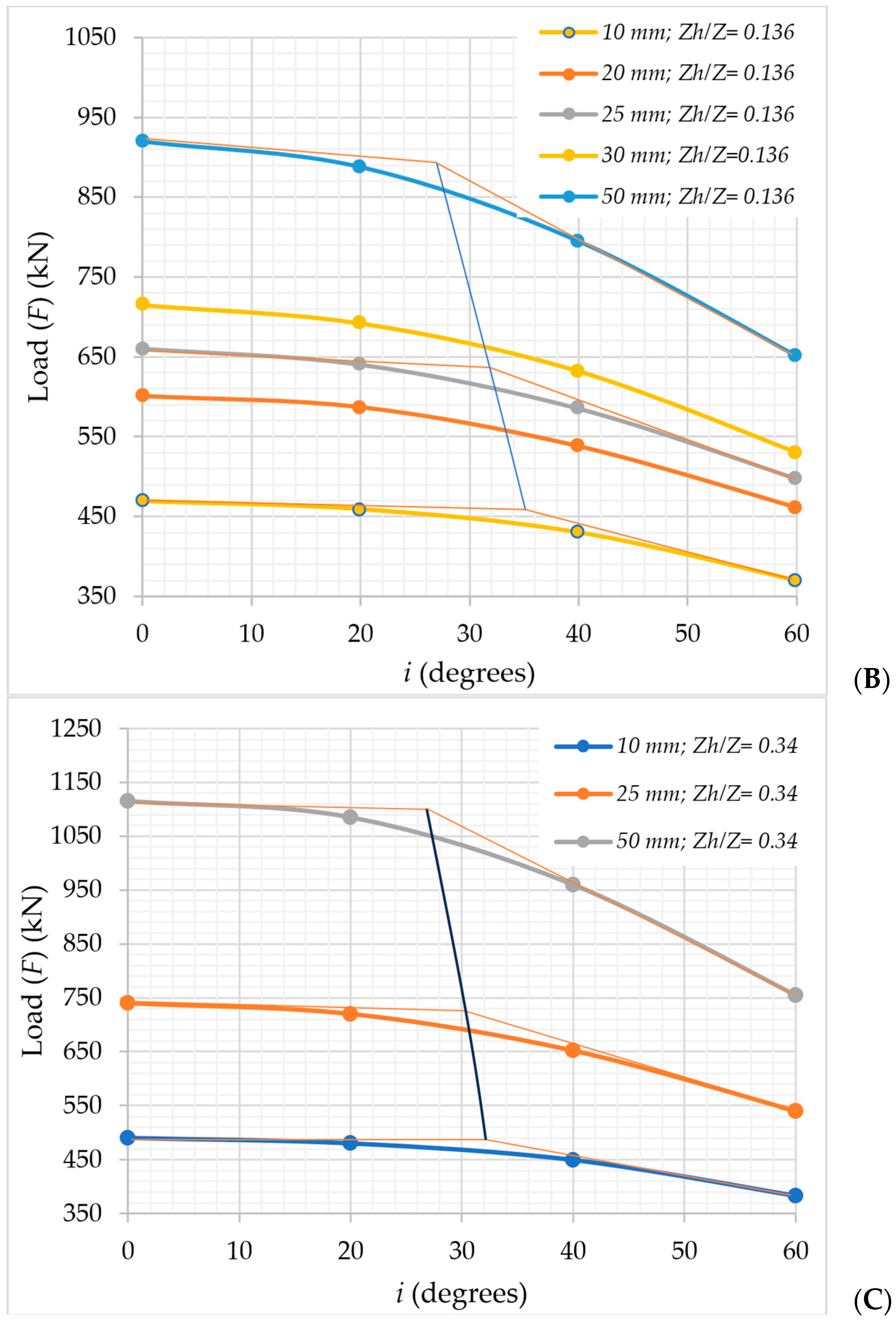
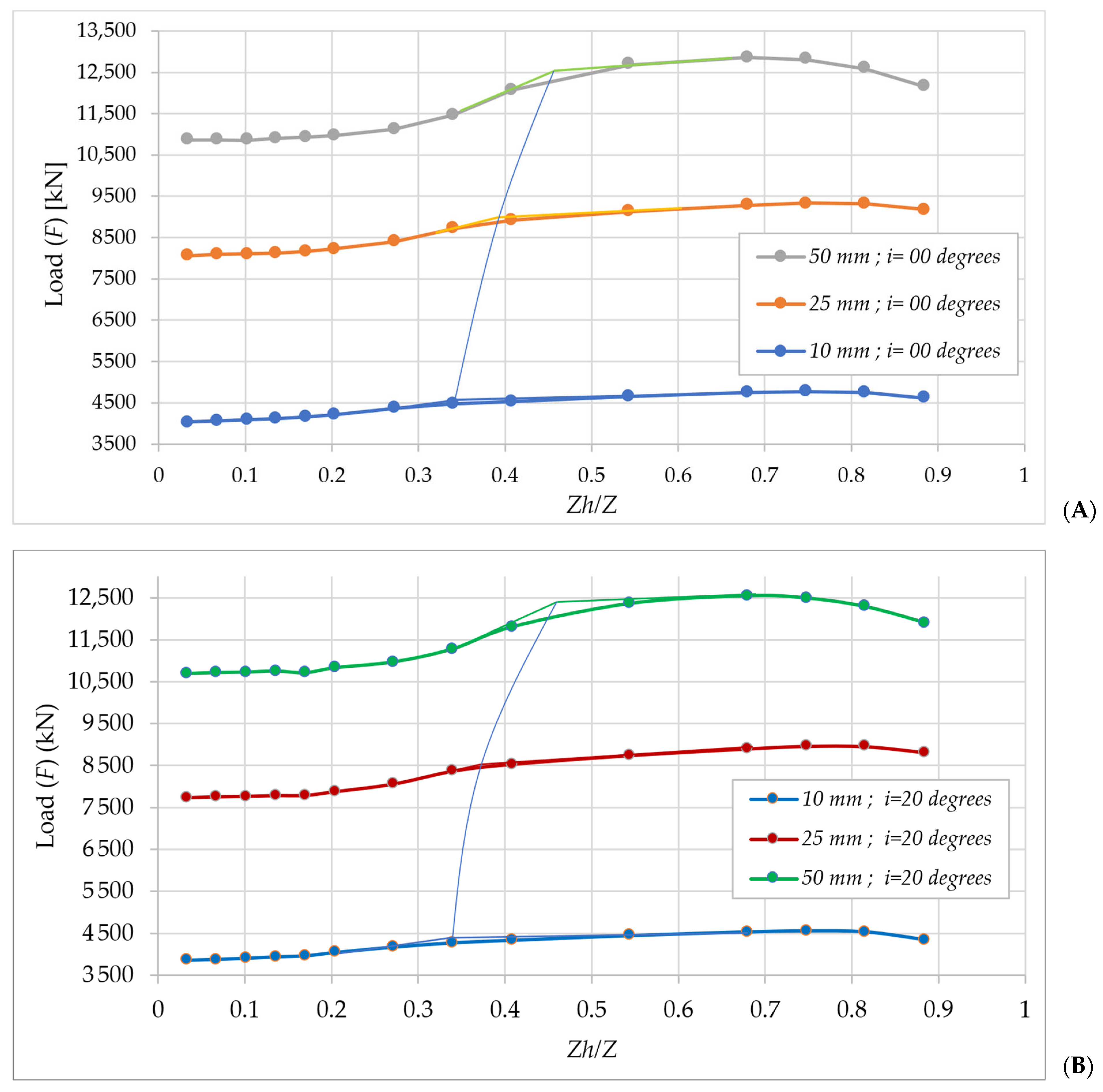
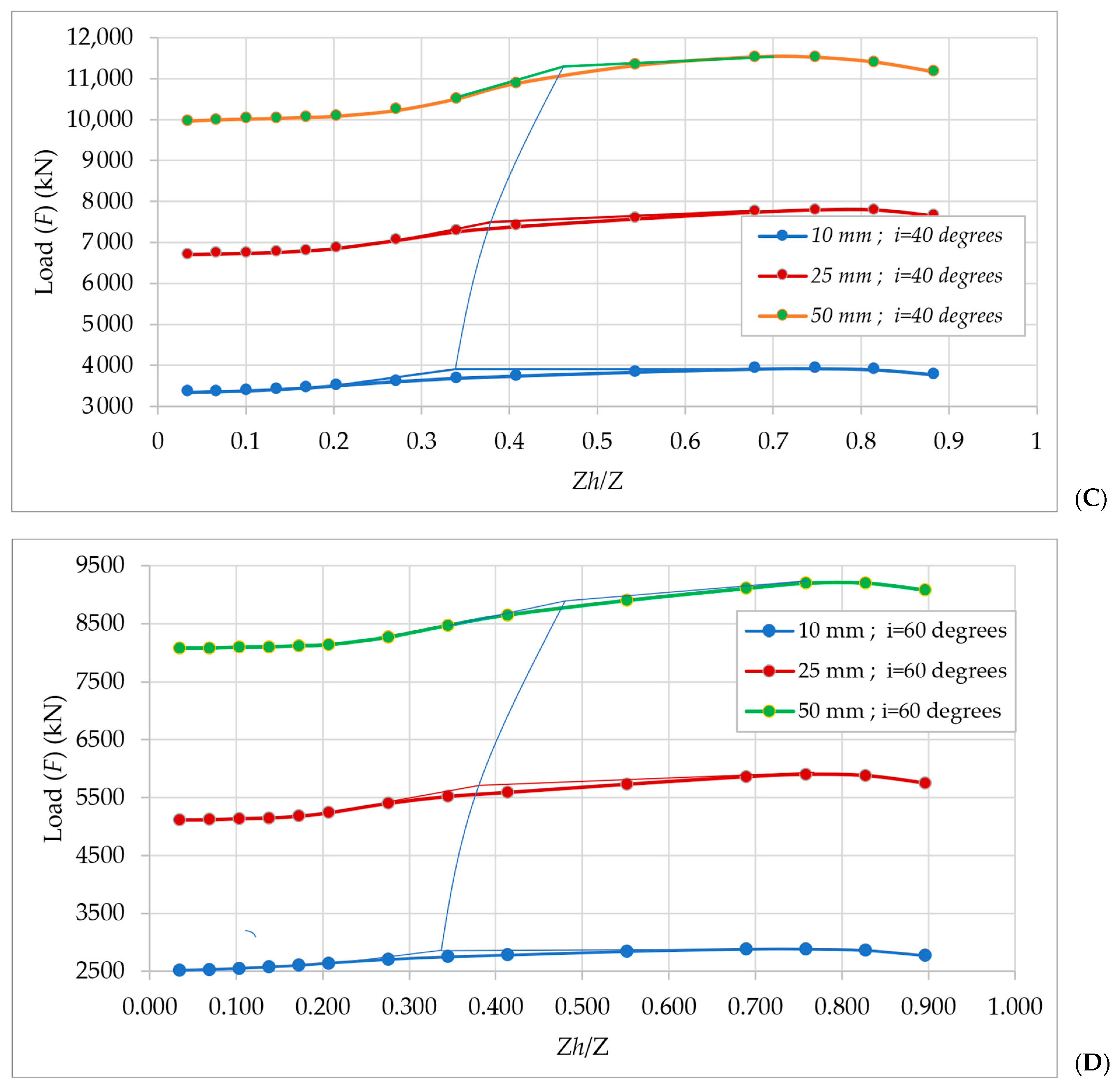
Impact of Load Inclination (i) on the Pullout Behavior of Large Diameter
Impact of the Top Helical Plate Location (Zh) on the Pullout Load (F) Behavior
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritchie, H.; Rosado, P.; Roser, M. Energy Mix. Our World in Data. 2024. Available online: https://ourworldindata.org/energy-mix (accessed on 7 April 2024).
- De Castro, M.; Salvador, S.; Gómez-Gesteira, M.; Costoya, X.; Carvalho, D.; Sanz-Larruga, F.J.; Gimeno, L. Europe, China and the United States: Three Different Approaches to the Development of Offshore Wind Energy. Renew. Sustain. Energy Rev. 2019, 109, 55–70. [Google Scholar] [CrossRef]
- Díaz, H.; Guedes Soares, C. Review of the Current Status, Technology and Future Trends of Offshore Wind Farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Rodrigues, S.; Restrepo, C.; Kontos, E.; Teixeira Pinto, R.; Bauer, P. Trends of Offshore Wind Projects. Renew. Sustain. Energy Rev. 2015, 49, 1114–1135. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application. In Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Poudineh, R.; Brown, C.; Foley, B. Background: Role of the Offshore Wind Industry. In Economics of Offshore Wind Power; Palgrave Macmillan: Cham, Switzerland, 2017; pp. 1–14. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Kapsali, M. Shifting towards Offshore Wind Energy-Recent Activity and Future Development. Energy Policy 2013, 53, 136–148. [Google Scholar] [CrossRef]
- Esteban, M.D.; Diez, J.J.; López, J.S.; Negro, V. Why Offshore Wind Energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Hevia-Koch, P.; Klinge Jacobsen, H. Comparing Offshore and Onshore Wind Development Considering Acceptance Costs. Energy Policy 2019, 125, 9–19. [Google Scholar] [CrossRef]
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.E.; Jiang, Z. Offshore Wind Turbine Operations and Maintenance: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK; Hoboken, NJ, USA, 2001; p. 780. [Google Scholar]
- Sun, X.; Huang, D.; Wu, G. The Current State of Offshore Wind Energy Technology Development. Energy 2012, 41, 298–312. [Google Scholar] [CrossRef]
- MacKinnon, D.; Dawley, S.; Steen, M.; Menzel, M.P.; Karlsen, A.; Sommer, P.; Hansen, G.H.; Normann, H.E. Path Creation, Global Production Networks and Regional Development: A Comparative International Analysis of the Offshore Wind Sector. Prog. Plan. 2019, 130, 1–32. [Google Scholar] [CrossRef]
- Johnston, B.; Foley, A.; Doran, J.; Littler, T. Levelised Cost of Energy, A Challenge for Offshore Wind. Renew. Energy 2020, 160, 876–885. [Google Scholar] [CrossRef]
- Markard, J.; Petersen, R. The Offshore Trend: Structural Changes in the Wind Power Sector. Energy Policy 2009, 37, 3545–3556. [Google Scholar] [CrossRef]
- WindEurope. Offshore Wind in Europe—Key Trends and Statistics 2020; WindEurope: Bilbao, Spain, 2021. [Google Scholar]
- Commission European. Directorate-General for Energy. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. An EU Strategy to Harness the Potential of Offshore Renewable Energy for a Climate Neutral Future; Commission European: Brussels, Belgium, 2020. [Google Scholar]
- WindEurope. Wind Energy in Europe: 2022 Statistics and the Outlook for 2023–2027; WindEurope: Bilbao, Spain, 2022; 58p. [Google Scholar]
- IRENA. Innovation Landscape for a Renewable-Powered Future: Solutions to Integrate Variable Renewables; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019; 164p. [Google Scholar]
- GWEC. Global Offshore Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021; p. 136. [Google Scholar]
- Babarit, A.; Gilloteaux, J.C.; Clodic, G.; Duchet, M.; Simoneau, A.; Platzer, M.F. Techno-Economic Feasibility of Fleets of Far Offshore Hydrogen-Producing Wind Energy Converters. Int. J. Hydrogen Energy 2018, 43, 7266–7289. [Google Scholar] [CrossRef]
- Kovalchuk, V. Techno-Economic Review of Offshore Wind Power. Master’s Thesis, Lappeenranta-Lahti University of Technology, Lappeenranta, Finland, 2021. [Google Scholar]
- Manwell, J.F. Offshore Wind Energy Technology Trends, Challenges, and Risks. In Power Stations Using Locally Available Energy Sources; Springer: New York, NY, USA, 2018; pp. 399–436. [Google Scholar] [CrossRef]
- Jiang, Z. Installation of Offshore Wind Turbines: A Technical Review. Renew. Sustain. Energy Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2022; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2023; 208p. [Google Scholar]
- IRENA. Renewable Energy Benefits Leveraging Local Capacity for Offshore Wind; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2018; 44p. [Google Scholar]
- Wang, X.; Zeng, X.; Li, J.; Yang, X.; Wang, H. A Review on Recent Advancements of Substructures for Offshore Wind Turbines. Energy Convers. Manag. 2018, 158, 103–119. [Google Scholar] [CrossRef]
- Buljan, A. Offshore Wind Turbines in 2023: 16 MW Model Installed Offshore, 18 MW WTGs Selected for New Project, 22 MW Turbine Announced. Available online: https://www.offshorewind.biz/2024/01/02/offshore-wind-turbines-in-2023-16-mw-model-installed-offshore-18-mw-wtgs-selected-for-new-project-22-mw-turbine-announced/ (accessed on 12 March 2024).
- Trojnar, K. Simplified Design of New Hybrid Monopile Foundations for Offshore Wind Turbines. Ocean Eng. 2021, 219, 108046. [Google Scholar] [CrossRef]
- Soares-Ramos, E.P.P.; de Oliveira-Assis, L.; Sarrias-Mena, R.; Fernández-Ramírez, L.M. Current Status and Future Trends of Offshore Wind Power in Europe. Energy 2020, 202, 117787. [Google Scholar] [CrossRef]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of Offshore Wind Turbines: A Review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Arshad, M.; O’kelly, B.C. Offshore Wind-Turbine Structures: A Review. Proc. Inst. Civ. Eng. Energy 2015, 166, 139–152. [Google Scholar] [CrossRef]
- Kaiser, M.J.; Snyder, B.F. Offshore Wind Energy System Components. In Offshore Wind Energy Cost Modeling; Green Energy and Technology; Springer: London, UK, 2012; pp. 13–30. [Google Scholar] [CrossRef]
- Igoe, D.; Gavin, K.; O’Kelly, B. An Investigation into the Use of Push-in Pile Foundations by the Offshore Wind Sector. Int. J. Environ. Stud. 2013, 70, 777–791. [Google Scholar] [CrossRef]
- Ørsted. Our Experience with Suction Bucket Jacket Foundations. Ørsted’s Experience with Suction Bucket Jacket Foundations. Available online: https://orsted.com/-/media/www/docs/corp/com/our-business/wind-power/bucket-jacket_long-version.ashx?la=en&hash=bb12170bd01a84543af54599146637e5 (accessed on 3 January 2024).
- Oh, K.Y.; Nam, W.; Ryu, M.S.; Kim, J.Y.; Epureanu, B.I. A Review of Foundations of Offshore Wind Energy Convertors: Current Status and Future Perspectives. Renew. Sustain. Energy Rev. 2018, 88, 16–36. [Google Scholar] [CrossRef]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A Review of Combined Wave and Offshore Wind Energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Horwath, S.; Hassrick, J.; Grismala, R.; Diller, E.; Krebs, J.; Manhard, R. ICF Comparison of Environmental Effects from Different Offshore Wind Turbine Foundations (2021 Revision)|Tethys; OCS Study BOEM 2021-053; U.S. Department of the Interior, Bureau of Ocean Energy Management: Sterling, VA, USA, 2020; p. 48. [Google Scholar]
- Fu, F. Design and Analysis of Tall and Complex Structures; Butterworth-Heinemann: Oxford, UK, 2018; ISBN 0081011210. [Google Scholar]
- Rystad Energy; WindEurope. The State of the European Wind Energy Supply Chain. A «What-Would-It-Take» Analysis of the European Supply Chain’s Ability to Support Ambitious Capacity Targets towards 2030; A Rystad Energy Report in Cooperation with, WindEurope; Rystad Energy: Oslo, Norway; WindEurope: Bilbao, Spain, 2023. [Google Scholar]
- Esteban, M.D.; López-Gutiérrez, J.S.; Negro, V. Gravity-Based Foundations in the Offshore Wind Sector. J. Mar. Sci. Eng. 2019, 7, 64. [Google Scholar] [CrossRef]
- Thomsen, K.E. What Is an Offshore Wind Farm? In Offshore Wind; Academic Press: London, UK; pp. 1–7. [CrossRef]
- Fischer, T.; De Vries, W.E.; Cordle, A. Executive Summary (WP4: Offshore Foundations and Support Structures). 2011. Available online: http://resolver.tudelft.nl/uuid:7ff42174-70ab-459d-b709-3bab9c2f9c4b (accessed on 14 January 2024).
- Passon, P.; Branner, K.; Larsen, S.E.; Hvenekaer Rasmussen, J. Offshore Wind Turbine Foundation Design; DTU Wind Energy PhD, No. 0044(EN); DTU Wind Energy: Roskilde, Denmark, 2015. [Google Scholar]
- WindEurope. Floating Offshore Wind Vision Statement; WindEurope: Bilbao, Spain, 2017; 16p. [Google Scholar]
- IRENA. Innovation Outlook Offshore Wind; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2016; 160p. [Google Scholar]
- Xu, S.; Murai, M.; Wang, X.; Takahashi, K. A Novel Conceptual Design of a Dynamically Positioned Floating Wind Turbine. Ocean Eng. 2021, 221, 108528. [Google Scholar] [CrossRef]
- Kopperstad, K.M.; Kumar, R.; Shoele, K. Aerodynamic Characterization of Barge and Spar Type Floating Offshore Wind Turbines at Different Sea States. Wind Energy 2020, 23, 2087–2112. [Google Scholar] [CrossRef]
- Meng, L.; He, Y.P.; Zhao, Y.S.; Yang, J.; Yang, H.; Han, Z.L.; Yu, L.; Mao, W.G.; Du, W.K. Dynamic Response of 6MW Spar Type Floating Offshore Wind Turbine by Experiment and Numerical Analyses. China Ocean Eng. 2020, 34, 608–620. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a Fully Coupled CFD Analysis Tool for Floating Offshore Wind Turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Kasyanov, V.N.; Kasyanova, E.V.; Jonkman, J.M.; Jonkman, B.J. FAST Modularization Framework for Wind Turbine Simulation: Full-System Linearization. J. Phys. Conf. Ser. 2016, 753, 082010. [Google Scholar] [CrossRef]
- Li, L.; Cheng, Z.; Yuan, Z.; Gao, Y. Short-Term Extreme Response and Fatigue Damage of an Integrated Offshore Renewable Energy System. Renew. Energy 2018, 126, 617–629. [Google Scholar] [CrossRef]
- Browning, J.R.; Jonkman, J.; Robertson, A.; Goupee, A.J. Calibration and Validation of a Spar-Type Floating Offshore Wind Turbine Model Using the FAST Dynamic Simulation Tool. J. Phys. Conf. Ser. 2014, 555, 012015. [Google Scholar] [CrossRef]
- Ruzzo, C.; Fiamma, V.; Collu, M.; Failla, G.; Nava, V.; Arena, F. On Intermediate-Scale Open-Sea Experiments on Floating Offshore Structures: Feasibility and Application on a Spar Support for Offshore Wind Turbines. Mar. Struct. 2018, 61, 220–237. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Avossa, A.M.; Riefolo, L.; Ricciardelli, F.; Musci, E.; D’Alessandro, F.; Vicinanza, D. Dynamic Modelling of a Spar Buoy Wind Turbine. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Trondheim, Norway, 25–30 June 2017; Volume 10. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Im, S.W.; Chang, I.H. Aero-Elastic-Control-Floater-Mooring Coupled Dynamic Analysis of Floating Offshore Wind Turbines; ISOPE: Mountain View, CA, USA, 2011. [Google Scholar]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in Semi-Submersible Floating Foundations Supporting Wind Turbines: A Comprehensive Review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
- Collu, M.; Borg, M.; Shires, A.; Brennan, F.P. FloVAWT: Progress on the Development of a Coupled Model of Dynamics for Floating Offshore Vertical Axis Wind Turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Nantes, France, 9–14 June 2013; Volume 8. [Google Scholar] [CrossRef]
- Roddier, D.; Cermelli, C.; Weinstein, A. WindFloat: A Floating Foundation for Offshore Wind Turbines—Part I: Design Basis and Qualification Process. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Honolulu, HI, USA, 31 May–5 June 2010; Volume 4, pp. 845–853. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Kim, H.C. Performance Changes of a Floating Offshore Wind Turbine with Broken Mooring Line. Renew. Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Kim, H.C.; Kim, M.H.; Lee, J.Y.; Kim, E.S.; Zhang, Z. Global Performance Analysis of 5MW WindFloat and OC4 Semi-Submersible Floating Offshore Wind Turbines (FOWT) by Numerical Simulations 2017. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Bae, Y.H.; Kim, M.H. Coupled Dynamic Analysis of Multiple Wind Turbines on a Large Single Floater. Ocean Eng. 2014, 92, 175–187. [Google Scholar] [CrossRef]
- Jang, H.K.; Park, S.; Kim, M.H.; Kim, K.H.; Hong, K. Effects of Heave Plates on the Global Performance of a Multi-Unit Floating Offshore Wind Turbine. Renew. Energy 2019, 134, 526–537. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, J.; He, Y. Preliminary Design of a Multi-Column TLP Foundation for a 5-MW Offshore Wind Turbine. Energies 2012, 5, 3874–3891. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Moan, T. Design Considerations for Tension Leg Platform Wind Turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Nihei, Y.; Fujioka, H. Motion Characteristics of TLP Type Offshore Wind Turbine in Waves and Wind. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Shanghai, China, 6–11 June 2010; Volume 3, pp. 283–292. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Shin, Y.S. Rotor-Floater-Mooring Coupled Dynamic Analysis of Mini TLP-Type Offshore Floating Wind Turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Shanghai, China, 6–11 June 2010; Volume 3, pp. 491–498. [Google Scholar] [CrossRef]
- Olondriz, J.; Elorza, I.; Jugo, J.; Alonso-Quesada, S.; Pujana-Arrese, A. An Advanced Control Technique for Floating Offshore Wind Turbines Based on More Compact Barge Platforms. Energies 2018, 11, 1187. [Google Scholar] [CrossRef]
- Floating Offshore Wind Farms; Green Energy and Technology; Springer International Publishing: Cham, Switzerland, 2016. [CrossRef]
- GWEC. Global Offshore Wind Report 2023; Global Wind Energy Council: Brussels, Belgium, 2023. [Google Scholar]
- IRENA. Renewable Power Generation Costs in 2019; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; 144p. [Google Scholar]
- Spagnoli, G.; de Hollanda Cavalcanti Tsuha, C. A Review on the Behavior of Helical Piles as a Potential Offshore Foundation System. Mar. Georesources Geotechnol. 2020, 38, 1013–1036. [Google Scholar] [CrossRef]
- Cerfontaine, B.; White, D.; Kwa, K.; Gourvenec, S.; Knappett, J.; Brown, M. Anchor Geotechnics for Floating Offshore Wind: Current Technologies and Future Innovations. Ocean Eng. 2023, 279, 114327. [Google Scholar] [CrossRef]
- Hao, D.; Wang, D.; O’loughlin, C.D.; Gaudin, C. Tensile Monotonic Capacity of Helical Anchors in Sand: Interaction between Helices. Can. Geotech. J. 2018, 56, 1534–1543. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Knappett, J.A.; Brown, M.J.; Davidson, C.S.; Al-Baghdadi, T.; Sharif, Y.U.; Brennan, A.; Augarde, C.; Coombs, W.M.; Wang, L.; et al. A Finite Element Approach for Determining the Full Load–Displacement Relationship of Axially Loaded Shallow Screw Anchors, Incorporating Installation Effects. Can. Geotech. J. 2020, 58, 565–582. [Google Scholar] [CrossRef]
- Ding, H.; Wang, L.; Zhang, P.; Le, C. Study on the Lateral Bearing Capacity of Single-Helix Pile for Offshore Wind Power. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Madrid, Spain, 17–22 June 2018; Volume 9. [Google Scholar] [CrossRef]
- Sharif, Y.U.; Brown, M.J.; Cerfontaine, B.; Davidson, C.; Ciantia, M.O.; Knappett, J.A.; Ball, J.D.; Brennan, A.; Augarde, C.; Coombs, W.; et al. Effects of Screw Pile Installation on Installation Requirements and In-Service Performance Using the Discrete Element Method. Can. Geotech. J. 2020, 58, 1334–1350. [Google Scholar] [CrossRef]
- Davidson, C.; Brown, M.J.; Cerfontaine, B.; Al-Baghdadi, T.; Knappett, J.; Brennan, A.; Augarde, C.; Coombs, W.; Wang, L.; Blake, A.; et al. Physical Modelling to Demonstrate the Feasibility of Screw Piles for Offshore Jacket-Supported Wind Energy Structures. Geotechnique 2022, 72, 108–126. [Google Scholar] [CrossRef]
- Bradshaw, A.S.; Cullen, L.; Miller, Z. Field Study of Group Effects on the Pullout Capacity of “Deep” Helical Piles in Sand. Can. Geotech. J. 2021, 59, 538–545. [Google Scholar] [CrossRef]
- Alsirawan, R.; Alnmr, A. Dynamic Behavior of Gravity Segmental Retaining Walls. Pollack Period. 2022, 18, 94–99. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Engin, E.; Engin, H.K. Validation of Empirical Formulas to Derive Model Parameters for Sands. In Numerical Methods in Geotechnical Engineering—Proceedings of the 7th European Conference on Numerical Methods in Geotechnical Engineering, Trondheim, Norway, 6 September 2006; 2010; pp. 137–142. Available online: https://www.researchgate.net/publication/267638739_Validation_of_empirical_formulas_to_derive_model_parameters_for_sands (accessed on 17 April 2024).
- Salem, T.N.; Hussein, M. Axial Tensile Capacity of Helical Piles from Field Tests and Numerical Study. Port-Said Eng. Res. J. 2017, 21, 111–119. [Google Scholar] [CrossRef]
- Brown, M.; Davidson, C.; Brennan, A.; Knappett, J.; Cerfontaine, B.; Sharif, Y. Physical Modelling of Screw Piles for Offshore Wind Energy Foundations. In Proceedings of the 1st International Symposium on Screw Piles for Energy Applications, Dundee, UK, 27–28 May 2019; pp. 31–38. [Google Scholar]
- Law, K.H.; Geotechnical, K.H.; Bhd, S. 3D Finite Element Analysis of a Deep Excavation Considering the Effect of Anisotropic Wall Stiffness Impact. In Proceedings of the 19th Southeast Asian Geotechnical Conference & 2nd AGSSEA Conference (19SEAGC & 2AGSSEA), Kuala Lumpur, Malaysia, 31 May–3 June 2016; p. 6. [Google Scholar]
- Al-Ani, W.; Wanatowski, D.; Chan, S.H. Numerical Analysis of Piled Embankments on Soft Soils. In Proceedings of the Geo-Shanghai 2014 International Conference, Shanghai, China, 26–28 May 2014; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2014; pp. 30–39. [Google Scholar]
- Hsiung, B.C.B.; Yang, K.H.; Aila, W.; Ge, L. Evaluation of the Wall Deflections of a Deep Excavation in Central Jakarta Using Three-Dimensional Modeling. Tunn. Undergr. Space Technol. 2018, 72, 84–96. [Google Scholar] [CrossRef]
- Alnmr, A. Material Models to Study the Effect of Fines in Sandy Soils Based on Experimental and Numerical Results. Acta Tech. Jaurinensis 2021, 14, 651–680. [Google Scholar] [CrossRef]
- Alsirawan, R.; Alnmr, A.; Koch, E. Experimental and Numerical Investigation of Geosynthetic-Reinforced Pile-Supported Embankments for Loose Sandy Soils. Buildings 2023, 13, 2179. [Google Scholar] [CrossRef]
- Salgado, R.; Mitchell, J.K.; Jamiolkowski, M. Cavity Expansion and Penetration Resistance in Sand. J. Geotech. Geoenvironmental Eng. 1997, 123, 344–354. [Google Scholar] [CrossRef]
- Krasiński, A. Numerical Simulation of Screw Displacement Pile Interaction with Non-Cohesive Soil. Arch. Civ. Mech. Eng. 2014, 14, 122–133. [Google Scholar] [CrossRef]
- Thiyyakkandi, S.; McVay, M.; Bloomquist, D.; Lai, P. Experimental Study, Numerical Modeling of and Axial Prediction Approach to Base Grouted Drilled Shafts in Cohesionless Soils. Acta Geotech. 2014, 9, 439–454. [Google Scholar] [CrossRef]
- Broere, W.; Van Tol, A.F. Modelling the Bearing Capacity of Displacement Piles in Sand. In Proceedings of the Institution of Civil Engineers-Geotechnical Engineering; Thomas Telford Ltd.: London, UK, 2015; Volume 159, pp. 195–206. [Google Scholar] [CrossRef]
- Li, Z.; Haigh, S.K.; Bolton, M.D. Centrifuge Modelling of Mono-Pile under Cyclic Lateral Loads. In Physical Modelling in Geotechnics, Two Volume Set; CRC Press: London, UK, 2010; Volume 2, pp. 965–970. [Google Scholar]
- Alnmr, A.; Ray, R.P.; Alsirawan, R. A State-of-the-Art Review and Numerical Study of Reinforced Expansive Soil with Granular Anchor Piles and Helical Piles. Sustainability 2023, 15, 2802. [Google Scholar] [CrossRef]
- Alnmr, A.; Ray, R.P.; Alsirawan, R. Comparative Analysis of Helical Piles and Granular Anchor Piles for Foundation Stabilization in Expansive Soil: A 3D Numerical Study. Sustainability 2023, 15, 11975. [Google Scholar] [CrossRef]
- Kaufmann, K.L.; Nielsen, B.N.; Augustesen, A.H. Finite Element Investigations on the Interaction between a Pile and Swelling Clay; DCE Technical Reports No. 104; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2010. [Google Scholar]





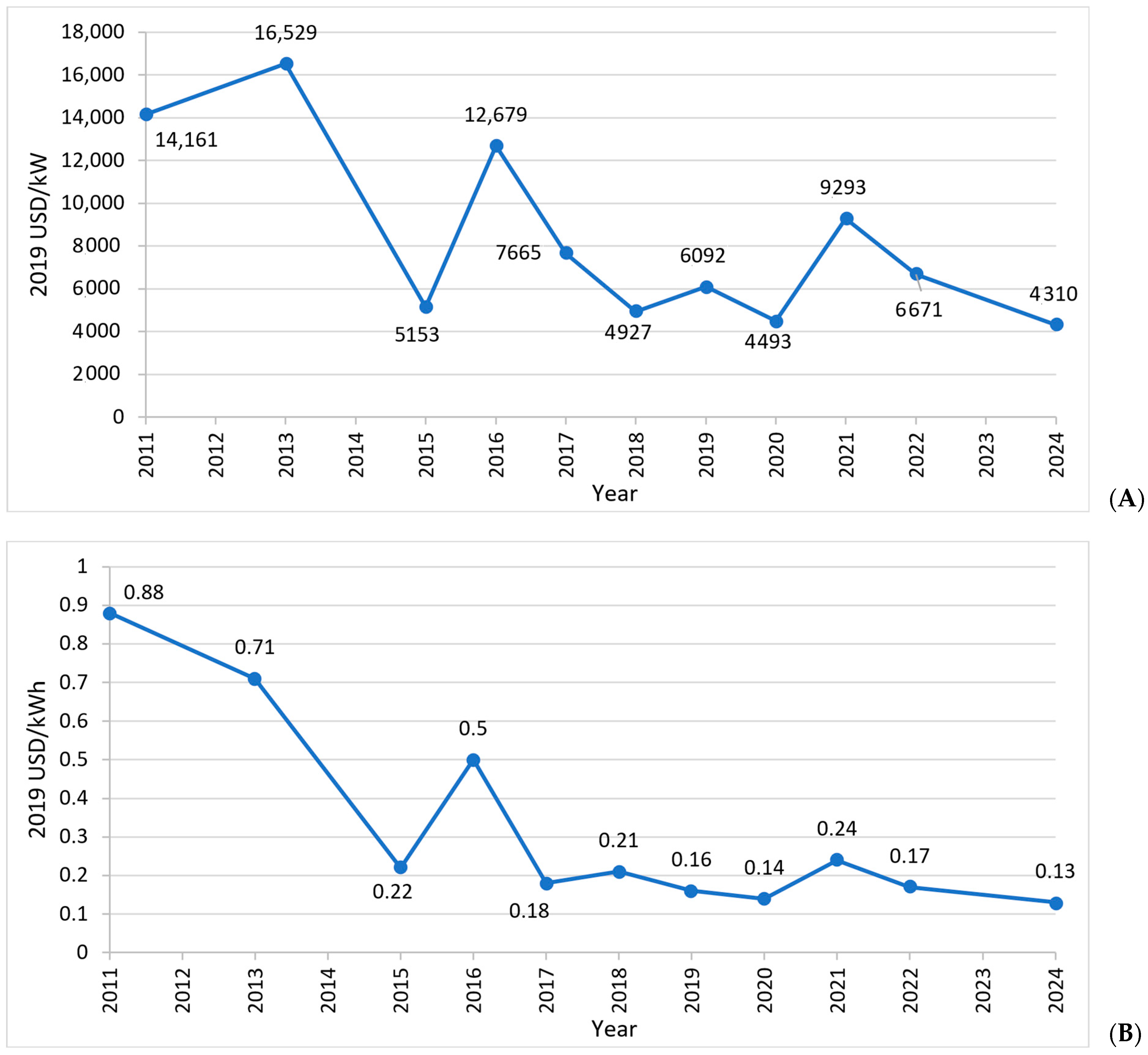








| Country | Number of OWFs | Number of Turbines Connected | Cumulated Capacity (MW) |
|---|---|---|---|
| The UK | 40 | 2294 | 10,428 |
| Germany | 29 | 1501 | 7689 |
| Denmark | 14 | 559 | 1703 |
| Belgium | 11 | 399 | 2261 |
| The Netherlands | 9 | 537 | 2611 |
| Sweden | 5 | 80 | 192 |
| Finland | 3 | 19 | 71 |
| Ireland | 1 | 7 | 25 |
| Portugal | 1 | 3 | 25 |
| Spain | 1 | 1 | 5 |
| Norway | 1 | 1 | 2 |
| France | 1 | 1 | 2 |
| Total | 116 | 5402 | 25,014 |
| Country (MW) | Year | |||
|---|---|---|---|---|
| 2024 | 2025 | 2026 | 2027 | |
| Belgium | - | - | 500 | 500 |
| Denmark | 190 | 210 | 800 | 900 |
| France | 530 | 990 | 300 | 800 |
| Germany | 1630 | 900 | 1420 | 2210 |
| Ireland | - | - | - | 560 |
| Italy | - | - | 250 | 520 |
| The Netherlands | 350 | 700 | 350 | 1000 |
| Poland | - | - | 920 | 1090 |
| Spain | - | - | - | 160 |
| Norway | - | 10 | - | - |
| The UK | 1670 | 1900 | 3890 | 3820 |
| Total | 4370 | 4710 | 8430 | 11,560 |
| Region | The Average Water Depth (m) | The Average Distance to Shore (km) |
|---|---|---|
| America | 25.5 | 4.5 |
| Europe | 17.4 | 23.3 |
| Asia | 6.7 | 6.9 |
| Soil Parameter | Sand Parameters Corresponding to Relative Density () |
|---|---|
| Drainage type | Drained |
| Oedometer stiffness, , at = 100 kPa | 60,000 |
| Secant stiffness, = 100 kPa | 60,000 |
| Unload/reload stiffness, = 100 kPa | 180,000 |
| Shear modulus at very small strains, | 60,000 + 68,000 |
| Reference shear strain | (2 − )/10,000 |
| Friction angle, (degrees) | 28 + 12.5 |
| Effective cohesion intercept c’ref (kPa) | - |
| Angle of dilation, Ψ (degrees) | −2 + 12.5 |
| Failure ratio, (−) | 1 − /8 |
| Unload–reload Poisson’s ratio, vur | 0.2 |
| Power of stress level dependency of stiffness, m (−) | 0.7 − (100/320) |
| Saturated unit weight, | 19 + 1.6 × |
| Unsaturated unit weight, | 15 + 4 |
| Case Study | Load Type | Shaft | Helical Plate | Helical Plate Number, N | Depth (m) | Plate Spacing Ratio (S/Dh) | |
|---|---|---|---|---|---|---|---|
| Dc (mm) | Dh (mm) | th (mm) | |||||
| Field study [82] | Pullout | 45 | 200 | 10 | 2 | 1.9 | 2.5 |
| Centrifuge test [83] | Pullout | 880 | 1700 | 110 | 2 | 13 | 2 |
| Model Parameter | HS | HS Small | |||
|---|---|---|---|---|---|
| Symbol | Soil Parameters | Disturbed Sand around Shaft (Drained Behavior) | Sand (Drained Behavior) | Disturbed Sand around Shaft (Drained Behavior) | Sand (Drained Behavior) |
| (kN/m3) | Saturated unit weight | 20 | 20 | 20 | 20 |
| (kN/m3) | Unsaturated unit weight | 18 | 18 | 18 | 18 |
| (kN/m2) | Reference secant stiffness | 30,000 | 46,700 | 30,000 | 46,700 |
| (kN/m2) | Reference tangent stiffness | 30,000 | 46,700 | 30,000 | 46,700 |
| (kN/m2) | Reference unloading–reloading stiffness | 90,000 | 140,000 | 90,000 | 140,000 |
| C′ (kN/m2) | Cohesion | 0.3 | 0.3 | 0.3 | 0.3 |
| (°) | Internal friction angle | 34.25 | 39 | 34.25 | 39 |
| Ψ (°) | Dilatancy angle | 6 | 12 | 6 | 12 |
| (−) | Unloading/reloading Poisson’s ratio | 0.2 | 0.2 | 0.2 | 0.2 |
| m (−) | Exponential power | 0.544 | 0.457 | 0.544 | 0.457 |
| (−) | Failure ratio | 0.938 | 0.903 | 0.938 | 0.903 |
| (kN/m2) | Shear modulus at very small strains | 94,000 | 112,900 | ||
| (−) | Reference shear strain (at = 0.722) | 0.00015 | 0.00012 | ||
| Model Parameter | HS | HS Small | |||
|---|---|---|---|---|---|
| Symbol | Soil Parameters | Disturbed Sand around Shaft (Drained Behavior) | Sand (Drained Behavior) | Disturbed Sand around Shaft (Drained Behavior) | Sand (Drained Behavior) |
| (kN/m3) | Saturated unit weight | 19.24 | 20.3 | 19.24 | 20.3 |
| (kN/m3) | Unsaturated unit weight | 18 | 18.4 | 18 | 18.4 |
| (kN/m2) | Reference secant stiffness | 21,000 | 50,400 | 21,000 | 50,400 |
| (kN/m2) | Reference tangent stiffness | 21,000 | 50,400 | 21,000 | 50,400 |
| (kN/m2) | Reference unloading–reloading stiffness | 63,000 | 151,200 | 63,000 | 151,200 |
| C′ (kN/m2) | Cohesion | 0.3 | 0.3 | 0.3 | 0.3 |
| (°) | Internal friction angle | 32 | 38.5 | 32 | 38.5 |
| Ψ (°) | Dilatancy angle | 0 | 8.5 | 0 | 8.5 |
| (−) | Unloading/reloading Poisson’s ratio | 0.2 | 0.2 | 0.2 | 0.2 |
| m (−) | Exponential power | 0.59 | 0.434 | 0.59 | 0.434 |
| (−) | Failure ratio | 0.938 | 0.895 | 0.938 | 0.895 |
| (kN/m2) | Shear modulus at very small strains | 83,800 | 117,120 | ||
| (−) | Reference shear strain (at ) | 0.00017 | 0.00012 | ||
| Movement (mm) | |||
|---|---|---|---|
| Zh/h | 10 | 25 | 50 |
| 0.034 | 35.5 | 32.5 | |
| 0.136 | 35 | 32 | 27 |
| 0.34 | 32.1 | 30.2 | 26.9 |
| U = 10 mm | U = 25 mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| i (°) | 0 | 20 | 40 | 60 | 0 | 20 | 40 | 60 | |
| Zh/Z | |||||||||
| 0.034014 | 430 | 423 | 405 | 350 | 591 | 580 | 538 | 464 | |
| 0.068027 | 440 | 432 | 412 | 360 | 605 | 590 | 542 | 468 | |
| 0.102041 | 458 | 450 | 425 | 365 | 628 | 610 | 560 | 484 | |
| 0.136054 | 469 | 460 | 431 | 370 | 660 | 642 | 590 | 496 | |
| 0.170068 | 473 | 464 | 436 | 373.2 | 685 | 664 | 610 | 508 | |
| 0.204082 | 477 | 469 | 440 | 375.6 | 701 | 681 | 622 | 518 | |
| 0.272109 | 485 | 475 | 445.5 | 380 | 727 | 708 | 640 | 532 | |
| 0.340136 | 490 | 480 | 450 | 381.6 | 740 | 720 | 652 | 540 | |
| 0.408163 | 492 | 485 | 452 | 382.4 | 752 | 728 | 662 | 545 | |
| 0.47619 | 497 | 487 | 454 | 382.8 | 761 | 738 | 670 | 549 | |
| 0.544218 | 500 | 490 | 457 | 383 | 770 | 750 | 678 | 553.2 | |
| 0.612245 | 502 | 493 | 459 | 383.4 | 781 | 756 | 684 | 557 | |
| 0.680272 | 509 | 496 | 460 | 384 | 789 | 762 | 688 | 561 | |
| 0.748299 | 510 | 499 | 461 | 384.8 | 793 | 770 | 692 | 564 | |
| 0.884354 | 511 | 500.5 | 464 | 386 | 785 | 760 | 692 | 569 | |
| Movement (mm) | |||
|---|---|---|---|
| i° | 10 | 25 | 50 |
| 0 | 0.12 | 0.22 | 0.26 |
| 20 | 0.12 | 0.21 | 0.26 |
| 40 | 0.12 | 0.215 | 0.26 |
| 60 | 0.11 | 0.215 | 0.26 |
| Zh/h | Movement (mm) | ||
|---|---|---|---|
| 10 | 25 | 50 | |
| 0.034 | 31.5 | 35 | 40 |
| 0.136 | 28 | 30 | 38.5 |
| 0.34 | 26.5 | 28 | 36 |
| U = 10 mm | U = 25 mm | U = 50 mm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i (°) | 0 | 20 | 40 | 60 | 0 | 20 | 40 | 60 | 0 | 20 | 40 | 60 | |
| Zh/Z | |||||||||||||
| 0.034 | 4035 | 3860 | 3340 | 2520 | 8062 | 7730 | 6710 | 5120 | 10,868 | 10,692 | 9970 | 8080 | |
| 0.069 | 4060 | 3880 | 3360 | 2530 | 8090 | 7750 | 6722 | 5121 | 10,866 | 10,715 | 10,002 | 8080 | |
| 0.103 | 4090 | 3908 | 3380 | 2550 | 8105 | 7762 | 6740 | 5140 | 10,852 | 10,725 | 10,020 | 8098 | |
| 0.138 | 4120 | 3940 | 3410 | 2575 | 8130 | 7780 | 6760 | 5150 | 10,907 | 10,750 | 10,035 | 8102 | |
| 0.172 | 4160 | 3965 | 3450 | 2602 | 8160 | 7785 | 6800 | 5182 | 10,930 | 10,711 | 10,060 | 8122 | |
| 0.207 | 4220 | 4042 | 3505 | 2640 | 8230 | 7873 | 6860 | 5240 | 10,968 | 10,830 | 10,090 | 8140 | |
| 0.276 | 4360 | 4170 | 3605 | 2705 | 8395 | 8058 | 7055 | 5402 | 11,130 | 10,970 | 10,230 | 8270 | |
| 0.345 | 4470 | 4270 | 3685 | 2750 | 8720 | 8365 | 7265 | 5520 | 11,463 | 11,280 | 10,510 | 8470 | |
| 0.414 | 4530 | 4330 | 3740 | 2781 | 8925 | 8530 | 7390 | 5582 | 12,070 | 11,797 | 10,885 | 8650 | |
| 0.552 | 4650 | 4440 | 3835 | 2842 | 9122 | 8835 | 7580 | 5730 | 12,682 | 12,355 | 11,322 | 8902 | |
| 0.690 | 4745 | 4528 | 3910 | 2883 | 9280 | 8895 | 7745 | 5860 | 12,862 | 12,540 | 11,530 | 9110 | |
| 0.759 | 4770 | 4553 | 3920 | 2885 | 9335 | 8960 | 7800 | 5900 | 12,810 | 12,485 | 11,520 | 9200 | |
| 0.828 | 4748 | 4530 | 3890 | 2860 | 9320 | 8953 | 7800 | 5880 | 12,588 | 12,280 | 11,402 | 9202 | |
| 0.897 | 4610 | 4345 | 3770 | 2770 | 9180 | 8810 | 7650 | 5750 | 12,160 | 11,900 | 11,160 | 9080 | |
| Movement (mm) | |||
|---|---|---|---|
| i° | 10 | 25 | 50 |
| 0 | 0.34 | 0.38 | 0.46 |
| 20 | 0.34 | 0.38 | 0.46 |
| 40 | 0.34 | 0.38 | 0.46 |
| 60 | 0.34 | 0.38 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnmr, A.; Mayassah, M. Innovations in Offshore Wind: Reviewing Current Status and Future Prospects with a Parametric Analysis of Helical Pile Performance for Anchoring Mooring Lines. J. Mar. Sci. Eng. 2024, 12, 1040. https://doi.org/10.3390/jmse12071040
Alnmr A, Mayassah M. Innovations in Offshore Wind: Reviewing Current Status and Future Prospects with a Parametric Analysis of Helical Pile Performance for Anchoring Mooring Lines. Journal of Marine Science and Engineering. 2024; 12(7):1040. https://doi.org/10.3390/jmse12071040
Chicago/Turabian StyleAlnmr, Ammar, and Mais Mayassah. 2024. "Innovations in Offshore Wind: Reviewing Current Status and Future Prospects with a Parametric Analysis of Helical Pile Performance for Anchoring Mooring Lines" Journal of Marine Science and Engineering 12, no. 7: 1040. https://doi.org/10.3390/jmse12071040








