Numerical Study of Hydrodynamic Characteristics of a Three-Dimensional Oscillating Water Column Wave-Power Device

Abstract

The impact of wave-induced forces on the integrity of stationary oscillating water column (OWC) devices is essential for ensuring their structural safety. In our study, we built a three-dimensional numerical model of an OWC device using the computational fluid dynamics (CFDs) software OpenFOAM-v1912. Subsequently, the hydrodynamic performance of the numerical model is comprehensively validated. Finally, the hydrodynamic performance data are analyzed in detail to obtain meaningful conclusions. Results indicate that the horizontal wave force applied to the OWC device is approximately 6.6 to 7.9 times greater than the vertical wave force, whereas the lateral wave force is relatively small. Both the horizontal and vertical wave forces decrease as the relative water depth increases under a constant wave period and height. In addition, the highest dynamic water pressure is observed at the interface between the water surface and device, both within and outside the front wall of the gas chamber. The dynamic water pressure at different locations on the front chamber increases and subsequently decreases as the wave frequency increases.

1. Introduction

Oceans have a variety of renewable energy sources, including ocean wind, wave, tidal, temperature, and salt. They are also the Earth’s greatest receivers of solar energy. Wave energy is particularly important for mitigating the energy crisis and environmental pollution, thus rendering its development and utilization essential. To extract and convert wave energy, various wave-energy-conversion technologies have been developed. Owing to its straightforward design, minimal undersea moving parts, and inexpensive upkeep, the OWC device is a viable choice [1]. Over the past few decades, a great deal of research has been conducted on the hydrodynamic performance of OWC devices. For example, Bayoumi et al. [2] developed a numerical wave-energy prediction tool that was experimentally validated for an offshore spar buoy OWC and discovered that the predictions aligned with the experimental results outside the resonance frequency. Evans [3] assumed that the water surface width within an OWC chamber was significantly smaller than the wavelength; thus, they disregarded the wave-surface variation within the chamber and reduced the wave-surface motion to a rigid piston motion to increase energy-conversion efficiency. Martins-rivas et al. [4] investigated the effects of the shoreline angle of incident and reflective waves on power-generation efficiency under a constant sea depth and a bluff coast. Nader et al. [5] used the finite-element approach to model single and multiple OWC devices and found that the closeness of the devices considerably influenced the power-generation efficiency. A basic three-dimensional (3D) OWC model based on potential flow theory was created by Dimakopoulos et al. [6] to study the impact of air compressibility on energy-conversion efficiency while taking air compressibility into account. Through physical model tests and theoretical research, Xu et al. [7] evaluated the wave-energy extraction of a 3D OWC device using a secondary power output model. They found that shorter waves were severely impacted by spatial non-uniformity and viscous losses. Hu et al. [8] established a two-dimensional (2D) model of an offshore OWC with a rectangular chamber and used theoretical and numerical methods to examine the effects of immersion depth and chamber width on energy-conversion efficiency; their results indicated that the frequency of the peak efficiency decreased with increasing immersion depth.

However, studies regarding forces exerted on OWC wave-energy devices and few related studies exist. Physical model studies were conducted by Ashlin et al. [9] on a fixed 2D OWC to examine wave forces in both horizontal and vertical orientations. They found that, on the OWC structure, the peak horizontal wave forces were 2.5–3 times greater than the peak vertical wave forces. Jakobsen et al. [10] investigated wave stress on a hemispherical point absorber using both physical model testing and simulations. Numerical simulations were used by Elhanafi [11] to study the wave force on a stationary, two-dimensional rectangular OWC. He discovered that, regardless of changes in the incident wave’s wavelength and height, the horizontal wave force is always greater than the vertical wave force. The effect of viscosity on wave force was investigated by adding an artificial viscous term to a 2D OWC through numerical simulation, which showed that the effect of viscosity on the total horizontal wave force at the front wall increased with the front wall draft [12]. Ning et al. [13] investigated the wave force on a 2D OWC via physical model tests and numerical simulations, where they demonstrated that the total wave force decreased with increasing wavelength and increased with increasing incident wave height. Additionally, they discovered that the wave force was affected significantly by the opening rate, with higher opening rates resulting in smaller wave forces in the low-frequency region, whereas the opposite trend was observed in the high-frequency region.

The 3D circular OWC device research has mostly concentrated on energy-conversion efficiency, with little attention given to force laws. Deng et al. [14] and Zhou et al. [15] investigated the energy-conversion efficiency of a 3D circular OWC using the eigenfunction expansion method. Huang et al. [16], as well as Xv and Huang [17], investigated the flow-field characteristics near an OWC device. He et al. [18,19] experimentally verified the energy-conversion efficiency of a 3D circular OWC using a physical model. Zhou et al. [20] investigated the energy-conversion efficiency and hydrodynamic performance of a 3D circular OWC device via numerical simulations. Zhou et al. [21] investigated the energy-conversion efficiency and force characteristics of a 3D circular OWC device both experimentally and numerically. Several researchers [22,23,24] integrated a circular OWC and investigated its power-generation efficiency.

Studies pertaining to 3D circular OWC devices focus primarily on energy-conversion efficiency [14,15,18,19,21,22,23,24,25] and flow-field characteristics [16,17], whereas force laws are focused less. Most previous studies regarding the force laws of OWC devices are restricted to 2D models, such as fixed 2D OWC devices [9,11,12,13]. These models cannot account for the complexity of 3D space; hence, their force characteristics cannot be utilized to analyze the forces of 3D OWC devices. In addition, experimentally verifying the overall forces of 3D OWC devices is difficult, thus rendering numerical simulations an ideal method for evaluating them.

In recent years, many OWC wave-energy-conversion devices [26] and marine structures [27] have been unable to operate normally due to various degrees of damage. Therefore, it has become especially critical to fully consider the wave loads on the devices to ensure their safe design and long-term stable operation [28]. Therefore, scholars began to consider the wave force characteristics of 3D OWCs. Li et al. [29] established a semi-analytical two-chamber OWC by using potential flow theory and the matched eigenfunction method and investigated the relationship between the angle of the incident wave and the wave load on the cavity but did not study the relationship between the forces on the whole device and the wave parameters. Although Ning et al. [30] investigated the force characteristics of 2D and 3D OWCs through experiments and numerical simulations, their findings are not generalizable to the type of waves studied, isolated waves. Huang et al. [31] investigated the forces exerted on 3D circular OWC devices under wave loading via numerical simulations. The results showed that wave loading is insensitive to changes in wavelength and period but increases with wave height. Although Huang et al. [31] extensively investigated the force law of a 3D circular OWC device, they did not provide a quantitative law for the variation in force with wave height of the OWC device. Moreover, they did not investigate the effects of water depth on the force of the OWC device or the variation in the dynamic water pressure of the device.

Therefore, the objective of this study is to perform a more detailed examination and analysis of 3D OWC force laws. In Section 2, the numerical modeling of a 3D circular OWC device is presented. In Section 3, the accuracy of the model is verified. In Section 4, the effects of wave period, wave height, and water depth on the forces in the OWC are analyzed, and conclusions about the effects of wave height on the forces in the OWC are provided; subsequently, the dynamic water pressure in the internal and external front walls of the OWC is analyzed. In Section 5, the conclusions are summarized, and future endeavors are presented.

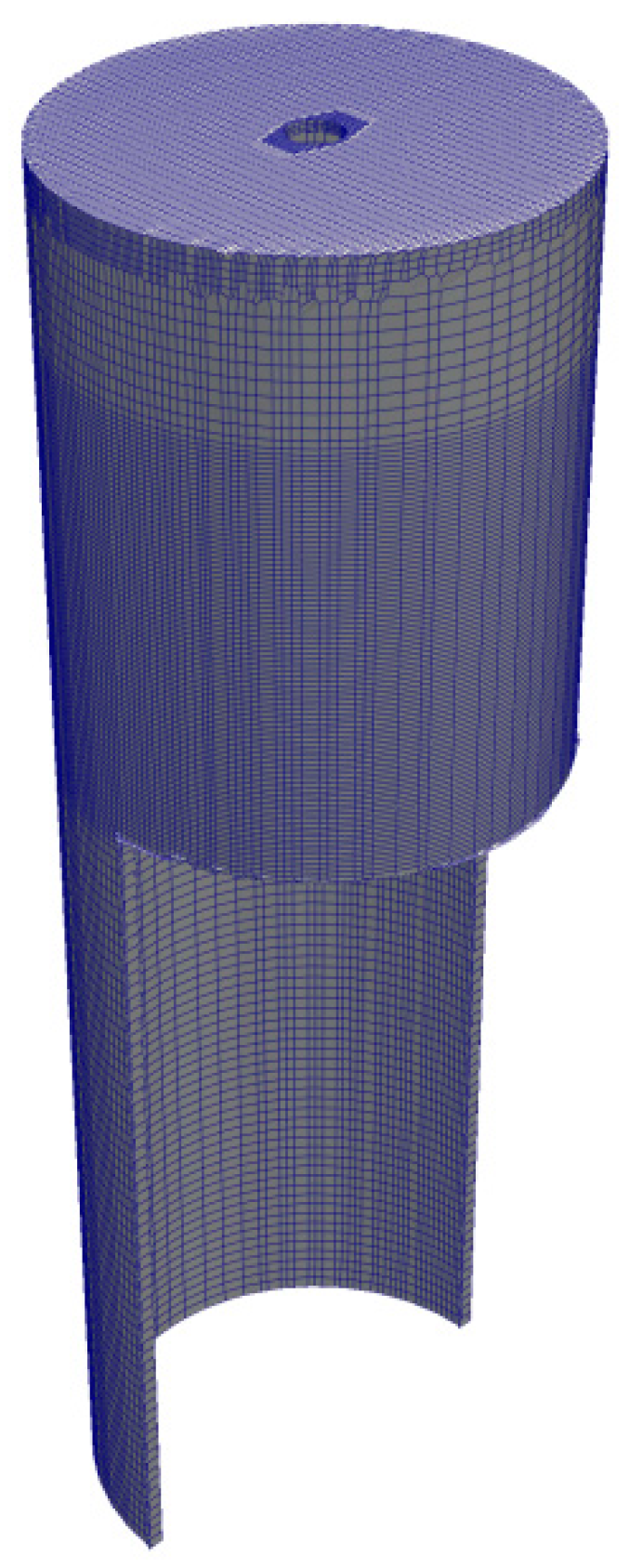
2. Materials and Methods

In this study, a 3D wave flume was developed using the finite-volume approach for wave interactions with a 3D circular OWC-type device supported by a bottom-sitting C-shaped structure. The Cartesian coordinate system was established at the intersection of the static water surface (water depth d = 0.30 m) and the midline of the flume side, i.e., the center point of the flume left-end rectangle, with the positive z-axis oriented vertically upward and the positive x-axis oriented horizontally to the right. A 3D diagram of the numerical wave tank is shown in Figure 1. The device was placed at the center of the sink’s calculation area. The outer diameter of the device D = 0.125 m, the diameter of the upper orifice D_O = 0.014 m, the size of the lower opening D_s = 0.244 m, and the column height D_h = 0.4 m (see Figure 2).

OpenFOAM was chosen for numerical modeling due to its open source nature and flexibility, with the numerical model incorporating free-slip wall boundaries at the front and back of the flume, the bottom, and the OWC units while applying no-slip conditions to the walls, and patch boundaries at the top, left, and right of the flume. The velocity inlet and pressure outlet were placed on the left and right sides of the flume, respectively, and the top of the flume was imposed with both the velocity-outlet and pressure-outlet boundary conditions (pressureInletOutletVelocity). Meanwhile, the waves2Foam relaxation zone technology was used to generate and eliminate waves [32]. The role of the relaxation zone is to distribute weights between the calculated and theoretical values, as well as to create and eliminate waves through the transition between analytical and CFD solutions; therefore, an appropriate length of the relaxation zone for wave creation and elimination is required.

All the above numerical parameters and boundary conditions were carefully designed according to the actual experimental conditions [7]. In order to ensure the accuracy of wave creation and dissipation, the length of the flume was set to 15 m, the width and height were set to 0.6 m, and the lengths of the left and right waveform relaxation zones were set to twice the wavelength $\lambda$. The spatial step $\Delta x$ in the x direction was set to $\Delta x/\lambda \approx 1/67$. In the z direction, z = 0 was set as the reference point. The area above and below the reference point at twice the length of the wave height 2H was encrypted, where the spatial step $\Delta z$ in the encrypted area was set to $\Delta z/H=0.5$ and the spatial step in the non-encrypted area was set to $\Delta z/H=1.3$. To ensure the accuracy of the device calculations, the grid on the surface of the OWC device was encrypted, as shown in Figure 3. The time step Δt was calculated using the time step Δt, which was automatically adjusted to improve model stability using adjustRunTime in the Controldict file.

3. Theory and Validation

3.1. Governing Equations

Under low water velocity, water is typically assumed to be an incompressible fluid, i.e., its density ρ = 1000 kg/m³ is constant, and the fluid satisfies the continuity and momentum equations.

$$\frac{\partial \overrightarrow{U}}{\partial t}+(\overrightarrow{U}\cdot \nabla )\overrightarrow{U}=-\frac{-\nabla p}{\rho }-\nabla gz,$$

(1)

In Equation (1), $\overrightarrow{U}$ is the fluid velocity, t is the time, $p$ is the pressure, $g$ is the acceleration owing to gravity, and z is the water surface height. The free surface of a liquid under a two-phase flow model can be modeled using the VOF method [33] as follows:

$$\frac{\partial C}{\partial t}+\nabla \cdot (\overrightarrow{U}C)=0,$$

(2)

In Equation (2), C is the volume fraction of the fluid. The wave force exerted on the device can be solved by integrating the pressure over the device surface as follows:

$$\overrightarrow{F}={\int }_{\tau }p\cdot \overrightarrow{n}d\tau ,$$

(3)

In Equation (3), $\overrightarrow{F}$ is the force applied to the structure, p is the pressure on the surface of the structure, $\overrightarrow{n}$ is the normal vector on the surface of the device, and τ is the surface area of the structure. Because the gas pressure is extremely low relative to the wave load, the wave force is expressed as $\overrightarrow{F}$ minus the hydrostatic load.

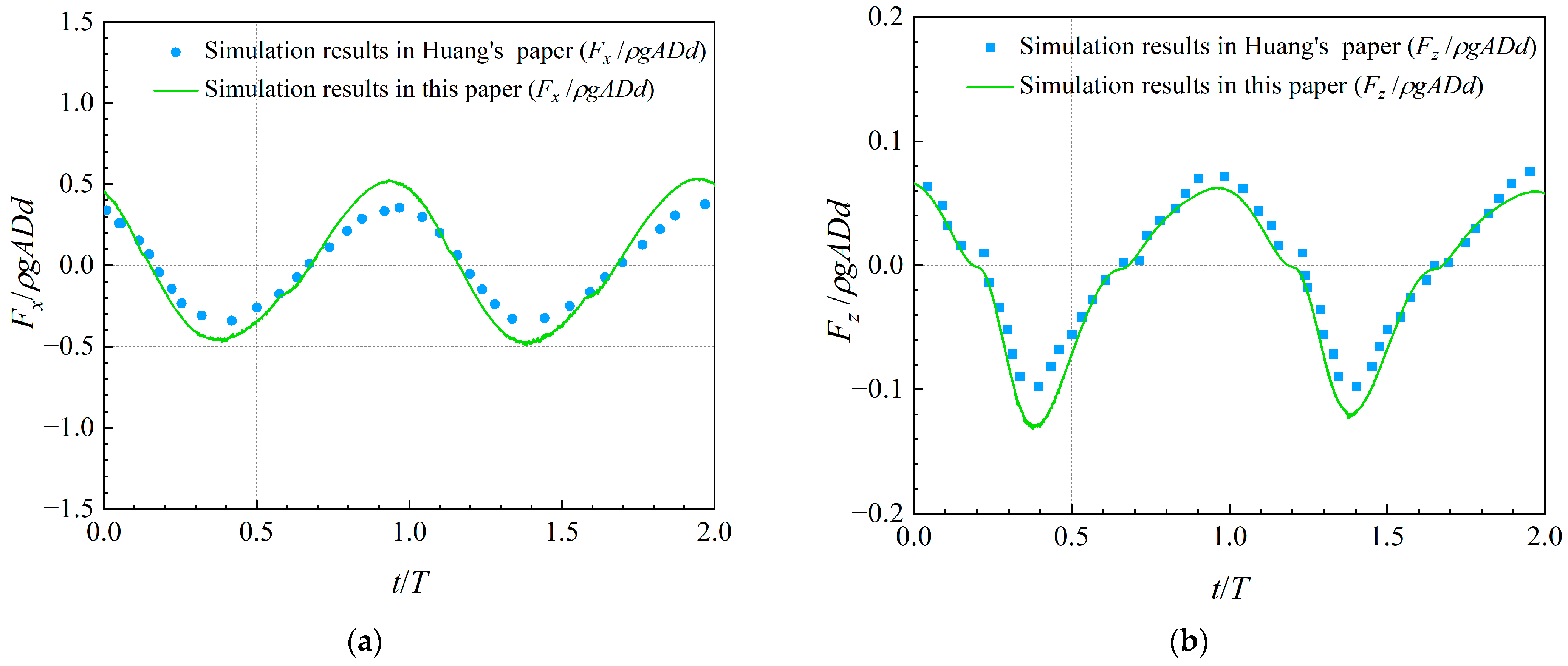
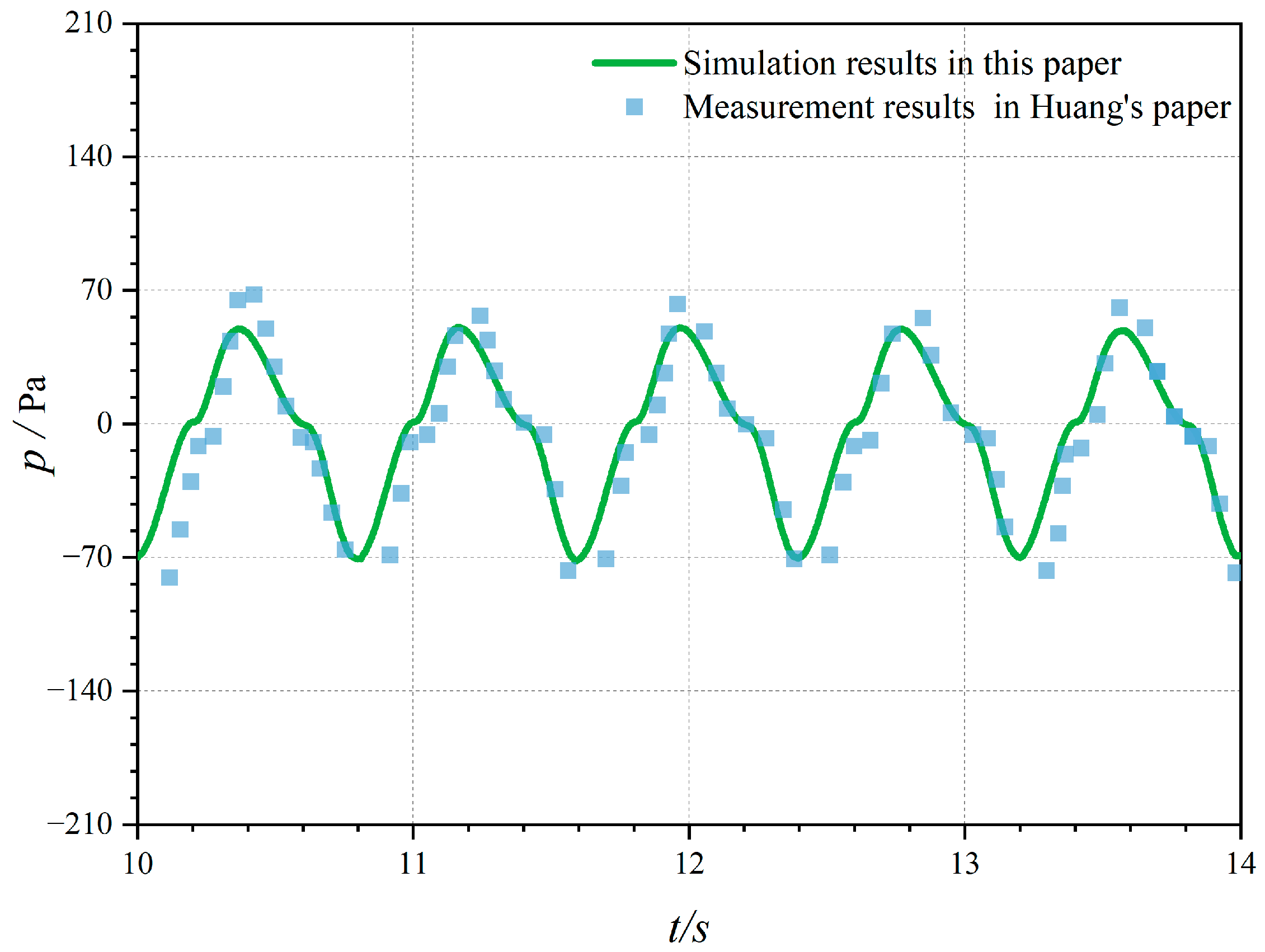
3.2. Model Validation

The numerical results of this study based on an incident wave period T of 1.40 s, a water depth d of 0.30 m, and H = 0.04 m for the horizontal wave force F_x and vertical wave force F_z are presented in Figure 4a for a comparison with the numerical results of Huang et al. [31]. Figure 4a,b shows that the numerical results agreed well with each other, thus indicating that the OWC wave-energy device established in this study can accurately simulate the wave load on the device.

As shown in Figure 5, six monitoring points, i.e., (S1 and S01), (S2 and S02), and (S3 and S03), were arranged at the hydrostatic water surface inside and outside the front wall of the device, at the midpoint of the inundation depth, and at 0.01 m from the bottom, respectively, to monitor the pressure. The dynamic water pressure is written as the sum of the first- and second-order dynamic water pressures, i.e., $p_w=p_1+p_2$, as a theoretical value to verify the numerical results of the dynamic water pressure at three points (i.e., S1, S2, and S3) on the front wall of the gas chamber of the installation.

$$p_1=\rho g\frac{H}{2}\frac{\cosh k(z+d)}{\cosh kd}\cos (kx-\omega t),$$

(4)

$$p_2=\frac{3\pi H^2}{4L}\frac{\rho g}{\sinh 2kd}[\frac{\cosh 2k(z+d)}{{\sinh }^{2}kd}-\frac{1}{3}]\cos 2(kx-\omega t)-\frac{\pi H^2}{4\lambda }\frac{\rho g}{\sinh 2kd}\cosh 2k(z+d),$$

(5)

In Equations (4) and (5), k denotes the wave number and ω denotes the circular frequency; the monitoring points on the front wall of the air chamber are shown in Figure 5.

Figure 6 shows a comparison between the numerical modeling results and the theoretical results of the dynamic water pressure at three monitoring points on the outside of the front wall at T = 1.40 s, d = 0.30 m, and H = 0.04 m. As shown in Figure 6, the numerical modeling results of the dynamic water pressure at the three monitoring points agreed well with the theoretical results, thereby indicating that the OWC wave-energy device established in this study can accurately simulate the dynamic water pressure on the front wall of the installation.

A comparison between the measured air pressure inside the chamber and the numerical model is provided in Figure 7, which shows the measured results [31] are consistent with the results of the numerical model, thus indicating that the numerical model established in this study can accurately simulate the relative pressure of air inside the air chamber.

4. Results

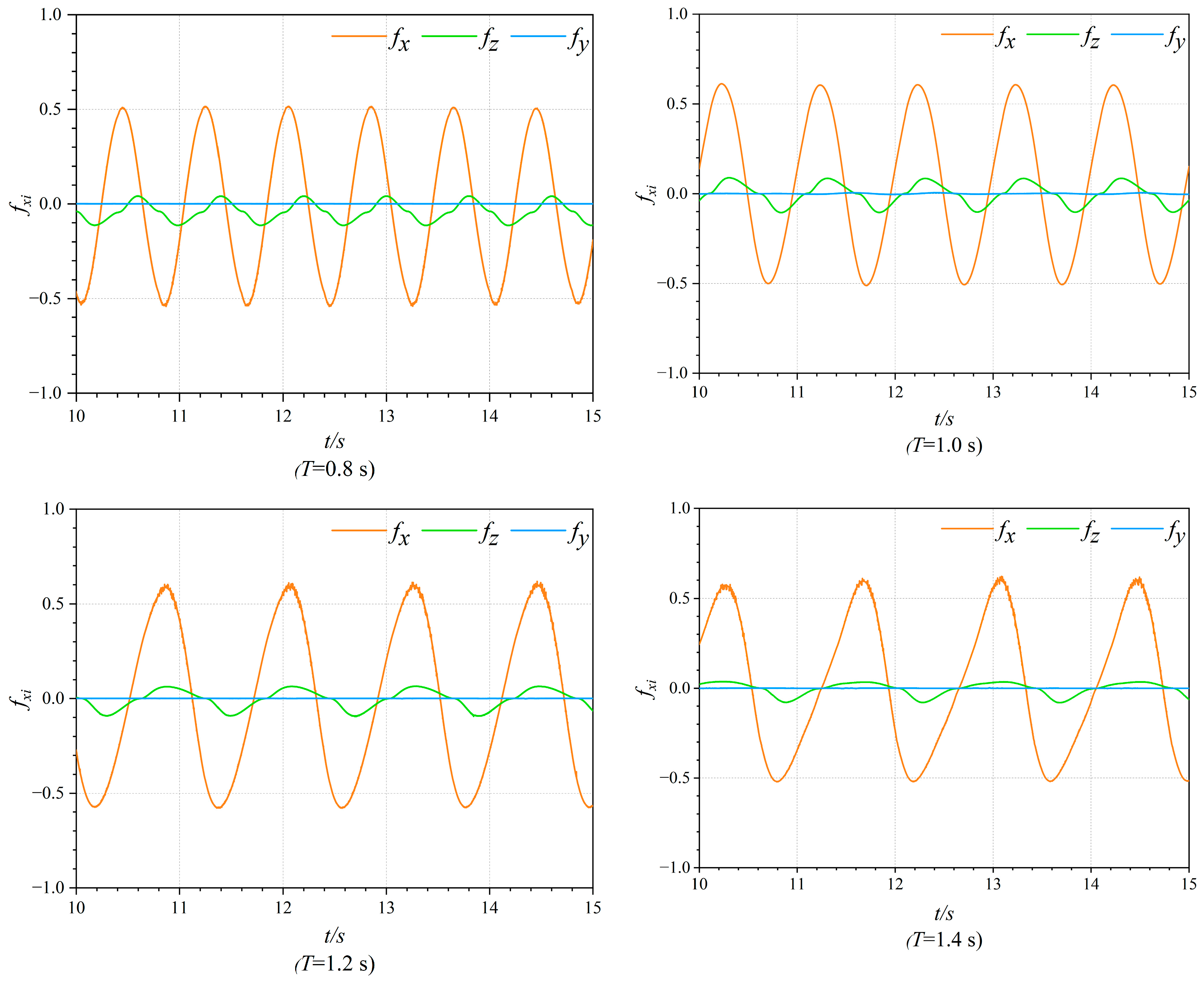
4.1. Effect of Wave Period on Forces in an OWC Device

At a water depth of 0.30 m, the wave height was set to 0.04 m, whereas the wave period was varied within the range of 0.80–1.40 s. This allowed for the determination of the relationship between the wave force and the wave period. To examine the wave force action law, the wave forces in the three directions were rendered dimensionless.

$$f_{x_i}=\frac{F_{x_i}}{\rho gADd},$$

(6)

Here, x_i (i = 1, 2, and 3) denotes the x-, y-, and z-directions, respectively; $f_{x_i}$ shows the dimensionless wave force in the three directions; and A is the wave amplitude.

Figure 8 shows the variation in the wave force on the OWC device in three directions (horizontal, vertical, and transverse) with time for different incident wave periods. The dimensionless wave force varied periodically in all three directions, with the same period as the incident wave. The horizontal dimensionless wave force f_x reflected a regular sine curve, whereas the vertical dimensionless wave force f_z presented clear peaks and troughs but did not present the typical sine curve. The magnitude of f_x was approximately 6.6 to 7.9 times that of f_z, and the horizontal dimensionless wave force f_y was approximately zero.

According to Huang et al. [31], the magnitude of f_y is directly related to the vorticity generated by the OWC pile, whereas vortex shedding on the device pile is related to the Keulegan–Carpenter number. Based on the model parameters of the installation, the vortex was not dislodged from the outer surface of the pile and main support structure, whereas vortex dislodgement occurred at the lower end of the pile skirt of the installation. Furthermore, because the waves were incident in the forward direction, the device was also placed on the centerline of the flume and symmetrical about the y = 0 cross-section, which explains the low f_y relative to f_x and f_z. Because f_y was extreme and thus minimally affected the device, it shall not be discussed herein.

For a more intuitive observation of the water level corresponding to the force case of the device at different moments, the variation in the liquid level near the OWC device on the y = 0 cross-section during one cycle (T = 0.80 s) is presented in Figure 9. As shown, the liquid levels on the outside of the OWC device and inside the chamber varied periodically within one cycle, which corresponded to the force case shown in Figure 8; f_x reached its maximum value when the water level on the outside of the front wall of the device reached its maximum, whereas the amplitude of f_z lagged slightly.

Figure 10 shows the maximum dimensionless wave force max (f_xi), the minimum dimensionless wave force min (f_x), and the corresponding mean value for wave frequencies kd of 0.80 to 1.96 (T = 0.80 to 1.40 s) after the wave propagation stabilized. As shown in Figure 10, the effect of period on the horizontal and vertical dimensionless wave forces to which the device was subjected was insignificant. At kd = 0.80–1.96, both the maximum and minimum wave forces did not vary significantly; thus, the mean values of the dimensionless wave forces at different periods can be a good estimate of the device wave force under a constant wave height and water depth.

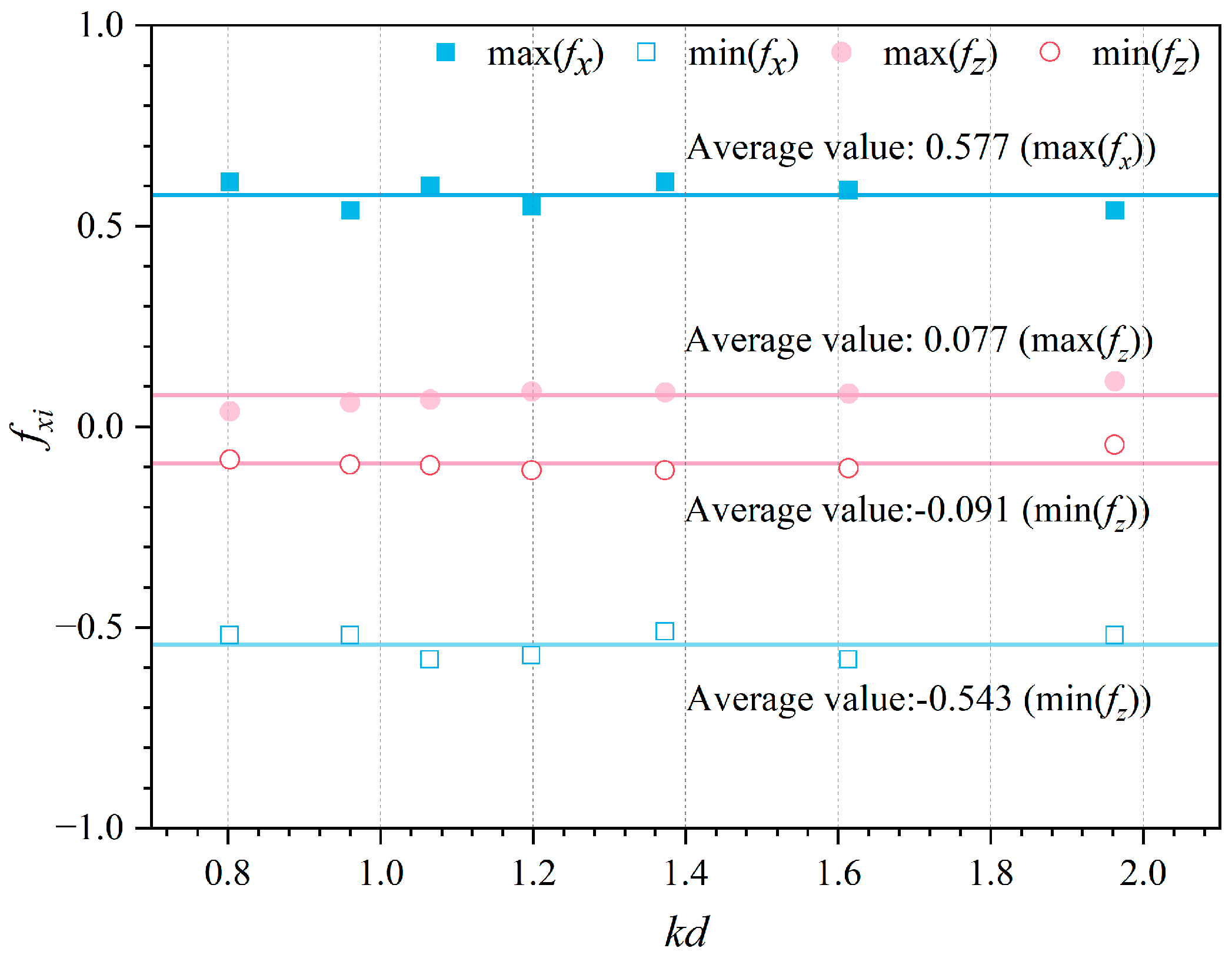
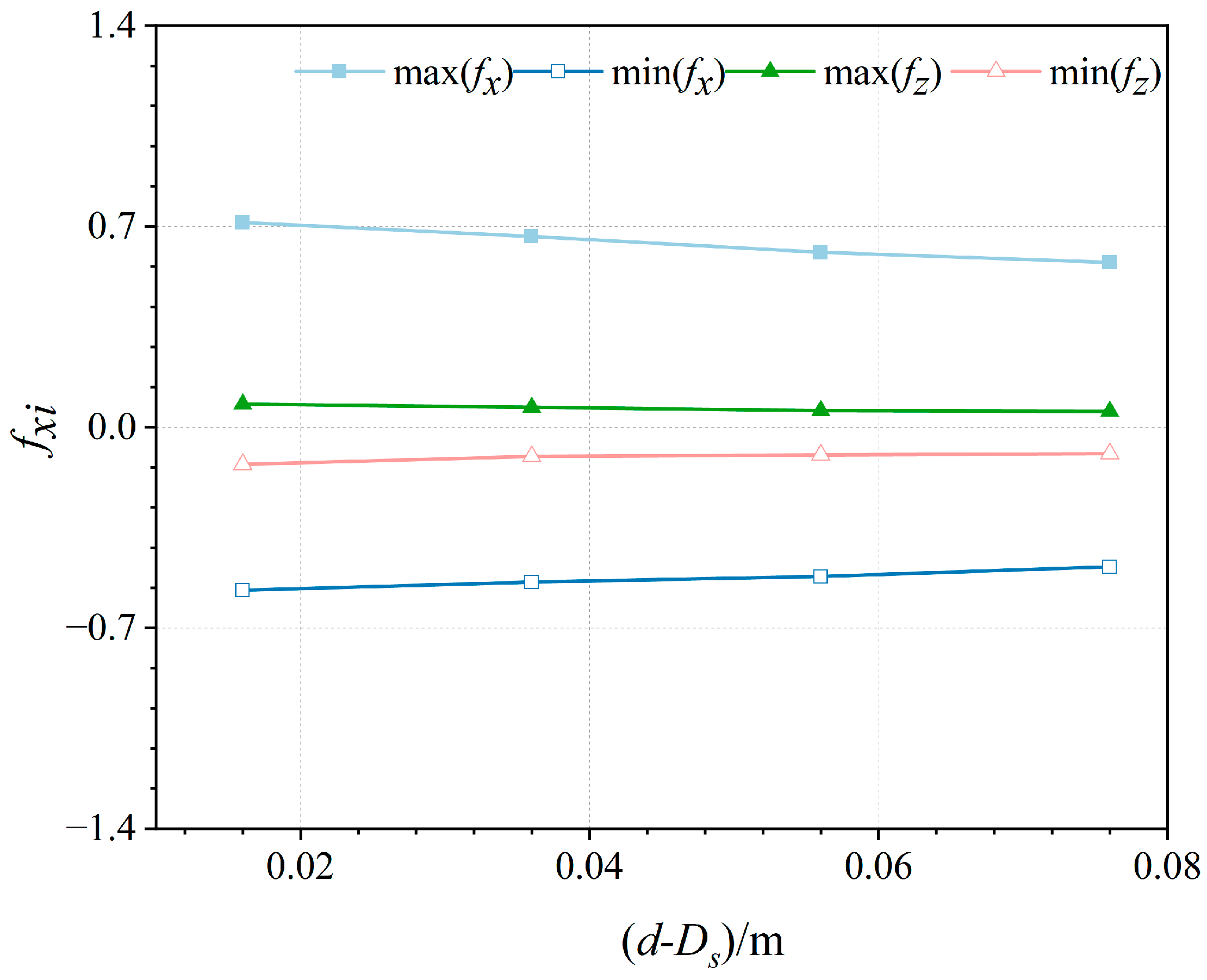
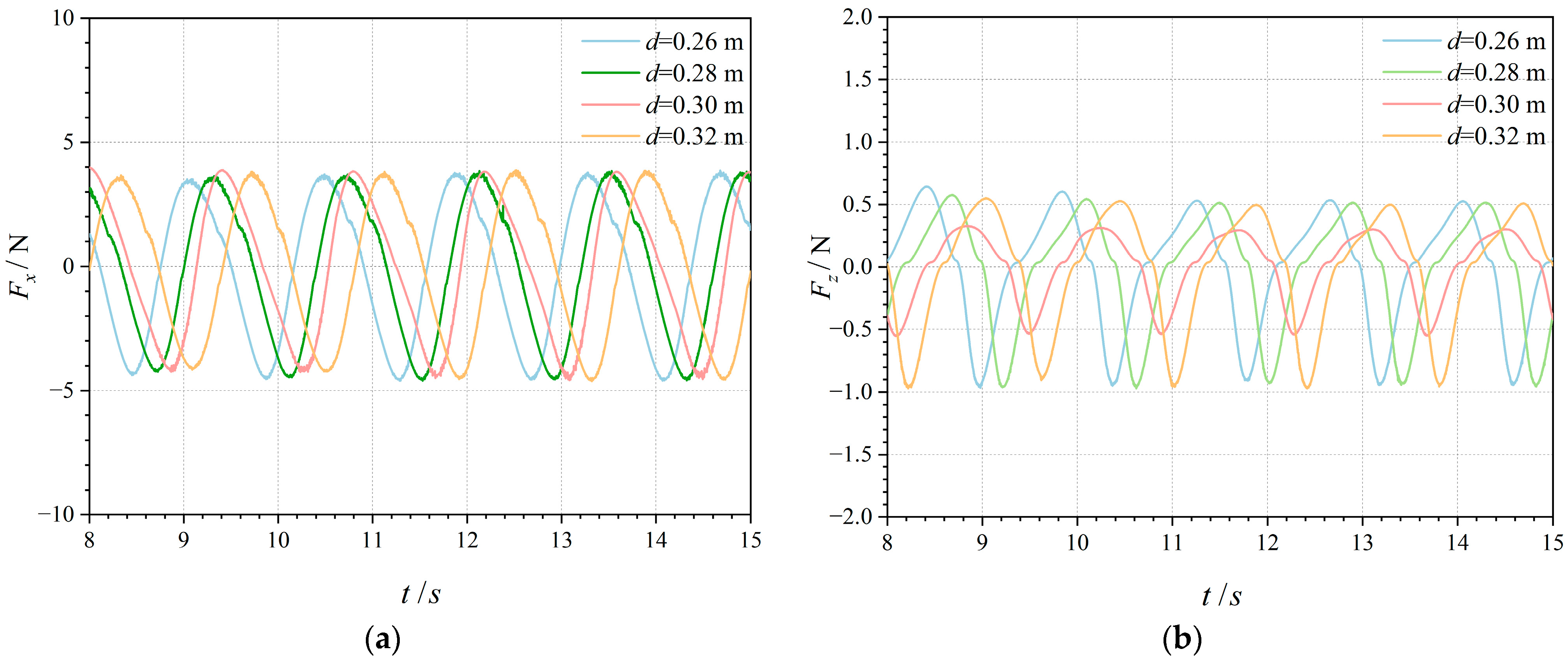
4.2. Effect of Water Depth on Forces in an OWC Device

At a wave period of 1.40 s and a fixed wave height of 0.04 m, the water depth varied within the range of 0.26–0.32 m. This allowed for the determination of the relationship between the wave force and water depth.

The maximum and minimum dimensionless wave loads after wave stabilization under different operating conditions are shown in Figure 11 as a function of the relative water depth d − D_s. As shown in Figure 11, the dimensionless wave force F_xi (i = 1 and 3) decreased as the relative water depth increased. However, the magnitudes of the horizontal and vertical wave forces exerted on the entire device were almost constant, as shown in Figure 12a,b. The submerged section of the OWC device comprised a hollowed-out half-cylinder section and a hollowed-out cylinder section. Because the OWC device requires the water surface to be above the skirt for power generation, the area of the circular cylindrical section submerged in the water increased with the water depth. The velocity of the water quality points decreased with increasing distance from the water surface, and the movement of the water quality points contributed primarily to the wave pressure. For a specified period and wave height, the velocity of the water-quality points at the free water surface was the highest, and it increased with the water depth at the horizontal surface. By focusing only on the wave force due to the water-point velocity on the outer surface, the size of the wave loads should increase with the water depth. Therefore, the wave force on the OWC device should not only be related to the water-point velocity outside the device but also to the force on the submerged section of the structure.

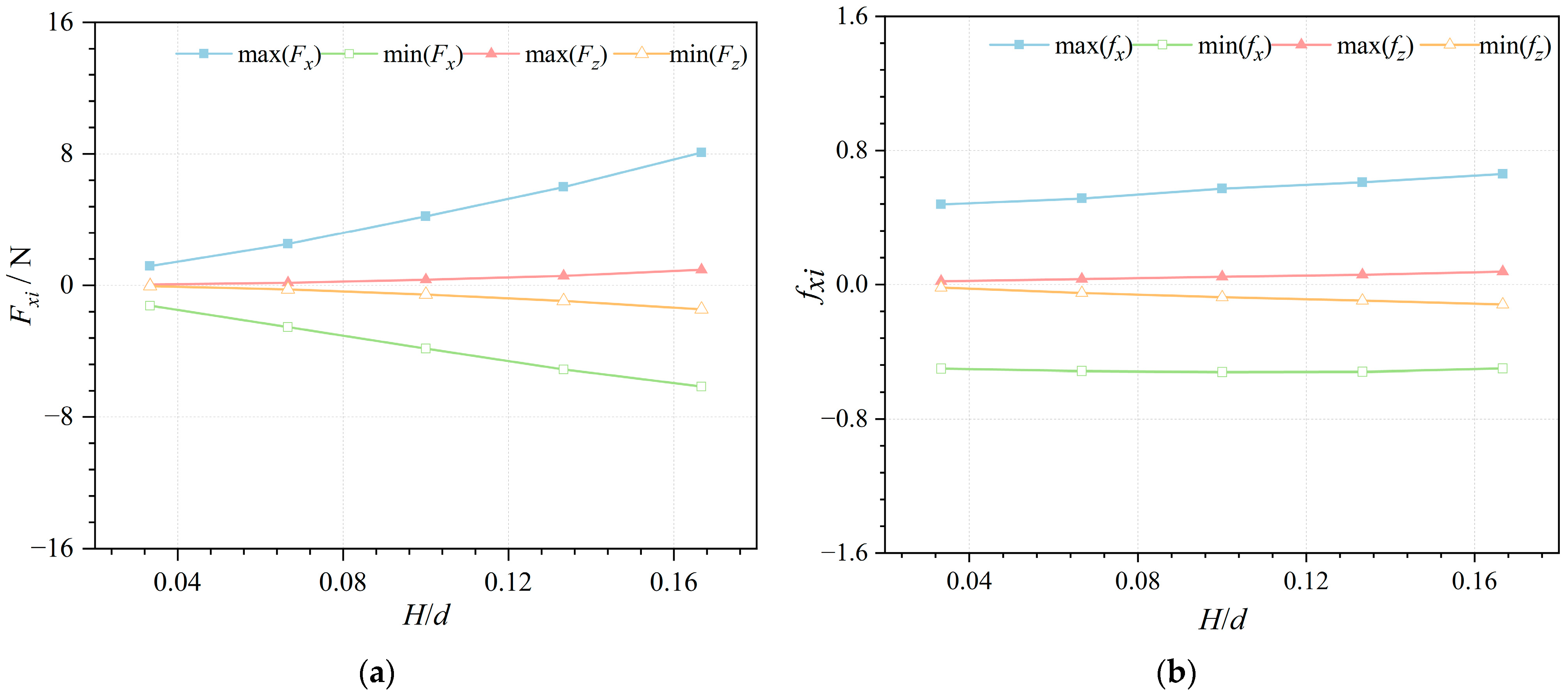
4.3. Effect of Wave Height on Forces in an OWC Device

The variation in pressure with the wave height was obtained by fixing the wave period to 1.40 s and varying the wave height from 0.01 to 0.05 m at a water depth of 0.30 m.

Figure 13 illustrates the changes in the maximum and lowest wave forces with the relative wave height H/d following wave-propagation stabilization under various wave height circumstances. As shown in Figure 13a, the dimensionless wave force grows with the relative wave height, with the minimum dimensionless horizontal wave force min (f_x) decreasing slightly at relative water depths H/d of 0.1 to 0.167; however, both the maximum and minimum dimensional wave forces on the device increased significantly with the relative wave height, as shown in Figure 13b.

To further investigate the relationship between the wave height and wave force, the average of the sum of the absolute values of the horizontal dimensionless wave force f_x and the vertical dimensionless wave force f_z crest and trough were set as the average horizontal wave force and average vertical wave force, respectively.

$$[f_x]=\frac{\left|min\left(f_x\right)\right|+\left|max\left(f_x\right)\right|}{2},$$

(7)

In Equation (7), [f_x] is the average horizontal wave force.

$$[f_z]=\frac{\left|min\left(f_z\right)\right|+\left|max\left(f_z\right)\right|}{2},$$

(8)

In Equation (8), [f_z] is the average vertical wave force.

The variations of [f_x]/[f_x]_{H=0.01 m} and [f_z]/[f_z]_{H=0.01 m} with the wave height are shown in Figure 14. [f_x]_{H=0.01 m} and [f_z]_{H=0.01 m} represent the average of the sum of the absolute values of the crests and troughs for incident wave heights of H = 0.01 m for the horizontal and vertical dimensionless wave forces, respectively. As illustrated in Figure 14, the mean horizontal wave force [f_x] increased linearly with the wave height, whereas the mean vertical wave force [f_z] increased with the square of the wave height.

To further examine the relationship between the wave force as well as wave height, the average value of the sum of the absolute values of the horizontal wave force F_x and the vertical wave force F_z peaks and troughs was set as the average horizontal wave force and the average vertical wave force $\left[F_z\right]$. Based on the force law of the device shown in Figure 14 and the conclusion that the water depth is not correlated significantly with the force of the device obtained in Section 3.2, we assumed that the magnitudes of $\left[F_x\right]$ and $\left[F_z\right]$ can be determined as follows, respectively:

$$\left[F_x\right]=\alpha \rho gDH,$$

(9)

$$\left[F_z\right]=\beta \rho gD{H}^2,$$

(10)

Here, $\alpha$ and $\beta$ are used to estimate the $\left[F_x\right]$ and $\left[F_z\right]$ empirical formula coefficients, respectively. Based on the data presented in Figure 13 and Figure 14, one obtains $\alpha =0.212\pm 0.018$ and $\beta =0.788\pm 0.038$.

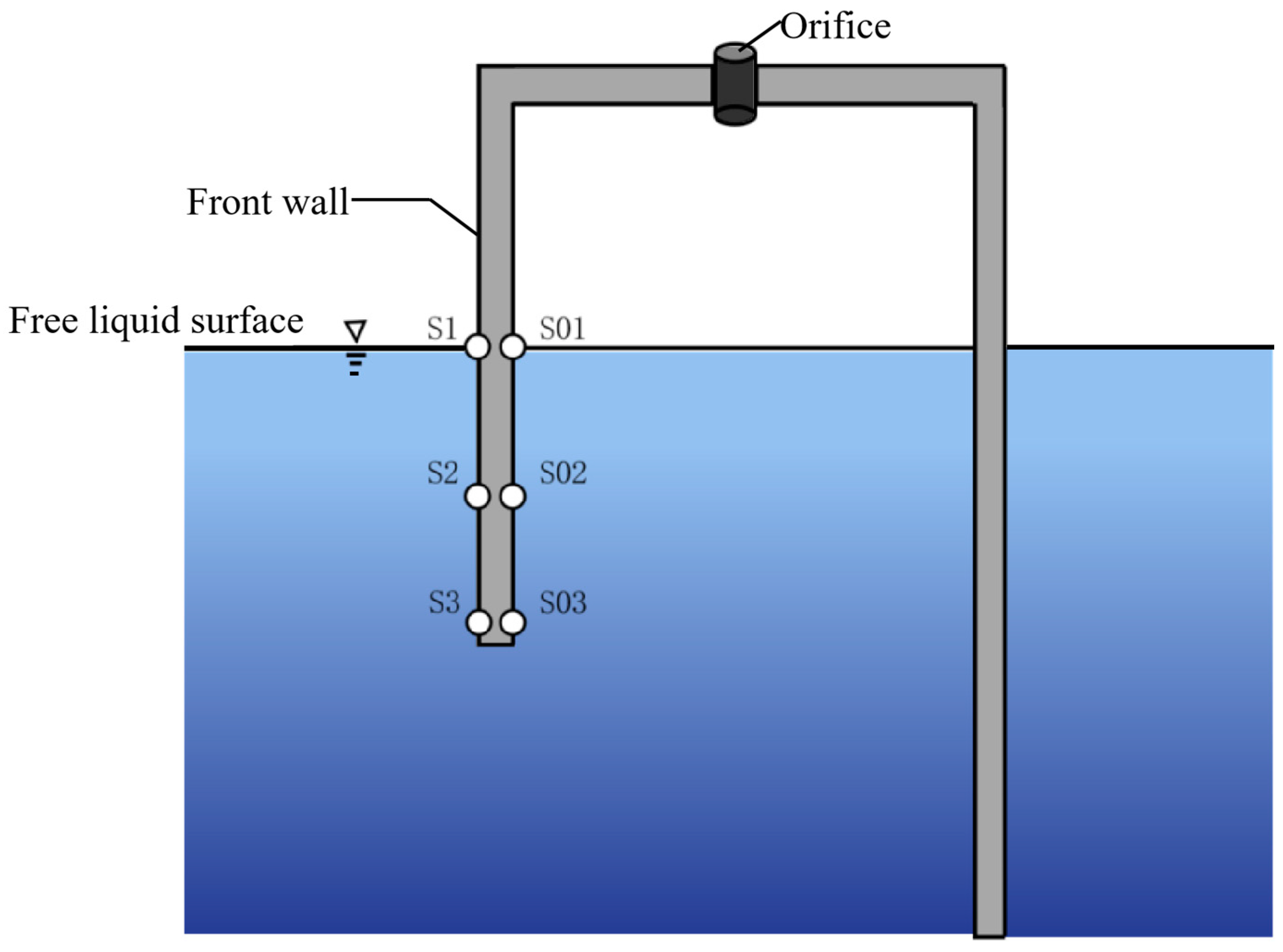
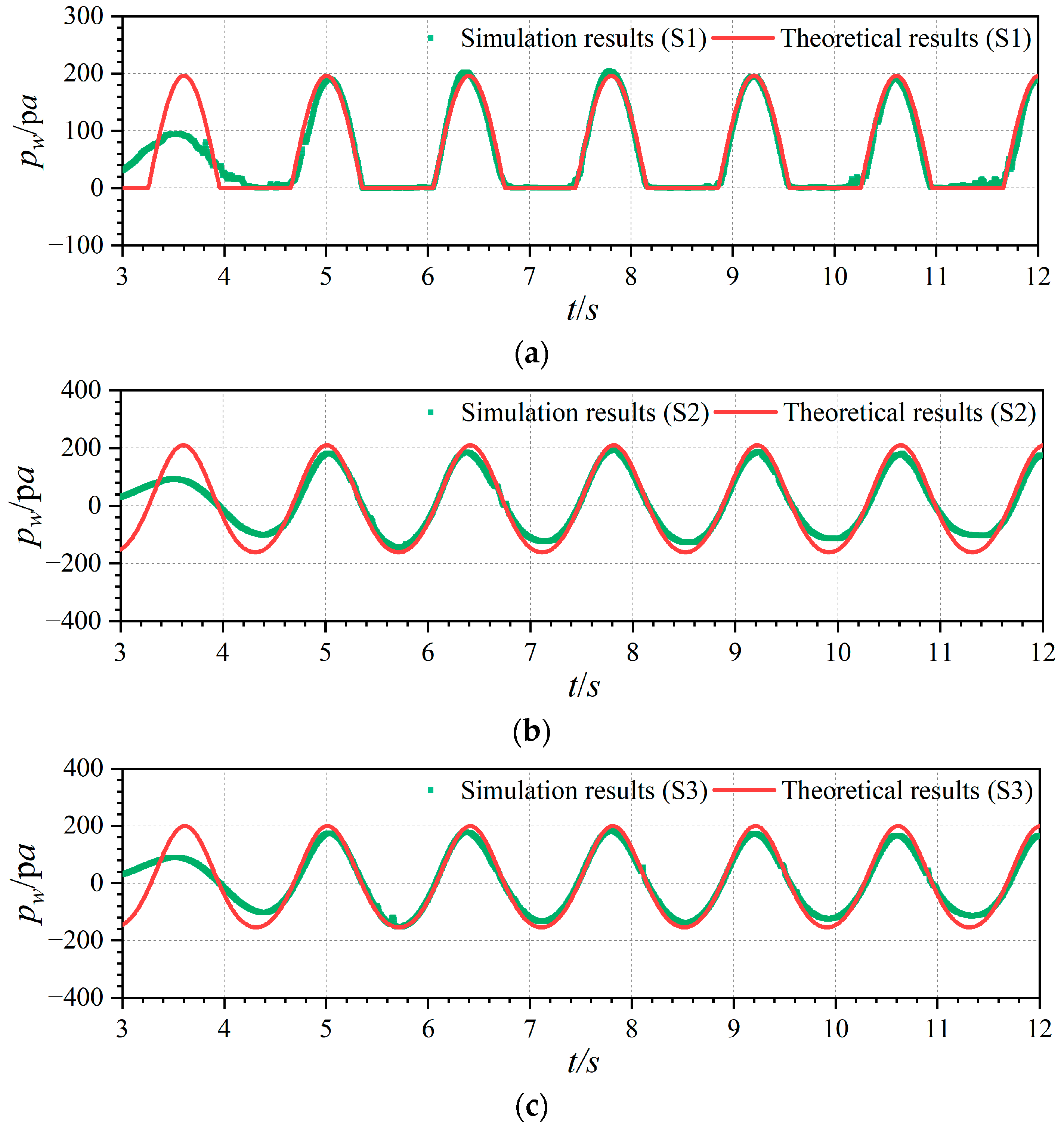
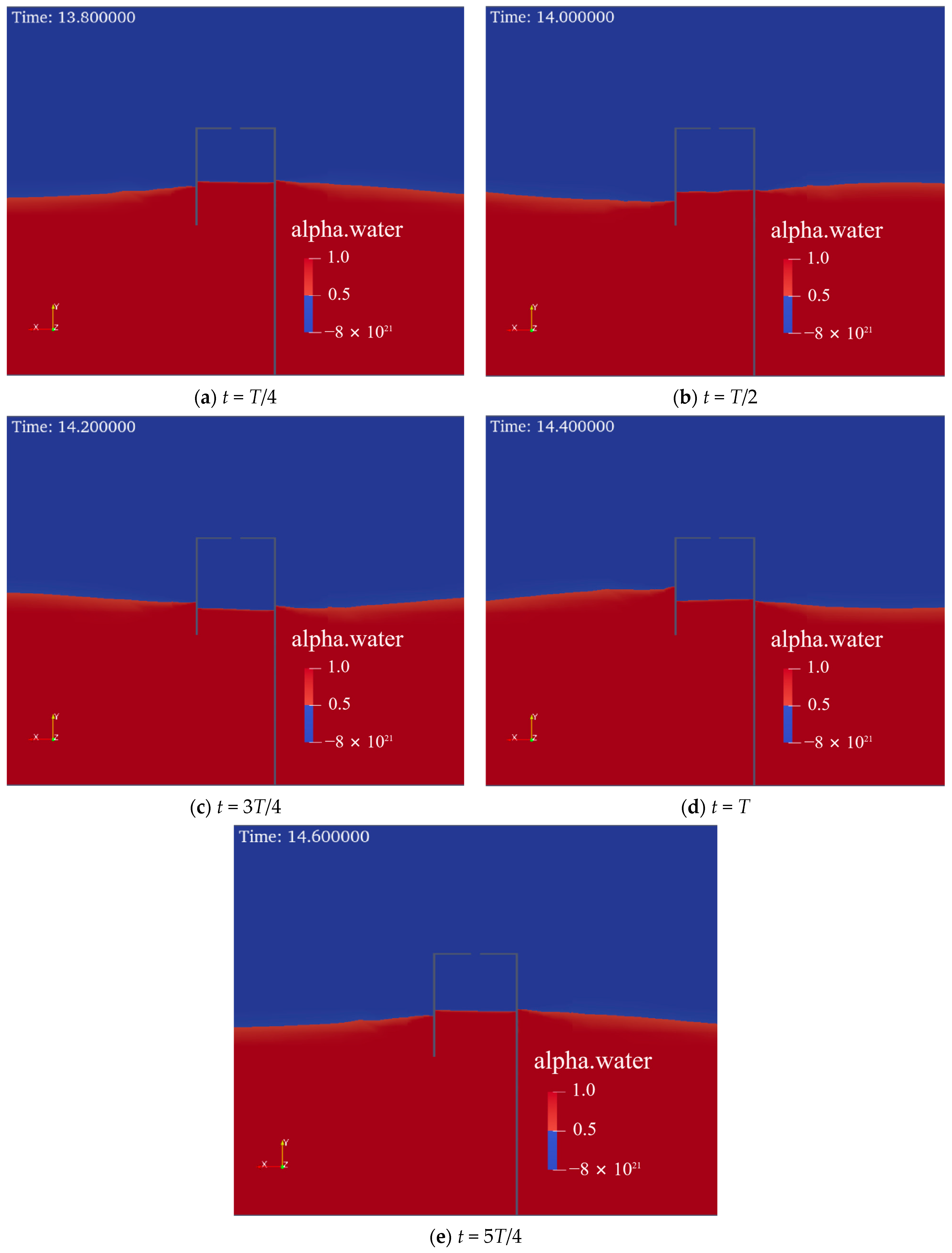
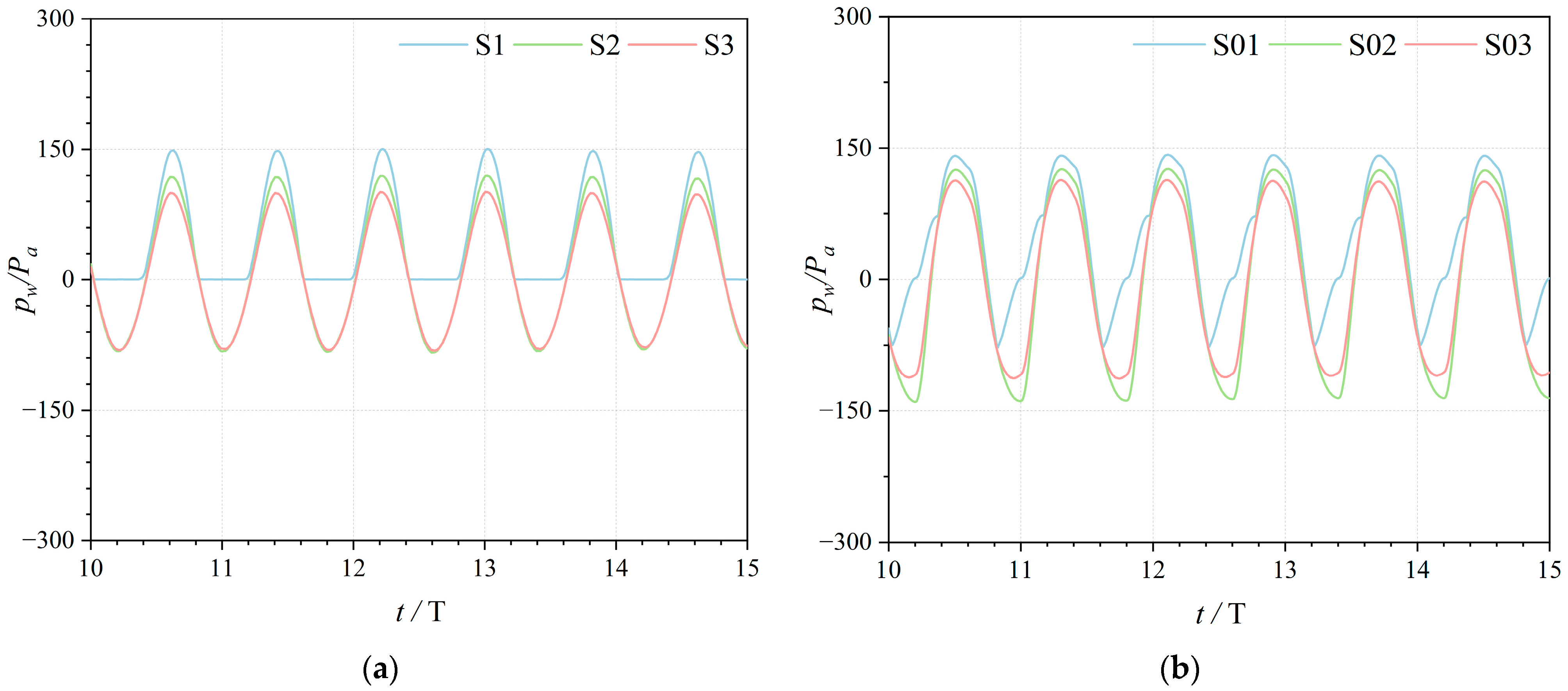
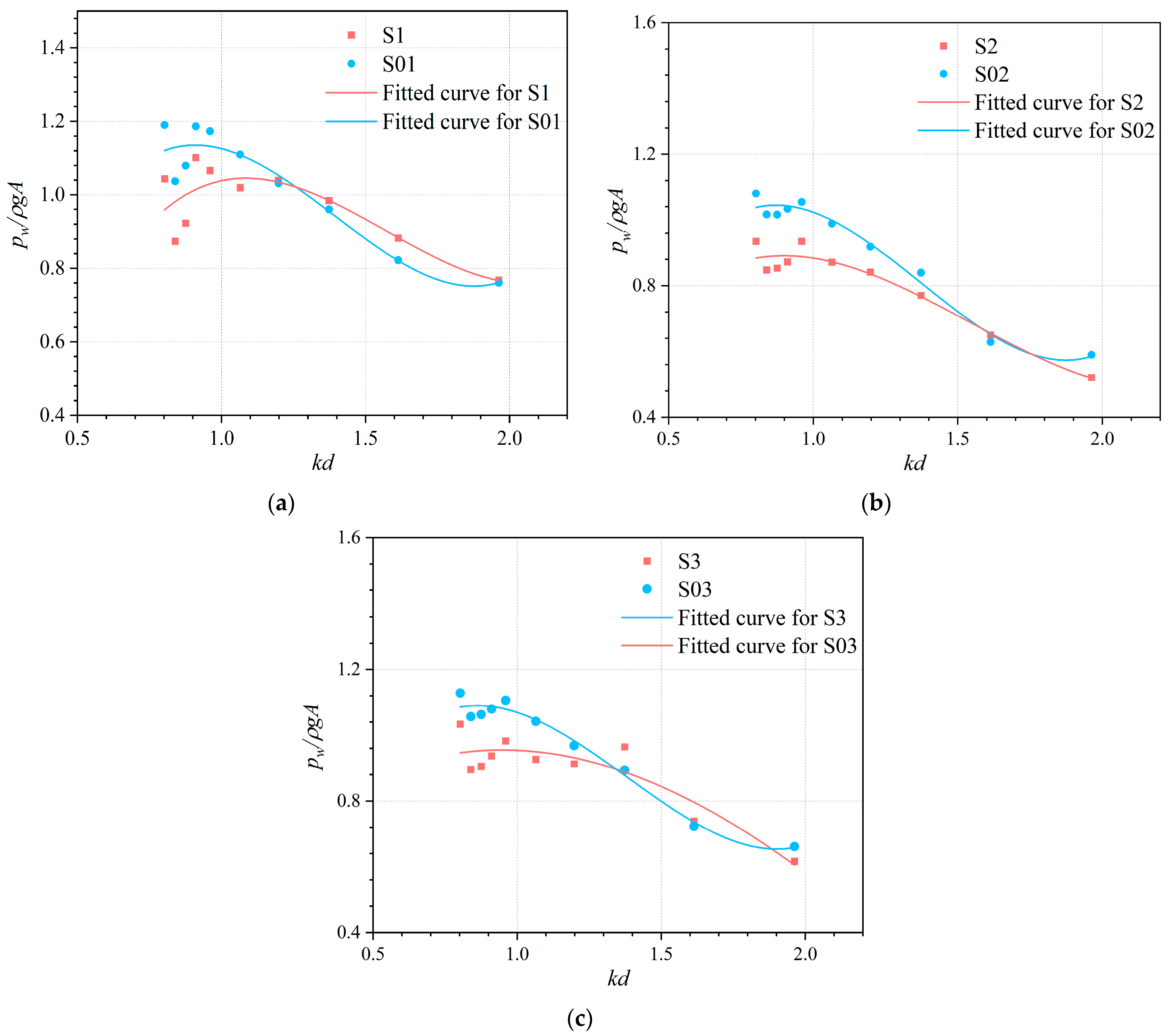
4.4. Dynamic Water Pressure at the Front Wall of the OWC Device

The dynamic water pressure monitoring points on the front wall of the gas chamber are shown in Figure 5. Figure 15 shows the results of the comparison of dynamic water pressure p_w histories at each measurement point inside and outside the front wall of the gas chamber. As shown in Figure 15a,b, the changes in the dynamic water pressure were cyclical, and the dynamic water pressure on the outside of the front wall of the gas chamber reflected a sinusoidal curve, whereas that on the inside changed relatively irregularly compared with the dynamic water pressure on the outside; this indicates that multiple wave reflections occurred inside the gas chamber of the device and were subject to the action of the air pressure inside the gas chamber. The maximum dynamic water pressure on both sides of the front wall of the gas chamber occurred at the point where it intersected the hydrostatic surface, i.e., the maximum pressures on the outside and inside occurred at points S1 and S01, respectively.

The mean value of the sum of the peaks and troughs of the dynamic water pressure at each pressure-monitoring point on the front wall is shown in Figure 16 as a function of kd. As shown in Figure 16, the dynamic water pressure at each point on the inside of the front wall of the air chamber p_w increased at kd = 0.80–1.0 and decreased at kd = 1.0–2.0. Notably, at kd less than 1.3 (low-frequency region), the dynamic water pressure amplitude on the inside of the front wall was greater than the outside pressure amplitude, whereas at kd greater than 1.3 (high-frequency region), the outside amplitude is likely to exceed the inside amplitude. Due to the limitations of the VOF method, the existing models fail to adequately simulate the behavior of the impinging rigid wall after wave entrainment into the air. The two-phase compression SPH method proposed by Rafiee et al. [34], with its advantages in dealing with complex hydrodynamics problems, may provide an important reference value for the improvement and refinement of our future work.

5. Conclusions

This study used OpenFOAM to simulate wave loads on an OWC device under forward-wave incidence conditions, as well as dynamic water pressures on the inside and outside of the device’s front wall. The following conclusions were drawn from this study:

(1)

The horizontal wave force was significantly greater than the lateral and vertical wave forces, which may be related to the forward incidence of the wave.

(2)

The horizontal and vertical wave forces on the device did not change significantly with the relative water depth. This suggests that the force on the submerged section of the device affected the force of the device.

(3)

The horizontal wave force changed linearly as the wave height increased, whereas the vertical wave force increased with the square of the wave height. Consequently, when designing installations in the face of large wave heights in the marine environment, special attention must be paid to the influence of the vertical wave force in order to ensure the stability and safety of the structure.

(4)

The maximum value of the dynamic water pressure on both sides of the front wall of the device occurred at the junction of the water surface and the device. The dynamic water pressure at each point of the front wall inside the gas chamber appeared to increase and then decrease with increasing wave frequency, which was very similar to the energy-conversion efficiency of the device. Therefore, the design of the device should consider more about the strength of the device along with its maximum energy-conversion efficiency. At the same time, more attention needs to be paid to the strength of the water surface junction.

The numerical simulation results of this study provide reference values for the design and optimization of OWC devices. Even though the force characteristics of OWC devices are complex, existing studies, including Li et al.’s [29] on the effect of incident wave angle, Ning et al.’s [30] on the force law of isolated waves, and Khakimzyanov et al.’s [35,36] on the interaction of surface waves with movable structures, provide a foundation for future work. These studies provide valuable references and point out areas for further exploration. For future endeavors, the following can be considered:

(1)

Extend the studies on the effects of different incidence angles to fully understand the force characteristics of OWC devices.

(2)

Utilize the existing studies as a theoretical foundation to gain a deeper understanding of the dynamic response of OWC devices under different sea states.

(3)

Based on the existing studies, explore the force law of a 3D floating OWC device under variable sea states and then improve its stability and energy-conversion efficiency.