Underwater Mapping and Optimization Based on Multibeam Echo Sounders
Abstract
1. Introduction
- Establishment of a Data Acquisition Platform: A data acquisition platform for the multibeam echo sounder is established, effectively reducing measurement errors and enabling convenient, fast, and stable high-quality data collection.
- Development of a Multibeam Data Processing System: A multibeam data processing system is developed under Linux, allowing for the modification and updating of sonar parameters, data stream format conversion, and enhanced system compatibility.
- Proposal of an Underwater Mapping Algorithm: An underwater mapping algorithm based on the iEKF is proposed, followed by further optimization through point cloud registration in the post-processing stage, achieving high-quality mapping results.
- Experimental Validation: The operability of the proposed algorithm is validated through on-site experiments, and its reliability is further confirmed through the precise calculation of trajectory and registration errors.
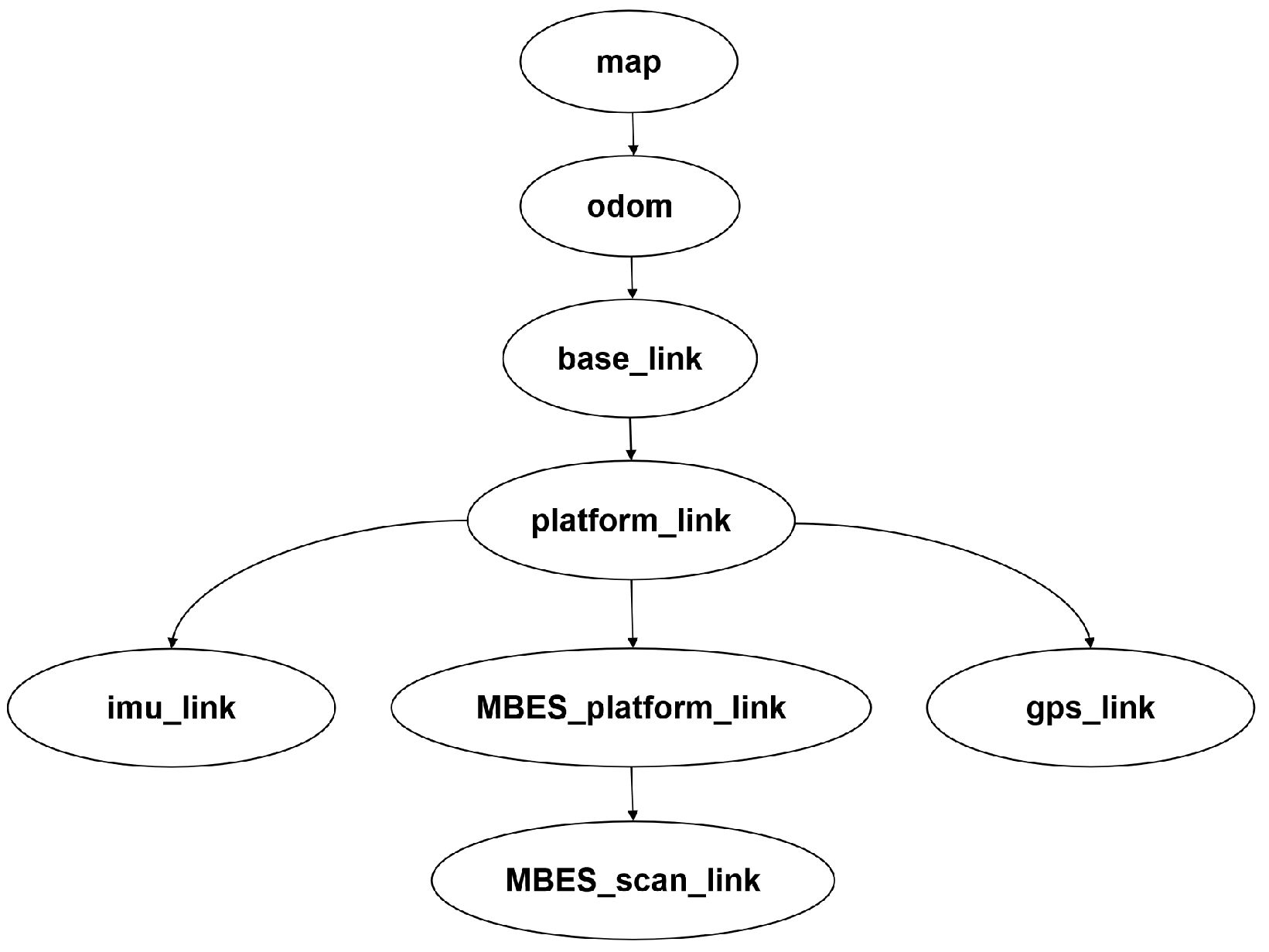
2. The Components of the Data Collection System
2.1. Hardware
- MBES, inclusive of the sonar head and interface modules;
- Inertial Navigation System (INS), encompassing satellite and 4G communication antennas, integrated gyroscopes, and accelerometers;
- Accumulator and power cord;
- Configuration computer and cable.
2.2. Software
3. Methods
3.1. Mapping
3.1.1. IMU Recursion Step
3.1.2. GPS Update Step
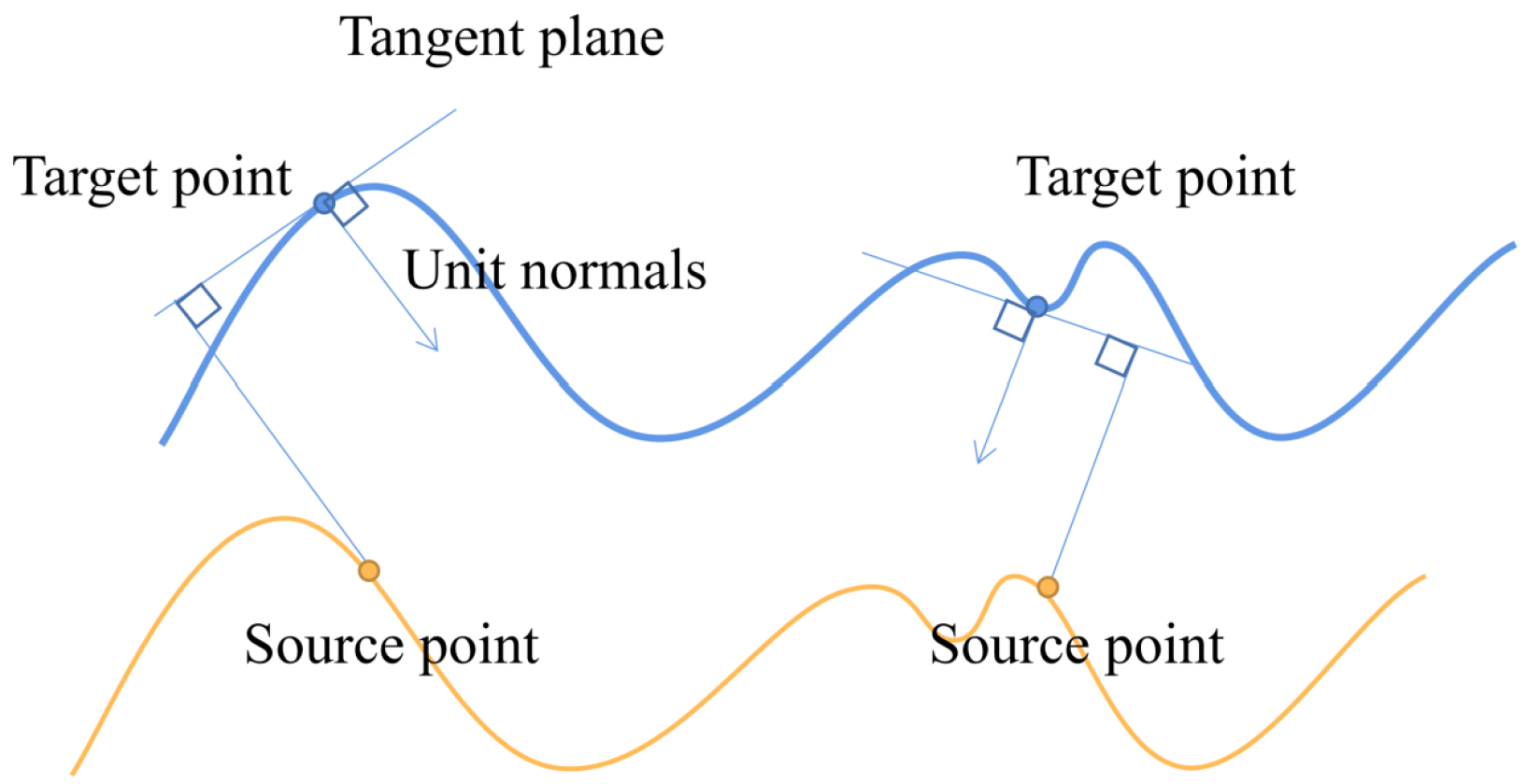
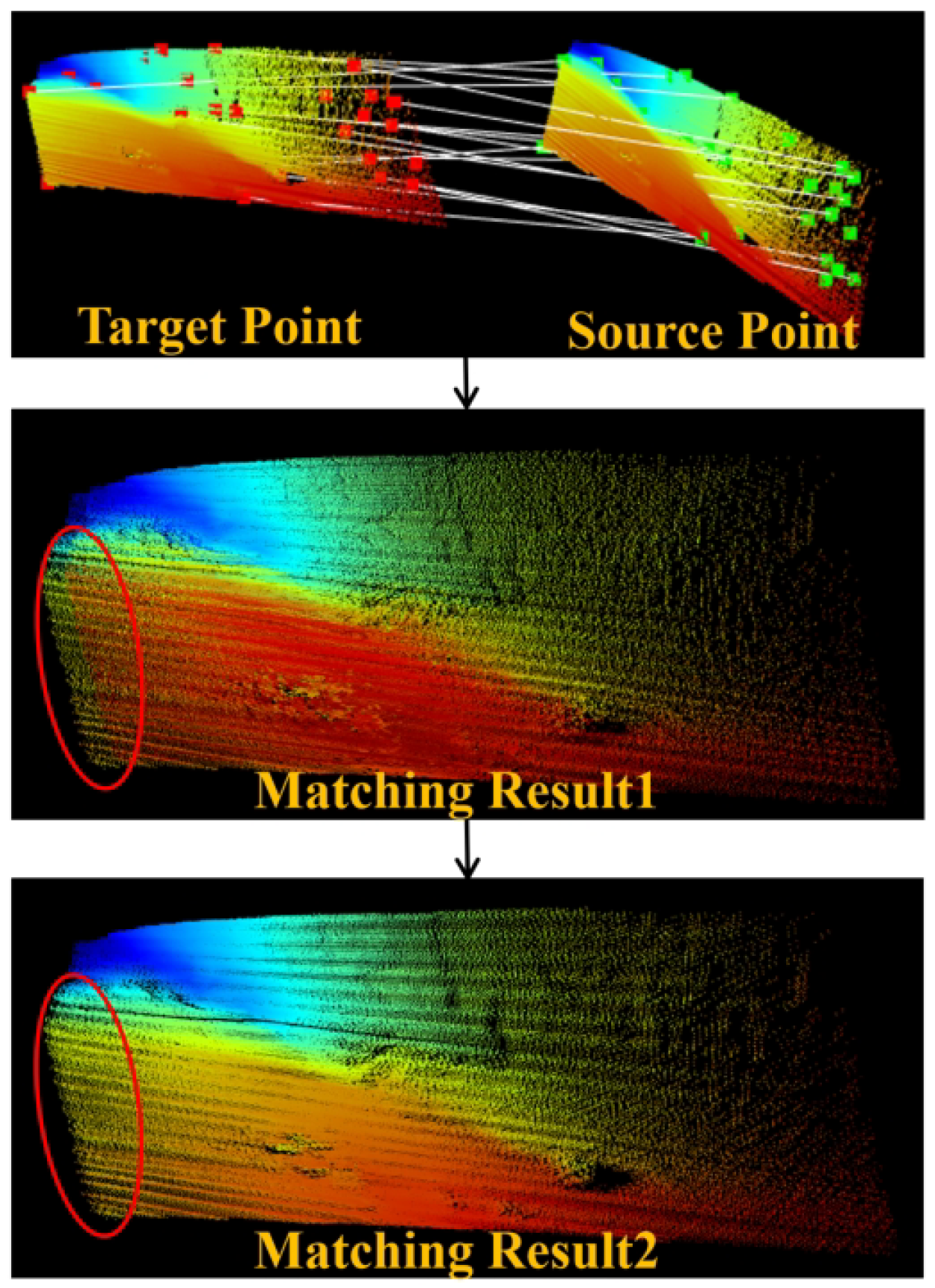
3.2. Point Cloud Registration
4. Experiments and Results
4.1. Experimental Description
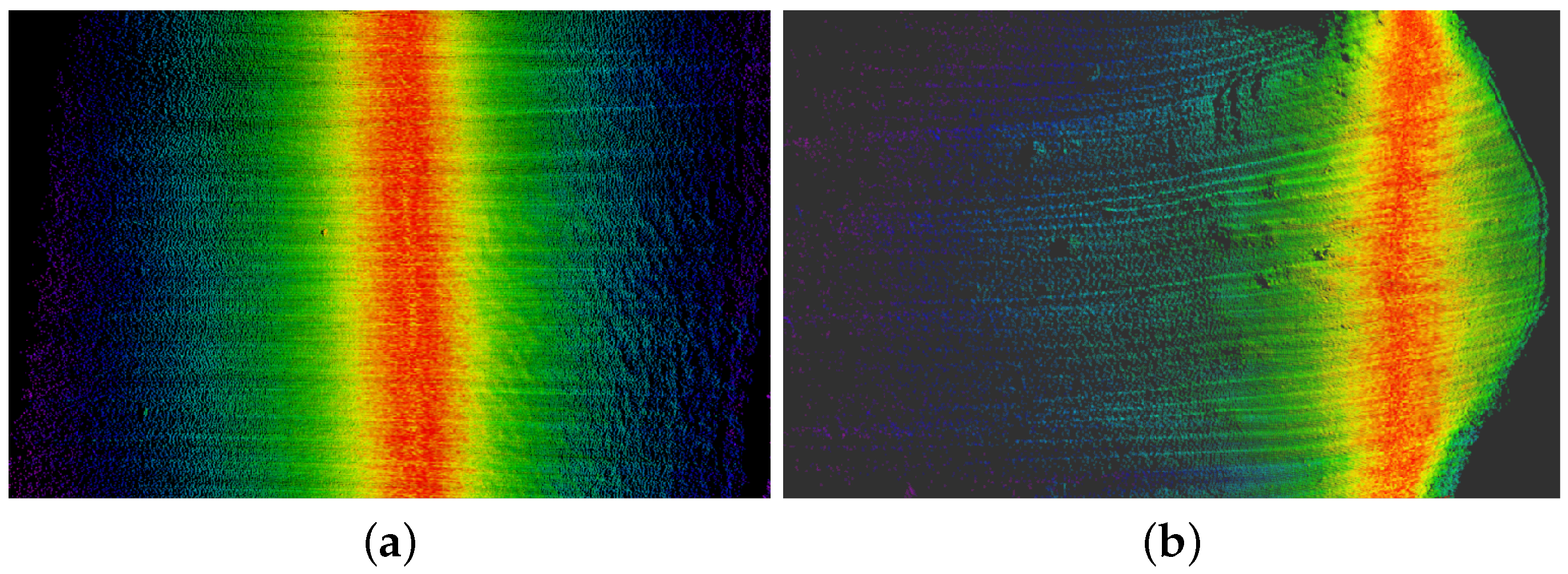
4.2. Mapping Results
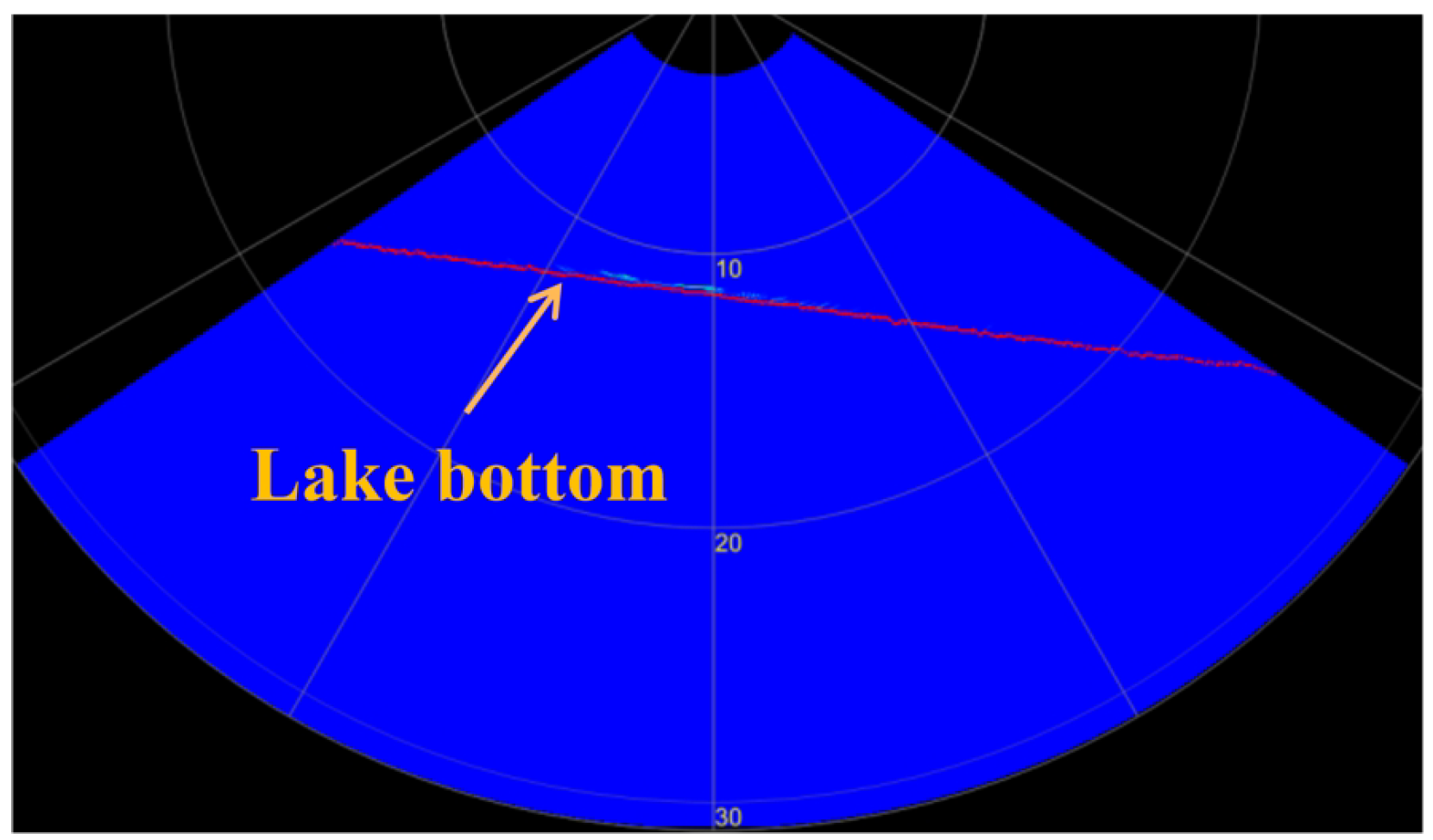
4.3. Target Scanning Results
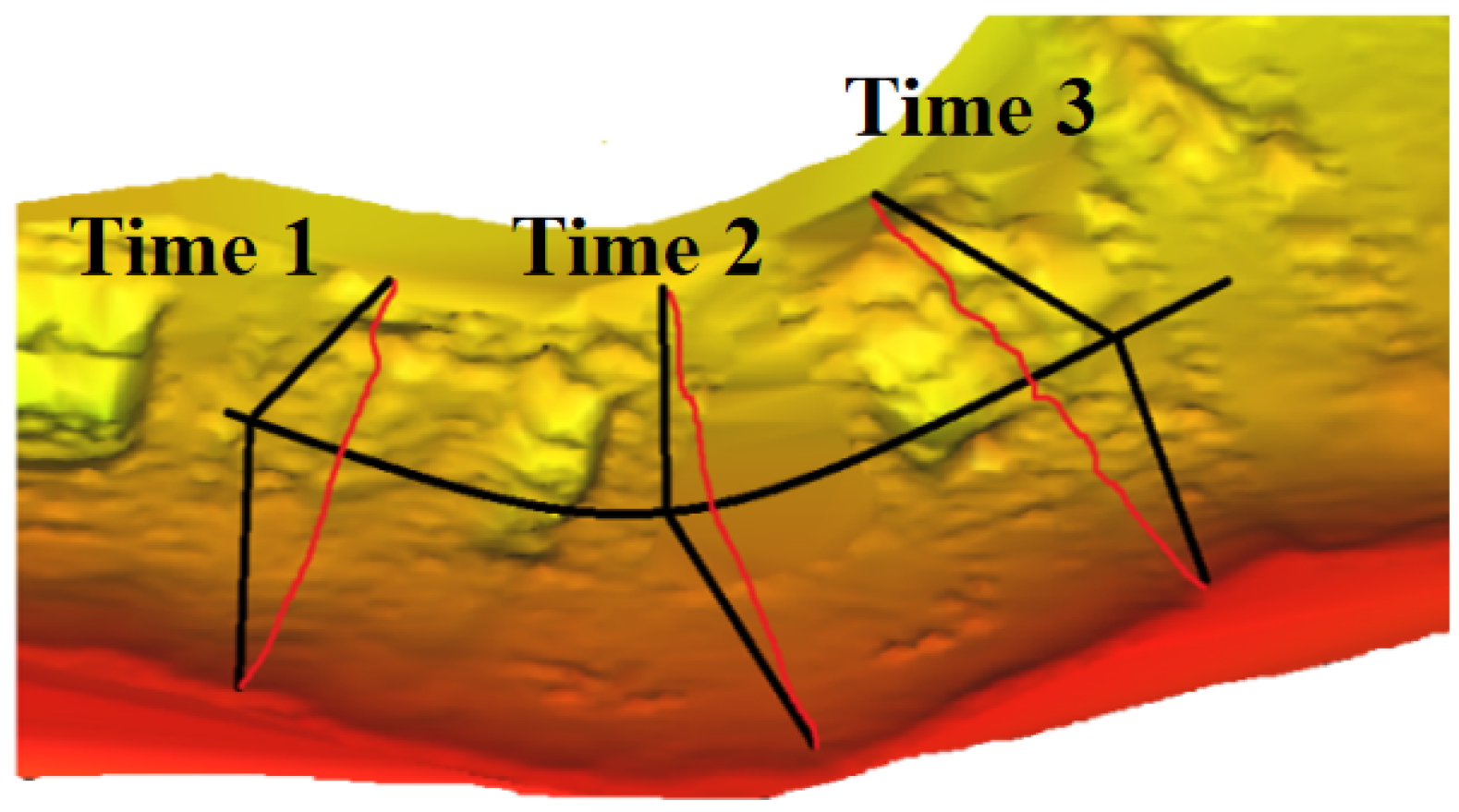
4.4. Registration Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MBES | Multibeam Echo Sounder |
| iEKF | Iterative Extended Kalman Filter |
| GICP | Global Informantion Consistency Point |
| INS | Inertial Navigation System |
| ROS | Robot Operating System |
| PPS | Pulse Per Second |
| ZDA | Zenith Total Delay Altimeter |
| GNSS | Global Navigation Satellite System |
| DVLs | Doppler Velocity Logs |
| PCL | Point Cloud Library |
| ATE | Absolute Trajectory Error |
References
- Mao, Z.; Zhang, Z. Taking the “UN Decade of Ocean Science for Sustainable Development” as an opportunity to help build a “Community with a Shared Future between China and Pacific Island Countries”. Mar. Policy 2024, 159, 105943. [Google Scholar] [CrossRef]
- Huy, D.Q.; Sadjoli, N.; Azam, A.B.; Elhadidi, B.; Cai, Y.; Seet, G. Object perception in underwater environments: A survey on sensors and sensing methodologies. Ocean Eng. 2023, 267, 113202. [Google Scholar] [CrossRef]
- Yan, Z.; Min, X.; Xu, D.; Geng, D. A novel method for underactuated UUV tracking unknown contour based on forward-looking sonar. Ocean Eng. 2024, 301, 117545. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y.; Ling, L.; Folkesson, J. A fully-automatic side-scan sonar simultaneous localization and mapping framework. IET Radar Sonar Navig. 2024, 18, 674–683. [Google Scholar] [CrossRef]
- Bore, N.; Folkesson, J. Neural shape-from-shading for survey-scale self-consistent bathymetry from sidescan. IEEE J. Ocean. Eng. 2022, 48, 416–430. [Google Scholar] [CrossRef]
- Rizzo, A.; De Giosa, F.; Donadio, C.; Scardino, G.; Scicchitano, G.; Terracciano, S.; Mastronuzzi, G. Morpho-bathymetric acoustic surveys as a tool for mapping traces of anthropogenic activities on the seafloor: The case study of the Taranto area, southern Italy. Mar. Pollut. Bull. 2022, 185, 114314. [Google Scholar] [CrossRef] [PubMed]
- Scardino, G.; De Giosa, F.; D’Onghia, M.; Demonte, P.; Fago, P.; Saccotelli, G.; Valenzano, E.; Moretti, M.; Velardo, R.; Capasso, G.; et al. The footprints of the wreckage of the Italian royal navy battleship leonardo da vinci on the mar piccolo sea-bottom (Taranto, Southern Italy). Oceans 2020, 1, 77–93. [Google Scholar] [CrossRef]
- Instruments, L.C.S. Multibeam Sonar Theory of Operation, 1st ed.; L-3 Communications SeaBeam Instruments: Boston, MA, USA, 2000. [Google Scholar]
- Teng, M.; Ye, L.; Yuxin, Z.; Zhang, Q.; Jiang, Y.; Zheng, C.; Zhang, T. Robust bathymetric SLAM algorithm considering invalid loop closures. Appl. Ocean Res. 2020, 102, 102298. [Google Scholar]
- Ji, X.; Yang, B.; Tang, Q. Acoustic seabed classification based on multibeam echosounder backscatter data using the PSO-BP-AdaBoost algorithm: A case study from Jiaozhou Bay, China. IEEE J. Ocean. Eng. 2020, 46, 509–519. [Google Scholar] [CrossRef]
- Trzcinska, K.; Janowski, L.; Nowak, J.; Rucinska-Zjadacz, M.; Kruss, A.; von Deimling, J.S.; Pocwiardowski, P.; Tegowski, J. Spectral features of dual-frequency multibeam echosounder data for benthic habitat mapping. Mar. Geol. 2020, 427, 106239. [Google Scholar] [CrossRef]
- Maleika, W.; Forczmański, P. Adaptive modeling and compression of bathymetric data with variable density. IEEE J. Ocean. Eng. 2019, 45, 1353–1369. [Google Scholar] [CrossRef]
- Seaman, P.; Sturkell, E.; Gyllencreutz, R.; Stockmann, G.J.; Geirsson, H. New multibeam mapping of the unique Ikaite columns in Ikka Fjord, SW Greenland. Mar. Geol. 2022, 444, 106710. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Y.; Jin, S.; Bian, G.; Zhao, X.; Peng, C. A Method for Multi-Beam Bathymetric Surveys in Unfamiliar Waters Based on the AUV Constant-Depth Mode. J. Mar. Sci. Eng. 2023, 11, 1466. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, T.; Guo, Q.; Xu, C.; Wang, T.; Peng, D.; Yu, X. Terrain matching positioning method for underwater vehicles based on curvature discrimination. Ocean Eng. 2022, 260, 111965. [Google Scholar] [CrossRef]
- Melo, J.; Matos, A. Survey on advances on terrain based navigation for autonomous underwater vehicles. Ocean Eng. 2017, 139, 250–264. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Wang, Y.; Liu, Y.; Yang, Y.; Zhou, T.; Bian, H. Subsea pipeline leak inspection by autonomous underwater vehicle. Appl. Ocean Res. 2021, 107, 102321. [Google Scholar] [CrossRef]
- Weber, T.C. A CFAR detection approach for identifying gas bubble seeps with multibeam echo sounders. IEEE J. Ocean. Eng. 2021, 46, 1346–1355. [Google Scholar] [CrossRef]
- Bello, J.; Eriksen, P.; Pocwiardowski, P. Oil leak detections with a combined telescopic fluorescence sensor and a wide band multibeam sonar. In Proceedings of the International Oil Spill Conference Proceedings. International Oil Spill Conference, Long Beach, CA, USA, 15–18 May 2017; pp. 1559–1573. [Google Scholar]
- Ghobrial, M. Fish Detection Automation from ARIS and DIDSON SONAR Data. Master’s Thesis, University of Oulu, Degree Programme in Computer Science and Engineering, Oulu, Finland, 2019. [Google Scholar]
- Solana Rubio, S.; Salas Romero, A.; Cerezo Andreo, F.; González Gallero, R.; Rengel, J.; Rioja, L.; Callejo, J.; Bethencourt, M. Comparison between the employment of a multibeam echosounder on an unmanned surface vehicle and traditional photogrammetry as techniques for documentation and monitoring of shallow-water cultural heritage sites: A case study in the bay of Algeciras. J. Mar. Sci. Eng. 2023, 11, 1339. [Google Scholar] [CrossRef]
- Jung, J.; Lee, Y.; Park, J.; Yeu, T.K. Multi-modal sonar mapping of offshore cable lines with an autonomous surface vehicle. J. Mar. Sci. Eng. 2022, 10, 361. [Google Scholar] [CrossRef]
- Thoms, A.; Earle, G.; Charron, N.; Narasimhan, S. Tightly Coupled, Graph-Based DVL/IMU Fusion and Decoupled Mapping for SLAM-Centric Maritime Infrastructure Inspection. IEEE J. Ocean. Eng. 2023, 48, 663–676. [Google Scholar] [CrossRef]
- Li, S.; Su, D.; Yang, F.; Zhang, H.; Wang, X.; Guo, Y. Bathymetric LiDAR and multibeam echo-sounding data registration methodology employing a point cloud model. Appl. Ocean Res. 2022, 123, 103147. [Google Scholar] [CrossRef]
- Stateczny, A.; Gronska, D.; Wlodarczyk-Sielicka, M.; Motyl, W. Multibeam echosounder and LiDAR in process of 360O numerical map production for restricted waters with HydroDron. In Proceedings of the 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018; pp. 288–292. [Google Scholar]
- Han, J.; Kim, J. Three-dimensional reconstruction of a marine floating structure with an unmanned surface vessel. IEEE J. Ocean. Eng. 2018, 44, 984–996. [Google Scholar] [CrossRef]
- Krasnosky, K.; Roman, C. A massively parallel implementation of Gaussian process regression for real time bathymetric modeling and simultaneous localization and mapping. Field Robot. 2022, 2, 940–970. [Google Scholar] [CrossRef]
- Torroba, I.; Sprague, C.I.; Bore, N.; Folkesson, J. PointNetKL: Deep inference for GICP covariance estimation in bathymetric SLAM. IEEE Robot. Autom. Lett. 2020, 5, 4078–4085. [Google Scholar] [CrossRef]
- Tan, J.; Torroba, I.; Xie, Y.; Folkesson, J. Data-driven loop closure detection in bathymetric point clouds for underwater slam. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3131–3137. [Google Scholar]
- Constantinoiu, L.F.; Bernardino, M.; Rusu, E. Autonomous Shallow Water Hydrographic Survey Using a Proto-Type USV. J. Mar. Sci. Eng. 2023, 11, 799. [Google Scholar] [CrossRef]
- Ling, Y.; Li, Y.; Ma, T.; Cong, Z.; Xu, S.; Li, Z. Active Bathymetric SLAM for autonomous underwater exploration. Appl. Ocean Res. 2023, 130, 103439. [Google Scholar] [CrossRef]
- Khan, M.U.; Zaidi, S.A.A.; Ishtiaq, A.; Bukhari, S.U.R.; Samer, S.; Farman, A. A comparative survey of lidar-slam and lidar based sensor technologies. In Proceedings of the 2021 Mohammad Ali Jinnah University International Conference on Computing (MAJICC), Karachi, Pakistan, 15–17 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8. [Google Scholar]
- Ribeiro, M.I. Kalman and extended kalman filters: Concept, derivation and properties. Inst. Syst. Robot. 2004, 43, 3736–3741. [Google Scholar]
- Krasnosky, K.; Roman, C.; Casagrande, D. A bathymetric mapping and SLAM dataset with high-precision ground truth for marine robotics. Int. J. Robot. Res. 2022, 41, 12–19. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, B.; Li, J.; Xu, Y. Map Boundary Optimization Based on Adaptive Iterative Extended Kalman Filter. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2979–2983. [Google Scholar]
- Xu, W.; Zhang, F. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Koide, K.; Yokozuka, M.; Oishi, S.; Banno, A. Voxelized gicp for fast and accurate 3d point cloud registration. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 11054–11059. [Google Scholar]
- Kam, H.R.; Lee, S.H.; Park, T.; Kim, C.H. Rviz: A toolkit for real domain data visualization. Telecommun. Syst. 2015, 60, 337–345. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. CloudCompare. In Proceedings of the 2nd International Workshop on Point Cloud Processing, Stuttgart, Germany, 4–5 December 2019; Available online: https://www.eurosdr.net/sites/default/files/images/inline/04-cloudcompare_pcp_2019_public.pdf (accessed on 9 July 2024).
- Schubert, D.; Goll, T.; Demmel, N.; Usenko, V.; Stückler, J.; Cremers, D. The TUM VI benchmark for evaluating visual-inertial odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1680–1687. [Google Scholar]
- Teng, M.; Ye, L.; Yuxin, Z.; Yanqing, J.; Qianyi, Z.; Pascoal, A.M. Efficient bathymetric SLAM with invalid loop closure identification. IEEE/ASME Trans. Mechatron. 2020, 26, 2570–2580. [Google Scholar] [CrossRef]











| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Length | 236 mm | Height | 316 mm |
| Width | 181 mm | Weight | 10.9 kg |
| Min. frequency | 400 kHz | Min.depth | 1 m |
| Max. frequency | 700 kHz | Max.depth | 200 m |
| Pulse width | 10 s–800 s | Ping rate | 50 Hz |
| Across-track Beam width | 1° | Along-track Beam width | 1° |
| Number of Beams | 256/512 (Equiangular/Equidistant) | Opening angle | 10°–180° |
| Interface | RS232/TSS1/NMEA0183 | IMU-supported | External |
| Parameters | Value |
|---|---|
| Heading accuracy (RMS) | 0.05° (Dynamic alignment of a single antenna); 0.1° (Low dynamic auxiliary with dual antennas, 2 m baseline) |
| Pitch/Roll accuracy | 0.01° (1 ) |
| Velocity accuracy | 0.02 m/s |
| Position accuracy: Single point | 3 m (1 ) |
| RTK | 2 cm + 1 ppm (1 ) |
| Gyroscope measurement range | 500°/s |
| Gyroscope zero bias stability | 0.1°/h |
| Accelerometer measurement range | 20 g |
| Accelerometer zero bias stability | 20 g |
| Maximum speed | 500 m/s |
| Command | Range | Description |
|---|---|---|
| set_mode | 0–2 | 0 = by range 1 = by depth 2 = by range and depth |
| set_opening_angle | 10–180 | Set opening angle in degrees. |
| set_range | 0–200 | Start and stop range/depth in meters |
| set_tx_freq | 400–700 | Set tx-pulse frequency in kHz |
| set_tx_amp | 0–15 | Set tx-pulse amplitude |
| Topic | Message | Type |
|---|---|---|
| odom | nav_msgs/Odometry | Subscribed |
| nav_gpsfix | sensor_msgs/NavSatFix | Subscribed |
| imu_raw | sensor_msgs/Imu | Subscribed |
| MBES_scan | sensor_msgs/PointCloud2 | Subscribed |
| cloud_map | sensor_msgs/PointCloud2 | Published |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Frequency | 400 khz | Range | 20 m |
| Pulse width | 240 s | Transmission amplitude | 7 |
| Sound velocity | 1486 m/s | Bandwidth | 80 kHz |
| Near-field Threshold | 1 | Beamwidth | 150 |
| Target | Placement Longitude | Placement Latitude | Depth | Is Discernible in This Experiment |
|---|---|---|---|---|
| Human-shaped model | 108.42743301 | 34.52545100 | 8.17 m | YES |
| Cylinder | 108.42626401 | 34.52634600 | 10.12 m | NO |
| Cube | 108.42716101 | 34.52620700 | 8.90 m | YES |
| Method | ATE (m) | Trajectory Error at Turns (m) | Trajectory Error of Straight-Line Driving (m) | Average Registration Error (m) | Location Error of Human-Shaped Model (m) | Location Error of Cube (m) |
|---|---|---|---|---|---|---|
| HydroMaster | 14.65 | 15.17 | 14.57 | × 1 | 3.89 | 5.50 |
| EKF | 16.91 | 17.75 | 16.67 | × | 4.35 | 6.31 |
| iEKF | 15.10 | 16.81 | 14.93 | × | 3.96 | 5.63 |
| EKF + GICP | 15.38 | 15.71 | 15.25 | 1.34 | 4.23 | 6.17 |
| iEKF + GICP(ours) | 13.74 | 14.03 | 13.57 | 0.97 | 3.77 | 5.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Tan, T.; Hou, X.; Zhao, L.; Cao, C.; Wang, Z. Underwater Mapping and Optimization Based on Multibeam Echo Sounders. J. Mar. Sci. Eng. 2024, 12, 1222. https://doi.org/10.3390/jmse12071222
Zhang F, Tan T, Hou X, Zhao L, Cao C, Wang Z. Underwater Mapping and Optimization Based on Multibeam Echo Sounders. Journal of Marine Science and Engineering. 2024; 12(7):1222. https://doi.org/10.3390/jmse12071222
Chicago/Turabian StyleZhang, Feihu, Tingfeng Tan, Xujia Hou, Liang Zhao, Chun Cao, and Zewen Wang. 2024. "Underwater Mapping and Optimization Based on Multibeam Echo Sounders" Journal of Marine Science and Engineering 12, no. 7: 1222. https://doi.org/10.3390/jmse12071222
APA StyleZhang, F., Tan, T., Hou, X., Zhao, L., Cao, C., & Wang, Z. (2024). Underwater Mapping and Optimization Based on Multibeam Echo Sounders. Journal of Marine Science and Engineering, 12(7), 1222. https://doi.org/10.3390/jmse12071222






