Fuzzy Fault Detection Observer Design for Unmanned Marine Vehicles Based on Membership-Function-Dependent H_∞/H_ Performance

Abstract

This paper studies the design problem of fault detection (FD) observer for unmanned marine vehicles (UMVs) based on the T-S fuzzy model. Firstly, T-S fuzzy systems are used to approximate the nonlinear dynamics in UMVs. Secondly, to improve the FD performance of UMVs, a new $H_{\infty }/H\_$ performance index, which depends on the membership functions, is defined. Then, based on the membership-function-dependent $H_{\infty }/H\_$ performance index, a new fuzzy FD observer strategy, where the fuzzy submodels are not all required to be with the same $H\_$ performance index, is developed to detect the sensor fault in UMVs; the corresponding synthesis conditions of the FD observer are derived based on the Lyapunov theory. Different from the conventional FD strategies, in the proposed membership-function-dependent FD method, the fuzzy submodels—which the system always works on—can have a larger $H\_$ performance index, such that the performance of the FD can be improved. In the end, an example is given to show the effectiveness of the presented method.

1. Introduction

As effective tools for ocean exploration and environmental monitoring, UMVs have received increasing attention in recent years [1,2,3,4,5,6,7] and significant progress has been made in the domain of UMVs. However, due to the complex ocean environment, UMVs are prone to failure [8], which hinders the further development of UMV technology. Failure has an adverse influence on UMVs, where it can decrease the performance of UMVs or even cause irreversible damage to their systems [9]. Therefore, it is necessary to study the FD problem for UMVs to detect faults occurring in the systems in a timely way, such that the safety and reliability of UMVs can be guaranteed.

However, achieving FD for UMVs is not an easy task. There exists strong nonlinear coupling between the interval variables of UMVs, such as the yaw angle and surge velocity. This will increase the difficulties in FD for UMVs. Fortunately, the T-S fuzzy system is a powerful tool to approximate nonlinear dynamics and has been widely used to deal with analysis and design problems for nonlinear engineering systems [10,11,12,13,14]. Therefore, it is promising to use the T-S fuzzy systems method to handle the nonlinear FD problem for UMVs. During the past few years, many researchers have devoted themselves to studying the FD problem in T-S fuzzy systems and many interesting FD results have been reported [15,16,17,18]. To mention a few, in [15], a switching-type FD filter is proposed for T-S fuzzy systems with unknown membership functions and, by using the switching mechanism which depends on the bound of unknown membership functions, the design of the FD observer is relaxed. In [16], the FD problem for T-S fuzzy systems in finite frequency is considered and the differential mean value theorem is used to reduce the conservatism of the FD observer design. A new fault isolation scheme is proposed for T-S fuzzy systems in [17], where false alarms caused by using incorrect sensor measurement information can be effectively avoided. Based on operator and input–output methods, the authors of [18] address the FD problem for T-S fuzzy systems with time delay. Although the theoretical study of the FD problem in T-S fuzzy systems has attained considerable development, the research in the FD of UMVs based on T-S fuzzy systems is still not sufficient, which is one of the motivations of this paper.

Another motivation of this paper is that there is still some space to improve the existing nonlinear FD methods based on T-S fuzzy systems. In some existing methods [19,20,21], the $H_{\infty }/H\_$ performance analysis method is considered to synthesize the FD observer. By optimizing the $H\_$ performance index, an optimal or sub-optimal FD performance can be obtained. However, the $H\_$ performance index in conventional FD schemes is considered to be constant, which may lead to some conservatism. The reason is that, due to the property that the $H\_$ performance index $\beta$ is constant, all the synthesis conditions of the FD observer, which are formulated in terms of linear matrix inequalities (LMIs), should be solvable on the basis of the common performance index $\beta$. In other words, all the subsystems of the T-S fuzzy system should satisfy the same FD performance no matter which subsystems the overall fuzzy system works on. However, in real applications, the fuzzy system always works on one certain fuzzy subsystem. If all the subsystems are still required to satisfy the same performance index $\beta$, it may increase the conservatism of the design.

To address the above problem, a membership-function-dependent performance analysis method is proposed in [22]. In [22], the robust control problem is considered and the robust performance index $\gamma$ is designed to depend on the membership functions. Then, the i-th fuzzy submodel corresponds to the performance index ${\gamma }_i$. By assuming that T-S fuzzy systems always work on a pre-specified subsystem, such as $A_1$, the value of index ${\gamma }_1$ is set as the smallest one. Then, if the system works on $A_1$ in practice, the robust performance index of the overall fuzzy systems will be the smallest so as to increase the robustness of the controller. However, there are still some problems to be addressed even if the membership-function-dependent performance analysis method is considered. In some cases, it is hard to determine that the system works on a certain subsystem even if the state of the system is limited to a local area. For example, consider the system with the membership functions $h_1={\displaystyle \frac{1+sin\left(x\left(t\right)\right)}{2}}$ and $h_2={\displaystyle \frac{1+sin\left(x\left(t\right)\right)}{2}}$; when the state $x\left(t\right)=0$, i.e., it is at equilibrium, then the dynamic of the T-S fuzzy system becomes $\dot{x}\left(t\right)=(0.5A_1+0.5A_2)x\left(t\right)$, which indicates that the system cannot work on subsystems $A_1$ or $A_2$. Therefore, whether we can establish a new membership-function-dependent index, which can not only improve the FD performance but also remove the aforementioned constraint, is an interesting problem, which is also another motivation of this paper.

In view of the above discussion, a membership-function-dependent FD observer scheme is proposed for UMVs based on T-S fuzzy systems. The design mainly focuses on how to take advantage of a membership-function-dependent performance index to improve the FD performance of UMVs. The contributions of the paper are listed as follows:

(1)

Inspired by the literature [22], a new membership-function-dependent $H_{\infty }/H\_$ FD strategy is proposed for UMVs in this paper. In the method developed, the fuzzy submodels, in which the system always works, can have a larger $H\_$ performance index; then, the property that the state of the system is limited to a local area can be fully made use of such that the FD performance for UMVs can be improved.

(2)

Motivated by set theory description [17], the FD performance index is designed to depend on the membership functions, which can take a relatively large value when the state is limited to a local area. Consequently, the FD performance can be improved as long as the state of the system is limited to a local area. Then, the constraint that the fuzzy systems are required to work on a certain subsystem in [22] can be removed by the proposed method.

The rest of the paper is organized as follows: In Section 2, the dynamic of UMVs is modeled by T-S fuzzy models. A membership-function-dependent $H_{\infty }/H\_$ FD observer scheme is proposed in Section 3. The sufficient conditions of the existence of the FD observer are presented in Section 4. In Section 5, an example is given to demonstrate the efficiency of the proposed FD strategies. Section 6 draws the conclusion.

Notation: For a matrix X, $X^T$ and $X^{-1}$ denote the transpose and inverse of the matrix X, respectively, and $He\left(X\right)=X+X^T$; $X>0$ denotes that the matrix X is positive definite. O and I represent zero matrix and identity matrix, respectively. The symbol “∗” in LMIs is the term which is induced by symmetry.

2. System Description

UMVs T-S Modeling

Following the work in [4], the mathematical model of UMVs is described as

$$\left\{\begin{array}{c}M\dot{\nu }\left(t\right)+N\nu \left(t\right)+G\phi \left(t\right)=u\left(t\right)+\omega \left(t\right)\hfill \\ \dot{\phi }\left(t\right)=\Omega \left(\psi \left(t\right)\right)\nu \left(t\right)\hfill \end{array}\right.$$

(1)

where $\nu \left(t\right)={\left[\rho \left(t\right)\upsilon \left(t\right)r\left(t\right)\right]}^T$ is the velocity vector in the body-fixed frame and its components $\rho \left(t\right)$, $\upsilon \left(t\right)$ and $r\left(t\right)$ represent the surge velocity, sway velocity, and yaw velocity, respectively; $\phi \left(t\right)={\left[\overline{x}\left(t\right)\overline{y}\left(t\right)\psi \left(t\right)\right]}^T$ is the earth-fixed orientation vector consisting of the components $\overline{x}\left(t\right)$ and $\overline{y}\left(t\right)$ and $\psi \left(t\right)$, which are the positions and yaw angle, respectively. The control input vector of UMVs is denoted by $u\left(t\right)={\left[u_1\left(t\right)u_2\left(t\right)u_3\left(t\right)\right]}^T$; $\omega \left(t\right)$ denotes the wave-induced disturbance signal; M represents the matrix of inertia and it is invertible satisfying $M=M^T>0$; N and G denote damping matrix and mooring force, respectively; $\Omega \left(\psi \right(t\left)\right)$, G, M, and N have the following form:

$$\begin{array}{cc}\hfill M=& \left[\begin{array}{ccc}{m}_{11}& 0& 0\\ 0& m_{22}& m_{23}\\ 0& m_{32}& m_{33}\end{array}\right],N=\left[\begin{array}{ccc}{n}_{11}& 0& 0\\ 0& n_{22}& n_{23}\\ 0& n_{32}& n_{33}\end{array}\right],\hfill \\ \hfill \Omega \left(\psi \right(t\left)\right)=& \left[\begin{array}{ccc}\cos \left(\psi \right(t\left)\right)& -\sin \left(\psi \right(t\left)\right)& 0\\ \sin \left(\psi \right(t\left)\right)& \cos \left(\psi \right(t\left)\right)& 0\\ 0& 0& 1\end{array}\right],G=\left[\begin{array}{ccc}{g}_{11}& 0& 0\\ 0& g_{22}& 0\\ 0& 0& g_{33}\end{array}\right].\hfill \end{array}$$

(2)

Let

$$\begin{array}{ccc}\hfill A& =-M^{-1}G=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right],B=-M^{-1}N=\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ b_{31}& b_{32}& b_{33}\end{array}\right],D\hfill & \hfill =M^{-1}=\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array}\right].\end{array}$$

Then, the system (1) becomes

$$\begin{array}{cc}\hfill & \dot{\nu }\left(t\right)=A\phi \left(t\right)+B\nu \left(t\right)+Du\left(t\right)+D\omega \left(t\right)\hfill \\ \hfill & \dot{\phi }\left(t\right)=\Omega \left(\psi \left(t\right)\right)\nu \left(t\right)\hfill \end{array}$$

(3)

Define $x\left(t\right)={\left[x_1\left(t\right)x_2\left(t\right)x_3\left(t\right)x_4\left(t\right)x_5\left(t\right)x_6\left(t\right)\right]}^T={\left[\overline{x}\left(t\right)\overline{y}\left(t\right)\psi \left(t\right)\rho \left(t\right)\upsilon \left(t\right)r\left(t\right)\right]}^T$ and taking (3) into consideration, the state equations of (3) are described by:

$$\begin{array}{cc}\hfill {\dot{x}}_1\left(t\right)=& \cos \left(x_3\left(t\right)\right)x_4\left(t\right)-\sin \left(x_3\left(t\right)\right)x_5\left(t\right)\hfill \\ \hfill {\dot{x}}_2\left(t\right)=& \sin \left(x_3\left(t\right)\right)x_4\left(t\right)+\cos \left(x_3\left(t\right)\right)x_5\left(t\right)\hfill \\ \hfill {\dot{x}}_3\left(t\right)=& x_6\left(t\right)\hfill \\ \hfill {\dot{x}}_4\left(t\right)=& a_{11}{x}_1\left(t\right)+a_{12}{x}_2\left(t\right)+a_{13}{x}_3\left(t\right)+b_{11}{x}_4\left(t\right)+b_{12}{x}_5\left(t\right)+b_{13}{x}_6\left(t\right)\hfill \\ \hfill & +d_{11}{u}_1\left(t\right)+d_{12}{u}_2\left(t\right)+d_{13}{u}_3\left(t\right)+d_{11}{\omega }_1\left(t\right)+d_{12}{\omega }_2\left(t\right)+d_{13}{\omega }_3\left(t\right)\hfill \\ \hfill {\dot{x}}_5\left(t\right)=& a_{21}{x}_1\left(t\right)+a_{22}{x}_2\left(t\right)+a_{23}{x}_3\left(t\right)+b_{21}{x}_4\left(t\right)+b_{22}{x}_5\left(t\right)+b_{23}{x}_6\left(t\right)\hfill \\ \hfill & +d_{21}{u}_1\left(t\right)+d_{22}{u}_2\left(t\right)+d_{23}{u}_3\left(t\right)+d_{21}{\omega }_1\left(t\right)+d_{22}{\omega }_2\left(t\right)+d_{23}{\omega }_3\left(t\right)\hfill \\ \hfill {\dot{x}}_6\left(t\right)=& a_{31}{x}_1\left(t\right)+a_{32}{x}_2\left(t\right)+a_{33}{x}_3\left(t\right)+b_{31}{x}_4\left(t\right)+b_{32}{x}_5\left(t\right)+b_{33}{x}_6\left(t\right)\hfill \\ \hfill & +d_{31}{u}_1\left(t\right)+d_{32}{u}_2\left(t\right)+d_{33}{u}_3\left(t\right)+d_{31}{\omega }_1\left(t\right)+d_{32}{\omega }_2\left(t\right)+d_{33}{\omega }_3\left(t\right)\hfill \end{array}$$

(4)

It is assumed that the yaw angle $\psi \left(t\right)$, i.e., $x_3\left(t\right)$ varies in the interval $[\underline{\psi },\overline{\psi }]$, where $\overline{\psi }>0$ and $\underline{\psi }>0$ represent the upper and lower bounds of $\psi \left(t\right)$, respectively. Select the premise variables as ${\chi }_1\left(t\right)=\sin \left(x_3\left(t\right)\right)$, ${\chi }_2\left(t\right)=\cos \left(x_3\left(t\right)\right)$, where ${\chi }_1\left(t\right)\in [{\underline{\chi }}_1,{\overline{\chi }}_1]$ and ${\chi }_2\left(t\right)\in [{\underline{\chi }}_2,{\overline{\chi }}_2]$. Then, the fuzzy rules of T-S fuzzy models of UMVs are given by

Plant Rule i: IF ${\chi }_1\left(t\right)$ is $M_{i1}$ and ${\chi }_2\left(t\right)$ is $M_{i2}$

Then

$$\left\{\begin{array}{cc}\hfill \dot{x}& \left(t\right)={\tilde{A}}_{i}x\left(t\right)+\overline{D}u\left(t\right)+\overline{D}\omega \left(t\right)\hfill \\ \hfill y& \left(t\right)=Cx\left(t\right)+Ff\left(t\right)\hfill \end{array}\right.$$

(5)

where ${\chi }_1\left(t\right)=\sin \left(x_3\left(t\right)\right)$ and ${\chi }_2\left(t\right)=\cos \left(x_3\left(t\right)\right)$ are premise variables; $M_{i1}$ and $M_{i2}$ ($i\in \{1,2,3,4\}$) denote fuzzy sets; $y\left(t\right)$ and $f\left(t\right)$ represent the measured output and the sensor faults, respectively; $\overline{D}$, F, and C are known real constant matrices with compatible dimensions;

$$\begin{array}{cc}\hfill {\mathcal{A}}_1=& \left[\begin{array}{ccc}{\overline{\chi }}_2& -{\overline{\chi }}_1& 0\\ {\overline{\chi }}_1& {\overline{\chi }}_2& 0\\ 0& 0& 1\end{array}\right],{\mathcal{A}}_2=\left[\begin{array}{ccc}{\underline{\chi }}_2& -{\overline{\chi }}_1& 0\\ {\overline{\chi }}_1& {\underline{\chi }}_2& 0\\ 0& 0& 1\end{array}\right],{\tilde{A}}_i=\left[\begin{array}{cc}{0}_{3\times 3}& {\mathcal{A}}_i\\ A& B\end{array}\right],\hfill \\ \hfill {\mathcal{A}}_3=& \left[\begin{array}{ccc}{\overline{\chi }}_2& -{\underline{\chi }}_1& 0\\ {\underline{\chi }}_1& {\overline{\chi }}_2& 0\\ 0& 0& 1\end{array}\right],{\mathcal{A}}_4=\left[\begin{array}{ccc}{\underline{\chi }}_2& -{\underline{\chi }}_1& 0\\ {\underline{\chi }}_1& {\underline{\chi }}_2& 0\\ 0& 0& 1\end{array}\right],\overline{D}=\left[\begin{array}{c}{0}_{3\times 3}\\ D\end{array}\right].\hfill \end{array}$$

By virtue of the standard T-S modeling process [23], the overall T-S fuzzy models can be derived as follows:

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\sum _{i=1}^4{g}_i\left(\chi \left(t\right)\right)\left[{\tilde{A}}_{i}x\left(t\right)+\overline{D}u\left(t\right)+\overline{D}\omega \left(t\right)\right]\hfill \\ \hfill y\left(t\right)& =Cx\left(t\right)+Ff\left(t\right)\hfill \end{array}\right.$$

(6)

where

$$\begin{array}{cc}\hfill g_i\left(\chi \left(t\right)\right)& ={\displaystyle \frac{{\vartheta }_i\left(\chi \left(t\right)\right)}{{\displaystyle \sum _{j=1}^4}{\vartheta }_j\left(\chi \left(t\right)\right)}}\ge 0,\chi ={\left[\begin{array}{cc}{\chi }_1& {\chi }_2\end{array}\right]}^T,\hfill \\ \hfill {\vartheta }_i\left(\chi \left(t\right)\right)& =M_{i1}\left({\chi }_1\left(t\right)\right)M_{i2}\left({\chi }_2\left(t\right)\right),\sum _{i=1}^4{g}_i\left(\chi \left(t\right)\right)=1.\hfill \end{array}$$

For further development, the T-S fuzzy system (6) is rewritten as

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& \sum _{i=1}^2\sum _{j=1}^2{h}_i\left(t\right){\lambda }_j\left(t\right)\left(A_{ij}x\left(t\right)+\overline{D}u\left(t\right)+\overline{D}\omega \left(t\right)\right)\hfill \\ \hfill y\left(t\right)=& Cx\left(t\right)+Ff\left(t\right)\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill h_1\left(t\right)=& {\displaystyle \frac{1+2sin\left(x_3\left(t\right)\right)}{2}},h_2\left(t\right)={\displaystyle \frac{1-2sin\left(x_3\left(t\right)\right)}{2}},A_{11}={\tilde{A}}_1,A_{12}={\tilde{A}}_2,g_1=h_1{\lambda }_1,g_2=h_1{\lambda }_2,\hfill \\ \hfill {\lambda }_1\left(t\right)=& {\displaystyle \frac{2cos\left(x_3\left(t\right)\right)-\sqrt{3}}{2-\sqrt{3}}},{\lambda }_2\left(t\right)={\displaystyle \frac{2-2cos\left(x_3\left(t\right)\right)}{2-\sqrt{3}}}{A}_{21}={\tilde{A}}_3,A_{22}={\tilde{A}}_4,g_3=h_2{\lambda }_1,g_4=h_2{\lambda }_2.\hfill \end{array}$$

Remark 1.

Motivated by the set theory [24], the T-S fuzzy system (6) is transformed into the equivalent model (7). The purpose of above-mentioned transformation is to take advantage of the property where the state of the system stays in local areas to improve the FD performance. A detailed discussion will be given in Remark 5.

3. Fault Detection Observer Design

3.1. Quantization Description

Due to the limitation of the communication resources of the network, the output of the system $y\left(t\right)$ should be quantized before it is transmitted. In this paper, logarithmic quantizer [25] is selected to quantize the output signal $y\left(t\right)$. Furthermore, the logarithmic quantizer has the following form:

$$\begin{array}{c}\hfill q\left(y\right)={\left[\begin{array}{c}{q}_1\left(y\right),\dots ,q_{n_y}\left(y\right)\end{array}\right]}^T\end{array}$$

(8)

The set of quantization level of each $q_i(.)$ is defined as

$$\begin{array}{c}\hfill U_i=\{\pm {\varpi }_i:{\varpi }_i={\overline{\rho }}^i{\varpi }_0,i=0,\pm 1,\pm 2,\dots \}\cup \{\pm {\varpi }_0\}\cup \left\{0\right\}\end{array}$$

(9)

where ${\overline{\rho }}^i\in (0,1)$, ${\varpi }_0>0$; ${\overline{\rho }}^i$ is called the quantization density.

The quantization function $q(.)$ is

$$q\left(y\right)=\left\{\begin{array}{cc}\hfill {\varpi }_i,if& {\displaystyle \frac{1}{1+\delta }}{\varpi }_i\le y\le {\displaystyle \frac{1}{1-\delta }}{\varpi }_i,\hfill \\ \hfill 0,if& y=0,\hfill \\ \hfill -q(-y)if& y<0,\hfill \end{array}\right.$$

where $\delta ={\displaystyle \frac{1-\overline{\rho }}{1+\overline{\rho }}}$.

Then, refer to the sector bounded method [25]; the output $y\left(t\right)$ with quantization is given by

$$\begin{array}{c}\hfill \overline{y}\left(t\right)=q\left(y\right)=(I+{▵}_y)y\left(t\right)\end{array}$$

(10)

where

$$\begin{array}{c}\hfill {\Delta }_y=diag\{{\Delta }_1,{\Delta }_2,\dots ,{\Delta }_{n_y}\},-{\overline{\tau }}_i\le {\Delta }_i\le {\overline{\tau }}_i(i=1,\dots ,n_y)\end{array}$$

Clearly, ${\Delta }_y$ satisfies

$$\begin{array}{c}\hfill |{\Delta }_y|\le \tilde{\tau }I\end{array}$$

(11)

where $\tilde{\tau }=max\{{\overline{\tau }}_1,{\overline{\tau }}_2,\dots ,{\overline{\tau }}_{n_y}\}$.

3.2. FD Observer Scheme

In this paper, consider the case that the output–feedback controller has been pre-designed by designers. Furthermore, the controller has the following form:

$$\begin{array}{c}\hfill u\left(t\right)=K\overline{y}\left(t\right)\end{array}$$

(12)

where K is the controller gain matrix to be determined.

Then substituting the control law (12) into the system dynamic (7), the following closed-loop control system can be obtained:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& \sum _{i=1}^m\sum _{j=1}^n{h}_i\left(t\right){\lambda }_j\left(t\right)\left[\left({\overline{A}}_{ij}+\mathsf{\Lambda }\Delta C\right)x\left(t\right)+\overline{D}\omega \left(t\right)+\mathsf{\Lambda }(I+\Delta )Ff\left(t\right)\right]\hfill \\ \hfill y\left(t\right)=& Cx\left(t\right)+Ff\left(t\right)\hfill \end{array}$$

(13)

where ${\overline{A}}_{ij}=A_{ij}+\overline{D}K,\mathsf{\Lambda }=\overline{D}K$.

Remark 2.

In this paper, we mainly focus on the design of FD observer and the controller synthesis problem is not main concern of this paper. Thus, in this paper, it is assumed that the controller has been designed previously. Indeed, to realize the design of the controller, the reader can refer to some effective control design strategies such as [25,26].

In this subsection, a membership-function-dependent $H_{\infty }/H\_$ FD observer will be designed.

Based on the closed-loop system (13), an FD observer is proposed as follows:

$$\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)=& \sum _{i=1}^m\sum _{j=1}^n{\overline{h}}_i\left(t\right){\overline{\lambda }}_j\left(t\right)\left({\overline{A}}_{ij}\widehat{x}\left(t\right)+L_{ij}\left(\overline{y}\left(t\right)-\widehat{\overline{y}}\left(t\right)\right)\right)\hfill \\ \hfill \widehat{\overline{y}}\left(t\right)=& C\widehat{x}\left(t\right)\hfill \\ \hfill \overline{r}\left(t\right)=& \overline{y}\left(t\right)-\widehat{\overline{y}}\left(t\right)\hfill \end{array}$$

(14)

where $\widehat{x}\left(t\right)$ and $\widehat{\overline{y}}\left(t\right)$ are the estimations of the state and the output, respectively; $L_{ij}$ ($i\in \{1,\dots ,m\},j\in \{1,\dots ,n\}$) is the FD observer gain matrix to be designed subsequently; $\overline{r}\left(t\right)$ is the residual signal.

Remark 3.

Since the premise variables of the FD observer (14) depend on the quantized signal $\overline{y}\left(t\right)$, the symbol ${\overline{h}}_i\left(t\right){\overline{\lambda }}_j\left(t\right)$ is used to represent the premise variables of the FD observer.

Then, based on the FD observer (14) and the closed-loop system (13), the following state estimation error dynamic can be obtained:

$$\begin{array}{cc}\hfill \dot{\eta }\left(t\right)=& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i\left(t\right){\lambda }_j\left(t\right){\overline{h}}_k\left(t\right){\overline{\lambda }}_l\left(t\right)\left[{\tilde{A}}_{ijkl}\eta \left(t\right)+\tilde{D}\omega \left(t\right)+{\tilde{G}}_{kl}f\left(t\right)\right]\hfill \\ \hfill \overline{r}\left(t\right)=& \tilde{C}\eta \left(t\right)+\tilde{F}f\left(t\right)\hfill \end{array}$$

(15)

where $\tilde{F}=\left(I+{\Delta }_y\right)F$, $\tilde{D}={\left[\begin{array}{cc}{\overline{D}}^T& {\overline{D}}^T\end{array}\right]}^T$, $\tilde{C}=\left[\begin{array}{cc}{\Delta }_{y}C& C\end{array}\right]$, $\eta \left(t\right)={\left[\begin{array}{cc}{x}^T\left(t\right)& e^T\left(t\right)\end{array}\right]}^T$,

$$\begin{array}{c}\hfill {\tilde{A}}_{ijkl}=\left[\begin{array}{cc}{\overline{A}}_{ij}+\mathsf{\Lambda }{\Delta }_{y}C& 0\\ {\overline{A}}_{ij}-{\overline{A}}_{kl}-L_{kl}{\Delta }_{y}C& {\overline{A}}_{ij}-L_{kl}C\end{array}\right],{\tilde{G}}_{kl}=\left[\begin{array}{c}\mathsf{\Lambda }\left(I+{\Delta }_y\right)F\\ \mathsf{\Lambda }\left(I+{\Delta }_y\right)F-L_{kl}\left(I+{\Delta }_y\right)F\end{array}\right].\end{array}$$

For simplicity, let $h_i=h_i\left(t\right)$, ${\lambda }_k={\lambda }_k\left(t\right)$, ${\overline{h}}_l={\overline{h}}_l\left(t\right)$, ${\overline{\lambda }}_j={\overline{\lambda }}_j\left(t\right)$.

To increase the performance of FD observer, the membership-function-dependent $H_{\infty }/H\_$ performance index is considered and the corresponding definitions are given as follows:

Definition 1.

The error dynamic system (15) is said to be with a membership-function-dependent $H\_$ performance index $\overline{\overline{\beta }}\left(\lambda \right)$, if the following condition is satisfied $\forall x\left(t\right)\in \Gamma$

$$\begin{array}{c}\hfill {\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds\ge {\overline{\overline{\beta }}}^2\left(\lambda \right){\int }_0^t{f}^T\left(s\right)f\left(s\right)ds\end{array}$$

(16)

where $\overline{\overline{\beta }}\left(\lambda \right)=min\left(\overline{\beta }\right)$ and $\overline{\beta }=\sqrt{\sigma {\lambda }_1+{\displaystyle \sum _{i=2}^n}{\lambda }_i}\beta$; $\sigma >1$ is a scalar to be optimized and $\beta >0$ is a given scalar; $\Gamma =\left\{x\left|\right||{\lambda }_1\left(x\right)\left|\right|>\kappa \right\}$ and $\kappa >0$.

Definition 2.

The error dynamic system (15) is said to be with an $H_{\infty }$ performance index γ, if the following inequality holds:

$$\begin{array}{c}\hfill {\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds\le {\gamma }^2{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds\end{array}$$

(17)

where $\gamma >0$ is a given scalar.

Remark 4.

It can be learned from (16) that $\overline{\overline{\beta }}$ depends on $\overline{\beta }$. When the state of the system is in the pre-specific local areas, the difference between $\overline{\beta }$ and $\overline{\overline{\beta }}$ is not big. Thus, we mainly discuss $\overline{\beta }$ instead of $\overline{\overline{\beta }}$ and serve the scalar $\overline{\beta }$ as the index reflecting the FD performance.

Remark 5.

Noted that in the condition (16), the $H\_$ performance index depends on the membership functions ${\lambda }_j$ rather than $h_i{\lambda }_j$. The purpose of the design is to handle with the problem where the fuzzy system cannot work on a certain subsystem. For example, on basis of the fuzzy model (6), if we consider the membership-function-dependent performance index in [22], then we have

$$\begin{array}{cc}\hfill {\overline{\beta }}^2\left(\lambda \right)=& \left(\sigma h_1{\lambda }_1+h_1{\lambda }_2+h_2{\lambda }_1+h_2{\lambda }_2\right){\beta }^2\hfill \\ \hfill =& \left(\sigma {\displaystyle \frac{1+2sin\left({\xi }_3\right)}{2}}{\displaystyle \frac{\left(2cos\left({\xi }_3\right)-\sqrt{3}\right)}{2-\sqrt{3}}}\right){\beta }^2+\left({\displaystyle \frac{1+2sin\left({\xi }_3\right)}{2}}{\displaystyle \frac{\left(2-2cos\left({\xi }_3\right)\right)}{2-\sqrt{3}}}\right){\beta }^2\hfill \\ \hfill & +\left({\displaystyle \frac{1-2sin\left({\xi }_3\right)}{2}}{\displaystyle \frac{\left(2cos\left({\xi }_3\right)-\sqrt{3}\right)}{2-\sqrt{3}}}\right){\beta }^2+\left({\displaystyle \frac{1-2sin\left({\xi }_3\right)}{2}}{\displaystyle \frac{\left(2-2cos\left({\xi }_3\right)\right)}{2-\sqrt{3}}}\right){\beta }^2.\hfill \end{array}$$

(18)

It can be known from (18) that it is difficult for (6) to work on the subsystem $A_{11}$ because the corresponding membership function $h_1{\lambda }_1$ cannot takes value 1. As a result, obtaining a large index $\overline{\beta }$ is difficult. To deal with the above-mentioned problem, a new performance index is proposed in (16). Obviously, the proposed index can take a relative large value as long as the state of the system stays at some local area. For example, when the system state is in the area nearby the equilibrium point, then the term $\sigma {\lambda }_1={\displaystyle \frac{\sigma (2cos\left({\xi }_3\right)-\sqrt{3})}{2-\sqrt{3}}}$ will be large while the other term $h_1{\lambda }_2+h_2{\lambda }_1+h_2{\lambda }_2$ are small which is helpful for improving the performance index $\overline{\beta }$. Based on the previous discussion, the membership functions, which can be selected as ${\lambda }_j$, should take a relatively large value when the state of the system is in the local objective area.

Remark 6.

It should be pointed out that, in the conditions (16) and (17), the $H\_$ performance index depends on the membership functions while $H_{\infty }$ performance index is a constant. Then, by fixing γ, the parameter $\overline{\beta }$ is optimized to improve the fault sensitivity of the residual signal to the fault. Compared with the performance index where γ and $\overline{\beta }$ both depend on the membership functions, less parameters are required to be optimized in the performance index (16) and (17), such that the analysis and design can be simplified.

3.3. Problem Formulation

The objective of this paper is to design the FD observer (14) such that the error dynamic system (15) satisfy the following requirements:

(1)

When $d\left(t\right)=0$, the error dynamic system (15) is asymptotically stable.

(2)

The error dynamic system (15) has an $H_{\infty }$ performance index $\gamma$ and has a membership-function-dependent $H\_$ performance index $\overline{\overline{\beta }}\left(\lambda \right)$.

For the development of the subsequent results, some useful assumptions and lemmas are given.

Assumption 1.

The state of the system (13) belongs to the compact set Ξ; meanwhile, the membership functions $h_i{\lambda }_j$ ($i=1,\dots ,m,j=1,\dots ,n$) are differentiable functions of the state $x\left(t\right)$ on the set Ξ and the partial derivative of $h_i{\lambda }_j$ with respect to $x\left(t\right)$ are bounded by ${\tau }_{ij}$.

According to Assumption 1, the following Lemma can be obtained:

Lemma 1.

Under Assumption 1, the following conditions hold on the compact set Ξ:

$$\begin{array}{c}\hfill \left|h_i{\lambda }_j-{\overline{h}}_i{\overline{\lambda }}_j\right|\le {\alpha }_{ij}\end{array}$$

(19)

where ${\alpha }_{ij}=min\{1,{\vartheta }_{ij}{\tilde{\tau }}_c\nu \}$ and ν is the upper bound of $\left|\right|x_q\left(t\right)\left|\right|$; $x_q$ represents the state vector, where the vector $x\left(t\right)$ removes the components which are not related with the membership functions; $\tilde{\tau }$ is defined in (11).

Proof. 

By virtue of differential mean value theorem [27], it can be derived that

$$\begin{array}{c}\hfill h_i{\lambda }_j-{\overline{h}}_i{\overline{\lambda }}_j={\displaystyle \frac{\partial h_i{\lambda }_j\left(x_q^a\right)}{\partial x_q}}\left(x_q-{\overline{x}}_q\right)\end{array}$$

(20)

where ${\overline{x}}_q$ is the quantized signal of $x_q$ and $x_q^a\in [{\overline{x}}_q,x_q]$.

Then, with Assumption 1 and the condition (20), it can be derived that

$$\begin{array}{c}\hfill \left|h_i{\lambda }_j-{\overline{h}}_i{\overline{\lambda }}_j\right|\le {\vartheta }_{ij}\left|\right|I-C+{\Delta }_y\left|\right|x_q\le {\vartheta }_{ij}\left(\left|\right|I-C\left|\right|+\tilde{\tau }\right)\nu ={\vartheta }_{ij}{\tilde{\tau }}_c\nu ={\alpha }_{ij}.\end{array}$$

(21)

where ${\vartheta }_{ij}$ is the upper bound of the function ${\displaystyle \frac{\partial h_i{\lambda }_j\left(x_q^a\right)}{\partial x_q}}$. □

Remark 7.

It should be mentioned that ${\overline{h}}_i{\overline{\lambda }}_j$, which are the membership functions of FD observer, are measured by the sensors. Consequently, ${\overline{h}}_i{\overline{\lambda }}_j$ depends on the quantized signal $\overline{x}\left(t\right)$. Additionally, in this paper, we assume that the sensors, which are used to measure the state related with the membership functions, are healthy. That is the reason why the error $h_i{\lambda }_j-{\overline{h}}_i{\overline{\lambda }}_j$ is not dependent on the fault signal $f\left(t\right)$.

4. FD Observer Analysis and Synthesis

In this section, the $H_{\infty }/H\_$ performance analysis for the FD observer (14) is made and the corresponding synthesis conditions are presented in Theorems 1 and 2, firstly. Then, the FD logic is given and an optimized algorithm is proposed to guarantee the FD performance.

4.1. Membership-Function-Dependent $H_{\infty }/H\_$ FD Observer Synthesis Conditions

Theorem 1.

For given scalars ${\alpha }_{ij}(i\in \{1,\dots ,m\},j\in \{1,\dots ,n\})$, the error dynamic system has the $H_{\infty }$ performance index (17), if there exist matrices ${\overline{P}}_1>0$, ${\overline{P}}_2>0$, $R>0$, $Q_{kl}$, scalars ${\epsilon }_1>0$, ${\epsilon }_2>0$ and diagonal matrices $W_{ijkl}$$(k\in \{1,\dots ,m\},l\in \{1,\dots ,n\left\}\right)$, such that the following inequalities hold:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\displaystyle \frac{{\Psi }_{ijkl}+{\Psi }_{klij}}{2}}+\overline{\overline{C}}R{\overline{\overline{C}}}^T& U_{ijkl}\\ \ast & -R\end{array}\right]<0,\forall i,k\in \{1,\dots ,m\},j,l\in \{1,\dots ,n\}\end{array}$$

(22)

where

$$\begin{array}{cc}\hfill {\Psi }_{ijkl}=& \left[\begin{array}{c}\begin{array}{ccc}{\tilde{\Xi }}_{ijkl}+({\epsilon }_1+{\epsilon }_2+1){\tilde{\tau }}^2{\overline{C}}_1^T{\overline{C}}_1& {\overline{M}}_{kl}& {\overline{N}}_1\\ \ast & -{\epsilon }_{1}I& 0\\ \ast & \ast & -{\epsilon }_{2}I\end{array}\end{array}\right],{\tilde{\Xi }}_{ijkl}=\left[\begin{array}{c}\begin{array}{ccc}He\left({\overline{P}}_1{\overline{A}}_{ij}\right)& {({\overline{A}}_{ij}-{\overline{A}}_{kl})}^T{\overline{P}}_2& {\overline{P}}_{1}D\\ \ast & He({\overline{P}}_2{\overline{A}}_{ij}-Q_{kl}C)& {\overline{P}}_{2}D\\ \ast & \ast & -{\gamma }^{2}I\end{array}\end{array}\right],\hfill \\ \hfill \overline{\overline{C}}=& {\left[\begin{array}{ccccc}0& C& 0& I& 0\end{array}\right]}^T\left[\begin{array}{c}{I}_{n_u}\dots I_{n_u}\end{array}\right],{\overline{N}}_1={\left[\begin{array}{ccc}{\left(P_1\mathsf{\Lambda }\right)}^T& {\left(P_2\mathsf{\Lambda }\right)}^T& 0\end{array}\right]}^T,{\overline{M}}_{kl}={\left[\begin{array}{ccc}0& {(C^T-Q_{kl})}^T& 0\end{array}\right]}^T,\hfill \\ \hfill U_{ijkl}=& {\left[\begin{array}{ccccc}0& I& 0& I& 0\end{array}\right]}^T\left[\begin{array}{cccc}{\alpha }_{11}(-Q_{11}+W_{ijkl})& {\alpha }_{12}(-Q_{12}+W_{ijkl})& \dots & {\alpha }_{mn}(-Q_{mn}+W_{ijkl})\end{array}\right]\hfill \end{array}$$

then, the FD observer gain matrix can be obtained by $L_{ijkl}={\overline{P}}_2^{-1}{W}_{ijkl}$.

Proof. 

First, consider the case $f\left(t\right)=0$; then, it follows from the dynamic (14) that:

$$\begin{array}{cc}\hfill \dot{\eta }\left(t\right)=& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left[{\tilde{A}}_{ijkl}\eta \left(t\right)+\tilde{D}d\left(t\right)\right]\hfill \\ \hfill \overline{r}\left(t\right)=& \tilde{C}\eta \left(t\right)\hfill \end{array}$$

(23)

Select the following Lyapunov function:

$$\begin{array}{c}\hfill V\left(t\right)={\eta }^T\left(t\right)\overline{P}\eta \left(t\right)\end{array}$$

(24)

where

$$\begin{array}{c}\hfill \overline{P}=\left[\begin{array}{cc}{\overline{P}}_1& 0\\ 0& {\overline{P}}_2\end{array}\right]>0\end{array}$$

Calculating the derivative of the function $V\left(t\right)$ yields:

$$\begin{array}{c}\hfill \dot{V}\left(t\right)={\dot{\eta }}^T\left(t\right)\overline{P}\eta \left(t\right)+{\eta }^T\left(t\right)\overline{P}\dot{\eta }\left(t\right)\end{array}$$

(25)

With (25) and taking the dynamic (14) into consideration, we have

$$\begin{array}{cc}\hfill & \dot{V}\left(t\right)+{\overline{r}}^T\left(t\right)\overline{r}\left(t\right)-{\gamma }^2{\omega }^T\left(t\right)\omega \left(t\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\eta }^T\left(t\right)\left\{\left(\overline{P}{\tilde{A}}_{ijkl}+{\tilde{A}}_{ijkl}^T\overline{P}+{\tilde{C}}^T\tilde{C}\right)\eta \left(t\right)+2\overline{P}\tilde{D}\omega \left(t\right)\right\}-{\gamma }^2{\omega }^T\left(t\right)\omega \left(t\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\overline{\psi }}^T\left(t\right)\left({\Xi }_{ijkl}+{\overline{C}}^T\overline{C}\right)\overline{\psi }\left(t\right)\hfill \end{array}$$

(26)

where $\overline{C}=\left[\begin{array}{ccc}\Delta C& C& 0\end{array}\right]$,

$$\begin{array}{c}\hfill \overline{\psi }=\left[\begin{array}{c}\eta \left(t\right)\\ d\left(t\right)\end{array}\right],{\Xi }_{ijkl}=\left[\begin{array}{ccc}He({\overline{P}}_1{\overline{A}}_{ij}+{\overline{P}}_1\mathsf{\Lambda }\Delta C)& {({\overline{P}}_2({\overline{A}}_{ij}-{\overline{A}}_{kl})+{\overline{P}}_2\mathsf{\Lambda }\Delta C-Q_{kl}\Delta C)}^T& {\overline{P}}_{1}D\\ \ast & He({\overline{P}}_2{\overline{A}}_{ij}-{\overline{P}}_2{L}_{kl}C)& {\overline{P}}_{2}D\\ \ast & \ast & -{\gamma }^{2}I\end{array}\right].\end{array}$$

By making the variables change $Q_{kl}={\overline{P}}_2{L}_{kl}$ and based on Lemma 1, the term $\left({\Xi }_{ijkl}+{\overline{C}}^T\overline{C}\right)$ in (26) can be rewritten as:

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left({\Xi }_{ijkl}+{\overline{C}}^T\overline{C}\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left({\tilde{\Xi }}_{ijkl}+He\left({\overline{M}}_{kl}{\Delta }_y{\overline{C}}_1\right)+He\left({\overline{N}}_1{\Delta }_y{\overline{C}}_1\right)\right)\hfill \\ \hfill \le & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left({\tilde{\Xi }}_{ijkl}\right)+{\epsilon }_1^{-1}\overline{M}\left(t\right){\overline{M}}^T\left(t\right)+{\epsilon }_2^{-1}{\overline{N}}_1{\overline{N}}_1^T+({\epsilon }_1+{\epsilon }_2+1)\left({\overline{C}}_1^T{\Delta }_y^2{\overline{C}}_1\right)\hfill \end{array}$$

(27)

where ${\overline{C}}_1=\left[\begin{array}{ccc}C& 0& 0\end{array}\right]$, $\overline{M}\left(t\right)={\displaystyle \sum _{k=1}^m}{\displaystyle \sum _{l=1}^n}{\overline{h}}_k{\overline{\lambda }}_l{\overline{M}}_{kl}$, ${\overline{N}}_1$, ${\tilde{\Xi }}_{ijkl}$ and ${\overline{M}}_{kl}$ are defined in (22).

Based on (26) and (27), it can be inferred that if the following condition is satisfied

$$\begin{array}{c}\hfill \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left({\tilde{\Xi }}_{ijkl}\right)+{\epsilon }_1^{-1}\overline{M}\left(t\right){\overline{M}}^T\left(t\right)+{\epsilon }_2^{-1}{\overline{N}}_1{\overline{N}}_1^T+({\epsilon }_1+{\epsilon }_2+1)\left({\overline{C}}_1^T{\Delta }_y^2{\overline{C}}_1\right)<0\end{array}$$

(28)

then, we have

$$\begin{array}{c}\hfill \dot{V}\left(t\right)+{\overline{r}}^T\left(t\right)\overline{r}\left(t\right)-{\gamma }^2{d}^T\left(t\right)d\left(t\right)<0\end{array}$$

(29)

Applying Shur complement twice for the condition (28), one has

$$\begin{array}{c}\hfill \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left(\underset{{\Psi }_{ijkl}}{\underbrace{\left[\begin{array}{ccc}{\tilde{\Xi }}_{ijkl}+({\epsilon }_1+{\epsilon }_2+1)\left({\overline{C}}_1^T{\Delta }_y^2{\overline{C}}_1\right)& {\overline{M}}_{kl}& {\overline{N}}_1\\ \ast & -{\epsilon }_{1}I& 0\\ \ast & \ast & -{\epsilon }_{2}I\end{array}\right]}}\right)<0\end{array}$$

(30)

Making some mathematical operations for the condition (30) leads to

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\Psi }_{ijkl}\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\Psi }_{ijkl}+\sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}{\Psi }_{ijpq}\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\displaystyle \frac{{\Psi }_{ijkl}+{\Psi }_{klij}}{2}}+\sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}{\displaystyle \frac{{\Psi }_{ijpq}+{\Psi }_{klpq}}{2}}\right)\hfill \end{array}$$

(31)

where $\Delta {\overline{\theta }}_{pq}=h_p{\lambda }_q-{\overline{h}}_p{\overline{\lambda }}_q$.

Using the method in [19], and considering the property ${\displaystyle \sum _{q=1}^m}{\displaystyle \sum _{p=1}^n}\Delta {\overline{\theta }}_{pq}=0$ and Lemma 1, one can obtain

$$\begin{array}{cc}\hfill & \sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}\left({\displaystyle \frac{{\Psi }_{ijpq}+{\Psi }_{klpq}}{2}}\right)\hfill \\ \hfill =& \sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}He\left({\displaystyle \frac{{\Psi }_{ijpq}+{\Psi }_{klpq}}{2}}\right)\hfill \\ \hfill =& He\left(\left[\begin{array}{c}0\\ C^T\\ 0\\ I\\ 0\end{array}\right]\left[\begin{array}{c}{I}_{n_u}\dots I_{n_u}\end{array}\right]\times diag\left\{\Delta {\overline{\theta }}_{11},\dots ,\Delta {\overline{\theta }}_{mn}\right\}\times \left[\begin{array}{c}-Q_{11}^T\\ -Q_{12}^T\\ ⋮\\ -Q_{mn}^T\end{array}\right]\left[\begin{array}{ccccc}0& I& 0& I& 0\end{array}\right]\right)\hfill \\ \hfill =& He\left(\left[\begin{array}{c}0\\ C^T\\ 0\\ I\\ 0\end{array}\right]\left[\begin{array}{c}{I}_{n_u}\dots I_{n_u}\end{array}\right]\times diag\left\{\Delta {\overline{\theta }}_{11},\dots ,\Delta {\overline{\theta }}_{mn}\right\}\times \left[\begin{array}{c}-Q_{11}^T+W_{ijkl}^T\\ -Q_{12}^T+W_{ijkl}^T\\ ⋮\\ -Q_{mn}^T+W_{ijkl}^T\end{array}\right]\left[\begin{array}{ccccc}0& I& 0& I& 0\end{array}\right]\right)\hfill \\ \hfill \le & \overline{\overline{C}}R{\overline{\overline{C}}}^T+U_{ijkl}{R}^{-1}{U}_{ijkl}^T\hfill \end{array}$$

(32)

where the definitions of $U_{ijkl}$ and $\overline{\overline{C}}$ are given in (22).

Combining (31) and (32), one can obtain

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\Psi }_{ijkl}\hfill \\ \hfill \le & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\displaystyle \frac{{\Psi }_{ijkl}+{\Psi }_{klij}}{2}}+\overline{\overline{C}}R{\overline{\overline{C}}}^T+U_{ijkl}{R}^{-1}{U}_{ijkl}^T\right)\hfill \end{array}$$

(33)

From (30) and (33), it can be known that, if the following condition is satisfied,

$$\begin{array}{c}\hfill \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\displaystyle \frac{{\Psi }_{ijkl}+{\Psi }_{klij}}{2}}+\overline{\overline{C}}R{\overline{\overline{C}}}^T+U_{ijkl}{R}^{-1}{U}_{ijkl}^T\right)<0\end{array}$$

(34)

then the condition (30) holds.

Clearly, applying a Shur complement for the condition (34), one can obtain the condition (22), which implies that the condition (28) can be guaranteed by the condition (22).

Once the condition (28) holds, the condition (29) is satisfied.

Integrating (29) from 0 to t and with the zero initial condition, we can obtain

$$\begin{array}{cc}\hfill & {\int }_0^t\dot{V}\left(s\right)ds+{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds-{\gamma }^2{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds<0\hfill \\ \hfill \Rightarrow & V\left(t\right)-V\left(0\right)+{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<{\gamma }^2{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds\hfill \\ \hfill \Rightarrow & V\left(t\right)+{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<{\gamma }^2{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds\hfill \end{array}$$

(35)

Due to the property $V\left(t\right)>0$, the condition (17) can be guaranteed by (35), which indicates that the system (15) satisfies $H_{\infty }$ performance (17). Here, the proof is completed. □

Next, the design condition of the membership-function-dependent $H\_$ FD observer will be presented in Theorem 2.

Theorem 2.

For given positive scalars ${\alpha }_{ij}(i\in \{1,\dots ,m\},j\in \{1,\dots ,n\})$, the error dynamic system (15) satisfies the $H\_$ performance index $\overline{\beta }\left(\lambda \right)$, if there exist matrices ${\overline{P}}_2>0$, ${\overline{P}}_3>0$, $\overline{R}>0$, $Q_{kl}$, positive scalars ${\epsilon }_3$, ${\epsilon }_4$, ${\epsilon }_5$, and diagonal matrices $W_{ijkl}$$(k\in \{1,\dots ,m\},l\in \{1,\dots ,n\left\}\right)$, such that the following inequalities hold:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\displaystyle \frac{{\overline{\Omega }}_{ijkl}+{\overline{\Omega }}_{klij}}{2}}+\overline{C_5}\overline{R}{\overline{C_5}}^T& {\overline{U}}_{ijkl}\\ \ast & -\overline{R}\end{array}\right]<0,\forall i,k\in \{1,\dots ,m,\},j,l\in \{1,\dots ,n\}\end{array}$$

(36)

where $\overline{\beta }\left(\lambda \right)=\sqrt{\sigma {\lambda }_1\left(t\right)+{\displaystyle \sum _{i=2}^n}{\lambda }_i\left(t\right)}\beta$

$$\begin{array}{cc}\hfill {\overline{\Omega }}_{ijkl}=& \left[\begin{array}{cccc}{{\rm Y}}_{ijkl}^{\left(3\right)}+{\epsilon }_4{\tilde{\tau }}^2{\overline{F}}^T\overline{F}& {\overline{M}}_{kl}& {\tilde{C}}_{kl}^T& {\overline{N}}_2^T\\ \ast & -{\epsilon }_{3}I& 0& 0\\ \ast & \ast & -{\epsilon }_{4}I& 0\\ \ast & \ast & \ast & -{\epsilon }_{5}I\end{array}\right],\overline{C_5}={\left[\begin{array}{ccccc}0& C& 0& I& 0\end{array}\right]}^T\left[\begin{array}{c}{I}_{n_u}\dots I_{n_u}\end{array}\right],\hfill \\ \hfill {{\rm Y}}_{ijkl}^{\left(3\right)}=& \left[\begin{array}{ccc}He\left({\overline{P}}_3{\overline{A}}_{ij}\right)+{\epsilon }_3{\tilde{\tau }}^2{C}^{T}C& {\left({\overline{P}}_2({\overline{A}}_{ij}-{\overline{A}}_{kl})\right)}^T& {\overline{P}}_3\mathsf{\Lambda }F\\ \ast & He({\overline{P}}_2{\overline{A}}_{ij}-Q_{kl}C)-C^{T}C& {\overline{P}}_2\mathsf{\Lambda }F-Q_{kl}F-C^{T}F\\ \ast & \ast & {\pi }_{i}I-F^{T}F+{\epsilon }_4{F}^T{J}^{2}F\end{array}\right],\hfill \\ \hfill {\overline{U}}_{ijkl}=& {\left[\begin{array}{cccccc}0& I& 0& 0& 0& 0\end{array}\right]}^T\left[\begin{array}{cccc}{\alpha }_{11}(-Q_{11}+W_{ijkl})& {\alpha }_{12}(-Q_{12}+W_{ijkl})& \dots & {\alpha }_{mn}(-Q_{mn}+W_{ijkl})\end{array}\right],\hfill \\ \hfill {\tilde{C}}_{kl}=& \left[\begin{array}{ccc}-C& -C-Q_{ij}^T& -2F\end{array}\right],{\overline{N}}_2={\left[\begin{array}{ccc}{\left(P_3\mathsf{\Lambda }\right)}^T& {\left(P_2\mathsf{\Lambda }\right)}^T& 0\end{array}\right]}^T,\overline{F}=\left[\begin{array}{ccc}0& 0& F\end{array}\right],\hfill \\ \hfill {\pi }_1=& \beta \sigma ,{\pi }_i=\beta (i=2,\dots ,m).\hfill \end{array}$$

Furthermore, the FD observer gain matrix can be obtained by $L_{ijkl}={\overline{P}}_2^{-1}{W}_{ijkl}$.

Proof. 

Consider the case $d=0$, the system (14) becomes:

$$\begin{array}{cc}\hfill \dot{\eta }\left(t\right)=& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left[{\tilde{A}}_{ijkl}\eta \left(t\right)+{\tilde{G}}_{kl}f\left(t\right)\right]\hfill \\ \hfill \overline{r}\left(t\right)=& \tilde{C}\eta \left(t\right)+\tilde{F}f\left(t\right)\hfill \end{array}$$

(37)

Construct the Lyapunov function as follows:

$$\begin{array}{c}\hfill V_2={\eta }^T\left(t\right)\tilde{P}\eta \left(t\right)\end{array}$$

(38)

where

$$\begin{array}{c}\hfill \tilde{P}=\left[\begin{array}{cc}{\overline{P}}_3& 0\\ 0& {\overline{P}}_2\end{array}\right]\end{array}$$

Calculating $\dot{V}\left(t\right)$, we can obtain

$$\begin{array}{c}\hfill \dot{V}\left(t\right)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\eta }^T\left(t\right)\left\{\left(\tilde{P}{\tilde{A}}_{ijkl}+{\tilde{A}}_{ijkl}^T\tilde{P}\right)\eta \left(t\right)+2\tilde{P}{\tilde{G}}_{kl}f\left(t\right)\right\}\end{array}$$

(39)

With (39), we can obtain the following function

$$\begin{array}{cc}\hfill & \dot{V}\left(t\right)+{\overline{\beta }}^2\left(t\right)f^T\left(t\right)f\left(t\right)-{\overline{r}}^T\left(t\right)\overline{r}\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\eta }^T\left(t\right)\left(\tilde{P}{\tilde{A}}_{ijkl}+{\tilde{A}}_{ijkl}^T\tilde{P}-{\overline{C}}^T\overline{C}\right)\eta \left(t\right)+f^T\left(t\right)\left({\overline{\beta }}^2\left(\lambda \right)I-{\tilde{F}}^T\tilde{F}\right)f\left(t\right)\hfill \\ \hfill & +\sum _{k=1}^m\sum _{l=1}^n{\overline{h}}_k{\overline{\lambda }}_l{\eta }^T\left(t\right)\left(\tilde{P}{\tilde{G}}_{kl}-{\overline{C}}^T\tilde{F}\right)f\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\varphi }^T\left(t\right)\left({{\rm Y}}_{ijkl}^{\left(1\right)}-{\overline{C}}_1^T{\Delta }_y^2{\overline{C}}_1\right)\varphi \left(t\right)\hfill \\ \hfill \le & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\varphi }^T\left(t\right){{\rm Y}}_{ijkl}^{\left(1\right)}\varphi \left(t\right)\hfill \end{array}$$

(40)

where $\varphi \left(t\right)={\left[\begin{array}{ccc}{x}^T\left(t\right)& e^T\left(t\right)& f^T\left(t\right)\end{array}\right]}^T$,

$$\begin{array}{c}\hfill {{\rm Y}}_{ijkl}^{\left(1\right)}=\left[\begin{array}{c}\begin{array}{ccc}He({\overline{P}}_3{\overline{A}}_{ij}+{\overline{P}}_3\mathsf{\Lambda }{\Delta }_{y}C)& {({\overline{P}}_2({\overline{A}}_{ij}-{\overline{A}}_{kl})+{\overline{P}}_2\mathsf{\Lambda }{\Delta }_{y}C-Q_{kl}{\Delta }_{y}C)}^T-C^T{\Delta }_{y}C& {\overline{P}}_3\mathsf{\Lambda }(I+{\Delta }_y)F-C^T{\Delta }_{y}F\\ \ast & He({\overline{P}}_2{\overline{A}}_{ij}-{\overline{P}}_2{L}_{kl}C)-C^{T}C& {\overline{P}}_2\mathsf{\Lambda }(I+{\Delta }_y)F-{\overline{P}}_2{L}_{kl}(I+{\Delta }_y)F-C^T(I+{\Delta }_y)F\\ \ast & \ast & {\overline{\beta }}^2\left(\lambda \right)I-F^T(I+2{\Delta }_y)F\end{array}\end{array}\right]\end{array}$$

By making the variables change $Q_{kl}={\overline{P}}_2{L}_{kl}$ and based on Lemma 1, the term $\left({\Xi }_{ijkl}+{\overline{C}}^T\overline{C}\right)$ in (26) can be rewritten as:

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{{\rm Y}}_{ijkl}^{\left(1\right)}\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left({{\rm Y}}_{ijkl}^{\left(2\right)}+He\left({\tilde{C}}_{kl}^T{\Delta }_y\overline{F}\right)+He\left(\overline{M}\left(t\right){\Delta }_y{\overline{C}}_1\right)+He\left({\overline{N}}_2{\Delta }_y{\overline{C}}_4\right)\right)\hfill \\ \hfill \le & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l({{\rm Y}}_{ijkl}^{\left(2\right)}+{\epsilon }_3^{-1}{\overline{M}}^T\left(t\right)\overline{M}\left(t\right)+{\epsilon }_3{\overline{C}}_1^T{\Delta }_y^2{\overline{C}}_1+{\epsilon }_4{\overline{F}}^T{\Delta }_y^2\overline{F}+{\epsilon }_4^{-1}{\tilde{C}}_{kl}^T{\tilde{C}}_{kl}\hfill \\ \hfill & +{\epsilon }_5^{-1}{\overline{N}}_2^T{\overline{N}}_2+{\epsilon }_5{\overline{C}}_4^T{\Delta }_y^2{\overline{C}}_4)\hfill \end{array}$$

(41)

where ${\tilde{C}}_{kl}$, ${\overline{C}}_4=\left[\begin{array}{ccc}C& 0& F\end{array}\right]$,

$$\begin{array}{cc}\hfill {{\rm Y}}_{ijkl}^{\left(2\right)}=& \left[\begin{array}{ccc}He\left({\overline{P}}_3{\overline{A}}_{ij}\right)& {\left({\overline{P}}_2({\overline{A}}_{ij}-{\overline{A}}_{kl})\right)}^T& {\overline{P}}_3\mathsf{\Lambda }F\\ \ast & He({\overline{P}}_2{\overline{A}}_{ij}-Q_{kl}C)-C^{T}C& {\overline{P}}_2\mathsf{\Lambda }F-Q_{kl}F-C^{T}F\\ \ast & \ast & {\overline{\beta }}^2\left(\lambda \right)I-F^{T}F\end{array}\right].\hfill \end{array}$$

Based on (41), the following inequality holds

$$\begin{array}{c}\hfill \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\varphi }^T\left(t\right){{\rm Y}}_{ijkl}^{\left(1\right)}\varphi \left(t\right)<0\end{array}$$

(42)

if we have

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{{\rm Y}}_{ijkl}^{\left(2\right)}+{\epsilon }_3^{-1}{\overline{M}}^T\left(t\right)\overline{M}\left(t\right)+{\epsilon }_3{\tilde{\tau }}^2{\overline{C}}_1^T{\overline{C}}_1+{\epsilon }_4{\tilde{\tau }}^2{\overline{F}}^T\overline{F}+{\epsilon }_4^{-1}{\tilde{C}}_{kl}^T{\tilde{C}}_{kl}+{\epsilon }_5^{-1}{\overline{N}}_2^T{\overline{N}}_2\hfill \\ \hfill & +{\epsilon }_5{\tilde{\tau }}^2{\overline{C}}_4^T{\overline{C}}_4<0.\hfill \end{array}$$

(43)

Applying the Shur complement for (43) gives

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l\left(\underset{{\overline{\Omega }}_{ijkl}}{\underbrace{\left[\begin{array}{cccc}{{\rm Y}}_{ijkl}^{\left(3\right)}+{\epsilon }_4{\tilde{\tau }}^2{\overline{F}}^T\overline{F}& {\overline{M}}_{kl}& {\tilde{C}}_{kl}^T& {\overline{N}}_2^T\\ \ast & -{\epsilon }_{3}I& 0& 0\\ \ast & \ast & -{\epsilon }_{4}I& 0\\ \ast & \ast & \ast & -{\epsilon }_{5}I\end{array}\right]}}\right)<0\hfill \end{array}$$

(44)

where ${{\rm Y}}_{ijkl}^{\left(3\right)}$ is defined in (36).

Similar to the process in Theorem 1, the term ${\displaystyle \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n}{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\overline{\Omega }}_{ijkl}$ in (44) can be rewritten as

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{\overline{h}}_k{\overline{\lambda }}_l{\overline{\Omega }}_{ijkl}\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\overline{\Omega }}_{ijkl}+\sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}{\overline{\Omega }}_{ijpq}\right)\hfill \\ \hfill =& \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\displaystyle \frac{{\overline{\Omega }}_{ijkl}+{\overline{\Omega }}_{klij}}{2}}+\sum _{q=1}^m\sum _{p=1}^n\Delta {\overline{\theta }}_{pq}{\displaystyle \frac{{\overline{\Omega }}_{ijpq}+{\overline{\Omega }}_{klpq}}{2}}\right)\hfill \\ \hfill \le & \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^m\sum _{l=1}^n{h}_i{\lambda }_j{h}_k{\lambda }_l\left({\displaystyle \frac{{\overline{\Omega }}_{ijkl}+{\overline{\Omega }}_{klij}}{2}}+\overline{C_5}\overline{R}{\overline{C_5}}^T+{\overline{U}}_{ijkl}{\overline{R}}^{-1}{\overline{U}}_{ijkl}^T\right)\hfill \end{array}$$

(45)

where ${\overline{U}}_{ijkl}$ and ${\overline{C}}_5$ are defined in (36) and $\overline{R}$ is a diagonal matrix.

It is easy to see from (45) that, if the following condition holds

$$\begin{array}{c}\hfill {\displaystyle \frac{{\overline{\Omega }}_{ijkl}+{\overline{\Omega }}_{klij}}{2}}+\overline{C_5}\overline{R}{\overline{C_5}}^T+{\overline{U}}_{ijkl}{\overline{R}}^{-1}{\overline{U}}_{ijkl}^T<0\end{array}$$

(46)

then one has

$$\begin{array}{c}\hfill \dot{V}\left(t\right)+{\overline{\beta }}^2\left(\lambda \right)f^T\left(t\right)f\left(t\right)-{\overline{r}}^T\left(t\right)\overline{r}\left(t\right)<0\end{array}$$

(47)

Using the Shur complement for (46), one can obtain (36), which implies that (47) holds if the condition (36) is satisfied.

Integrating both sides of (47) from 0 to t and with the zero initial condition, we have

$$\begin{array}{cc}\hfill & {\int }_0^t\dot{V}\left(s\right)ds+{\int }_0^t{\overline{\beta }}^2\left(\lambda \right)f^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<0\hfill \\ \hfill \Rightarrow & V\left(t\right)-V\left(0\right)+{\int }_0^t{\overline{\beta }}^2\left(\lambda \right)f^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<0\hfill \\ \hfill \Rightarrow & V\left(t\right)+{\int }_0^t{\overline{\beta }}^2\left(\lambda \right)f^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<0\hfill \\ \hfill \Rightarrow & {\int }_0^t{\overline{\beta }}^2\left(\lambda \right)f^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<0\hfill \end{array}$$

(48)

Obviously, from (48), we have

$$\begin{array}{c}\hfill {\overline{\overline{\beta }}}^2\left(\lambda \right){\int }_0^t{f}^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<{\int }_0^t{\overline{\beta }}^2\left(\lambda \right)f^T\left(s\right)f\left(s\right)ds-{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds<0\end{array}$$

(49)

where $\overline{\overline{\beta }}\left(\lambda \right)$ is defined in (16).

According to (49), one can see that the system (15) satisfies the membership-function-dependent $H\_$ performance (16). □

4.2. FD Logic and Optimized Algorithm

To achieve the purpose of FD, based on the method, the residual evaluation function $J_r$ and the threshold $J_{th}$ are selected as

$$\begin{array}{cc}\hfill J_{\overline{r}}\left(t\right)=& \sqrt{{\displaystyle \frac{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}{t}}},\hfill \\ \hfill J_{th}=& \underset{f\left(t\right)=0,0\ne \omega \in L_2}{sup}{J}_{\overline{r}}\left(t\right)\hfill \end{array}$$

By comparing the residual evaluation function $J_{\overline{r}}$ with $J_{th}$, the occurrence of the fault signal can be observed by the following fault detection logic:

$$\begin{array}{cc}\hfill J_{\overline{r}}>J_{th}⟹& \mathrm{sensor} \mathrm{fault} \mathrm{alarm}\hfill \\ \hfill J_{\overline{r}}\le J_{th}⟹& \mathrm{no} \mathrm{sensor} \mathrm{fault}\hfill \end{array}$$

(50)

The gain matrices $L_{ij},(i=1,\dots ,mandj=1,\dots ,n)$ of FD observer (14) can be determined by solving the following optimization problem:

$$\begin{gathered} max\sigma \\ \mathrm{s}.\mathrm{t}. (22) \mathrm{and} (36). \end{gathered}$$

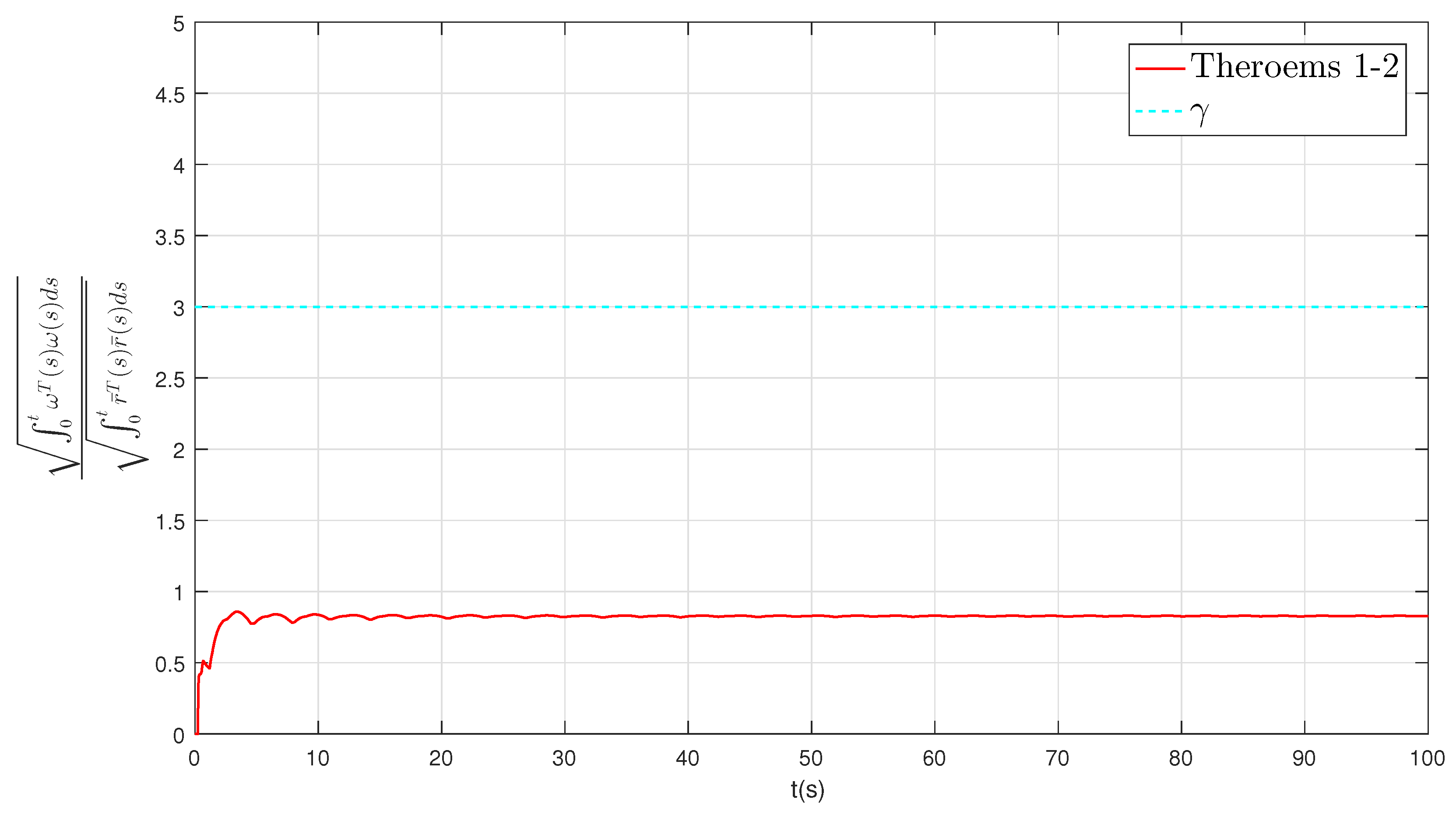
5. Example

In this section, an example with respect to UMVs is provided to show the effectiveness of the presented method. Refer to [28], the matrices M, G, and N are provided as follows:

$$\begin{array}{c}\hfill M=\left[\begin{array}{c}\begin{array}{ccc}1.0852& 0& 0\\ 0& 2.0575& -0.04087\\ 0& -0.4087& 0.2153\end{array}\end{array}\right],G=\left[\begin{array}{c}\begin{array}{ccc}0.0389& 0& 0\\ 0& 0.0266& 0\\ 0& 0& 0\end{array}\end{array}\right],N=\left[\begin{array}{c}\begin{array}{ccc}0.0865& 0& 0\\ 0& 0.0762& 0.0151\\ 0& 0.151& 0.0031\end{array}\end{array}\right].\end{array}$$

Correspondingly, by using (3), the matrices A, D and B can be obtained as follows:

$$\begin{array}{c}\hfill A=\left[\begin{array}{c}\begin{array}{ccc}-0.0358& 0& 0\\ 0& -0.0208& 0\\ 0& -0.0394& 0\end{array}\end{array}\right],D=\left[\begin{array}{c}\begin{array}{ccc}0.9215& 0& 0\\ 0& 0.7802& 1.4811\\ 0& 1.4811& 7.4562\end{array}\end{array}\right],B=\left[\begin{array}{c}\begin{array}{ccc}-0.0797& 0& 0\\ 0& -0.0818& -0.1224\\ 0& -0.2254& -0.2468\end{array}\end{array}\right].\end{array}$$

Other matrices of the system (13) are given as follows:

$$\begin{array}{c}\hfill F={\left[\begin{array}{c}\begin{array}{cccccc}0& 0& 0& 0& 6& 0\end{array}\end{array}\right]}^T,\mathsf{\Lambda }=\left[\begin{array}{c}\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ -2.5250& 0& 0& -3.0592& 0& 0\\ 0& -1.9635& -0.7524& 0& -2.9476& -0.2853\\ 0& -1.3835& -4.0222& 0& -1.1512& -3.4042\end{array}\end{array}\right].\end{array}$$

Let $\gamma =3$ and ${\beta }^2=3.6$ and assume that $\underline{\psi }=-{30}^{\circ }$ and $\overline{\psi }={30}^{\circ }$ [29,30], solving the LMIs (22) and (36) in Theorems 1 and 2, the FD observer gain matrices and the optimized parameter $\sigma$ can be obtained as follows:

$$\begin{array}{cc}\hfill L_{11}=& \left[\begin{array}{c}\begin{array}{cccccc}374.4281& -18.5380& -109.6260& 713.0683& 3.2597& -19.6527\\ 0.1325& 164.2773& 37.4165& -14.0361& -29.3229& -28.0563\\ 0.0086& 8.9454& 2.8725& -0.7664& -1.6583& -1.0469\\ 185.5099& -9.5102& -55.8698& 418.7376& 1.4572& -9.8093\\ 0.3128& 389.5008& 89.8453& -33.6793& -73.8098& -62.9532\\ -0.0478& -43.1203& -10.4880& 3.7688& 6.2639& 14.6171\end{array}\end{array}\right],\hfill \\ \hfill L_{12}=& \left[\begin{array}{c}\begin{array}{cccccc}376.1083& -0.0691& 33.2222& 472.4253& -9.9260& 0.0205\\ -0.2785& 163.2217& 35.1480& -8.5601& -21.6449& -28.3399\\ -0.0137& 8.9043& 2.7927& -0.5319& -1.2309& -1.0795\\ 186.3607& 0.1828& 17.9891& 297.3008& -6.7109& -0.4095\\ -0.6421& 387.0900& 84.5674& -20.7604& -55.5328& -63.6440\\ 0.1248& -42.5896& -9.5858& 2.3012& 3.8387& 14.6368\end{array}\end{array}\right],\hfill \\ \hfill L_{21}=& \left[\begin{array}{c}\begin{array}{cccccc}374.4281& 18.5380& 109.6260& 713.0683& -3.2597& 19.6528\\ -0.1325& 164.2773& 37.4165& 14.0361& -29.3229& -28.0563\\ -0.0086& 8.9454& 2.8725& 0.7664& -1.6583& -1.0469\\ 185.5099& 9.5102& 55.8698& 418.7376& -1.4572& 9.8093\\ -0.3128& 389.5008& 89.8453& 33.6793& -73.8098& -62.9532\\ 0.0478& -43.1203& -10.4880& -3.7688& 6.2639& 14.6171\end{array}\end{array}\right],\hfill \\ \hfill L_{22}=& \left[\begin{array}{c}\begin{array}{cccccc}376.1083& 0.0691& -33.2222& 472.4253& 9.9260& -0.0205\\ 0.2785& 163.2217& 35.1480& 8.5601& -21.6449& -28.3399\\ 0.0137& 8.9043& 2.7927& 0.5319& -1.2309& -1.0795\\ 186.3607& -0.1828& -17.9891& 297.3008& 6.7109& 0.4095\\ 0.6421& 387.0900& 84.5674& 20.7604& -55.5328& -63.6440\\ -0.1248& -42.5896& -9.5858& -2.3012& 3.8387& 14.6368\end{array}\end{array}\right],\hfill \\ \hfill \sigma =& 2.1727.\hfill \end{array}$$

With the parameters $\sigma$ and $\beta$ obtained previously, the membership-function-dependent $H\_$ performance index $\overline{\beta }\left(\lambda \right)$ is:

$$\begin{array}{c}\hfill \overline{\beta }\left(\lambda \right)=\sqrt{(\sigma {\lambda }_1+{\lambda }_2)\times {\beta }^2}=\sqrt{(2.1727{\lambda }_1+{\lambda }_2)\times 3.6}\end{array}$$

(51)

Next, with the help of Equation (51), the relationships between the membership functions $\lambda \left(t\right)$ and the $H\_$ performance index ${\overline{\beta }}^2\left(\lambda \right)$ are investigated. The results of the investigation are shown in

Table 1. The $H\_$ performance index obtained by the proposed method and [19].

	The proposed method	[19]	[22]
$H\_$ performance bound	[3.6, 7.8218]	6.1236	[5.5, 7.6993]

and Figure 1. Table 1 lists the $H\_$ performance index calculated by the presented FD strategy and the FD method in [19]. It can be inferred from Table 1 that the $H\_$ performance index computed by [19] is a fixed value; however, $H\_$ performance index computed by the proposed method belongs to the interval $[3.6,7.8218]$ because it depends on the time-varying membership functions ${\lambda }_1$ and ${\lambda }_2$. As the membership function ${\lambda }_1$ increased, ${\overline{\beta }}^2\left(\lambda \right)$ will also be increased. When ${\lambda }_1$ takes its maximum value, i.e., ${\lambda }_1=1$, ${\overline{\beta }}^2$ also takes its maximum value $7.8218$. That is to say, if the fuzzy system (13) always works on the subsystem $A_{11}$ or $A_{21}$, then ${\lambda }_1$ will keep at relative large values which leads to a large ${\overline{\beta }}^2\left(\lambda \right)$. Consequently, with a large ${\lambda }_1$, a good FD performance will be obtained. Figure 1 demonstrates the relationship between ${\lambda }_1$ and $\overline{\beta }\left(\lambda \right)$. Here, it can be learned that, when ${\lambda }_1$ increases, $\overline{\beta }\left(\lambda \right)$ is also increased, which also verifies the validity of the analysis for Table 1. On the other hand, Table 1 also shows the $H\_$ performance bound obtained by [22]. It can be learned that the $H\_$ performance bound obtained by [22] also belongs to an interval rather than a constant.

Furthermore, with zero initial conditions and assume that the system (13) is subjected with the external disturbance and fault signal which takes the following form:

$$\omega \left(t\right)=0.4sin\left(t\right),f\left(t\right)=\left\{\begin{array}{cc}\hfill 0,& 0\le t\le 30,\hfill \\ \hfill 0.0175(t-30),& 30<t<70,\hfill \\ \hfill 0.7,& t\ge 70\hfill \end{array}\right.$$

To further illustrate the effectiveness of the developed approach, Simulations are made and the results of simulations are shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

The real-time trajectories of $x_3\left(t\right)$ and ${\lambda }_1\left(t\right)$ are plotted in Figure 2. It can be seen from Figure 2 that the system state $x_3\left(t\right)$ is in the area nearby the equilibrium point, such that the membership function ${\lambda }_1>0.75$. Figure 3 shows the real-time trajectories of $H\_$ performance indices ${\overline{\beta }}^2\left(\lambda \right)$ (obtained by the proposed method), the $H\_$ performance index ${\beta }^2$ (obtained by [19]) and the $H\_$ performance index ${\beta }^2\left(h\lambda \right)$ (obtained by [22]), respectively. By comparison, it can be seen that ${\overline{\beta }}^2\left(\lambda \right)$ is larger than ${\beta }^2$ and ${\beta }^2\left(h\lambda \right)$ which illustrates that the proposed FD method is more sensitive to the fault signal than [19,22] in theory. The reason is that the membership function ${\lambda }_1$ can take a large value. Then, based on the analysis for Table 1, we have ${\overline{\beta }}^2\left(\lambda \right)=(\sigma {\lambda }_1+{\lambda }_2)\times {\beta }^2=(2.1727{\lambda }_1+{\lambda }_2)\times 3.6>6.8>{\beta }^2$. Additionally, it can also be obtained from Figure 3 that ${\overline{\overline{\beta }}}^2=6.78$, which is also larger than ${\beta }^2$ obtained by [19]. Figure 4 shows the residual evaluation functions generated by our method and the methods presented by [19,22], respectively. It is clear to see from Figure 4 that the fault is detected at 47.6 s by the proposed method while the fault is detected at 48.9 s and 48 s by the methods proposed in [19,22], respectively. It means that, compared with [19,22], the fault can be detected earlier by the proposed membership-function-dependent $H\_$ FD observer. Thus, FD performance of membership-function-dependent $H\_$ observer is better than those of the traditional observer method.

Remark 8.

A discussion about the superiority of the proposed method is given.

The superiority of the presented method is that the $H\_$ performance index $\overline{\beta }\left(\lambda \right)$ depends on the membership functions ${\lambda }_i$. This fact can help the designers to better make use of the property where the state of the system always stays in some local areas such that the FD performance can be improved. Just as is shown in this example, the $H\_$ performance index $\overline{\beta }\left(\lambda \right)$ depends on the membership function ${\lambda }_1$ which can take a relatively large value when the state of the system is in the local area nearby the equilibrium point. Consequently, compared with the constant performance index β, the proposed performance index $\overline{\beta }$ can take a larger value such that a better FD performance can be obtained. On the other hand, it should be mentioned that $H\_$ performance index in [22] also depends on the membership functions. However, it depends on $h_i{\lambda }_j,(i\in \{1,\dots ,m\},i\in \{1,\dots ,n\},)$ which is not very suitable for the case in this example. As is stated in Remark 5, when the state $x_3$ is in the area nearby the the equilibrium point, $h_1{\lambda }_1$ cannot take a relatively large value such that $\overline{\beta }\left(\lambda \right)$ is also not large. That is the reason why is the FD performance of the proposed strategy is better than that of [22].

In the following, we will verify that the real-time ratio ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}$ and ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\omega \left(s\right)\omega \left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}$ satisfy the conditions

$$\begin{array}{c}\hfill {\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}\ge \overline{\beta }\left(\lambda \right)\mathrm{and}{\displaystyle \frac{\sqrt{{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}\le \gamma \end{array}$$

(52)

The first step is to verify ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}\ge \overline{\beta }\left(\lambda \right)$. To achieve the objective, consider $\omega \left(t\right)=0$ and the fault scenario as: $f\left(t\right)=0.7$. The real-time trajectory of ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}$ is shown in Figure 5. From Figure 5, we can see that the real-time ratio ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}$ is larger than the maximum value of the membership-function-dependent $H\_$ performance index, i.e., ${\overline{\beta }}_{max}\left(\lambda \right)$, which illustrates that the $H\_$ performance index (16) can be guaranteed. Additionally, the real-time ratio ${\displaystyle \frac{\sqrt{{\int }_0^t{f}^T\left(s\right)f\left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}$ generated by the proposed strategy is larger than those generated by [19,22] which further demonstrates that compared with [19,22], the proposed FD observer is more sensitive to the fault signal.

Next, to verify ${\displaystyle \frac{\sqrt{{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}\le \gamma$, consider the case where the disturbance signal $\omega \left(t\right)=0.7$ and fault signal $f\left(t\right)=0$. The result of Simulation is presented in Figure 6. From Figure 6, it is obvious that ${\displaystyle \frac{\sqrt{{\int }_0^t{\omega }^T\left(s\right)\omega \left(s\right)ds}}{\sqrt{{\int }_0^t{\overline{r}}^T\left(s\right)\overline{r}\left(s\right)ds}}}\le \gamma =3$. It verifies that the system (15) satisfies the $H_{\infty }$ performance (17).

6. Conclusions

In this paper, the problem of the FD observer design is studied for UMVs. First, to describe the nonlinearity in UMVs, the dynamic of UMVs is modeled by T-S fuzzy systems. Based on the T-S fuzzy models, a new FD observer and the residual generator are designed. To improve the performance of FD, the membership-function-dependent $H_{\infty }/H\_$ performance index is defined. Then, the synthesis conditions of the membership-function-dependent $H_{\infty }/H\_$ performance are obtained. Finally, examples are given to demonstrate the efficacy of the developed method. In the future, we will investigate the finite-time FD problem for UMVs by using the T-S fuzzy model method to increase the transient performance of the systems.