Research on the Optimization of Ship Trajectory Clustering Based on the OD–Hausdorff Distance
Abstract
:1. Introduction
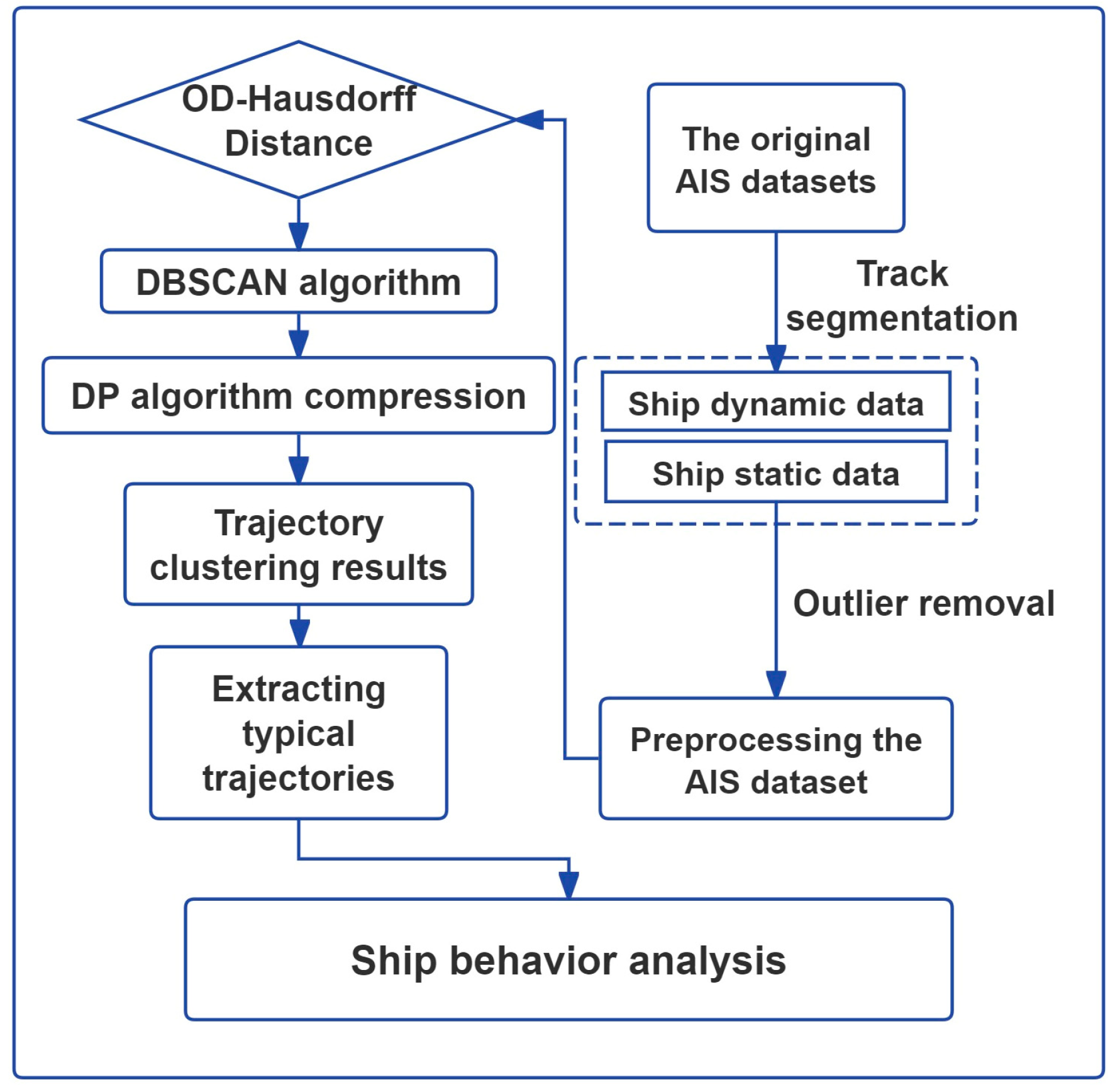
2. Methods
2.1. AIS Data Preprocessing
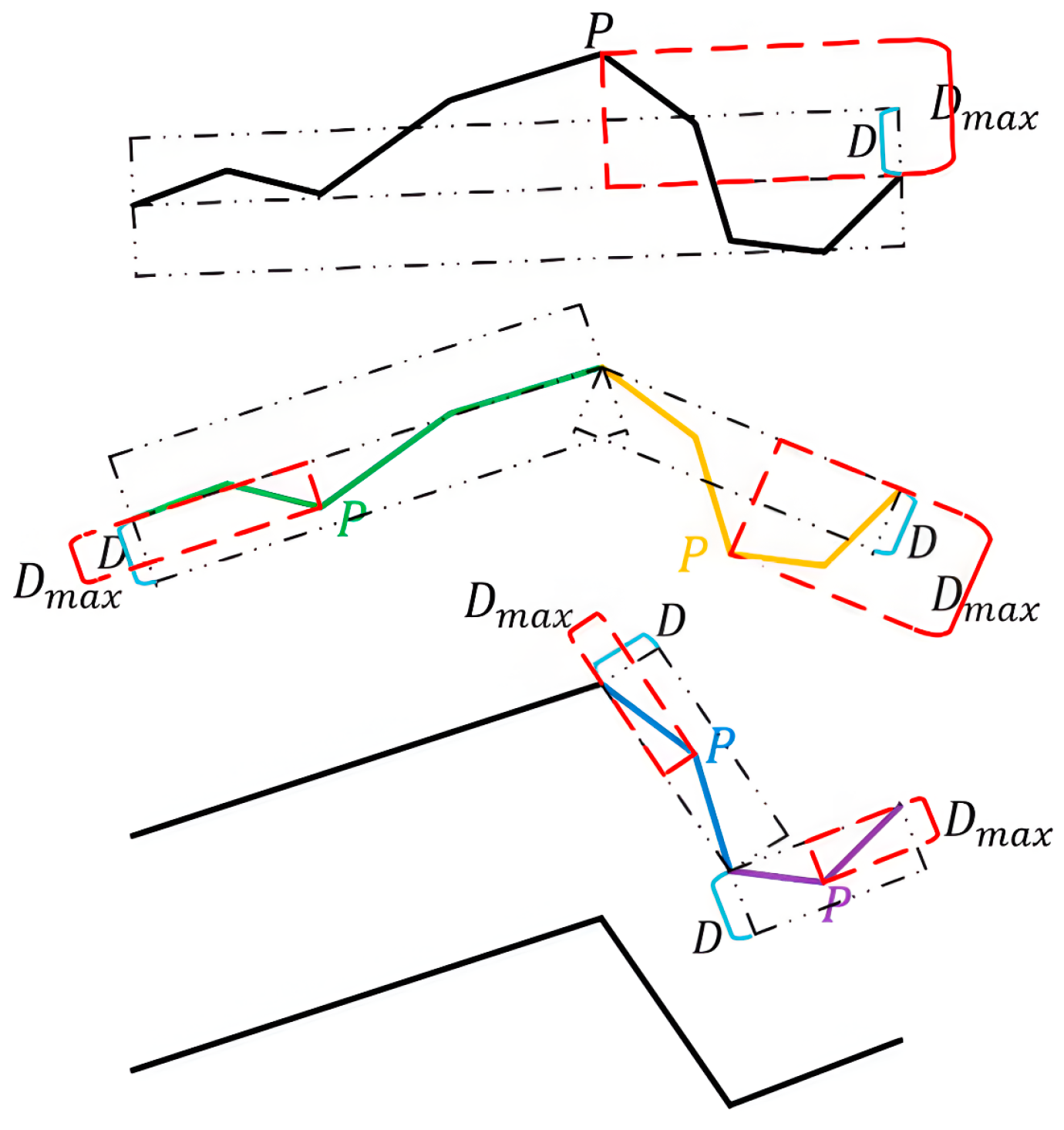
2.2. OD–Hausdorff Distance
Extraction of Typical Ship Trajectories
3. Results
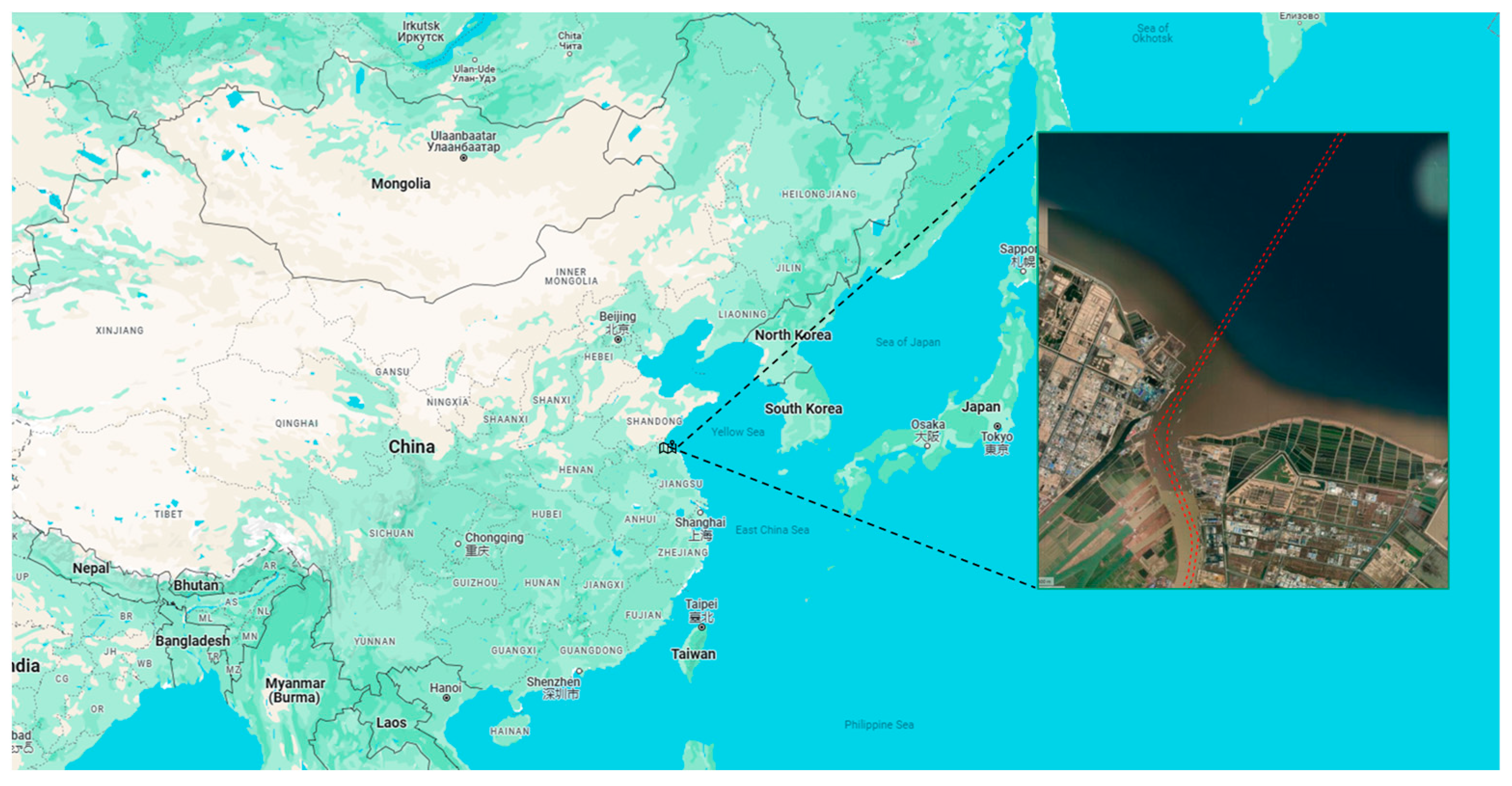
3.1. Environment and Data Setup
3.2. Clustering Parameter Settings Comparison
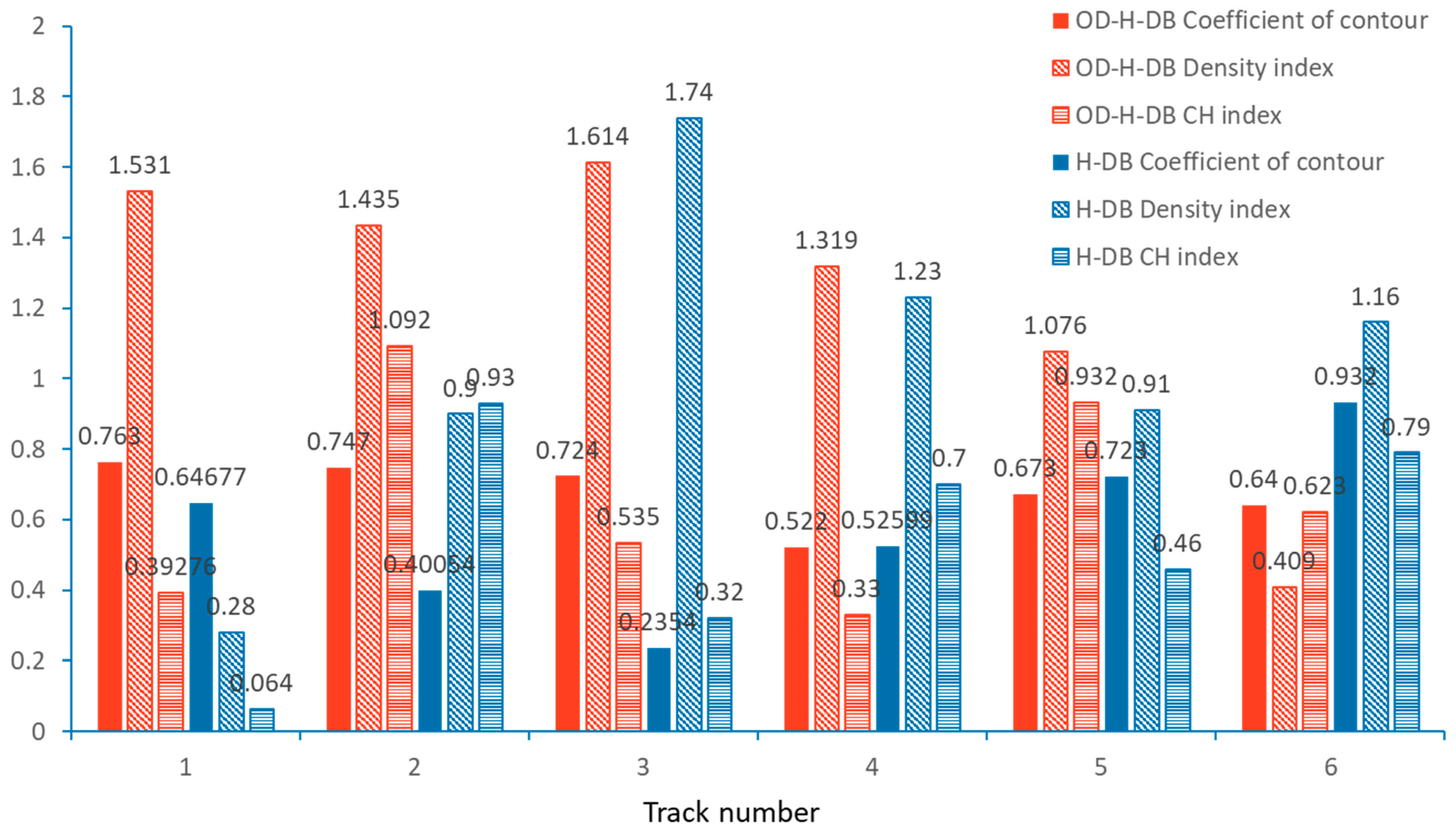
Cluster Quality Evaluation
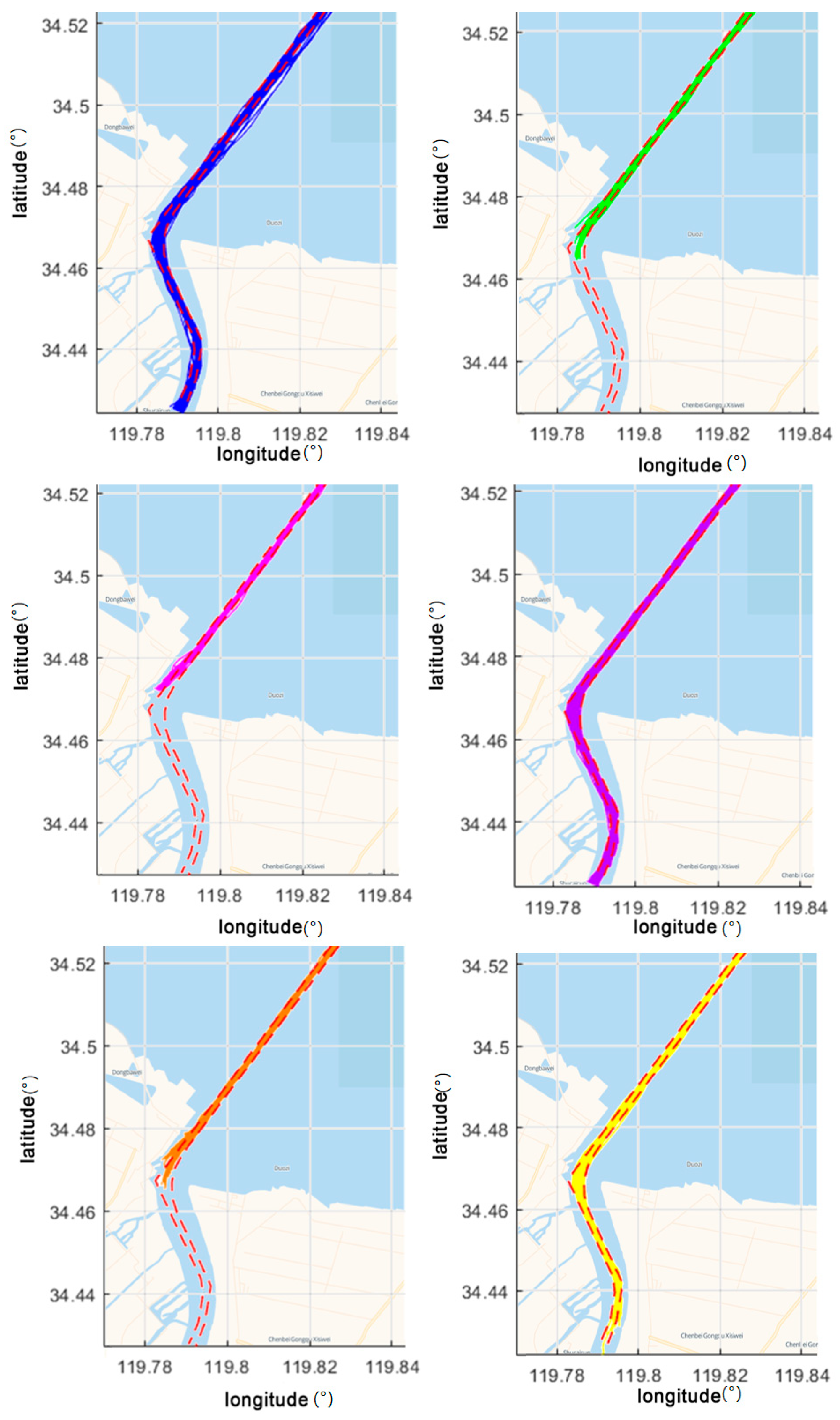
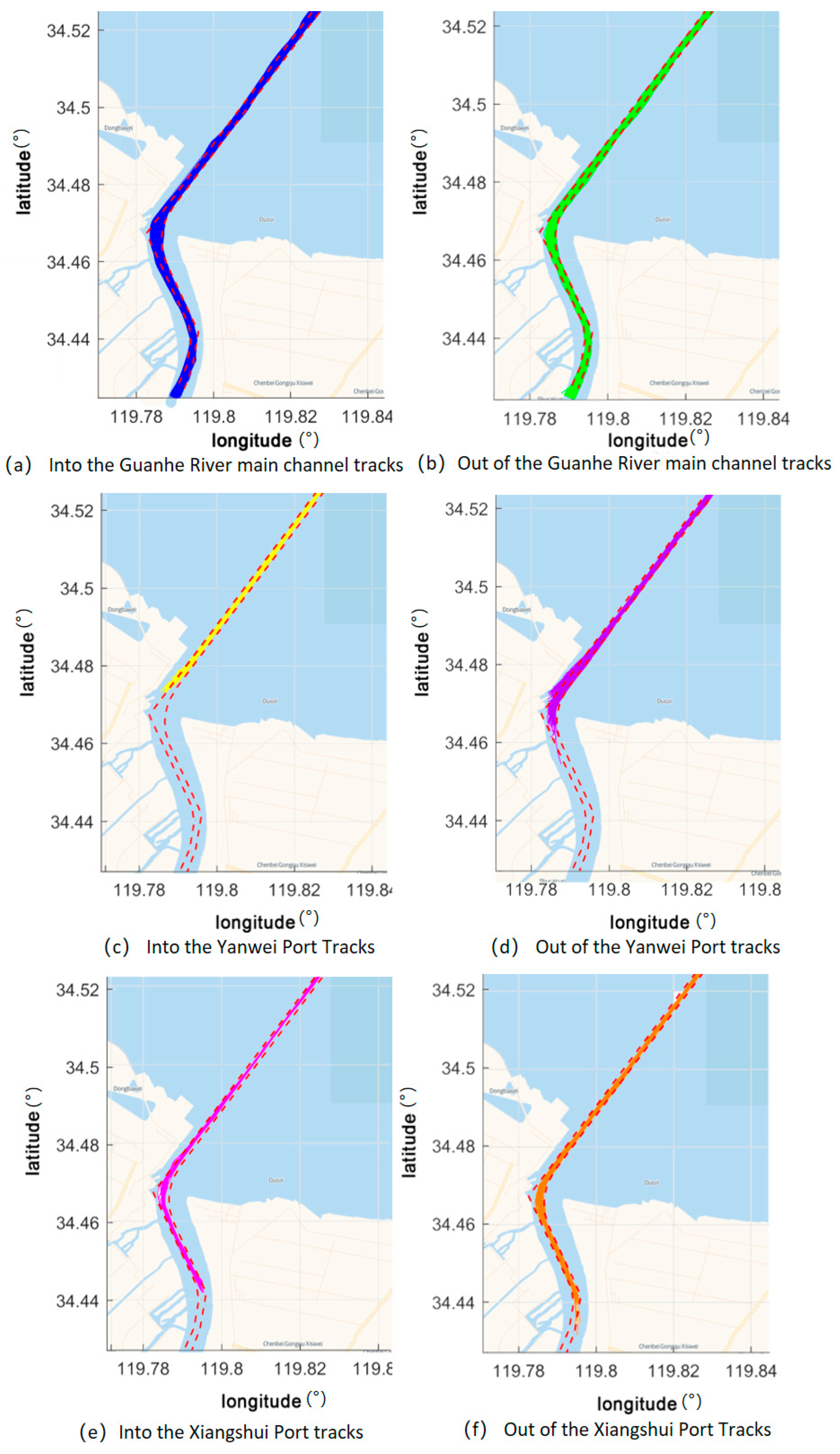
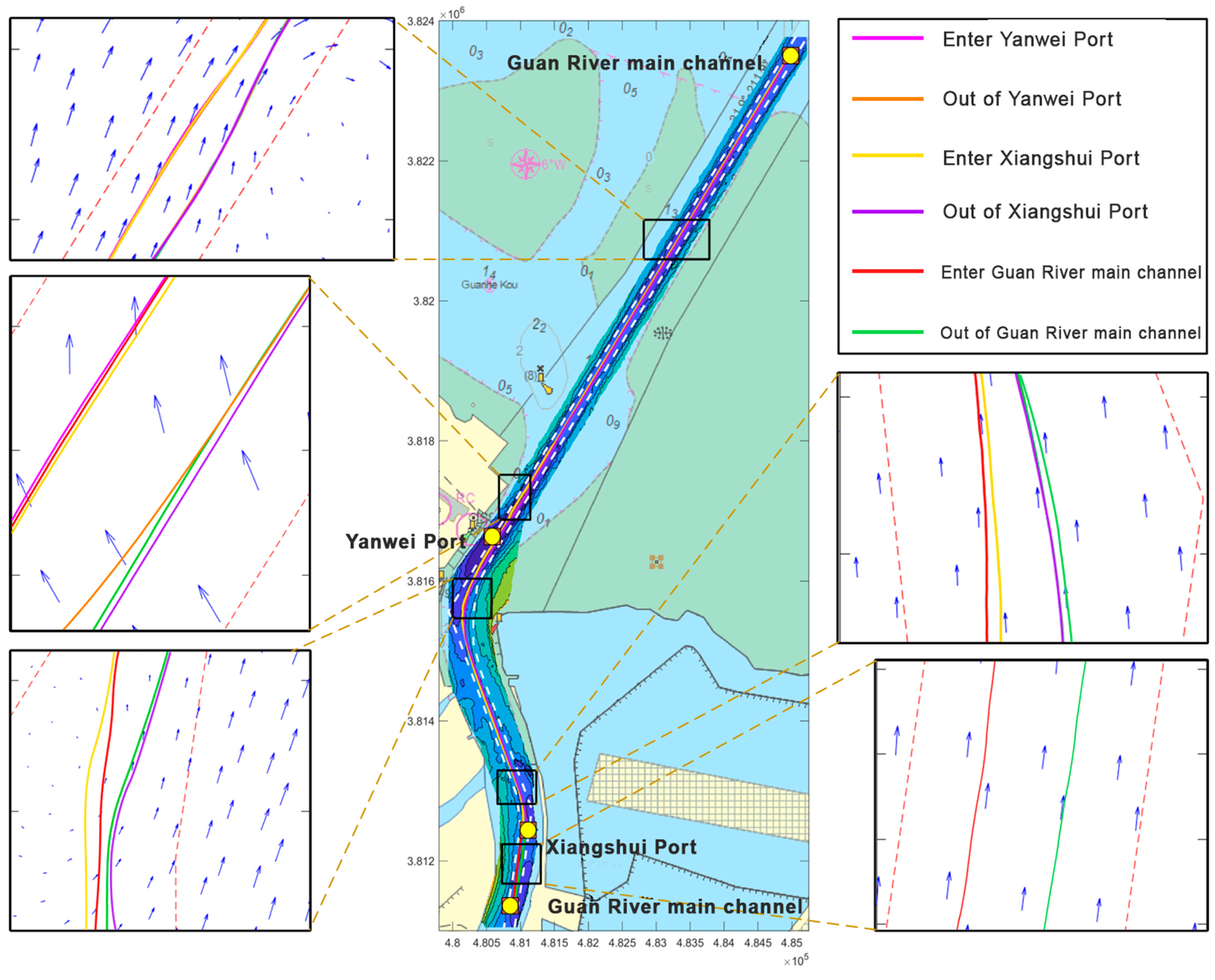
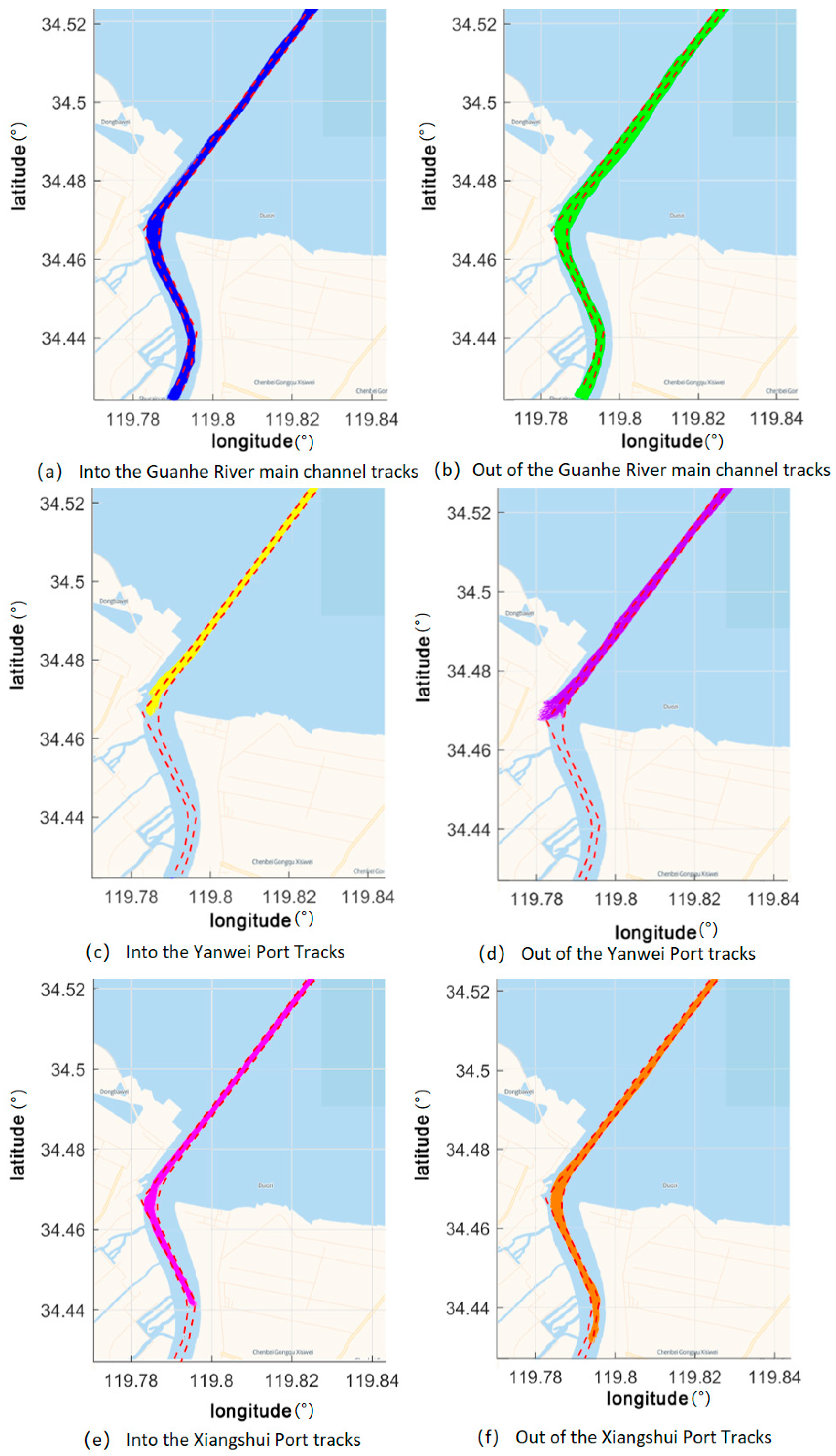
3.3. Clustering Results of Ship Trajectories
3.3.1. Clustering and Trajectories of Ships under 60 m
3.3.2. Clustering and Trajectories of Ships over 60 m
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mazzarella, F.; Vespe, M.; Damalas, D.; Osio, G. Discovering vessel activities at sea using AIS data: Mapping of fishing footprints. In Proceedings of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014; pp. 1–7. [Google Scholar]
- Shelmerdine, R.L. Teasing out the detail: How our understanding of marine AIS data can better inform industries, developments, and planning. Mar. Policy 2015, 54, 17–25. [Google Scholar] [CrossRef]
- Simsir, U.; Ertugrul, S. Prediction of manually controlled vessels’ position and course navigating in narrow waterways using Artificial Neural Networks. Appl. Soft Comput. 2009, 9, 1217–1224. [Google Scholar] [CrossRef]
- Raja, M.; Hasan, P.; Mahmudunnobe, M.; Saifuddin, M.; Hasan, S.N. Membership determination in open clusters using the DBSCAN Clustering Algorithm. Astron. Comput. 2024, 47, 100826. [Google Scholar] [CrossRef]
- Vespe, M.; Visentini, I.; Bryan, K.; Braca, P. Unsupervised learning of maritime traffic patterns for anomaly detection. In Proceedings of the 9th IET Data Fusion & Target Tracking Conference (DF&TT 2012): Algorithms & Applications, London, UK, 16–17 May 2012; pp. 1–5. [Google Scholar]
- Bakdi, A.; Glad, I.K.; Vanem, E.; Engelhardtsen, Ø. AIS-Based Multiple Vessel Collision and Grounding Risk Identification based on Adaptive Safety Domain. J. Mar. Sci. Eng. 2019, 8, 5. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, W.; Liu, Q.; Wang, W. AIS data repair model based on generative adversarial network. Reliab. Eng. Syst. Saf. 2023, 240, 109572. [Google Scholar] [CrossRef]
- Knorr, E.M.; Ng, R.T.; Tucakov, V. Distance-based outliers: Algorithms and applications. VLDB J. Int. J. Very Large Data Bases 2000, 8, 237–253. [Google Scholar] [CrossRef]
- Lin, B.; Zheng, M.; Chu, X.; Zhang, M.; Mao, W.; Wu, D. A novel method for the evaluation of ship berthing risk using AIS data. Ocean Eng. 2024, 293, 116595. [Google Scholar] [CrossRef]
- Yang, J.; Bian, X.; Qi, Y.; Wang, X.; Yang, Z.; Liu, J. A spatial-temporal data mining method for the extraction of vessel traffic patterns using AIS data. Ocean Eng. 2024, 293, 116454. [Google Scholar] [CrossRef]
- Laxhammar, R.; Falkman, G.; Sviestins, E. Anomaly detection in sea traffic—A comparison of the Gaussian Mixture Model and the Kernel Density Estimator. In Proceedings of the 2009 12th International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009; pp. 756–763. [Google Scholar]
- Qian, J.; Zhou, Y.; Han, X.; Wang, Y. MDBSCAN: A multi-density DBSCAN based on relative density. Neurocomputing 2024, 576, 127329. [Google Scholar] [CrossRef]
- Newaliya, N.; Singh, Y. Multivariate hierarchical DBSCAN model for enhanced maritime data analytics. Data Knowl. Eng. 2024, 150, 102282. [Google Scholar] [CrossRef]
- Ouyang, T.; Shen, X. Online structural clustering based on DBSCAN extension with granular descriptors. Inf. Sci. 2022, 607, 688–704. [Google Scholar] [CrossRef]
- Ros, F.; Guillaume, S.; Riad, R.; El Hajji, M. Detection of natural clusters via S-DBSCAN a Self-tuning version of DBSCAN. Knowl.-Based Syst. 2022, 241, 108288. [Google Scholar] [CrossRef]
- Zhu, Q.; Tang, X.; Elahi, A. Application of the novel harmony search optimization algorithm for DBSCAN clustering. Expert Syst. Appl. 2021, 178, 115054. [Google Scholar] [CrossRef]
- de Moura Ventorim, I.; Luchi, D.; Rodrigues, A.L.; Varejão, F.M. BIRCHSCAN: A sampling method for applying DBSCAN to large datasets. Expert Syst. Appl. 2021, 184, 115518. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, S.; Bouguila, N.; Wang, C.; Du, J.; Li, H. A fast clustering algorithm based on pruning unnecessary distance computations in DBSCAN for high-dimensional data. Pattern Recognit. 2018, 83, 375–387. [Google Scholar] [CrossRef]
- Chen, H.; Liang, M.; Liu, W.; Wang, W.; Liu, P.X. An approach to boundary detection for 3D point clouds based on DBSCAN clustering. Pattern Recognit. 2022, 124, 108431. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.F. Anomaly Detection Based on Enhanced DBScan Algorithm. Procedia Eng. 2011, 15, 178–182. [Google Scholar] [CrossRef]
- Gan, L.; Yan, Z.; Zhang, L.; Liu, K.; Zheng, Y.; Zhou, C.; Shu, Y. Ship path planning based on safety potential field in inland rivers. Ocean Eng. 2022, 260, 111928. [Google Scholar] [CrossRef]
- Shu, Y.; Xiong, C.; Zhu, Y.; Liu, K.; Liu, R.W.; Xu, F.; Gan, L.; Zhang, L. Reference path for ships in ports and waterways based on optimal control. Ocean Coast. Manag. 2024, 253, 107168. [Google Scholar] [CrossRef]
- Guo, Z.; Qiang, H.; Xie, S.; Peng, X. Unsupervised knowledge discovery framework: From AIS data processing to maritime traffic networks generating. Appl. Ocean Res. 2024, 146, 103924. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, W.; Yuan, Y. 3D DBSCAN detection and parameter sensitivity of the 2022 Yangtze river summertime heatwave and drought. Atmos. Ocean. Sci. Lett. 2023, 16, 100324. [Google Scholar] [CrossRef]
- Vikhrov, A. Denseness of metric spaces in general position in the Gromov–Hausdorff class. Topol. Its Appl. 2024, 342, 108771. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, C.; Jiang, C. An improvement method of DBSCAN algorithm on cloud computing. Procedia Comput. Sci. 2019, 147, 596–604. [Google Scholar] [CrossRef]
- Gan, L.; Ye, B.; Huang, Z.; Xu, Y.; Chen, Q.; Shu, Y. Knowledge graph construction based on ship collision accident reports to improve maritime traffic safety. Ocean Coast. Manag. 2023, 240, 106660. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Xing, H. A novel method for ship trajectory prediction in complex scenarios based on spatio-temporal features extraction of AIS data. Ocean Eng. 2023, 281, 114846. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, S.; Guo, M.; Liu, Y. A novel ship trajectory clustering analysis and anomaly detection method based on AIS data. Ocean Eng. 2023, 288, 116082. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhang, C. Data mining approach for automatic ship-route design for coastal seas using AIS trajectory clustering analysis. Ocean Eng. 2021, 236, 109535. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C. A framework for ship abnormal behaviour detection and classification using AIS data. Reliab. Eng. Syst. Saf. 2024, 247, 110105. [Google Scholar] [CrossRef]
- Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS Trajectory Clustering: An HDBSCAN-Based Approach. J. Mar. Sci. Eng. 2021, 9, 566. [Google Scholar] [CrossRef]
- Wolsing, K.; Roepert, L.; Bauer, J.; Wehrle, K. Anomaly Detection in Maritime AIS Tracks: A Review of Recent Approaches. J. Mar. Sci. Eng. 2022, 10, 112. [Google Scholar] [CrossRef]
- Jon, M.H.; Kim, Y.P.; Choe, U. Determination of a safety criterion via risk assessment of marine accidents based on a Markov model with five states and MCMC simulation and on three risk factors. Ocean Eng. 2021, 236, 109000. [Google Scholar] [CrossRef]
- Liu, K.; Yuan, Z.; Xin, X.; Zhang, J.; Wang, W. Conflict detection method based on dynamic ship domain model for visualization of collision risk Hot-Spots. Ocean Eng. 2021, 242, 110143. [Google Scholar] [CrossRef]
- Shu, Y.; Han, B.; Song, L.; Yan, T.; Gan, L.; Zhu, Y.; Zheng, C. Analyzing the spatio-temporal correlation between tide and shipping behavior at estuarine port for energy-saving purposes. Appl. Energy 2024, 367, 123382. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Cui, F.; Liu, Y.; Liu, Z.; Dong, J. Research into Ship Trajectory Prediction Based on An Improved LSTM Network. J. Mar. Sci. Eng. 2023, 11, 1268. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Yang, Y.; Wang, P.; Wang, Z.; Li, Z.; Mei, Q.; Sun, Y. Maritime greenhouse gas emission estimation and forecasting through AIS data analytics: A case study of Tianjin port in the context of sustainable development. Front. Mar. Sci. 2023, 10, 1308981. [Google Scholar] [CrossRef]
- Shu, Y.; Hu, A.; Zheng, Y.; Gan, L.; Xiao, G.; Zhou, C.; Song, L. Evaluation of ship emission intensity and the inaccuracy of exhaust emission estimation model. Ocean Eng. 2023, 287, 115723. [Google Scholar] [CrossRef]
- Ferrara, R.; Virdis, S.G.P.; Ventura, A.; Ghisu, T.; Duce, P.; Pellizzaro, G. An automated approach for wood-leaf separation from terrestrial LIDAR point clouds using the density based clustering algorithm DBSCAN. Agric. For. Meteorol. 2018, 262, 434–444. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.-Y. Ship-handling behavior pattern recognition using AIS sub-trajectory clustering analysis based on the T-SNE and spectral clustering algorithms. Ocean Eng. 2020, 205, 106919. [Google Scholar] [CrossRef]



| Parameters | MinNum | ||||||
|---|---|---|---|---|---|---|---|
| Values | 42 | 0.6 | 0.1 | 0.3 | 0.5 | 0.4 | 0.1 |
| eps | Number of Clusters | Noise Ratio | DB Index |
|---|---|---|---|
| 0.0010 | 5 | 28.12% | 1.67 |
| 0.0014 | 6 | 15.35% | 0.88 |
| 0.0018 | 6 | 12.21% | 0.97 |
| 0.0022 | 5 | 10.63% | 1.26 |
| 0.0025 | 5 | 8.59% | 1.33 |
| 0.0030 | 4 | 6.87% | 1.46 |
| Parameters | eps | MinNum | ||||||
|---|---|---|---|---|---|---|---|---|
| Values | 0.0014 | 50 | 0.6 | 0.3 | 0.5 | 0.4 | 0.1 |
| POINT | 1 | 2 | 3 | 4 | 5 | 6 | ... | 33 | 34 | 35 | ... | 98 | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE (m) | |−7| | |−8| | |−5| | |−6| | |−6| | |−5| | ... | |−18| | |−20| | |−17| | ... | |−9| | |−10| | |−11| |
| Parameters | eps | MinNum | ||||||
|---|---|---|---|---|---|---|---|---|
| Values | 0.0014 | 42 | 0.6 | 0.3 | 0.5 | 0.4 | 0.1 |
| POINT | 1 | 2 | 3 | 4 | 5 | 6 | ... | 39 | 40 | 41 | ... | 98 | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE (m) | |−7| | |−6| | |−4| | |−3| | |−3| | |−4| | ... | |−23| | |−25| | |−22| | ... | |−16| | |−15| | |−14| |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yang, H.; Xiong, C.; Xu, F.; Gan, L.; Yan, T.; Shu, Y. Research on the Optimization of Ship Trajectory Clustering Based on the OD–Hausdorff Distance. J. Mar. Sci. Eng. 2024, 12, 1398. https://doi.org/10.3390/jmse12081398
Liu Z, Yang H, Xiong C, Xu F, Gan L, Yan T, Shu Y. Research on the Optimization of Ship Trajectory Clustering Based on the OD–Hausdorff Distance. Journal of Marine Science and Engineering. 2024; 12(8):1398. https://doi.org/10.3390/jmse12081398
Chicago/Turabian StyleLiu, Zhiyao, Haining Yang, Chenghuai Xiong, Feng Xu, Langxiong Gan, Tao Yan, and Yaqing Shu. 2024. "Research on the Optimization of Ship Trajectory Clustering Based on the OD–Hausdorff Distance" Journal of Marine Science and Engineering 12, no. 8: 1398. https://doi.org/10.3390/jmse12081398
APA StyleLiu, Z., Yang, H., Xiong, C., Xu, F., Gan, L., Yan, T., & Shu, Y. (2024). Research on the Optimization of Ship Trajectory Clustering Based on the OD–Hausdorff Distance. Journal of Marine Science and Engineering, 12(8), 1398. https://doi.org/10.3390/jmse12081398






