Trajectory Tracking Control for an Underactuated AUV via Nonsingular Fast Terminal Sliding Mode Approach
Abstract
:1. Introduction
2. Problem Formulation
3. Main Results
3.1. Trajectory Tracking Error Equation
3.2. Design of Controller
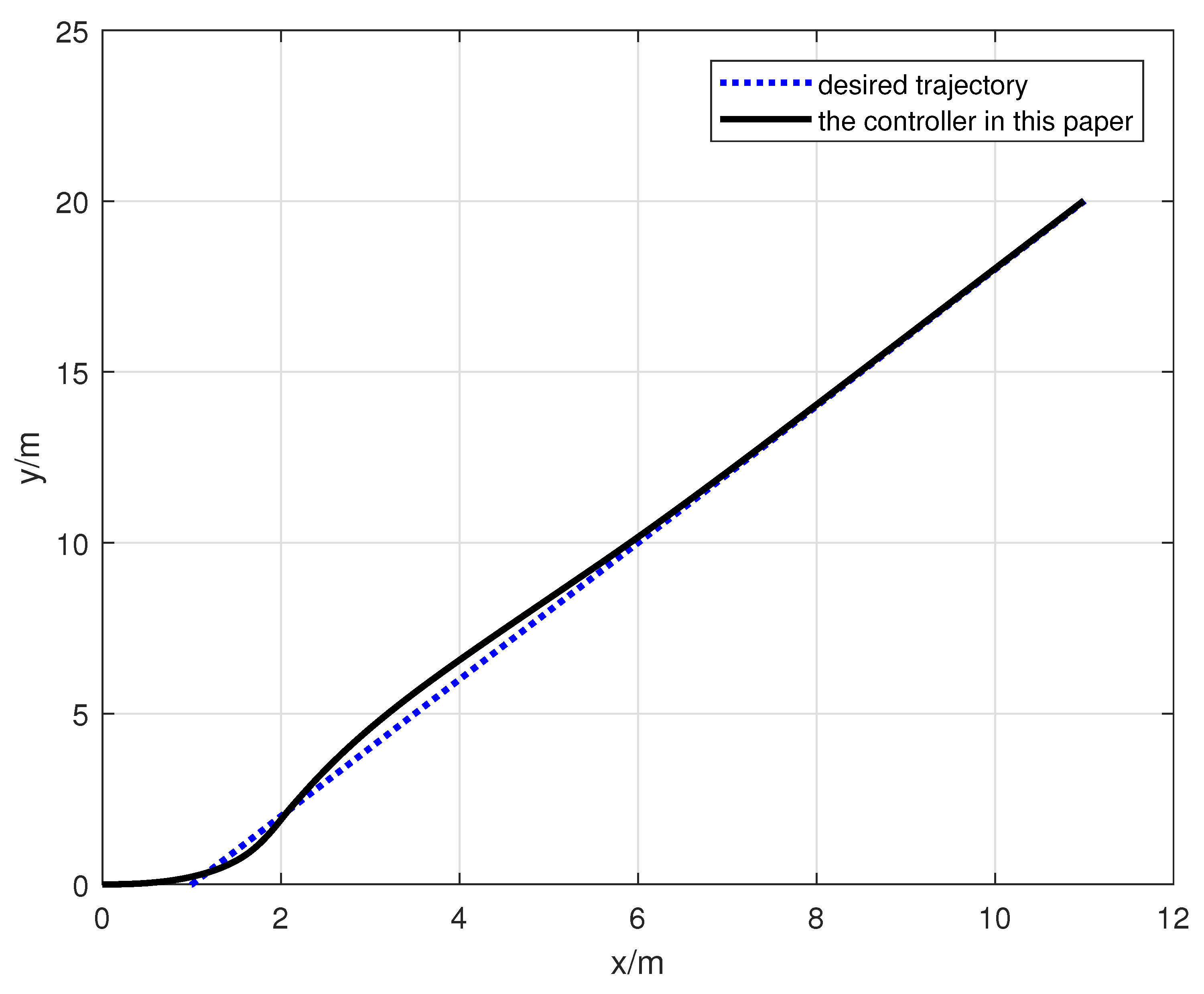
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, J.; Yang, J.; Zhang, C.; Zhang, J.; Zhang, T. Autonomous Underwater Vehicle Trajectory Prediction with the Nonlinear Kepler Optimization Algorithm–Bidirectional Long Short-Term Memory–Time-Variable Attention Model. J. Mar. Sci. Eng. 2024, 12, 1115. [Google Scholar] [CrossRef]
- Shao, G.; Wan, L.; Xu, H. Formation Control of Autonomous Underwater Vehicles Using an Improved Nonlinear Backstepping Method. J. Mar. Sci. Eng. 2024, 12, 878. [Google Scholar] [CrossRef]
- Gutnik, Y.; Groper, M. Terminal Phase Navigation for AUV Docking: An Innovative Electromagnetic Approach. J. Mar. Sci. Eng. 2024, 12, 192. [Google Scholar] [CrossRef]
- Hedayati Khodayari, M.; Pariz, N.; Balochian, S. Admissibility analysis for autonomous underwater vehicle based on descriptor model with time-varying delay. J. Vib. Control 2022, 28, 3302–3314. [Google Scholar] [CrossRef]
- Huang, H.; Wen, X.; Niu, M.; Miah, M.S.; Wang, H.; Gao, T. Multi-Objective Path Planning of Autonomous Underwater Vehicles Driven by Manta Ray Foraging. J. Mar. Sci. Eng. 2024, 12, 88. [Google Scholar] [CrossRef]
- Zhang, B.; Ji, D.; Liu, S.; Zhu, X.; Xu, W. Autonomous Underwater Vehicle navigation: A review. Ocean Eng. 2023, 273, 113861. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P.S. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Jiang, X.S.; Feng, X.S.; Wang, D.T. Unmanned Underwater Vehicles; Liaoning Science and Technology Press: Shenyang, China, 2000. [Google Scholar]
- Cho, G.R.; Li, J.H.; Park, D.; Jung, J.H. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation. Ocean Eng. 2020, 201, 107131. [Google Scholar] [CrossRef]
- Xu, J.; Wang, M.; Qiao, L. Backstepping-based controller for three-dimensional trajectory tracking of underactuated unmanned underwater vehicles. Control Theory Appl. 2014, 31, 1589–1596. [Google Scholar]
- Yan, Z.; Wang, M.; Xu, J. Global adaptive neural network control of underactuated autonomous underwater vehicles with parametric modeling uncertainty. Asian J. Control 2019, 21, 1342–1354. [Google Scholar] [CrossRef]
- Xia, G.Q.; Yang, Y. FNN-based L2 following control of underactuated autonomous underwater vehicles. Control Decis. 2013, 28, 351–356. [Google Scholar]
- Ma, L.M. Global chattering-free sliding mode trajectory tracking control of underactuated autonomous underwater vehicles. CAAI Trans. Intell. Syst. 2016, 11, 200–207. [Google Scholar]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef]
- Ma, C.; Jia, J.; Zhang, T.; Wu, S.; Jiang, D. Horizontal trajectory tracking control for underactuated autonomous underwater vehicles based on contraction theory. J. Mar. Sci. Eng. 2023, 11, 805. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Fei, S. Nonsingular terminal sliding mode guidance law. J. Southeast Univ. 2009, 39, 87–90. [Google Scholar]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y.; Liu, L.; Fang, Y. Fuzzy multiple hidden layer recurrent neural control of nonlinear system using terminal sliding-mode controller. IEEE Trans. Cybern. 2021, 52, 9519–9534. [Google Scholar] [CrossRef] [PubMed]
- Nekoukar, V.; Dehkordi, N.M. Robust path tracking of a quadrotor using adaptive fuzzy terminal sliding mode control. Control Eng. Pract. 2021, 110, 104763. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Hua, C.; Guan, X. Trajectory tracking control of autonomous underwater vehicle with unknown parameters and external disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1054–1063. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems: Guidance, Navigation, and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Park, B.S. Adaptive formation control of underactuated autonomous underwater vehicles. Ocean Eng. 2015, 96, 1–7. [Google Scholar] [CrossRef]
- Tang, S.C. Modeling and Simulation of the Autonomous Underwater Vehicle, Autolycus. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Alberti, J. Modeling and Model Identification of Autonomous Underwater Vehicles. Ph.D. Dissertation, Naval Postgraduate School, Monterey, CA, USA, 2015. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Brockett, R.W. Asymptotic stability and feedback stabilization. Differ. Geom. Control. Theory 1983, 27, 181–191. [Google Scholar]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, Y.; He, K.; Chen, C. Fast terminal sliding-mode control based on unknown input observer for the tracking control of underwater vehicles. Ocean Eng. 2022, 264, 112480. [Google Scholar] [CrossRef]
- Herman, P. Trajectory Tracking Nonlinear Controller for Underactuated Underwater Vehicles Based on Velocity Transformation. J. Mar. Sci. Eng. 2023, 11, 509. [Google Scholar] [CrossRef]
- Zhou, B.; Su, Y.; Huang, B.; Wang, W.; Zhang, E. Trajectory tracking control for autonomous underwater vehicles under quantized state feedback and ocean disturbances. Ocean Eng. 2022, 256, 111500. [Google Scholar] [CrossRef]

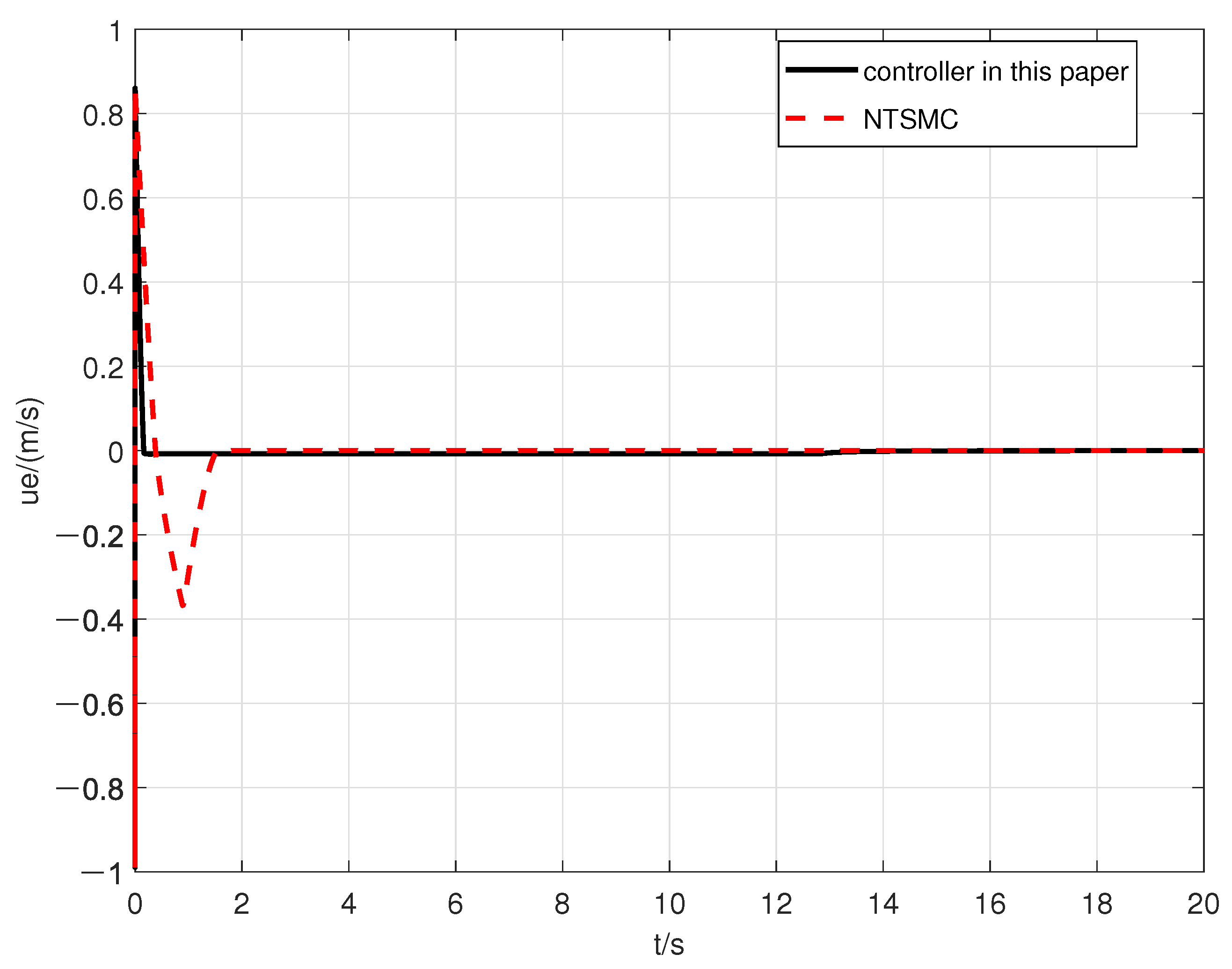
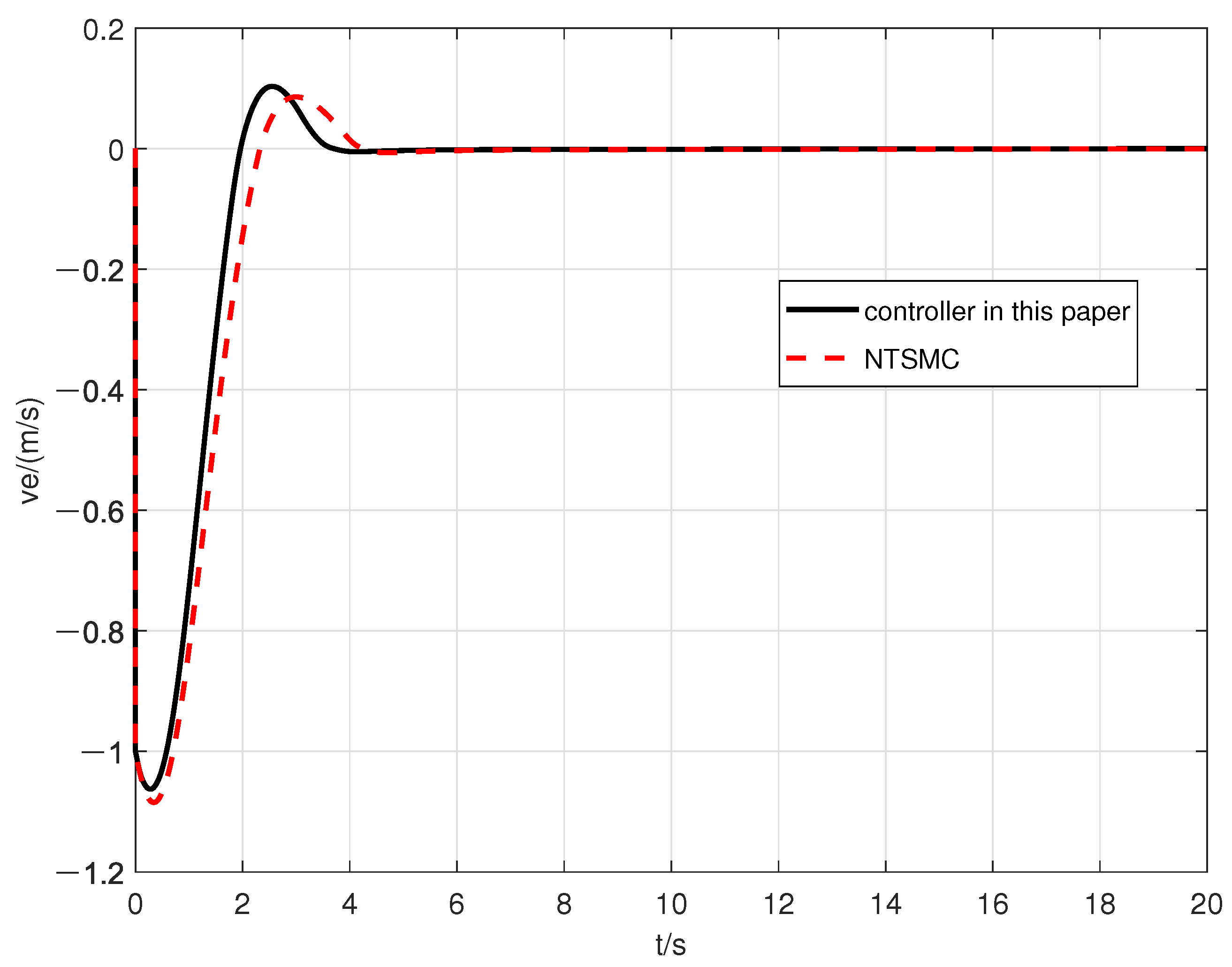
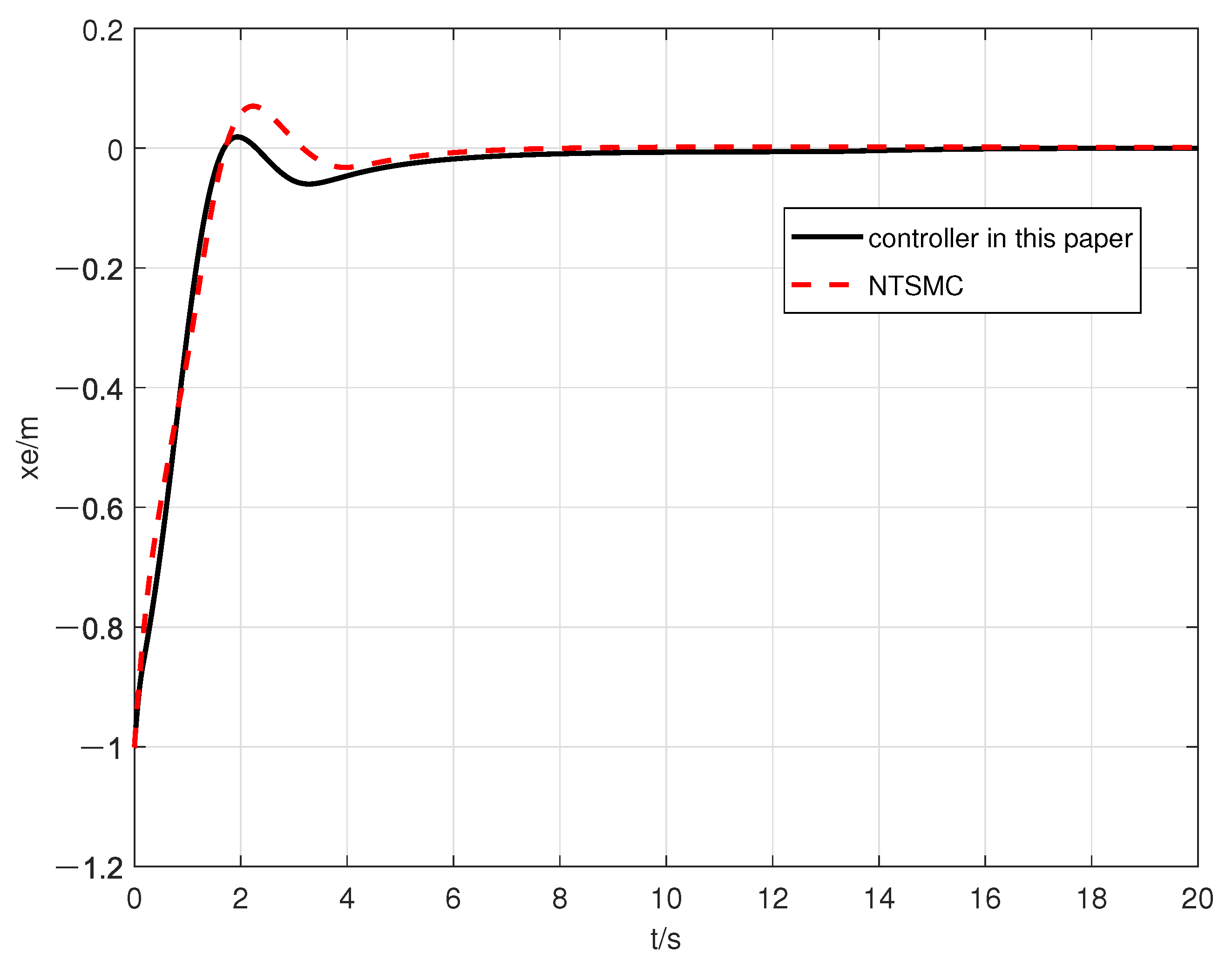
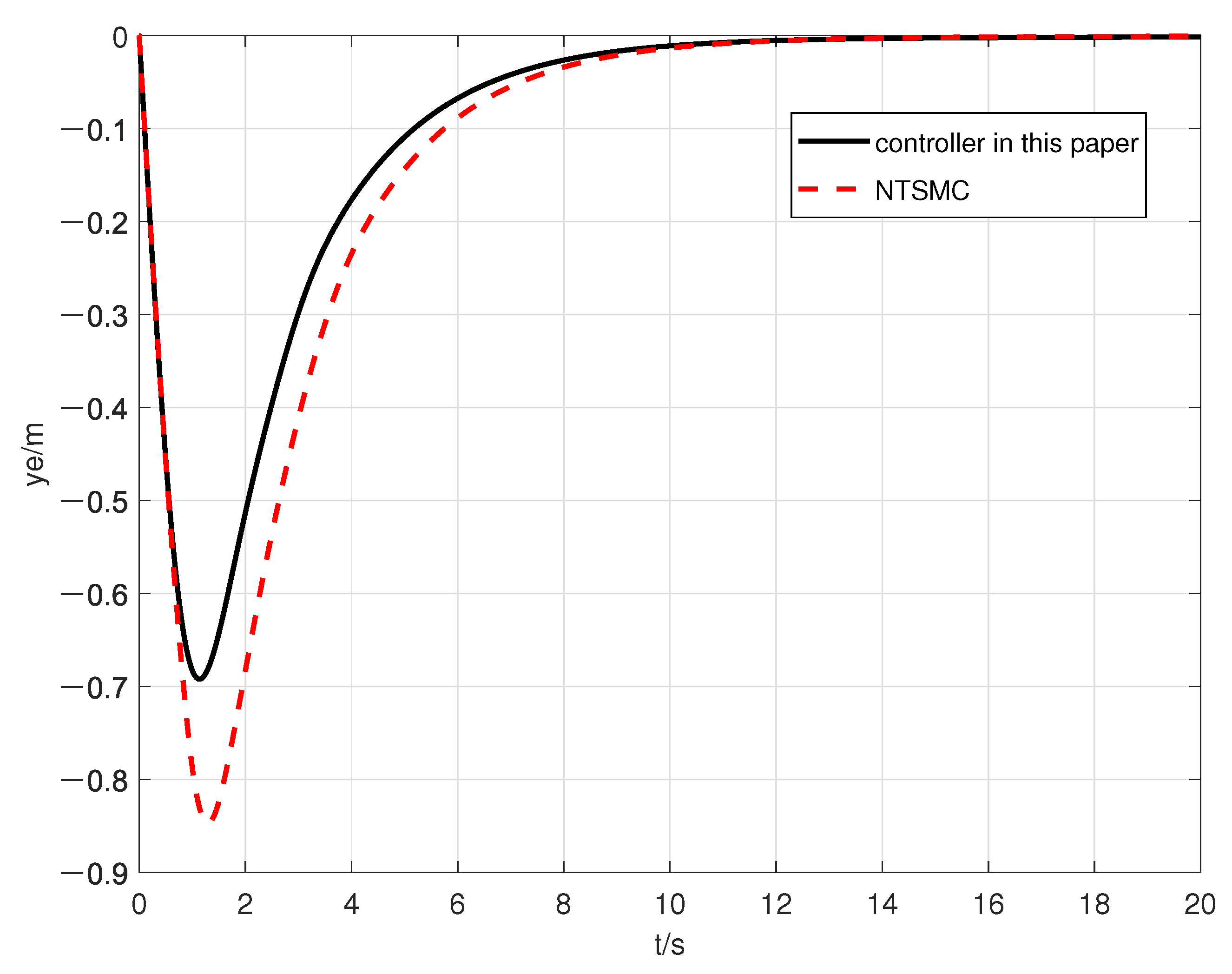
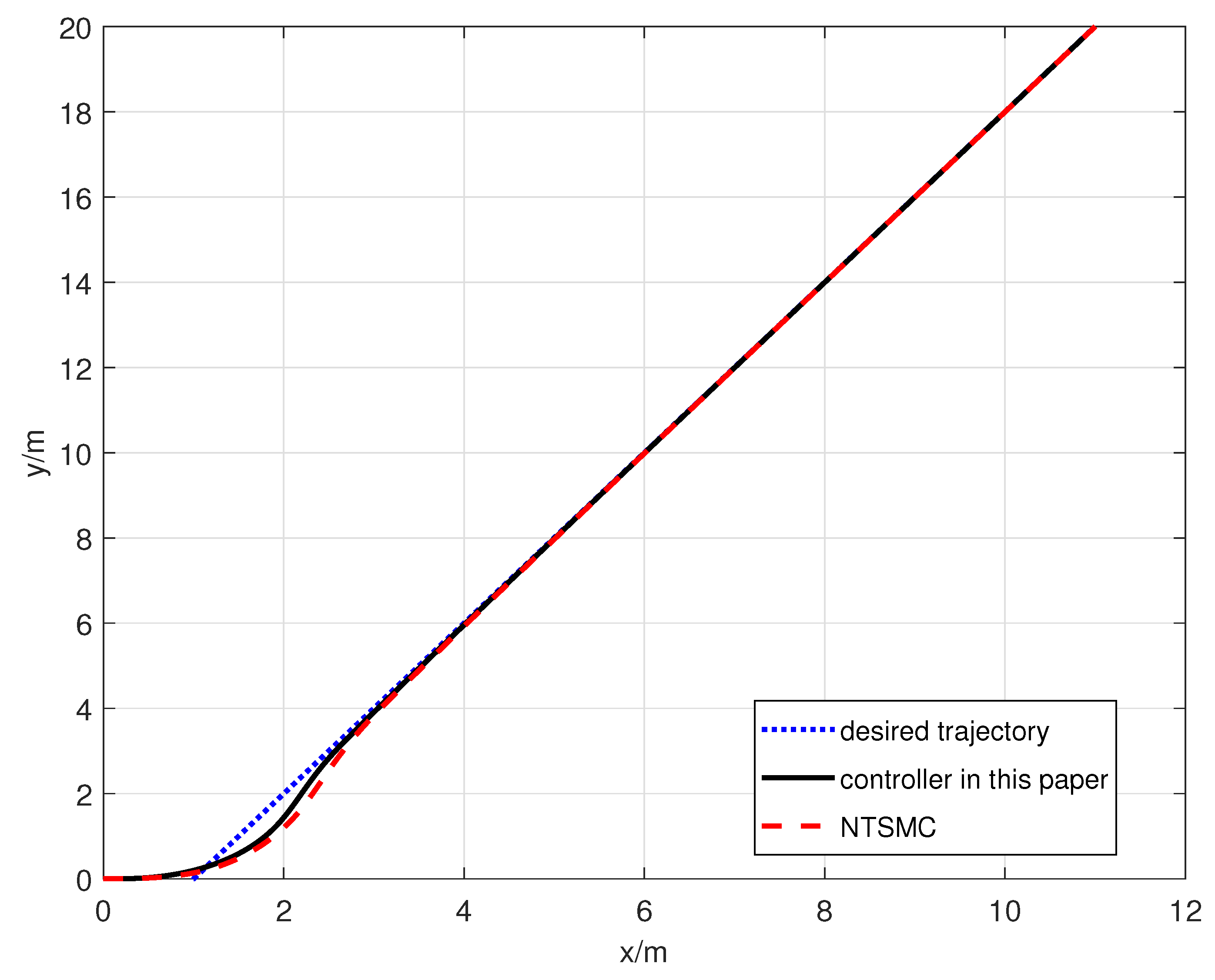
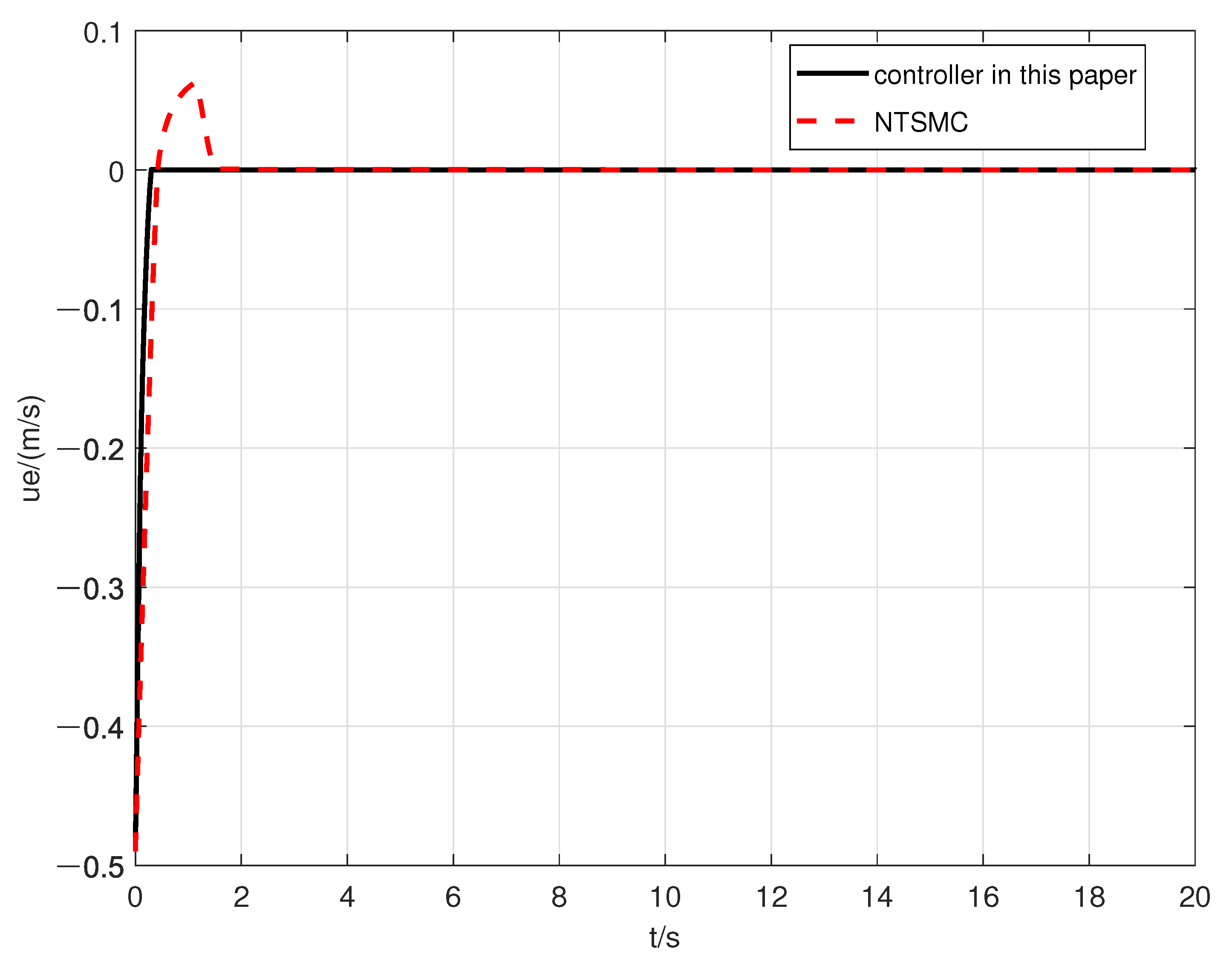
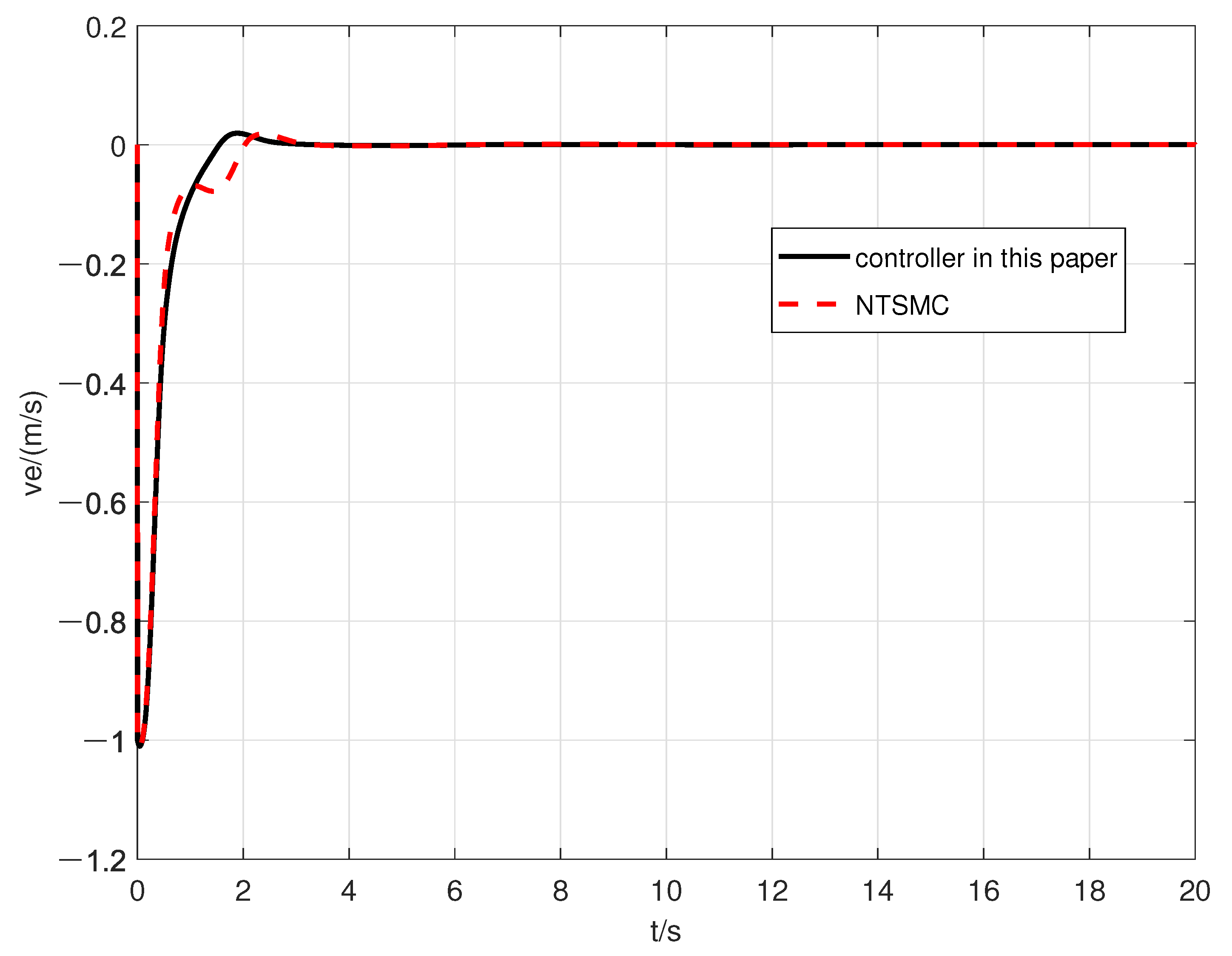
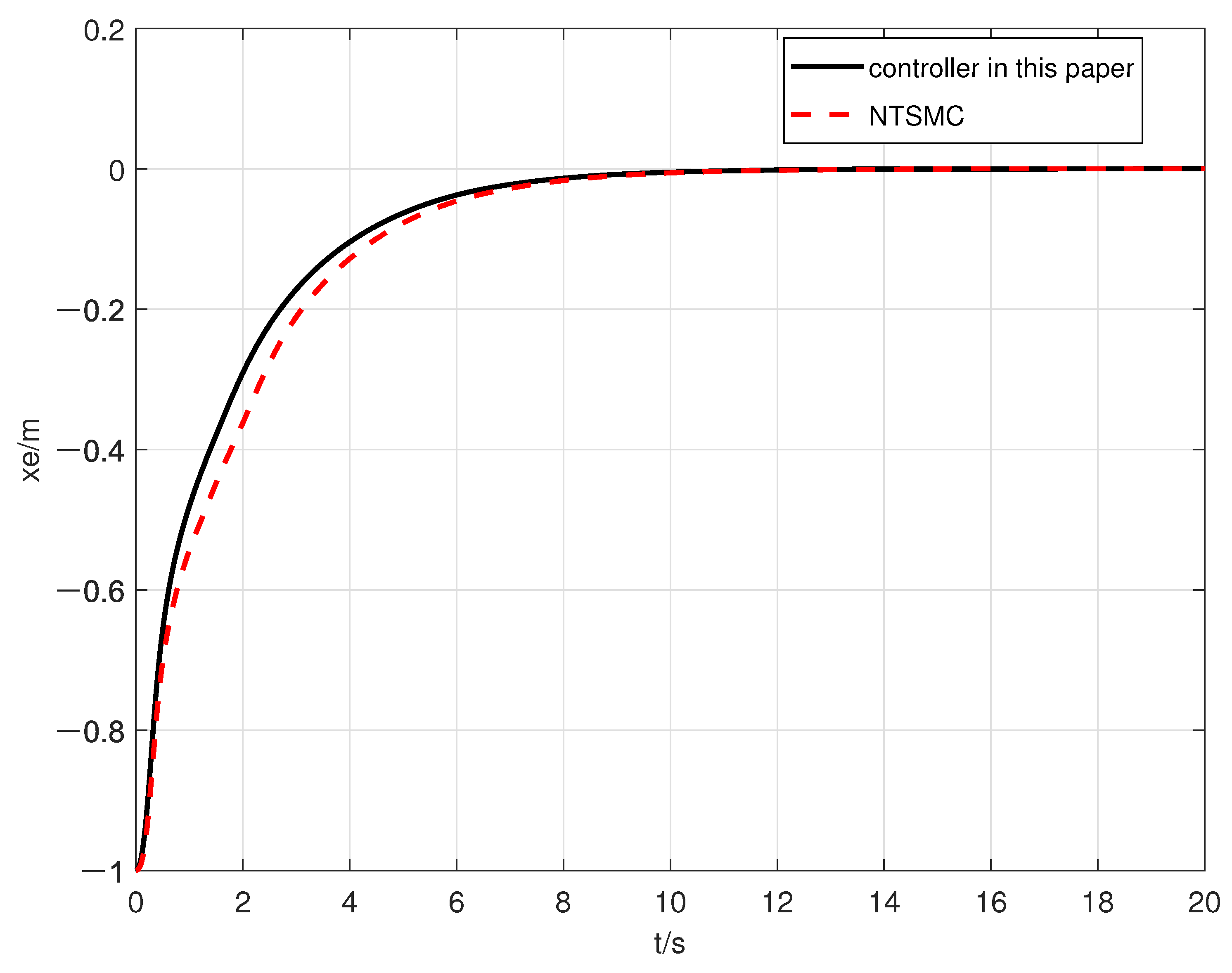
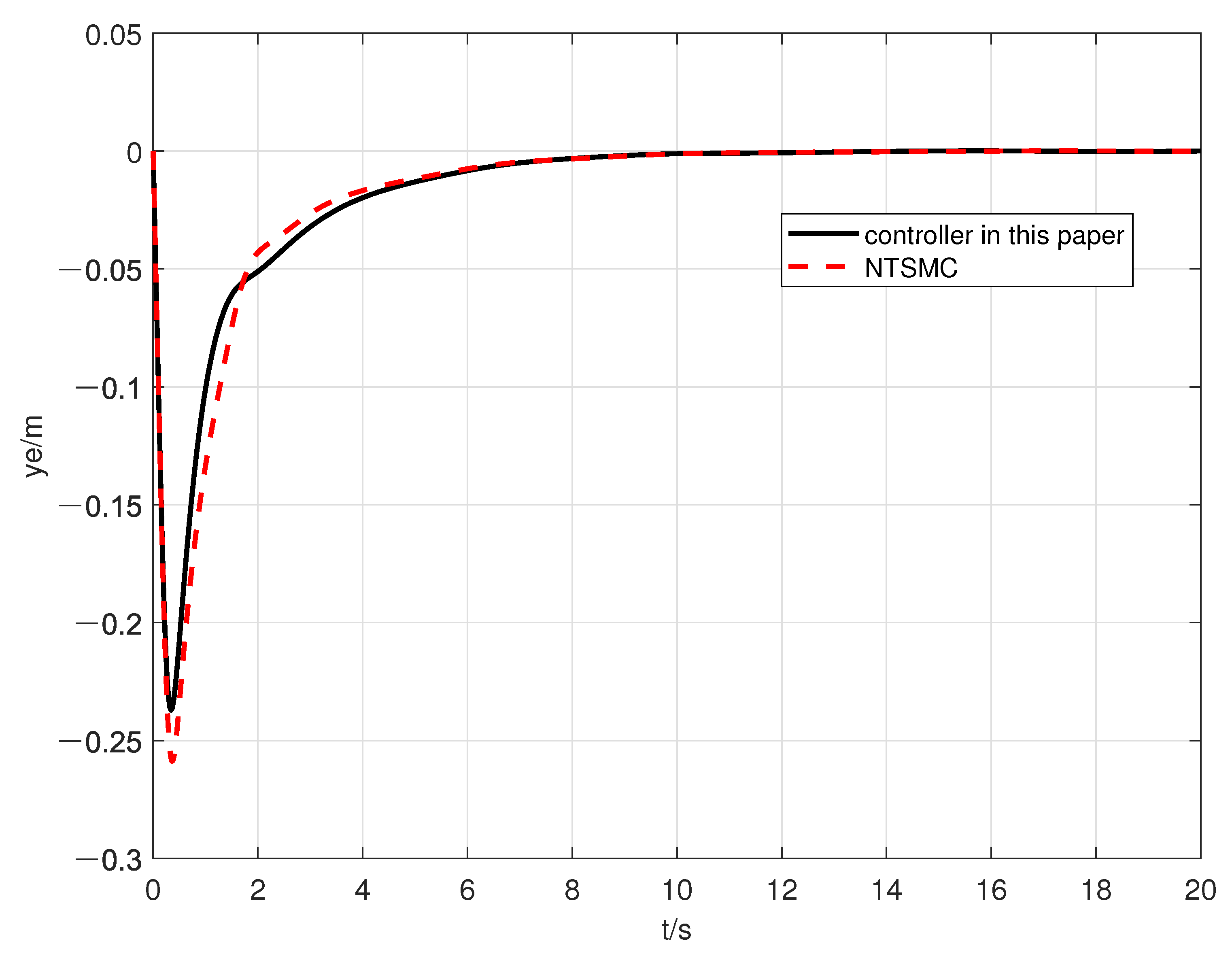
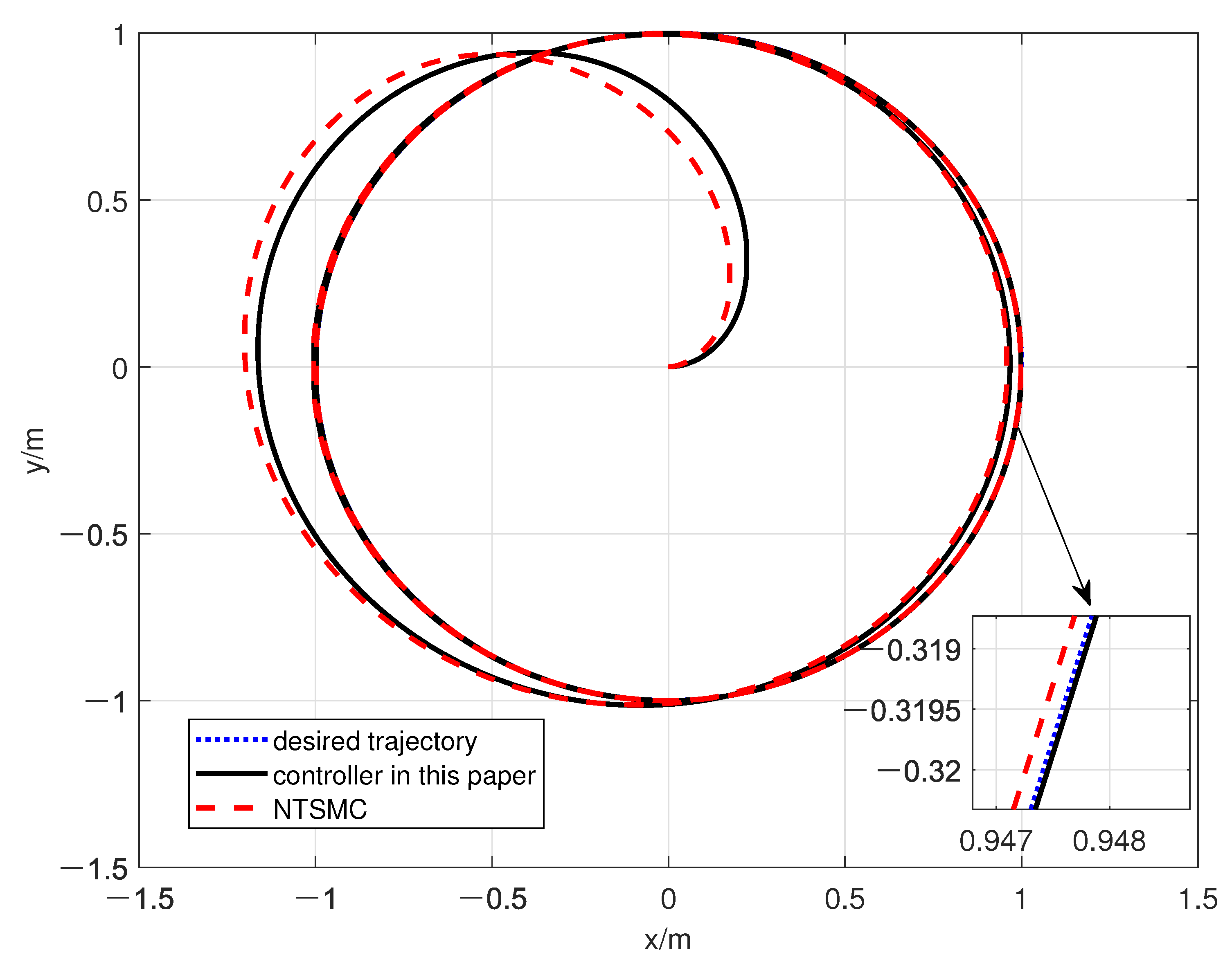

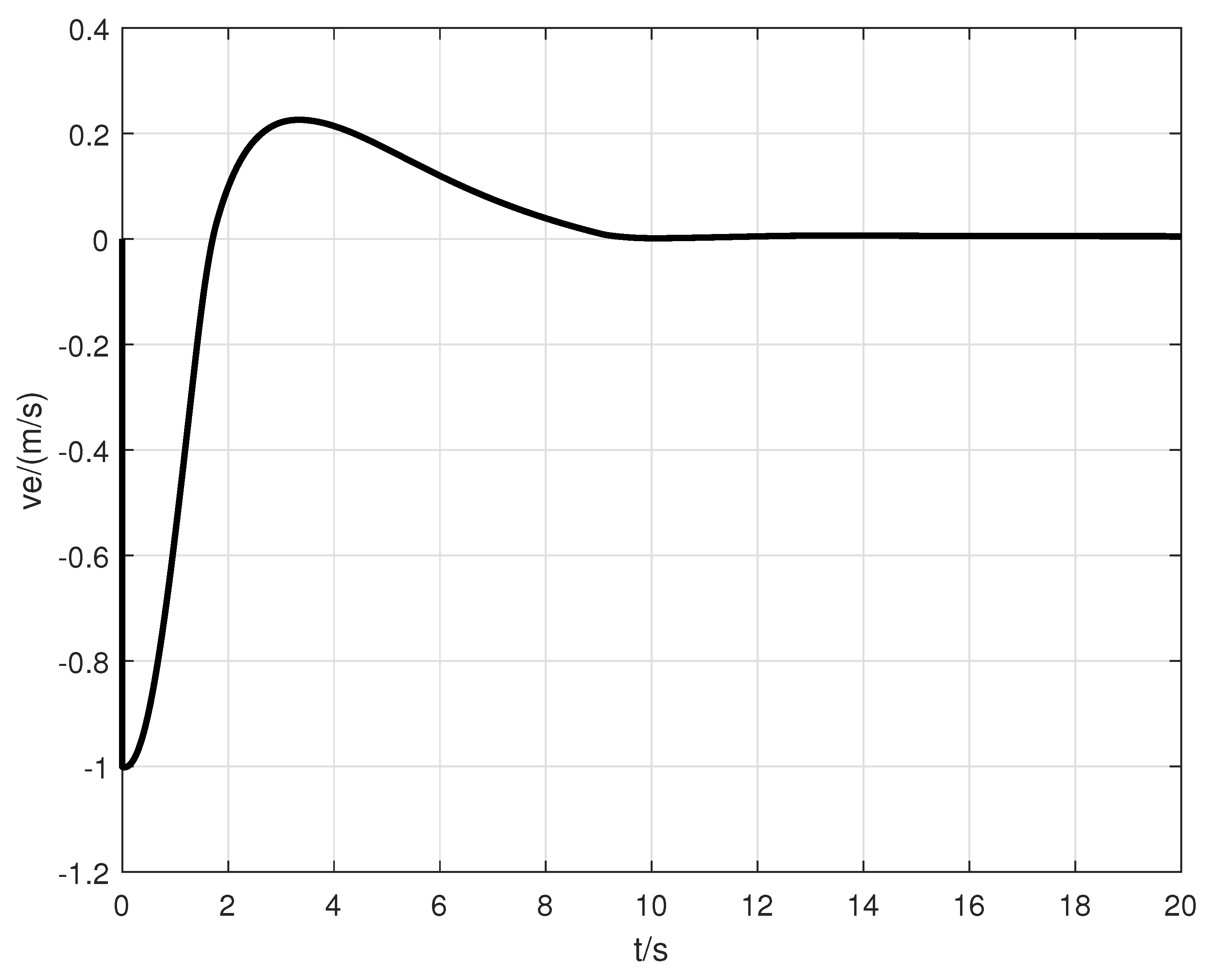

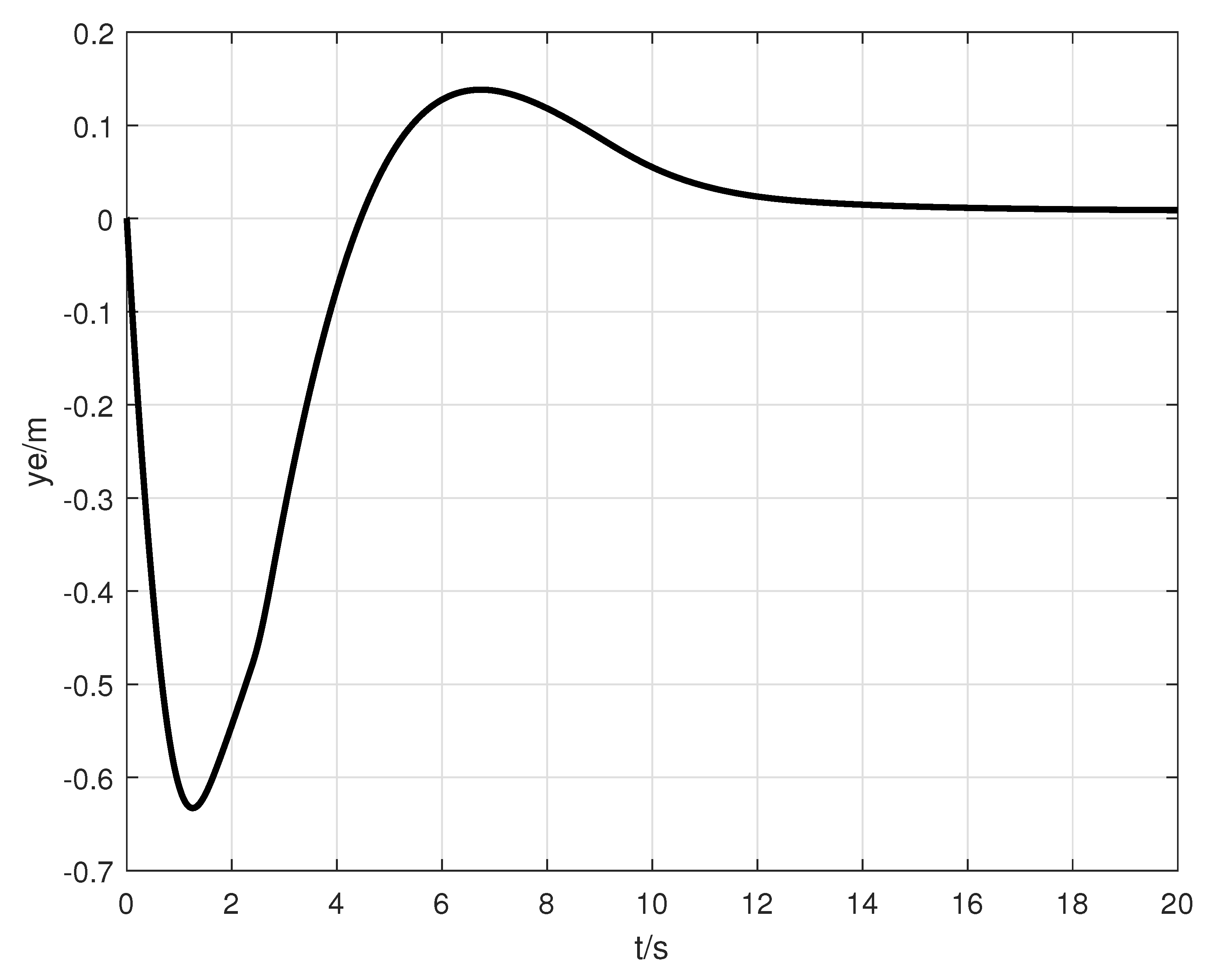
| Error | The Designed Controller in This Paper | The Controller in [21] |
|---|---|---|
| 0.25 s | 1.5 s | |
| 3.6 s | 4.5 s |
| Error | The Designed Controller in This Paper | The Controller in [21] |
|---|---|---|
| 0.4 s | 1.58 s | |
| 2.5 s | 3.3 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Du, Z. Trajectory Tracking Control for an Underactuated AUV via Nonsingular Fast Terminal Sliding Mode Approach. J. Mar. Sci. Eng. 2024, 12, 1442. https://doi.org/10.3390/jmse12081442
Wang Y, Du Z. Trajectory Tracking Control for an Underactuated AUV via Nonsingular Fast Terminal Sliding Mode Approach. Journal of Marine Science and Engineering. 2024; 12(8):1442. https://doi.org/10.3390/jmse12081442
Chicago/Turabian StyleWang, Yuan, and Zhenbin Du. 2024. "Trajectory Tracking Control for an Underactuated AUV via Nonsingular Fast Terminal Sliding Mode Approach" Journal of Marine Science and Engineering 12, no. 8: 1442. https://doi.org/10.3390/jmse12081442




