On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures
Abstract
:1. Introduction
2. Ice Loading on Fixed and Floating Offshore Structures
2.1. Vertical Structures
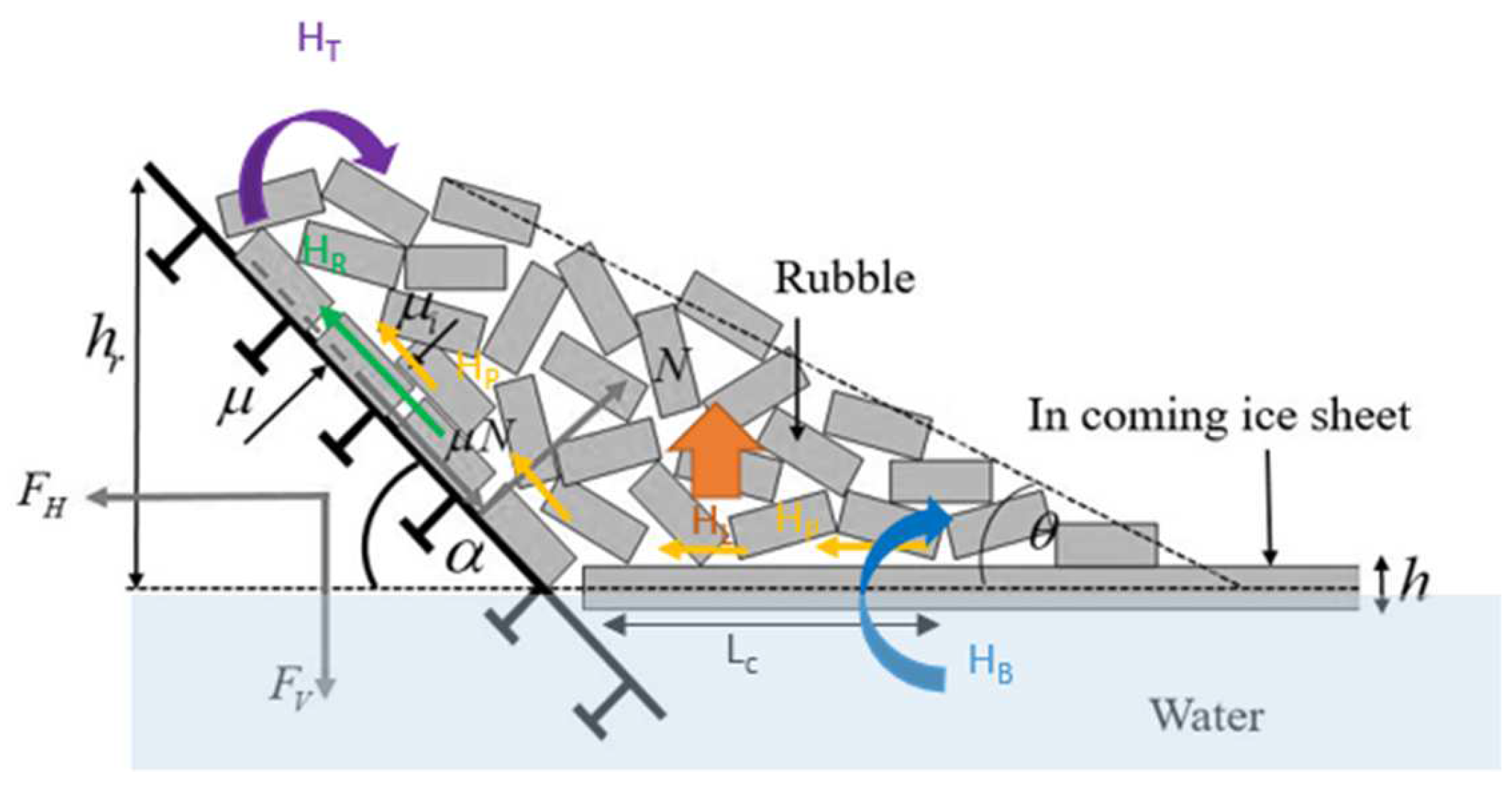
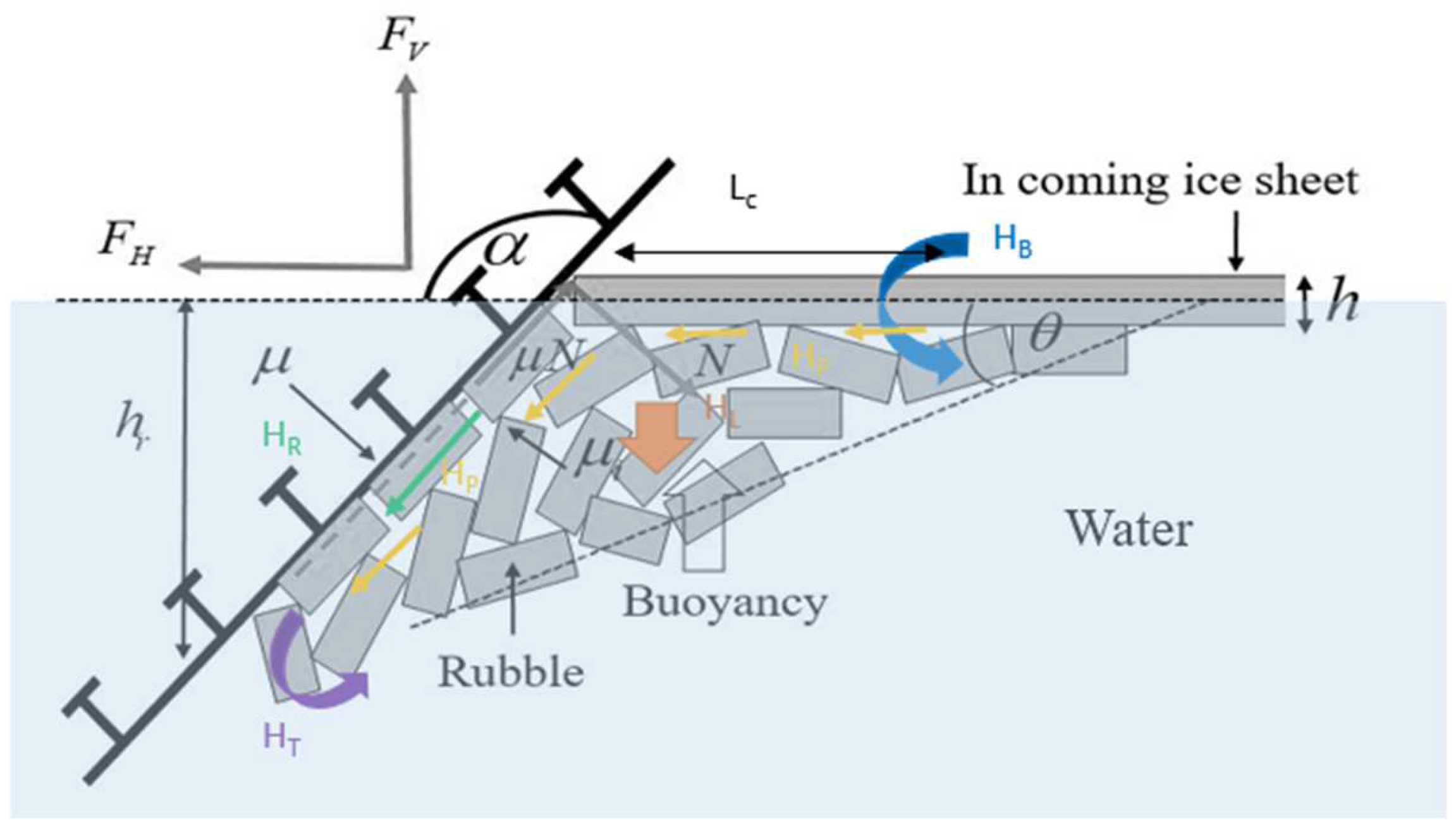
2.2. Sloping Structures
- Breaking load (HB).
- The load component required to push the sheet ice through the ice rubble (HP).
- The load required in order to push the ice blocks up the slope through the ice rubble (HR).
- The load required to lift the ice rubble on top of the advancing ice sheet prior to breaking it (HL).
- The load needed to turn the ice block at the top of the slope (HT).
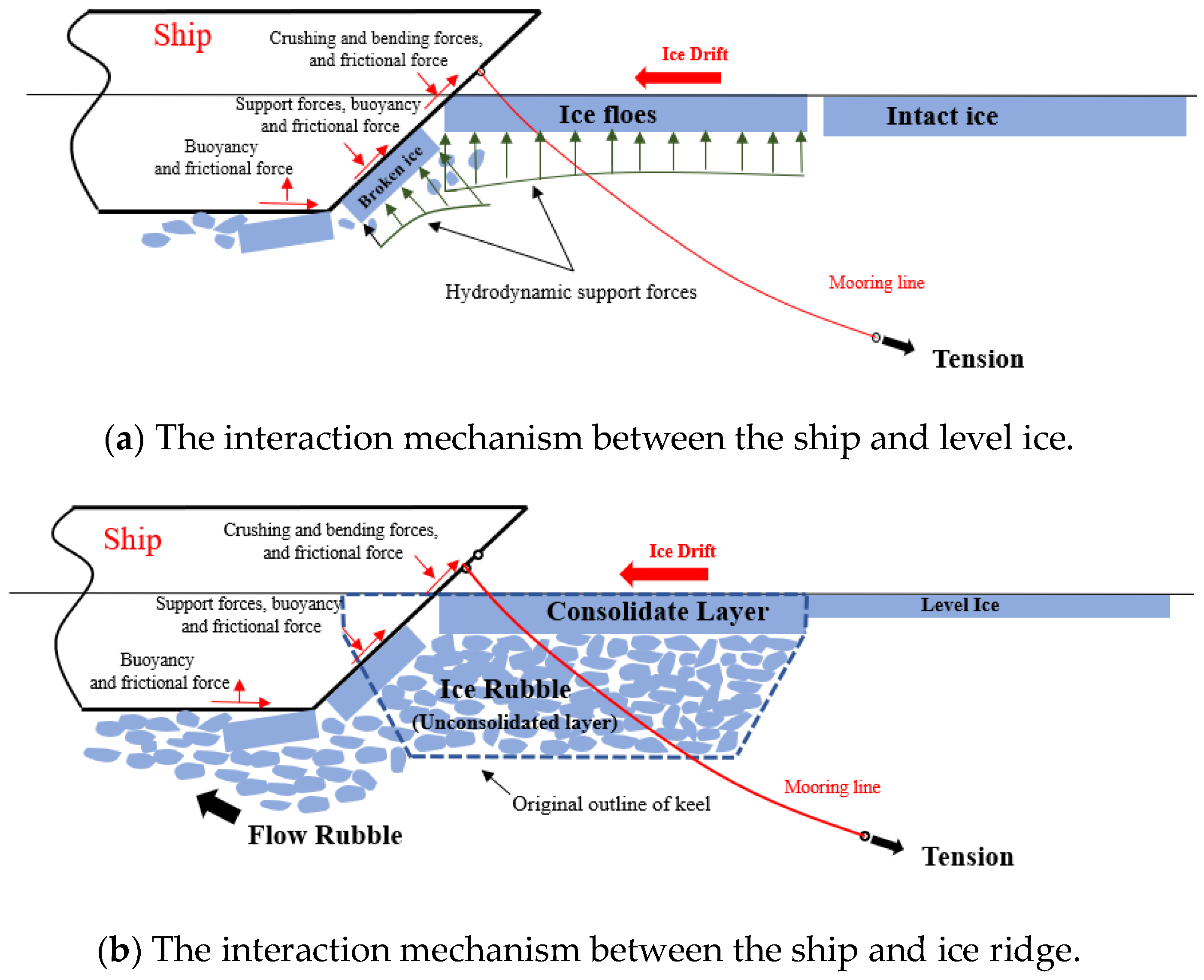
2.3. Ice Load on Vessel Station-Keeping
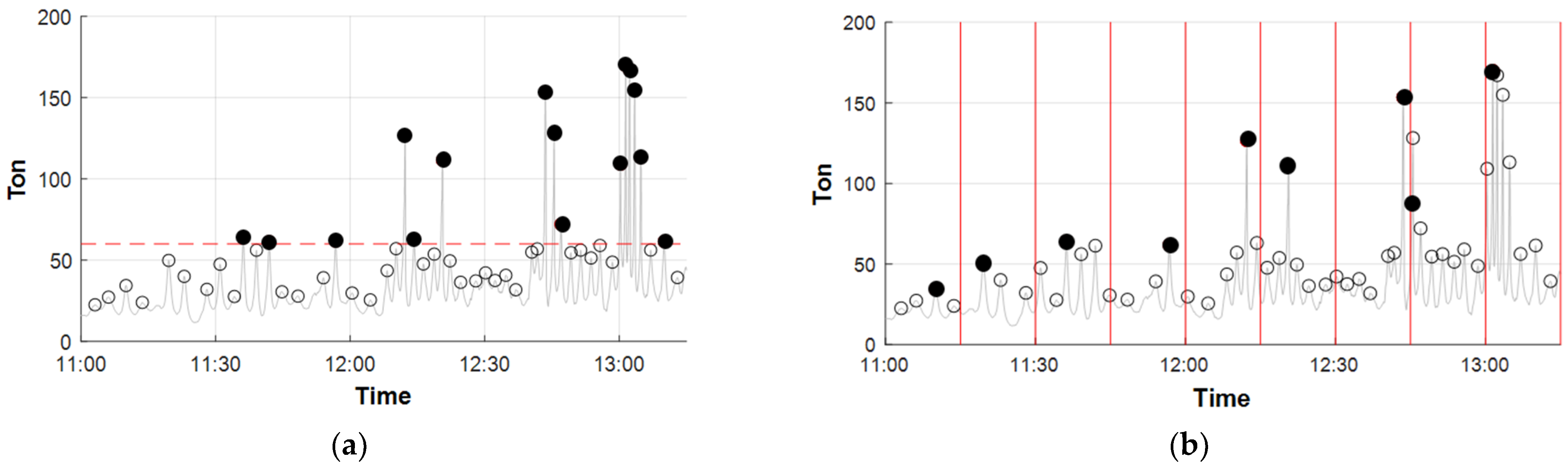
2.4. Detection of Load Peaks in Measured Data
3. Probabilistic Assessment
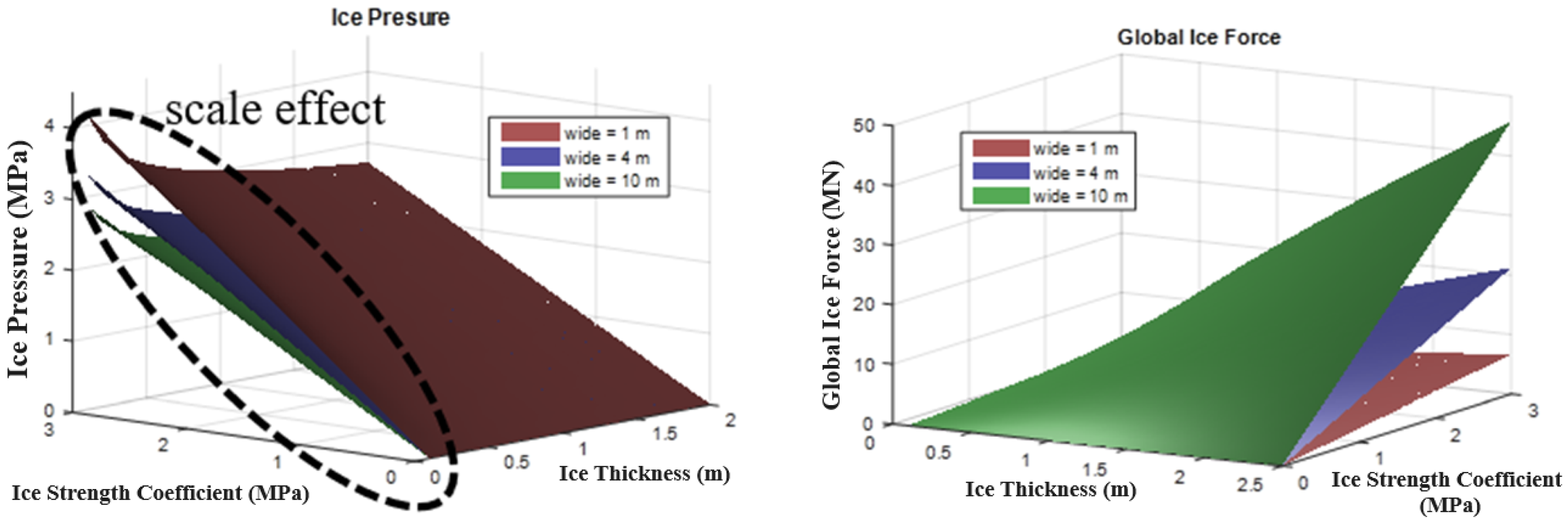
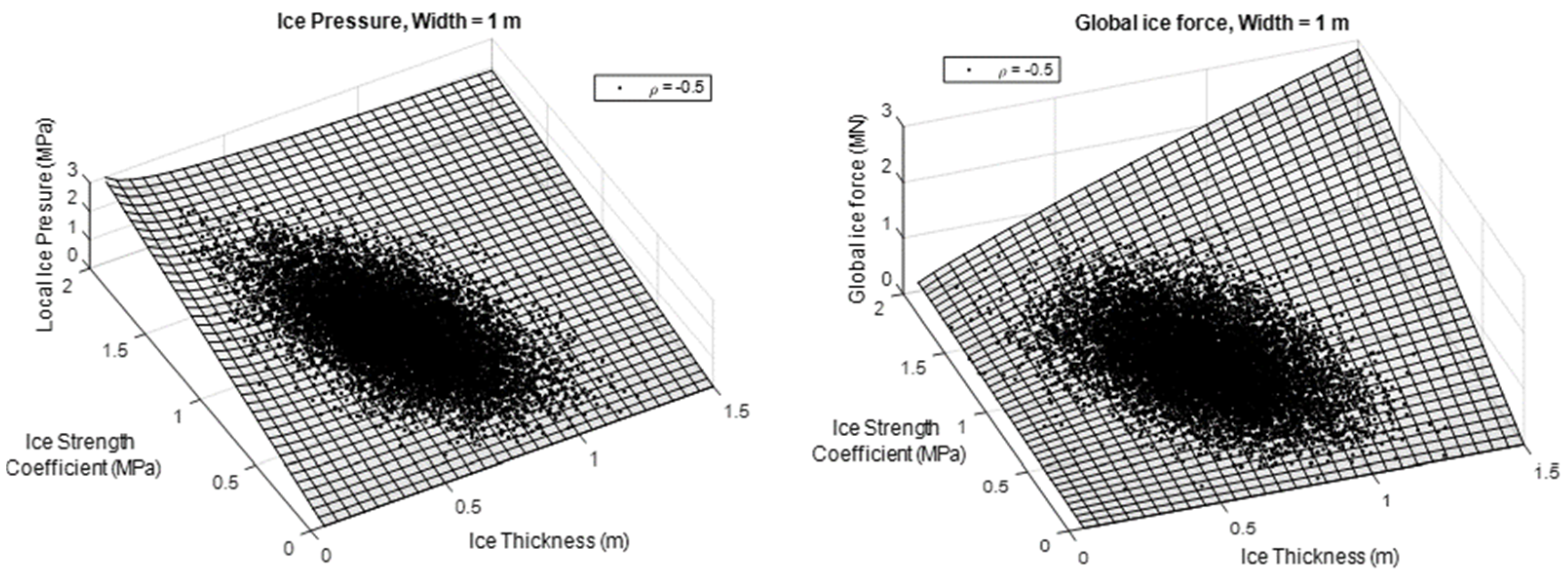
3.1. Monte Carlo Simulation
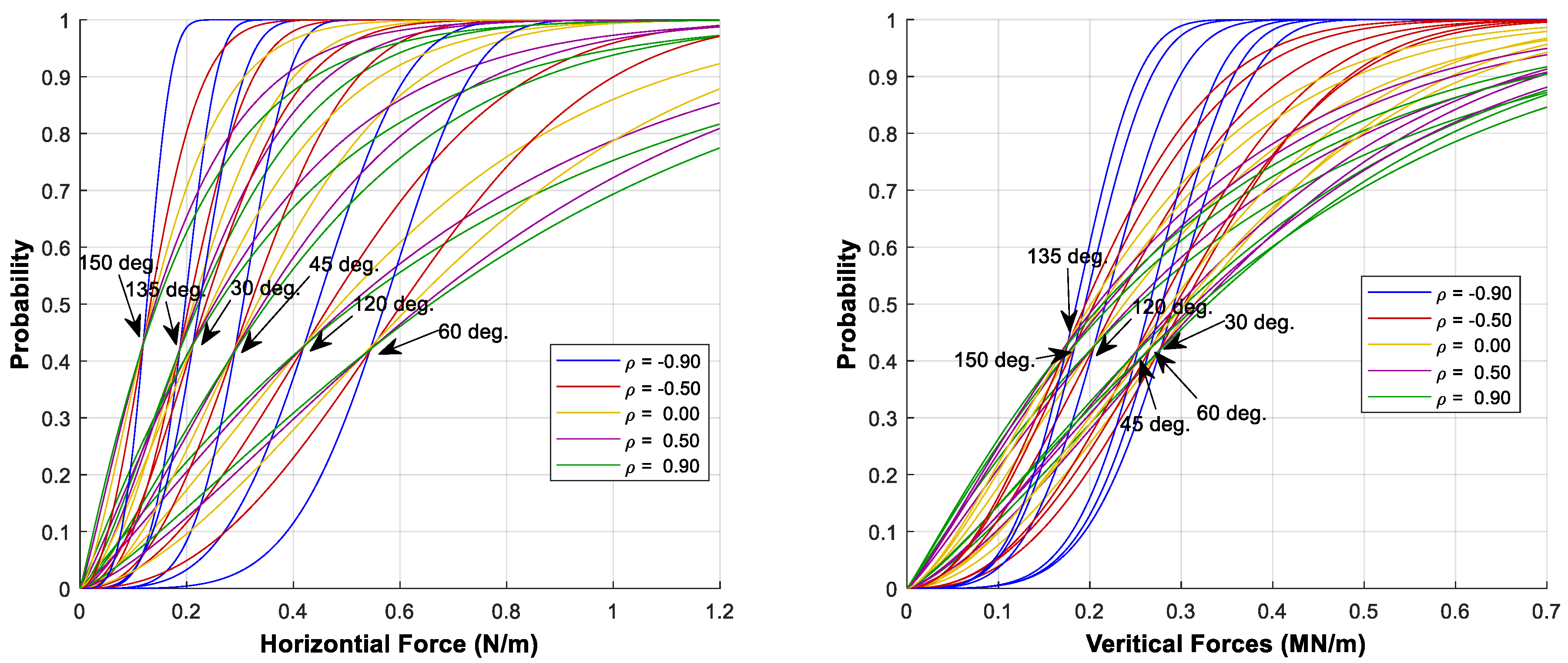
3.2. NATAF Transformation Model
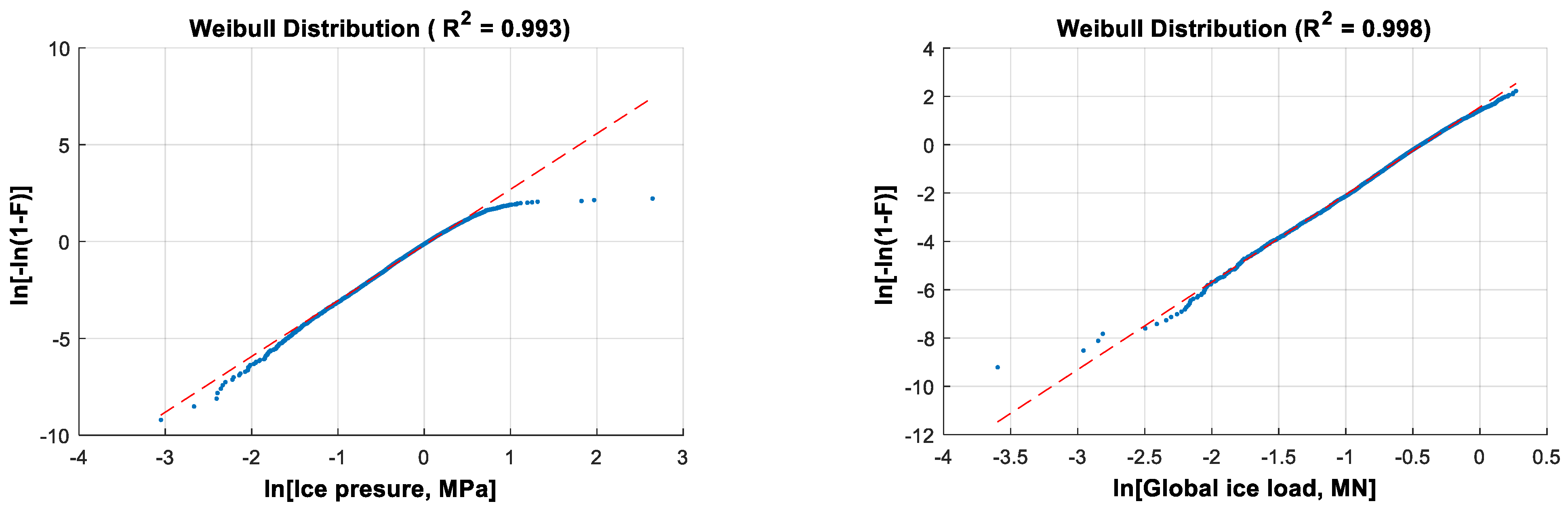
3.3. Implementation of Extreme Value Analysis
3.3.1. The Peaks-over-Threshold and Block Maxima Methods
3.3.2. The ACER Method
4. Case Study
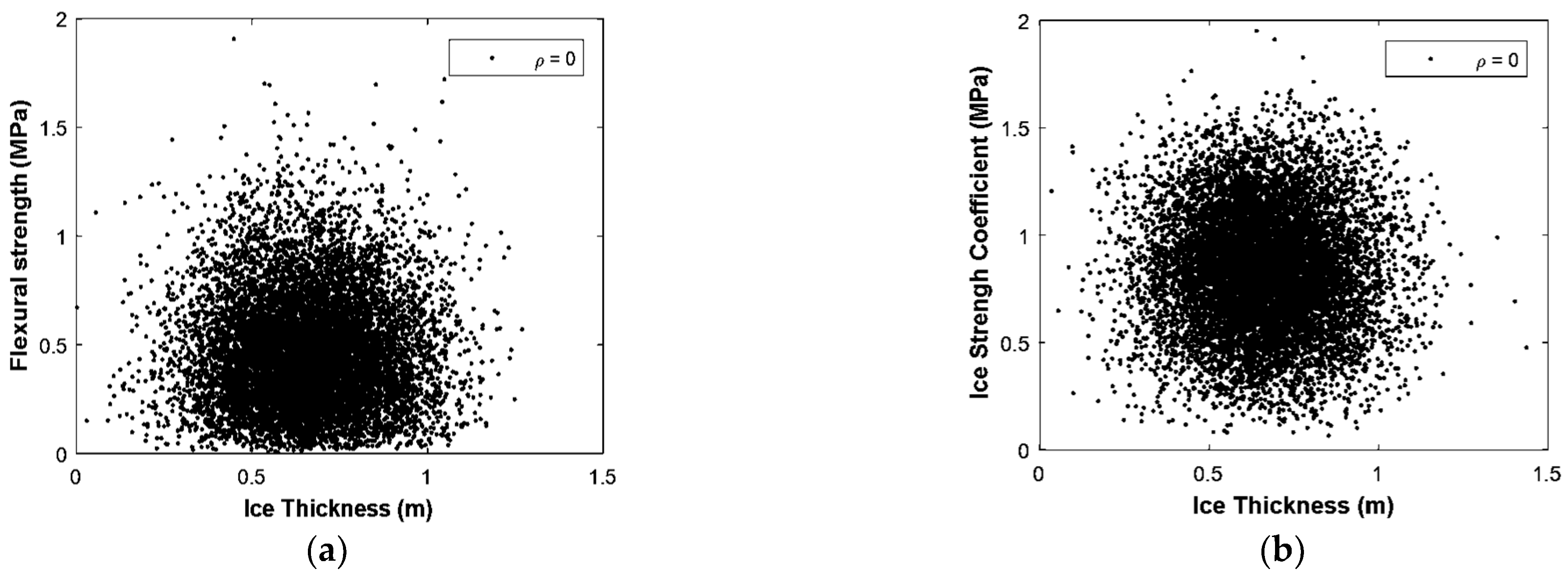
4.1. Probabilistic Assessment of a Fixed Offshore Structure under Ice Loading
4.1.1. Vertical Structures
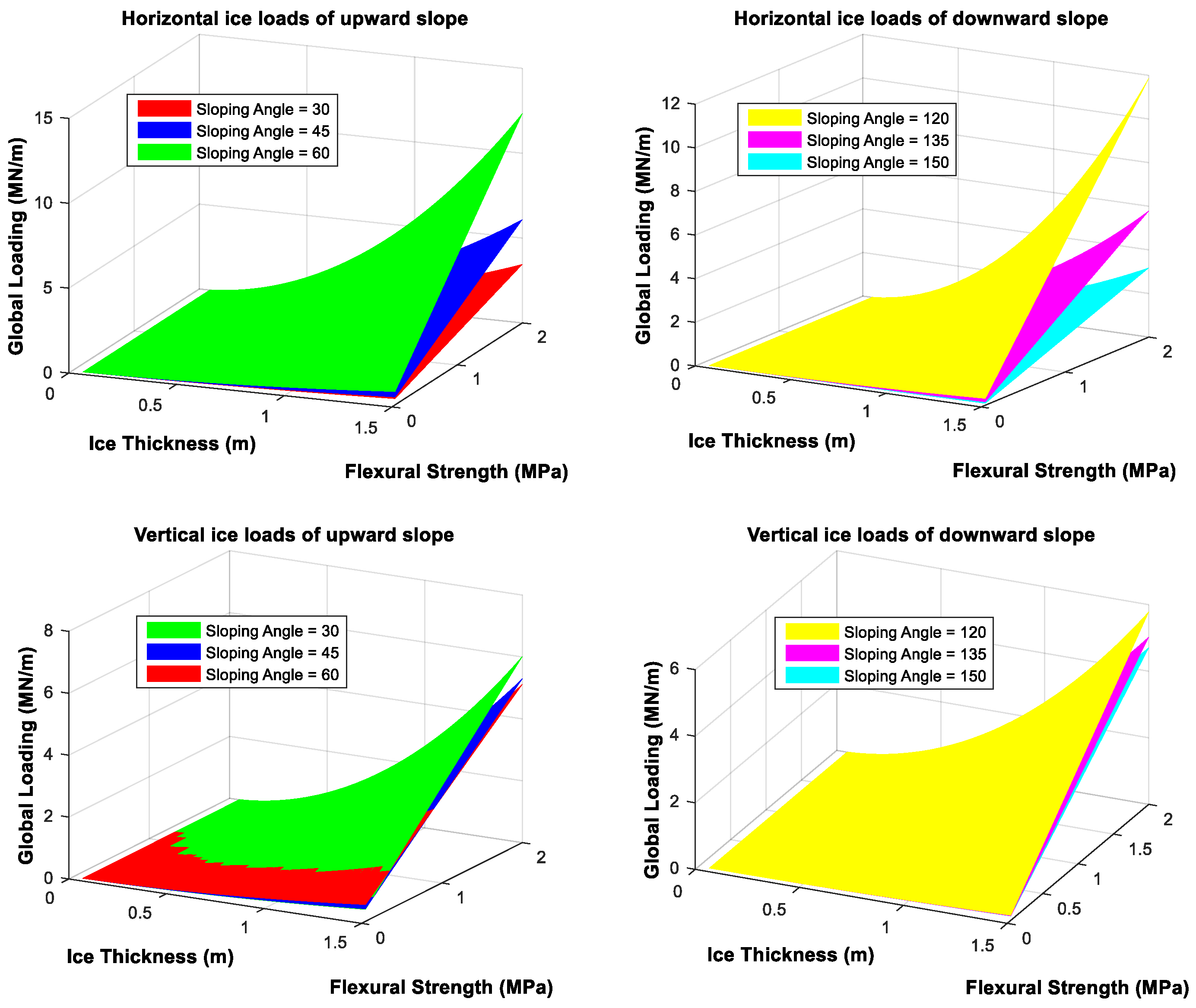
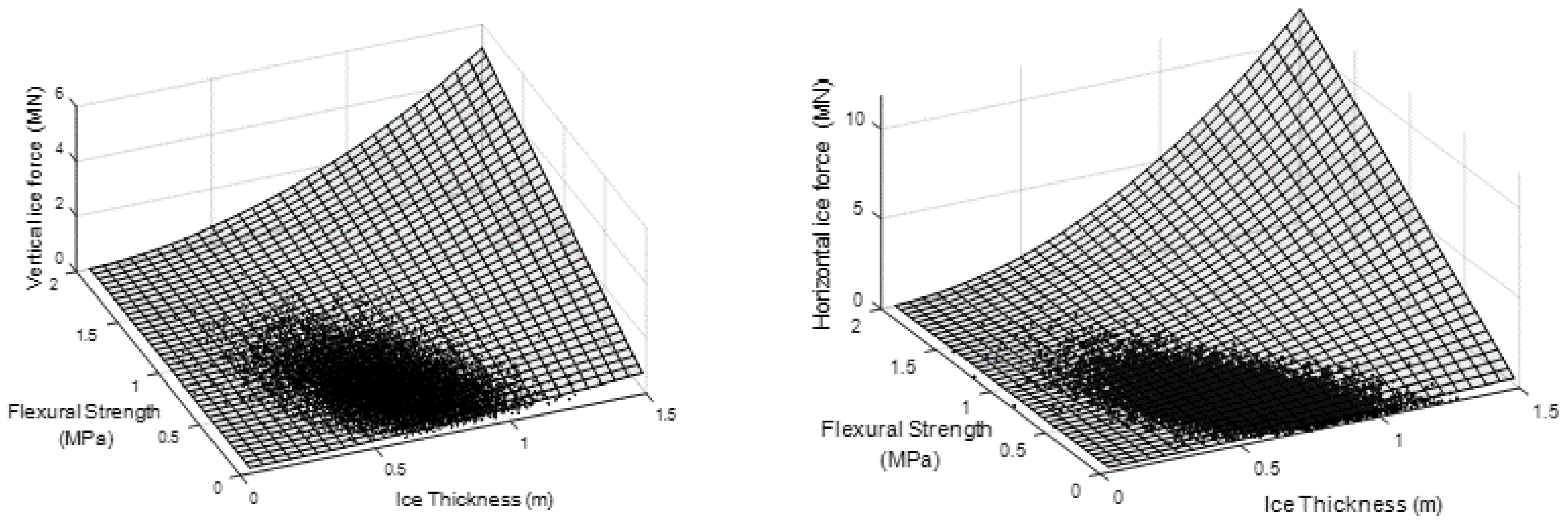
4.1.2. Sloping Structures
4.2. Extreme Value Analysis of Ice Loading on Fixed and Floating Offshore Structures
4.2.1. Ice Management Operations
4.2.2. Ice Breaker Deployment Patterns for Ice Management
4.2.3. Weather Conditions
4.2.4. Estimation of Global Ice Loading
4.3. Extreme Value Estimation
4.3.1. The POT and PM Methods
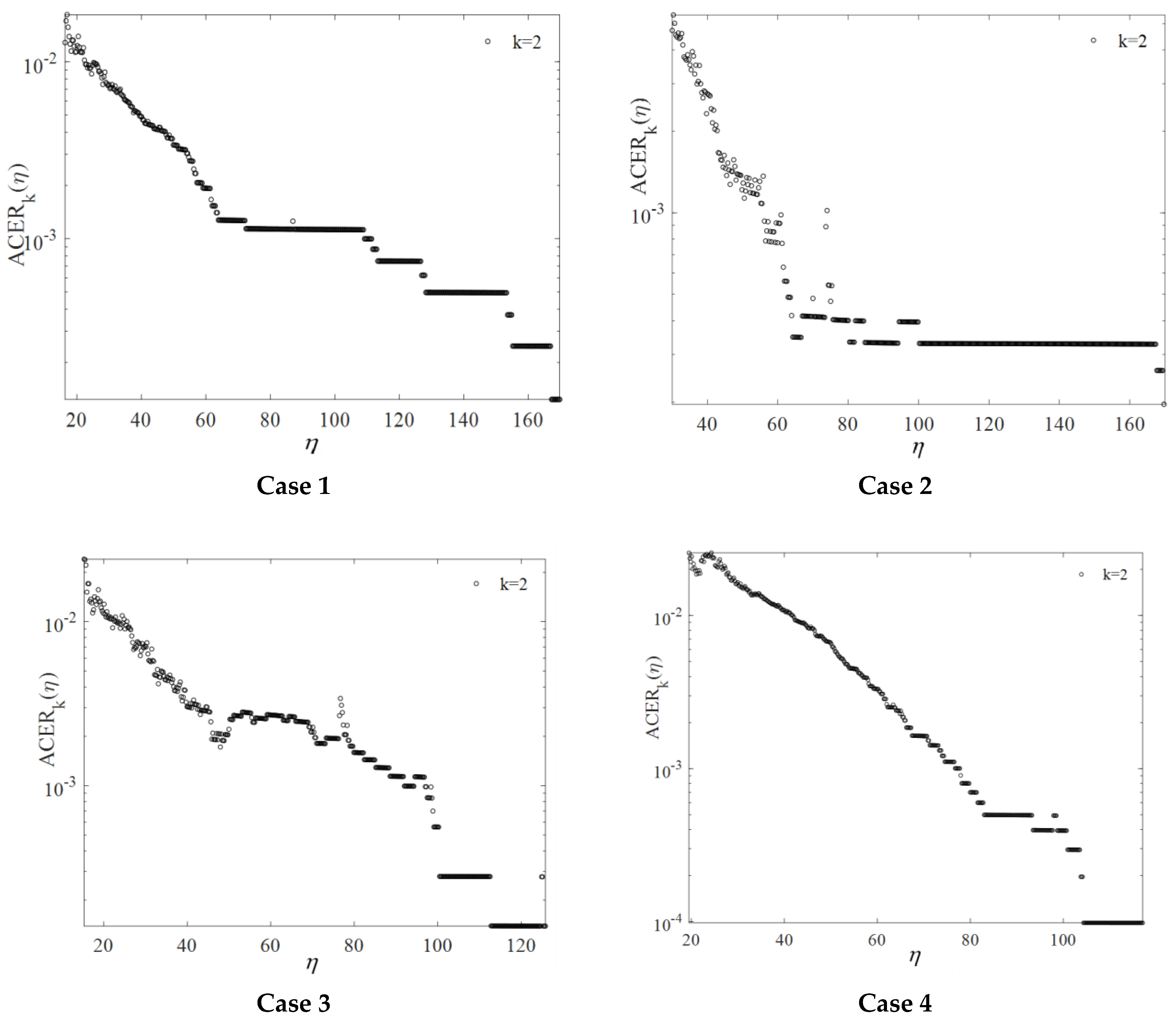
4.3.2. The ACER Method
5. Discussion
5.1. Probabilistic Assessment of Fixed Offshore Structures
5.1.1. Vertical Structures
5.1.2. Sloping Structures
5.2. Extreme Value Analysis of Mooring Lines for Stationary Keeping in Ice
6. Conclusions
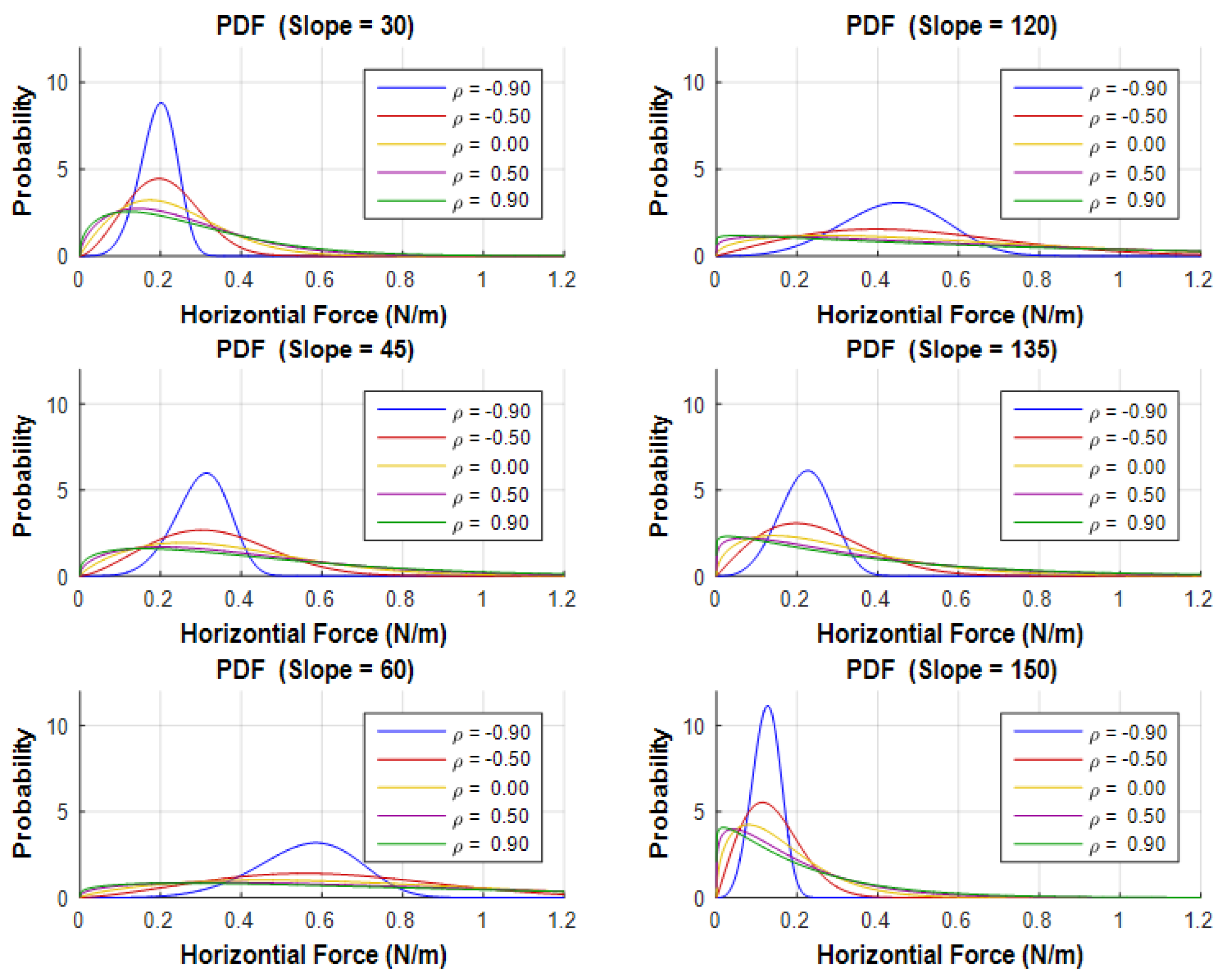
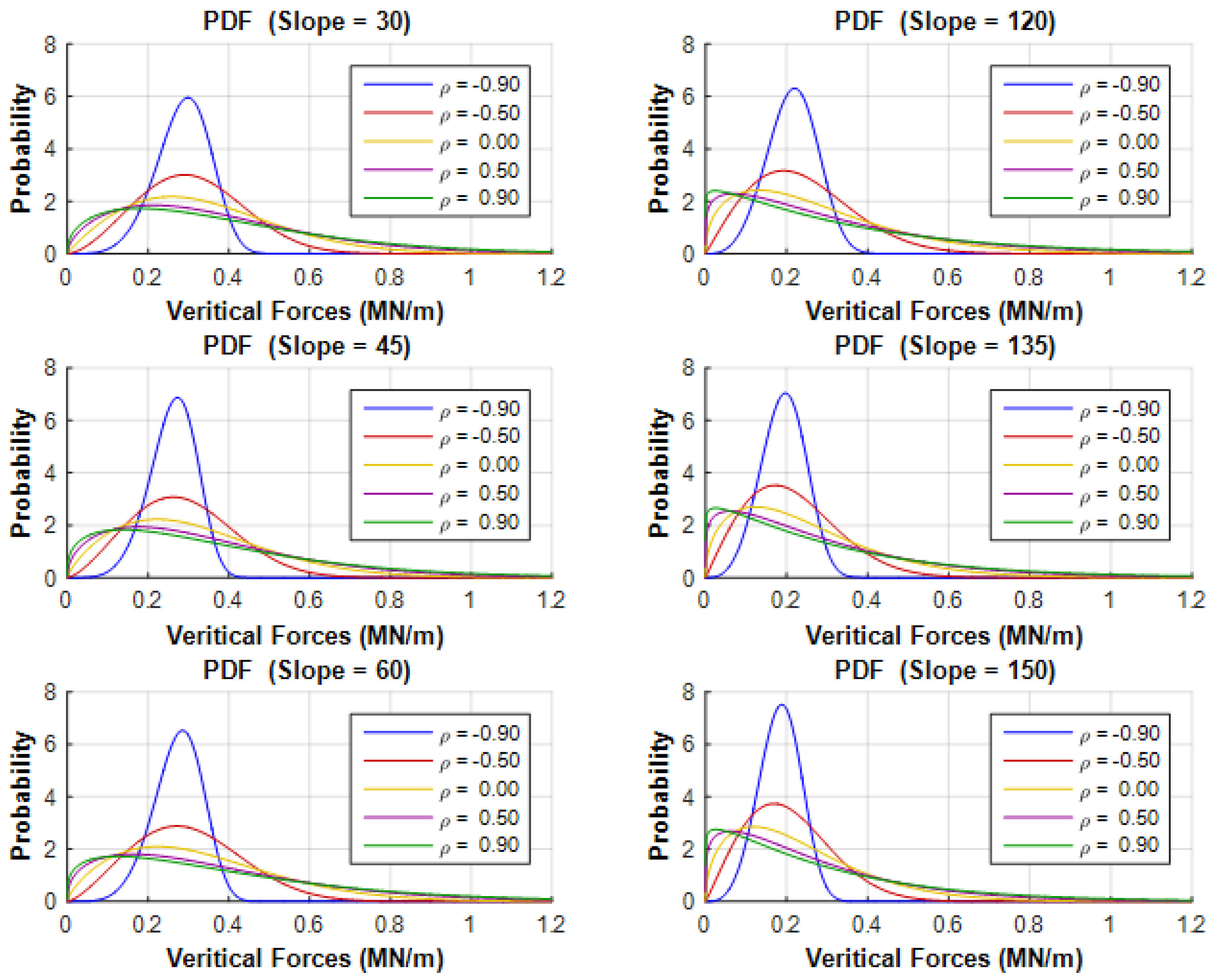
- For vertical structures, a transition from a correlation coefficient of 0 to 0.9 resulted in approximately 10% and 40% increases in mean values and standard deviations.
- Sloping structures showed approximately 20% and 60% increases in mean value and standard deviation of horizontal and vertical global forces, respectively, as correlation coefficients increased from 0 to 0.9.
- Higher sloping angles correlated with an increased standard deviation (uncertainty) of global forces.
- Changes in slope angle exerted a more pronounced effect on mean values and standard deviations of global forces in the horizontal direction compared to the vertical direction.
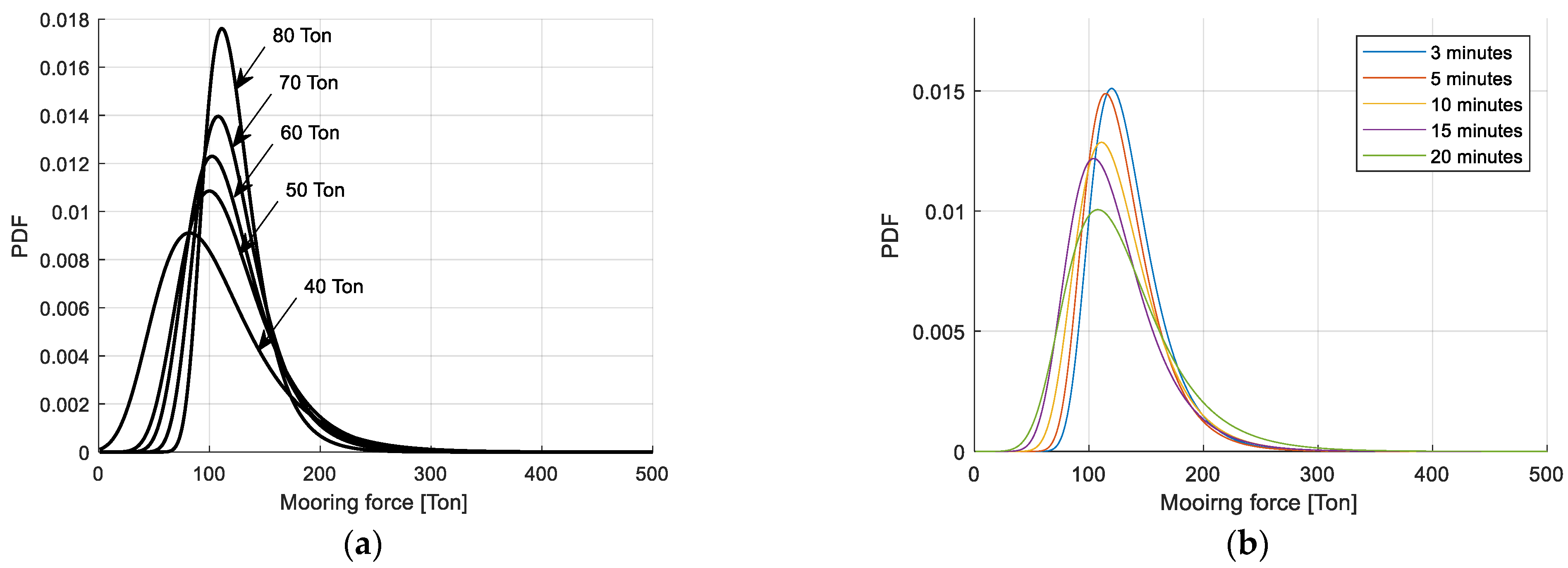
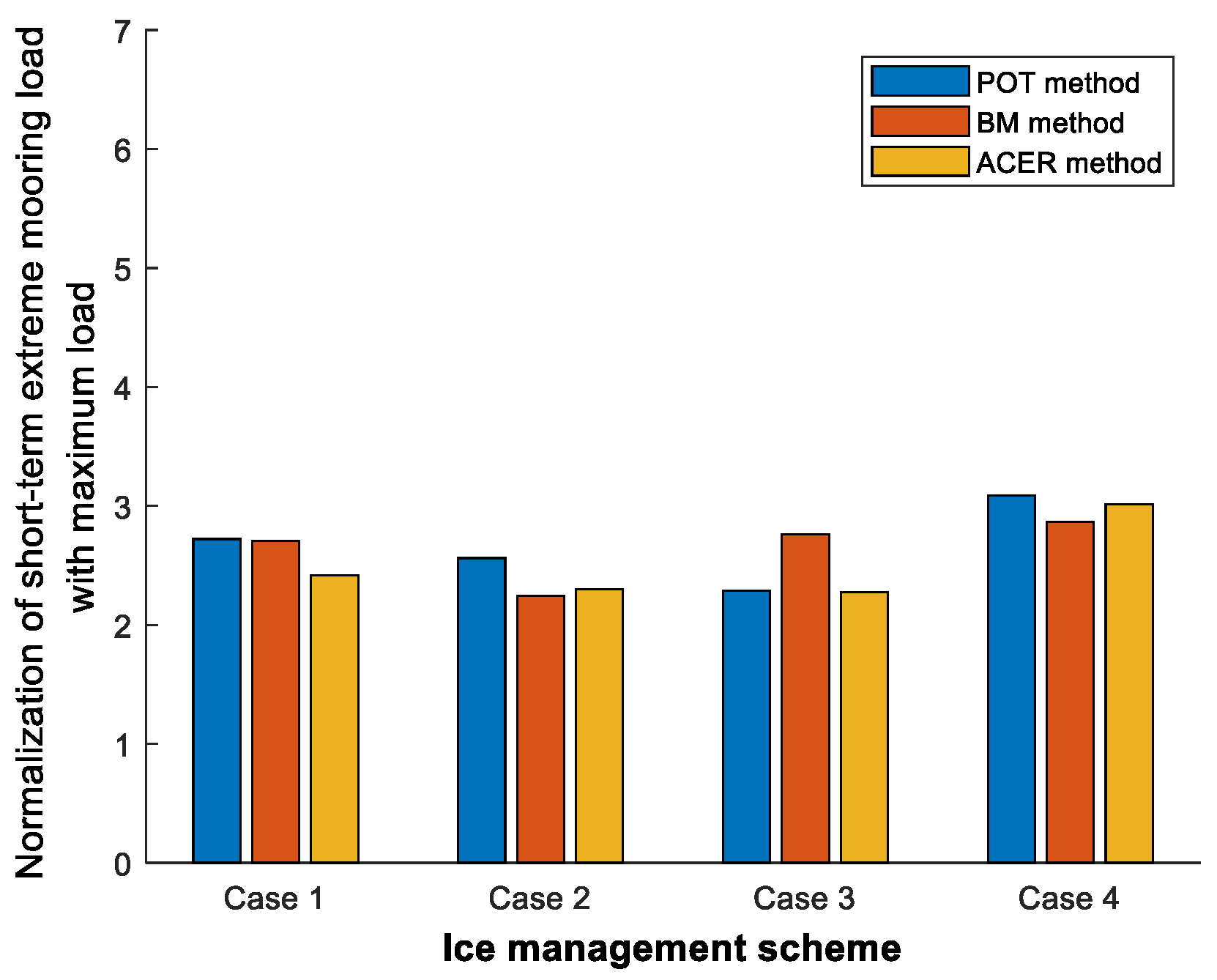
- The results are notably sensitive to the POT threshold and the time window width applied in the BM method.
- Extreme mooring loads estimated for a three-month return period, adjusted with a reduction factor R for an operational frequency of 0.375, exhibit consistent agreement across all methods.
- Differences among results from the various methods do not exceed 20%, primarily influenced by variability in peak mooring loads (also correlating with total ice loads on the MV supply vessel).
- Case 3, employing the circular updrift pattern, demonstrates the highest efficiency among the ice management schemes, followed by case 4 utilizing the linear updrift pattern. Case 2, employing the round circular pattern, displays the lowest efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pfaffling, A.; Haas, C.; Reid, J.E. Direct helicopter EM—Sea-ice thickness inversion assessed with synthetic and field data. Geophysics 2007, 72, F127–F137. [Google Scholar] [CrossRef]
- Li, H.; Bjerkås, M.; Høyland, K.V.; Nord, T. Panel loads and weather conditions at Norströmsgrund lighthouse. In Proceedings of the 23rd IAHR International Symposium on Ice, Ann Arbor, MI, USA, 31 May–3 June 2016. [Google Scholar]
- Zvyagin, P. A method for the probabilistic modelling of ice pressure. Cold Reg. Sci. Technol. 2015, 118, 112–119. [Google Scholar] [CrossRef]
- ISO19906:2010; Petroleum and Natural Gas Industries–Arctic Offshore Structures. ISO: Geneva, Switzerland, 2010.
- Ranta, J.; Polojärvi, A.; Tuhkuri, J. Ice loads on inclined marine structures-Virtual experiments on ice failure process evolution. Mar. Struct. 2018, 57, 72–86. [Google Scholar] [CrossRef]
- Sinsabvarodom, C.; Chai, W.; Leira, B.J.; Høyland, K.V.; Naess, A. Uncertainty assessments of structural loading due to first year ice based on the ISO standard by using Monte-Carlo simulation. Ocean Eng. 2020, 198, 106935. [Google Scholar] [CrossRef]
- Lemström, I.; Polojärvi, A.; Puolakka, O.; Tuhkuri, J. Load distributions in the ice-structure interaction process in shallow water. Ocean Eng. 2022, 258, 111730. [Google Scholar] [CrossRef]
- Hamilton, J.; Holub, C.; Blunt, J.; Mitchell, D.; Kokkinis, T. Ice management for support of arctic floating operations. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 5–7 November 2018. [Google Scholar]
- Gürtner, A.; Baardson, B.H.H.; Kaasa, G.-O.; Lundin, E. Aspects of importance related to Arctic DP operations. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 617–623. [Google Scholar]
- American Petroleum Institute. Recommended Practice for Design and Analysis of Stationkeeping Systems for Floating Structures; American Petroleum Institute: Washington, DC, USA, 1996. [Google Scholar]
- Liferov, P.; McKeever, T.; Scibilia, F.; Teigen, S.H.; Kjøl, A.; Almkvist, E.; Lindvall, J.K. Station-keeping trials in ice: Project overview. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V008T007A029. [Google Scholar]
- Croasdale, K.R.; Cammaert, A.B. An improved method for the calculation of ice loads on sloping structures in first-year ice. Hydrotech. Constr. 1994, 28, 174–179. [Google Scholar] [CrossRef]
- Brown, T.G.; Määttänen, M. Comparison of Kemi-I and Confederation Bridge cone ice load measurement results. Cold Reg. Sci. Technol. 2009, 55, 3–13. [Google Scholar] [CrossRef]
- Riska, K. Performance of Merchant Vessels in Ice in the Baltic; Sjöfartsverket: Norrkoping, Sweden, 1997. [Google Scholar]
- Erceg, S.; Ehlers, S. Semi-empirical level ice resistance prediction methods. Ship Technol. Res. 2017, 64, 1–14. [Google Scholar] [CrossRef]
- Sinsabvarodom, C.; Leira, B.J.; Høyland, K.V.; Næss, A.; Chai, W. A generalized ice drift spectrum based on measurements in the Beaufort Sea. Ocean Eng. 2024, 296, 116832. [Google Scholar] [CrossRef]
- Riska, K. Design of Ice Breaking Ships. 2011. Available online: https://www.eolss.net/sample-chapters/C05/E6-178-45-00.pdf (accessed on 24 July 2024).
- Kämäräinen, J. Evaluation of Ship Ice Resistance Calculation Methods. Licentiate Thesis, Helsinki University of Technology, Otaniemi, Finland, 1993. [Google Scholar]
- Ionov, B. Ice Resistance and Its Composition; Arctic and Antarctic Research Institute: Saint Petersburg, Russia, 1988. [Google Scholar]
- Lindquist, A. Straightforward method for calculation of ice resistance of ships. In Proceedings of the 10th International Conference, Port and Ocean Engineering under Arctic Conditions, POAC’89, Luleaa, Sweden, 12–16 June 1989. [Google Scholar]
- Mellor, M. Ship resistance in thick brash ice. Cold Reg. Sci. Technol. 1980, 3, 305–321. [Google Scholar] [CrossRef]
- Kuuliala, L.; Kujala, P.; Suominen, M.; Montewka, J. Estimating operability of ships in ridged ice fields. Cold Reg. Sci. Technol. 2017, 135, 51–61. [Google Scholar] [CrossRef]
- Hopkins, M.A.; Hibler, W., III; Flato, G. On the numerical simulation of the sea ice ridging process. J. Geophys. Res. J. Geophys. Res. Ocean. 1991, 96, 4809–4820. [Google Scholar] [CrossRef]
- Liu, P.-L.; Der Kiureghian, A. Multivariate distribution models with prescribed marginals and covariances. Probabilistic Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Goda, Y. On the methodology of selecting design wave height. Coast. Eng. 1989, 1988, 899–913. [Google Scholar]
- Far, S.S.; Wahab, A.K.A. Evaluation of peaks-over-threshold method. Ocean Sci. Discuss. 2016, 2016, 1–25. [Google Scholar]
- Næss, A.; Gaidai, O. Estimation of extreme values from sampled time series. Struct. Saf. 2009, 31, 325–334. [Google Scholar] [CrossRef]
- Naess, A.; Gaidai, O.; Karpa, O. Estimation of extreme values by the average conditional exceedance rate method. J. Probab. Stat. 2013, 2013, 797014. [Google Scholar] [CrossRef]
- El Bakkay, B.; Coche, E.; Riska, K. Efficiency of Ice Management for Arctic Offshore Operations. Int. Conf. Offshore Mech. Arct. Eng. 2014, 45561, V010T007A041. [Google Scholar] [CrossRef]
- Kjøl, A.; Liferov, P.; Almkvist, E.; Lindvall, J.K.; McKeever, T. Station-keeping trials in ice: Marine spread. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V008T007A023. [Google Scholar]
- Neville, M.; Almkvist, E.; Scibilia, F.; Lindvall, J.K.; Liferov, P. Station-keeping trials in ice: Overview of ice management support. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V008T007A027. [Google Scholar]
- Sinsabvarodom, C.; Leira, B.J.; Chai, W.; Naess, A. Extreme Value Estimation of Mooring Loads Based on Station-Keeping Trials in Ice. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Online, 3–7 August 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar]
- Teigen, S.H.; Lindvall, J.K.; Samardzija, I.; Hansen, R.I. Station-keeping trials in ice: Ice and metocean conditions. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V008T007A030. [Google Scholar]
- Sinsabvarodom, C.; Chai, W.; Leira, B.J.; Høyland, K.V.; Naess, A. Probabilistic Assessment of Ice Rose Diagrams for Ice Drift in the Beaufort Sea. In Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019. [Google Scholar]
- Fenz, D.; Younan, A.; Piercey, G.; Barrett, J.; Ralph, F.; Jordaan, I. Field measurement of the reduction in local pressure from ice management. Cold Reg. Sci. Technol. 2018, 156, 75–87. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.J.; Riska, K. Non Parametric Probabilistic Approach of Ice Load Peaks on Ship Hulls. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 415–423. [Google Scholar]
- Chai, W.; Leira, B.J.; Naess, A. Probabilistic methods for estimation of the extreme value statistics of ship ice loads. Cold Reg. Sci. Technol. 2018, 146, 87–97. [Google Scholar] [CrossRef]
- Ronkainen, I.; Lehtiranta, J.; Lensu, M.; Rinne, E.; Haapala, J.; Haas, C. Interannual sea ice thickness variability in the Bay of Bothnia. Cryosphere 2018, 12, 3459–3476. [Google Scholar] [CrossRef]
- DNV-OS-H101; Marine Operations, General. October 2011. Available online: https://rules.dnv.com/docs/pdf/dnvpm/codes/docs/2011-10/Os-H101.pdf (accessed on 2 July 2024).
- Sinsabvarodom, C.; Leira, B.J.; Chai, W.; Næss, A. Short-term extreme mooring loads prediction and fatigue damage evaluation for station-keeping trials in ice. Ocean Eng. 2021, 242, 109930. [Google Scholar] [CrossRef]
- DNVGL-OS-E301; Position Mooring. DNV GL: Oslo, Norway, 2015.
- ABS. Guide for Position Mooring Systems; American Bureau of Shipping Incorporated by Act of Legislature of the State of New York: New York, NY, USA, 2018.
- GL Noble Denton. Technical Policy Board Guidelines for Moorings, GL Noble Denton 0032/ND; GL Noble Denton: Loughborough, UK, 2013. [Google Scholar]
- NR493; Classification of Mooring Systems for Permanent and Mobile Offshore Units. Bureau Veritas Marine & Offshore: Paris, France, 2005.








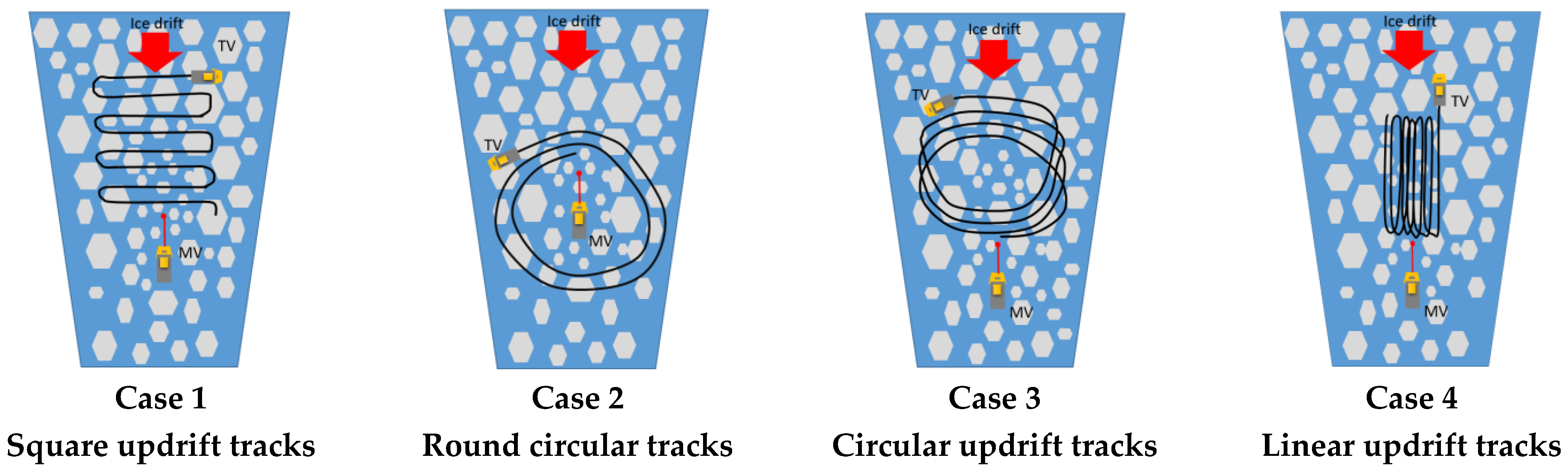
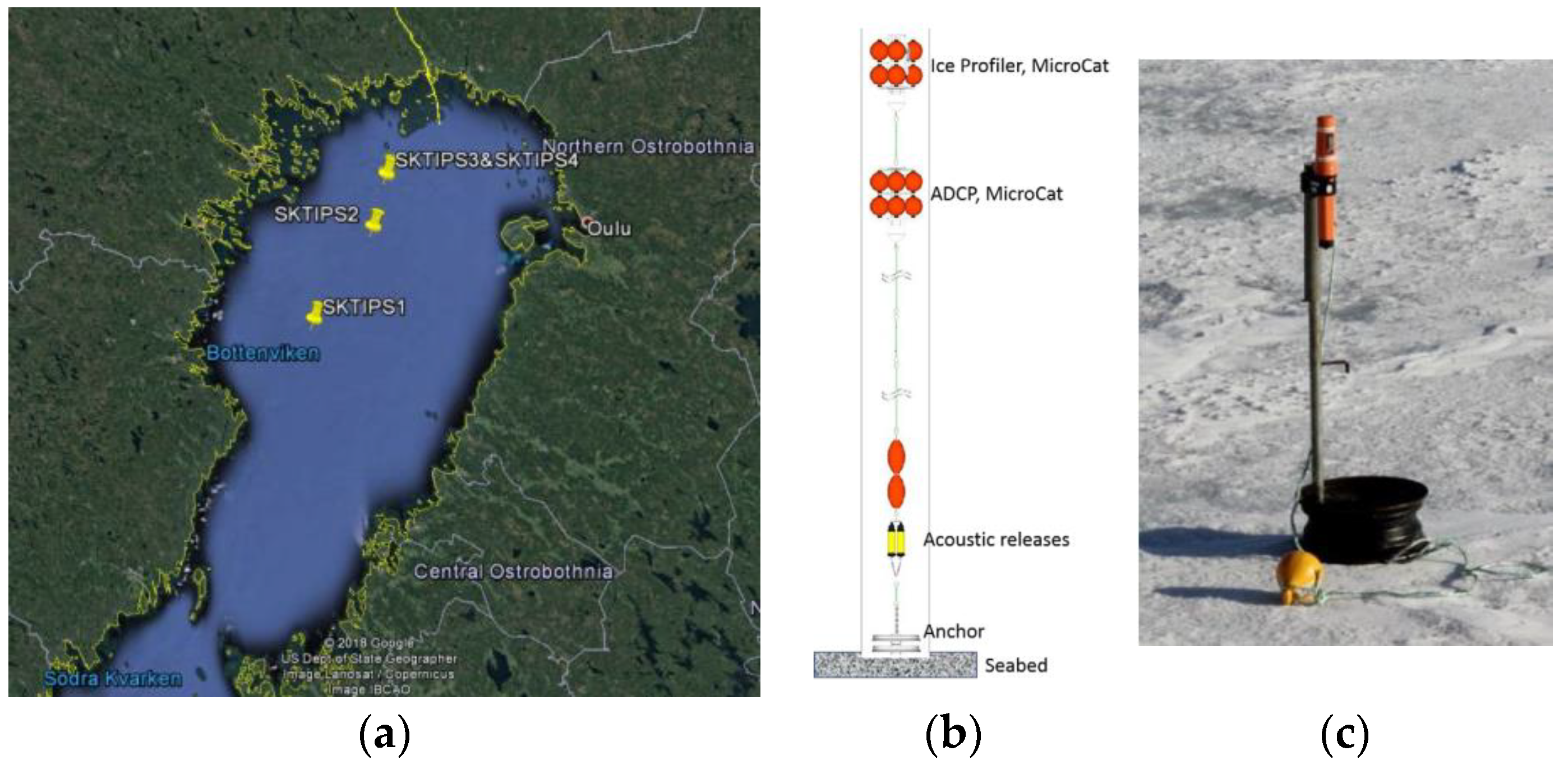
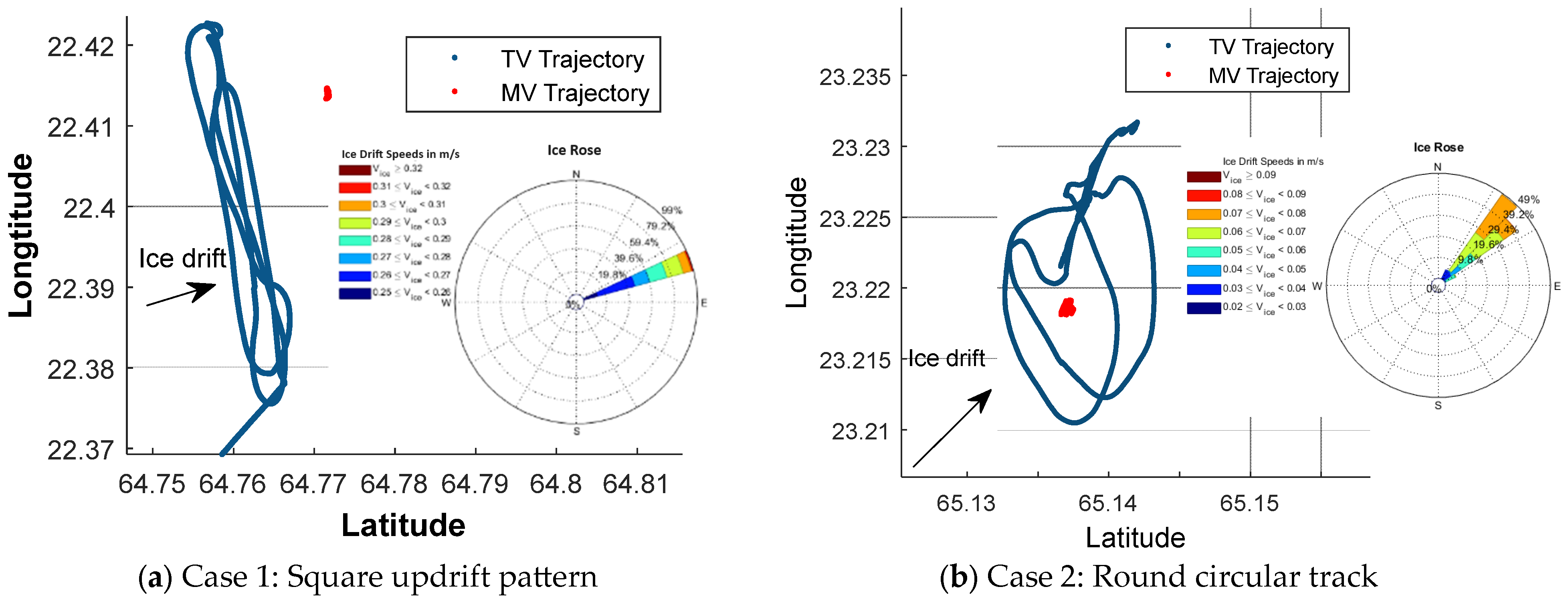
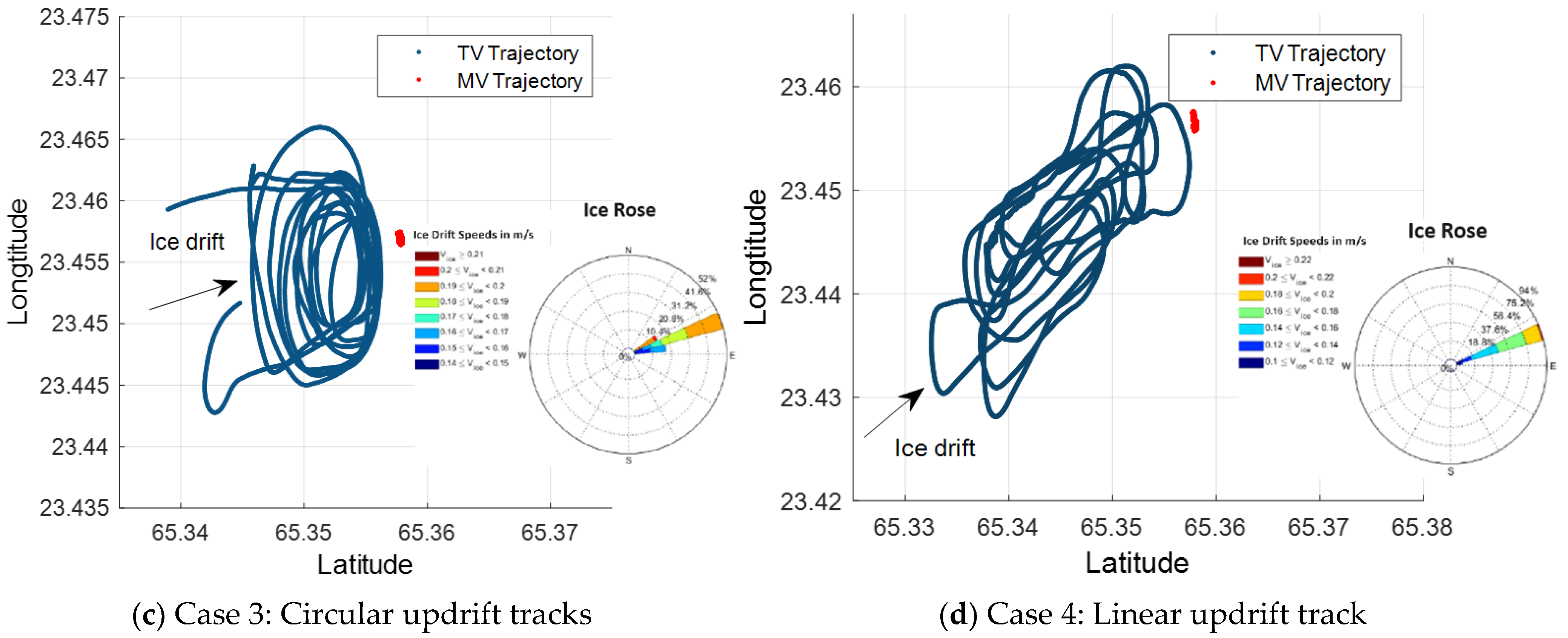
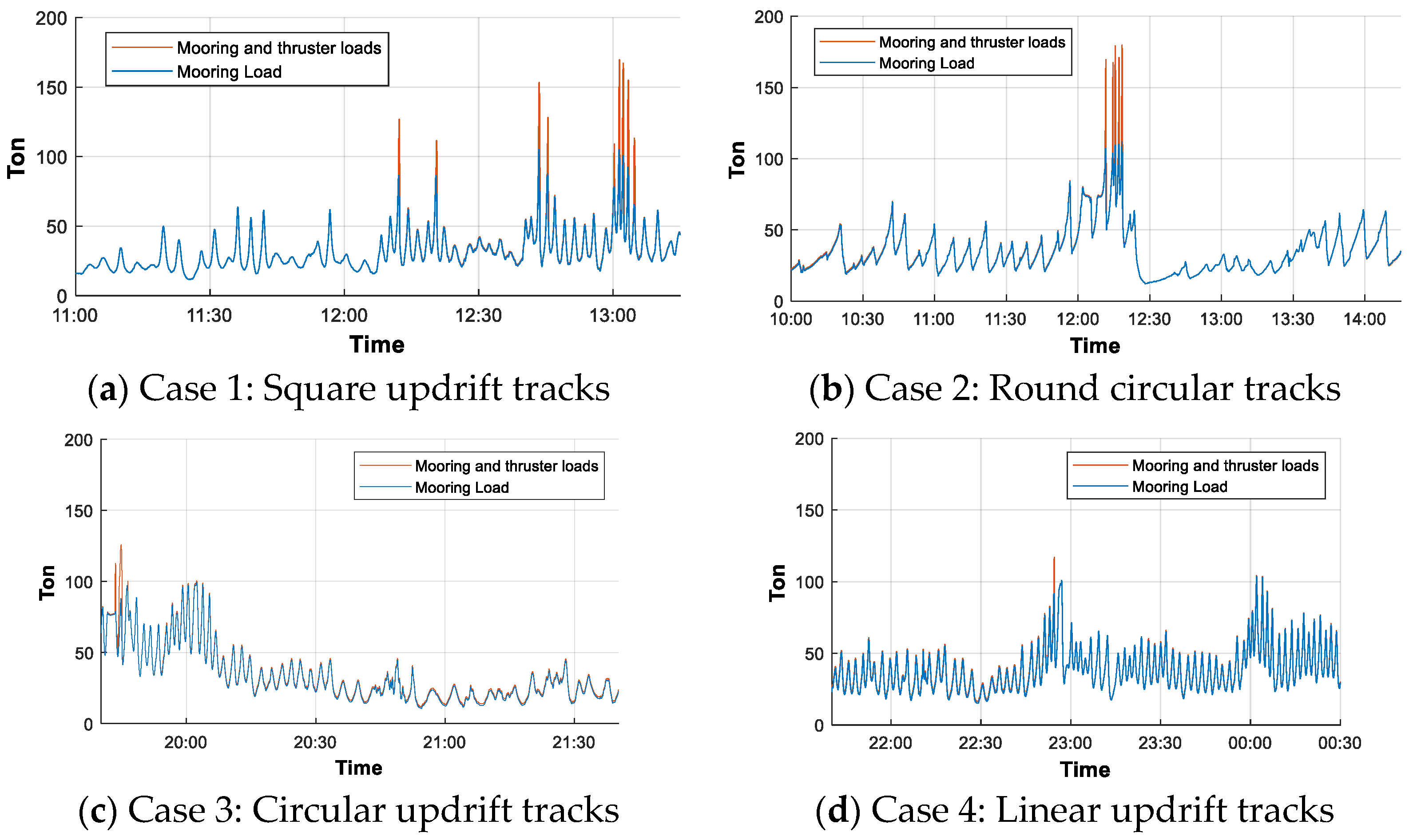
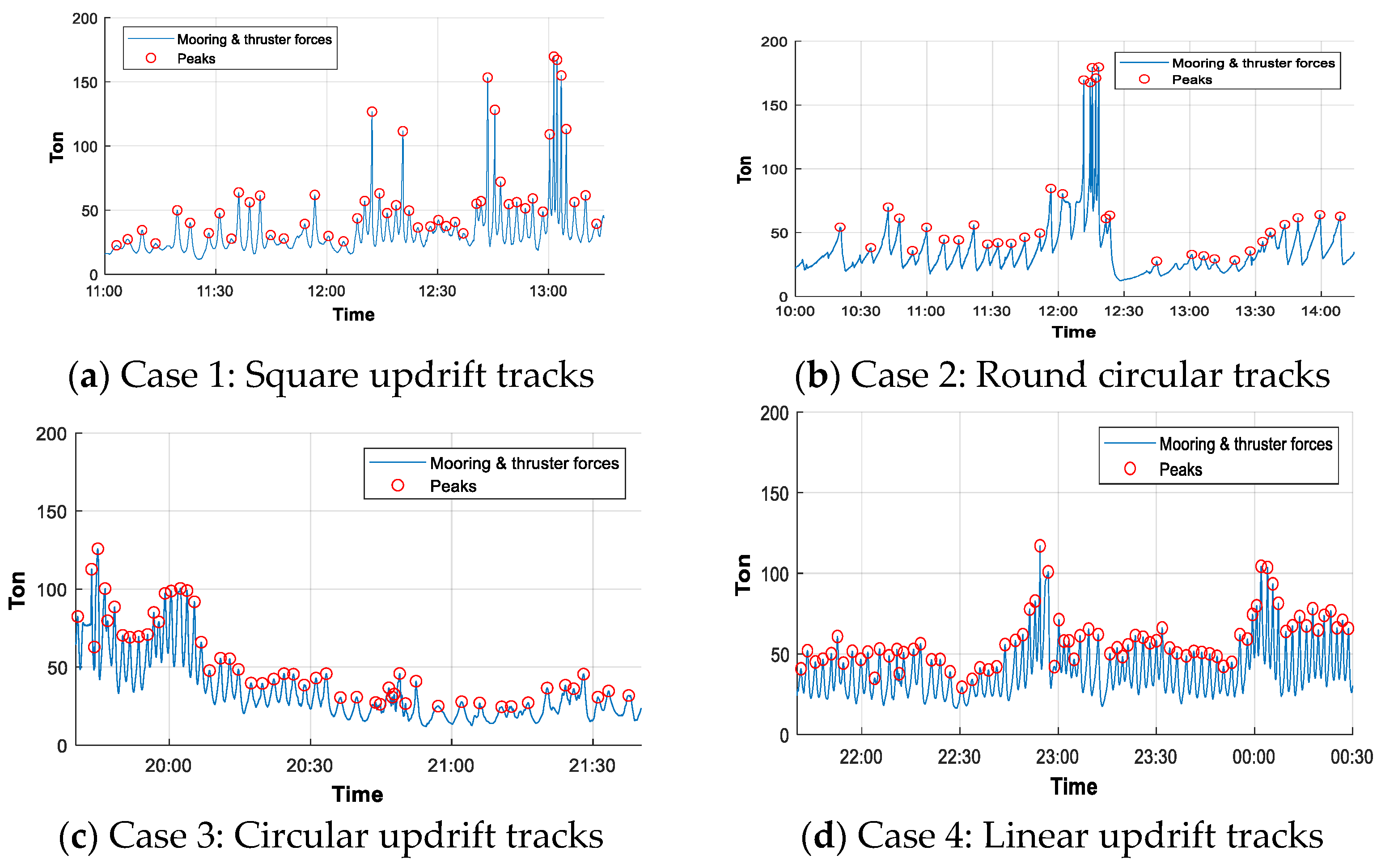






| Ice Management Operation | Date | Time |
|---|---|---|
| Square updrift pattern | 9 March 2017 | 11:00:00–13:15:00 |
| Round circular pattern | 12 March 2017 | 10:00:00–14:25:00 |
| Circular updrift pattern | 16 March 2017 | 19:40:00–21:40:00 |
| Linear updrift pattern | 16 March 2017 | 21:40:00–00:30:00 |
| Case | Measured Load [Ton] | Calculated Load [Ton] | ||||
|---|---|---|---|---|---|---|
| Mean | STD | COV % | Mean | STD | COV % | |
| 1 | 32.22 | 17.03 | 52.85 | 24.92 | 16.11 | 64.63 |
| 2 | 35.08 | 17.99 | 51.29 | 41.63 | 18.99 | 45.61 |
| 3 | 34.89 | 20.15 | 57.76 | 55.13 | 26.88 | 48.76 |
| 4 | 39.07 | 14.69 | 37.60 | 52.30 | 27.02 | 51.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinsabvarodom, C.; Leira, B.J.; Høyland, K.V.; Næss, A.; Samardžija, I.; Chai, W.; Komonjinda, S.; Chaichana, C.; Xu, S. On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures. J. Mar. Sci. Eng. 2024, 12, 1458. https://doi.org/10.3390/jmse12081458
Sinsabvarodom C, Leira BJ, Høyland KV, Næss A, Samardžija I, Chai W, Komonjinda S, Chaichana C, Xu S. On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures. Journal of Marine Science and Engineering. 2024; 12(8):1458. https://doi.org/10.3390/jmse12081458
Chicago/Turabian StyleSinsabvarodom, Chana, Bernt J. Leira, Knut V. Høyland, Arvid Næss, Ilija Samardžija, Wei Chai, Siramas Komonjinda, Chatchawan Chaichana, and Sheng Xu. 2024. "On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures" Journal of Marine Science and Engineering 12, no. 8: 1458. https://doi.org/10.3390/jmse12081458
APA StyleSinsabvarodom, C., Leira, B. J., Høyland, K. V., Næss, A., Samardžija, I., Chai, W., Komonjinda, S., Chaichana, C., & Xu, S. (2024). On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures. Journal of Marine Science and Engineering, 12(8), 1458. https://doi.org/10.3390/jmse12081458








