Investigating the Structural and Power Performance of a 15 MW Class Wind Energy Generation System under Experimental Wind and Marine Loading
Abstract
:1. Introduction
Literature Survey
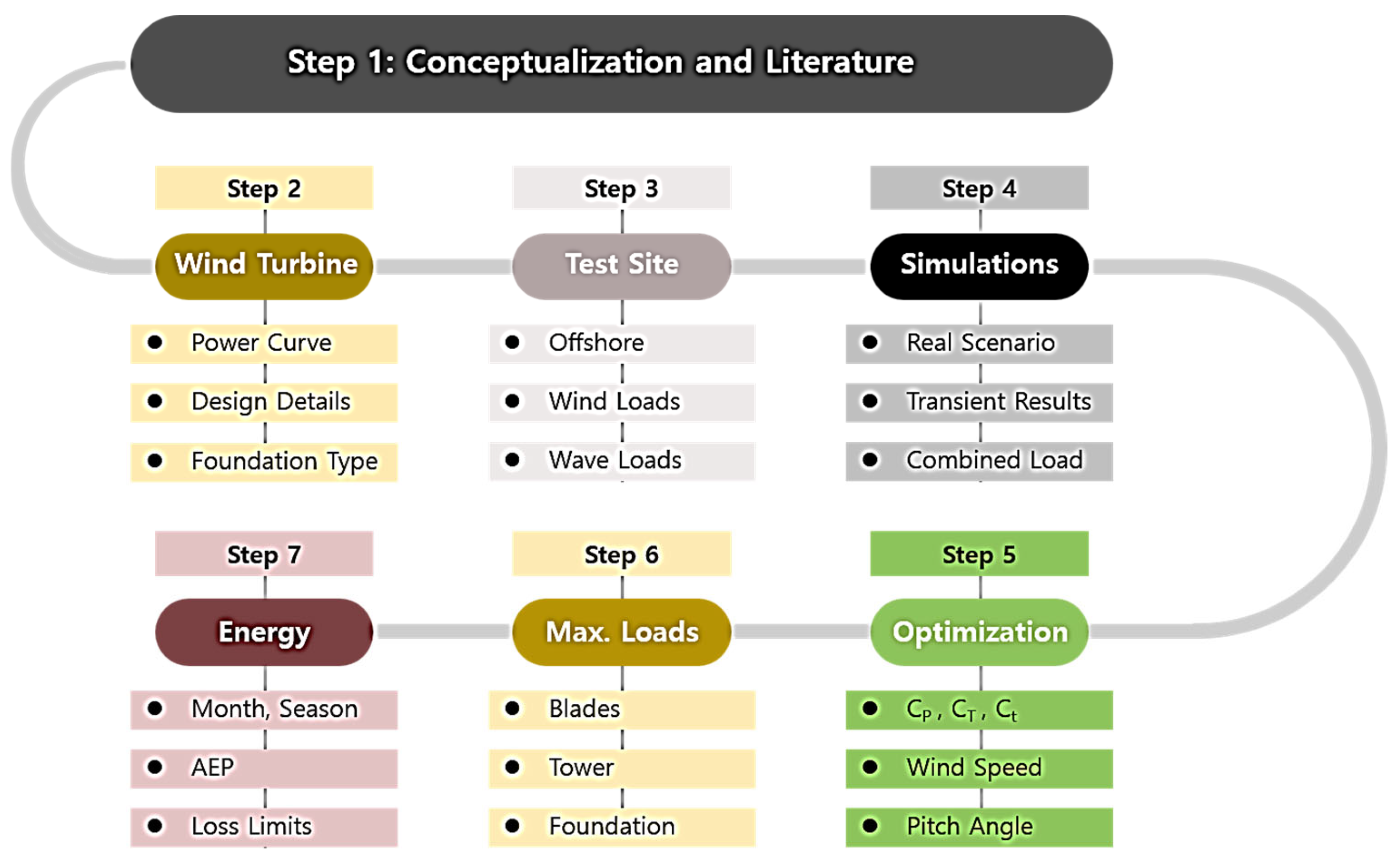
2. Materials and Methods
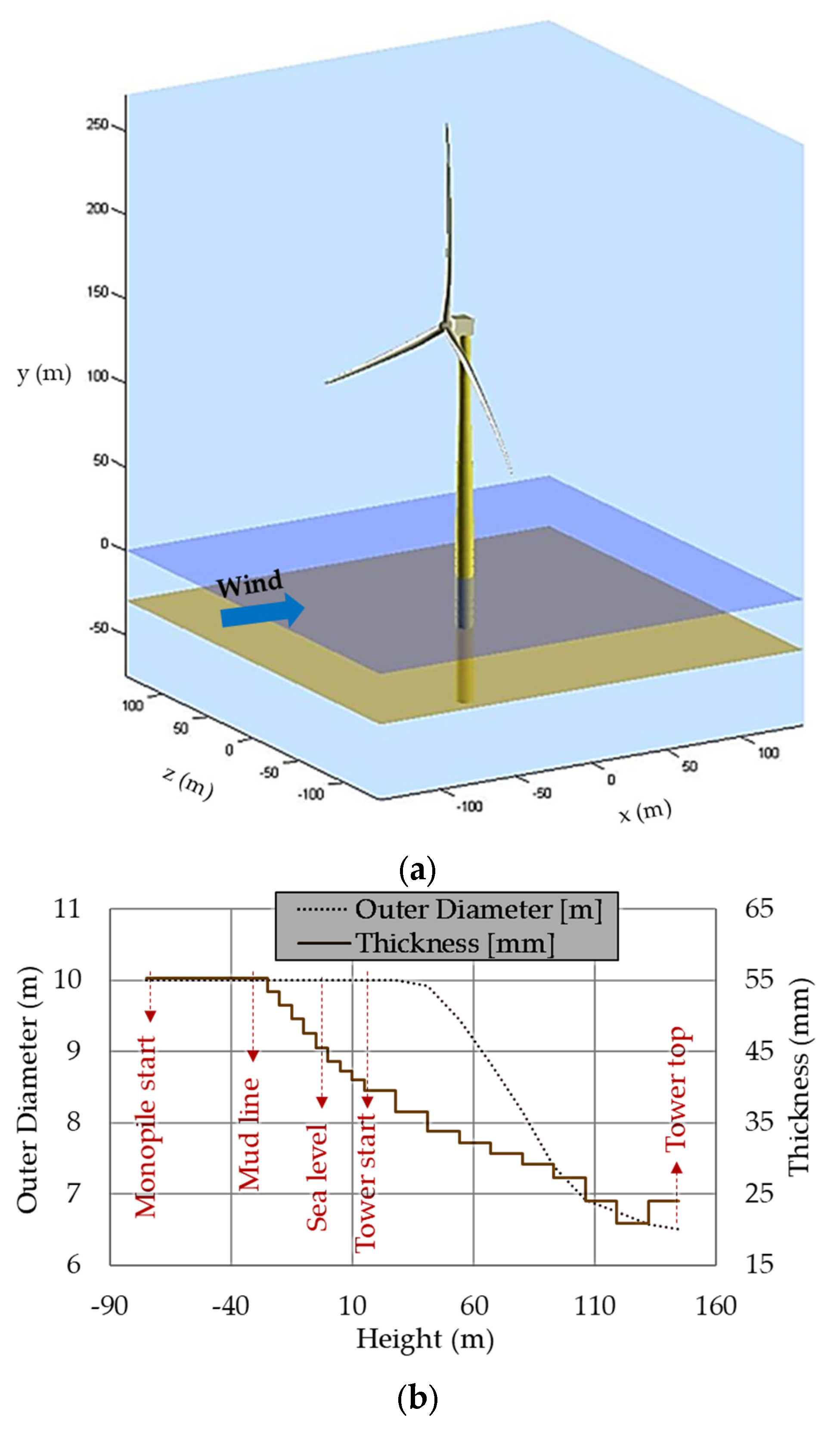
2.1. Wind Turbine Model
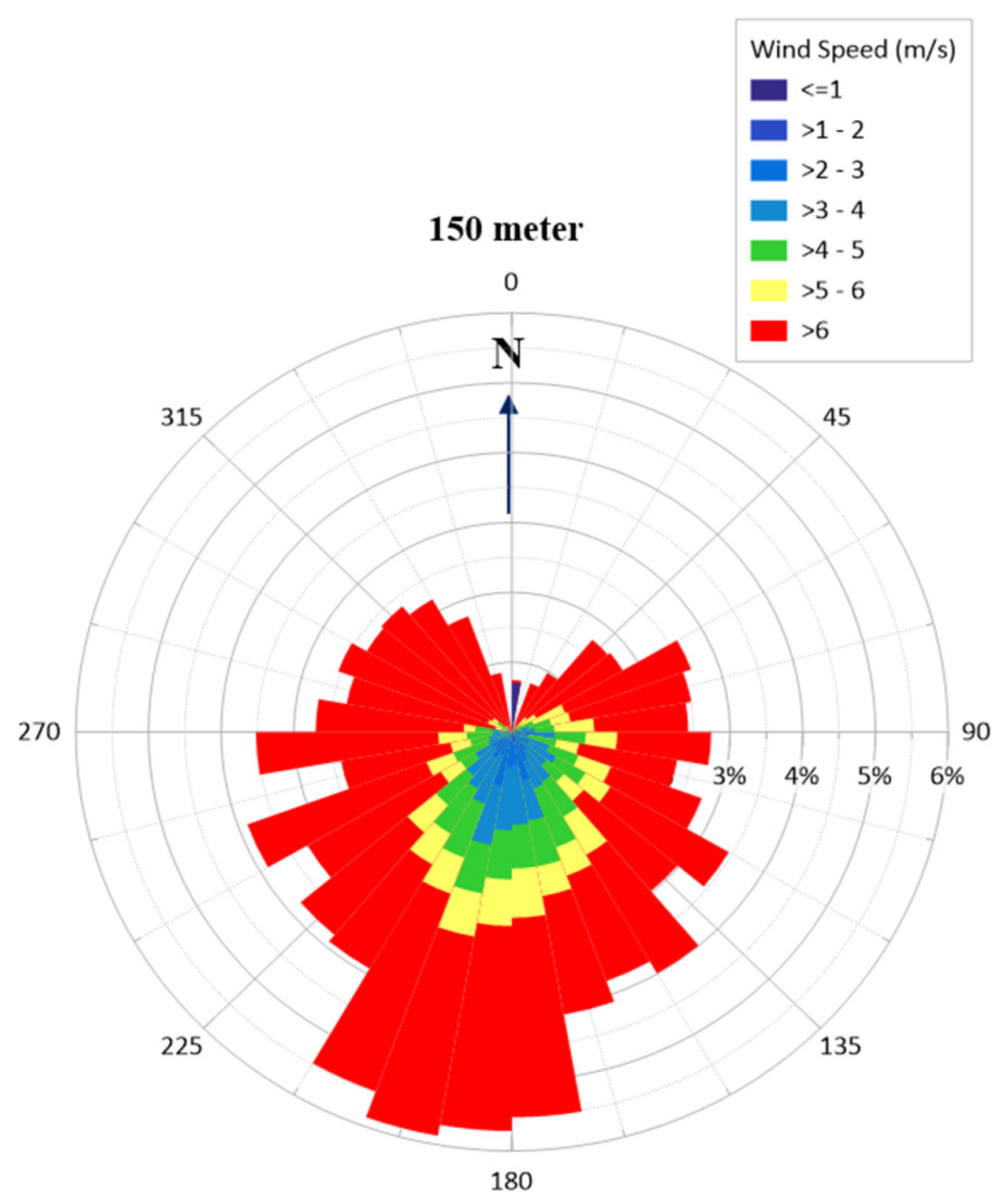
2.2. Data Site
- This site is completely offshore having extremely dynamic wind and wave conditions.
- The wave angle is very important for the structural integrity of the wind turbine tower and monopile foundation. Buan is one of very few sites where the wave angle data were available as measured by KMA.
- The South Korean government is interested in developing a large wind farm on the south-west coast of the country. Therefore, the present study analysis will help many stakeholders in the country.
- The proposed wind farm site has potential for monopile foundations in shallow waters not exceeding 30 m in depth.
2.3. Mathematical Modeling
3. Results
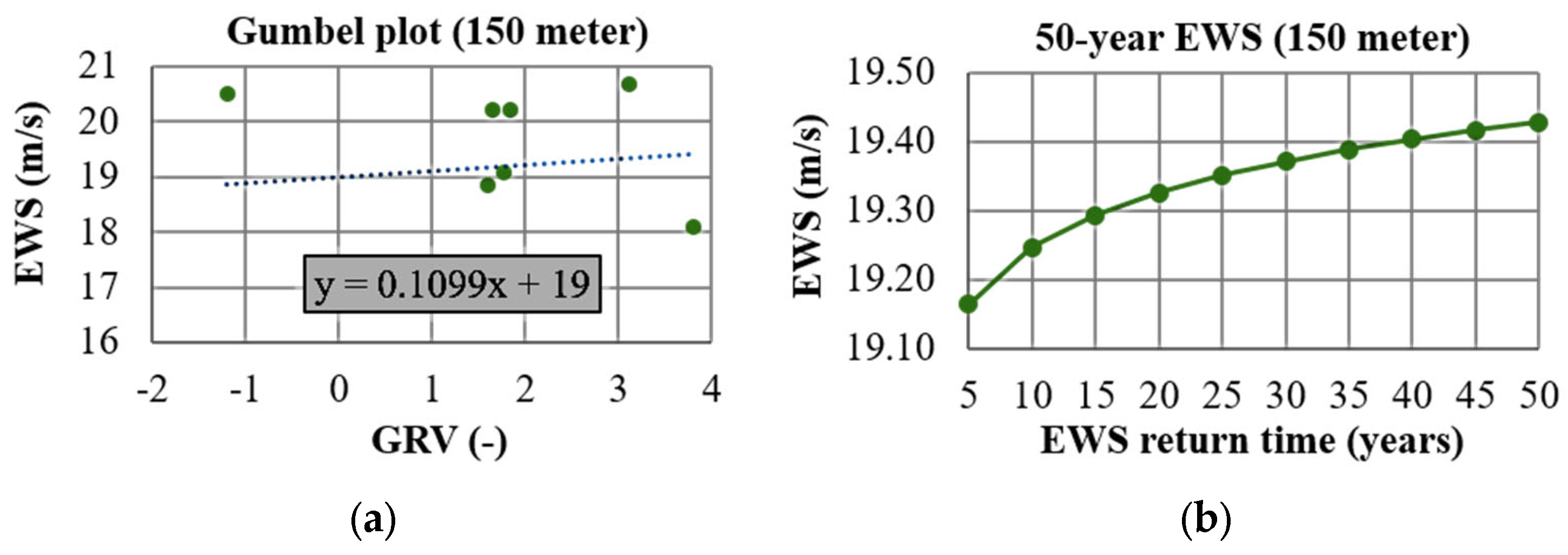
3.1. Environemt Conditions
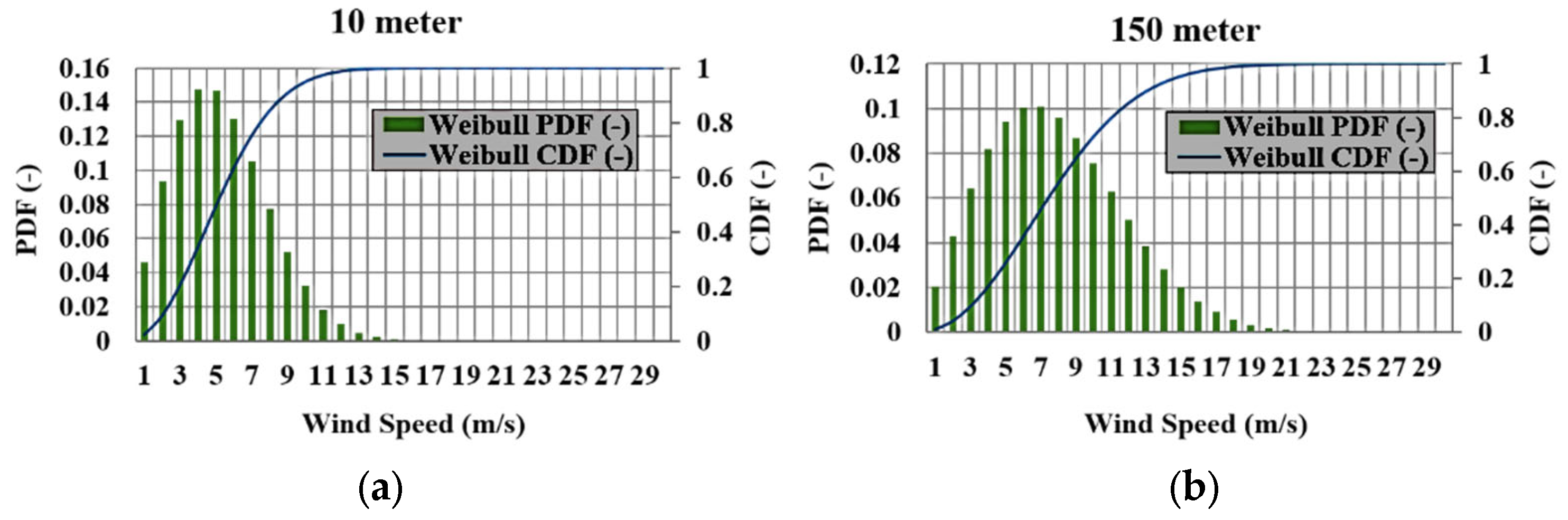
3.1.1. Wind Characteristics
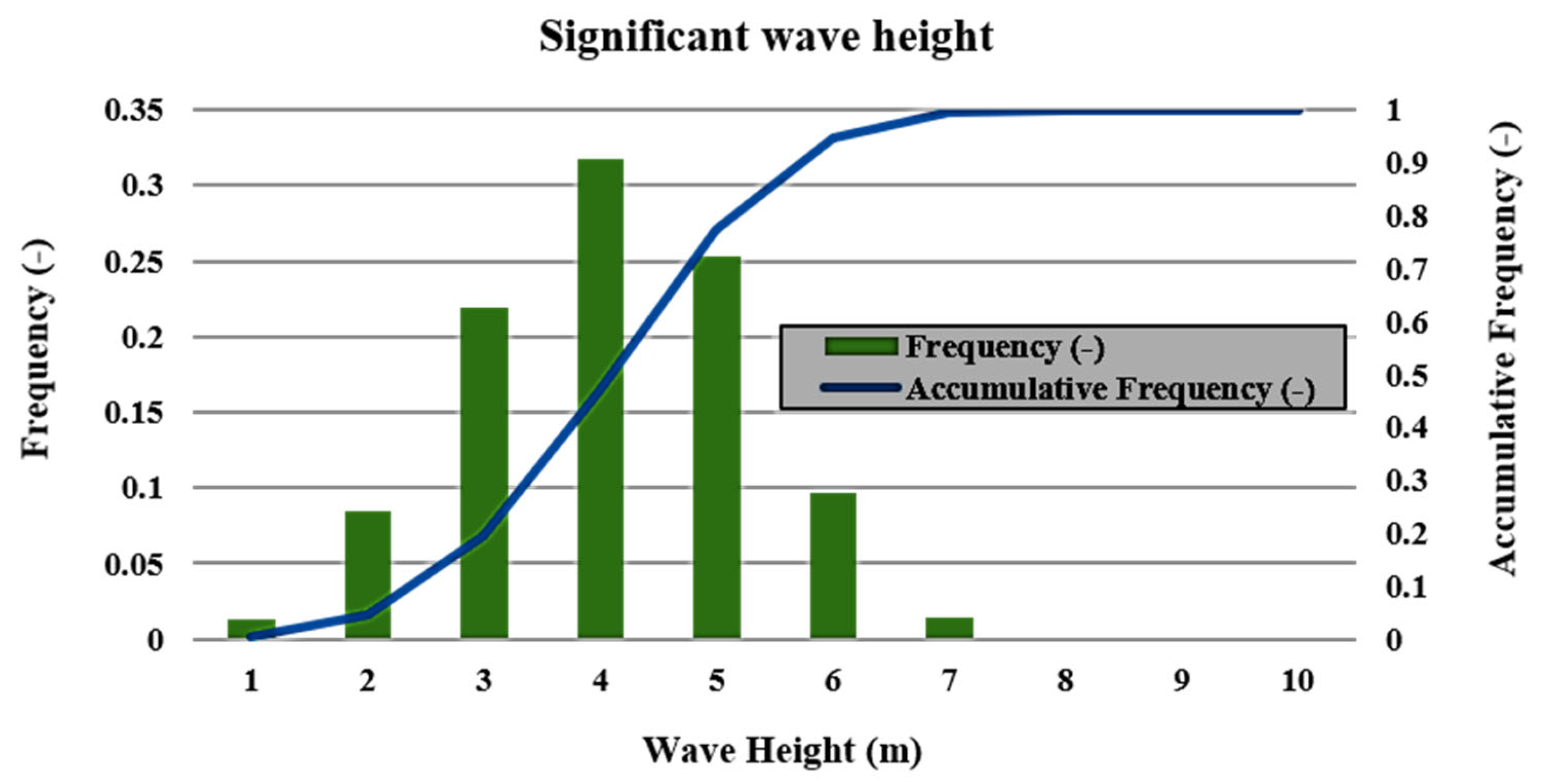
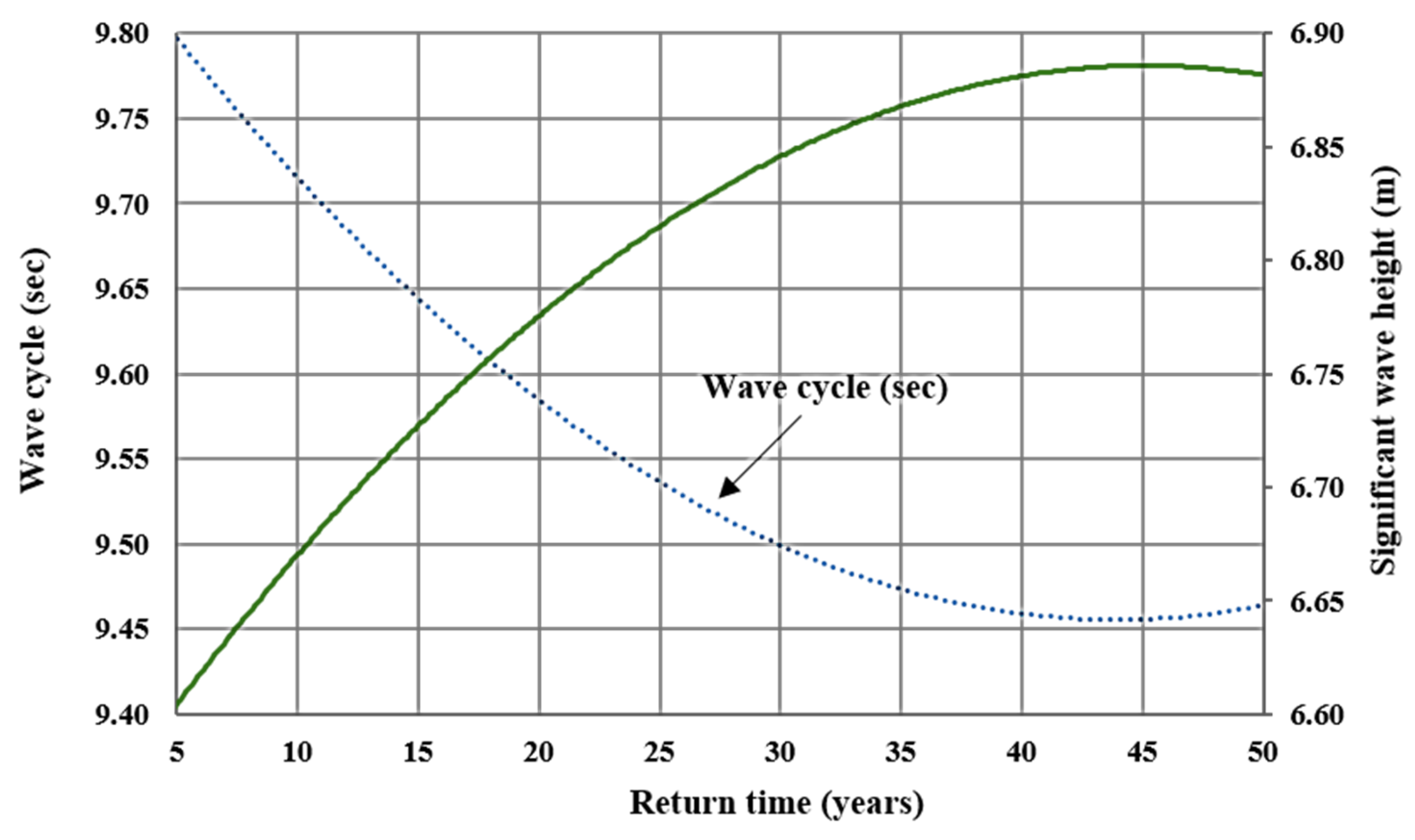
3.1.2. Hydro Characteristics
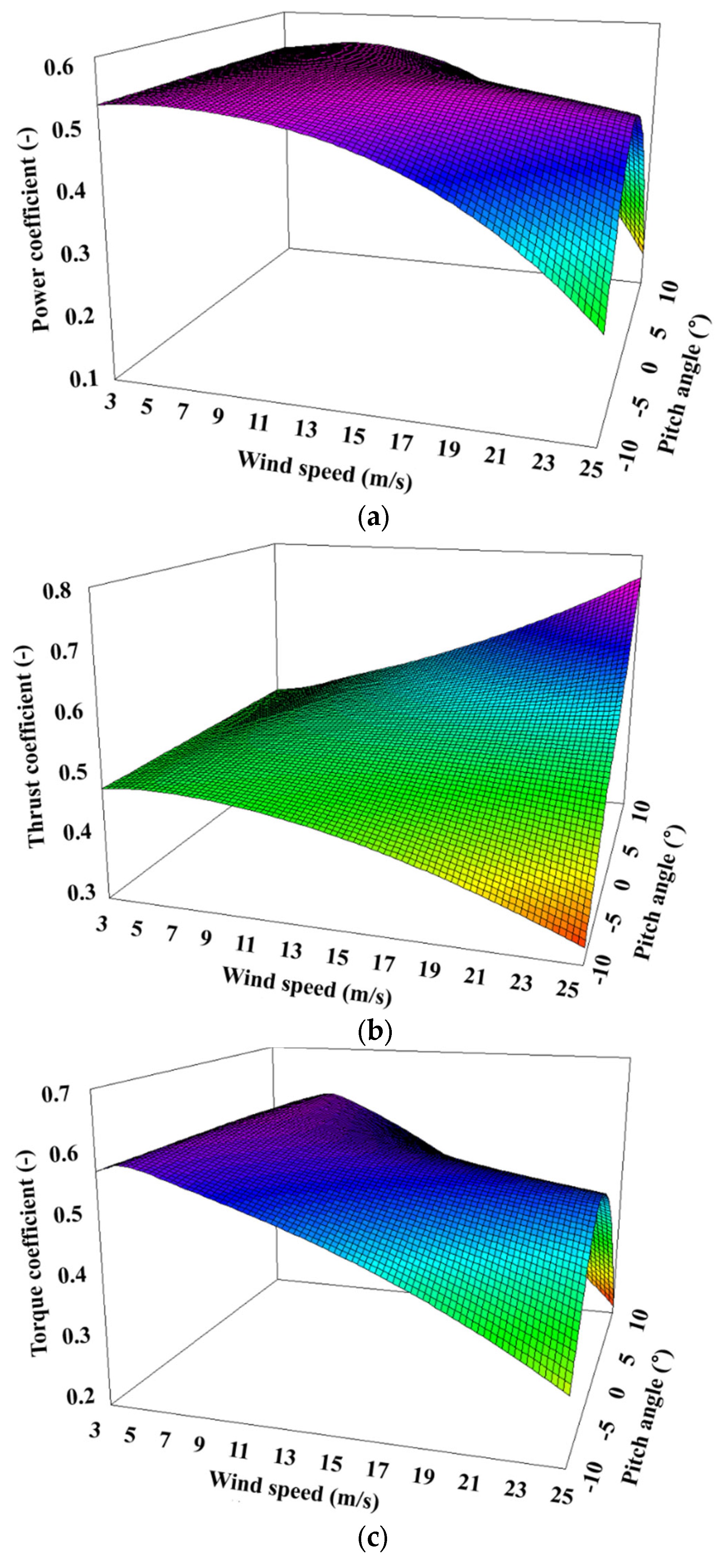
3.2. Performance Coefficients
3.3. Structural Loads
3.3.1. Monopile Foundation
3.3.2. Tower
3.3.3. Blades
3.4. Energy Production
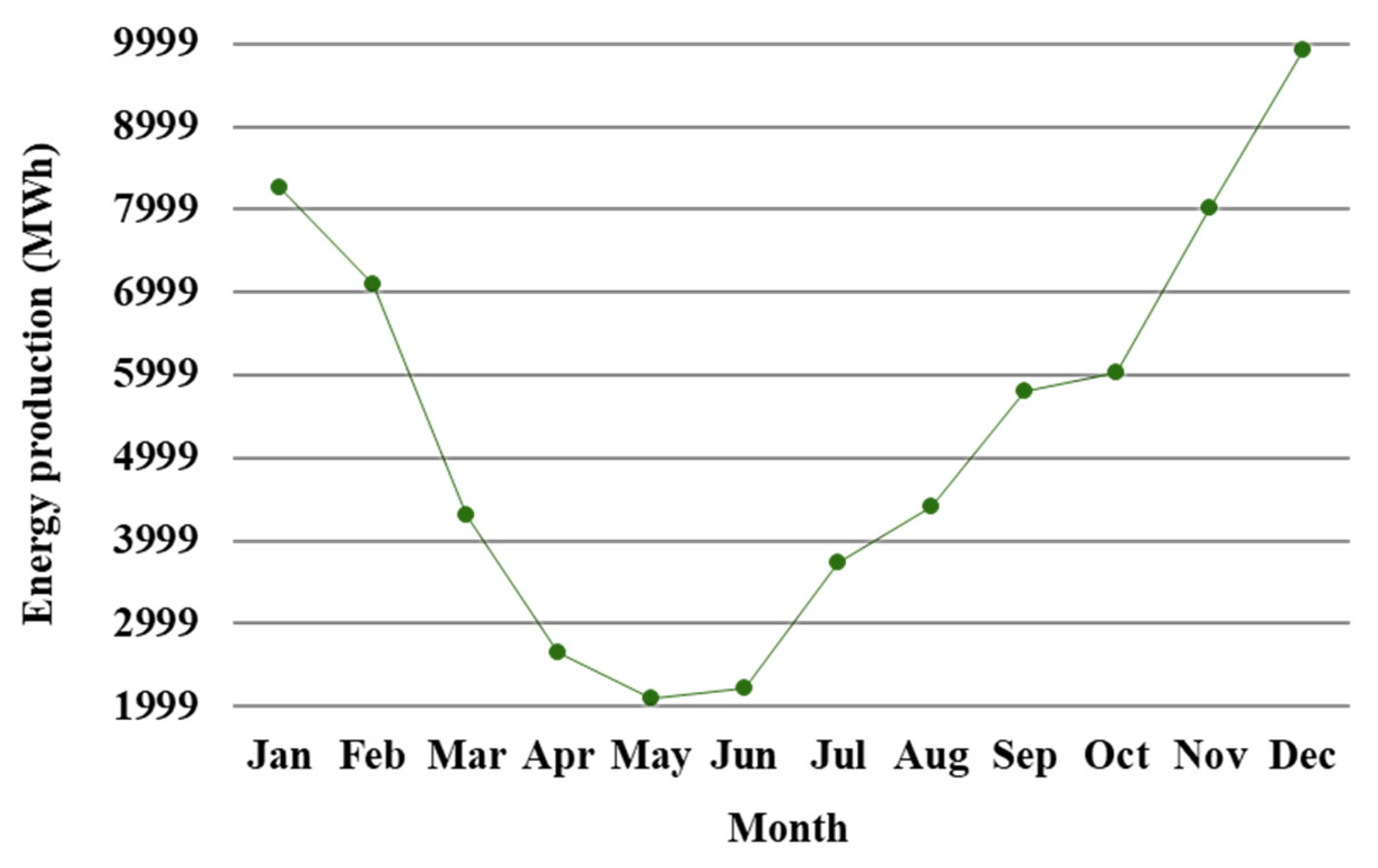
3.4.1. Monthly Basis
3.4.2. Season Basis
- Autumn: September to October;
- Summer: May to August;
- Spring: March to April;
- Winter: November to February.
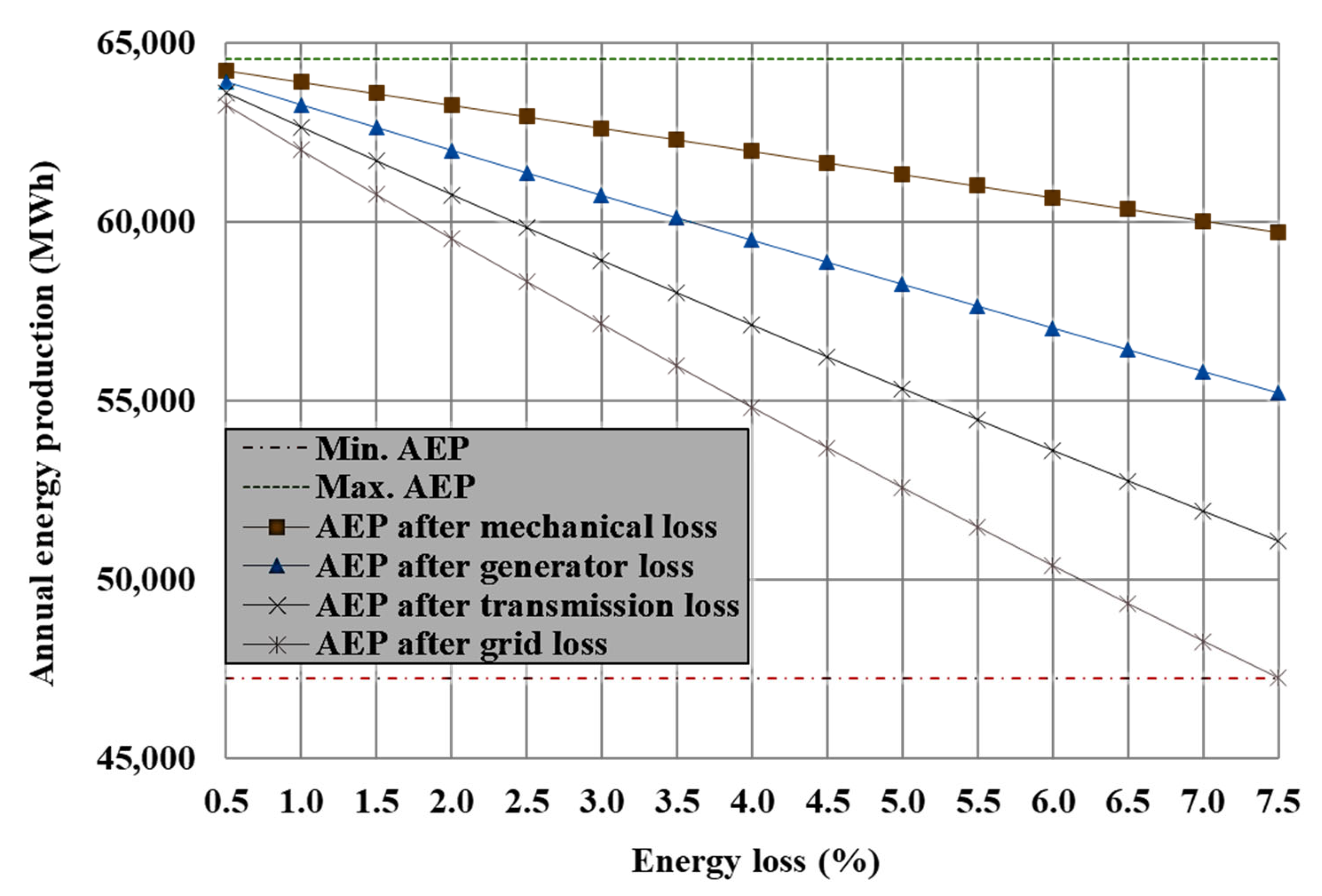
3.4.3. Annual Energy Production (AEP)
4. Discussion and Future Recommendations
- Typhoon Khanun (2023): Winds up to 43.89 m/s.
- Typhoon Hinnamnor (2022): Maximum sustained winds around 43.61 m/s.
- Typhoon Maysak (2020): Maximum sustained winds around 43.06 m/s.
- Typhoon Haishen (2020): Winds up to 44.44 m/s.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sánchez, S.; López-Gutiérrez, J.S.; Negro, V.; Esteban, M.D. Foundations in offshore wind farms: Evolution, characteristics and range of use. Analysis of main dimensional parameters in monopile foundations. J. Mar. Sci. Eng. 2019, 7, 441. [Google Scholar] [CrossRef]
- Dromant Bellver, B. An EU Strategy to Harness the Potential of Offshore Renewable Energy for a Climate Neutral Future. Available online: https://roderic.uv.es/items/9fdb5f40-edbd-410e-912c-25d8234547a1 (accessed on 12 July 2024).
- Bento, N.; Fontes, M. Emergence of floating offshore wind energy: Technology and industry. Renew. Sustain. Energy Rev. 2019, 99, 66–82. [Google Scholar] [CrossRef]
- Duffy, A.; Hand, M.; Wiser, R.; Lantz, E.; Dalla Riva, A.; Berkhout, V.; Stenkvist, M.; Weir, D.; Lacal-Arántegui, R. Land-based wind energy cost trends in Germany, Denmark, Ireland, Norway, Sweden and the United States. Appl. Energy 2020, 277, 114777. [Google Scholar] [CrossRef]
- Li, X.; Wu, Z.; Su, D.; Zhang, L. Reliability analysis of offshore monopile foundations considering multidirectional loading and soil spatial variability. Comput. Geotech. 2024, 166, 106045. [Google Scholar] [CrossRef]
- Shields, M.; Beiter, P.; Nunemaker, J.; Cooperman, A.; Duffy, P. Impacts of turbine and plant upsizing on the levelized cost of energy for offshore wind. Appl. Energy 2021, 298, 117189. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Ishihara, T. Upscaling and levelized cost of energy for offshore wind turbines supported by semi-submersible floating platforms. J. Phys. Conf. Ser. 2019, 1356, 012033. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef]
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Jiang, Z.; Gao, Z.; Ren, Z.; Li, Y.; Duan, L. A parametric study on the final blade installation process for monopile wind turbines under rough environmental conditions. Eng. Struct. 2018, 172, 1042–1056. [Google Scholar] [CrossRef]
- Chitteth Ramachandran, R.; Desmond, C.; Judge, F.; Serraris, J.J.; Murphy, J. Floating offshore wind turbines: Installation, operation, maintenance and decommissioning challenges and opportunities. Wind Energy Sci. Discuss. 2021, 2021, 903–924. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine; Danish Wind Power Research: Fredericia, Denmark, 2013. [Google Scholar]
- Sieros, G.; Chaviaropoulos, P.; Sørensen, J.D.; Bulder, B.H.; Jamieson, P. Upscaling wind turbines: Theoretical and practical aspects and their impact on the cost of energy. Wind Energy 2012, 15, 3–17. [Google Scholar] [CrossRef]
- Ashuri, T. Beyond Classical Upscaling: Integrated Aeroservoelastic Design and Optimization of Large Offshore Wind Turbines; NARCIS: The Hague, The Netherlands, 2012. [Google Scholar]
- Leimeister, M.; Bachynski, E.E.; Muskulus, M.; Thomas, P. Rational upscaling of a semi-submersible floating platform supporting a wind turbine. Energy Procedia 2016, 94, 434–442. [Google Scholar] [CrossRef]
- Ferri, G.; Marino, E.; Borri, C. Optimal dimensions of a semisubmersible floating platform for a 10 MW wind turbine. Energies 2020, 13, 3092. [Google Scholar] [CrossRef]
- Butterfield, S.; Musial, W.; Jonkman, J.; Sclavounos, P. Engineering Challenges for Floating Offshore Wind Turbines; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007.
- Jonkman, J.M. Loads Analysis of a Floating Offshore Wind Turbine Using Fully Coupled Simulation; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007.
- Jonkman, J. Influence of control on the pitch damping of a floating wind turbine. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 1306. [Google Scholar]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, W.; Shi, W.; Li, X. Effects of second-order hydrodynamics on an ultra-large semi-submersible floating offshore wind turbine. Structures 2020, 28, 2260–2275. [Google Scholar] [CrossRef]
- Offshore Wind Website. Available online: https://www.offshorewind.biz/2020/02/14/nrel-unveils-15mw-reference-offshore-wind-turbine/ (accessed on 14 August 2024).
- Gaertner, E. Definition of the IEA 15-Megawatt Offshore Reference Wind; National Renewable Energy Laboratory: Golden, CO, USA, 2020.
- Jonkman, J.M.; Matha, D. Dynamics of offshore floating wind turbines—Analysis of three concepts. Wind Energy 2011, 14, 557–569. [Google Scholar] [CrossRef]
- Jiang, Z. Installation of offshore wind turbines: A technical review. Renew. Sustain. Energy Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- Butterfield, C.P.; Musial, W.P.; Simms, D.A. Combined Experiment Phase 1. Final Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1992.
- Simms, D.A.; Hand, M.M.; Fingersh, L.J.; Jager, D.W. Unsteady Aerodynamics Experiment Phases II–IV Test Configurations and Available Data Campaigns; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1999.
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2001.
- Schepers, J.G.; Snel, H. Model Experiments in Controlled Conditions; ECN Report: ECN-E-07-042; Energy Research Center of the Netherlands (ECN): Petten, The Netherlands, 2007.
- Boorsma, K.; Schepers, J.G. Description of Experimental Set-Up; Mexico Measurements; ECN: Petten, The Netherlands, 2009.
- Boorsma, K.; Schepers, J.G. Description of Experimental Setup, New Mexico Experiment; Technical Report ECN-X–15-093; ECN: Petten, The Netherlands, 2015.
- Schepers, J.G.; Schreck, S.J. Aerodynamic measurements on wind turbines. Wiley Interdiscip. Rev. Energy Environ. 2019, 8, e320. [Google Scholar] [CrossRef]
- Xiao, J.P.; Wu, J.; Chen, L.; Shi, Z.Y. Particle image velocimetry (PIV) measurements of tip vortex wake structure of wind turbine. Appl. Math. Mech. 2011, 32, 729–738. [Google Scholar] [CrossRef]
- Cho, T.; Kim, C. Wind tunnel test for the NREL phase VI rotor with 2 m diameter. Renew. Energy 2014, 65, 265–274. [Google Scholar] [CrossRef]
- Cho, T.; Kim, C. Wind tunnel test results for a 2/4.5 scale MEXICO rotor. Renew. Energy 2012, 42, 152–156. [Google Scholar] [CrossRef]
- Schepers, J.G.; Boorsma, K.; Cho, T.; Gomez-Iradi, S.; Schaffarczyk, P.; Jeromin, A.; Shen, W.Z.; Lutz, T.; Meister, K.; Stoevesandt, B.; et al. Analysis of Mexico Wind Tunnel Measurements: Final Report of IEA Task 29, Mexnext (Phase 1); Energy Research Center of the Netherlands (ECN): Petten, The Netherlands, 2012.
- Berger, F.; Kröger, L.; Onnen, D.; Petrović, V.; Kühn, M. Scaled wind turbine setup in a turbulent wind tunnel. J. Phys. Conf. Ser. 2018, 1104, 012026. [Google Scholar] [CrossRef]
- Berger, F.; Onnen, D.; Schepers, J.G.; Kühn, M. Experimental analysis of radially resolved dynamic inflow effects due to pitch steps. Wind Energy Sci. Discuss. 2021, 2021, 1341–1361. [Google Scholar] [CrossRef]
- Langidis, A.; Nietiedt, S.; Berger, F.; Kröger, L.; Petrović, V.; Wester, T.T.; Gülker, G.; Göring, M.; Rofallski, R.; Luhmann, T.; et al. Design and evaluation of rotor blades for fluid structure interaction studies in wind tunnel conditions. J. Phys. Conf. Ser. 2022, 2265, 022079. [Google Scholar] [CrossRef]
- Nietiedt, S.; Wester, T.T.; Langidis, A.; Kröger, L.; Rofallski, R.; Göring, M.; Kühn, M.; Gülker, G.; Luhmann, T. A Wind Tunnel Setup for Fluid-Structure Interaction Measurements Using Optical Methods. Sensors 2022, 22, 5014. [Google Scholar] [CrossRef]
- Fontanella, A.; Bayati, I.; Mikkelsen, R.; Belloli, M.; Zasso, A. UNAFLOW: A holistic experiment about the aerodynamics of floating wind turbines under imposed surge motion. Wind Energy Sci. Discuss. 2021, 2021, 1169–1190. [Google Scholar] [CrossRef]
- Taruffi, F.; Novais, F.; Viré, A. An experimental study on the aerodynamic loads of a floating offshore wind turbine under imposed motions. Wind Energy Sci. 2024, 9, 343–358. [Google Scholar] [CrossRef]
- Fontanella, A.; Facchinetti, A.; Di Carlo, S.; Belloli, M. Wind tunnel investigation of the aerodynamic response of two 15 MW floating wind turbines. Wind Energy Sci. Discuss. 2022, 2022, 1711–1729. [Google Scholar] [CrossRef]
- Allen, C.; Viscelli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Lab. (NREL): Golden, CO, USA; University of Maine: Orono, ME, USA, 2020.
- Kimball, R.; Robertson, A.; Fowler, M.; Mendoza, N.; Wright, A.; Goupee, A.; Lenfest, E.; Parker, A. Results from the FOCAL experiment campaign 1: Turbine control co-design. J. Phys. Conf. Ser. 2022, 2265, 022082. [Google Scholar] [CrossRef]
- Phengpom, T.; Kamada, Y.; Maeda, T.; Murata, J.; Nishimura, S.; Matsuno, T. Study on blade surface flow around wind turbine by using LDV measurements. J. Therm. Sci. 2015, 24, 131–139. [Google Scholar] [CrossRef]
- Phengpom, T.; Kamada, Y.; Maeda, T.; Murata, J.; Nishimura, S.; Matsuno, T. Experimental investigation of the three-dimensional flow field in the vicinity of a rotating blade. J. Fluid Sci. Technol. 2015, 10, JFST0013. [Google Scholar] [CrossRef]
- Phengpom, T.; Kamada, Y.; Maeda, T.; Matsuno, T.; Sugimoto, N. Analysis of wind turbine pressure distribution and 3D flows visualization on rotating condition. IOSR J. Eng. 2016, 6, 18–30. [Google Scholar]
- Akay, B.; Ragni, D.; Simão Ferreira, C.J.; Van Bussel, G.J. Experimental investigation of the root flow in a horizontal axis wind turbine. Wind Energy 2014, 17, 1093–1109. [Google Scholar] [CrossRef]
- Lignarolo, L.E.; Ragni, D.; Krishnaswami, C.; Chen, Q.; Ferreira, C.S.; Van Bussel, G.J. Experimental analysis of the wake of a horizontal-axis wind-turbine model. Renew. Energy 2014, 70, 31–46. [Google Scholar] [CrossRef]
- Micallef, D.; Akay, B.; Ferreira, C.S.; Sant, T.; van Bussel, G. The origins of a wind turbine tip vortex. J. Phys. Conf. Ser. 2014, 555, 012074. [Google Scholar] [CrossRef]
- Micallef, D.; Ferreira, C.S.; Sant, T.; Bussel, G.V. Experimental and numerical investigation of tip vortex generation and evolution on horizontal axis wind turbines. Wind Energy 2016, 19, 1485–1501. [Google Scholar] [CrossRef]
- Del Campo, V.; Ragni, D.; Micallef, D.; Akay, B.; Diez, F.J.; Simão Ferreira, C. 3D load estimation on a horizontal axis wind turbine using SPIV. Wind Energy 2014, 17, 1645–1657. [Google Scholar] [CrossRef]
- Del Campo, V.; Ragni, D.; Micallef, D.; Diez, F.J.; Ferreira, C.S. Estimation of loads on a horizontal axis wind turbine operating in yawed flow conditions. Wind Energy 2015, 18, 1875–1891. [Google Scholar] [CrossRef]
- NREL Wind Turbines. Available online: https://www.nrel.gov/docs/fy20osti/75698.pdf (accessed on 7 June 2024).
- Akdağ, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
- Akgül, F.G.; Şenoğlu, B.; Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: Inverse Weibull distribution. Energy Convers. Manag. 2016, 114, 234–240. [Google Scholar] [CrossRef]
- Carneiro, T.C.; Melo, S.P.; Carvalho, P.C.; Braga, A.P. Particle swarm optimization method for estimation of Weibull parameters: A case study for the Brazilian northeast region. Renew. Energy 2016, 86, 751–759. [Google Scholar] [CrossRef]
- Hennessey, J.P., Jr. Some aspects of wind power statistics. J. Appl. Meteorol. Climatol. 1977, 16, 119–128. [Google Scholar] [CrossRef]
- Corotis, R.B.; Sigl, A.B.; Klein, J. Probability models of wind velocity magnitude and persistence. Sol. Energy 1978, 20, 483–493. [Google Scholar] [CrossRef]
- Justus, C.G.; Hargraves, W.R.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Deaves, D.M.; Lines, I.G. On the fitting of low mean windspeed data to the Weibull distribution. J. Wind Eng. Ind. Aerodyn. 1997, 66, 169–178. [Google Scholar] [CrossRef]
- Garcia, A.; Torres, J.L.; Prieto, E.; De Francisco, A. Fitting wind speed distributions: A case study. Sol. Energy 1998, 62, 139–144. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramirez, P.; Velazquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Bañuelos-Ruedas, F.; Angeles-Camacho, C.; Rios-Marcuello, S. Analysis and validation of the methodology used in the extrapolation of wind speed data at different heights. Renew. Sustain. Energy Rev. 2010, 14, 2383–2391. [Google Scholar] [CrossRef]
- Pinheiro, E.C.; Ferrari, S.L. A comparative review of generalizations of the Gumbel extreme value distribution with an application to wind speed data. J. Stat. Comput. Simul. 2016, 86, 2241–2261. [Google Scholar] [CrossRef]
- Mendoza, N.; Robertson, A.; Wright, A.; Jonkman, J.; Wang, L.; Bergua, R.; Ngo, T.; Das, T.; Odeh, M.; Mohsin, K.; et al. Verification and Validation of Model-Scale Turbine Performance and Control Strategies for the IEA Wind 15 MW Reference Wind Turbine. Energies 2022, 15, 7649. [Google Scholar] [CrossRef]
- Fritz, E.; Ribeiro, A.; Boorsma, K.; Ferreira, C. Aerodynamic characterisation of a thrust-scaled IEA 15 MW wind turbine model: Experimental insights using PIV data. Wind Energy Sci. 2024, 9, 1173–1187. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.M.; Jang, C.M. Techno-economic assessment of wind energy potential at three locations in South Korea using long-term measured wind data. Energies 2017, 10, 1442. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.M.; Jang, C.M. Determination of the most optimal on-shore wind farm site location using a GIS-MCDM methodology: Evaluating the case of South Korea. Energies 2017, 10, 2072. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.M.; Jang, C.M. Statistical analysis of wind characteristics using Weibull and Rayleigh distributions in Deokjeok-do Island–Incheon, South Korea. Renew. Energy 2018, 123, 652–663. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, J.; Baniotopoulos, C.; Wang, X.; Deng, X. Dynamic analysis of offshore steel wind turbine towers subjected to wind, wave and current loading during construction. Ocean Eng. 2020, 216, 108084. [Google Scholar] [CrossRef]
- Papi, F.; Bianchini, A. Technical challenges in floating offshore wind turbine upscaling: A critical analysis based on the NREL 5 MW and IEA 15 MW Reference Turbines. Renew. Sustain. Energy Rev. 2022, 162, 112489. [Google Scholar] [CrossRef]
- Lapa, G.V.; Neto, A.G.; Franzini, G.R. Effects of blade torsion on IEA 15MW turbine rotor operation. Renew. Energy 2023, 219, 119546. [Google Scholar] [CrossRef]
- Riviera Maritime Webpage. Available online: https://www.rivieramm.com/news-content-hub/news-content-hub/second-siemens-gamesa-turbine-certified-lsquotyphoon-resistantrsquo-66444 (accessed on 24 July 2024).
- Vestas Wind Turbines. Available online: https://www.vestas.com/content/dam/vestas-com/global/en/sustainability/environment/LCA%20of%20Electricity%20Production%20from%20an%20offshore%20V236-15MW.pdf.coredownload.inline.pdf (accessed on 12 August 2024).
- NREL Website. Available online: https://www.nrel.gov/docs/fy24osti/88195.pdf (accessed on 12 August 2024).








| Wind | Wave | ||
|---|---|---|---|
| Site Name | Buan | Site Name | Buan |
| Latitude (°) | 35.667 | Latitude (°) | 35.667 |
| Longitude (°) | 125.733 | Longitude (°) | 125.733 |
| Data Period (Years) | 2017–2023 | Data Period (Years) | 2017–2023 |
| Height (m) | 10 | Water Temperature | Yes |
| Time Interval (min) | 10 | Maximum Wave Height | Yes |
| Wind Speed | Yes | Significant Wave Height | Yes |
| Wind Direction | Yes | Average Wave Height | Yes |
| Temperature | Yes | Wave Cycle | Yes |
| Parameter | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|---|
| Temperature (°C) | 13.9 | 13.87 | 13.93 | 13.86 | 12.01 | 11.56 | 13.67 |
| Wind Angle (degrees) | 191.57 | 174.76 | 200.94 | 192.15 | 184.39 | 176.9 | 190.49 |
| Mean Wind Speed (m/s) | 5.25 | 5.06 | 5.16 | 5.47 | 5.6 | 5.4 | 5.23 |
| Max. Wind Speed (m/s) | 12.78 | 12.27 | 12.92 | 14.01 | 13.69 | 13.7 | 13.89 |
| Min. Wind Speed (m/s) | 0 | 0 | 1.03 | 0 | 1.28 | 0 | 0 |
| St. Dev. (m/s) | 2.55 | 2.38 | 2.54 | 2.8 | 2.74 | 2.77 | 2.79 |
| TI (-) | 0.49 | 0.47 | 0.49 | 0.51 | 0.49 | 0.51 | 0.53 |
| k (-) | 2.19 | 2.27 | 2.15 | 2.06 | 2.17 | 2.06 | 1.98 |
| c (m/s) | 5.92 | 5.72 | 5.82 | 6.17 | 6.32 | 6.09 | 5.9 |
| Vmp (m/s) | 4.49 | 4.43 | 4.36 | 4.48 | 4.76 | 4.42 | 4.13 |
| VmaxE (m/s) | 7.96 | 7.55 | 7.9 | 8.57 | 8.53 | 8.47 | 8.4 |
| Parameter | Sea-Water Temperature (°C) | Sea-Water Density (kg/m3) | Significant Wave Height (m) | Wave Cycle (s) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Max. | Mean | Max. | Mean | Max. | Mean | Max. | |
| Jan | 8.55 | 11.34 | 999.8 | 1000 | 2.1 | 6.8 | 5.5 | 8.7 |
| Feb | 6.76 | 8.93 | 999.9 | 1000 | 1.9 | 7.3 | 5.5 | 8.9 |
| Mar | 7.52 | 11.75 | 999.9 | 1000 | 1.4 | 4.7 | 4.9 | 7.8 |
| Apr | 10.67 | 19.31 | 999.6 | 999.9 | 1 | 4.1 | 4.8 | 11.9 |
| May | 16.59 | 28.33 | 998.8 | 999.8 | 0.9 | 3.2 | 4.9 | 8.3 |
| Jun | 22.36 | 29.09 | 997.7 | 999 | 0.9 | 3.5 | 5.4 | 10.4 |
| Jul | 25.02 | 28.71 | 997 | 998.2 | 1 | 3.2 | 5.1 | 8.3 |
| Aug | 25.21 | 30.65 | 997 | 998.6 | 1.3 | 4.2 | 5.3 | 9.8 |
| Sep | 20.97 | 26.88 | 998 | 999.3 | 1.5 | 6.4 | 5 | 8.6 |
| Oct | 16.78 | 21.24 | 998.8 | 999.7 | 1.7 | 6 | 5.1 | 8.7 |
| Nov | 14.36 | 17.56 | 999.2 | 999.7 | 2 | 6.2 | 5.5 | 8.7 |
| Dec | 11.32 | 14.2 | 999.6 | 999.8 | 2.7 | 7.4 | 5.9 | 9.1 |
| Wind Speed (m/s) | Fx (N) | Fy (N) | Fxy (N) | Mx (Nm) | My (Nm) | Mxy (Nm) |
|---|---|---|---|---|---|---|
| 8 | 1.33 × 106 | 1.23 × 102 | 1.33 × 106 | 1.14 × 107 | 2.36 × 108 | 2.36 × 108 |
| 9 | 1.64 × 106 | 6.75 × 102 | 1.64 × 106 | 1.42 × 107 | 2.90 × 108 | 2.91 × 108 |
| 10 | 1.95 × 106 | 1.28 × 103 | 1.95 × 106 | 1.73 × 107 | 3.47 × 108 | 3.47 × 108 |
| 11 | 2.14 × 106 | 9.65 × 102 | 2.14 × 106 | 2.03 × 107 | 3.79 × 108 | 3.79 × 108 |
| 12 | 1.80 × 106 | −2.12 × 103 | 1.80 × 106 | 2.07 × 107 | 3.18 × 108 | 3.19 × 108 |
| 13 | 1.62 × 106 | −3.82 × 103 | 1.62 × 106 | 2.10 × 107 | 2.85 × 108 | 2.86 × 108 |
| 14 | 1.49 × 106 | −5.00 × 103 | 1.49 × 106 | 2.11 × 107 | 2.62 × 108 | 2.63 × 108 |
| Annual Energy Production (MWh) | Mean Annual Generated Power (MW) |
|---|---|
| 64,540.13 | 7.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.; Park, H.; Lee, D. Investigating the Structural and Power Performance of a 15 MW Class Wind Energy Generation System under Experimental Wind and Marine Loading. J. Mar. Sci. Eng. 2024, 12, 1485. https://doi.org/10.3390/jmse12091485
Ali S, Park H, Lee D. Investigating the Structural and Power Performance of a 15 MW Class Wind Energy Generation System under Experimental Wind and Marine Loading. Journal of Marine Science and Engineering. 2024; 12(9):1485. https://doi.org/10.3390/jmse12091485
Chicago/Turabian StyleAli, Sajid, Hongbae Park, and Daeyong Lee. 2024. "Investigating the Structural and Power Performance of a 15 MW Class Wind Energy Generation System under Experimental Wind and Marine Loading" Journal of Marine Science and Engineering 12, no. 9: 1485. https://doi.org/10.3390/jmse12091485
APA StyleAli, S., Park, H., & Lee, D. (2024). Investigating the Structural and Power Performance of a 15 MW Class Wind Energy Generation System under Experimental Wind and Marine Loading. Journal of Marine Science and Engineering, 12(9), 1485. https://doi.org/10.3390/jmse12091485







