Design of a Trajectory Tracking Controller for Marine Vessels with Asymmetric Constraints Using a New Universal Barrier Function
Abstract
:1. Introduction
2. Preliminaries
2.1. Vessel Mathematical Model
2.2. Control Objective
2.3. Universal Asymmetric Barrier Function
3. Constrained Controller Design
4. Simulations
4.1. Control Setting
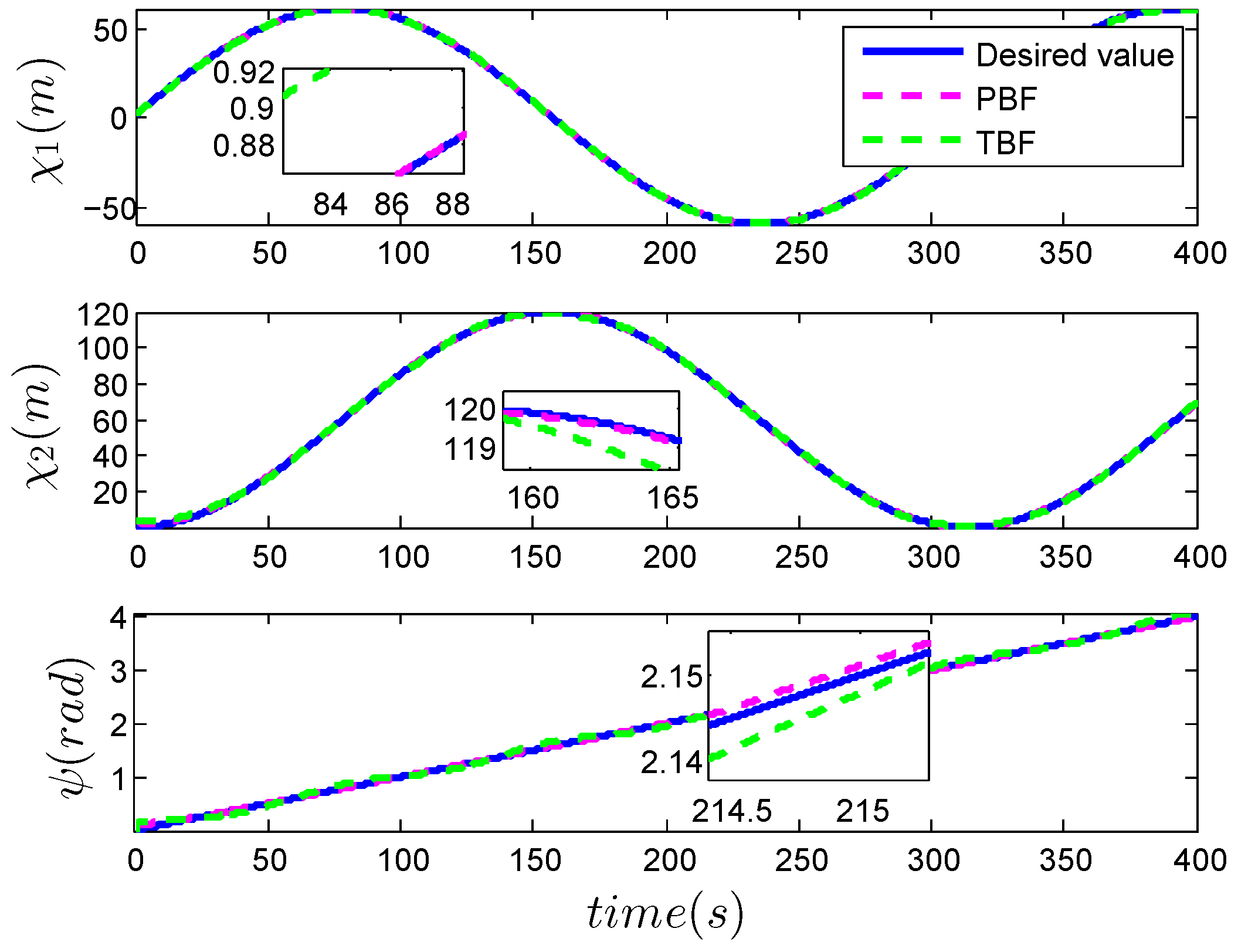
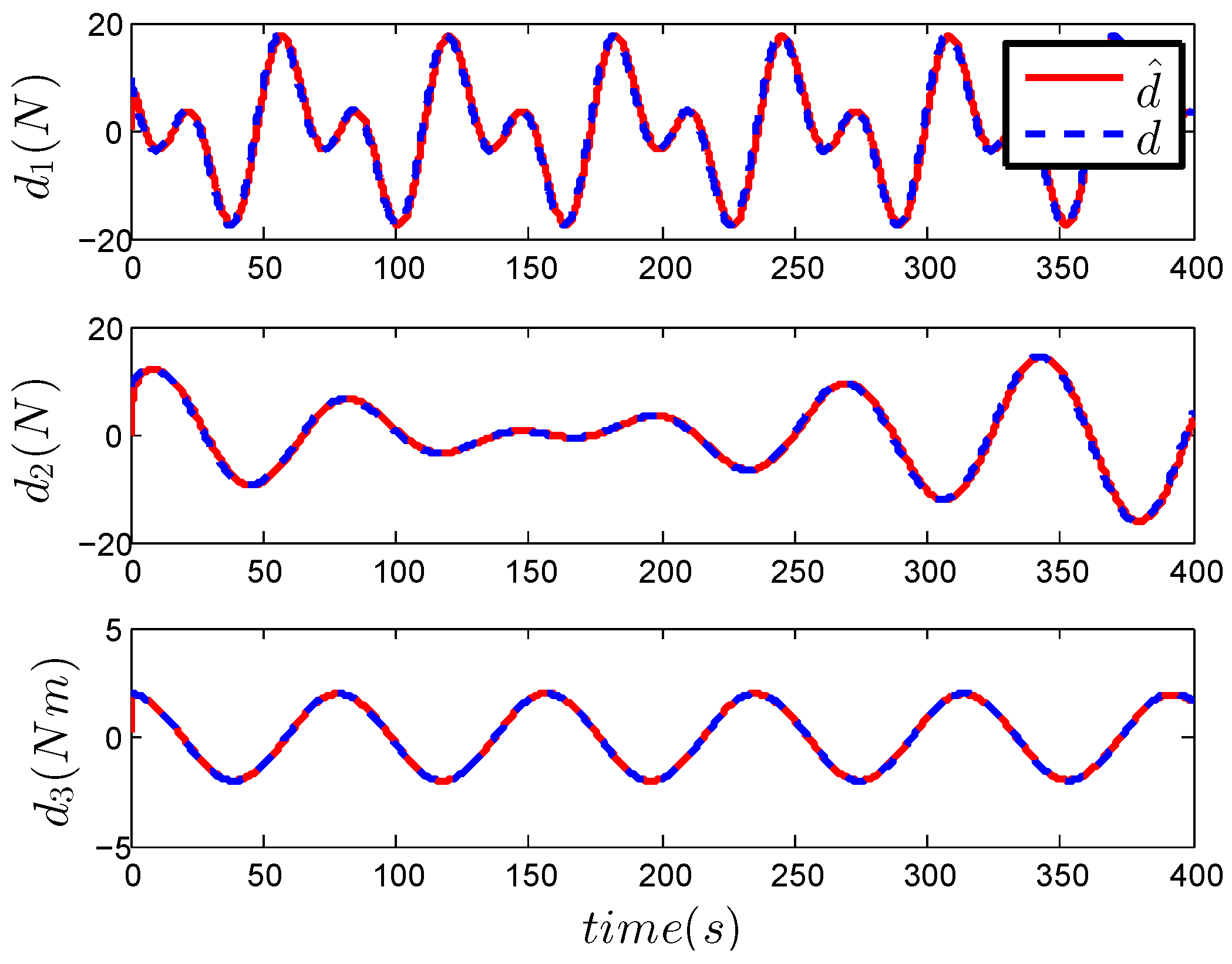
4.2. Simulation Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Donaire, A.; Romero, J.G.; Perez, T. Trajectory tracking passivity-based control for marine vehicles subject to disturbances. J. Frankl. Inst. 2017, 354, 2167–2182. [Google Scholar] [CrossRef]
- Ellenrieder, K.D. Dynamic surface control of trajectory tracking marine vehicles with actuator magnitude and rate limits. Automatica 2019, 105, 433–442. [Google Scholar] [CrossRef]
- Li, M.-Y.; Xie, W.-B.; Wang, Y.-L.; Hu, X. Prescribed performance trajectory tracking fault-tolerant control for dynamic positioning vessels under velocity constraints. Appl. Math. Comput. 2022, 431, 127348. [Google Scholar] [CrossRef]
- Li, M.-Y.; Xu, J.; Xie, W.-B.; Wang, H.-B. Finite-time composite learning control for trajectory tracking of dynamic positioning vessels. Ocean Eng. 2022, 262, 112288. [Google Scholar] [CrossRef]
- Bidikli, B.; Tatlicioglu, E.; Zergeroglu, E. Observer-based adaptive output feedback tracking control of dynamically positioned surface vessels. J. Mar. Sci. Technol. 2017, 22, 376–387. [Google Scholar] [CrossRef]
- Lin, Y.; Du, J.; Zhu, G.; Fang, H. Thruster fault-tolerant control for dynamic positioning of vessels. Appl. Ocean Res. 2018, 80, 118–124. [Google Scholar] [CrossRef]
- ⌀veraas, H.; Halvorsen, H.S.; Landstad, O.; Smines, V.; Johansen, T.A. Dynamic Positioning Using Model Predictive Control with Short-Term Wave Prediction. IEEE J. Ocean. Eng. 2023, 48, 1065–1077. [Google Scholar]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdahl, J.T.; Sorensen, A.J.; Milovanovic, M.; Bruzzone, B. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Barragan-Alcantar, D.; Collado-Gonzalez, I.; Garrido, L. Adaptive dynamic programming and deep reinforcement learning for the control of an unmanned surface vehicle: Experimental results. Control Eng. Pract. 2021, 111, 1623–1642. [Google Scholar] [CrossRef]
- Zheng, Z. Moving path following control for a surface vessel with error Constraint. Automatica 2020, 118, 109040. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, Z.; Wang, T.; Song, S.; Xiang, J.; Zhang, X. Multi-model predictive control strategy for path-following of unmanned surface vehicles in wide-range speed variations. Ocean Eng. 2024, 295, 116845. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, C.; Yin, Y.; Wang, J. Safety-certified constrained control of maritime autonomous surface ships for automatic berthing. IEEE Trans. Veh. Technol. 2023, 72, 8541–8552. [Google Scholar] [CrossRef]
- Shojaei, K. Observer-based neural adaptive formation control of autonomous surface vessels with limited torque. Robot. Auton. Syst. 2016, 78, 83–96. [Google Scholar] [CrossRef]
- Jin, X. Fault tolerant finite-time leader-follower formation control for autonomous surface vessels with LOS range and angle constraints. Automatica 2016, 68, 228–236. [Google Scholar] [CrossRef]
- Tran, Q.V.; Lee, C.; Kim, J.; Nguyen, H.Q. Robust bearing-based formation tracking control of underactuated surface vessels: An output regulation approach. IEEE Trans. Control Netw. Syst. 2023, 10, 2048–2059. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Z.; Chen, F. Adaptive output-constrained finite-time formation control for multiple unmanned surface vessels with directed communication topology. Ocean Eng. 2024, 292, 116552. [Google Scholar] [CrossRef]
- Abdelaal, M.; Franzle, M.; Hahn, A. Nonlinear Model Predictive Control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean Eng. 2018, 160, 168–180. [Google Scholar] [CrossRef]
- Kinjo, L.M.; Menard, T.; Wirtensohn, S.; Gehan, O.; Reuter, J. Tracking Control of Docking Maneuvers for a Fully Actuated Surface Vessel Using Backstepping. IEEE Trans. Control Syst. Technol. 2024, 32, 1920–1927. [Google Scholar] [CrossRef]
- Aguilar-Ibanez, C.; Suarez-Castanon, M.S.; Garcia-Canseco, E.; Robio, J.J.; Barron-Fernandez, R.; Martinez, J.C. Trajectory Tracking Control of an Autonomous Vessel in the Presence of Unknown Dynamics and Disturbances. Mathematics 2024, 12, 2239. [Google Scholar] [CrossRef]
- Manzanilla, A.; Ibarra, E.; Salazar, S.; Zamora, A.E.; Lozano, R.; Munoz, F. Super-twisting integral sliding mode control for trajectory tracking of an Unmanned Underwater Vehicle. Ocean Eng. 2021, 234, 109164. [Google Scholar] [CrossRef]
- Londhe, P.S.; Patre, B.M. Adaptive fuzzy sliding mode control for robust trajectory tracking control of an autonomous underwater vehicle. Intel. Serv. Robot. 2019, 12, 87–102. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Yang, J.; Zhang, W. Research on the sliding mode control for underactuated surface vessels via parameter estimation. Nonlinear Dyn. 2018, 91, 1163–1175. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, S. Disturbance observer-based prescribed performance super-twisting sliding mode control for autonomous surface vessels. ISA Trans. 2023, 135, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Wen, G.; Ge, S.S.; Chen, C.P.; Tu, F.; Wang, S. Adaptive tracking control of surface vessel using optimized backstepping technique. IEEE Trans. Cybern. 2018, 49, 3420–3431. [Google Scholar] [CrossRef]
- Jiao, J.; Wang, G. Event driven tracking control algorithm for marine vessel based on backstepping method. Neurocomputing 2016, 207, 669–675. [Google Scholar] [CrossRef]
- Fetzer, K.L.; Nersesov, S.; Ashrafiuon, H. Full-state nonlinear trajectory tracking control of underactuated surface vessels. J. Vib. Control 2013, 26, 1286–1296. [Google Scholar] [CrossRef]
- Chen, X.; Tan, W.W. Tracking control of surface vessels via fault-tolerant adaptive backstepping interval type-2 fuzzy control. Ocean Eng. 2020, 70, 97–109. [Google Scholar] [CrossRef]
- Shen, Z.; Li, A.; Li, L.; Yu, H. Prescribed performance LOS guidance-based dynamic surface path following control of surface vessel with position and heading errors constraint. J. Navig. 2013, 76, 255–285. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, T.; Liu, Z. Robust model predictive control for path-following of underactuated surface vessels with roll constraints. Ocean Eng. 2017, 143, 125–132. [Google Scholar] [CrossRef]
- Cui, S.; Zhao, T. Uncertain surface vessels tracking control based on linear active disturbance rejection control and finite time convergence. Ocean Eng. 2024, 298, 117263. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Y.; Huang, B.; Su, Y. Finite-time trajectory tracking control for under-actuated unmanned surface vessels with saturation constraint. Ocean Eng. 2022, 249, 110745. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended state observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Wu, D.; Yan, Y. Nonsingular fixed-time terminal sliding mode trajectory tracking control for marine surface vessels with anti-disturbances. Ocean Eng. 2020, 217, 108158. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J. Model predictive control for tracking of underactuated vessels based on recurrent neural networks. IEEE J. Ocean. Eng. 2012, 37, 717–726. [Google Scholar] [CrossRef]
- Zhu, G.; Du, J.; Kao, Y. Robust adaptive neural trajectory tracking control of surface vessels under input and output constraints. J. Frankl. Inst. 2020, 357, 8591–8610. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, B.; Su, Y.; Zheng, Y.; Zheng, S. Fixed-time neural network trajectory tracking control for underactuated surface vessels. Ocean Eng. 2021, 236, 109416. [Google Scholar] [CrossRef]
- Li, M.; Long, Y.; Li, T.; Bai, W. Observer-based adaptive fuzzy event-triggered path following control of marine surface vessel. Int. J. Fuzzy Syst. 2021, 23, 2021–2036. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Tee, K.P.; Ren, B.; Ge, S.S. Control of nonlinear systems with time-varying output constraints. Automatica 2011, 47, 2511–2516. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, Y.; Ouyang, Y.; Yin, Z.; Peng, K. Adaptive neural control for robotic manipulators with output constraints and uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5554–5564. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Zhang, Y.; Yang, C.; Wang, M.; Annamalai, A. An improved adaptive online neural control for robot manipulator systems using integral Barrier Lyapunov functions. Int. J. Syst. Sci. 2019, 50, 638–651. [Google Scholar] [CrossRef]
- Yu, X.; He, W.; Li, H.; Sun, J. Adaptive fuzzy full-state and output-feedback control for uncertain robots with output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6994–7007. [Google Scholar] [CrossRef]
- Yin, Z.; He, W.; Yang, C. Tracking control of a marine surface vessel with full-state constraints. Int. J. Syst. Sci. 2017, 48, 535–546. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Wang, N. Adaptive trajectory tracking algorithm of unmanned surface vessel based on anti-windup compensator with full-state constraints. Ocean Eng. 2020, 200, 106906. [Google Scholar] [CrossRef]
- McIlvanna, S.; Van, M.; Sun, Y.; Naeem, W.; Liu, Z. Adaptive fixed-time control for uncertain surface vessels with output constraints using barrier Lyapunov function. Ocean Eng. 2024, 116740. [Google Scholar] [CrossRef]
- Thanh, P.N.N.; Thuyen, N.A.; Anh, H.P.H. Adaptive fuzzy 3-D trajectory tracking control for autonomous underwater vehicle (AUV) using modified integral barrier lyapunov function. Ocean Eng. 2023, 283, 115027. [Google Scholar] [CrossRef]
- Li, L.; Dong, K.; Guo, G. Trajectory tracking control of underactuated surface vessel with full state constraints. Asian J. Control 2021, 23, 1762–1771. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Li, X.; Du, Y.; Deng, Z. Finite-time trajectory tracking control of unmanned surface vessel with error constraints and input saturations. J. Frankl. Inst. 2020, 357, 11472–11495. [Google Scholar] [CrossRef]
- He, W.; Yin, Z.; Sun, C. Adaptive neural network control of a marine vessel with constraints using the asymmetric barrier Lyapunov function. IEEE Trans. Cybern. 2016, 47, 1641–1651. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, J.; Wang, D.; Fang, J.; Chen, R. Design of trajectory tracking controller for surface vessels with/without output limitations. Ocean Eng. 2024, 307, 118207. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, D.; Zhang, J.; Yan, P. Improved Barrier Function with Adjustable Parameter-based Tracking Control for Robot under Position Constraints. IEEE Access 2023, 11, 100137–100145. [Google Scholar] [CrossRef]
- Zheng, Z.; Jin, C.; Zhu, M.; Sun, K. Trajectory tracking control for a marine surface vessel with asymmetric saturation actuators. Robot. Auton. Syst. 2017, 97, 83–91. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L. Path following control for marine surface vessel with uncertainties and input saturation. Neurocomputing 2016, 177, 158–167. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Zhang, G.; Zhang, J. Design of a Trajectory Tracking Controller for Marine Vessels with Asymmetric Constraints Using a New Universal Barrier Function. J. Mar. Sci. Eng. 2024, 12, 1545. https://doi.org/10.3390/jmse12091545
Zhang T, Zhang G, Zhang J. Design of a Trajectory Tracking Controller for Marine Vessels with Asymmetric Constraints Using a New Universal Barrier Function. Journal of Marine Science and Engineering. 2024; 12(9):1545. https://doi.org/10.3390/jmse12091545
Chicago/Turabian StyleZhang, Tan, Gang Zhang, and Jinzhong Zhang. 2024. "Design of a Trajectory Tracking Controller for Marine Vessels with Asymmetric Constraints Using a New Universal Barrier Function" Journal of Marine Science and Engineering 12, no. 9: 1545. https://doi.org/10.3390/jmse12091545




