Experimental Study of Omnidirectional Scattering Characteristics of Complex Scale Targets Based on Coded Signals
Abstract
:1. Introduction
2. Theory and Experimental Method
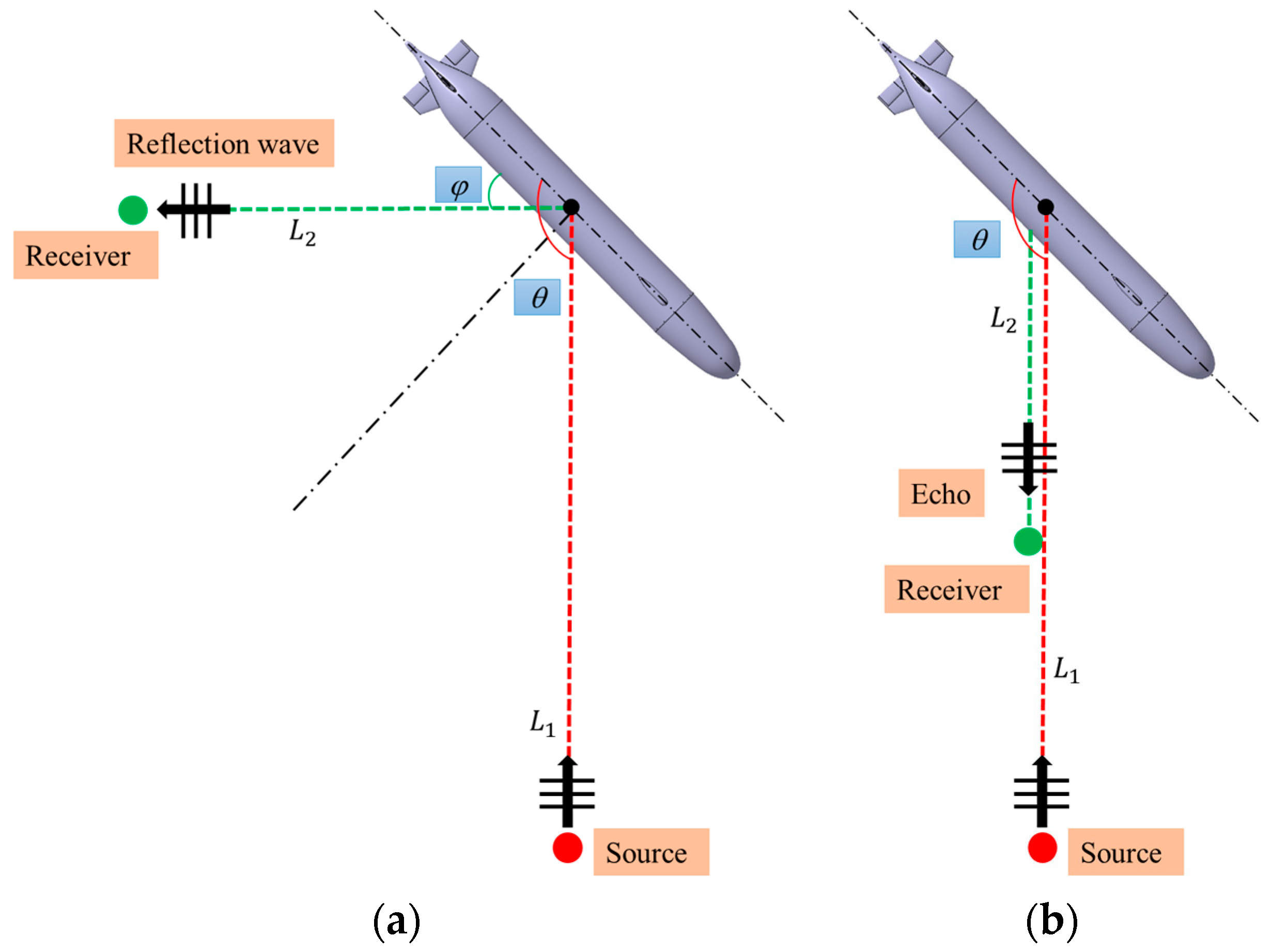
2.1. Experimental Layout and Plan
2.2. Simulation Method and Broadband Scattering Strength
2.3. Direct Path Interference Suppression Method
3. Test Results and Discussion
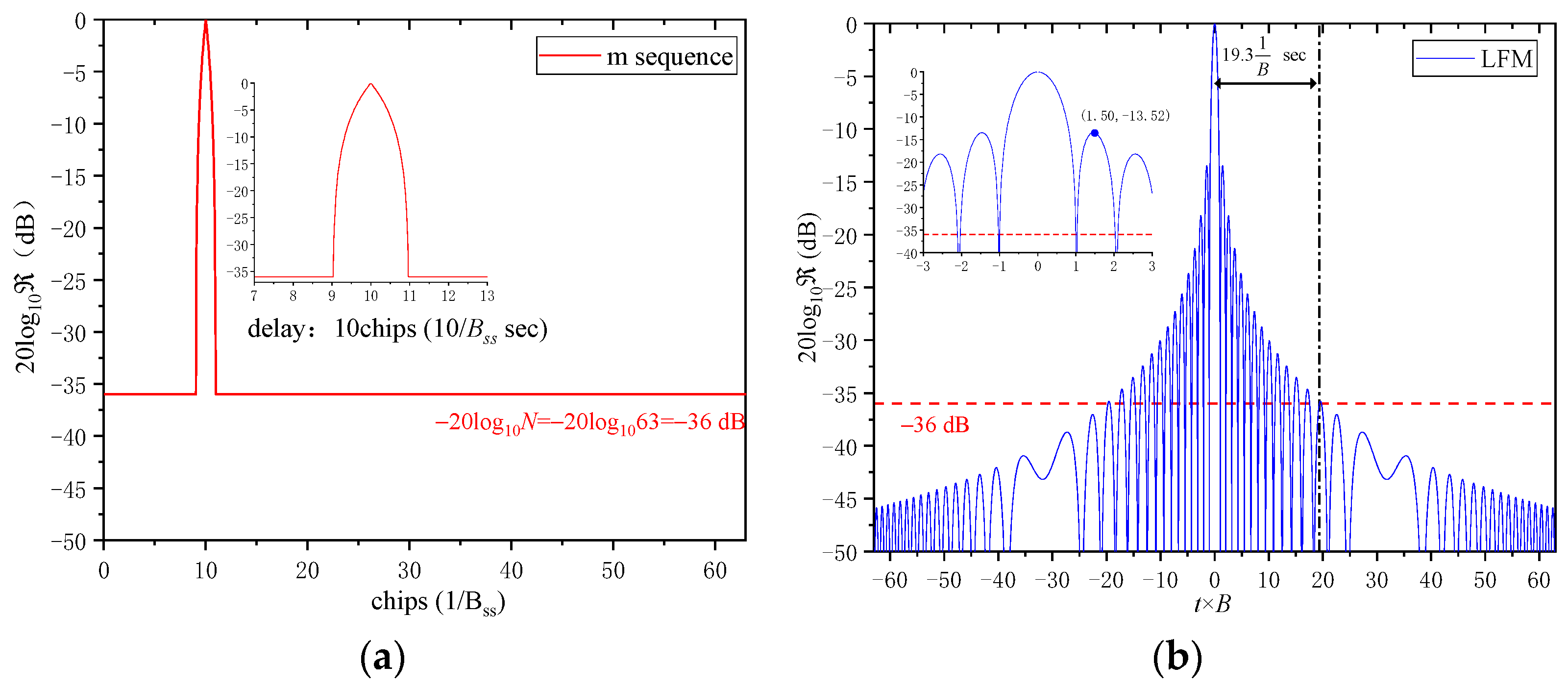
3.1. Verification of BPSK Signal Highlight Feature Acquisition
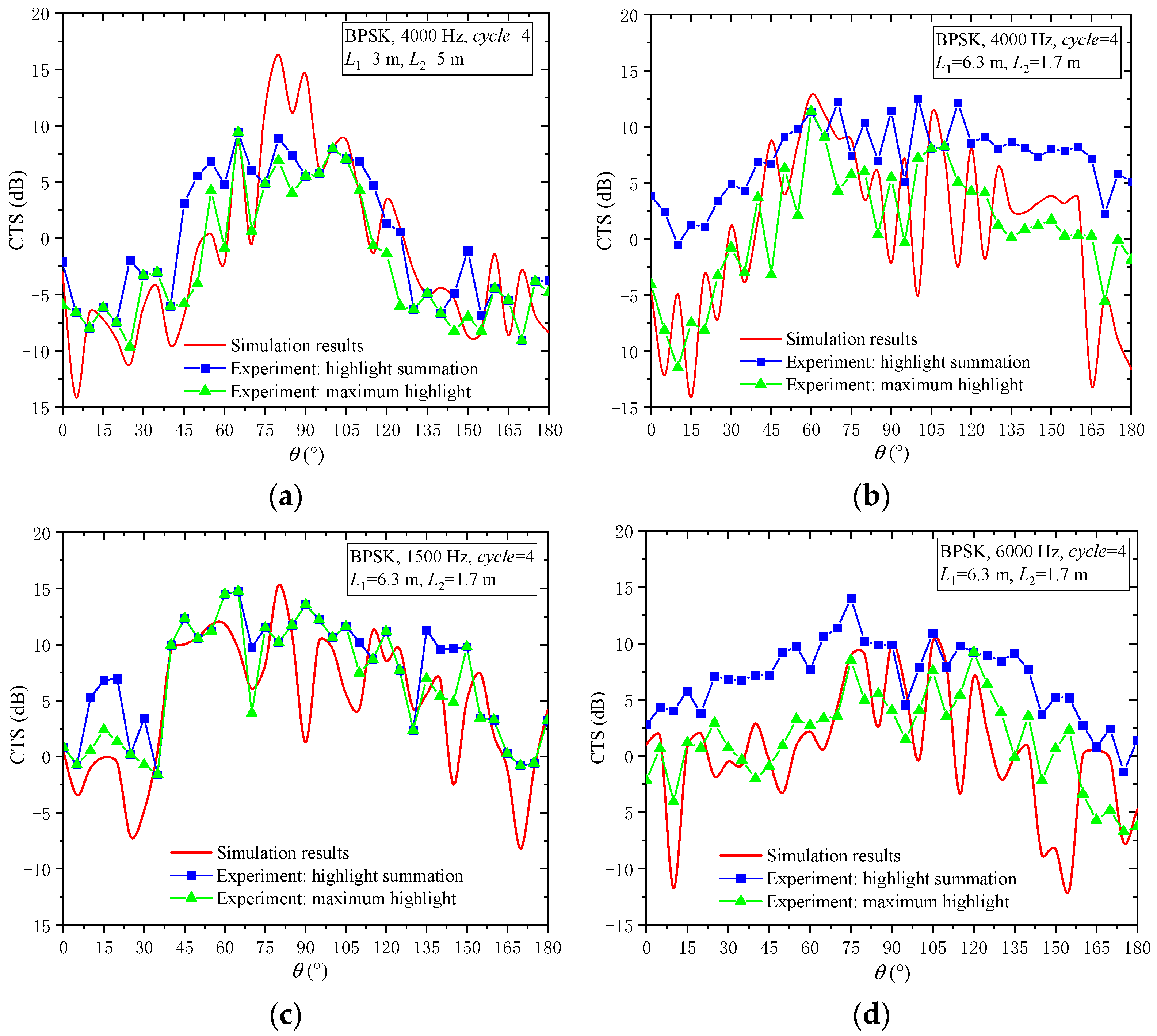
3.2. Echo Azimuth Characteristics of BPSK Signals
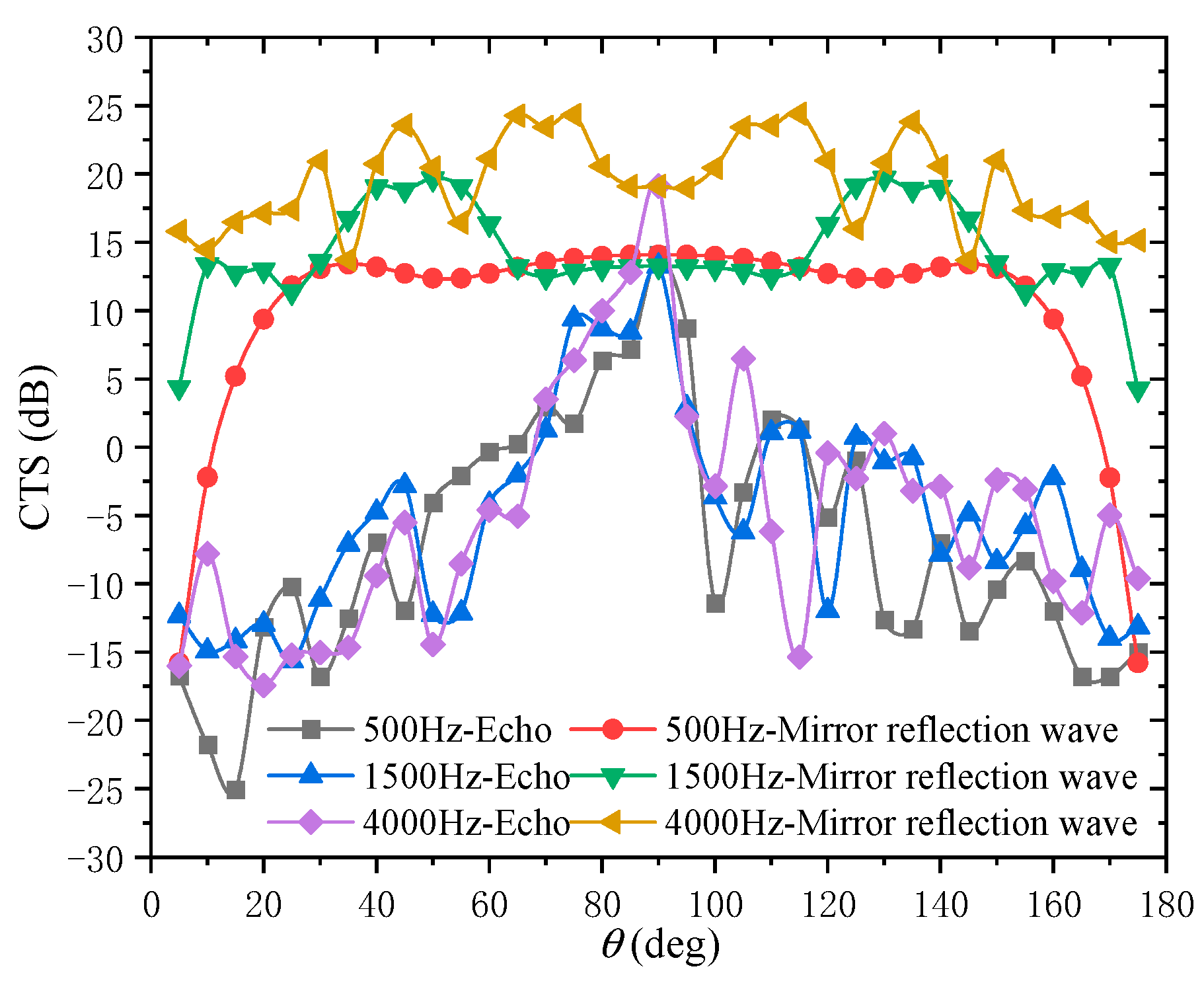
3.3. Multistatic Scattering Feature Acquisition of BPSK Signals
3.4. Active Detection Performance of BPSK Signals
4. Conclusions
- The echo azimuth characteristics of broadband BPSK signals were generally consistent with the steady-state characteristics in the frequency domain. In the time domain, the correlation scattering strength of the maximum highlight in the echo was roughly equal to that in the frequency domain. Due to the averaging effect of broadband, the interference of the echo strength curve of BPSK signals was smaller.
- The strength of mirror reflection and its scattering in the nearby directions was much greater than that of the echo. The difference in the far-field strength between these two could reach 15–30 dB. Moreover, strong mirror reflection was maintained at most incidence angles. This was the most prominent feature of multistatic scattering. At high frequencies, the scattering strength in the mirror reflection direction reached its maximum value. Only at low frequencies and small grazing angles, the maximum angle shifted due to interference.
- A high proportion of scattering waves were found in the fan-shaped area where the mirror reflection direction was located. These scattering waves were much stronger than the echo. Scattering waves stronger than the echo were also observed within the fan-shaped area where the echo direction was located.
- Frequency was the dominant factor in the scattering strength distribution. The higher the frequency, the smaller the beam angle of the strong scattering distribution in the mirror reflection direction. At low frequencies, strong scattering had a wider distribution and slightly lower strength, but the reflection wave strength was still significantly greater than the echo strength.
- The effective dimensionless frequency of the submarine model detected by low-frequency BPSK signals could reach ka = 1.88.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Hou, H.; Wang, K.; Meng, C. Overview of Underwater Target Feature Extraction Methods. In Proceedings of the 6th International Conference on Mechatronics and Intelligent Robotics (ICMIR2022), Kunming, China, 20–22 May 2022; SPIE: Paris, France, 2022; Volume 12301, pp. 678–686. [Google Scholar]
- Wu, Y.; Li, X.; Wang, Y. Extraction and classification of acoustic scattering from underwater target based on Wigner-Ville distribution. Appl. Acoust. 2018, 138, 52–59. [Google Scholar] [CrossRef]
- Wang, J.; Lin, H.; Zhang, Q.; Guo, H.; Ge, J. Acoustic compact test range system for large-scale target characteristic testing in a shorter distance. Appl. Acoust. 2023, 206, 109307. [Google Scholar] [CrossRef]
- Tran-Van-Nhieu, M. Scattering from a ribbed finite cylindrical shell. J. Acoust. Soc. Am. 2001, 110, 2858–2866. [Google Scholar] [CrossRef]
- Gong, Z.; Li, W.; Chai, Y.; Zhao, Y.; Mitri, F.G. T-matrix method for acoustical Bessel beam scattering from a rigid finite cylinder with spheroidal endcaps. Ocean Eng. 2017, 129, 507–519. [Google Scholar] [CrossRef]
- Pan, A.; Fan, J.; Wang, B.; Chen, Z.G.; Zheng, G.Y. Acoustic scattering from the finite periodically ribbed two concentric cylindrical shells. Acta Phys. Sin. 2014, 63, 214301. [Google Scholar] [CrossRef]
- Zhou, F.; Fan, J.; Wang, B.; Zhou, Y.; Huang, J. Acoustic barcode based on the acoustic scattering characteristics of underwater targets. Appl. Acoust. 2022, 189, 108607. [Google Scholar] [CrossRef]
- Maxit, L.; Oudot, G.; Audoly, C. Target Strength Modeling of Submarines. In Proceedings of the Undersea Defence Technology Conference (UDT 2004), Nice, France, 22–25 June 2004. [Google Scholar]
- Nijhofa, M.; Fillingera, L.; Gilroyb, L.; Ehrlichc, J.; Schäferc, I. BETSSI IIB: Submarine Target Strength Modeling Workshop. In Proceedings of the 4th Underwater Acoustics Conference and Exhibition, Skiathos, Greece, 3–8 September 2017. [Google Scholar]
- Sun, X.; Fan, W.; Fan, J. Simulation and experimental verification of acoustic image of echo bright spots for single hull submarine targets. J. Nav. Univ. Eng. 2012, 24, 26–31. [Google Scholar]
- Liu, J.; Peng, Z.; Fan, J. Acoustic Scattering Prediction Method of Underwater Vehicles Based on Slice-parameterized Multi-highlight Model. Acta Armamentarii 2023, 44, 517–525. [Google Scholar]
- Wang, W.; Wang, B.; Fan, J.; Zhou, F.; Zhao, K.; Jiang, Z. A simulation method on target strength and circular SAS imaging of X-rudder UUV including multiple acoustic scattering. Def. Technol. 2023, 23, 214–228. [Google Scholar] [CrossRef]
- Agounad, S.; Décultot, D.; Chati, F.; Léon, F.; Khandouch, Y. Experimental study of the bistatic acoustic scattering from cylindrical shell. Mech. Syst. Signal Process. 2023, 186, 109892. [Google Scholar] [CrossRef]
- Agounad, S.; Aassif, E.H.; Khandouch, Y.; Maze, G.; Décultot, D. Investigation into the bistatic evolution of the acoustic scattering from a cylindrical shell using time-frequency analysis. J. Sound Vib. 2018, 412, 148–165. [Google Scholar] [CrossRef]
- Fischell, E.M.; Schmidt, H. Supervised machine learning for estimation of target aspect angle from bistatic acoustic scattering. IEEE J. Ocean. Eng. 2017, 42, 759–769. [Google Scholar] [CrossRef]
- Wang, B.; Wang, W.H.; Fan, J.; Zhao, K.Q.; Zhou, F.L.; Tan, L.W. Modeling of bistatic scattering from an underwater non-penetrable target using a Kirchhoff approximation method. Def. Technol. 2022, 18, 1097–1106. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, T.; Hou, G.X. Finite-difference time-domain modeling for underwater acoustic scattering applications based on immersed boundary method. Appl. Acoust. 2022, 193, 108764. [Google Scholar] [CrossRef]
- Pakdel Azar, O.; Amiri, H.; Razzazi, F. Enhanced target detection using a new combined sonar waveform design. Telecommun. Syst. 2021, 77, 317–334. [Google Scholar] [CrossRef]
- DeFerrari, H.; Wylie, J. Ideal signals and processing for continuous active sonar. In Proceedings of the Meetings on Acoustics, Montreal, QC, Canada, 2–7 June 2013; AIP Publishing: Melville, NY, USA, 2013; Volume 19. [Google Scholar]
- DeFerrari, H.; Birdsall, T. The application of M sequences to sonar. J. Acoust. Soc. Am. 2001, 109, 2418. [Google Scholar] [CrossRef]
- DeFerrari, H.A. The application of m-sequences to bi-static active sonar. J. Acoust. Soc. Am. 2003, 114, 2399–2400. [Google Scholar] [CrossRef]
- Jourdain, G.; Henrioux, J.P. Use of large bandwidth-duration binary phase shift keying signals in target delay Doppler measurements. J. Acoust. Soc. Am. 1991, 90, 299–309. [Google Scholar] [CrossRef]
- Jobst, W.; Whited, L.; Smith, D.W. Acoustic clutter removal. IEEE J. Ocean. Eng. 2021, 46, 1000–1007. [Google Scholar] [CrossRef]
- Colin, M.E.G.D.; Beerens, S.P. False-alarm reduction for low-frequency active sonar with BPSK pulses: Experimental results. IEEE J. Ocean. Eng. 2011, 36, 52–59. [Google Scholar] [CrossRef]
- Jiang, L.; Yan, S.; Wu, Y.; Ma, X. Sonar Detection Performance with LFM-BPSK Combined Waveforms. In Proceedings of the OCEANS 2016-Shanghai, Shanghai, China, 10–13 April 2016; IEEE: New York, NY, USA, 2016; pp. 1–4. [Google Scholar]
- Wang, Z.S. Statistical feature of underwater target echo highlight. Acta Phys. Sin. 2013, 62, 084302. [Google Scholar]
- Urick, R.J. Principles of Underwater Sound; Peninsula Publishing: Westport, CT, USA, 1975; p. 1083. [Google Scholar]
- Tang, W.L.; Fan, J.; Ma, Z.C. Acoustic Scattering of Underwater Target; Science Press: Beijing, China, 2018. [Google Scholar]
- Xie, A.; Liu, X.; Zhao, F.; Liu, Z.; Xiao, S. Waveform design and processing method of pulse signal in anechoic chamber measurement. Measurement 2022, 203, 111938. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Xu, Z.; Ai, X.; Xiao, S. Design and experimental research of precession target micro-Doppler measurement using pulse signal in anechoic chamber. Measurement 2021, 184, 109948. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Zhao, F.; Ai, X.; Wang, G. An equivalent simulation method for pulse radar measurement in an anechoic chamber. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1081–1085. [Google Scholar] [CrossRef]
- Jia, H.; Li, X.; Meng, X.; Yang, Y. Extraction of echo characteristics of underwater target based on cestrum method. J. Mar. Sci. Appl. 2017, 16, 216–224. [Google Scholar] [CrossRef]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA SUBOFF Models; David Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Tang, Y.; Zhou, Q.; Lü, X.; Ji, G.; Tan, L. A Numerical Method for Scattering from Multi-domain Structures Based on Near-Field Artificial Boundary. J. Vib. Eng. Technol. 2024, 12, 7021–7033. [Google Scholar] [CrossRef]
- Ginolhac, G.; Jourdain, G. Principal component inverse algorithm for detection in the presence of reverberation. IEEE J. Ocean. Eng. 2022, 27, 310–321. [Google Scholar] [CrossRef]
- Fan, Z.; Liang, G.L.; Wang, Y.L. Robust adaptive beamforming with null widening. J. Electron. Inf. Technol. 2013, 35, 2764–2770. [Google Scholar] [CrossRef]
- He, C.; Zheng, Y.; Ma, Y. Analysis and application of the acoustic interfered field distortion for acoustic forward-scattering detection of underwater targets. Acta Acust. 2021, 46, 939–949. [Google Scholar]
- Feng, B.; Xu, W.; Cai, J.; Wu, R.; Wang, H. Phase-preserving theory and its linearization approximation for forward scattering field of scalar acoustic wave equation. Acta Phys. Sin. 2023, 72, 159101. [Google Scholar] [CrossRef]


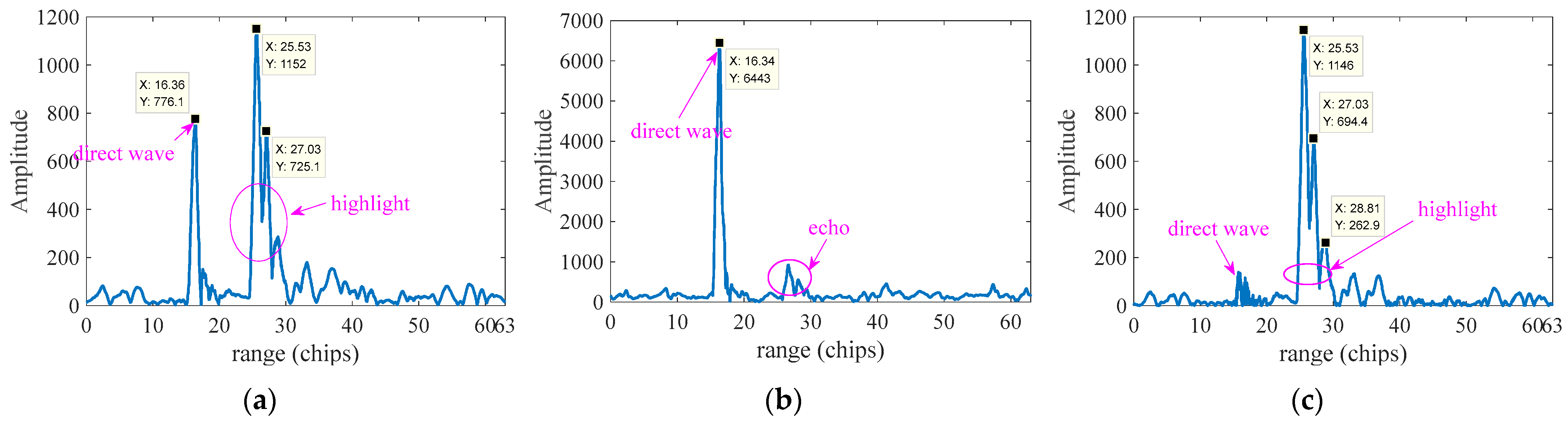


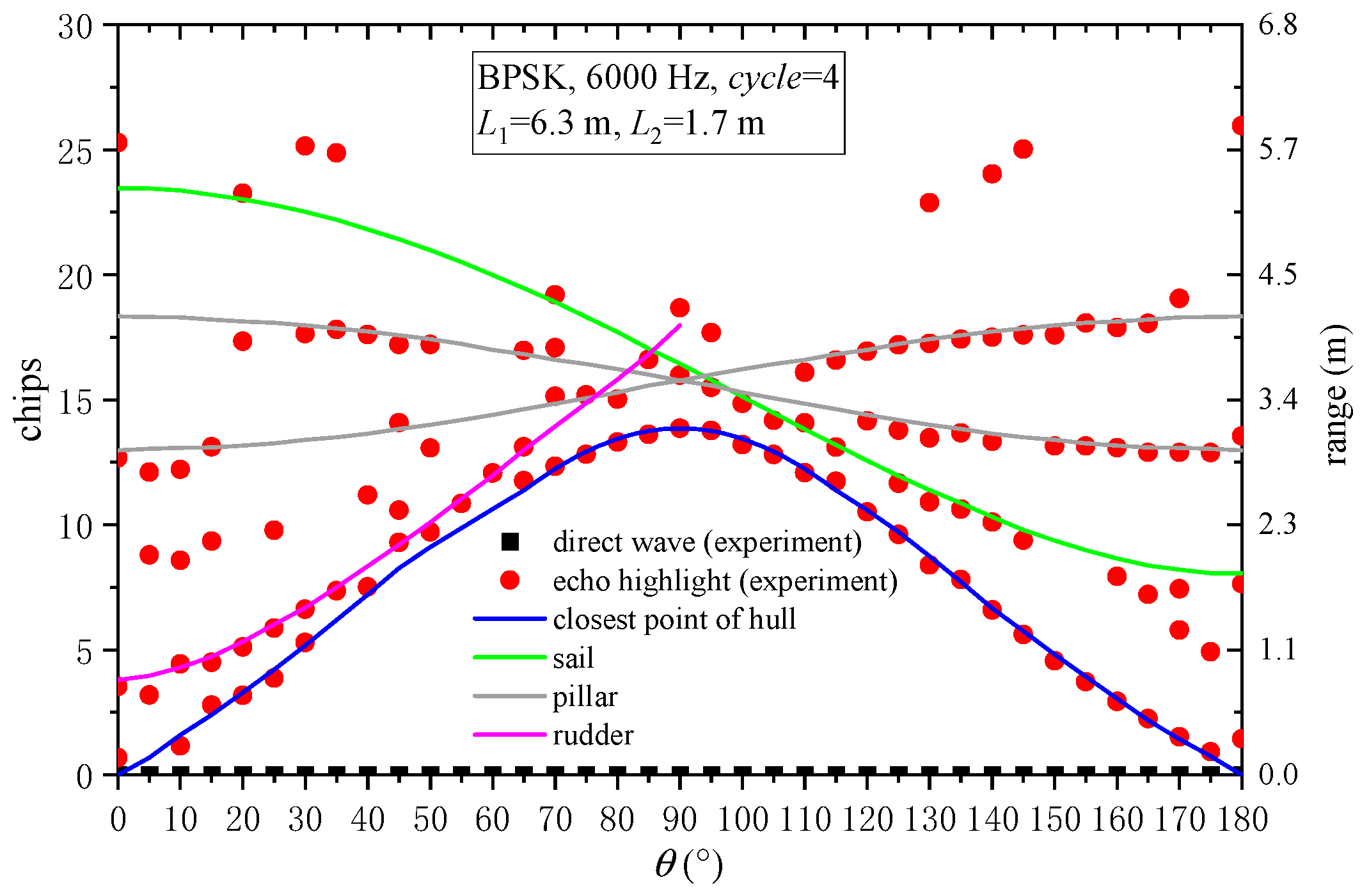
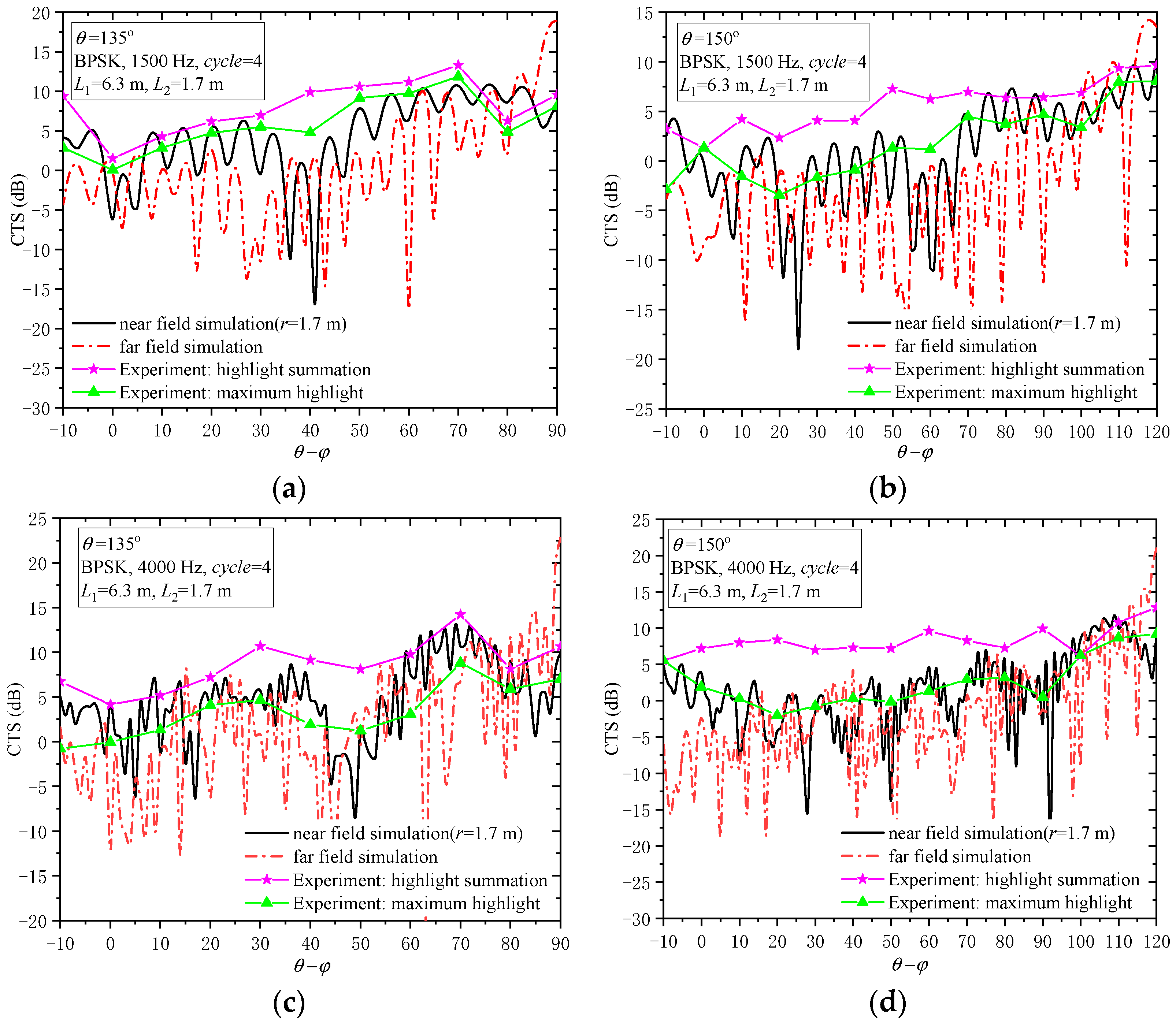
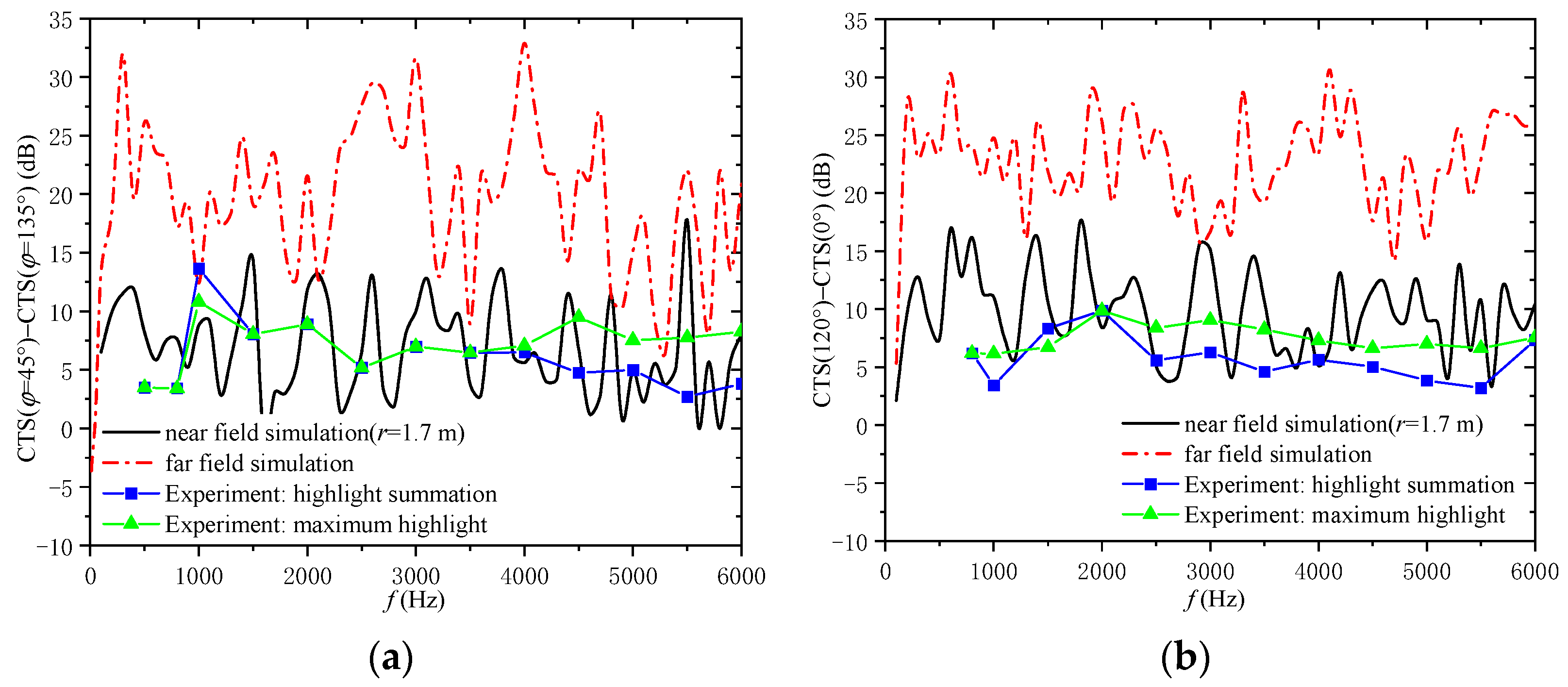
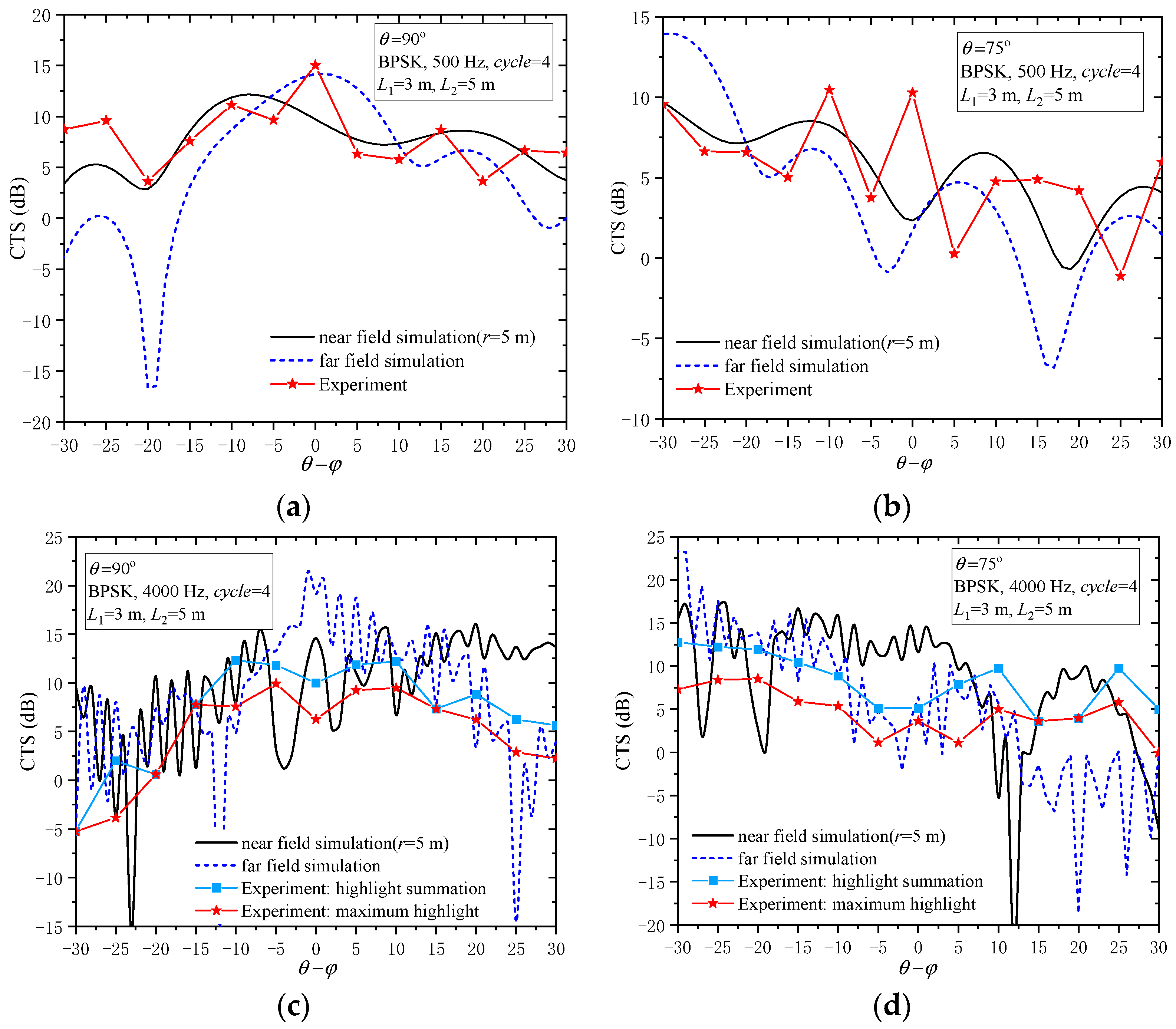


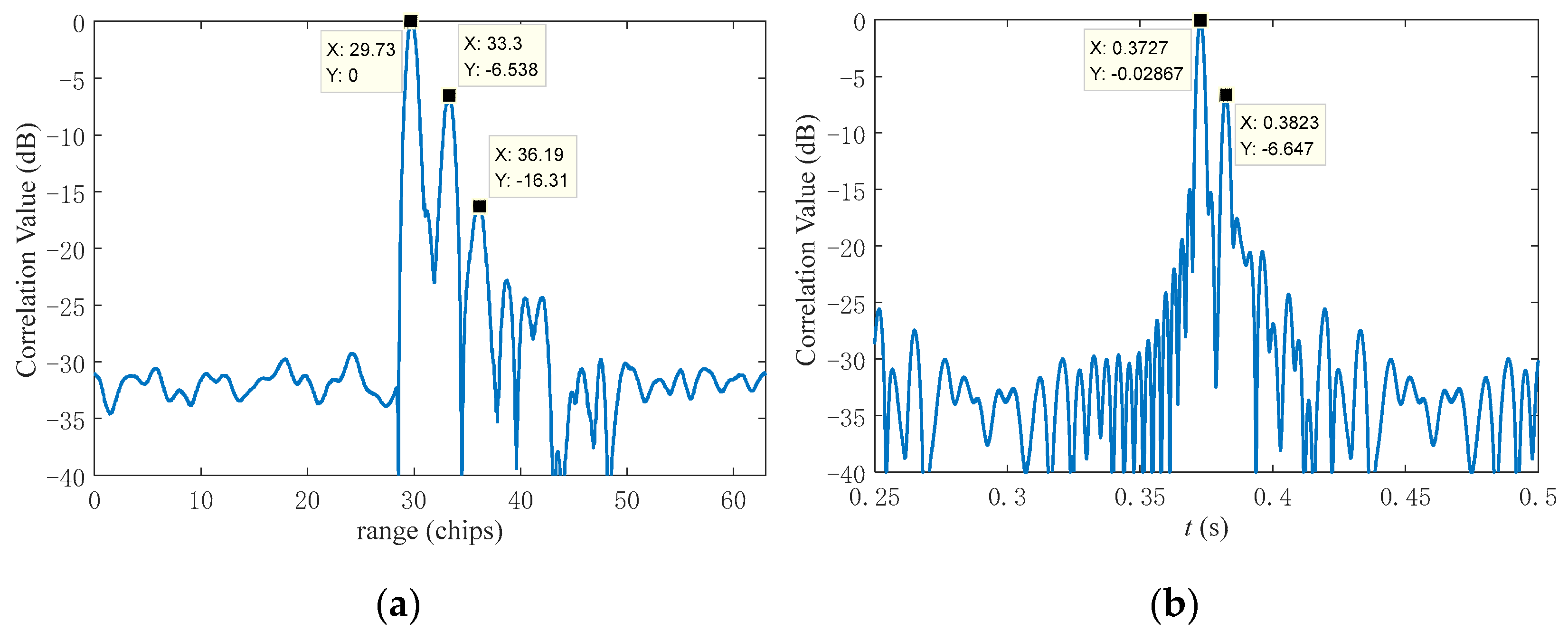
| θ | Highlight Position | d1 (m) | d2 (m) | Direct Wave and Highlight Echo Acoustic Path (m) | Test Value (m) | Error |
|---|---|---|---|---|---|---|
| 90° | Nearest hull highlight | 1.56 | 1.56 | 3.12 | 3.14 | 0.6% |
| Sail | 1.75 | 1.977 | 3.727 | 3.622 | 2.8% | |
| Farthest hull highlight | 1.764 | 2.48 | 4.244 | 4.26 | 0.4% | |
| 135° | Nearest hull highlight | 0.578 | 1.168 | 1.746 | 1.77 | 1.4% |
| Sail | 1.144 | 1.317 | 2.461 | 2.41 | 2.1% | |
| Pillar 1 | 1.561 | 1.574 | 3.135 | 3.07 | 2.0% | |
| Pillar 2 | 1.986 | 2.0 | 3.986 | 3.95 | 0.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhou, Q.; Pan, Y.; Lü, X.; Wang, X. Experimental Study of Omnidirectional Scattering Characteristics of Complex Scale Targets Based on Coded Signals. J. Mar. Sci. Eng. 2024, 12, 1590. https://doi.org/10.3390/jmse12091590
Tang Y, Zhou Q, Pan Y, Lü X, Wang X. Experimental Study of Omnidirectional Scattering Characteristics of Complex Scale Targets Based on Coded Signals. Journal of Marine Science and Engineering. 2024; 12(9):1590. https://doi.org/10.3390/jmse12091590
Chicago/Turabian StyleTang, Yongzhuang, Qidou Zhou, Yucun Pan, Xiaojun Lü, and Xiaowei Wang. 2024. "Experimental Study of Omnidirectional Scattering Characteristics of Complex Scale Targets Based on Coded Signals" Journal of Marine Science and Engineering 12, no. 9: 1590. https://doi.org/10.3390/jmse12091590
APA StyleTang, Y., Zhou, Q., Pan, Y., Lü, X., & Wang, X. (2024). Experimental Study of Omnidirectional Scattering Characteristics of Complex Scale Targets Based on Coded Signals. Journal of Marine Science and Engineering, 12(9), 1590. https://doi.org/10.3390/jmse12091590





