Parametric Estimation of Directional Wave Spectra from Moored FPSO Motion Data Using Optimized Artificial Neural Networks
Abstract
1. Introduction
2. Data Collection
2.1. Numerical FPSO Model
2.2. Environmental Conditions
2.3. Synthetic Data Generation
2.4. FPSO Motions from Numerical Simulation
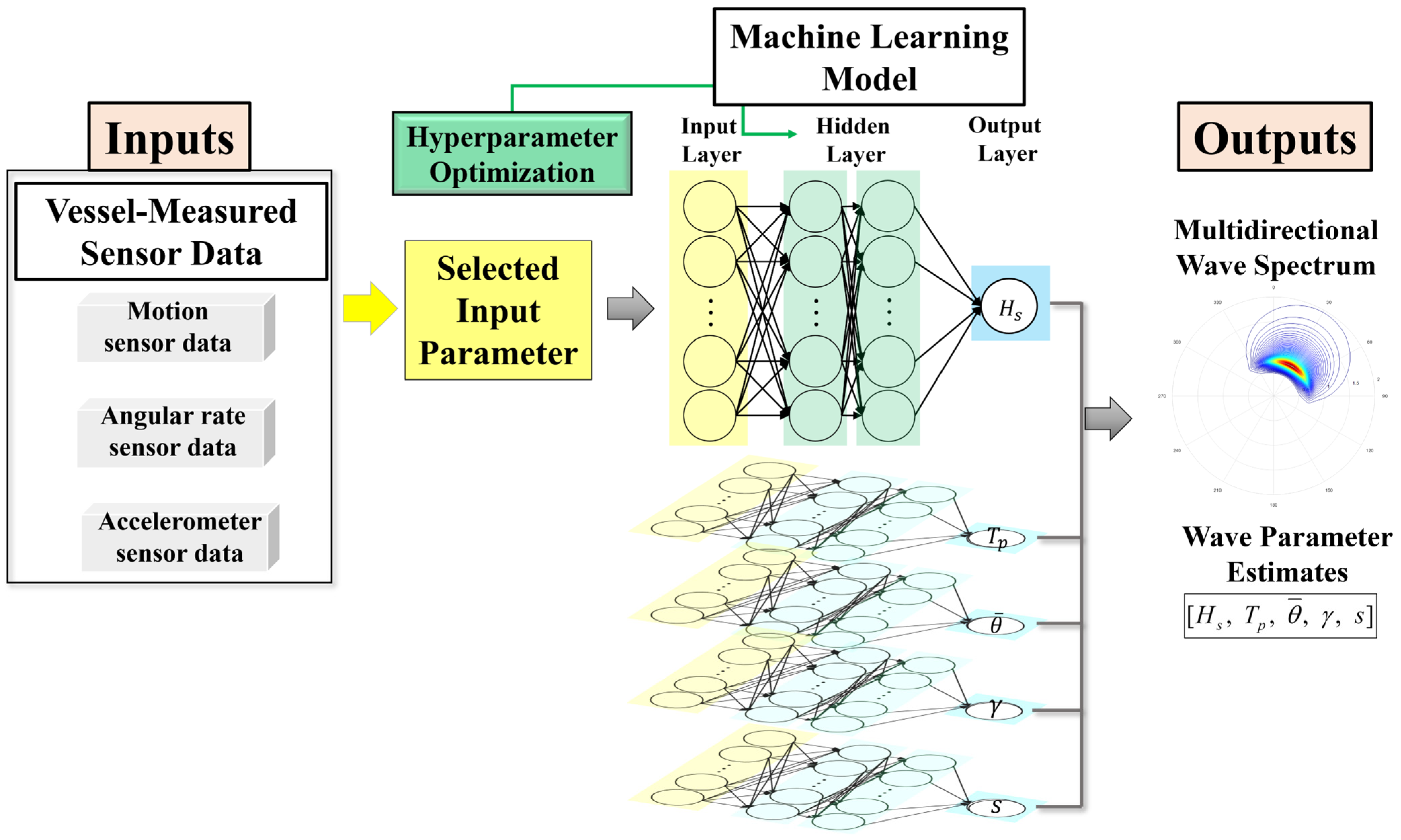
3. ANN for Inverse Wave Estimation from Motion Sensor
3.1. Applied Methodology
3.2. Feature Correlation
3.3. Hyperparameter Selection
4. Results and Discussion
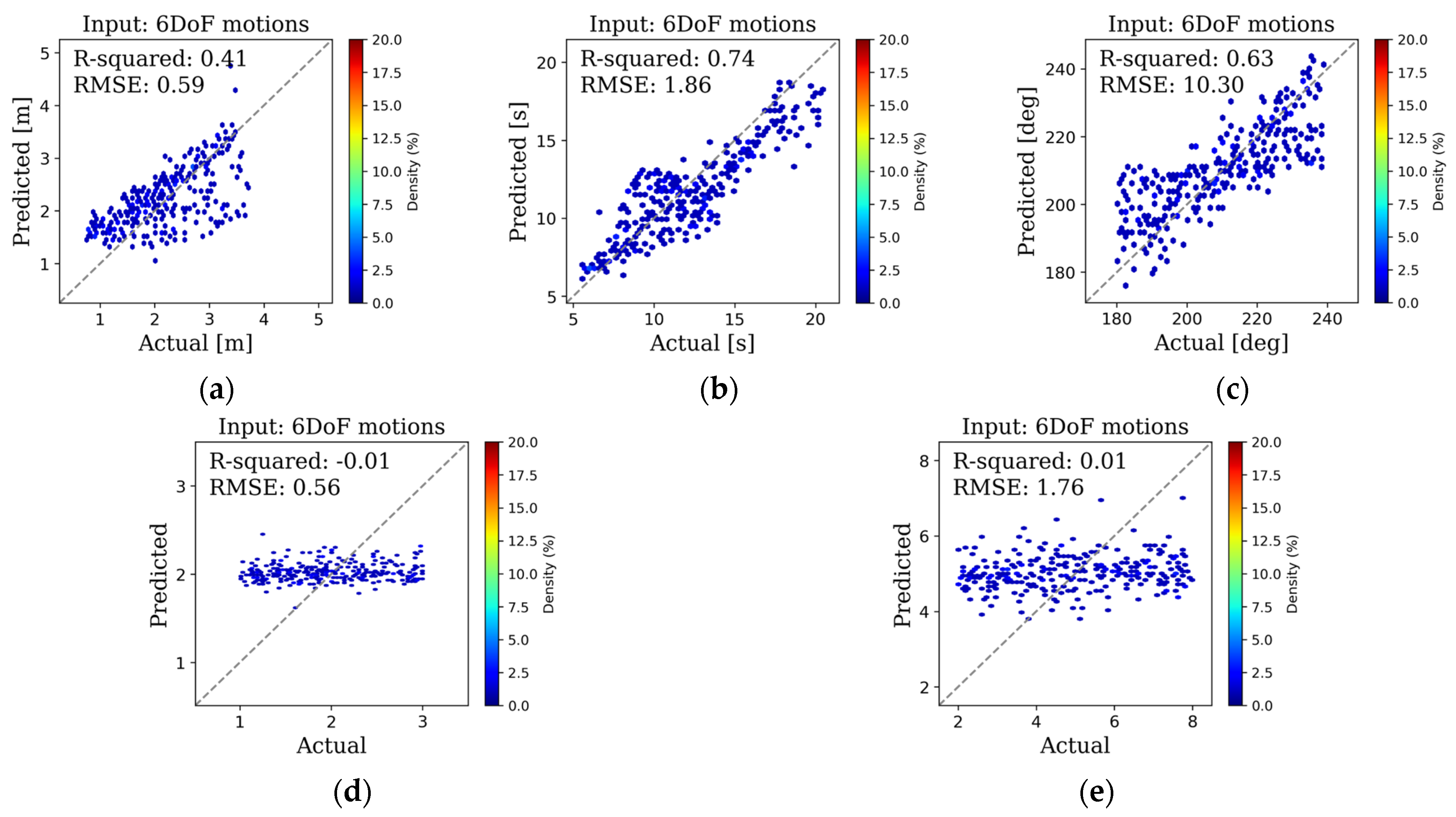
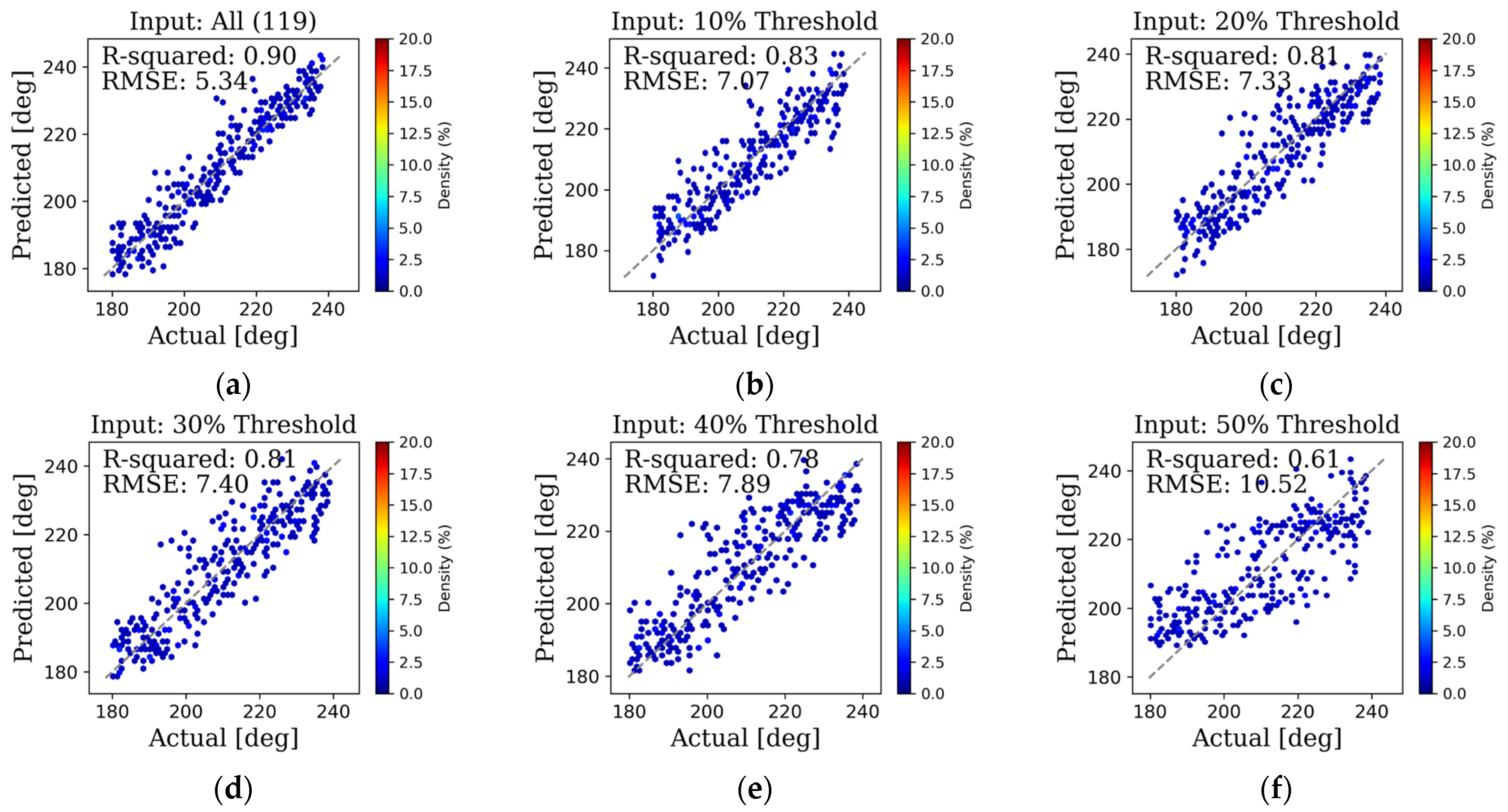
4.1. Sensitivity Analysis with Respect to Input
| All | N | 119 | 119 | 119 | 119 | 119 |
| 0.99 | 1.00 | 0.90 | 0.48 | 0.39 | ||
| Threshold 10 | N | 85 | 94 | 68 | 4 | 8 |
| 0.96 | 0.99 | 0.83 | 0.26 | 0.03 | ||
| Threshold 20 | N | 64 | 76 | 46 | 1 | |
| 0.95 | 0.98 | 0.81 | 0.14 | |||
| Threshold 30 | N | 58 | 56 | 30 | ||
| 0.95 | 0.99 | 0.81 | ||||
| Threshold 40 | N | 42 | 48 | 24 | ||
| 0.93 | 0.99 | 0.78 | ||||
| Threshold 50 | N | 28 | 35 | 5 | ||
| 0.95 | 0.99 | 0.61 |
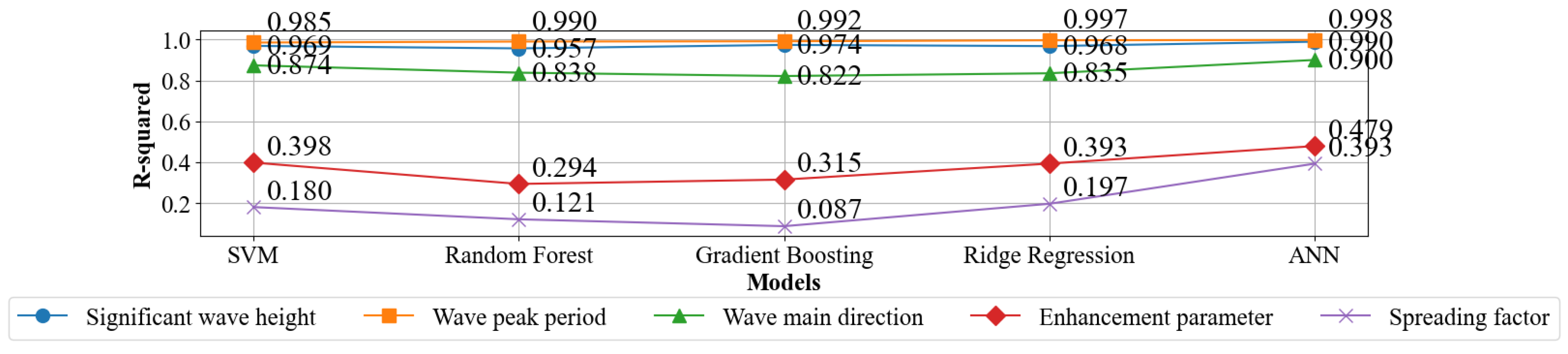
4.2. Comparison with Other ML Methods
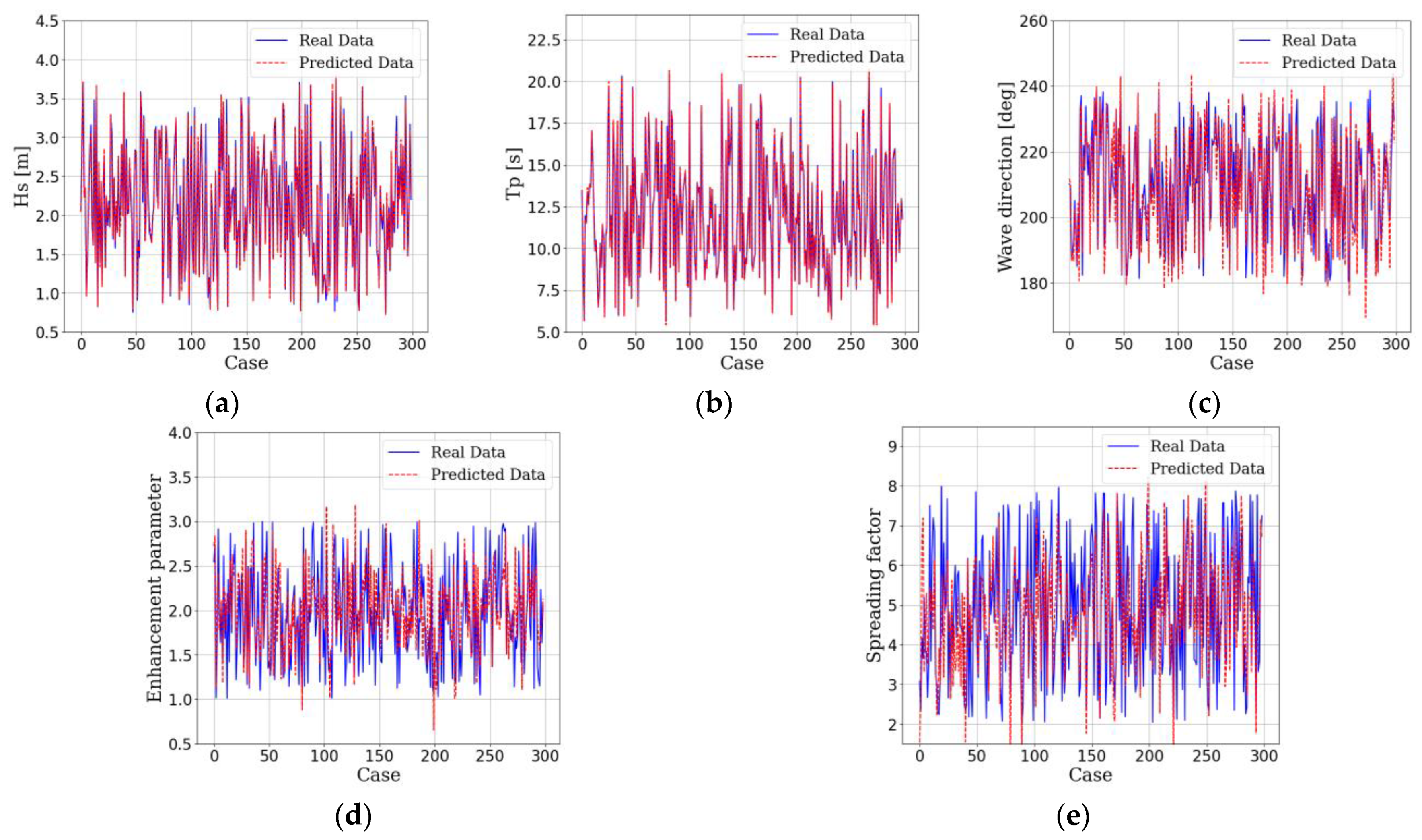
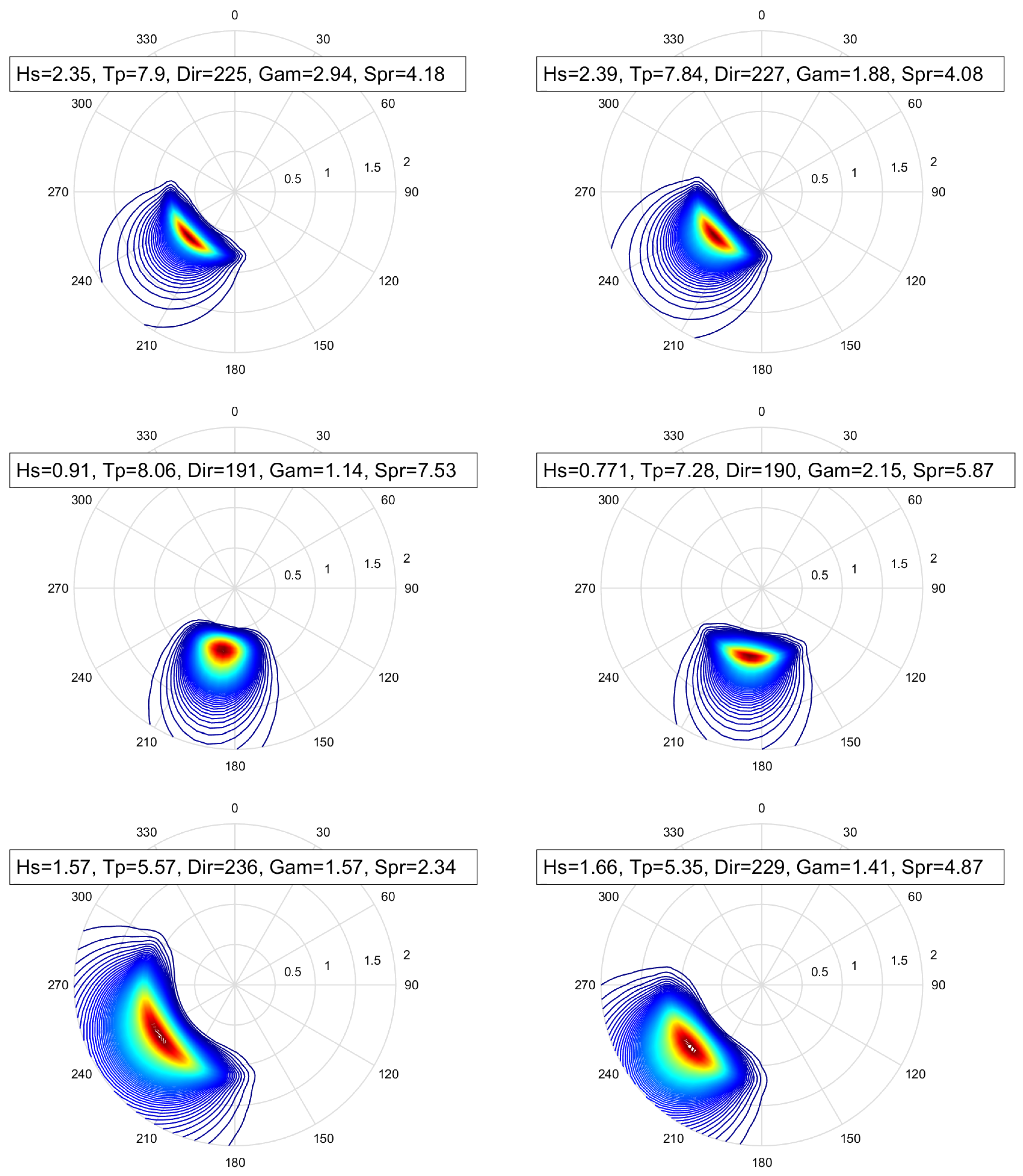
4.3. Estimation of Directional Wave Spectrum
5. Conclusions
- Additional information from accelerations and angular velocities improves the overall prediction accuracy of the significant wave height, peak period, and main wave direction compared to in cases with only 6DOF motions as input.
- Introducing additional multiple motion-based statistical variables to have more correlated inputs significantly enhances the estimation accuracy of all wave parameters.
- Sensitivity tests regarding thresholds show the best performance when using all variables as inputs, with accuracy tending to decrease as the threshold increases, indicating a decrease in accuracy with fewer adopted inputs.
- The optimized ANN algorithms estimate the significant wave height, peak period, and main wave direction with high accuracy, while the enhancement parameter and spreading factor are estimated with reduced accuracy.
- A comparative analysis with other ML methods demonstrates the superiority of ANNs in accurately estimating wave parameters, highlighting their capability to capture complex nonlinear patterns inherent in data.
- Having more relevant statistical parameters as input improves estimation accuracy to some degree with more data processing, but there is a trade-off between accuracy and practicality depending on the data amount and quality needed to collect and process input variables.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | |
| significant wave height | |
| wave peak period | |
| wave direction | |
| enhancement parameter | |
| spreading factor | |
| mean_ | mean value |
| std_ | standard deviation |
| relative standard deviation | |
| max_ | one-tenth max value |
| m0_ | zeroth moments of the spectrum |
| m2_ | second moments of the spectrum |
| m4_ | fourth moments of the spectrum |
| _ | mean crest period |
| _ | mean up-crossing period |
| absolute maximum cross-correlation between and | |
| BW_ | bandwidth |
| : 1–6 | surge, sway, heave, roll, pitch, and yaw displacements |
| : 7–9 | angular velocities with respect to x, y, and z axes |
| : 10–12 | x, y, and z accelerations |
| Abbreviations | |
| FPSO | Floating Production Storage and Offloading |
| ML | machine learning |
| ANN | artificial neural network |
| DOF | degree of freedom |
| RMSE | Root-Mean-Square Error |
| R2 | R-squared values |
| ERA5 | fifth-generation ECMWF atmospheric reanalysis of the global climate |
| HYCOM | Hybrid Coordinate Ocean Model |
| NN | neural network |
| MSE | mean squared error |
| ReLU | Rectified Linear Unit |
| ELU | Exponential Linear Unit |
| SVM | Support Vector Machines |
| RF | Random Forest |
| GB | Gradient Boosting |
References
- Bisinotto, G.A.; Cotrim, L.P.; Cozman, F.G.; Tannuri, E.A. Sea state estimation with neural networks based on the motion of a moored fpso subjected to campos basin metocean conditions. In Proceedings of the Brazilian Conference on Intelligent Systems, Online, 29 November–3 December 2021; pp. 294–308. [Google Scholar]
- Duz, B.; Mak, B.; Hageman, R.; Grasso, N. Real time estimation of local wave characteristics from ship motions using artificial neural networks. In Proceedings of the Practical Design of Ships and Other Floating Structures: Proceedings of the 14th International Symposium, PRADS 2019, Yokohama, Japan, 22–26 September 2019; Volume III, pp. 657–678. [Google Scholar]
- Mak, B.; Düz, B. Ship As a Wave Buoy: Estimating Relative Wave Direction From In-Service Ship Motion Measurements Using Machine Learning. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, UK, 9–14 June 2019. [Google Scholar]
- Nielsen, U.D.; Mittendorf, M.; Shao, Y.; Storhaug, G. Wave spectrum estimation conditioned on machine learning-based output using the wave buoy analogy. Mar. Struct. 2023, 91, 103470. [Google Scholar] [CrossRef]
- Scholcz, T.; Düz, B.; Hageman, R.; Mak, B. Consistency assessment of wave directional spectrum predictions from machine learning based ship-as-a-wave-buoy methods. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Boston, MA, USA, 7–8 December 2022; p. V05BT06A004. [Google Scholar]
- Scholcz, T.; Mak, B. Ship as a wave buoy: Estimating full directional wave spectra from in-service ship motion measurements using deep learning. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Virtual, 3–7 August 2020; p. V001T001A006. [Google Scholar]
- Chen, X.; Okada, T.; Kawamura, Y.; Mitsuyuki, T. Estimation of on-site directional wave spectra using measured hull stresses on 14,000 TEU large container ships. J. Mar. Sci. Technol. 2020, 25, 690–706. [Google Scholar] [CrossRef]
- Han, P.; Li, G.; Cheng, X.; Skjong, S.; Zhang, H. An uncertainty-aware hybrid approach for sea state estimation using ship motion responses. IEEE Trans. Ind. Inform. 2021, 18, 891–900. [Google Scholar] [CrossRef]
- Han, P.; Li, G.; Skjong, S.; Wu, B.; Zhang, H. Data-driven sea state estimation for vessels using multi-domain features from motion responses. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 2120–2126. [Google Scholar]
- Mittendorf, M.; Nielsen, U.D.; Bingham, H.B. The prediction of sea state parameters by deep learning techniques using ship motion data. In Proceedings of the 7th World Maritime Technology Conference (WMTC’22), Copenhagen, Denmark, 26–28 April 2022. [Google Scholar]
- Nielsen, U.D.; Bingham, H.B.; Brodtkorb, A.H.; Iseki, T.; Jensen, J.J.; Mittendorf, M.; Mounet, R.E.; Shao, Y.; Storhaug, G.; Sørensen, A.J. Estimating waves via measured ship responses. Sci. Rep. 2023, 13, 17342. [Google Scholar] [CrossRef]
- Cheng, X.; Li, G.; Ellefsen, A.L.; Chen, S.; Hildre, H.P.; Zhang, H. A novel densely connected convolutional neural network for sea-state estimation using ship motion data. IEEE Trans. Instrum. Meas. 2020, 69, 5984–5993. [Google Scholar] [CrossRef]
- Han, P.; Li, G.; Skjong, S.; Zhang, H. Directional wave spectrum estimation with ship motion responses using adversarial networks. Mar. Struct. 2022, 83, 103159. [Google Scholar] [CrossRef]
- Kawai, T.; Kawamura, Y.; Okada, T.; Mitsuyuki, T.; Chen, X. Sea state estimation using monitoring data by convolutional neural network (CNN). J. Mar. Sci. Technol. 2021, 26, 947–962. [Google Scholar] [CrossRef]
- Mittendorf, M.; Nielsen, U.D.; Bingham, H.B.; Storhaug, G. Sea state identification using machine learning—A comparative study based on in-service data from a container vessel. Mar. Struct. 2022, 85, 103274. [Google Scholar] [CrossRef]
- Mounet, R.E.; Chen, J.; Nielsen, U.D.; Brodtkorb, A.H.; Pillai, A.C.; Ashton, I.G.; Steele, E.C. Deriving spatial wave data from a network of buoys and ships. Ocean. Eng. 2023, 281, 114892. [Google Scholar] [CrossRef]
- Nielsen, U.D.; Dietz, J. Estimation of sea state parameters by the wave buoy analogy with comparisons to third generation spectral wave models. Ocean. Eng. 2020, 216, 107781. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.-H. Dynamic behaviors of conventional SCR and lazy-wave SCR for FPSOs in deepwater. Ocean. Eng. 2015, 106, 396–414. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.; Kang, H. Turret location impact on global performance of a thruster-assisted turret-moored FPSO. Ocean Syst. Eng. Int. J 2016, 6, 265–287. [Google Scholar] [CrossRef]
- Orcina, L. OrcaFlex User Manual; Version 11.0 B; Orcina: Ulverston, UK, 2016. [Google Scholar]
- Lee, C.-H. WAMIT Theory Manual; Massachusetts Institute of Technology, Department of Ocean Engineering: Cambridge, MA, USA, 1995. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Huang, Y.; He, Y.; Liu, Y.; Qiu, M.; Li, M.; Luo, Z.; Xu, J. Study of the response characteristics of a spread moored FPSO in the bidirectional sea state. Ocean. Eng. 2022, 264, 112453. [Google Scholar] [CrossRef]
- Lopez, J.T.; Tao, L.; Xiao, L.; Hu, Z. Experimental study on the hydrodynamic behaviour of an FPSO in a deepwater region of the Gulf of Mexico. Ocean. Eng. 2017, 129, 549–566. [Google Scholar] [CrossRef]
- Kim, H.; Kang, H.; Kim, M.-H. Real-time inverse estimation of ocean wave spectra from vessel-motion sensors using adaptive kalman filter. Appl. Sci. 2019, 9, 2797. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Jin, C.; Kim, M.; Lee, D. Real-time inverse estimation of multi-directional random waves from vessel-motion sensors using Kalman filter. Ocean. Eng. 2023, 280, 114501. [Google Scholar] [CrossRef]
- Keras Documentation. 2015. Available online: https://keras.io/ (accessed on 2 December 2024).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- George, A.; Poguluri, S.K.; Kim, J.; Cho, I.H. Design optimization of a multi-layer porous wave absorber using an artificial neural network model. Ocean. Eng. 2022, 265, 112666. [Google Scholar] [CrossRef]
- Velasco-Gallego, C.; Lazakis, I. Real-time data-driven missing data imputation for short-term sensor data of marine systems. A comparative study. Ocean. Eng. 2020, 218, 108261. [Google Scholar] [CrossRef]
- Xie, J.; Xue, X. A novel hybrid model based on grey wolf optimizer and group method of data handling for the prediction of monthly mean significant wave heights. Ocean. Eng. 2023, 284, 115274. [Google Scholar] [CrossRef]
- Juan, N.P.; Matutano, C.; Valdecantos, V.N. Uncertainties in the application of artificial neural networks in ocean engineering. Ocean. Eng. 2023, 284, 115193. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, W.; Li, J.; Li, X.; Cheng, Z. A data-driven methodology for wave time-series measurement on floating structures. Ocean. Eng. 2024, 303, 117629. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z.; Ding, N.; Gu, Y.; Liu, X.; Huo, Y.; Qiu, J.; Yao, Y.; Zhang, A.; Zhang, L. Pre-trained models: Past, present and future. AI Open 2021, 2, 225–250. [Google Scholar] [CrossRef]
- Panda, J. Machine learning for naval architecture, ocean and marine engineering. J. Mar. Sci. Technol. 2023, 28, 1–26. [Google Scholar] [CrossRef]
- Schmidgall, S.; Ziaei, R.; Achterberg, J.; Kirsch, L.; Hajiseyedrazi, S.; Eshraghian, J. Brain-inspired learning in artificial neural networks: A review. APL Mach. Learn. 2024, 2, 021501. [Google Scholar] [CrossRef]
- Kwon, D.-S.; Jin, C.; Kim, M.; Guha, A.; Esenkov, O.E.; Ryu, S. Inverse wave estimation from measured FPSO motions through artificial neural networks. In Proceedings of the SNAME Offshore Symposium, Houston, TX, USA, 20 February 2024; p. D011S004R003. [Google Scholar]

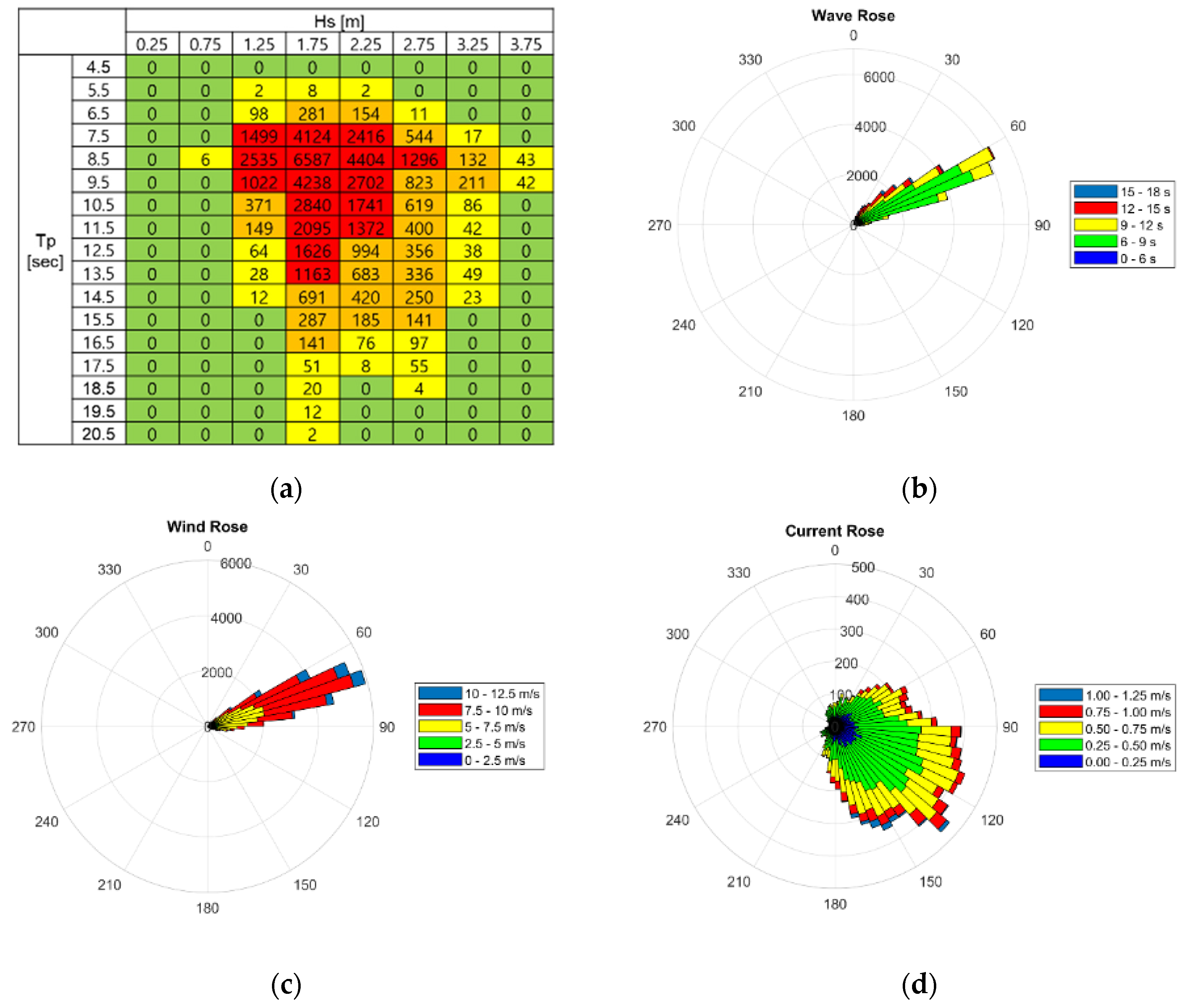
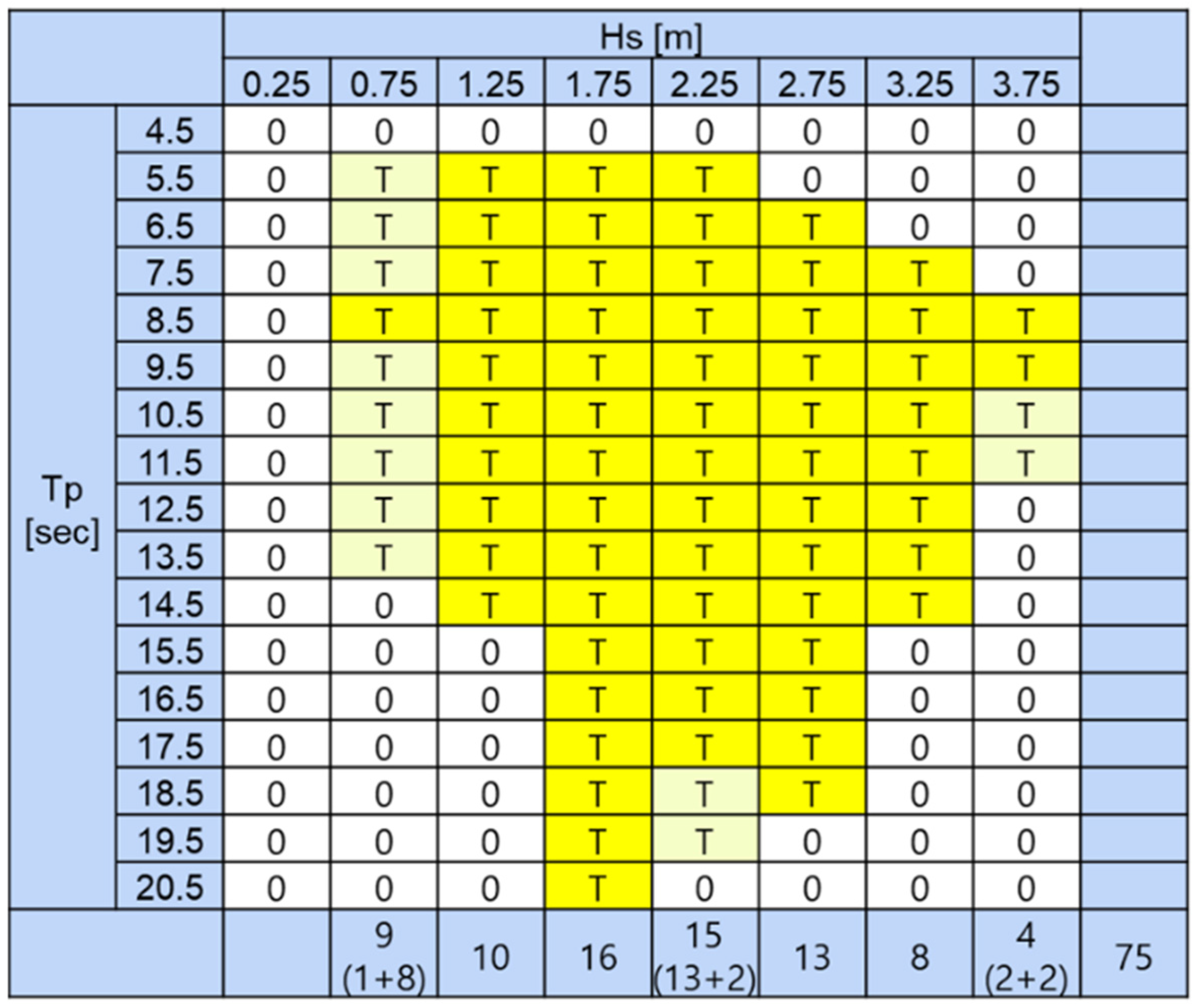

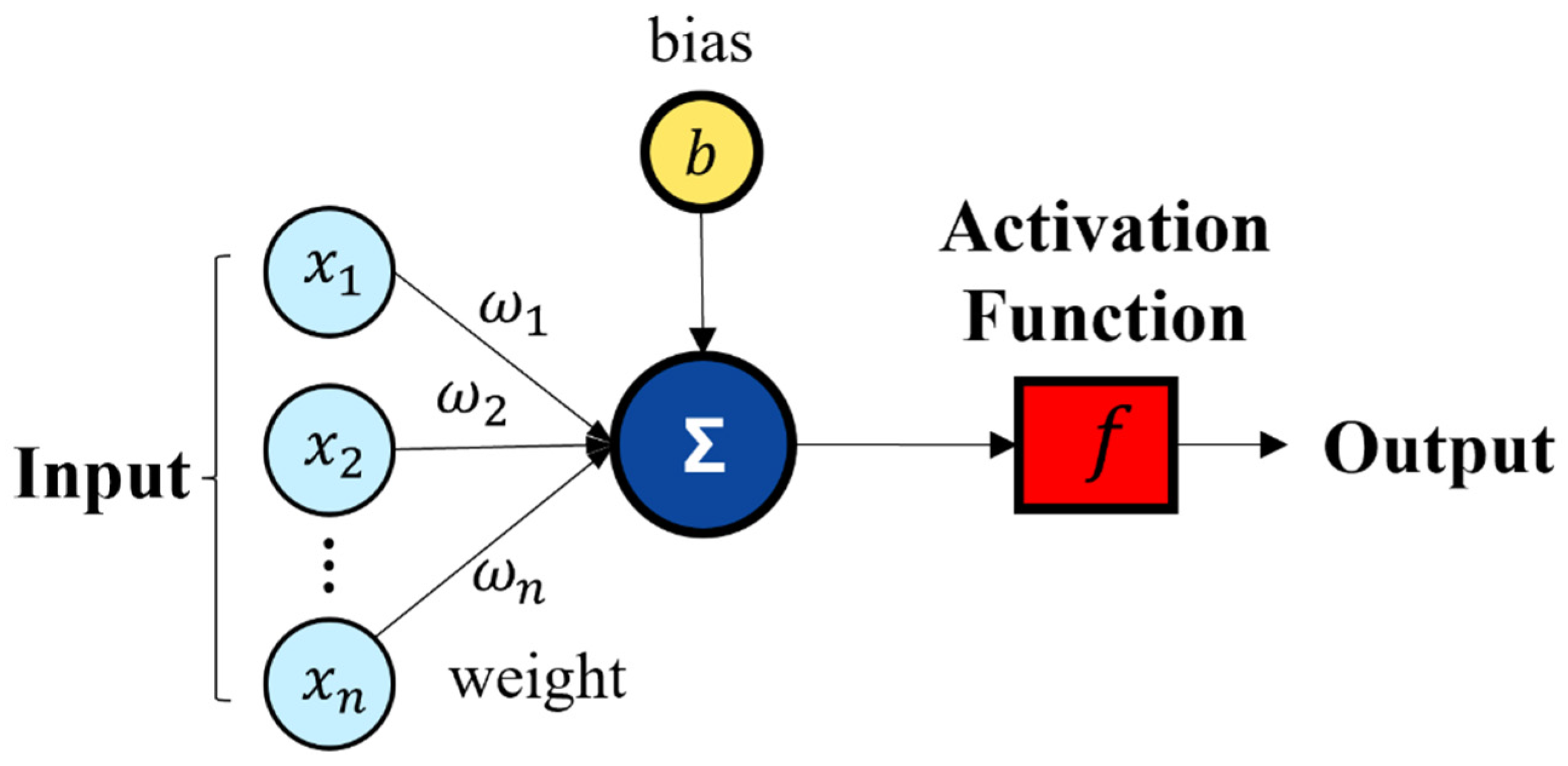



| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Length between perpendicular | Lpp | m | 310 |
| Breadth | B | m | 47.17 |
| Depth | H | m | 28.04 |
| Draft | d | m | 18.90 |
| Displacement | - | MT | 240,869 |
| Center of gravity above base | KG | m | 13.30 |
| Roll radius of gyration at CG | Rxx | m | 14.77 |
| Pitch radius of gyration at CG | Ryy | m | 77.47 |
| Yaw radius of gyration at CG | Rzz | m | 79.30 |
| Heave natural period | Tn3 | s | 14.62 |
| Roll natural period | Tn4 | s | 12.88 |
| Pitch natural period | Tn5 | s | 11.79 |
| Parameter | Unit | Segment 1 (Chain) | Segment 2 (Polyester) | Segment 3 (Chain) |
|---|---|---|---|---|
| Length | m | 120.0 | 2290 | 90.0 |
| Diameter | cm | 9.52 | 16.0 | 9.52 |
| Dry weight | N/m | 1856 | 168.7 | 1856 |
| Wet weight | N/m | 1615 | 44.1 | 1615 |
| Axial stiffness | kN | 912,081 | 186,825 | 912,081 |
| Minimum breaking load | kN | 7553 | 7429 | 7553 |
| Parameter | |||||
|---|---|---|---|---|---|
| Number of layers | 4 | 4 | 3 | 1 | 3 |
| Number of neurons | 128 | 256 | 256 | 128 | 64 |
| Activation function | ELU | ELU | ELU | ELU | ELU |
| Optimizer | Nadam | Adam | Adam | Adam | Nadam |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, D.-S.; Kim, S.-J.; Jin, C.; Kim, M. Parametric Estimation of Directional Wave Spectra from Moored FPSO Motion Data Using Optimized Artificial Neural Networks. J. Mar. Sci. Eng. 2025, 13, 69. https://doi.org/10.3390/jmse13010069
Kwon D-S, Kim S-J, Jin C, Kim M. Parametric Estimation of Directional Wave Spectra from Moored FPSO Motion Data Using Optimized Artificial Neural Networks. Journal of Marine Science and Engineering. 2025; 13(1):69. https://doi.org/10.3390/jmse13010069
Chicago/Turabian StyleKwon, Do-Soo, Sung-Jae Kim, Chungkuk Jin, and MooHyun Kim. 2025. "Parametric Estimation of Directional Wave Spectra from Moored FPSO Motion Data Using Optimized Artificial Neural Networks" Journal of Marine Science and Engineering 13, no. 1: 69. https://doi.org/10.3390/jmse13010069
APA StyleKwon, D.-S., Kim, S.-J., Jin, C., & Kim, M. (2025). Parametric Estimation of Directional Wave Spectra from Moored FPSO Motion Data Using Optimized Artificial Neural Networks. Journal of Marine Science and Engineering, 13(1), 69. https://doi.org/10.3390/jmse13010069







