Time-Domain Simulation of Coupled Motions for Five Fishing Vessels Moored Side-by-Side in a Harbor
Abstract
1. Introduction
2. Theoretical Background
2.1. Wind Load
2.2. Hydrodynamic Wave Loads
2.3. Dynamic Catenary Mooring Line Model
2.4. Fender Load
2.5. Time-Domain Motion Control Equation
3. Side-by-Side Moored Model for Fishing Vessels in the Harbor
3.1. Fishing Vessel Parameters and Arrangements
3.2. Fishing Vessel Configuration
3.3. Environmental Conditions
4. Results and Discussion
4.1. Coupled Motions Analysis of S-L-S Side-by-Side Mooring System
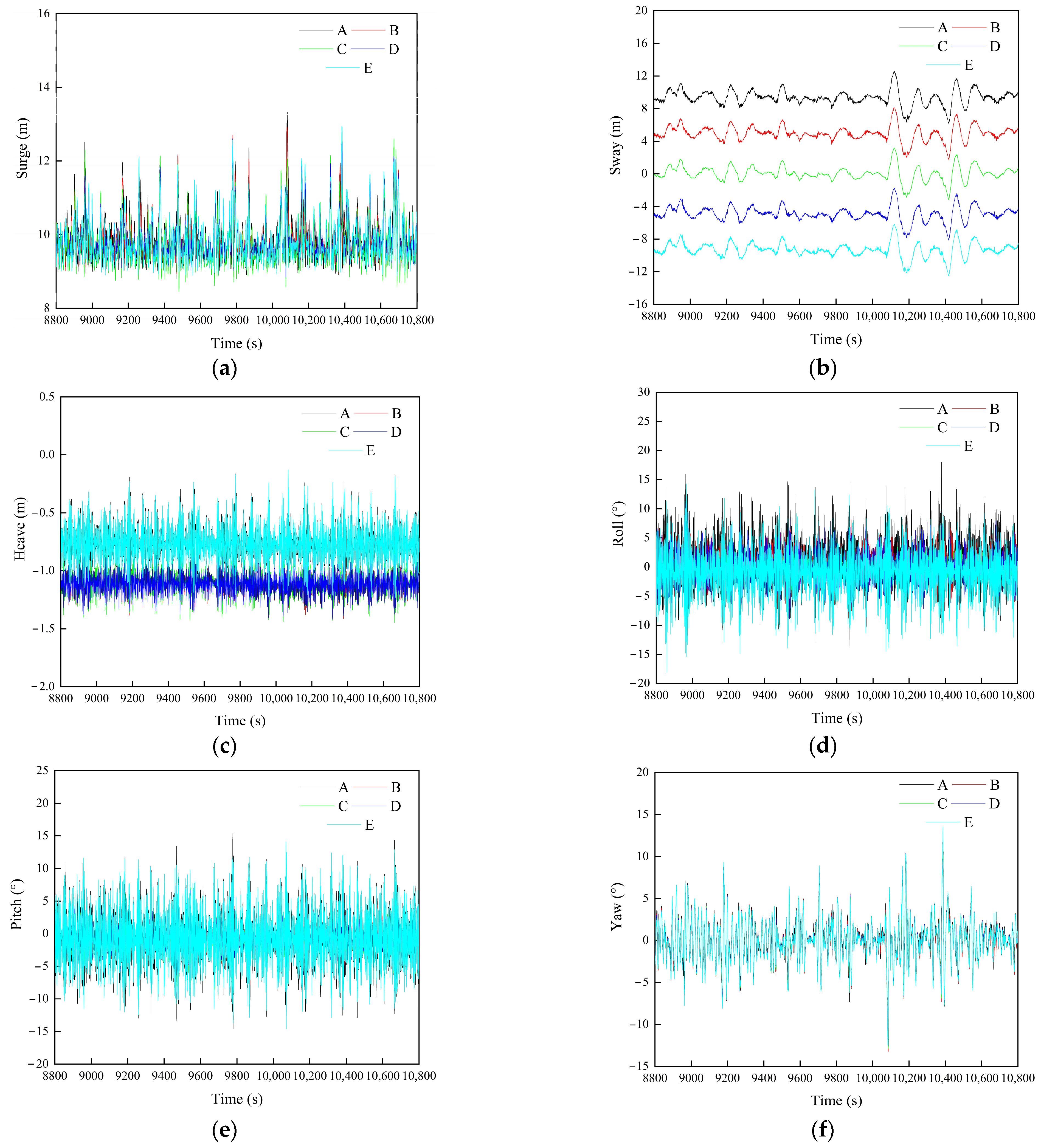
4.1.1. Analysis of Motion Responses
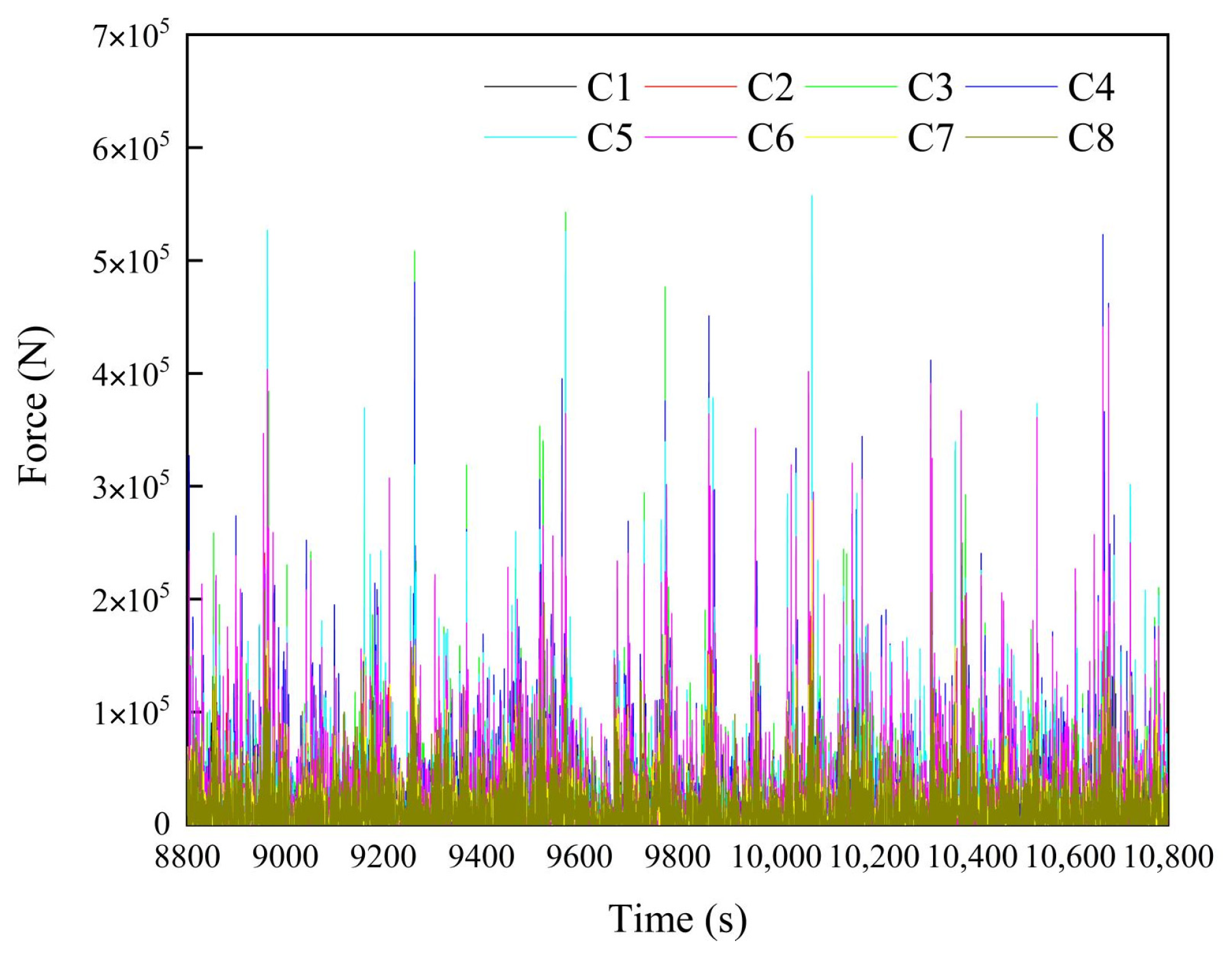
4.1.2. Analysis of Hawsers, Fenders, and Mooring Loads
4.2. Coupled Motions Analysis of the S-L-S Side-by-Side System at Different Wind Direction Angles
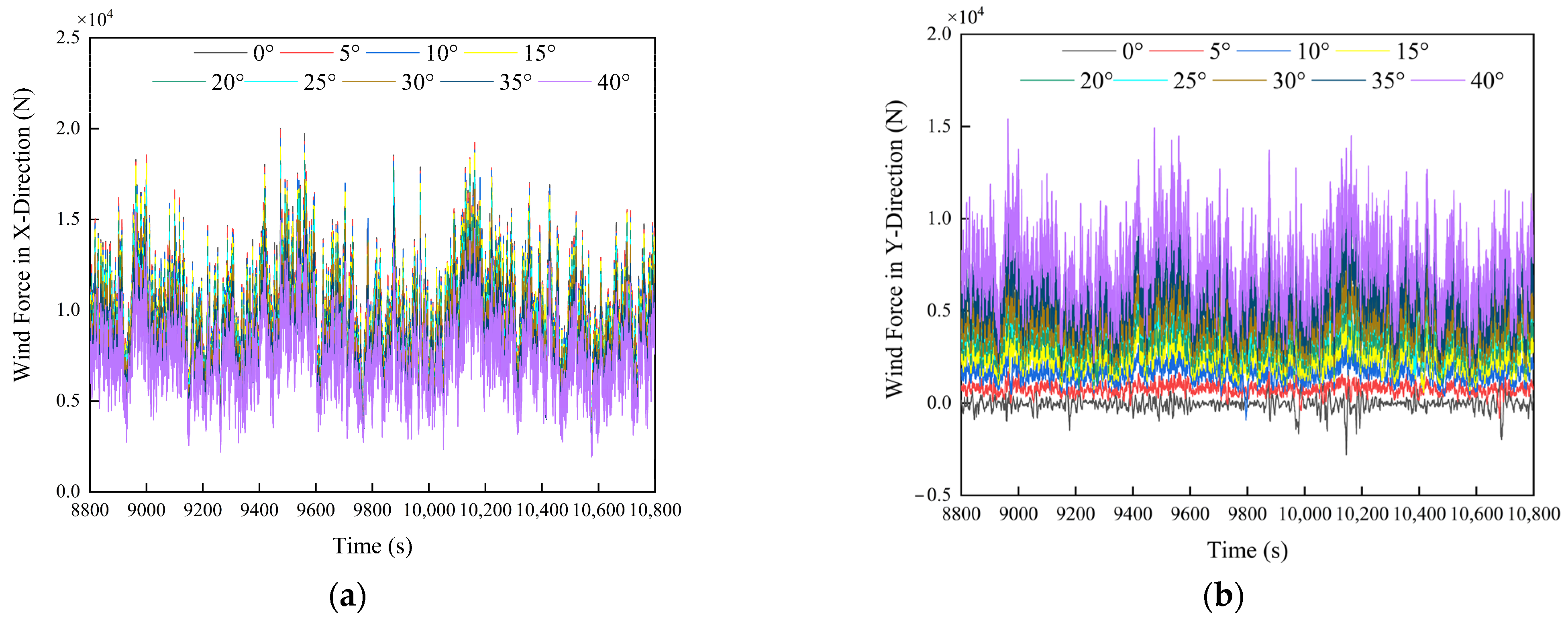
4.2.1. Analysis of the Motion Responses
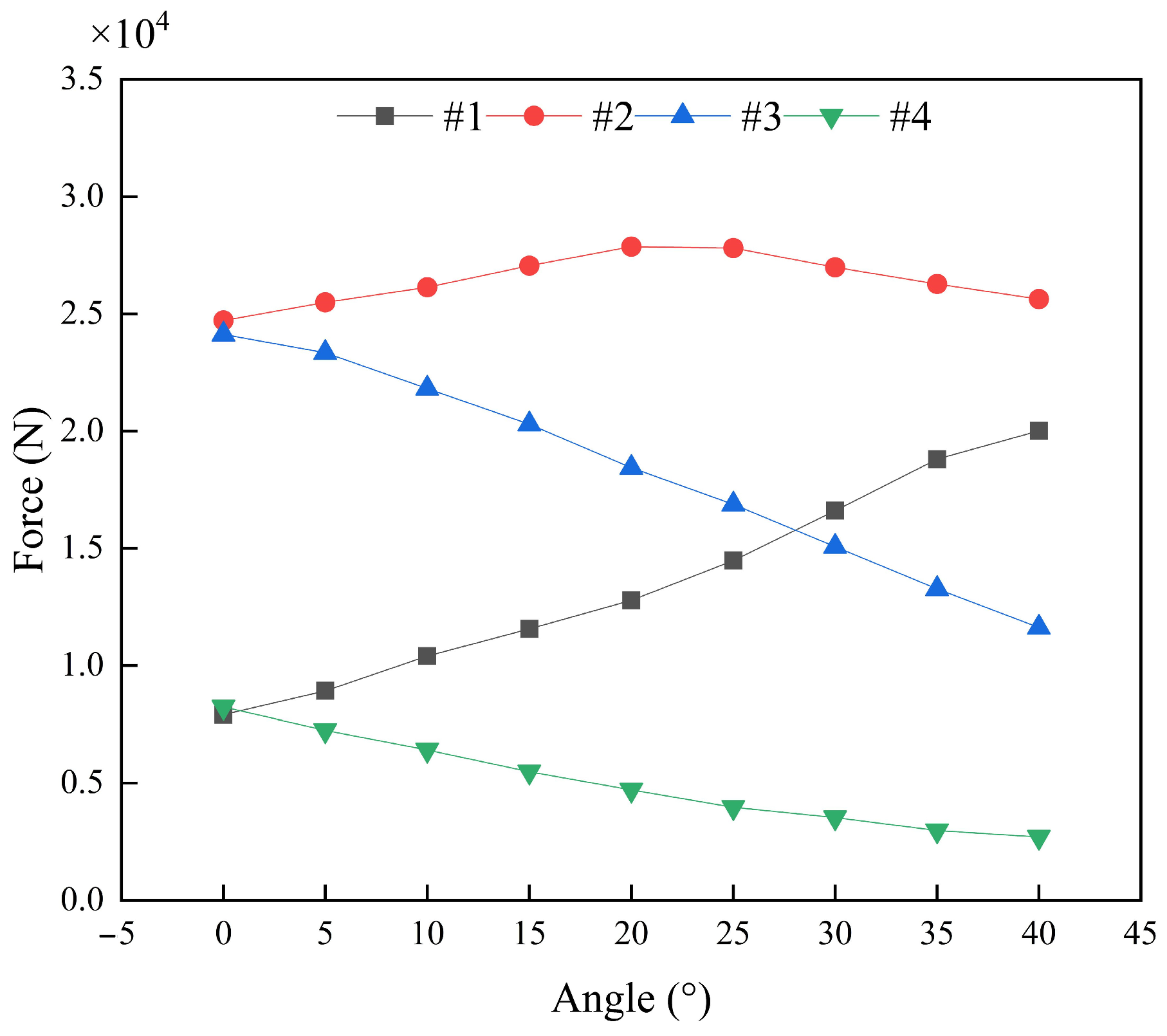
4.2.2. Analysis of Hawsers, Fenders, and Mooring Loads
5. Conclusions
- In the 6DOF motion of the S-L-S side-by-side system, the surge, roll, and pitch responses are relatively large, while the other motion responses are smaller. The roll and pitch angles of two small-scale vessels on both sides are significantly higher than those of the other vessels, indicating that their dynamic responses are more pronounced;
- The forces acting on the hawsers, fenders, and mooring system are all represented as impulse loads. Under combined wind and wave conditions, collisions between the fishing vessels are relatively intense. The maximum loads on these mechanical components remain below their safe working limits, ensuring that they can operate safely;
- With the increase in the wind-wave angles, the surge relative motion of the fishing vessels gradually decreases, while the sway relative motion increases. The wind-wave angle has minimal impact on the heave and pitch motion responses. The forces acting on the hawsers, fenders, and mooring system exhibit distinct characteristics at different angles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Yu, D.; Xiong, Y.; Wang, G.; Li, X. Experimental Investigations on the Roll Motion Characteristics of Multi-Fishing Boats Anchored Side by Side. China Ocean Eng. 2024, 38, 1071–1081. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, R.; Zhang, P.; Xi, Y.; Ma, Q. Wave characteristics and berthing capacity evaluation of the offshore fishing port under the influence of typhoons. Appl. Ocean Res. 2021, 106, 102447. [Google Scholar] [CrossRef]
- Ma, K.-T.; Luo, Y.; Kwan, C.-T.T.; Wu, Y. Mooring System Engineering for Offshore Structures; Gulf Professional Publishing: Houston, TX, USA, 2019. [Google Scholar]
- Feng, X.; Bai, W. Hydrodynamic analysis of marine multibody systems by a nonlinear coupled model. J. Fluids Struct. 2017, 70, 72–101. [Google Scholar] [CrossRef]
- Sun, S.; Li, W. Experimental investigation on the coupling response of a multi-floating side-by-side system between a single-point mooring carrier and an articulated floating platform. Ocean Eng. 2023, 281, 114700. [Google Scholar] [CrossRef]
- Bai, X.; Luo, H.; Xie, P. Experimental investigation on hydrodynamic performance of side-by-side three barges in topsides floatover installation in beam seas. Ocean Eng. 2021, 236, 109516. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, J.; Lu, H.; Li, X.; Lu, W.; Liu, L. Dynamic Response of a Gangway Between Two Floating Bodies in a Side-by-Side Configuration. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; p. V07AT06A027. [Google Scholar]
- Mirzaei, M.; Shafieefar, M.; Moharrami, M.R. Hull-Mooring Coupled Dynamic Analysis of Two Side-by-Side Operating Vessels. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 639–644. [Google Scholar]
- Chitrapu, A.M.; Mordfin, T.G.; Chance, H.M. Efficient time-domain simulation of side-by-side moored vessels advancing in waves. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 871–879. [Google Scholar]
- Pessoa, J.; Fonseca, N.; Soares, C.G. Numerical study of the coupled motion responses in waves of side-by-side LNG floating systems. Appl. Ocean Res. 2015, 51, 350–366. [Google Scholar] [CrossRef]
- Pessoa, J.; Fonseca, N.; Soares, C.G. Side-by-side FLNG and shuttle tanker linear and second order low frequency wave induced dynamics. Ocean Eng. 2016, 111, 234–253. [Google Scholar] [CrossRef]
- Sen, D. Time domain simulation of side-by-side floating bodies using a 3D numerical wave tank approach. Appl. Ocean Res. 2016, 58, 189–217. [Google Scholar]
- Zhou, K.; Hu, Z.; Zhao, D. Time-domain analysis of the relative motions between side-by-side FLNG and LNGC under oblique waves. J. Mar. Sci. Appl. 2018, 17, 519–530. [Google Scholar] [CrossRef]
- Yue, J.; Kang, W.; Mao, W.; Chen, P.; Wang, X. Prediction of dynamic responses of FSRU-LNGC side-by-side mooring system. Ocean Eng. 2020, 195, 106731. [Google Scholar] [CrossRef]
- Ok, H.; Lee, S.; Choi, J. Numerical simulation of motion of single and side-by-side vessels in regular waves using OpenFOAM. Ships Offshore Struct. 2017, 12, 793–803. [Google Scholar] [CrossRef]
- Hong, S.; Kim, J.; Cho, S.; Choi, Y.; Kim, Y. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels. Ocean Eng. 2005, 32, 783–801. [Google Scholar] [CrossRef]
- Naciri, M.; Waals, O.; de Wilde, J. Time domain simulations of side-by-side moored vessels: Lessons learnt from a benchmark test. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 801–811. [Google Scholar]
- Jin, Y.; Chai, S.; Duffy, J.; Chin, C.; Bose, N. Hydrodynamics of a conceptual FLNG system in side-by-side offloading operation. Ships Offshore Struct. 2019, 14, 104–124. [Google Scholar] [CrossRef]
- Patel, M.; Liew, M.; Mustaffa, Z.; Al-Yacouby, A.; Abdurrasheed, A.S.; Whyte, A. Downtime cost analysis of offloading operations considering vessel motions and mooring responses in Malaysian waters. In Proceedings of the 2019 IEEE student conference on research and development (SCOReD), Bandar Seri Iskandar, Malaysia, 15–17 October 2019; pp. 63–68. [Google Scholar]
- Tong, B.; Chang, R.; Kang, Z.; Sui, H.; Li, S. A Numerical Study of TAD and TLP Platforms Operating Side by Side. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Virtual, 3–7 August 2020; p. V06AT06A031. [Google Scholar]
- Xu, X.; Yang, J.-m.; Li, X.; Xu, L.-y. Time-domain simulation for coupled motions of three barges moored side-by-side in floatover operation. China Ocean Eng. 2015, 29, 155–168. [Google Scholar] [CrossRef]
- Chen, M.; Guo, H.; Wang, R.; Tao, R.; Cheng, N. Effects of gap resonance on the hydrodynamics and dynamics of a multi-module floating system with narrow gaps. J. Mar. Sci. Eng. 2021, 9, 1256. [Google Scholar] [CrossRef]
- Zou, M.Y.; Chen, M.S.; Zhu, L.; Yun, Q.H.; Zhao, W.H.; Liang, Q.Y.; Zhao, Y.J. Experimental and numerical investigation of gap resonances between side-by-side fixed barges under beam sea excitation. Ocean Eng. 2024, 297, 117150. [Google Scholar] [CrossRef]
- Wang, G.; Bar, D.; Schreier, S. The potential of end-of-life ships as a floating seawall and the methodical use of gap resonance for wave attenuation. Ocean Eng. 2024, 298, 117246. [Google Scholar] [CrossRef]
- Zhou, H.X.; Wang, F.; Hu, W.L.; Grifoll, M.; Liu, J.; Du, W.J.; Zheng, P.J. A Novel Framework for Identifying Major Fishing Vessel Accidents and Their Key Influencing Factors. Sustainability 2024, 16, 8246. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.; Koo, K.; Kwon, S. Human Reliability Analysis for Fishing Vessels in Korea Using Cognitive Reliability and Error Analysis Method (CREAM). Sustainability 2024, 16, 3780. [Google Scholar] [CrossRef]
- Palomba, V.; Dino, G.E.; Ghirlando, R.; Micallef, C.; Frazzica, A. Decarbonising the Shipping Sector: A Critical Analysis on the Application of Waste Heat for Refrigeration in Fishing Vessels. Appl. Sci. 2019, 9, 5143. [Google Scholar] [CrossRef]
- Notti, E.; Figari, M.; Sala, A.; Martelli, M. Experimental assessment of the fouling control coating effect on the fuel consumption rate. Ocean Eng. 2019, 188, 106233. [Google Scholar] [CrossRef]
- Zhang, X.; Lv, J.J.; He, D.C.; Wang, K.; Liu, Y.; Zhi, J. Hydrodynamic characteristics and internal flow field of a perforated fishing vessel under wave conditions. Ocean Eng. 2024, 314, 119611. [Google Scholar] [CrossRef]
- Zhang, F.; Cui, M.C.; Liu, H.; Zhang, C. The Effect of Corner Structure on the Optimisation of Fishable Flow Field in Aquaculture Tanks. J. Mar. Sci. Eng. 2024, 12, 1185. [Google Scholar] [CrossRef]
- Standal, D.; Ahlquist, I.H. Transforming coastal fisheries in Norway: Institutional implications of green technology implementation. Mar. Policy. 2025, 171, 106471. [Google Scholar] [CrossRef]
- Jankowsky, M.; Morroni, D.A.; Mendonca, J.T. Importance of fishing permits in no-take marine protected area overlapping with fishing grounds. Bol. Inst. Pesca 2024, 50, e824. [Google Scholar] [CrossRef]
- Chureev, E.A. Study of the Geometric Shape of A Small Fishing Trawler In An Effort to Improve Its Sea-Keeping Characterisics. Mar. Intellect. Technol. 2018, 3, 36–43. [Google Scholar]
- Jonsson, I.M.; Leifsson, L.; Koziel, S.; Tesfahunegn, Y.A.; Bekasiewicz, A. Shape Optimization of Trawl-Doors Using Variable-Fidelity Models and Space Mapping. In Proceedings of the 15th Annual International Conference on Computational Science (ICCS), Reykjavik, Iceland, 1–3 June 2015; pp. 905–913. [Google Scholar]
- Gammon, M.A. Optimization of fishing vessels using a Multi-Objective Genetic Algorithm. Ocean Eng. 2011, 38, 1054–1064. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Xiong, Y.Z.; An, X.T.; Yu, D.S.; Wang, G. Experimental study on roll motion of small-scale multi-vessel anchored side by side in waves. Ocean Eng. 2024, 42, 130–140. (In Chinese) [Google Scholar]
- Liu, X. China Fishery Statistical Yearbook; China Agriculture Press: Beijing, China, 2024. (In Chinese) [Google Scholar]
- Wang, K.; Chu, Y.; Huang, S.; Liu, Y. Preliminary design and dynamic analysis of constant tension mooring system on a 15 MW semi-submersible wind turbine for extreme conditions in shallow water. Ocean Eng. 2023, 283, 115089. [Google Scholar] [CrossRef]
- ANSYS, Inc. AQWA Theory Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Mohapatra, S.C.; Amouzadrad, P.; Bispo, I.B.d.S.; Guedes Soares, C. Hydrodynamic Response to Current and Wind on a Large Floating Interconnected Structure. J. Mar. Sci. Eng. 2025, 13, 63. [Google Scholar] [CrossRef]
- Neisi, A.; Ghassemi, H.; Iranmanesh, M.; He, G. Effect of the multi-segment mooring system by buoy and clump weights on the dynamic motions of the floating platform. Ocean Eng. 2022, 260, 111990. [Google Scholar] [CrossRef]
- GB/T 20848-2017; Mooring Chain; China State Shipbuilding Corporayion Limted. Standardization Administration of the People’s Republic of China: Beijing, China, 2017. (In Chinese)
- Q/ZJSX 001-2016; Polypropylene Rope for Ships. Zhejiang Four Brothers Rope Co., Ltd.: Beijing, China, 2016. (In Chinese)
- T/CNASI 31-2020; Type Selection and Installation Requirements of Marine Rubber Fender; CSSC Huangpu Wenchong Shipbuilding Company Limted. China Association of the National Shipbuilding Industry: Beijing, China, 2020. (In Chinese)
- Zhoushan Maritime Safety Administration Has Initiated a Level IV Maritime Typhoon Emergency Response. Available online: https://news.qq.com/rain/a/20240721A03XV700 (accessed on 9 January 2025). (In Chinese).
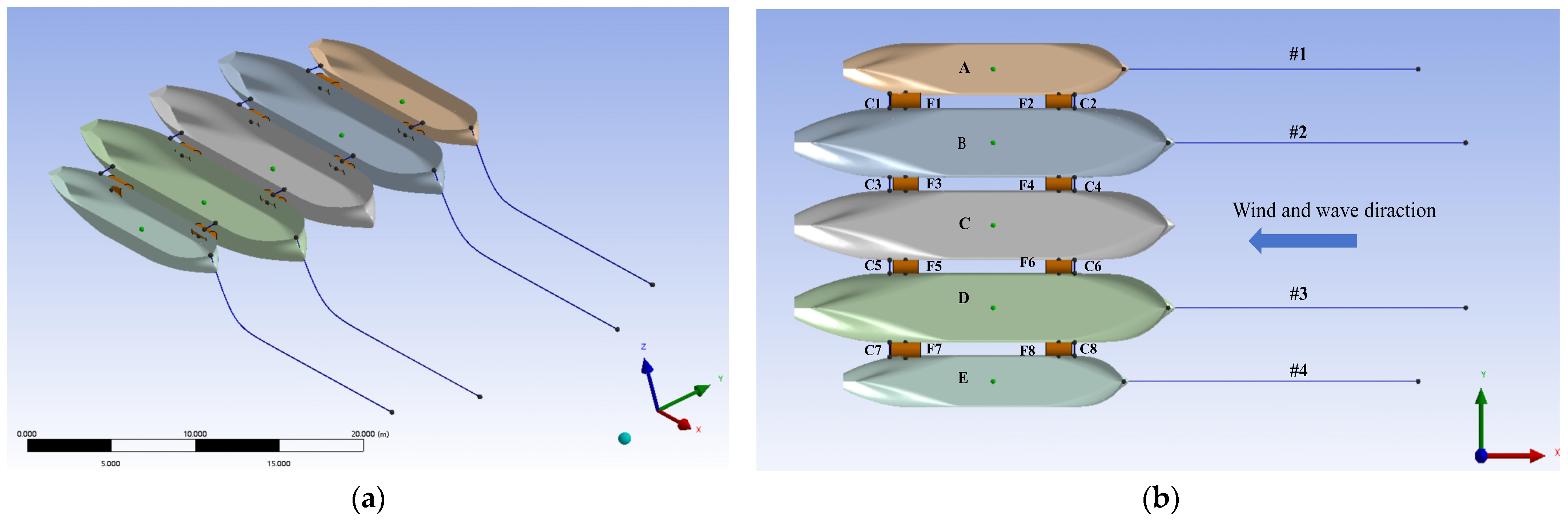






| Parameter | Large-Scale Fishing Vessel | Small-Scale Fishing Vessel |
|---|---|---|
| length/m | 24 | 18 |
| beam/m | 4.18 | 3.14 |
| depth/m | 1.8 | 1.35 |
| draft/m | 1 | 0.75 |
| displacement/t | 102.83 | 43.45 |
| Parameter | Value |
|---|---|
| mass/unit length | 10.53 kg/m |
| axial stiffness | 1.18 × 108 N |
| initial tension | 2.019 × 105 N |
| added mass coefficient | 1.0 |
| drag coefficient | 1.2 |
| axial drag coefficient | 0.4 |
| diameter | 0.054 m |
| length | 22 m |
| Vessel and COG | Surge (m) | Sway (m) | Heave (m) | Roll (°) | Pitch (°) | Yaw (°) | |
|---|---|---|---|---|---|---|---|
| A (12.15, 9.41, −0.2) | Max | 13.33 | 12.57 | −0.16 | 11.98 | 9.53 | 9.52 |
| Min | 9.00 | 6.32 | −1.28 | −13.83 | −14.63 | −13.15 | |
| Mean | 9.85 | 9.37 | −0.77 | 2.98 | 3.41 | 1.86 | |
| RM | 2.30 | 0.04 | 0.57 | --- | --- | --- | |
| B (12.15, 4.97, −0.45) | Max | 12.70 | 8.07 | −0.81 | 8.04 | 8.70 | 10.38 |
| Min | 9.02 | 1.86 | −1.42 | −8.79 | −10.71 | −13.25 | |
| Mean | 9.88 | 4.96 | −1.11 | 1.96 | 2.27 | 1.84 | |
| RM | 2.27 | 0.01 | 0.66 | --- | --- | --- | |
| C (12.15, 0, −0.45) | Max | 12.03 | 2.23 | −0.77 | 2.50 | 7.94 | 7.59 |
| Min | 8.84 | −3.18 | −1.45 | −4.01 | −9.72 | −12.90 | |
| Mean | 9.77 | 0.63 | −1.11 | 0.82 | 2.33 | 1.82 | |
| RM | 2.38 | 0.63 | 0.66 | --- | --- | --- | |
| D (12.15, −4.97, −0.45) | Max | 11.90 | −1.70 | −0.79 | 10.51 | 6.63 | 8.99 |
| Min | 9.06 | −8.15 | −1.42 | −8.90 | −10.69 | −12.60 | |
| Mean | 9.88 | −4.89 | −1.11 | 2.00 | 2.29 | 1.83 | |
| RM | 2.27 | 0.08 | 0.66 | --- | --- | --- | |
| E (12.15, −9.41, −0.2) | Max | 12.85 | −6.15 | −0.13 | 8.12 | 10.83 | 11.39 |
| Min | 8.97 | −12.52 | −1.28 | −18.10 | −14.63 | −12.60 | |
| Mean | 9.84 | −9.30 | −0.77 | 2.99 | 3.38 | 1.84 | |
| RM | 2.31 | 0.11 | 0.57 | --- | --- | --- |
| Stern Hawsers | Bow Hawsers | |||||||
|---|---|---|---|---|---|---|---|---|
| C1 | C3 | C5 | C7 | C2 | C4 | C6 | C8 | |
| Max (kN) | 213.95 | 542.73 | 557.60 | 287.61 | 256.03 | 523.122 | 457.98 | 208.06 |
| Mean (kN) | 15.02 | 17.78 | 18.45 | 14.68 | 12.47 | 16.72 | 16.34 | 11.99 |
| Stern Fenders | Bow Fenders | |||||||
|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | |
| Max (kN) | 106.01 | 97.57 | 146.55 | 152.60 | 155.49 | 166.01 | 109.96 | 111.29 |
| Mean (kN) | 14.01 | 11.53 | 15.16 | 17.85 | 14.65 | 18.33 | 13.79 | 11.19 |
| #1 | #2 | #3 | #4 | |
|---|---|---|---|---|
| Max (kN) | 588.95 | 1070.17 | 1281.20 | 584.65 |
| Mean (kN) | 8.14 | 25.06 | 24.48 | 8.48 |
| DOF | 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | Surge (m) | 2.32 | 2.31 | 2.30 | 2.14 | 1.99 | 1.75 | 1.44 | 1.12 | 0.96 |
| Sway (m) | 0.69 | 1.25 | 2.32 | 3.68 | 4.81 | 6.09 | 7.27 | 8.41 | 9.12 | |
| Heave (m) | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | |
| Roll (°) | 3.03 | 3.11 | 3.21 | 3.08 | 3.09 | 2.96 | 2.95 | 2.98 | 2.87 | |
| Pitch (°) | 3.34 | 3.37 | 3.35 | 3.31 | 3.28 | 3.26 | 3.24 | 3.22 | 3.19 | |
| Yaw (°) | 1.89 | 2.11 | 2.54 | 2.90 | 3.14 | 3.67 | 4.25 | 4.64 | 4.90 | |
| B | Surge (m) | 2.27 | 2.26 | 2.24 | 2.04 | 1.90 | 1.65 | 1.31 | 1.01 | 0.88 |
| Sway (m) | 0.64 | 1.23 | 2.26 | 3.60 | 4.84 | 6.01 | 7.18 | 8.33 | 9.07 | |
| Heave (m) | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | |
| Roll (°) | 1.96 | 2.05 | 2.02 | 1.86 | 1.88 | 1.97 | 1.83 | 1.89 | 1.79 | |
| Pitch (°) | 2.27 | 2.25 | 2.24 | 2.24 | 2.23 | 2.24 | 2.27 | 2.28 | 2.27 | |
| Yaw (°) | 1.83 | 1.94 | 2.41 | 2.85 | 3.06 | 3.58 | 4.14 | 4.70 | 4.72 | |
| C | Surge (m) | 2.40 | 2.36 | 2.28 | 2.08 | 1.90 | 1.62 | 1.23 | 0.94 | 0.83 |
| Sway (m) | 0.68 | 1.19 | 2.25 | 3.61 | 4.74 | 6.02 | 7.19 | 8.32 | 9.04 | |
| Heave (m) | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | |
| Roll (°) | 0.84 | 0.88 | 0.98 | 1.05 | 1.06 | 1.17 | 1.18 | 1.28 | 1.25 | |
| Pitch (°) | 2.32 | 2.33 | 2.33 | 2.33 | 2.32 | 2.32 | 2.33 | 2.34 | 2.34 | |
| Yaw (°) | 1.85 | 2.06 | 2.48 | 2.80 | 3.01 | 3.53 | 4.01 | 4.45 | 4.70 | |
| D | Surge (m) | 2.28 | 2.22 | 2.14 | 1.93 | 1.74 | 1.46 | 1.12 | 0.85 | 0.81 |
| Sway (m) | 0.68 | 1.16 | 2.20 | 3.57 | 4.70 | 5.98 | 7.15 | 8.28 | 9.00 | |
| Heave (m) | 0.66 | 0.66 | 0.67 | 0.67 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | |
| Roll (°) | 2.01 | 2.10 | 2.03 | 1.93 | 1.82 | 1.82 | 1.76 | 1.73 | 1.77 | |
| Pitch (°) | 2.27 | 2.30 | 2.32 | 2.35 | 2.36 | 2.37 | 2.40 | 2.43 | 2.44 | |
| Yaw (°) | 1.86 | 2.08 | 2.52 | 2.85 | 3.06 | 3.59 | 4.15 | 4.50 | 4.75 | |
| E | Surge (m) | 2.31 | 2.25 | 2.14 | 1.91 | 1.69 | 1.40 | 1.09 | 0.87 | 0.83 |
| Sway (m) | 0.69 | 1.14 | 2.17 | 3.54 | 4.67 | 5.94 | 7.11 | 8.24 | 8.96 | |
| Heave (m) | 0.57 | 0.57 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | |
| Roll (°) | 3.11 | 3.20 | 3.27 | 3.14 | 3.18 | 3.15 | 3.08 | 3.01 | 2.97 | |
| Pitch (°) | 3.35 | 3.41 | 3.42 | 3.46 | 3.46 | 3.46 | 3.48 | 3.50 | 3.50 | |
| Yaw (°) | 1.87 | 2.06 | 2.46 | 2.76 | 2.95 | 3.46 | 4.01 | 4.36 | 4.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, X.; He, J.; Jiao, B.; Zhu, G.; Lin, H.; Sun, H. Time-Domain Simulation of Coupled Motions for Five Fishing Vessels Moored Side-by-Side in a Harbor. J. Mar. Sci. Eng. 2025, 13, 307. https://doi.org/10.3390/jmse13020307
Men X, He J, Jiao B, Zhu G, Lin H, Sun H. Time-Domain Simulation of Coupled Motions for Five Fishing Vessels Moored Side-by-Side in a Harbor. Journal of Marine Science and Engineering. 2025; 13(2):307. https://doi.org/10.3390/jmse13020307
Chicago/Turabian StyleMen, Xuran, Jinlong He, Bo Jiao, Guibing Zhu, Haihua Lin, and Hongyuan Sun. 2025. "Time-Domain Simulation of Coupled Motions for Five Fishing Vessels Moored Side-by-Side in a Harbor" Journal of Marine Science and Engineering 13, no. 2: 307. https://doi.org/10.3390/jmse13020307
APA StyleMen, X., He, J., Jiao, B., Zhu, G., Lin, H., & Sun, H. (2025). Time-Domain Simulation of Coupled Motions for Five Fishing Vessels Moored Side-by-Side in a Harbor. Journal of Marine Science and Engineering, 13(2), 307. https://doi.org/10.3390/jmse13020307







