A Numerical Study for the Self-Propulsion Performance of a Propulsion System Using the Coanda Effect
Abstract
:1. Introduction
2. Numerical Set-Up
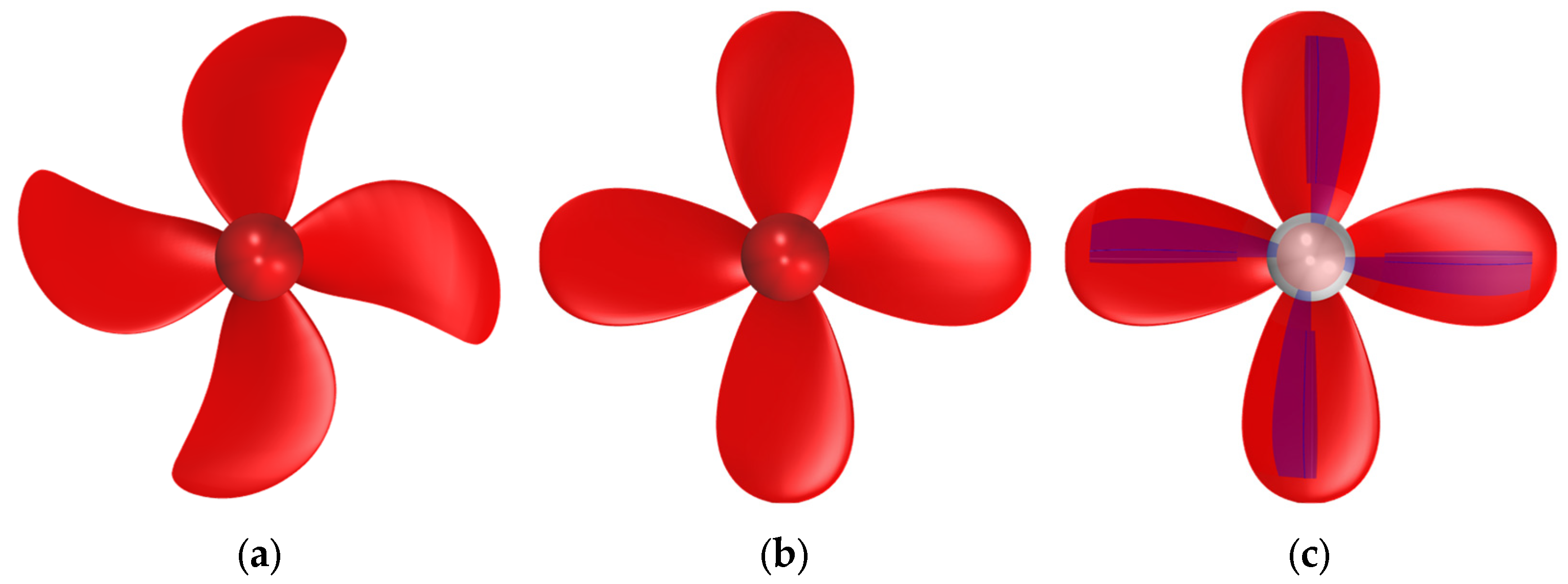
2.1. Geometries of Target Ship and Propellers
2.2. Governing Equations
2.3. Numerical Scheme
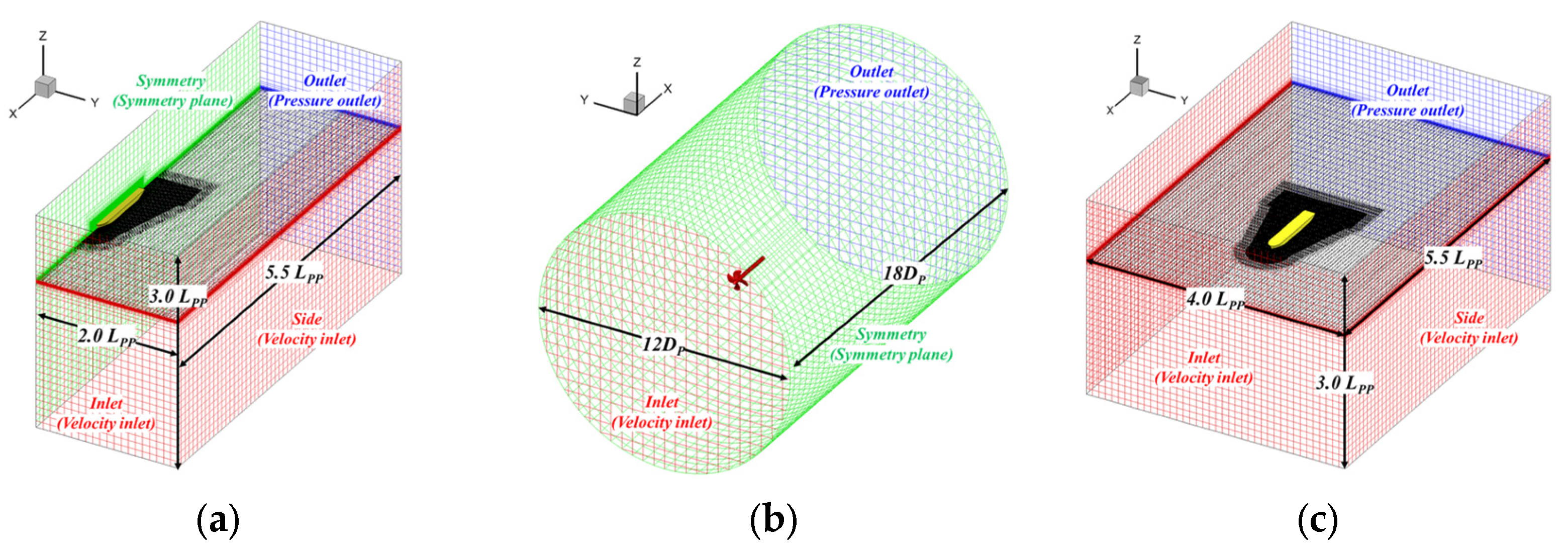
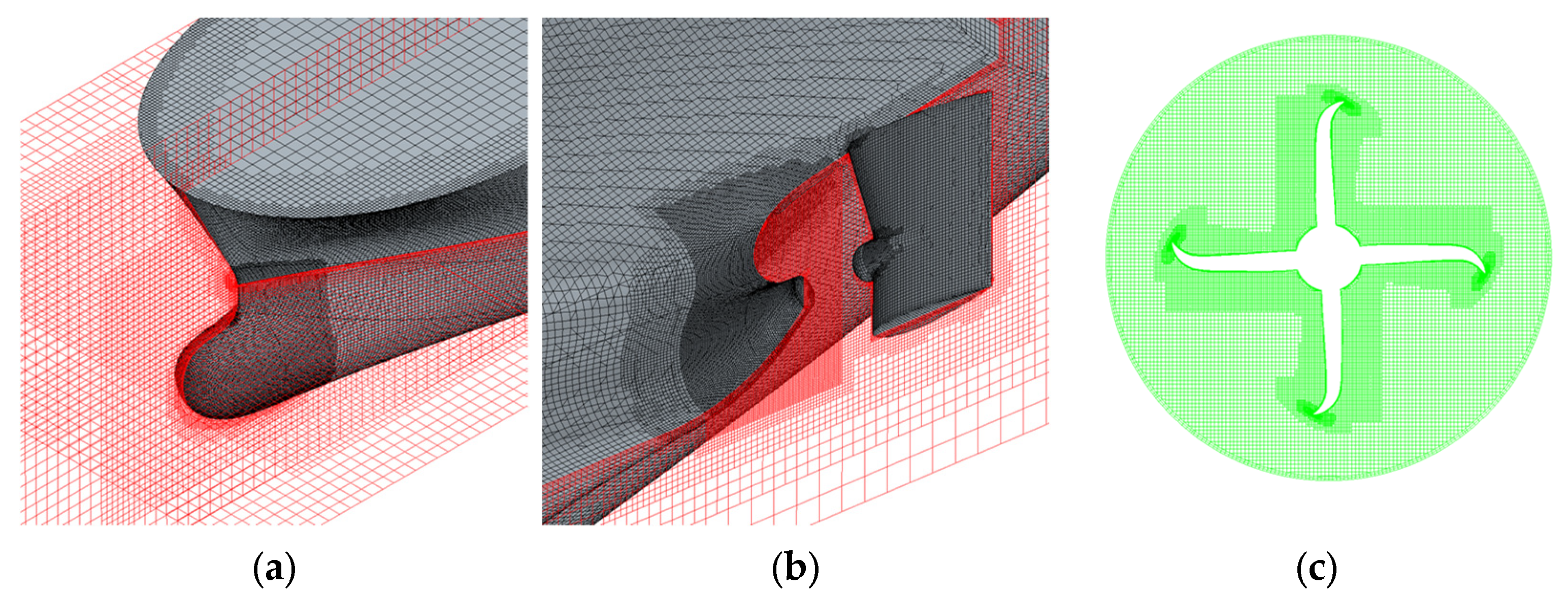
2.4. Computation Domain and Grid System
2.5. Verification and Validation
2.5.1. Verification
2.5.2. Validation of Resistance Simulation
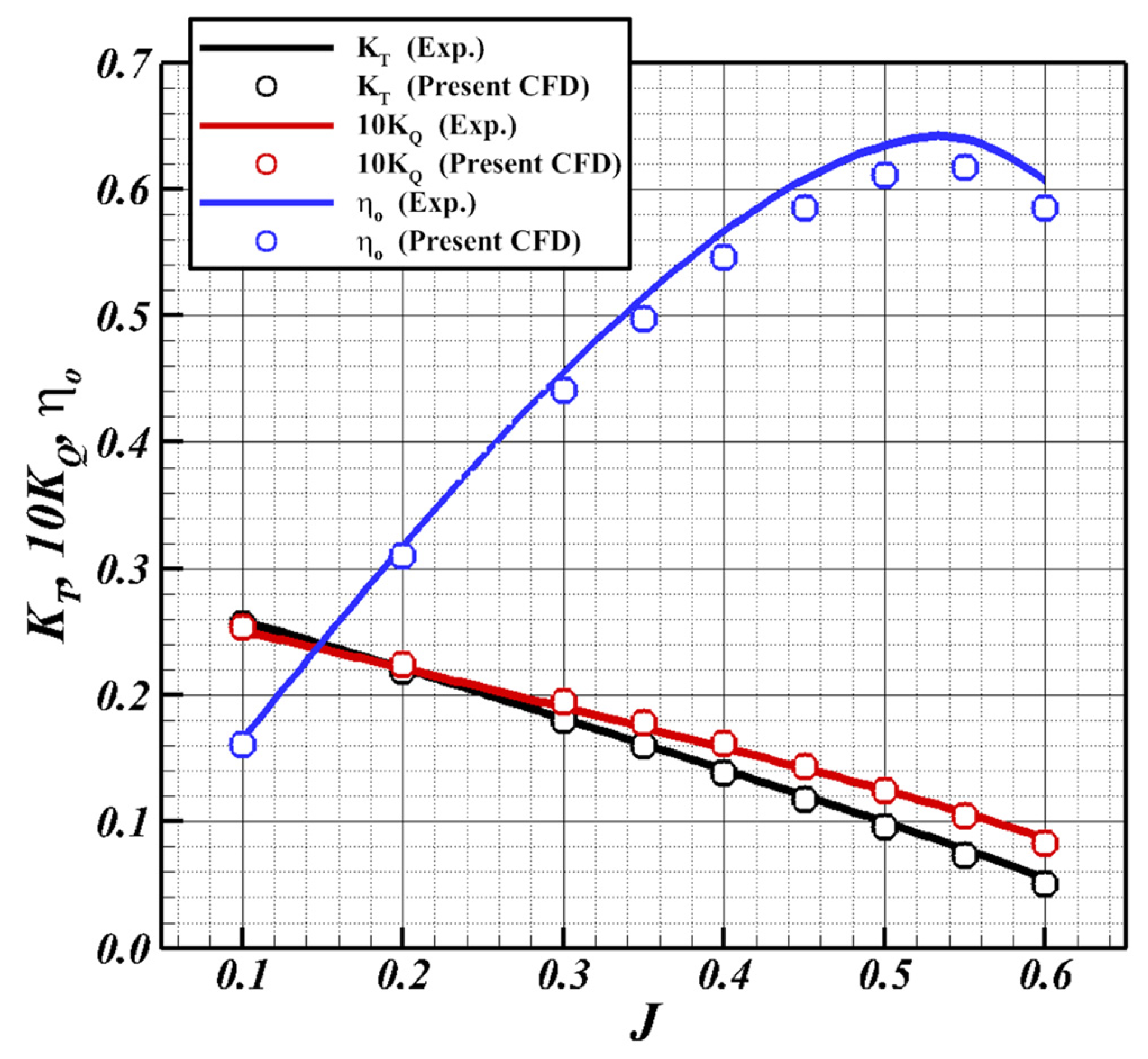
2.5.3. Validation of Propeller Open-Water Simulation
2.5.4. Validation of Self-Propulsion Simulation
3. Methodology
3.1. Procedures for the Coanda Effect Performance Decision
3.2. Procedures for Pump Performance
4. Results of the Simulation
5. Conclusions
- The Coanda propeller showed significant improvements in the self-propulsion performance compared to the normal and original propellers. The self-propulsion analysis indicated that the required power of the Coanda propeller was reduced by approximately 7.8% compared to the original propeller. These results suggest that additional force is generated on the suction side because of jet injection, enabling efficient propulsion even at lower rotational speeds.
- The numerical scheme used in this study was based on the URANS equations and showed a correlation with the model experimental results. This approach effectively reproduced key flow phenomena and accurately modeled the flow characteristics of jet injection because of the Coanda effect, allowing precise thrust and torque calculations.
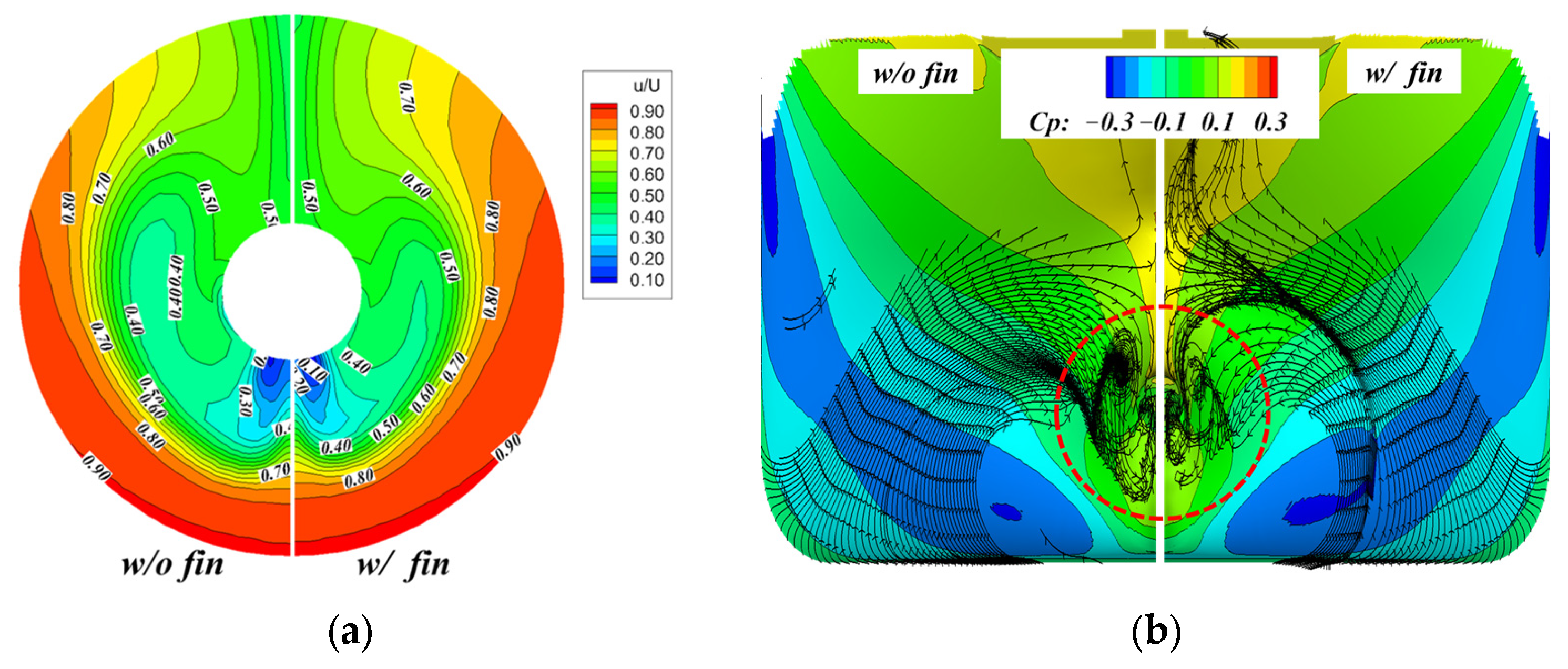
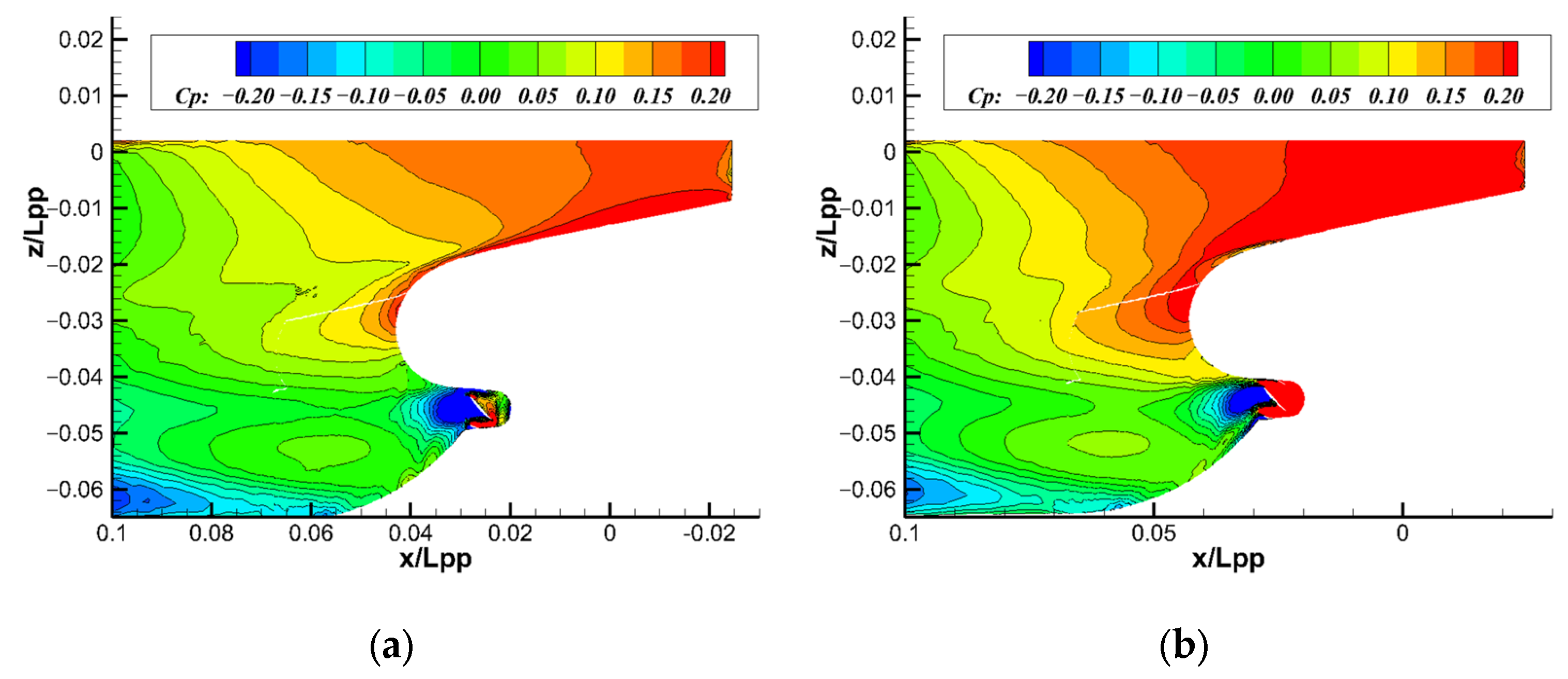
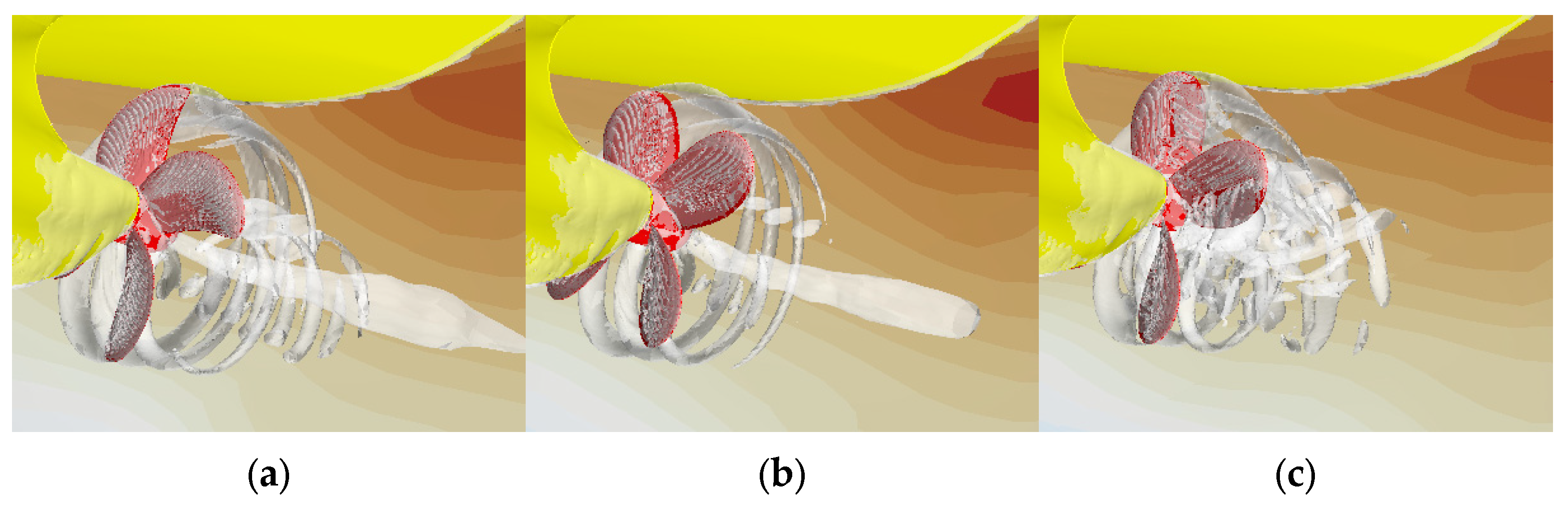
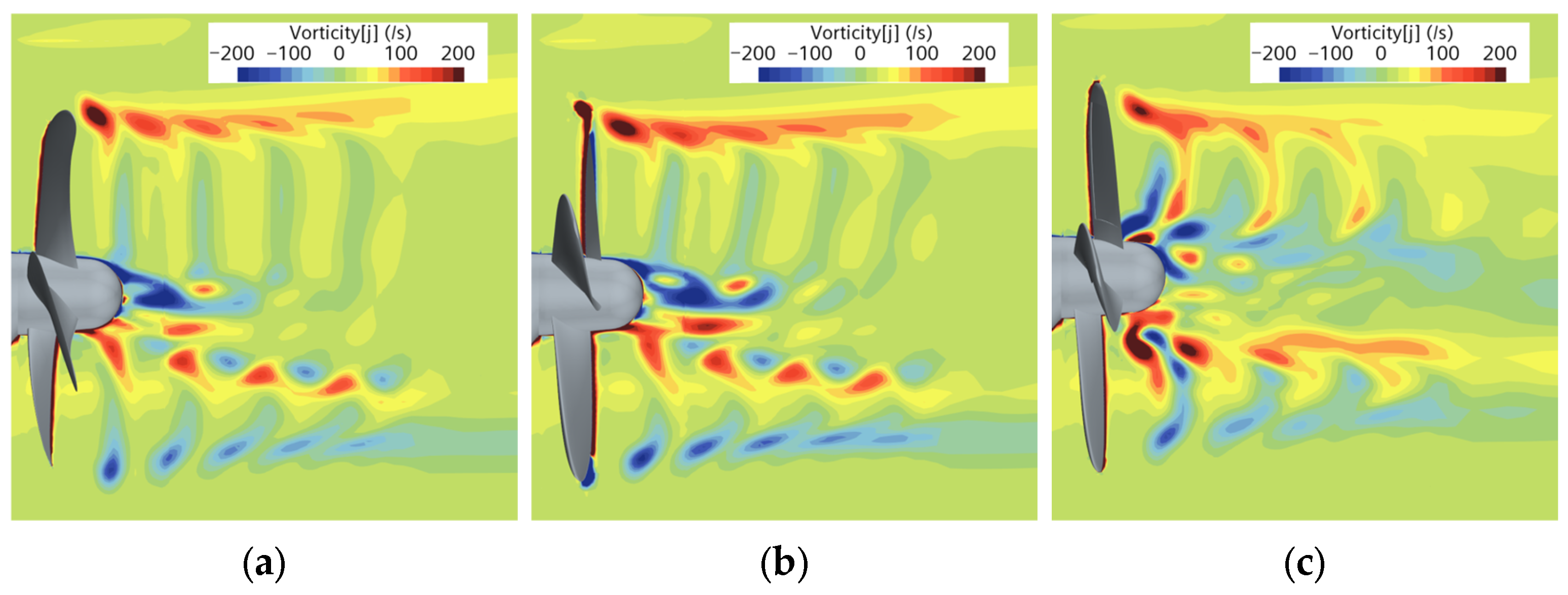
- The numerical results confirmed that the Coanda effect positively influenced the flow characteristics by stabilizing the wake and enhancing pressure recovery. In the wake region, the interactions between tip vortices and the jet flow were observed, promoting vortex dissipation, reducing resistance, and improving propulsion efficiency. Furthermore, pressure fluctuations showed that the Coanda propeller exhibited lower pressure variations than normal and original propellers, indicating its potential for cavitation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, J.Y. International Maritime Organization (IMO) 82nd Marine Environment Protection Committee (MEPC). J. Soc. Nav. Archit. Korea 2024, 61, 12–21. [Google Scholar]
- Kim, J.H.; Choi, J.H. A study on impact and countermeasures of marine fuels in the FuelEU Maritime regulation. J. Soc. Nav. Archit. Korea 2024, 61, 88–97. [Google Scholar] [CrossRef]
- Su, Y.M.; Lin, J.F.; Zhao, D.G.; Guo, C.Y.; Guo, H. Influence of a pre-swirl stator and rudder bulb system on the propulsion performance of a large-scale ship model. Ocean Eng. 2020, 218, 108189. [Google Scholar] [CrossRef]
- Koushan, K.; Krasilnikov, V.; Nataletti, M.; Sileo, L.; Spence, S. Experimental and numerical study of pre-swirl stators (PSS). J. Mar. Sci. Eng. 2020, 8, 47. [Google Scholar] [CrossRef]
- Kang, J.G.; Kim, M.C.; Shin, I.R.; Jin, W.S. Feasibility study on effect of structural flexibility of asymmetric pre-swirl stator on propulsion performance for kriso container ship (Kcs). Brodogradnja 2021, 72, 103–119. [Google Scholar] [CrossRef]
- Gaggero, S. Design of PBCF energy saving devices using optimization strategies: A step towards a complete viscous design approach. Ocean Eng. 2018, 159, 517–538. [Google Scholar] [CrossRef]
- Ouchi, K.; Ogura, M.; Kono, Y.; Orito, H.; Shiotsu, T.; Tamashima, M.; Koizuka, H. A research and development of PBCF (propeller boss cap fins): Improvement of flow from propeller boss. J. Soc. Nav. Archit. Jpn. 1988, 163, 66–78. [Google Scholar] [CrossRef]
- Ouchi, K.; Tamashima, M.; Kawasaki, T.; Koizuka, H. A research and development of PBCF (propeller boss cap fins), 2nd report: Study on propeller slipstream and actual ship performance. J. Soc. Nav. Archit. Jpn. 1989, 165, 43–53. [Google Scholar] [CrossRef]
- Xu, K.; Su, X.; Bensow, R.; Krajnovic, S. Drag reduction of ship airflow using steady Coanda effect. Ocean Eng. 2022, 266, 113051. [Google Scholar] [CrossRef]
- Pfingsten, K.C.; Radespiel, R. Numerical simulation of a wing with a gapless high-lift system using circulation control. In New Results in Numerical and Experimental Fluid Mechanics VI: Contributions to the 15th STAB/DGLR Symposium; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Burnazzi, M.; Radespiel, R. Design and analysis of a droop nose for Coanda flap applications. J. Aircr. 2014, 51, 1567–1579. [Google Scholar] [CrossRef]
- Lee, H.; Han, S.; Lee, H.; Jeon, J.; Lee, C.; Kim, Y.B.; Choi, H.R. Design optimization, modeling, and control of unmanned aerial vehicle lifted by Coandă effect. IEEE/ASME Trans. Mechatron. 2017, 22, 1327–1336. [Google Scholar] [CrossRef]
- Jun, H.C.; Kim, S.H.; Kim, H.J.; Park, H.P. An experimental study on the effect of increasing rudder force on the turning ability of a short sea shipping ship. J. Korean Soc. Mar. Environ. Saf. 2012, 18, 591–596. [Google Scholar] [CrossRef]
- Maltsev, L.I.; Dimitrov, V.D.; Milanov, E.M.; Zapryagaev, I.I.; Timoshevskiy, M.V.; Pervunin, K.S. Jet control of flow separation on hydrofoils: Performance evaluation based on force and torque measurements. J. Eng. Thermophys. 2020, 29, 424–442. [Google Scholar] [CrossRef]
- Oh, J.K.; Noh, J.K. On the lift enhancement technique of the trailing edge rotor of two-dimensional hydrofoil. J. Korean Soc. Mar. Environ. Saf. 2015, 21, 200–206. [Google Scholar] [CrossRef]
- Oh, J.K.; Kim, H.C. A study on the high lifting device equipped with the trailing edge rotor for the enhancement of circulation control. J. Soc. Nav. Archit. Korea 2010, 47, 533–542. [Google Scholar]
- Pant, C.S.; Frankel, S.H. Interaction between surface blowing and re-entrant jet in active control of hydrofoil cavitation. Ocean Eng. 2021, 242, 110087. [Google Scholar] [CrossRef]
- Wang, W.; Tang, T.; Zhang, Q.D.; Wang, X.F.; An, Z.Y.; Tong, T.H.; Li, Z.J. Effect of water injection on the cavitation control: Experiments on a NACA66 (MOD) hydrofoil. Acta Mech. Sin. 2020, 36, 999–1017. [Google Scholar] [CrossRef]
- Chowdhury, N.E.; Hossain, M.F.; Karim, M.M.; Islam, M.R.; Bhuiyan, A.A. Numerical investigation for mitigation of cavitation in high-speed marine propeller using mass injection approach. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1693–1709. [Google Scholar] [CrossRef]
- Yang, C.; Yao, H.D.; Sun, C.; Guo, C.; Wang, C.; Ren, W. Injection of micro jets to improve hydrodynamic performance of a ducted propeller. Ocean Eng. 2024, 309, 118502. [Google Scholar] [CrossRef]
- Eom, M.J.; Paik, K.J.; Lee, J.H. Numerical study on the lift-drag and cavitation performances of a two-dimensional hydrofoil using the Coanda effect. J. Adv. Mar. Eng. Technol. 2020, 44, 457–466. [Google Scholar] [CrossRef]
- Eom, M.J.; Paik, K.J.; Lee, J.H.; Kang, S.M.; Kim, D.Y. A study on the performance variation of a three-dimensional hydrofoil using jet flow. J. Ocean Eng. Technol. 2021, 35, 24–37. [Google Scholar] [CrossRef]
- Lee, J.H.; Paik, K.J.; Lee, S.H.; Kim, G.H.; Cho, J.H. Experimental and numerical study on the performance change of a simple propeller shape using the Coanda effect. Appl. Sci. 2021, 11, 4112. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, J.H.; Kim, M.M.; Oh, D.; Paik, K.J. A numerical study on the optimization of the slit shape of a jet injection propeller. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100578. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Lee, S.H.; Paik, K.J.; Cho, J.H.; Kim, G.H.; Kim, H.S.; Kim, S.H. A Numerical Study on Self-Propulsion Performance in Regular Waves and Power Prediction in Irregular Waves. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100454. [Google Scholar] [CrossRef]
- Grlj, C.G.; Degiuli, N.; Martić, I. Experimental and numerical assessment of the effect of speed and loading conditions on the nominal wake of a containership. Brodogradnja 2024, 75, 75405. [Google Scholar] [CrossRef]
- Simens. STAR-CCM+ User Guide, Version 16.06; Simens: Munich, Germany, 2021. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- ITTC. Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. ITTC-Rcomm. Proced. 7.5-03-01-01.4. 2021. Available online: https://www.ittc.info/media/11950/75-03-01-01.pdf (accessed on 23 February 2025).
- ITTC. 1978 ITTC Performance Prediction Method. ITTC-Rcomm. Proced. 7.5-02-03-01.4. 2018. Available online: https://www.wartsila.com/encyclopedia/term/ittc-performance-prediction-method (accessed on 23 February 2025).




| Main Specifications | Full Scale | CFD Model |
|---|---|---|
| Ship speed (Fr) | 0.219 | |
| Scale ratio | 1 | 20 |
| Length between perpendiculars, LPP (m) | 102 | 5.10 |
| Breadth, BWL (m) | 18.6 | 0.93 |
| Draft, d (m) | 6.65 | 0.3325 |
| Displacement, ∇ (m3) | 9366 | 1.171 |
| Vertical center of gravity, KG (m) | 2672 | 6.680 |
| Moment of inertia, Ixx/B, Iyy/LPP, Izz/LPP | 0.40, 0.25, 0.25 | |
| Main Specifications | KP1364 |
|---|---|
| Full-scale diameter (m) | 3.600 |
| Model-scale diameter (m) | 0.180 |
| Pitch ratio, P/DP (0.7RP) | 0.632 |
| Thickness ratio, t/D (0.7RP) | 0.044 |
| Chord ratio, c/DP (0.7RP) | 0.300 |
| Number of blades | 4 |
| Hub ratio | 0.180 |
| Direction of rotation | Right-handed |
| Variables | Fine Grid | Medium Grid | Coarse Grid |
|---|---|---|---|
| Number of grids (at resistance test) | 5,697,248 | 2,976,710 | 1,553,994 |
| Number of grids (at POW test) | 7,068,215 | 3,787,544 | 2,028,383 |
| Time step [s] (at resistance test) | 0.005 | 0.010 | 0.025 |
| Resistance Test | POW Test (J = 0.35) | POW Test (J = 0.40) | POW Test (J = 0.45) | |
|---|---|---|---|---|
| ε21 | 0.711 | 4.785 | 2.066 | 1.530 |
| ε32 | 1.000 | 11.425 | 4.418 | 2.584 |
| r | 1.242 | 1.231 | 1.231 | 1.231 |
| R | 0.710 | 0.419 | 0.468 | 0.592 |
| , % | 3.626 | 2.747 | 1.691 | 2.451 |
| Case | CTM (×103) | τ (deg) | σ/LPP (×102) |
|---|---|---|---|
| Exp. | 4.558 | - | - |
| Present CFD | 4.503 | 0.234 | −0.217 |
| Diff. | −1.21% |
| Case | VS (knots) | CTM (×103) | τ (deg) | σ/LPP (×102) |
|---|---|---|---|---|
| Exp. | 12.0 | 4.207 | 0.158 | −0.131 |
| Present CFD | 4.186 | 0.177 | −0.180 | |
| Diff. | −0.49% | 0.019 | −0.049 | |
| Exp. | 13.0 | 4.301 | 0.185 | −0.157 |
| Present CFD | 4.311 | 0.220 | −0.218 | |
| Diff. | 0.23% | 0.035 | −0.061 | |
| Exp. | 13.5 | 4.441 | 0.203 | −0.175 |
| Present CFD | 4.451 | 0.225 | −0.235 | |
| Diff. | 0.23% | 0.023 | −0.061 | |
| Exp. | 14.0 | 4.612 | 0.215 | −0.190 |
| Present CFD | 4.709 | 0.237 | −0.255 | |
| Diff. | 1.90% | 0.022 | −0.065 | |
| Exp. | 15.0 | 4.908 | 0.255 | −0.220 |
| Present CFD | 4.970 | 0.269 | −0.300 | |
| Diff. | 1.26% | 0.014 | −0.080 |
| Exp. | Present CFD | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| J | KT | 10KQ | ηO | KT | Diff. | 10KQ | Diff. | ηO | Diff. |
| 0.10 | 0.2590 | 0.2505 | 0.1646 | 0.2565 | −1.0% | 0.2541 | 1.4% | 0.1606 | −2.4% |
| 0.20 | 0.2211 | 0.2214 | 0.3179 | 0.2190 | −0.9% | 0.2245 | 1.4% | 0.3106 | −2.3% |
| 0.30 | 0.1813 | 0.1902 | 0.4551 | 0.1801 | −0.7% | 0.1948 | 2.4% | 0.4414 | −3.0% |
| 0.35 | 0.1612 | 0.1744 | 0.5150 | 0.1597 | −1.0% | 0.1787 | 2.5% | 0.4976 | −3.4% |
| 0.40 | 0.1410 | 0.1584 | 0.5667 | 0.1387 | −1.6% | 0.1617 | 2.1% | 0.5460 | −3.6% |
| 0.45 | 0.1205 | 0.1420 | 0.6078 | 0.1173 | −2.6% | 0.1436 | 1.1% | 0.5850 | −3.8% |
| 0.50 | 0.0997 | 0.1250 | 0.6347 | 0.0957 | −4.0% | 0.1246 | −0.3% | 0.6112 | −3.7% |
| 0.55 | 0.0781 | 0.1068 | 0.6397 | 0.0735 | −5.8% | 0.1042 | −2.4% | 0.6175 | −3.5% |
| 0.60 | 0.0552 | 0.0868 | 0.6073 | 0.0506 | −8.3% | 0.0826 | −4.8% | 0.5852 | −3.6% |
| WTM | WTS | 1−t | ηH | ηR | ηO | ηD | RPM | PD (kW) | |
|---|---|---|---|---|---|---|---|---|---|
| Exp. | - | - | - | 1.128 | 1.002 | 0.569 | 0.643 | 204.5 | 2399 |
| Present CFD | 0.356 | 0.305 | 0.795 | 1.145 | 1.046 | 0.548 | 0.656 | 203.3 | 2344 |
| Diff. (%) | 1.5 | 4.4 | −3.7 | 2.0 | −0.6 | −2.3 |
| Case | Original Prop. | Normal Prop. | Coanda Prop. |
|---|---|---|---|
| RPSM | 15.865 | 16.724 | 15.012 |
| KTM | 0.163 | 0.145 | 0.176 |
| QTM (Nm) | 0.833 | 0.859 | - |
| PW (W) | - | - | 24.7 |
| wTM | 0.372 | 0.326 | 0.280 |
| tM | 0.159 | 0.150 | 0.128 |
| ηH | 1.340 | 1.261 | 1.211 |
| ηR | 1.035 | 1.031 | 1.000 |
| ηO | 0.506 | 0.494 | 1.881 |
| ηP | - | - | 0.500 |
| ηM | - | - | 0.667 |
| ηD | 0.701 | 0.643 | 0.759 |
| PE (W) | 56.3 | 56.3 | 56.3 |
| PD (W) | 80.2 | 87.6 | 74.1 |
| Diff. of PD (%) | - | 9.0 | −7.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Paik, K.-J.; Oh, D.-H. A Numerical Study for the Self-Propulsion Performance of a Propulsion System Using the Coanda Effect. J. Mar. Sci. Eng. 2025, 13, 437. https://doi.org/10.3390/jmse13030437
Lee J-H, Paik K-J, Oh D-H. A Numerical Study for the Self-Propulsion Performance of a Propulsion System Using the Coanda Effect. Journal of Marine Science and Engineering. 2025; 13(3):437. https://doi.org/10.3390/jmse13030437
Chicago/Turabian StyleLee, Jun-Hee, Kwang-Jun Paik, and Do-Han Oh. 2025. "A Numerical Study for the Self-Propulsion Performance of a Propulsion System Using the Coanda Effect" Journal of Marine Science and Engineering 13, no. 3: 437. https://doi.org/10.3390/jmse13030437
APA StyleLee, J.-H., Paik, K.-J., & Oh, D.-H. (2025). A Numerical Study for the Self-Propulsion Performance of a Propulsion System Using the Coanda Effect. Journal of Marine Science and Engineering, 13(3), 437. https://doi.org/10.3390/jmse13030437










