A Symbol Conditional Entropy-Based Method for Incipient Cavitation Prediction in Hydraulic Turbines
Abstract
1. Introduction
- (1)
- An SCE method is proposed to extract fault information in complex nonlinear time series by classifying the state modes. The information gain of the hydroacoustic signal is increased, which is more conducive to improving the prediction performance.
- (2)
- An IM algorithm is proposed to detect the initial prediction point, which can avoid missing pivotal information or including unnecessary noise.
- (3)
- The effectiveness of the proposed method is validated with hydroacoustic signals collected from a hydraulic turbine model test bench. The results of comparisons with different prediction algorithms show that the proposed SCE has excellent trend prediction performance and high precision, as evaluated using RMSE, MAE, and MAPE as performance metrics.
2. Problem Descriptions
2.1. The Hydroacoustic Signal in Cavitation States
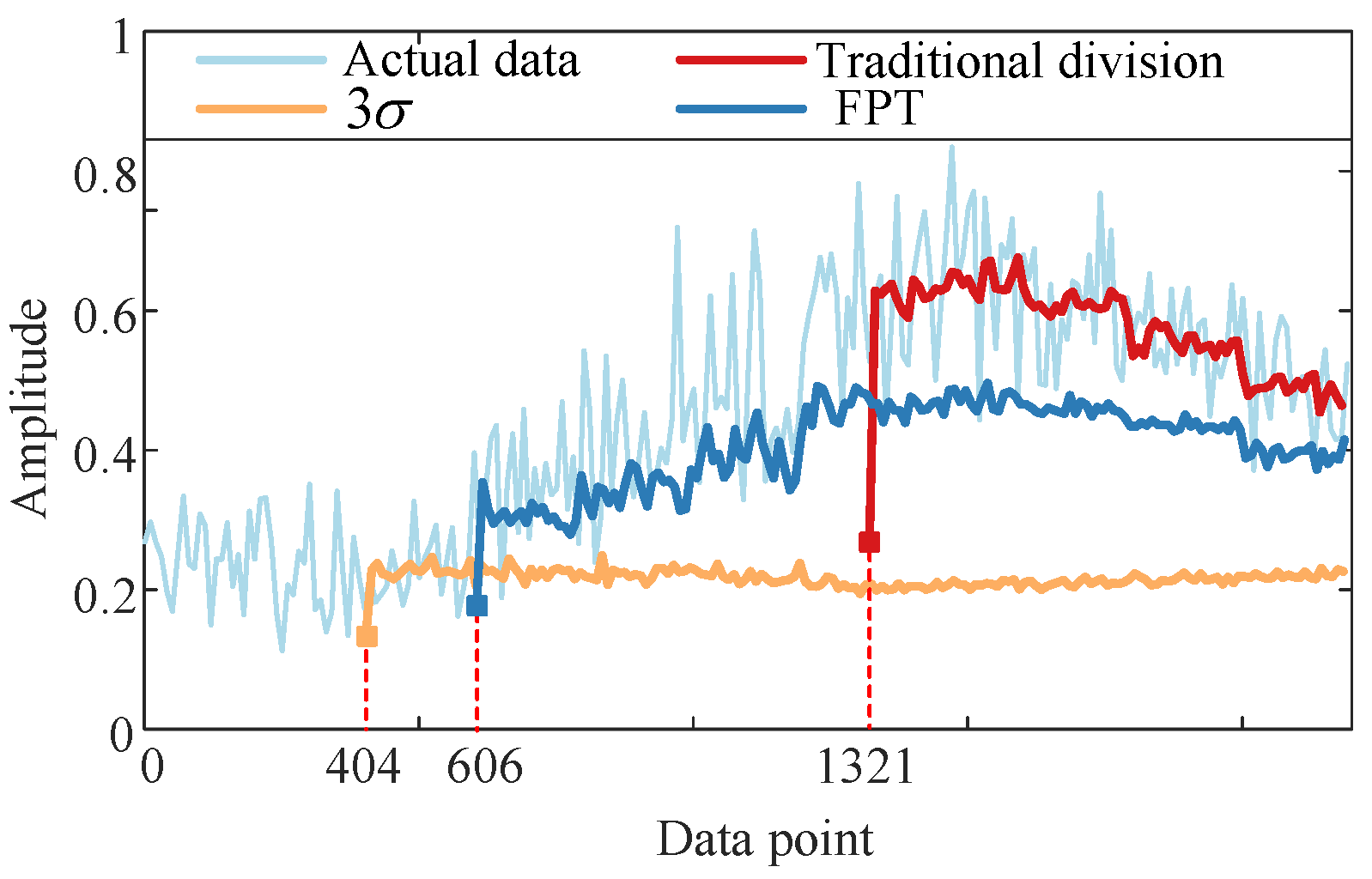
2.2. Determination of Initial Prediction Point
3. The Symbol Conditional Entropy (SCE)
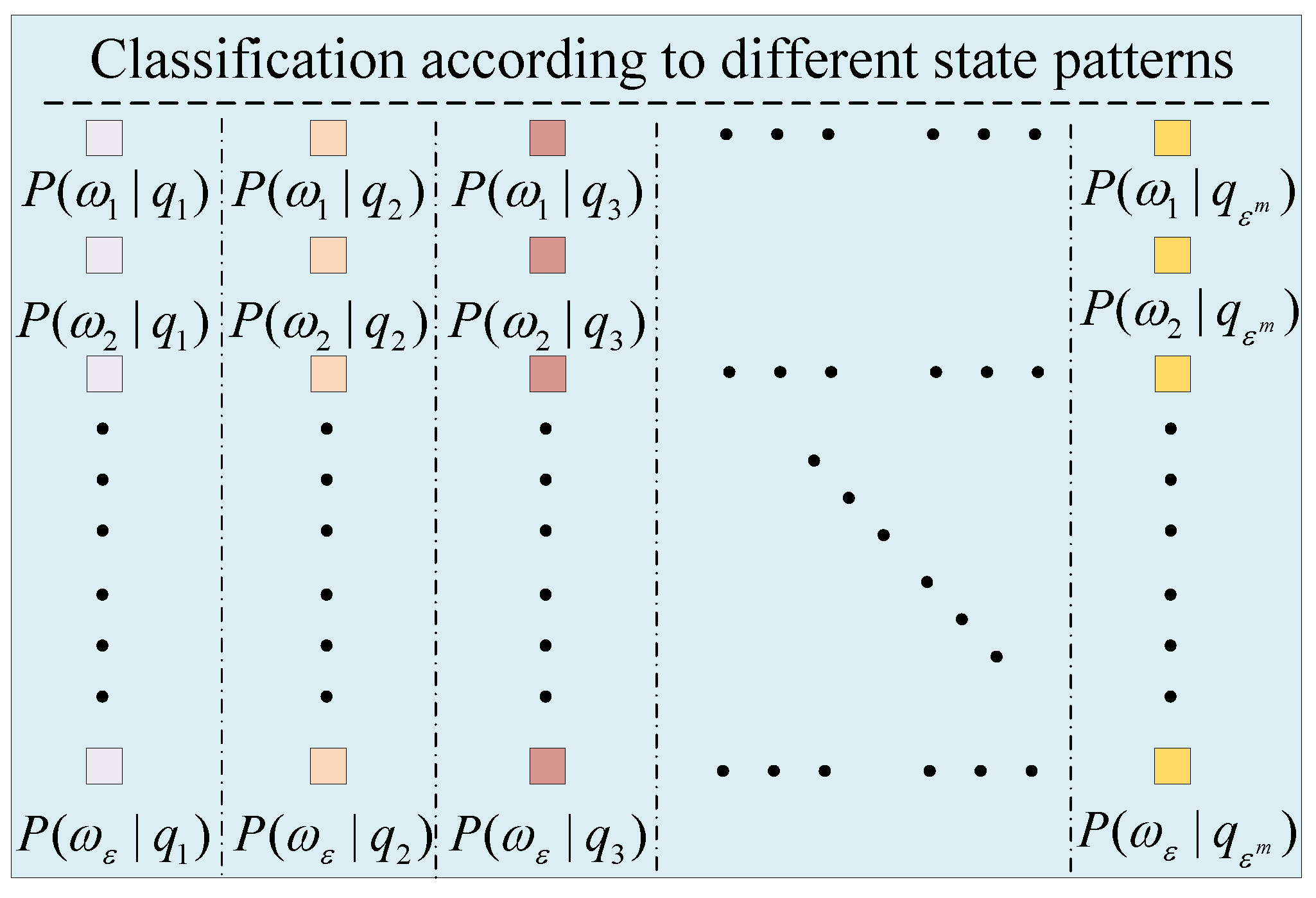
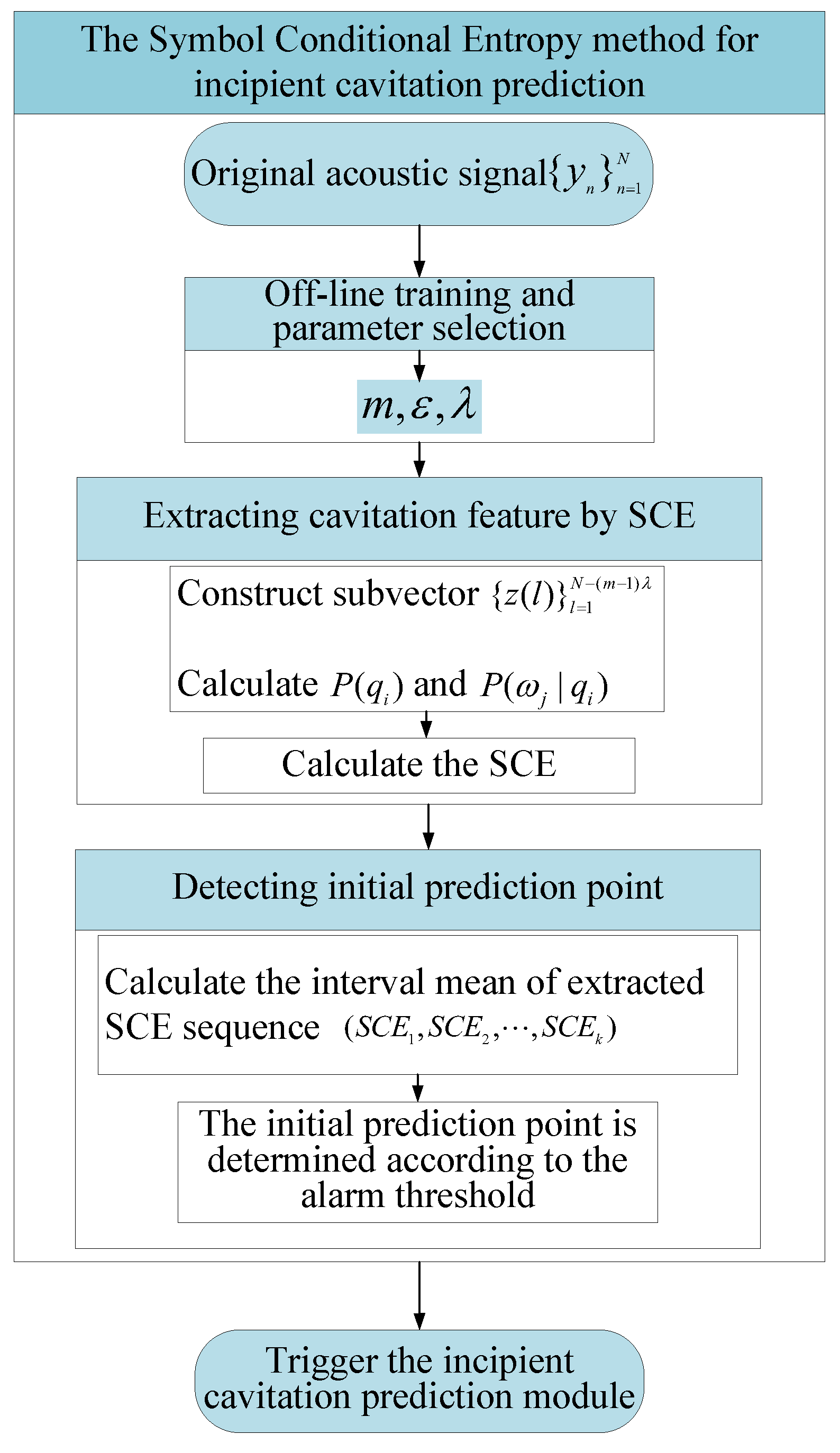
3.1. The SCE Method for Cavitation Feature Extraction
3.2. The IM Algorithm for Initial Prediction Point Detection
3.3. Incipient Cavitation Prediction
| Algorithm 1 Feature extraction using SCE. |
|
4. Experimental Results and Analysis
4.1. Data Description
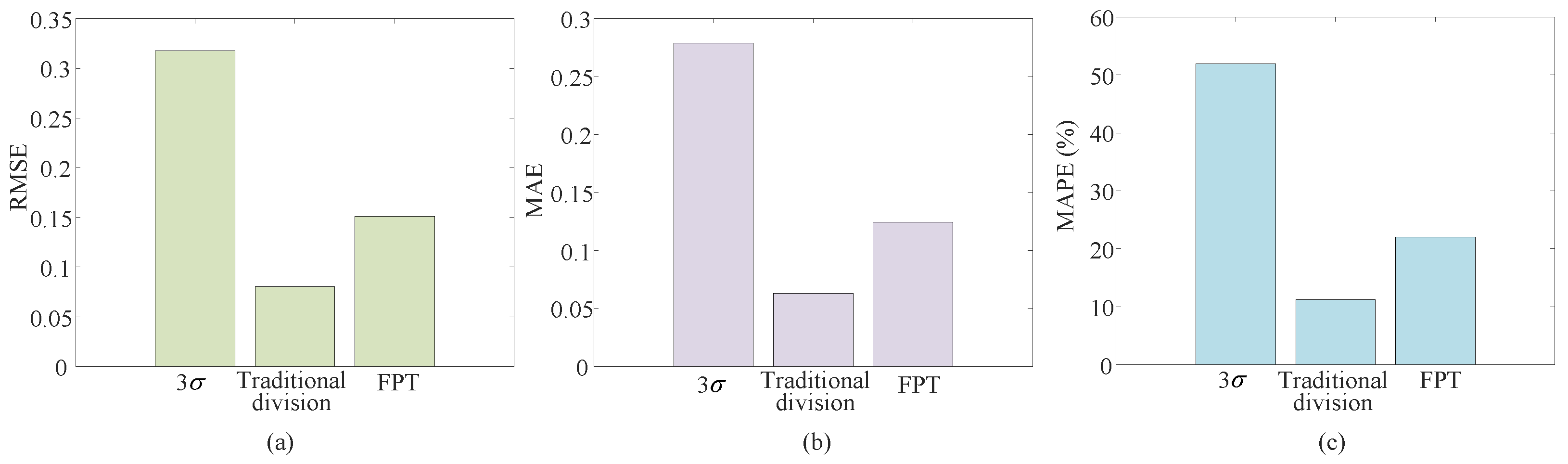
4.2. The Performance Evaluation of the SCE
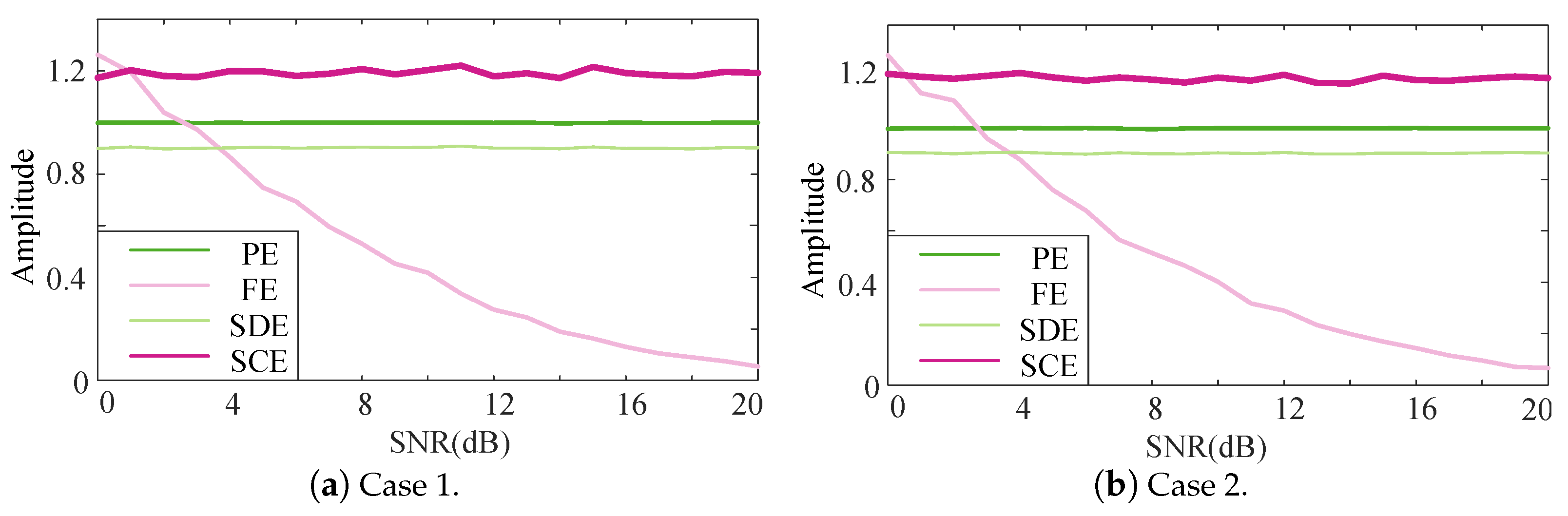
4.2.1. Robustness Test
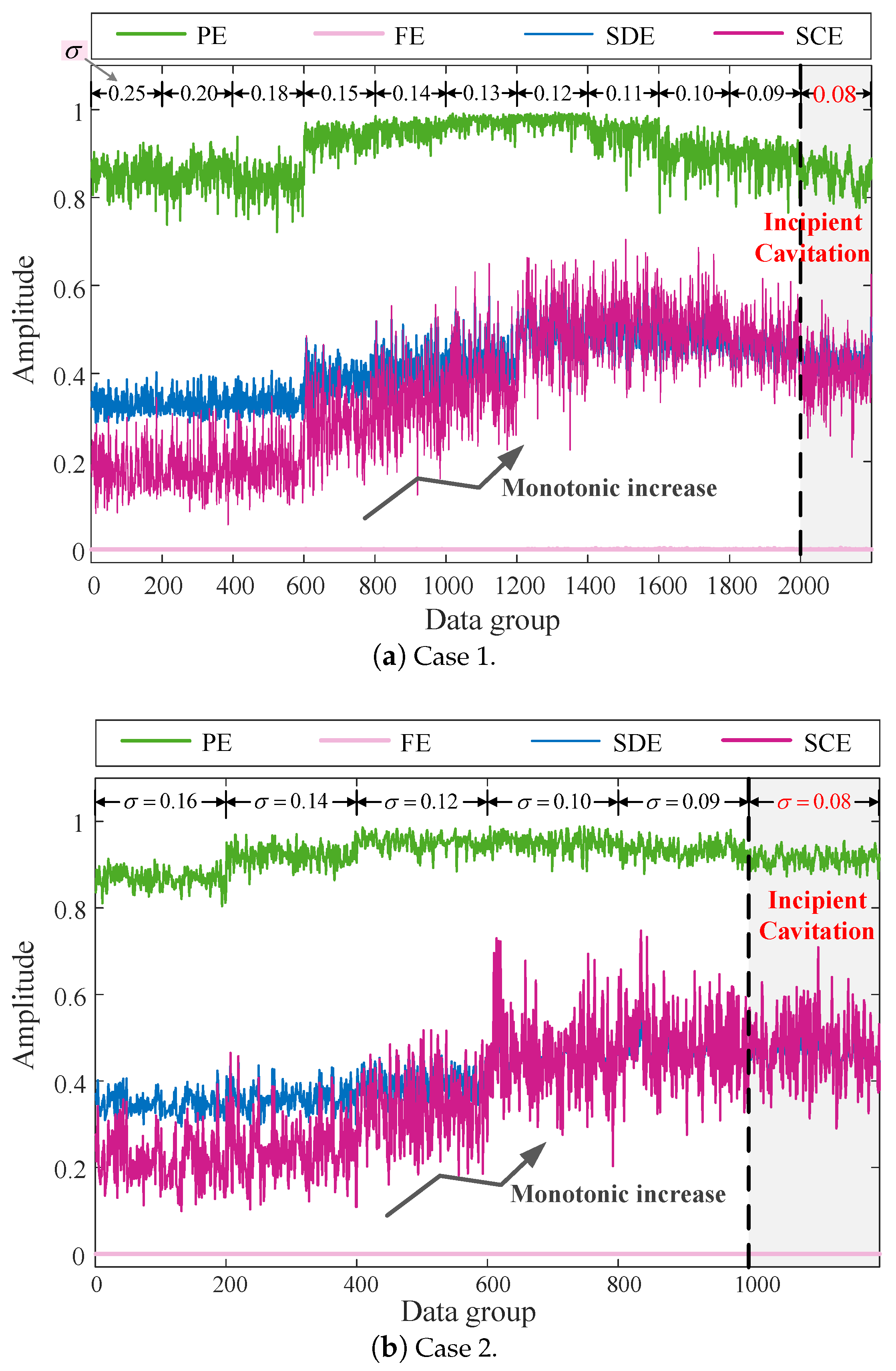
4.2.2. Monotonicity Test
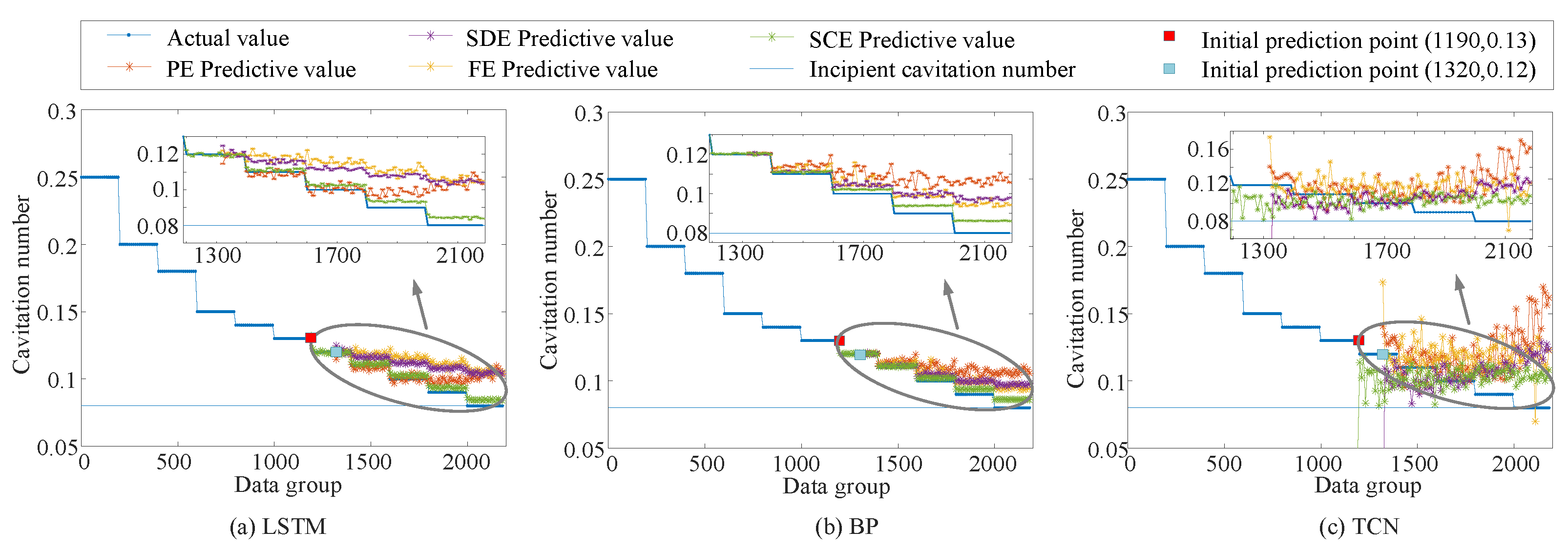
4.3. The Comparison Results of Incipient Cavitation Prediction
5. Conclusions and Perspectives
- (1)
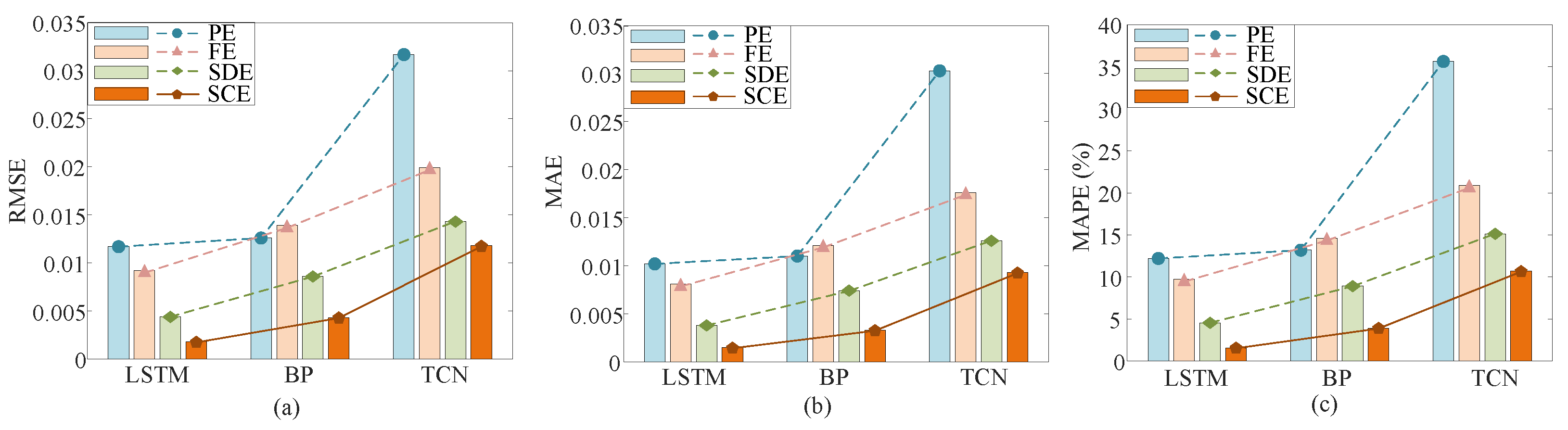
- By classifying state patterns, the SCE method can reduce the uncertainty of information and increase the information gain of the hydroacoustic signal. The prediction performance has been enhanced due to the improved capability to extract cavitation features from complex and nonlinear time series. The RMSE, MAE, and MAPE of the proposed SCE decreased by 84.62%, 85.29%, and 87% compared with the PE method.
- (2)
- The SCE is used to extract cavitation features from real-time signals effectively, and the initial prediction point is determined using the IM algorithm for trend prediction. The detection of the initial prediction point can focus on cavitation information, which is useful for predicting the evolution trend. The prediction accuracy is improved consequently.
- (3)
- The proposed SCE is used to predict the incipient cavitation of the hydroacoustic signal collected from a hydraulic turbine test bench. The results show that the proposed method is superior to other used entropy algorithms in fitting the distribution of real feature points and predicting accuracy with different prediction algorithms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCE | Symbol Conditional Entropy |
| IM | Interval mean |
| PE | Permutation Entropy |
| FE | Fuzzy Entropy |
| SDE | Symbol Dynamic Entropy |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MEP | Maximum entropy partitioning |
| ED | Euclidean Distance |
| LSTM | Long Short-Term Memory |
| BP | Back Propagation |
| TCN | Temporal Convolutional Network |
References
- Zhou, T.; Kao, S.C.; Xu, W.; Gangrade, S.; Voisin, N. Impacts of climate change on subannual hydropower generation: A multi-model assessment of the United States federal hydropower plant. Environ. Res. Lett. 2023, 18, 034009. [Google Scholar] [CrossRef]
- Kumar, K.; Saini, R.P. A review on operation and maintenance of hydropower plants. Sustain. Energy Technol. Assess. 2022, 49, 101704. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Y.; Tang, Q.; Cai, J.; Zhao, L.; Ge, X. Energy analysis of Francis turbine for various mass flow rate conditions based on entropy production theory. Renew. Energy 2022, 183, 447–458. [Google Scholar] [CrossRef]
- Feng, J.; Zhao, N.; Zhu, G.; Wu, G.; Li, Y.; Luo, X. Cavitation identification in a hydraulic bulb turbine based on vibration and pressure fluctuation measurements. Mech. Syst. Signal Process. 2024, 208, 111042. [Google Scholar] [CrossRef]
- Kadivar, E.; Timoshevskiy, M.V.; Nichik, M.Y.; el Moctar, O.; Schellin, T.E.; Pervunin, K.S. Control of unsteady partial cavitation and cloud cavitation in marine engineering and hydraulic systems. Phys. Fluids 2020, 32, 052108. [Google Scholar] [CrossRef]
- Murovec, J.; Curovic, L.; Novakovic, T.; Prezelj, J. Psychoacoustic approach for cavitation detection in centrifugal pumps. Appl. Acoust. 2020, 165, 107323. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, J.; Chen, B.; Cheng, X.; Yang, J. Fluid cavitation detection method with phase demodulation of ultrasonic signal. Appl. Acoust. 2015, 87, 198–204. [Google Scholar] [CrossRef]
- Firly, R.; Inaba, K.; Triawan, F.; Kishimoto, K.; Hayabusa, K.; Nakamoto, H. Numerical prediction of cavitation damage based on shock-induced single bubble collapse near solid surfaces. Eur. J. Mech. B-Fluids 2023, 98, 143–160. [Google Scholar] [CrossRef]
- Favrel, A.; Pereira Junior, J.G.; Landry, C.; Mueller, A.; Yamaishi, K.; Avellan, F. Dynamic modal analysis during reduced scale model tests of hydraulic turbines for hydro-acoustic characterization of cavitation flows. Mech. Syst. Signal Process. 2019, 117, 81–96. [Google Scholar] [CrossRef]
- Mousmoulis, G.; Yiakopoulos, C.; Aggidis, G.; Antoniadis, I.; Anagnostopoulos, I. Application of Spectral Kurtosis on vibration signals for the detection of cavitation in centrifugal pumps. Appl. Acoust. 2021, 182, 108289. [Google Scholar] [CrossRef]
- Kan, K.; Binama, M.; Chen, H.; Zheng, Y.; Zhou, D.; Su, W.; Muhirwa, A. Pump as turbine cavitation performance for both conventional and reverse operating modes: A review. Renew. Sustain. Energy Rev. 2022, 168, 112786. [Google Scholar] [CrossRef]
- Tiwari, G.; Kumar, J.; Prasad, V.; Patel, V.K. Utility of CFD in the design and performance analysis of hydraulic turbines—A review. Energy Rep. 2020, 6, 2410–2429. [Google Scholar] [CrossRef]
- Karaalioglu, M.S.; Bal, S. Performance prediction of cavitating marine current turbine by BEMT based on CFD. Ocean. Eng. 2022, 255, 111221. [Google Scholar] [CrossRef]
- Brijkishore; Khare, R.; Prasad, V. Prediction of cavitation and its mitigation techniques in hydraulic turbines—A review. Ocean. Eng. 2021, 221, 108512. [Google Scholar] [CrossRef]
- Sun, H.; Si, Q.; Chen, N.; Yuan, S. HHT-based feature extraction of pump operation instability under cavitation conditions through motor current signal analysis. Mech. Syst. Signal Process. 2020, 139, 106613. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, D.; Tao, R.; Xiao, R.; Liu, W. Analysis of two-phase flow in cavitation condition of pump-turbine based on dynamic mode decomposition method in turbine mode. J. Energy Storage 2022, 56, 106107. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Tang, S.; Wang, R.; Su, H.; Wang, C. Acoustic signal-based fault detection of hydraulic piston pump using a particle swarm optimization enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]
- Sha, Y.; Faber, J.; Gou, S.; Liu, B.; Li, W.; Schramm, S.; Stoecker, H.; Steckenreiter, T.; Vnucec, D.; Wetzstein, N.; et al. A multi-task learning for cavitation detection and cavitation intensity recognition of valve acoustic signals. Eng. Appl. Artif. Intell. 2022, 113, 104904. [Google Scholar] [CrossRef]
- Kang, Z.; Feng, C.; Liu, Z.; Cang, Y.; Gao, S. Analysis of the incipient cavitation noise signal characteristics of hydroturbine. Appl. Acoust. 2017, 127, 118–125. [Google Scholar] [CrossRef]
- Feng, J.; Men, Y.; Zhu, G.; Li, Y.; Luo, X. Cavitation detection in a Kaplan turbine based on multifractal detrended fluctuation analysis of vibration signals. Ocean. Eng. 2022, 263, 112232. [Google Scholar] [CrossRef]
- Feng, J.; Liu, B.; Luo, X.; Zhu, G.; Li, K.; Wu, G. Experimental investigation on characteristics of cavitation-induced vibration on the runner of a bulb turbine. Mech. Syst. Signal Process. 2023, 189, 110097. [Google Scholar] [CrossRef]
- Yang, C.; Gabbouj, M.; Jia, M.; Li, Z. Hierarchical Symbol Transition Entropy: A Novel Feature Extractor for Machinery Health Monitoring. IEEE Trans. Ind. Inform. 2022, 18, 6131–6141. [Google Scholar] [CrossRef]
- Huo, Z.; Martinez-Garcia, M.; Zhang, Y.; Yan, R.; Shu, L. Entropy Measures in Machine Fault Diagnosis: Insights and Applications. IEEE Trans. Instrum. Meas. 2020, 69, 2607–2620. [Google Scholar] [CrossRef]
- Yang, C.; Jia, M. Hierarchical multiscale permutation entropy-based feature extraction and fuzzy support tensor machine with pinball loss for bearing fault identification. Mech. Syst. Signal Process. 2021, 149, 107182. [Google Scholar] [CrossRef]
- Minhas, A.S.; Singh, G.; Singh, J.; Kankar, P.K.; Singh, S. A novel method to classify bearing faults by integrating standard deviation to refined composite multi-scale fuzzy entropy. Measurement 2020, 154, 107441. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Z.; Cui, H.; Wang, C. MMC-HVDC grids transmission line protection method: Based on permutation entropy algorithm. Int. J. Electr. Power Energy Syst. 2024, 162, 110296. [Google Scholar] [CrossRef]
- Saravanan, B.; Mohanraj, V.; Senthilkumar, J. A fuzzy entropy technique for dimensionality reduction in recommender systems using deep learning. Soft Comput. 2019, 23, 2575–2583. [Google Scholar] [CrossRef]
- Hou, S.; Zheng, J.; Pan, H.; Feng, K.; Liu, Q.; Ni, Q. Multivariate multi-scale cross-fuzzy entropy and SSA-SVM-based fault diagnosis method of gearbox. Meas. Sci. Technol. 2024, 35, 056102. [Google Scholar] [CrossRef]
- Zhou, X.; Yuan, R.; Lv, Y.; Li, B.; Fu, S.; Li, H. Hierarchical Multiscale Fluctuation-Based Symbolic Fuzzy Entropy: A Novel Tensor Health Indicator for Mechanical Fault Diagnosis. IEEE Sens. J. 2025, 25, 5013–5030. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Yang, C.; Jia, M.; Li, Z.; Gabbouj, M. Enhanced hierarchical symbolic dynamic entropy and maximum mean and covariance discrepancy-based transfer joint matching with Welsh loss for intelligent cross-domain bearing health monitoring. Mech. Syst. Signal Process. 2022, 165, 108343. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, T.; Li, Y.; Pan, E. A hybrid prognostic method based on gated recurrent unit network and an adaptive Wiener process model considering measurement errors. Mech. Syst. Signal Process. 2021, 158, 107785. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Sang, L.; Xu, Y.; Long, H.; Hu, Q.; Sun, H. Electricity Price Prediction for Energy Storage System Arbitrage: A Decision-Focused Approach. IEEE Trans. Smart Grid 2022, 13, 2822–2832. [Google Scholar] [CrossRef]
- Li, N.; Xu, P.; Lei, Y.; Cai, X.; Kong, D. A self-data-driven method for remaining useful life prediction of wind turbines considering continuously varying speeds. Mech. Syst. Signal Process. 2022, 165, 108315. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, C.; Cheng, B. Butterfly valve erosion prediction based on LSTM network. Flow Meas. Instrum. 2024, 98, 102652. [Google Scholar] [CrossRef]
- Wu, Y.; Tao, R.; Zhu, D.; Xiao, R. Analysis and prediction of force characteristics of tubular turbine based on Hankel-DMD-LSTM. Eng. Appl. Comput. Fluid Mech. 2025, 19, 2443122. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, J.; Yang, F.; Zhu, Q.; Zuo, M. Optimization design of centrifugal pump cavitation performance based on the improved BP neural network algorithm. Measurement 2025, 245, 116553. [Google Scholar] [CrossRef]
- Zhao, Z.; Lin, W. Short-term electric load forecasting based on empirical wavelet transform and temporal convolutional network. IET Gener. Transm. Distrib. 2024, 18, 1672–1683. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, L.; Wei, H.; Li, D.; Li, X. A Comparative Study of LSTM and Temporal Convolutional Network Models for Semisubmersible Platform Wave Runup Prediction. J. Offshore Mech. Arct. Eng.-Trans. ASME 2025, 147, 011202. [Google Scholar] [CrossRef]
- Shamsuddeen, M.M.; Park, J.; Choi, Y.S.; Kim, J.H. Unsteady multi-phase cavitation analysis on the effect of anti-cavity fin installed on a Kaplan turbine runner. Renew. Energy 2020, 162, 861–876. [Google Scholar] [CrossRef]
- Ma, C.; Wang, L.; Gao, J.; Cui, Y.; Peng, C.; Zhang, S. Time of arrival estimation for underwater acoustic signal using multi-feature fusion. Appl. Acoust. 2023, 211, 109475. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yan, S.; Shi, W.; Yang, X.; Guo, Y.; Gulliver, T.A. A Novel Underwater Acoustic Signal Denoising Algorithm for Gaussian/Non-Gaussian Impulsive Noise. IEEE Trans. Veh. Technol. 2021, 70, 429–445. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Z.; Li, Y.; Dong, L.; Du, W.; Wang, J.; Zhang, X.; Shi, H. Two-stage prediction technique for rolling bearings based on adaptive prediction model. Mech. Syst. Signal Process. 2024, 206, 110931. [Google Scholar] [CrossRef]
- Rajagopalan, V.; Ray, A. Symbolic time series analysis via wavelet-based partitioning. Signal Process. 2006, 86, 3309–3320. [Google Scholar] [CrossRef]


| Operating Condition | None Cavitation | Incipient Cavitation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 0.250 | 0.200 | 0.180 | 0.150 | 0.140 | 0.130 | 0.120 | 0.110 | 0.100 | 0.09 | 0.08 |
| Case 2 | 0.160 | 0.140 | 0.120 | 0.100 | 0.09 | 0.08 | |||||
| Operating Condition | Methods | |||
|---|---|---|---|---|
| PE | FE | SDE | SCE | |
| Case 1 | 0.9991 | 0.3633 | 0.9976 | 0.9916 |
| Case 2 | 0.9994 | 0.3684 | 0.9975 | 0.9915 |
| Operating Condition | Methods | |||
|---|---|---|---|---|
| PE | FE | SDE | SCE | |
| Case 1 | −0.1075 | 0.00008 | 0.0715 | 0.1690 |
| Case 2 | −0.0713 | 0.00002 | 0.0912 | 0.1910 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
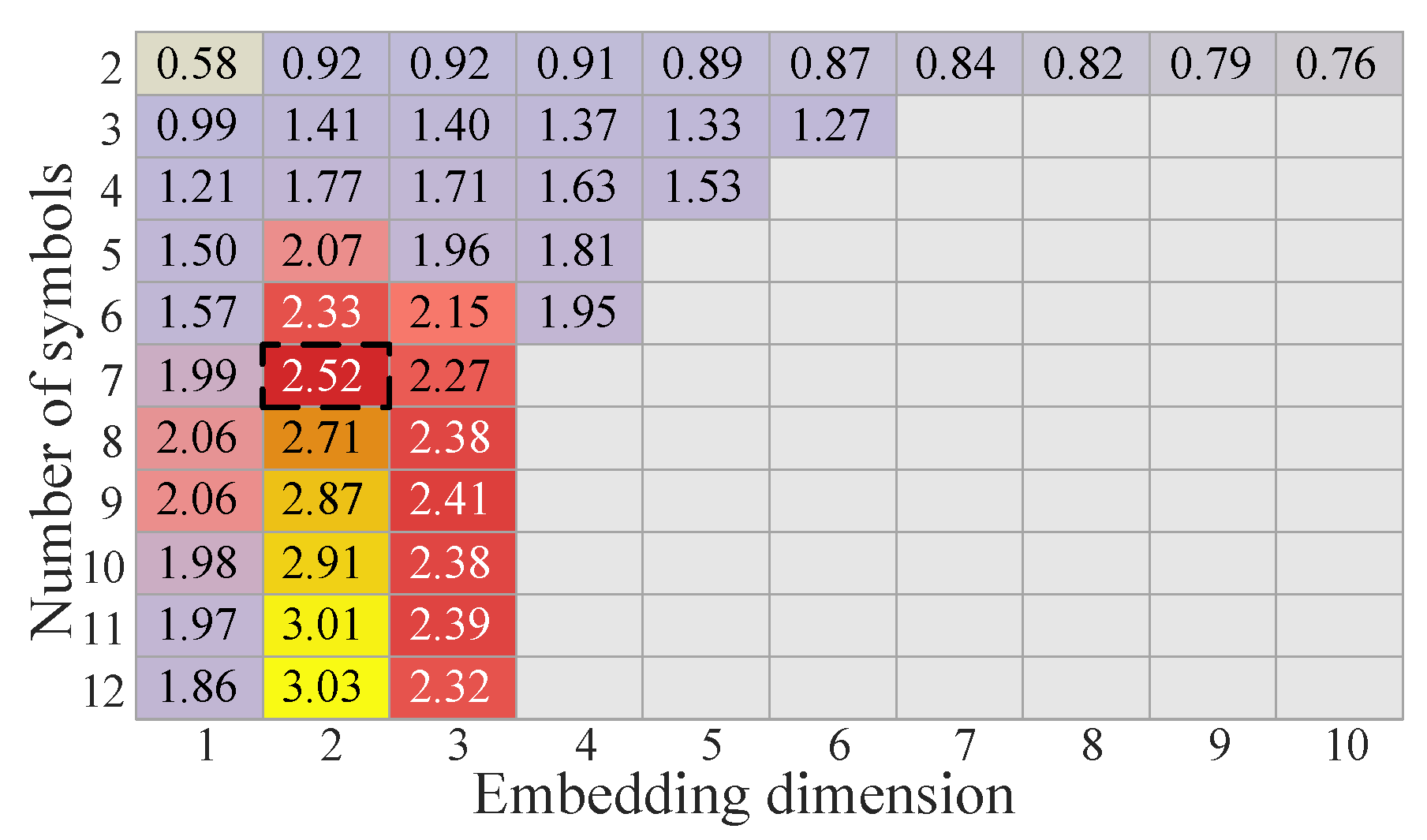
| ED | 2.1544 | 2.1505 | 2.1459 | 2.1476 | 2.1486 | 2.1473 |
| 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|
| Time (s) | 0.2878 | 0.4417 | 0.3729 | 0.9897 | 1.1046 | 1.1453 |
| Parameter | Value |
|---|---|
| 50 | |
| MaxEpochs | 300 |
| LearnRateDropPeriod | 50 |
| Number of LSTM hidden units | 27 |
| Number of TCN numFilters | 128 |
| Number of TCN filterSize | 3 |
| Methods | LSTM | BP | TCN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | |
| PE | 0.0117 | 0.0102 | 12.23 | 0.0126 | 0.0110 | 13.22 | 0.0317 | 0.0303 | 35.67 |
| FE | 0.0092 | 0.0081 | 9.72 | 0.0139 | 0.0121 | 14.61 | 0.0199 | 0.0176 | 20.91 |
| SDE | 0.0044 | 0.0038 | 4.56 | 0.0086 | 0.0074 | 8.92 | 0.0143 | 0.0126 | 15.13 |
| Proposed SCE | 0.0018 | 0.0015 | 1.59 | 0.0043 | 0.0033 | 3.93 | 0.0118 | 0.0093 | 10.69 |
| Methods | LSTM | BP | TCN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | |
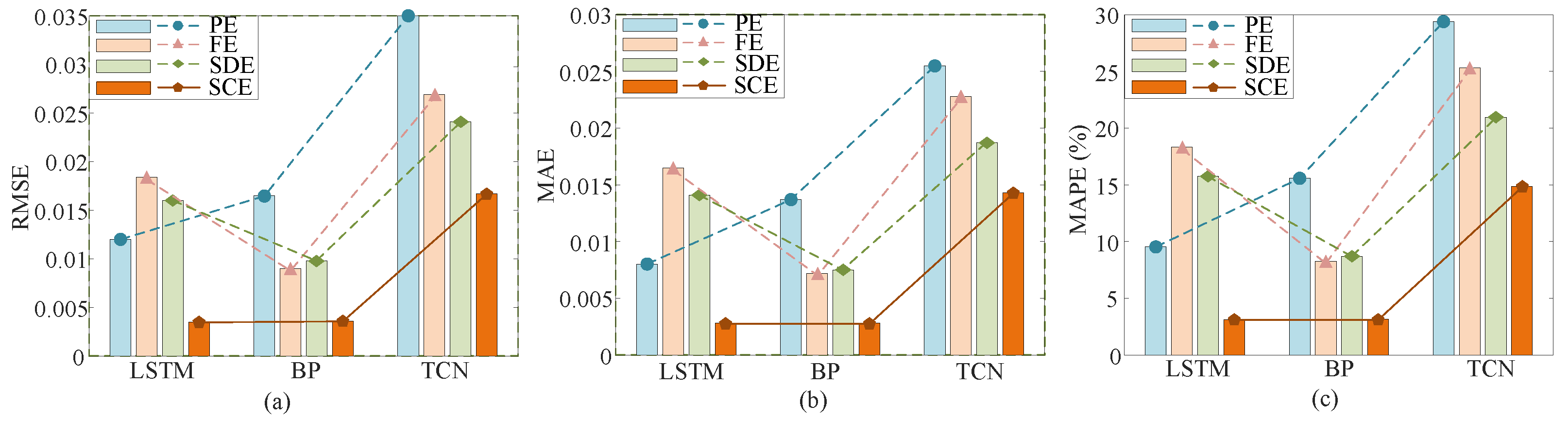
| PE | 0.0120 | 0.0080 | 9.53 | 0.0165 | 0.0137 | 15.57 | 0.0350 | 0.0255 | 29.39 |
| FE | 0.0184 | 0.0165 | 18.34 | 0.0090 | 0.0072 | 8.26 | 0.0269 | 0.0228 | 25.32 |
| SDE | 0.0160 | 0.0141 | 15.78 | 0.0098 | 0.0075 | 8.7 | 0.0241 | 0.0187 | 20.95 |
| Proposed SCE | 0.0035 | 0.0028 | 3.11 | 0.0036 | 0.0028 | 3.16 | 0.0167 | 0.0143 | 14.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, M.; Li, F.; Wang, Y.; Wang, T.; Diallo, D.; Wang, X. A Symbol Conditional Entropy-Based Method for Incipient Cavitation Prediction in Hydraulic Turbines. J. Mar. Sci. Eng. 2025, 13, 538. https://doi.org/10.3390/jmse13030538
Lv M, Li F, Wang Y, Wang T, Diallo D, Wang X. A Symbol Conditional Entropy-Based Method for Incipient Cavitation Prediction in Hydraulic Turbines. Journal of Marine Science and Engineering. 2025; 13(3):538. https://doi.org/10.3390/jmse13030538
Chicago/Turabian StyleLv, Mengge, Feng Li, Yi Wang, Tianzhen Wang, Demba Diallo, and Xiaohang Wang. 2025. "A Symbol Conditional Entropy-Based Method for Incipient Cavitation Prediction in Hydraulic Turbines" Journal of Marine Science and Engineering 13, no. 3: 538. https://doi.org/10.3390/jmse13030538
APA StyleLv, M., Li, F., Wang, Y., Wang, T., Diallo, D., & Wang, X. (2025). A Symbol Conditional Entropy-Based Method for Incipient Cavitation Prediction in Hydraulic Turbines. Journal of Marine Science and Engineering, 13(3), 538. https://doi.org/10.3390/jmse13030538








