Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty
Abstract
:1. Introduction
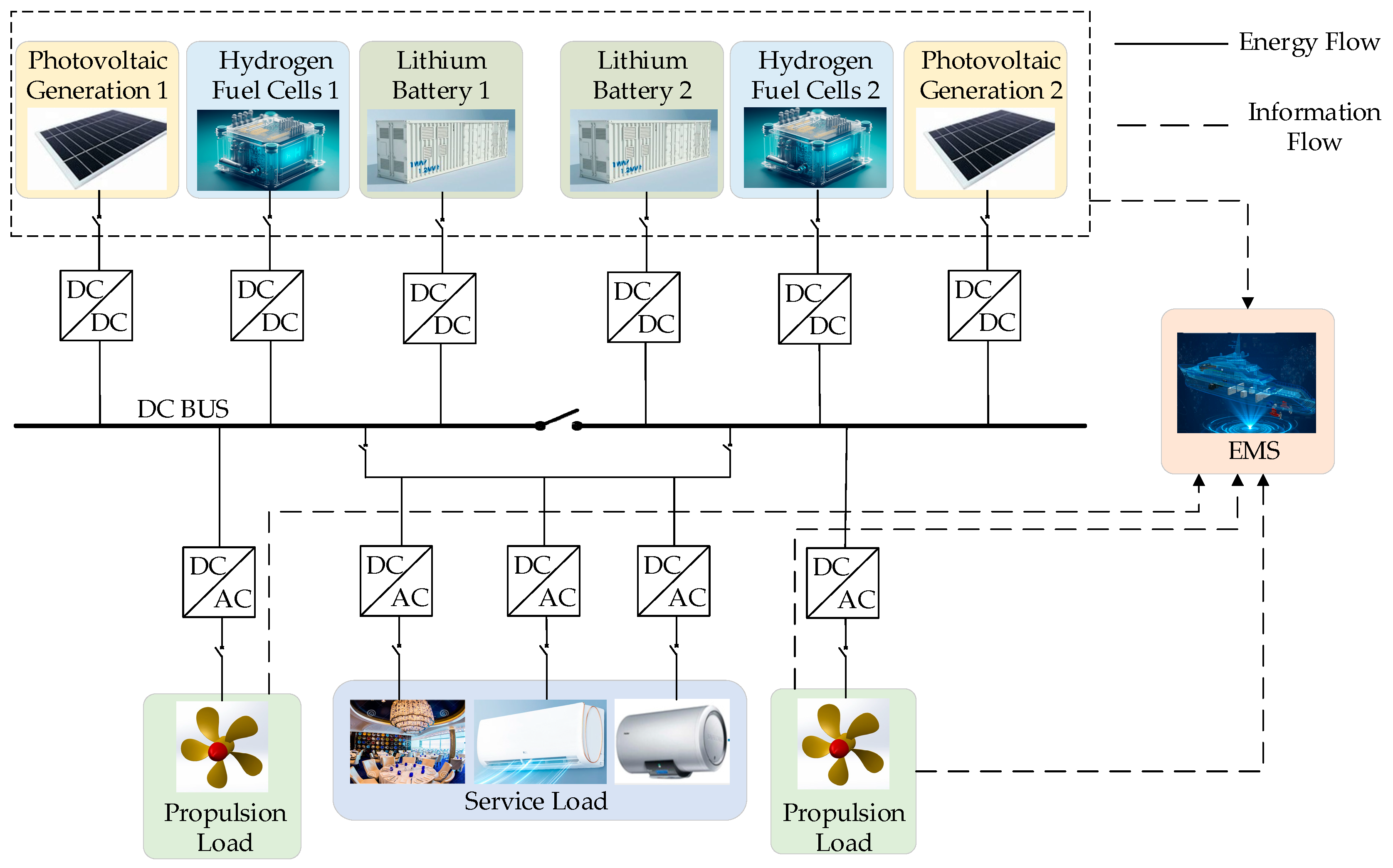
2. Modeling of Hybrid Ship Power System
2.1. Photovoltaic Generation Model
2.2. Hydrogen Fuel Cell Model
2.3. Shipboard Lithium Battery Model
2.4. Propulsion Load Model
2.5. Service Load
3. Optimal Energy Management for Hybrid Ship
3.1. Objective Function
3.2. Constraints
3.2.1. Generation Constraints
- PV generation system limits:
- HFCs limits:
- Shipboard ESS limits:
3.2.2. Voyage Constraints
3.2.3. Power Balance Constraint
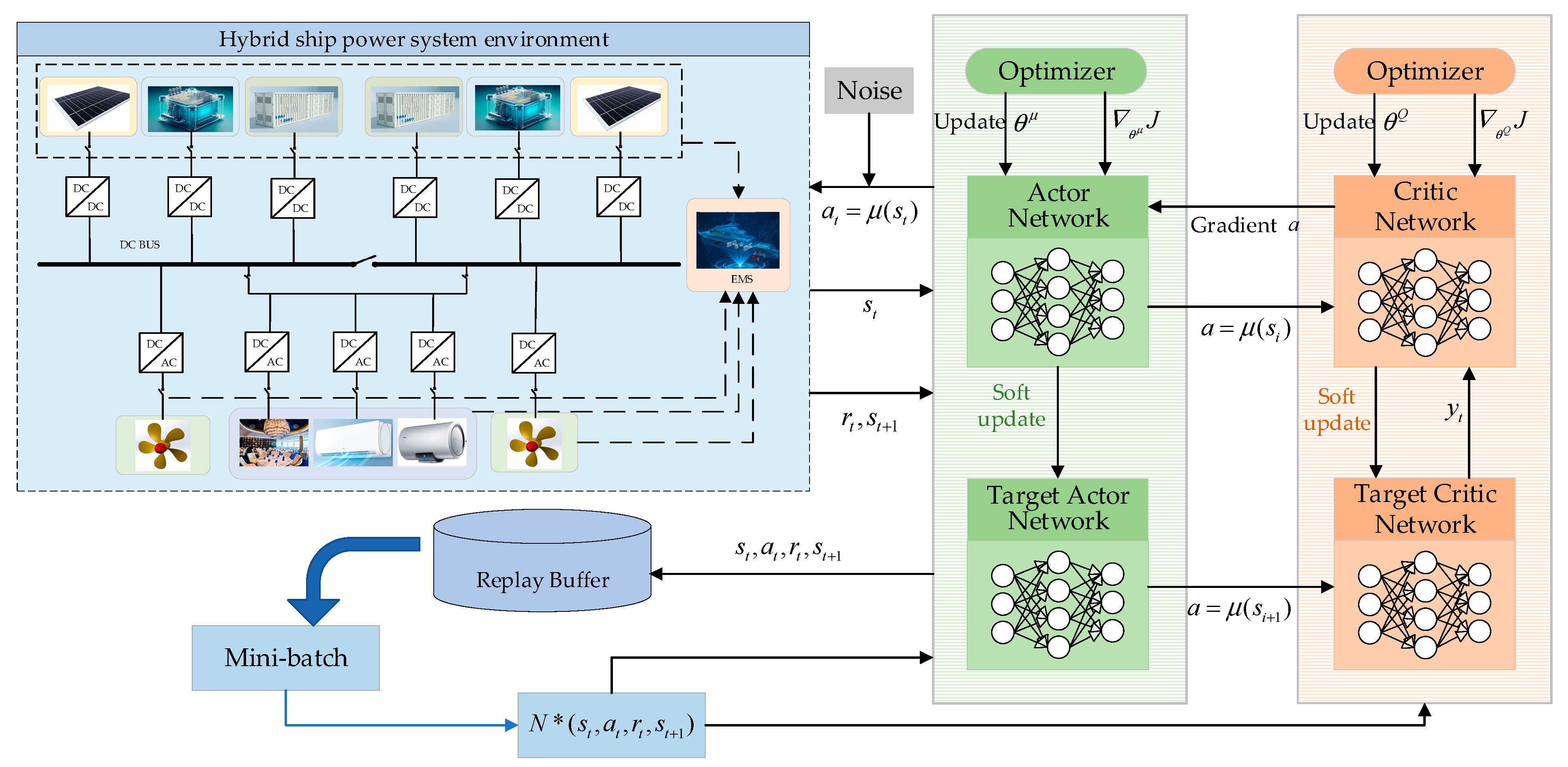
4. DDPG-Algorithm-Based EMS
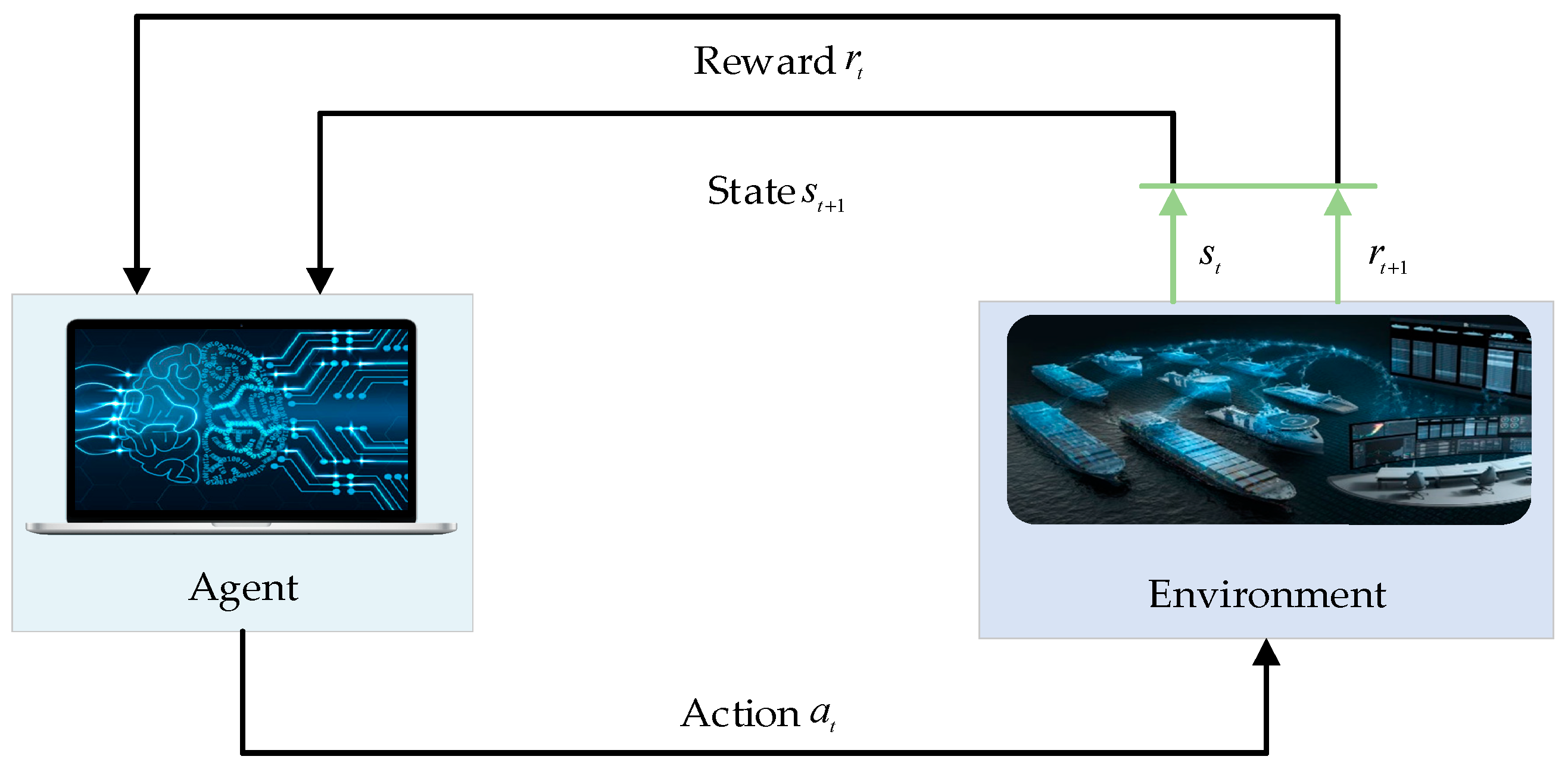
4.1. DDPG Algorithms
4.1.1. State Space Definition
4.1.2. Action Space Definition
4.1.3. Reward Function Definition
5. Results and Discussion
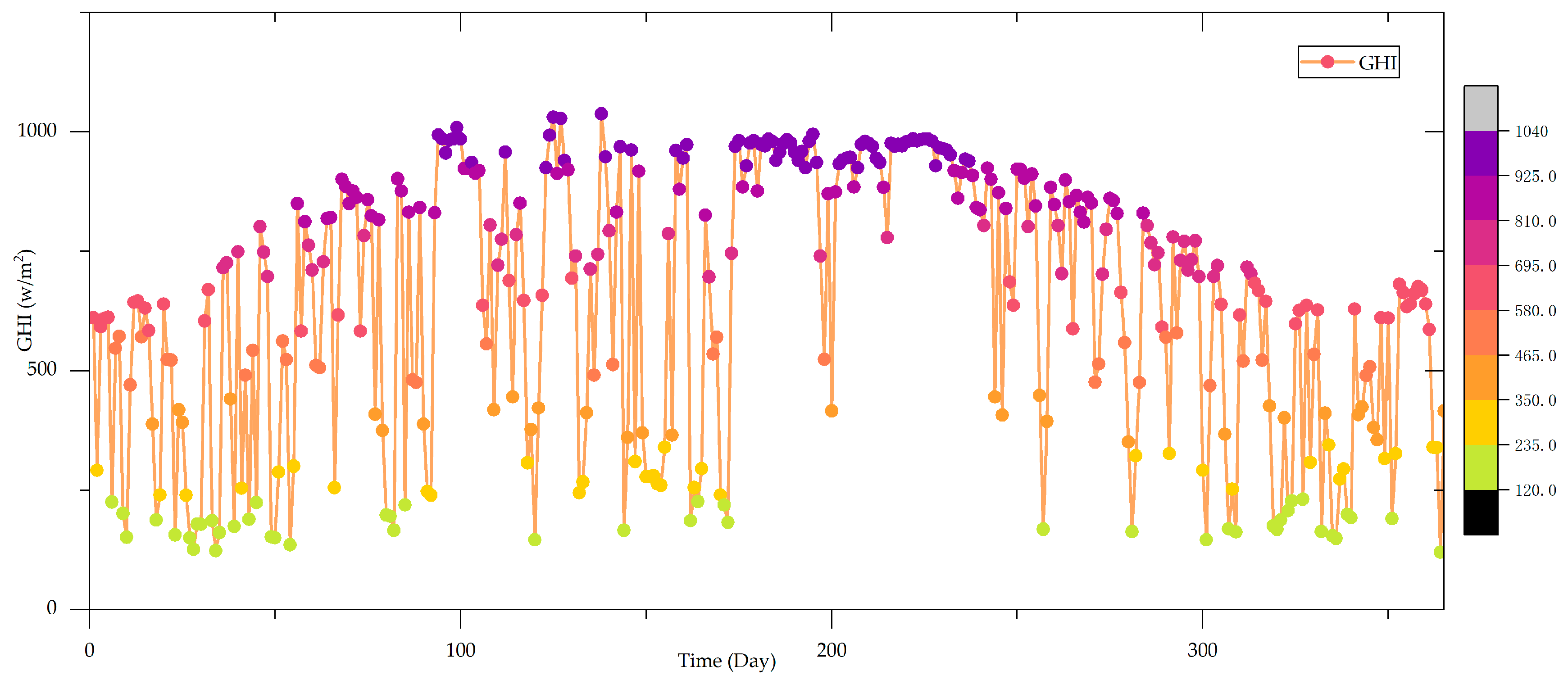
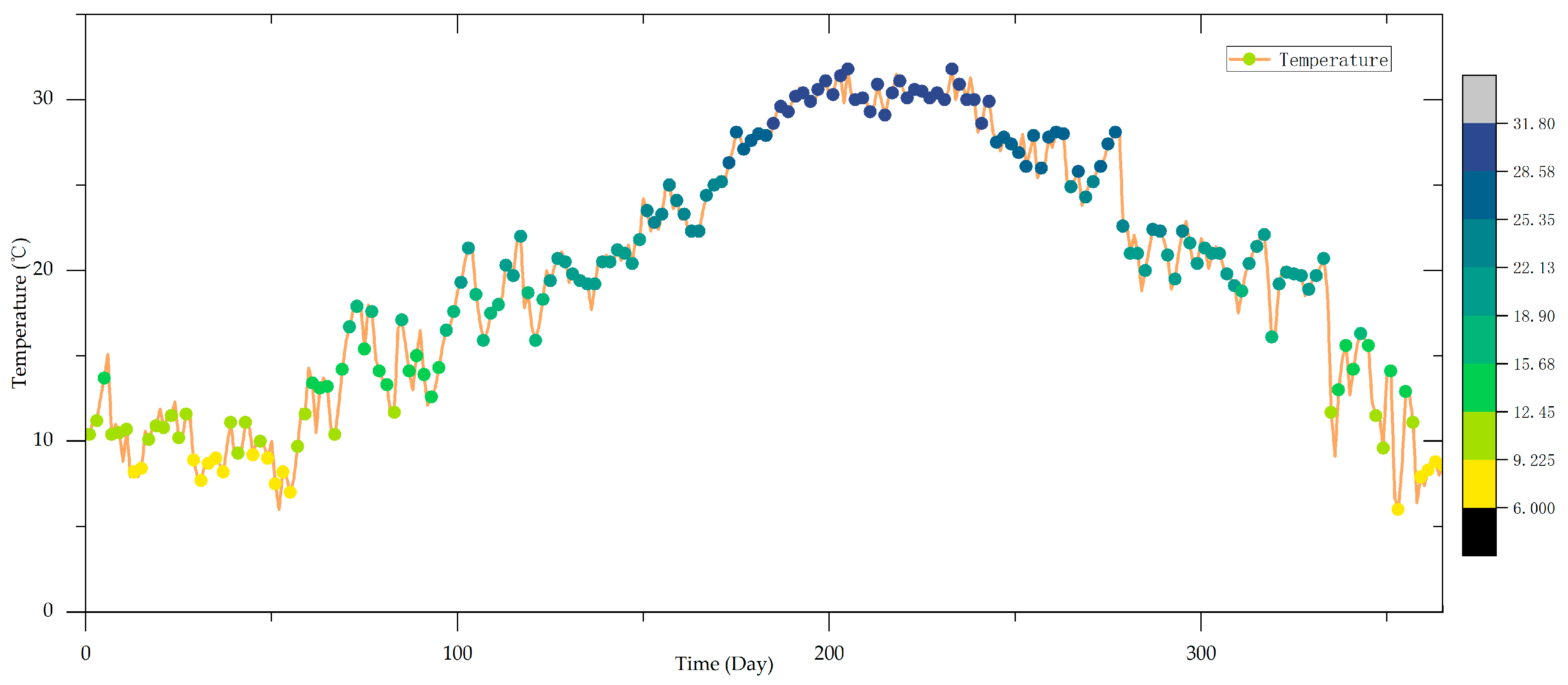
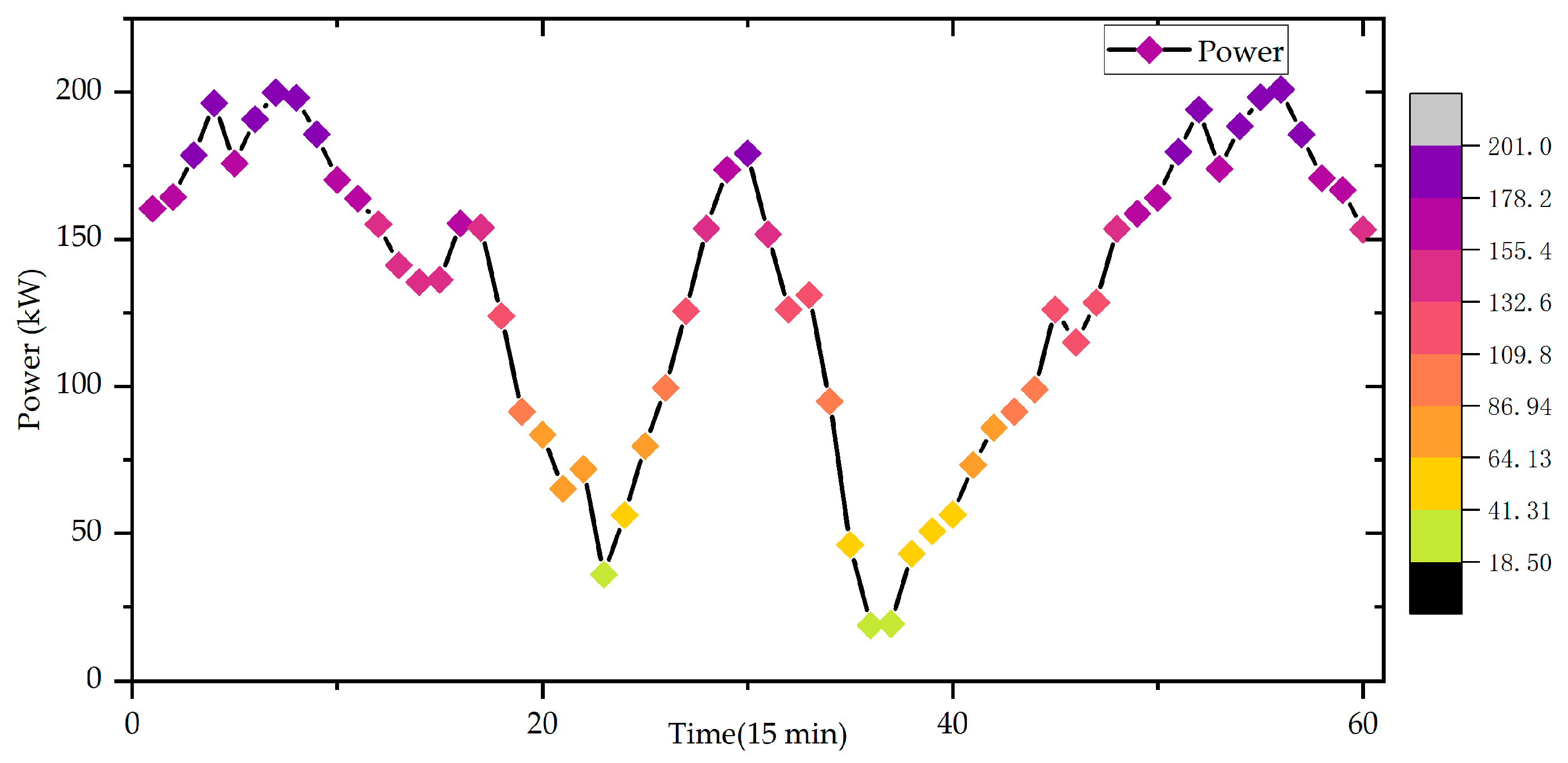
5.1. Data Set
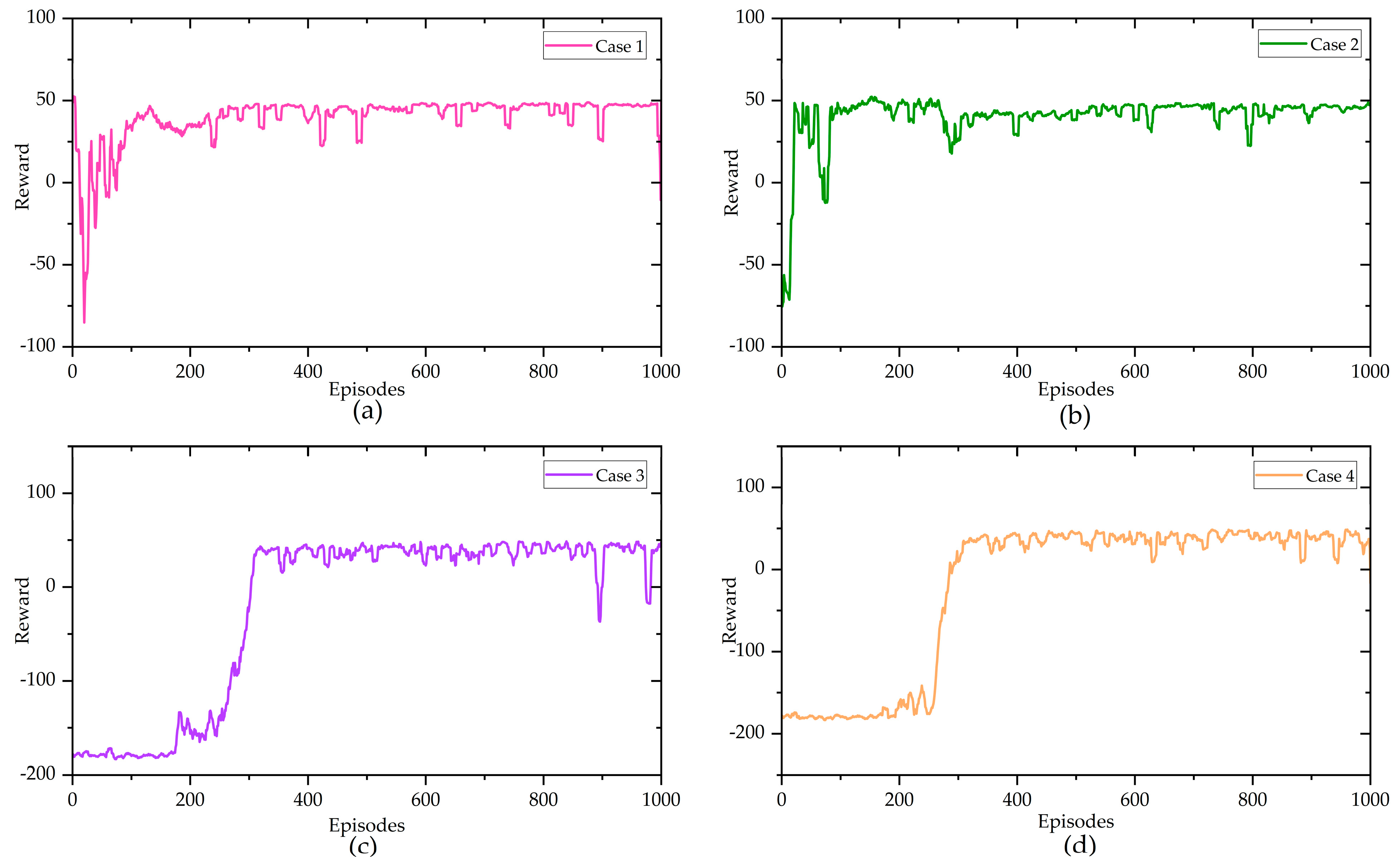
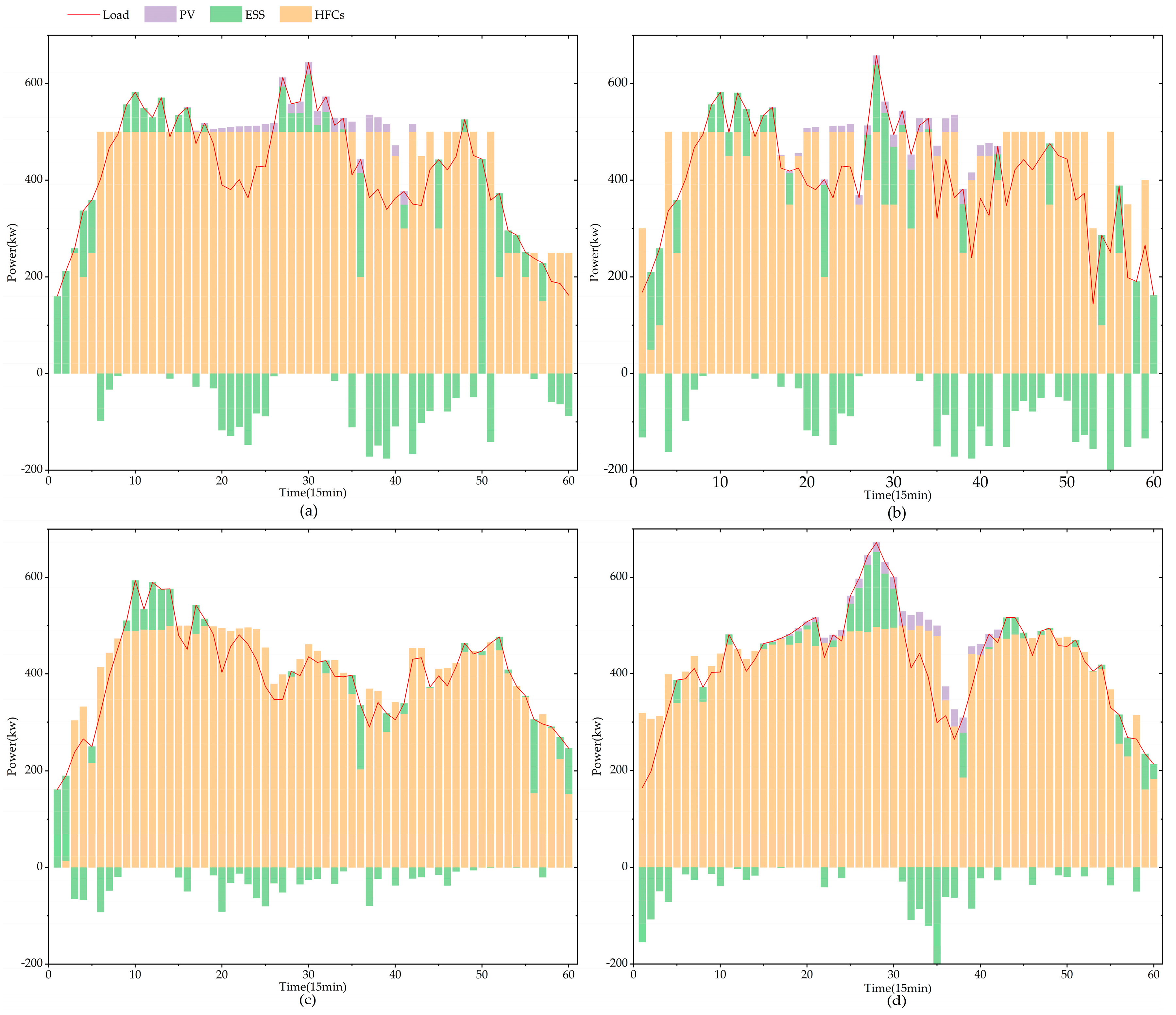
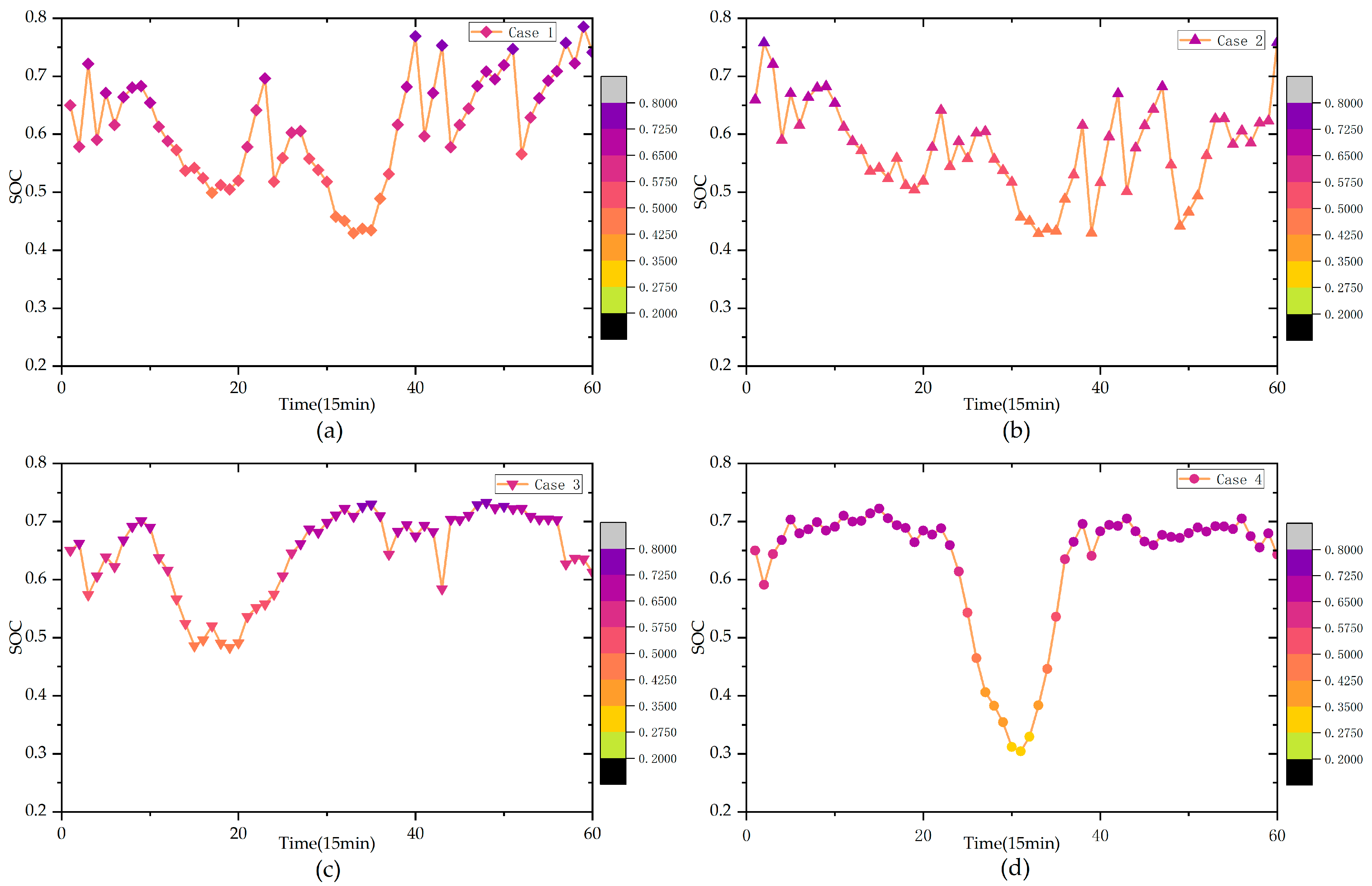
5.2. Case Study
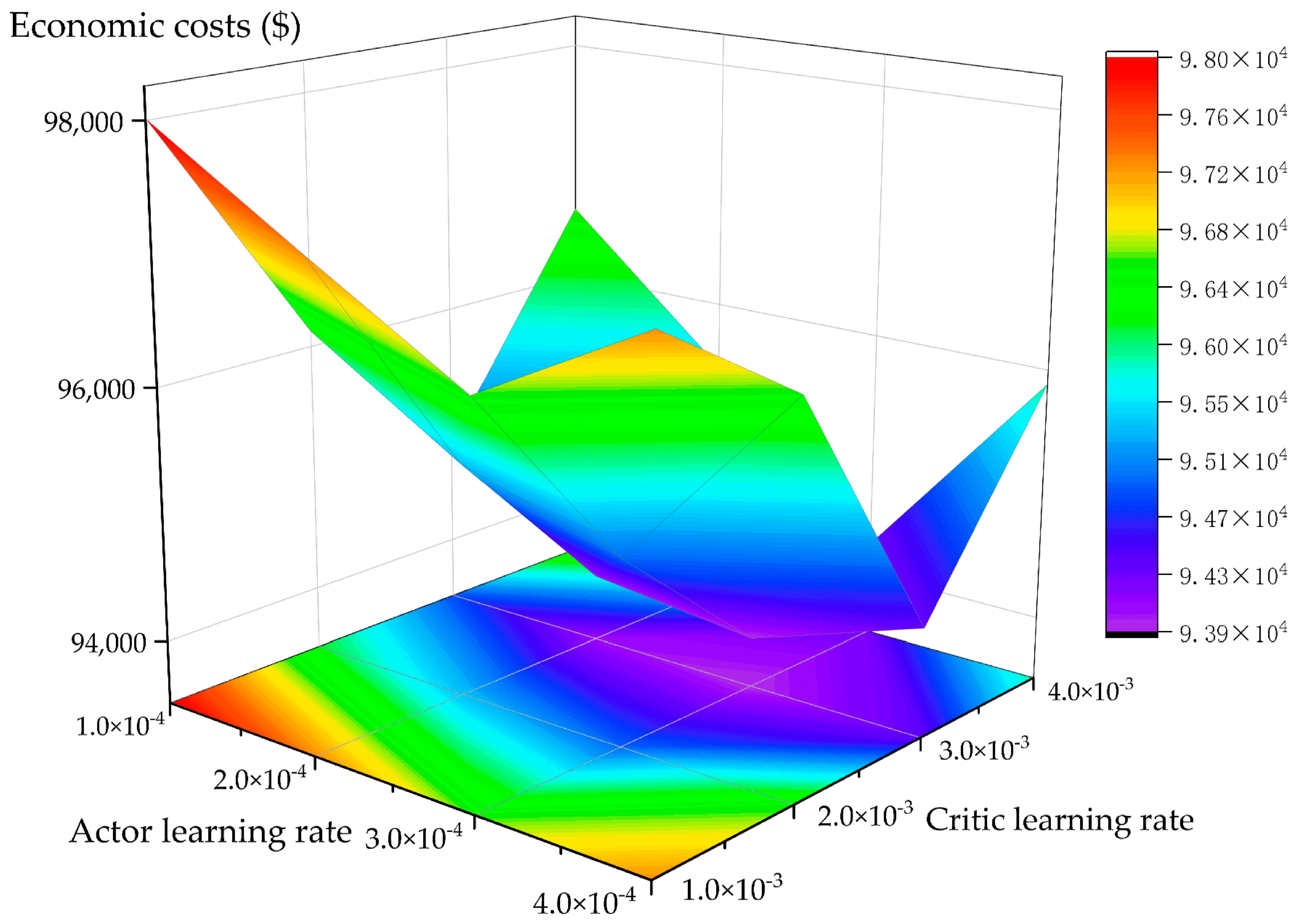
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms: | |
| DDPG | Deep deterministic policy gradient |
| DRL | Deep reinforcement learning |
| DQN | Deep Q network |
| HFCs | Hydrogen fuel cells |
| GHI | Global horizontal irradiance |
| PV | Photovoltaic |
| EMS | Energy management system |
| SOC | State of charge |
| ESS | Energy storage system |
| Parameters: | |
| Time step | |
| Generator efficiency/reference generator efficiency of the shipboard PV system | |
| Efficiency of the maximum power point tracking equipment | |
| Effective area of the PV module | |
| Temperature coefficient of efficiency of the PV system | |
| Reference temperature of the PV system | |
| Diffuse component constant/reflection index/zenith angle | |
| Angle between the panel and the sunlight/tilt angle relative to the horizontal plane | |
| Standard voltage of the HFCs | |
| Gas constant | |
| Faraday constant | |
| Partial pressure of hydrogen/oxygen/water vapor | |
| Empirical coefficients for ohmic loss | |
| Output current and internal resistance of the HFCs | |
| Empirical coefficients for concentration loss of the HFCs | |
| The number of individual cells in an HFC stack | |
| Efficiency of the HFCs | |
| Maximum heating value of hydrogen | |
| Fuel utilization rate | |
| Maximum capacity of the ESS | |
| Charging/discharging efficiency of the ESS | |
| SOC initial value | |
| SOC at time | |
| Propulsion coefficients | |
| Molar mass | |
| Unit price of hydrogen fuel | |
| Maintenance factors of the HFCs/ESS/PV system | |
| Minimum/maximum output power of the PV system | |
| Minimum/maximum total chemical power of the HFCs | |
| Minimum/maximum actual power of the HFCs | |
| Minimum/maximum SOC of the ESS | |
| Minimum/maximum charge/discharge power of the ESS | |
| Maximum SOC deviation | |
| Minimum/maximum speed of the ship | |
| Minimum allowable cruising speed of the ship | |
| Target voyage of the ship at time t | |
| Terminal voyage of the ship | |
| Total voyage of the ship | |
| Maximum allowable voyage variation of the ship | |
| Total economic cost reward/power fluctuation penalty/SOC safety constraint penalty | |
| Penalty coefficients | |
| Discount factor | |
| Actor network | |
| Target actor network | |
| Critic network | |
| Target critic network | |
| Soft update parameter | |
| Parameters of the critic/target critic networks | |
| Parameters of the actor/target actor networks | |
| Parameters of the actor/target networks | |
| Batch size | |
| Gradient | |
| Penalty coefficient of the power balance/safety | |
| Variables: | |
| Output power of the shipboard PV system at time t | |
| Global horizontal irradiance, direct horizontal irradiance and diffuse irradiance at time t | |
| Temperature of the PV system/HFCs at time t | |
| Actual output voltage/open-circuit voltage/activation loss voltage/ohmic loss voltage/concentration loss voltage of the HFCs at time t | |
| Output current of the HFCs at time t | |
| Hydrogen mass flow rate at time t | |
| Total chemical power/actual output power of the HFCs at time t | |
| ESS capacity at time t | |
| SOC at time t | |
| Theoretical charging/discharging power of the ESS at time t | |
| Charging/discharging power of the ESS at time t | |
| Propulsion power demand at time t | |
| Ship speed at time t | |
| Voyage of the ship at time t | |
| Service load at time t | |
| Total load of the ship at time t | |
| Total cost | |
| Cost of the HFCs/ESS and/or the PV system at time t | |
| Cost of hydrogen fuel at time t | |
| Installation cost of the PV system at time t | |
| Maintenance cost of the HFCs/ESS/PV systems at time t | |
| Scaling factor for the HFC load at time t | |
| Installation cost of the ESS/PV systems at time t | |
| Supply/demand of total power at time t | |
| Reward of the DDPG algorithm at time t | |
| Loss function of the critic network at time t | |
| Gradient of the actor network at time t | |
| Loss function of the critic network at time t | |
| State space of the system | |
| Action space of the system | |
| Reward function of the system | |
| Reward of the cost/power balance/safety | |
| Power of the supply/demand at time t |
References
- Soni, G.; Neto, R.C.; Moreira, L. Hydrodynamic Simulation of Green Hydrogen Catamaran Operating in Lisbon, Portugal. J. Mar. Sci. Eng. 2023, 11, 2273. [Google Scholar] [CrossRef]
- Inal, O.B.; Charpentier, J.-F.; Deniz, C. Hybrid Power and Propulsion Systems for Ships: Current Status and Future Challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
- Díaz-Secades, L.A. Enhancement of Maritime Sector Decarbonization through the Integration of Fishing Vessels into IMO Energy Efficiency Measures. J. Mar. Sci. Eng. 2024, 12, 663. [Google Scholar] [CrossRef]
- Magkouris, A.; Belibassakis, K. A Novel BEM for the Hydrodynamic Analysis of Twin-Hull Vessels with Application to Solar Ships. J. Mar. Sci. Eng. 2024, 12, 1776. [Google Scholar] [CrossRef]
- Lu, F.; Tian, Y.; Liu, H.; Ling, C. Distributionally Robust Optimal Scheduling of Hybrid Ship Microgrids Considering Uncertain Wind and Wave Conditions. J. Mar. Sci. Eng. 2024, 12, 2087. [Google Scholar] [CrossRef]
- Balsamo, F.; Capasso, C.; Lauria, D.; Veneri, O. Optimal Design and Energy Management of Hybrid Storage Systems for Marine Propulsion Applications. Appl. Energy 2020, 278, 115629. [Google Scholar] [CrossRef]
- Dawoud, S.M.; Selim, F.; Lin, X.; Zaky, A.A. Techno-Economic and Sensitivity Investigation of a Novel Perovskite Solar Cells Based High Efficient Hybrid Electric Sources for Off-Shore Oil Ships. IEEE Access 2023, 11, 41635–41643. [Google Scholar] [CrossRef]
- Wu, C.-H.; Wang, H.-C.; Chang, H.-Y. Greenhouse Gas Emissions Reduction and Energy Savings for a Dredger at Port Area Using Hybrid Photovoltaic Power System Onboard. Energy Sustain. Dev. 2024, 78, 101354. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, L. A Probabilistic Multi-Objective Design Method of Sail-Photovoltaic-Hybrid Power System for an Unmanned Ocean Surveillance Trimaran. Appl. Energy 2023, 350, 121604. [Google Scholar] [CrossRef]
- A Hybrid Ensemble Model for Interval Prediction of Solar Power Output in Ship Onboard Power Systems. Available online: https://ieeexplore.ieee.org/abstract/document/8946708 (accessed on 25 December 2024).
- Gaber, M.; Hamad, M.S.; El-banna, S.H.; El-Dabah, M. An intelligent energy management system for ship hybrid power system based on renewable energy resources. J. Al-Azhar Univ. Eng. Sect. 2021, 16, 712–723. [Google Scholar] [CrossRef]
- Tang, R.; Li, X.; Lai, J. A Novel Optimal Energy-Management Strategy for a Maritime Hybrid Energy System Based on Large-Scale Global Optimization. Appl. Energy 2018, 228, 254–264. [Google Scholar] [CrossRef]
- Maaruf, M.; Khalid, M. Hybrid Solar/PEM Fuel Cell/and Water Electrolyzer Energy System for All-Electric Ship. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022; pp. 1–5. [Google Scholar]
- Study and Analysis of a Solar Electric Boat with Dynamic Design Strategy in Efficient Way by Tawheed Hasan, Shahrizan Jamaludin, WB Wan Nik, Mehedi Hasan Rajib: SSRN. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4446339 (accessed on 25 December 2024).
- Abdelrahman, M.S.; Hussein, H.; Mohammed, O.A. Rule-Based Power and Energy Management System for Shipboard Microgrid with HESS to Mitigate Propulsion and Pulsed Load Fluctuations. In Proceedings of the 2023 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 19–21 April 2023; pp. 224–228. [Google Scholar]
- Song, T.; Fu, L.; Zhong, L.; Fan, Y.; Shang, Q. HP3O Algorithm-Based All Electric Ship Energy Management Strategy Integrating Demand-Side Adjustment. Energy 2024, 295, 130968. [Google Scholar] [CrossRef]
- Yiğit, K.; Acarkan, B. A New Ship Energy Management Algorithm to the Smart Electricity Grid System. Int. J. Energy Res. 2018, 42, 2741–2756. [Google Scholar] [CrossRef]
- Hein, K. Emission-Aware and Data-Driven Many-Objective Voyage and Energy Management Optimization of Solar-Integrated All-Electric Ship. Electr. Power Syst. Res. 2022, 213, 108718. [Google Scholar] [CrossRef]
- Identifying Hybrid Renewable Energy Power Management and Speed Control on Catamaran Ship|IEEE Conference Publication|IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/10335546 (accessed on 27 December 2024).
- Fang, S.; Xu, Y.; Wen, S.; Zhao, T.; Wang, H.; Liu, L. Data-Driven Robust Coordination of Generation and Demand-Side in Photovoltaic Integrated All-Electric Ship Microgrids. IEEE Trans. Power Syst. 2020, 35, 1783–1795. [Google Scholar] [CrossRef]
- Igder, M.A.; Rafiei, M.; Boudjadar, J.; Khooban, M.-H. Reliability and Safety Improvement of Emission-Free Ships: Systemic Reliability-Centered Maintenance. IEEE Trans. Transp. Electrif. 2021, 7, 256–266. [Google Scholar] [CrossRef]
- Wen, S.; Zhao, T.; Tang, Y.; Xu, Y.; Zhu, M.; Huang, Y. A Joint Photovoltaic-Dependent Navigation Routing and Energy Storage System Sizing Scheme for More Efficient All-Electric Ships. IEEE Trans. Transp. Electrif. 2020, 6, 1279–1289. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ölçer, A.I.; Vakili, S. The Application of Hybrid Energy System (Hydrogen Fuel Cell, Wind, and Solar) in Shipping. Renew. Energy Focus 2023, 46, 197–206. [Google Scholar] [CrossRef]
- Comparative Study Based on Techno-Economics Analysis of Different Shipboard Microgrid Systems Comprising PV/Wind/Fuel Cell/Battery/Diesel Generator with Two Battery Technologies: A Step toward Green Maritime Transportation—ScienceDirect. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0960148123015859 (accessed on 27 December 2024).
- Probabilistic Coordination of Optimal Power Management and Voyage Scheduling for All-Electric Ships. Available online: https://ieeexplore.ieee.org/abstract/document/10246416 (accessed on 27 December 2024).
- Lan, H.; Gao, J.; Hong, Y.-Y.; Yin, H. Interval Forecasting of Photovoltaic Power Generation on Green Ship under Multi-Factors Coupling. Sustain. Energy Technol. Assess. 2023, 56, 103088. [Google Scholar] [CrossRef]
- Wang, Z.; Liao, P.; Liu, S.; Ji, Y.; Han, F. Scenario-Based Energy Management Optimization of Hydrogen-Electric-Thermal Systems in Sustainable Shipping. Int. J. Hydrog. Energy 2025, 99, 566–578. [Google Scholar] [CrossRef]
- Hou, H.; Gan, M.; Wu, X.; Xie, K.; Fan, Z.; Xie, C.; Shi, Y.; Huang, L. Real-Time Energy Management of Low-Carbon Ship Microgrid Based on Data-Driven Stochastic Model Predictive Control. CSEE J. Power Energy Syst. 2023, 9, 1482–1492. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, H.; Hong, Y.-Y.; Wen, S.; Fang, S. Joint Voyage Scheduling and Economic Dispatch for All-Electric Ships with Virtual Energy Storage Systems. Energy 2020, 190, 116268. [Google Scholar] [CrossRef]
- Lan, H.; Wen, S.; Hong, Y.-Y.; Yu, D.C.; Zhang, L. Optimal Sizing of Hybrid PV/Diesel/Battery in Ship Power System. Appl. Energy 2015, 158, 26–34. [Google Scholar] [CrossRef]
- Liang, H.; Pirouzi, S. Energy Management System Based on Economic Flexi-Reliable Operation for the Smart Distribution Network Including Integrated Energy System of Hydrogen Storage and Renewable Sources. Energy 2024, 293, 130745. [Google Scholar] [CrossRef]
- Ship Energy Scheduling with DQN-CE Algorithm Combining Bi-Directional LSTM and Attention Mechanism—ScienceDirect. Available online: https://www.sciencedirect.com/science/article/pii/S0306261923007420 (accessed on 28 February 2025).
- Drungilas, D.; Kurmis, M.; Senulis, A.; Lukosius, Z.; Andziulis, A.; Januteniene, J.; Bogdevicius, M.; Jankunas, V.; Voznak, M. Deep Reinforcement Learning Based Optimization of Automated Guided Vehicle Time and Energy Consumption in a Container Terminal. Alex. Eng. J. 2023, 67, 397–407. [Google Scholar] [CrossRef]
- Shang, C.; Fu, L.; Bao, X.; Xu, X.; Zhang, Y.; Xiao, H. Energy Optimal Dispatching of Ship’s Integrated Power System Based on Deep Reinforcement Learning. Electr. Power Syst. Res. 2022, 208, 107885. [Google Scholar] [CrossRef]
- Long, L.N.B.; You, S.-S.; Cuong, T.N.; Kim, H.-S. Optimizing Quay Crane Scheduling Using Deep Reinforcement Learning with Hybrid Metaheuristic Algorithm. Eng. Appl. Artif. Intell. 2025, 143, 110021. [Google Scholar] [CrossRef]
- Li, W.; Cui, H.; Nemeth, T.; Jansen, J.; Ünlübayir, C.; Wei, Z.; Feng, X.; Han, X.; Ouyang, M.; Dai, H.; et al. Cloud-Based Health-Conscious Energy Management of Hybrid Battery Systems in Electric Vehicles with Deep Reinforcement Learning. Appl. Energy 2021, 293, 116977. [Google Scholar] [CrossRef]


| Component | Type | Numerical | Unit |
|---|---|---|---|
| PV [30] | 0.18 | / | |
| 300 | |||
| 1 | / | ||
| 25 | |||
| 0.0048 | / | ||
| 180 | |||
| HFCs [31] | 500 | kW | |
| 0.5 | / | ||
| 0.75 | / | ||
| 5 | USD/kg | ||
| 142 | MJ/kg | ||
| ESS [32] | 200 | kW | |
| 0.99/0.99 | / | ||
| 0.2/0.8 | / | ||
| Ship speed [32] | 20 | knot |
| Parameters | Type | Numerical |
|---|---|---|
| Actor learning rate | Actor_lr | 0.0003 |
| Critic learning rate | Critic_lr | 0.003 |
| Soft update parameter | 0.005 | |
| Discount factor | 0.98 | |
| Standard deviation for gaussian noise | 0.01 | |
| Replay buffer size | RB | 10,000 |
| Minimum number of training starts | MS | 1000 |
| Number of samples | NS | 64 |
| Dimensions of the hidden layer | Hidden_dim | 64 |
| Component | Economic Costs (USD) | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|---|
| PV | Installation | 2400 | 2400 | 0 | 2400 |
| Maintenance | 121.64 | 121.64 | 0 | 121.64 | |
| HFCs | Hydrogen fuel | 85,507.76 | 85,035.12 | 90,886.68 | 84,804.01 |
| Maintenance | 5937.50 | 5905.22 | 6711.58 | 5889.17 | |
| ESS | Maintenance | 1219.47 | 1339.95 | 633.78 | 676.93 |
| Total economic costs | 95,186.37 | 94,801.93 | 98,232.04 | 93,891.75 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wen, S.; Zhao, Q.; Zhang, B.; Huang, Y. Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty. J. Mar. Sci. Eng. 2025, 13, 565. https://doi.org/10.3390/jmse13030565
Zhao Y, Wen S, Zhao Q, Zhang B, Huang Y. Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty. Journal of Marine Science and Engineering. 2025; 13(3):565. https://doi.org/10.3390/jmse13030565
Chicago/Turabian StyleZhao, Yunxiang, Shuli Wen, Qiang Zhao, Bing Zhang, and Yuqing Huang. 2025. "Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty" Journal of Marine Science and Engineering 13, no. 3: 565. https://doi.org/10.3390/jmse13030565
APA StyleZhao, Y., Wen, S., Zhao, Q., Zhang, B., & Huang, Y. (2025). Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty. Journal of Marine Science and Engineering, 13(3), 565. https://doi.org/10.3390/jmse13030565







