Evaluation of Measurement Uncertainty for the Wave Buoy Calibration Device Using a Vertical Lifting Method
Abstract
:1. Introduction
2. Design of the Standard Instrument for the Wave Buoy Calibration Device
2.1. Introduction of Wave Buoy Calibration Devices
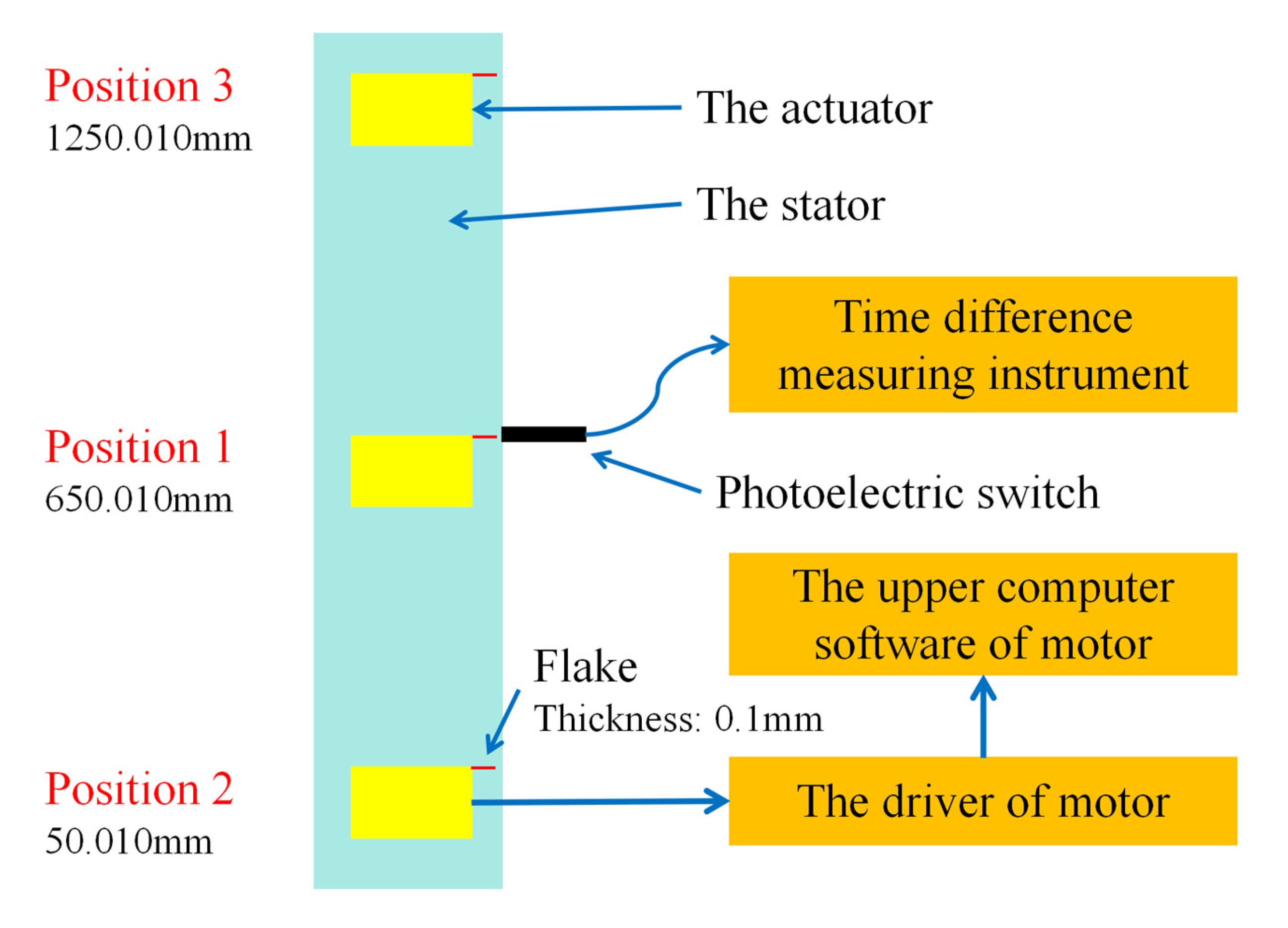
2.2. Wave Height Measuring Standard Instrument Design
2.3. Wave Period Measuring Standard Instrument Design
3. Evaluation of Measurement Uncertainty
3.1. Evaluation of Wave Height Measurement Uncertainty
- (a)
- The uncertainty introduced by the measurement repeatability of the standard steel tape
- (b)
- The uncertainty introduced by the smallest division measure of the standard steel tape
- (c)
- The uncertainty introduced by the linear expansion coefficient of the standard steel tape
- (d)
- The uncertainty introduced by the influence of ambient temperature
- (e)
- The uncertainty introduced the measurement of the standard steel tape
- (f)
- The combined standard uncertainty
- (g)
- The extended measurement uncertainty
3.2. Evaluation of Wave Period Measurement Uncertainty
- (a)
- The uncertainty introduced by the response time of the photoelectric switch
- (b)
- The uncertainty introduced by the sampling interval of the motor upper computer software
- (c)
- The uncertainty introduced by the digital output transmission delay of the driver
- (d)
- The uncertainty introduced by the measurement of the motor upper computer software
- (e)
- The combined standard uncertainty
- (f)
- The extended measurement uncertainty
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pradal, M.A.; Gnanadesikan, A. How does the Redi parameter for mesoscale mixing impact global climate in an Earth System Model? J. Adv. Model. Earth Syst. 2014, 6, 586–601. [Google Scholar] [CrossRef]
- Rossby, T.; Flagg, C.; Chafik, L.; Harden, B.; Soiland, H. A Direct Estimate of Volume, Heat, and Freshwater Exchange Across the Greenland-Iceland-Faroe-Scotland Ridge. J. Geophys. Res. Ocean. 2018, 123, 7139–7153. [Google Scholar] [CrossRef]
- Torsethaugen, K.; Haver, S.K.; Norway, S. Simplified Double Peak Spectral Model For Ocean Waves. In Proceedings of the International Ocean and Polar Engineering Conference, Toulon, France, 23–28 May 2004; ISOPE-I-04-289. [Google Scholar]
- Wang, D.; Mitchell, D.A.; Teague, W.J.; Jarosz, E.; Hulbert, M. Extreme Waves Under Hurricane Ivan. Science 2005, 309, 896. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.C.; Chen, H.S.; Doong, D.-J.; Kao, C.C.; HSU, Y.-J.G. Monstrous ocean waves during typhoon Krosa. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2008; Volume 26, pp. 1327–1329. [Google Scholar]
- Hanafin, J.; Quilfen, Y.; Ardhuin, F.; Sienkiewicz, J.; Queffeulou, P.; Obrebski, M.; Chapron, B. Phenomenal sea states and swell radiation: A comprehensive analysis of the 12-16 February 2011 North Atlantic storms. Bull. Am. Meteorol. Soc. 2012, 93, 1825–1832. [Google Scholar] [CrossRef]
- Husson, R.; Ardhuin, F.; Chapron, B.; Collard, F.; Balanche, A. Swells throughout the pacific: A combined view using the global seismic network and Envisat’s wave mode ASAR data. Geophys. Res. Lett. 2012, 39, L15609. [Google Scholar] [CrossRef]
- Ardhuin, F.; Molero, B.; Bohé, A.; Nouguier, F.; Collard, F.; Houghton, I.; Hay, A.; Legresy, B. Phase-Resolved Swells Across Ocean Basins in SWOT Altimetry Data: Revealing Centimeter-Scale Wave Heights Including Coastal Reflection. Geophys. Res. Lett. 2024, 51, 109658. [Google Scholar] [CrossRef]
- Thomson, J. Wave propagation in the marginal ice zone: Connections and feedback mechanisms within the air-ice-ocean system. Philos. T. R. Soc. A 2022, 380, 20210251. [Google Scholar] [CrossRef]
- Nose, T.; Katsuno, T.; Waseda, T.; Ushio, S.; Rabault, J.; Kodaira, T.; Voermans, J. Observation of wave propagation over 1000 km into Antarctica winter pack ice. Coast. Eng. J. 2023, 66, 115–131. [Google Scholar] [CrossRef]
- Jangir, P.K.; Ewans, K.C.; Young, I.R. Comparative Performance of Radar, Laser, and Waverider Buoy Measurements of Ocean Waves. Part II: Time-Domain Analysis. J. Atmos. Ocean. Technol. 2023, 40, 939–956. [Google Scholar] [CrossRef]
- Xue, C.; Guo, J.S.; Jiang, S.M.; Wang, Y.F.; Guo, Y.L.; Li, J. Performance Characteristics of Newly Developed Real-Time Wave Measurement Buoy Using the Variometric Approach. J. Mar. Sci. Eng. 2024, 12, 2032. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C. Comparison of HF Radar Fields of Directional Wave Spectra Against In Situ Measurements at Multiple Locations. J. Mar. Sci. Eng. 2019, 7, 271. [Google Scholar] [CrossRef]
- Timmermans, B.; Shaw, A.G.P.; Gommenginger, C. Reliability of Extreme Significant Wave Height Estimation from Satellite Altimetry and In Situ Measurements in the Coastal Zone. J. Mar. Sci. Eng. 2020, 8, 1039. [Google Scholar] [CrossRef]
- Directional Waverider 4. Available online: https://datawell.nl/products/directional-waverider-4 (accessed on 1 January 2025).
- Raghukumar, K.; Chang, G.; Spada, F.; Jones, C.; Janssen, T.; Gans, A. Performance Characteristics of “Spotter”, a Newly Developed Real-Time Wave Measurement Buoy. J. Atmos. Ocean. Technol. 2019, 36, 1127–1141. [Google Scholar] [CrossRef]
- Rabault, J.; Nose, T.; Hope, G.; Müller, M.; Breivik, Ø.; Voermans, J.; Hole, L.R.; Bohlinger, P.; Waseda, T.; Kodaira, T.; et al. OpenMetBuoy-v2021: An easy-to-build, affordable, customizable, open-source instrument for oceanographic measurements of drift and waves in sea ice and the open ocean. Geosciences 2022, 12, 110. [Google Scholar] [CrossRef]
- Thomson, J.; Bush, P.; Castillo Contreras, V.; Clemett, N.; Davis, J.; de Klerk, A.; Iseley, E.; Rainville, E.J.; Salmi, B.; Talbert, J. Development and testing of microSWIFT expendable wave buoys. Coast. Eng. J. 2023, 66, 168–180. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.; Jin, Y.X.; Chen, Y.H.; Liu, Y.J. Investigation of an Ironless Permanent Magnet Linear Synchronous Motor with Cooling System. Appl. Sci. 2016, 6, 422. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chien, Z.J.; Wang, W.Y.; Chiang, H.H. Contour Tracking Control of a Linear Motors-Driven X-Y-Y Stage Using Auto-Tuning Cross-Coupled 2DOF PID Control Approach. Appl. Sci. 2020, 10, 9036. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Cheng, Y.B.; Gao, H.T.; Sun, S.H.; Zhang, X.D.; Xue, L.; Tang, J.W.; Tang, Y.Q. High-Precision Measurement of Microscales Based on Optoelectronics and Image Integration Method. Micromachines 2024, 15, 1162. [Google Scholar] [CrossRef]
- Cheng, Y.B.; Wang, Z.Y.; Chen, X.H.; Li, Y.; Li, H.Y.; Li, H.L.; Wang, H.B. Evaluation and Optimization of Task-oriented Measurement Uncertainty for Coordinate Measuring Machines Based on Geometrical Product Specifications. Appl. Sci. 2019, 9, 6. [Google Scholar] [CrossRef]
- de Groot, P.J. A review of selected topics in interferometric optical metrology. Rep. Prog. Phys. 2019, 82, 056101. [Google Scholar] [CrossRef]
- JJG 741-2022; Standard Steel Tapes. State Market Regulatory Administration of China: Beijing, China, 2022.
- Yan, T.; Li, F. A Tide Gauge Verification Device Based On Image Recognition. J. Astronaut. Metrol. Meas. 2021, 41, 20–21. [Google Scholar]
- JJG 2007-2015; Time and Frequency Measuring Instruments. State Market Regulatory Administration of China: Beijing, China, 2015.
- IEC 60444-1:1986; Measurement of Quartz Crystal Unit Parameters by Zero Phase Technique in a -Network; Part 1: Basic Method for the Measurement of Resonance Frequency and Resonance Resistance of Quartz Crystal Units by Zero Phase Technique in a -Network. International Electrotechnical Committee: Singapore, 1986.
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. JCGM Member Organizations (BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML): Sèvres Cedex, France, 2008.
- Huang, Y.F.; Gao, C.H.; Wen, Z.P.; Qian, F.; He, L.J. Design and Performance Analysis of Meteorological Temperature Sensor Calibration Device Using Gas Cavities. Atmosphere 2024, 15, 1475. [Google Scholar] [CrossRef]


| Serial Number | The Value of the Standard Steel Tape Measure for the Motor at Its Lowest Point (mm) | The Value of the Standard Steel Tape Measure for the Motor at Its Highest Point (mm) | Standard Wave Height (mm) | Experimental Standard Deviation (mm) | Uncertainty u1h (mm) |
|---|---|---|---|---|---|
| 1 | 14.83 | 1014.85 | 1000.02 | 0.0082 | 0.0033 |
| 2 | 14.84 | 1014.84 | 1000.00 | ||
| 3 | 14.84 | 1014.85 | 1000.01 | ||
| 4 | 14.83 | 1014.84 | 1000.01 | ||
| 5 | 14.83 | 1014.85 | 1000.02 | ||
| 6 | 14.84 | 1014.84 | 1000.00 |
| Serial Number | Wave Height (m) | u2h (mm) | u3h (mm) | u4h (mm) | u5h (mm) | uch (mm) | Uh (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 0.03 | 0.0289 | 0.0000 | 0.0004 | 0.0026 | 0.0290 | 0.058 |
| 2 | 0.1 | 0.0289 | 0.0001 | 0.0013 | 0.0028 | 0.0291 | 0.059 |
| 3 | 1 | 0.0289 | 0.0012 | 0.0133 | 0.0050 | 0.0322 | 0.065 |
| 4 | 5 | 0.0289 | 0.0058 | 0.0664 | 0.0150 | 0.0742 | 0.149 |
| 5 | 20 | 0.0289 | 0.0231 | 0.2656 | 0.0525 | 0.2732 | 0.547 |
| 6 | 40 | 0.0289 | 0.0462 | 0.5312 | 0.1025 | 0.5437 | 1.088 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhao, D.; Gao, C.; Yan, T.; He, L. Evaluation of Measurement Uncertainty for the Wave Buoy Calibration Device Using a Vertical Lifting Method. J. Mar. Sci. Eng. 2025, 13, 605. https://doi.org/10.3390/jmse13030605
Huang Y, Zhao D, Gao C, Yan T, He L. Evaluation of Measurement Uncertainty for the Wave Buoy Calibration Device Using a Vertical Lifting Method. Journal of Marine Science and Engineering. 2025; 13(3):605. https://doi.org/10.3390/jmse13030605
Chicago/Turabian StyleHuang, Yafei, Donglei Zhao, Chenhao Gao, Tian Yan, and Lijun He. 2025. "Evaluation of Measurement Uncertainty for the Wave Buoy Calibration Device Using a Vertical Lifting Method" Journal of Marine Science and Engineering 13, no. 3: 605. https://doi.org/10.3390/jmse13030605
APA StyleHuang, Y., Zhao, D., Gao, C., Yan, T., & He, L. (2025). Evaluation of Measurement Uncertainty for the Wave Buoy Calibration Device Using a Vertical Lifting Method. Journal of Marine Science and Engineering, 13(3), 605. https://doi.org/10.3390/jmse13030605






