Optimization Strategy for Container Transshipment Between Yards at U-Shaped Sea-Rail Intermodal Terminal
Abstract
:1. Introduction
2. Literature Review
2.1. Automated Terminal Multilevel Operations
2.2. Sea-Rail Intermodal Transportation
- CT scheduling at seaport terminals: Although CTs play a crucial role in terminal operations, especially in sea-rail intermodal transportation, few studies have explicitly addressed CT scheduling within seaport terminals. Most research focuses on isolated aspects, failing to consider the comprehensive scope of terminal operations.
- Multi-level operations in sea-rail intermodal transportation: Most research on terminal operations is limited to the loading and unloading of containers from vessels, with very few studies addressing the multi-level operations of sea-rail intermodal transportation.
- Integration of U-ACT and sea-rail operations: Although U-ACT offers significant potential advantages, such as streamlined operations and space optimization, existing research lacks a comprehensive evaluation of how sea-rail intermodal transportation can be integrated into U-ACT frameworks. The potential benefits of such integration remain underexplored.
3. Mathematical Model Formulation
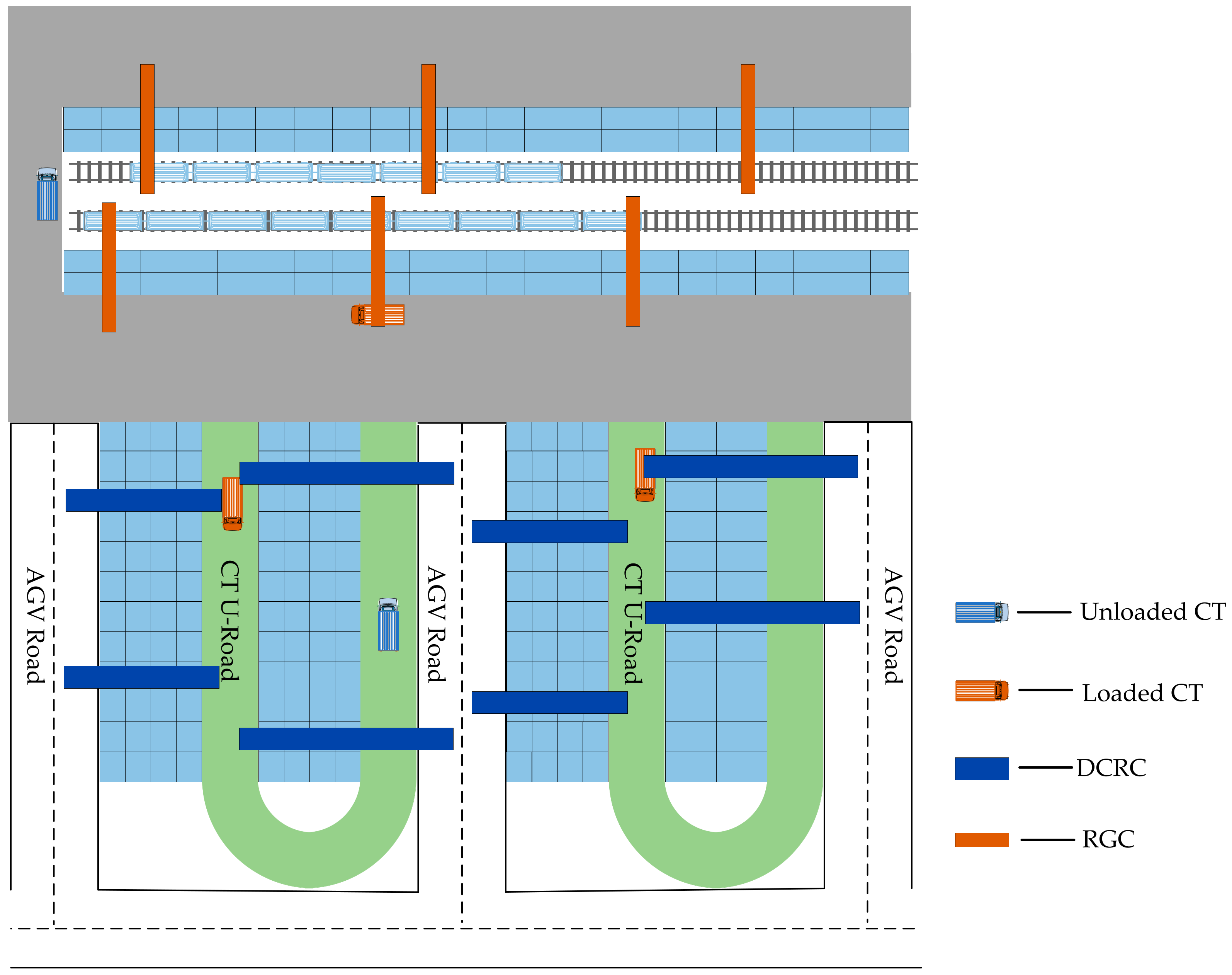
3.1. Problem Description
- Scheduling of DCRC: The UY consists of multiple container blocks, each equipped with two DCRCs. Unlike traditional operations, DCRCs do not have to return to the ends of the yard after each operation. Instead, they can conduct loading and unloading operations directly inside the yard. This approach can effectively reduce the idle time of the DCRC, which effectively improves the efficiency of the operation and reduces its energy consumption.
- Scheduling of CTs: The utilization rate of CTs is related to the efficiency and energy consumption of the overall operation. Therefore, the idle distance of CTs should be minimized. CTs should be allowed to transport export containers and import containers alternately, forming a double-cycle pattern.
- Scheduling of RGC: U-ACT is equipped with yards for train operation, and each yard is equipped with three RGCs. Normally, the train transporting export containers will arrive at the terminal in advance and temporarily be stored in the RY through the RGC. The operations of the RGC are in side loading and unloading mode, which can reduce the waiting time of CT and the empty time of RGC. This mode effectively improves the operation efficiency and reduces the operation’s energy consumption.
- Assignment of tasks: Task assignment in U-ACT is flexible, encompassing both the selection of CTs and the sequencing of tasks. Therefore, tasks should be distributed as evenly as possible to avoid congestion caused by centralized operations.
3.2. Assumptions
- Each CT, RGC, and DCRC can handle only one container at a time.
- The operating speeds of CTs, RGCs, and DCRCs are known and remain constant.
- The transshipment of containers within the yard is not considered.
- All container storage points can be determined according to the distribution plan.
3.3. Notations
3.4. Integrated Scheduling Model
3.5. Path Planning Model
4. Solution Approach
4.1. Selection Layer Algorithm Design
4.1.1. Hyper-Heuristic Algorithm
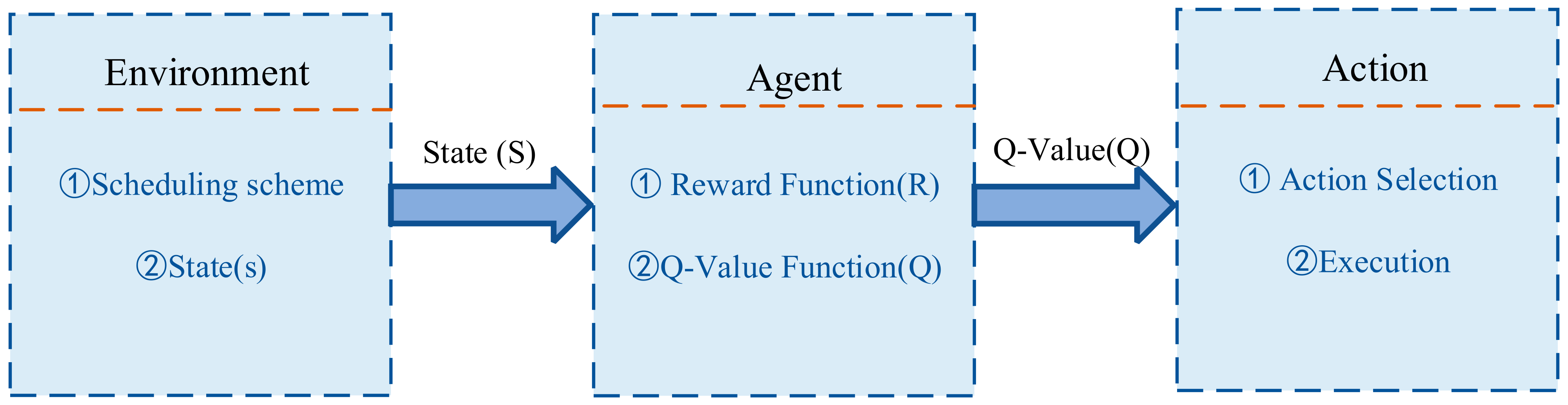
4.1.2. Q-Learning Algorithm
- I.
- The Q-value is initialized and all state-actions are set to zero.
- II.
- The heuristic algorithm is selected based on the selection layer. Then, solve and compute the model described in Chapter 3 to generate the current solution.
- III.
- Based on the results of the scheduling program, the reward value is calculated and the Q-value is updated.
- IV.
- Iterate and optimize the scheduling scheme until the termination criteria are reached.
4.2. Scheduling Layer Algorithm Design
4.3. Path Planning Layer Algorithm Design
5. Simulation Experiments and Analysis
5.1. Parameter Design
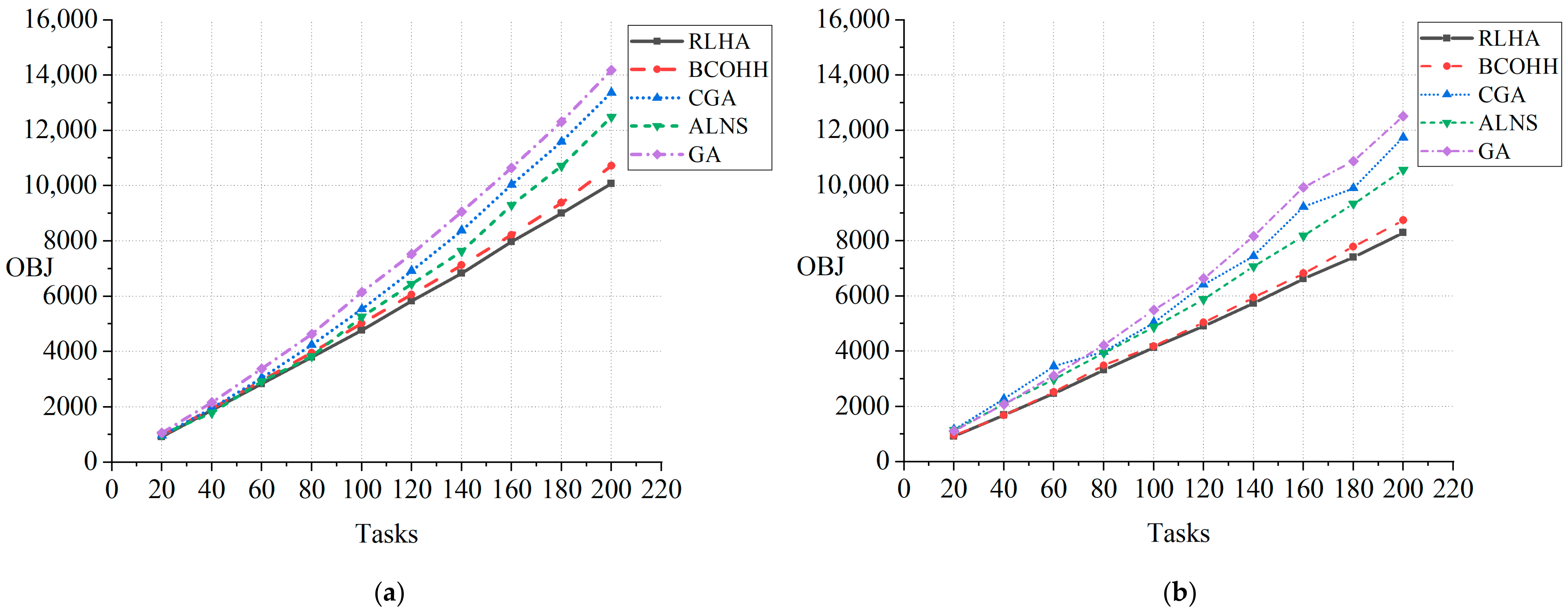
5.2. Algorithm Comparison
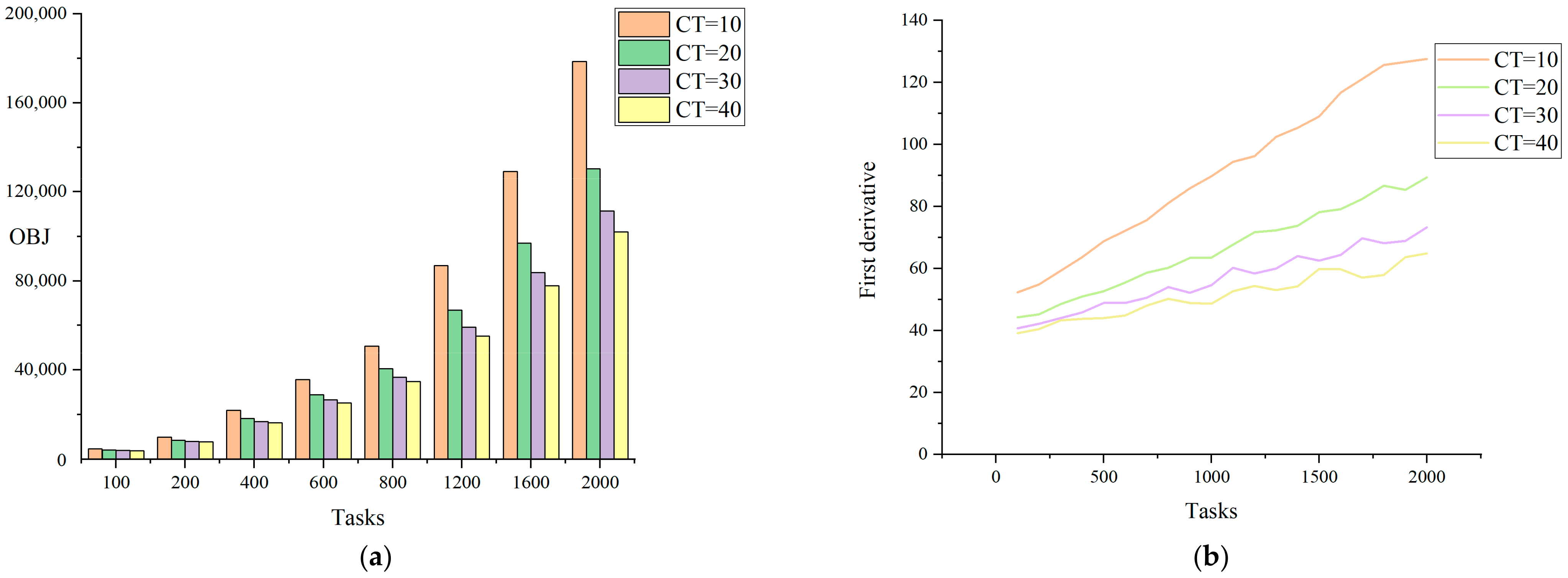
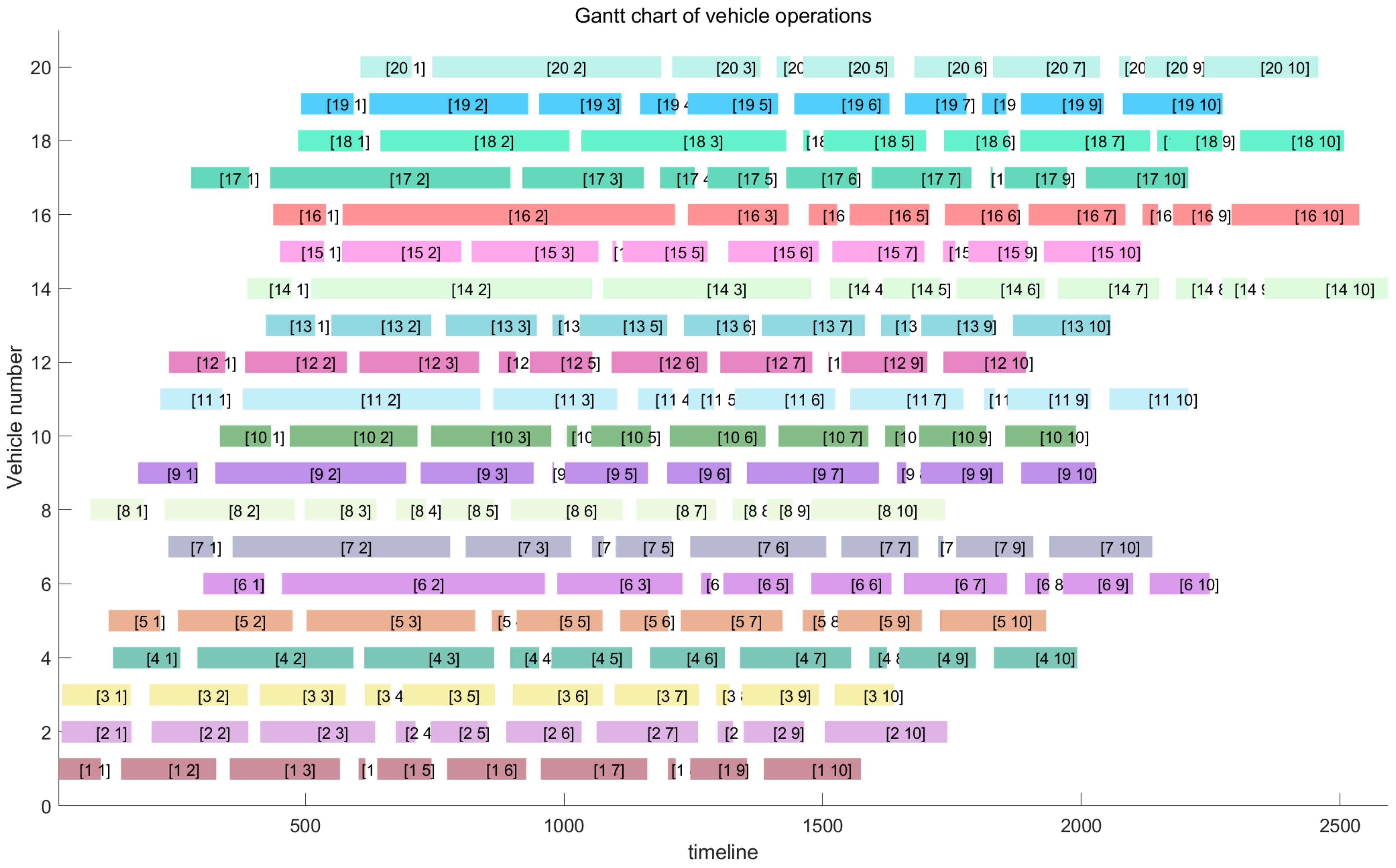
5.3. Large-Scale Experiment
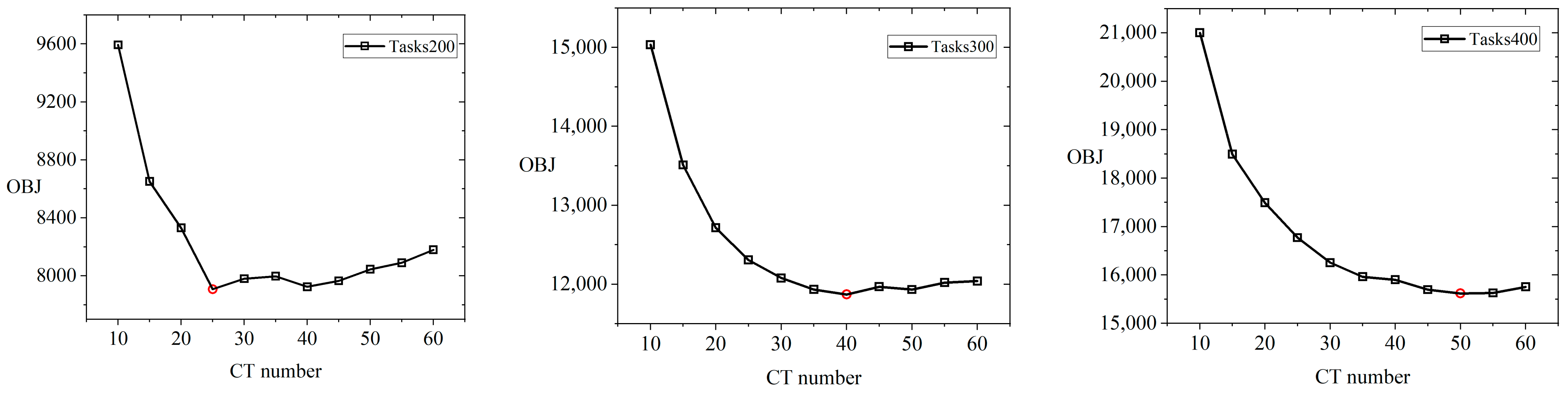
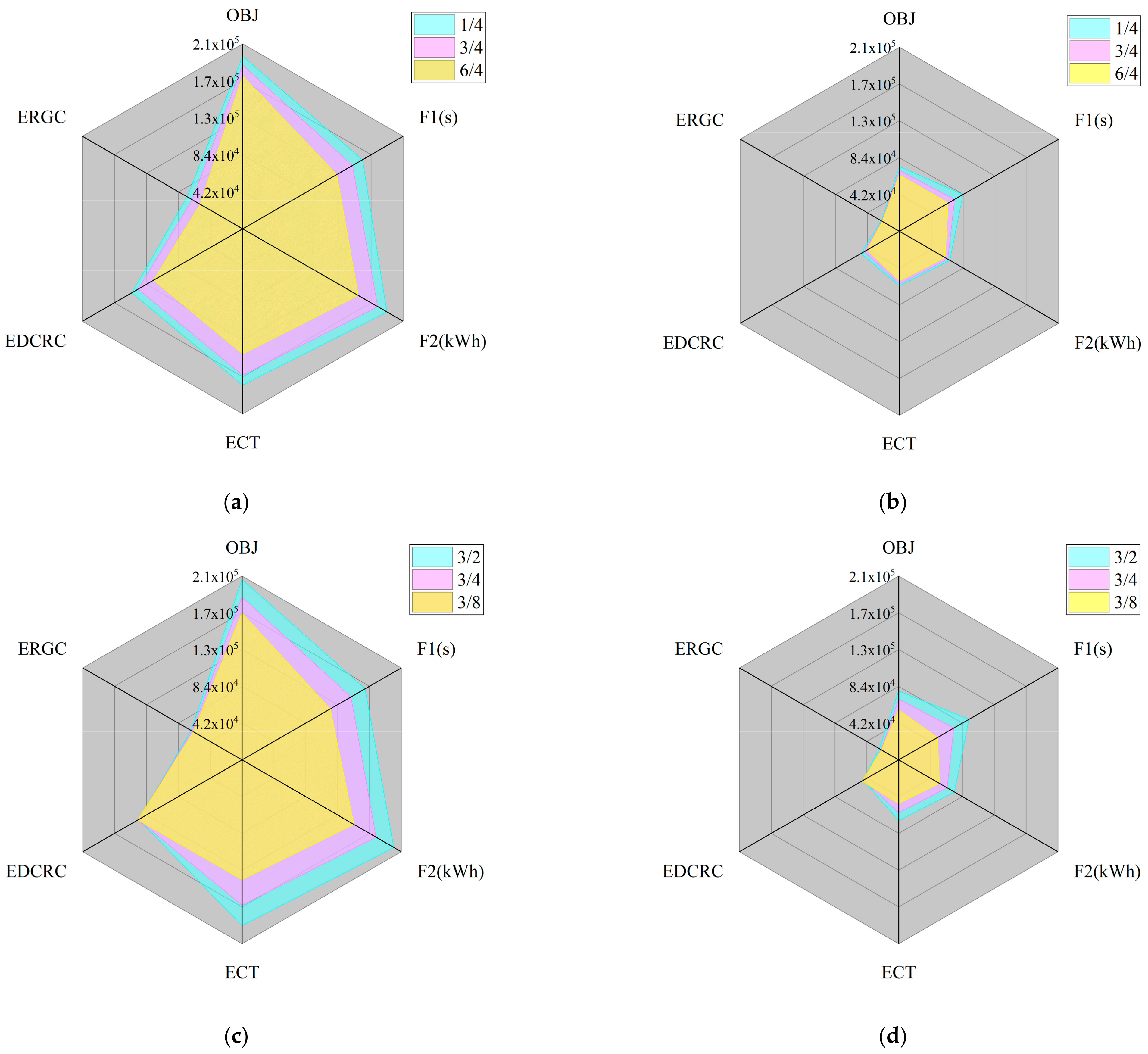
5.4. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| TASKS | CT | RGC/DCRC | Method | OBJ | CPT (s) |
|---|---|---|---|---|---|
| 20 | 10 | 3/4 | RLHA | 927.34 | 46.74 |
| BCOHH | 965.81 | 55.25 | |||
| ACGA | 950.09 | 8.58 | |||
| ALNS | 998.71 | 18.58 | |||
| GA | 1057.89 | 12.32 | |||
| 40 | 10 | 3/4 | RLHA | 1878.76 | 60.03 |
| BCOHH | 1943.36 | 93.26 | |||
| ACGA | 1977.97 | 13.67 | |||
| ALNS | 1779.87 | 26.25 | |||
| GA | 2156.75 | 17.64 | |||
| 60 | 10 | 3/4 | RLHA | 2829.72 | 80.88 |
| BCOHH | 2937.89 | 108.23 | |||
| ACGA | 3039.62 | 17.51 | |||
| ALNS | 2915.49 | 33.80 | |||
| GA | 3373.20 | 22.41 | |||
| 80 | 10 | 3/4 | RLHA | 3791.01 | 108.52 |
| BCOHH | 3957.93 | 140.61 | |||
| ACGA | 4236.74 | 22.00 | |||
| ALNS | 3822.37 | 40.80 | |||
| GA | 4626.90 | 27.00 | |||
| 100 | 10 | 3/4 | RLHA | 4772.53 | 103.46 |
| BCOHH | 5017.74 | 160.65 | |||
| ACGA | 5531.28 | 25.37 | |||
| ALNS | 5258.06 | 46.37 | |||
| GA | 6150.21 | 32.03 | |||
| 120 | 10 | 3/4 | RLHA | 5823.69 | 111.12 |
| BCOHH | 6059.06 | 171.26 | |||
| ACGA | 6950.86 | 28.72 | |||
| ALNS | 6442.65 | 52.36 | |||
| GA | 7527.36 | 40.09 | |||
| 140 | 10 | 3/4 | RLHA | 6829.73 | 141.07 |
| BCOHH | 7026.40 | 170.62 | |||
| ACGA | 8434.83 | 35.04 | |||
| ALNS | 7628.35 | 58.11 | |||
| GA | 9061.73 | 39.10 | |||
| 160 | 10 | 3/4 | RLHA | 7979.53 | 125.13 |
| BCOHH | 8220.62 | 235.41 | |||
| ACGA | 9789.28 | 36.90 | |||
| ALNS | 9296.57 | 61.79 | |||
| GA | 10,640.52 | 44.30 | |||
| 180 | 10 | 3/4 | RLHA | 9003.86 | 162.26 |
| BCOHH | 9180.67 | 209.34 | |||
| ACGA | 11,582.00 | 40.42 | |||
| ALNS | 10,713.51 | 66.14 | |||
| GA | 12,315.47 | 64.94 | |||
| 200 | 10 | 3/4 | RLHA | 10,071.85 | 133.37 |
| BCOHH | 10,516.29 | 273.19 | |||
| ACGA | 13,258.22 | 45.49 | |||
| ALNS | 12,488.00 | 70.21 | |||
| GA | 14,178.40 | 49.78 |
| Tasks | CTs | Method | OBJ |
|---|---|---|---|
| 100 | 10 | RLHA | 4763.78 |
| 200 | 10 | RLHA | 10,024.05 |
| 400 | 10 | RLHA | 21,883.57 |
| 600 | 10 | RLHA | 35,640.61 |
| 800 | 10 | RLHA | 50,747.29 |
| 1200 | 10 | RLHA | 86,803.77 |
| 1600 | 10 | RLHA | 129,084.80 |
| 2000 | 10 | RLHA | 178,611.60 |
| 100 | 20 | RLHA | 4157.00 |
| 200 | 20 | RLHA | 8583.77 |
| 400 | 20 | RLHA | 18,291.08 |
| 600 | 20 | RLHA | 28,838.55 |
| 800 | 20 | RLHA | 40,567.03 |
| 1200 | 20 | RLHA | 66,789.70 |
| 1600 | 20 | RLHA | 96,879.10 |
| 2000 | 20 | RLHA | 130,427.93 |
| 100 | 30 | RLHA | 3970.01 |
| 200 | 30 | RLHA | 8042.12 |
| 400 | 30 | RLHA | 16,841.44 |
| 600 | 30 | RLHA | 26,616.61 |
| 800 | 30 | RLHA | 36,724.70 |
| 1200 | 30 | RLHA | 59,193.52 |
| 1600 | 30 | RLHA | 83,681.12 |
| 2000 | 30 | RLHA | 111,404.48 |
| TASKS | CT | RGC/DCRC | OBJ | F1 (s) | F2 (kWh) | ECT | EDCRC | ERGC |
|---|---|---|---|---|---|---|---|---|
| 2000 | 10 | 1/4 | 195,903 | 74,622 | 251,816 | 236,259 | 10,371 | 5185 |
| 2000 | 10 | 3/4 | 185,854 | 68,455 | 235,780 | 221,295 | 9776 | 4709 |
| 2000 | 10 | 6/4 | 173,503 | 58,649 | 201,815 | 189,516 | 8334 | 3965 |
| 1000 | 10 | 1/4 | 73,814 | 39,876 | 88,511 | 83,197 | 3613 | 1700 |
| 1000 | 10 | 3/4 | 69,276 | 34,600 | 85,044 | 80,079 | 3323 | 1641 |
| 1000 | 10 | 6/4 | 64,114 | 30,609 | 80,045 | 75,392 | 3037 | 1615 |
| 2000 | 10 | 3/2 | 206,048 | 77,337 | 266,960 | 252,434 | 9736 | 4790 |
| 2000 | 10 | 3/4 | 185,854 | 68,455 | 235,780 | 221,295 | 9776 | 4709 |
| 2000 | 10 | 3/8 | 167,556 | 55,436 | 196,704 | 182,334 | 9806 | 4564 |
| 1000 | 10 | 3/2 | 78,767 | 44,093 | 97,883 | 92,728 | 3331 | 1824 |
| 1000 | 10 | 3/4 | 69,276 | 34,600 | 85,044 | 80,079 | 3323 | 1641 |
| 1000 | 10 | 3/8 | 57,073 | 24,322 | 71,693 | 66,650 | 3441 | 1602 |
References
- Arvis, J.-F.; Ojala, L.; Shepherd, B.; Ulybina, D.; Wiederer, C. Connecting to Compete 2023: Trade Logistics in an Uncertain Global Economy—The Logistics Performance Index and Its Indicators; World Bank: Washington, DC, USA, 2023. [Google Scholar]
- Yu, N.; Wang, R. Comparative Study on Infrastructure Layout Plan of Container Rail-Water Intermodal Transport in China and Abroad. In Proceedings of the International Conference on Frontiers of Traffic and Transportation Engineering (FTTE 2022), Lanzhou, China, 17–19 June 2022; Ma, C., Ed.; SPIE: Lanzhou, China, 2022; p. 16. [Google Scholar]
- Angeloudis, P.; Bell, M.G.H. An Uncertainty-Aware AGV Assignment Algorithm for Automated Container Terminals. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 354–366. [Google Scholar] [CrossRef]
- Norouzi, N.; Sadegh-Amalnick, M.; Alinaghiyan, M. Evaluating of the Particle Swarm Optimization in a Periodic Vehicle Routing Problem. Measurement 2015, 62, 162–169. [Google Scholar] [CrossRef]
- Kong, L.; Ji, M.; Yu, A.; Gao, Z. Scheduling of Automated Guided Vehicles for Tandem Quay Cranes in Automated Container Terminals. Comput. Oper. Res. 2024, 163, 106505. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Meng, Q. Autonomous Truck Scheduling for Container Transshipment Between Two Seaport Terminals Considering Platooning and Speed Optimization. Transp. Res. Part B Methodol. 2021, 154, 289–315. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, K.; Tang, M.; Yuan, X.; Heilig, L.; Song, J.; Fang, H.; Tian, Y. An Efficient and Eco-Friendly Operation Mode for Container Transshipments through Optimizing the Inter-Terminal Truck Routing Problem. J. Clean. Prod. 2023, 430, 139644. [Google Scholar] [CrossRef]
- Vinh, N.Q.; Kim, H.-S.; Long, L.N.B.; You, S.-S. Robust Lane Detection Algorithm for Autonomous Trucks in Container Terminals. J. Mar. Sci. Eng. 2023, 11, 731. [Google Scholar] [CrossRef]
- Jin, J.; Cui, T.; Bai, R.; Qu, R. Container Port Truck Dispatching Optimization Using Real2Sim Based Deep Reinforcement Learning. Eur. J. Oper. Res. 2024, 315, 161–175. [Google Scholar] [CrossRef]
- Chu, L.; Gao, Z.; Dang, S.; Zhang, J.; Yu, Q. Optimization of Joint Scheduling for Automated Guided Vehicles and Unmanned Container Trucks at Automated Container Terminals Considering Conflicts. J. Mar. Sci. Eng. 2024, 12, 1190. [Google Scholar] [CrossRef]
- Dang, Q.-V.; Singh, N.; Adan, I.; Martagan, T.; van de Sande, D. Scheduling Heterogeneous Multi-Load AGVs with Battery Constraints. Comput. Oper. Res. 2021, 136, 105517. [Google Scholar] [CrossRef]
- Drungilas, D.; Kurmis, M.; Senulis, A.; Lukosius, Z.; Andziulis, A.; Januteniene, J.; Bogdevicius, M.; Jankunas, V.; Voznak, M. Deep Reinforcement Learning Based Optimization of Automated Guided Vehicle Time and Energy Consumption in a Container Terminal. Alex. Eng. J. 2023, 67, 397–407. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Wang, C.-N.; Thanh Tam Nguyen, T.; Dang, T.-T.; Pan, Y.-J. Hybridizing WOA with PSO for Coordinating Material Handling Equipment in an Automated Container Terminal Considering Energy Consumption. Adv. Eng. Inform. 2024, 60, 102410. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Tai, H.-H.; Wang, C.-N.; Chou, C.-C. Scheduling of Collaborative Operations of Yard Cranes and Yard Trucks for Export Containers Using Hybrid Approaches. Adv. Eng. Inform. 2021, 48, 101292. [Google Scholar] [CrossRef]
- Kong, L.; Ji, M.; Gao, Z. Joint Optimization of Container Slot Planning and Truck Scheduling for Tandem Quay Cranes. Eur. J. Oper. Res. 2021, 293, 149–166. [Google Scholar] [CrossRef]
- Li, H.; Peng, J.; Wang, X.; Wan, J. Integrated Resource Assignment and Scheduling Optimization With Limited Critical Equipment Constraints at an Automated Container Terminal. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7607–7618. [Google Scholar] [CrossRef]
- Zhu, S.; Tan, Z.; Yang, Z.; Cai, L. Quay Crane and Yard Truck Dual-Cycle Scheduling with Mixed Storage Strategy. Adv. Eng. Inform. 2022, 54, 101722. [Google Scholar] [CrossRef]
- Tang, K.; Zhang, Y.; Yang, C.; He, L.; Zhang, C.; Zhou, W. Optimization for Multi-Resource Integrated Scheduling in the Automated Container Terminal with a Parallel Layout Considering Energy-Saving. Adv. Eng. Inform. 2024, 62, 102660. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, M.; Dessouky, Y.; Postolache, O. An Integrated Scheduling Method for AGV Routing in Automated Container Terminals. Comput. Ind. Eng. 2018, 126, 482–493. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Zhou, Y.; Postolache, O. Application of Hybrid GA-PSO Based on Intelligent Control Fuzzy System in the Integrated Scheduling in Automated Container Terminal. J. Intell. Fuzzy Syst. 2020, 39, 1525–1538. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Zhang, Y.; Tong, L.; Shang, P.; Zhou, X. Yard Crane and AGV Scheduling in Automated Container Terminal: A Multi-Robot Task Allocation Framework. Transp. Res. Part C Emerg. Technol. 2020, 114, 241–271. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Lee, L.H.; Chew, E.P. Performance Estimation and Design Optimization of a Congested Automated Container Terminal. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2437–2449. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Xu, B.; Yang, Y.; Wen, F.; Song, H. Hybrid Scheduling for Multi-Equipment at U-Shape Trafficked Automated Terminal Based on Chaos Particle Swarm Optimization. J. Mar. Sci. Eng. 2021, 9, 1080. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Wang, S. Multiple Equipment Scheduling and AGV Trajectory Generation in U-Shaped Sea-Rail Intermodal Automated Container Terminal. Measurement 2023, 206, 112262. [Google Scholar] [CrossRef]
- Niu, Y.; Yu, F.; Yao, H.; Yang, Y. Multi-Equipment Coordinated Scheduling Strategy of U-Shaped Automated Container Terminal Considering Energy Consumption. Comput. Ind. Eng. 2022, 174, 108804. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Yang, Y.; Wen, F.; Song, H. Integrated Scheduling Optimization of U-Shaped Automated Container Terminal under Loading and Unloading Mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Madudova, E.; Dávid, A. Identifying the Derived Utility Function of Transport Services: Case Study of Rail and Sea Container Transport. Transp. Res. Procedia 2019, 40, 1096–1102. [Google Scholar] [CrossRef]
- Xie, Y.; Song, D.-P. Optimal Planning for Container Prestaging, Discharging, and Loading Processes at Seaport Rail Terminals with Uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2018, 119, 88–109. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Hao, C.; Hong, C. Research on the Scheduling in Sea-Rail Intermodal Trains Based on Full-Length and Full-Occupied Strategy. Res. Transp. Bus. Manag. 2025, 59, 101301. [Google Scholar] [CrossRef]
- Hu, Q.; Corman, F.; Wiegmans, B.; Lodewijks, G. A Tabu Search Algorithm to Solve the Integrated Planning of Container on an Inter-Terminal Network Connected with a Hinterland Rail Network. Transp. Res. Part C Emerg. Technol. 2018, 91, 15–36. [Google Scholar] [CrossRef]
- Mashayekhi, Z.; Verma, M. An Analytical Approach to Rail-Truck Intermodal Network Design. Transp. Res. Procedia 2025, 82, 356–366. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, X.; Lee, D.-H.; Jin, J.G.; Wang, L. Transshipment Operations Optimization of Sea-Rail Intermodal Container in Seaport Rail Terminals. Comput. Ind. Eng. 2020, 141, 106296. [Google Scholar] [CrossRef]
- Lei, Z.; Ma, Z.; de Sousa, J.S.S.; Zhu, Y. Research on the Plan of Container Train Operation in Sea-Rail Intermodal Transportation Under the Uncertain Demand. In Proceedings of the Green Connected Automated Transportation and Safety, Beijing, China, 17–19 October 2020; Wang, W., Chen, Y., He, Z., Jiang, X., Eds.; Springer: Singapore, 2022; pp. 549–561. [Google Scholar]
- Rathi, P.; Upadhyay, A. Container Retrieval and Wagon Assignment Planning at Container Rail Terminals. Comput. Ind. Eng. 2022, 172, 108626. [Google Scholar] [CrossRef]
- Xia, T.; Wang, L.; Liu, W.; Zhang, Q.; Dong, J.-X.; Zhu, X. Train Assignment and Handling Capacity Arrangement in Multi-Yard Railway Container Terminals: An Enhanced Adaptive Large Neighborhood Search Heuristic Approach. Comput. Ind. Eng. 2024, 198, 110733. [Google Scholar] [CrossRef]
- Song, X.; Chen, N.; Zhao, M.; Wu, Q.; Liao, Q.; Ye, J. Novel AGV Resilient Scheduling for Automated Container Terminals Considering Charging Strategy. Ocean Coast. Manag. 2024, 250, 107014. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, S.; Zhong, M.; Feng, J.; Wen, F.; Song, H. A Refined Collaborative Scheduling Method for Multi-Equipment at U-Shaped Automated Container Terminals Based on Rail Crane Process Optimization. J. Mar. Sci. Eng. 2023, 11, 605. [Google Scholar] [CrossRef]
- Adriaensen, S.; Brys, T.; Nowé, A. Fair-Share ILS: A Simple State-of-the-Art Iterated Local Search Hyperheuristic. In Proceedings of the Annual Conference on Genetic And Evolutionary Computation, Vancouver, BC, Canada, 12–16 June 2014; pp. 1303–1310. [Google Scholar] [CrossRef]
- Kallestad, J.; Hasibi, R.; Hemmati, A.; Sörensen, K. A General Deep Reinforcement Learning Hyperheuristic Framework for Solving Combinatorial Optimization Problems. Eur. J. Oper. Res. 2023, 309, 446–468. [Google Scholar] [CrossRef]


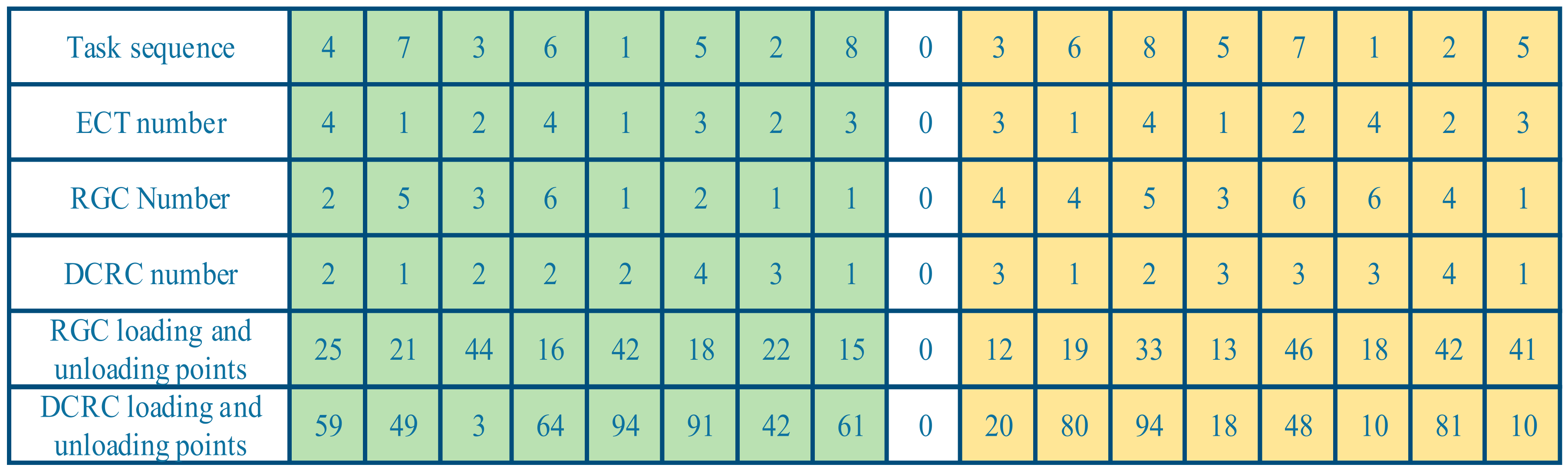

| Notation | Description of Notation |
|---|---|
| Set of import containers to be transferred | |
| Set of export containers to be transferred | |
| Set of containers to be transported by CT | |
| Set of all containers, , indexed by | |
| Set of CTs, indexed by | |
| Set of RGCs, indexed by | |
| Set of DCRCs, indexed by | |
| Set of DCRC Tasks | |
| Set of RGC Tasks | |
| Set of paths, indexed by | |
| Set of nodes, indexed by | |
| The starting node of the container | |
| The destination node for the container | |
| Set of all nodes on the path | |
| Set of times for CT to reach all nodes on the path | |
| Set of conflicting nodes in space for path and path | |
| Set of times for CT to reach conflicting nodes in path and path | |
| Speed of CT | |
| Speed of RGC | |
| Speed of DCRC | |
| Energy consumption per unit time for CT operation | |
| Energy consumption per unit time for CT waiting | |
| Energy consumption per unit time for RGC operation | |
| Energy consumption per unit time for DCRC operation | |
| RGC processing time for container | |
| DCRC processing time for container | |
| Distance from node . to node |
| Notation | Description of Notation |
|---|---|
| Total energy consumption of CT | |
| Total energy consumption of DCRC | |
| Total energy consumption of RGC | |
| The time when CT arrives at the designated loading point for the container | |
| The time when CT starts processing the container , which means the CT receives the container from the RGC or DCRC | |
| The time when CT arrives at the designated unloading point for the container | |
| The time when CT completes the container task | |
| The time when DCRC . moves to the designated loading and unloading point of the container | |
| The time when DCRC begins processing the container | |
| The time when DCRC completes processing the container | |
| The time when RGC moves to the designated loading and unloading point of the container | |
| The time when RGC begins processing the container | |
| The time when RGC completes processing the container | |
| The total time for CTs to complete container transfers | |
| The time taken by CT to choose path from node to | |
| When a path conflict occurs for the CT, the distance that needs to be passed by changing speed | |
| The safe distance between two CTs |
| Notation | Description of Notation |
|---|---|
| When the container is to be transferred by CT , , otherwise | |
| When CT . passes node and then passes through node , , otherwise | |
| When the CT performs container task and then performs container task otherwise, | |
| When the DCRC performs container task and then performs container task ; otherwise, | |
| When the RGC performs container task and then performs container task ; otherwise, |
| Index | RLHA | BCOHH | ACGA | ALNS | GA |
|---|---|---|---|---|---|
| GAP | — | 5.14% | 15.90% | 10.17% | 28.87% |
| Completion time | 3467.00 | 3826.00 | 3640.00 | 3761.00 | 3874.00 |
| Total energy consumption | 5269.66 | 6409.27 | 6341.83 | 6437.71 | 6570.58 |
| CPT | 103.46 | 160.65 | 25.37 | 46.37 | 32.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, J. Optimization Strategy for Container Transshipment Between Yards at U-Shaped Sea-Rail Intermodal Terminal. J. Mar. Sci. Eng. 2025, 13, 608. https://doi.org/10.3390/jmse13030608
Liu Z, Li J. Optimization Strategy for Container Transshipment Between Yards at U-Shaped Sea-Rail Intermodal Terminal. Journal of Marine Science and Engineering. 2025; 13(3):608. https://doi.org/10.3390/jmse13030608
Chicago/Turabian StyleLiu, Zeyi, and Junjun Li. 2025. "Optimization Strategy for Container Transshipment Between Yards at U-Shaped Sea-Rail Intermodal Terminal" Journal of Marine Science and Engineering 13, no. 3: 608. https://doi.org/10.3390/jmse13030608
APA StyleLiu, Z., & Li, J. (2025). Optimization Strategy for Container Transshipment Between Yards at U-Shaped Sea-Rail Intermodal Terminal. Journal of Marine Science and Engineering, 13(3), 608. https://doi.org/10.3390/jmse13030608




