Experimental and Numerical Simulation Studies on the Flow Field Effects of Three Artificial Fish Reefs
Abstract
1. Introduction
2. Material and Methods
2.1. Reef Model
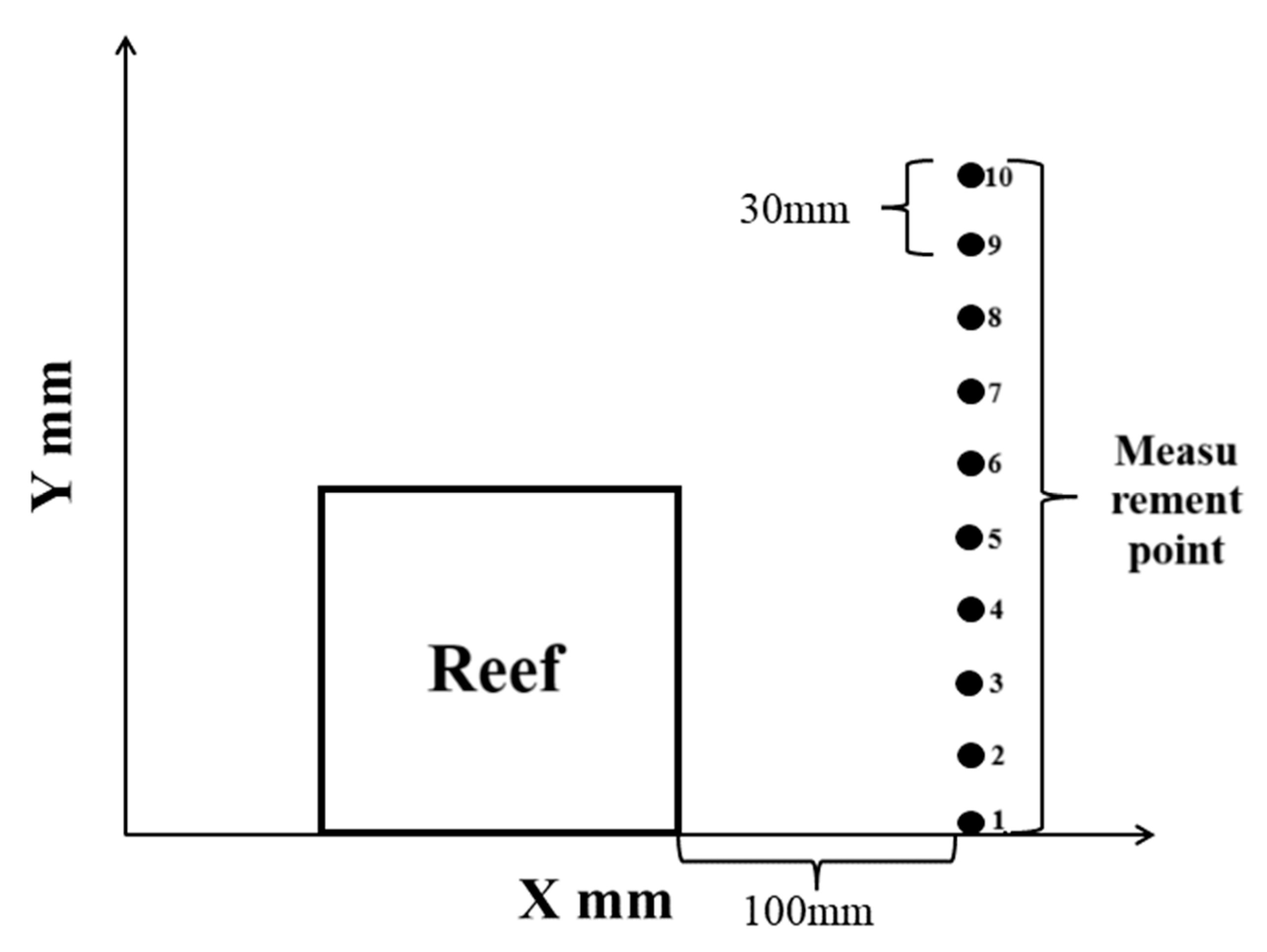
2.2. PIV Test
- (1)
- The fish reef model was placed 0°, 15°, 30° and 45° to the flow angle, the target flow velocity was set, and the flow-making device was turned on;
- (2)
- After the flow velocity was stabilized, a high-speed camera was used to take pictures and collect image data, see Figure 4.
- (3)
- The obtained particle images were first imported into PIV lab (2022) for processing, and the transient flow field map was obtained by selecting the image region to be analyzed for image correction, image analysis, error vector rejection, and data smoothing.
- (4)
- The data processed by PIVlab were imported into Tecplot (2022 R1) software for further detailed processing and analysis.
2.3. Numerical Simulation Methods
2.3.1. Governing Equations
- (1)
- The rotational and cyclonic flow cases in the mean flow are taken into account by correcting the turbulent viscosity.
- (2)
- An additional coefficient C1 is calculated in the ε equation, thus reflecting the time-averaged strain rate Si,j of the main flow, such that the resulting term in the RNG k-ε model is not only related to the flow situation but also a function of the spatial coordinates in the same problem.
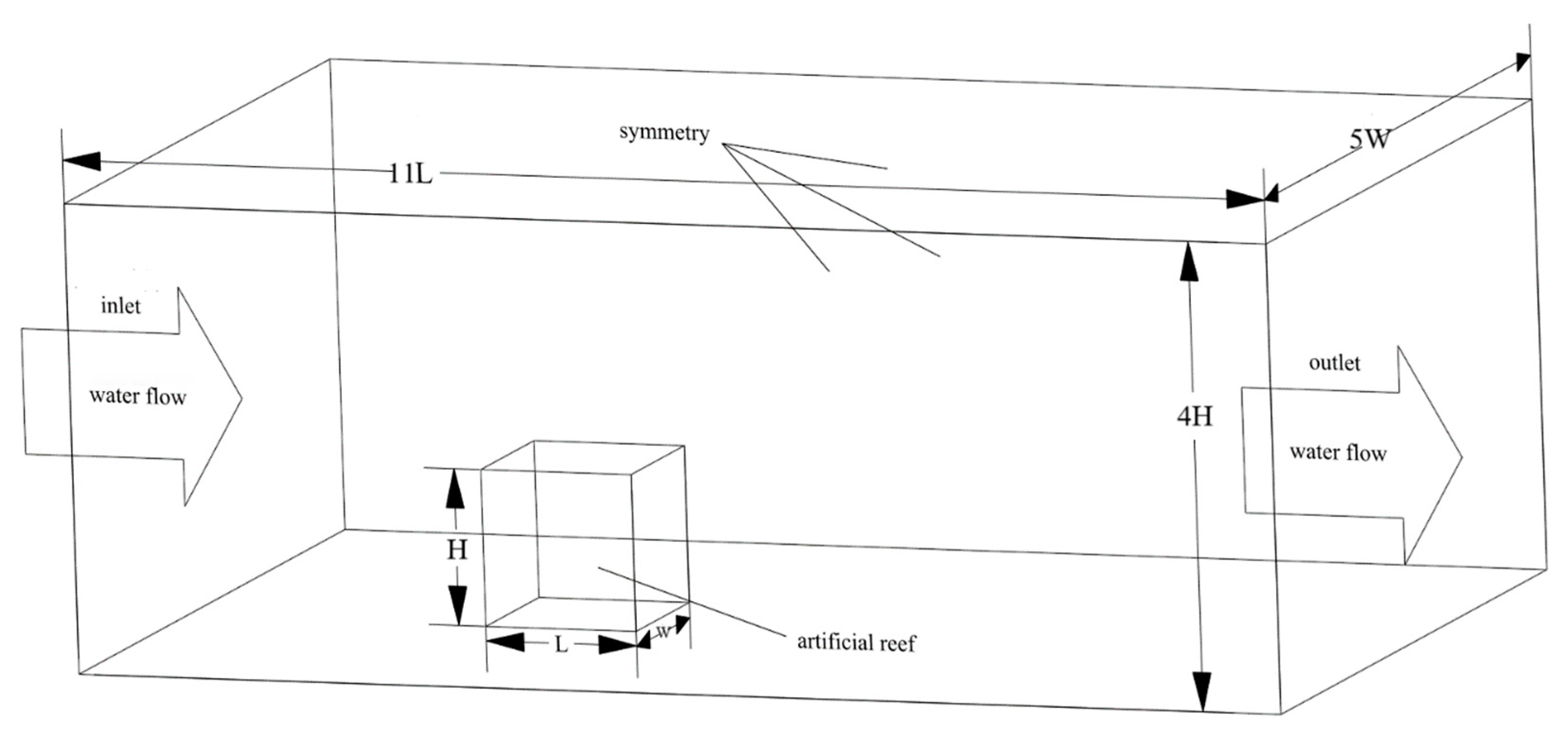
2.3.2. Computational Domain and Boundary Conditions
- (1)
- The inlet boundary condition is a velocity inlet. The corresponding incoming velocity is set, and the turbulence intensity and turbulent viscosity ratio on the boundary are calculated and given.
- (2)
- The outlet boundary is a pressure outlet.
- (3)
- The bottom surface of the computational domain and the surface of the artificial reef body are set as wall boundary conditions, the side walls are symmetric, and the standard wall boundary parameters of static no-slip are used.
2.3.3. Meshing
2.3.4. Selection of Indicators for the Flow Field Region
3. Results
3.1. Test Results
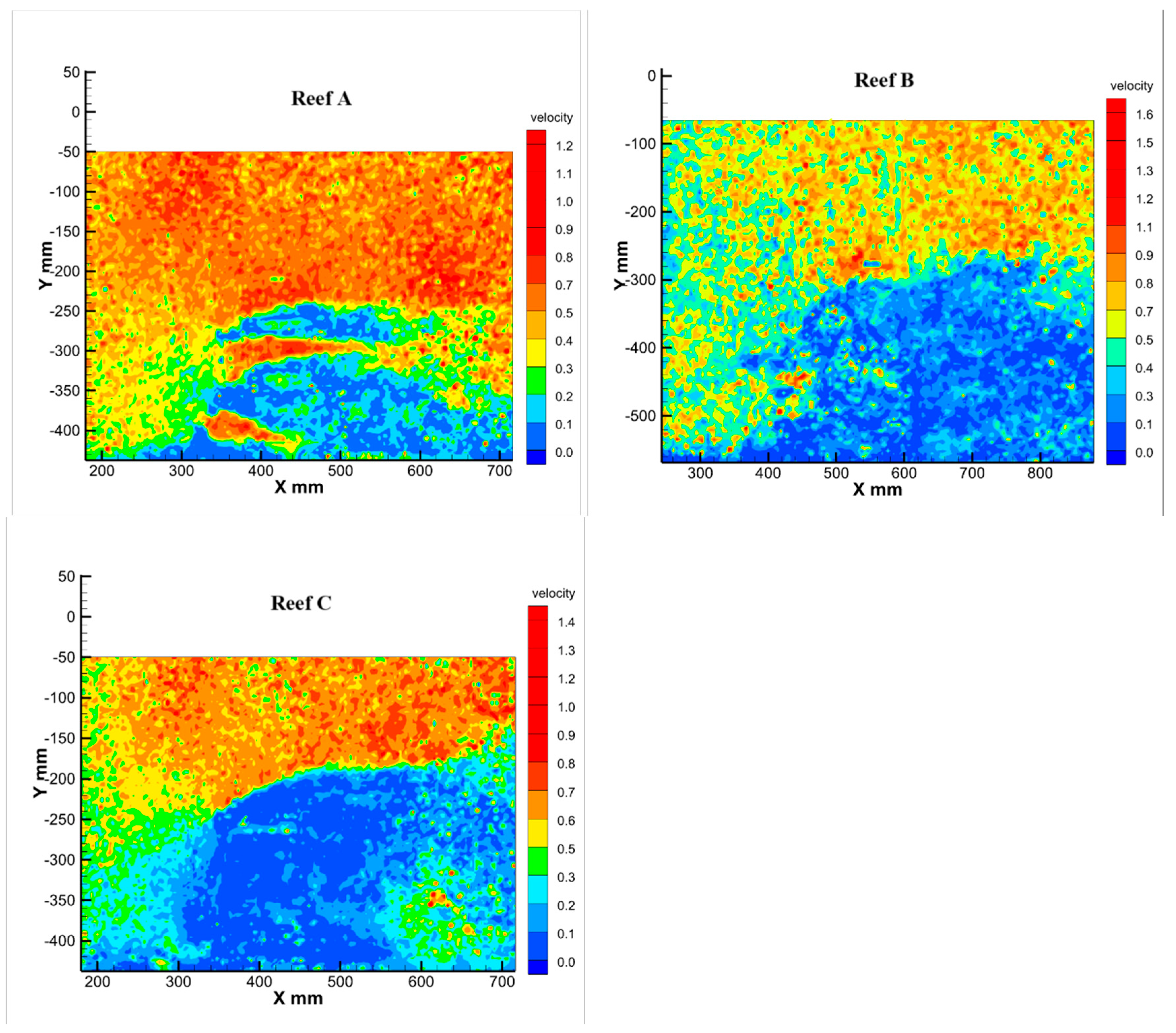
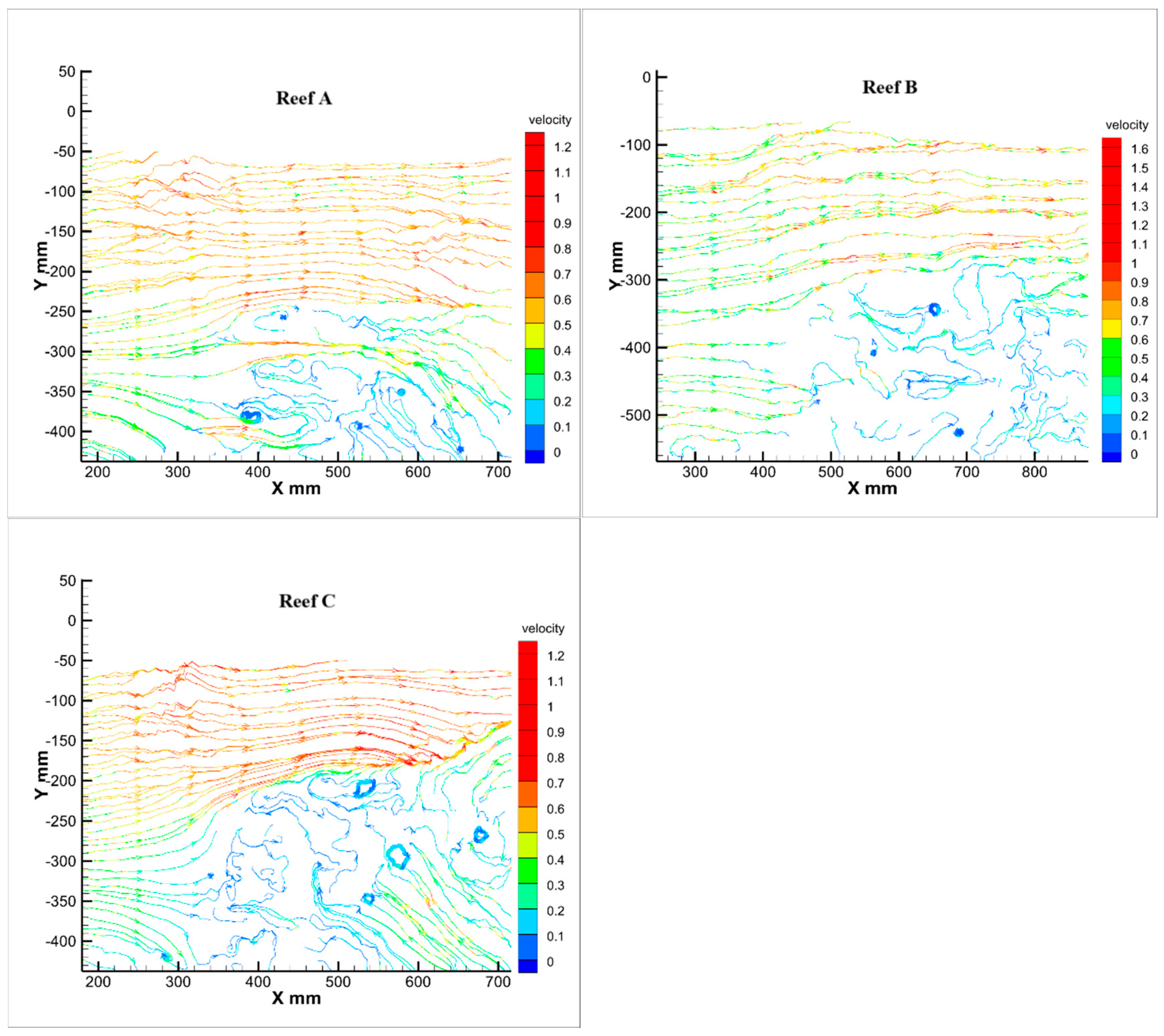
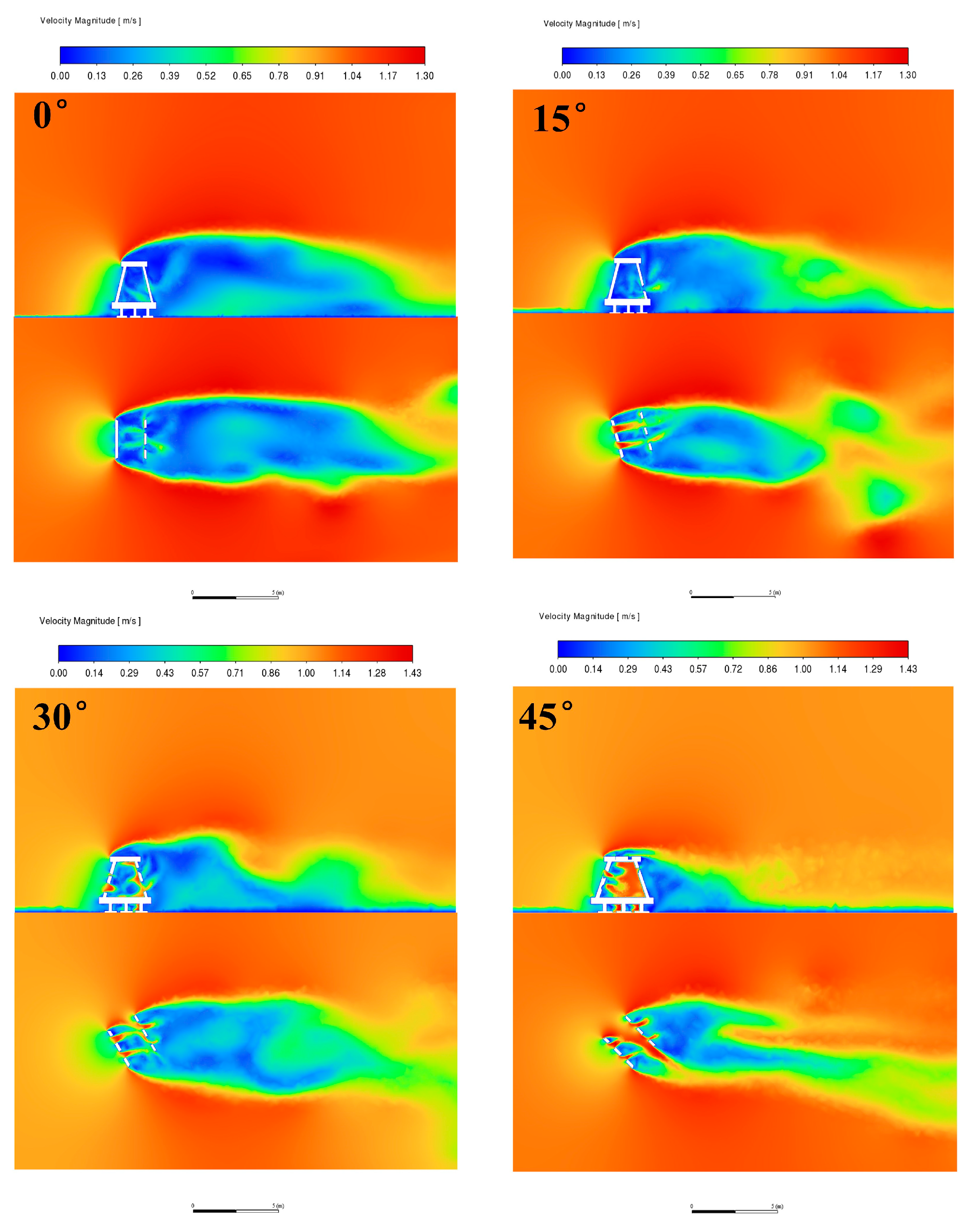
3.1.1. Characterization of Flow Patterns in the Mid-Axial Plane
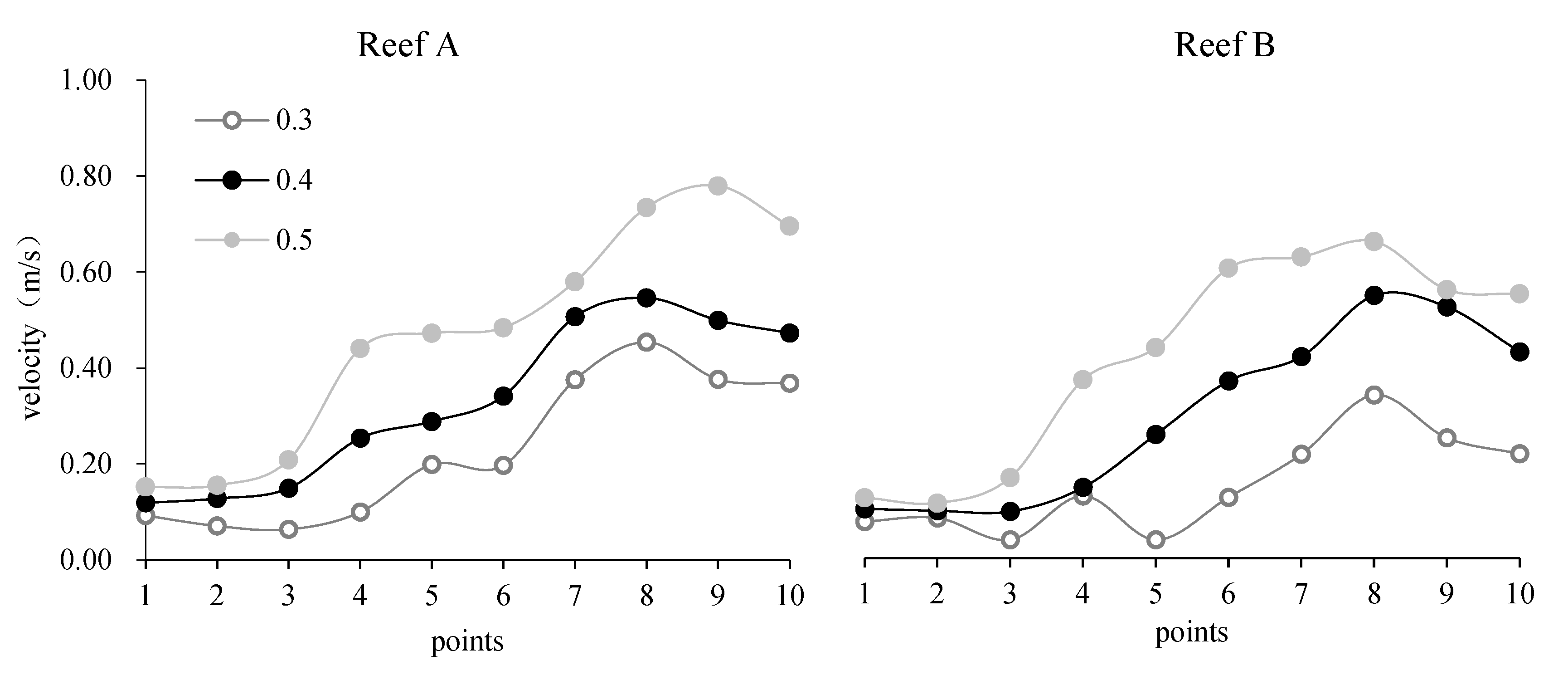
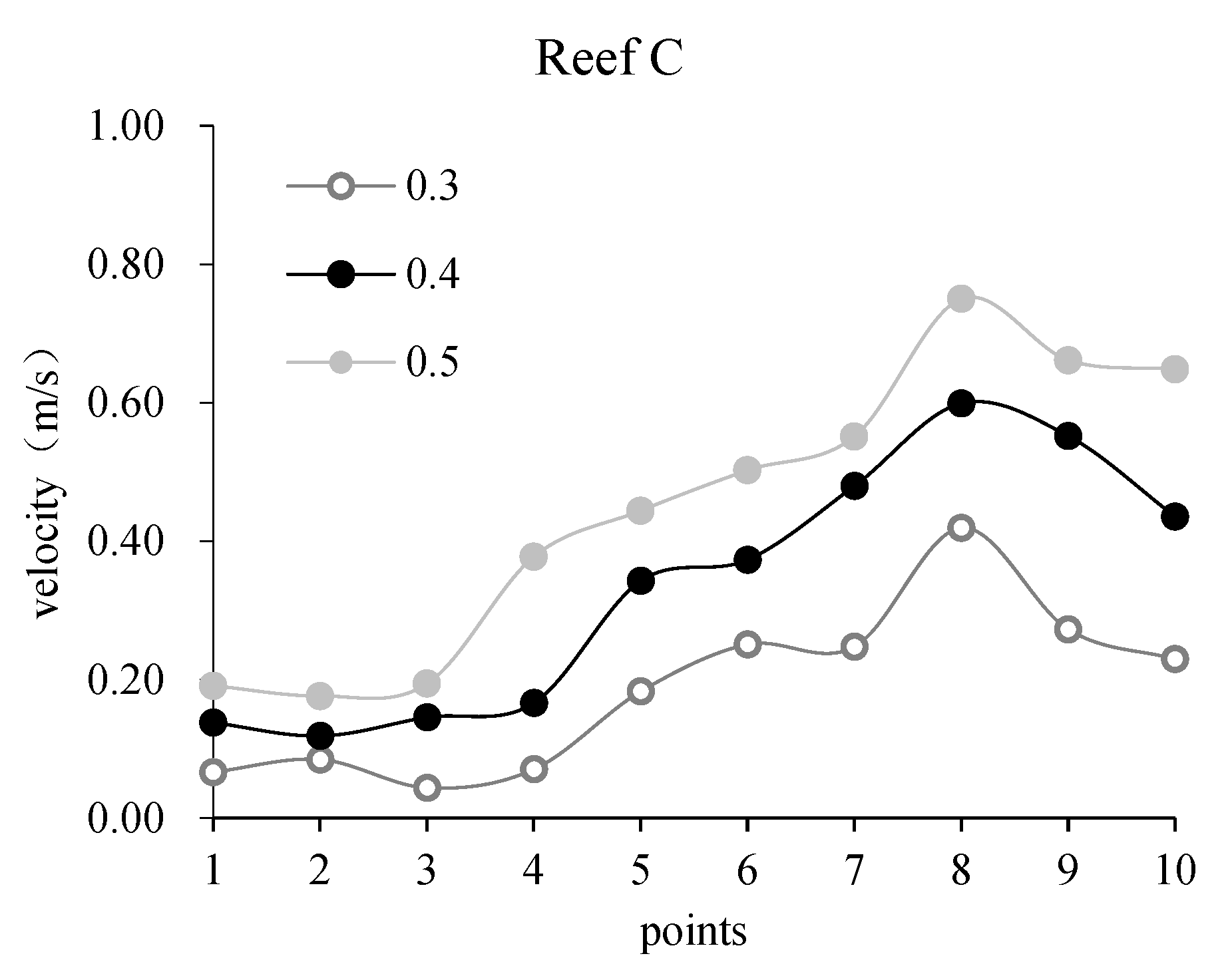
3.1.2. Point Velocity Results
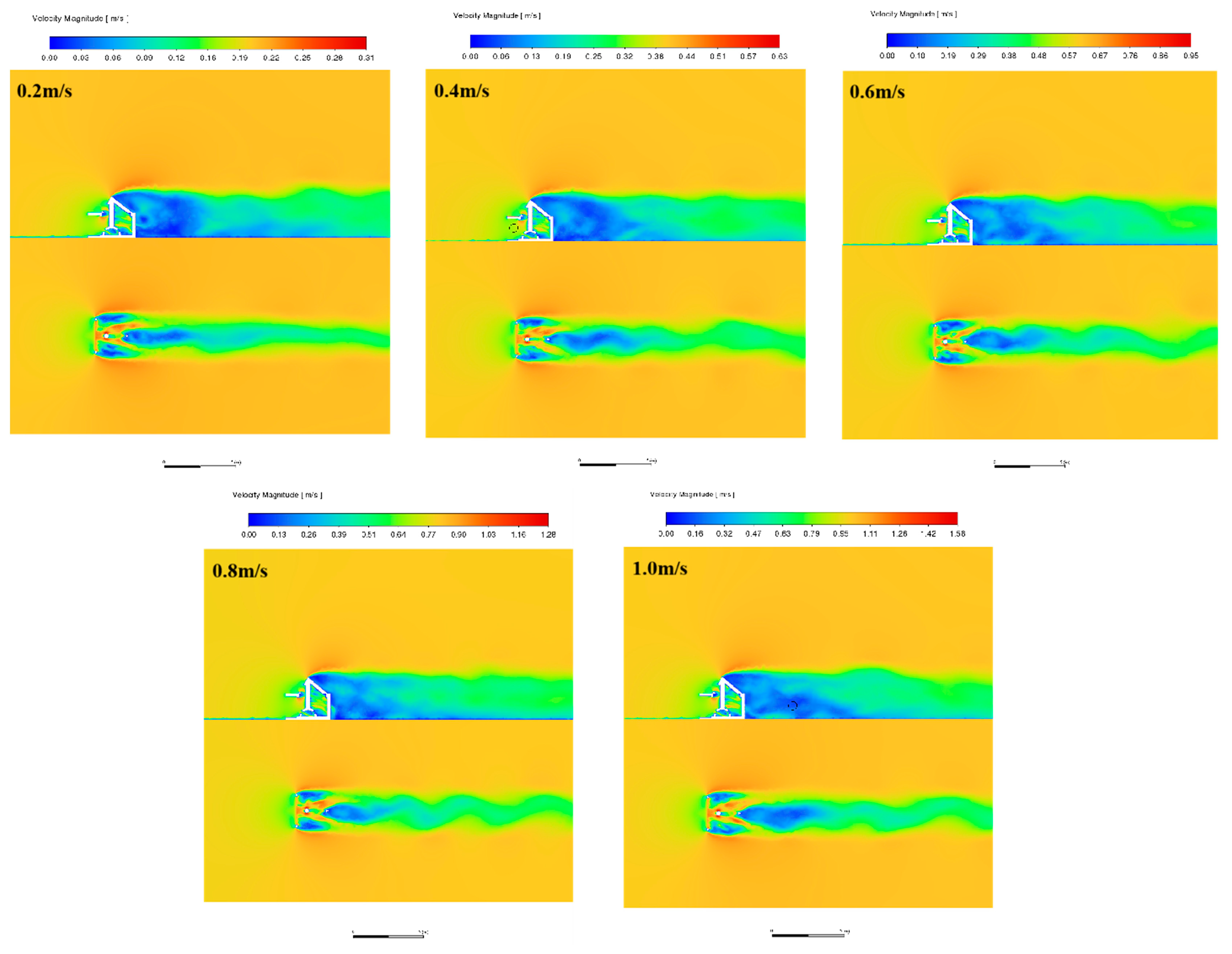
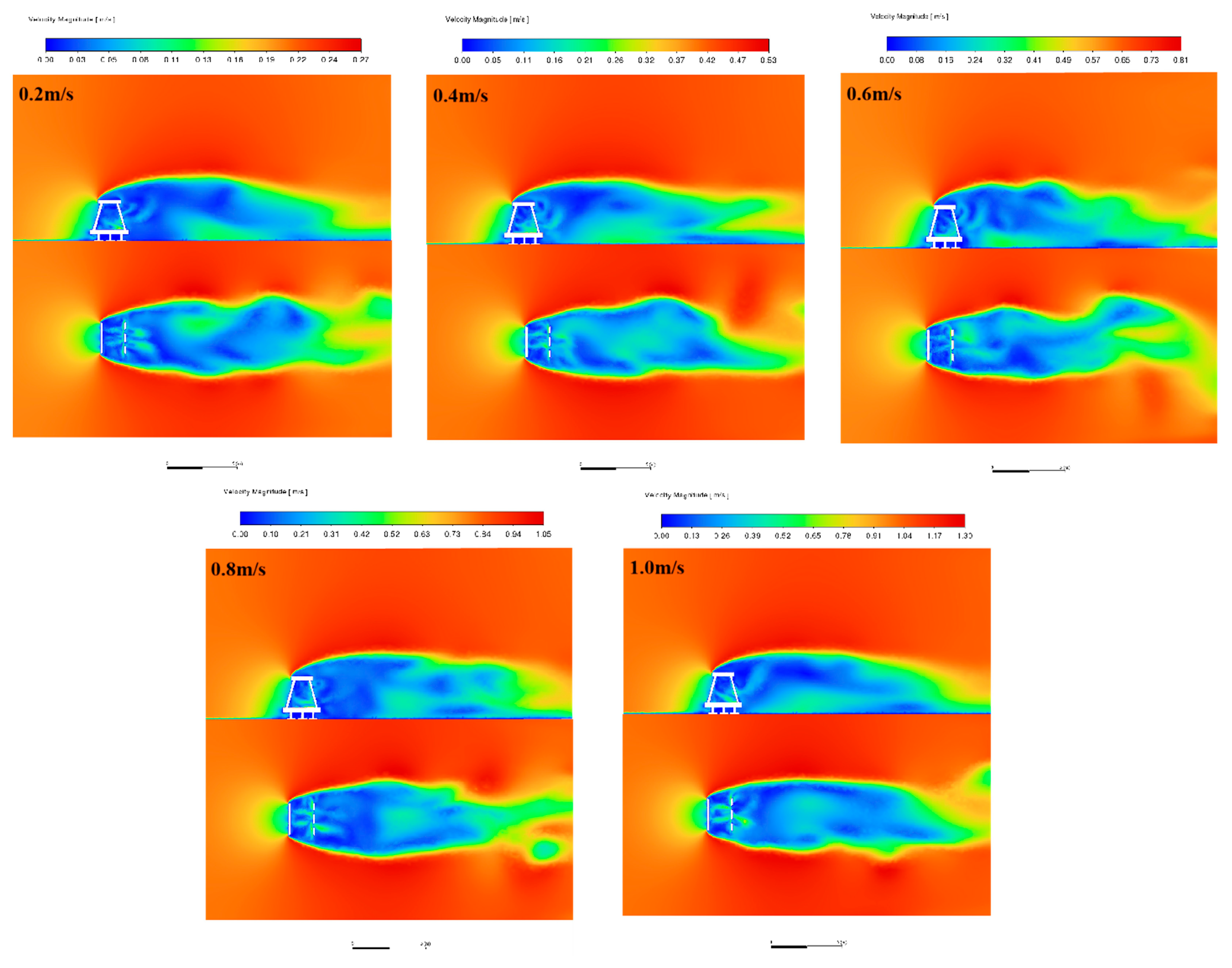
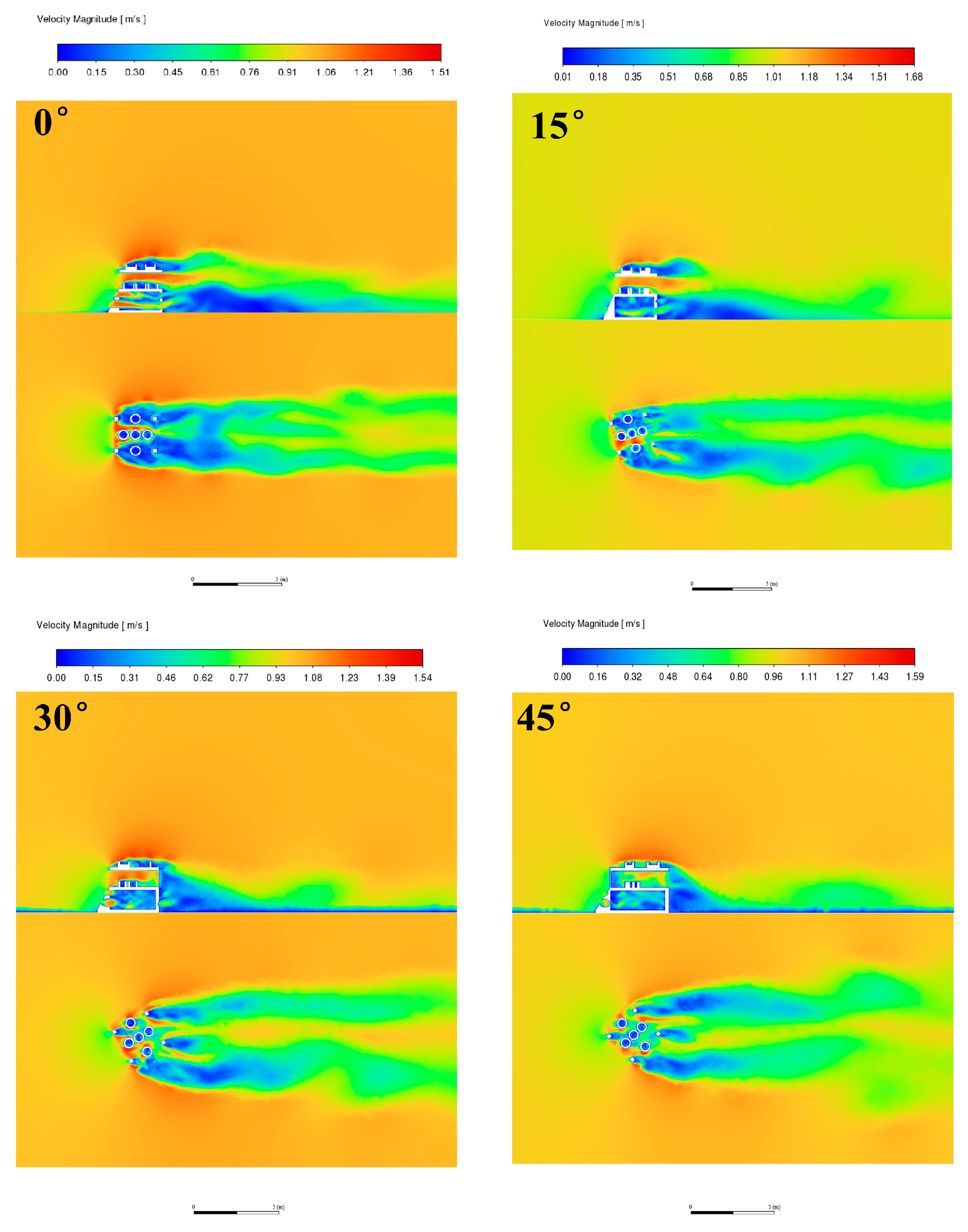
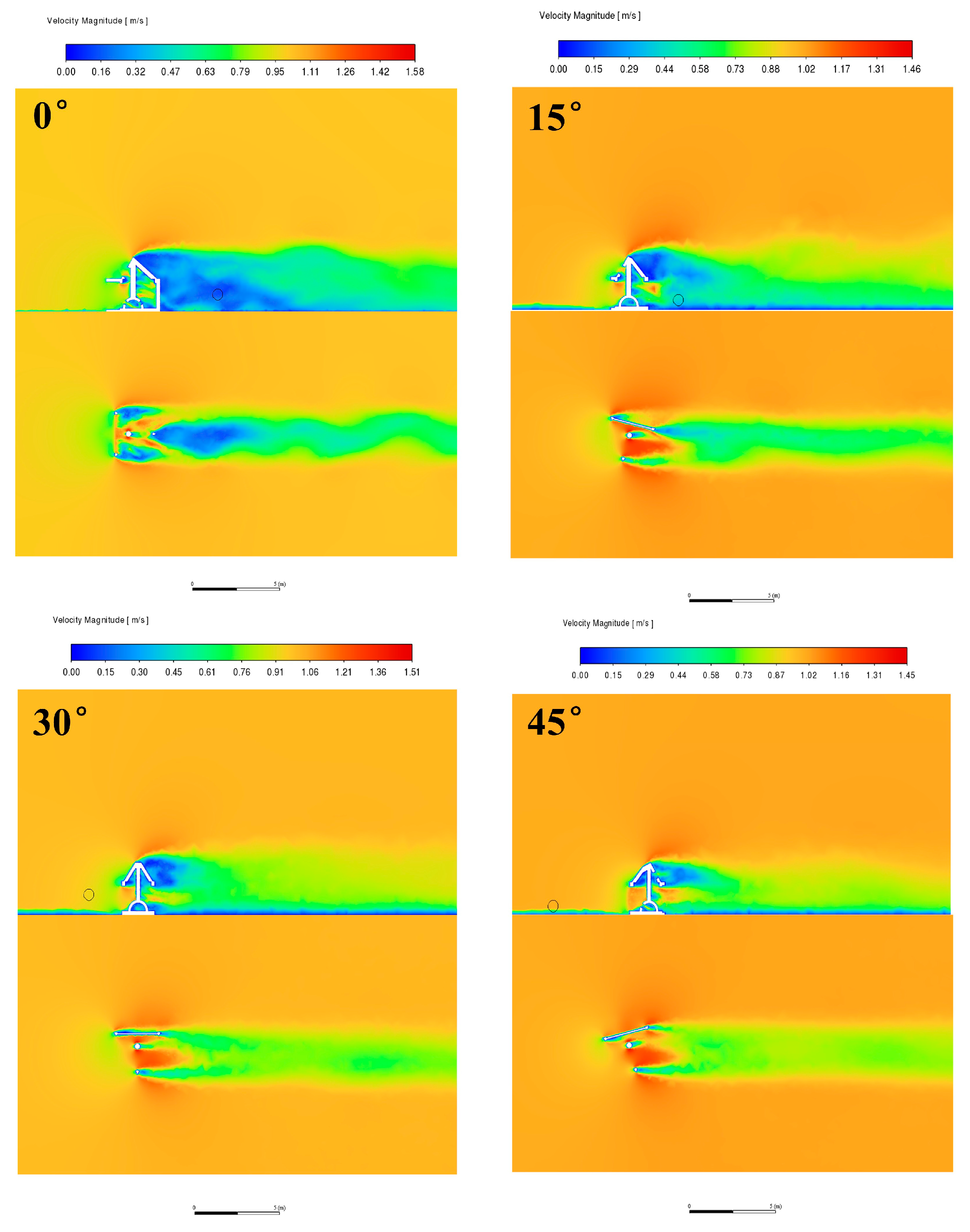
3.2. Numerical Results
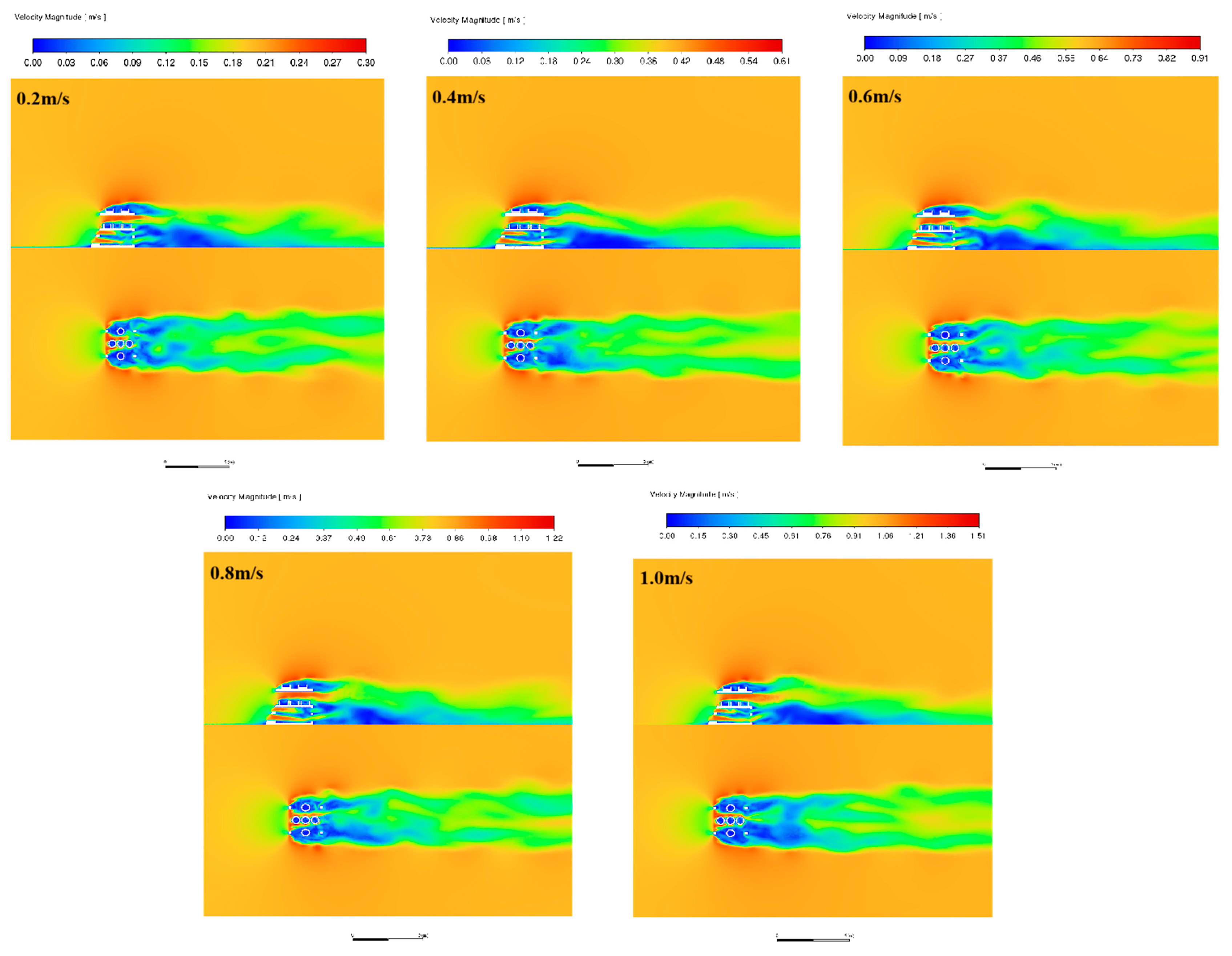
3.2.1. Cross-Sectional Flow Characteristics
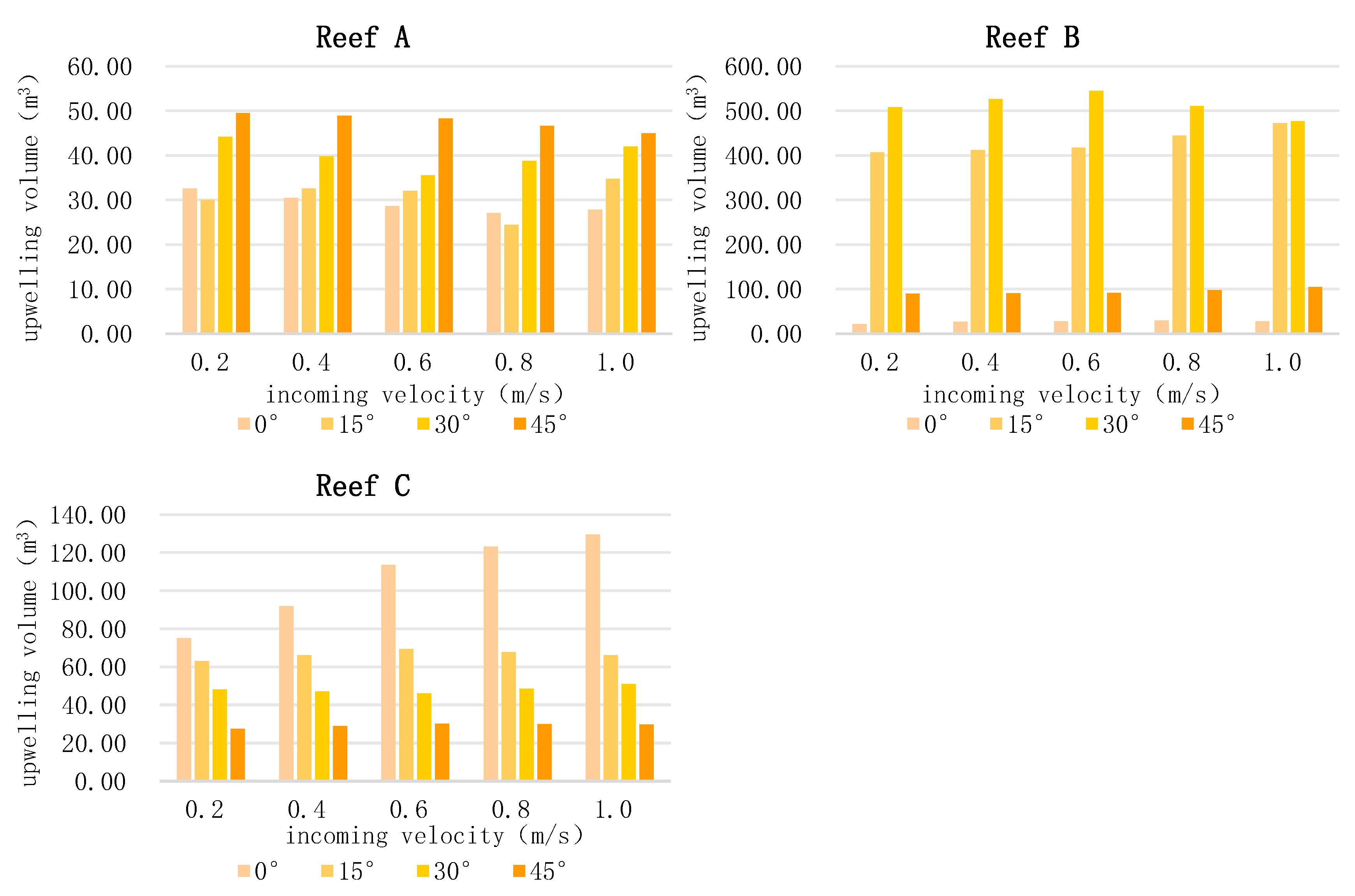
3.2.2. Volume Characteristics of the Flow Field for Different Incoming Velocities
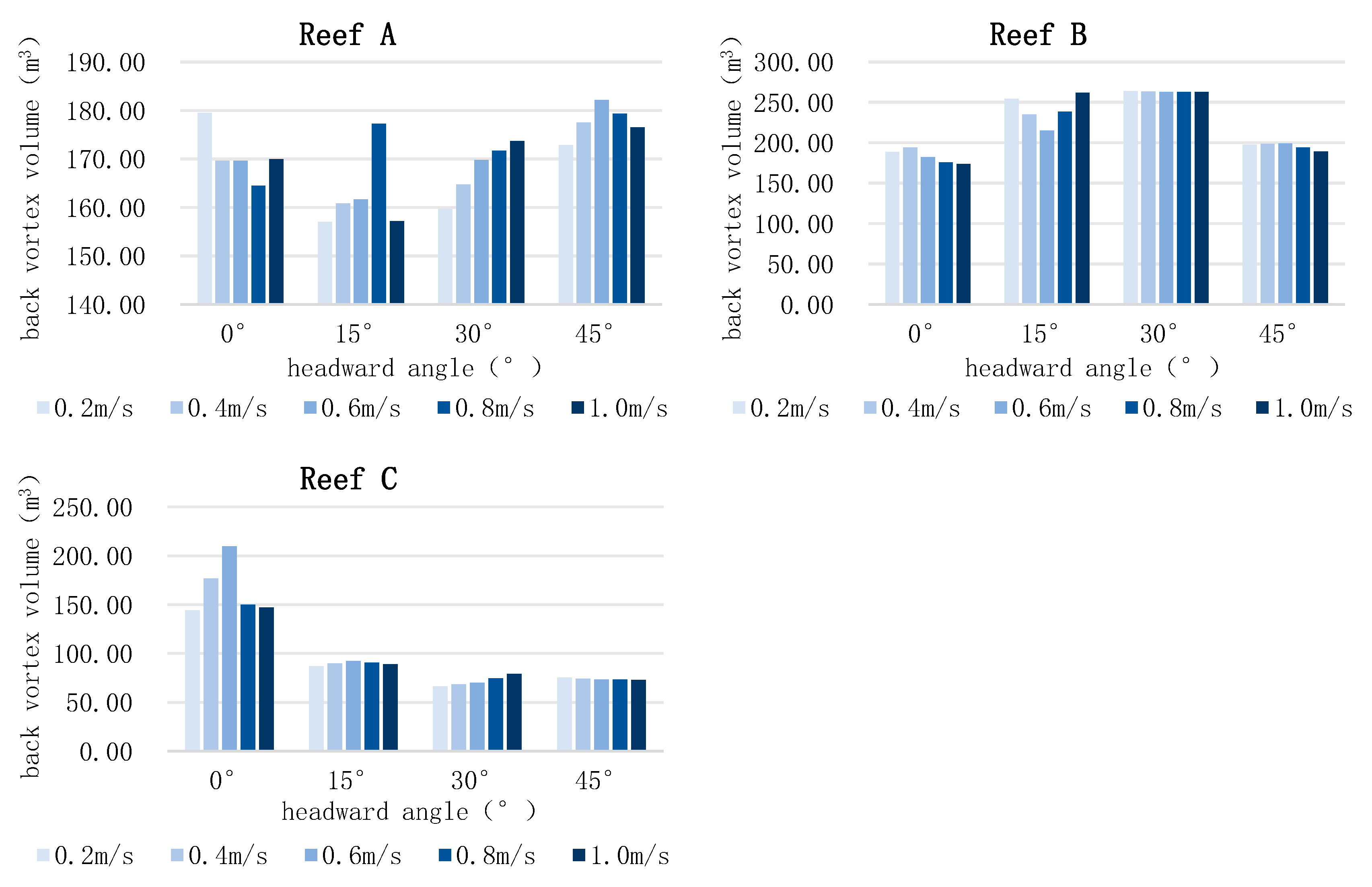
3.2.3. Volume Characteristics of the Flow Field for Different Flowing Angle
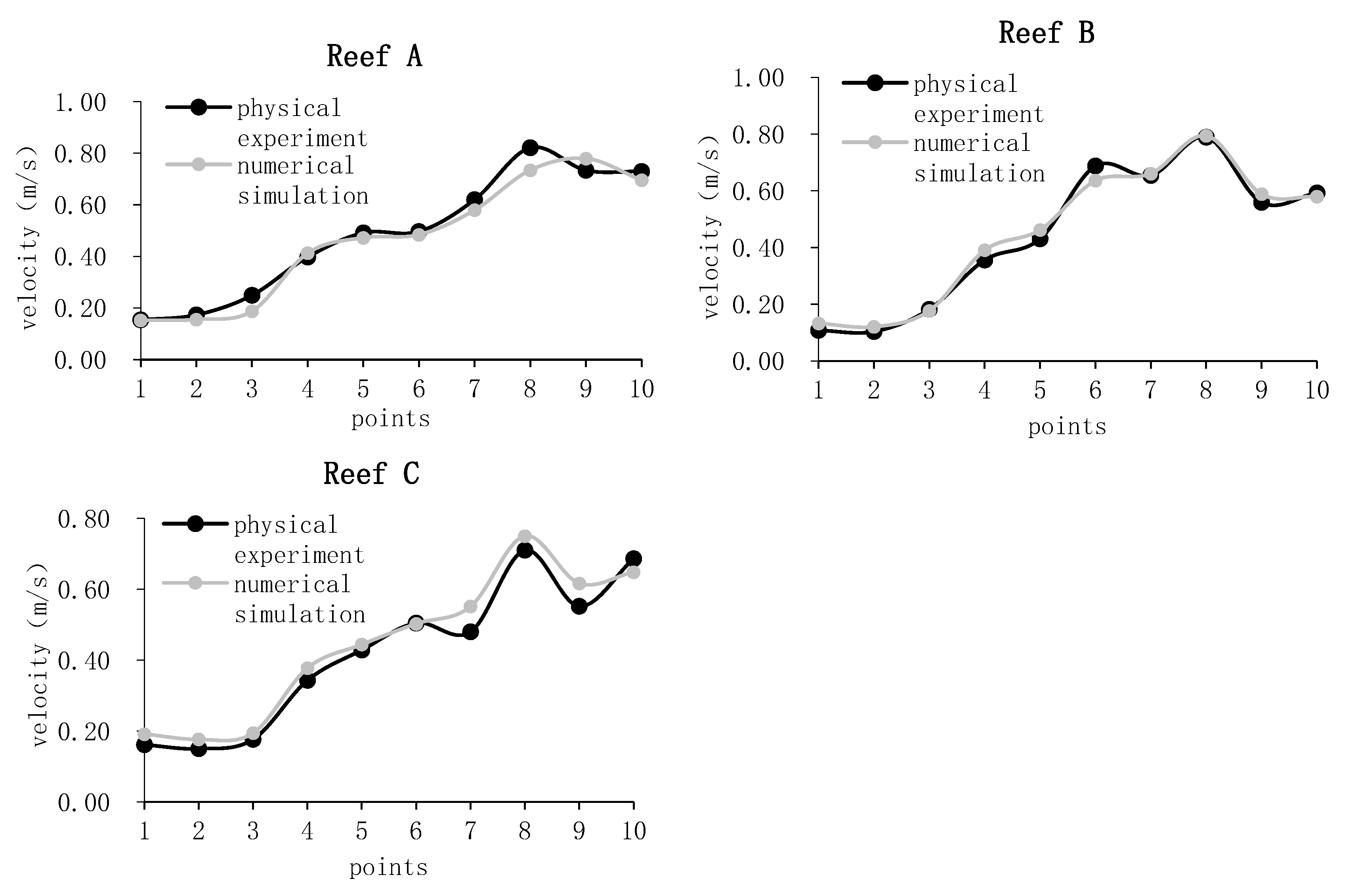
3.3. Validation of Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, K.X. Analysis of Economic Benefits of Marine Resource Utilization in China. Master’s Thesis, Anhui University of Finance and Economics, Bengbu, China, 2020. [Google Scholar]
- Hong, H.X.; Lin, L.M. Problems and Countermeasures of Fishery in China. J. Jimei Univ. (Nat. Sci. Ed.) 2002, 1, 5–10. [Google Scholar]
- Fariñas-Franco, J.M.; Roberts, D. Early faunal successional patterns in artificial reefs used for restoration of impacted biogenic habitats. Hydrobiologia 2014, 727, 75–94. [Google Scholar] [CrossRef]
- Gatts, P.; Franco, M.; Dos Santos, L.; Rocha, D.; de Sá, F.; Netto, E.; Machado, P.; Masi, B.; Zalmon, I. Impact of artificial patchy reef design on the ichthyofauna community of seasonally influenced shores at Southeastern Brazil. Aquat. Ecol. 2015, 49, 343–355. [Google Scholar] [CrossRef]
- Chua, C.; Chou, L.M. The use of artificial reefs in enhancing fish communities in Singapore. Hydrobiologia 1994, 285, 177–187. [Google Scholar] [CrossRef]
- Yu, D.Y.; Yang, Y.H.; Li, Y.J. Research on hydrodynamic characteristics and reef stability of artificial fish reefs with different opening ratios. J. Ocean Univ. China (Nat. Sci. Ed.) 2019, 49, 128–136. [Google Scholar]
- Seaman, W.J. Artificial Reef Evaluation: With Application to Natural Marine Habitats; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Jiang, Z.Y.; Liang, Z.L.; Huang, L.Y.; Liu, Y.; Tang, Y.L. Characteristics from a hydrodynamic model of a trapezoidal artificial reef. Chin. J. Oceanol. Limnol. 2014, 32, 1329–1338. [Google Scholar] [CrossRef]
- Liu, T.L.; Su, D.T. Numerical analysis of the influence of reef arrangements on artificial reef flow fields. Ocean Eng. 2013, 74, 81–89. [Google Scholar] [CrossRef]
- Li, J.; Lin, J.; Zhang, S.Y. Numerical experiments on the permeability of a square artificial reef and its effect on the flow field around the reef. J. Shanghai Ocean. Univ. 2010, 19, 836–840. [Google Scholar]
- Kageyama, M.; Osaka, H.; Yamada, H. Experiences of a fish reef with a perforated cubic fish tank and the feasibility of its perforation. J. Fish. Eng. Technol. 1982, 17, 1–10. [Google Scholar]
- Shao, W.J.; Liu, C.G.; Nie, H.T. Hydrodynamic characterization and flow field effect analysis of artificial reefs. Hydrodyn. Res. Prog. Ser. A 2014, 29, 580–585. [Google Scholar]
- Fu, D.W.; Chen, C.; Chen, Y.S. PIV experimental study on the flow field effect of a square artificial reef. J. Dalian Ocean. Univ. 2014, 29, 82–85. [Google Scholar]
- Wang, G.; Wan, R.; Wang, X.X.; Zhao, F.F. Study the influence of cut-opening ratio, cut-opening shape, and cut-opening number on the flow field of a cubic artificial reef. Ocean Eng. 2018, 162, 341–352. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Guan, C.T.; Song, X.F.; Liang, Z.L.; Cui, Y.; Li, Q. Numerical simulation of flow field effect of the star-shaped artificial reef. J. Agric. Eng. 2012, 28, 185–193+297–298. [Google Scholar]
- Zhang, S.; Hu, F.X.; Chu, W.H.; Huang, C.Y.; Liu, F.F.; Zhang, Q.C. Comparative study of numerical simulation and model test on the drag coefficient of the hexagonal open square artificial reef. Chin. Aquat. Sci. 2020, 11, 1350–1359. [Google Scholar]
- Jiang, Z.Y.; Guo, Z.S.; Zhu, L.X.; Liang, Z.L. Artificial fish reef structural design principles and research progress. J. Aquat. Prod. 2019, 9, 1881–1889. [Google Scholar]
- Guan, C.T.; Li, M.J.; Zheng, Y.X.; Li, J.; Cui, Y.; Li, Z.Z.; Wang, T.T. Guan Numerical simulation and physical stability study on the spacing of three-circle tube-type artificial reef deployment. J. Ocean Univ. China (Nat. Sci. Ed.) 2016, 9, 9–17. [Google Scholar]
- Lu, M.; Sun, X.H.; Li, Y.J.; Fan, Z.G. Turbulence numerical simulation method and its characteristic analysis. J. Hebei Univ. Archit. Technol. 2006, 2, 106–110. [Google Scholar]
- Fu, D.W. PIV Experimental Study on the Flow Field Effect of Artificial Reefs. Master’s Thesis, Dalian Ocean University, Dalian, China, 2013. [Google Scholar]
- Liu, J. Research on the Current Field Effect of the Hexagonal Artificial Reef. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Kim, D.; Jung, S.; Na, W.B. Evaluation of turbulence models for estimating the wake region of artificial reefs using particle image velocimetry and computational fluid dynamics. Ocean Eng. 2021, 223, 108673. [Google Scholar] [CrossRef]
- La Ode, M.A.; Iba, W.; Ingram, B.A.; Gooley, G.J.; de Silva, S.S. Mariculture in SE Sulawesi, Indonesia: Culture practices and the socio-economic aspects of the major commodities. Ocean Coast. Manag. 2015, 116, 44–57. [Google Scholar]
- Afero, F.; Miao, S.; Perez, A.A. Economic analysis of tiger grouper Epinephelus fuscoguttatus and humpback grouper Cromileptes altivelis commercial cage culture in Indonesia. Aquac. Int. 2010, 18, 725–739. [Google Scholar] [CrossRef]
- Albasri, H.; Iba, W.; Gooley, G.; De Silva, S. Mapping of Existing Mariculture Activities in South-East Sulawesi “Potential, Current and Future Status”. Indones. Aquac. J. 2010, 5, 173–186. [Google Scholar] [CrossRef]
- Aslan, L.O.M.; Hutauruk, H.; Zulham, A.; Effendy, I.; Atid, M.; Phillips, M.; Olsen, L.; Larkin, B.; Silva, S.S.D.; Gooley, G. Mariculture development opportunities in SE Sulawesi, Indonesia. Aquac. Asia 2008, 13, 36–41. [Google Scholar]
- Moreno-Sanchez, X.G.; Perez-Rojo, P.; Irigoyen-Arredondo, M.S.; Marin-Enriquez, E.; Abitia-Cárdenas, L.A.; Escobar-Sanchez, O. Feeding habits of the leopard grouper, Mycteroperca rosacea (Actinopterygii: Perciformes: Epinephelidae), in the central Gulf of California, BCS, Mexico. Acta Ichthyol. Piscat. 2019, 49, 9–22. [Google Scholar] [CrossRef]
- Kim, D.H.; Woo, J.H.; Yoon, H.S.; Na, W.B. Efficiency, tranquillity and stability indices to evaluate performance in the artificial reef wake region. Ocean Eng. 2016, 122, 253–261. [Google Scholar] [CrossRef]
- Gou, Y. Research on the Scale Effect of Artificial Reefs Based on Flow field Simulation Experiment. Ph.D. Thesis, Shanghai Ocean University, Shanghai, China, 2020. [Google Scholar]
- Liu, H.S.; Ma, X.; Zhang, Z.Y.; Yu, H.B.; Huang, H.J. Modeling experiment on artificial reef flow field effect. Aquat. J. Hydrogr. 2009, 33, 229–236. [Google Scholar]
- Zhang, B.H.; Zhang, X.Q.; Zheng, X.L. Study on the flow field effect of reef-building on offshore decommissioned oil platforms. Ocean Eng. 2024, 42, 86–95. [Google Scholar]
- Wei, L.Y.; Zhang, N.C. Numerical simulation of flow field effect of the hexagonal artificial reef. China Water Transp. 2023, 2, 110–112. [Google Scholar]
- Kim, D.H.; Woo, J.H.; Yoon, H.S.; Na, W.B. Wake lengths and structural responses of Korean general artificial reefs. Ocean Eng. 2014, 92, 83–91. [Google Scholar] [CrossRef]
- Fang, J.H.; Lin, J.; Yang, W. Numerical simulation of the flow field effect of a double-layer cross-wing artificial reef. J. Shanghai Ocean. Univ. 2021, 4, 743–754. [Google Scholar]
- Tan, S.F.; Wang, X.C.; Zhang, M.L. Flow field effects of a rectangular frame-type artificial reef. J. Appl. Mech. 2024, 12, 1–13. [Google Scholar]
- Lv, Z.M.; Lai, Q.K.; Zhan, D.Q. Comparative analysis of flow field near permeable and impermeable structures. Taiwan Water Resour. 2005, 54, 46–52. [Google Scholar]
- Liu, J.; Xu, L.X.; Zhang, S.; Hang, H.L. Experimental study on the drag coefficient of artificial reef model. J. Ocean Univ. China (Nat. Sci. Ed.) 2011, 41, 35–39. [Google Scholar]
- Sherman, R.L.; Gillian, D.S.; Spieler, R.E. Artificial reef design: Void space, complexity, and attractants. ICES J. Mar. Sci. 2002, 59, S196–S200. [Google Scholar] [CrossRef]
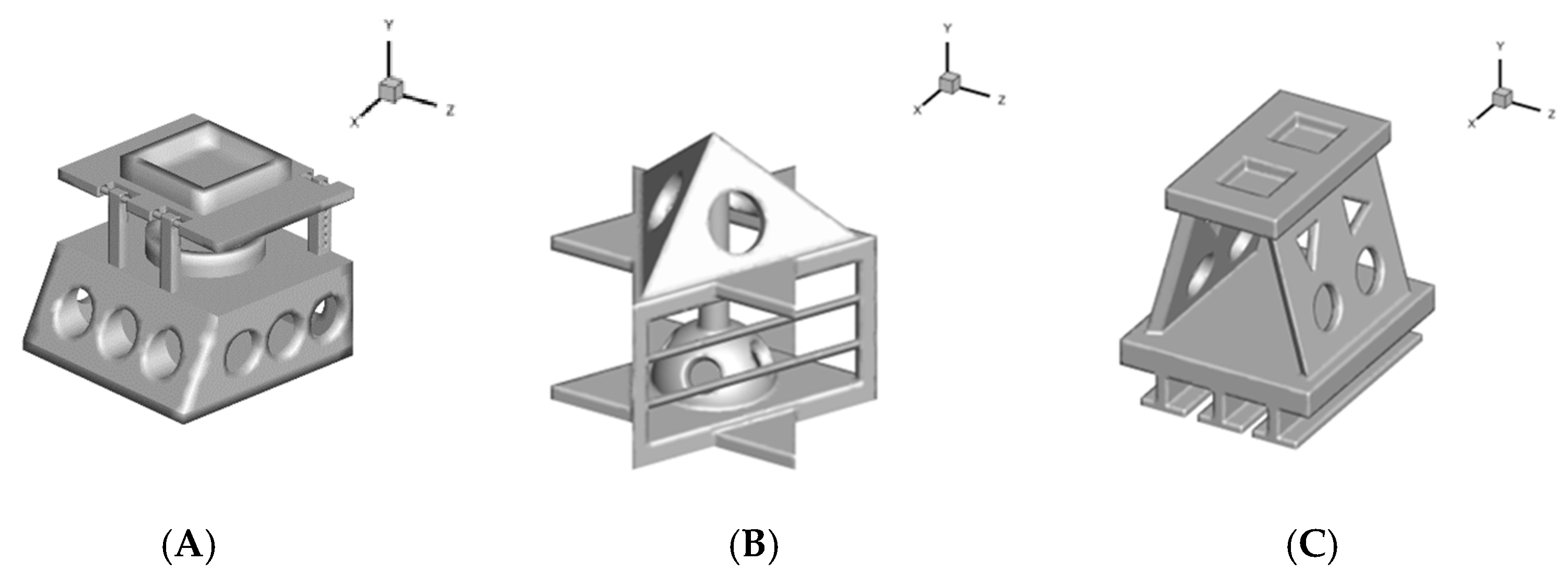







| Type | Dimensions/mm (L × W × H) | Material |
|---|---|---|
| A | 200 × 200 × 200 | plexiglass |
| B | 180 × 180 × 150 | |
| C | 200 × 180 × 200 |
| Structured Grid | Unstructured Grid | |
|---|---|---|
| Advantages | Fast generation, high generation quality, and simple structure | Wide range of applications and simple generation |
| Disadvantages | Limited scope of application; only for regular shapes | Higher requirements for hardness and precision |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, P.; Zhang, S.; Zhu, S.; Jiang, Z. Experimental and Numerical Simulation Studies on the Flow Field Effects of Three Artificial Fish Reefs. J. Mar. Sci. Eng. 2025, 13, 612. https://doi.org/10.3390/jmse13030612
Guo P, Zhang S, Zhu S, Jiang Z. Experimental and Numerical Simulation Studies on the Flow Field Effects of Three Artificial Fish Reefs. Journal of Marine Science and Engineering. 2025; 13(3):612. https://doi.org/10.3390/jmse13030612
Chicago/Turabian StyleGuo, Peng, Shuo Zhang, Shishi Zhu, and Zhaoyang Jiang. 2025. "Experimental and Numerical Simulation Studies on the Flow Field Effects of Three Artificial Fish Reefs" Journal of Marine Science and Engineering 13, no. 3: 612. https://doi.org/10.3390/jmse13030612
APA StyleGuo, P., Zhang, S., Zhu, S., & Jiang, Z. (2025). Experimental and Numerical Simulation Studies on the Flow Field Effects of Three Artificial Fish Reefs. Journal of Marine Science and Engineering, 13(3), 612. https://doi.org/10.3390/jmse13030612







