Scale Effects on Nominal Wake Fraction in Shallow Water: An Experimental and CFD Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Ship Models and Range of Scales
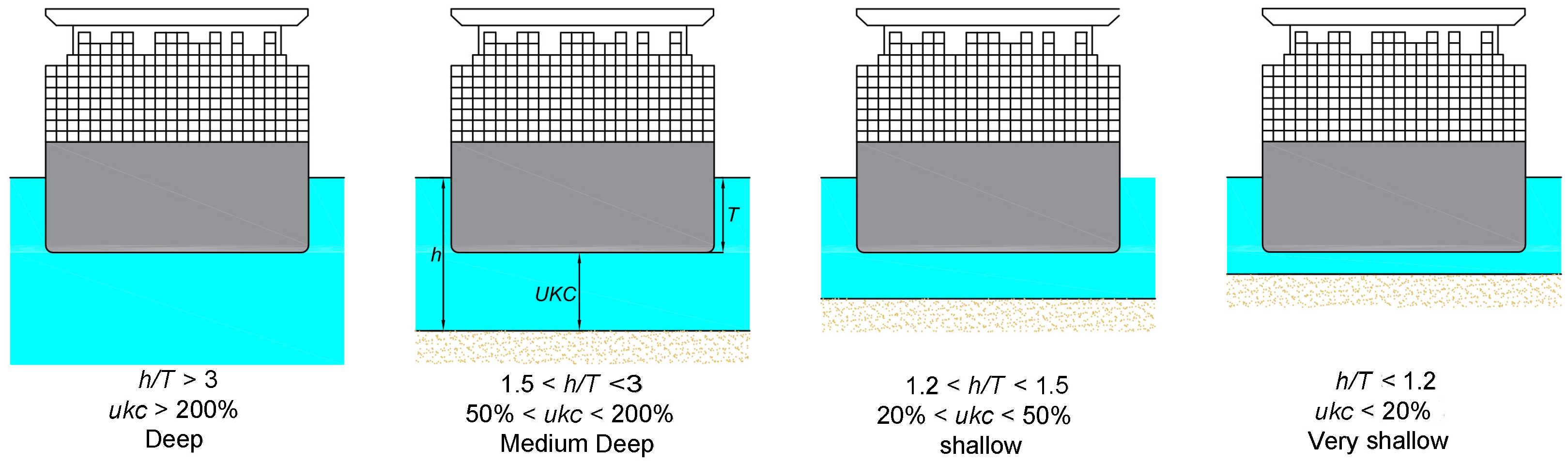
2.2. Experimental Setup and Benchmarking Data for Shallow Water Validation
2.3. Numerical Simulations Methodology
2.3.1. Governing Equations
2.3.2. Computation Domain and Boundary Conditions
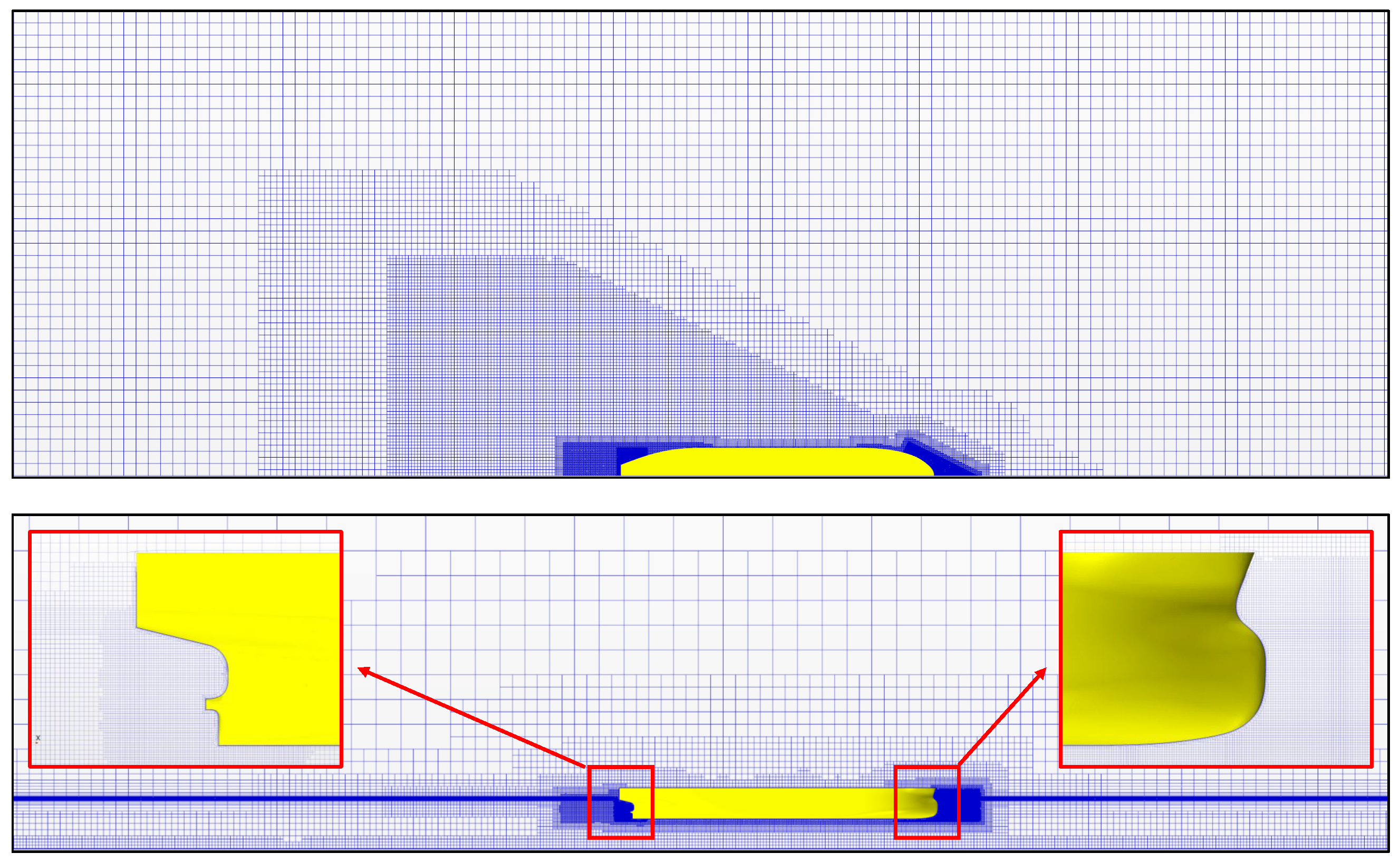
2.3.3. Mesh Generation
- : Viscous sublayer, dominated by laminar effects, where no wall functions are needed.
- : Buffer layer, a transitional zone where turbulence gradually increases.
- : Logarithmic layer, where wall functions are typically employed to model turbulence.
2.3.4. Physics Setup
2.4. Verification and Validation Study —V&V
2.4.1. Verification Study
- Round-off errors: These errors arise from the finite precision of numerical representations within a computer. While typically minor, they can accumulate during computations, especially as grid refinement increases, potentially impacting the results in certain scenarios. In this study, double-precision calculations were employed to mitigate round-off errors, rendering them negligible in most practical cases.
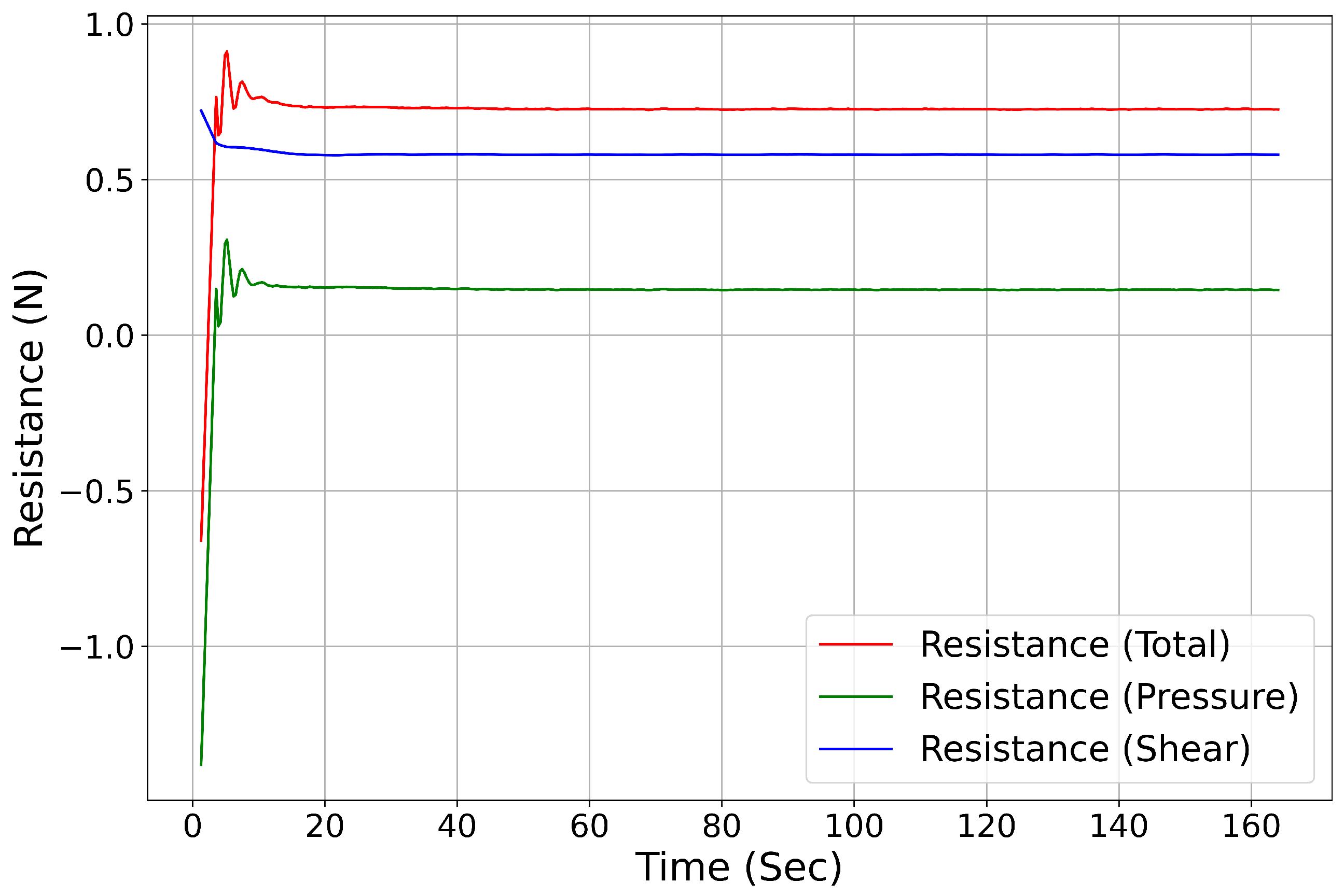
- Convergence errors: Convergence errors occur when iterative methods, often used to solve discretized mathematical models, fail to achieve full convergence. This is particularly relevant when dealing with nonlinear equations or for computational efficiency. To address convergence errors, double-precision schemes were used, and an adequate number of iterations were ensured. Total and frictional resistance values were closely monitored, confirming that convergence errors were negligible once these parameters stabilized or exhibited periodic behavior, indicating sufficient convergence of the solution, as shown in Figure 12.
- Programming errors: Programming errors can introduce unpredictable results if not identified and addressed. However, in this study, no specific analysis of programming errors was performed, as the simulation software used has already undergone rigorous verification and validation, ensuring its accuracy and reliability.
- Discretization errors and representation errors: Considering the above, the verification process primarily focused on discretization errors, covered in Section 2.4.2, which typically constitute the largest component of numerical error in CFD simulations. These errors stem from the approximation of continuous equations into discrete forms, introducing numerical inaccuracies.
2.4.2. Discretization Error Analysis
- Spatial Convergence Study: The impact of grid resolution on numerical accuracy was evaluated through systematic mesh refinement, commonly known as a grid/mesh sensitivity study, with convergence rates quantified using methods such as Richardson extrapolation.
- Temporal Convergence Study: The influence of time step size on simulation accuracy was analyzed to ensure temporal resolution independence, balancing numerical precision and computational efficiency.
2.4.3. Validation Study
- Validation using experimental results for the Aframax model ship in shallow water, with total resistance as the reference parameter.
- Validation against EFD/CFD results from the literature for the KVLCC2 hull form (both model and full scale) in deep water, using total resistance as the reference parameter.
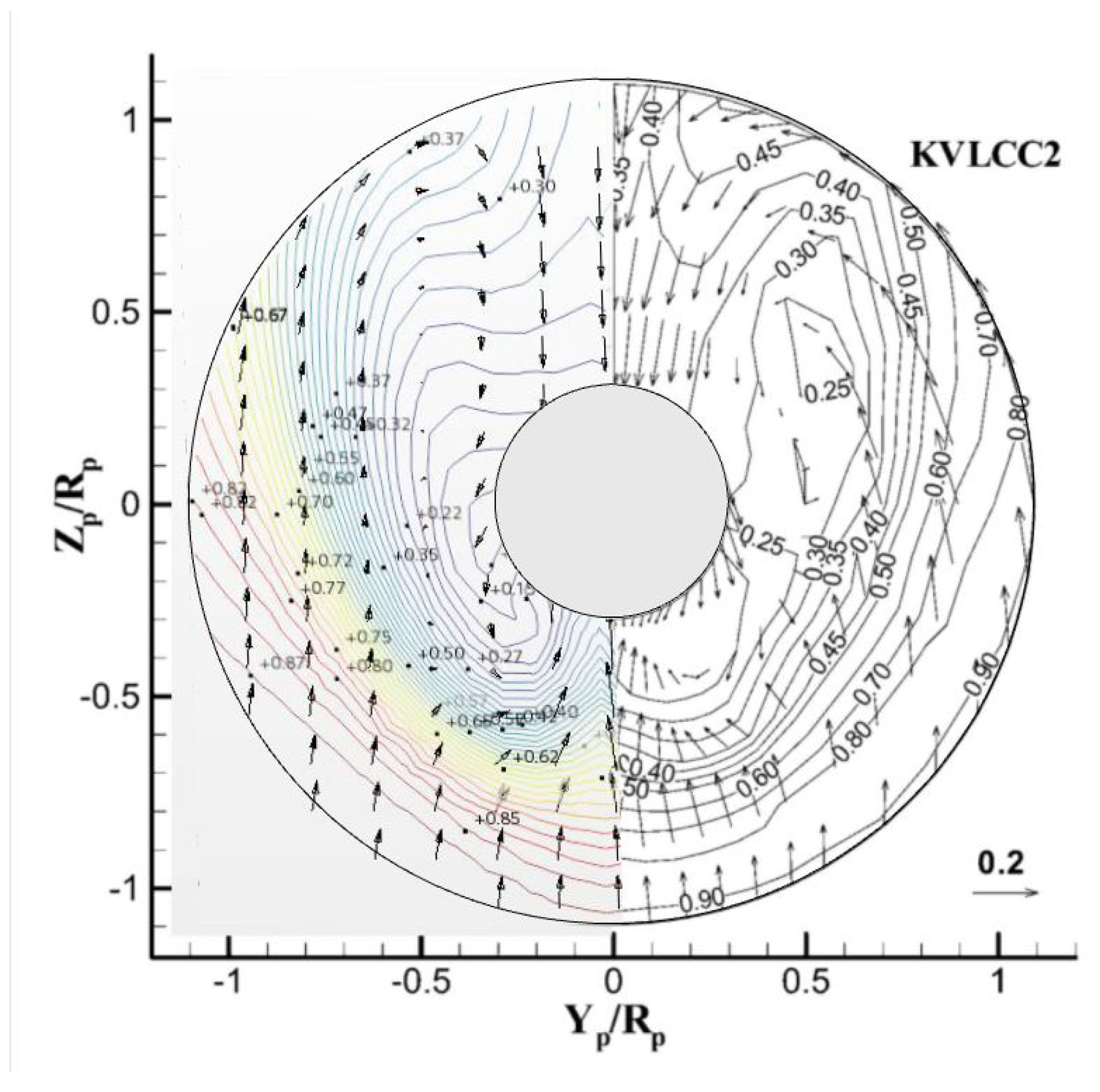
- Validation of the wake field distribution against experimental results for the KVLCC2 model ship in deep water.
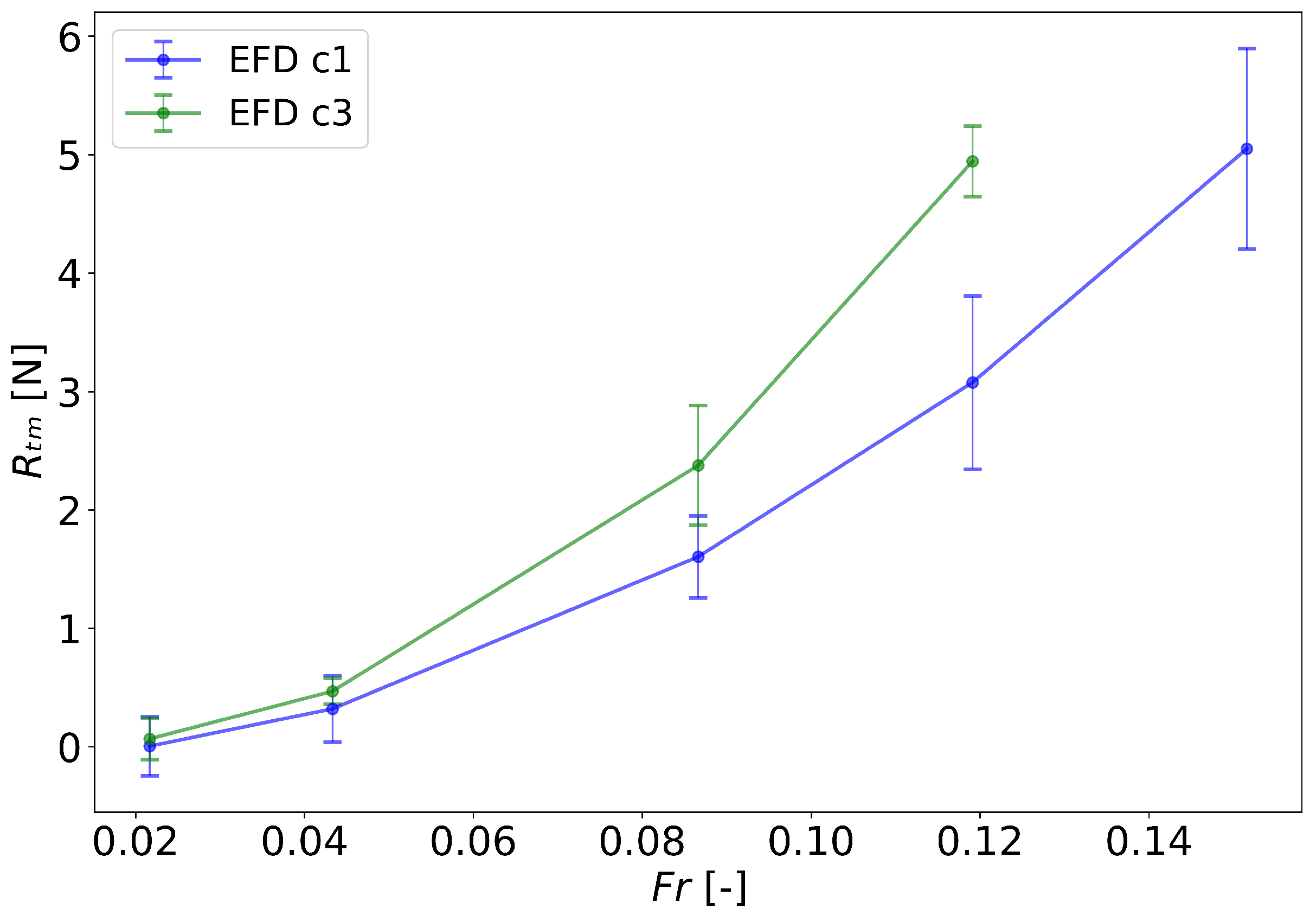
2.4.4. Validation with Aframax Hull Form—Shallow Water
2.4.5. Validation with KVLCC2 Hull Form—Deep Water and Full Scale
3. Results and Discussion
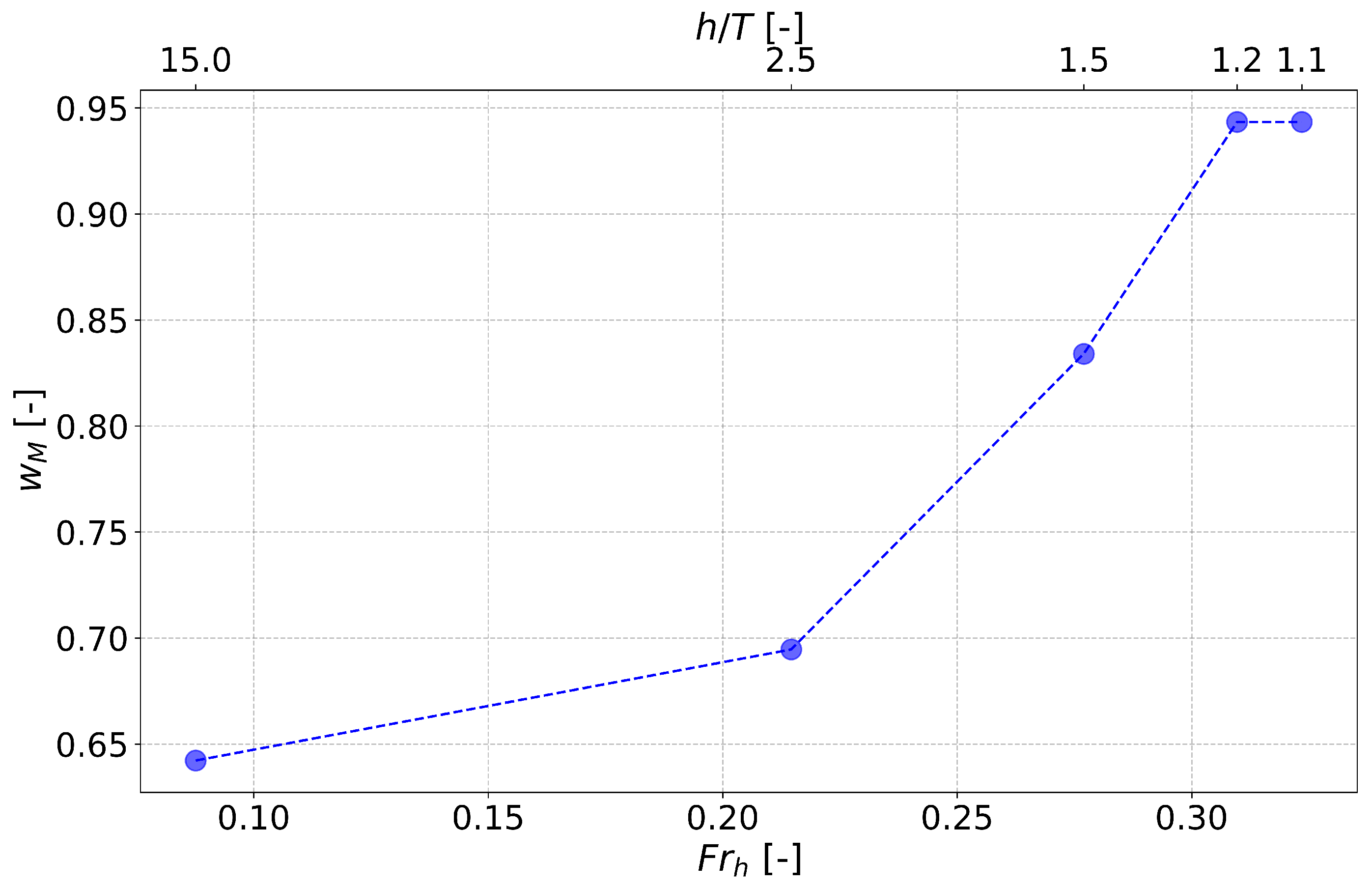
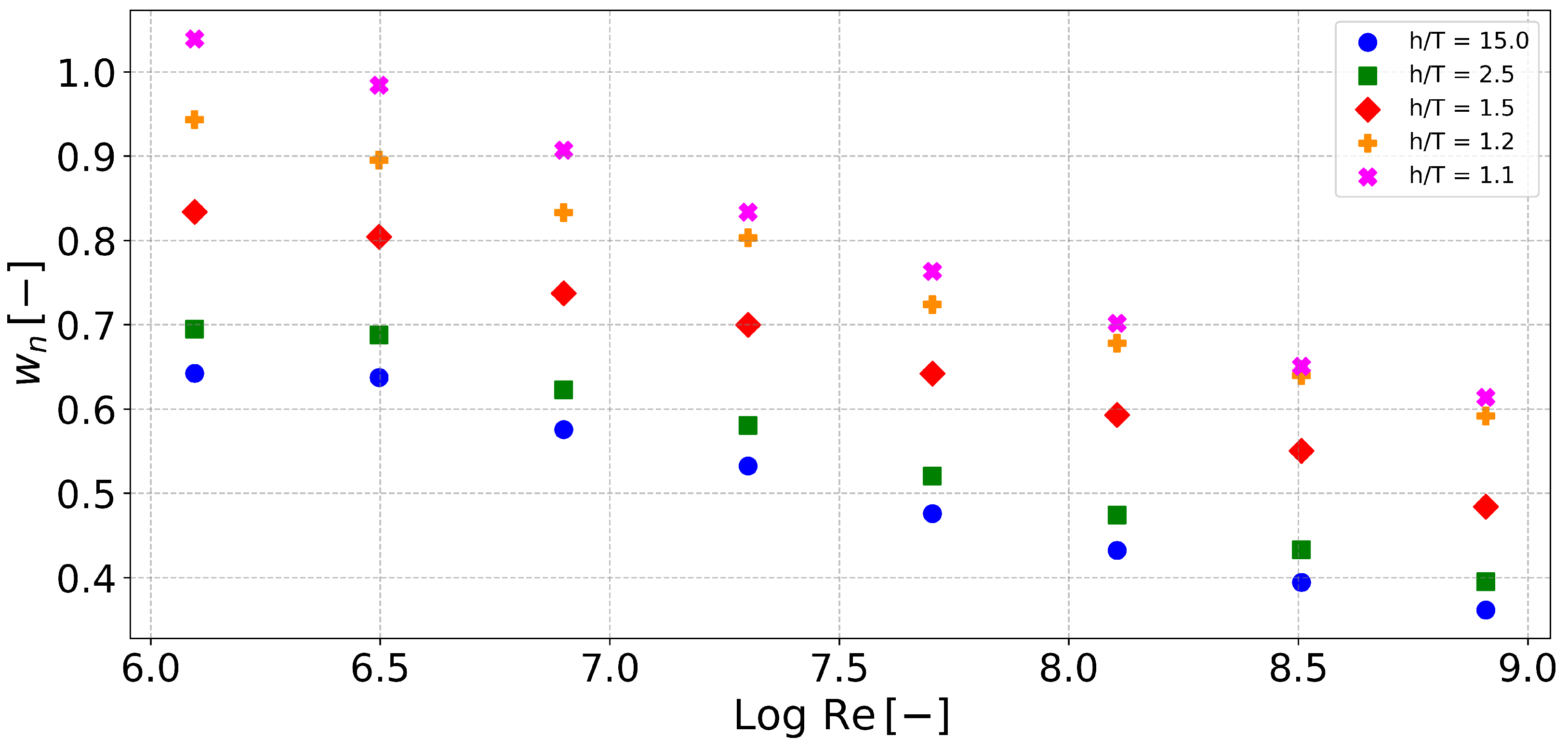
3.1. Water Depth Effect on Nominal Wake Fraction
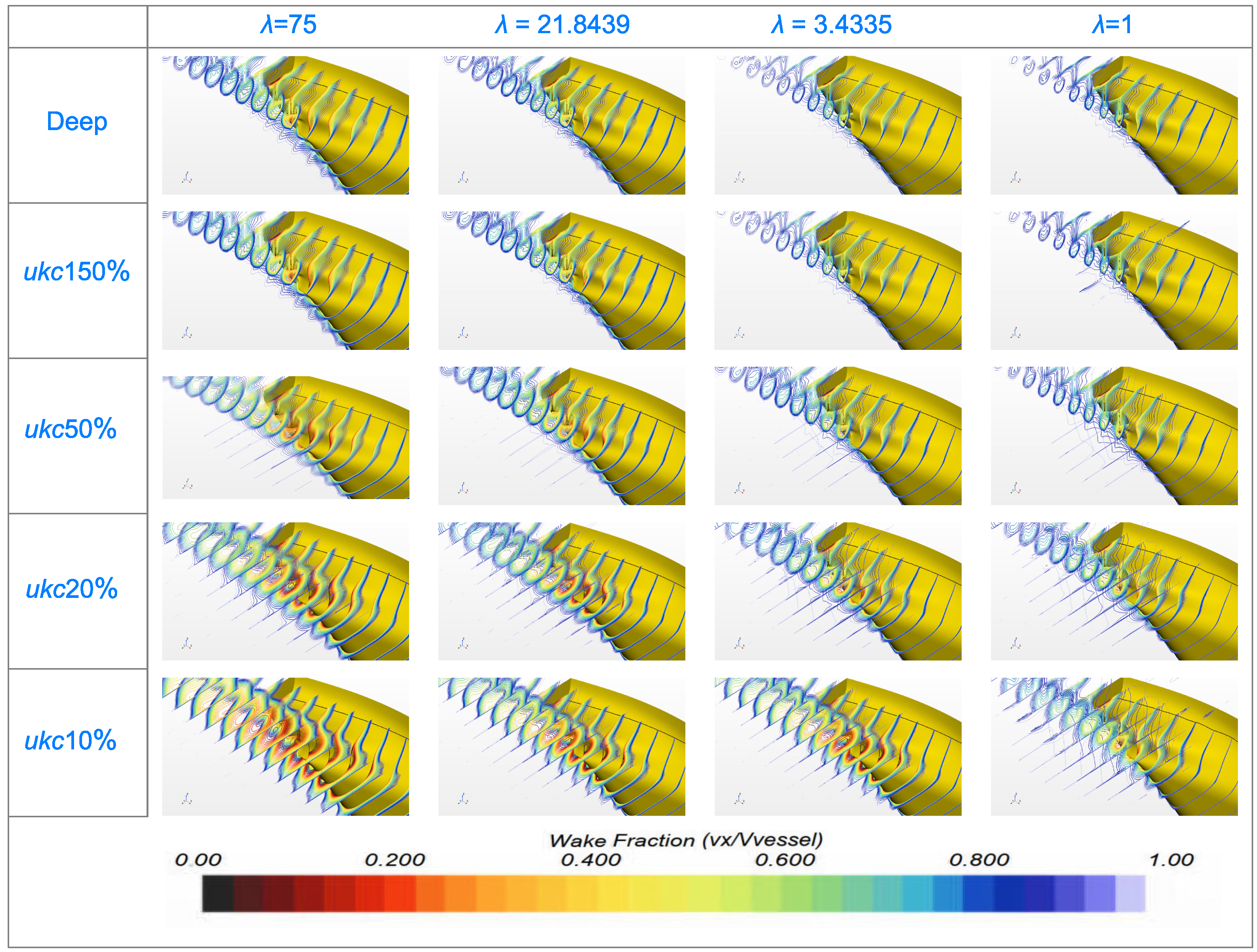
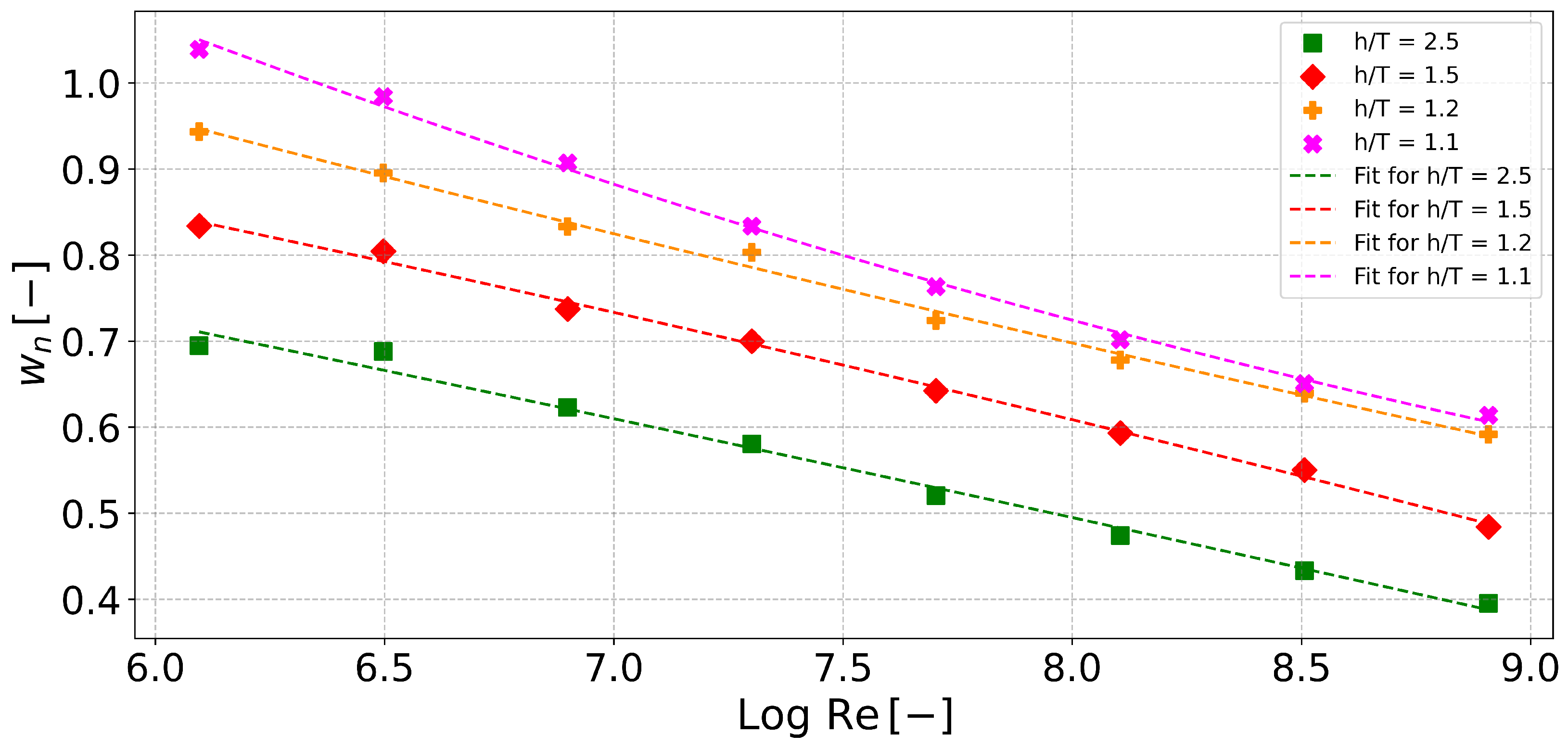
3.2. Scale Effect on Nominal Wake Fraction in Shallow Water
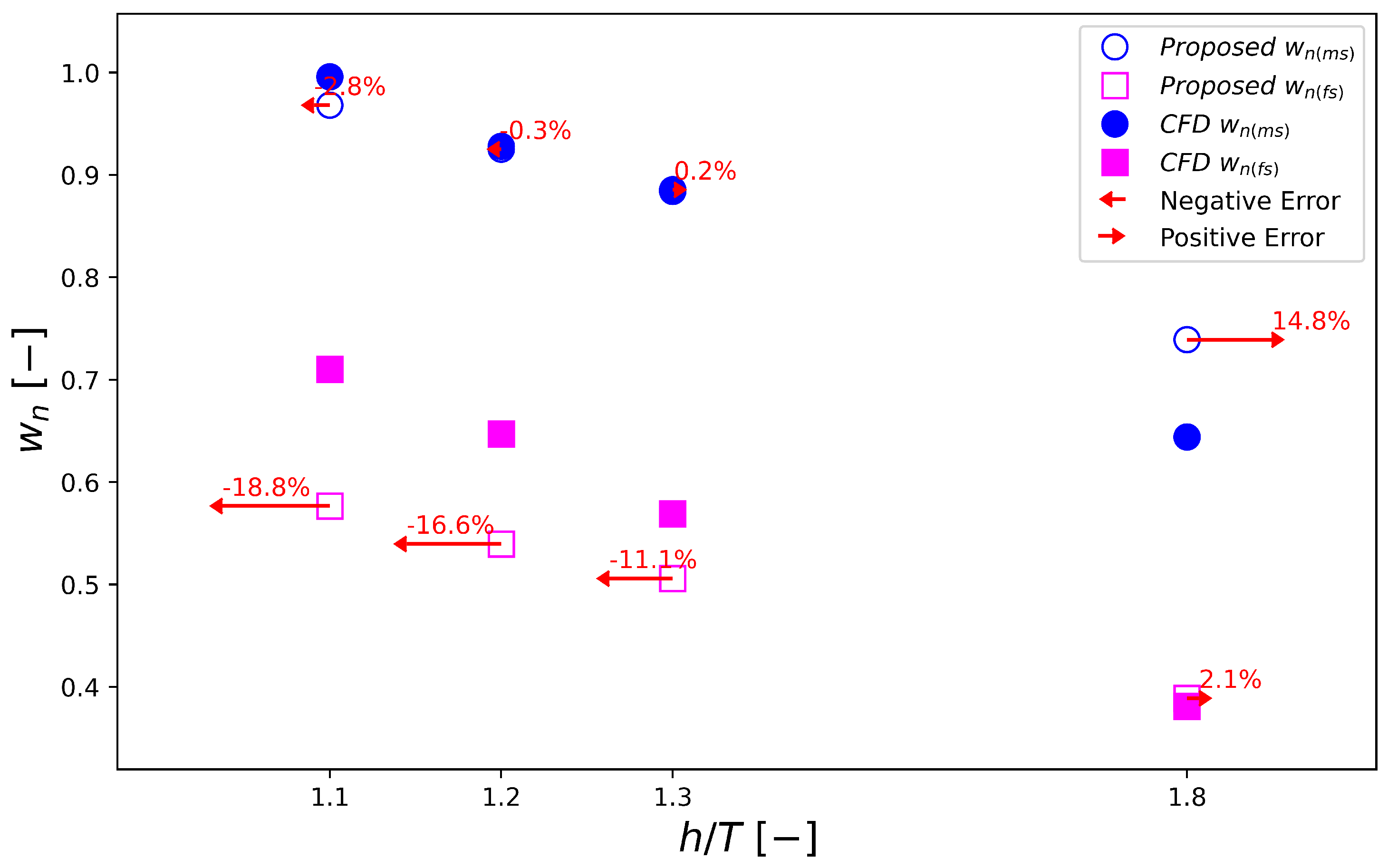
3.3. Application of the Proposed Equation for Nominal Wake in Shallow Water
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- PIANC. Capability of Ship Manoeuvring Simulation Models for Approach Channels and Fairways in Harbours: Report of Working Group no. 20 of Permanent Technical Committee II; General Secretariat of PIANC: Brussels, Belgium, 1992; 49p. [Google Scholar]
- Lackenby, H. The effect of shallow water on ship speed. Nav. Eng. J. 1964, 76, 21–26. [Google Scholar] [CrossRef]
- Eloot, K.; Vantorre, M. Ship behaviour in shallow and confined water: An overview of hydrodynamic effects through EFD. In Proceedings of the Assessment of Stability and Control Prediction Methods for NATO Air and Sea Vehicles, Portsdown, UK, 12–14 October 2011; p. 20. [Google Scholar]
- Robbins, A.; Macfarlane, G.; Allsop, D.; Leaper, P. When is Water Shallow? Int. J. Marit. Eng. 2013, 155, A116–A130. [Google Scholar] [CrossRef]
- Duarte, H.; López Droguett, E.; Martins, M.R.; Lutzhoft, M.; Pereira, P.S.; Lloyd, J. Review of practical aspects of shallow water and bank effects. Int. J. Marit. Eng. 2016, 158, 177–186. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Xiong, Y.; Wang, R.; Shen, X.R.; Zhong, C.H. Numerical study on scale effect of nominal wake of single screw ship. Ocean Eng. 2015, 104, 437–451. [Google Scholar] [CrossRef]
- Sasajima, H.; Tanaka, I. On the estimation of wakes of ships. In Proceedings of the 11th ITTC, Tokyo, Japan, 11–20 October 1966. [Google Scholar]
- Hoekstra, M. Prediction of full scale wake characteristics based on model wake survey. Int. Shipbuild. Prog. 1975, 22, 204–219. [Google Scholar]
- Tanaka, I. Scale effects on wake distribution of ships with bilge vortices. J. Soc. Nav. Archit. Jpn. 1983, 1983, 78–85. [Google Scholar]
- Tanaka, I. Scale effects on wake distribution and viscous pressure resistance of ships. J. Soc. Nav. Archit. Jpn. 1979, 1979, 53–60. [Google Scholar]
- García Gómez, A. Predicción y Análisis de la Configuración de la Estela en Buques de Una Hélice. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 1990. [Google Scholar]
- Choi, J.E.; Min, K.S.; Kim, J.H.; Lee, S.B.; Seo, H.W. Resistance and propulsion characteristics of various commercial ships based on CFD results. Ocean Eng. 2010, 37, 549–566. [Google Scholar] [CrossRef]
- Wang, J.B.; Yu, H.; Zhang, Y.F.; Cai, R. Numerical simulation of viscous wake field and resistance prediction around slow-full ships. Chin. J. Hydrodyn. 2010, 25, 648–654. [Google Scholar]
- Min, K.S.; Kang, S.H. Study on the form factor and full-scale ship resistance prediction method. J. Mar. Sci. Technol. 2010, 15, 108–118. [Google Scholar] [CrossRef]
- Castro, A.M.; Carrica, P.M.; Stern, F. Full scale self-propulsion computations using discretized propeller for the KRISO container ship KCS. Comput. Fluids 2011, 51, 35–47. [Google Scholar] [CrossRef]
- Sun, S.; Wang, C.; Chang, X.; Zhi, Y.c. Analysis of ship resistance and flow field characteristics in shallow water. J. Harbin Eng. Univ. 2017, 38, 499–505. [Google Scholar]
- Gaggero, S.; Villa, D.; Viviani, M. An extensive analysis of numerical ship self-propulsion prediction via a coupled BEM/RANS approach. Appl. Ocean. Res. 2017, 66, 55–78. [Google Scholar] [CrossRef]
- Pereira, F.S.; Eça, L.; Vaz, G. Verification and Validation exercises for the flow around the KVLCC2 tanker at model and full-scale Reynolds numbers. Ocean Eng. 2017, 129, 133–148. [Google Scholar] [CrossRef]
- Dogrul, A. Numerical prediction of scale effects on the propulsion performance of Joubert BB2 submarine. Brodogr. Teor. Praksa Brodogr. Pomor. Teh. 2022, 73, 17–42. [Google Scholar] [CrossRef]
- Starke, B.; Windt, J.; Raven, H.C. Validation of viscous flow and wake field predictions for ships at full scale. In Proceedings of the 26th ONR Symposium on Naval Hydrodynamics, Rome, Italy, 17–22 September 2006; pp. 17–22. [Google Scholar]
- Visonneau, M. A Step Towards the Numerical Simulation of Viscous Flows Around Ships at Full Scale-Recent Achievements Within the European Union Project Effort; Royal Institute of Naval Architecture Marine CFD: Southampton, UK, 2005. [Google Scholar]
- Sun, S.; Qin, T.; Li, X. Research of scale effect on propeller bearing force of a four-screw ship in oblique flow. Phys. Fluids 2024, 36, 107145. [Google Scholar] [CrossRef]
- Uzun, D.; Sezen, S.; Ozyurt, R.; Atlar, M.; Turan, O. A CFD study: Influence of biofouling on a full-scale submarine. Appl. Ocean. Res. 2021, 109, 102561. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Lai, M.Y.; Ni, Y.; Feng, L. CFD study of hull wakes in oblique flow at model and full scales. Appl. Ocean. Res. 2021, 112, 102689. [Google Scholar] [CrossRef]
- Tat, H.L.; Tran, V.T. Numerical Investigation of the Scale Effect on the Flow around the Ship by using RANSE Method. CFD Lett. 2023, 15, 67–78. [Google Scholar] [CrossRef]
- Delen, C.; Can, U.; Bal, S. Prediction of Resistance and Self-Propulsion Characteristics of a Full-Scale Naval Ship by CFD-Based GEOSIM Method. J. Ship Res. 2020, 65, 346–361. [Google Scholar] [CrossRef]
- Can, U.; Delen, C.; Bal, S. Effective wake estimation of KCS hull at full-scale by GEOSIM method based on CFD. Ocean Eng. 2020, 218, 108052. [Google Scholar] [CrossRef]
- Sun, S.; Hu, Z.; Wang, C.; Guo, Z.; Li, X. Numerical prediction of scale effect on propeller bearing force of a four-screw ship. Ocean Eng. 2021, 229, 108974. [Google Scholar] [CrossRef]
- Pena, B.; Muk-Pavic, E.; Thomas, G.; Fitzsimmons, P. An approach for the accurate investigation of full-scale ship boundary layers and wakes. Ocean Eng. 2020, 214, 107854. [Google Scholar] [CrossRef]
- Ma, Z. Influence of scale effect on flow field offset for ships in confined waters. Brodogradnja 2024, 75, 75106. [Google Scholar] [CrossRef]
- Sakamoto, N.; Kobayashi, H.; Ohashi, K.; Kawanami, Y.; Windén, B.; Kamiirisa, H. An overset RaNS prediction and validation of full scale stern wake for 1,600TEU container ship and 63,000 DWT bulk carrier with an energy saving device. Appl. Ocean. Res. 2020, 105, 102417. [Google Scholar] [CrossRef]
- Ma, W.; Chang, X.; Sun, S.; Jia, X. Numerical research on the effect of brackets installation angle on the propeller wake field and propulsion performance in a four-screw ship. Ocean Eng. 2022, 266, 112303. [Google Scholar] [CrossRef]
- Ma, W.; Chang, X.; Wang, W.; Sun, S.; Chen, Q. Study on the influence of shaft brackets on the scale effect of the four-screw ship wake field. Ocean Eng. 2023, 287, 115881. [Google Scholar] [CrossRef]
- Liu, J.Z.; Guo, H.P.; Zou, Z.J.; Liu, Y. A study on interaction among hull, diesel engine and propellers of a twin-screw ship during turning circle maneuver. Appl. Ocean. Res. 2023, 135, 103517. [Google Scholar] [CrossRef]
- International Towing Tank Conference (ITTC). ITTC – Recommended Procedures and Guidelines: Ship Models. Technical Report 7.5-01-01-01, ITTC. 2017. Available online: https://www.ittc.info/media/7975/75-01-01-01.pdf (accessed on 20 January 2025).
- International Towing Tank Conference (ITTC). ITTC – Recommended Procedures: Fresh Water and Seawater Properties. Technical Report 7.5-02-01-03, ITTC. 2011. Available online: https://ittc.info/media/4048/75-02-01-03.pdf (accessed on 20 January 2025).
- ITTC. Procedures and Guidelines: Practical Guidelines for Ship CFD Applications, 7.5; ITTC: Boulder, CO, USA, 2011. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 271–275. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2003; Volume 153. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.-J. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. Diffuse-Interface Methods in Fluid Mechanics. Annu. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef]
- Quérard, A.; Temarel, P.; Turnock, S.R. Influence of Viscous Effects on the Hydrodynamics of Ship-Like Sections Undergoing Symmetric and Anti-Symmetric Motions, Using RANS. In Proceedings of the OMAE 2008: 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 5, pp. 683–692. [Google Scholar] [CrossRef]
- Salim, S.M.; Cheah, S.C. Wall y+ Strategy for Dealing with Wall-bounded Turbulent Flows. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2009, Hong Kong, 18–20 March 2009; pp. 2165–2170. [Google Scholar]
- Lin, T.Y.; Kouh, J.s. On the scale effect of thrust deduction in a judicious self-propulsion procedure for a moderate-speed containership. J. Mar. Sci. Technol. 2014, 20, 373–391. [Google Scholar] [CrossRef]
- Tezdogan, T.; Incecik, A.; Turan, O. Full-scale unsteady RANS simulations of vertical ship motions in shallow water. Ocean Eng. 2016, 123, 131–145. [Google Scholar] [CrossRef]
- Dashtimanesh, A.; Tavakoli, S.; Kohansal, A.; Khosravani, R.; Ghassemzadeh, A. Numerical study on a heeled one-stepped boat moving forward in planing regime. Appl. Ocean. Res. 2020, 96, 102057. [Google Scholar] [CrossRef]
- Yang, B.; Lefrançois, E.; Kaidi, S. Numerical Investigation of the Effect of Confined Curved Waterways on Ship Hydrodynamics. J. Mar. Sci. Eng. 2021, 9, 112–124. [Google Scholar]
- Yang, B.; Kaidi, S.; Lefrançois, E. CFD Method to Study Hydrodynamic Forces Acting on a Ship Navigating in Confined Curved Channels. J. Mar. Sci. Eng. 2022, 10, 1263. [Google Scholar] [CrossRef]
- Wang, H.; Zou, Z. Numerical Prediction of Hydrodynamic Forces on a Ship Passing Through a Lock with Different Configurations. J. Hydrodyn. 2022, 26, 1–9. [Google Scholar]
- He, N.V.; Hien, N.V. Viscous Resistance Acting on a Symmetrical Hull with Different Turbulent Viscous Models. In Proceedings of the NAFOSTED Conference on Information and Computer Science, Ho Chi Minh City, Vietnam, 31 October–1 November 2022; pp. 414–418. [Google Scholar] [CrossRef]
- Yuan, Z.M.; Incecik, A.; Alexander, D. Verification of a new radiation condition for two ships advancing in waves. Appl. Ocean. Res. 2014, 48, 186–201. [Google Scholar] [CrossRef]
- Lewis, E.V. Principles of Naval Architecture; Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 1988. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998. [Google Scholar]
- Richardson, L.F. The Approximate Arithmetical Solution by Finite Differences of Physical Problems Involving Differential Equations with an Application to the Stress in a Masonry Dam. Philos. Trans. R. Soc. Lond. Ser. A 1911, 210, 307–357. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.; Shao, J. Quantitative V&V of CFD simulations and certification of CFD codes. Int. J. Numer. Methods Fluids 2006, 50, 1335–1355. [Google Scholar] [CrossRef]
- ITTC. Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures; 25th ITTC 2008, Resistance Committee; ITTC: Boulder, CO, USA, 2008. [Google Scholar]
- Suez Canal Authority. Suez Canal Rules of Navigation. 2020. Available online: https://www.suezcanal.gov.eg/ (accessed on 20 January 2025).
- Panama Canal Authority. Panama Canal Rules of Navigation (N-1-2023). 2023. Available online: https://pancanal.com/ (accessed on 20 January 2025).
- Kim, W.J.; Van, S.H.; Kim, D.H. Measurement of flows around modern commercial ship models. Exp. Fluids 2001, 31, 567–578. [Google Scholar] [CrossRef]
- Song, K.w.; Guo, C.y.; Wang, C.; Sun, C.; Li, P.; Zhong, R.f. Experimental and numerical study on the scale effect of stern flap on ship resistance and flow field. Ships Offshore Struct. 2019, 15, 981–997. [Google Scholar] [CrossRef]
- Dogrul, A.; Song, S.; Demirel, Y.K. Scale effect on ship resistance components and form factor. Ocean Eng. 2020, 209, 107428. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. An investigation into the effect of hard fouling on the ship resistance using CFD. Appl. Ocean. Res. 2020, 100, 102205. [Google Scholar] [CrossRef]
- Sheng, Z.; Liu, Y. Chuanbo Yuanli; Shanghai Jiao Tong University Press: Shanghai, China, 2003. [Google Scholar]












| Aframax | KVLCC2 | ||||||
|---|---|---|---|---|---|---|---|
| Particulars | Units | Model Scale | Full Scale | Model Scale | Full Scale | ||
| Scale | - | 75 | 1 | 75 | 58 | 1 | |
| Length overall | [m] | 3.16 | 237 | 4.33 | 5.60 | 325 | |
| Length b/w perpendiculars | [m] | 3.067 | 230 | 4.27 | 5.52 | 320 | |
| Breadth | B | [m] | 0.56 | 42 | 0.77 | 1.00 | 58 |
| Draught | T | [m] | 0.2 | 15 | 0.28 | 0.36 | 20.8 |
| Block Coefficient | [-] | 0.767 | 0.767 | 0.81 | 0.81 | 0.81 | |
| Scale factor [-] | Length L [m] | Beam B [m] | Draught T [m] | Velocity V [m/s] | Froude Number [-] | Reynolds Number [-] |
|---|---|---|---|---|---|---|
| 75 | 3.07 | 0.56 | 0.2 | 0.48 | 0.09 | |
| 40.5 | 5.68 | 1.04 | 0.37 | 0.65 | 0.09 | |
| 21.8 | 10.53 | 1.92 | 0.69 | 0.88 | 0.09 | |
| 11.8 | 19.51 | 3.56 | 1.27 | 1.20 | 0.09 | |
| 6.4 | 36.15 | 6.6 | 2.36 | 1.63 | 0.09 | |
| 3.4 | 66.99 | 12.23 | 4.37 | 2.22 | 0.09 | |
| 1.9 | 124.13 | 22.67 | 8.10 | 3.02 | 0.09 | |
| 1 | 230.00 | 42.00 | 15.0 | 4.12 | 0.09 |
| 150% | 50% | 20% | 10% | |
|---|---|---|---|---|
| Model Ship Speed [m/s] | Depth Froude Number | |||
| 0.1188 | 0.054 | 0.031 | 0.020 | 0.014 |
| 0.2376 | 0.107 | 0.063 | 0.041 | 0.028 |
| 0.4752 | 0.215 | 0.125 | 0.082 | 0.055 |
| 0.6534 | 0.295 | 0.172 | 0.112 | - |
| 0.8316 | 0.375 | 0.219 | - | - |
| Surface | Boundary Conditions |
|---|---|
| Inlet | Velocity inlet at |
| Outlet | Pressure Outlet |
| Top | Velocity inlet |
| Bottom | Non-slip moving wall (with the same speed as the incoming flow) |
| Side | Velocity inlet |
| Symmetry plane | Symmetry |
| Ship Hull | Non slip stationary wall |
| Method | Mass Conservation | Topological Changes | Computational Cost | References |
|---|---|---|---|---|
| VOF | Excellent | Excellent | Low to Moderate | [39] |
| Level Set | Moderate | Excellent | High | [40] |
| SPH | Moderate | Excellent | High | [41] |
| Front Tracking | Good | Moderate | High | [42] |
| Phase Field | Moderate | Excellent | High | [43] |
| Parameters | Mesh | Time-Step |
|---|---|---|
| 2.840 M | 0.0239 s | |
| 0.752 M | 0.0338 s | |
| 0.203 M | 0.0478 s | |
| 1.56 | 1.41 | |
| 1.55 | 1.41 | |
| 2.76143 | 2.76143 | |
| 2.72728 | 2.76242 | |
| 3.6217 | 2.76858 | |
| 0.894 | 0.00616 | |
| −0.034 | 0.00099 | |
| R | −0.038 | 0.16 |
| Oscillatory convergence | Monotonic convergence | |
| s | −1 | 1 |
| (%) | 0.012 | 0.036 |
| q | 0.04 | 0 |
| p | 7.47 | 5.283 |
| (%) | 0.059 | 0.009 |
| EFD (N) | CFD (N) | % Difference | ||||
|---|---|---|---|---|---|---|
| Fr [-] | ||||||
| 0.0217 | 0.0056 | 0.0672 | 0.0060 | 0.0700 | 7.78 | 4.12 |
| 0.0433 | 0.3206 | 0.4693 | 0.4023 | 0.4125 | 25.50 | −12.11 |
| 0.0866 | 1.6048 | 2.3764 | 1.5504 | 2.0492 | −3.39 | −13.77 |
| 0.1191 | 3.0771 | 4.9436 | 2.8672 | 4.3274 | −6.82 | −12.46 |
| 0.1516 | 5.0503 | 4.5700 | −9.51 | |||
| Scale | × 10−3 | × 10−3 (Literature) | Source | %Diff |
|---|---|---|---|---|
| Model Scale | 4.100 | 4.110 | EFD [61] | −0.24 |
| 4.176 | CFD [62] | −1.82 | ||
| 4.176 | CFD [63] | −1.82 | ||
| Full Scale | 1.907 | 1.722 | CFD [64] | +6.26 |
| 1.806 | CFD [62] | +5.61 | ||
| 1.810 | CFD [63] | +5.38 |
| Scale | Source | %Diff | ||
|---|---|---|---|---|
| Model Scale | 0.524 | 0.487 | Corrected EFD [61] | +7.57 |
| 0.550 | CFD [62] | −4.70 | ||
| Full Scale | 0.310 | 0.336 | Corrected EFD [61] | −7.71 |
| 0.320 | CFD [62] | −3.24 |
| 1.3076 | −0.1049 | −0.0002 |
| 2.88604 | −0.21110 | −0.95672 | 0.00313 | 0.02097 | 0.17098 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Zeng, Q.; Van Hoydonck, W. Scale Effects on Nominal Wake Fraction in Shallow Water: An Experimental and CFD Investigation. J. Mar. Sci. Eng. 2025, 13, 619. https://doi.org/10.3390/jmse13030619
Raza A, Zeng Q, Van Hoydonck W. Scale Effects on Nominal Wake Fraction in Shallow Water: An Experimental and CFD Investigation. Journal of Marine Science and Engineering. 2025; 13(3):619. https://doi.org/10.3390/jmse13030619
Chicago/Turabian StyleRaza, Asif, Qingsong Zeng, and Wim Van Hoydonck. 2025. "Scale Effects on Nominal Wake Fraction in Shallow Water: An Experimental and CFD Investigation" Journal of Marine Science and Engineering 13, no. 3: 619. https://doi.org/10.3390/jmse13030619
APA StyleRaza, A., Zeng, Q., & Van Hoydonck, W. (2025). Scale Effects on Nominal Wake Fraction in Shallow Water: An Experimental and CFD Investigation. Journal of Marine Science and Engineering, 13(3), 619. https://doi.org/10.3390/jmse13030619







